Mechanical response of human female breast skin under uniaxial stretching

Abstract

Skin is a complex material covering the entire surface of the human body. Studying the mechanical properties of skin to calibrate a constitutive model is of great importance to many applications such as plastic or cosmetic surgery and treatment of skin-based diseases like decubitus ulcers. The main objective of the present study was to identify and calibrate an appropriate material constitutive model for skin and establish certain universal properties that are independent of patient-specific variability. We performed uniaxial tests performed on breast skin specimens freshly harvested during mastectomy. Two different constitutive models – one phenomenological and another microstructurally inspired – were used to interpret the mechanical responses observed in the experiments. Remarkably, we found that the model parameters that characterize dependence on previous maximum stretch (or preconditioning) exhibited specimen-independent universal behavior.

Graphical Abstract

The Rausch-Humphrey model is fitted to the intrinsic elastic response of human skin specimens. The blue circular symbols represent experimental measurements, and the red lines are best-fit of the Hart-Smith constitutive model. The best-fit model parameters were demonstrated to depend only on the previous maximum stretch and to not exhibit patient specific variability.

1. Introduction

The skin is the largest organ of the human body. Its main function is to protect the body against external influences. Depending on its purpose and location on the body, the mechanical behavior and thickness of skin vary. For example, the eyelids, whose main function is to blink (folding and unfolding), have a thickness of only 0.5 mm, while the skin on the soles of the feet, which must be able to resist cuts and abrasions, is at least 4 mm thick. Understanding the mechanical behavior of skin is important to many applications, such as cosmetic and reconstructive surgery, healing issues following surgical operations, and the treatment of skin-based diseases. The in vivo mechanical behavior of skin is described as heterogeneous, anisotropic, non-linear, and viscoelastic [Lanir and Fung, 1974; Dunn et al, 1983; Silver et al, 2001, Annaidh et al 2012]. Many factors such as age, biological sex, and hydration also affect the skin’s response.

Tensile tests – uniaxial and biaxial – are important methods for characterizing soft tissues such as skin. Such mechanical tests help to develop an understanding of the normal functional response of this organ and predict its response in cases of medical interventions such as surgery. Many experiments have been performed on skin to understand its complex mechanical behavior [see for example, porcine: Shergold et al, 2006 and Khatam et al, 2014; murine: Munoz et al, 2008; human: Abas and Barbenel, 1982, Dunn and Silver, 1983, Escoffier et al, 1989, Clark et al, 1996, Reihsner and Menzel, 1996, Bischoff et al, 2000, Silver et al, 2001, Hendriks et al, 2003, Kvistedal and Nielsen, 2009, Annaidh et al, 2012, and Tonge et al, 2013; and rabbit: Lanir and Fung, 1974]. Although it is generally accepted that uniaxial tension tests are insufficient to characterize skin completely, such tests are still typically performed on skin specimens in vitro (see for example, Moronkeji and Akhtar, 2015). There are numerous in vivo tests on skin as well since this will provide important characterization under physiologically correct conditions (see for example, Abas and Barbenel, 1982; Manschott and Brakkee, 1986; Escoffier et al 1989, Kvistedal et al, 2009).

The microstructure and biomechanical properties of skin (and other soft biological tissues) have been studied by numerous investigators, and there exists a common understanding of both (see for example, Gibson et al, 1965; Fung, 1967; Harkness, 1971; Wilkes et al, 1973; Sanders and Goldstein, 1995; Annaidh, 2012: Menon 2012; Tonge et al. 2013a,b; Caro-Bretelle et al, 2015, 2016; Bancelin et al, 2015). A succinct summary of skin composition is provided by Sanders and Goldstein (1995): skin is composed of collagen (27 to 39% by volume, 75 to 80% of fat-free dry weight), elastin (0.2 to 0.6% by volume, 4% of fat-free dry weight), glycosaminoglycans (0.03 to 0.35% by volume), and water (60 to 72% by volume). Different constituents govern the typical mechanical response of skin at different load levels. In addition, skin contains cells such as fibroblasts (for generating capillary and thermoregulatory blood vessels and elastin, collagen, and glycosaminoglycans as needed for growth, adaptation, and remodeling), and macrophages, and leukocytes; however, these are considered not to influence the mechanical response directly (see discussion in Pegg, 2006).

The structure of the constituents of skin is important for determining its response to mechanical stress. Elastin fibers form a network and provide the ability to recoil; this network is embedded in the network of crimped collagen fibers that are themselves cross-linked. While early research suggested that the collagen fibers are initially randomly oriented (see Figure 5 of Dunn et al, 1985), more recent work has provided measurements that indicate a systematic orientation distribution (Annaidh et al, 2012, Bancelin et al. 2015). Nevertheless, a sharp increase in stiffness with deformation is generated as the average stretch increases beyond some threshold, primarily due to uncrimping and reorientation of the collagen fibers with deformation. The remaining constituents, water and the glycosaminoglycans, provide viscous properties to skin. This composite structure of skin results in nonlinear, time-dependent mechanical behavior that can include elastic response, viscoelasticity, and damage (Dunn et al. 1985; Sanders and Goldstein, 1995; Bischoff et al, 2000; Silver et al, 2001; Munoz et al, 2008).

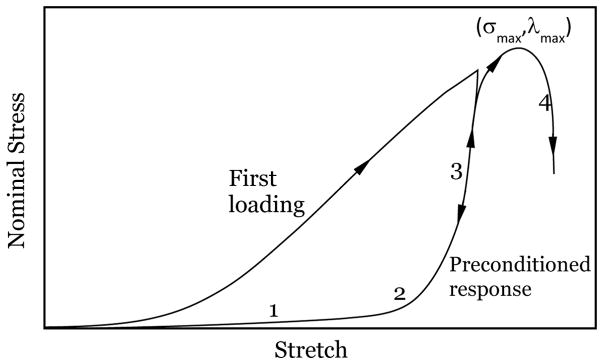
According to Fung (1967), the intrinsic elastic response of a biomaterial (such as skin), devoid of any time-dependent or inelastic response, can be extracted from a preconditioned specimen. This intrinsic elastic response plays a crucial role in the overall physiological response. A schematic diagram of the typical uniaxial response of skin is shown in Figure 1, indicating the variation of the nominal stress with the stretch: Four different phases are commonly identified in stress-stretch diagrams of preconditioned response. Phase 1 corresponds to the stretching of the elastin network, the most compliant of the skin constituents. Typical modulus in Phase 1 is in the range of 15–20 kPa and this low modulus persists until a stretch level of about 1.3. Note that this network modulus is significantly smaller than the elastic modulus of elastin itself, which is around 0.6 MPa (Fung, 1993) and retains a nearly linear elastic behavior for a stretch of about 1.6. Beyond this phase, the collagen fibers begin reorienting and uncrimping themselves in the direction of the stretching, exhibiting their higher resistance to stretching and contributing to a nonlinear, stiffening response; hence, Phase 2 represents a transition region where more and more collagen fibers become aligned with increasing stretch. We will examine this through a fiber recruitment model in Section 2.3. Phase 3 represents the stiffest response observed, corresponding to nearly fully oriented collagen; the response is nearly linear with a modulus of about few hundred MPa, about three to four orders of magnitude greater than in Phase 1. Finally, damage to the network occurs beyond a maximum stress level corresponding to the strength of the skin, and a softening response is observed in Phase 4. It is commonly considered that the physiological state of the skin lies somewhere between Phases 2 and 3 (Abas and Barbenel, 1982). It should be noted that the roles of elastin and collagen are similar in the preconditioned and first (native) loading responses; the only differences are slightly larger moduli in each segment and a smaller stretch level at which these transitions occur in the first loading response. The unloading and reloading response stabilizes along the line ‘1-2-3’ and corresponds to the preconditioned response up to the maximum stretch imposed.

Figure 1.

Typical variation of the nominal stress with stretch for skin specimens for the first loading, the preconditioned response and loading up to failure. Phases 1 through 4 are identified in the preconditioned response. The maximum stress σ_max occurs at a stretch λ_max that corresponds to the maximum possible stretch without generating permanent damage.

The significant difference in the stress level at a given stretch between the first loading response and the preconditioned response (sometimes called strain-softening) is attributed to viscoelasticity (Lanir and Fung, 1974) or to damage that is analogous to Mullins’s effect in rubber (Emery et al, 1997; Munoz et al, 2008; Johnson and Beatty, 1993, Caro-Bretelle et al. 2015, 2016). Lanir and Fung (1974) observed full recovery of strain-softening in rabbit skin after several hours, if all the strains experienced were always positive (note that this is violated in simple uniaxial tension where the transverse strain is negative). If loading is continued monotonically, a peak stress level is attained beyond which the skin becomes damaged and fails (Phase 4). While preconditioned specimens provide a repeatable characterization of subsequent response, it is not apparent that this is the response that is important in vivo in all applications, especially if there is long-term recovery of both dimensions (as indicated in Lanir and Fung, 1974) and response. In addition, in a recent article, Tonge et al (2013) investigated the behavior of human skin under biaxial loading in a bulge test where the specimen experiences non-uniform strain distribution; their results indicate that the effects of preconditioning on the structural response are negligible.

The use of constitutive models, posed in the framework of the theory of finite elasticity through a strain-energy density function, brings consistency to the measured data and provides a way to generalize the specific results obtained in the uniaxial tensile tests. There are numerous strain energy density functions that have been proposed to model material behavior for soft materials, for example, the neo-Hookean, Mooney-Rivlin, Ogden, Valanis-Landel (see Ogden, 1997 for a discussion of these models), Lopez-Pamies (2010), and other models describe the strain energy density functions applicable to typical elastomers. For soft tissues, Fung (1967) introduced a model that captures the exponential dependence of the stress on the deformation; many others have followed this model and there exists a vast array of such strain-energy density functions in the literature. Some of these models are derived from micromechanical considerations of the anisotropic structure of the materials, while others are purely phenomenological. Here, we consider two models, one by Hart-Smith (1966) and another by Rausch and Humphrey (2016) for interpreting experimental measurements; these models are described fully in Section 2.3.

Using these models, we investigated the mechanical response of human female breast skin obtained during mastectomy. While the anisotropic material behavior of skin necessitates the use of biaxial testing to capture its constitutive behavior fully, the lack of availability of large areas of skin for such testing limits biaxial testing to a few samples. Therefore, we embarked on uniaxial tests first to understand and characterize the mechanical response under tensile loading so that future biaxial tests could be performed more efficiently on the few available specimens. The main objective of the present study was to identify and calibrate an appropriate material constitutive model for skin and establish certain universal properties that are independent of patient-specific variability. While there are numerous phenomenological and mechanistic models of the mechanical behavior of soft tissues in general, and skin in particular, we will demonstrate that a universal model of response can be obtained with material properties dependent only on the previous maximum stretch level attained.

2. Materials and Methods

2.1. Patient characteristics and skin specimens

Breast skin specimens were collected and tests were performed in accordance with the institutional review board-approved protocols at The University of Texas MD Anderson Cancer Center and The University of Texas at Austin. The specimens used for mechanical testing were obtained from breast cancer patients who underwent mastectomy at MD Anderson Cancer Center and who provided informed consent. The inclusion criteria consisted of women aged 21 years or older who underwent mastectomy between July 2014 and April 2015 and who had enough excess breast skin to donate for testing (length ~5–7 cm and width ~1–3 mm). Patient demographics, specimen dimensions, test protocols, etc. of all six patients are shown in Table 1; note that multiple specimens were obtained from some participants. The patients were women 45 to 67 years old; four were Caucasian and two African-American; one had scar tissue from previous surgery and another had undergone prior surgery and radiation therapy. This demographic distribution permits assessment of patient-specific variability and benchmarking of reference material properties of human skin. The specimens were collected from the operating room and taken to the testing center; no measurements were made prior to excising the skin, and hence the prestretch characteristics in vivo were not known. The specimens were kept in water at room temperature for anywhere from 30 min to 90 min to remove any residual blood. The specimens were cleaned in warm water, and the subcutaneous fat was sharply removed from just below the dermis. Tissue thickness and width were determined as the average of three to four measurements taken at the center of the specimen using a manual Vernier caliper. The specimens were then wrapped in moist towels and stored inside a sealed bag in a 2°C refrigerator until testing up to 24 hours later. For storage more than 1 day, the specimens were frozen at −20°C^*. In this study, we have included results from some specimens that were frozen for different time periods, but tested after attaining a temperature of 38 – 40 °C.

Table 1.

Patient samples and loading protocols^†

Patient-Sample Number	Age	Race	Days to test	Sample thickness (mm)	Sample width (mm)	Segment	Cycles	Peak displacement (mm)
US1-P1-Jan-1313	54	Caucasian	170	1.5	12	1	1–3	7
						2	4–6	23
US1-P1-May-0000	54	Caucasian	288	1.5	12	1	1–3	7
						2	4–7	23
US2-P1-Jan-1334	54	Caucasian	170	1.5	12	1	1–3	7
						2	4–7	23
US1-P2-Feb-scarred	66	Caucasian	106	2.1	12.5	1	1–3	7
						2	4–6	10
US1-P3-Feb-0000	59	Caucasian	1	1.28	7	1	1–3	10
						2	4–6	15
US1-P4-Mar-Irrad	67	African American	0	1.42	10.5	1	1–3	3
						2	4–6	4
						3	7–9	5
						4	10–12	6
						5	13–15	7
						6	16–18	8
US1-P4-May-Irrad	67	African American	45	1.42	10.5	1	1–3	3
						2	4–6	4
						3	7–9	5
						4	10–12	6
						5	13–15	7
						6	16–18	10
US2x-P4-May-Irrad	67	African American	45	1.23	11.63	1	1–3	3
						2	4–6	4
						3	7–9	5
						4	10–12	6
						5	13–15	7
						6	16–18	8
US1-P5-Apr-1605	45	African American	0	1.85	15	1	1–3	1
						2	4–6	2
						3	7–9	3
						4	10–12	4
						5	13–15	5
						6	16–18	6
						7	19	7
US1-P5-Apr-1644	45	African American	0	1.85	15	1	1–3	5
						2	4–6	6
						3	7–9	7
						4	10–12	8
						5	13–15	9
						6	16–18	10
						7	19	11
US2-P5-Apr-1716	45	African American	0	1.05	11	1	1–3	5
						2	4–6	7
						3	7–9	8
						4	10–12	9
						5	13–14	10
						6	15–16	11
						7	17–18	12
US2-P5-Apr-1747	45	African American	0	1.05	11	1	1–3	5
						2	4–6	6
						3	7–9	7
						4	10–12	8
						5	13–14	9
						6	15–16	10
						7	17–18	11
						8	19	12
US2-P5-May1040	45	African American	25	1.05	11	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19
US3-P5-Apr-1811	45	African American	0	1.85	12	1	1–3	5
						2	4–6	6
						3	7–9	7
						4	10–12	8
						5	13–14	9
						6	15–16	10
						7	17	11
						8	18	12
US3-P5-Apr-1829	45	African American	0	1.85	12	1	1–3	5
						2	4–6	7
						3	7–9	9
						4	10–12	11
						5	13–15	13
						6	16–18	15
US1-P6-Apr-1527	52	Caucasian	0	1.95	13.83	1	1–3	5
						2	4–6	6
						3	7–9	7
						4	10–12	8
						5	13–15	9
						6	16–18	10
US1-P6-Apr-1550	52	Caucasian	0	1.95	13.83	1	1–3	8
						2	4–6	9
						3	7–9	10
						4	10–12	11
						5	13–15	12
						6	16–18	13
US1-P6-Apr-1627	52	Caucasian	0	1.95	13.83	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19
US2-P6-Apr-1651	52	Caucasian	0	1.25	13.33	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19
US2-P6-Apr-1715	52	Caucasian	0	1.25	13.33		1–3	8
						2	4–6	9
						3	7–9	10
						1	10–12	11
						5	13–15	12
						6	16–18	13
US3-P6-Apr-1744	52	Caucasian	0	1.2	10.5	1	1–3	8
						2	4–6	9
						3	7–9	10
						4	10–12	11
						5	13–15	12
						6	16–18	13
US3-P6-Apr-1808	52	Caucasian	0	1.2	10.5	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19
US3-P6-May-0000	52	Caucasian	20	1.2	10.5	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19
US4-P6-Apr-1834	52	Caucasian	0	1.65	12.25	1	1–3	8
						2	4–6	9
						3	7–9	10
						4	10–12	11
						5	13–15	12
						6	16–18	13
US4-P6-Apr-1857	52	Caucasian	0	1.65	12.25	1	1–3	8
						2	4–6	11
						3	7–9	13
						4	10–12	15
						5	13–15	17
						6	16–18	19

^†Abbreviations used here are explained as follows: US1-P1-Mon-xxx stands for Uniaxial Specimen 1 from Patient 1 followed by the month the specimen was tested and time (four digits); here Jan-1313 stands for test performed in January at 13:13 hours.

2.2. Device set-up and operation

We built a special uniaxial testing machine designed for mobility, simplicity, and low-force capability. A torsional ratcheting actuator (Model TRA25CC, Newport Corporation, Irvine, CA; displacement resolution of up to 0.0305 μm) was used to stretch the specimens. A miniature load cell (Model LSB200, Futek Corporation, Irvine, CA; 0.04448 N resolution, 44.5 N range) was used to measure the force in the testing machine. A photograph of the test setup with a specimen is shown in Figure 2. The ends of the specimens were held by screws between two stainless steel plate grips covered with sandpaper to prevent slippage. During design of the device, trials were conducted on pigskin samples, with digital image correlation for monitoring the displacement and identifying possible occurrence of slip. The procedure used for gripping was robust enough that no slipping occurred. Also, in the tests performed, any occurrence of slip would manifest itself a change in the slope of the nominal stress vs stretch variation that could be readily identified; none occurred in the tests reported. The minimum gauge length between the upper and lower grips was 43 mm, and the maximum stroke of the machine was 25 mm; this allowed a stretch of up to 1.58 to be imposed. All specimens were gripped at the minimum gage length of 43 mm. The displacement rate used in all the uniaxial tests was 0.4 mm/sec, and the strain rate thus observed was 0.0093/sec. The displacement of the actuator was controlled by means of a LabVIEW program (National Instruments Corporation, Austin, Texas), which also controlled the data acquisition system to record the force and displacement. The general practice in biological tissue testing is to place the specimen in a body-temperature hydration bath to maintain the physiological temperature and to avoid excessive drying. This is assumed to simulate the in vivo hydration condition of skin, even though skin is not in contact with water on both sides. Therefore, all tests were performed in a bath/beaker where the water temperature was set between 38°C and 40°C^†. This machine was sufficient for determining the stress-stretch response but not for causing failure. Therefore, we did not explore specimen failure in these tests. The mechanical stress-stretch response within and slightly above the physiological limits was explored; in vivo measurements obtained by Abas and Barbenel (1982) indicated stretch levels between 1.1 and 1.3. In vitro tests have been performed to even greater levels (see Dunn et al, 1985; Bischoff et al. 2000; Annaidh et al. 2012). In the present work we explored stretches in the range of 1 to 1.58.

Figure 2.

Experimental device with specimen mounted. The red line shows the 43 mm gage length of the specimen.

2.3. Material mechanical response

The deformation in the uniaxial stretching experiment is characterized by a single quantity, the stretch, λ, defined as the ratio of the current length to the initial length. The force applied is indicated by the nominal stress, T = P/A₀, which is the force divided by the initial cross-sectional area. Therefore, the results from the uniaxial test protocols will be presented in terms of the nominal stress versus stretch.

While the uniaxial stress-stretch is readily characterized as described, in order to generalize our results to biaxial conditions, and to perform comparative evaluations between the different participants, specimens, and test conditions, it is useful to provide the framework of a constitutive model within which the results can be examined. We will consider two different constitutive models, the Hart-Smith model and the Rauch and Humphrey model, to address this generalization.

2.3.1. Exponential model of Hart-Smith

Hart-Smith (1966) proposed a strain energy density function W(I₁, I₂), for isotropic incompressible rubber that is taken to obey

$$\frac{\partial W}{\partial I_1}=aexp\left[b{(I_1-3)}^2\right],\frac{\partial W}{\partial I_2}=\frac{c}{I_2},$$ (1)

where I₁ and I₂ are the first and second fundamental invariants of the right Cauchy-Green tensor C= F^T F, F, F^T are the deformation gradient tensor and its transpose, and a,b,c are material constants to be calibrated (see Ogden, 1997). Note that a,c have the dimension of force per unit area (modulus), and b is dimensionless. This model has been used, for example, by Sahay et al. (1992) to model brain tissue. The Hart-Smith model is unusual in the sense that it describes the derivatives of the strain energy function with respect to the invariants rather than the function itself (see Humphrey, 2002). However, from Eq.(1), it is seen that the strain energy density depends on I₁ through the error function erf and on I₂ logarithmically. Through many trials with the data obtained in the present work, we found that the best fit to human skin response was obtained when the dependence on I₂ was eliminated by making c = 0. With this restriction, the relationship between the nominal stress and stretch can be derived using standard procedures (see Treloar, 1949; Ogden, 1997) and expressed as

$$T=2aexp\left[b{\left({\lambda }^2+\frac{2}{\lambda }-3\right)}^2\right]\left(\lambda -\frac{1}{{\lambda }^2}\right),$$ (2)

This now leaves two parameters, a and b to be determined by fitting to experimental data to Eq.(2). We assume that dependence on previous maximum stretch may be introduced by considering the parameters a and b to be functions of the previous maximum stretch λ_m: a(λ_m), b(λ_m) and will explore this further through the data collected in the present work.

2.3.2. Fiber recruitment and damage model of Rausch and Humphrey

The microstructurally inspired damage model presented recently by Rausch and Humphrey (2016) will also be used to interpret the uniaxial test data. We provide a brief description of the model to facilitate the discussion; details may be found in Rausch and Humphrey (2016). In this model, the strain energy density function is represented in the following form:

$$W=W_g(\mathbf{C})+\underset{S}{\int }\phi (\theta ,\mathrm{\Phi })W_f(\mathbf{C},\mathbf{N}(\theta ,\mathrm{\Phi }))d\theta d\mathrm{\Phi }-p(J-1),$$ (3)

where W_g(C) is the strain energy density of the ground substance, C is the right Cauchy-Green tensor, φ (θ, Φ) is the fiber bundle orientation distribution function with (θ, Φ) representing the azimuthal and polar angles, and W_f(C, N(θ, Φ)) is the strain energy density of the fiber bundles oriented in the direction N(θ, Φ). The integral in the second term over the orientation distribution provides the strain energy density of the fibers integrated over the appropriate distribution function. J = detF is the Jacobian; incompressibility of the material is assumed, resulting in a pressure, p, to be determined. In order to evaluate this constitutive model further, it is necessary to determine the fiber bundle orientation distribution. However, this was not measured in our specimens, and therefore we will use the approximate procedure suggested by Rausch and Humphrey (2016). As the skin is stretched, fiber bundles rotate towards the stretching direction and further become uncrimped; this is the fiber recruitment process. If there is an initial distribution of fiber bundle orientations stretched to different crimp levels, the stored energy may be written approximately in terms of the uniaxial fiber bundle properties as follows:

$$W_f=\int \rho \left({\lambda }_s\right)W_0\left(\mathbf{C},0\right)d{\lambda }_s,$$ (4)

where ρ(λ_s) is the distribution function for the effective density of uniaxially oriented fibers at a stretch of λ_s, and W₀ is the strain energy density function for an individual straight fiber bundle. This effectively assumes that reorientation of the fiber bundles occurs without any energy penalty and that only after the bundles are reoriented in the direction of stretch do they contribute to the skin response. It is expected that ρ(λ_s) will depend on the initial orientation of the specimen relative to the material anisotropy and the initial crimp distribution. Again, following Rausch and Humphrey (2016), we take ρ(λ_s) to be a Weibull distribution:

$$\rho \left({\lambda }_s\right)=\frac{\beta }{\delta }{\left(\frac{{\lambda }_s-\gamma }{\delta }\right)}^{\beta -1}exp\left[-{\left(\frac{{\lambda }_s-\gamma }{\delta }\right)}^{\beta }\right]$$ (5)

with the shape parameter β > 1, the scale parameter δ > 0, and the location parameter γ > 0. The ground substance and fiber are taken to be neo-Hookean, with W_g = μ_g (λ² + 2λ⁻¹ −3) and W₀ = μ_f (λ̄² + 2λ̄⁻¹ −3), respectively, where λ̄ = λ/λ_s enforces the fact that due to the initial crimp, fibers contribute to the overall energy only after they exceed the recruitment stretch. The nominal stress can then be obtained as

$$T=2{\mu }_g\left(\lambda -{\lambda }^{-2}\right)+2{\mu }_0{\lambda }^{-1}\underset{\gamma }{\overset{\lambda }{\int }}\rho \left({\lambda }_s\right)\left({\overline{\lambda }}^2-{\overline{\lambda }}^{-1}\right)d{\lambda }_s.$$ (6)

Rausch and Humphrey (2016) introduced damage into this model by assuming that the Weibull scale parameter δ would depend on the previously attained maximum stretch, λ_m, such that we may replace the effective fiber density function with ρ(λ_s, δ(λ_m)), where δ(λ_m) is to be obtained through direct calibration to measurements. With the assumption that the material behavior can be represented by an equivalent one-dimensional fiber recruitment model, we now have the following material parameters to calibrate: μ_g, μ_f, which define the modulus of the ground substance and the fiber bundles, respectively, and β, γ, δ(λ_m), the Weibull parameters that define the effective fiber recruitment stretch distribution. While it might be argued that this is a physically based model of material behavior, it also contains more material parameters (five) available for calibration than phenomenological models such as the Hart-Smith model (Section 2.3.1). However, the usefulness of this model increases if the Weibull parameters as well as ρ(λ_s) can be measured independently from the microstructure of the collagen fiber bundles.

2.4. Specimen test protocols

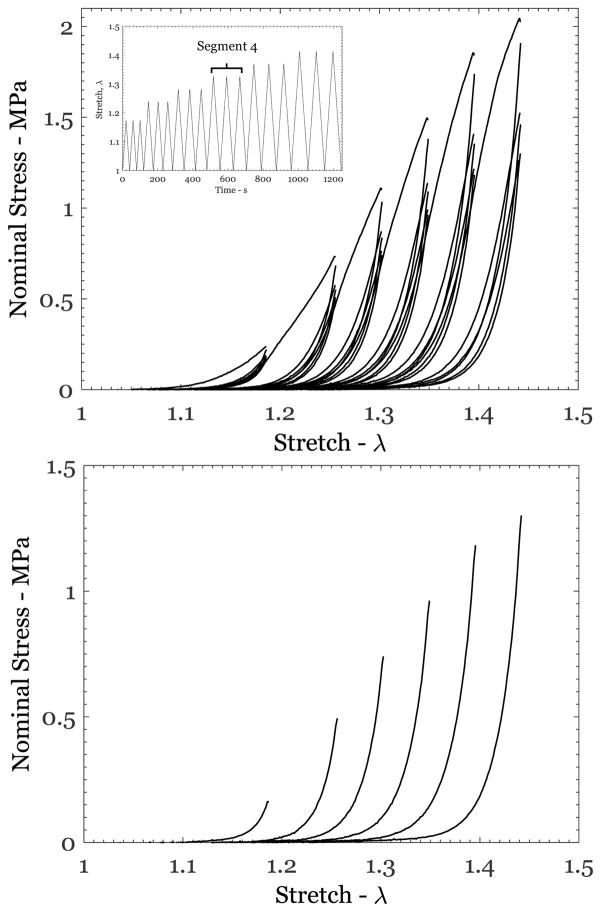
Each specimen was subjected to load-unload cycling as indicated in Table 1. A graphical example of one of these protocols is shown in Figure 3a (inset). Protocols similar to this have been used by others (see for example Emery et al. 1997; Munoz et al. 2008). The protocol for each test consisted of a number of segments; each segment consists of three repeat loading-unloading cycles up to a constant maximum stretch λ_m ; loading-unloading cycles in subsequent segments were performed with increasing levels of maximum stretch. The unloading response from the last step of each segment was collected in order to fit the models described in Section 2.3. Since we sought to show that the constitutive response is only a function of the previous maximum stretch, λ_m, the protocol could be varied from one test to another, with two caveats: first that the magnitude of the previous maximum stretch, λ_m, must be known and second that the last unloading response of each segment is considered as the preconditioned intrinsic elastic response to be modeled.

Figure 3.

(a) Response of specimen US2-P6-Apr-1651 subjected to the protocol shown in the inset; each segment consisted of three loading-unloading cycles to a constant maximum stretch λ_m, with subsequent steps at increasing stretch levels. (b) The unloading response from the last unloading step of each segment is shown; this was the response used in calibrating the two models.

3. Results and Discussion

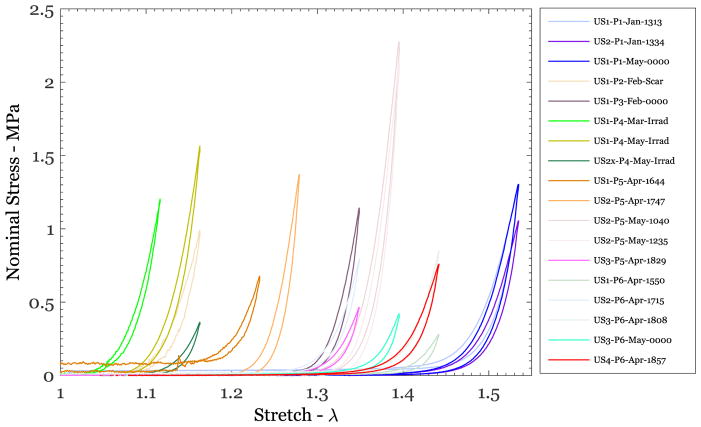
A typical response of human skin under uniaxial cyclic loading-unloading loading is shown in Figure 3a for specimen US2-P6-Apr-1651. The maximum stretch attained in each segment was 1.186, 1.256, 1.302, 1.349, 1.395, and 1.442. All features of the stress-stretch response discussed in Figure 1, except the failure, were observed in each specimen tested. In particular, the stiffening stress-stretch behavior was consistently observed in all specimens. The response of the last unloading cycle from each segment is shown in Figure 3b; this was taken to be the preconditioned response corresponding to the respective maximum stretch levels in each segment. Similar response curves were obtained from all the test protocols listed in Table 1, providing a large data set for determining the patient-specific variability of the mechanical response. This variability is explored first through a graphical comparison of the cyclically stabilized responses from all specimens as shown in Figure 4. For clarity, this figure shows only one selected loading-unloading cycle with a maximum nominal stress level in the range of 0.25 to ~1.5 MPa from 18 of 25 different tests of six different patients and 13 different specimens. It includes specimens that were tested immediately after extraction and specimens that were kept frozen for nearly 6 months. In addition, it includes specimens that contained surgical scar tissue and two that included skin from a patient who had undergone radiation therapy to the breast. Two things are clear from the results displayed in Figure 4: first, the general shape of the stress-stretch curve (monotonically increasing nominal stress with stretch) appears to be quite similar in all specimens, independent of the patient, prior freezing history, or irradiation and scarring. Second, the stretch level at which the skin stiffness increases rapidly varies significantly by patient and was in the range of about 1.1 to about 1.6. Anisotropy will influence this stretch level, but it could not be addressed through these uniaxial tests.

Figure 4.

Nominal stress vs stretch variation from uniaxial tests on different breast skin specimens

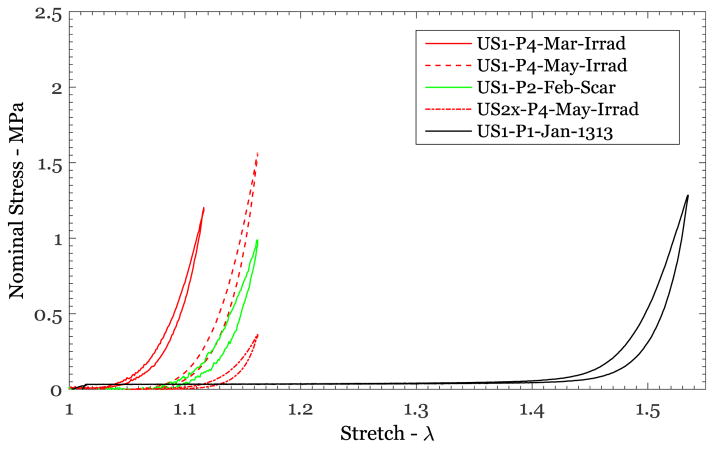
Scarred and irradiated tissues are considered to be less extensible and stiffer than normal skin (see Fung, 1967; Dunn and Silver, 1983). The nominal stress vs stretch responses for the skin specimens that were scarred (US1-P2-Feb-Scar) and irradiated (US1-P4-Mar-Irrad; US1-P4-May-Irrad) are shown in Figure 5 along with the response of a normal skin specimen (US1-P1-Jan-1313). These nominal stress-stretch responses corresponded to the preconditioned response of specimens loaded to nearly the same nominal stress level. Quantitative comparison of the unloading response of each of these specimens shows that the stretch level at which the skin begins its exponential increase in stiffness has decreased significantly owing to both scarring and irradiation: the rapid increase in stiffness began at a stretch level of 1.48 for the natural specimen shown, while it occurred at 1.05 – 1.15 for the scarred and irradiated skin specimens (Figure 5). It appears that the anecdotal observance of “stiffening from scarring” is primarily due to the elimination of the early part of the soft response. These differences must be reflected in the material model.

Figure 5.

Nominal stress vs stretch variation from uniaxial tests of normal, irradiated, and scarred breast skin specimens.

The data obtained from the breast skin specimens are consistent with the behavior of skin that has been reported earlier in the literature (Abas and Barbenel, 1982; Dunn et al. 1985, Clark et al, 1996; Edsberg et al. 1999; Bischoff et al, 2000; Annaidh et al, 2012; Caro-Betelle et al. 2016 and others). This data has significant patient-specific variability and contains data on the influence of specimen storage on the mechanical response. In order to analyze the data, we will fit the two models discussed in Section 2.3 to the experimental data and explore the underlying similarities in the response of skin.

3.1. Optimal fitting of the Hart-Smith model to experimental data

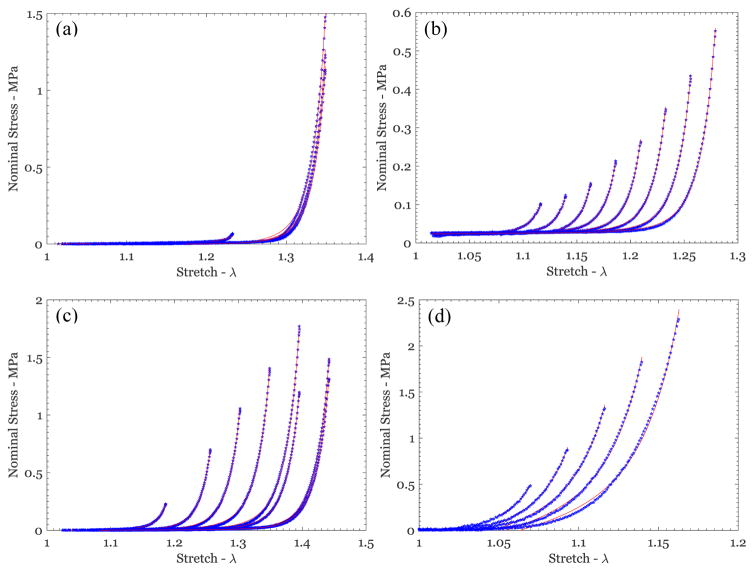
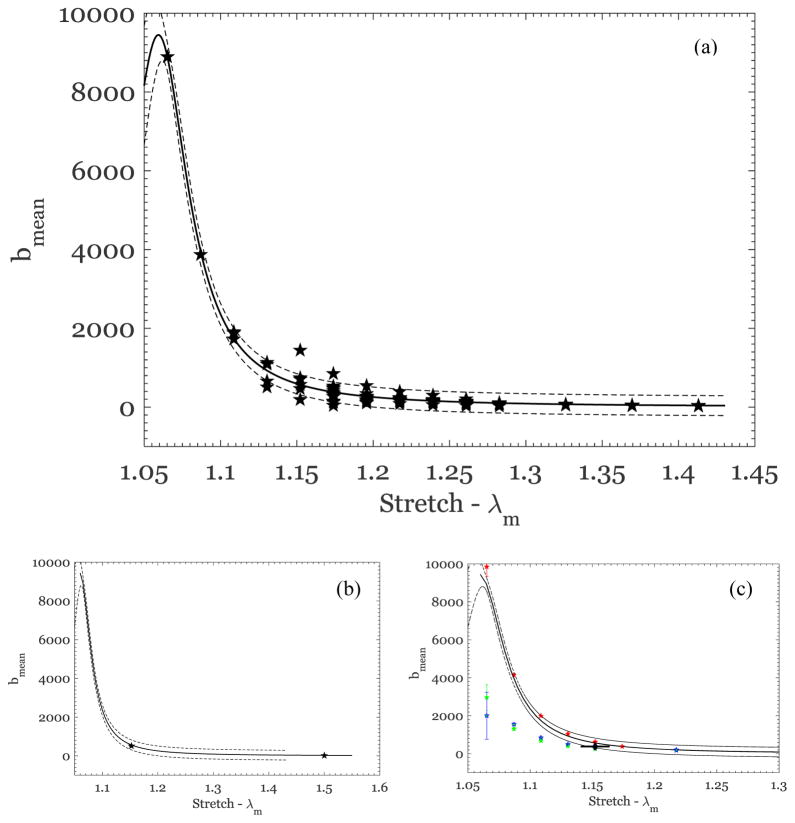
For the Hart-Smith model, the parameters a(λ_m), b(λ_m) in Eq.(2) were fitted to the experimental data from all the tests listed in Table 1 through the nonlinear least-squared error fitting algorithm lsqcurvefit in MATLAB (Mathworks, Natick, MA); the fitted curves are shown in Figure 6 for different loading cycles of four different selected specimens. All of the curves indicate exceptionally good fit to all data on the basis of an r² correlation coefficient in the range of 0.97 to 0.999; even the irradiated specimen (US1-P4-May-Irrad) showed good fitting. Similar agreement was obtained for all tests in which the specimen had been stretched beyond the “toe” region of the stress-stretch curve (to a stress level above 0.75 MPa). This agreement suggests that the form of the constitutive model in Eq. (2) is appropriate to represent the material response. These curve fits indicated a systematic dependence of the model coefficients on λ_m that provides further insight into the model. The parameter a was found to be nearly independent of λ_m within the scatter in the experimental data but dependent on the individual patient; from Eq.(2), a is clearly seen to set the scale for the magnitude of the stress (or equivalently the modulus) and hence should depend on the patient. The dependence of b on λ_m is shown for subjects P3, P5 and P6 in Figures 7a; all of these specimens were tested on the same day the tissue was excised, without any freeze-thaw cycles. Some of the specimens were tested more than once on the same day, with a recovery period of about 2 hours. Before interpreting this result, we make two important observations: first, the scatter arises primarily from errors in consistently identifying λ_m from one specimen to the next, but within each specimen, different trials have little scatter. Second, the plot in Figure 7a contains results for model constant b from fits to more than 135 uniaxial tests that had different cycles with different peak stretch in each cycle, to different specimens, and to three different participants. The collapse of all datasets into this one representation suggests a dependence of b on λ_m that can be represented by a simple function; after numerous trials, it was determined that a rational polynomial of the following form:

$$b\left({\lambda }_m\right)=p_1/\left({\lambda }_m^2+q_1{\lambda }_m+q_2\right)$$ (7)

provided the best fit over the range of stretch levels considered. The fitted curve is shown in Figure 7a as a solid black line; a global fit to these data yields a 95% confidence interval with p₁ =5.212±0.695, q₁ = −2.119 ± 0.007 and q₂ =1.123±0.008. This confidence interval is shown in Figure 7a by the black dashed lines. This fit implies that as λ_m increases, b → 0 and a nearly linear stress-stretch response is achieved, corresponding to the fully stretched fiber response.

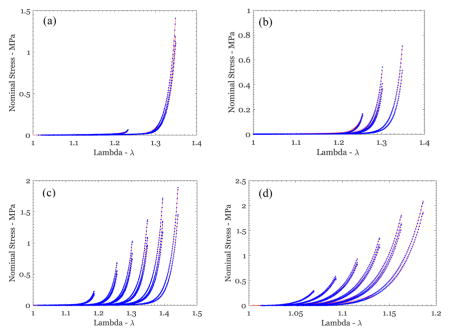
Figure 6.

Nominal stress vs stretch variation from uniaxial tests on different breast skin specimens (blue symbols), along with the fit of the Hart-Smith model (red lines) for (a) US1-P3-Feb-000, (b) US3-P5-1811, (c) US2-P6-1627, and (d) US1-P4-May-Irrad.

Figure 7.

(a) Dependence of the Hart-Smith model parameter b on the previous maximum stretch; the symbols represent the best estimates for b from each test for patients P3, P5 and P6. The solid line is the best fit Eq.(2), and the dashed lines show the 95% confidence interval. (b) The best-fit parameter b for P1, where all specimens were tested after freezing and storage for 106 to 288 days. (c) The best-fit parameter b for P4 in different irradiated specimens, subjected to protocols indicated in Table 1; while one specimen (red pentagrams) follows the trend of the unirradiated specimens, the other two trials (blue and green pentagrams) fall outside the 95% confidence interval. One set of results from specimen P2 (with a scar) is also shown by the diamond symbols (at a stretch of ~1.15, identified by the horizontal line attached to the symbol).

We now turn to specimens that were frozen, or were obtained from irradiated and scarred subjects. Specimens from subject P1 were kept frozen for different periods of time from 106 days to 288 days, and tested three different times; the best-fit parameter b of the Hart-Smith model for the data from these specimens are shown in Figure 7b. These values are well within 95% confidence intervals for the parameter b obtained from the normal specimens (subjects P3, P5, and P6), as shown in Figure 7b. Next, the subject P4 with radiation treatment also exhibited a mechanical response that could be fitted well by the Hart-Smith model; the best-fit model parameter b exhibited dependence on λ_m that is similar to that of the normal specimens as indicated in Figure 7c but with some specimen dependence. Finally, the Hart-Smith model could also fit the stress-stretch response of specimens from subject P2, with a scarred tissue. Only one test result was available, and it was within the 95% confidence interval established by the normal specimens. While model parameters from frozen specimens, irradiated and scarred tissues exhibit a Hart-Smith model with model parameters that fall mostly within the confidence interval of the normal specimens, the number of samples is small and these aspects require greater scrutiny with a larger number of samples.

It is important to explore why the best-fit parameters from normal skin of different patients fall onto the form of the curve in Eq.(7). While the response at large stretch is governed by the uncrimped collagen fibers, the initial differences between the specimens arise from two related sources: (i) the initial orientation (or its distribution) relative to the tension direction varies from specimen to specimen and (ii) the stretch at which different fibers begin to align in the direction of loading and begin uncrimping varies. From the initial configuration, the specimen stretches by a certain amount before beginning the process of uncrimping; let us indicate this stretch level by λ_R. Therefore we have an effective stretch, λ_m/λ_R, in each specimen at the time at which the uncrimping begins. The major upshot of this result is that the parameter b(λ_m) would have a universal form given in Eq.(7) and that one set of uniaxial tests is adequate to calibrate the material model and identify the patient-specific parameter, a. We have not been able to identify the use of the Hart-Smith model to skin the literature, but given the good fit to the experimental data from the present work, it would appear that the model is suitable for use in capturing the mechanical response of skin. However, the connection between this dependence of b(λ_m) and the fiber orientation distribution remains to be explored quantitatively in order to fully exploit this constitutive model.

3.2. Optimal fitting of the Rausch-Humphrey model to experimental data

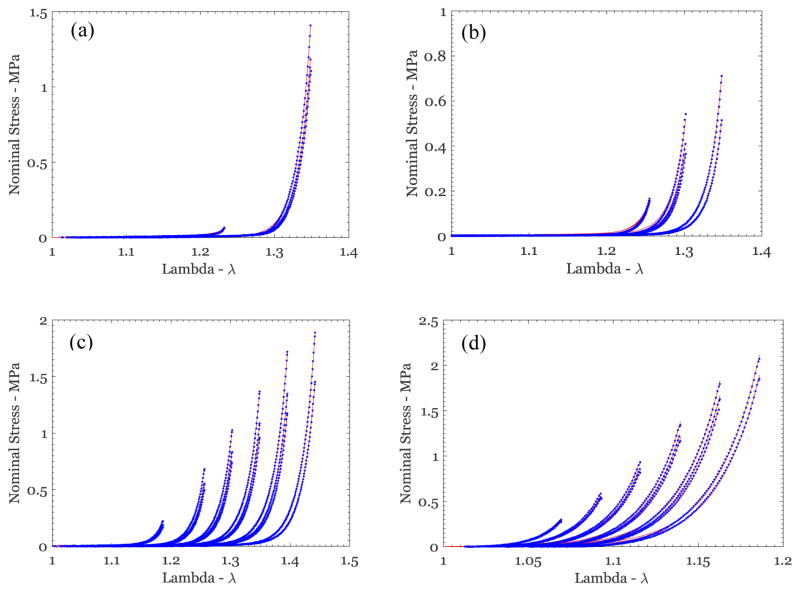
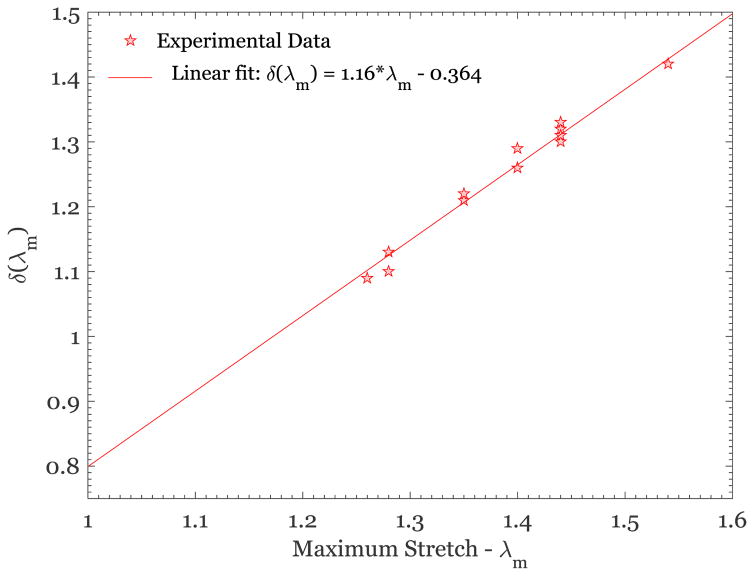
Next, we turn to a calibration of the Rausch-Humphrey model, where the following material parameters were calibrated: μ_g, μ _f, which define the modulus of the ground substance and the fiber bundles, respectively, and β, γ, δ(λ_m), the Weibull parameters that define the effective fiber recruitment stretch distribution. Parameter identification based on curve fitting to the experimental data was accomplished through the nonlinear least-squared error fitting algorithm lsqcurvefit in MATLAB. Since there are five parameters to identify, it is important to provide good starting estimates for the parameters; we fixed γ = 0.2 (based on numerous preliminary trial fits), provided starting values of μ₀ = 0.01 MPa and μ₁ = 900 MPa to account for the difference in stiffness values of the ground substance and the fiber bundles, used β = 40 to provide a steep rise in recruitment as the stretch increases, and used δ =1. The fitted curves are shown in Figure 8 for different loading cycles of four selected specimens, and all indicate good fits to data, even for the irradiated specimen (US1-P4-May-Irrad). Similar agreement was obtained for all tests in which the specimen had been stretched beyond the “toe” region of the stress-stretch curve (to a stress level above 0.75 MPa). The parameters extracted from the fits for specimens that met the above stress level criterion are shown in Table 2. The modulus μ₀ varies significantly from one specimen to another because it sets the scale for the initial slope of the stress-stretch curve and therefore depends on the initial orientation of the fibers in each specimen. On the other hand, the modulus μ₁ should represent the fully oriented fiber property; we found that the fiber bundle modulus is constant at μ₁=870±11 MPa (95% confidence interval) within the scatter in the fitting process. The dependence of β on the previous maximum stretch, λ_m, for all specimens that met the stress-level-based selection criterion was also nearly constant, with β =66.2±4.9. It should be recalled that this data set contains specimens from different participants and different specimens from each participant, and hence variability in the initial orientation; despite this, the variability in the model parameters was small. Finally, the scale parameter, δ, exhibits systematic dependence on the previous maximum stretch λ_m, as shown in Figure 9; as demonstrated by Rausch and Humphrey (2016) for thrombus, this dependence can be represented as

Figure 8.

Nominal stress vs stretch variation from uniaxial tests on different breast skin specimens (blue symbols), along with the fit of the Rausch-Humphrey model (red lines) for (a) US1-P3-Feb-0000, (b) US3-P5-1829, (c) US2-P6-1627, and (d) US1-P4-May-Irrad.

Table 2.

Best fit material parameters for the Rausch-Humphrey model^†

Patient sample number	Parameters of the Rausch-Humphrey model See Eqs.(5) and (6)
	λ	μ0	μ1	β	δ
US1-P3-Feb-0000	1.35	4.12E-03	873	70	1.21
US3-P5-Apr-1811	1.28	6.46E-03	891	75	1.13
US2-P6-Apr-1627	1.44	9.27E-03	903	60	1.31
US1-P4-Mar-Irrad	1.16	1.33E-03	892	31	1.10
US1-P4-May-Irrad	1.19	4.07E-04	825	41	1.08
US1-P2-Feb-Scarred	1.16	5.19E-03	899	33	1.11
US1-P1-Jan-1313	1.54	2.75E-02	859	57	1.42
US1-P1-May-0000	1.54	1.77E-03	866	57	1.42
US1-P5-Apr-1644	1.26	1.34E-01	895	81	1.09
US2-P5-Apr-1716	1.28	1.95E-02	892	90	1.10
US2-P5-Apr-1747	1.28	3.49E-04	867	71	1.13
US2-P5-May-1040	1.40	6.60E-04	834	62	1.26
US2-P5-May-1235	1.44	3.06E-04	812	62	1.30
US2-P6-Apr-1715	1.44	4.25E-03	867	53	1.32
US3-P6-Apr-1808	1.44	1.72E-02	868	71	1.31
US3-P6-May-000	1.40	8.25E-03	886	65	1.29
US4-P6-Apr-1857	1.44	4.75E-03	867	58	1.33
US2-P1-Jan-1334	1.54	1.33E-03	869	58	1.42
US3-P5-Apr-1829	1.35	5.57E-03	879	70	1.22
Average		0.015	870	66.2	1.27
Standard deviation		0.033	23	9.81	0.111
Count		16	16	16	16
95% confidence interval		0.016	11	4.90	0.06

^†The sample numbering scheme is the same as identified in Table 1. The rows in bold, italics have been excluded in obtaining the average, standard deviation, etc.

Figure 9.

Variation of the Weibull scale parameter δ with maximum stretch, λ_m. Data from the scarred and irradiated tissue specimens have been excluded.

$$\delta \left({\lambda }_m\right)=c_1+c_2{\lambda }_m,$$ (8)

with c₁ = −0.364 and c₂ =1.16. The above equation represents the evolution of the scale parameter of the Weibull distribution in Eq.(5) and thus is a measure of the change in distribution of recruitment stretches with prior stretch. Comparing these results to the original work of Rausch and Humphrey (2016), where this model was proposed for thrombus, we see that the most important feature of the model – the linear dependence of the scale parameter δ, on the previous maximum stretch λ_m over the range of stretches considered – is similar in both cases. It would be of interest to pursue microstructural studies to determine the underlying cause of the changes in the scale parameter with stretch.

From the above model fitting results, it is evident that both models are capable of representing the experimental data and providing a path towards generating a constitutive model of human skin. It is difficult to choose between the two models; while the Hart-Smith model has fewer parameters, and is therefore easier to calibrate, the Rausch-Humphrey model has the attractive feature that it could be connected to the material microstructure, provided additional measurements are made of the initial orientation of the fiber bundle structure.

4. Conclusion

We performed uniaxial tensile tests on skin excised during breast surgery. Twenty-five tests were performed on 13 specimens obtained from six participants. Each test corresponded to multiple cycles of loading and unloading, at increasing stretch levels. The uniaxial tests were performed on a specially built testing machine that had the capacity to resolve the low-load-level response of the skin. The main conclusions from the experiments are given below.

• The experimental stress-stretch curves from different patients, tested either immediately after extension or after freezing for a duration of up to 288 days, exhibited remarkably similar behavior.

• These stress-stretch responses were modeled through the phenomenological model of Hart-Smith (1967) and the microstructurally inspired damage model of Rausch and Humphrey (2016). It was found that both models fit the experimental data quite well.

• The material parameters were found to be a function only of the previous maximum stretch experienced for both material models, and remarkably, these parameters exhibited very little variability between specimens or storage conditions. Hence, a certain universality in the response of skin to uniaxial tensile deformation has been demonstrated; the reasons for such universality remain to be explored.

Finally, we note that a major limitation in the work presented arises from the fact that uniaxial tensile tests are performed and analyzed using an isotropic elastic model. The model calibration needs further examination through biaxial tests and anisotropic material models.

Highlights.

• The phenomenological Hart-Smith model fits the uniaxial stress-stretch response of human skin.

• The damage-based Rauch-Humphrey model fits the uniaxial stress-stretch response of human skin.

• The best-fit model parameters depend universally on the previous maximum stretch.