Measurement of phase resetting curves using optogenetic barrage stimuli

Abstract

Background

The phase resetting curve (PRC) is a primary measure of a rhythmically firing neuron’s responses to synaptic input, quantifying the change in phase of the firing oscillation as a function of the input phase. PRCs provide information about whether neurons will synchronize due to synaptic coupling or shared input. However, PRC estimation has been limited to in vitro preparations where stable intracellular recordings can be obtained and background activity is minimal, and new methods are required for in vivo applications.

New method

We estimated PRCs using dense optogenetic stimuli and extracellular spike recording. Autonomously firing neurons in substantia nigra pars reticulata (SNr) of Thy1-channelrhodopsin 2 (ChR2) transgenic mice were stimulated with random barrages of light pulses, and PRCs were determined using multiple linear regression.

Results

The PRCs obtained were type-I, showing only phase advances in response to depolarizing input, and generally sloped upward from early to late phases. Secondary PRCs, indicating the effect on the subsequent ISI, showed phase delays primarily for stimuli arriving at late phases. Phase models constructed from the optogenetic PRCs accounted for a large fraction of the variance in ISI length and provided a good approximation of the spike-triggered average stimulus.

Comparison with existing methods

Compared to methods based on intracellular current injection, the new method sacrifices some temporal resolution. However, it should be much more widely applicable in vivo, because only extracellular recording and optogenetic stimulation are required.

Conclusions

These results demonstrate PRC estimation using methods suitable for in vivo applications.

1. Introduction

The phase resetting curve (PRC) measures the input-sensitivity of an oscillating neuron’s spike timing, as a function of the oscillation phase at which the input arrives. Thus, the PRC is a primary measure of the input-output relationship of a neuron that fires autonomously, or any neuron operating at an average level of excitation above its rheobase. It has been shown that PRC shapes can predict the tendency of neurons to synchronize or remain asynchronous in response to synaptic or electrical coupling, as well as the strength of synchronization by correlated input (Marella and Ermentrout 2008, Achuthan and Canavier 2009, Smeal et al. 2010, Stiefel and Ermentrout 2016). However, doubt has persisted about the applicability of these findings to in vivo conditions, for two main reasons. First, PRCs have traditionally been measured in neurons firing with great regularity, using single, widely separated stimuli with little resemblance to the barrages of synaptic input thought to occur in vivo. Second, the condition of the cells may be altered by damage during brain slice preparation, deviations from normal physiological temperature or oxygenation, and/or lack of critical neuromodulators.

To address these concerns, it would be valuable to obtain PRCs in vivo. In principle, this could be accomplished by extracellular synaptic stimulation, intracellular current injection, or either direct or synaptic optogenetic stimulation. With any of these methods, it is expected that accurate PRC estimation would be difficult to achieve by the traditional method of low-frequency single-pulse stimulation, because of high levels of ongoing synaptic input producing inter-spike interval (ISI) variability. Even in brain slice preparations, this method requires a long period of data acquisition and generally yields PRCs with a large standard error. However, this limitation has recently been overcome by noise-based methods of PRC estimation, which utilize much higher stimulus densities (Ermentrout et al. 2007, Ota et al. 2009, Wilson et al., 2014). Phase models based on noise-derived PRCs have been shown to predict a large fraction of the observed ISI variance, even with large-amplitude stimuli that one might expect to violate the weak-input assumption of most theoretical studies (Wilson et al., 2014). Because high-density stimuli produce relatively large ISI variance, they should compete better with ongoing synaptic activity, allowing PRC estimation under a wider range of conditions.

In the present study, we extend noise-based PRC estimation to utilize direct optogenetic barrage stimulation of recorded neurons. Because intracellular recording is not required to deliver highly controlled stimuli, extracellular spike recording is sufficient. The method was tested using substantia nigra pars reticulata (SNr) neurons in brain slices from Thy1-channelrhodopsin 2 (ChR2) transgenic mice (Arenkiel et al. 2007), which express ChR2 in multiple brain regions including SNr.

2. Materials and Methods

Animals

Studies utilized Thy1-ChR2 homozygous and heterozygous transgenic mice (line 18, B6.Cg-Tg(Thy1-COP4/EYFP)18Gfng/J). Mice were obtained from Jackson Laboratories and bred in-house. The University of Texas at San Antonio Institutional Animal Care and Use Committee approved all animal procedures, and all procedures were carried out in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Brain slice preparation

Mice were deeply anesthetized with isoflurane and euthanized by decapitation. The brain was removed, and coronal midbrain slices (300 μm) containing substantia nigra were prepared using a vibratome, in cold cutting solution containing (in mM) 2.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂, 10 MgSO₄, 10 D-glucose, 26 NaHCO₃, and 202 sucrose (pH 7.4). After cutting, slices were maintained at 28°C in artificial cerebrospinal fluid (ACSF) containing (in mM) 126 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 2 MgSO₄, 10 D-glucose, 26 NaHCO₃, and bubbled with 95% O₂, 5% CO₂. The slice storage ACSF, but not the recording ACSF, also contained (in mM) 0.005 L-glutathione, 1 Na-pyruvate, and 1 Na-ascorbate.

Recording

A slice was transferred to the recording chamber of an upright microscope (Olympus BX51WI) and superfused with ACSF containing 5 μM 2,3-dioxo-6-nitro-1,2,3,4-tetrahydrobenzo[f]quinoxaline-7-sulfonamide (NBQX) to block AMPA/kainate receptors, 5 μM (CPP) to block NMDA receptors, and 100 μM picrotoxin to block GABA_A receptors. On-cell and whole-cell recordings were obtained in voltage-clamp mode using a MultiClamp 700B amplifier (Molecular Devices) and an ITC-18 analog/digital converter (HEKA Instruments) controlled by custom software written in Igor Pro (WaveMetrics). Patch pipettes were pulled from borosilicate glass (Warner Instruments G150-4) using a Sutter P-97 puller and usually had resistances of 3–6 MΩ. For spike recordings in the on-cell mode, pipettes were filled with 150 mM NaCl, the holding potential was maintained at 0 mV, and data were band-pass filtered on-line at 300 Hz-2 kHz. For whole-cell recording of ChR2 currents, pipettes were filled with solution containing (in mM) 140.5 K-methanesulfonate, 7.5 NaCl, 10 HEPES, 0.2 EGTA, 2 Mg-ATP, and 0.21 Na-GTP, and data were low-pass filtered at 10 kHz. All data were sampled at 20 kHz.

Optogenetic barrage stimulation

Random trains of blue light pulses (~0.3 mW/mm²) were delivered through a 5× microscope objective. A white LED (Mightex MLS-5500-OL1) was used to generate light pulses, and the blue light band (460–490 nm) was selected using an Olympus U-MWB2 filter cube. The pulses were 0.5 or 1 ms in duration and were separated by random, exponentially distributed inter-pulse intervals (mean interval = 5 ms). Up to 100 traces 10 s in duration were recorded at a 15 s start-to-start interval. Each trace included 1 s of baseline firing activity and 9 s of continuous barrage stimulation. The timing of pulses was different for each trace but was the same for each recorded cell.

Spike detection

All analysis was performed in Mathematica 10.2 (Wolfram). The on-cell recordings provided a high signal-to-noise ratio, making spike detection unambiguous. The initial negative-going phase of each spike was detected at a level of −20 times the standard deviation of the noise, which was estimated by Gaussian fitting of the histogram of current values between −5 and +5 pA. The spike time was taken at the detection point. Only one spike detection was allowed in a 2 ms window, which was much shorter than the observed ISIs.

PRC estimation

Data from the near-steady-state responses from 4–9 s after the onset of each optogenetic barrage were analyzed essentially as described previously (Wilson et al. 2014), with the addition of a secondary PRC measurement. Briefly, the time-varying phase of the neuron was estimated as the fraction of the ISI elapsed. Thus, each ISI was divided into n bins, where the bin index (i) corresponded to the estimated phase [ϕ_i = (i − 0.5)/n]. The value of n was set to the mean ISI length in milliseconds (rounded to the nearest whole number) or a maximum of 50. The number of pulses (p_α,i) delivered in each bin of each ISI (indexed by α) was counted, and the mean pulse count was subtracted, giving Δp_α,i. A multiple regression analysis was then performed, where the independent variables were the Δp values from the two ISIs prior to each spike (ISIs α and α − 1), the dependent variable was ISI_α, and the residual error was ε_α.

$$\mathrm{\Delta }{p}_{\alpha ,i}=p_{\alpha ,i}-\overline{p}$$

$$IS{I}_{\alpha }=\overline{I}\overline{S}\overline{I}-{\displaystyle \sum _{i=1}^n\mathrm{\Delta }{p}_{\alpha ,i}Z}\left({\varphi }_i\right)-{\displaystyle \sum _{i=1}^n\mathrm{\Delta }{p}_{\alpha -1,i}{Z}_2}\left({\varphi }_i\right)+{\epsilon }_{\alpha }$$

The regression coefficients, Z(ϕ_i) and Z₂(ϕ_i) provide a unique solution for the primary and secondary PRC, respectively. The primary PRC quantifies the effect of a single light pulse on the present ISI, whereas the secondary PRC measures the effect on the following ISI. Mathematica code for the PRC analysis is available on request.

Phase models

To test the ability of optogenetic PRCs to predict spike timing, phase models were constructed based on the experimentally determined primary PRCs for individual SNr neurons. A phase model includes an oscillation rate ω and a PRC function z(ϕ), where ϕ(t) is the phase. The evolution of ϕ(t) in response to a stimulus current I(t) is governed by the following differential equation:

$$\frac{d\varphi }{dt}=\omega +I(t)z[\varphi (t)]$$

ϕ(t) is taken as cyclic; thus, when ϕ(t) reaches 1, it is reset to 0 and the spike time is collected. To construct the phase model for an individual neuron, ω was taken as the mean firing rate for the period analyzed, and z(ϕ) was obtained by linear interpolation of the experimental primary PRC, appending end points (ϕ = 0, z = 0) and (ϕ = 1, z = 0). The experimental stimulus waveforms were also interpolated, and the models were simulated by numerical integration (Mathematica NDSolve). To test the ability of a phase model to predict individual ISIs (between spike times t₁ and t₂), the model was initialized at ϕ = 0 and then integrated from t₁ to t₂. If a spike was not generated by t₂, the model was allowed to advance at the unperturbed rate ω until ϕ = 1.

Materials

Unless otherwise specified, all chemicals were obtained from Sigma-Aldrich (St. Louis, MO). NBQX was purchased from Tocris Bioscience (Bristol, UK).

3. Results

Current responses to optogenetic barrages

SNr neurons in brain slices from Thy1-ChR2 transgenic mice were stimulated with 9 s barrages of wide-field blue light stimuli, which directly activate ChR2 located on the soma and dendrites of the recorded cell. Potential activation of glutamatergic and GABAergic synaptic inputs was blocked by NBQX, CPP, and picrotoxin. The stimuli were barrages of 0.5 or 1 ms light pulses separated by random inter-pulse intervals with a mean of 5 ms, producing current waveforms that were dense in large-amplitude fluctuations. Each barrage was 9 s in duration, and up to 100 barrages were applied to each cell at a 15 s start-to-start interval. To examine the current waveforms produced by the barrages, the ChR2 current was recorded in whole-cell voltage-clamp mode at −80 mV (Fig. 1A). The mean and standard deviation (SD) of the currents were measured in 1 s windows (Fig. 1B, C). Both the mean current and the SD were largest at the onset of stimulation and then desensitized partially, reaching nearly constant levels for the second half of each barrage. We observed little change in the mean current or the SD over repeated barrages, and multiple cells were tested sequentially in the same illuminated area without apparent degradation of the responses.

Figure 1. ChR2 current responses to optogenetic barrage stimulation.

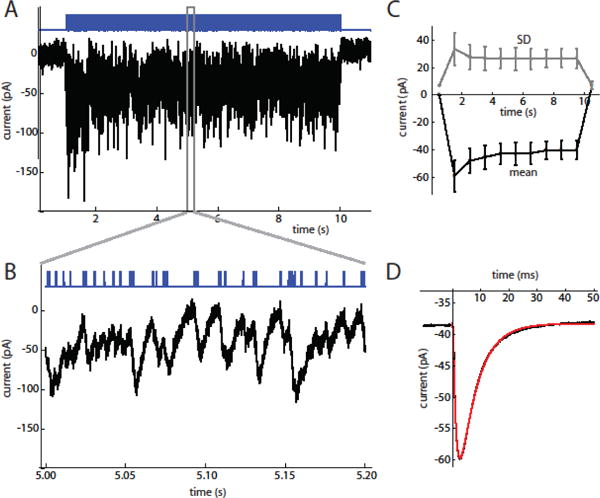
A. 9 s stimulus barrage (top, blue trace) and current response (bottom trace) in an SNr neuron (V = −80 mV). The baseline holding current was subtracted from the trace.

B. Expanded view of stimulus barrage and steady-state response, showing the summated fluctuations produced by individual stimulus pulses. C. Mean (bottom, black line) and SD (top, gray line) of stimulus current measured in 1 s bins (n = 6 cells). D. Average current response to a stimulus pulse in the example cell during the steady-state period. The average response rises from a non-zero baseline resulting from the decay of responses to previous stimulus pulses. The fitted function (red line) is the convolution of a double exponential, I₀ + A exp(−t/τ_rise) − A exp(−t/τ_decay), with the square-pulse waveform of an individual stimulus pulse. For this cell, τ_rise = 1.23 ms and τ_decay = 6.13 ms.

To examine the average response to each stimulus pulse, we measured the average current response to each stimulus pulse during the steady-state response (4–9 s from the onset of each barrage) (Fig. 1D). The average current responses were well fitted by the convolution of a double-exponential waveform (time constants τ_rise and τ_decay) with the square-pulse waveform of the light stimulus. In six cells tested with 0.5 ms pulses, we obtained τ_rise = 1.25 ± 0.21 ms (mean ± SD) and τ_decay = 5.43 ± 1.07 ms. This time course likely overestimates the duration of the ChR2 conductance, because of electrotonic filtering of current flowing through the long dendrites of SNr neurons to the somatic voltage clamp electrode. The illustrated cell also shows a small slow component that deviates slightly from the fit. A similar deviation was observed in three of the six cells, and would be predicted to result in slightly more accumulation of ChR2 current than predicted by the fits.

Spike responses and PRC estimation

Spike responses of SNr neurons were recorded in the cell-attached mode. Out of 24 cells recorded, 18 showed stable, rhythmic autonomous firing and were therefore considered suitable for PRC analysis. An example of the initial response and the steady-state response is shown in Fig. 2A, and the ISIs for that trial are plotted in Fig. 2B. Cells responded to the optogenetic barrages with increases in firing rate (Fig. 2C) and CV_ISI (Fig. 2D). Because of initial ChR2 desensitization and likely cellular adaptation, analysis was restricted to the steady-state portion of the response from 4–9 s after onset of each barrage. On average, the stimuli increased the mean firing rate from a baseline autonomous rate of 13.9 ± 6.1 spikes/s to 28.2 ± 11.1 spikes/s (n = 18), and increased CV_ISI from 0.072 ± 0.013 to 0.212 ± 0.090.

Figure 2. Spike responses to optogenetic barrage stimulation.

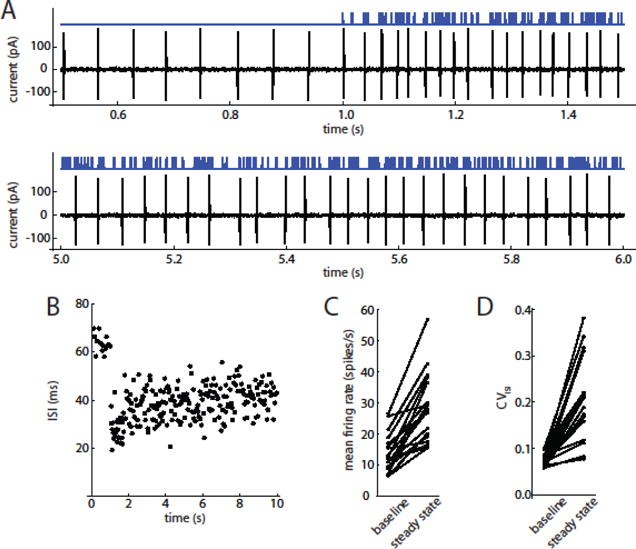
A. Optogenetic pulse barrage (top, blue trace) and corresponding spike response of an SNr neuron recorded in the on-cell voltage-clamp mode (bottom, black trace). Top panel shows the autonomous firing before stimulus onset (up to 1 s) and the initial response. Bottom panel includes a portion of the steady-state response, showing the sustained increase in firing rate and variability of ISIs. B. ISIs of this cell during this barrage. C. Effect of optogenetic barrages on mean firing rate (steady-state) (n = 18 cells). D. Effect of optogenetic barrages on CV_ISI.

Primary and secondary phase resetting curves were estimated using a multiple linear regression method (Wilson et al. 2014; see Materials and Methods). To reserve a portion of the data for predictive analysis (see below), PRCs were calculated using the data from every other stimulus trial. An example of the primary and secondary PRCs is shown in Fig. 3A. The error bars indicate the standard error of the estimated PRC value for each phase bin. The primary PRC is the portion of the plot to the right of the vertical axis, and the secondary PRC is the portion to the left, following the convention of Butera and Preyer (2005). The PRCs obtained from 18 SNr neurons are overlaid in Fig. 3B. All were type-1, showing only phase advances in response to depolarizing stimulus pulses. The primary PRCs generally sloped upward to the right, indicating that the input-sensitivity increased over most of the ISI before falling to zero as the phase approached 1. The steep negative slope at late phases is consistent with the cells approaching the causal limit, where the input elicits an immediate spike. This property of the PRC could facilitate synchronization of these neurons by a periodic stimulus with a frequency similar to the cells’ oscillation frequency.

Figure 3. Primary and secondary PRCs measured by optogenetic barrage stimulation.

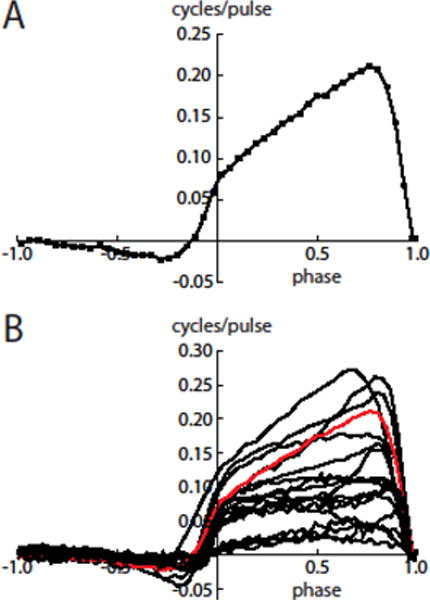
A. PRC of an example SNr neuron. The primary PRC is the portion to the right of the vertical axis (phases of 0–1), and the secondary PRC is the portion to the left of the axis. Typical features seen in this cell are the upward slope and lack of a negative region in the primary PRC and the relatively small negativity in the secondary PRC. Error bars are smaller than the size of the symbols. B. Primary and secondary PRCs of 18 SNr neurons. The PRC from panel A is shown in red.

As an overall measure of PRC skew, we measured the centroid, or center-of-mass, of each primary PRC. On average, the centroid phase was 0.54 ± 0.08. It is perhaps surprising that the centroid was not further to the right of center; however, this is explained by the non-zero values of the PRC from phase zero, combined with the fall to zero at the right side. To test whether heterogeneity of PRC shape resulted from differences in stimulation intensity, perhaps from variation of ChR2 expression, we correlated the centroid with the mean PRC value across 12 neurons tested with barrages of 1 ms light pulses of identical intensity. The correlation was not significant (r = −0.18, p = 0.59). Thus, our data did not indicate a dependence of PRC shape on stimulus strength. Rather, PRC shape heterogeneity is likely to arise from variation in neuronal dynamics, as observed previously in other cell types using highly controlled current stimuli (e.g. Burton et al. 2012, Wilson et al. 2014).

The secondary PRCs showed negative values at middle-to-late phases and then rose into positive territory as the phase approached 1. The ends of the secondary PRCs were continuous with the beginnings of the primary PRCs, presumably because of the duration of the ChR2 conductance waveform, which continues into the next ISI after a late-phase stimulus. Even prior to the late rise, the secondary PRCs were not mirror images of the primary PRCs. Thus, lengthening of the second ISI was not simply a consequence of shortening the first ISI, but must arise from ionic mechanisms whose activation is altered by middle-to-late-phase input. The overall amplitudes of the secondary PRCs were much lower than the primary PRC amplitudes. Based on the root-mean-square (RMS) value, the ratios of secondary PRC amplitude to primary PRC amplitude were 0.147 ± 0.031. These data indicate that overall, stimulus pulses had a much larger effect on the first ISI compared to the second ISI.

Performance of PRC-based phase models

As a type of input-output relationship, the PRC is of interest only if it can predict spike output (timing) in response to specified input. To test the ability of SNr neuron PRCs to predict spike timing, phase models were constructed using the primary PRC of each individual cell (see Materials and Methods). Phase models were obtained from the odd-numbered stimulus trials and tested for their ability to predict the spike responses recorded on the even-numbered trials.

The phase models were first tested for their ability to predict each individual inter-spike interval separately, setting the phase to 0 at each spike time and running the model with the stimulus waveform delivered during the subsequent ISI. If the model phase reached 1 during the ISI, the model spike time was taken at that point. If the model phase did not reach 1 during the experimental ISI, it was then allowed to advance at the unperturbed oscillation rate until the phase reached 1. An example of the predictive analysis is shown in Fig. 4. The model for this cell used the primary PRC shown in Fig. 3A. The model phase trajectories for a subset of the ISIs are shown in Fig. 4A, and the experimental and model ISI lengths are compared in Fig. 4B. In the example, the model predicted 81.5% of the ISI variance. On average, across the sample of 18 neurons, the phase models predicted 81.2 ± 14.1% of the ISI variance. The unpredicted fraction of ISI variance could arise from intrinsic cellular noise, secondary and higher-order PRCs, and complex dynamics that are not captured by a simple phase model.

Figure 4. Prediction of individual ISI lengths by phase models with experimental PRCs.

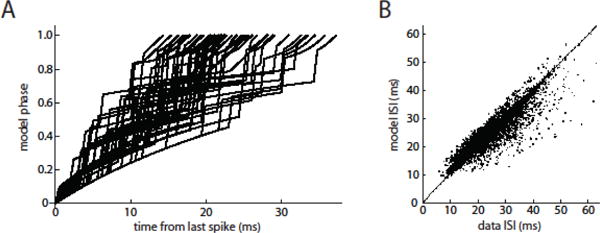
A. A subset of phase trajectories generated by the model for the example cell. The individual stimulus pulses produce rapid phase increases, with the largest increases occurring where the phase corresponds to the peak of the PRC. The curvature of the intervening phase trajectories results from a below-average stimulus (where the average includes pulses and inter-pulse intervals) interacting with the PRC and thereby slowing the rate of phase advance. B. Individual model-generated ISIs compared to the corresponding real ISIs of the example neuron. For this test, the model phase was set to 0 at the beginning of each ISI. In this cell, r = 0.883.

As a second test of the phase models, we evaluated their ability to reproduce the spike-triggered average (STA) stimuli leading up to spikes during barrages. This test was performed in free-running mode without any forced resetting of the model phase during the stimulus barrage. Because of accumulation of errors across multiple ISIs, the models did not follow the real spike trains precisely, but instead appeared to show sequences of well-matched spike times mixed with sequences of spikes that were unlocked from the real spike data (Fig. 5A). However, there were substantial correlations between the real and model-generated spike trains, as indicated by the distribution of model phases at the real spike times (Fig. 5B). Despite the differences in spike times, the models produced STA stimuli similar to those of the corresponding real neurons (Fig. 5C), indicating that the input features associated with spiking were largely preserved in the models. To compare the data and model STA waveforms quantitatively, we calculated the point-by-point correlation coefficient over a 100 ms window before the spike time. On average, we obtained r = 0.87 ± 0.16 (n = 18), indicating a reasonably good correspondence between the real and phase model-based STAs.

Figure 5. Prediction of the spike-triggered average stimulus by phase models with experimental PRCs.

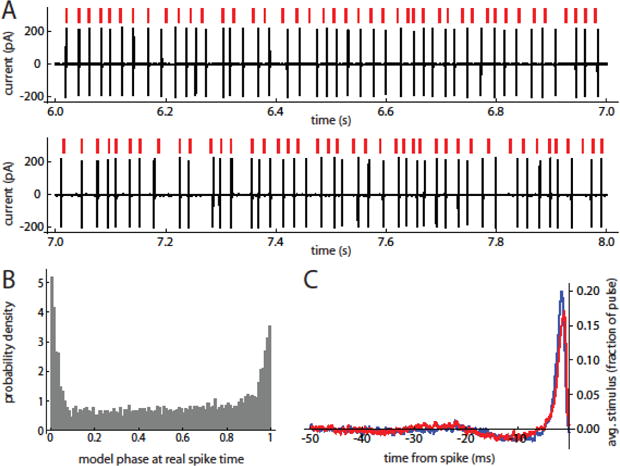
A. Free-running model prediction of spike response to stimulus barrage. Red marks indicate model spike times. Black trace is spike response of SNr neuron with the PRC used to generate the model. B. Probability density of model phase at real spike times. Note the large peak around phases of 0/1, showing substantial correspondence between model and cell oscillations. C. Spike-triggered average stimuli for the example cell (blue trace) and the corresponding model (red trace).

4. Discussion

The results of the present study show that PRCs of oscillating neurons in SNr can be estimated using non-invasive spike recording, direct stimulation using ChR2, and multiple linear regression analysis. Phase models based on these PRCs capture a great deal of the input-output relationship for these cells. Models incorporating the second-order PRCs could potentially allow even better spike time prediction, but would require further investigation to understand how the primary and secondary perturbations interact. Because the PRC estimation method described here requires only extracellular spike recording and optogenetic stimulation, it should be widely applicable to other cell types and may be possible to apply in vivo.

Comparison to previous methods of PRC estimation

The classic, definitional method of PRC estimation used single-pulse stimuli – either intracellular current injection or extracellular stimulation of synaptic afferents – delivered at low frequency to measure the change in ISI length produced by a single brief input. To our knowledge, PRC estimation in neurons was first reported by Perkel (1964) and was later performed in cortical neurons by Reyes and Fetz (1993). In the simplest analysis, the lengths of stimulus-perturbed ISIs are compared to the lengths of unperturbed ISIs to obtain the degree of ISI shortening as a function of the stimulus delay from the previous spike, and the stimulus phase is taken as the stimulus delay divided by the average length of the unperturbed ISIs. Because of intrinsic noise present in neurons, in addition to synaptic noise in experiments where synaptic inputs are not blocked, a large number of stimuli (usually hundreds to thousands) must be delivered to obtain a discernable PRC. To estimate the so-called infinitesimal PRC employed in many theoretical studies, small stimulus amplitudes are preferred, but the number of stimuli required increases further as the amplitudes are reduced.

To estimate PRCs more rapidly and precisely using small individual stimulus pulses, several investigators have used current noise, thereby delivering much denser perturbations (Ermentrout et al. 2007, Ota et al. 2009, Wilson et al. 2014). During noise stimulation there are no unperturbed or singly perturbed ISIs. Thus, different methods of analysis are required. Two methods are related to the spike-triggered average current (I_STA). First, it was shown analytically that as the amplitude of white-noise input approaches zero, the PRC becomes proportional to the negative time-derivative of I_STA(t) over one ISI (Ermentrout et al. 2007). Second, it was demonstrated that the PRC could be computed as a weighted average of the stimulus currents in the previous ISIs, re-scaling the time-axis of each ISI from length T_i to a uniform period T_avg and weighting by (T_avg-T_i)/T_i (Ota et al. 2009). Related to this method, it was shown that the PRC could be computed by multiple linear regression, where the independent variables represent the charge injected in subdivisions of each ISI and the dependent variable is the ISI length (Izhikevich, 2007; Wilson et al., 2014). This method accurately reproduced the PRC of a phase model subjected to strong perturbation by noise, and produced experimentally derived phase models that accurately predicted ISI lengths in oscillating neurons of the rat subthalamic nucleus.

In the present study PRCs were estimated using optogenetic barrages rather than injected current noise. Two limitations of this approach are that the optogenetic stimuli are unidirectional, and that, because of the opsin kinetics, the stimulus bandwidth is not arbitrarily high. Unlike directly injected noise current, which can have zero mean, the ChR2 current is always depolarizing. Given analog control of the light stimulus (which is generally available with LED sources but not with simple laser sources), it would be possible to apply a stimulus similar to previously applied current noise, but with a non-zero mean level in addition to fluctuations. However, to apply Gaussian-distributed fluctuations without substantially truncating the lower part of the distribution, the mean level would need to be at least twice the standard deviation. In addition, unless each pulse was relatively long (unlike the near-white noise applied previously), the kinetics of ChR2 would substantially reduce the amplitude of current fluctuations produced.

More generally, the kinetics of any opsin limit the bandwidth of the stimulus current produced. This effect limits the ability of optogenetic stimuli to resolve sharp features of the PRC. In general, the sharpest elements of the PRC are found at very early or late phases, near to or during the action potential. In the frequency domain, the PRC can be considered as a sum of sinusoidal modes (Goldberg et al., 2013), and the sharp features can be represented only with the inclusion of high-frequency modes. To permit estimation of these modes or their time-domain counterparts, the stimulus must have power at the corresponding frequency.

To maximize the amplitude and bandwidth of the current fluctuations produced by ChR2, we chose a random-pulse stimulus in preference to Gaussian noise waveforms. Using short pulses maximizes the bandwidth obtained with a given opsin. The mean inter-pulse interval of 5 ms was chosen as similar to the decay time constant of the ChR2 current, to produce current barrages that were dense in fluctuations (i.e. did not have long gaps with no stimulus current), but also had a relatively high coefficient of variation (CV). Based on voltage clamp recordings of the ChR2 current barrages, the CV of the ChR2 conductance produced by these stimuli was ~0.6. This was sufficient to produce a useful degree of ISI variation with a moderate increase in average firing rate. To increase the temporal resolution of the stimulus, one could use a different opsin such as Chronos (Klapoetke et al. 2014), which could be expressed in the target area/cell type by viral transduction. With faster opsin kinetics, a Gaussian noise stimulus might also become more practical.

To scale the optogenetic PRC in more meaningful units, we would ideally like to know the exact relationship between the light stimulus and the time-varying current produced in the neuron. If this were known, the PRC could be calculated as a function of current over time (i.e. charge) rather than arbitrary unit stimuli. We investigated the ChR2 current produced by our random stimulus trains by whole-cell voltage clamp recording. These experiments showed the amplitude and time course of the current produced by each light pulse. However, the current amplitudes varied substantially among neurons, presumably due to differences in ChR2 expression. In addition, we found that the recorded current waveforms could not be substituted for the corresponding light stimulus trains for purposes of PRC estimation, as the resulting PRCs were dominated by noise (data not shown). This finding suggests that the time course of ChR2 current recorded in voltage clamp in one group of SNr neurons may have been substantially different from that of the ChR2 current received during active firing in another group of cells. The causes of this difference are likely to include changes in driving force caused by the subthreshold membrane potential trajectory, voltage-dependent ChR2 kinetics (Williams et al., 2013), and differences in dendritic charge redistribution (i.e. filtering) between voltage-clamp and unclamped conditions. For these reasons, our reported analyses were limited to considering each light pulse as a unit input, much like an artificial EPSC.

Considerations for future in vivo application

It has been debated whether regular oscillatory firing observed in basal ganglia neurons in brain slices is relevant to real brain function or becomes unimportant as firing is made irregular by massive synaptic bombardment. Are these neurons still oscillating in vivo, or is the fundamental nature of the oscillator altered or obliterated by large synaptic conductances? To answer this question for each class of oscillator neuron, it would be valuable to obtain PRCs in vivo and compare them to PRCs measured in the slice preparation.

For PRC estimation using optogenetics, the main differences between the in vivo and slice preparations are the greater barriers to light penetration and the higher degree of background synaptic activity. Thus, it will be important to deliver stimuli strong enough to compete with the natural synaptic inputs. If LED stimuli delivered by an optical fiber were insufficient, a laser could be used to deliver the same pulse barrages. The sufficiency of the fluctuating stimulus can be evaluated by the R-squared value of the multiple-regression analysis used to determine the PRC, which represents the proportion of ISI variance caused by the stimulus and captured by the linear model. If the background input is large, this will yield a small number. In this case the PRC should still be unbiased but will be noisy. By increasing the stimulus strength and monitoring R-squared, one could tune stimulus intensity to obtain PRC data with sufficient precision.

To determine whether any differences between in vivo and in vitro PRCs result from background synaptic activity, it would be useful to block synaptic inputs by local infusion of glutamate and GABA receptor antagonists. For recording, any technique providing well-isolated single units should be sufficient. For direct optogenetic stimulation of recorded neurons in the absence of synaptic blockers, it will be important to ensure that opsin is not expressed in afferent fibers, or that the stimulus is weak enough to preclude axonal excitation.

5. Conclusions

The methods described here provide an approach that may be useful for obtaining PRCs in vivo. Such measurements could provide insight into network interactions that influence neuronal oscillations. When a population of neurons is stimulated by shared, time-varying optogenetic input, the common input is likely to produce correlated firing. The degree to which this occurs will depend on the properties of the individual neurons – firing rates, PRC shapes and overall sensitivities – and the homogeneity or heterogeneity of the population (Burton et al. 2012). Correlations of firing activity will also depend on synaptic coupling among the stimulated cells. With strong coupling, PRCs estimated in the absence of synaptic blockers will reflect the network interactions as well as the properties of individual neurons. The combination of pharmacology and optogenetic stimulation will provide a powerful approach to investigate the cellular properties and network interactions regulating oscillations in neuronal networks.

Highlights.

• Optogenetic methods were adapted to measure phase resetting curves (PRCs).

• The PRCs yielded phase models that predicted inter-spike intervals.

• Optogenetic PRC estimation is potentially suitable for in vivo applications.