Human movement, cooperation and the effectiveness of coordinated vector control strategies

Abstract

Vector-borne disease transmission is often typified by highly focal transmission and influenced by movement of hosts and vectors across different scales. The ecological and environmental conditions (including those created by humans through vector control programmes) that result in metapopulation dynamics remain poorly understood. The development of control strategies that would most effectively limit outbreaks given such dynamics is particularly urgent given the recent epidemics of dengue, chikungunya and Zika viruses. We developed a stochastic, spatial model of vector-borne disease transmission, allowing for movement of hosts between patches. Our model is applicable to arbovirus transmission by Aedes aegypti in urban settings and was parametrized to capture Zika virus transmission in particular. Using simulations, we investigated the extent to which two aspects of vector control strategies are affected by human commuting patterns: the extent of coordination and cooperation between neighbouring communities. We find that transmission intensity is highest at intermediate levels of host movement. The extent to which coordination of control activities among neighbouring patches decreases the prevalence of infection is affected by both how frequently humans commute and the proportion of neighbouring patches that commits to vector surveillance and control activities. At high levels of host movement, patches that do not contribute to vector control may act as sources of infection in the landscape, yet have comparable levels of prevalence as patches that do cooperate. This result suggests that real cooperation among neighbours will be critical to the development of effective pro-active strategies for vector-borne disease control in today's commuter-linked communities.

1. Introduction

Effective prevention and mitigation of outbreaks of infectious diseases relies on being able to predict patterns in the dynamics of spread of exposure risks over space and time. For vector-borne diseases, this implies understanding the factors that influence both host and vector ecologies, and the epidemiological patterns that emerge as a result. In a world with shifting climates [1], altered habitats [2] and increasing travel distances in the course of many people's normal lives [3–5] with associated human-mediated transport of both diseases and vectors [6,7], even just understanding the basic ecological drivers of the system can be complicated. Naturally, understanding mitigation and control adds yet another layer of complexity.

Interruption of ongoing transmission can, in principle, target any stage in the parasite's life cycle. Medical interventions that focus on hosts target either infected individuals through treatment, or susceptible hosts through prophylaxis or vaccination. Physical interventions, such as bed nets, can prevent vectors from biting hosts, disrupting transmission between hosts and vectors in both directions. There are also a myriad of interventions that focus on the vector directly. While there are ongoing efforts to control some diseases by decreasing vector competence (e.g. through the release of mosquitoes harboring infection-blocking Wolbachia strains [8,9]), most vector-targeted interventions focus on decreasing vector population sizes or vector longevity. This can be done by purposefully altering habitat availability, for instance through environmental management or by removal of vessels holding standing water [10]. Populations can also be controlled actively, through sterile male releases, or application of adulticides or larvicides [11–13].

In the case of newly emerging vector-borne pathogens, the vast majority of our epidemic-fighting toolkit relies on the vector-targeted strategies for the simple reason that we rarely have existing medical treatments or preventive measures that are effective against novel threats. This does not, however, imply that these strategies are without their own set of challenges. Vector-targeted strategies, by their nature, have localized geographical regions of direct effect. Any broader secondary or community-level impacts, either ecologically or epidemiologically, are driven by the direct impact of a local intervention on a local area. In some cases, such as when eliminating potential larval habitat by removing or chemically treating standing water, those performing the intervention can focus on as small a scale as a single residence. Even wider-scale efforts are frequently still relatively geographically limited in their immediate effect, such as spraying insecticides from trucks or releasing them from low-flying airplanes: decisions frequently made by city-, county-, district- or state-level public health or vector control agencies, or at a smaller scale, by private contractors.

There have been some very successful instances of large-scale coordinated vector control efforts. These notably include the mass scaling up of insecticide-treated bed net coverage across sub-Saharan Africa [14,15], or the Aedes aegypti elimination efforts in Latin America in the 1930s [16]. However, it is still the case that local/regional vector control efforts are most frequently undertaken at the same level as their direct effect. In other words, two neighbouring municipalities may undertake very different control strategies, despite facing similar risks. These differences may be more drastic, even between regions that are geographically close to each other, if they face different risks from vector populations. Such differences could be due to, for instance, different distributions in land usage, or unequal access to resources needed for effective control. Control decisions may reasonably diverge, even among neighbours, based on many factors. These include differences in ecological viability of vector habitat, epidemiological susceptibility of the resident population, different sizes in resident host populations, different access to medical resources for prevention and/or treatment and even different perceptions of risk associated with vector populations and/or infection. Even if there is consensus among decision-makers across regions about the need for vector control efforts, the timing, frequency and efficacy of control measures may vary.

Unfortunately, local/regional vector population sizes are not the only drivers of epidemiological dynamics across the broader landscape. Even if the vector species responsible for transmission of a particular pathogen does not disperse far or frequently enough to cause concern for neighbouring regions about the efficacy of adjacent regions' control decisions, humans themselves routinely travel across distances that are likely to span areas controlled by different decision-makers. Especially around dense urban centres, people routinely travel many miles each day as they commute to employment or school. The result of this confluence of patchy habitat manipulations of vector populations, with varying levels of travel by hosts who may be carrying infection, is a textbook case of potential metapopulation dynamics for the disease [17–19].

Considering the question of epidemiological control via vector-targeted intervention as a question of metapopulation ecology leads us to a natural set of important immediate questions. How much movement of humans across control region borders yields a metapopulation dynamic? Do adjacent regions need to coordinate with each other in the timing or method of their vector control strategies to avoid inadvertently supporting longer durations of ongoing pathogen transmission among their populations? Can heightened local surveillance efforts that allow regional decision-makers to be responsive to disease within their own population more rapidly compensate for lack of coordination in vector control across regions that occurs without the need for any knowledge of population health status? Most critically, asking these questions also allows us to frame control issues in the language of biological control. If we understand the disease metapopulation dynamics, can we decrease the resources and effort dedicated to local control within each region, so long as we allow for strategic coordination in those efforts to achieve a global impact on disease incidence? To begin to address these questions, we here present a simplified spatial model of a system that reflects only the most basic elements of such a system.

2. Model

We developed a spatial model of vector (e.g. Ae. aegypti) and host (e.g. human) populations arranged as patches on a 10 × 10 grid. We consider a microparasite such as the Zika virus, such that infection in vectors and hosts can be modelled using a compartmental approach. Thus, within each patch (indicated by subscript k), the vector population, N_v,k, consists of immature (L_v,k), susceptible (S_v,k), exposed (E_v,k) and infectious (I_v,k) mosquitoes. The human population, N_h,k, consists of susceptible (S_h,k), exposed (E_h,k), infectious (I_h,k) and recovered (R_h,k) individuals. A description of the parameters and their values is provided in table 1. The parameter values were based on the literature, varied in order to explore their impact, or set in order to lead to desired mosquito:host ratios. Transitions between these compartments are governed by the following set of equations:

2.1

where 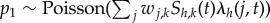, the number of susceptible hosts from patch k that become infected at time t (see below).

2.2

where p₂ ∼ Poisson(τ_hE_h,k(t)) gives the number of latent hosts that progress to the infective state.

2.3

where p₃ ∼ Poisson(γI_h,k(t)) gives the number of infectious hosts that progress to the recovered or immune state.

2.4

Table 1.

Description of parameters.

parameter	description	value	dim.	source
δ	proportion of exposure experienced away from the home patch	0–1	d−1	varied
a	inverse of gonotrophic cycle duration	0.33	d−1	[20]
c	probability of a vector becoming infected upon biting an infective host	0.31	—	[21]
b	probability of a host becoming infected upon receiving an infectious bite	0.35	—	[21]
τh	inverse of human latent period	1/5.8	d−1	[22]
γ	inverse of human infectious period	1/5.8	d−1	[22]
μ1	adult mosquito death rate	1/13	d−1	[23]
τv	inverse of extrinsic incubation period	1/9.1	d−1	[22]
μ2	base immature mosquito death rate	0.05	d−1	—
μ3	density-dependent modifier of immature mortality	0.001	d−1	—
ϕ	fecundity	10	d−1	[24]
η	rate of larval development	1/7	d−1	[25]

The focus of the model is on the short term, so that human demography and any possible waning of immunity can be ignored. Vector populations are described as follows:

2.5

Here, the number of immature mosquitoes dying per time step is given by p₄ ∼ Poisson(μ₂ + (μ₃L_v,k(t))L_v,k(t)). The number of immature mosquitoes added each step are given by p₅ ∼ Poisson(ϕN_v,k). Juvenile development is given by p₆ ∼ Poisson(η(L_v,k(t) − p₄)). Changes in the population size of susceptible (uninfected) mosquitoes are given by

2.6

where losses are due to mortality: p₇ ∼ Poisson(μ₁S_v,k(t)), and due to infection: p₈ ∼ Poisson(λ_v(k, t)(S_v,k(t) − p₇)).

2.7

Mosquitoes leave the exposed class by dying: p₉ ∼ Poisson(μ₁E_v,k(t)), and by becoming infectious following the extrinsic incubation period: p₁₀ ∼ Poisson(τ_v(E_v,k(t) − p₉)).

2.8

Infectious mosquitoes remain so until they die: p₁₁ ∼ Poisson(μ₁I_v,k(t)).

2.1. Force of infection and movement

The model operates at a scale where mosquito dispersal can safely be ignored, through the assumption that mosquito travel between patches is negligible. For dengue and Zika vectors such as Ae. aegypti this implies that patches capture communities or neighbourhoods that are separated in space by a few hundred metres or are sufficiently large so that movement across edges is minimal relative to each patch's mosquito population [26–29]. Hosts are assumed to have a home patch (k), but commute and can potentially be exposed to infective bites in other patches (j) with a probability of δ, which we vary across a wide range. The distribution of hosts that commute from a given home patch to other patches in the metapopulation depends on both the distance to and population size of other patches, following a gravity-type model:

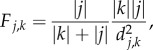2.9

where 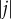and are the respective sizes of the populations that call patches j and k home, and d_j,k represents the Euclidean distance on the grid between these patches. These probabilities are then normalized over all patches that could be visited (figure 1a). For each patch, we then have a matrix W with probabilities of remaining in the home patch with probability w_k,k = 1 − δ, or to any other patch with probability w_j,k = δF*_j,k. The distribution of hosts per time step over patches is based on draws from a multinomial distribution with these probabilities.

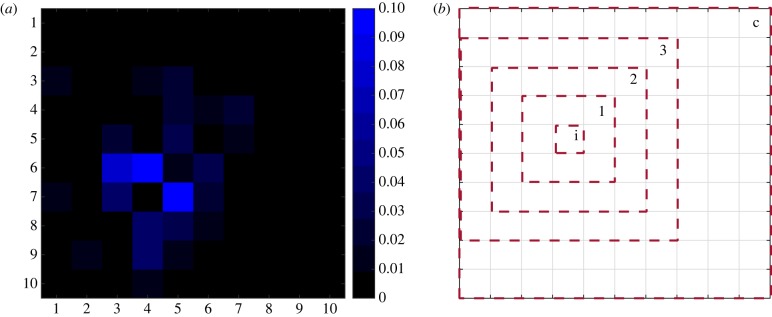
Figure 1.

(a) An example of the commuting probabilities (F*_j,k) for an arbitrary patch (with coordinates 4,7); (b) an example of the different levels of coordination in terms of larval control, where control is either implemented at the individual-patch level (i), or by a patch and its nearest neighbours (1), its neighbours two steps (2) or three steps (3) removed, or collectively by the entire metapopulation (c).

It follows that the forces of infection on hosts (λ_h) and vectors (λ_v) are

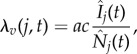2.10

where 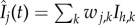and 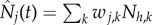. That is to say that the force of infection on vectors in a given patch depends on the biting rate (a), the probability of a vector becoming infected when biting an infective person (c), and the proportion of hosts present in patch j that are infective.

The force of infection on hosts, λ_h is given by

2.11

That is, the force of infection on humans present in patch j depends on the biting rate (a), the probability of a human becoming infected following an infective bite (b) and the density of infective vectors in that patch over all hosts that are present there that day.

2.2. Control

We focus on the use of larval control. Interventions targeting immature mosquitoes are commonly employed against species such as Ae. aegypti that lay eggs in small containers with water that are often encountered in private yards (e.g. bird baths, buckets, etc.). Larval control can take the form of source management, the removal or emptying of containers or the application of larvicides, such as Bacillus thuringiensis israelensis [30]. We focus on the latter: a method that increases the rate of larval mortality in patches where it is deployed. In our simulations, we introduce a single infected host into an arbitrarily chosen, but always the same, patch. We assumed that following detection of at least two infected hosts (so that the initial introduced case does not invoke a response in the absence of active transmission) in a given patch, larval control would be implemented the following day and remain effective for 10 days. Within a given patch, we assumed that 80% of immatures would succumb to the larvicide per day, so that the base death rate in the presence of the larvicide becomes μ_c =−log(0.2) + μ₂ (i.e. an arbitrarily chosen high level of efficacy, which allows us to focus on community-level effects of vector control, rather than local efficacy).

We varied two components of community-level responses to infection: whether individual patches contribute to surveillance and vector control or not (referred to as cooperation), and the extent to which patches acted collectively (which we refer to as coordination). For cooperation, we assumed that a given, randomly assigned number of patches would not contribute to surveillance and control. This assignment was fixed, so that the patches that did or did not contribute to control did not change over time. This percentage was typically set to 20% of the communities, but a greater proportion of non-cooperation (50%) was also investigated. Non-cooperation here could represent, for instance, a lack of resources at a local level. The extent to which patches acted collectively was varied from a control response targeted at the individual patch where infection was witnessed, to a response in the patch with infection as well as its immediate neighbours, to its neighbours that are two or three steps removed, or to all patches in the metapopulation (figure 1b). Coordination here therefore gives insight into the value of extending control activities to increasingly large areas around a focal infection. Thus, we investigate how the extent to which hosts commute affects the dynamics of Zika infection as it spreads through a metapopulation as well as the efficacy of coordinated control responses aimed at halting the epidemic.

3. Results

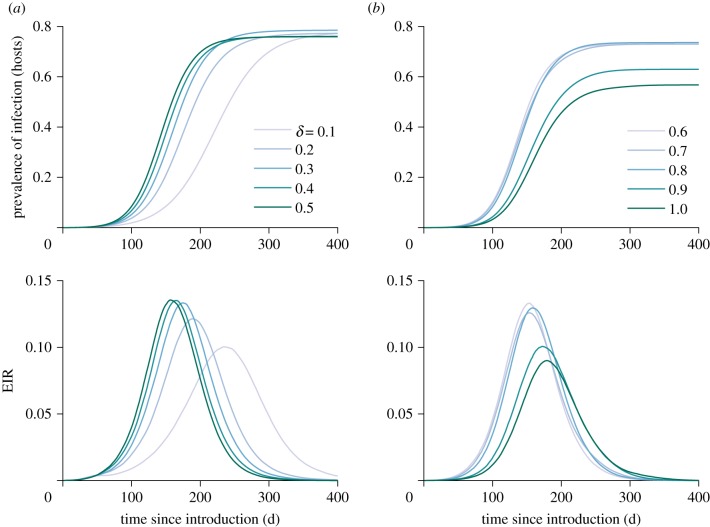
The course of the epidemic spreading through the metapopulation is consistent with typical SIR dynamics: a pathogen burns through a population and then limits its own transmission as immunity is built up. This is illustrated in figure 2, where the entomological inoculation rate (a relevant metric of exposure for vector-borne diseases which indicates the average number of infectious bites received per person per unit of time) increases sharply before falling. The extent to which hosts commute was varied by changing δ from 0.1 to 1 (i.e. each host has a daily probability of δ of commuting to a different patch, where that host is then exposed to mosquito bites). At intermediate levels of commuting, we see the steepest rise in prevalence and the most intense transmission.

Figure 2.

The mean prevalence of infection (latent, infected and immune hosts) in hosts over time in the absence of vector control, for levels of human commuting (δ) ranging from 0.1–0.5 (a) and 0.6–1.0 (b). The lower panels show the corresponding mean entomological inoculation rate (EIR), i.e. the mean number of infectious bites received per human per day, over time.

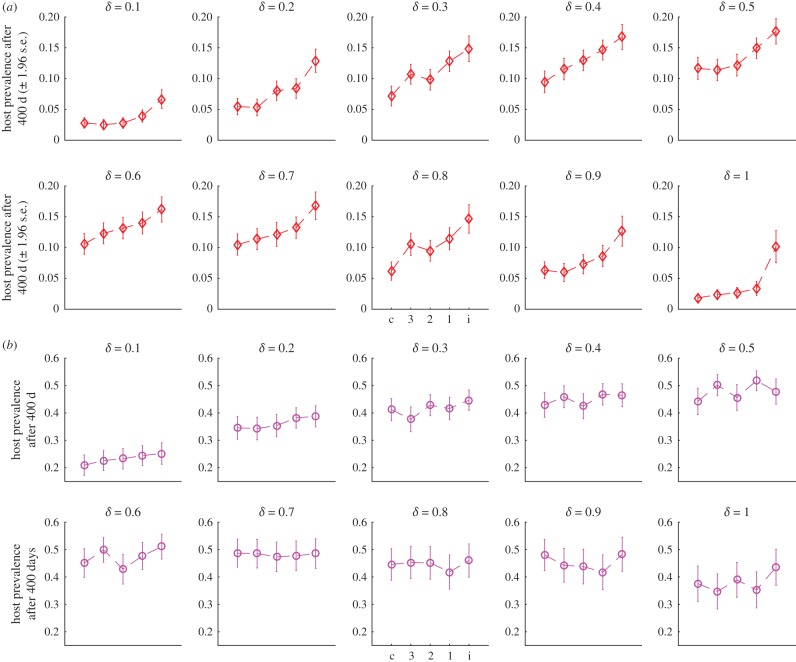
With vector control, the mean prevalence after 400 days likewise remains higher at intermediate levels of movement (figure 3). We varied the extent to which vector control responses were coordinated and the extent to which patches contributed to surveillance and control. Impressions from figure 3 are that the usefulness of coordination depends both on the rate of commuting and on the extent to which patches are capable or willing to implement surveillance and control.

Figure 3.

(a) Mean prevalence ±1.96 s.e. of infection in hosts 400 days following introduction of a single infected case at different levels of human commuting (δ). Dashed lines merely provide a visual cue. Control is implemented as a collective response targeting all patches in the environment (c); at the individual patch level and all neighbours three steps or less removed (3); the patch and all neighbours two steps or less removed (2); the patch and its nearest neighbours (1); or only at the individual patch level (i). Control can occur in up to 80% of patches, with 20% not cooperating. (b) The same, except treatment only occurs in 50% of the patches. (Online version in colour.)

For instance in figure 3a we see that at both the lowest and the highest rates of δ, there is relatively little gain to be made by using a more coordinated strategy (although the individual patch response is still worse than the other strategies), while at intermediate levels increasing levels of coordination appear to be more effective. At a lower level of cooperation, where only half the patches implement surveillance and control (figure 3b), control is not only less effective in general but also the relative efficacy of more coordinated responses is diminished compared to patch-level responses.

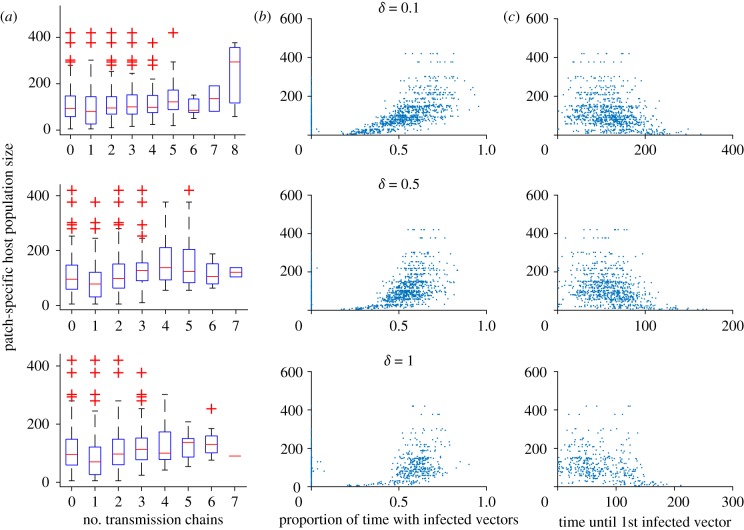
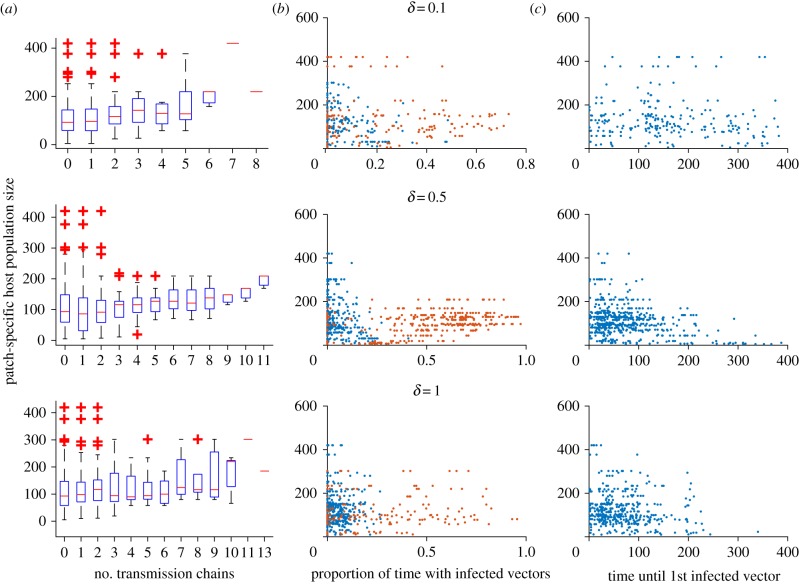
To understand why the overall metapopulation disease dynamics are as they are, patch-level responses are of interest. In figure 4, three aspects of the epidemic are explored in the absence of control. The number of introductions of the pathogen resulting in active transmission (i.e. distinct chains of infection in the vector population) appears to not rely much on the host population size of each patch. The proportion of time that a patch undergoes active transmission does, however, depend on the patch's population size, with more populous patches having proportionally longer periods of ongoing transmission, though this effect becomes less pronounced at the highest level of commuting. There appears to be an inverse relation between patch size and the time until the first infected vectors appear. It is possible that the proportion of time with ongoing transmission may be a result of earlier introduction and therefore a longer transmission window, though we cannot rule out that (in addition or instead) smaller patches simply exhaust their susceptible population more rapidly.

Figure 4.

Patch-level transmission dynamics as a function of patch size for three levels of commuting (δ = 0.1, 0.5 or 1). (a) The distinct number of transmission chains (periods with continuous infected vector populations, or, how many introductions of active transmission occurred); (b) the proportion of time (out of 400 days) that each patch had infected vectors; (c) the time in days until the first infected vector was observed per patch. (Online version in colour.)

We can look at the same statistics when control is being implemented, to understand how patch-level outcomes are affected. These are shown for the individual-patch response in figure 5. When control is implemented at the patch level, the number of pathogen introductions increases along with community size. However, this is only evident at low and moderate levels of movement. A notable difference compared to the outcomes without control interventions is in the proportion of time patches undergo active transmission, where the patches divide into those that are and are not effectively controlled. The patches that are not effectively controlled tend to be non-cooperating patches, those that did not implement surveillance or control, and the distinction between cooperating and non-cooperating patches appears sharpest under moderate levels of commuting (δ = 0.5).

Figure 5.

Patch-level transmission dynamics as a function of patch size for three levels of commuting (δ = 0.1, 0.5 or 1), when larval control is implemented at the patch level in 80% of patches. (a) The distinct number of transmission chains (periods with continuous infected vector populations, or, how many introductions of active transmission occurred); (b) the proportion of time (out of 400 days) that each patch had infected vectors; patches that did implement control are shown in blue, while patches that did not implement control are shown in red; (c) the time in days until the first infected vector was observed per patch.

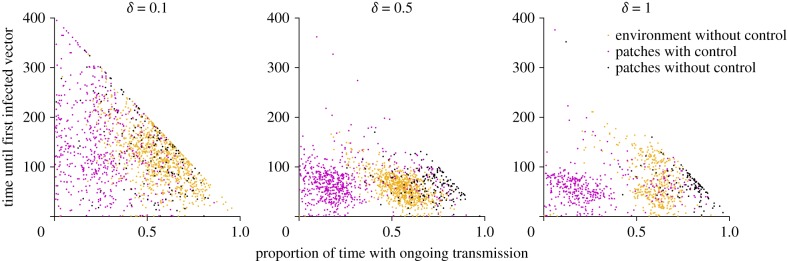
When we plot the time of first introduction against the proportion of time that patches had ongoing transmission (i.e. infected vectors), we see that, in the absence of control, there is indeed a correlation between these two outcomes (figure 6). With control, this effect disappears. The bimodal aspect of the patch-level control scenario for the higher levels of commuting is apparent here as well. Figure 6 suggests that a subset of patches (particularly, but not exclusively, those that did not implement control) can actually be subjected to a longer period of active transmission than patches in the absence of any control.

Figure 6.

The time in days until the first infected vector occurs in a given patch plotted against the proportion of time (out of 400 days) that a patch had ongoing transmission. Different panels represent simulations for varying levels of commuting, δ. Orange dots represent patches from the scenario without any intervention. Magenta dots represent those patches from the scenario with individual patch-level larval control which implemented control, while black dots represent patches from the same environment which did not implement control.

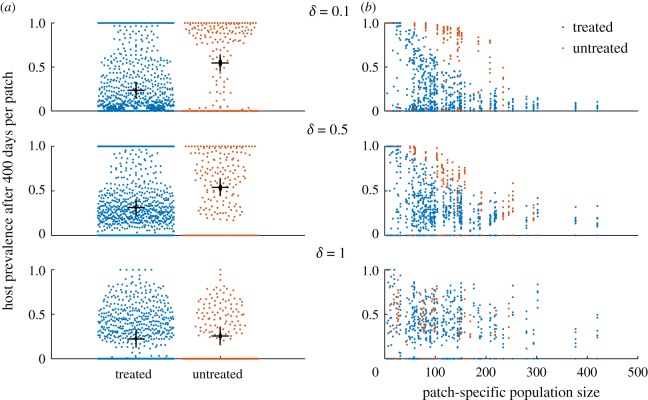
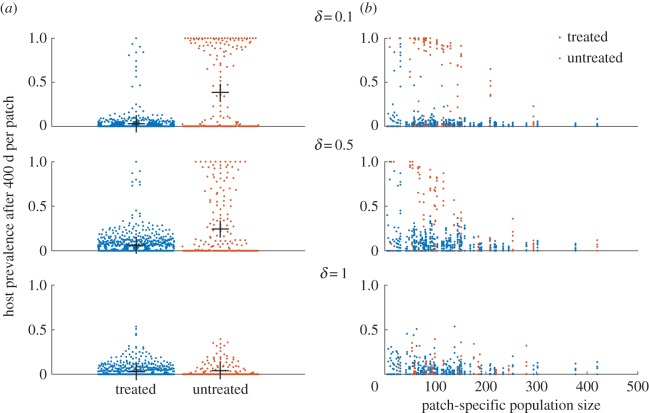
Looking at the prevalence of infection in hosts adds to this picture (figure 7). When δ is 0.1, prevalence of infection in hosts in untreated patches is greater than that in treated patches, but this difference diminishes as commuting intensifies. This is further highlighted by the prevalence by population size scatter plots. At low levels of movement, there is a clear separation between treated and untreated patches, and a correlation between patch size and prevalence. As expected, at higher levels of movement when hosts are mixed more thoroughly, the infection status of hosts from particular patches has seemingly little bearing to their patch characteristics (treatment or size). When control is performed collectively, overall prevalence is lower, but otherwise the conclusions remain largely the same (figure 8).

Figure 7.

Prevalence at the patch level in hosts after 400 days (based on 10 replicates). Control was done at the individual patch level, i.e. without coordination. (a) Dots represent the proportion of hosts that are infected in individual patches. The mean prevalence of infection and standard error over all patches are indicated by the black bars. (b) The proportion of hosts that are infected in individual patches of varying host population sizes.

Figure 8.

Prevalence at the patch level in hosts after 400 days (based on 10 replicates). Control was done collectively for 80% of the patches. (a) Prevalence of patches with the mean and standard error. (b) A scatter plot of prevalence and population size of each patch.

4. Discussion

Vector-borne diseases are often highly focal in space and/or time, and are typically characterized by strong heterogeneity in exposure among host populations [31,32]. This is no different for Aedes-transmitted arboviruses in urban settings [33–37]. Such heterogeneity can theoretically be masked, alleviated, compounded or even shaped by movement of both vectors and hosts. In the case of mosquitoes, the extent of movement will be determined by species-specific characteristics and environmental or ecological conditions. For humans, socio-economic and cultural conditions probably shape movement patterns. While it is becoming increasingly clear that these factors can influence the intensity and dynamics of vector-borne diseases [6,38–41], understanding the ramifications for control and surveillance efforts of the combined effects of movement and heterogeneity remains at the forefront of vector-borne disease ecology. A metapopulation dynamic, particularly the occurrence of rescue events, where infection is re-established following local extinctions, thereby allowing for longer persistence of an epidemic outbreak, would have particular repercussions for how we structure control programmes [42–44]. This has been recognized in the context of pathogen eradication programmes (e.g. [45]), yet for the control of arboviruses such as dengue, chikungunya and Zika, control efforts remain largely focal and reactive. Adapting control strategies to consider heterogeneous exposure and human movement may be challenging, but could be done by incorporating contact tracing, or targeting high-risk groups or areas [46]. In the case of a metapopulation dynamic, questions regarding cooperation among nearby communities become much more relevant. For instance, to what extent are control efforts hampered by the inability or unwillingness of adjacent communities to participate in a control effort? To what extent does coordination of control efforts in time affect the usefulness of the interventions? And are there situations where vector control can inadvertently prolong the period of ongoing transmission in certain areas?

Our model was run over a relatively short term, namely that in which an initial epidemic outbreak tended to run its course and deplete susceptible hosts. Even so, certain aspects associated with metapopulation dynamics were evident. These aspects were that we found the highest entomological inoculation rates and the fastest spread of infection at intermediate levels of host movement. Likewise, when vector control was implemented, the prevalence of infection remained higher at these intermediate levels of movement. This is reminiscent of findings that persistence of directly transmitted pathogens tends to be maximized at intermediate levels of connectivity between patches, such that the number of introductions in uninfected patches relies on both movement and the synchronization of dynamics between patches [47]. In this study, the peak at intermediate levels of movement may be because the basic reproduction number of vector-borne disease in metapopulations can decrease with stronger connectivity [19], while greater rates of movement can reduce heterogeneity of exposure, and therefore increase prevalence of infection [41]. Further studies on the dynamics of immunity in relation to control effect sizes of interventions are warranted. Additionally, we found that individual patches in our simulations frequently lost and reacquired infections, either due to stochastic extinctions (probably short-lived chains of infection that stuttered and died out before taking hold) or due to vector control. The number of active transmission events per patch appeared to be relatively unaffected by the host population size of individual patches. In the absence of vector control, the duration of ongoing active transmission in a given patch, as indicated by the presence of infective vectors, was associated with the host population size of that patch (i.e. the number of humans that called that patch home). Because larger patches would have attracted a larger proportion of commuters, this is probably explained by earlier introductions of infections (figure 4).

Our study has a number of limitations. Certain of these are due to our assumptions regarding control interventions. For instance, we have focused only on the use of larval control, which is a commonly used Aedes spp. abatement strategy. In reality, once an arboviral outbreak has been identified, adult control (e.g. perifocal or indoor spraying with residual insecticides) is likely to be used in addition to larval control [30]. However, the focus on larval control represents a targeting of the least mobile stage of the mosquitoes. Thus, it allows for easy comparison to models applied at a different scale where adult mosquito movement could come into play, or to mosquito species which disperse over greater distances. Models that have investigated the role of mosquito movement suggest that additional complexities related to control can emerge. For instance, clustering of certain interventions can lead to a lower overall efficacy than a uniformly distributed intervention [48], or increase mosquito populations in adjacent areas [49]. Another example of a simplifying assumption is that patches in our model either contributed to both population surveillance of infection in hosts and vector control or to neither. The rationale behind this choice was that we assumed such a lack of investment to be driven largely by socio-economic conditions (e.g. communities which are less likely to implement vector control are also less likely to invest in active surveillance or have worse access to healthcare providers). In reality, surveillance and vector control may be organized at different scales, such that humans still have access to healthcare and would be tested for Zika, but vector control might not be implemented in their community. Alternatively, members of a community may be less likely to see physicians for relatively mild symptoms, but have access to city-wide vector control interventions. Whether this distinction matters probably depends on the extent to which communities share information regarding infected cases and whether a case in a community which does not implement vector control would trigger a response in neighbouring communities. A further limitation relates to the use of a gravity model to describe human commuting. While use of such an approach is reasonable and often fits commuting data well, this may not always be the case (for instance in the case of socially structured movements), and use of mobile phone data or a radiation model may be more appropriate [50]. Finally, we note that we assumed that human behaviour does not change as a function of infection or throughout an outbreak. In reality, it is likely that a proportion of symptomatic cases would be less mobile, or that active transmission in an area may lead to avoidance behaviour or increased use of personal repellents. As including adaptive human behaviour in epidemic models can have large implications [51], such refinements should be explored in models adapted and parametrized to explore such questions in specific situations and well-defined spatial scales.

The importance of (re-)introductions of infection and host movement suggest an important role for coordination of control activities and cooperation among communities. We have investigated these two aspects here in the following sense: that coordination implies that surrounding communities would implement vector control at the same time as the focal community where an infection in humans was detected, in order to more effectively limit spread of the pathogen. Cooperation was investigated in the sense of the ability or willingness to pay for control activities among different communities, with potential repercussions of non-cooperation being either that such communities could act as sources of (re-)infection or simply diminish the community-level effects (as opposed to the direct, local effects) of control. Our main result is that the efficacy of coordination depends strongly both on how frequently humans commute, and on the overall level of cooperation among communities. Importantly, we found that while more coordinated responses tend to lead to significantly lower prevalence levels after the 400-day period we simulated, this is not the case at low levels (less than or equal to 50%) of cooperation. In that case, a focal, individual-patch response is not much less effective than a collective response targeting the entire metapopulation, and both lead to high proportions of hosts becoming infected over this time period.

Worrisome also is the finding that at higher levels of commuting, implementing vector control at the individual-patch level only leads to a bimodal pattern with regard to the proportion of time that patches experience active transmission (figure 5). In fact, these patches often may have active transmission for a longer period than they would be in the absence of control altogether (figure 6). Intuitively, this could be because of an influx of susceptible hosts from nearby patches that do implement control, resulting in a decreased likelihood of transmission dying out in these source patches.

When commuting occurs with high frequency, patches that do not participate in surveillance and treatment can putatively keep transmission going for a longer time, but do not necessarily suffer a higher disease burden themselves, as the location of exposure becomes less associated with the control activities undertaken in the home patch. Thus, the time a patch continues to have active transmission differs from the effects on host prevalence. Under high levels of movement, there is potentially a tension between achieving high levels of coordination (e.g. multiple communities enacting vector control to limit the spread of Zika) and maintaining a high level of cooperation (i.e. the proportion of communities that is willing to participate in vector control and surveillance activities). This is because at high levels of coordination, the community-level impact of vector control will be stronger, potentially providing an incentive to not participate to individual communities. This suggests that control of vector-borne diseases such as Zika could, under certain conditions, lead to a situation reminiscent of a tragedy of the commons. Improving vector control operations may thus have to rely not only on a realistic understanding of vector populations, human movement and factors leading to heterogeneous risk of exposure, but also on the social determinants that drive demand (e.g. [52]) for vector control in specific communities.

Data accessibility

Code is available at Dryad: http://dx.doi.org/10.5061/dryad.nn28v [53].

Author's contributions

All authors conceived of and designed the study. C.M.S. and N.H.F. developed the model. C.M.S. performed the simulations. C.M.S. and N.H.F. drafted the manuscript. All authors contributed to the writing of the manuscript and gave their final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by National Science Foundation (NSF) RAPID grant no. 1640951.