Analysis of longitudinal data from animals where some data are missing in SPSS

Abstract

Testing of therapies for disease or injury often involves analysis of longitudinal data from animals. Modern analytical methods have advantages over conventional methods (particularly where some data are missing) yet are not used widely by pre-clinical researchers. We provide here an easy to use protocol for analysing longitudinal data from animals and present a click-by-click guide for performing suitable analyses using the statistical package SPSS. We guide readers through analysis of a real-life data set obtained when testing a therapy for brain injury (stroke) in elderly rats. We show that repeated measures analysis of covariance failed to detect a treatment effect when a few data points were missing (due to animal drop-out) whereas analysis using an alternative method detected a beneficial effect of treatment; specifically, we demonstrate the superiority of linear models (with various covariance structures) analysed using Restricted Maximum Likelihood estimation (to include all available data). This protocol takes two hours to follow.

Introduction

In many laboratory studies using animals, an outcome is measured repeatedly over time (“longitudinally”) in each animal subject within the study. There are a variety of different experimental designs (e.g., before/after, cross-over), different data types (e.g., continuous, categorical; see Box 1 for definitions of terms) and, accordingly, a number of different methods of analysis (e.g., survival analysis, growth curve analysis). Reviews of many of these have been given elsewhere^1–4. Here, we provide a protocol for researchers who obtain quantitative (“continuous variable”) measurements (e.g., number of pellets eaten) at time points common to each animal in an experiment and who are interested in answering questions of the following types: Is there a difference between groups in performance on the task?; Does performance on the task change over time?; Do groups differ in performance on the task at particular times?

Box 1. SPSS Glossary.

• “Categorical”: In SPSS, independent variables may be Ordinal or Nominal. “Ordinal” categories have ordered levels (e.g., Low, Medium, High) whereas “Nominal” categories have no ordering (e.g., experimental drug, vehicle control). The SPSS “mixed model framework” cannot handle dependent variables that are categorical: other software packages must be used (e.g., MLwiN)²² or the “GENLINMIXED” command in SPSS version 19 or later may be used.

• “Compound symmetric”: This “covariance structure” assumes that the errors have equal variance at each occasion and that the errors have equal covariances between all possible pairs of occasions. See also “covariance structure”.

• “Covariate”: This is an independent variable whose influence you are studying. Covariates are any continuous variables you may have obtained that may predict your “Repeated” measure. If a covariate is included in a repeated measures analysis of variance, the analysis becomes a Repeated Measures Analysis Of Covariance (RM ANCOVA). The effect of a covariate is “fixed” if its impact is consistent across animals (e.g., if mouse age predicts task performance) but the effect of a covariate is “random” if its impact varies across animals (e.g., if different mice learn a task at different rates). In vivo researchers often acquire baseline measurements of performance prior to an intervention, and including these as a covariate in the analysis can improve the power of a study by controlling for individual differences in task performance²⁴,²⁵. This is recommended even when researchers randomise animals to intervention (because only in very large groups will randomisation adequately control for mean baseline differences at the level of the group). Even if there is no significant difference between groups in mean baseline measurement, it is still worthwhile including the covariate in the analysis because it accounts for some of the variability in the data: this reduces the residual variability and accordingly improves the power of the analysis to detect other effects (e.g., post-treatment differences in performance between groups). In our Case Study, the covariate was the mean number of foot faults per step measured prior to stroke and treatment.

• “Covariance”: Covariance is a statistical measure of how much two variables change together. “Variance” is the special case of covariance when the two variables are identical.

• “Covariance structure”: Different analytical models make different assumptions about the variance and covariance of the errors and these assumptions can be summarised using notation referred to as “covariance structures”. Real-world longitudinal data can have a range of difference variance and covariance structures and the mixed model framework allows researchers to analyse their data using the covariance structure most appropriate for their data. See also “Compound symmetric”, “Diagonal”, “First-order autoregressive” and “Unstructured”. The complete list can be found by searching SPSS’s “Online Help” for “Covariance Structure” and “Covariance Structure List (MIXED command)”. See Introduction for more information.

• “Diagonal”: The “Diagonal” covariance structure has heterogeneous variances for each repeated measure and zero correlation between other repeated measures. See also “covariance structure”.

• “Error”: See Introduction for a detailed discussion.

• “Estimation methods”: Population parameters (e.g., mean weight of the population of three-month old female rats) need to be estimated from sample data (e.g., weights of 50 three-month old female rats). Different estimation methods exist including “ordinary least squares”, “maximum likelihood” and “restricted maximum likelihood” estimation methods. See Introduction for more details.

• “Factor”: This is an independent variable whose influence you are studying. Factors are categorical and not continuous predictors and have a number of discrete “levels”. For in vivo research, one factor might be “gender”, with two levels (male and female). A factor is “fixed” when each level has a similar slope (e.g., “gender” is a fixed factor if males and female rats learn to perform a task at the same rate over time). A factor is “random” if it varies across levels (e.g., “gender” is a random factor if male and female rats learn to perform a task at different rates over time). Conventional methods of analysis (e.g., RM ANOVA) determine whether one or more fixed factors predict the outcome variable whereas “mixed models” determine whether fixed and random factors predict the outcome variable. In our Case Study, the main factor of interest was treatment group: the four levels were “sham”, “young AAV-NT3”, “aged AAV-NT3” and “aged AAV-GFP”.

• “First-order autoregressive”: This “covariance structure”, also known as AR(1), has homogeneous variances. The correlation between any two other elements is equal to ρ for adjacent elements, ρ² for elements that are separated by one other element, and so on. ρ is constrained so that –1<ρ<1. See also “covariance structure”.

• “Fixed factor”: See “Factor” and “Covariate”.

• “Homogeneity of error variances”: The variance of the errors is said to be homogeneous in a longitudinal data set if they are similar for each group within each “wave” of data.

• “Mixed model”: A mixed model is one which includes both fixed and random factors. Our Protocol uses SPSS’s mixed model framework to access ML and REML estimation methods. For simplicity, we omit random factors from the model: technically, this is not a mixed model but rather a linear model with a variety of covariance structures.

• “Maximum Likelihood” or “ML”: This is a statistical method used to fit a model to data and to estimate the model’s parameters. It does not reject cases where one or more data items are missing. See also “Restricted Maximum Likelihood”.

• “Parameter”: Population parameters (e.g., mean, variance) need to be estimated from sample data. See “Estimation methods” for more details.

• “Random factor”: See “Factor” and “Covariate”.

• “Residual”: Also known as “error”. See Introduction for a detailed discussion.

• “Restricted Maximum Likelihood” or “REML”: This is a statistical method used to fit a model to data and to estimate the model’s parameters. It does not reject cases where one or more data items are missing. Our protocol uses REML estimation because this generates unbiased estimates of the population covariance parameters and is therefore more suitable for comparing linear models with differing covariance structures. Furthermore, REML estimation is preferred to ML estimation where there are smaller numbers of subjects or groups (p.18, ¹⁵) which is likely to be the case in most in vivo studies (e.g., total n<100).

• “Repeated” measure: The dependent variable (or “outcome measure”) you measured longitudinally in each of your animals. (See also “Wave”). In general, measurements can be categorical (e.g., neurological score from A to E) or continuously varying (e.g., animal weight). This protocol requires the Repeated Measure to be quantitative, continuous variables (SPSS refers to these as “scale” variables). At present, SPSS cannot use the mixed model framework to analyse categorical data: other packages must be used (e.g., MLwiN)²² or the “GENLINMIXED” command in SPSS version 19 or later may be used. In our Case Study, the “Repeated Measure” was the mean number of foot faults per step on the “horizontal ladder” behavioural test of sensorimotor function.

• “Scale”: SPSS refers to interval or ratio (continuous) data as “scale”.

• “Subject”: This is the variable which identifies your individual animals. In our Case Study, the variable “rat” was used to identify each subject (from 1 to 53).

• “Unstructured”: This “covariance structure” is the most general and makes no assumptions at all about the pattern of measurement errors within individuals. See also “covariance structure”.

• “Variable”: In SPSS, variables may be “Categorical” or “Scale”. See these terms for more information.

• “Variance”: Variance is a statistical method of the range over which a variable changes. It is a special case of “Covariance” when the two variables are identical.

• “Wave”: Repeated measures are usually obtained in two or more waves². In our Case Study, we obtained eight waves of data. Note one does not include the pre-treatment baseline measure as one of these waves if one is testing the hypothesis that treatment will affect post-treatment performance (see Procedure Step 1): inappropriate inclusion of the baseline data as a post-treatment outcome measure will reduce the chance that an effect of treatment will be detected.

By way of example, in my laboratory we use elderly rats to identify potential therapies that overcome limb disability after brain injury (focal cortical stroke)^5–7. We typically measure sensorimotor performance using a battery of tests weekly for several months after stroke. In one recent study, we used this protocol to examine whether injection of a putative therapeutic into muscles affected by stroke overcomes disability in adult or aged rats, when treatment is initiated 24 hours after stroke⁷. (see ‘Experimental design of the Case Study’, below) Crucially, 3 (out of 53) rats had to be withdrawn near the end of the study due to age-related ill-health (and unrelated to the treatment). Our desire to handle this “missing data” appropriately led us to compare different analytical approaches (including some linear models with advanced methods for estimation of population parameters where data are missing). The goal of our protocol is to introduce readers to using these procedures in SPSS to analyse real-world behavioural data, particularly where some data are missing.

How to handle missing data powerfully and without bias (and why you need to know about estimation methods)

When you obtain measurements from a sample of animals, your goal is often to learn something more general about the population of animals from which the sample was obtained. Statistical algorithms estimate population parameters (e.g., means, variances; Box 1) from sample data, and different algorithms use different estimation methods to do this. Many commonly used methods of analysis use an estimation method called “ordinary least squares” (including, for example, repeated measures analysis of variance; RM ANOVA). This method works well where there are no missing data values and where all animals were measured at all the same time points. (This method was popular historically because one did not need much computer power to perform the calculations.) However, if data is missing for an animal for even a single time point then all data for all time points for that animal are excluded from the analysis^8,9. In a longitudinal study, data can be missing through “drop-out” (where all remaining observations are missing) or as “incidents” (where one or more data points are missed but remaining observations are not missing). Where data are missing, researchers have a dilemma and have to choose whether to omit animals with missing data or whether to estimate (impute) the missing outcome data. Omission of animals causes loss of statistical power (e.g., to detect a beneficial effect of treatment) and may introduce bias that may cause incorrect conclusions to be drawn^1,9–11. Moreover, analysis on an “Intention to Treat” basis requires that all randomised subjects are included in the analysis, even where there are missing data¹⁰. One attempt to deal with missing data is to perform analysis with “Last Value Carried Forward” but analysis using simulated data shows that this method can incorrectly estimate the treatment effect and it can misrepresent the results of a trial, and so is not a good choice for primary analysis¹². Additionally, analysis with “Last Value Carried Forward” implicitly assumes that behavioural data have reached plateau, which may not be the case.

Thankfully, there are alternative estimation methods which can handle missing data effectively^8,9,11 (but require modern computers to perform the iterative calculations). SPSS provides a choice between “Maximum Likelihood” (ML) and “Restricted Maximum Likelihood” (REML) estimation methods. These methods are unlikely to result in serious misinterpretation unless the data was “Missing Not At Random” (i.e., that the probability of drop-out was related to the missing value: for example, where side effects of a treatment cause drop-out)¹². These estimation methods can handle data that are “Missing At Random” (e.g., where the probability of drop-out does not depend on the missing value)¹³. In SPSS, these estimation methods are available by running an analysis procedure called “MIXED”. Our goal is to show readers how to use these modern estimation methods: our Case Study confirms that this approach improved our ability to detect a beneficial effect of our candidate therapy.

Why you need to choose a model carefully

We would encourage readers that are suspicious of apparently “fancy stats” to reflect a moment on the statistics they already know. For example, when we ask a computer to perform a t-test on two groups of sample data, it assumes that the two sample groups came from the same population and then uses an algorithm to calculate a p-value which represents how extreme the sample data is. In order to work at all, the algorithm needs to make some assumptions about the data. For example, analysis of variance (ANOVA) assumes that the measurements are independent of one another. A good researcher will check whether the assumptions are valid or whether they are violated, knowing that this will help ensure he or she chooses a test which balances the risks of false positive and false negative conclusions¹⁴. At the heart of this is the desire to draw conclusions from data that will be reproducible. It can come as a surprise to researchers that many of their statistical analyses depend on a theoretical model and that their inferences may be invalid unless these underlying theoretical assumptions are met. However, this recognition should motivate wise researchers to select an appropriate model with care¹. Our goal is to help readers select between different analytical methods, given a set of data.

Many models exist and the type you choose will reflect the type of question you are trying to answer and the type of data that you have. Longitudinal models can treat time as a categorical variable (a fixed factor: e.g., week) or as a continuous variable (a covariate: e.g., real time; see Box 1). Models that treat time as a continuous variable are sometimes referred to as “growth” models. Some models can even handle covariates that vary over time. A major advantage of models which treat time as a continuous variable is that non-linear models can be built so that curved trajectories can be modelled appropriately² (to learn to build these models in SPSS, see http://www.ats.ucla.edu/stat/spss/seminars/Repeated_Measures/default.htm). Our protocol will demonstrate linear models that treat time as a categorical variable (“wave”) in order to answer the three types of research question posed at the beginning of the Introduction. Specifically, we will show users how to use the “MIXED” procedure to analyse longitudinal data from animals using a linear model with a variety of “covariance structures” (Box 1) and using methods for estimating population parameters that cope with missing data values. (Technically, this is not a “mixed model” as it does not include any random factors; we refer readers to other references that show how to implement true mixed models in SPSS^2,15–20; see Box 2 (Enders’ “SPSS Mixed: Point and Click” article)[AU: Can you provide any further citation information on where this document originates from/where readers can access it/who this is attributable to as I don’t think there’s any information on the document itself?]: www.lawrencemoon.co.uk/resources/Pointandclick.pdf).

Box 2. Recommended Resources.

We recommend two very short articles designed to teach SPSS users to analyse repeated measures data using RM ANOVA and mixed models²⁶,²⁷. SPSS also has a useful set of dynamic tutorials that can be accessed by clicking “Help>Case Studies>Advanced Statistics Option>Linear Mixed Models”.

We have saved in PDF form many of the webpages cited below in case they move or are no longer available (http://www.lawrencemoon.co.uk/resources/mixedmodels2.asp).

David Garson’s on-line resource “StatNotes” is highly recommended, now available through Statistical Associates (http://www.statisticalassociates.com/booklist.htm), including chapters called “Longitudinal Analysis” and “Univariate GLM” (General Linear Model).

There are also some excellent online and residential courses (e.g., http://www.cmm.bristol.ac.uk). Singer and Willett have provided comprehensive theoretical guides for analysing longitudinal data with mixed models²,¹⁸ and several online resources provide a guide to implementing these in SPSS¹⁷ although usually via programming code.

1. Using SAS Proc Mixed to Fit Multilevel Models, Hierarchical Models, and Individual Growth Models: http://www.ats.ucla.edu/stat/spss/paperexamples/singer/default.htm.

2. Textbook examples for Applied Longitudinal Data Analysis: http://www.ats.ucla.edu/stat/examples/alda.htm.

3. Repeated measures analysis with SPSS: http://www.ats.ucla.edu/stat/spss/seminars/Repeated_Measures/default.htm, (2010).

4. Enders’ “SPSS Mixed: Point and Click” http://www.lawrencemoon.co.uk/resources/Pointandclick.pdf

5. Linear Mixed-Effects Modeling in SPSS: An Introduction to the MIXED Procedure: http://www.spss.ch/upload/1126184451_Linear%20Mixed%20Effects%20Modeling%20in%20SPSS.pdf.

6. Painters’ “Designing Multilevel Models Using SPSS” (especially see the Appendix): http://samba.fsv.cuni.cz/~soukup/ADVANCED_STATISTICS/lecture3/texts/SPSSLinearMixedModelsv3.pdf

Don Hedeker’s website is also a rich source of theoretical and practical information concerning longitudinal data analysis in SPSS, available at http://tigger.uic.edu/~hedeker/long.html. Some clustered histological and molecular data from animals has been analysed using mixed models: see the “rat pup” and “rat brain” examples (see ¹⁹ and http://www-personal.umich.edu/~bwest/almmussp.html). A small number of resources provide a click-by-click guide to using SPSS to analyse a variety of linear models¹⁵,²⁸. There is also a free statistics package (InVivoStat: http://invivostat.co.uk/) which can analyse longitudinal data using a mixed model approach (“Repeated Measures Parametric Module”). However, to date, we could not find a resource showing researchers how to analyse longitudinal data from animals where data were missing. Our goal was to fill this gap.

Why you need to know about covariance structures in longitudinal data

When you measure an animal’s performance, there is always some degree of measurement error. As the difference between “true performance” and “measured performance” is unknown and variable, statistical algorithms must make some assumptions about the errors in order to model the “true” trajectory of change. (These errors are also called “residuals” because they account for what is left-over between the model and reality.) For example, many algorithms assume that the errors are normally distributed and independent over time and across persons. However, with longitudinal data, it is likely that the errors for a given individual correlate between measurement occasions (rather than being independent of one another)². Two important issues are: whether the variance of all the errors for all the individuals is similar at each occasion and whether the covariance of these errors for all the individuals is similar between all possible pairs of occasions (see Box 1 for definitions of terms including “variance” and “covariance”). For example, RM ANOVA assumes that the errors have equal variance at each occasion and that the errors have equal covariances between all possible pairs of occasions. This is referred to as assuming that the “covariance structure” has “compound symmetry”⁴ (this a special case of the assumption of “sphericity”¹⁶, p.181). However, much real-world data does not have equal error covariances between time points (e.g., if points are widely separated in time²). Therefore, RM ANOVA is not be suitable for analysis of all longitudinal data and can cause incorrect conclusions to be drawn when the assumption of sphericity is violated (also see TROUBLESHOOTING). Happily, other linear models are highly flexible and can accommodate a wide range of real-world longitudinal data using more general covariance structures. For example, some models make no assumptions at all about the pattern of errors within individuals: this is referred to as assuming “unstructured” covariance structure. The rich variety of models have been reviewed elsewhere (15, p.163)². Our click-by-click protocol will show readers how to select the approach that is best suited for analysis of their data. Again, this is important because it helps researchers avoid drawing false conclusions from their data ^14,16.

How to analyse data using a linear model with general covariance structures

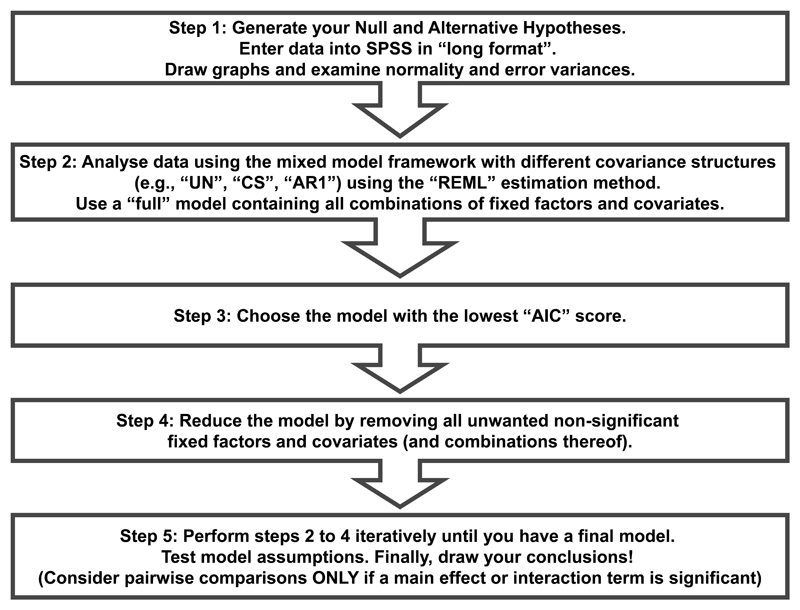
We and others^2,15 recommend a stepwise approach to analysing data using a linear model with different general covariance structures (Figure 1). In stage one, formulate your hypothesis, enter your data into SPSS, explore it graphically and ensure that your data do not violate the assumptions of the linear model. In stage two, analyse your data using a variety of different “full” models (including all combinations of factors and covariates). In our Case Study we will show the results from three different models that vary in the covariance matrix that they assume for the errors, called “Compound Symmetric” (CS), “Unstructured” (UN) and “First-order autoregressive” (AR1) (Box 1). In stage three, decide which of these models best fits your sample data by using a statistic called “Akaike’s Information Criteria” (AIC)¹⁵. AIC takes into account the number of parameters that the model estimates and allows the more parsimonious model to be selected: the smaller the AIC, the better the fit. In stage four, analyse your data using “reduced” models (made more parsimonious by removing combinations of factors and covariates that do not contribute significantly to the model). In stage five, select your model with best-fit to obtain final results upon which to base your conclusions.

Figure 1.

Flow chart showing five-stage approach to analysing longitudinal data where some data are missing

Experimental design of the Case Study

In our Case Study^7,21, stroke was induced in 35 elderly rats (18 months old) and 15 young adult rats (4 months old). This causes a moderate, persistent disability in limb function on the other side of the body⁵. We set out to test the hypothesis that limb disability can be overcome with a gene therapy treatment (an adenoviral vector expressing neurotrophin-3; AAV-NT3) relative to control treatment (AAV expressing green fluorescent protein; GFP). Twenty aged rats were treated with AAV-NT3 and 15 aged rats were treated with AAV-GFP, 24 hours following stroke. We have shown in previous work that young adult rats recover after smaller strokes following treatment with AAV-NT3 relative to AAV-GFP. In the present study we wanted to reproduce these findings and accordingly included as a positive control 15 young adult rats with smaller strokes treated with AAV-NT3. To reduce the number of animals used in the study, no young adult rats were treated with AAV-GFP. Three young adult rats without surgery (“shams”) were also included. To investigate recovery of sensorimotor function following stroke, rats were videotaped while they crossed a 1 m long horizontal ladder with irregularly spaced rungs. Any paw slips or rung misses were scored as foot faults. The mean number of foot faults per step were calculated and averaged for each limb for three runs each week. Each rat was assessed weekly for eight weeks. Three aged rats had to be killed humanely by overdose of anaesthetic two or three weeks before the end of the study because of tumours that are common in this strain of elderly rat. These data can be considered “Missing Completely at Random” because drop-out occurrences were unrelated to the missing data items¹². All procedures were carried out in accordance with the Animals (Scientific Procedures) Act of 1986, using anaesthesia and postoperative analgesia, in accordance with relevant governmental legislation and regulations and with Institutional approval. All surgeries and behavioural testing were conducted using a randomized block design. Surgeons and assessors were blinded to treatment.

The future

It is simply not possible to give an in-depth, comprehensive overview of this enormous field. We encourage readers to suggest improvements and additional protocols via the interactive Feedback / Comments link associated with this article on the Nature Protocols’ website. Links to additional resources are equally welcome: we have provided a list of resources relevant to SPSS users in Box 2 including datasets and other protocols. Ultimately, the key goal of research is to draw conclusions from data that will be reproducible. Proper use of statistics can inform a researcher’s decision whether or not to plough additional resources (time, and money) into a project. We hope this protocol enables scientists to use animals optimally in basic and preclinical research.

Materials

EQUIPMENT

• A computer with SPSS/PASW (IBM) version 18 or later.

CRITICAL: There is no need for special configuration. However, some of the analyses involve iterative computation and therefore the more powerful the processor, the quicker results will be obtained.

CAUTION Screenshots presented in this protocol were obtained using a PC running SPSS/PASW version 18 or later. Versions of SPSS earlier than version 11 may not be able to run these linear models at all, or may generate different results. SPSS version 19 or later can run generalized linear mixed models (GENLINMIXED).

EQUIPMENT SETUP

• Download data files. To work through our Case Study, download the “short format” and “long format” data files from Supplementary Tutorial (slide 3) [AU: Edits correct? Slide number correct?] or from www.lawrencemoon.co.uk/resources/linearmodels.asp.

CAUTION All experiments performed using animals must be performed in accordance with relevant governmental legislation and regulations and with Institutional approval.

Procedure

Reflect upon your experimental design · TIMING 15 minutes if novice, 5 minutes if experienced.

• 1Specify your Null and Alternative hypotheses. This will help you decide what statistical tests to select and run. For our Case Study, we framed our hypotheses as follows:

  Null hypothesis: After controlling for individual differences in baseline performance on the ladder test, there will be no difference in post-treatment performance (from weeks 1 to 8) between the group of aged rats with stroke treated with AAV-NT3 and the group treated with AAV-GFP.

  Alternative hypothesis: After controlling for individual differences in baseline performance, there will be a significant improvement in post-treatment performance (from weeks 1 to 8) by the group of aged rats with stroke treated with AAV-NT3 compared to the group treated with AAV-GFP.

• 2Recognise the variables in your study using the SPSS terms defined in Box 1. In our Case Study, “Subjects” were rats, the “Repeated” measure obtained was the number of foot faults on the horizontal ladder test, and 8 “Waves” of measures were obtained after treatment in addition to a baseline performance measure which will be used as a “Covariate”. There was one “Fixed factor” (group) with four levels (aged AAV-NT3, aged AAV-GFP, young AAV-NT3 and sham).

Loading data and understanding data structure in SPSS · TIMING 10 minutes if loading a file; longer if entering data manually.

• 3Open SPSS. Click “Cancel” (Supplementary Tutorial, slide 1). We will analyse the data from our Case Study first using RM ANCOVA and then using the MIXED procedure to implement linear models with general covariance structures and an estimation method known as REML (Figure 1). To jump to the MIXED procedure directly and to skip RM ANCOVA, go to Step 26. In SPSS, longitudinal data has to be arranged in “short format” for RM ANCOVA but in “long format” for the MIXED procedure (although formats can be interconverted using Data>Restructure; see Supplementary Tutorial, slides 75-82).
• 4To open our “short format” Case Study datafile for analysis by RM ANCOVA, click “File>Open>Data>short_format.sav” and click “OK” (Supplementary Tutorial, slides 2 and 3). This will open in “Data View” (Supplementary Tutorial, slide 4 and Figure 2a). You will see that “short format” requires all outcome measures from a given “Subject” (rat) to be entered on a single row.
• 5Click the “Variable View” tab at the bottom left (Supplementary Tutorial, slide 4). You will see each line corresponds to a variable (Supplementary Tutorial, slide 5). In the penultimate column these are specified as either Categorical (“Nominal” or “Ordinal”) or “Scale” (see Box 1). In our Case Study, the variables are either “Nominal” categorical (rat, group) or “Scale” (mean_preop, mean_postop1 to 8). These specifications are important, including for the purposes of drawing graphs in SPSS. You will see missing values are coded as a number which falls outside of the measurement range (coded here as “999.00”). Click on the cell at the intersection of the “Values” column and the “group” row (Supplementary Tutorial, slide 5). This reveals the names of the Levels of your Factor “group” (Supplementary Tutorial, slide 6). Click “Cancel” to go back without changing anything.
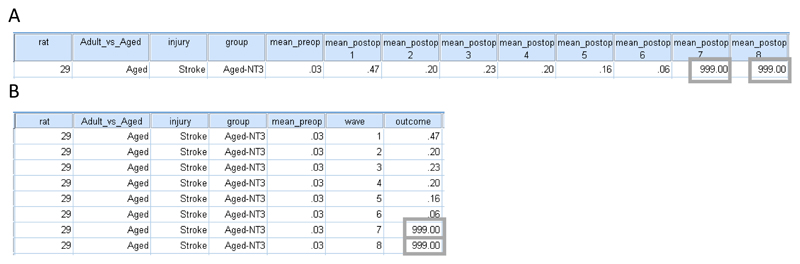
• 6Click the “Data View” tab at the bottom left and scroll down through your lines of data. You will see that missing values for rats 29, 33 and 52 are coded 999.00 (Supplementary Tutorial, slide 7 and Figure 2a).
• 7To open our “long format” Case Study datafile for analysis using the “MIXED” procedure, click “File>Open>Data>long_format.sav”. In “Data View” you will see that “long format” involves one outcome measure (from one animal) per line so that all outcomes from a single animal occupy multiple lines and that the baseline measure is entered identically on each line. For our Case Study, each animal occupies eight lines and the baseline measure “mean_pre-op” is entered identically on each of these eight lines (Supplementary Tutorial, slide 8 and Figure 2b).
• 8Click “Variable View” (Supplementary Tutorial, slide 9). You will see that, as before, “group” is a Nominal categorical variable and “mean_preop” is a Scale (continuous) variable. In long format, the Repeated Measure is “outcome” with multiple “waves” of data per animal. “Wave” is defined as an “Ordinal categorical” variable because it has a rank order (Box 1).

Figure 2.

Screenshots showing arrangement of data in SPSS. (A) short and (B) long formats. The eight measurements for a single animal (rat 29) are shown. Missing data are entered as a value lying outside of the dataset, here 999.00 (grey boxes). All experiments using animals were performed in accordance with relevant UK legislation and regulations and with Institutional approval.

Graph and explore your data - TIMING 45 minutes if novice, 20 minutes if experienced.

• 9Graphs are easily generated using data arranged in long format. To generate graphs showing the performance of individual animals over time, click Graph>Chart Builder (Supplementary Tutorial, slide 10). At the warning window, click OK (see Supplementary Tutorial, slide 11). Under the “Gallery” tab, click on “Line” and drag the second icon (bearing three lines) into the “Chart preview” window at the top (Supplementary Tutorial, slide 12). Drag your Repeated Measure (“outcome”) into the “Y-axis?” box and “wave” into the “X-axis?” box. Drag “rat” into “Set color” box. Click on “Groups/Point ID” tab and click on the box marked “Rows panel variable” (a tick should appear). Drag “group” into “Panel?” box (Supplementary Slideshow, slide 13). Click “OK”. A new window called “Output” should appear. Scroll down to see graphs of individual rat performances over time arranged by group and colour coded according to rat identity number (Supplementary Tutorial, slide 14).
• 10To generate graphs showing the mean performance of each group over time, click Graph>Chart Builder and at the warning window, click OK. Click on “Groups/Point ID” tab and, by clicking, remove the tick from the box marked “Rows panel variable”. Drag “group” over to the “Set color” box and it will replace “rat”. In the right hand “Element Properties” panel, ensure “Mean” is selected from the “Statistic” drop-down box and place a tick in the box marked “Display Error bars”, click on the radio button marked “Standard Error”, change the “Multiplier” to 1 (to indicate plus or minus one standard error) and click “Apply” (Supplementary Tutorial, slides 15-17). Click OK.
• 11We saw in the Introduction that analytical models have to make assumptions about the variance and covariance of the residuals at different time points. We will test some of these assumptions here and then we will test some other assumptions once the final model has been chosen (Steps 24 and 25). To test whether the variance of groups is similar at each occasion (so-called “homogeneity of group variances”), we can look at box plots of the data. Click on GRAPH>CHART BUILDER (Supplementary Tutorial, slide 18). At the warning window, click OK (see Supplementary Tutorial, slide 19). Under the “Gallery” tab, click on “Box Plot” and drag the middle icon (bearing blue and green box plots) into the “Chart preview” window at the top (Supplementary Tutorial, slide 20). Drag “outcome” into the “Y-axis?” box, drag “group” into the “X-axis?” box and drag “wave” into the box marked “Cluster on X: set color” (Supplementary Tutorial, slide 21). Then click “OK”. In the Output window, you should see your box plot (Supplementary Tutorial, slide 22). To modify this graph, double-click on the graph and the “Chart Editor” will open (Supplementary Tutorial, slide 23). Double click on one of the box plots and the “Properties” window will open (Supplementary Tutorial, slide 23). Click on the “Chart size” tab and adjust the Width to 600. Now click on the “Bar Options” tab and move the slider for “Bar size” up to 100% (Supplementary Tutorial, slide 24). Click “Apply” and then Click “Close” (Supplementary Tutorial, slide 25). The Box Plots for our Case Study (Supplementary Tutorial, slide 26) show similar variances for Aged-NT3 and Aged-GFP groups and smaller variances for Young-NT3 and Sham groups. These variances are reasonably similar, however (e.g., not more than 10-fold different). Further, within each group, there is not much change in variance over time. Accordingly, the assumption of similar group variances is reasonable. Circles with numbers (e.g., 150) identify outliers by data line number.

CRITICAL STEP: If Box Plots of your data show highly dissimilar variances between groups, double check that your data is entered correctly, being particularly thorough with outliers.

?TROUBLESHOOTING

• 12To assist with selection of a covariance structure, we can look at our sample data to see how the time points correlate with each other (p.207, ¹⁶). We recommend doing this for all the data considered together (omit Step 13 and follow Step 14) rather than for each group separately (follow Steps 13 and 14) because in many in vivo studies, the number of animals per group may be too small for a group-wise analysis to be powerful. Load a data file in “short format” (using File>Open).
• 13OPTIONAL: Click “Data>Split File” (Supplementary Tutorial, slide 27). Click on “Organise output by groups” and drag “group” to the “Groups based on” window (Supplementary Tutorial, slide 28).
• 14The correlation structure between each pair of time points is calculated by clicking “Analyze>Correlate>Bivariate” (Supplementary Tutorial, slide 29). Drag all your outcome measurements into the “Variables” window. Click on “Options” and ensure the radio button “Exclude cases pairwise” is pressed for “Missing Values”. Click “Continue” and ensure “Pearson” is ticked (Supplementary Tutorial, slide 30). We will postpone consideration of the results (Supplementary Tutorial, slide 31) until ANTICIPATED RESULTS.

Analyse data using Repeated Measures Analysis of Covariance - TIMING 30 minutes if novice, 15 minutes if experienced.

• 15There are two ways to analyse data in SPSS: via point-and-click or via Syntax (Box 3). We will start with point-and-click and will consider Syntax later. As noted above, RM ANCOVA requires data to be in short format. To open our “short format” Case Study datafile for analysis by RM ANCOVA, click “File>Open>Data>short_format.sav” and click “OK” (Supplementary Tutorial, slides 2 and 3).
• 16Click Analyze>General Linear Model>Repeated Measures (Supplementary Tutorial, slide 32). Enter “wave” as “Within-Subject Factor Name” and enter the number of waves of data that you collected for each animal in “Number of Levels” then click “Add” and “Define”. In our Case Study, we had eight waves of data, so we entered “8” as the “Number of Levels” (Supplementary Tutorial, slide 33).
• 17Now drag your baseline measurement to the “Covariates” box. Drag your outcome measurements to the “Within-Subjects Variables” box. A good way to do this (if all the waves are consecutively ordered) is to click on the first wave and then Shift-click on the last wave. Now drag them over. Now drag your Factor(s) of interest to “Between-Subjects Factor(s)”. In our Case Study, the baseline measurement was “mean_preop”. We had 8 waves of data named mean_postop1 to mean_postop8. We had one factor of interest, “group”, which had four levels (Supplementary Tutorial, slide 34).
• 18One assumption of RM ANCOVA is that the errors (“residuals”) come from a normal distribution. To test this assumption (in Step 24) we need to save the computed residuals. Click “Save” and click “Unstandardised” in the Residuals box (Supplementary Tutorial, slide 35) before clicking “Continue”.
• 19Click “Options”. To obtain means and pairwise comparisons for any significant effect of group or wave then click “(OVERALL)” and Shift-click the bottom item in the list. Drag these to “Display Means for:” and click on the box marked “Compare main effects” (a tick should appear). Leave “Confidence interval adjustment” as the default setting “LSD(none)” (Supplementary Tutorial, slide 36). See Box 4 for rationale for selecting “LSD(none)” and for more information. When using point-and-click, SPSS allows you to perform pairwise comparisons for main effects (e.g., group or wave) but does not allow you to perform pairwise comparisons for any means defined by significant interaction terms (e.g., group by wave). Instead, the latter can be generated using Syntax and we will return to this in step 21.
• 20Another assumption of RM ANCOVA is “homogeneity of error variances” (see Introduction). To test this assumption, click on the box marked “Homogeneity tests” (a tick should appear) (Supplementary Tutorial, slide 36) and “Continue”. This tells SPSS to run Levene’s tests to check whether groups have similar variances for each wave.
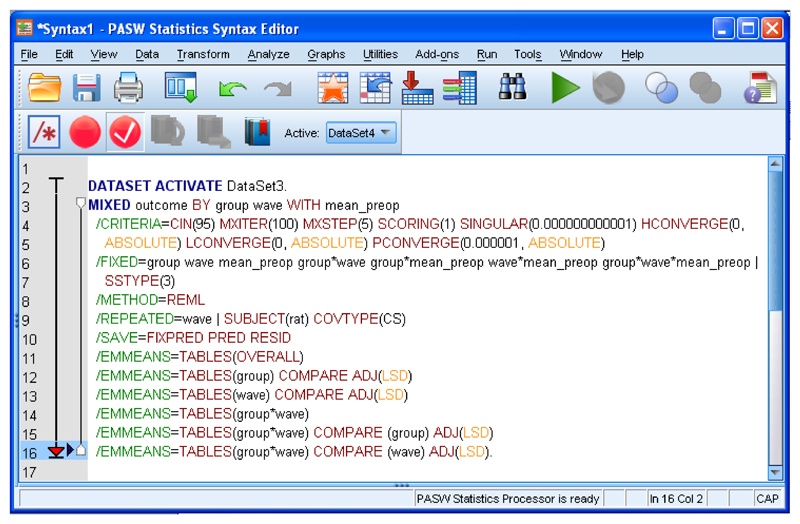
• 21Let’s also ask SPSS to perform pairwise comparisons for means defined by any significant interactions. This cannot be done through point-and-click, so it is necessary to enter this as Syntax. Click “Paste”. This opens a new window listing the Syntax you have already created (Supplementary Tutorial, slide 37). Delete the final full stop (period). On the next lines, type the following, including the full stop on the last line.

  • /EMMEANS=TABLES(group*wave) WITH(mean_preop=MEAN)COMPARE (group) ADJ(LSD)

  • /EMMEANS=TABLES(group*wave) WITH(mean_preop=MEAN)COMPARE (wave) ADJ(LSD).

  The first line generates a table listing pairwise comparisons between each group for each wave of data. The second line generates a table listing pairwise comparisons between each wave of data for each group. For example, in our Case Study, the first line will generate comparisons that allow the experimenter to decide whether AAV-NT3 and AAV-GFP differed in performance at wave 1 or 2 or 3, etc. The second line will generate comparisons that allow the experimenter to decide whether performance of the AAV-NT3 differed between wave 1 and 2, etc. (Supplementary Tutorial, slide 38).

  For more information, see http://www.ats.ucla.edu/stat/spss/faq/sme.htm and

  http://www.ats.ucla.edu/stat/spss/seminars/Repeated_Measures/default.htm.

Box 3. How to get the most out of SPSS using Syntax.

• When you use the point-and-click interface in SPSS, the computer generates syntax behind-the-scenes, and it is this syntax that SPSS uses for analysis. You can view the syntax you are currently generating by clicking “Paste”. Save Syntax for future use by clicking “File>Save”.

• Any Syntax that you have saved or downloaded can be loaded directly. Click “File>Open>Syntax” and navigate to the folder containing your Syntax. Click on the item and click “Open” and then “Run>All”. Syntax for analysing our Case Study data can be downloaded from www.lawrencemoon.co.uk/resources/linearmodels.asp. Syntax for analysing other Case Studies can be downloaded from various webpages (see Box 2).

• Syntax can also be copied from peer-reviewed publications (see Box 2). Click “File>New>Syntax”. Then simply enter syntax (making sure there is only one full stop/period, at the end). Click “Run>All”.

Box 4. How to enhance analytical power whilst striving for reproducibility.

A result is deemed significant when the analysis returns a p-value which is less than the threshold for significance, alpha, which is conventionally set to 0.05. When making multiple statistical comparisons on a single data set, analysts increase their risk of drawing false positive conclusions. This protocol recommends the use of statistical tests appropriate for multiple groups (RM ANCOVA and mixed models) and if these show significant effects or interactions, then secondary pairwise comparisons are warranted. SPSS offers three options for pairwise comparisons: a “Least Significant Differences” (LSD) method that does not control for multiple testing and “Sidak” and “Bonferroni” methods which do.

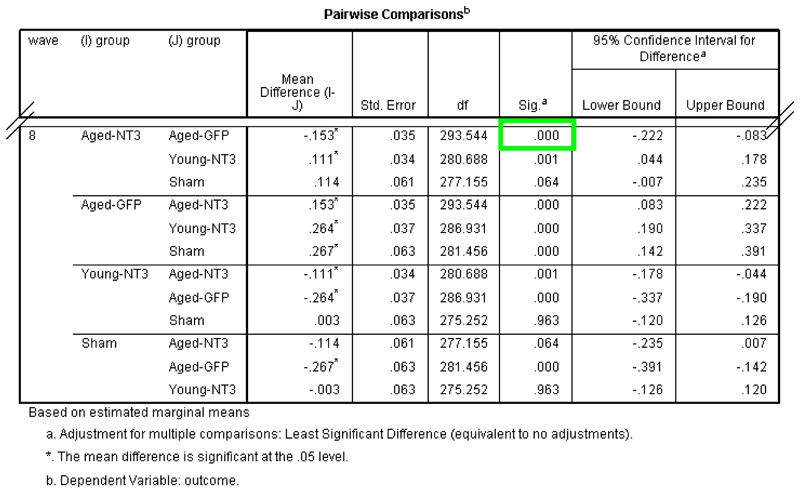
In longitudinal studies with animals, researchers may be interested to know whether particular groups differed one from another at particular times. Statistically, this is warranted if there is a significant interaction of “group” with “wave”. However, this may involve a large number of pairwise comparisons. In our Case Study, eight waves of data for four groups of rats would result in 48 unique pairwise comparisons. The Bonferroni method involves adjusting the threshold for significance by dividing by the number of tests conducted: in our Case Study, this would mean that the p-value for any one comparison would have to be <0.00104 to reach significance. Thus, the Bonferroni (and the related Sidak) corrections are very conservative. Researchers can avoid “throwing out the baby with the bathwater” by specifying a priori what pairwise comparisons are of primary interest. We recommend that you instruct SPSS to perform pairwise comparisons using the LSD method, and then manually divide the resulting p-values of interest by the number of tests scrutinised. For example, in our Case Study, we were interested a priori in knowing whether the two aged groups had similar deficits one week after stroke surgery (as a surrogate measure of similar mean lesion volumes) and then at what time thereafter (if any) they differed one from another: this involved eight pairwise comparisons, so we divide the threshold for significance for the eight comparisons of interest by 8 (i.e., 0.00625).

CAUTION It is vital to recognise these two lines of code can generate an enormous number of pairwise comparisons and the experimenter is at risk of drawing false positive conclusions due to an inflated Type I error. See Box 4 for tips on how to avoid this.

• 22Save this Syntax for future use by clicking “File>Save” and then selecting an appropriate file name. See Box 3 for tips on how to re-load and run this Syntax in the future.
• 23You can now run your analysis. Ensure the Syntax window is uppermost and active. Click “OK”. Click “Run>All”. The results of the analysis will be placed in a new “Output” window. For assistance with interpreting SPSS output (Supplementary Tutorial, slides 41 – 45), see ANTICIPATED RESULTS.
• 24It is advisable to run some diagnostic checks to determine whether the assumptions of the model are met. Residuals were saved in Step 18. To check the assumption that the errors (residuals) come from a normal distribution, we recommend plotting a histogram. Click Graph>Chart Builder>OK. Click on Gallery>Histogram and drag the “Simple Histogram” icon into the “Chart Preview” window. Now drag “Residual for mean_postop 1” into the “X-axis?” box. In the “Element Properties” window, put a tick in the box next to “Display normal curve” and click “Apply” (Supplementary Tutorial, slide 39). Click “OK”. Inspect the histogram for deviations from normality (see below). Repeat this for each set of residuals (e.g., Residual for mean_postop 2, etc.) In our Case Study, there were eight sets of residuals (one for each wave of data). The residuals for mean_postop 1 appear to have come from a normal distribution (Supplementary Tutorial, slide 40). Laboratory experiments tend to have relatively low numbers of independent subjects (typically, number of animals <50) and accordingly histograms will rarely appear perfectly normal.

CRITICAL STEP: Distributions are non-normal if they do not follow a bell-shaped (“Gaussian”) distribution: non-normal distributions may have more than one peak, appear skewed or have extreme kurtosis.

?TROUBLESHOOTING

• 25To check the assumption that the group variances are similar, we recommend generating box plot diagrams (Step 11) and using Levene’s test (Step 20). See ANTICIPATED RESULTS for a guide on how to interpret these results.

CRITICAL STEP: RM ANCOVA is robust to differences between groups in variance but if the ratio of the largest to smallest group variance exceeds 10, then there is a substantial violation of the assumption of homogeneity of variances (see for more information http://www.statisticalassociates.com/assumptions.pdf)

?TROUBLESHOOTING

Analyse data using linear models with general covariance structures - TIMING 30 minutes per model for novices, 10 minutes per model for the experienced.

• 26We next show how to use SPSS’s “MIXED” procedure to analyse longitudinal data from animals using a “linear model with general covariance structure” because this procedure provides access to estimation methods that can handle missing data effectively. You will recall that these models require data to be arranged in “long format”. To open our Case Study data file, click “File>Open>Data>long_format.sav”. Alternatively, short format data can be restructured (Supplementary Tutorial, slides 75 - 82).
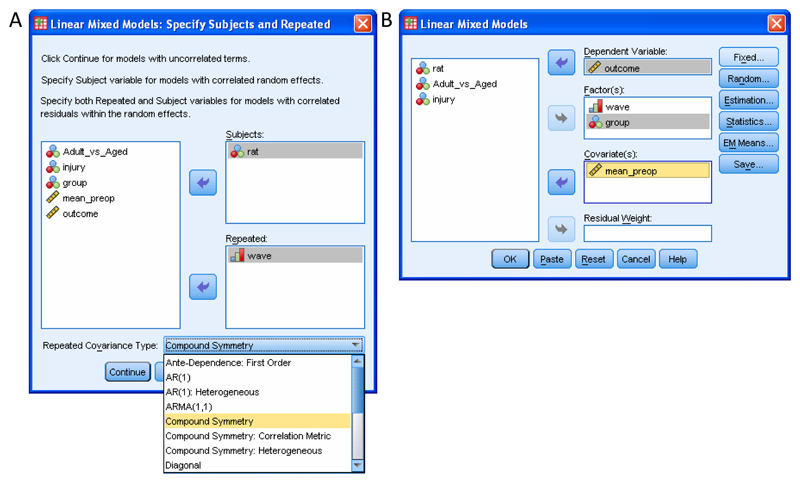
• 27Click Analyze>Mixed Models>Linear (Supplementary Tutorial, slide 46). This invokes the “MIXED” procedure. Click on the variable which identifies the entities (usually animals) that you obtained repeated measurements from, and drag this into “Subjects:”. Next, click on the variable which identifies the testing sessions and drag this into “Repeated” (Supplementary Tutorial, slide 47 and Figure 3a). In our Case Study, the variable “rat” was used to identify each subject and the variable “wave” was used to identify the session of testing. Wave had eight levels, corresponding to the eight post-treatment testing sessions. Note that the baseline testing session is not included as we are testing the hypothesis that post-treatment performance differs between groups after controlling for differences in baseline.

Figure 3.

Screenshots showing SPSS windows involved in specification of a model using the “MIXED” procedure. (A) Specification of the variable which identifies the subjects in the study (“rat”) and the variable which identifies the sessions during which repeated measurements were obtained (“wave”). Covariance structure is specified from the drop-down window. (B) Specification of the dependent variable (“outcome”) and the factor(s) and covariate(s) (“group”, “wave” and “mean_preop”) that are hypothesised to affect the dependent variable.

CAUTION This protocol requires the Repeated Measure to be quantitative, continuous data (SPSS refers to these as “Scale”) and not “categorical” data. At present, SPSS cannot use the “MIXED” procedure to analyse categorical data: other packages must be used (e.g., MLwiN)²² or the “GENLINMIXED” command in SPSS version 19 or later may be used. GENLINMIXED may also be used to fit linear models with general error covariance structures and different variance components for different groups of cases (Supplementary Tutorial, slide 83).

• 28Click on the drop-down menu labelled “Repeated Covariance Type”. The default is “Diagonal” (see Box 1). We recommend comparing different covariance structures, starting with “Compound Symmetry”¹⁶ because this covariance structure is similar to that assumed by RM ANCOVA (see Introduction). Select “Compound Symmetry” (Supplementary Tutorial, slide 47 and Figure 3a). Later, for comparison, you can also select “Unstructured” and “First-order autoregressive” or any of the other covariance structures (See Box 1).
• 29Optional: Clicking “Help” at this point provides a list of all covariance structures available in SPSS. Additionally, search SPSS’s “Online Help” for “Covariance Structure” and “Covariance Structure List (MIXED command)”.
• 30Click on “Continue”. In the new window, drag your Covariate(s) (e.g., baseline measurement) to the “Covariates” box and drag your outcome measure to the “Dependent Variables” box. Now drag your Factor(s) of interest to “Factor(s):”. In our Case Study, the baseline measurement was “mean_preop” and the dependent variable was “outcome”. We are interested to know whether ladder performance depended on “group” or “wave” and whether there was an interaction of group with wave. Accordingly we dragged both of these to “Factor(s)” (Supplementary Tutorial, slide 48 and Figure 3b).
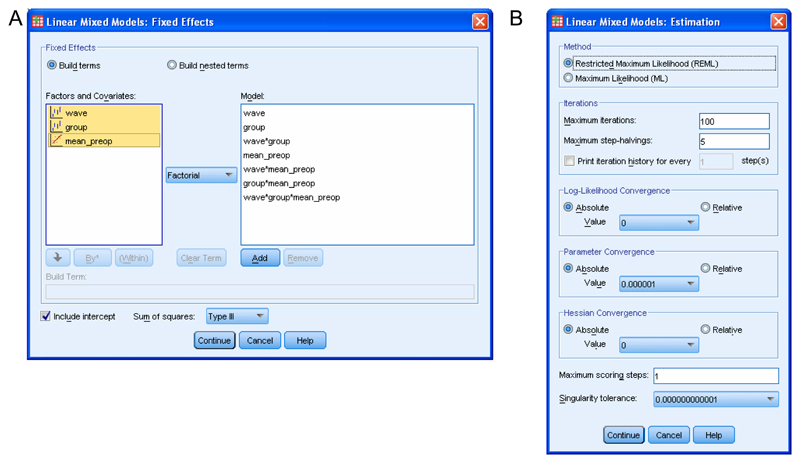
• 31Now click “Fixed”. You will see a list of your Factor(s) and your Covariate(s). This allows you to specify which covariate(s), which factor(s) and which combination of factors (if any) account for differences between animals in their test performance. We recommend that you include all factors, covariates and interactions thereof in the model to start with (referred to as a “Full model”). Factors, covariates and combinations thereof that the analysis does not identify as significant can be removed from subsequent models if desired^2,19 (see http://www.statisticalassociates.com/longitudinalanalysis.htm and ANTICIPATED RESULTS for more information). Ensure the drop-down menu in the middle of the screen shows “Factorial” (the default). Click on your first factor and Shift-click on your last factor. Now click “Add”. (Supplementary Tutorial, slide 49 and Figure 4a). Click “Continue”. We omit “Random” factors and covariates from this analysis for reasons given in the Introduction and Anticipated Results sections.
• 32Click on “Estimation”. Click the radio button next to “Restricted Maximum Likelihood (REML)” (Supplementary Tutorial, slide 50 and Figure 4b) and click “Continue”. (See Introduction and Box 1 for more information).
• 33Click on “EM Means”. In the new window labelled “Factor(s) and Factor Interactions”, click “(OVERALL”), then Shift-click the last factor in this list and click the blue arrow pointing right. Now click on the box marked “Compare main effects” and a tick should appear. Leave “Confidence Interval Adjustment” as “LSD (none)” (the default). (Supplementary Tutorial, slide 51 and Figure 5a). See Box 4 for more information. Click on “Continue”. This step asks SPSS to perform pairwise comparisons between group means for any significant effects.
• 34Next, save the values predicted by the model (and the residuals) so that you can graph them later. Click on “Save”. In the new window, below “Fixed predicted values:” put a tick next to “Predicted Values” and below “Predicted Values & Residuals:” put a tick next to “Predicted Values” and “Residuals” (Supplementary Tutorial, slide 52 and Figure 5b) (p. 220, ¹⁶).
• 35You could just click “OK” to run the analysis but let’s also ask SPSS to run pairwise comparisons between means defined by any significant interaction(s). This cannot be done through point-and-click, so it is necessary to enter this as Syntax. Click “Paste”. This opens a new window listing the Syntax you have already created (Supplementary Tutorial, slide 53). Delete the final full stop (period). On the next lines, type the following, including the full stop on the last line.

  • /EMMEANS=TABLES(group*wave) COMPARE (group) ADJ(LSD)

  • /EMMEANS=TABLES(group*wave) COMPARE (wave) ADJ(LSD).

  The first line generates a table listing pairwise comparisons between each group for each wave of data. The second line generates a table listing pairwise comparisons between each wave of data for each group. For example, in our Case Study, the first line will generate comparisons that allow the experimenter to decide whether AAV-NT3 and AAV-GFP differed in performance at wave 1 or 2 or 3, etc. The second line will generate comparisons that allow the experimenter to decide whether performance of the AAV-NT3 differed between wave 1 and 8. (Supplementary Tutorial, slide 54 and Figure 6). See, for more information, http://www.ats.ucla.edu/stat/spss/faq/sme.htm and http://www.ats.ucla.edu/stat/spss/seminars/Repeated_Measures/default.htm.

Figure 4.

Screenshots showing SPSS windows involved in defining the model. (A) Specification of the factor(s), covariate(s) and interactions thereof that are hypothesised to affect the dependent variable. (B) SPSS allows users to estimate parameters using either Maximum Likelihood or Restricted Maximum Likelihood, by iteration to convergence based on the parameters and variables specified in the lower panels.

Figure 5.

Screenshots showing SPSS windows involved in developing the linear model. (A) How to obtain pairwise comparisons of any significant factor(s), and (B) how to save a list of the model-based predicted and residual values.

Figure 6.

Screenshot showing SPSS Syntax window defining linear model estimated using REML and with two additional lines of code requesting pairwise comparisons for the interaction of group by wave.

CAUTION! It is vital to recognise these two lines of code can generate an enormous number of pairwise comparisons and the experimenter is at risk of drawing false positive conclusions due to an inflated Type I error. See Box 4 for tips on how to avoid this.

• 36Save this Syntax for future use by clicking “File>Save”.
• 37To run this Syntax, click “Run>All”. (See Box 3 for tips on how to re-load and run this Syntax in the future.)

CRITICAL STEP: Warning messages regarding iteration convergence require additional action (see Troubleshooting, Table 1).

Table 1. Troubleshooting.

Step	Problem	Possible reason	Solution
11	Box Plot ranges are highly dissimilar	Group variances are highly dissimilar	If group variances differ by, say, more than threefold then there is increased risk of drawing false positive conclusions from the data, especially where group sizes differ (See StatNotes, Box 3). SPSS is not easily able to make adjustments for violations of this assumption. Transforming data (e.g., log transformation) may make variances more similar. See “42 or 43” below.
24	Histogram of a set of residuals appears non-normal	Residuals may not follow a normal distribution	RM ANCOVA is robust in the face of moderate deviations from this assumption but may not be valid if histogram of residuals shows extreme kurtosis or skew (See StatNotes, Box 3).
25	Levene’s test is significant for one or more wave of data	Group variances are highly dissimilar.	RM ANCOVA is robust in the face of moderate deviations from this assumption if the study is balanced. However, if group variances differ by, say, more than threefold then there is increased risk of drawing false positive conclusions from the data. SPSS is not easily able to make adjustments for violations of this assumption. Transforming data (e.g., log transformation) may make variances more similar. See “42 or 43” below.
37	“Iteration was terminated but convergence has not been achieved. The MIXED procedure continues despite this warning. Subsequent results produced are based on the last iteration. Validity of the model fit is uncertain.”	Algorithm was not able to fit your sample data according to the criteria you specified. Model may be over-parameterised (for example, you may have specified a factor that is redundant).	Reanalyse the model using a simpler covariance structure that requires fewer parameters to be estimated (p.295 19). Alternatively, try a model with fewer covariates, factors and/or interactions. You can also try changing the variables in the Estimation window: try increasing the “Maximum interations” or increasing the “Parameter convergence value” (page 217 16) See also StatNotes (Box 3).
37	“The final Hessian matrix is not positive definite although all convergence criteria are satisfied. The MIXED procedure continues despite this warning. Validity of subsequent results cannot be ascertained.”	Algorithm was not able to fit your sample data according to the criteria you specified in the Estimation window.	Re-run the analysis but after clicking on Estimation, increase the “Maximum scoring steps”, for example to 5 (page 217 16). See also StatNotes (Box 3).
41	The residuals do not appear to come from a normal distribution (histogram or Kolmogorov-Smirnov / Shapiro-Wilks tests).	Skewed data (perhaps lots of ceiling or floor values: does your test have a fixed upper and lower score?)	Data that shows a skewed distribution may benefit from transformation prior to analysis. Slight deviations from normality will likely be tolerated. Methods for analysing non-normal longitudinal data can be found elsewhere22.
42 or 43	Plots or Levene’s test indicates that some groups have bigger variation of the residuals than others	Data genuinely has greater spread in some groups than in others.	If the sample size is small (<100), as is usually the case in in vivo studies, then the evidence may not be reliable (p.132 2). At present SPSS cannot fit models which allow groups to have different covariance parameters and other packages must be used19. For ways to deal with non-similar variances between groups or over time, see 23, available from Don Hedeker’s website (Box 3).
Anticipated Results	I have run a RM ANOVA / RM ANCOVA and Mauchly’s test has a p value less than 0.05.	Evidence that the errors do not have a “compound symmetry variance/ covariance structure” (i.e., is not “spherical”). The assumption of sphericity is likely to be violated if there are long intervals (as the covariance between distant points most likely will be less similar than proximal points)	Mauchly’s test is very sensitive and should be handled with caution. If Mauchly’s test provides strong evidence against sphericity then one has a number of options. One can base one’s conclusions on an adjusted F-ratio (e.g., using the Greenhouse-Geisser correction) 15(p.143). Alternatively, one can base one’s conclusions on the Multivariate Analysis of Variance (MANOVA) output which only assumes an unstructured error covariance structure (StatNotes, Box 3). However, our recommended approach would be to use a linear model which allows you to choose the error covariance structure with best fit.

? TROUBLESHOOTING

• 38The Output window should contain the results from your new model. You should now re-analyse the data using at least two other covariance structures (e.g., “unstructured” and “first-order autoregressive”). In other words, re-run Steps 27-37 and choose different covariance structures at Step 28. You would then select the model with lowest AIC. Effects and interactions that do not account for significant variation may be removed (at step 31) to make the model more parsimonious. We provide an introduction to interpreting SPSS Output in ANTICIPATED RESULTS.
• 39OPTIONAL: One can formally test whether one model is a significant improvement over another, by comparing their “-2 Log Likelihood” Information Criteria (Supplementary Tutorial, slides 57-59) using a Chi squared test. Click “Transform>Compute Variable” (Supplementary Tutorial, slide 57) and then in “Function group” click “CDF and noncentral CDF” and then in the “Functions and Special Variables” box click “Cdf.Chisq”. Now click the blue “up” arrow and “CDF.CHISQ(?,?)” will appear in the “Numeric Expression” window. Type “1-“ before this (Supplementary Tutorial, slide 58). By hand, calculate the difference between the -2LL scores of the two models you wish to compare. Enter this as the first “?”. Now calculate the difference between the number of parameters of these two models: if ML was used then enter the difference between the number of fixed plus covariance parameters and if REML was used then enter the number of covariance parameters only. Enter this as the second “?”. Now enter “Improvement” as the “Target Variable” name and click “OK”. Look in the “Data View” for a new column called “Improvement” containing your result (Supplementary Tutorial, slide 59). For example, our first full model with CS covariance structure had a -2LL of -711 (66 parameters) and our second full model with unstructured covariance structure had a -2LL of -738 (100 parameters). The chi squared test gives p=0.80 (Supplementary Tutorial, slide 59) which provides no statistical evidence that the first model is a better model. This is not surprising, given the large difference in the number of parameters estimated and the relatively small difference in -2LL (2 p. 122). Nevertheless, because the second model has a smaller AIC and requires many fewer parameters to be estimated, we opt to proceed with the first model.

CAUTION! This option is only appropriate when one model is “nested” within the other (i.e., when the parameters of one model are special cases of the parameters of the second model; see 16 or ¹⁹ p. 34 for more information) and when Information Criteria were generated using the same estimation method. Many models are not nested and therefore this option is not appropriate for many comparisons. Nevertheless, we provide this option for advanced users.

• 40It’s also important to run some diagnostics for your preferred model to check that the assumptions of the linear model are not violated (see for more information http://www.statisticalassociates.com/longitudinalanalysis.htm). You need to have used Save to save the Predicted Values (RESID_1) and Residuals (PRED_1) in step 34. To determine whether the residuals might come from a normal distribution, we recommend plotting a histogram. Click Graph>Chart Builder>OK. Click on Gallery>Histogram and drag the “Simple Histogram” icon into the “Chart Preview” window. Now drag “Residuals [RESID_1]” into the “X-axis?” box. In the “Element Properties” window, put a tick in the box next to “Display normal curve” and click “Apply” (Supplementary Tutorial, slide 63). Click “OK” (Supplementary Tutorial, slide 64).
• 41Normality can also be examined using the Kolmogorov-Smirnov tests (see ¹⁹ p. 212). Type the following lines into Syntax and “Run>All”.

  • NPAR TESTS

  •    /K-S(NORMAL)= RESID_1

  •    /MISSING ANALYSIS.

  In Output, look for “Asymp. Sig. (2-tailed)”. If p>0.05 then the assumption is reasonable (Supplementary Tutorial, slide 65).

CRITICAL STEP: If p<0.05 then there is evidence that the residuals do not follow a normal distribution.

? TROUBLESHOOTING

• 42Normality can also be examined using “Normal Q-Q plots of the residuals”. Type the following lines into Syntax.

  • PPLOT

  •    /VARIABLES=RESID_1

  •    /NOLOG

  •    /NOSTANDARDIZE

  •    /TYPE=Q-Q

  •    /FRACTION=BLOM

  •    /TIES=MEAN

  •    /DIST=NORMAL.

  If the circles mostly lie close to the diagonal line then the assumption of normality is reasonable (Supplementary Tutorial, slide 66).

CRITICAL STEP: If many circles significantly deviate from the 45 degree line then there is evidence to suggest your residuals do not follow a normal distribution.

? TROUBLESHOOTING

• 43To determine whether the residuals of the groups have equal variance (so-called “homogeneity of error variances”), you can examine a scatterplot of the conditional residuals versus the conditional predicted values (arranged by “group”). If there is no pattern in the data for each group then it is likely that the assumption is met (Supplementary Tutorial, slide 67). In Syntax, type

  • GRAPH

  •      / SCATTERPLOT(BIVAR)=PRED_1 WITH RESID_1 BY group

  •      / MISSING=LISTWISE

CRITICAL STEP: If there is a strong asymmetry or pattern in the data then the residuals within each group may have different variance.

? TROUBLESHOOTING

TIMING

• Steps 1 to 2: Reflect upon your experimental design: Novice, 15 minutes: Expert, 5 minutes.

• Steps 3 to 8: Loading data and understanding data structure in SPSS. 10 minutes if loading a file; much longer if entering data manually.

• Steps 9 to 14: Graph and explore your data. Novice, 45 minutes; Expert, 20 minutes.

• Steps 15 to 25: Analyse data using Repeated Measures Analysis of Covariance. Novice, 30 min; Expert 15 min.

• Steps 26 to 43: Analyse data using the “MIXED” procedure. Novice, 30 minutes per model; Expert, 10 minutes per model.

Anticipated Results

Repeated measures analysis of covariance (RM ANCOVA)

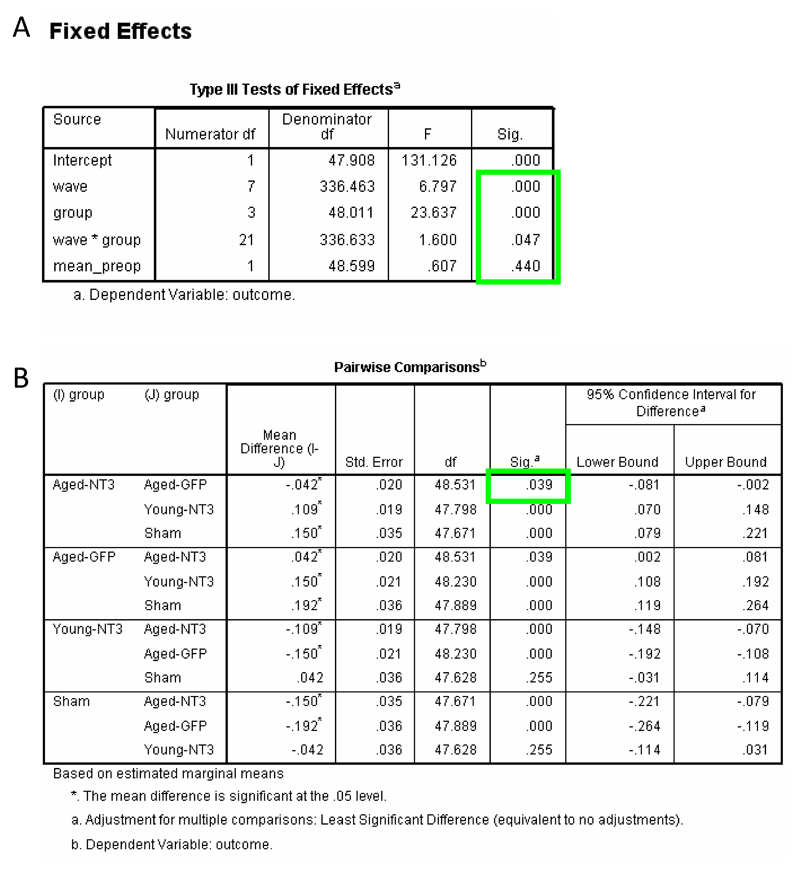
We first analysed our Case Study data using RM ANCOVA (steps 1 – 25). Regarding assumptions of the model, histograms showed that the dependent variables and residuals largely followed normal distributions (e.g., Supplementary Tutorial, slide 40). Although Levene’s tests showed that “group” variances were dissimilar in six out of eight waves (p<0.05; Supplementary Tutorial, slide 43), box plots showed that variances were similar between the two key groups (AAV-NT3 and AAV-GFP) (Supplementary Tutorial, slide 26). In any event, RM ANCOVA is robust to differences in group variances when the number of animals per group is similar (which it is here for three of the four groups). There was no evidence indicating a violation of sphericity (Mauchly’s W=0.675; df=27, p=0.94; Supplementary Tutorial, slide 42) indicating that the covariance structure of the model was appropriate (see TROUBLESHOOTING if sphericity is violated). Thus, the assumptions of RM ANCOVA were reasonably met. We therefore proceeded with interpreting the results. RM ANCOVA showed there was an effect of group (F_3,45=21.1; p<0.001) and of wave (F_7,315=4.03, p<0.001) (Supplementary Tutorial, slides 42 and 43). Differences between group means were explored using pairwise comparisons and these revealed no overall difference between aged rats treated with AAV-NT3 and those treated with AAV-GFP (p=0.107) (Supplementary Tutorial, slide 44). However, there was also a significant interaction of wave and group (F_21,315=1.69, p=0.032; Supplementary Tutorial, slide 42), meaning that the effect of time (wave) differed by group: this warrants consideration because it means that the group mean trajectories were not parallel. Differences between means defined by the interaction of wave and group were examined using pairwise comparisons: these revealed a difference between the aged AAV-NT3 group and the aged AAV-GFP at week 8 (p<0.001) (Supplementary Tutorial, slide 45) but at no other time (p>0.05). Some statisticians are uncomfortable with multiple pairwise comparisons for means defined by a significant interaction. Indeed, this may be the reason why SPSS does not offer pairwise comparisons for the interaction term via point-and-click. Accordingly, one might conservatively conclude that RM ANCOVA provides no strong evidence that recovery after stroke in aged rats results from treatment with AAV-NT3 (relative to AAV-GFP).

Pairwise comparison of group means did identify an overall difference between the aged AAV-NT3 group and shams as well as between the aged AAV-GFP group and shams (p<0.05, Supplementary Tutorial, slide 44) reflecting persistent disabilities due to stroke. Importantly, no overall difference was detected between young AAV-NT3 rats and sham rats (p=0.276; Supplementary Tutorial, slide 44) indicating that after stroke, young AAV-NT3 rats recovered back to the performance level of sham rats. Pairwise comparison of means defined by the significant interaction of group and wave showed that at week 1, all three stroke groups were impaired relative to the sham group (all p<0.013) and also that there was no difference between the aged AAV-NT3 group and the aged-AAV-GFP group at week 1 (p=0.272), indicating that disabilities were similar in aged rats immediately after stroke. As an aside, there was no effect of baseline performance (mean_preop; F_1,45=0.16, p=0.694; Supplementary Tutorial, slide 43) but we kept this term in the analysis because it partitions away some of the residual variance and improves the power of the test to detect a benefit of treatment. Ultimately, however, it is vital to recall that RM ANCOVA excludes all data from a subject where even a single data point is missing^8,9. In our study, three rats had two or three missing data points:

• Rat 29 (aged rat, AAV-NT3) had the last two values missing.

• Rat 33 (aged rat, AAV-GFP) had the last two values missing.

• Rat 52 (aged rat; AAV-GFP) had the last three values missing.

Inspection of the “Between-Subjects Factors” box in the Output confirms that n=50 (rather than 53) showing that all the data from these three rats were omitted (Supplementary Tutorial, slide 41). This reduction in n causes a loss of statistical power (i.e., reduces the chance of detecting a real effect). We therefore investigated methods of analysis which avoid exclusion of rats with missing values.

Linear models with alternative covariance structures and REML estimation

We next analysed the data using linear models with alternative covariance structures and REML estimation, which automatically includes all available data from all 53 rats (Supplementary Tutorial, slide 55, green circle) and allows us to compare between covariance structures. We first compared various “full” linear models.

Covariance Structure 1: We know from the “Bivariate” correlation analysis of our Case Study data (step 12 to 14; Supplementary Tutorial, slide 31) that there is a significant and positive correlation between most pairs of time points (considering all groups together). The size of the correlation stays similar with increasing separation of time points. This suggests that a compound symmetric (CS) covariance structure may be appropriate¹⁶. The full model with CS covariance structure required 66 different parameters to be estimated (Supplementary Tutorial, slide 55, blue circle) and was associated with an AIC score of -707 (Supplementary Tutorial, slide 55, orange ellipse) (n.b., AIC scores can be negative or positive: better fit is indicated by a more negative AIC score).

Covariance Structure 2: We next evaluated a general “unstructured” (UN) covariance structure which neither requires that the variances of the data at all time points are equal nor that the covariances between any two time points are equal. Accordingly, many variance and covariance parameters (here, 100) had to be estimated. This resulted in an AIC score of -666 (i.e., this is a less good fit than the first model because the AIC score is more positive than -707).

Covariance Structure 3: We also evaluated a “first-order autoregressive” covariance structure (AR1) which has been recommended for longitudinal data¹⁸. This also required 66 parameters to be estimated but resulted in an intermediate AIC score of -689.

Thus, amongst these full models, the model with CS covariance structure had the best fit. These models are considered “full” because they included all possible combinations of factors and covariates (Supplementary Tutorial, slide 49). However, many of the combinations with the covariate were not significant (Supplementary Tutorial, slide 56) and were removed from the analysis (step 31) to make the model more parsimonious (reducing the number of parameters tested from 66 to 35). We left the baseline performance measure as a covariate in the model for reasons given in Box 1 and because our hypothesis specifically stipulated the need to control for baseline differences in performance at the level of the animal (Step 1). However, for parsimony we removed all combinations of this covariate with other factors (Supplementary Tutorial, slides 68 to 71): including only the covariate adds only a single parameter to the model. We also left the interaction of group by wave in the model because this is of key experimental interest (see the third question in the Introduction). We then compared this model with the three different covariance structures described above (UN, CS, AR1): amongst these, the model with CS still had the lowest AIC score.

Other models: We also evaluated other covariance structures (referred to here by their abbreviations: AD1, ARH1, ARMA1, CSH, DIAG, HF, ID, TPH and UNR) but none had a smaller AIC than CS. It is also possible to build a linear model that models time as a continuous variable (i.e., real time) rather than as a categorical variable (e.g., “week”). This requires far fewer parameters to be estimated when time is specified as a linear parameter (2 p.246) and is therefore parsimonious. However, it does not allow pairwise comparisons to be made easily between groups at particular time points and because these are of particular interest we do not present a model of that kind here. It is also possible to build models where the intercept and/or slope for each animal is allowed to vary from animal to animal (e.g., a random effects model): however, for our data, analysis showed this to be redundant and we omit this model for simplicity. Finally it is also possible to use the GENLINMIXED command in SPSS to fit linear models with general error covariance structures and different variance components for different groups of subjects (Supplementary Tutorial, slide 83); however, further guidance is beyond the scope of this article.

Summary

Longitudinal behavioural data were analysed using SPSS’s “MIXED” procedure and REML estimation to accommodate data from rats with occasional missing values⁸. The covariance structure with best fit, identified using Akaike’s Information Criterion, was the “compound symmetry” structure. Fixed factors included in the final model were group, wave and the group by wave interaction. Baseline score was used as covariate. For hypothesis testing, significant effects and interactions were explored using Least Significant Differences tests. The threshold for significance for main effects and interactions was 0.05. The threshold for significance for eight selected pairwise comparisons of the interaction of wave by group was adjusted to 0.00625.

After controlling for baseline differences in performance, there was an effect of group (F_3,48.0=23.6, p<0.001) and of wave (F_7,336=6.80, p<0.001) and an interaction of group with wave (F_21,337=1.60, p=0.047) (Supplementary Tutorial, slides 60 and 72 and Figure 7). Pairwise comparisons of group means showed a difference between the aged AAV-NT3 group and the aged AAV-GFP group (p=0.039) and also between the aged AAV-NT3 group and both the young AAV-NT3 group (p<0.001) and sham rats (p<0.001) (Supplementary Tutorial, slides 61 and 73 and Figure 7). Overall, there was no difference between the young AAV-NT3 group and sham rats (p=0.255). Pairwise comparisons of the means defined by the group by wave interaction showed the following: 1) a deficit was evident at week one in the young and aged stroke groups (young AAV-NT3 p=0.014, aged AAV-NT3 p<0.001, aged AAV-GFP p<0.001, all versus sham), 2) there was a difference between aged rats treated with AAV-NT3 and with AAV-GFP at week eight (p<0.001; Supplementary Tutorial, slide 74 and Figure 8), 3) There was no difference between the two groups of aged rats in the deficit at week one, prior to treatment (p=0.43), 4) After stroke, the young AAV-NT3 group completely recovered to sham levels by week 5 (comparisons from week 2 to week 8, all p>0.33). Finally, we checked the assumptions underlying our model. The residuals appeared to come from a normal distribution (Kolmogorov-Smirnov p>0.05; Supplementary Tutorial, slides 63 to 66) and (although the sham and young AAV-NT3 groups had smaller variance), the variances of the residuals were reasonably similar between groups (Supplementary Tutorial, slide 67). Therefore, the assumptions of the model were reasonably met.

Figure 7.

Screenshot of SPSS Output. (A) Results of significance testing for Fixed Effects (i.e., factor(s),covariate(s) and interaction(s) specified in Figure 4A). There is a significant effect of wave, group and an interaction of wave by group but no effect of covariate (green box). (B) Results of pairwise comparisons of any significant main effect(s) (as requested in Figure 5A) showing a difference between aged stroke rats treated with AAV-NT3 and those treated with AAV-GFP (green box).

Figure 8.

Screenshot of SPSS Output. Results of pairwise comparison of significant interaction of wave by group. Top panel shows table header and bottom panel shows results for wave eight (bottom of table, after intervening part of table removed for clarity). There was a significant difference between aged stroke rats treated with AAV-NT3 and those treated with AAV-GFP at week eight (green box).

Conclusions

Our alternative hypothesis stated that, after stroke, aged rats treated with AAV-NT3 would perform better on the ladder test than those treated with AAV-GFP (after controlling for baseline differences in performance). Whereas RM ANCOVA did not identify any difference between these two groups (unless pairwise comparisons of the interaction were considered), an overall beneficial effect of AAV-NT3 was identified by the linear model using REML estimation.

We are confident that the latter analysis identified a true positive effect of treatment, for two reasons. First, an additional behavioural test (the bilateral tactile stimulation test) also showed a positive benefit of treatment in this study ^7,21. Second, we also showed in this and another study that AAV-NT3 in young adult rats also improves function on these two behavioural tests back to pre-stroke levels of performance. ^7,21.

An important benefit of using the “MIXED” procedure is that animal lives were used to best effect. Data from animals with missing values were included rather than needlessly omitted. In our experiment, inclusion of the three rats with missing values enabled a positive benefit of treatment to be detected: the alternative would be that the study had not shown any positive benefit of treatment and that the 53 rat lives would, essentially, have been wasted. We conclude that the “MIXED” procedure (using REML estimation) performs better than RM ANCOVA where animals have even a few missing data points.

Troubleshooting

Troubleshooting advice can be found in Table 1.

Supplementary Material

Supplementary Tutorial: A click-by-click guide to analysing longitudinal data from animals where some data are missing. Slides 1 to 31) How to enter and explore data graphically. Slides 32 to 45) Analysis using RM ANCOVA. Slides 46 to 74) Analysis using linear models with general covariance structures. Slides 75 to 82) Restructuring data.