Nonlinear electroelasticity: material properties, continuum theory and applications

Abstract

In the last few years, it has been recognized that the large deformation capacity of elastomeric materials that are sensitive to electric fields can be harnessed for use in transducer devices such as actuators and sensors. This has led to the reassessment of the mathematical theory that is needed for the description of the electromechanical (in particular, electroelastic) interactions for purposes of material characterization and prediction. After a review of the key experiments concerned with determining the nature of the electromechanical interactions and a discussion of the range of applications to devices, we provide a short account of the history of developments in the nonlinear theory. This is followed by a succinct modern treatment of electroelastic theory, including the governing equations and constitutive laws needed for both material characterization and the analysis of general electroelastic coupling problems. For illustration, the theory is then applied to two simple representative boundary-value problems that are relevant to the geometries of activation devices; in particular, (a) a rectangular plate and (b) a circular cylindrical tube, in each case with compliant electrodes on the major surfaces and a potential difference between them. In (a), an electric field is generated normal to the major surfaces and in (b), a radial electric field is present. This is followed by a short section in which other problems addressed on the basis of the general theory are described briefly.

1. Introduction

In 1880, Röntgen reported the effect of electric forces on the behaviour of dielectric solids and fluids following his presentation of experimental results at the Versammlung Deutscher Naturforscher und Ärzte in 1879 under the title ‘Über die elektrische Ausdehnung’, which can be translated as ‘On the electric stretching’. In particular, he described an experimental set-up in which a thin rubber sheet having an initial length of 1 m, width of 16 cm and unspecified thickness was stretched to double its length by holding one end fixed and applying a constant load to the other. Once equilibrium was established, the sheet was electrically charged, as a result of which the rubber sheet elongated by several centimetres [1]. This is the first documented experiment in which elongation is induced by electric forces in a pre-stretched dielectric rubber, but it is only in recent years that it has been recognized that such nonlinear electromechanical coupling can be used in the development of transducers such as actuators and sensors and in many other applications of electro-sensitive polymers.

To fully understand the electromechanical coupling effects and to aid the design of devices, it is necessary to be able to predict the behaviour of these polymers under different mechanical and electrical loading conditions. For this purpose, a theory of nonlinear electromechanical interactions is required. In particular, constitutive laws that describe the material properties based on experimental data form a key part of this theory, but it must be emphasized that there is at present a lack of comprehensive datasets for this purpose.

The mathematical theory appropriate for the description of the nonlinear coupling of electric forces and mechanical deformation was developed more recently than the early work of Röntgen and began with the classic paper of Toupin [2]. This combines the theories of continuum mechanics and electrostatics in order to develop a framework for the analysis of the nonlinear response of isotropic dielectric materials. Röntgen’s work was not mentioned in Toupin’s paper although he did refer to the work of Voigt on piezoelectricity (which was summarized in Voigt’s book [3]).

The present paper provides a review, in §2, of the history of the experiments relating to large deformation electromechanical effects in polymeric materials and their development for use in applications, particularly as actuators, their basic theoretical analysis and a short discussion of instability phenomena. Section 3 follows with a brief description of the various contributions to the nonlinear theory of electromechanical interactions as a prelude to a full but succinct modern development of the main aspects of the theory in the subsequent sections. In particular, the basic equations of static nonlinear continuum mechanics are summarized in §4, the appropriate specialization of Maxwell’s equations in §5 and the equations that combine the two theories leading to the general theory of nonlinear electroelastic interactions are provided in §6. This is followed, in §7, by a discussion of constitutive equations for electroelastic materials and then their specialization to isotropic electroelasticity, thus providing a framework for material characterization and the construction of specific constitutive laws. The theory is then applied to the simple case of pure homogeneous strain with a uniform electric field aligned with one of the principal directions of strain, followed by an application to a parallel plate actuator with compliant electrodes coated on the major surfaces of the plate and a potential difference between the electrodes.

In §8, a general electroelastic boundary-value problem is formulated and then applied to a representative example involving a non-homogeneous deformation and electric field. Specifically, the problem involving the extension and inflation of a circular cylindrical tube with compliant electrodes on its curved inner and outer surfaces is analysed in some detail. This is followed by a brief summary of other boundary-value problems for electroelastic bodies that have been examined in the literature. Finally, §9 contains some concluding comments.

2. Material properties, geometrical configurations and instability phenomena

Considerable interest has developed in the last few years in the possibilities for using dielectric elastomers as electromechanical transducers, as has been summarized in the collection of papers edited by Carpi et al. [4] and the reviews by O’Halloran et al. [5] and Brochu & Pei [6]. In particular, O’Halloran et al. [5] summarize the operating principles of dielectric elastomer actuators, but with the restriction to uniaxial deformations with linear electric and mechanical properties. They review representative configurations, discuss existing and potential applications and challenges that need to be overcome in the use of compliant electrodes, the high electric field requirements and the selection of optimal elastomeric materials. Brochu & Pei [6] provide a detailed account of actuator materials and, more specifically, an extensive summary of dielectric material properties, and conclude with a detailed list of actuator configurations and applications, including sensors and generators. The attractive Scientific American article by Ashley [7], while focusing on artificial muscle, highlights the potential for a wide range of possible applications of electroactive polymers.

A set of guidelines for possible standards for the manufacturing and testing of dielectric elastomer transducers was published recently [8] with a brief discussion of modelling in which the mechanical response of the material was taken to be linearly elastic with the Maxwell stress providing the electrostatic contribution to the response.

The purpose of the present section is to highlight the main important contributions that focus on the experimental characterization of dielectrics of various geometries that are capable of achieving large strains on application of an electric field, and on their use as actuators.

(a). Planar geometries

Following Röntgen [1], the next significant work was the short contribution by Stark & Garton [9], who considered the reduction in thickness of rubber-like sheets under electric fields normal to the sheets. They reported that as the magnitude of the electric field increased, the thickness reduced continuously until either a stable configuration was reached, at a reduced thickness, or until no stable thickness existed and a breakdown in electrical strength occurred.

On a similar theme, Blok & LeGrand [10] noted that the major surfaces of a dielectric film, when subjected to a uniform electric field in the direction normal to the top and bottom surfaces, become effectively charged and attract one another with an electrostatic stress, which they refer to as a ‘pressure’ p, given by

$$p=\frac{1}{2}{\epsilon }_{\mathrm{r}}{\epsilon }_0{\left(\frac{V}{t}\right)}^2=\frac{1}{2}\epsilon E^2,$$ 2.1

where t is the deformed thickness of the dielectric, V is the potential difference between the surfaces (the electrodes), ε₀ is the vacuum permittivity, ε_r is the relative permittivity of the dielectric (in this case a constant independent of the deformation), ε=ε_rε₀ is the actual permittivity of the material, and the electric field between the surfaces, denoted by E, is given by E=−V/t. They found that as the magnitude of the electric field approached a critical value, the film became susceptible to non-uniform thinning. They interpreted this as being caused by microscopic imperfections in the material that experience higher than average fields, resulting in confined indentations so that the intensity of the electric field ceases to be uniform, increases locally, and induces electromechanical instability and inhomogeneous deformations.

Equation (2.1) was used by Ma & Reneker [11] to determine the attractive electrostatic force between two electrodes attached to the top and bottom surfaces of a circular dielectric elastomer sample. Measurements were obtained on five different rubber compounds and, assuming linearly elastic behaviour, they reported a linear relation between strain and the square of the electric field.

Pelrine et al. [12] described the effect of a potential difference applied between flexible electrodes that sandwich an elastomeric polymer film as compressing the film by the resulting electrostatic pressure and, because of incompressibility, stretching in the lateral directions. Assuming elastic behaviour, they balanced the change in electrostatic energy with the mechanical work (a dielectric elastomer actuator converts electrical energy to mechanical energy) to derive the electrostatic stress (the effective Maxwell stress) as

$$p={\epsilon }_{\mathrm{r}}{\epsilon }_0{\left(\frac{V}{t}\right)}^2=\epsilon E^2,$$ 2.2

which is double that given in (2.1). Equation (2.2), not (2.1), is the correct expression and is a particular example arising from the general theory discussed in §7d.

On the basis of the linear theory of elasticity, Pelrine et al. [12] used expression (2.2) to approximate the strain of thin dielectric films in the thickness direction. Measurements of the in-plane deformation, combined with the incompressibility condition, were also used to determine the strain in the thickness direction and, on use of (2.2), to determine the electrostatic stress in various polymer dielectrics.

Pelrine et al. [13] characterized the behaviour of three types of polymeric elastomer films. In particular, they used a set-up in which compliant electrodes were coated on the top and bottom surfaces of radially pre-strained circular films over a relatively small centrally located circular area, followed by application of a potential difference between the electrode surfaces. Importantly, it was shown that the applied pre-strain amplifies the magnitude of the actuation strain due to the potential difference. An acrylic elastomer known as VHB 4910 from 3M was identified as a dielectric capable of particularly large actuation strains and high electromechanical pressure and pre-strains. In [14], the actuation performances of a large number of dielectric elastomers were determined using the same biaxial experimental set-up as in Pelrine et al. [13] and compared with other electric actuation technologies. The magnitude of the actuation strains reported has increased steadily, as exemplified in [15].

Similar experiments were conducted by Wissler & Mazza [16,17] using the polymer VHB 4910. They adopted a number of different nonlinear isotropic hyperelastic material models to describe the mechanical effects and used the stress given by (2.2) to provide the electromechanical coupling. They then compared the predictions of the models with the experimental results and obtained good agreement while noting that the selection of the material model had a strong influence on the predictions. Clearly, equation (2.2) shows that the electrostatic stress increases as the film thickness decreases. If the corresponding increase in material stiffness does not compensate for the increase in the electrostatic stress then an electromechanical instability can occur in the form of further decrease in the film thickness or electrical breakdown, as noted in [16] and earlier in [9,10,13]. These effects are strongly dependent on the amount of pre-strain.

Wissler & Mazza [18,19] obtained further experimental data for VHB 4910 with the same set-up for different pre-strains and actuation potentials with particular reference to equation (2.2), and also considered the time-dependent response of the materials. The final section in [19] shows that the relative dielectric permittivity ε_r of VHB 4910 is not a constant but depends on the pre-strain.

Kofod et al. [20] performed experiments on pre-strained rectangular films of the acrylic polymer VHB 4910 to validate the expression for the electrostatic stress (2.2), which they derived from the components of the Maxwell stress tensor. In particular, they applied different amounts of pre-strain to investigate the onset of mechanical instability and electric breakdown. Consistent with the results in Pelrine et al. [13], they showed that the electrical breakdown strength, actuation strain and efficiency increase with increasing pre-strain normal to the thickness direction. They also found that the relative dielectric permittivity ε_r decreased with the increase in pre-strain and considered that the differences between the theoretical predictions of (2.2) and their experimental data could, in part, arise because ε_r was assumed to be independent of strain in (2.2). The mechanical properties of VHB 4910 were used by Kofod [21] to assess the electromechanical coupling as a function of pre-strain in the pure shear deformation of a cuboid subject to different boundary conditions in the direction transverse to the pure shear and thickness directions.

Experimental results for VHB 4910 were also reported by Díaz-Calleja et al. [22], and they adopted an isotropic hyperelastic model for the mechanical response of the material, which they fitted successfully to the data. They also examined wrinkling instability, both theoretically and experimentally.

Plante & Dubowsky [23] focused on the characterization of failure modes of dielectric elastomer film actuators and, in particular, how they are influenced by pre-strain and the strain rate, each of dielectric breakdown, pull-in instability and material instability being dominant under different loading conditions. They considered both circular and diamond-shaped actuator geometries, the properties and performance of which were further assessed in [24,25].

The three types of failure considered, expressed in simple form, are

• — pull-in failure: this occurs after the film thickness falls below a critical value, leading to an unstable configuration with the film assuming a complex wrinkling pattern, which is followed by either material or dielectric strength failure;

• — dielectric failure: this happens when the electric field in the material exceeds a critical value (the dielectric strength), and electrical discharge occurs between the electrodes. The dielectric strength may be defined as the maximum electric field that the material can support without failure of its insulating capacity; and

• — material failure: this occurs when the stress in the material exceeds a critical value (the material strength). The material strength is the capacity of the material to support stress without failure.

Failure mechanisms also formed a key consideration in [26], which was concerned with the theoretical analysis of the extent to which dielectric elastomers can be used to generate electrical energy from mechanical deformation. Theoretical analysis of electromechanical instability has been considered by many authors, exemplified in [27–42]. Based on the theory of small deformations superimposed on large deformations for a general electroelastic material following the development of Dorfmann & Ogden [43], an analysis of the stability of an electroelastic plate was performed by the same authors in [44]. They noted, in particular, that the restricted Hessian criterion for the onset of instability adopted in several previous papers was neither able to capture the full range of instability modes, nor to account for the plate (or film) thickness or for inhomogeneous instabilities, and they found that their predictions of instability were often quite different from those obtained with the Hessian approach.

As mentioned earlier, in [19], it was found that the relative dielectric permittivity ε_r of VHB 4910 is strain dependent. The effect of a deformation-dependent permittivity on material response has been discussed in [42,45,46], and its influence on stability has been examined in [30,42–44,47,48], and on small amplitude electroelastic wave propagation in [49].

Puglisi & Zurlo [50] evaluated the effect of thickness imperfections and curvature on electromechanical instabilities, while Zurlo [51] proposed a simple constitutive dependence on the second gradient of the deformation for the analysis of non-homogeneous deformations in order to estimate the onset of pull-in instability in electroelastic films and found that the resulting non-local effects can significantly decrease the instability threshold.

Full discussion and analysis of instability and failure phenomena is not attempted in the present article, however, because a much more extensive review would be needed than the space limitations allow. Indeed, a detailed analysis and separate review of such phenomena is highly desirable.

(b). Cylindrical geometries

Thus far, cylindrical geometries have been considered less frequently than planar geometries, the first example being that of Carpi & De Rossi [52], who tested a cylindrical tube actuator of silicone dielectric elastomer with flexible electrodes applied to the inner and outer curved surfaces. For modelling the response, they adopted the electrostatic pressure given by the formula (2.2) combined with linear elasticity, and to simplify the modelling further, the electrostatic pressure was assumed constant during activation. With limited pre-strain and activation strain a good comparison was obtained between the theoretical predictions and experimental results. In [53], a cylindrical tube actuator with helical compliant electrodes was presented for which the activation generates axial contraction and radial expansion. In [54], Arora et al. also use silicone for very small diameter cylindrical tubes in order to evaluate the axial and radial actuation strains as functions of uniaxial and uniform pre-strains.

A mathematical model based on hyperelasticity was developed in [55,56] for the finite deformation analysis of thin-walled cylindrical dielectric elastomer sensors and actuators, again using the Maxwell stress for the electromechanical pressure. The cylindrical tubes were fibre-reinforced, with the fibres symmetrically and helically arranged. The dynamic response of tubes without fibre reinforcement was examined in [57]. In each of these papers, the experiments were conducted with tubes made from silicone and polyacrylate VBH 4905, and a good correlation was obtained between the theoretical predictions and experimental results.

For thick-walled cylinders of neo-Hookean elastic material with different wall thicknesses, Zhu et al. [58] analysed their activation after axial stretching without internal pressure and assessed the conditions leading to loss of electromechanical stability. In the absence of extension, an analysis of bifurcation instability for a tube under inflating pressure and a radial electric field was provided by Díaz-Calleja et al. [59] for two electroelastic material models.

A recent paper [60] provides a theoretical analysis of the bifurcation and post-bifurcation bulging of a cylindrical dielectric elastomer membrane tube under finite deformation and electromechanical loading based on a simple electroelastic constitutive law. The predictions of the theory gave good agreement with experiments they performed on tubes subject to internal pressure, axial load and potential difference.

(c). Other geometries

Many other geometrical arrangements have been considered for the design of dielectric elastomer actuators, the specification and performance of some of which have been reviewed in [61]. Here, we mention just a small selection of subsequent works involving different geometries. In adopting silicone elastomers as materials for actuators, the effects of pre-strain, hardener concentration and dielectric filler were investigated by Zhang et al. [62] for both planar and spring-roll actuators, while a variable geometry hexagonal frame design for pre-straining dielectric actuators with several degrees of freedom was used by Wingert et al. [63]. Kofod et al. [64] investigated the formation of complex out-of-plane electroelastic structures for use as claws in robotic gripping technology.

An analytical approach was developed by Moscardo et al. [65] for optimizing the design parameters of dielectric elastomer actuators so as to avoid the failure modes noted earlier and to maximize the range of actuation, and for illustration they considered the homogeneous deformation of a spring-roll actuator. The problem of programming the design of actuator geometries for different functions involving inhomogeneous deformations, including gripper actions, was also investigated by Zhao & Suo [66]. Inhomogeneous out-of-plane deformations of dielectric elastomer actuators were examined by He et al. [67], with particular reference to the avoidance of potential failure modes.

Some recent attention has been focused on layered beam-like actuators. For example, Wissman et al. [68], by minimizing the energy comprising the sum of hyperelastic and electrical contributions, predicted the principal curvatures of the beam as functions of the applied potential difference and obtained good agreement with their experimental measurements performed on a GaIn–PDMS composite. Balakrisnan et al. [69] analysed the bending of multilayered dielectric elastomer actuators, but their analysis was limited in several respects—in particular, it was restricted to plane strain and did not include material nonlinearity or electromechanical coupling.

Spherical elastomer balloons have been considered because of their ability in the absence of an electric field to ‘snap through’ to form balloons with increased radius. When coated with electrodes on their inner and outer surfaces, application of an electric field between the electrodes can be used to trigger this instability phenomenon, with the critical pressure at which snap-through occurs reducing as the field strength increases, as the analysis in [70] has demonstrated. The stability of a thick-walled ideal dielectric elastomer spherical shell has been analysed in [71], while the dynamic response of a radially pre-stressed spherical shell was analysed by Yong et al. [72], who considered the stability of oscillations of the shell for a constant or periodic potential difference.

An analysis of the radial response of a thick-walled spherical shell with compliant electrodes on its surfaces was provided in [73] within the framework of the general theory of nonlinear electroelasticity with examples illustrated for three forms of electroelastic energy function.

Experiments relating to snap-through were conducted by Keplinger et al. [15] and Li et al. [74], who observed that for inflated membrane balloons instabilities can be generated, where the balloon expands suddenly and either reaches a stable configuration or causes electrical breakdown due to the increase in the electric field between the electrodes on its surfaces. The experimental results were compared favourably with their theoretical predictions using the elastic Gent model [75]. Recent results for initially flat inflated membranes [76] have shown that rather complex geometrical bifurcation patterns can arise.

Membrane theory was also used by Xie et al. [77] to investigate how, under electrical actuation, bifurcation of a spherical balloon can lead to pear-shaped configurations for material models with either a deformation-dependent or deformation-independent permittivity.

An extensive list of references on large deformations and instabilities of soft dielectrics from both experimental and theoretical perspectives was provided by Zhao & Wang [78], who also discussed creasing, cratering and cavitation instabilities.

(d). Viscoelasticity

Much of the theoretical research on dielectric elastomers is based on elasticity, and while it is our intention to focus on the elastic behaviour of dielectric materials in this paper, it is well known that their behaviour can be significantly viscoelastic and dissipative. We, therefore, mention briefly that this has led to the development of electro-viscoelastic models of different degrees of complexity with a variety of applications, as discussed variously in [79–91].

Detailed experiments aimed at characterizing the electro-viscoelastic properties of VHB 4910 under application of purely mechanical and electromechanically coupled loadings have been carried out in [92]. The data show that the electric loading has a profound effect on the time-dependent behaviour of this electroactive polymer. This is a valuable contribution because it is very important to have comprehensive data on the properties of these materials to inform the modelling process. This is one of the few papers that provides such information and highlights the need for more data for various materials that are used for dielectric elastomer transducers. Most of the materials used in actuators are silicone and acrylics and the comparative performance of a particular silicone and acrylic has been evaluated by Michel et al. [93].

There is a clear need for more detailed characterization of the properties of dielectric polymers, and elastomers in particular. The appropriate basis for this characterization is a sound underpinning constitutive theory within the framework of continuum electromechanics which can be used in the processes of prediction and design. Such a framework is described in the following sections after a brief historical discussion of the main contributions to the continuum theory of electromechanical interactions in §3.

3. Continuum theories of nonlinear electromechanics

The modern development of the nonlinear theory of continuum electromechanics began with the seminal work of Toupin [2] in 1956 on the elasticity of dielectric materials. In the static context, with a stored energy depending on the deformation and the polarization per unit mass as independent variables, he used the principle of virtual work to derive constitutive laws for the electric field and a non-symmetric measure of stress together with the field equations in the material and the surrounding space, and associated boundary and continuity conditions. Particular attention was accorded to the constitutive equations for homogeneous isotropic dielectric materials expressed in terms of invariants, and the theory was illustrated by application to two simple boundary-value problems. The equations governing the dynamics of elastic dielectrics were derived in a subsequent paper by Toupin [94] in 1963 and then applied, in particular, to the study of linearized incremental deformations and weak electromagnetic fields superimposed on a finitely deformed configuration in a strong electromagnetic field.

Also in 1963, Eringen [95], in a paper that closely followed the theoretical development in [2], formulated the equations governing elastic dielectrics, the main difference being that he used the polarization per unit reference volume as his independent field variable instead of the polarization per unit mass. For the particular case of an isotropic dielectric, he applied his theory to the problem of extension of an incompressible thick-walled circular cylindrical tube subjected to a radial electric field.

Tiersten is also considered to be one of the founders of continuum electrodynamics, and he made fundamental contributions to the modelling of nonlinearly electroelastic materials, including thermal effects [96], and simplified the formulation of Toupin [2] and Eringen [95]. In particular, he used the theory of quasi-electrostatics to examine electroelastic wave propagation, a theory that was also used by Baumhauer & Tiersten [97] to derive the nonlinear equations and boundary conditions for small fields superimposed on a large static biasing field. Tiersten made significant contributions to the theory of piezoelectricity and its applications, and highlighted in [98,99] the differences between the linear piezoelectric equations and the linear electroelastic equations for small fields superposed on a biasing field.

Lax & Nelson [100] developed a theory of nonlinear electrodynamics for anisotropic dielectrics, with particular reference to acoustic wave interactions. In [101], they introduced Lagrangian versions of the electromagnetic fields and the associated forms of Maxwell’s equations and boundary conditions. These were used by Nelson [102] in deriving the field equations, constitutive equations and corresponding boundary conditions of nonlinear electroacoustics in dielectrics, without restriction to the quasi-electrostatic approximation. The theory was then specialized by considering second-order approximations in the elastic strain and electric field variables and finally to the quasi-electrostatic approximation. More details of Nelson’s contributions can be found in his monograph [103].

McMeeking & Landis [104] derived the governing equations for quasi-electrostatics in Eulerian form based on a principle of virtual work somewhat simpler than that of Toupin [2] and Eringen [95], and also adopted a free energy function dependent on the deformation gradient and the polarization. By use of the second law of thermodynamics for non-dissipative materials, they obtained the associated constitutive equations for the electric field and the (symmetric) total Cauchy stress. They applied the theory to the analysis of the response of an electroelastic plate with flexible electrodes on its major faces, based on a specialization of the constitutive law consisting of a purely elastic term supplemented by a term quadratic in the polarization. The principle of virtual work was also used by McMeeking et al. [105] to expand the formulation in [104] to dissipative materials.

A novel Lagrangian formulation was provided by Dorfmann & Ogden [106] based on the notion of a total energy function, leading to relatively simple and compact forms of the governing equations of equilibrium and constitutive equations in terms of the total Cauchy stress and its Lagrangian counterpart, the total nominal stress, thus facilitating the formulation and solution of a number of boundary-value problems. This is the formulation that will be adopted in the subsequent sections of this paper. A particular case of the theory in [106] was developed later from a different starting point by Suo et al. [107].

Vertechy et al. [108] presented a thermodynamically consistent nonlinear thermo-electro-mechanical model for analysing isotropic thermoelastic dielectrics. They obtained invariant-based constitutive equations for the polarization vector, the total Cauchy stress tensor and the heat flux vector as functions of the deformation gradient, the Eulerian form of the electric field and the temperature. A particular form of their constitutive equations was used to illustrate the efficacy of the model when compared with experimental data on membranes of natural rubber infused with electro-sensitive particles. They also discussed the similarities with and differences from the theories developed by Toupin [2], Hutter et al. [109], Pao [110], Eringen & Maugin [111], Dorfmann & Ogden [106], McMeeking & Landis [104] and McMeeking et al. [105], inter alia. A thermodynamically consistent coupled theory of nonlinear electro-thermo-viscoelasticity including hysteresis, ageing and damage effects was formulated by Chen [112], and more recently Mehnert et al. [113] have developed a general thermodynamically consistent time-independent constitutive framework for thermal and electromechanical interactions, and the theory was applied to the extension and inflation of a circular cylindrical tube to illustrate the coupling effects.

A quite different approach to the modelling of dielectric elastomers was presented by Skatulla et al. [114], who introduced the electromechanical coupling by means of a multiplicative decomposition of the deformation gradient into two parts, the first related to the elastic behaviour of the material, and the second to the deformation induced by the electric field. Standard free energy functions were then adapted for the formulation of constitutive equations based on a free energy function depending on the deformation gradient and the Lagrangian electric field. The free energy function was specialized into the sum of a purely mechanical part and a coupled electromechanical term quadratic in the electric field. This was used within a variational formulation to illustrate numerically the solution of a number of representative problems.

Bustamante & Rajagopal [115] extended the novel implicit theory of elasticity of Rajagopal [116] to an implicit theory of electroelasticity with the constitutive equations involving the total Cauchy stress tensor, the left Cauchy–Green deformation tensor, and the electric displacement and electric field vectors. In general, this theory is somewhat unwieldy because, even for isotropic materials, it involves a total of 21 invariants. To reduce the number of material functions, the theory was restricted to the case of linearized strains, and then used to exhibit strain-limiting material behaviour and polarization saturation. Several boundary-value problems were solved assuming a homogeneous distribution of the total stress and the electric field in [117], while numerical solutions were given for the case of a non-homogeneous distribution of stresses.

A general incremental theory for small deformations and electric fields superposed on a finite deformation and electric field was developed by Dorfmann & Ogden [43] based on the theory in [106] and extended to allow for incremental motions within the quasi-electrostatic approximation by Dorfmann & Ogden [49].

Finally, in this section, we mention that different aspects of the theories discussed earlier and their applications are discussed in the texts by Landau & Lifshitz [118], which was restricted to the linearly elastic context, Nelson [103], Maugin [119], Eringen & Maugin [111], Hutter et al. [109] and Dorfmann & Ogden [120].

4. The equations of nonlinear elastic equilibrium

We begin by defining the kinematic quantities that are required for describing the geometry of large deformations of general solid continua. Consider a material body in a stress-free undeformed configuration, which is referred to as the reference configuration and here denoted by ${\mathcal{B}}_{\mathrm{r}}$. Its boundary is denoted by $\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$. Material points are labelled by their position vectors X in ${\mathcal{B}}_{\mathrm{r}}\cup \mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$. In this paper, we consider only time-independent deformations and describe the deformation from ${\mathcal{B}}_{\mathrm{r}}$ to the deformed configuration, denoted by $\mathcal{B}$, with the vector mapping function χ, so that x=χ(X) is the deformed position vector of the material point X. The boundary of $\mathcal{B}$ is denoted by $\mathrm{\partial }\mathcal{B}$.

In the neighbourhood of a point X the deformation is described in terms of the deformation gradient tensor, the gradient of x=χ(X) with respect to X, denoted by F and given by

$$\mathbf{\text{F}}=\mathrm{Grad}\hspace{0.17em}\mathbf{\text{x}}=\mathrm{Grad}\hspace{0.17em}\mathit{\chi }(\mathbf{\text{X}}),$$ 4.1

Grad being the gradient operator with respect to X, which should be distinguished from grad, the usual gradient with respect to x, which is used later. The standard notation $J=det\mathbf{\text{F}}$ with the convention that J>0 is adopted here.

Two important symmetric tensors are formed from F, namely the left and right Cauchy–Green deformation tensors, denoted by B and C, respectively, and defined by

$$\mathbf{\text{B}}=\mathbf{\text{F}}{\mathbf{\text{F}}}^{\mathrm{T}}\mathrm{and}\mathbf{\text{C}}={\mathbf{\text{F}}}^{\mathrm{T}}\mathbf{\text{F}},$$ 4.2

where superscript T signifies the transpose of a second-order tensor.

Let n denote the unit outward normal vector on the surface $\mathrm{\partial }\mathcal{B}$ and t the force per unit area of $\mathrm{\partial }\mathcal{B}$. Then, Cauchy’s theorem allows us to write t=σn, where σ is a second-order tensor independent of n known as the Cauchy stress tensor. In the absence of couple stresses σ is symmetric, but without modification this is no longer the case when forces generated by an electric field are accounted for, as will be discussed in §6.

Let ρ denote the mass density of the material in $\mathcal{B}$ and f the (mechanical) body force acting on $\mathcal{B}$ per unit mass. Then, for mechanical equilibrium σ satisfies the equation

$$\mathrm{div}\hspace{0.17em}\mathbf{\sigma }+\mathrm{\rho }\mathbf{\text{f}}=\mathbf{\text{0}},$$ 4.3

where div is the divergence operator with respect to x. An important alternative measure of stress is the nominal stress tensor, denoted by S and given in terms of the Cauchy stress by

$$\mathbf{\text{S}}=J{\mathbf{\text{F}}}^{-1}\mathbf{\sigma }.$$ 4.4

This connection arises from the formula for the traction t per unit area of $\mathrm{\partial }\mathcal{B}$ via

$$\mathbf{\text{t}}\hspace{0.17em}\mathrm{d}a=\mathbf{\sigma }\mathbf{\text{n}}\hspace{0.17em}\mathrm{d}a=J\mathbf{\sigma }{\mathbf{\text{F}}}^{-\mathrm{T}}\mathbf{\text{N}}\hspace{0.17em}\mathrm{d}A={\mathbf{\text{S}}}^{\mathrm{T}}\mathbf{\text{N}}\hspace{0.17em}\mathrm{d}A,$$ 4.5

which makes use of Nanson’s formula

$$\mathbf{\text{n}}\hspace{0.17em}\mathrm{d}a=J{\mathbf{\text{F}}}^{-\mathrm{T}}\mathbf{\text{N}}\hspace{0.17em}\mathrm{d}A$$ 4.6

relating an area element dA on $\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$ to an area element da on $\mathrm{\partial }\mathcal{B}$ under the deformation, where N is the unit outward normal on $\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$.

In terms of S, the equilibrium equation (4.3) can be written as

$$\mathrm{Div}\hspace{0.17em}\mathbf{\text{S}}+{\mathrm{\rho }}_{\mathrm{r}}\mathbf{\text{f}}=\mathbf{\text{0}},$$ 4.7

where Div is the divergence operator with respect to X and ρ_r is the mass per unit volume in ${\mathcal{B}}_{\mathrm{r}}$, and we note the connection ρ_r=Jρ.

For an elastic material for which there is a strain-energy function, denoted by W(F) and defined per unit volume, the nominal stress is given simply by

$$\mathbf{\text{S}}=\frac{\mathrm{\partial }W}{\mathrm{\partial }\mathbf{\text{F}}}$$ 4.8

and from (4.4), the corresponding formula for the Cauchy stress is

$$\mathbf{\sigma }=J^{-1}\mathbf{\text{F}}\frac{\mathrm{\partial }W}{\mathrm{\partial }\mathbf{\text{F}}}.$$ 4.9

We emphasize that, at this point, we are considering a purely elastic material with no electromechanical coupling. The latter will be introduced in §6. The formulae (4.8) and (4.9) apply when there is no internal constraint on the material, i.e. no constraint on F. However, many materials, such as rubber-like materials and electroactive elastomers, that are capable of large elastic deformations can be regarded as incompressible, in which case the constraint of incompressibility is adopted. This takes the form

$$J=det\mathbf{\text{F}}\equiv 1.$$ 4.10

This means, in particular, that not all the components of F are independent, and (4.8) requires modification by the introduction of a Lagrange multiplier to accommodate the constraint (4.10). The resulting modifications of (4.8) and (4.9) are

$$\mathbf{\text{S}}=\frac{\mathrm{\partial }W}{\mathrm{\partial }\mathbf{\text{F}}}-p{\mathbf{\text{F}}}^{-1}\mathrm{and}\mathbf{\sigma }=\mathbf{\text{F}}\frac{\mathrm{\partial }W}{\mathrm{\partial }\mathbf{\text{F}}}-p\mathbf{\text{I}},$$ 4.11

where p is the required Lagrange multiplier and I is the identity tensor.

One fundamental condition that the strain-energy function W and its various generalizations considered later have to satisfy is the principle of objectivity, or just objectivity for brevity. This requires that W be invariant with respect to rotations superimposed on the deformation, a condition that C satisfies automatically. Thus, for objectivity to be satisfied, W must depend on F through C. This is always assumed to be the case in the remainder of this paper, even though the argument of the energy function is often written as F. For more detailed background on solid continuum mechanics, see [121,122].

5. Maxwell’s equations for electrostatics

(a). Eulerian forms

We consider purely electrostatic fields in this section, and as a prerequisite for the nonlinear theory of electroelasticity, we summarize the appropriate specializations of Maxwell’s equations, first in Eulerian form, i.e. in the configuration $\mathcal{B}$. Let E and D denote the electric field and electric displacement vectors, respectively. These fields are in general functions of x. In a polarized material medium, there is an additional vector, denoted by P and called the polarization density (per unit volume in $\mathcal{B}$). It is defined by

$$\mathbf{\text{P}}=\mathbf{\text{D}}-{\epsilon }_0\mathbf{\text{E}},$$ 5.1

where, as indicated following equation (2.1), ε₀ is the vacuum permittivity (or electric permittivity of free space). In polarizable materials, there are thus two independent vector fields and one when the electric properties of the material are specified by a constitutive equation, which expresses one of the three vectors in terms of another (and also, in general, the deformation). In vacuum or non-polarizable material this reduces to

$$\mathbf{\text{D}}={\epsilon }_0\mathbf{\text{E}},$$ 5.2

in which case there is only one independent vector and (5.2) can be regarded as a special form of constitutive equation. Some specializations of the constitutive equations will be considered in §§7 and 8.

The vector fields E and D satisfy two fundamental differential equations, namely

$$\mathrm{curl}\hspace{0.17em}\mathbf{\text{E}}=\mathbf{\text{0}}\mathrm{and}\mathrm{div}\hspace{0.17em}\mathbf{\text{D}}={\mathrm{\rho }}_{\mathrm{f}},$$ 5.3

where ρ_f is the density of free charges (per unit volume in $\mathcal{B}$) and the operation of curl is with respect to x. In vacuum ρ_f=0, and in dielectric materials, on which we shall focus in this paper, this is also the case.

Consider a (stationary) surface $\mathcal{S}$, which may either be within $\mathcal{B}$ or form (part of) the boundary $\mathrm{\partial }\mathcal{B}$ and let the unit vector n denote a normal to $\mathcal{S}$ (the outward unit normal in the case of $\mathrm{\partial }\mathcal{B}$). The two sides of $\mathcal{S}$ are distinguished as side + and side − with the vector n pointing from side − to side +. The field vectors on the two sides of $\mathcal{S}$ are identified by subscripts + and −. Then, a discontinuity (or ‘jump’) in a vector on $\mathcal{S}$ is the difference between its values on side + and side −, evaluated on $\mathcal{S}$. Thus, E, for example, has the discontinuity E₊−E₋, which is denoted by [[E]], and similarly for other quantities. The discontinuity conditions associated with equations (5.3) are given by the standard formulae

$$\mathbf{\text{n}}\times [[\mathbf{\text{E}}]]=\mathbf{\text{0}}\mathrm{and}\mathbf{\text{n}}\cdot [[\mathbf{\text{D}}]]={\sigma }_{\mathrm{f}},$$ 5.4

where σ_f is the free surface charge density per unit area on the surface $\mathcal{S}$.

Excellent sources of reference for the theory of electrostatics and more generally electromagnetic theory are the classical texts of Jackson [123], Becker & Sauter [124] and Stratton [125].

(b). Lagrangian forms

The vector fields E and D (and P) may be referred to as Eulerian fields because they are defined in $\mathcal{B}$. For the development of the theory governing the interaction of mechanical and electric effects it will be convenient to make use of the Lagrangian counterparts of E and D, which we denote by E_L and D_L, where the label L signifies ‘Lagrangian’. Given that the configuration $\mathcal{B}$ is obtained by deformation from ${\mathcal{B}}_{\mathrm{r}}$ with deformation gradient F, these are the pull-back versions of E and D from $\mathcal{B}$ to ${\mathcal{B}}_{\mathrm{r}}$ defined by

$${\mathbf{\text{E}}}_{\mathrm{L}}={\mathbf{\text{F}}}^{\mathrm{T}}\mathbf{\text{E}}\mathrm{and}{\mathbf{\text{D}}}_{\mathrm{L}}=J{\mathbf{\text{F}}}^{-1}\mathbf{\text{D}},$$ 5.5

for a derivation of which see [106] or [120]. We shall also make use of the density ρ_F of free charges per unit volume in ${\mathcal{B}}_{\mathrm{r}}$, which is defined by ρ_F=Jρ_f.

In terms of the Lagrangian fields, the Eulerian equations in (5.3) can be transformed into their Lagrangian counterparts

$$\mathrm{Curl}\hspace{0.17em}{\mathbf{\text{E}}}_{\mathrm{L}}=\mathbf{\text{0}}\mathrm{and}\mathrm{Div}\hspace{0.17em}{\mathbf{\text{D}}}_{\mathrm{L}}={\mathrm{\rho }}_{\mathrm{F}},$$ 5.6

which are equivalent to (5.3) provided that the deformation is sufficiently regular.

The jump conditions associated with these equations are analogous to their Eulerian counterparts (5.4), and, on use of elementary vector identities, can be written as

$$\mathbf{\text{N}}\times [[{\mathbf{\text{E}}}_{\mathrm{L}}]]=\mathbf{\text{0}}\mathrm{and}\mathbf{\text{N}}\cdot [[{\mathbf{\text{D}}}_{\mathrm{L}}]]={\sigma }_{\mathrm{F}},$$ 5.7

where σ_F=σ_f da/dA is the surface charge density per unit area of the surface ${\mathcal{S}}_{\mathrm{r}}$, which is the pre-image of $\mathcal{S}$, and N is the unit normal vector on ${\mathcal{S}}_{\mathrm{r}}$ corresponding to n on $\mathcal{S}$, with n and N related by Nanson’s formula (4.6).

We may also define a Lagrangian version P_L of P as P_L=JF⁻¹P by the same transformation as for D_L, and hence for later reference, from (5.1),

$${\mathbf{\text{P}}}_{\mathrm{L}}={\mathbf{\text{D}}}_{\mathrm{L}}-{\epsilon }_{0}J{\mathbf{\text{C}}}^{-1}{\mathbf{\text{E}}}_{\mathrm{L}}.$$ 5.8

By virtue of the deformation x=χ(X), we may regard the Lagrangian fields as functions of X in ${\mathcal{B}}_{\mathrm{r}}$.

6. The equations of electroelasticity

In this section, we focus on electrostatics and the interaction between electric fields and nonlinear elastic deformations in order, first, to generalize the equilibrium equation (4.3) so as to accommodate the electromechanical coupling with appropriate boundary conditions and, second, to prepare for the discussion of constitutive equations in §7.

(a). Equilibrium equations

To generalize the equilibrium equation (4.3), we must first of all include body forces associated with the electric field. The electric field also contributes to the Cauchy stress σ, the definition of which depends on the particular form of the electric body force adopted, as highlighted in [126,127].

From classical electrostatics, the force acting on charge e in an electric field E is eE and the force acting on a dipole of strength p located at a point in an electric field E is (p⋅grad)E. The generalizations of these forces at a point x in a polarized continuum $\mathcal{B}$ are ρ_fE and (P⋅grad)E, respectively, per unit volume in $\mathcal{B}$. By incorporating these into (4.3), we obtain the equilibrium equation for an electroelastic material in the form

$$\mathrm{div}\hspace{0.17em}\mathbf{\sigma }+\mathrm{\rho }\mathbf{\text{f}}+{\mathbf{\text{f}}}_{\mathrm{e}}=\mathbf{\text{0}}\text{in }\hspace{0.17em}\mathcal{B},$$ 6.1

where σ is a form of the Cauchy stress tensor, different from that in the purely elastic case, dependent on the electric field and not in general symmetric, while f_e is the electric body force defined by

$${\mathbf{\text{f}}}_{\mathrm{e}}={\mathrm{\rho }}_{\mathrm{f}}\mathbf{\text{E}}+(\mathbf{\text{P}}\cdot \mathrm{grad})\mathbf{\text{E}},$$ 6.2

f again being the mechanical body force per unit mass.

In fact, on use of (5.3), it can be seen that f_e can be expressed as the divergence of a second-order tensor, specifically

$${\mathbf{\text{f}}}_{\mathrm{e}}=\mathrm{div}\hspace{0.17em}{\mathbf{\tau }}_{\mathrm{m}},$$ 6.3

where τ_m is a form of electrostatic Maxwell stress given by

$${\mathbf{\tau }}_{\mathrm{m}}=\mathbf{\text{D}}\otimes \mathbf{\text{E}}-\frac{1}{2}{\epsilon }_0(\mathbf{\text{E}}\cdot \mathbf{\text{E}})\mathbf{\text{I}}$$ 6.4

and I is again the identity tensor. We emphasize that, in the literature, there are different definitions of the Maxwell stress within a polarizable body; this is just one of them, and we refer the readers to [126,127] for further discussion.

The equilibrium equation (6.1) may now be written in the form

$$\mathrm{div}\hspace{0.17em}\mathbf{\tau }+\mathrm{\rho }\mathbf{\text{f}}=\mathbf{\text{0}}\text{in }\mathcal{B},$$ 6.5

where we have introduced the total Cauchy stress tensor τ defined by

$$\mathbf{\tau }=\mathbf{\sigma }+{\mathbf{\tau }}_{\mathrm{m}},$$ 6.6

which incorporates the electric body force. Whereas neither σ nor τ_m is in general symmetric, τ has the advantage that it is symmetric. This symmetry comes from the balance of angular moments in the absence of intrinsic couples.

Expressed in the form (6.5), the equilibrium equation has the same structure as for a purely mechanical theory and, as will be shown in §7, τ can be expressed in terms of an energy function in a way that is exactly analogous to that used for pure elasticity. This has considerable advantages when it comes to formulating and solving particular boundary-value problems because it avoids the need for defining a Maxwell stress within a polarizable material. In a non-polarizable material or in free space, this is not an issue since the Maxwell stress is uniquely defined in such cases, and we provide its definition in the following subsection.

Analogously to the connection (4.4) between the nominal stress and Cauchy stress in pure elasticity theory, it is natural to define a total nominal stress tensor with the same connection in the present setting. This is denoted by T and is given by

$$\mathbf{\text{T}}=J{\mathbf{\text{F}}}^{-1}\mathbf{\tau }.$$ 6.7

Similarly to equation (4.7), the equation of equilibrium (6.5) translates into the equivalent form

$$\mathrm{Div}\hspace{0.17em}\mathbf{\text{T}}+{\mathrm{\rho }}_{\mathrm{r}}\mathbf{\text{f}}=\mathbf{\text{0}}\text{in }\hspace{0.17em}{\mathcal{B}}_{\mathrm{r}}.$$ 6.8

(b). Exterior fields

To distinguish the fields E and D within a polarizable material from those in the exterior (non-polarizable) region, we use the notations E^★ and D^★ for the latter, with the simple connection D^★=ε₀E^★ holding. The (symmetric) Maxwell stress, denoted by τ^★_m, in the exterior region is defined unambiguously by

$${\mathbf{\tau }}_{\mathrm{m}}^{\star }={\epsilon }_0{\mathbf{\text{E}}}^{\star }\otimes {\mathbf{\text{E}}}^{\star }-\frac{1}{2}{\epsilon }_0({\mathbf{\text{E}}}^{\star }\cdot {\mathbf{\text{E}}}^{\star })\mathbf{\text{I}},$$ 6.9

the superscript ^★ being used for all quantities in the exterior region.

The fields E^★ and D^★ must satisfy the equations in (5.3) appropriately specialized, i.e.

$$\mathrm{curl}\hspace{0.17em}{\mathbf{\text{E}}}^{\star }=\mathbf{\text{0}}\mathrm{and}\mathrm{div}\hspace{0.17em}{\mathbf{\text{D}}}^{\star }=0$$ 6.10

with D^★=ε₀E^★, from which it follows that div τ^★_m=0.

(c). Boundary conditions

In terms of Eulerian fields, the jump conditions across a discontinuity surface are given by (5.4). For a polarizable body $\mathcal{B}$ and its exterior, these jump conditions form boundary conditions, which we write here as

$$\mathbf{\text{n}}\times ({\mathbf{\text{E}}}^{\star }-\mathbf{\text{E}})=\mathbf{\text{0}}\mathrm{and}\mathbf{\text{n}}\cdot ({\mathbf{\text{D}}}^{\star }-\mathbf{\text{D}})={\sigma }_{\mathrm{f}},$$ 6.11

evaluated on the boundary $\mathrm{\partial }\mathcal{B}$. The corresponding Lagrangian forms of the boundary conditions are, from (5.7),

$$\mathbf{\text{N}}\times ({\mathbf{\text{F}}}^{\mathrm{T}}{\mathbf{\text{E}}}^{\star }-{\mathbf{\text{E}}}_{\mathrm{L}})=\mathbf{\text{0}}\mathrm{and}\mathbf{\text{N}}\cdot (J{\mathbf{\text{F}}}^{-1}{\mathbf{\text{D}}}^{\star }-{\mathbf{\text{D}}}_{\mathrm{L}})={\sigma }_{\mathrm{F}},$$ 6.12

evaluated on $\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$. Note that the deformation has not been defined in the exterior region and the deformation gradient terms in (6.12) come from the transformation of the unit normal according to Nanson’s formula (4.6).

By integrating (6.5) over $\mathcal{B}$ and applying the divergence theorem, we see that τn is the traction per unit area of the boundary $\mathrm{\partial }\mathcal{B}$ formed from the value of τ on the inside of $\mathrm{\partial }\mathcal{B}$, and this must match the exterior traction that combines the applied mechanical and electrical loads. Let t_a be the applied mechanical traction. We denote the electrical traction by ${\mathbf{\text{t}}}_{\mathrm{m}}^{\star }$. This is due to the Maxwell stress τ^★_m, and is given by ${\mathbf{\text{t}}}_{\mathrm{m}}^{\star }={\mathbf{\tau }}_{\mathrm{m}}^{\star }\mathbf{\text{n}}$, so that the total traction on $\mathrm{\partial }\mathcal{B}$ is ${\mathbf{\text{t}}}_{\mathrm{a}}+{\mathbf{\text{t}}}_{\mathrm{m}}^{\star }$. Hence, where t_a is prescribed, the traction boundary condition is

$$\mathbf{\tau }\mathbf{\text{n}}={\mathbf{\text{t}}}_{\mathrm{a}}+{\mathbf{\text{t}}}_{\mathrm{m}}^{\star }\text{on}\hspace{0.17em}\mathrm{\partial }\mathcal{B}.$$ 6.13

The traction boundary condition may also be written in Lagrangian form, as follows. With N denoting the unit outward normal to $\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}}$, and with dA the associated area element, Nanson’s formula (4.6) enables (6.13) to be transformed into

$${\mathbf{\text{T}}}^{\mathrm{T}}\mathbf{\text{N}}={\mathbf{\text{t}}}_{\mathrm{A}}+{\mathbf{\text{t}}}_{\mathrm{M}}^{\star }\text{on}\hspace{0.17em}\mathrm{\partial }{\mathcal{B}}_{\mathrm{r}},$$ 6.14

where t_A and t^★_M are defined via t_A dA=t_a da and ${\mathbf{\text{t}}}_{\mathrm{M}}^{\star }\hspace{0.17em}\mathrm{d}A={\mathbf{\text{t}}}_{\mathrm{m}}^{\star }\hspace{0.17em}\mathrm{d}a$.

We have now introduced the required stress tensors for electroelastic deformation that will be used subsequently. The next step, in the following section, is to relate the stresses to the deformation and field variables through constitutive equations that define the material properties. For this purpose, we regard the electric field E and electric displacement D vectors as basic field variables because they satisfy the field equations (5.3), with the polarization P given by (5.1).

Thus, for a polarizable material there are three vector fields to consider. To characterize the properties of a polarizable material and to distinguish between different materials, a framework for the development of constitutive equations is required, and this may be based on either one of the three variables as the independent electric variable, expressed as a function of one of the others together with (5.1). Two main options for such a framework are considered in §7 based on the Lagrangian fields E_L and D_L rather than E and D themselves.

Before proceeding, we note that the simplest example of a constitutive equation for a polarizable material is that of a linear isotropic material with constant permittivity ε. This has the form

$$\mathbf{\text{D}}=\epsilon \mathbf{\text{E}},$$ 6.15

with ε=ε_rε₀ and ε_r the relative dielectric permittivity, as used in (2.1). It follows that the polarization is a linear function of the electric displacement and equation (5.1) is replaced by

$$\mathbf{\text{P}}=\frac{{\epsilon }_{\mathrm{r}}-1}{{\epsilon }_{\mathrm{r}}}\mathbf{\text{D}},$$ 6.16

so that the vector field P is parallel to the electric displacement D. In vacuo or in non-polarizable material ε_r=1, while in polarizable materials ε_r>1. Note that ε_r−1 is referred to as the susceptibility, which is often denoted by χ_e.

7. Electroelastic constitutive equations

The stress tensor σ in (6.1) has been identified in [127] as the same as the stress tensor used in Toupin [2], albeit in different notation. Toupin obtains this, and the electric field E, from an energy function Σ(F,π), defined per unit mass, in the form

$$\mathbf{\sigma }=\mathrm{\rho }\mathbf{\text{F}}\frac{\mathrm{\partial }\mathit{\Sigma }}{\mathrm{\partial }\mathbf{\text{F}}}\mathrm{and}\mathbf{\text{E}}=\frac{\mathrm{\partial }\mathit{\Sigma }}{\mathrm{\partial }\mathbf{\pi }},$$ 7.1

where π=P/ρ is the polarization per unit mass. Note that E is denoted by E_M in [2], which is the sum of the Maxwell self field and the external field.

It is convenient in the present context to define the energy per unit reference volume and, as in [120], to use the polarization in the form ρ_rπ=JP, which we denote by P_r (the polarization per unit reference volume). We write the energy, per unit reference volume, as U(F,P_r)=ρ_rΣ(F,π), and the formulae in (7.1) can be recast as

$$\mathbf{\sigma }=J^{-1}\mathbf{\text{F}}\frac{\mathrm{\partial }U}{\mathrm{\partial }\mathbf{\text{F}}},\mathbf{\text{E}}=\frac{\mathrm{\partial }U}{\mathrm{\partial }{\mathbf{\text{P}}}_{\mathrm{r}}}.$$ 7.2

Here, it is the polarization that is used as the independent electric variable. Equally, this can be replaced by the electric field E or the electric displacement D, leading to variants of the constitutive laws, details of which can be found in [127]. However, it turns out that it is particularly convenient for several purposes to make use of the Lagrangian forms of the field variables defined in §5b in the construction of constitutive equations and the formulation of boundary-value problems, and we now focus on this approach.

(a). Lagrangian field-based energy functions

Our aim now is to obtain a compact formula for the total Cauchy stress τ analogous to the formula (4.9) for σ in pure elasticity. Two such formulae were derived in [106] and involved the use of the Lagrangian fields and a sequence of changes of independent variable. By combining these changes into a single step, we consider first a formulation which replaces U(F,P_r) by a function Ω of F and E_L, defined per unit reference volume. This is given by

$$\mathit{\Omega }(\mathbf{\text{F}},{\mathbf{\text{E}}}_{\mathrm{L}})=U(\mathbf{\text{F}},{\mathbf{\text{P}}}_{\mathrm{r}})-({\mathbf{\text{F}}}^{-\mathrm{T}}{\mathbf{\text{E}}}_{\mathrm{L}})\cdot {\mathbf{\text{P}}}_{\mathrm{r}}-\frac{1}{2}{\epsilon }_{0}J{\mathbf{\text{E}}}_{\mathrm{L}}\cdot ({\mathbf{\text{C}}}^{-1}{\mathbf{\text{E}}}_{\mathrm{L}}),$$ 7.3

which may be referred to as a total energy function. This leads to the equations

$$\mathbf{\text{T}}=\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }\mathbf{\text{F}}}\mathrm{and}{\mathbf{\text{D}}}_{\mathrm{L}}=-\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}},$$ 7.4

the detailed derivations of which can be found in [106,120]. The Eulerian counterparts, based on the use of Ω(F,E_L), are

$$\mathbf{\tau }=J^{-1}\mathbf{\text{F}}\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }\mathbf{\text{F}}}\mathrm{and}\mathbf{\text{D}}=-J^{-1}\mathbf{\text{F}}\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}}.$$ 7.5

An alternative to E_L as the independent electric variable is D_L with the definition of an energy function Ω*(F,D_L) (per unit reference volume) via

$${\mathit{\Omega }}^{\ast }(\mathbf{\text{F}},{\mathbf{\text{D}}}_{\mathrm{L}})=U(\mathbf{\text{F}},{\mathbf{\text{P}}}_{\mathrm{r}})+\frac{1}{2}{\epsilon }_0^{-1}{J}^{-1}{\mathbf{\text{D}}}_{\mathrm{L}}\cdot (\mathbf{\text{C}}{\mathbf{\text{D}}}_{\mathrm{L}})-{\epsilon }_0^{-1}{J}^{-1}(\mathbf{\text{F}}{\mathbf{\text{D}}}_{\mathrm{L}})\cdot {\mathbf{\text{P}}}_{\mathrm{r}}+\frac{1}{2}{\epsilon }_0^{-1}{J}^{-1}{\mathbf{\text{P}}}_{\mathrm{r}}\cdot {\mathbf{\text{P}}}_{\mathrm{r}}$$ 7.6

or more simply by means of the Legendre transform

$${\mathit{\Omega }}^{\ast }(\mathbf{\text{F}},{\mathbf{\text{D}}}_{\mathrm{L}})=\mathit{\Omega }(\mathbf{\text{F}},{\mathbf{\text{E}}}_{\mathrm{L}})+{\mathbf{\text{D}}}_{\mathrm{L}}\cdot {\mathbf{\text{E}}}_{\mathrm{L}}$$ 7.7

in the electric variables. This leads to formulae analogous to those in (7.4) and (7.5), specifically

$$\mathbf{\text{T}}=\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }\mathbf{\text{F}}},{\mathbf{\text{E}}}_{\mathrm{L}}=\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }{\mathbf{\text{D}}}_{\mathrm{L}}}$$ 7.8

and

$$\mathbf{\tau }=J^{-1}\mathbf{\text{F}}\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }\mathbf{\text{F}}},\mathbf{\text{E}}={\mathbf{\text{F}}}^{-\mathrm{T}}\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }{\mathbf{\text{D}}}_{\mathrm{L}}}.$$ 7.9

The variables (T,−D_L) and (F,E_L) are ‘work conjugate’ with respect to Ω, while (T,E_L) and (F,D_L) are work conjugate with respect to Ω*.

In passing, it should be mentioned that it is not possible to construct an energy function depending on just F and P_L, the latter given by (5.8), for which a pair of equally compact formulae can be obtained, and, for this reason, we do not adopt P_L as an independent variable.

Following the pattern of (4.11) for a purely elastic material, the appropriate modifications for incompressible materials of the expressions for T and τ given by (7.4)₁ and (7.5)₁ are

$$\mathbf{\text{T}}=\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }\mathbf{\text{F}}}-p{\mathbf{\text{F}}}^{-1}\mathrm{and}\mathbf{\tau }=\mathbf{\text{F}}\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }\mathbf{\text{F}}}-p\mathbf{\text{I}},$$ 7.10

respectively, with p a Lagrange multiplier as in (4.11). The expressions for D_L and D in (7.4)₂ and (7.5)₂ are unchanged except that J=1.

For Ω* the equations in (7.10) are replaced by

$$\mathbf{\text{T}}=\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }\mathbf{\text{F}}}-p^{\ast }{\mathbf{\text{F}}}^{-1}\mathrm{and}\mathbf{\tau }=\mathbf{\text{F}}\frac{\mathrm{\partial }{\mathit{\Omega }}^{\ast }}{\mathrm{\partial }\mathbf{\text{F}}}-p^{\ast }\mathbf{\text{I}},$$ 7.11

where p* is also a Lagrange multiplier, in general, not the same as p. The formulae for E_L and E in (7.8)₂ and (7.9)₂ are unchanged except that again J=1.

(b). Isotropic electroelasticity

Let us first of all consider the energy function Ω, which, by objectivity, is a function of the right Cauchy–Green deformation tensor C and E_L. If the underlying material in the absence of an electric field is isotropic, then the effect of an electric field is similar from the mechanical point of view to a preferred direction in a transversely isotropic elastic material, although E_L is not in general a unit vector (for details of the transversely isotropic theory for purely elastic materials, see [128]). Similarly to the case of a transversely isotropic elastic material, an electroelastic material is said to be isotropic if Ω is an isotropic function of the two tensors C and E_L⊗E_L. For an isotropic electroelastic material, Ω depends on six independent invariants of C and E_L⊗E_L, typically denoted by I₁,I₂,I₃,I₄,I₅,I₆ and defined here, respectively, by

$$I_1=\mathrm{tr}\hspace{0.17em}\mathbf{\text{C}},I_2=\frac{1}{2}[{(\mathrm{tr}\hspace{0.17em}\mathbf{\text{C}})}^2-\mathrm{tr}({\mathbf{\text{C}}}^2)],I_3=det\hspace{0.17em}\mathbf{\text{C}}=J^2$$ 7.12

and

$$I_4={\mathbf{\text{E}}}_{\mathrm{L}}\cdot {\mathbf{\text{E}}}_{\mathrm{L}},I_5=(\mathbf{\text{C}}{\mathbf{\text{E}}}_{\mathrm{L}})\cdot {\mathbf{\text{E}}}_{\mathrm{L}},I_6=({\mathbf{\text{C}}}^2{\mathbf{\text{E}}}_{\mathrm{L}})\cdot {\mathbf{\text{E}}}_{\mathrm{L}}.$$ 7.13

Thus, Ω=Ω(I₁,I₂,I₃,I₄,I₅,I₆) and for an unconstrained material the total nominal and Cauchy stresses can be expressed as

$$\mathbf{\text{T}}=\sum _{i=1,i\ne 4}^6{\mathit{\Omega }}_i\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }\mathbf{\text{F}}}\mathrm{and}\mathbf{\tau }=J^{-1}\mathbf{\text{F}}\sum _{i=1,i\ne 4}^6{\mathit{\Omega }}_i\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }\mathbf{\text{F}}},$$ 7.14

where Ω_i=∂Ω/∂I_i, i=1,2,…,6. We now give an explicit expression for the total Cauchy stress, which requires the derivatives of the invariants (7.12) and (7.13) with respect to F in the form

$$\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_1}{\mathrm{\partial }\mathbf{\text{F}}}=2\mathbf{\text{B}},\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_2}{\mathrm{\partial }\mathbf{\text{F}}}=2I_1\mathbf{\text{B}}-2{\mathbf{\text{B}}}^2,\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_3}{\mathrm{\partial }\mathbf{\text{F}}}=2I_3\mathbf{\text{I}},$$ 7.15

and

$$\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_5}{\mathrm{\partial }\mathbf{\text{F}}}=2\mathbf{\text{BE}}\otimes \mathbf{\text{BE}},\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_6}{\mathrm{\partial }\mathbf{\text{F}}}=2(\mathbf{\text{BE}}\otimes {\mathbf{\text{B}}}^2\mathbf{\text{E}}+{\mathbf{\text{B}}}^2\mathbf{\text{E}}\otimes \mathbf{\text{BE}}),$$ 7.16

where we recall that B=FF^T is the left Cauchy–Green deformation tensor. Hence (noting that ∂I₄/∂F vanishes),

$$\mathbf{\tau }=2J^{-1}[{\mathit{\Omega }}_1\mathbf{\text{B}}+{\mathit{\Omega }}_2(I_1\mathbf{\text{B}}-{\mathbf{\text{B}}}^2)+I_3{\mathit{\Omega }}_3\mathbf{\text{I}}+{\mathit{\Omega }}_5\mathbf{\text{BE}}\otimes \mathbf{\text{BE}}+{\mathit{\Omega }}_6(\mathbf{\text{BE}}\otimes {\mathbf{\text{B}}}^2\mathbf{\text{E}}+{\mathbf{\text{B}}}^2\mathbf{\text{E}}\otimes \mathbf{\text{BE}})].$$ 7.17

For an incompressible material (with I₃=1) this changes to

$$\mathbf{\tau }=2{\mathit{\Omega }}_1\mathbf{\text{B}}+2{\mathit{\Omega }}_2(I_1\mathbf{\text{B}}-{\mathbf{\text{B}}}^2)-p\mathbf{\text{I}}+2{\mathit{\Omega }}_5\mathbf{\text{BE}}\otimes \mathbf{\text{BE}}+2{\mathit{\Omega }}_6(\mathbf{\text{BE}}\otimes {\mathbf{\text{B}}}^2\mathbf{\text{E}}+{\mathbf{\text{B}}}^2\mathbf{\text{E}}\otimes \mathbf{\text{BE}}).$$ 7.18

For the electric displacement we have, similarly, as I₁,I₂,I₃ are independent of E_L,

$${\mathbf{\text{D}}}_{\mathrm{L}}=-\sum _{i=4}^6{\mathit{\Omega }}_i\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}},\mathbf{\text{D}}=-J^{-1}\mathbf{\text{F}}\sum _{i=4}^6{\mathit{\Omega }}_i\frac{\mathrm{\partial }{I}_i}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}},$$ 7.19

with

$$\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_4}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}}=2\mathbf{\text{BE}},\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_5}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}}=2{\mathbf{\text{B}}}^2\mathbf{\text{E}},\mathbf{\text{F}}\frac{\mathrm{\partial }{I}_6}{\mathrm{\partial }{\mathbf{\text{E}}}_{\mathrm{L}}}=2{\mathbf{\text{B}}}^3\mathbf{\text{E}}.$$ 7.20

Hence,

$$\mathbf{\text{D}}=-2J^{-1}({\mathit{\Omega }}_4\mathbf{\text{BE}}+{\mathit{\Omega }}_5{\mathbf{\text{B}}}^2\mathbf{\text{E}}+{\mathit{\Omega }}_6{\mathbf{\text{B}}}^3\mathbf{\text{E}})$$ 7.21

and we note that the Cayley–Hamilton theorem B³−I₁B²+I₂B−I₃I=O can be used to replace B³ if required. Equation (7.21) holds for an incompressible material with J=1.

When Ω*(F,D_L) is adopted as the energy function, then, for an isotropic material, Ω* again depends on the invariants I₁,I₂,I₃, but the invariants I₄,I₅,I₆ are replaced by invariants that depend on D_L. These are denoted by K₄,K₅,K₆ and defined by

$$K_4={\mathbf{\text{D}}}_{\mathrm{L}}\cdot {\mathbf{\text{D}}}_{\mathrm{L}},K_5={\mathbf{\text{D}}}_{\mathrm{L}}\cdot (\mathbf{\text{C}}{\mathbf{\text{D}}}_{\mathrm{L}})\mathrm{and}{K}_6={\mathbf{\text{D}}}_{\mathrm{L}}\cdot ({\mathbf{\text{C}}}^2{\mathbf{\text{D}}}_{\mathrm{L}}).$$ 7.22

Then, for an unconstrained and incompressible material, respectively, τ is given by

$$\mathbf{\tau }=2J^{-1}[{\mathit{\Omega }}_1^{\ast }\mathbf{\text{B}}+2{\mathit{\Omega }}_2^{\ast }(I_1\mathbf{\text{B}}-{\mathbf{\text{B}}}^2)+I_3{\mathit{\Omega }}_3^{\ast }\mathbf{\text{I}}+{\mathit{\Omega }}_5^{\ast }\mathbf{\text{D}}\otimes \mathbf{\text{D}}+2{\mathit{\Omega }}_6^{\ast }(\mathbf{\text{D}}\otimes \mathbf{\text{BD}}+\mathbf{\text{BD}}\otimes \mathbf{\text{D}})$$ 7.23

and

$$\mathbf{\tau }=2{\mathit{\Omega }}_1^{\ast }\mathbf{\text{B}}+2{\mathit{\Omega }}_2^{\ast }(I_1\mathbf{\text{B}}-{\mathbf{\text{B}}}^2)-p^{\ast }\mathbf{\text{I}}+2{\mathit{\Omega }}_5^{\ast }\mathbf{\text{D}}\otimes \mathbf{\text{D}}+2{\mathit{\Omega }}_6^{\ast }(\mathbf{\text{D}}\otimes \mathbf{\text{BD}}+\mathbf{\text{BD}}\otimes \mathbf{\text{D}}),$$ 7.24

where Ω*_i is defined as ∂Ω*/∂I_i, for i=1,2,3 and as ∂Ω*/∂K_i, for i=4,5,6. In each case, the formula for the electric field is

$$\mathbf{\text{E}}=2({\mathit{\Omega }}_4^{\ast }{\mathbf{\text{B}}}^{-1}\mathbf{\text{D}}+{\mathit{\Omega }}_5^{\ast }\mathbf{\text{D}}+{\mathit{\Omega }}_6^{\ast }\mathbf{\text{B}}\mathbf{\text{D}}).$$ 7.25

(c). The case of homogeneous biaxial deformation

As a first example, we consider the pure homogeneous strain of an incompressible material defined in Cartesian components by

$$x_1={\mathrm{\lambda }}_1{X}_1,x_2={\mathrm{\lambda }}_2{X}_2\mathrm{and}{x}_3={\mathrm{\lambda }}_3{X}_3,$$ 7.26

where λ₁,λ₂,λ₃ denote the principal stretches satisfying the incompressibility condition

$${\mathrm{\lambda }}_1{\mathrm{\lambda }}_2{\mathrm{\lambda }}_3=1.$$ 7.27

We also assume that the electric field is aligned with the x₃ direction with Eulerian component E₃ denoted by E and D₃ denoted by D, and corresponding Lagrangian components E_L3 and D_L3 denoted by E_L and D_L, respectively.

We work in terms of the energy function Ω(I₁,I₂,I₄,I₅,I₆) with the isotropic dependence expressed in terms of the stretches. From (7.18) and (7.21), we then obtain the only non-zero components of τ as

$$\begin{array}{rl}{\tau }_{11}& ={\mathrm{\lambda }}_1\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }{\mathrm{\lambda }}_1}-p,{\tau }_{22}={\mathrm{\lambda }}_2\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }{\mathrm{\lambda }}_2}-p,\end{array}$$ 7.28

$$\begin{array}{rl}{\tau }_{33}& ={\mathrm{\lambda }}_3\frac{\mathrm{\partial }\mathit{\Omega }}{\mathrm{\partial }{\mathrm{\lambda }}_3}-p+2{\mathit{\Omega }}_5{\mathrm{\lambda }}_3^2{E}_{\mathrm{L}}^2+4{\mathit{\Omega }}_6{\mathrm{\lambda }}_3^4{E}_{\mathrm{L}}^2\end{array}$$ 7.29

and D has just a single component

$$D=D_{\mathrm{L}}{\mathrm{\lambda }}_3=-2({\mathit{\Omega }}_4+{\mathit{\Omega }}_5{\mathrm{\lambda }}_3^2+{\mathit{\Omega }}_6{\mathrm{\lambda }}_3^4){\mathrm{\lambda }}_3{E}_{\mathrm{L}},$$ 7.30

with E_L=λ₃E.

In terms of two independent stretches, say λ₁ and λ₂, the invariants I₁, I₂, I₄, I₅ and I₆ are written

$$I_1={\mathrm{\lambda }}_1^2+{\mathrm{\lambda }}_2^2+{\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2},I_2={\mathrm{\lambda }}_1^{-2}+{\mathrm{\lambda }}_2^{-2}+{\mathrm{\lambda }}_1^2{\mathrm{\lambda }}_2^2$$ 7.31

and

$$I_4=E_{\mathrm{L}}^2,I_5={\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2}{I}_4,I_6={\mathrm{\lambda }}_1^{-4}{\mathrm{\lambda }}_2^{-4}{I}_4.$$ 7.32

By the incompressibility condition, it follows that Ω depends on just three independent variables, namely λ₁,λ₂ and I₄, and we introduce the notation $\tilde{\mathit{\Omega }}=\tilde{\mathit{\Omega }}({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,I_4)$ to represent this. Then, by forming the stress differences from (7.28) and (7.29), we obtain the compact formulae

$${\tau }_{11}-{\tau }_{33}={\mathrm{\lambda }}_1\frac{\mathrm{\partial }\tilde{\mathit{\Omega }}}{\mathrm{\partial }{\mathrm{\lambda }}_1}\mathrm{and}{\tau }_{22}-{\tau }_{33}={\mathrm{\lambda }}_2\frac{\mathrm{\partial }\tilde{\mathit{\Omega }}}{\mathrm{\partial }{\mathrm{\lambda }}_2},$$ 7.33

while, from (7.30),

$$D=-2\frac{\mathrm{\partial }\tilde{\mathit{\Omega }}}{\mathrm{\partial }{I}_4}{\mathrm{\lambda }}_1^{-1}{\mathrm{\lambda }}_2^{-1}{E}_{\mathrm{L}}=-2\frac{\mathrm{\partial }\tilde{\mathit{\Omega }}}{\mathrm{\partial }{I}_4}{\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2}E.$$ 7.34

A particular special class of models within this framework has the form

$$\tilde{\mathit{\Omega }}=\tilde{\omega }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2)-\frac{1}{2}\epsilon {\mathrm{\lambda }}_1^2{\mathrm{\lambda }}_2^2{I}_4,$$ 7.35

where ε is a constant and we note that ${\mathrm{\lambda }}_1^2{\mathrm{\lambda }}_2^2{I}_4=E^2$, and $\tilde{\omega }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2)$ is any (incompressible) isotropic strain-energy function arising in pure elasticity theory. Then, (7.34) simplifies to D=εE, with ε having the interpretation as the permittivity of the material. Also, the formulae in (7.33) become

$${\tau }_{11}-{\tau }_{33}={\mathrm{\lambda }}_1\frac{\mathrm{\partial }\tilde{\omega }}{\mathrm{\partial }{\mathrm{\lambda }}_1}-\epsilon E^2\mathrm{and}{\tau }_{22}-{\tau }_{33}={\mathrm{\lambda }}_2\frac{\mathrm{\partial }\tilde{\omega }}{\mathrm{\partial }{\mathrm{\lambda }}_2}-\epsilon E^2.$$ 7.36

The counterpart of (7.35) for the energy function Ω*, with variables λ₁,λ₂ and K₄ is denoted ${\tilde{\mathit{\Omega }}}^{\ast }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,K_4)$ and obtained by specializing (7.7) as

$${\tilde{\mathit{\Omega }}}^{\ast }={\tilde{\omega }}^{\ast }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2)+\frac{1}{2\epsilon }{\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2}{K}_4,$$ 7.37

where ${\tilde{\omega }}^{\ast }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2)=\tilde{\omega }({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2)$ and ${\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2}{K}_4=D^2$. This yields again the expressions for the stress differences given in (7.36).

(d). Application: a parallel plate actuator

We now apply the earlier equations to the deformation of a rectangular plate with reference geometry defined by

$$-L_1\le X_1\le L_1\mathrm{and}-L_2\le X_2\le L_2,0\le X_3\le H,$$ 7.38

where L₁,L₂,H are constants, the thickness H being small compared with the lateral dimensions so that electric end effects are negligible, as is usually assumed in the literature for thin films.

The deformed plate has uniform thickness h=λ₃H and is defined by

$$-l_1\le x_1\le l_1\mathrm{and}-l_2\le x_2\le l_2,0\le x_3\le h,$$ 7.39

where l₁=λ₁L₁,l₂=λ₂L₂.

Flexible electrodes coated on the surfaces X₃=0,H deform into the surfaces x₃=0,h and a uniform electric field E normal to the faces is generated by a potential difference, say V , between the electrodes so that V =Eh=Eλ₃H. This is accompanied by free surface charges on the electrodes with densities ±σ_f per unit deformed area (the positive sign applies to x₃=0). By Gauss’s theorem, there is no electric field outside the plate and hence, by the boundary condition (6.11)₂, D=σ_f

We now specialize to equibiaxial deformation with the notation λ₁=λ₂=λ, so that λ₃=λ⁻². A reduced form of energy function, defined by $\omega (\mathrm{\lambda },I_4)=\tilde{\mathit{\Omega }}(\mathrm{\lambda },\mathrm{\lambda },I_4)$, that depends only on λ and I₄=E²_L is then introduced. The two components τ₁₁ and τ₂₂ of the total stress tensor are then each denoted by τ, where

$$\tau -{\tau }_{33}=\frac{1}{2}\mathrm{\lambda }\frac{\mathrm{\partial }\omega }{\mathrm{\partial }\mathrm{\lambda }},$$ 7.40

while D is given by

$$D=-2{\mathrm{\lambda }}^{-4}\frac{\mathrm{\partial }\omega }{\mathrm{\partial }{I}_4}E.$$ 7.41

If there are no lateral tractions applied, then τ=0, and if no traction is applied on the faces, then τ₃₃=0 also so that ∂ω/∂λ=0, which condition provides a balance between the internal electric stress and mechanical stress in the x₃ direction.

For definiteness we now consider ω to be based on (7.35) with $\tilde{\omega }(\mathrm{\lambda },\mathrm{\lambda })$ corresponding to a neo-Hookean contribution, such that

$$\omega (\mathrm{\lambda },I_4)=\frac{1}{2}\mu (2{\mathrm{\lambda }}^2+{\mathrm{\lambda }}^{-4}-3)-\frac{1}{2}\epsilon {\mathrm{\lambda }}^4{I}_4,$$ 7.42

where μ>0 is the constant shear modulus of the neo-Hookean material in the reference configuration and ε is the constant permittivity of the material, with the linear relation D=εE, which follows from (7.41).

Then, (7.40) gives

$$\tau -{\tau }_{33}=\mu ({\mathrm{\lambda }}^2-{\mathrm{\lambda }}^{-4})-\epsilon E^2.$$ 7.43

For τ=0, this can be written as

$${\tau }_{33}=\epsilon E^2-\mu ({\mathrm{\lambda }}^2-{\mathrm{\lambda }}^{-4})=\epsilon E^2+\mu ({\mathrm{\lambda }}_3^2-{\mathrm{\lambda }}_3^{-1}),$$ 7.44

with the right-hand side consisting of the effective Maxwell stress εE²>0, as in (2.2), and the mechanical stress $\mu ({\mathrm{\lambda }}_3^2-{\mathrm{\lambda }}_3^{-1})$, which must be negative when τ₃₃=0 for internal stress balance. This, of course, requires λ>1 and λ₃<1, so the plate thins as a result of the applied potential difference.

If we denote by A and a the reference and deformed areas of the plate, then by incompressibility ah=AH and hence a=λ²A. Let Q be the total charge on an electrode. Then, Q=aσ_f=Aλ²D, and with E=V/h=λ²V/H we obtain

$$Q=\epsilon {\mathrm{\lambda }}^4\frac{A}{H}V.$$ 7.45

The stress balance τ₃₃=0 is then expressed in terms of the potential difference or charge as

$$\mu ({\mathrm{\lambda }}^{-2}-{\mathrm{\lambda }}^{-8})=\epsilon \frac{V^2}{H^2}\mathrm{and}\mu ({\mathrm{\lambda }}^6-1)=\frac{Q^2}{\epsilon A^2}.$$ 7.46

An interesting feature of these equations is that the potential has a maximum with respect to λ where λ³=2, but the corresponding electric field increases monotonically with λ. This type of behaviour and its connection with material instability and electrical breakdown has been discussed in detail in [129], to which we refer for further references.

The neo-Hookean model can be replaced by any appropriate strain-energy function for an elastomeric material. However, for simplicity we retain the neo-Hookean model but consider a slightly more general version of the electric contribution to ω, by replacing ελ⁴ in (7.42) by αλ⁴+β, where α and β are positive constants (with α=ε when β=0). Then, we obtain D=ε(λ)E, where ε(λ)=α+βλ⁻⁴ is a deformation-dependent permittivity, while the expressions in (7.46) are replaced by

$$\mu ({\mathrm{\lambda }}^{-2}-{\mathrm{\lambda }}^{-8})=\alpha \frac{V^2}{H^2}\mathrm{and}\mu ({\mathrm{\lambda }}^6-1)=\alpha \frac{Q^2}{A^2\epsilon {(\mathrm{\lambda })}^2}.$$ 7.47

Note that the above form of ε(λ) is consistent with the experimentally observed reduction in the permittivity of the material with increasing stretch [19].

8. Formulation of boundary-value problems

In the above example, we have considered a very simple boundary-value problem in which the deformation is homogeneous and the electric field uniform. For a general boundary-value problem, the deformation will be inhomogeneous and the electric field non-uniform, and we now state the equations and boundary conditions for the general case before their application to a specific problem in the following section. In particular, we consider only the situation in which there is no volumetric charge distribution, as is appropriate for a dielectric material.

When the constitutive law is expressed in terms of Ω(F,E_L), as in the above example, the total nominal stress tensor is given by (7.4)₁ and the associated equilibrium equation is (6.8), while D_L is given by (7.4)₂ and satisfies Div D_L=0. These equations are associated with the boundary conditions (6.12) and (6.14). Moreover, E_L satisfies (5.6), and hence is expressible in the form E_L=−Grad Φ, where Φ is a scalar function of X. This Lagrangian formulation is for an unconstrained material and requires the solution of the equations for the deformation χ(X) and Φ(X). The formulation for an incompressible material follows the same pattern, with appropriate adjustments to accommodate the incompressibility constraint (4.10) and specialization to isotropy.

Alternatively, with the constitutive law expressed in terms of Ω*(F,D_L), the total nominal stress tensor is given by (7.8)₁ and again has to satisfy the equilibrium equation (6.8), while E_L is given by (7.8)₂ and has to satisfy (5.6). The independent electric variable in this case, namely D_L, has to satisfy Div D_L=0, which, if required, allows D_L to be expressed in terms of a vector potential, but this is not pursued here.

(a). Illustrative example: extension and inflation of a tube

We now analyse a prototype example involving a non-homogeneous deformation and non-uniform electric field, namely that of the problem of extension and inflation of a circular cylindrical tube of incompressible isotropic electroelastic material, with the material properties based on the formulation using the energy function Ω*(F,D_L) with D_L as the independent electric variable. The mechanical loads on the tube consist of an internal pressure and an axial load, while a potential difference is applied between flexible electrodes coated on its inner and outer cylindrical surfaces which generate a radial electric field. The analysis in this section follows closely that in [130].

(i). The deformation

Prior to deformation the geometry of the tube is described in its reference configuration in terms of cylindrical polar coordinates R, Θ, Z by 0<A≤R≤B, 0≤Θ≤2π, 0≤Z≤L, A and B being the internal and external radii, respectively, and L the length of the tube. The tube is deformed radially and axially in such a way that the circular symmetry is maintained and the geometry is described in terms of cylindrical polar coordinates r, θ, z by a≤r≤b, 0≤θ≤2π, 0≤z≤l, where a, b and l are, respectively, the internal and external radii and the length of the tube in the deformed configuration.

Because of incompressibility, the deformation is described by the equations

$$r^2=a^2+{\mathrm{\lambda }}_z^{-1}(R^2-A^2),\theta =\mathit{\Theta },z={\mathrm{\lambda }}_{z}Z,$$ 8.1

where λ_z is the axial stretch, which is a constant (i.e. independent of the radius R). It is convenient to write the first of the above equations as r=f(R), so that

$$b=f(B)=\sqrt{a^2+{\mathrm{\lambda }}_z^{-1}(B^2-A^2)}.$$ 8.2

The associated deformation gradient F is diagonal with respect to the cylindrical polar axes, with diagonal components λ_r,λ_θ,λ_z, which are the principal stretches of the deformation, with the azimuthal stretch given by λ_θ=r/R and henceforth denoted by λ. Then, by the incompressibility condition (7.27), the radial stretch λ_r is given by ${\mathrm{\lambda }}_{\mathrm{r}}={\mathrm{\lambda }}^{-1}{\mathrm{\lambda }}_z^{-1}$, and we consider λ and λ_z to be the independent stretches. The invariants I₁ and I₂ are then expressed in terms of λ and λ_z as

$$I_1={\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}+{\mathrm{\lambda }}^2+{\mathrm{\lambda }}_z^2\mathrm{and}{I}_2={\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^2+{\mathrm{\lambda }}^{-2}+{\mathrm{\lambda }}_z^{-2}.$$ 8.3

(ii). The electric field

A radial electric field is generated within the material of the tube by means of a potential difference applied between the electrodes on R=A and R=B, and this produces equal and opposite charges on the two electrodes. Gauss’s theorem ensures that there is no radial field outside the tube. This assumes that end effects are negligible, which is a reasonable assumption normally adopted for a tube whose length is significantly larger than its thickness. Thus, the electric field has only a radial component E_r, which is independent of θ and z. The corresponding electric displacement component D_r=D_r(r) is a function of r only. The equation curl E=0 is then satisfied identically and div D=0 reduces to d(rD_r)/dr=0, so that rD_r(r) is a constant, equal to its value on either boundary, i.e.

$$r{D}_{\mathrm{r}}(r)=a{D}_{\mathrm{r}}(a)=b{D}_{\mathrm{r}}(b).$$ 8.4

Let Q and −Q be the total charges on r=a and r=b, respectively. The charges per unit area of the surfaces are then Q/(2πal) and −Q/(2πbl), and hence, on specialization of the boundary condition (6.11)₂, equation (8.4) yields

$$r{D}_{\mathrm{r}}(r)=\frac{Q}{2\pi l}.$$ 8.5

Let D_L denote the corresponding (radial) component of D_L, which, on specialization of (5.5)₂, is given in terms of D_r by $D_{\mathrm{L}}={\mathrm{\lambda }}_{\mathrm{r}}^{-1}{D}_{\mathrm{r}}=\mathrm{\lambda }{\mathrm{\lambda }}_z{D}_{\mathrm{r}}=Q/(2\pi LR)$. Then, the invariants K₄, K₅ and K₆ defined in (7.22) reduce to

$$K_4=D_{\mathrm{L}}^2,K_5={\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}{K}_4\mathrm{and}{K}_6={\mathrm{\lambda }}^{-4}{\mathrm{\lambda }}_z^{-4}{K}_4.$$ 8.6

The radial component E_r of the electric field E is obtained by specializing the constitutive relation (7.25) as

$$E_r=2({\mathit{\Omega }}_4^{\ast }{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^2+{\mathit{\Omega }}_5^{\ast }+{\mathit{\Omega }}_6^{\ast }{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2})D_r.$$ 8.7

The associated Lagrangian component, denoted by E_L, is obtained by specializing (5.5)₁ as $E_{\mathrm{L}}={\mathrm{\lambda }}_{\mathrm{r}}{E}_{\mathrm{r}}={\mathrm{\lambda }}^{-1}{\mathrm{\lambda }}_z^{-1}{E}_{\mathrm{r}}$.

(iii). Stress components and equilibrium

For the considered deformation and electric field, the total Cauchy stress tensor has no shear components with respect to the cylindrical polar coordinates r,θ,z, and its normal components are obtained by specializing (7.24) as

$$\begin{array}{rl}{\tau }_{rr}& =2{\mathit{\Omega }}_1^{\ast }{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}+2{\mathit{\Omega }}_2^{\ast }({\mathrm{\lambda }}_z^{-2}+{\mathrm{\lambda }}^{-2})-p^{\ast }+2{\mathit{\Omega }}_5^{\ast }{D}_{\mathrm{r}}^2+4{\mathit{\Omega }}_6^{\ast }{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}{D}_{\mathrm{r}}^2,\end{array}$$ 8.8

$$\begin{array}{rl}{\tau }_{\theta \theta }& =2{\mathit{\Omega }}_1^{\ast }{\mathrm{\lambda }}^2+2{\mathit{\Omega }}_2^{\ast }[{\mathrm{\lambda }}_z^{-2}+{\mathrm{\lambda }}_z^2{\mathrm{\lambda }}^2]-p^{\ast }\end{array}$$ 8.9

$$\begin{array}{rl}\text{and}{\tau }_{zz}& =2{\mathit{\Omega }}_1^{\ast }{\mathrm{\lambda }}_z^2+2{\mathit{\Omega }}_2^{\ast }[{\mathrm{\lambda }}^{-2}+{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^2]-p^{\ast }.\end{array}$$ 8.10

The invariants in equations (8.3) and (8.6) depend on the two independent stretches λ and λ_z together with K₄, and it is therefore advantageous to define a reduced energy function, denoted by ${\tilde{\mathit{\Omega }}}^{\ast }$ and defined by

$${\tilde{\mathit{\Omega }}}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z,K_4)={\mathit{\Omega }}^{\ast }(I_1,I_2,K_4,K_5,K_6),$$ 8.11

where I₁,I₂,K₅,K₆ on the right-hand side are given by (8.3) and (8.6).

Elimination of the Lagrange multiplier p* from equations (8.8)–(8.10) then yields the formulae

$${\tau }_{\theta \theta }-{\tau }_{rr}=\mathrm{\lambda }\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }\mathrm{\lambda }}\mathrm{and}{\tau }_{zz}-{\tau }_{rr}={\mathrm{\lambda }}_z\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }{\mathrm{\lambda }}_z}$$ 8.12

for the stress differences, while equation (8.7) simplifies to

$$E_{\mathrm{r}}=2{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^2\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }{K}_4}{D}_{\mathrm{r}}.$$ 8.13

Henceforth, it will be convenient to use the shorthand notations

$${\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }=\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }\mathrm{\lambda }},{\tilde{\mathit{\Omega }}}_{{\mathrm{\lambda }}_z}^{\ast }=\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }{\mathrm{\lambda }}_z}\mathrm{and}{\tilde{\mathit{\Omega }}}_4^{\ast }=\frac{\mathrm{\partial }{\tilde{\mathit{\Omega }}}^{\ast }}{\mathrm{\partial }{K}_4}.$$ 8.14

There is no electric field, and hence no Maxwell stress, outside the tube, so that the boundary condition (6.13) has only a mechanical contribution, which is taken to consist of an applied pressure P on the inner surface r=a and no traction on r=b, so that

$${\tau }_{rr}=-P\text{on}\hspace{0.17em}r=a\mathrm{and}{\tau }_{rr}=0\text{on}\hspace{0.17em}r=b.$$ 8.15

We also assume that there is no mechanical body force so that, in view of the radial symmetry, the equilibrium equation (6.5) has just a radial component, which, on use of (8.12)₁, we write as

$$r\frac{\mathrm{d}{\tau }_{rr}}{\mathrm{d}r}={\tau }_{\theta \theta }-{\tau }_{rr}=\mathrm{\lambda }{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }.$$ 8.16

On application of the boundary conditions (8.15), integration of the latter equation leads to an expression for the pressure P, namely

$$P={\int }_a^b\mathrm{\lambda }{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }\frac{\mathrm{d}r}{r}.$$ 8.17

As ${\tilde{\mathit{\Omega }}}^{\ast }$ depends on λ, λ_z and K₄=D²_L with D_L=Q/(2πLR), λ=r/R=f(R)/R, and b=f(B) depends on a via (8.2), equation (8.17) is an expression for the pressure P in terms of the inner radius a and the charge Q for any given initial geometry A, B, L and axial stretch λ_z.

An axial load is required on the ends of the tube in order to maintain the deformation. The tube is assumed to have closed ends, so that there is a contribution to the total axial load from the pressure P. When this contribution is subtracted, the result is the so-called reduced axial load, which we denote by F. By a standard procedure, this can be shown to have the form

$$F=\pi {\int }_a^b(2{\mathrm{\lambda }}_z{\tilde{\mathit{\Omega }}}_{{\mathrm{\lambda }}_z}^{\ast }-\mathrm{\lambda }{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast })r\hspace{0.17em}\mathrm{d}r.$$ 8.18

Like P, this depends on a and the charge Q for any given initial geometry and axial stretch.

(iv). Application to a class of material models

In order to set the stage for more detailed illustrations, we consider the class of energy functions introduced in (7.37), but with λ₁ and λ₂ replaced by λ and λ_z, respectively. Thus,

$${\tilde{\mathit{\Omega }}}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z,K_4)={\tilde{\omega }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)+\frac{1}{2}{\epsilon }^{-1}{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}{K}_4$$ 8.19

and we recall that ${\tilde{\omega }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)$ is a purely (isotropic) elastic contribution to the total energy which will be specialized later.

In the expressions for P and F in (8.17) and (8.18) the terms

$$\mathrm{\lambda }{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }=\mathrm{\lambda }{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast }-{\epsilon }^{-1}{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}{K}_4\mathrm{and}{\mathrm{\lambda }}_z{\tilde{\mathit{\Omega }}}_{{\mathrm{\lambda }}_z}^{\ast }={\mathrm{\lambda }}_z{\tilde{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }-{\epsilon }^{-1}{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}{K}_4$$ 8.20

are required. In each case, the term in K₄ can be integrated explicitly, and, on introduction of the notations

$$\eta =\frac{B}{A},q={\left(\frac{Q}{2\pi AL}\right)}^2,$$ 8.21

the formulae for P and F become, respectively,

$$P={\int }_a^b\mathrm{\lambda }{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast }\frac{\mathrm{d}r}{r}-\frac{q({\eta }^2-1)}{2\epsilon {\eta }^2{\mathrm{\lambda }}_z^3{\mathrm{\lambda }}_a^2{\mathrm{\lambda }}_b^2}$$ 8.22

and

$$F=\pi {\int }_a^b(2{\mathrm{\lambda }}_z{\tilde{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }-\mathrm{\lambda }{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast })r\hspace{0.17em}\mathrm{d}r-\frac{\pi q{A}^2}{\epsilon {\mathrm{\lambda }}_z^2}\log \left(\frac{\eta {\mathrm{\lambda }}_b}{{\mathrm{\lambda }}_a}\right),$$ 8.23

where the notations

$${\mathrm{\lambda }}_a=\frac{a}{A}\mathrm{and}{\mathrm{\lambda }}_b=\frac{b}{B}$$ 8.24

have been introduced. Equations (8.22) and (8.23) are equivalent to equations (45) and (46) in [130].

Instead of being expressed in terms of the charge via Q, P and F can equally be written in terms of the potential difference between the electrodes. Let V denote the electrostatic potential function, so that E=−grad V , which has only the radial component E_r with V =V (r). Thus, from (8.13), we obtain

$$\frac{\mathrm{d}V}{\mathrm{d}r}=-2{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^2{\tilde{\mathit{\Omega }}}_4^{\ast }{D}_{\mathrm{r}}.$$ 8.25

With the help of equation (8.5), this may be integrated to obtain the potential difference

$$V(b)-V(a)=-\frac{Q}{\pi l}{\mathrm{\lambda }}_z^2{\int }_a^b{\mathrm{\lambda }}^2{\tilde{\mathit{\Omega }}}_4^{\ast }\frac{\mathrm{d}r}{r}.$$ 8.26

In respect of (8.19) this yields the explicit formula

$$V(b)-V(a)=-\frac{Q}{2\pi l\epsilon }\log \left(\frac{\eta {\mathrm{\lambda }}_b}{{\mathrm{\lambda }}_a}\right).$$ 8.27

The mean value of the electric field through the undeformed thickness is denoted by E₀ and given by

$$E_0=\frac{V(b)-V(a)}{B-A}$$ 8.28

and is related to the charge by

$$\epsilon E_0^2=\frac{q{[\log (\eta {\mathrm{\lambda }}_b/{\mathrm{\lambda }}_a)]}^2}{\epsilon {\mathrm{\lambda }}_z^2{(\eta -1)}^2}.$$ 8.29

This connection enables (8.22) and (8.23) to be recast in terms of the potential difference as

$$P={\int }_a^b{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast }\frac{\mathrm{d}r}{r}-\frac{\epsilon E_0^2({\eta }^2-1){(\eta -1)}^2}{2{\mathrm{\lambda }}_z{\mathrm{\lambda }}_a^2{\mathrm{\lambda }}_b^2{\eta }^2{[\log (\eta {\mathrm{\lambda }}_b/{\mathrm{\lambda }}_a)]}^2}$$ 8.30

and

$$F=\pi {\int }_a^b(2{\mathrm{\lambda }}_z{\tilde{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }-\mathrm{\lambda }{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast })r\hspace{0.17em}\mathrm{d}-\pi A^2\frac{\epsilon E_0^2{(\eta -1)}^2}{\log (\eta {\mathrm{\lambda }}_b/{\mathrm{\lambda }}_a)}.$$ 8.31

Note that λ_a and λ_b are not independent but are connected by $({\mathrm{\lambda }}_b^2{\mathrm{\lambda }}_z-1){\eta }^2={\mathrm{\lambda }}_a^2{\mathrm{\lambda }}_z-1$, which follows from (8.2) on use of (8.24).

(v). Numerical results

For numerical illustration of the preceding formulae, we now choose a particular form of ${\tilde{\omega }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)$, namely that based on the model of Gent [75], for which

$${\tilde{\omega }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)=-\frac{\mu G}{2}\log [1-\frac{({\mathrm{\lambda }}^2+{\mathrm{\lambda }}_z^2+{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}-3)}{G}],$$ 8.32

where G is a positive dimensionless material constant and μ (also positive) is the shear modulus of the material in the undeformed configuration. It follows that

$$\mathrm{\lambda }{\tilde{\omega }}_{\mathrm{\lambda }}^{\ast }=\frac{\mu G({\mathrm{\lambda }}^2-{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2})}{G+3-({\mathrm{\lambda }}^2+{\mathrm{\lambda }}_z^2+{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2})}\mathrm{and}{\mathrm{\lambda }}_z{\tilde{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }=\frac{\mu G({\mathrm{\lambda }}_z^2-{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2})}{G+3-({\mathrm{\lambda }}^2+{\mathrm{\lambda }}_z^2+{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2})},$$ 8.33

expressions required in the formulae for P and F in §8a(iv).

It is convenient to present the results in non-dimensional form, and for this purpose we adopt non-dimensional versions of P, F, q and $E_0^2$ defined by

$$P^{\ast }=\frac{P}{\mu },F^{\ast }=\frac{F}{(\pi \mu A^2)},q^{\ast }=\frac{q}{(\mu \epsilon )}\mathrm{and}{e}^{\ast }=\frac{\epsilon E_0^2}{\mu }.$$ 8.34

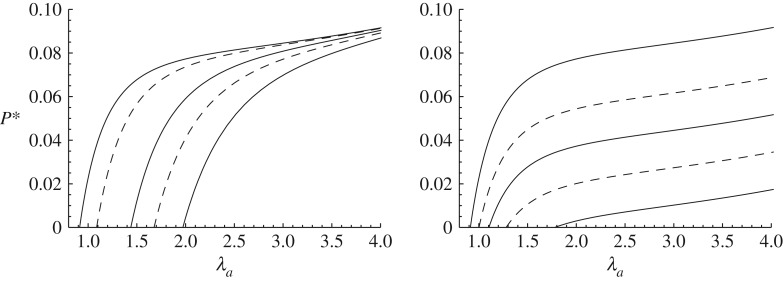
For definiteness, calculations were performed using Mathematica [131] based on the representative value λ_z=1.2 of the axial stretch, the geometrical ratio η=1.1 corresponding to a relatively thin-walled tube, and with G set to the value 97.2, which was obtained by Gent in modelling the elastic response of vulcanized rubber. The dependence of P* on λ_a is based on equations (8.22) and (8.30) and of F* on λ_a on equations (8.23) and (8.31).

In figure 1a, P* is plotted against λ_a for five selected values of q* and in figure 1b for five values of e*.

Figure 1.

Plots of the dimensionless pressure P* against λ_a based on equations (8.22) and (8.30) for the Gent model (8.32) with G=97.2, η=1.1 and λ_z=1.2: (a) for q*=0,1,5,10,20; (b) for e*=0,0.2,0.35,0.5,0.65. In each case, the uppermost curve corresponds to the purely elastic case and the value of P* decreases as the magnitude of the field measure, q* or e*, increases.

For each value of q* and e*, the pressure is clearly a monotonic increasing function of λ_a. Because of the limiting chain characteristic of the Gent model, λ_a approaches a limiting value (not shown in the figure) with $P^{\ast }\to \mathrm{\infty }$. The uppermost curve in each case corresponds to the absence of an electric field, while application of an electric field without pressure induces an increase in the tube radius and then the pressure needed to achieve a given radius is lower than in the absence of an electric field.

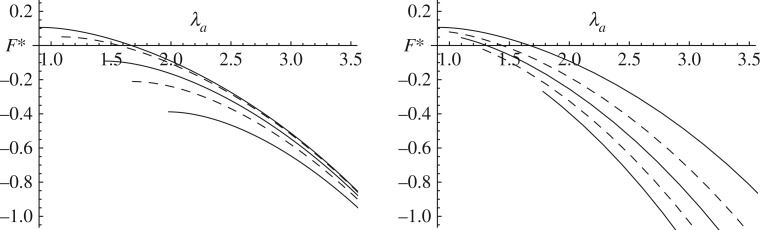
Figure 2 is the counterpart of figure 1 for the reduced axial load, with F* plotted against λ_a for the same values of the parameters. First, with λ_z set at 1.2, an electric field is applied which causes an increase in λ_a at zero pressure, which is then taken as the starting point for application of the pressure, which is different for each electric field, as measured by q* in figure 2a and e* in figure 2b, the same values of which are used as in figure 1.

Figure 2.

Plots of dimensionless reduced axial load F* against λ_a based on equations (8.23) and (8.31) for the Gent model (8.32) with G=97.2, η=1.1 and λ_z=1.2: (a) for q*=0,1,5,10,20; (b) for e*=0,0.2,0.35,0.5,0.65. In each case, the uppermost curve corresponds to the purely elastic case and the value of F* decreases as the magnitude of the field measure, q* or e*, increases.

As in figure 1, the uppermost curve corresponds to the purely elastic case. On application of an electric field, the value of F* associated with a given value of λ_a as the pressure increases reduces as the magnitude of q* or e* increases. It decreases monotonically as λ_a increases, and its sign changes from positive to negative as λ_a increases for small electric fields, so initially the pressure and/or electric field tends to decrease the tube length (so a positive F* is required to maintain the length), but thereafter tends to increase it. For larger electric fields the latter is the case, and a compressive axial load is required to prevent extension.

It is worth noting, by reference to figures 1 and 2, that, for both P* and F*, the influence of the electric field for fixed charge (through q*) declines as λ_a increases, whereas for fixed potential (through e*) the electric field has a significant effect.

It was shown in [130] that the results for both thinner- and thicker-walled tubes are qualitatively very similar to those shown in figures 1 and 2 in respect of the Gent model, the main difference being in the magnitudes of P* and F*. This also applies to the neo-Hookean and Ogden models that were also considered in [130] although the P* versus λ_a behaviour exhibits some differences, as is well known for the purely elastic response. We refer the readers to [130] for further details.

Because the results are qualitatively very similar for different tube thicknesses, including very thin tubes, it is advantageous to adopt the thin-walled approximation for P* and F* because this allows explicit formulae to be obtained that do not involve integrals and without specializing the energy function further, thus providing more insight. This approximation is now considered.

(vi). The thin-walled tube approximation and activation

As a measure of the wall thickness for a thin-walled tube, it is appropriate to introduce the small parameter δ defined by δ=(B−A)/A. It follows that A/R=1+O(δ) and, from (8.2), the expansion $b=(1+\delta {\mathrm{\lambda }}_z^{-1}{\mathrm{\lambda }}_a^{-2})a$ is obtained correct to the first order in δ, while, on use of (8.1)₁, λ=λ_a[1+O(δ)]. From (8.6)₁ and definition (8.21)₂ of q, it follows that K₄=qA²/R², and hence, by also approximating (8.29), we obtain

$$K_4=q[1+\mathrm{O}(\delta )],\epsilon E_0^2=\frac{q}{\epsilon {\mathrm{\lambda }}_z^4{\mathrm{\lambda }}^4}[1+\mathrm{O}(\delta )],$$ 8.35

the subscript a now being dropped from λ_a.

Then, to the first order in δ, the formulae for P and F from (8.17) and (8.18) yield

$$P=\delta {\mathrm{\lambda }}_z^{-1}{\mathrm{\lambda }}^{-1}{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z,q)\mathrm{and}F=\delta \pi A^2[2{\tilde{\mathit{\Omega }}}_{{\mathrm{\lambda }}_z}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z,q)-\mathrm{\lambda }{\mathrm{\lambda }}_z^{-1}{\tilde{\mathit{\Omega }}}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z,q)].$$ 8.36

These formulae do not involve specializing ${\tilde{\mathit{\Omega }}}^{\ast }$, but when specialized in respect of (8.19) in dimensionless form, they become

$$P^{\ast }={\mathrm{\lambda }}^{-1}{\mathrm{\lambda }}_z^{-1}{\overline{\omega }}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-{\mathrm{\lambda }}^{-4}{\mathrm{\lambda }}_z^{-3}{q}^{\ast },F^{\ast }=2{\overline{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-\mathrm{\lambda }{\mathrm{\lambda }}_z^{-1}{\overline{\omega }}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-3}{q}^{\ast },$$ 8.37

based on (8.22) and (8.23), and

$$P^{\ast }={\mathrm{\lambda }}^{-1}{\mathrm{\lambda }}_z^{-1}{\overline{\omega }}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-{\mathrm{\lambda }}_z{e}^{\ast },F^{\ast }=2{\overline{\omega }}_{{\mathrm{\lambda }}_z}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-\mathrm{\lambda }{\mathrm{\lambda }}_z^{-1}{\overline{\omega }}_{\mathrm{\lambda }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)-{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z{e}^{\ast },$$ 8.38

based on (8.30) and (8.31), where the following non-dimensionalizations have been adopted

$$q^{\ast }=\frac{q}{\mu \epsilon },e^{\ast }=\frac{\epsilon E_0^2}{\mu },{\overline{\omega }}^{\ast }=\frac{{\tilde{\omega }}^{\ast }}{\mu },{\overline{P}}^{\ast }=\frac{P^{\ast }}{\delta }\mathrm{and}{\overline{F}}^{\ast }=\frac{F^{\ast }}{\delta }.$$ 8.39

These formulae formed the basis for explicit results obtained in [130] for the activation response in respect of the neo-Hookean model, for which

$${\overline{\omega }}^{\ast }(\mathrm{\lambda },{\mathrm{\lambda }}_z)=\frac{1}{2}({\mathrm{\lambda }}^2+{\mathrm{\lambda }}_z^2+{\mathrm{\lambda }}^{-2}{\mathrm{\lambda }}_z^{-2}-3).$$ 8.40

In particular, for ${\overline{P}}^{\ast }=0$ we then have

$${\mathrm{\lambda }}^4{\mathrm{\lambda }}_z^2-1=q^{\ast }={\mathrm{\lambda }}^4{\mathrm{\lambda }}_z^4{e}^{\ast },{\overline{F}}^{\ast }=2({\mathrm{\lambda }}_z-{\mathrm{\lambda }}^2{\mathrm{\lambda }}_z^{-1})$$ 8.41

and hence

$${\overline{F}}^{\ast }=2{\mathrm{\lambda }}_z-2{\mathrm{\lambda }}_z^{-2}{(1-{\mathrm{\lambda }}_z^2{e}^{\ast })}^{-1/2}\text{or}{\overline{F}}^{\ast }=2{\mathrm{\lambda }}_z-2{\mathrm{\lambda }}_z^{-2}{(1+q^{\ast })}^{1/2}$$ 8.42

in terms of e* and q*, respectively, and we note that λ_z>λ for ${\overline{F}}^{\ast }>0$.

On the other hand, if ${\overline{F}}^{\ast }=0,$ we have

$$q^{\ast }={\mathrm{\lambda }}^4{\mathrm{\lambda }}_z^4{e}^{\ast }=2{\mathrm{\lambda }}_z^4{\mathrm{\lambda }}^2-{\mathrm{\lambda }}^4{\mathrm{\lambda }}_z^2-1,{\overline{P}}^{\ast }=2{\mathrm{\lambda }}_z^{-1}-2{\mathrm{\lambda }}_z{\mathrm{\lambda }}^{-2}$$ 8.43

and then, on solution of the quadratic (8.43)₁ for λ², we obtain, analogously,

$${\overline{P}}^{\ast }=2{\mathrm{\lambda }}_z^{-1}-\frac{2{\mathrm{\lambda }}_z^2({\mathrm{\lambda }}_z^2{e}^{\ast }+1)}{{\mathrm{\lambda }}_z^3+\sqrt{{\mathrm{\lambda }}_z^6-{\mathrm{\lambda }}_z^2{e}^{\ast }-1}}\text{or}{\overline{P}}^{\ast }=2{\mathrm{\lambda }}_z^{-1}-\frac{2{\mathrm{\lambda }}_z^2}{{\mathrm{\lambda }}_z^3+\sqrt{{\mathrm{\lambda }}_z^6-1-q^{\ast }}}$$ 8.44

and we note that λ>λ_z for ${\overline{P}}^{\ast }>0$.

For ${\overline{P}}^{\ast }=0$ and several fixed positive values of ${\overline{F}}^{\ast }$ and for ${\overline{F}}^{\ast }=0$ and several fixed positive values of ${\overline{P}}^{\ast }$, the interdependence of e* or q* and λ_z was illustrated in [130]. In the case ${\overline{P}}^{\ast }=0$, in terms of different variables similar results were provided in [58] for different values of the initial axial stretch (equivalently, different values of F*) but for a thick-walled tube with B/A=2.

Illustrations of the above formulae for the neo-Hookean model were provided in [130] with the proviso that the applicability of the neo-Hookean model is limited to moderate strains, and we refer the reader to the latter paper for further discussion.

(b). Other problems addressed in the literature

The general theory summarized in §6 has been used by a number of investigators to study specific problems related to the response of dielectric elastomers, and we therefore here briefly review a representative selection of these.

The homogeneous deformation discussed in §6c,d was examined in [120] for the energy function Ω* instead of Ω. References to the literature concerning the deformation of a thin rectangular plate induced by an electric field normal to its major faces and associated stability analysis have been detailed in §2a and are not repeated here. The same problem, without compliant electrodes and with the Maxwell stress exterior to the plate, has also been examined for a particular material model on the basis of the implicit theory of Bustamante & Rajagopal [117].

Homogeneous simple shear of a slab for an incompressible material, also with an electric field normal to the slab, was examined in [106] for a general energy function and the dependence of the shear stress on the electric field was illustrated for a particular material model. Based on the same theory, the inhomogeneous shear of a slab was examined by Kumar & Kumar [132]. Using the constitutive theory of Rajagopal & Wineman [133], Bortone [134] also studied inhomogeneous shear in the presence of an electric field.

For a circular cylindrical tube several problems have been examined. First, the radial expansion and/or axial extension have been analysed by Dorfmann & Ogden [135] with either an axial or a radial electric field or their combination and with the Maxwell stress exterior to the tube accounted for, giving expressions for the internal pressure and axial load for a general incompressible isotropic electroelastic material model. The same theory, for a number of specific material models, was applied by Díaz et al. [59] in studying the pressure–radius relation for the purely radial expansion (without axial extension) of an incompressible isotropic tube subjected to a radial electric field. Bustamante & Rajagopal [117] considered the same problem for a specific material model within their general implicit theory, and obtained numerical results for the stress distribution in the tube for given values of the internal radial traction and radial electric field, also accounting for the Maxwell stresses. For the situation in which the inner and outer circular boundaries of the tube are coated with compliant electrodes, this problem was treated at length by Melnikov & Ogden [130] and Zhu et al. [58] and discussed in §8a.

Second, pure axial shear deformation of a thick-walled tube with a radial electric field has been analysed by Dorfmann & Ogden [106] for an incompressible isotropic electroelastic material, and, when combined with radial inflation, by Kumar & Kumar [132]. Dorfmann & Ogden [135] similarly evaluated the influence of a radial electric displacement field on the azimuthal shear response. The combination of axial and azimuthal shear, namely helical shear, was studied in Dorfmann & Ogden [120] with both radial and axial electric field components. In each of these problems, the general results were illustrated for a particular choice of constitutive law.

Inflation of a thick-walled spherical shell with radial electric field and an internal pressure has been examined in several papers, without compliant electrodes [34,135] with the exterior Maxwell stress accounted for, and with compliant electrodes on its inner and outer surfaces [71,73]. Rudykh et al. [70] examined the snap-through instability of a thin-walled spherical balloon.

Recognizing that composites can improve the response characteristics of electroactive materials, a number of authors have analysed different aspects of the influence of composite structures. For example, deBotton et al. [136] showed that the response of a laminated composite actuator can be better than that of its constituents. The instability of multilayered dielectric composites has been investigated by Bertoldi & Gei [137], Rudykh & deBotton [138] and Rudykh et al. [139] using the theory of linearized incremental deformations and electric fields superimposed on a known underlying deformation and electric field formulated by Dorfmann & Ogden [43]. Spinelli & Lopez-Pamiez [140] have examined the stability of laminated composites via the macroscopic strong ellipticity condition and the method of homogenization.

Homogenization has been used to determine the effective overall electroelastic properties of two-phase composites consisting of a periodic array of rigid polarizable ellipsoidal particles in an elastomer dielectric matrix by Castañeda & Siboni [141,142], while Siboni & Castañeda [143] and Siboni et al. [144] obtained homogenization estimates for the effective properties of composites with aligned long rigid dielectric fibres of elliptical cross-section embedded in an elastomer dielectric matrix, and investigated different stability criteria. As an application, in [143] a thin dielectric elastomer composite sandwiched between two flexible electrodes was considered, while in [144] the stability of a dielectric composite subjected to all around dead electromechanical loading was examined. Lopez-Pamies [145] used homogenization to predict the macroscopic behaviour of an elastic dielectric two-phase composite under large deformations and electric fields with various distributions of deformable particles embedded within a matrix.

Several papers dealing with small-amplitude waves and motions superposed on finite deformations in the presence of an electric field have been investigated by Shmuel & deBotton [146,147], Shmuel et al. [148], Shmuel [149,150], Su et al. [151] and Wu et al. [152] based on the general quasi-electrostatic approximation theory in Dorfmann & Ogden [49], wherein the theory was applied to electroelastic surface waves propagating on a half-space.

Finally, we mention that the solution of non-trivial boundary-value problems for electroelastic bodies requires the use of computational approaches such as those initiated by Vu et al. [153] and Vu & Steinmann [154], in particular finite-element methods based on variational principles. Extensive discussions of electroelastic variational principles are contained in the papers by Bustamante et al. [155] and Vogel et al. [156].

9. Concluding remarks

In this paper, we have reviewed some of the history of the development of electroactive materials capable of large deformations with particular reference to their use as actuators together with the general theory of electroelastic theory. We then went on to describe a particular theory in some detail together with representative and illustrative applications. The final subsection above provides a brief account of some of the many boundary-value problems that have been tackled on the basis of the theory. We have focused on the macroscopic continuum theory without discussion of microscopic or multiscale approaches. These are major topics which require more detailed consideration than the space available here allows. Indeed, a separate review of each of these topics would be timely and very welcome, and, as mentioned at the end of §2a, this is also the case for the analysis of instability and failure phenomena.

Finally, it should be mentioned that at present relatively simple material models have been used to illustrate the behaviour of electroactive polymers for a variety of geometries and combined mechanical and electrical loading conditions because there are not enough experimental data available to justify the use of more refined models. In order to inform and improve the modelling and to provide a basis for more realistic predictions, it is important to obtain a more detailed characterization of the properties of electroactive polymers for a wide range of deformations and electric fields.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors contributed equally in all aspects.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.