Benchmarking Quantum Chemical Methods: Are We Heading in the Right Direction?

Abstract

Theoreticians and experimentalists should work together more closely to establish reliable rankings and benchmarks for quantum chemical methods. Comparison to carefully designed experimental benchmark data should be a priority. Guidelines to improve the situation for experiments and calculations are proposed.

Over the last years a subtle but profound change has taken place in chemical research. Electronic structure calculations have become ubiquitous, with much of the work published in the field today making use of theoretical results. The chemistry curricula have also been accompanying this change, incorporating a growing number of courses on quantum chemistry and computational chemistry, slowly but surely. The reasons behind this quiet revolution are all well known. The computing hardware has undergone significant developments, such that even a mobile phone surpasses the performance of computing clusters from 30 years back. This allows us to compute more and in less time, translating into larger systems, longer timescales. Furthermore, the computer algorithms have improved significantly, expanding the realm of application and the quality of the calculations performed.

We find ourselves at a perceived turning point where quantum chemical calculations are believed by many to be on par with experimental methods. Even if the reader may not share this view, it is not difficult to find reasons why others would. Already in the 1960s we observe examples of theory competing with experiment in terms of accuracy. A seminal example is the H₂ adiabatic dissociation energy computed by Kolos and Wolniewicz.1 The authors carried out a variational calculation and found their value (36 117.4 cm⁻¹) to exceed the best experimental estimate at the time (36 113.6±0.6 cm⁻¹).2 Given that the theoretical estimate would necessarily give an upper bound to the true energy of H₂, and thus a lower bound to its dissociation energy, the experimental value was questioned. The episode was only concluded after a further experiment confirmed the theoretical result.3 Since then, there have been several cases where theory has made predictions which were only later confirmed by experiment,4, 5, 6, 7, 8, 9 and many more where theory played an essential role in the interpretation of experimental results.

Already the early H₂ story points to a fascinating aspect, in particular now that the agreement between theory and experiment has progressed to eight significant digits.10 In contrast to other fields of science, where a model is mostly used as a framework to break down and understand complex systems, electronic structure methods are regarded as quantitative‐data providers. This is a completely different scenario from that faced in biology or economics, just to name two examples. In many fields, the ruling equations are still unknown, or the conditions are ill‐defined. An exact monthly weather forecast is unthinkable, but we chemists dare to believe that our theoretical models will be able to provide us with a reaction mechanism involving hundreds of atoms. This line of thought is fertile ground for illusions of grandeur, and calls for a critical analysis of the relation between experiment and theory in chemistry (Figure 1).

Figure 1.

A false change of paradigm. Experience has taught us that one should be critical on both ends.

Since we are not philosophers of science (nor pretend to be), we will focus on a pragmatic view and only briefly touch on fundamental issues. In the language of Thomas Kuhn, quantum chemistry is largely in a rather unspectacular state of normal science.11 Apart from subtle issues such as parity violation,12 the Schrödinger equation and its relativistic variants are assumed to be essentially correct and complete for all practical purposes.13 Currently the cutting edge of quantum chemistry is simply modeling larger and larger systems in an increasingly quantitative way.

Our concern is thus evolutionary rather than revolutionary. Beyond the usual method validations within the theoretical community, we address the relation between quantum chemical calculations and experiments. In order to guarantee a fruitful interplay, we need to define how to experimentally evaluate and benchmark the numerous methods in the best way. We argue that this subject is frequently neglected, and that this neglect leads to a slower development of quantum chemistry and the field of chemistry as a whole. While we are unable to provide unique and final recipes, we would like to share some of our thoughts and discussions with the community and conclude with some recommendations. Without prejudice against any of the methodologies covered under the general designation of theoretical/computational chemistry,14 this essay deals exclusively with electronic‐structure methods, given their particular appeal and promise towards a first‐principles description of chemical systems. Mechanical force fields and topological methods, for example, have a more pragmatic relation to experiment, and do not warrant the same type of discussion. The dynamics and statistics needed to connect the electronic‐structure information to the real world would also be an important and critical topic of its own. This is beyond our scope, just like conceptual models and other qualitative theories.

Theory Benchmarking Theory

One permanent issue in quantum chemistry is to establish a practical overview of the many different approximations to the Schrödinger equation. Literally hundreds of electronic‐structure methods are available at our fingertips, and it can be a cumbersome task to compare them or even to select one for a particular application. One way to deal with this question has been to establish a hierarchy of models. In the case of wave‐function methods, the process can be rather straightforward. For single‐reference correlated methods there are widely accepted orderings. The latter can be better understood through the use of diagrammatic representations. Generally, the method that includes the greater number of terms lies higher in the ranking. However, this is not necessarily true, since the nature of each term is different along with the impact on the overall performance. While a ranking for coupled cluster (CC) methods such as CCSD<CCSDT<CCSDTQ<CCSDTQP is rather straightforward, the ordering within the Møller–Plesset perturbation series (MP2, MP3, MP4, …) will depend on the system being studied, since it is not necessarily convergent.15 And although CCSDT is a more expensive approach, the CCSD(T) method is for most application purposes a more robust method than the full triples variant. This results from a quite favorable cancellation of error between the overestimated triples contribution and the neglect of quadruple excitations.16

Also in the case of density functional theory (DFT) there have been attempts at establishing similar hierarchies. The most well‐known example is the DFT Jacob's Ladder, proposed by Perdew,17 which defines a set of steps featuring the different levels of approximation in the exchange‐correlation kernels. Even for artificial molecules, such hierarchies have been shown to shine through.18 It is, however, relatively easy to find individual examples where a functional from a lower rank may be able to outperform methods higher up in the ladder19and truth be told, this was not the intended purpose of Perdew's proposal.

Although such hierarchies can be questionable, they provide a very welcome order amidst the chaos of modern‐day quantum chemistry toolboxes. They have also created the possibility to carry out theory benchmarks with theory as reference. The quality of a model is thereby no longer measured through any relation to experiment, but purely to the similarity to another model. This practice has become so popular that many manuscripts dedicated to quantum chemistry benchmarks do not feature a single experimental result.20 Sometimes, the word “experiment” is missing from the entire manuscript, or may at best be found once in the outlook. The current most complete set of benchmark sets, the GMTKN30,21 includes only a small amount of experimental reference data (Figure 2). The acceptance of CCSD(T) as a “gold standard”22 has been a particular encouragement to the practice, from DFT benchmarking23, 24 up to theory‐only blind‐test challenges.25 As further evidence, if one looks again at the GMTKN30 database, 14/30 sets use as reference data estimated CCSD(T)/CBS limits. Even improvements beyond CCSD(T) are sometimes judged without any reference to experiment.26 This is certainly related to the fact that most such calculations refer to a fixed geometry, although the importance of structural relaxation at least for selected degrees of freedom has been emphasized.27

Figure 2.

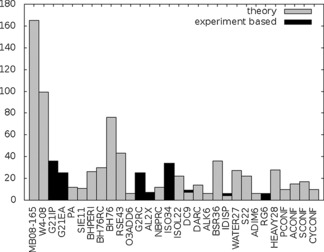
Reference points in the GMTKN30 database, classified according to their origin (pure theoretical values or experiment‐based).

There are good reasons for theory‐only benchmarking. Even weather forecasters can develop a reasonable sense for their simulation error by just comparing the results of disparate numerical models for the same starting conditions. Another obvious application is the comparison of different codes and numerical strategies within a model family.28 For the identification of isolated experimental database errors, sometimes even superficial comparisons between different computational predictions suffice.29 One may also be interested in a single quantity which is ill‐defined or hard/impossible to measure experimentally (e.g., harmonic spectra,30 or transition‐state structures31, 32) so that the best (or only) reference is the result of another calculation. Or there may simply be no satisfactory experimental data available or in reach for a specific class of compounds.33 Current state‐of‐the‐art quantum chemical methods depend on a wide variety of approximations. They range from more technical issues such as density fitting34, 35 and numerical grids,36 up to developments such as explicit correlation,37 trying to reach the complete basis set limit. All these require the comparison to internal standards.

However, the literature is filled with examples where the comparison to experiment is completely disregarded for no particularly good reason. There are many causes for this fault. On one hand, we have the focused education of theoretical chemists, who dedicate several years to equations and little time to lab experience. In other cases, one may find it difficult to establish relations between what has been measured in experiment and the results of calculations, or even in understanding the approximations the experiment itself involves. More trivially, insufficient time is spent in searching the literature due to the all too well known publication pressure.38 All of these issues can result in misguided comparisons (oranges and apples) leading to frustration or flawed benchmarking, or to a complete neglect of the published experimental data.

There are also cases where the appropriate experimental literature is cited but not really digested by the theory/theory benchmark. As an example, we pick the ethanol dimer, which was shown semi‐experimentally to revert the conformational preference of its monomer (trans) to a homochiral double‐gauche arrangement in the lowest‐energy pair structure.39, 40 The driving force is obviously a compact, dispersion‐optimizing packing. A recent computational study claiming accurate (1 kJ mol⁻¹) ab initio approximations for longer‐chain alcohol clusters41 uses ethanol dimer as a stepping stone for the validation of their methods, which is not an unreasonable approach. Based on the results of a series of calculations of perceived increasing accuracy, the authors argue that in contrast to all the cited experimental and high‐level computational evidence, the double‐trans dimer is systematically the most stable dimer. This is due to a range of misconceptions, not the least of which is the overlooked difference between homo‐ and heterochiral pairings and the resulting apparently decreased importance of dispersion corrections. Even if some of the targeted cluster quantities happen to be close to older thermodynamic data, this is clearly no match for the right reason. Careful comparison to available spectroscopic data would immediately have revealed the flaws in this laborious study.

We end this section with a little story told by Coulson42 about an exhibition of quantum chemistry in Paris after World War II. There were lovely diagrams of resonance structures of benzene and excellent numerical illustrations of the lowering in energy produced by them. But Linus Pauling, as he went round that exhibition and came to these diagrams, said, “Why don't you put a bottle of the stuff by the side of the diagrams?”

Experiment Benchmarking Theory

At the end of the day, any weather‐forecasting model has to be tested against reality, and success for one season or region is no guarantee for further successful predictions. Chemists also want reliable forecasts for exotic conditions,43 not only for well‐trod paths. And even for those, there may be occasional surprises. In the end, there is no way around some experimental benchmarking. The benefits of this practice are obvious, when one looks back at the development of electronic‐structure methods. Even though quantum chemists will often find shortcomings in their methods when performing theory/theory benchmarks, it is usually the hard test against experiment that brings about a change in practice. A recent example of this is the description of dispersion forces. Although conventional DFT functionals were well known to fail in the description of weakly bound van der Waals complexes,44 until about ten years ago a large community regarded this as a minor inconvenience for computational studies on “realistic” systems. Looking at the interaction curves of rare‐gas dimers was not convincing enough, and it was uncertain whether these small contributions would cancel out or add up. A real change only came about when a series of benchmark studies with increasing system sizes, supported by experimental evidence, unequivocally showed that the DFT functionals in use at the time were systematically biased, and that the errors were in fact adding up.45, 46, 47, 48, 49, 50, 51

Obviously, experiments aiming to benchmark theory need to be carefully designed, and the right questions have to be posed. For the macroscopic properties of a multilayer insulation material, quantum chemistry may at the start not be more quantitative than models in biology or economics. Reductionism is called for. Experimentalists must provide answers to popular excuses from the theory side (Figure 3): System too big? Let's boil it down to the essentials to meet theory.^52] Thermal motion? Let's cool down the sample for a start.53 Environmental effects? Let's move into the gas phase for a reliable comparison.54 Experimentalists offer lots of elegant solutions for the apparently contradicting requirements of gas‐phase isolation and low temperature. Other complications, such as relativistic or quantum‐electrodynamic effects, cannot be removed by the experimentalist.

Figure 3.

Experimentalists can also play a role in removing complexity in different chemical systems and providing the best conditions for benchmarking.

There is something less exotic which is hard for experimentalists to get rid of: zero‐point vibrational energy (ZPVE), or separated quantum delocalization of the nuclei, an artifact of the Born–Oppenheimer approximation which is so fruitful in electronic structure theory (Figure 4). At least for the study of intermolecular interactions, where theory/theory benchmarking is very popular, this can limit the system size more than one would wish for. Progress is definitely needed from both sides in this area and it is helpful to have careful analyses on how to best bridge this.55, 56

Figure 4.

A resilient obstacle between theory and experiment: the ZPVE.

Experimental benchmarking requires a special state of mind. The first goal is to identify any possible weakness in the experimental approach chosen to test quantum chemical methods. This requires phases of intense interaction with theory but also events of blind competition,57 because, as Feynman justly emphasized:58 The first principle is that you must not fool yourself—and you are the easiest person to fool. If the experimental result is known beforehand to the theoretician or the theoretical prediction known to the experimentalist, there is a non‐zero risk of mutual influence, however rationally the scientists may approach the challenge. Another useful factor is molecular diversity, something chemists are very good at generating. A single match between theory and experiment is almost worthless, because it could always be the result of fortuitous error cancellation. A broad, disparate data set is usually needed, and this means a lot of work at the laboratory bench. Because it has become widespread to train density functionals on such benchmark data sets (so far mostly theoretical ones, we regret), there is a continuous demand for new, reliable experiments.

While the credo of the theoretical benchmarker is “calculate observables!”, the motto of the benchmark experimentalist should be “measure fundamental quantities!”. The hyperpolarizability of a nonlinear optical material or the third virial coefficient of a polar gas may be highly relevant quantities to which quantum mechanics contributes importantly, but whether or not a particular quantum chemical method captures the essentials can often be seen most transparently by simply looking at structures56 and energies,59, 60 properties of the stationary points on the potential energy hypersurface. This explains why spectroscopic methods play a central role in benchmarking. No higher‐order property can be predicted correctly for the correct reason, if the predicted structure or energetics is far off. Therefore, benchmarking experimentalists must sometimes make an effort to move away from their favorite observables and system conditions and try to address more basic ones. In this way, the possibilities for error compensation are minimized. A meaningful approach to the judging bench usually means more effort at the laboratory bench. This also allows much higher levels of computation to be used and validated.61 Ideally, these could subsequently serve as secondary standards for theory/theory comparisons.62

In organic chemistry, absolute energies are often less important than conformational preferences. Therefore, experiments on such energy rankings of different structures for a given system may also be useful for benchmarking purposes. Again, it is beneficial for the comparison to quantum chemistry to remove thermal excitation and the environment. For intramolecular isomerism, the case of glucose may be mentioned,54 although one should remember that the global‐minimum structure for C₆O₆H₁₂ is a completely different one.63 Solvation preferences can be studied by intermolecular balance experiments as a function of chemical substitution.64 It turns out the balance between π‐cloud and oxygen solvation of anisoles is not captured correctly by the M06‐2X functional, whereas the B3LYP‐D3 functional performs satisfactorily. Whether this is for a good reason can be found out by extending the data base.

Numerous good‐practice examples of benchmark comparisons to experiment may be found in the literature and only a few recent examples can be mentioned here. The Hättig group compared different methods for calculating adiabatic electronic excitation energies based on a large high‐resolution experimental database compiled by Leutwyler.65 Vibrational frequencies can be compared rather rigorously to experiment, at least for small molecules, and their benchmarking66, 67 contributes to a resolution of the ZPVE problem. Grimme's group compared experimental rotational constants (after ZPVE correction) to theoretical predictions68 and also cautiously explored back‐corrected experimental noncovalent interactions for very large systems.69 Such attempts to bring experiment and theory together despite environmental effects can be challenged in a subsequent step by other theoretical methods,70 leading to a healthy competition between different approaches. A recurrent conclusion from such scientific dialogues is the need for more accurate low‐temperature gas‐phase reference data for complex formation energies.53 Thermodynamic data in the gas phase provide a particularly rich and frequently explored source for stable‐molecule energetics.71 On the other end, periodic solids offer access to interaction energies through experimental sublimation enthalpies.72

Chemistry is about change and it would be far too restrictive for benchmarking activities to stay at the static level of structures and energies. It is worth mentioning the counterpart to the H₂ energy challenge in reaction dynamics and kinetics: the H+H₂ reaction. Ever since the archetypical representation of its reaction surface73 it has been the subject of countless detailed experimental benchmarking efforts.74 Scattering experiments and time‐resolved spectroscopy continue to provide the most valuable reference data for chemical dynamics and thus the time‐dependent Schrödinger equation. This also brings us to another point. Advances are not only made through benchmark databases. Exemplary comparisons between theory and experiment for selected molecules are also valuable, because they have the potential to push the frontiers of methodology. Impressive examples include alanine,75 butane,76 anionic gold clusters,77 and even condensed water.78 It then remains to investigate whether such frontier methods/approaches are generally applicable to other chemical systems.

In this context, the role of benchmarking experiments is occasionally reversed.79 Rather than challenging theory, it may be that a persistent gap turns out to be an experimental misinterpretation, or even measurement error. When this happens, quantum chemists have done their homework with careful model assessment, or experimentalists have simply been too optimistic in their assumptions. The latter is more often the case for old experimental reference values,80, 81 which are easily shown to be inconsistent with state‐of‐the‐art quantum chemical predictions.82, 83 Today, countless experimental misinterpretations never surface because they are resolved before publication through intense interaction with theory, which is of course an excellent practice beyond benchmarking. Sometimes, there is a very fundamental and illuminating reason why theory and experiment cannot match, such as for the gap between electronic states of weakly bound dimers.84 More often, the opposite situation is found: Experiment and theory agree perfectly with each other for a specific quantity, but for no good reason, because two or more errors cancel.85 A recent example is the switch from stretched linear alkanes to dispersion‐driven hairpin conformations as a function of chain length. The MM2 force field prediction is within experimental error,86 but only because it overestimates the conformational folding energy and the dispersion attraction between the two chain ends by similar amounts.89 Anyone can be lucky in predicting snow for next Christmas! Different variants of CCSD(T) calculations also agree with experiment86, 87, 88 but now for much better reasons. It is actually quite possible that these calculations are more accurate than the experiment, which retains an estimated error bar of ±1 chain segments.89 This remains a possibility despite multiple spectroscopic evidence and the ZPVE bottleneck in the calculations. But we will probably only know for sure once a fundamentally improved experiment becomes available—possibly some kind of clever action spectroscopy on ultracold trapped molecules.

Conclusions

Like powerful action spectroscopies which have to be sufficiently validated by linear spectroscopies with more limited application range, powerful approximate models have to be carefully checked by higher‐quality (but size‐limited) approximations in quantum mechanics. In view of such important and straightforward intradisciplinary calibration activities, the more sophisticated and more tedious cross‐disciplinary benchmarking between theory and experiment tends to be neglected. This must change for the good of science, because both disciplines profit enormously from periodic cross‐fertilization. We advocate that it would be very helpful if junior quantum chemists and experimentalists were co‐educated for the activity of benchmarking in research‐training groups and research units. Weather forecasters should learn to check the real weather and weather‐dependent activities profit from a deeper understanding of the forecasting models.

In the end, we are all sinners, but in order to provide the best possible conditions for quantum chemistry to improve, some guidelines could perhaps be of use. Based on our views and the recent history detailed above, we would like to suggest:

• Theoreticians should focus on measurable quantities, and/or a well‐defined connection between the computed quantity and the experimental data. They should keep in touch with experimental colleagues and seek advice.

• In the case of theory/theory benchmarks, reviewers should also play a role in verifying whether pertinent experimental data are missing. Editors can contribute by regularly assigning an extra experimental reviewer.

• Experimentalists should contact theory colleagues and work collaboratively to establish realistic theory/experiment comparisons. They should insist that theoretical results and methods can and should be experimentally tested and in some cases even disqualified.

• Theoreticians should challenge published experimental results whenever the results of their calculations are in contradiction although they have strong reasons to believe that they should not be. The ensuing discussion can only benefit both communities.

• Regular blind challenges should be established on selected experimental benchmark results.

• To help in all the above mentioned points, there should be an effort to establish experimental‐benchmark data sets for use in the quantum chemistry community, rather than only the popular theory‐based data sets. This effort should be supported by scientific chemical societies.

• National institutes of standards should play an active role in the latter point, managing cross‐checking and critical reviews, supporting efforts in interrelating databases from different subfields of chemistry. Crystallographic databases may serve as good‐practice examples.

Apart from the benchmark studies, theoreticians and experimentalists alike could also contribute by changing some of their habits, so as to lower existing barriers:

Theoreticians should:

• not only mention the “successful” methods, but also take the opportunity to address the approaches that fail, in particular those with wide acceptance in the community

  (Reviewers should be open to this type of additions.)

• document their work properly

  (They should provide all needed material to ensure reproducibility and make proper use of the Supporting Information (provide structures, energies). This has to be supported by the editors of scientific journals. There is no current guideline on what a theoretical study should provide in the Supporting Information, and there is little involvement of the editors/referees in defining what should be included there. A universal file format for storing energy and coordinates would be helpful.)

• provide whenever possible estimates and comments on error sources and crucial approximations in the calculations carried out.

Experimentalists should

• promote to the quantum chemistry community results that are particularly amenable to computation and benchmarking

• promote to the quantum chemistry community conflicting experimental results where theory (or adjudicating experiments) could help in a decision

• present talks or posters on specialized theoretical chemistry conferences (WATOC, Symposium für Theoretische Chemie, …) to support the former points

• rectify outdated experimental data by the available publication instruments of revisit, critical review, erratum, retraction, comment.

This discussion leaves out, nonetheless, perhaps the biggest threat to benchmarking activities in quantum chemistry: the growing political pressure in several countries to focus only on immediately useful, applied science. Experimentalists and theoreticians alike have to fight for the freedom to contemplate the fundamental meeting points between their methods. And on this note we conclude, with the reminder that fortuitous success will not take us very far.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Ricardo Mata has been a research group leader at the University of Göttingen since 2009, working in the field of theoretical chemistry. His main topics of interest include weak molecular interactions, incremental/fragment‐based approaches to wave function methods, and applications in enzymatic catalysis. Among some of his main concerns are the applicability and accuracy of computational approaches moving from small to complex chemical systems.

Biographical Information

Martin Suhm likes to bring experiment closer to theory in the field of intermolecular interactions, to assist in identifying weaknesses and strengths in standard quantum chemical approaches. Over the last two decades, his Göttingen‐based group has combined linear IR and Raman spectroscopy tools with supersonic jet expansions to unravel the structure, vibrational dynamics, and energetics of flexible molecules and van der Waals complexes. He is a member of the Editorial Board of Angewandte Chemie.

R. A. Mata, M. A. Suhm, Angew. Chem. Int. Ed. 2017, 56, 11011.