Network Analysis on Attitudes

Abstract

In this article, we provide a brief tutorial on the estimation, analysis, and simulation on attitude networks using the programming language R. We first discuss what a network is and subsequently show how one can estimate a regularized network on typical attitude data. For this, we use open-access data on the attitudes toward Barack Obama during the 2012 American presidential election. Second, we show how one can calculate standard network measures such as community structure, centrality, and connectivity on this estimated attitude network. Third, we show how one can simulate from an estimated attitude network to derive predictions from attitude networks. By this, we highlight that network theory provides a framework for both testing and developing formalized hypotheses on attitudes and related core social psychological constructs.

Network theory might be the most interdisciplinary framework to date (e.g., Barabási, 2011; Borgatti, Mehra, Brass, & Labianca, 2009; Wasserman & Faust, 1994; Watts & Strogatz, 1998). In the past decade, network analysis has become increasingly important in psychology, where it was introduced as a psychometric framework for the representation of clinical and cognitive psychological constructs (e.g., Borsboom, 2008; Cramer, Waldorp, van der Maas, & Borsboom, 2010; Boschloo, van Borkulo, Borsboom, & Schoevers, 2016; McNally et al., 2015; van Borkulo, Boschloo, Borsboom, Penninx, & Schoevers, 2015; van de Leemput et al., 2014; van der Maas et al., 2006). More recently, network modeling has also been introduced into social psychology in the form of the Causal Attitude Network (CAN) model, which conceptualizes attitudes as networks of causally interacting evaluative reactions (i.e., beliefs, feelings, and behaviors toward an attitude object; Dalege et al., 2016).

The CAN model provides a promising theoretical framework for research on attitudes and other related social psychological core constructs, such as self-concept, prejudice, and interpersonal attraction. The generality of the data-analytic framework and simulation techniques that the CAN model uses, invites the application of the model to many different attitude objects. The model may be thus useful to researchers with various substantive interests, and here, we provide a brief tutorial on how to apply network theory to attitudes. While we focus on attitude networks, the techniques discussed here can easily be transferred to related constructs.

The outline of this article is as follows. First, we briefly discuss what a network is. We then illustrate network estimation from data on attitudes and calculation of standard network measures. Finally, we show how one can use simulations to investigate consequences of manipulating structural properties of an estimated network. The tutorial provides code in the programming language R (R Core Team, 2013), and we assume basic familiarity with R. Readers, who are not familiar with R, are referred to Torfs and Bauer (2014) for an excellent introduction to R.

What is a Network?

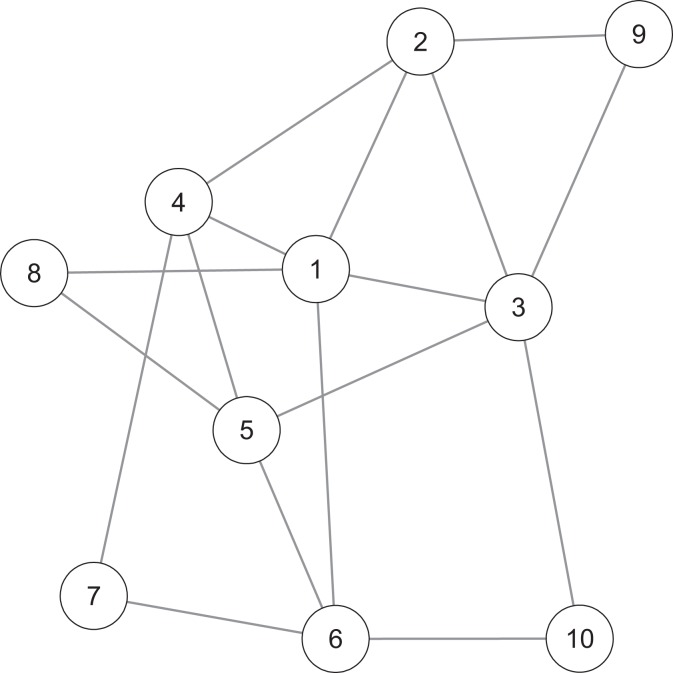
A network (called a graph in the mathematical literature) is an abstract representation of a system of entities or variables (i.e., nodes) that have some form of connection with each other (i.e., edges). Nodes can represent any entity or variable, like people, brain regions, or evaluative reactions, and edges can represent any form of connection, like friendship, associations in blood flow, or direct causal connections. Figure 1 shows an example of a simple network. Networks can be unweighted (i.e., edges are either present or absent) or weighted (i.e., edges can also differ in magnitude), and networks can be directed (i.e., edges indicate the direction of the connection) or undirected (i.e., edges show no direction). Here we focus on weighted undirected networks because the techniques for estimating directed networks from correlational data require assumptions that are often not tenable in psychological data (e.g., there are no reciprocal influences between variables; Costantini et al., 2014). Excellent and thorough introductions to network theory are provided in Kolaczyk (2009) and Newman (2010).

Figure 1.

Example of a simple undirected and unweighted network with 10 nodes (represented by circles) and 17 edges (represented by lines).

From a network perspective, attitudes are systems of causally interacting evaluative reactions that strive for a coherent representation of the attitude object (Dalege et al., 2016). Based on this basic idea, Dalege et al. (2016) developed the CAN model that links research on attitudes to network theory. Important tenets of the CAN model are that attitude networks show a high degree of clustering, with similar evaluative reactions exerting stronger influence on each other than dissimilar evaluative reactions (e.g., judging a person as honest exerts a stronger influence on judging this person as caring and vice versa than judging this person as intelligent) and that strong attitudes correspond to highly connected attitude networks. The CAN model further assumes that the dynamics of attitude networks can be captured by the Ising (1925) model, which originated from statistical physics. Here we use this assumption to simulate attitude networks based on the CAN model.

Network Analysis

In this section, we show how networks can be estimated from responses to attitude items and how one can calculate common network measures on these estimated networks. We focus on binary data, as the simulation based on the estimated networks that we discuss later is based on a model of binary variables. For estimating networks from continuous data or from data involving different types of variables, the interested reader is referred to Epskamp (2016) and Haslbeck and Waldorp (2016), respectively, and to the Supplemental Materials for examples. For the illustration of the techniques, we use the open-access data from the American National Election Study (ANES) of 2012 (available at www.electionstudies.org) on evaluative reactions toward Barack Obama (see Table 1 for an overview of the evaluative reactions). In the ANES of 2012, 5,914 individuals, representative of the adult U.S. American population, participated.

Table 1.

List of Items Tapping Evaluative Reactions and Their Abbreviations.

Item	Abbreviation
Items tapping beliefs
“Is moral”	Mor
“Would provide strong leadership”	Led
“Really cares about people like you”	Car
“Is knowledgeable”	Kno
“Is intelligent”	Int
“Is honest”	Hns
Items tapping feelings
“Angry”	Ang
“Hopeful”	Hop
“Afraid of him”	Afr
“Proud”	Prd

Note. Participants rated whether the items tapping beliefs described Barack Obama and whether they ever felt the feelings described by the items tapping feelings toward Obama.

Estimation of Attitude Networks

For the estimation of attitude networks, we use the eLasso procedure (van Borkulo et al., 2014). The eLasso procedure regresses each variable on all other variables in turn, and each regression function is subjected to regularization to reduce the size of the statistical problem of regressing a variable on a large number of variables and cope with the problem of multicollinearity in a data set involving a large number of variables (see Friedman, Hastie, & Tibshirani, 2008; Tibshirani, 1996). The best-fitting regression function is selected using the extended Bayesian information criterion as described in Foygel and Drton (2010). The independent variables included in the selected regression function define the nodes that the dependent variable is connected to by edges, which are weighted by the regression parameters.

If the observed data are indeed realizations of a (sparse) network structure, this technique provides an accurate estimation of this network (van Borkulo et al., 2014). In this case, the resulting network can also be regarded as a causal skeleton, in which the edges represent putative causal associations that can be either directed or reciprocal.

If one does not want to make the assumption that a causal network underlies the data, a network may still be highly useful, because the edges represent how well the connected variables predict each other if all other observed variables are being held constant. Thus, networks can be used to gain insight into the causal structure of the data, but also to merely describe the pattern of predictive relations in a dataset, or to represent the correlation structure of the data (Epskamp et al., 2012). In some instances, one might be willing to make the assumption that some of the variables measured form a causal system, while other variables might be worth controlling for without making the assumption that they form part of the causal system (i.e., covariates). We included a description in the Supplemental Material how to deal with covariates in network estimation.

Simulation studies have shown that for binary data, sample sizes of 500 are generally sufficient to estimate networks of low and moderate size (i.e., networks consisting of 10–30 nodes) and that for large networks (i.e., networks consisting of 100 nodes), a sample size of 1,000 is needed (van Borkulo et al., 2014). Regarding networks based on continuous data, sample sizes of 250 are generally sufficient for networks of moderate size (e.g., 25 nodes; Epskamp, 2016).

To estimate a network on the responses to the attitude items, which are stored in the data frame Obama (see the Supplementary R code), we can use the function IsingFit, available in the R package IsingFit (van Borkulo & Epskamp, 2015) and save the results in the object ObamaFit:

• ObamaFit <- IsingFit(Obama)

The object ObamaFit now contains the estimated network in the form of a weight adjacency matrix. A weight adjacency matrix has the same number of columns and rows as the number of nodes in the network, and the values in the matrix represent the edge weights between the different nodes (see the Supplemental Material for how to assess the stability of edge weights). The weight adjacency matrix of the Obama network can be called by using the command ObamaFit$weiadj (see Table 2). Each value above (below) the diagonal represents an edge from the node in the given row (column) to the node in the given column (row). As the Obama network is undirected, the weight adjacency matrix is symmetric. The values on the diagonal represent self-loops of the nodes, and these are all 0 in the Obama network, as self-loops cannot be estimated using cross-sectional data. The object ObamaFit also contains the thresholds of the different nodes that are the slopes of the regression equations of predicting a given node. The thresholds can be called with the command ObamaFit$thresholds.

Table 2.

Weight Adjacency Matrix of the Obama Network.

Node	Mor	Led	Car	Kno	Int	Hns	Ang	Hop	Afr	Prd
Mor	0	0.38	1.23	0.49	1.13	1.76	−0.22	0.19	−0.42	0.52
Led	0.38	0	0.8	1.38	0.58	0.93	−0.84	0.33	−0.46	0.82
Car	1.23	0.8	0	0.65	0.68	1.38	−0.49	0.78	−0.48	0.86
Kno	0.49	1.38	0.65	0	2.66	0.67	0	0.56	−0.23	0.39
Int	1.13	0.58	0.68	2.66	0	0.86	0	0.31	0.24	0.25
Hns	1.76	0.93	1.38	0.67	0.86	0	−0.36	0.34	−0.73	0.42
Ang	−0.22	−0.84	−0.49	0	0	−0.36	0	−0.28	2.21	0
Hop	0.19	0.33	0.78	0.56	0.31	0.34	−0.28	0	−0.78	2.32
Afr	−0.42	−0.46	−0.48	−0.23	0.24	−0.73	2.21	−0.78	0	−0.16
Prd	0.52	0.82	0.86	0.39	0.25	0.42	0	2.32	−0.16	0

Note. See Table 1 for the abbreviations of the nodes.

To plot the network, we can use the function qgraph, available in the R package qgraph (Epskamp et al., 2016). The following command produces the network shown in Figure 2 (except for the color of the nodes; we come back to this issue in the section on community detection):

Figure 2.

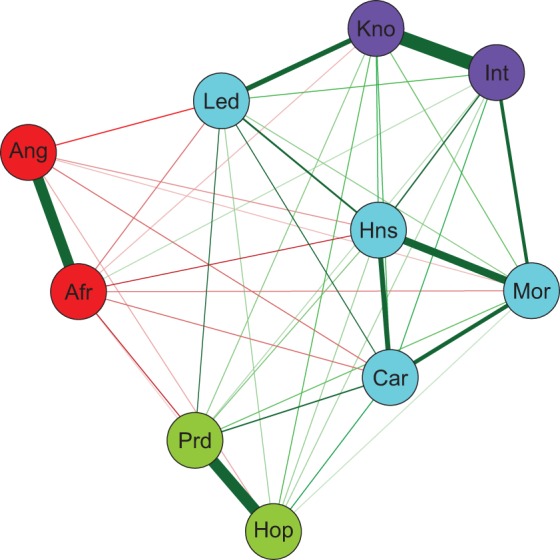
Network of the attitude toward Barack Obama. Nodes represent evaluative reactions and edges represent connections between evaluative reactions, with the edge width and color density corresponding to the strength of the connections. Green (red) edges represent positive (negative) connections. Colors of the nodes correspond to detected communities in the network. See Table 1 for the abbreviations of the nodes. See the online article for the color version of this figure.

• ObamaGraph <- qgraph(ObamaFit$weiadj, layout = ‘spring’, cut = .8)

The first argument in the function specifies the weight adjacency matrix to plot. The layout argument is used to plot the network using the Fruchterman–Reingold algorithm (Fruchterman & Reingold, 1991) that places strongly connected nodes close to each other. The cut argument specifies which edges should be plotted with higher width. All edges higher than the value specified in the cut argument are plotted with width according to their magnitude. Edges below the value specified in the cut argument only differ in color density. In the Supplementary R code, we also show how to plot a network using other color pallets.

Community Detection

Looking at the network shown in Figure 2, one can immediately recognize that nodes differ in their interconnectedness. To formalize this impression, we can use an algorithm that detects communities (or clusters) within the network. We use the walktrap algorithm (Pons & Latapy, 2005), as this algorithm performs well on psychological networks (Gates, Henry, Steinley, & Fair, 2016; Golino & Epskamp, 2016). An advantage of this algorithm compared to factor analyses is that it can detect dimensions of variables very well even when the different dimensions are highly correlated (Golino & Epskamp, 2016). To run the walktrap algorithm on the Obama network, we can use the function cluster_walktrap, available in the R package igraph (Amestoy et al., 2015). Before doing so, we have to create an igraph object containing the information on the Obama network and we have to take the absolute values of the edge weights because the walktrap algorithm can only deal with positive edge values:

• ObamaiGraph<- graph_from_adjacency_matrix(abs (ObamaFit$weiadj), ‘undirected’, weighted = TRUE, add.colnames = FALSE)

This command creates the igraph object ObamaiGraph containing the Obama network with absolute edge weights. The first argument specifies the input adjacency matrix, which is the weighted adjacency matrix of the Obama network with absolute values. The second and third arguments specify that we want an undirected and weighted network, respectively. The add.colnames argument can be ignored at the moment. We can now run the walktrap algorithm on the ObamaiGraph object:

• ObamaCom <- cluster_walktrap(ObamaiGraph)

This function runs the walktrap algorithm on the Obama network and saves the results to the object ObamaCom. We can extract the found communities using the following command:

• communities (ObamaCom)

To plot the network with the nodes being colored according to their community membership, we can use the following command, which creates Figure 2:

• qgraph(ObamaFit$weiadj, layout = ‘spring’, cut = .8, groups = communities(ObamaCom), legend = FALSE)

The groups argument is used to assign nodes to groups and the communities function extracts a list containing the community membership of each node. Here, the add.colnames = FALSE argument of the graph_from_adjacency_matrix function comes into play because this argument results in the nodes being numbered instead of having the variable names. This is needed, because the groups argument can only handle numeric values. The legend = FALSE argument is used because plotting the legend of the communities would not be informative.

The interpretation of the results of the community detection algorithm is straightforward: The red nodes represent negative feelings toward Barack Obama; the green nodes represent positive feelings toward Obama; the light blue nodes represent judgments pertaining mainly to interpersonal warmth (with judging Obama as a good leader also belonging to this community); and the purple nodes represent judgments pertaining to Obama’s competence. The community structure of the Obama network is also in line with the postulate of the CAN model that similar evaluative reactions are likely to cluster (Dalege et al., 2016).

Node Centrality

While community detection can be used to inspect the global structure of the network, centrality of nodes can be used to inspect the structural importance of the different nodes. Centrality of nodes can, for example, be used to infer which evaluative reactions most likely influence decision-making (Dalege, Borsboom, van Harreveld, Waldorp, & van der Maas, 2017) and which evaluative reactions would be the most effective targets for persuasion attempts (see section on network simulation). The probably most popular measures of centrality are degree (called strength in weighted networks), closeness, and betweenness (Barrat, Barthélemy, Pastor-Satorras, & Vespignani, 2004; Freeman, 1978; Opsahl, Agneessens, & Skovretz, 2010). The most straightforward of these indices is strength, as it is the sum of the absolute edge values connected to a given node and therefore represents the direct influence a given node has on the network.

Closeness and betweenness both depend on the concept of shortest path lengths. The shortest path length between two given nodes refers to the shortest distance between these two nodes based on the edges that directly or indirectly connect these two nodes. Dijkstra’s algorithm is used to find shortest path lengths in weighted networks (Brandes, 2001; Dijkstra, 1959; Newman, 2001). Based on this algorithm, shortest path lengths represent the inverse of edge weights that have to be “travelled” on the shortest path (see the Supplemental Material for an illustration of shortest path lengths). Closeness sums the shortest path lengths between a given node and all other nodes in the network and takes the inverse of the resulting value. Therefore, closeness represents how likely it is that information from a given node “travels” through the whole network either directly or indirectly. Betweenness represents how strongly a given node can disrupt information flow in the network, as betweenness calculates the number of shortest paths a given node lies on.

To calculate the different centrality estimates for the Obama network, we can use the function centralityTable and to plot these indices, we can use the function centralityPlot, both available in the R package qgraph (see the Supplemental Material for how to assess the stability of centrality indices):

• ObamaCen <- centralityTable(ObamaGraph, standardized = FALSE)

• centralityPlot(ObamaGraph, scale = ‘raw’)

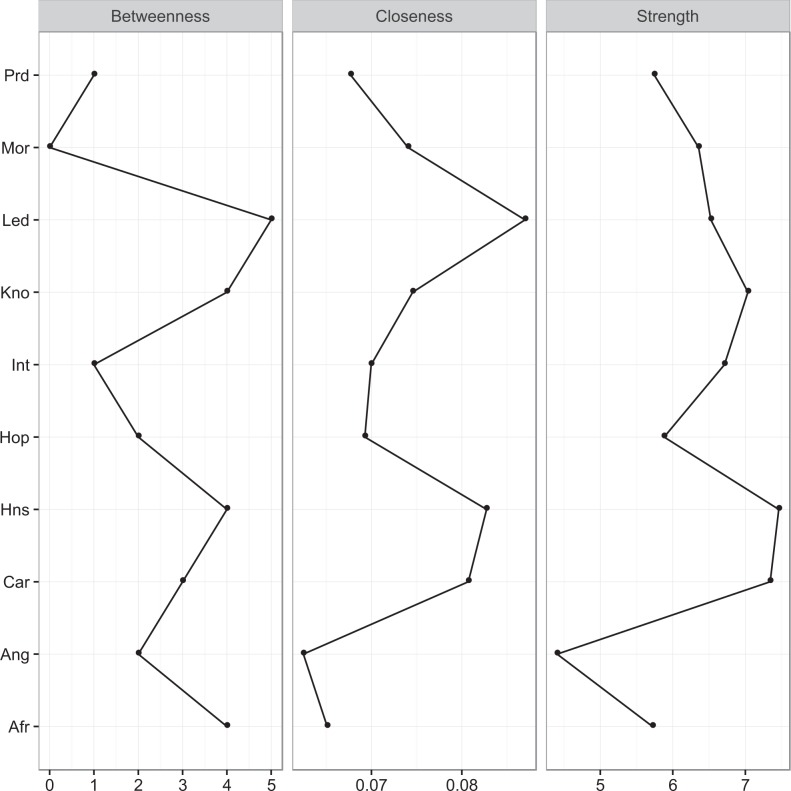
The first argument in these functions specifies the network for which we want to calculate the centrality indices, and the standardized = FALSE and scale = ‘raw’ arguments specify that we want unstandardized centrality estimates. The plots produced by the centralityPlot function are shown in Figure 3. As can be seen, two nodes seem to have high structural importance: The node Led has the highest betweenness and the highest closeness, while the node Hns has the highest strength. Looking back at Figure 2, we can see that the reason for the node Led having the highest betweenness is probably that, while it belongs to the warmth community, it is also relatively closely connected to the two feeling communities and to the competence community. This node thus connects the different communities and changes in the different communities probably only affect the other communities when the Led node also changes. That the node Led is closely connected to all communities also explains why it is the node with the highest closeness. Change in this node is thus likely to affect large parts of the network. Hns has the highest strength because it has strong connections to the nodes Mrl, Car, Int, and Led. Change in the node Hns would thus strongly affect many other nodes.

Figure 3.

Centrality plot of the Obama network. Left (middle) [right] panel shows the betweenness (closeness) [strength] estimates for each node of the Obama network. See Table 1 for the abbreviations of the nodes.

Network Connectivity

While centrality of nodes provides information on how change in a given node would affect the rest of the network, network connectivity provides general information on the dynamics of the network, as network connectivity and dynamics are closely connected (e.g., Kolaczyk, 2009; Manrubia & Mikhailov, 1999; Scheffer et al., 2012; Watts, 2002).

A common index of network connectivity is the average shortest path length (L; West, 1996), which is the average of all shortest path lengths between all nodes in the network. A low L indicates high connectivity. To calculate the L of the Obama network, we first have to calculate the matrix, containing all shortest path lengths. This can be done using the function centrality, available in the R package qgraph. Then we need to select the upper triangle of this matrix and take the mean of the resulting values:

• ObamaSPL <- centrality(ObamaGraph) $ShortestPathLengths

• ObamaSPL <- ObamaSPL[upper.tri(ObamaSPL)]

• ObamaASPL <- mean(ObamaSPL)

The object ObamaASPL now contains the L of the Obama network, which is equal to 1.53. In the section on network simulation, we illustrate some of the differences between highly and weakly connected networks.

Comparison of Networks

While it can be informative to study one attitude network, in many instances we want to compare networks of different attitudes. To do this, we can use the recently developed Network Comparison Test (NCT; van Borkulo, Epskamp, & Millner, 2016). The NCT utilizes permutations (i.e., rearranging of samples) to test whether two networks are invariant with respect to global strength (i.e., the sum of all edge weights), network structure, and specific edge values. We illustrate the use of the NCT by comparing the network of the attitude toward Barack Obama to the network of the attitude toward Mitt Romney. To do so, we created two matched data frames on the evaluative reactions toward Barack Obama (ObamaComp) and Mitt Romney (RomneyComp), respectively (see the Supplementary R code). To run the NCT on these data frames, we can use the function NCT, available in the R package NetworkComparisonTest (van Borkulo et al., 2016):

• NCTObaRom <- NCT(ObamaComp, RomneyComp, it = 1000, binary.data = TRUE, paired = TRUE, test.edges = TRUE, edges = ‘all’)

The first two arguments specify the data frames, we want to use to compare networks, the it argument specifies how many permutations will be performed, the binary.data argument specifies that we use binary data, the paired argument specifies that the two data frames contain responses of the same group of individuals, the test.edges argument specifies that we want to also test invariance of single edges, and the edges argument specifies that we want to test the invariance of all edges in the network.

The NCT indicated that the global strengths of the networks did not differ significantly but that the structures of the networks and some specific edges differed significantly. The difference in global strength was 1.12, p = .111. These values can be called using the commands NCTObaRom$glstrinv.real and NCTObaRom$glstrinv.pval. The structure of the networks was not invariant, as the maximum difference in edge weights of 0.72 was significant, p = .021. These values can be called using the commands NCTObaRom$nwinv.real and NCTObaRom$nwinv.pval. To investigate whether specific edges differed, we can use the command NCTObaRom$einv.pvals that gives us the Bonferroni corrected p values for each edge. As can be seen in Figure 4, four edge weights differed significantly between the two networks, three of which are connected to the node Led. From this, we can conclude that the node Led has a different role in the Romney network than in the Obama network. In the Romney network, the node Led is more strongly (positively) connected to other beliefs, while in the Obama network, it is more strongly (negatively) connected to the feeling of anger.

Figure 4.

Edges that differ significantly between the Obama and the Romney network. Red (green) edges indicate edges that had a higher value in the Obama (Romney) network. Values indicate the difference between the edges in the Obama network and the Romney network. See the online article for the color version of this figure.

Network Simulation

While network analysis can be used to describe systems, such as attitudes, network simulation can be used to make inferences on the dynamics of the system. Simulation of attitude networks can therefore help researchers to derive concrete hypotheses that in many instances cannot be derived by only studying the descriptives of the network. In this section, we first show how to simulate networks with varying connectivity and then show, as an illustration, how to simulate the results of change in nodes of varying centrality. This is helpful in determining at which nodes a persuasion attempt should be targeted.

To model dynamics of attitude networks, we make use of the Ising (1925) model, which represents an idealized model of probabilities that nodes in the network will be “on” or “off” (e.g., whether evaluative reactions will be endorsed or not). The Ising model consists of three classes of parameters. The first class represents continuous edge weights between nodes in the network that can be positive, negative, or 0. Positive (negative) edge weights make it more likely that the connected nodes assume the same (different) state and the higher the magnitude of the weights, the more likely it is that nodes assume the same (different) state. The second class represents continuous thresholds of nodes that also can be positive, negative, or 0. A positive (negative) threshold of a given node indicates that the node has the disposition to be “on” (“off”) and the higher the magnitude, the stronger the disposition of the given node. Finally, the Ising model utilizes a temperature parameter that scales the entropy of the network model (Epskamp, Maris, Waldorp, & Borsboom, in press; Wainwright & Jordan, 2008). High (low) temperature makes the network behave more (less) randomly by decreasing (increasing) the influence of both edge weights and thresholds. In attitude networks, temperature can be seen as formal conceptualization of consistency pressures (Dalege, Borsboom, van Harreveld, Waldorp, et al., 2017).

Network Connectivity

To simulate dynamics of estimated networks, we can use the function IsingSampler, available in the R package IsingSampler (Epskamp, 2015). This function requires the network from which we want to simulate as input (i.e., the edge weights as well as the thresholds of nodes). We can extract this information from the object ObamaFit, and we saved the relevant information in the object SimInput (see the Supplementary R code). Note that we rescaled the negative evaluative reactions Ang and Afr, so that a positive (negative) score on all evaluative reactions indicates a positive (negative) evaluation.

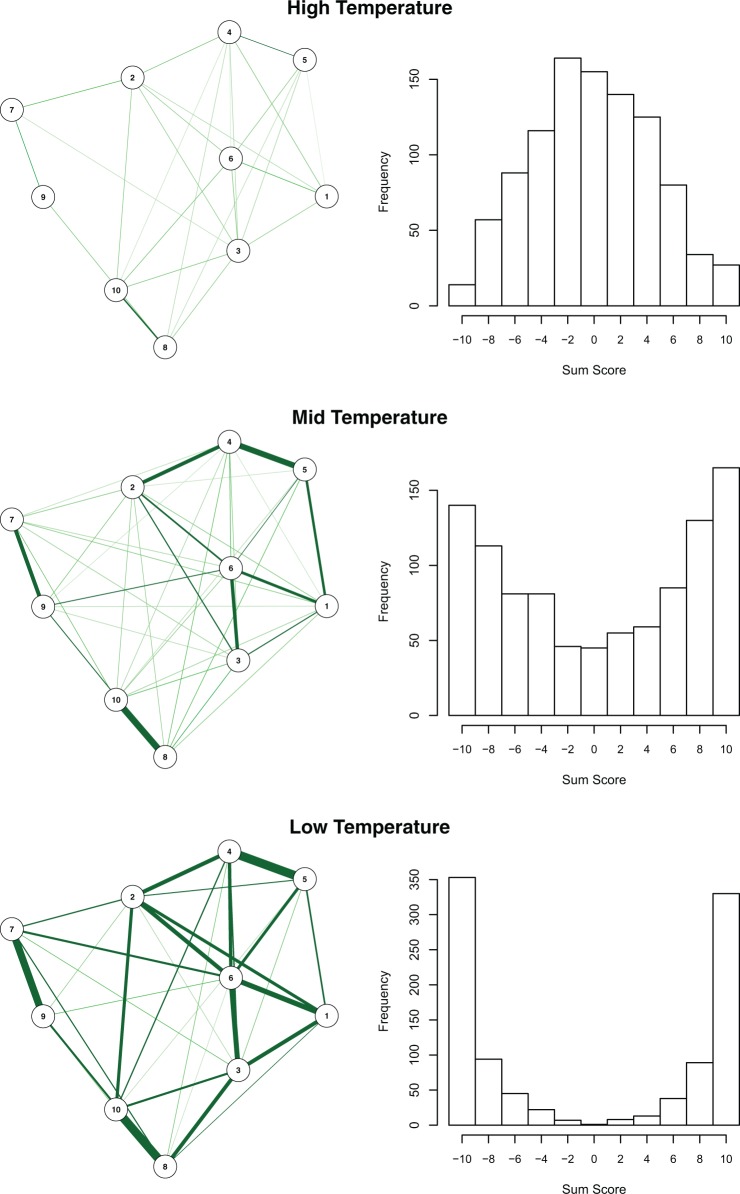
To illustrate the consequences of varying network connectivity, we set all thresholds to 0 (implying all nodes have no disposition to be in a given state) and we manipulate the temperature of the network model. To simulate cases based on the Obama network with three different temperatures, we can use the following commands:

• sampleHighTemp <- IsingSampler(1000, SimInput$ graph, rep(0,10), .4, responses = c(-1L,1L))

• sampleMidTemp <- IsingSampler(1000, SimInput$ graph, rep(0,10), .8, responses = c(-1L,1L))

• sampleLowTemp <- IsingSampler (1000, SimInput$ graph, rep(0,10), 1.2, responses = c(-1L,1L))

The first argument of the IsingSampler function specifies the number of cases we want to simulate, the second argument specifies the network from which we want to simulate, the third argument specifies the thresholds, and the fourth argument specifies the inverse temperature. The responses argument is used to indicate that the network and thresholds we are simulating from are based on −1 and +1 responses. As can be seen in Figure 5, the connectivity of a network has fundamental implications for the distributions of the sum scores. The sum score is a useful measure of the overall state of the attitude and represents a measure of the global attitude toward Barack Obama in the current example. While the sum scores of a weakly connected network are normally distributed, sum scores of a highly connected network are distributed bimodally. This illustrates that psychological constructs, which are based on networks, can be regarded either as dimensions or categories depending on the connectivity of the network (cf., Borsboom et al., 2016). In the case of attitudes, this would mean that weakly connected attitude networks behave as dimensions (i.e., attitudes can take any evaluation ranging from negative to positive), while highly connected attitude networks behave as categories (i.e., attitudes are generally either positive or negative). For a thorough discussion of the implications of network connectivity for attitudes and especially attitude strength, the interested reader is referred to Dalege, Borsboom, van Harreveld, and van der Maas (2017).

Figure 5.

Networks with different temperatures based on the Obama network and their associated distributions of sum scores.

Node Centrality

To illustrate the consequences of influencing nodes with different centrality, we show how to simulate targeting nodes differing in strength. As can be seen in Figure 3, the node with the highest (lowest) strength is the node Hns (Ang). Let us assume we want individuals to have a more positive attitude toward Obama and we focus on individuals who have a moderately negative attitude toward Obama. We can simulate a group of individuals with moderately negative attitudes by setting all thresholds of the evaluative reactions to a moderately negative value (e.g., −.1):

• SampleNeg <- IsingSampler(1000, SimInput$graph, rep(-.1,10), responses = c(-1L,1L))

The mean sum score of this sample is −5.63 with a standard deviation (SD) of 6.54. To simulate a strong persuasion attempt focusing on the node Hns (Ang), we can set the node’s threshold to 1. This represents a persuasion attempt to make individuals judge Obama as more honest (feel less angry toward Obama):

• SampleHns <- IsingSampler(1000, SimInput$ graph, c(rep(-.1,5),1,rep(-.1,4)), responses = c(-1L,1L))

• SampleAng <- IsingSampler (1000, SimInput$ graph, c(rep(-.1,6),7,rep(-.1,3)), responses = c(-1L,1L))

Important to note here is that the persuasion attempt in both situations was equally strong. Yet the persuasion attempts significantly differed in their effectiveness reflected by the sum scores, t(1,998) = 6.27, p < .001, 95% Confidence Interval [1.53, 2.91], d = 0.28. The persuasion attempt on the central node Hns resulted in a more positive attitude (M = 1.18, SD = 7.99) than the persuasion attempt on the peripheral node Ang (M = −1.04, SD = 7.84). From this simulation, we can thus derive the hypothesis that persuasion targeted at a node with high strength would result in higher attitude change than persuasion targeted at a node with low strength.

Testing Predictions From Simulations

In a recent study, Dalege, Borsboom, van Harreveld, Waldorp, et al. (2017) used the Ising model to derive predictions regarding network structure and prediction of behavior. Simulations showed that highly connected attitude networks are more predictive of behavior than weakly connected attitude networks. To test this prediction, Dalege, Borsboom, van Harreveld, Waldorp, et al. (2017) estimated attitude networks based on nonbehavioral evaluative reactions toward presidential candidates (like the network discussed in the current article) and correlated the network connectivity with how well the attitude (based on the sum score of the evaluative reactions) predicted the voting decision. They found an almost perfect correlation between network connectivity and predictability of voting decisions, supporting the hypothesis derived from simulations on the Ising model. This study provides an illustration of how network simulation can aid hypothesis generation and also how to devise research on behavior prediction in the attitude network framework.

Discussion

In this article, we provided a brief tutorial on estimating, analyzing, and simulating attitude networks. The combination of network analysis and simulation illustrates that network theory provides a framework to both test and develop formalized hypotheses on attitudes. It is our view that this makes network theory a unique framework, as it bridges the current gap between social psychological theorizing and psychometric theory.

Network analysis is a novel and still developing field in psychology. An important issue that needs to be tackled in the future is to devise strategies to make sure that all relevant nodes in a (attitude) network are measured. While currently the focus on questionnaire construction lies on selecting items that are highly interrelated (resulting in high reliability of the questionnaire), the network perspective on psychological constructs implies that the most important issue in questionnaire construction is to select items that provide a comprehensive picture of the measured construct. Such items might not be highly interrelated, which implies that validity and reliability of a questionnaire might in some instances be incompatible (Dalege et al., 2016).

With this tutorial, we aimed to provide an accessible introduction to network analysis and simulation on attitudes. While we have focused on attitudes in this tutorial, the techniques outlined here can also be applied to several other core social psychological constructs such as self-concept, prejudice, and interpersonal attraction. It is therefore our view that network theory provides a promising framework to move our field forward.

Author Biographies

Jonas Dalege is a PhD student at the University of Amsterdam. His research focuses on applying network theory and analysis to attitudes.

Denny Borsboom is a full professor at the University of Amsterdam. His work has focused on conceptual analyses of psychometric models.

Frenk van Harreveld is an associate professor at the University of Amsterdam and specializes in attitudes, decision-making, risk, and uncertainty.

Han L. J. van der Maas is a full professor at the University of Amsterdam. He works on the formalization of psychological theories in diverse fields of psychology.

Handling Editor: Kate Ratliff