Abstract
Multiple imputation is a popular method for addressing missing data, but its implementation is difficult when data have a multilevel structure and one or more variables are systematically missing. This systematic missing data pattern may commonly occur in meta-analysis of individual participant data, where some variables are never observed in some studies, but are present in other hierarchical data settings. In these cases, valid imputation must account for both relationships between variables and correlation within studies. Proposed methods for multilevel imputation include specifying a full joint model and multiple imputation with chained equations (MICE). While MICE is attractive for its ease of implementation, there is little existing work describing conditions under which this is a valid alternative to specifying the full joint model. We present results showing that for multilevel normal models, MICE is rarely exactly equivalent to joint model imputation. Through a simulation study and an example using data from a traumatic brain injury study, we found that in spite of theoretical differences, MICE imputations often produce results similar to those obtained using the joint model. We also assess the influence of prior distributions in MICE imputation methods and find that when missingness is high, prior choices in MICE models tend to affect estimation of across-study variability more than compatibility of conditional likelihoods.
Keywords: chained equations, fully conditional specification, joint model, systematic missingness
1. Introduction
Several analytic approaches have been proposed to address missing data with inherent multilevel (hierarchical) structure, but their relative operating characteristics have not, to our knowledge, been extensively studied. Practical guidelines on their use is timely, as an increasing number of analyses are based on data with this structure, where individual observations are nested in larger groups and thus have characteristics that are correlated with members of the same group. These types of data occur in, for example, individual participant data (IPD) meta-analysis of multiple medical studies and joint analysis of individual electronic health records from multiple health systems. Missing data often present an unusual challenge in such hierarchical data because some variables may be unavailable in some groups due to group-level design or data availability. This type of “systematic missingness” occurs whenever variables are not measured identically across studies; for example, sites might use different indices to measure socioeconomic status, or record-keeping protocol might differ across hospitals [1]. Because we expect systematic missingness to be prevalent in IPD meta-analysis, we focus on analytical methods for that setting; however, the general principles are more broadly applicable.
When systematic missingness is found in important outcomes, covariates or confounders, appropriate methods are essential to sound analyses. Simply ignoring the missing data, or implementing a complete case analysis, is typically inappropriate, as it could result in biased results even for a missing data mechanism that is missing at random [2]. For systematic missingness, a complete case data analysis is particularly problematic because it would require dropping entire studies from the analysis. If there are enough important systematically missing variables, the complete case approach would result in dropping most or even all datasets from the model, thus undermining the meta-analytic undertaking.
Under the assumption of an ignorable missing data mechanism, multiple imputation is frequently the preferred method of handling missing values since it is often relatively easy to implement, allows use of all available data, and is theoretically unbiased. For the case of multilevel data described above, it is important for the imputation model to correctly reflect the hierarchical covariance structure of the data. For analysis of full IPD data, the meta-analysis literature overwhelmingly promotes the use of mixed-effect models that include a study identifier as a random effect, as this type of model accounts for the variability of individual responses across studies while allowing fixed relationships between covariates in multiple studies (see, e.g., [3]). Recent work has led to similar recommendations for imputation models. For example, Andridge showed that both omitting the effect of study and modeling the effect of study as a fixed effect can lead to bias in estimating regression coefficients even when the intra-class correlation is small [4]; for this reason, random effect models that appropriately account for the hierarchical structure of participants within studies are preferred.
While Andridge’s suggestions are directly applicable to sporadic missingness, systematic missingness complicates imputation models because certain relationships are never observed in some studies. As such, these studies do not contribute to some covariance estimates. Nonetheless, if we assume some across-study homogeneity in the within-study covariance structures, random effect models can be used to impute systematically missing values. In fact, Siddique, et al. demonstrated that IPD meta-analysis with systematic missingness that excludes consideration of hierarchical structure can result in attenuated estimates of regression coefficients [5].
Two types of imputation methods for hierarchical data have been proposed – joint multivariate models for all the variables with missing data [6, 7], and iterative univariate approaches that use multiple imputation with chained equations (MICE), also referred to as “fully conditional specification” (FCS) [1, 8]. Each approach has its advantages and drawbacks. The multivariate modeling approach, although it is a proper multivariate model for imputation, requires estimating many parameters from the observed data, which can lead to computational limitations and large variances. In addition, specification of the joint model can be quite difficult, especially for extensions that include different types of variables. FCS methods are attractive because they are easy to implement, particularly in cases where a corresponding joint imputation model is not obvious. For example, it is straightforward to impose conditional independence between subsets of variables or, in extensions to the multivariate normal case, specify univariate conditional models for a multivariate response containing many different types of variables. A disadvantage to FCS is that it is often difficult to characterize the theoretical properties of the resulting distribution of the missing values because it makes use of a series of conditional distributions that need not correspond to any joint model. (See, for example, [9].) A notable exception is a simple multivariate normal model, where an appropriately defined FCS has been shown to result in imputation procedures that are equivalent to the joint model [10, 11]. However, this conclusion does not obviously extend to hierarchical normal models. If such a joint model does not exist, it is not clear that the completed data resulting from imputation will have desirable properties. In addition, standard implementations of the univariate approach may not adequately capture correlation induced by the hierarchical data structure.
Multiple imputation implementations specific to random effects models include Schafer [6] and Schafer and Yucel[7]’s joint multivariate normal model, an FCS adaptation of Schafer and Yucel [7]’s approach implemented by van Buuren and Groothuis-Oudshoorn in the “mice” R package [8], and a different FCS implementation proposed by Resche-Rigon, et al[1]. Siddique, et al discussed the use of the joint multivariate model to synthesize a collection of studies with systematic missingness, emphasizing the limitations of this approach when there are many systematically missing variables that are jointly measured in a small number of studies [12]. Resche-Rigon, et al show that their FCS imputation model with random effects outperforms a corresponding fixed effects model when data are systematically missing and normally distributed [1]. Jolani, et al extend the method and results to binary and categorical predictors in a generalized linear model framework and show through simulations that their method has better coverage properties when compared to complete-case analysis, multiple imputation ignoring between-study heterogeneity, and multiple imputation including study as a fixed effect [13]. However, neither Resche-Rigon, et al nor Jolani, et al compared their FCS methods to a joint multivariate model. Enders, Mistler and Keller provide such a comparison for a multivariate normal model with sporadic missing values in the response and conclude based on congeniality arguments that joint model and FCS imputation are both appropriate for random intercepts analysis models, while the two methods are each preferred for contextual effects and random slopes in the analysis model, respectively [14]. van Buuren, et al studied FCS in a multivariate normal model, logistic regression, and quadratic regression [9]. The latter two cases are known to not correspond with a joint model, yet simulation showed that imputations from these models nonetheless achieve nominal confidence levels in all studied cases.
The original formulations for these methods focus on missing individual-level (“level 2”) variables, as opposed to missing variables that are common to all members of a group, or “level 1” variables. We also focus on this situation. However, we note that several authors have studied imputation methods for missing ‘level 1’ variables [15, 16, 17]. In this setting, Kline, Andridge and Kaizar showed that aggregating “level 2” variables to construct a FCS conditional regression models for each “level 1” variable (as proposed by [15]) results in underestimates of the association between the missing variables and the observed level 2 covariates [17]. This result suggests that for similar multilevel models, it may prove difficult to appropriately capture a complex dataset’s covariance structure using an FCS approach, whereas corresponding joint models can reflect structured relationships among variables.
We fill the gap in direct comparisons of joint and FCS imputation procedures for multilevel models by comparing the joint multivariate model proposed by Schafer [6] with the two implementations of FCS for imputing multilevel data with systematic missingness. We particularly focus on the multivariate normal case because of its analytic tractability. We believe that trends observed in this case are likely to extend to or be exacerbated by other families of distributions. We discuss some cases where an iterative approach will not be exactly equivalent to the full joint model and examine the consequences of these differences in practice. The paper is organized as follows: Section 2 presents the joint model and the corresponding univariate conditional models, and Section 3 discusses the question of exact equivalence between the two models. In Section 4, we present simulation studies to demonstrate the comparative differences between joint and FCS models, and demonstrate practical differences in a meta-analysis of pediatric traumatic brain injury studies in Section 5. Finally, we discuss the implication of our results and make practical recommendations in Section 6. Because our presentation includes notation for the detailed specification of two separate models, we include a notation summary as an Appendix. R code for the simulation and analysis can be found at https://zenodo.org/badge/latestdoi/92626197.
2. Imputation model for multilevel missing values
Mimicking a usual IPD meta-analysis setting, we assume the data are consistent with a hierarchical model with two levels – “level-2” individuals nested within “level-1” groups or studies. Specifically, we consider m studies indexed by i = 1, …, m, each of which contains ni individuals. Among the collection of studies, there are r ≥ 2 systematically missing variables Y that are not observed for any individual in one or more study, so that a joint imputation model for each study i has a matrix response: Yi = (Yi1, …, Yir) ∈ Rni×r, where Yir is a vector of individual measurements of variable r for all ni individuals in study i. Following [7], we specify a random effects model for Yi. Conditional on (fully observed) covariates Xi ∈ Rni×p and Zi ∈ Rni×q, the joint imputation model for an r-dimensional response variable can be written as:
| (1) |
where the response Yi and error εi are ni × r matrices, β ∈ Rp×r is the matrix of fixed effects, and Bi ∈ Rq×r is the matrix of random effects. The matrices Xi and Zi may contain some or all of the same explanatory variables. Again following typical IPD meta-analytical practice, we assume independent normal distributions on the random effects and errors:
where the vec(Bi) function stacks the columns of the matrix Bi on top of each other to create an rq-length column vector. Under this assumption, the distribution of Yi (not conditional on the random effects) can be written in vectorized form as a Ni = rni-dimensional normal distribution:
where Ini is the ni × ni identity matrix and ⊗ denotes the Kronecker product.
We follow standard random effects modeling to assume that Bi and εij are identically distributed across studies and Yi is conditionally independent of Yi′ for i ≠ i′. The distribution above fully specifies the joint imputation model for all data with potentially systematically missing values and is parameterized by the matrices β, Σ, and Ψ, which together we denote θ. Under this model, the study-specific variables with systematic missingness, Yi, each have identical error covariances and the random effect covariances differ across studies only through differences in the random effect covariates Zi.
To concretely illustrate ideas, we also consider a special case of model (1) where Xi = Zi = 1ni, a column vector of all ones, and Bi and β are both row vectors of length r. That is, this random intercepts model assumes a common mean β across all studies with an additional random (mean zero) study effect vector for each study-specific Yi. When r = 2, the joint model for Yi can be written:
| (2) |
where Jni is a ni × ni matrix of ones.
Model (1) and its special case (2) can be considered to be the true data generation model for Y conditional on X and Z. We now turn to imputation models, which may reflect the conditional distribution of the missing values of Y, loosely denoted Ymis given the observed values of Y, loosely denoted Yobs, and fully observed covariates X and Z.
2.1. Joint imputation
Following [7], our joint multivariate imputation model begins with the complete data likelihood specified in (1). To create a proper imputation procedure that reflects all the variability in the conditional distribution of Ymis, we additionally specify prior distributions for the parameters in model (1).We denote prior distributions for the covariance matrices Σ and Ψ and the regression coefficients β with the generic function πJ, where the superscript signifies that it is part of the joint imputation model. A Gibbs sampler algorithm can be used to produce imputations from the marginal posterior distribution of the missing data Ymis|Yobs by sequentially sampling from the full conditional distributions of the parameters θ, random effects B, and missing data Ymis. One sample can be represented as follows, where the variables in the conditioning set are either observed or the most recently sampled value in the sequential sample:
| (3) |
Schafer and Yucel [7] provide a specific sampling algorithm to implement this for the imputation model (1). The specified prior distributions are flat on the mean parameters β and conjugate inverse-Wishart (IW) priors for the variance parameters Σ and Ψ. These prior choices result in full conditional distributions that can each be sampled in closed form. Software that implements this method with Schafer and Yucel’s prior distributions is available in the “pan” package in R [18].
2.2. FCS imputation overview
A chained equations or fully conditional specification method is an alternative approach to imputing missing individual values in r variables by specifying a reasonable conditional model (often a generalized linear model) for each variable with missing values given the remaining observed or imputed variables. Each of the r conditional models, denoted gk, k = 1, …, r, is parameterized by a variable-specific object (analogous to θ in the joint imputation model; we use asterisks to differentiate entities that appear in the FCS models from entities that have similar interpretations in the joint model). Upon choosing prior distributions for each , one sample from the FCS imputation sequential sampling algorithm for a random effects model is drawn as follows (loosely following notation found in [11] and [19]):
| (4) |
where Y(−k) denotes Y with the kth variable removed, Y(k) denotes the portion of Y that includes only the kth variable, and is a m × q* random effect matrix associated with variable k.
The full conditional distribution for the parameters g̃k is determined by the prior and full conditional likelihood gk. When proper priors are used, sequential samples from each pair of full conditional distributions {g̃k, gk} would produce draws from a well-defined predictive distribution of conditional on fixed , Y(−k). As noted in the introduction, however, neither the functional form of gk nor its corresponding parameterization needs to correspond to a joint r-variate distribution on the full array Y. As a consequence, there is no guarantee that the variables in Ymis are drawn from any proper joint imputation distribution. This is a well-known potential limitation of such algorithms, and their behavior in this area is understood in relatively few particular cases.
2.3. FCS implementation
The FCS algorithms we consider use a series of univariate mixed-effect regression models to impute missing values one variable at a time. With model (1) in mind, the conditional distribution gk for the kth variable is the product of study-specific conditional distributions, gik. In turn, these are specified as random effects regression models with conditional mean and a study-specific random effect :
| (5) |
where ℳk is the collection of indices for studies where variable k is systematically missing, Yik is a length ni vector, is a ni × p* matrix that may include Yi(−k) or transformations of Yi(−k) and is a length p* vector, is a ni × q* matrix that also may include Yi(−k) or transformations of Yi(−k) and is a length q* vector, and φ(·,·) is the multivariate normal density function. The random effects are independently and identically distributed (iid) as N(0, ). Each gk is parameterized by the collection .
With the special case model (2) in mind, the fully conditional models gi1 and gi2 for Y consistent with (5) can be written as regressions with random intercepts, where for this special case we follow usual practice to define the matrices and .
| (6) |
Each multilevel conditional model implies a structured variance-covariance matrix when the latent random effects are removed from the conditioning set: the covariance of Yi1|Yi2, for instance, is equal to .
We consider two implementations of FCS using the imputation model described in (4) and (5) above. These two use the same likelihood functions gk but differ in the procedure used to sample from g̃k in the first step of the algorithm in (4) above. The first method is presented by Resche-Rigon, et al and at each iteration samples from the estimated asymptotic sampling distribution of its maximum likelihood estimator [1]. The second method is the MICE implementation of multilevel normal imputation as available in the R “mice” package [8] using the “2l.impute.pan” imputation function. The next sections provide additional detail about these two methods, and in Section 3.3, we compare the implications of the differences in prior distributions. To differentiate among the general and specific features of FCS models and implementations, when our discussion applies to any MICE algorithm using the model (6), we refer to the method as simply MICE or FCS. When the distinction between these two implementations is important, we will refer to the method in [1] as “MICE-ML” and the “2l.impute.pan” method in the “mice” R package as “MICE-IW”.
2.3.1. MICE-ML FCS implementation
For each sequential sample in the MICE-ML method, one first calculates the maximum likelihood estimator of conditional on and and imputes each variable using the full conditional likelihood gk in (5). In the r = 2 case, the steps for drawing ( , B(1)i) from g̃1 corresponding to the likelihood g1 shown in (6) above are:
where , the estimated covariance matrix of , is obtained by evaluating the Fisher information at . This method specifies no prior information about , instead using the data alone to define g̃k. Once such an algorithm converges, the steps here will approximate a draw from the posterior distribution of (B(1)i, ) given ( , Y(2), X, Z). Sampling from these data-driven full conditional distributions raises two practical problems. First, the estimated variance-covariance matrix may not be positive definite, and thus may not be used to generate samples. In this case, Resche-Rigon, et al recommend using the maximum likelihood estimates directly instead of sampling from the normal distribution [1]. Second, draws of and may not be positive. To prevent this situation, we implement an algorithm that truncates the normal distribution at zero.
2.3.2. MICE-IW Implementation
The MICE-IW method uses existing functionality from the R package “pan” [18], typically used for joint model imputation of multivariate normal models as in section 2.1, to perform univariate imputations. That is, each pair of full conditional univariate distributions {g̃k, gk} is defined using the same family of priors and conditional sampling methods as the distributions {Pθ, PB, PY} defined for the joint procedure (3). Under this method, the prior distributions are flat on and inverse-Wishart on and with degrees of freedom and prior scales νk and Vk for each variable k. This prior specification results in a closed form expression for the full conditional distributions. For our specific case where r = 2, draws of the parameters and random effects ( , B(1)i) are sampled as:
These conditional draws will, upon convergence, represent a sample from the posterior distribution g̃ of ( , B(1)i) as determined by the likelihood g1 and prior distributions . The algorithm for drawing ( , B(2)i) is similar.
3. Equivalence of joint and conditional imputation models
If the joint and FCS imputation procedures can be shown to be equivalent for the normal hierarchical model, then one could choose the most convenient algorithm without being concerned about relative statistical properties of the procedures. If not, an understanding of situations where differences are substantial will be helpful in guiding algorithmic choices. Imputation procedures are equivalent when the posterior distribution of the missing variables used to sample imputed values, or imputation distribution, is identical across procedures. Studying such equivalence, or lack of equivalence, can be segmented into three considerations. First, because FCS procedures are ad hoc specifications, any possible equivalence relies on the existence of a stationary posterior distribution in the FCS algorithm. Second, if such a posterior distribution exists, it must be compatible with the joint imputation model in order for the two imputation methods to be asymptotically equivalent [11]. Finally, the choice of prior distributions may impact finite sample imputations.
We describe these three items in more detail below, and address each for the joint and FCS procedures for imputing variables in the context of the hierarchical multivariate normal data model. In particular, we compare the two imputation methods given by a fully Bayesian joint model, described in 3), and the analogous MICE procedure (4). For ease of presentation, we focus on the special two-dimensional case shown in (2) and (6) above. As noted in the text below, we sometimes also assume that β = 0; i.e., we assume there are no fixed effects in the joint model and that E(Yik) = 0 for k = 1, 2. Throughout, we continue to denote the data distribution (i.e., the likelihood) for the joint model with P(Y|θ) where θ = (β, Σ, Ψ). The MICE conditional models for the data are denoted g1, g2 and are parameterized by and , respectively. The prior distributions are πJ(θ) for the joint model and ; k = 1, 2 for MICE. We assume that the model for the data P(Y|θ) implied by (2) is correctly specified, so that imputations from the joint model will lead to consistent estimates in the final model.
3.1. Existence
The sequence of conditional draws in an FCS method must converge to some stationary posterior distribution in order for it to be meaningful to evaluate its implied imputation distribution. Arnold and Press have shown that two conditional densities g1 and g2 on y1 and y2, respectively, will together specify a joint distribution if and only if their ratio can be factorized as g(y1)h(y2) [10]. (See also [20].) For FCS conditional models (6), this factorization condition will hold when the conditional parameters are functions of θ as necessary for compatibility with P, as discussed in the next subsection. In this case, the unique joint distribution will be the distribution given by (2).
3.2. Compatibility of models (2) and (6)
Loosely speaking, a full conditional imputation approach would be called compatible with a joint model if the full conditional distributions for the missing data are identical to those that would be derived from the joint model, and their parameters can be derived from the parameters for the joint model. To more precisely define compatibility, we follow definitions given in [11] and [21] and first define Pk(Y(k)|Y(−k), θk) to be the full conditional distribution of the variable Y(k) that is derived from the full joint model P(Y|θ). This conditional distribution is parameterized by θk, possibly a subset of θ. Then, a family of conditional models {g1, …gr}, where gk is parameterized by , is said to be compatible with P if gk = Pk for all k, and θ is surjective with [11].
Compatibility is an important consideration for evaluating imputation procedures because if the FCS distributions {g1, …, gr} are not compatible with any joint model, the posterior predictive distribution of the resulting imputations will generally not correspond to any Bayesian model. Compatibility implies the asymptotic equivalency of imputation distributions for Ymis, whenever suitable asymptotic conditions ensure the choice of prior distributions for the model parameters θ have no asymptotic impact [11].
We first consider the compatibility requirement that gk = Pk for all k when P is the multivariate normal model in (2) and the FCS analogs {g1, g2} are given in (6). Let P1, P2 denote the conditional distributions of Yi1 and Yi2 based on P. The following expressions give the conditional mean and covariance of P1(Yi1|Yi2, θ1) when the mean of the joint distribution is zero, i.e., β = 0:
| (7) |
where the parameters (β1.2,1, σ1.2, ) are functions of the covariance matrix of Yi, as defined below. We use the subscript notation k.k′ to denote a parameter corresponding to the conditional distribution Pk(Y(k)|Y(k′), θ), and as necessary, additional indices in the subscript identify subsets of a multidimensional parameter. The correspondence of these conditional parameters to those of the joint distribution are as follows:
| (8) |
The expressions in (7) indicate that, as long as the FCS parameter is equal to the joint parameter defined in (8), it is possible to express the full conditional distribution Pk as a mixed-effects regression model of the form of the FCS model (6). The multilevel structure of this model, however, creates two unusual features in the conditional distributions. First, the conditional mean is not a simple linear regression model. The term creates a multilevel structure in the conditional mean, so that for individual j, the mean of Yi1j|Yi2j is linear in both the jth value of Yi2 and the within-study sum , or, equivalently, its within-study mean. An FCS model gk must include this additional within-study sum as a covariate in the regression function in order to be compatible with model (2). An analogous result holds for models with a random slope associated with a continuous predictor Zi: the conditional mean is linear in and compatibility requires that this term should be included in as a fixed effect.
Carpenter and Kenward note the need to include the study-specific mean, and show that this implies exact equality of Pk and gk in the case of equal numbers of “level 1” measurements per “level 2” group. (i.e, ni = n for all i) [22]. While this is a reasonable assumption for the analysis of a single repeated measures study, it becomes untenable for IPD meta-analysis or hierarchical models that include random effects. When study sizes vary, the conditional distributions are heterogeneous across studies: Equations (8) show that although the joint model specifies homogeneous error and random effect variances, its corresponding conditional distribution P1 has parameters that depend on , which need not be the same for each study. In particular, for this random intercept model, the parameters of and depend on , and a model assuming these values are constant across study cannot be compatible with the model (2).
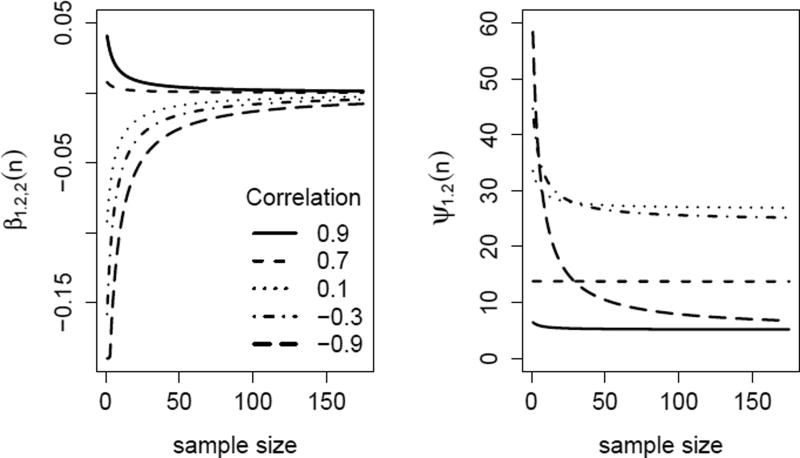
Figure 1 depicts the practical influence of heterogeneous sample size on the magnitude of these two parameters, (left panel) and (right panel) for a case where the joint model covariance matrices Σ and Ψ are of similar magnitude to those estimated from the TBI data in Section 5. In each plot, the horizontal axis represents the study size and the vertical represents the value of the conditional parameter for a study of that value of ni. Each line shows the effect of increasing sample size for one particular value of the intraclass correlation in Ψ, defined as . The dashed line represents a case where Σ and Ψ have similar correlations (0.65 and 0.7, respectively), and both plots show nearly flat lines, indicating that for this case the parameters vary little with study size. Conversely, when the random effects are extremely negatively correlated (ρ = −.90), the conditional distributions can differ dramatically across studies with different sample sizes. Consequently the MICE model (6) that assumes complete homogeneity of conditional distributions is theoretically incompatible with P. The magnitude of differences across conditional distributions depends on both the model covariances and the variability of ni across studies (or, if a random slope is used, the across-study variability of ). For both parameters, the lines tend to grow flat for ni sufficiently large; the effect of sample size on the parameters diminishes as studies grow.
Figure 1.
True values of and when ψ11 = 27, ψ22 = 33, σ11 = 122, σ22 = 147, σ12 = 100. Lines shown depict varying values of .
When some variables are systematically missing, it is nonetheless necessary to assume some homogeneity in the coefficients across studies for FCS formulations that are based on standard generalized linear models. In a practical sense, then, compatibility will not be possible. The simulation study in Section 4 examines the potential consequences of this trade-off in several situations.
In addition to equivalent forms of Pk and gk, compatibility requires a surjective map t that maps the joint parameterization to the conditional parameterization. That is, if gk is compatible with P, it must be parameterized by a valid value of t(θ). The reparameterization t for the simple two-variable case with β = 0 is given in (8). The inverse of t maps an 8-dimensional parameter to two covariance matrices θ = {Σ, Ψ}. Because these are positive definite matrices, θ has only 6 free parameters, one of which must satisfy an additional constraint that ensures a positive determinant of Ψ. As a result, each lies in a specific subspace of R4, and values outside of this space will not correspond to a valid value of θ. In practice, draws of these parameters should fall in the correct space with high probability for large sample sizes. It is nonetheless possible for an FCS algorithm to draw parameter values outside of the correct subspace, particularly if the chosen priors put high probability on incompatible θ* values.
3.3. Priors
If the FCS models {g1, …, gr} are compatible with a joint model P, both methods will draw imputations from a posterior predictive distribution of Ymis|Yobs. For finite samples, however, each method’s predictive distribution will depend on the prior distributions placed on the model parameters, πFCS(θ*) and πJ(θ). Liu, et al show that under several technical conditions, these differences will disappear asymptotically [11]. In many multilevel applications, however, asymptotic results are unlikely to be relevant. For example, in an IPD meta-analysis synthesizing a small number of studies, the prior distribution on the model’s study-level parameters may be particularly influential, and the asymptotic result would depend on unrealistic increases in the number of studies. A practical comparison of the methods, then, requires an assessment of how the priors influence imputations in finite samples.
To aid in comparison of πFCS and πJ, we first reconcile the two parameterizations of the model. Note that when the models are compatible, for any k, the joint distribution P can be written , where gk is the compatible FCS distribution parameterized by , and is a function of θ [11]. It is possible to transform any prior distribution on the joint parameterization πJ(θ) to find the corresponding prior . Integrating θ̃k out of πJ gives the joint model prior distribution on that can be readily compared to the FCS prior on the same parameter. We make this comparison using the parameterization because this involves only specifying the marginal priors , while the reverse comparison would require specifying a joint prior on .
We assume the FCS model (4) is chosen to be compatible with (2), so that the fixed-effect design includes as discussed in Section 3.2. Then the joint and conditional parameters can be represented, following the notational conventions in (8) and again fixing β = 0:
| (9) |
| (10) |
| (11) |
It is straightforward to show the one-to-one correspondence between θ and . We consider the prior distributions for the parameters that were proposed for the three imputation procedures described in Section 2.3 above. First, we look at weakly-informative inverse-Wishart prior on θ as proposed by [6] and implemented in the ‘pan’ R package [18]. We compare this prior on θ to two sets of FCS priors on : a univariate analog to the inverse-Wishart priors on θ used in the MICE-IW method, and the implicitly non-informative prior that leads to the large-sample conditional sampling distributions used in the MICE-ML method. Our comparison of these priors considers only , omitting the redundant study of . We begin by precisely describing the three sets of prior distributions, then examine the shape and influence of the various prior distribution specifications.
Joint Model Prior Distributions
In their fully Bayesian proposal for imputation within a multilevel model, Schafer and Yucel use conditionally conjugate and a priori independent inverse-Wishart prior distributions on the covariance matrices Σ and Ψ and improper flat prior distributions on fixed regression coefficients β [7]. An inverse-Wishart (IW(ν, V)) prior has two hyperparameters: the scale matrix V and the degrees of freedom ν. For our two-variable example, we use the “minimally informative” ν = 2, and choose prior scale as V = I2 to follow the default implementation used in the analogous MICE-IW procedure. The joint prior distribution for θ = (Σ, Ψ) under these settings, up to a normalizing constant, is:
| (12) |
This distribution implies a prior distribution in the FCS parameterization:
| (13) |
where ℐ is the indicator function.
MICE-IW Prior Distributions
The R “mice” package implements an analogous FCS algorithm that uses univariate versions of the inverse-Wishart joint model prior distributions for the parameters in each full conditional specification to iteratively generate imputations one variable at a time. That is, each step of the FCS algorithm implements the joint imputation model proposed by [6] as if only one variable in the dataset had missing values. As such, the prior distribution has the same functional form as πJ, but differs in dimension and the parameterization to which it applies. MICE-IW imposes independent improper flat distributions on each column of β2.1, and independent inverse Chi-squared distributions with ν = 1 degree of freedom for the variance parameters ψ2.1 and σ2.1. This prior distribution for the vector can be written:
| (14) |
MICE-ML Prior Distributions
The MICE method in [1] does not explicitly specify priors for , but instead directly specifies their full conditional distributions for the sequential sampling procedure:
| (15) |
| (16) |
where the estimated parameters β̂2.1,1, β̂2.1,2, σ̂2.1 and ψ̂2.1 are maximum likelihood estimates and the estimated variances are asymptotic variance estimates derived from the Fisher information. All are available in closed form for the normal model [23]. This specification for β2.1 is equivalent to using an improper flat prior distribution, but it is less straightforward to identify a corresponding prior distribution for the variance parameters.
The absence of a prior distribution here means that it is not necessary to provide subjective information about model parameters, but posterior draws of model parameters are dependent on the maximum likelihood estimates alone. One possible disadvantage to the procedure described above is that it relies on a large-sample distribution of both σ1.2 and ψ1.2, which may not be a close approximation if either the number of studies and number of observations per study are small. In addition, any bias in the maximum likelihood estimator may be present in posterior draws of . But there may be a unique advantage to a data-driven approach: as discussed below, it is possible for standard priors on to put substantial mass in regions where these parameters are incompatible with the joint model. Estimates from data should, with high probability, avoid these regions.
Comparisons among Prior Distributions
Direct comparison of the prior distributions in (13) and (14) would require integrating over σ11 and ψ11; instead, we examine the two expressions and note a few differences. Our inability to factor out the marginal parameters σ11, ψ11 suggests that the joint model imposes a relationship between the conditional and marginal parameters that any FCS prior on alone would be unable to model directly. A notable feature of this relationship is the indicator function in (13), which truncates the support of the parameter β2.1,2 at . This restriction is necessary in order for Ψ to be positive definite and often requires that β2.1,2 be small in magnitude. Note that a similar constraint does not hold for β2.1,1; σ2.1 > 0 is sufficient to ensure Σ is positive definite. The FCS flat prior samples β2.1,2 from an unrestricted normal distribution; as a consequence, if this parameter is poorly estimated, sampled values might be outside of the support under πJ. As discussed in more detail in Section 4, simulations suggest that this might lead to unstable estimates when data are limited and the number of studies is small.
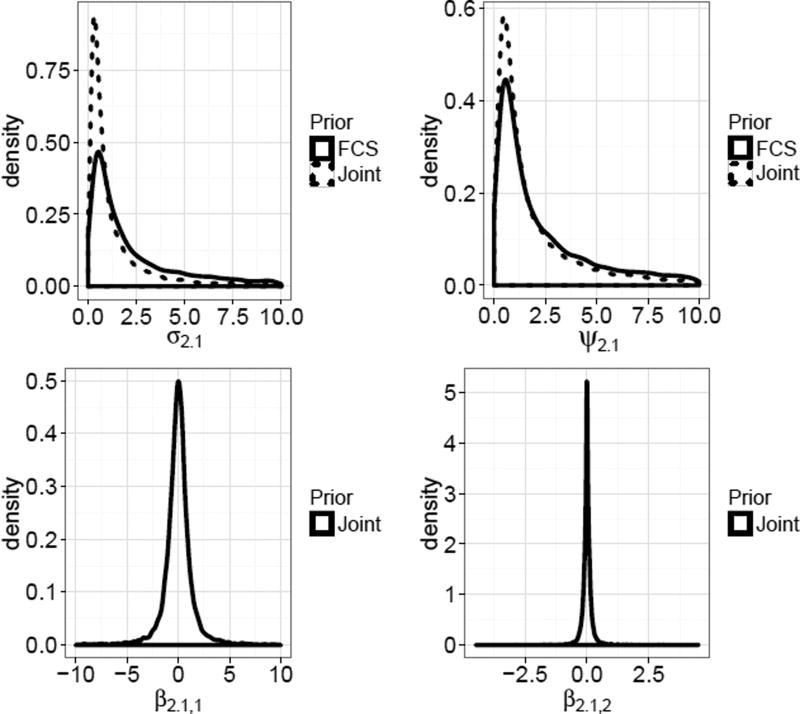
Figure 2 shows marginal prior density estimates of the each element of under πJ and, when applicable, the MICE-IW FCS prior distribution for the same parameter. The prior density on β2.1,2, when averaged over the other parameters, is highly concentrated near zero. The prior for the slope β2.1,1 is more diffuse than β2.1,2, but still not uninformative. For both of the variance parameters σ2.1 and ψ2.1, the densities are similarly shaped, with heavier tails in the FCS priors.
Figure 2.
Marginal density estimates from samples of . Improper flat prior densities for β2.1 parameters under the FCS model are not shown.
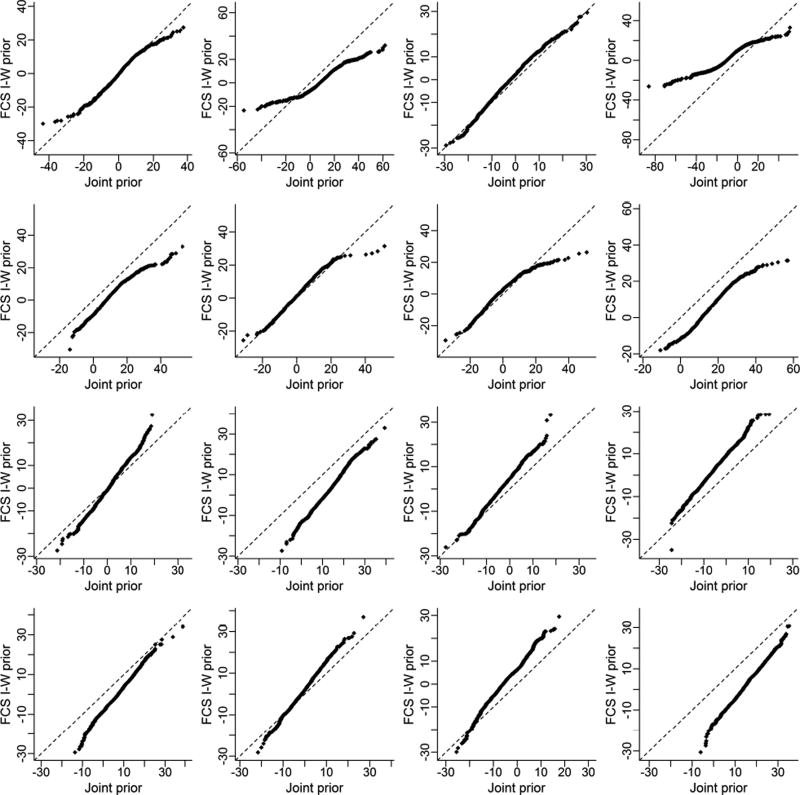
To explore the practical effects of the prior differences we simulated values from each posterior predictive distribution of a new observation Y̌i1j given one simulated data set Y1, Y2, with no missing values. These samples are obtained by sampling many values of the parameters θ and from their posterior distributions Pθ and g̃1, respectively and evaluating the conditional likelihoods P1 and g1 at each sampled value. Draws from these likelihoods are samples from the posterior predictive distribution. The quantile-quantile plots in Figure 3 compare the predictive distributions associated with the joint and MICE-IW priors. Each column of the figure shows samples of the predictive distribution of a particular observation Y̌i1j conditional on Y2. The rows represent varying values of the study size (n) and number of studies (m). These plots show that for small values of m in particular, the joint predictive distributions can often have much heavier tails than the FCS counterpart. The plots in the upper rows show that as samples grow large, these differences are less pronounced. We note that although each plot represents the predictive distribution for only four randomly chosen individuals in the dataset, the results were similar for those not displayed.
Figure 3.
Quantile quantile plots for the joint and MICE-IW predictive distributions for selected individuals Yij. Row 1: n=10, m=5; Row 2: n=30, m=5; Row 3: n = 10, m = 30; Row 4: n=30, m = 30. Ψ takes the same values as in Figure 1 with ρ = .85. Σ is the matrix used in Figure 1 with correlation 0.65, but scaled by 1/1.75.
4. Simulations
We present five simulation studies that compare joint model imputation to the FCS implementations discussed above. The goal is to assess the impact of incompatibility and prior influence on the performance of these methods when using default software settings. Each study compares four imputation models: the joint model (2) with fully observed predictors and random effects Xi and zi, MICE-ML as described in section 2.3.1, and MICE-IW as described in section 2.3.2 using two separate definitions of , the fixed effects in the conditional regressions. The first uses and the second includes the within-study sums as predictors, so that . The second model ensures theoretical compatibility when each study has equal sample sizes, so we refer to this as “compatible MICE-IW” (or MICE-IW-c) and to the first method as “MICE-IW”. The “MICE-ML” method was also implemented using the compatible regression with . We used R to implement all methods: we used the R “pan” package [18] for the joint imputation, the R “mice” package [8] for MICE-IW, and the “lme4” package to obtain maximum likelihood estimates for the MICE-ML method.
In the first four studies, we simulated datasets with r = 3 mean-zero variables as Yij = εij + zibi, where εij ~ N3 ((0 0 0)T, Σ) and bi ~ N3 ((0 0 0)T, Ψ). We used twelve combinations of the covariance matrices Σ and Ψ, the first nine of which have the form
with σ = 10 and ψ = 1 fixed and varying values of ρ1, ρ2, ρ3, and ρ4. For settings 10 – 12, we allowed Y1 and Y2 to have different marginal error variances, so that the diagonal elements of Σ are equal to (10, 1, 10) and the diagonal elements of Ψ are equal to (10, 10, 10). These are of the form
where ψ = 10. The values of ρ1, ρ2, ρ3 and ρ4 are all shown in Table 2.
Table 2.
Correlation settings used for simulation studies 1–4
| Setting | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ1 | 0.15 | 0.75 | −0.55 | 0.15 | 0.75 | −0.55 | 0.15 | 0.75 | −0.55 | −0.55 | −0.55 | 0.75 |
| ρ2 | 0.15 | 0.15 | 0.15 | 0.75 | 0.75 | 0.75 | −0.55 | −0.55 | −0.55 | 0.75 | −0.55 | 0.75 |
| ρ3 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | −0.40 | −0.40 | 0.40 |
| ρ4 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | −0.40 | 0.40 |
In each dataset we generated systematic missingness in Y1 and Y2 according to a missing at random (MAR) mechanism, requiring that no study is missing both variables, and compared all results to the full data set before the missingness was generated. Specifically, we randomly chose studies in which to impose missingness, and then randomly assigned the variable (Y1 or Y2) that would be missing. Thus, the missing data mechanism is MAR given study membership. This mechanism mimics the real world situation where the choice of variables to measure made that is within each study reflects the goals of the study, but does not depend on the underlying values of those variables.
We imputed Y1 and Y2 with the the goal of correct inference for parameters of the analysis model
| (17) |
where the variable Y3 is fully observed and is the only fixed effect to be used in the imputation models; that is, the joint imputation model is (2) with Xi = (1ni, Yi3).
In simulations 1, 2, and 3, we used the random intercept model with zi = 1ni, so the additional fixed effect is equal to the within-study sum . The studies used varying numbers of studies and size of studies, which are shown in Table 1. Simulation 1 compares methods in a best-case scenario where sample sizes are moderate within study (ni = 30) and there are many studies (m = 35), while Simulation 2 uses a more realistic case of moderate number of studies (m = 15) and few without systematic missingness. Simulation 3 uses a moderate number of studies and studies of varying sizes, so that the conditional FCS distributions cannot be compatible with the joint model because their parameters depend on . Simulation 4 further investigates the effect of incompatibility by taking zi to be a vector of independent standard normal random variables, so that bi is a random slope. In this study, as in Simulation 3, the conditional parameters will vary across studies, even with equal study sizes. In both Simulations 3 and 4, the imputation models that include in are not strictly compatible with the joint model, but we continue to refer to these as the “compatible” models. We expect that the additional fixed effect makes the imputation model a close approximation to the true compatible model.
Table 1.
Description of the simulation studies
| Simulation | Study sizes | m |
|
Studies missing Y1, Y2 |
|
|---|---|---|---|---|---|
| 1. Balanced, large m | ni = 30 for all i | 35 | 1050 | 8, 9 | |
| 2. Balanced, small m | ni = 30 for all i | 15 | 450 | 8, 3 | |
| 3. Unbalanced, small m | ni varying in [15, 150] | 15 | 450 | 8, 3 | |
| 4. Balanced, small m, random slope on zi ~ N (0, 1) | ni = 30 for all i | 15 | 450 | 8, 3 | |
| 5a. Unbalanced, small m | 49,18,15,29, 60 | 5 | 171 | 1,1 | |
| 5b. Unbalanced, small m | Replacates of 5a | 35 | 1197 | 7,7 |
In Simulation 5, we assess the influence of the prior hyperparameters on and when MICE is used with inverse-Wishart priors in both small and large data settings. We performed this comparison using the same linear generative model Yij = εij + zibi, but with a single value of Σ and Ψ:
These values were chosen to produce a covariance structure similar to that estimated from the TBI dataset discussed in Section 5. In setting A, we again mimicked the TBI dataset and used five studies with sample sizes of 49, 18, 15, 29, and 60. We generated systematic missingness in study 2 (missing Y1) and study 5 (missing Y2). Setting B used datasets that were identical in structure and missingness pattern, but contained a much larger number of studies in order to minimize prior influence. We replicated the sample sizes in setting A seven times to get a total of m = 35 studies and generated missingness in Y1 for the studies of size 18 and in Y2 for the studies of size 60. The analysis model used was the same as for Simulations 1–3, given in (17).
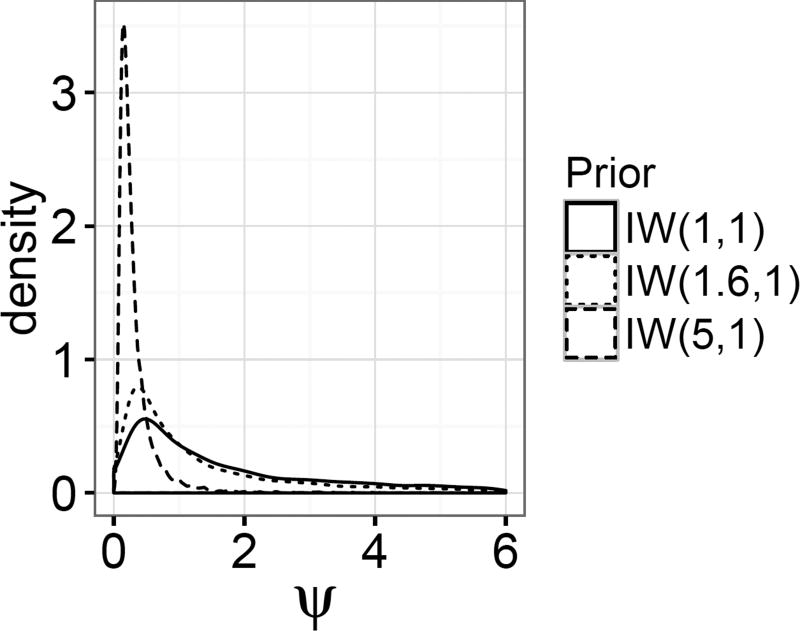
Three inverse-Wishart priors with different degrees of freedom were used to impute missing values for the MICE-IW and MICE-IW-c methods: the default IW(1, 1) prior and the more concentrated IW(1.6, 1) and IW(5, 1) priors. The IW(1.6, 1) prior was chosen because samples from this distribution are distributed similarly to samples of ψ1.2 and ψ2.1 when the priors on Σ and Ψ are both the default used in the joint distribution, IW(2,I2) (shown in Figure 2). These prior distribution are displayed in Figure 4.
Figure 4.
Densities of the three priors used for the random effect variances in Simulation 5.
A total of 200 datasets were constructed for each simulation study. Following [24], we chose D = 60 imputations for each method to exceed the number necessary to produce reasonable Monte Carlo error across all of our simulations. Imputations were stored following a burn-in period of 45 iterations. Parameter estimates for the substantive models were combined using Rubin’s rules [2].
4.1. Results
Because many of the simulation results were similar, we present only a subset here. Full results can be found in the supplemental appendix.
Simulations 1 and 2, Balanced Random Intercept
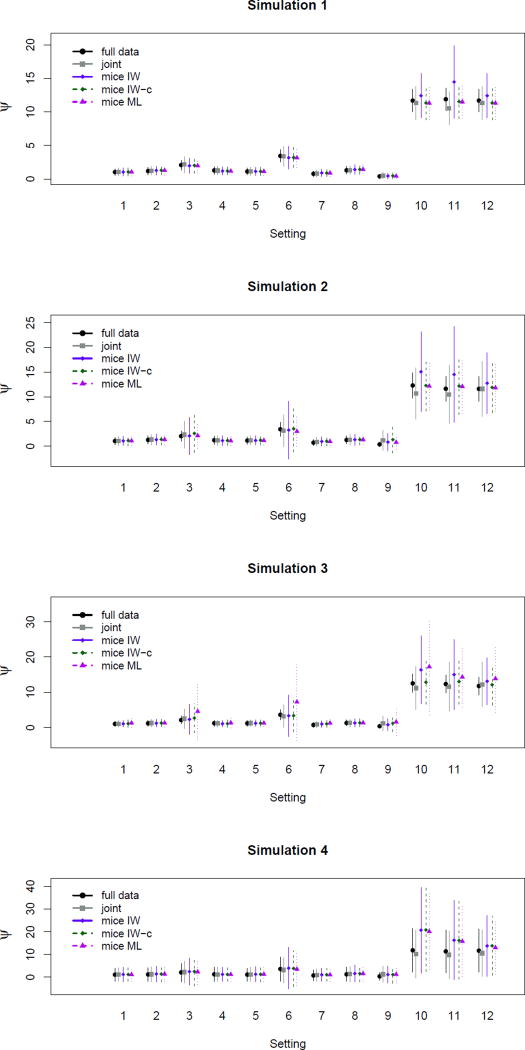
Table 3 shows summaries of parameter estimates and Monte Carlo estimates of standard errors for Simulation 1. We see that, with the exception of the random effect variance ψ, the four imputation methods produce nearly identical estimates and standard errors for all model parameters, and these are in turn close to the full data estimates. Table 4 shows similar results for Simulation 2; in fact, for all correlation settings in Simulations 1, 2 and 3, only results for ψ differ substantially, and so we focus our presentation on this single parameter.
Table 3.
Simulation 1, correlation setting 6 mean parameter estimates and Monte Carlo (standard errors)
| β0 | β1 | β2 | σ | ψ | |
|---|---|---|---|---|---|
| Full data | −0.039 (0.32) | 1.164 (0.02) | 1.035 (0.02) | 3.753 (0.17) | 3.440 (0.46) |
| Joint | −0.042 (0.35) | 1.164 (0.03) | 1.036 (0.03) | 3.741 (0.23) | 3.369 (0.73) |
| MICE-IW | −0.055 (0.40) | 1.163 (0.03) | 1.035 (0.03) | 3.759 (0.23) | 3.167 (0.84) |
| MICE-IW-c | −0.043 (0.35) | 1.164 (0.03) | 1.035 (0.03) | 3.761 (0.23) | 3.206 (0.73) |
| MICE-ML | −0.046 (0.35) | 1.164 (0.03) | 1.035 (0.03) | 3.756 (0.23) | 3.152 (0.71) |
Table 4.
Simulation 2, correlation setting 6 mean parameter estimates and Monte Carlo (standard errors)
| β0 | β1 | β2 | σ | ψ | |
|---|---|---|---|---|---|
| Full data | −0.047 (0.48) | 1.166 (0.04) | 1.036 (0.04) | 3.783 (0.26) | 3.420 (0.69) |
| Joint | −0.049 (0.59) | 1.168 (0.06) | 1.036 (0.06) | 3.791 (0.47) | 3.155 (1.59) |
| MICE-IW | −0.034 (0.80) | 1.164 (0.06) | 1.031 (0.06) | 3.837 (0.48) | 3.264 (2.91) |
| MICE-IW-c | −0.064 (0.68) | 1.166 (0.06) | 1.033 (0.06) | 3.830 (0.48) | 3.514 (2.35) |
| MICE-ML | −0.062 (0.60) | 1.169 (0.06) | 1.036 (0.05) | 3.808 (0.46) | 2.993 (1.51) |
The first panels of Figure 5 show estimates for the random effect variance ψ in the balanced Simulations 1 and 2, and Table 5 contains these estimates for Simulation 2. All methods seem to perform similarly for settings 1–9 when m = 35, but when m = 15 there is a slight discrepancy across methods in settings 3, and 6, unusual cases in which the within-study correlation is negative and the between-study correlation is positive. In particular, the MICE-IW methods both seem to be somewhat less efficient in estimating ψ for these settings. This does not appear to be the case for the regular MICE-ML method. An interesting pattern emerges in settings 10–12, where the true error variance of Y2 is small in comparison to the other parameters: MICE-IW tended to overestimate the random effect variance and its estimates are highly variable. The MICE-IW-c and MICE-ML method are more accurate: including the fixed effect to ensure compatibility appears to alleviate the problem in all three of these settings. These differences may be particularly evident in settings 10 and 11 because the true value of the coefficient associated with the study sums is relatively large in these settings. In settings 10 and 11, we also see a small downward bias in estimating ψ for the joint model imputation.
Figure 5.
Estimates of random effect variance for Simulations 1–4. Lines represent two standard errors from the point estimate. Note the different scales across graphs.
Table 5.
Estimate of ψ; Simulation 2
| Full data | Joint | MICE-IW | MICE-IW-c | MICE-ML | |
|---|---|---|---|---|---|
| 1 | 1.041 (0.38) | 1.057 (0.48) | 1.075 (0.48) | 1.131 (0.53) | 1.081 (0.48) |
| 2 | 1.270 (0.42) | 1.326 (0.52) | 1.318 (0.53) | 1.373 (0.55) | 1.340 (0.52) |
| 3 | 2.039 (0.53) | 2.326 (1.38) | 2.094 (1.88) | 2.584 (1.91) | 2.139 (1.25) |
| 4 | 1.218 (0.41) | 1.171 (0.49) | 1.123 (0.48) | 1.144 (0.49) | 1.100 (0.46) |
| 5 | 1.133 (0.39) | 1.172 (0.46) | 1.158 (0.45) | 1.203 (0.48) | 1.146 (0.44) |
| 6 | 3.420 (0.69) | 3.155 (1.59) | 3.264 (2.91) | 3.514 (2.35) | 2.993 (1.51) |
| 7 | 0.715 (0.31) | 0.884 (0.43) | 0.960 (0.45) | 1.008 (0.48) | 0.954 (0.43) |
| 8 | 1.261 (0.41) | 1.268 (0.51) | 1.330 (0.57) | 1.343 (0.54) | 1.313 (0.51) |
| 9 | 0.369 (0.23) | 1.202 (1.00) | 0.830 (0.86) | 1.333 (1.35) | 0.773 (0.68) |
| 10 | 12.287 (1.28) | 10.678 (2.59) | 15.063 (4.05) | 12.274 (2.55) | 12.155 (2.42) |
| 11 | 11.619 (1.25) | 10.469 (2.94) | 14.514 (4.84) | 12.188 (2.90) | 12.088 (2.70) |
| 12 | 11.598 (1.25) | 11.607 (2.78) | 12.749 (3.09) | 11.890 (2.53) | 11.819 (2.37) |
Simulation 3, Unbalanced Random Intercept
This simulation study highlights the effect of FCS imputation models that require ψ1.2, β1.2,2, ψ2.1, and β2.1,2 to be equal across studies of different sizes. Figure 5 and Table 6 shows that again, the methods performed similarly in estimating ψ except in all but a few settings. As in Simulations 1 and 2, there is a slight inefficiency of MICE-IW in settings 3 and 6, and an upward bias of MICE-IW in settings 10 and 11. Unlike the previous simulations, however, the performance of MICE-ML is notably worse for several cases, producing estimates that are inflated and inefficient for settings 3, 6, 10, and 12. It is not surprising these cases highlight these differences because the conditional parameters in settings 3,6,10, and 12 vary considerably as sample size changes, decreasing in magnitude as within-study sample sizes increase. The relatively poor performance of MICE-ML suggests that drawing these parameters from empirical procedures can lead to estimates that are heavily influenced by the smaller studies.
Table 6.
Estimates of ψ; Simulation 3
| Full data | Joint | MICE-IW | MICE-IW-c | MICE-ML | |
|---|---|---|---|---|---|
| 1 | 1.040 (0.38) | 1.070 (0.46) | 1.076 (0.46) | 1.126 (0.50) | 1.298 (0.65) |
| 2 | 1.214 (0.40) | 1.271 (0.50) | 1.253 (0.52) | 1.301 (0.53) | 1.305 (0.55) |
| 3 | 2.133 (0.54) | 2.499 (1.40) | 2.335 (2.16) | 2.704 (2.07) | 4.587 (4.03) |
| 4 | 1.245 (0.41) | 1.150 (0.48) | 1.096 (0.47) | 1.129 (0.50) | 1.364 (0.70) |
| 5 | 1.201 (0.40) | 1.258 (0.48) | 1.233 (0.46) | 1.273 (0.49) | 1.267 (0.49) |
| 6 | 3.642 (0.70) | 3.221 (1.61) | 3.362 (2.94) | 3.371 (2.25) | 7.270 (5.46) |
| 7 | 0.752 (0.32) | 0.933 (0.43) | 1.014 (0.45) | 1.059 (0.48) | 1.276 (0.69) |
| 8 | 1.310 (0.42) | 1.305 (0.52) | 1.305 (0.56) | 1.344 (0.55) | 1.363 (0.60) |
| 9 | 0.387 (0.23) | 1.198 (1.00) | 0.815 (0.87) | 1.219 (1.20) | 1.596 (1.93) |
| 10 | 12.537 (1.29) | 11.211 (3.06) | 16.351 (4.82) | 12.837 (3.09) | 17.239 (6.81) |
| 11 | 12.343 (1.28) | 11.583 (3.51) | 15.025 (4.95) | 13.045 (3.22) | 14.337 (4.22) |
| 12 | 11.784 (1.25) | 12.184 (3.18) | 13.132 (3.30) | 12.147 (2.88) | 13.887 (4.74) |
The results of both Simulations 2 and 3 suggest that in some situations, MICE-IW-c and can perform notably better than MICE-IW, and so there is at times a benefit to including the study-specific sums in the univariate regression models. Even if the MICE-IW-c model is not truly “compatible” in Simulation 3, its relatively good performance suggests that including the study sums in the imputation model produces an adequate approximation to the true full conditionals. The reduced efficiency of the MICE-ML method in this study suggests that for some unusual covariances, using a proper prior on variance parameters might offer advantageous stabilization.
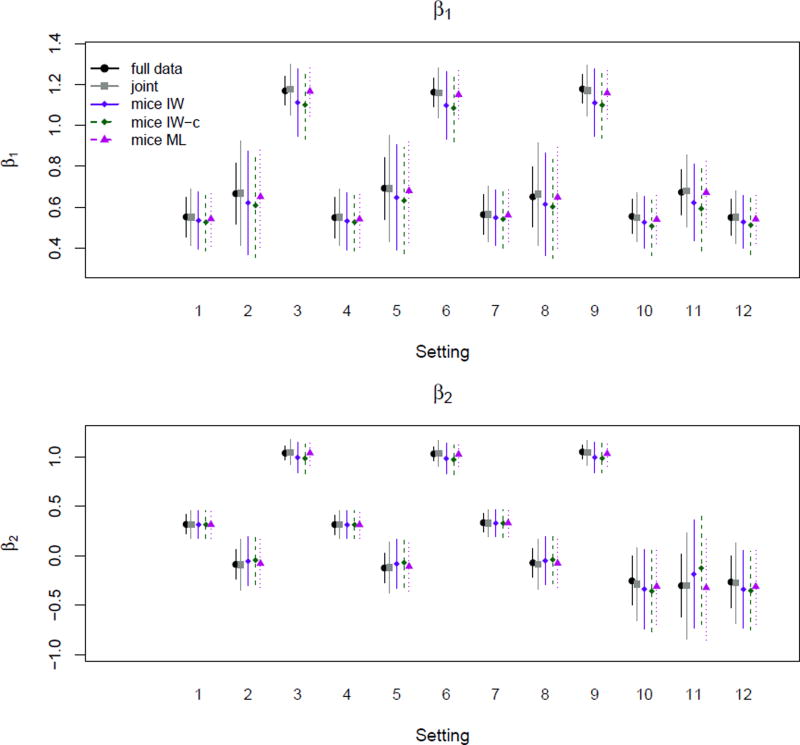
Simulation 4, Balanced Random Slope
The fourth panel of Figure 5 shows estimates of ψ, the variance of the random slope. All of the MICE methods inflate estimates for settings 10 and 11, but there is no notable difference across these methods. Table 7 details these findings. As shown in Figure 6, we also see a discrepancy across methods in estimating β1 and β2, the regression coefficients associated with the variables with missing variables. The differences are more apparent in β1, the coefficient associated with the variable with higher missingness: both of the MICE-IW methods tend to underestimate the strength of association, particularly the compatible model, and this is seen to some degree in all settings except 1, 4, and 7, the settings where Y1 and Y2 are most weakly associated. The joint model and MICE-ML both yield estimates reasonably close to the full data for this parameter.
Table 7.
Estimates of ψ; Simulation 4
| Full data | Joint | MICE-IW | MICE-IW-c | MICE-ML | |
|---|---|---|---|---|---|
| 1 | 1.096 (1.45) | 1.121 (1.50) | 1.200 (1.56) | 1.204 (1.56) | 1.165 (1.53) |
| 2 | 1.203 (1.51) | 1.300 (1.62) | 1.418 (1.72) | 1.397 (1.71) | 1.417 (1.72) |
| 3 | 2.091 (2.02) | 2.240 (2.39) | 2.431 (2.96) | 2.490 (3.18) | 2.337 (2.79) |
| 4 | 1.269 (1.56) | 1.204 (1.54) | 1.219 (1.56) | 1.225 (1.56) | 1.198 (1.54) |
| 5 | 1.114 (1.44) | 1.217 (1.56) | 1.284 (1.61) | 1.276 (1.61) | 1.292 (1.62) |
| 6 | 3.609 (2.65) | 3.154 (2.78) | 3.971 (4.53) | 3.841 (3.98) | 3.523 (3.60) |
| 7 | 0.754 (1.19) | 0.924 (1.35) | 1.067 (1.47) | 1.065 (1.47) | 1.029 (1.44) |
| 8 | 1.251 (1.53) | 1.350 (1.65) | 1.595 (1.85) | 1.579 (1.84) | 1.560 (1.82) |
| 9 | 0.369 (0.84) | 1.261 (1.77) | 1.145 (1.86) | 1.148 (1.89) | 1.214 (1.88) |
| 10 | 11.827 (4.78) | 10.221 (5.31) | 20.685 (9.43) | 20.778 (9.20) | 20.073 (8.35) |
| 11 | 11.360 (4.70) | 9.812 (5.19) | 16.268 (8.70) | 16.145 (8.53) | 15.765 (7.72) |
| 12 | 11.667 (4.76) | 10.546 (5.13) | 13.745 (6.69) | 13.785 (6.53) | 13.039 (5.90) |
Figure 6.
Estimates of β1 and β2 for simulation study 4.
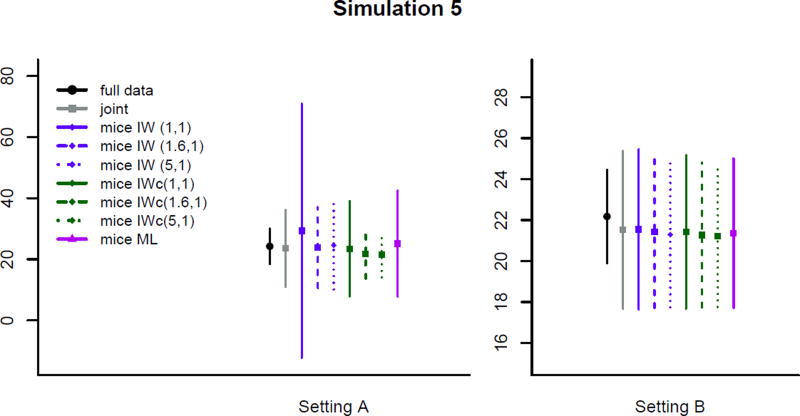
Simulation 5, Different prior distributions
Figure 7 shows the effect of different choices of prior distributions for both small and large numbers of studies. For the small number of studies in Setting A, we clearly see that the prior distributions can change both the point estimates for the random effects variance and, more dramatically, the variability of such estimates. The effect for the “incompatible” MICE-IW method is most striking, where the estimate and its variance become nearly identical to the approximately unbiased joint model results when the similar inverse-Wishart prior with 1.6 degrees of freedom, is employed. In this case, stronger prior distributions have little effect. However, for the “compatible” version, MICE-IW-c, the stronger priors in the imputation procedure results in dramatically more efficient, though slightly downward biased, estimates of random effect variance. As expected, when the number of studies grows to m = 35, comparable to Simulation 1, the choice of prior distribution has little effect. While we did not study the sensitivity to choice of prior distribution for the joint model, the comparability of the joint imputation-based estimates to the estimates with no missing data suggest that the default prior distribution performs relatively well in realistic situations, as in the example presented in Section 5.
Figure 7.
Estimates of ψ for simulation study 5.
5. Example: Traumatic brain injury data
We now apply these methods to data from two multi-site longitudinal studies of children who experience traumatic brain injuries. Previous research has shown that traumatic brain injuries are often associated with psychological and behavioural problems later in life, particularly when the injury is severe [25], and so symptoms observed weeks and months after injury are of interest. Our dataset contains records from two studies: one of preschool-aged children (pTBI) and another of school aged children (TBI) at three sites in Ohio (Cincinnati, Cleveland, and Columbus). Information about these studies can be found in [25] and [26], respectively. While data at several time points are available for some of the participants, we focus on a cross-sectional analysis of the long-term outcomes at 12 months post-injury.
We combine information from these two studies using the multilevel models described above. For the purpose of illustration we treat each site/study combination as a pseudo-study. This approach will both improve algorithmic stability in estimating between-study covariance and better mimic the between-study variability seen in usual IPD meta-analyses. A summary of sample sizes within each pseudo-study is in Table 8. It is reasonable to assume that data within each of these pseudo-studies might be correlated, although the assumption of independent random effects might be less plausible because some pseudo-studies share the same site or study. While a fixed effect for study and site would alleviate some of this concern, the number of studies precludes this solution.
Table 8.
Sample sizes and numbers of missing values for each pseudo-study at the 12-month followup visit. Boldface indicated systematic missingness.
| Study | pTBI | pTBI | pTBI | TBI | TBI | |
|---|---|---|---|---|---|---|
| Site | Site 1 | Site 2 | Site 3 | Site 2 | Site 3 | |
| Pseudo-Study Indicator | 1 | 2 | 3 | 4 | 5 | |
|
| ||||||
| Sample Size | ||||||
| 51 | 21 | 16 | 32 | 64 | 184 | |
|
| ||||||
| Number of missing values for each variable | ||||||
| Injury Group | 0 | 0 | 0 | 0 | 0 | |
| Sex | 0 | 0 | 0 | 0 | 0 | |
| Age | 0 | 0 | 0 | 0 | 0 | |
| Race | 0 | 0 | 0 | 0 | 0 | |
| Maternal Education | 0 | 0 | 0 | 2 | 1 | |
| CBC Internalizing | 0 | 3 | 0 | 0 | 0 | |
| CBC Externalizing | 0 | 3 | 0 | 0 | 0 | |
| BSI Score | 2 | 1 | 1 | 1 | 3 | |
| Hollingshead | 51 | 21 | 16 | 0 | 0 | |
| z-ses | 0 | 0 | 0 | 0 | 0 | |
These datasets illustrate typical missing data issues in IPD meta-analysis, where some measures are taken in both the pTBI and TBI studies, and others are recorded in only one of the two, thus producing systematic missingness. In addition, of course there was also sporadic missingness where some measures are not available due to missed appointments or other individual circumstances, as summarized in Table 8. We used the MICE-IW-c method to easily impute sporadically missing values for the 13 subjects with incomplete data. We do not expect our treatment of this very small amount of missing data to substantially effect our results.
We have chosen two example analyses to specifically illustrate two different types of modeling settings discussed in Section 4. The first analysis focuses on psychological scale outcomes using standard Child Behavior Checklist (CBC) sub-scales, where we generate missingness so as to be able to compare results from the imputation techniques to the ‘true’ estimates with no missing data. The second focuses on measures of socioeconomic status – a particular area of concern for IPD meta-analysis in medical and social science due to immense variation across studies in the choice of which measure to use.
Example 1: CBC scores
In our first example, we consider the relationship between the Brief Symptom Inventory (BSI) overall score [27] and the internalizing and externalizing subscales of the Child Behavior Checklist (CBC) [28, 29]. The BSI provides a summary measure for general psychological wellness. The CBC internalizing score captures indications of internalizing problems such as anxiety or depression, and the externalizing score captures indications of externalizing problems such as aggressive behavior. Higher CBC scores indicate greater prevalence of problem behaviors. Both instruments and all three summaries are well-established, often used in psychological studies, and potentially related to long-term behavioral effects of head injury. In these two studies, both questionnaires were completed by each child’s primary caregiver. Although the versions of the CBC used among the pTBI differed from the TBI, due to the ages of the children, both versions provide a summary score related to the same underlying constructs. Further, the CBC subscale scores are standardized so that systematic differences between the versions should be minimized. Finally, we follow usual practice by including in the analysis both demographic variables (age, sex, race, maternal education) and a binary group variable that indicates whether the injury was “severe” or “mild/moderate”. Summaries of these variables are shown in Table 9.
Table 9.
Proportions or means and (standard deviations) of variables by pseudo-study
| Pseudo-Study | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Group (1 = mild/moderate injury) | 0.863 | 0.571 | 0.688 | 0.500 | 0.578 |
| Sex (1 = male) | 0.588 | 0.714 | 0.438 | 0.750 | 0.734 |
| Age | 6.006 (1.08) | 6.129 (1.31) | 6.282 (1.16) | 10.824 (2.18) | 10.843 (1.95) |
| Race (1 = Caucasian) | 0.765 | 0.714 | 0.500 | 1.000 | 0.703 |
| Maternal Education | 4.412 (1.28) | 4.238 (1.00) | 4.750 (1.06) | 4.167 (1.02) | 4.683 (1.16) |
| CBC Internalizing | 53.755 (10.40) | 53.200 (11.54) | 48.000 (11.58) | 56.516 (10.22) | 53.230 (11.41) |
| CBC Externalizing | 48.392 (9.46) | 53.667 (14.77) | 49.875 (11.82) | 56.594 (11.05) | 52.906 (10.70) |
| BSI Score | 53.569 (12.26) | 55.111 (18.77) | 48.062 (10.27) | 55.188 (11.88) | 52.703 (12.12) |
| Hollingshead | NA (NA) | NA (NA) | NA (NA) | 32.281 (12.88) | 36.125 (15.55) |
| z-ses | −0.237 (1.00) | −0.326 (0.88) | −0.087 (1.12) | −0.013 (0.87) | 0.190 (1.07) |
Our goal in this first example is to mimic a case where a subset of different psychological scale measures are used in different studies. Both CBC subscale scores were fully observed in both the pTBI and TBI studies, so we generated systematic missingness by deleting the externalizing subscale in pseudo-study 2 and the internalizing subscale in pseudostudy 5. Because these two scores are derived from the same checklist, it is unlikely in practice that one would be systematically missing; nonetheless, it is plausible that systematically missing variables may have a similar association, such as scores from two different indices of injury severity or methods of summarizing the same checklist.
We imputed missing values according to the four methods described in Section 2. For the joint imputation model in Equation 1, we specified the outcome Yi to be the CBC internalizing and externalizing scores and the covariate matrix Xi to comprise the injury group, sex, age, race, maternal education, and BSI score. For the MICE-IW imputations based on Equation 5, we specified the covariate matrix to comprise Xi and the CBC externalizing score, Y(2)i, and similarly the covariate matrix to comprise Xi and the CBC internalizing score, Y(1)i. The MICE-IW-c and MICE-ML imputations add the study-specific averages of the appropriate CBC score, Ȳ(k)i to the fixed effect covariates of the MICE-IW model. For all imputation models, the random effects covariates, Zi and , are simply study indicators corresponding to random intercepts models. We analyzed completed datasets using a random intercepts regression of the BSI score on the CBC subscale scores and the baseline variables listed in Table 10. Summaries of parameter estimates are also shown in Table 10.
Table 10.
Parameter estimates and (standard errors) for Example 1 analysis of BSI score on listed covariates.
| Full data | Joint | MICE-IW | MICE-IW (c) | MICE-ML | |
|---|---|---|---|---|---|
| Intercept | 26.001 (5.79) | 24.443 (5.89) | 24.288 (6.04) | 24.391 (6.31) | 23.101 (6.49) |
| CBC Internalizing | 0.225 (0.08) | 0.287 (0.09) | 0.260 (0.10) | 0.290 (0.10) | 0.255 (0.09) |
| CBC Externalizing | 0.302 (0.07) | 0.278 (0.08) | 0.294 (0.09) | 0.268 (0.09) | 0.317 (0.08) |
| Group (1 = mild/moderate injury) | 1.084 (1.45) | 1.339 (1.50) | 0.960 (1.50) | 1.073 (1.51) | 1.214 (1.51) |
| Sex (1=male) | −0.200 (1.46) | −0.266 (1.52) | −0.199 (1.53) | −0.382 (1.54) | 0.175 (1.60) |
| Age | 0.407 (0.26) | 0.337 (0.29) | 0.402 (0.29) | 0.393 (0.30) | 0.380 (0.31) |
| Race (1=Caucasian) | −1.518 (1.62) | −1.694 (1.71) | −1.736 (1.70) | −1.882 (1.75) | −1.671 (1.72) |
| Maternal Education | −0.759 (0.63) | −0.706 (0.67) | −0.602 (0.66) | −0.629 (0.70) | −0.680 (0.70) |
| Error variance | 81.389 (8.60) | 76.884 (8.62) | 76.656 (8.84) | 77.716 (9.11) | 79.261 (9.52) |
| Random effect variance | 0.919 (0.53) | 1.415 (1.49) | 1.421 (1.44) | 2.186 (2.59) | 1.424 (1.77) |
The parameter estimates suggest a positive association between both the internalizing and externalizing CBC scores and BSI score. Relative to the full data, most of the imputation methods produce coefficients that are slightly overestimated for the internalizing scores and underestimated for the externalizing scores. The exception is the MICE-ML method, which slightly overestimates the CBC externalizing score. Several other variables’ coefficients (e.g., sex and race) differ more substantially between full data and imputations. However, all of these differences are small relative to the estimated standard errors. Consistent with the simulation results, the four imputation methods vary in their estimates of the random effect variance. All methods over-estimate the between-study variability by at least 50%, but MICE-IW-c produces an estimate nearly 150% larger than the full data estimate. The standard error of this estimate is also substantially larger than for the other estimates. We note that this relative instability of estimates using MICE-IW-c can be alleviated if the “compatible” study means are omitted from the imputation models for sporadically missing values, reducing the number of parameters that must be estimated. We expect that in most cases, there is little to be gained by requiring compatible imputation models for sporadically missing variables. The four imputation methods were in agreement for the error variance parameter, which is much larger than the random effect; the model fit suggests that the between-study variability of this example is relatively small in magnitude.
Example 2
Our second example considers imputing socioeconomic status (SES) variables for a prognostic model of CBC internalizing score. In particular, we consider imputing the Hollingshead index, a measure of socioeconomic status observed only in the school-aged children of the TBI study (pseudo-studies 4 and 5). While many psychological studies rely on census tract median income or maternal education to capture SES, the Hollingshead index (and related measures, such as the Duncan score) also incorporate occupational information. Thus, the Hollingsead index may be a more accurate measure of SES, but is much more difficult to measure and construct in practice. SES was measured using other metrics in both the pTBI and TBI studies; each report maternal education and a normed composite, which we call the “z-ses” score. (Although the z-ses score is based on different variables across the studies, the measures are normed to the sample and thus should be comparable for this example.) To mimic the motivating example of two variables with systematic missingness, we also imposed artificial missingness on z-ses in pseudo-study 4.
We again imputed missing values according to the four methods described in Section 2. For the joint imputation model in Equation 1, we specified the outcome Yi to be the Hollingshead index and the z-ses composite measure and the covariate matrix Xi to comprise the injury group, sex, age, race, and maternal education. For the MICE-IW imputations based on Equation 5, we specified the covariate matrix to comprise Xi and z-ses, Y(2)i, and similarly the covariate matrix to comprise Xi and the Hollingshead index, Y(1)i. The MICE-IW-c imputation adds the study-specific averages of the appropriate scores, Ȳ(k)i to the fixed effect covariates of the MICE-IW model. The MICE-ML imputation adds only the study-specific Hollingshead average to the imputation model for z-ses; because only one study includes both the Hollingshead and z-ses measures, adding the study-specific z-ses averages to the Hollingshead imputation would have resulted in unstable maximum likelihood estimates in the imputation algorithm. The need for this adjustment highlights a computational limitation of the MICE-ML approach for sparse overlap in fully observed parameters across studies. Again, for all imputation models, the random effects covariates, Zi and , are simply study indicators corresponding to appropriate random intercepts models. Our target model for analysis is a regression of CBC internalizing score on the Hollingshead score and the baseline variables listed in Table 11. The parameter estimates based on the four imputation procedures are also shown in Table 11. Because we have no “true” complete data analysis with which to compare our results, this table also includes the estimated fraction of missing information for each coefficient [2].
Table 11.
Parameter estimates, (standard errors), and [estimated fraction of missing information] for Example 2 regression of CBC internalizing score on listed covariates.
| Joint | MICE-IW | MICE-IW (c) | MICE-ML | |
|---|---|---|---|---|
| Intercept | 57.089 (5.13) | 57.810 (5.50) | 58.102 (5.34) | 57.483 (6.56) |
| [0.118] | [0.234] | [0.116] | [0.268] | |
| Hollingshead | 0.631 (1.13) | 0.233 (1.14) | 0.435 (1.08) | 0.322 (1.15) |
| [0.369] | [0.331] | [0.425] | [0.419] | |
| Group (1 = Mild/moderate injury) | −0.286 (0.10) | −0.229 (0.10) | −0.262 (0.09) | −0.270 (0.10) |
| [0.040] | [0.059] | [0.036] | [0.047] | |
| Sex (1 = male) | −1.619 (1.71) | −1.551 (1.74) | −1.420 (1.72) | −1.481 (1.81) |
| [0.046] | [0.049] | [0.037] | [0.060] | |
| Age | 0.416 (1.74) | 0.643 (1.74) | 0.468 (1.73) | 0.247 (1.88) |
| [0.137] | [0.166] | [0.215] | [0.182] | |
| Race (1 = Caucasian) | 0.361 (0.37) | 0.245 (0.41) | 0.245 (0.40) | 0.262 (0.45) |
| [0.133] | [0.113] | [0.176] | [0.301] | |
| Maternal Education | −0.580 (2.16) | −1.387 (2.15) | −0.868 (2.11) | −0.321 (2.47) |
| [0.255] | [0.230] | [0.303] | [0.258] | |
| Error variance | 109.520 (11.86) | 112.019 (12.15) | 110.357 (11.85) | 121.777 (28.96) |
| Random effect variance | 3.998 (2.91) | 8.995 (3.56) | 8.223 (10.04) | 20.917 (53.39) |
The baseline indicator of injury group has the strongest relationship with the CBC internalizing score, with the mild/moderate group showing lower prevalence of behavioral problems than the severe injury group. The coefficient associated with Hollingshead index suggests a negative association between socioeconomic status and long-term behavioral effects of TBI, but this coefficient is highly variable due to the high missingness, as indicated by estimated fractions of missing information near 40%. As in Example 1, and expected from our simulation study, most of the coefficient estimates are fairly similar across imputation methods. For this model, the data are considerably more variable than in Example 1. Estimates of both error variance and random effect variance are large, for example 110 and 4 for the joint imputation results, respectively. Again, the magnitude of between-study variability is small compared to the within-study variability. While the error variance estimates are relatively similar across the imputation methods, the estimates of the random effect variance differ considerably. The joint method produces the smallest estimate. Based on the simulation results, we expect this estimate to be closest to the truth. The MICE methods all estimate the random effect variance to be larger, with MICE-IW and MICE-IW-c indicating variances close to 8 or 9. Our modified MICE-ML procedure results in a substantially larger estimate of the random effect variance of 20, with an accompanying large standard error over 50. Because the MICE-ML algorithm relies on ML estimates, we are not surprised that it performs relatively poorly in this sparse imputation example.
6. Discussion
In this paper we compared joint model imputation and MICE in terms of their theoretical equivalence and empirical performance for the multilevel multivariate normal model with systematically missing data in the structure commonly seen for IPD meta-analysis. We showed in Section 3 that the two methods may not be theoretically equivalent in most MICE models; namely, the equivalent full conditionals require a study-specific term in the regression function, and some of the conditional parameters are typically specific to a study even if the joint model specifies homogeneous parameters. These features, in particular the second, mean that it is not realistic to use a fully compatible model for systematically missing covariates. Nonetheless, simulations in Section 4 suggest that in these examples, similar to findings in [9], incompatible conditional FCS models will often still lead to reasonable imputations; analyses based on imputations from joint and FCS procedures do not tend to differ substantially in many common settings. When there are differences, it is in estimating the variance of the random effect. Including the sum for a compatible (or approximately compatible) imputation model can often prevent such difficulties. Our work also suggests that when the conditional parameters vary considerably across studies, use of prior information can improve performance of FCS methods.
Because both models account for variables’ multilevel structure, Enders, Mistler and Keller conclude that both FCS and joint model imputation are appropriate for multilevel random intercepts models [14]. Although we agree that FCS is typically able to produce good imputations, our work reveals some features of the full conditional models that might on occasion lead to biased or inefficient estimators. These problems tend to be mild, but might be exacerbated by small samples sizes or unequal error and random effect variances in the presence of systematic missingness. In addition, we found that joint model and FCS methods can diverge in small samples due the the influence of priors. Standard “weakly-informative” inverse-Wishart priors on the joint parameterization, for example, translate to concentrated distributions on the conditional parameterization, and the same priors applied directly to the conditional parameterization often lead to predictive distributions with heavier tails. The results of Simulation 5 suggest that a data-driven approach with no prior influence, as in the MICE-ML method, can at times mitigate this influence. Nonetheless, in the same situations when prior influence is large, data-based hyperparameters may also be unreliable. Our work regarding these priors is not comprehensive, however, and other families of distributions might result in improved performance. Overall, because the prior distribution specification can substantially effect the analytical results, robust sensitivity analyses are particularly important for small collections of studies. Comparing results across a range of prior distributions does not reveal the ‘best’ prior distribution for any particular analysis, but can convey the level of caution one should take in making inference based on any one chosen prior distribution.
Existing work has emphasized the importance of accounting for data’s multilevel structure when accounting for missingness, and multiple imputation using a chained equations approach is often the most flexible and user-friendly method. For example, an approach by The Fibrinogen Studies Collaboration addresses systematic missingness by directly modelling the relationship between estimates from fully observed studies and those with missing values, but requires likelihood calculations that are not easily adapted to differing patterns of missingness [30]. FCS, on the other hand, can easily adapt to a variety of missingness patterns and typically requires specification of only simple regression models. Our results suggest that the multiple imputation FCS alternatives will typically perform adequately for a random intercepts model. Although the random slopes case was not our primary focus, the results of simulation 4 suggest that joint model imputation is slightly better suited to capture all associations for this model when missingness is high.
Here we considered only the multivariate normal model where both methods are easily implemented and derivations are analytically tractable. In practice, FCS is often used in cases where an appropriate joint model is less straightforward, such as when missing values occur in both continuous and categorical variables, where a joint model is much less easily implemented. The work of Enders, Mistler and Keller [14] and Kline, Andridge and Kaizar [17] suggest that a latent variable imputation scheme may be an effective method of utilizing joint normal imputation methods to impute categorical variables, and the authors showed promising improvement over a chained equations approach based on rounding. Their work did not address systematic missingness, however. For systematic missingness, Jolani, et al provides a framework for FCS imputation in a method analogous to those discussed here, but within a generalized linear model framework that is appropriate for binary and categorical variables [13]. Future work might compare the latent variable joint imputation to this approach to non-normally distributed data.
Even though our comparisons in the continuous case are not directly applicable to model non-normally distributed variables, we believe that our results here, nonetheless, do reveal properties of fully conditional models that are applicable to other problems. First, it is likely that homogeneity assumptions in the fully conditional model will be misspecified for multilevel models, which may negatively affect imputations in some cases. Second, prior influence can be strong on the parameters corresponding to the higher level of the hierarchy.
In sum, we have found that for many cases of multivariate normal hierarchical data with systematic missingness, the joint or conditional specification of imputation procedures in itself has little impact on analytical results. However, especially in cases with few groups or studies consistent with typical IPD meta-analyses, the choice of prior distributions substantially affects the results. As such, ‘default’ prior distributions should be used only with caution. In absence of other guidelines, we believe that using joint model imputation with default priors, or FCS priors that are similar to the joint priors, will often work well. Nonetheless, we recommend that researchers carefully consider prior specifications and their implications regardless of the chosen imputation method, and explore the importance of this choice via sensitivity analyses.
Supplementary Material
Acknowledgments
The authors thank Drs. Terry Stancin, H. Gerry Taylor, Shari Wade, and Keith Yeates for providing data and assistance related to the example.
Contract/grant sponsor: This work was supported in part by the Eunice Kennedy Shriver National Institute of Child Health and Human Development under award number R03HD080033. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix
Notation
| Data Structure | Constant Objects | |
|---|---|---|
|
|
|
|
| i = 1, …, m | Index for ‘level-1’ group, or study | 1n Column vector of ones, length n |
| j = 1, …, ni | Index for ‘level-2’ individuals, or participants within study i | In Square identity matrix of dimension n |
| k = 1, …, r | Index for variable | Jn Square matrix of dimension n of all ones |
| Ymis | The portion of {Yi}i=1,…,m where the values are missing | |
| Yobs | The portion of {Yi}i=1,…,m where the values are observed | |
| ℳk ⊂ {1, …, m} | Collection of indices for studies where variable k is systematically missing | |
| Objects Used in Models | ||||
|---|---|---|---|---|
|
| ||||
| Joint Imputation Model for Y (Equation (1)) | Full Conditional Specification (FCS) Imputation Models for Y(k) (Equations (4)) |
|||
| Likelihood or Conditional Likelihood Functions | ||||
|
| ||||
| Yi = (Yi1, …, Yir) ∈ Rni×r | Matrix of r partially observed variables for each of ni individuals participating in study i | Y(k) | The portion of {Yi}i=1,…,m that only includes the kth variable | |
| Y(−k) | {Yi}i=1,…,m with the kth variable removed | |||
| Xi ∈ Rni×p | Matrix of p fully observed fixed effects covariates for each of ni individuals participating in study i |
|
Matrix of p* fixed effect covariates; possibly includes Yi(−k) or transformations of Yi(−k). | |
| Zi ∈ Rni×q | Matrix of q fully observed variables for each of ni individuals participating in study i; typically associated with random effects. |
|
Matrix of q* random effect covariates for the conditional model of response variable Y(k); possibly includes Yi(−k) or transformations of Yi(−k). | |
| εi = (εi1, …, εini)′ ∈ Rni×r | Matrix of errors, where each row represents the vector of errors for individual j in group i. | |||
| β ∈ Rp×r | Matrix of fixed effects |
|
Vector of fixed effects | |
| Bi ∈ Rq×r | Matrix of random effects for study i |
|
Random effects matrix | |
| Σ ∈ Rr×r | Variance-covaraince matrix for the individual-specific error vector εij |
|
Scalar error variance | |
| Ψ = {ψab}a=1,…,rq;b=1,…,rq ∈ Rrq×rq | Variance-covariance matrix for the stacked vector of random effects, vec (Bi) |
|
Random effect variance | |
| θ = {β, Σ, Ψ} | All parameters for the likelihood of the variables with missing values, Y |
|
Vector of parameters for the fully conditional specified likelihood for variable with missing values Y(k) | |
|
| ||||
| Prior Distributions | ||||
|
| ||||
| πJ | Prior distribution for θ in the joint imputation model |
|
Prior distribution for the parameters ϕk and latent random effects | |
| νk | Degrees of freedom for inverse-Wishart prior on variance parameters | |||
| Vk | Scale for inverse-Wishart prior on variance parameters | |||
|
| ||||
| Conditional Distributions for Sampling Algorithm | ||||
|
| ||||
| P• | Full conditional distribution of the parameter or latent variable • in the Gibbs sampler derived from the joint imputation model and prior distribution πJ | |||
| Pk (Y(k)|Y(−k), θk) | Full conditional distribution for the parameters θk and latent random effects as derived from the joint likelihood and prior | g̃k | Pseudo-full conditional distribution for the parameters and latent random effects as derived from the fully conditional specified likelihood and prior | |
| θk | Parameters for the full conditional distribution | gk | Pseudo-full conditional distribution for the missing values for variable k, as derived from the fully conditional specified likelihood | |
References
- 1.Resche-Rigon M, White IR, Bartlett JW, Peters SAE, Thompson SG. Multiple imputation for handling systematically missing confounders in meta-analysis of individual participant data. Statistics in Medicine. 2013;32:4890–4905. doi: 10.1002/sim.5894. [DOI] [PubMed] [Google Scholar]
- 2.Rubin D, Little RJA. Statistical Analysis with Missing Data. John Wiley and Sons; Hoboken, New Jersey: 2002. [Google Scholar]
- 3.Thompson SG, Higgins JPT. How should meta-regression analyses be undertaken and interpreted? Statistics in Medicine. 2002;21:1559–1573. doi: 10.1002/sim.1187. [DOI] [PubMed] [Google Scholar]
- 4.Andridge RR. Quantifying the impact of fixed effects modeling of clusters in multiple imputation for cluster randomized trials. Biometrical Journal. 2011;53:57–74. doi: 10.1002/bimj.201000140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Siddique J, Reiter JP, Brincks A, Gibbons RD, Crespi CM, Brown CH. Multiple imputation for harmonizing longitudinal non-commensurate measures in individual participant data meta-analysis. Statistics in Medicine. 2015;34(26):3399–3414. doi: 10.1002/sim.6562. URL http://dx.doi.org/10.1002/sim.6562, sim.6562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schafer JL. Technical Report 97-04. The Pennsylvania State University; 1997. Imputation of missing covariates under a multivariate linear mixed model. [Google Scholar]
- 7.Schafer JL, Yucel RM. Computational strategies for multivariate linear mixed-effects models with missing values. Journal of Computational and Graphical Statistics. 2002;11(2):437–457. doi: 10.1198/106186002760180608. [DOI] [Google Scholar]
- 8.van Buuren S, Groothuis-Oudshoorn K. mice: Multivariate imputation by chained equations in R. Journal of Statistical Software. 2011;45(1):1–67. doi: 10.18637/jss.v045.i03. [DOI] [Google Scholar]
- 9.van Buuren S, Brand JPL, Groothuis-Oudshoorn CGM, Rubin DB. Fully conditional specification in multivariate imputation. Journal of Statistical Computation and Simulation. 2006;76(12):1049–1064. doi: 10.1177/096228020607446. [DOI] [Google Scholar]
- 10.Arnold B, Press SJ. Compatible conditional distributions. Journal of the American Statistical Association. 1989;84(405):152–156. doi: 10.1080/01621459.1989.10478750. [DOI] [Google Scholar]
- 11.Liu J, Gelman A, Hill J, Su YS, Kropko J. Stationary distribution of iterative imputations. Biometrika. 2013:1–19. doi: 10.1093/biomet/ast044. [DOI] [Google Scholar]
- 12.Siddique J, de Chavez PJ, Howe G, Cruden G, Brown CH. Limitations in using multiple imputation to harmonize individual participant data for meta-analysis. Prevention Science. 2017:1–14. doi: 10.1007/s11121-017-0760-x. URL http://dx.doi.org/10.1007/s11121-017-0760-x. [DOI] [PMC free article] [PubMed]
- 13.Jolani S, Debray TPA, Koffijberg H, van Buuren S, Moons KGM. Imputation of systematically missing predictors in an individual participant data meta-analysis: a generalized approach using mice. Statistics in Medicine. 2015;34:1841–1863. doi: 10.1002/sim.6451. [DOI] [PubMed] [Google Scholar]
- 14.Enders CK, Mistler SA, Keller BT. Multilevel multiple imputation: A reivew and evaluation of join modeling and chained equations imputation. Psychological Methods. 2015 doi: 10.1037/met0000063. [DOI] [PubMed] [Google Scholar]
- 15.Yucel R. Multiple imputation inference for multivariate multilevel contnuous data with ignorable non-response. Philosophical Transactions of the Royal Society A. 2008;366(1874):2389–2403. doi: 10.1098/rsta.2008.0038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kline D, Andridge R, Kaizar E. Comparing multiple imputation methods for systematically missing subject-level data. Research Synthesis Methods. 2015 doi: 10.1002/jrsm.1192. [DOI] [PubMed] [Google Scholar]
- 17.Kline D, Andridge R, Kaizar E. PhD Thesis. The Ohio State University; 2016. Systematically missing subject-level data in longitudinal research synthesis. [Google Scholar]
- 18.Zhao JH, Schafer JL. pan: Multiple imputation for multivariate panel or clustered data 2016. R package version 1.4 [Google Scholar]
- 19.Hughes R, White IR, Seaman SR, Carpenter JR, Tilling K, Sterne JAC. Jont modelling rationalie for chained equations. BMC Medical Research Methodology. 2014;14 doi: 10.1186/1471-2288-14-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Arnold BC, Castillo E, Sarabia JM. Conditionally specified distributions: An introduction. Statistical Science. 2001;16(3):249–274. doi: 10.1214/ss/1009213728. [DOI] [Google Scholar]
- 21.Bartlett J, Seaman SR, White IR, Carpenter JR. Multiple imputation of covariates by fully conditional specification: Accommodating the substantive model. Statistical Methods in Medical Research. 2015;24(4):462–487. doi: 10.1177/0962280214521348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Carpenter J, Kenward M. Multiple Imuptation and its Application. John Wiley and Sons; 2013. [Google Scholar]
- 23.Demidenko E. Mixed Models. John Wiley and Sons; Hoboken New Jersey: 2004. [Google Scholar]
- 24.White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Statistics in Medicine. 2011;30(4):377–399. doi: 10.1002/sim.4067. [DOI] [PubMed] [Google Scholar]
- 25.Chapman LA, Wade SL, Walz NC, Taylor HG, Stancin T, Yeates KO. Clinically significant behavior problems during the initial 18 months following early childhood traumatic brain injury. Journal of Rehabilitation Psychology. 2010;55:48–57. doi: 10.1037/a0018418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fay TB, Yeates KO, Wade SL, Drotar D, Stancin T, Taylor HG. Predicting longitudinal patterns of functional deficits in children with traumatic brain injury. Neuropsychology. 2009;23:271–282. doi: 10.1037/a0014936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Derogatis L, Melisaratos N. The brief symptom inventory: an introductory report. Psychological Medicine. 1983;13:595–605. [PubMed] [Google Scholar]
- 28.Achenbach T, Rescorla L. Manual for the ASEBA Preschool Forms and Profiles. University of Vermont Department of Psychiatry; Burlington, VT: 2001. [Google Scholar]
- 29.Achenbach T, Rescorla L. Manual for the ASEBA School-Age Forms and Profiles. University of Vermont Department of Psychiatry; Burlington, VT: 2001. [Google Scholar]
- 30.The Fibrinogen Studies Collaboration. Systematically missing confounders in individual participant data meta-analysis of observational cohort studies. Statistics in Medicine. 2009;28(8):1218–1237. doi: 10.1002/sim.3540. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.