Angular reconstitution-based 3D reconstructions of nanomolecular structures from superresolution light-microscopy images

Significance

Superresolution imaging techniques have become an essential tool to study the organization and structure of biological molecules with previously unimagined detail. It is becoming clear, however, that structural heterogeneity, dynamics, and low labeling densities can impede the potential of such technologies. Here, we describe a model-free method based on single-particle reconstruction algorithms to extract 3D isotropic structural information from 2D superresolution images of nanometer-sized supramolecular structures, such as DNA origami or protein complexes. We expect our work will help bridge the gap between superresolution microscopy and conventional electron microscopy.

Abstract

Superresolution light microscopy allows the imaging of labeled supramolecular assemblies at a resolution surpassing the classical diffraction limit. A serious limitation of the superresolution approach is sample heterogeneity and the stochastic character of the labeling procedure. To increase the reproducibility and the resolution of the superresolution results, we apply multivariate statistical analysis methods and 3D reconstruction approaches originally developed for cryogenic electron microscopy of single particles. These methods allow for the reference-free 3D reconstruction of nanomolecular structures from two-dimensional superresolution projection images. Since these 2D projection images all show the structure in high-resolution directions of the optical microscope, the resulting 3D reconstructions have the best possible isotropic resolution in all directions.

With recent advances in electron detection and image processing, electron microscopy (EM) now enables the exploration of supramolecular architectures at nanoscale resolutions (1–3). The resolution in conventional fluorescence light microscopies is limited by diffraction to a few hundred nanometers. Recently, several superresolution microscopy methods were developed to surpass the intrinsic resolution limit of conventional fluorescence microscopy (4). Uniquely, superresolution microscopies enable imaging of man-made materials and biological objects in complex environments with chemical specificity and previously unimagined detail (5–7). However, the dissection of structural heterogeneity, dynamics, and low labeling densities, most noticeable at the nanoscale, limit the full potential of current superresolution analysis methods.

Recently, single-particle averaging approaches were successfully applied to superresolution optical microscopy images to unravel ultrastructural details of the nuclear pore complex (8), the endosomal sorting complexes required for transport (ESCRT) machinery at HIV assembly sites (6), and the machinery of the centrosome (9). Typically, these methods relied on the use of structural templates to seed the reconstruction process and used cylindrical or spherical symmetries to reveal information on the radial distribution of components within complexes. These approaches are thus not easily transferable to de novo systems and may lead to structures that are biased toward those of templates.

Here, we present a model-free method adapted from conventional EM single-particle reconstruction (EM SPR) algorithms to extract 3D isotropic structural information from 2D single-molecule localization microscopy (SMLM) (10) images of supramolecular structures. We demonstrate the applicability of this method by solving the 3D structures of DNA origami (11, 12) and of simulated large protein complexes.

Results

Superresolution Imaging of Model DNA Origami.

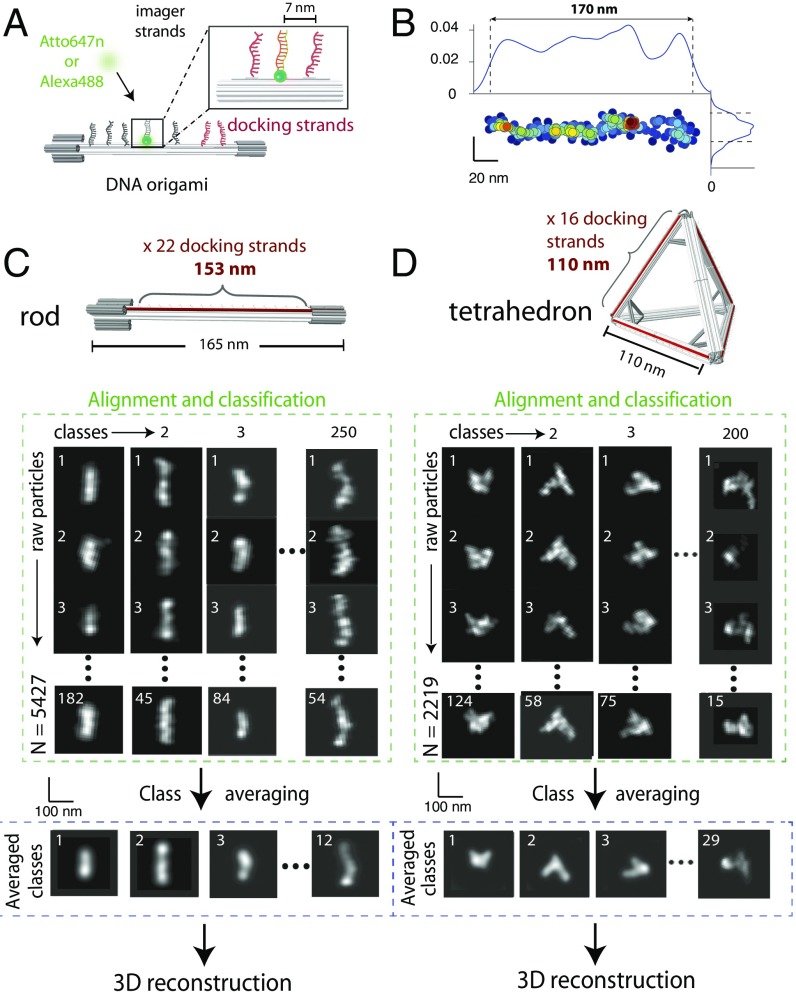
DNA origami were labeled by DNA-PAINT (13, 14). Equally spaced “docking” strands were placed to provide high-density labeling using Atto647n- or Alexa488-labeled “imager” strands (Fig. 1A and SI Appendix, Figs. S1, S3, and Materials and Methods). Two distinct DNA origami structures were used to demonstrate our approach on 1D and 3D architectures: a linear rod of 165 nm in length and a tetrahedron of 110-nm edge length (14) (Fig. 1 C and D and SI Appendix, Figs. S1–S4). Linear rods were immobilized on a flat biotin-PEG surface by specific biotin-neutravidin-biotin-PEG interactions at the two extremities along the long axis, thus most rods laid flat on the surface (SI Appendix, Fig. S5B). Tetrahedrons were immobilized by nonspecific interactions with a rough poly-l-lysine surface, ensuring random orientations with respect to the optical axis (SI Appendix, Fig. S5C).

Fig. 1.

Self-assembly of DNA origami and single-particle averaging. (A) Schematic representation of DNA origami and DNA-PAINT strategy. Docking strands were positioned on the surface of the origami at regular spacings; imager strands were localized with nanometer precision. (B) Single, surface-bound DNA origami can be visualized by DNA-PAINT (Left and Right). The typical profile width was 14 nm (Bottom). (C and D, Top) Schematic representations of linear rod and tetrahedron. (Bottom) Raw particles were reoriented and retranslated, aligned, and classified to obtain class averages. Total number of raw particles from over 20 independent experiments: 5,427 for linear rod and 2,219 for tetrahedron.

After surface immobilization, we performed DNA-PAINT imaging in a microfluidics chamber (SI Appendix, Fig. S5). For each structure, thousands of monodisperse single DNA origami particles were obtained by DNA-PAINT at a localization precision of 15 ± 3 nm (Fig. 1B, SI Appendix, Fig. S6, and Materials and Methods) covering 153 nm of the rod length and the full 110 nm of the tetrahedron side.

Single-Particle 3D Reconstructions from Single-Molecule Datasets.

Localizations from single particles were converted to images by calculating the probability density of localization. The labeling spacing (7 nm) was lower than the localization precision (15 nm, SI Appendix, Fig. S6). Images from single particles were aligned and classified into class averages by multivariate statistical analysis (MSA) classification. Well-defined class averages were then selected as references for multireference alignment (MRA), followed by resubmission to MSA classification (15). After a small number of iterative cycles (typically ∼5) of MRA and MSA classification, class averages did not evolve. Class averages were obtained from the sum of images representing particles in the same orientation, resulting in a more uniformly distributed fluorescence signal than that of raw particles, and leading to overall better projections (Fig. 1 C and D and SI Appendix, Figs. S7 and S8 and Materials and Methods).

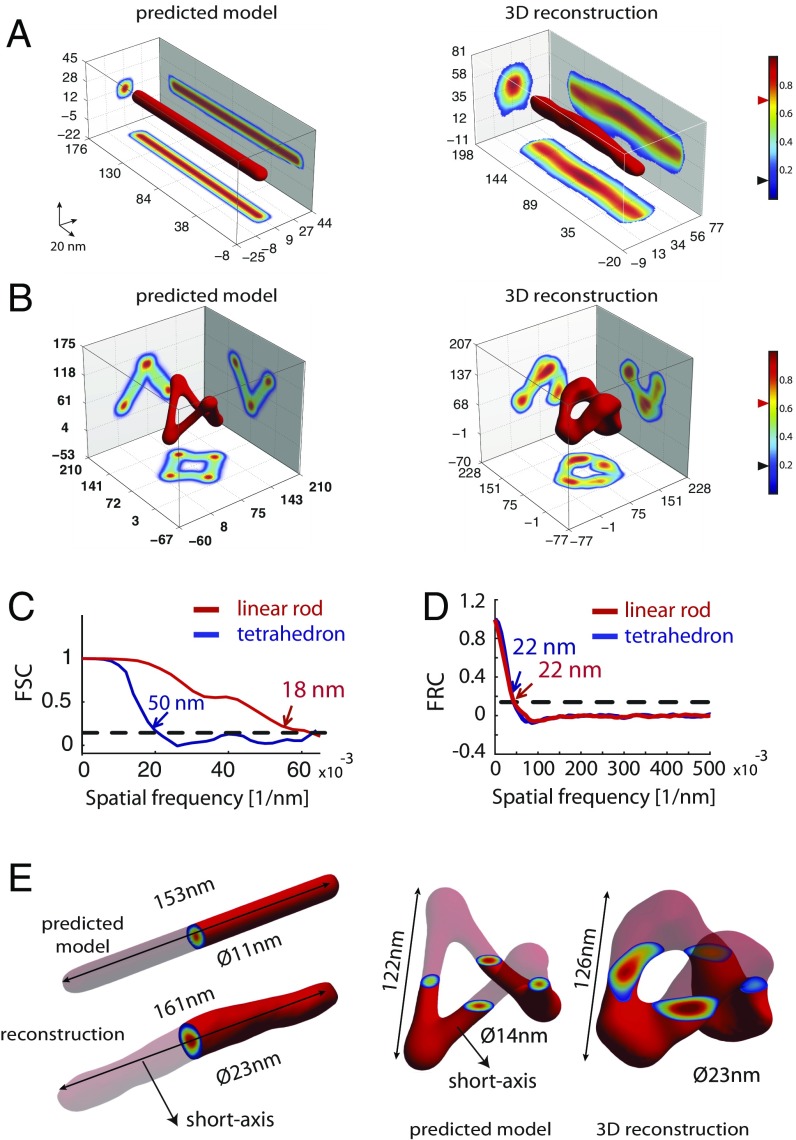
The best class averages were used to compute 3D reconstructions using the angular reconstitution method (SI Appendix, Fig. S9) (16). This technique uses the data in the projection images to find the relative spatial orientations of the projection images without using any instrumentally driven projection direction. These orientations are then used to derive a 3D model. Strikingly, both DNA origami structures could be successfully reconstructed from 5,427 and 2,219 individual particles without relying on initial models (Fig. 2B). We then performed 3D reconstructions using theoretical models of DNA origami. Reconstructions with or without initial models yielded very similar 3D structures (SI Appendix, Figs. S10 and S11 and Fig. 2 A, B, E, and F, respectively), supporting the robustness of the reconstruction method without an initial 3D template.

Fig. 2.

Three-dimensional structures of DNA origami by single-particle reconstruction. (A and B, Left) Three-dimensional structures of linear rod and tetrahedron from theoretical models. (Right) Template-free 3D reconstructions. Black and red triangles on colormaps represent the threshold and iso values used for the intensity projections and 3D representation of the structures, respectively. (C) FSC of the final 3D reconstructions. (D) Average FRC obtained by averaging the FRC curves of 100 single particles for the linear rod and the tetrahedron. (E) Direct comparison of the reference model and 3D reconstructions.

This method was robust with respect to total particle number, localization precision of single events, the density of localizations, and background levels (SI Appendix, Fig. S13). To further assess the robustness of reconstructions, we split raw particles into two sets and calculated the correlation between the final reconstructions obtained from each set of particles as a function of resolution using Fourier shell correlation (FSC; Fig. 2C and SI Appendix, Fig. S11) (17). The resolution of the reconstructions was estimated using the criterion of Rosenthal (18) and resulted in 18 ± 2 and 50 ± 4 nm for the linear rod and tetrahedron, respectively (Fig. 2C). Fourier ring correlation (FRC) (19), which applies the computational principles of FSC to 2D datasets, was used to evaluate the resolution of DNA-PAINT localization data. Averaging 100 FRC curves corresponding to single linear rod and tetrahedron localization datasets yielded resolutions of 22 ± 9 and 22 ± 10 nm, respectively (Fig. 2D and SI Appendix, Fig. S12). The lateral resolution in DNA-PAINT (or other SMLM methods) is 2–3× better than the axial resolution, leading to the acquisition of 3D volumes with anisotropic resolutions. Notably, our 3D reconstructions displayed isotropic resolution as the detection method relies on the use of 2D superresolution projection images that have the best resolution attainable by SMLM.

Additionally, direct measurements of each 3D structure were compared with theoretical predictions. For the linear rod, lengths were 161 ± 8 and 153 ± 5 nm (mean ± interquartile range, Fig. 2E) for the reconstruction and the model, respectively. Similar agreements were found in the lengths of the tetrahedron (126 ± 11 and 122 ± 5 nm, Fig. 2E). Further validation of 3D reconstructions was made by computing their FSC against reference 3D models, resulting in 23 nm for the linear rod and 35 nm for the tetrahedron (SI Appendix, Fig. S11). Overall, these data suggest that the reconstructions were highly accurate and recovered the 3D structure of the model.

Three-Dimensional Reconstructions of Large Protein Complexes from Simulated Datasets.

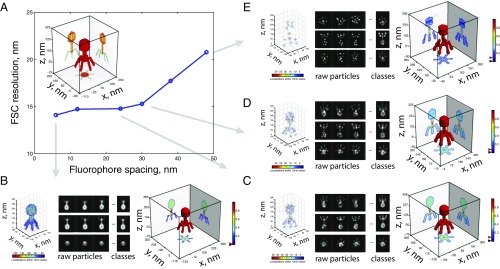
To test whether this method was applicable to reconstruct the ultrastructures of large protein complexes, we produced a high-resolution structural model of the T4 bacteriophage (Fig. 3A, Inset) and applied the single-particle reconstruction algorithm to retrieve 3D reconstructions from simulated SMLM experiments. We investigated the robustness of the method with respect to labeling density by reconstructing the model from very high (6-nm average distance between emitters; Fig. 3B, Left) to extremely low-labeling density SMLM datasets (∼48 nm between emitters; Fig. 3E, Left). Strikingly, reconstructions were successful across the whole range of densities tested (Fig. 3 B–E and SI Appendix, Fig. S14). Robustness of the reconstructions was assessed by performing the FSC of single-particle 3D reconstructions against the high-resolution theoretical model and by calculating Euler angle distributions (Fig. 3A and SI Appendix, Fig. S14). Reconstructions were robust even when the average distance between labeling sites was considerably larger than the localization precision, and comparable to the size of the object itself (Fig. 3 A and E). At these low densities, the original shape of the object was hardly recognizable from individual raw particles, but the stochasticity of labeling sites combined with single-particle classification and averaging led to properly reconstructed classes and successful 3D reconstructions (Fig. 3E and SI Appendix, Fig. S14). Similar results were observed when a model was used as a template (SI Appendix, Fig. S15).

Fig. 3.

Fidelity of 3D single-particle reconstructions for different labeling spacings. (A) Robustness of the 3D single-particle reconstruction as a function of labeling spacing measured as the FSC resolution obtained by correlating the high-resolution theoretical model and the 3D reconstruction. (Inset) Three-dimensional structure of the high-resolution model of the T4 bacteriophage (250 nm in height, 150 nm in diameter). (B–E) Reconstruction results for different labeling spacings. (Left) Three-dimensional representation of single-molecule localizations from a single simulated particle. (Middle) Projections of raw particles and class averages. (Right) Final 3D single-particle analysis reconstruction. A total of 4,000 raw particles were used for each labeling spacing. Black and red triangles on colormaps represent the threshold and iso values used for the intensity projections and 3D representation of the structures, respectively.

Next, we tested the robustness of this approach to noise contamination and decreasing specific labeling densities to simulate realistic experimental conditions. Most notably, SMLM based on the use of fluorescently labeled antibodies can contain a considerable proportion of nonspecific localizations. Thus, we generated various densities of contaminating localizations in conjunction with reduced specific labeling densities. With a single cycle of MRA and MSA classification, class averages of the most distinct structure orientations could be successfully retrieved without a model and at high signal-to-noise ratios in all tested conditions (SI Appendix, Fig. S16). MSA classification is thus very robust to noise contamination by background emitters typically obtained with light microscopy approaches. Overall, these simulations strongly suggest that our method will be able to reconstruct large protein complexes from experimental SMLM datasets.

Three-Dimensional Reconstructions of Asymmetric Structures from Simulated Datasets.

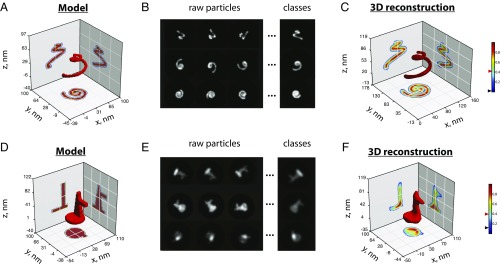
Finally, we investigated the effect of symmetry in 3D reconstructions. To this end, we first reconstructed the structures of the DNA linear rod, the DNA tetrahedron, and the T4 bacteriophage without imposing symmetry constraints (SI Appendix, Fig. S17). These successful reconstructions show that our method is able to reconstruct complex shapes even in the absence of symmetry constraints. Next, we simulated SMLM experiments of intrinsically asymmetric structures (spiral and duckling, Fig. 4 A, B, D, and E, respectively, and SI Appendix, Fig. S18) and applied our method to reconstruct them. Again, we were able to successfully reconstruct complex asymmetric 3D shapes with excellent resolutions and fidelities (Fig. 4 C and F and SI Appendix, Fig. S19). All in all, we conclude that the method can be applied to asymmetric shapes and that symmetry considerations are not necessary to retrieve the original structure.

Fig. 4.

Three-dimensional reconstructions of asymmetric structures. (A and D) High-resolution structural models of a spiral-shaped and a duckling-shaped structure. (B and E) Class averages produced by cumulating similar projections of the spiral-shaped and duckling structures generated with a 6- and 5-nm labeling spacing, respectively. (C and F) Three-dimensional reconstructions of the spiral and duckling structures. Black and red triangles on colormaps represent the threshold and iso values used for the intensity projections and 3D representation of the structures, respectively.

Discussion

Recently, single-particle averaging methods used 3D single-molecule localization images to reveal the 3D structures of several biological objects, such as the nuclear pore complex (8), the ESCRT machinery at HIV assembly sites (6), and the centrosome machinery (9). These objects were highly symmetrical (cylindrical or spherical) and the previous approaches used relied on the use of templates, making it difficult to apply similar methodologies to more complex biological objects or to unknown structures. More recently, it was shown that 3D single-molecule localization data can be directly used to reconstruct a 3D shape (20), making it a valuable approach when raw 3D localizations are available. This method, however, requires a template structure to detect and align single-particle images and does not explicitly deal with sample heterogeneity or particle symmetry.

Here, we present a method that is able to reconstruct the 3D structures of well-characterized DNA origami and protein complexes with 3D isotropic resolutions. Our results demonstrate that conventional single-particle reconstruction algorithms can be adapted to solve several issues inherent to superresolution microscopies, despite recent reports (20). First, we were able to automatically discard particles that were not efficiently labeled, displayed structural inhomogeneities due to the fabrication process, or to the immobilization conditions. Second, the ability to obtain different projections from the particles allowed us to reach isotropic 3D resolutions, with high resolutions in all directions. Third, the reconstruction method did not rely on a priori information about the structure, which minimized template dependence. We note, however, that knowledge of the particle symmetry was important to converge faster to accurate reconstructions. Finally, the resolution of the reconstruction far outstripped the resolution of the individual particles lacking labeling sampling, highlighting the ability of the method to further surpass the Nyquist resolutions attainable by direct superresolution methods.

Reference-free cross-correlation-based alignment and classification methods with MRA/MSA tend to perform poorly for datasets with low signal-to-noise ratios (SNRs). However, SMLM data sets are highly contrasted due to the relatively good SNR of each detected single fluorescent molecule with respect to the background noise. In fact, our simulations of various densities of contaminating localizations in conjunction with reduced specific labeling densities showed that reference-free cross-correlation-based alignment and classification methods are very robust to noise in SMLM datasets. It is also worth noting that the depth of field in single-molecule localization microscopy is typically 300–800 nm, depending on the emission intensity of the fluorophore (21–23). Thus, imaging of objects larger than the depth of field will require the acquisition and averaging of images at different axial positions to obtain projection images containing information from the whole particle volume.

A correct angular reconstitution requires an even distribution of single particles with random orientations on the support onto which the specimen is adsorbed so that all views are well represented. However, as observed in the field of EM SPR, the angular distribution of projections may be uneven due to physical effects, such as interactions with the support, or to the specific cellular distribution of the complex under study. Under these conditions, an angular imbalance of projections can result in an anisotropic resolution and distortions (e.g., stretching) of the structure (24, 25). To overcome this problem, iterative image-processing procedures to retrieve rare views have been developed in the EM SPR community (26) and can be adapted to SMLM-based imaging. After an iterative procedure of image processing and a collection of substantially larger data sets, rare views are brought to statistical significance to achieve reliable isotropic reconstructions. This method has been widely used and may be future directions of this work (27–30). Similarly to approaches taken in the EM SPR community (31–33), exploration of different support chemistries will help prevent any preferred orientations during image acquisition.

In addition to imaging DNA origami nanostructures, our method is directly applicable to protein assemblies labeled by genetic fusions, antibodies, and exchange-PAINT (34). By using iPAINT (35) as a generic imaging method, our approach should allow for the exploration of 3D isotropic supramolecular structures in other fields, such as nanotechnology, colloid science, interface science, and soft-matter physics. The ability of our method to reconstruct structures labeled with extremely low labeling densities could alleviate many problems such as low photoactivation efficiency, probe accessibility, and steric hindrance. Excitingly, the combination of our approach with multicolor acquisition could be used in the future to retrieve the 3D structures of supramolecular complexes in their natural environments at unsurpassed resolutions.

Materials and Methods

Design and Assembly of DNA Origami Structures.

DNA origami nanostructures were designed using the honeycomb-lattice version of the caDNAno software (cadnano.org). Assembly of DNA nanostructures was accomplished in a one-pot reaction by mixing scaffold strands derived from M13 bacteriophage at 20 nM with 200 nM of each oligonucleotide staple strand in a folding buffer containing 5 mM Tris, 1 mM EDTA, pH 8, and a concentration of MgCl2 adjusted for each nanostructure. MgCl2 conditions listed in parentheses: linear-rod origami (18 mM), tetrahedron (12 mM). The strand mixture was then annealed in a PCR thermal cycler using a fast linear cooling step from 80 to 65 °C over 1 h, then 42-h linear cooling ramp from 64 to 24 °C.

Agarose Gel Electrophoresis.

Annealed samples were subjected to gel electrophoresis in 1% Tris-borate-EDTA buffer including 11 mM MgCl₂, at 70 V for 3 h in an ice-water bath. Gels were stained with SyberR Safe before imaging. Bands corresponding to the correctly folded structures were then visualized with UV light and cut out from the gel. Excised bands were crushed and transferred into DNA gel extraction spin column (BIO-RAD, catalog number: 732–6166). The DNA structure solution was recovered by centrifugation of the loaded column for 10 min at 10,000 × g.

Transmission Electron Microscopy Imaging.

For imaging, 2.5 μL of annealed sample was adsorbed for 2 min onto glow-discharged, carbon-coated transmission electron microscopy (TEM) grids. The grids were then stained for 60 s using a 2% aqueous uranyl formate solution containing 25 mM NaOH. Imaging was performed at 80 keV.

Imager Strands for DNA-PAINT Imaging.

Atto647n/Alexa488 imager strand sequence: 5′–TATGTAGATC–3′ Dye (Eurogentec). Sequence of biotin-oligo: 5′–GAATCGGTCACAGTACAACCG–3′ biotin (Eurogentec).

Microfluidics Channel Functionalization.

Linear rods were immobilized by using specific biotin/neutravidin interactions. Biotin-silane-PEG/Silane-PEG/neutravidin coating was performed in several steps: (i) the glass coverslip surface of the microfluidics channels was activated by incubating in a solution of KOH (1 M for 20 min) and then rinsed by flushing a solution of borate potassium buffer; (ii) 5 µl of Biotin-silane-PEG [20 mg of Biotin-silane-PEG (Laysan Bio) diluted in 220 µl of methanol] were mixed with 150 µl of silane-PEG [10 mg of silane-PEG (Laysan Bio) diluted in 200 µl of borate potassium buffer] and were injected into microfluidics channels; (iii) channels were incubated overnight; (iv) channels were rinsed several times with ddH2O; (v) a 1 mg/mL solution of neutravidin in PBS was injected and incubated for 30 min; (vi) channel was extensively rinsed with ddH2O. Tetrahedrons were immobilized onto poly-l-Lysine-coated microfluidics channels. Channels were then filled with a solution of 0.01% (vol/vol) of poly-l-Lysine, incubated for 20 min, and rinsed several times with ddH2O.

Setup for Superresolution Experiments.

Superresolution imaging was carried out on a custom-built PALM microscope, using objective-type total internal reflection fluorescence. Two laser lines were used for excitation: 488 nm (OBIS, LX 488–50, Coherent Inc.) and 640 nm (OBIS, LX 640–100, Coherent Inc.) depending on the fluorophore being excited. Laser beams were expanded, passed through an acoustooptic tunable filter (AOTFnc-400.650-TN, AA optoelectronics), and coupled into the back focal plane of an oil-immersion objective (Plan-Apocromat, 100×, 1.4 N.A. oil, Zeiss) using achromatic lenses. A multiband dichroic mirror (zt405/488/561/638rpc, Chroma) was used to decouple excitation and emission. Fluorescence signal was spectrally filtered by emission filters (ET525/50m and ET700/75m, Chroma Technology) and imaged on an electron-multiplying charge-coupled-device camera (iXon ×3 DU-897, Andor Technologies). A 1.5× telescope was used in the emission path to obtain a final imaging magnification of ∼150-fold, corresponding to a pixel size of 105 nm. Acquisition software controlling lasers, filter wheels, and camera were homemade using LabVIEW 2010 (National Instruments). For more details see Cattoni et al. (36).

DNA-PAINT Imaging.

Experiments were performed in a custom-made poly-di-methyl-siloxane microfluidics flow chamber (SI Appendix, Fig. S5). Surface functionalization is described above. Origami were flushed into a channel of the chamber (inner volume capacity of ∼5 µl) at a concentration of 250 pM and incubated for 30 min. Next, 100-nm TetraSpeck beads (Invitrogen) were flushed into the chamber and used as fiducial marks for drift correction. Finally, imager strands (oligo-Alexa488, for linear rod and oligo-Atto647n for tetrahedron) were diluted to a final concentration of 5 nM in imaging buffer [Tris⋅HCl pH 8, 10 mM MgCl2, 1 mM EDTA, 0.05% Tween 20 (34)] and injected into the channel.

Camera gain was fixed at 200. Movies (typically 15,000–20,000 frames) were recorded at a rate of 5 Hz in frame-transfer mode with ∼50 mW of continuous laser illumination (488-nm laser for linear rod, and 642 nm for tetrahedron).

Single-Fluorophore Localization, Drift Correction, and Image Reconstruction.

Image processing was performed using MATLAB 2011 (MathWorks, Inc.). Single-molecule localizations and fiducial marks were detected using multiple target tracing analysis (37). A minimum-intensity threshold was applied to filter localizations derived from background noise. Drift correction was assessed using vPALM, a custom-made software where fiducial marks trajectories were extracted [for more details refer to Fiche et al. (38)]. Experiments with a drift-correction precision larger than 20 nm were discarded.

Further analysis of single-molecule localizations was performed with several custom-made algorithms. Localizations were plotted in a single image (pointillist representation), and drift corrected. Drift correction involved the following steps: (i) for each field of view, the trajectories of at least four fiducial marks were chosen and the mean trajectory was calculated by averaging their trajectories; (ii) the quality of the drift correction was estimated by subtracting the mean trajectory to all of the trajectories and calculating the SDs along x and y for the beads used for correction; (iii) when the SD of the corrected trajectories was acceptable (<10 nm), the coordinates of the localizations corresponding to DNA-PAINT events were corrected by using the mean trajectory. Otherwise, the experiment was discarded.

Drift-corrected localizations were then sorted into clusters using an algorithm described elsewhere (36). For each cluster, the main axes were determined by using eigenvector decomposition. Clusters were aligned to match the major axis with the x direction and the minor axis with the y direction. Cluster dimensions were measured as follows: length was defined as the maximum distance between localizations along the x axis, while width was calculated from the FWHM of the distribution of localizations along the y coordinate. Clusters with less than a minimum number of localizations (100 for linear rod and 50 for tetrahedron) were discarded to eliminate imager strands bound nonspecifically to the surface. For linear rods, only clusters with a length >25 nm and <250 nm, and a maximum width of 100 nm were considered to avoid single imager strands or large aggregates of origami. For tetrahedron, only clusters with dimensions >25 nm and <200 nm were considered. Clusters passing this minimal criterion were converted into probability density images using a superresolution pixel size of 2.2 nm for linear rod and 3.3 nm for tetrahedron (36).

Localization coordinates and uncertainties were used to estimate the probability distribution of localization for each single emitter. Probability density images were thus obtained by superimposing the contributions of all of the detected localizations after drift correction (39–42). This probability density is the most commonly used approach to representing the underlying structure as it provides the probability of having a fluorescent molecule at a given position.

Particle Averaging Analysis and 3D Reconstruction.

Particle averaging analysis was implemented using iMagic (43) (Image Science Software, GmBH). This choice was made because iMagic allows access to modify the scripts used for each step in the process, which was critical to find the most optimal procedure for particle classification and reconstruction from SMLM data. Most operations can be implemented on other EM software packages (see the extensive list in www.emdatabank.org/emsoftware.html). Initial data sets of images were obtained from a stack of individual probability density images derived from single-molecule localization analysis. The probability density of localization from each selected cluster (particle) was represented as a 100 × 100-pixels image in TIFF format. These images were converted to Medical Research Council format using ImageJ (44). Final image stacks had 5,427 particles for linear rods, 2,219 particles for tetrahedrons, and 4,000 particles for simulated structures. We ensured that these numbers of raw particles produced robust reconstructions by evaluating the FSC between two independent reconstructions derived from half the total number of particles. Subsequently, particles were band-pass filtered, aligned, and classified using MSA classification (15). For unbiased reconstructions (without initial model), selected references from these classes (based on the visual match between the class average and the individual particles) were further used to perform MRA of the images. To perform biased reconstructions (with initial model) a set of 2D forward projection images with known Euler angles was implemented as references (“anchor set”). After three cycles of MRA/MSA, final class averages were obtained (200 and 250 classes for linear rod and tetrahedron, respectively) for the unbiased reconstruction, and 250 and 400 for the biased reconstructions.

References (best projections) derived from the final class averages were selected to apply angular reconstitution. For the linear rod, 12 (unbiased) and 15 (biased) references were selected. For the tetrahedron, 29 (unbiased) and 55 (biased) references were used. C2 and C6 symmetries were applied for 3D reconstructions of origami and bacteriophage simulations reconstructions, respectively. For unbiased template-free reconstructions, 3D reconstructions were back-projected with different angles to serve as references (anchor set) for further iterative refinement cycles of reconstructions. Template-free reconstructions were performed with a single model generation iteration. Note that the quality of the final 3D reconstructions could be further improved by using models of increasing quality to obtain classes. This analysis scheme allowed for the characterization of sample heterogeneity, including different orientations of the same species (i.e., projections) or different species.

Fourier Ring and Shell Correlations.

The resolution of 3D reconstructions was evaluated by FSC (43, 45, 46). The initial set of single particles was divided into two independent groups, each containing half the particles (chosen randomly). Three-dimensional reconstructions were computed for each independent group of single particles. The resolution was assigned from the FSC curve by estimating the point where the FSC crosses a threshold of 0.143 (18) and is similar to that used for superresolution imaging using the FRC (19).

To validate our 3D reconstructions we additionally computed their FSC against their respective models. FSCs between theoretical high-resolution models and 3D reconstructions were calculated using freely accessible software provided by the Protein Data Bank (https://www.ebi.ac.uk/pdbe/emdb/validation/fsc).

FRC of localizations obtained for single linear rods and tetrahedron origamis using DNA-PAINT was performed in MATLAB using routines developed in ref. 19. Each origami cluster time series was divided into blocks of 100–1,000 frames and assigned randomly to two distinct half-sets to computed the FRC. The operation was performed 5 times and averaged for 100 random origami structures to get a resulting mean resolution value.

Simulations of DNA-PAINT Datasets.

The effect of labeling spacing on the robustness of the single-particle reconstruction method was tested using computer simulations. A high-resolution theoretical model of the T4 bacteriophage was produced at 5-nm resolution. From this model, we designed a series of simulated docking strands spanning the whole structure at a minimum distance of 5 nm. To generate a simulated DNA-PAINT model, we sequentially and randomly chose docking strands in the model and populated them with an average of 15 localizations. An iterative process ensured that the distance between the selected docking strands was not smaller than the labeling spacing being simulated. This process was repeated for each DNA-PAINT model until no more docking strands satisfying these conditions were available. Three-dimensional DNA-PAINT models were converted into 2D projected densities as described above generating the raw particles. For each labeling spacing, 4,000 single particles were generated and used to obtain a 3D reconstruction as described above. In case noise was considered in the simulation, additional nonspecific binding sites were randomly added within a 150-nm radius of each structure center and populated with an average of 15 localizations (similar to specific sites). The number of nonspecific binding sites was chosen as a percentage of the total number of specific binding sites used to label the structure.

The same procedure was applied to the spiral and duckling structures (with a labeling spacing and a localization precision of 6 and 15 nm for the spiral and of 5 and 10 nm for the duckling, respectively) to validate our approach with asymmetric structures.

Software and Scripts.

MATLAB m-files and iMagic scripts are accessible at Github under project name 3DreconstructionSMLM (https://github.com/marcnol/3DreconstructionSMLM).