Summary
Activity in striatal direct- and indirect-pathway spiny projection neurons (SPNs) is critical for proper movement. However, little is known about the spatiotemporal organization of this activity. We investigated the spatiotemporal organization of SPN ensemble activity in mice during self-paced, natural movements using microendoscopic imaging. Activity in both pathways showed predominantly local but also some long-range correlations. Using a novel approach to cluster and quantify behaviors based on continuous accelerometer and video data, we found that SPN ensembles active during specific actions were spatially closer and more correlated overall. Furthermore, similarity between different actions corresponded to the similarity between SPN ensemble patterns, irrespective of movement speed. Consistently, the accuracy of decoding behavior from SPN ensemble patterns was directly related to the dissimilarity between behavioral clusters. These results identify a predominantly local, but not spatially compact, organization of direct- and indirect-pathway SPN activity that maps action space independently of movement speed.
Keywords: basal ganglia, direct pathway, indirect pathway, caudate, putamen, calcium imaging, neural correlation, population activity, action space, behavior decoding
Highlights
-
•
Direct- and indirect-pathway SPNs show locally biased spatiotemporal organization
-
•
SPNs active during a particular behavior are more correlated and spatially closer
-
•
SPN ensembles encode action identity independently of movement speed
-
•
Distance between behaviors corresponds to distance between SPN ensemble patterns
Klaus, Martins et al. image neural activity from direct- and indirect-pathway neurons of dorsal striatum during self-paced, natural behaviors. They find that striatal neurons form ensembles that are spatiotemporally organized and map action space independently of movement speed.
Introduction
The initiation and execution of self-paced, natural behaviors depends on intact circuits of the basal ganglia. The striatum, the main input nucleus of the basal ganglia, forms two largely separate projection pathways that are positioned to differentially control downstream basal ganglia and thalamocortical areas (Alexander and Crutcher, 1990, Gerfen et al., 1990). About half of the striatal spiny projection neurons (SPNs) directly target basal ganglia output structures, whereas the other half indirectly influences basal ganglia output via the external segment of the globus pallidus and subthalamic nucleus (Parent et al., 1984). Although activation of direct- and indirect-pathway SPNs can facilitate and suppress movements, respectively (Durieux et al., 2012, Kravitz et al., 2010), recent studies demonstrated that both pathways are co-active during movement (Barbera et al., 2016, Cui et al., 2013, Isomura et al., 2013, Tecuapetla et al., 2014), suggesting that concerted activity in both SPN pathways is required for proper action performance (Tecuapetla et al., 2014, Tecuapetla et al., 2016). Thus, not only the rate of SPN activity, but also the precise functional organization of SPN ensembles, may be important for motor control (Klaus and Plenz, 2016). Here, we studied the spatiotemporal organization of direct- and indirect-pathway SPNs during self-paced, natural behaviors using one-photon microendoscopy in freely moving mice. We recorded intracellular calcium transients in populations of up to 350 direct- or indirect-pathway SPNs selectively expressing the genetically encoded calcium indicator GCaMP6f (Chen et al., 2013, Resendez and Stuber, 2015). Calcium dynamics were recorded simultaneously with motor behavior using video and body acceleration (BA) and were analyzed using two independent methods to remove background fluctuations from somatic SPN signals. The average population activity of both direct- and indirect-pathway SPNs increased during movement, and positively correlated with total body movement during self-paced, natural behaviors in line with previous observations during learned actions (Cui et al., 2013, Isomura et al., 2013). Further analysis of spatial correlations between background-corrected, somatic SPN signals as a function of inter-neuronal distance revealed networks with predominantly local but also some long-range correlations in both pathways. That is, in contrast to a recent report (Barbera et al., 2016), SPNs did not form spatially compact clusters but instead covered spatially overlapping areas within the imaging field of view.
In order to investigate if activity in SPN ensembles encodes mainly the vigor or speed of movements (Barbera et al., 2016, Dudman and Krakauer, 2016), or can encode specific behaviors, we clustered the behavior data using a novel approach that allowed the quantification of behavioral similarity based on video and acceleration measurements. SPNs that were active during particular behaviors showed increased overall cross-correlations (CCs) between them, and showed an increased likelihood of being nearby. Importantly, the similarity between different behaviors corresponded to the similarity between SPN ensemble patterns, independent of the speed of the movements. Accordingly, using a binary classifier, we found that the accuracy of decoding behavior from SPN ensemble activity patterns was directly related to the dissimilarity between behavioral clusters. These results identify a locally biased spatiotemporal organization of striatal activity that represents the action space, independently of movement speed, with similar actions being encoded by similar striatal ensemble activity. This organization might support further aspects of striatal function during learning and skilled motor control.
Results
Striatal Direct- and Indirect-Pathway SPNs Are Co-active during Self-Paced Movements
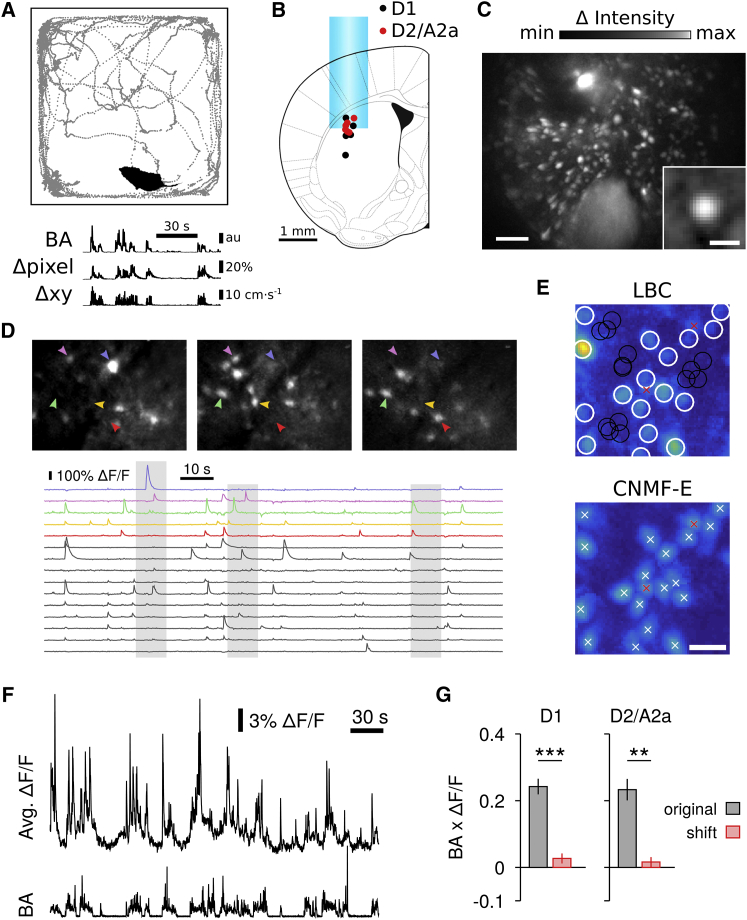
To study neuronal activities in identified striatal populations of SPNs, we used microendoscopic one-photon calcium imaging of GCaMP6f (AAV5-Flex) selectively expressed in direct-pathway SPNs (D1-Cre, FK150) or indirect-pathway SPNs (D2-Cre, ER43; A2a-Cre, KG139) in mice during self-paced, natural movements in an open field arena (Figure 1A, top). Neuronal activity was monitored through a gradient index (GRIN) lens chronically implanted into the dorsolateral striatum (Figures 1B, 1C, and S1A) from up to 350 SPNs with single-cell resolution (Figures 1C–1E). Calcium dynamics were recorded simultaneously with motor behavior using video and a head-mounted three-axis accelerometer (Figure 1A, bottom). Total BA correlated with video pixel change (Δpixel, Spearman correlation ρ = 0.57 ± 0.03, n = 10 mice, p < 0.001) and the movement speed in the open field (Δxy, ρ = 0.49 ± 0.03, n = 10 mice, p < 0.01).
Figure 1.
Direct and Indirect-Pathway SPNs Show Increased Activity during Self-Paced Movements
(A) Example of a single open field session with mouse position (top panel) and corresponding body acceleration (BA; bottom panel), video pixel change (Δpixel), and speed (Δxy).
(B) Reconstructed GRIN lens position for all D1 (n = 5), D2 (n = 3), and A2a mice (n = 2).
(C) Activity image (maximum deviation from average fluorescence; STAR Methods) for a 10 min recording (scale bar, 100 μm). Inset: average neuron shape for a single recording (n = 186 neurons normalized to unity peak amplitude; scale bar, 20 μm).
(D) Top: detailed views of activity images (maximum deviation from average image) for 10 s long segments in a D1 mouse, showing diverse activation of SPN ensembles. Bottom: ΔF/F traces for a subset of 15 neurons extracted with LBC for the same animal. The gray shaded areas correspond to the time periods in the top activity images. The top five traces are color-coded and correspond to the neurons marked by arrowheads in the top panels.
(E) Top: example of manually selected ROIs (white circles) in the activity image (maximum deviation from average image) and automatically determined background regions (black circles; STAR Methods). Bottom: spatial footprints obtained with CNMF-E within the same field of view. White crosses mark the center of each detected neuron. Red crosses mark neurons not detected with the manual ROI selection used for LBC (the position of these neurons is replicated in the top panel for comparison). Shown is the maximum projection over the spatial footprints. Scale bar, 30 μm.
(F) Example of simultaneously recorded average ΔF/F in 98 neurons (top, LBC) and BA (bottom trace) in a D1-Cre mouse.
(G) Average ΔF/F is correlated with BA in direct- and indirect-pathway SPNs (D1, n = 5 mice; D2/A2a, n = 5 mice; paired t test for comparison to time-shifted control, ∗∗p < 0.01, ∗∗∗p < 0.001). Bars represent mean ± SEM.
Intracellular calcium transients of single neurons were estimated from changes in GCaMP6f fluorescence (Chen et al., 2013, Grienberger and Konnerth, 2012). Because one-photon imaging suffers from stronger background signals compared to two-photon imaging due to increased out-of-focus contamination (Zhou et al., 2017), we used two independent methods to correct raw, somatic fluorescence. First, manually selected somatic regions of interest (ROIs, 35–263 neurons/session, median = 120 neurons/session) were automatically adjusted using local background and baseline correction (LBC; STAR Methods) (Klaus and Plenz, 2016) and relative changes in fluorescence, ΔF/F, were extracted (Figure 1D, bottom; Figure 1E, top). To better account for background signals directly superimposed onto the neuron’s soma fluorescence and for overlapping neuronal sources (Figure 1E), we applied constrained non-negative matrix factorization for endoscopic data (CNMF-E) (Pnevmatikakis et al., 2016, Zhou et al., 2017) to the same dataset (Figure 1E, bottom; Figure S1C; Movie S1). CNMF-E, which models the spatial and temporal background statistics superimposed on the neuronal signals, showed a slightly superior performance for the estimation of calcium transients from simulated ground truth data (Figure S1C).
The average rate of intracellular calcium transients was similar in direct- and indirect-pathway SPNs (D1, 0.13 ± 0.02 s−1, n = 5 mice; D2/A2a, 0.17 ± 0.02 s−1, n = 5 mice; two-sample t test, t(8) = −1.38, p = 0.21; threshold crossings of the time derivative of ΔF/F > 3 SDs of baseline; STAR Methods). The average amplitude of the corresponding ΔF/F transients was also similar in direct- and indirect-pathway SPNs (D1, 9.4% ± 0.52%, n = 5 mice; D2, 10.1% ± 1.13%, n = 5 mice; two-sample t test, t(8) = −0.53, p = 0.61; LBC). Average intracellular calcium transients increased during movement initiation (Figure S1D), and positively correlated with self-paced movements in the open field for both direct- and indirect-pathway SPNs (Figures 1F and 1G), in line with previous reports on SPN activity during learned actions (Cui et al., 2013, Isomura et al., 2013) and during head movements (Tecuapetla et al., 2014). In summary, intracellular calcium transients in SPNs can be extracted reliably with single-cell resolution from endoscopic data, and show co-activation of direct- and indirect-pathway SPNs during self-paced movements (Barbera et al., 2016, Cui et al., 2013, Tecuapetla et al., 2014).
Locally Biased, but Not Spatially Compact, Spatiotemporal Patterns of Activity in Direct- and Indirect-Pathway SPNs
To study the precise spatiotemporal organization of SPN ensemble activity underlying the observed transient increases in average ΔF/F (Figure 1F), we measured CCs between SPNs at the temporal resolution of the calcium imaging (Figure 2A; bin duration, 100–143 ms; Figure S2A). SPNs in direct- and indirect-pathway populations showed low average correlations (D1, 0.08 ± 0.02, n = 5 mice; D2/A2a, 0.07 ± 0.01, n = 5 mice; comparison D1 versus D2/A2a, two-sample t test, t(8) = 0.31, p = 0.77; continuous ΔF/F time series) that were significantly larger than zero (one-tailed t test; D1, t(4) = 2.87, p = 0.023; D2/A2a, t(4) = 5.26, p = 0.003; corrected for chance-level correlations by inter-event interval shuffling of events in the ΔF/F time derivative; STAR Methods). Despite this low average CC, SPN activity showed, on average, increased CCs for nearby neurons (Figure 2B, D1 example). This monotonic decrease in CC with increasing neuron distance was found when using continuous ΔF/F (Figure 2C, top) or time series including only significant ΔF/F peak events (STAR Methods), which remove the influence of baseline fluctuations and the GCaMP6f decay on the CC measure (Figure 2C, bottom). As expected, spatially shuffled control data resulted in a flat CC-distance relationship (Figure 2C, black lines). In addition, a significant decrease in CC for increasing distances was still observed when restricting the analysis to the 20% largest events and when only neurons with a distance larger than three times the average neuron diameter were considered, thus further reducing potential crosstalk between nearby neurons (Figure S2B). In contrast to the background-corrected somatic fluorescence intensities, raw somatic fluorescence intensities were highly correlated and showed little decrease within a 100 μm radius (Figure S2C). In line with the findings from the LBC method, intracellular calcium transients extracted with CNMF-E showed a monotonic decrease in CC with increasing neuronal distance, and CC values approached shuffled data at a distance of ∼80–100 μm (Figure 2D). To further investigate that spatially localized CCs can be extracted from endoscopic data using appropriate background corrections, we tested the LBC and CNMF-E methods using simulated ground truth data (Figure S1C) with locally clustered or non-clustered activities. Indeed, the spatial profile of CCs could be recovered for both conditions (Figures S2D and S2E). Despite the local organization in activity in the direct and indirect pathway during self-paced movements, nearby SPNs in both pathways showed a wide distribution of CCs (Figures 2E and 2F). Furthermore, even SPNs far from each other can exhibit relatively high CCs (Figures 2B, S2F, and S2G).
Figure 2.
Local Spatiotemporal Correlations in Functional Networks of Direct- and Indirect-Pathway SPNs
(A) Left: example network of 91 direct-pathway SPNs showing the spatial distribution of ROIs. Right: ΔF/F traces for four neurons showing diverse activity even for nearby neurons (traces were calculated using LBC).
(B) Left: two-dimensional view showing the relative position of neuronal pairs and corresponding CCs between ΔF/F traces for a single session in a D1 mouse. Each dot corresponds to one neuronal pair: the coordinates represent the relative position of one neuron to another neuron in the center of the coordinate system, and the color represents the CC between the neurons. Pairs were plotted in order of increasing CC. Right: CCs plotted as a function of inter-neuronal distance for the same session (red, individual pairs; black, average). For better visualization, the distance axis was logarithmically scaled.
(C) Top: average CCs between continuous ΔF/F for all D1 (n = 5 mice) and D2/A2a-Cre (n = 5 mice) mice obtained using LBC. Bottom: same as above for CCs between ΔF/F peak events. Data represent mean ± SEM.
(D) Same as (C) for activity traces, C, obtained with CNMF-E. Data represent mean ± SEM.
(E) Probability density functions (PDFs) of CC for different ranges of neuronal distance. Data represent mean ± SEM.
(F) Same as (E) for traces extracted with CNMF-E. Data represent mean ± SEM.
See also Figure S2.
The above data suggest an organization of SPN activities that is characterized by a local bias in correlated activities but seems to be at odds with a spatially compact organization as recently described by Barbera et al. (2016), who reported spatially compact and non-overlapping clusters of SPNs during self-paced movements. We applied the same clustering algorithm to our data and obtained locally biased but spatially extended, i.e., not spatially compact, clusters of SPNs (Figure S2H) in line with the finding from Figure 2. We found that such spatially compact clusters were observed in the raw signals without background correction (Figures S2H–S2J), which would be expected because background contains low spatial frequencies and dominates signals in endoscopic one-photon imaging data (Zhou et al., 2017). Furthermore, we found that the background signals alone, i.e., the signals that were removed with CNMF-E, organized in spatially compact clusters (Figures S2H and S2J), similar to the ones reported by Barbera et al. (2016). This analysis demonstrates that adequate background and baseline corrections are required to separate somatic from background signals (for further discussion, see STAR Methods).
Taken together, the above results suggest that during self-paced movements, direct- and indirect-pathway SPNs form functional groups with predominantly local but also some long-range correlations.
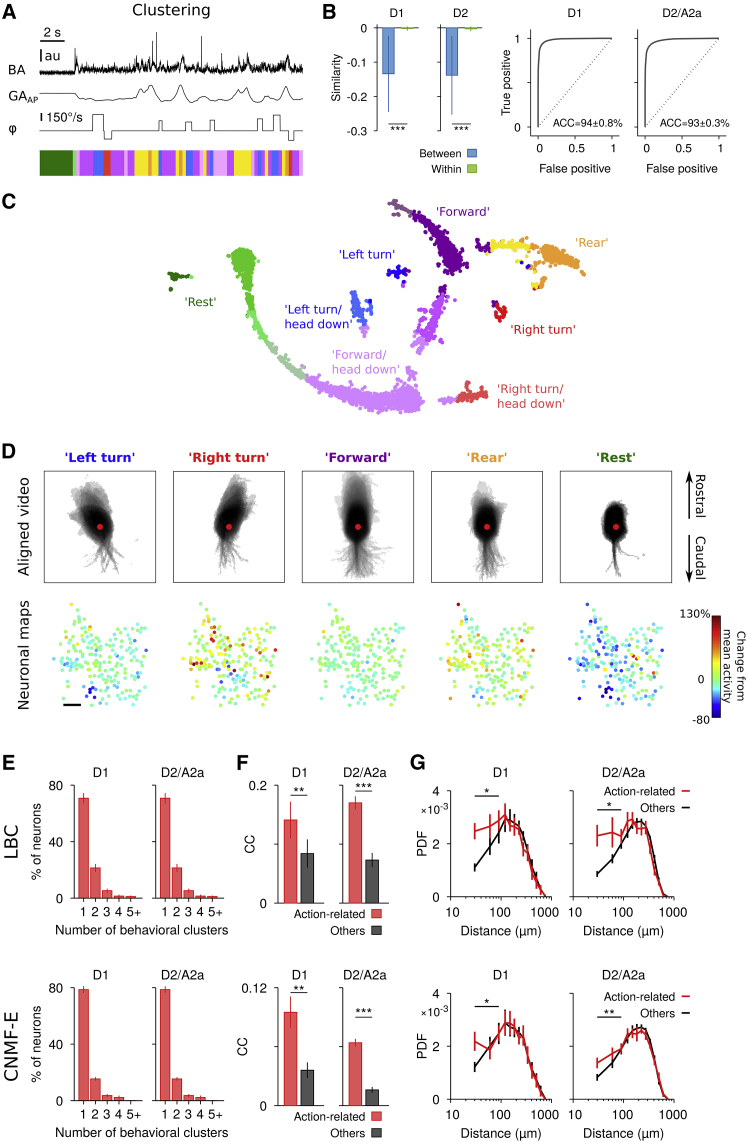
SPN Ensembles Active during Particular Actions Are More Correlated and Spatially Closer
We next investigated the spatial organization of SPN activity in more detail with respect to different behaviors. To this end, we analyzed behaviors using continuous video and acceleration measurements based on the following features: (1) total BA, which captures periods of movement versus rest; (2) gravitational acceleration along the anterio-posterior axis (GAAP), which captures changes in posture, e.g., during rearing; and (3) video rotation angle (φ) to measure changes in body and head orientation (Figure 3A). The BA, GAAP, and φ time series were binned (300 ms) and discretized to obtain a low-dimensional histogram representation of each behavioral time bin (STAR Methods). These “behavioral” histograms were then used to quantify the similarity between all behavioral time bins (Figures S3A and S3B). This approach allowed us to cluster the entire range of behaviors observed during a single recording session (Figures 3A–3C) rather than focusing on a pre-defined set of behaviors. In the following, we used a similarity measure based on the so-called earth mover’s (EM) distance (Rubner et al., 2000), which compares discretized histograms of the above features and takes into account the smoothness of the animal’s movements (STAR Methods). Thus, EM similarity is zero for identical behavioral histograms and more negative for more dissimilar behavioral histograms. For example, a “left turn” or “right turn” versus “straight” is assigned a higher similarity in behavioral (i.e., action) space compared to “left turn” versus “right turn.” Behavioral clusters were obtained by affinity propagation (Frey and Dueck, 2007) on the EM similarity of the behavioral histograms (Figure S3A, 300 ms; STAR Methods) and showed low between-cluster and high within-cluster similarity (Figures 3B and S3D), suggesting specificity of our behavioral clustering approach. Although some clusters obtained using the above features are difficult to fully describe in terms of words and two-dimensional video, other clusters corresponded to known behaviors like “left” or “right” turn, “forward” locomotion, “rearing,” or “rest” (Figures 3C and 3D, top; Movie S2).
Figure 3.
Action-Related SPNs Are Locally Biased and More Correlated Overall
(A) Behavioral clustering using BA, GAAP, and body/head rotation φ. Top: BA, GAAP, and φ time series. Bottom: corresponding behavioral clusters obtained by affinity propagation on similarity of discretized time series (STAR Methods).
(B) Left: behavior similarity between segments belonging to different (“between”) versus the same (“within”) cluster for a single D1 and D2 session, respectively. Smaller values indicate less similarity. Zero indicates equality (i.e., highest similarity). Bars denote mean ± SD. Right panels: ROC analysis demonstrating high accuracy (ACC) of determining whether two behavior segments belong to different behavioral clusters (“true positive”) using a single threshold. “False positive” denotes the fraction of behavior segments from the same cluster classified as belonging to different clusters. Shown is the average for all mice (D1, n = 5; D2/A2a, n = 5).
(C) Two-dimensional projection of all behavioral feature vectors during a single recording session (STAR Methods). Each dot represents a behavioral segment of 300 ms duration. Color code represents cluster identity obtained by affinity propagation. A subset of clusters was labeled according to the dominant feature (“left turn,” “right turn,” “rear,” etc.).
(D) Top: aligned video segments (300 ms after segment start) for a subset of behavioral clusters within a single session (same as C). All occurrences were merged into a single movie (number of occurrences: “Left turn,” 45; “Right turn,” 46; “Forward,” 243; “Rear,” 95; “Rest,” 21), and pixel intensities were logarithmically scaled for better visualization. Colors match the color code in (C). The red dot indicates the center of mass of the mouse at behavior onset. Bottom: neuronal maps showing, for each behavioral cluster, the relative changes in activity compared to each neuron’s mean activity and the neuron positions in the field of view. Note that SPNs were recorded in the left striatum. Scale bar, 100 μm.
(E) Average percentage of action-related neurons participating in 1, 2, 3, 4, or 5 and more behavioral clusters (D1, n = 5; D2/A2a, n = 5 mice). Bars represent mean ± SEM.
(F) Average CC between action-related SPNs is significantly higher than average CC between remaining SPNs (paired t test, ∗∗p < 0.01, ∗∗∗p < 0.001). Bars represent mean ± SEM.
(G) PDF of inter-neuronal distances for action-related and other SPNs (paired t test, ∗p < 0.05, ∗∗p < 0.01). Data represent mean ± SEM.
We found that different behavioral clusters were accompanied by distinct changes in SPN activity (Figures 3D, S3G, S4A, and S4B). To test whether the changes in activity during specific behavioral clusters reflected the spatiotemporal organization identified in Figure 2, we determined action-related SPNs for each behavioral cluster that showed significant increases in activity (>3 SDs from average activity; STAR Methods). We found that SPN activity at the single-neuron level was rather action specific (Figure 3E; for neurons with significant decrease in activity, see Figure S3H). Although action-related SPNs are, by our definition, co-active during specific behavioral clusters, they do not need to be co-active at fine timescales and hence could show low zero-lag CCs (behavioral segments can last multiple seconds; Figure S4C; though see also Brody, 1999 for further discussion of this issue) and low common activity across different behavioral clusters. We therefore calculated, as done in Figure 2, the CC for the entire imaging session and found that SPNs of both pathways that were active during a specific behavior showed significantly increased CCs compared to neurons that did not show action-specific activity (Figures 3F and S3H). In addition, SPNs that were active during particular behaviors formed ensembles with a local bias yet a notable number of distant SPN pairs (Figure 3G; neurons that decreased firing rate did not show a significant local bias; see Figure S3H), which contrasts with the idea of spatially compact and non-overlapping functional clusters. This result suggests that the locally biased organization of SPN correlations identified at the general population level (Figure 2) has functional significance in terms of action-related activity.
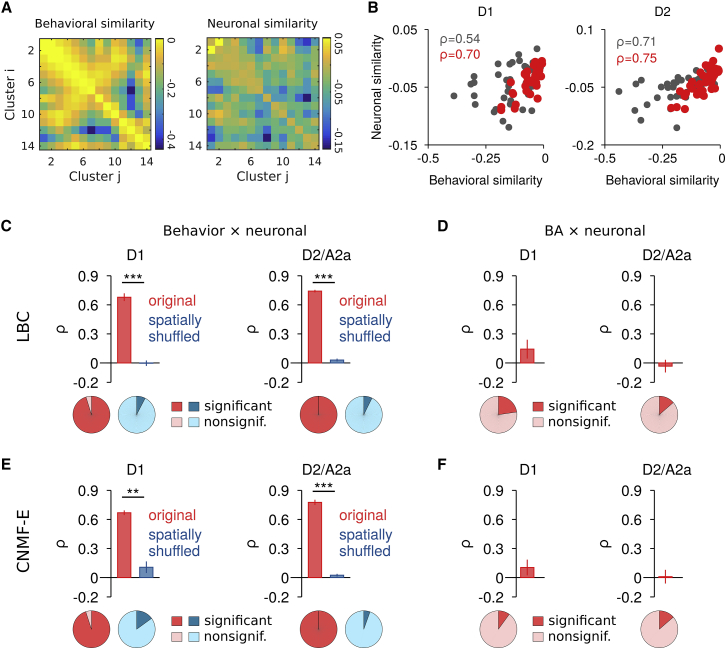
Direct- and Indirect-Pathway SPN Ensembles Map Action Space
We showed above at the single-neuron level that action-related SPNs in the two pathways show high action specificity, are more correlated overall, and exhibit a local bias. While our definition of “action related” is based on a threshold for each neuron, SPNs were differently modulated during different behaviors. We therefore tested at the neuronal ensemble level if different behaviors would be encoded by distinct, non-overlapping SPN groups, or rather if behavior would be mapped more continuously in SPN activity space. To investigate this, we quantified the similarity between SPN ensemble patterns (i.e., “neuronal similarity”) for different behavioral clusters as the cross-validated (Walther et al., 2016) Euclidean similarity and compared it to the similarity between behavioral clusters (i.e., “behavioral similarity”). Figure 4A shows the pairwise similarity matrices for all behavioral clusters and the corresponding SPN ensemble patterns for a single D1 session (left and right panels, respectively). In both direct- and indirect-pathway SPNs, we found a strong positive correlation between behavioral and neuronal similarity (Figure 4B, gray). Importantly, the correlation between behavioral similarity and neuronal similarity persisted when only clusters with relatively rapid movements were analyzed (Figures 4B, 4C, and 4E, red), and was abolished when neurons were spatially shuffled for each behavioral segment (Figures 4C and 4E, blue; see Figure S4D for the summary, including both move and rest behavioral clusters). The correlation between behavioral and neuronal similarity was significantly different from zero on a single-session level for the majority of recordings for the original, but not spatially shuffled, data (Figures 4C and 4E, bottom). Furthermore, when analyzing the correlation between speed similarity (BA similarity) and neuronal similarity during the behavioral clusters, the correlations were small and largely non-significant (Figures 4D, 4F, and S4D), further suggesting that speed alone did not account for the observed relationship between behavioral and neuronal similarity. We additionally confirmed that the positive correlation between behavioral and neuronal similarity remained for more general movement features using the cumulative body/head rotation angle and median-filtered, raw acceleration time series (Figure S4E). These results identify a particular relationship between the SPN ensemble activity and behaviors that extends beyond changes in average SPN activity and movement speed (Figures 1F and 1G). It argues against the encoding of different actions by compact, non-overlapping SPN ensembles, and suggests a more continuous representation, in which the degree of overlap in neuronal ensemble representation reflects the similarity/dissimilarity between behaviors.
Figure 4.
Similarity in SPN Ensemble Activity Correlates with Similarity in Behaviors
(A) Left: matrix of the pairwise EM similarity between behavioral clusters i and j based on BA, GAAP, and body/head rotation φ for a single recording session (D1, n = 14 behavioral clusters). Right: corresponding neuronal similarity calculated as the cross-validated Euclidean similarity between the normalized SPN ensemble patterns (continuous ΔF/F, LBC) during the behavioral clusters from the left panel. Note that smaller values indicate less similarity.
(B) Relationship between behavioral similarity and neuronal (i.e., SPN ensemble pattern) similarity and corresponding Spearman correlation coefficients, ρ, for a single session (left, D1; right, D2) for all behavioral clusters (moving and resting, gray) and behavioral clusters during movement (red).
(C) Average correlation between behavioral similarity and neuronal similarity during movement (top; D1, n = 5 mice; D2/A2a, n = 5 mice) and fraction of significant (p < 0.05) versus nonsignificant (p ≥ 0.05) correlation coefficients (bottom; D1, 21 sessions; D2/A2a, 22 sessions) for original (red) and spatially shuffled control (blue) data. Neuronal activity was extracted using LBC. Paired t test for comparison to spatially shuffled control data (∗∗p < 0.01, ∗∗∗p < 0.001). Bars represent mean ± SEM.
(D) Same as (C) for the average correlation between BA similarity and neuronal similarity. Bars represent mean ± SEM.
(E and F) Same as (C) and (D), respectively, for neuronal activity extracted with CNMF-E (D1, n = 5 mice, 20 sessions; D2/A2a, n = 5 mice, 22 sessions). Bars represent mean ± SEM.
See also Figure S4.
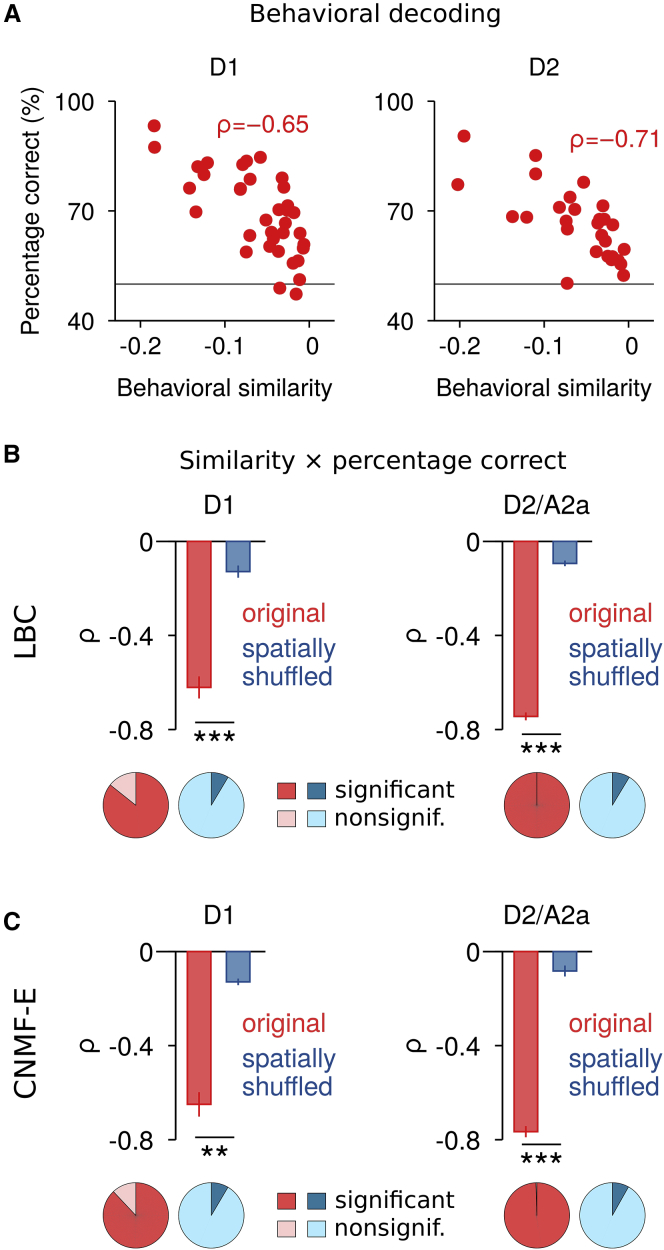
To test whether differences in the SPN ensemble activity were predictive of the difference in behavior, we trained a support vector machine (SVM) for binary classification. Instead of using the time-averaged SPN ensemble activity during each behavioral cluster, which smooths out the variability of SPN firing at shorter timescales, we performed the behavior decoding at the timescale of individual behavioral segments (Figure S4C). That is, for each pair of behavioral clusters, the SVM uses a subset of the data to find a linear separation that best distinguishes the SPN ensemble patterns between the two behaviors. The SVM can then be used to decode the behavior from the remaining data and to evaluate the decoding accuracy (for details, see STAR Methods). We found that decoding accuracy was very high for very different behaviors, and decreased for similar behaviors (Figure 5A; see also Figure S4B), confirming that the difference between SPN ensemble activity corresponds to the dissimilarity between behaviors. To control for possible confounds of average changes in SPN activity, we performed spatial shuffling, which preserved the differences in average SPN activity between behavioral clusters. The negative correlation between behavioral similarity and decoding accuracy observed in the original data was not seen in spatially shuffled data (Figures 5B and 5C), indicating that, indeed, different SPN ensembles underlie the encoding of different behaviors.
Figure 5.
Behavior Decoding Based on SPN Ensemble Activity
(A) Relationship between behavioral similarity and decoding performance of a support vector machine (SVM) for binary classification. The decoding performance was measured as the percentage of correct classifications and was corrected for differences in the sample size between behavioral clusters (STAR Methods). Shown are clusters during movement in a single session for each pathway (D1 and D2) with the corresponding ρ. The dashed lines indicate chance level.
(B) Average correlation between behavioral similarity and percentage correct during movement (top; D1, n = 5 mice; D2/A2a, n = 5 mice) and fraction of significant (p < 0.05) versus nonsignificant (p ≥ 0.05) correlation coefficients (bottom; D1, 21 sessions; D2/A2a, 22 sessions) for original (red) and spatially shuffled control (blue) data. Neuronal activity was extracted using LBC. Paired t test for comparison to spatially shuffled control data (∗∗p < 0.01, ∗∗∗p < 0.001). Bars represent mean ± SEM.
(C) Same as (B) for neuronal activity extracted with CNMF-E (D1, n = 5 mice, 20 sessions; D2/A2a, n = 5 mice, 22 sessions). Bars represent mean ± SEM.
Taken together, these results suggest a particular organization of striatal activity that covers the action space with spatially overlapping SPN ensembles, and where similar behaviors are encoded by closer population representations and more dissimilar behaviors by more distant representations.
Discussion
In the current study, we measured the spatiotemporal neuronal dynamics of the two major striatal projection pathways in the dorsal striatum during self-paced, natural movements. Our results demonstrate a locally biased, but not spatially compact, organization of SPN activity, in which action-specific SPNs are more correlated and spatially closer to each other. Importantly, we found that different actions are not encoded by discrete, non-overlapping SPN ensembles, but are represented continuously in the neural activity space by overlapping SPN ensembles, with more similar actions being encoded by closer ensemble representations and more dissimilar actions by more distant representations.
Microendoscopic in vivo imaging can record SPNs with high density at single-cell resolution and allowed us to quantify the spatiotemporal organization of SPN ensembles in the two pathways. Although we confirmed that SPNs exhibit low average CCs (Bakhurin et al., 2016, Klaus and Plenz, 2016), the recording of neurons at all spatial distances including distances below 50 μm revealed increased correlations within a radius of up to 80–100 μm in both direct- and indirect-pathway SPNs (Bakhurin et al., 2016, Barbera et al., 2016). This locally biased organization was reflected in the activity of action-related SPNs, suggesting functional significance. Quantifying the microstructure in the spatiotemporal organization of SPN activity therefore reveals new principles in addition to average measures of network synchrony, which could potentially be interesting for the study of pathological conditions.
The functional SPN networks we identified in our study also showed some long-range spatial correlations and thus differed from an organization with purely compact SPN clusters as recently described in a study by Barbera et al. (2016). The difference between the results in the current study and Barbera et al. (2016) could stem from the different approaches in correcting the intracellular calcium measurements. The calculation of CCs in our study was based on measurements of intracellular calcium activity in populations of hundreds of SPNs obtained with one-photon microendoscopic imaging. Such data inherently suffer from strong background signals and contamination caused by neuronal overlap (Pnevmatikakis et al., 2016, Zhou et al., 2017), which require adequate correction methods. Multiple lines of evidence suggest that the local correlations we observed accurately reflect SPN firing and are not simply a result of background signals, neuronal overlap, or optical aberrations. First, spatially local CCs between SPNs were found with two independent methods verified using simulated ground truth data. Second, strong CCs were found throughout the imaging field of view. Third, not all nearby SPNs showed strong CCs. And fourth, a decrease in CC with increasing SPN distance was also found when only the largest calcium transients at distances larger than three times the average neuron diameter were analyzed, further reducing potential crosstalk between signals from neighboring SPNs. In addition, a decrease of average CCs with increasing neuronal distance was recently described in resting activity using extracellular recordings (Bakhurin et al., 2016). Different possible mechanisms could lead to the increased CC between nearby neurons. Converging cortical inputs (Alexander and DeLong, 1985, Brown, 1992, Hintiryan et al., 2016, Hunnicutt et al., 2016) provide an anatomical substrate to modulate local striatal domains. However, the actual moment-to-moment activation that SPNs receive will also depend on the spatiotemporal dynamics of the corticostriatal input. Independent experimental evidence suggests that cortical neurons exhibit a local CC profile similar to the one observed in our study (Bellay et al., 2015, Prevedel et al., 2016, Rosenbaum et al., 2017; but see Sakata and Harris, 2009 for differences between cortical layers obtained with high temporal resolution extracellular recordings). Additionally, the local organization of striatal activity might be shaped by intrastriatal inhibition (Carrillo-Reid et al., 2008, Tepper et al., 2004), including lateral inhibition between SPNs (Czubayko and Plenz, 2002, Klaus and Plenz, 2016, Planert et al., 2010) with overlapping dendritic and axonal fields extending radially between 150 and 400 μm and more (Kawaguchi et al., 1990).
An important aspect of our study was the clustering of natural behaviors (Berman et al., 2014, Wiltschko et al., 2015) based on video data and BA measurements and the quantification of similarity between behavioral clusters. We found that SPNs related to specific actions showed an increased likelihood of being closer together and were more correlated in general, indicating that the overall organization of striatal activity is related to its representation of action space. In particular, the quantification of similarity allowed us to demonstrate a mapping between SPN ensemble activity and self-paced, natural actions in the two pathways, in which more similar SPN ensemble patterns were associated with more similar behaviors. While this seems intuitive, it is not possible to know a priori the mapping between neuronal activity space and action space. SPNs could be organized in discrete, non-overlapping clusters (Barbera et al., 2016) that would correspond to different actions. Instead, we found that SPNs are organized in overlapping ensembles that represent the action space, and the amount of overlap in the neuronal activity space is progressively less for more dissimilar behaviors. Consequently, behaviors could be discriminated from SPN ensemble activity with increasing accuracy proportionally to the degree of dissimilarity. Importantly, this relationship reflected the activation of specific SPN ensembles and not simply changes in average activity, and was independent of movement speed (Jin et al., 2014). Thus, our findings extend beyond the existing view of striatal function in regulating movement speed (Dudman and Krakauer, 2016) and suggest a representation of action space in the activity of SPN ensembles.
The observation that action similarity is encoded in the similarity between SPN ensemble activities might have important implications for reinforcement learning. At early stages of learning, it can be difficult to repeat the exact same action that previously led to a positive outcome. We hypothesize that being able to repeat similar actions would facilitate learning and could be supported by the retrieval of similar SPN ensemble states and avoiding the retrieval of very different ensembles, thus circumventing the need for the consistent retrieval of a very specific SPN ensemble early in learning.
Some basal ganglia models propose a pro- versus antikinetic (i.e., “go” versus “no-go”) function for direct- and indirect-pathways SPNs, respectively (Durieux et al., 2012, Kravitz et al., 2010, Yttri and Dudman, 2016), whereas other models suggest that both pathways contribute in concert to generate movements (Cui et al., 2013, Tecuapetla et al., 2016). Here, we found that both direct- and indirect-pathway SPNs show a very similar organization that encodes action space. This finding suggests that indirect-pathway SPNs do not represent a general “no-go” signal (Durieux et al., 2012, Kravitz et al., 2010, Yttri and Dudman, 2016), or an “inhibit all competing movements” signal (because the activity patterns are as action specific as those of the direct pathway), but instead proposes a more specific relationship between the activity of indirect-pathway SPNs and specific behaviors. The idea that indirect-pathway SPNs inhibit unwanted movements should perhaps be revisited in the context of action selection, in which the selection of a particular movement requires both the facilitation and the inhibition of specific movement features (for example, flexor/extensor muscle pairs). This finding also constrains the possibilities of how independent the activity in the two SPN pathways can be. That is, the coordination of direct- and indirect-pathway SPN activities is not only present at the average activity level but should also be reflected in the precise spatiotemporal activity patterns in the two pathways. Simultaneous measurement of direct- and indirect-pathway SPNs and a more detailed knowledge of effects on downstream nuclei will be required to further the understanding of striatal function. In summary, our results identify a predominantly local organization in striatal ensemble activity that encodes action space beyond movement speed.
STAR★Methods
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Rabbit anti-GFP Alexa Fluor-488 conjugate | Molecular Probes | Cat#A-21311; RRID: AB_221477 |
| Bacterial and Virus Strains | ||
| AAV5.CAG.Flex.GCaMP6f.WPRE.SV40 | University of Pennsylvania Vector Core | Cat#AV-5-PV2816 |
| Experimental Models: Organisms/Strains | ||
| Mouse: D1-Cre: Tg(Drd1a-cre)FK150Gsat/Mmucd | MMRRC | RRID: MMRRC_029178-UCD |
| Mouse: D2-Cre: Tg(Drd2-cre)ER43Gsat/Mmucd | MMRRC | RRID: MMRRC_017268-UCD |
| Mouse: A2a-Cre: B6.FVB(Cg)-Tg(Adora2a-cre)KG139Gsat/Mmucd | MMRRC | RRID: MMRRC_036158-UCD |
| Software and Algorithms | ||
| CNMF-E | This paper; Pnevmatikakis et al., 2016, Zhou et al., 2017, Friedrich et al., 2017 | N/A |
| LBC | This paper; Klaus and Plenz, 2016 | N/A |
| Unsupervised behavior classification algorithm | This paper; Frey and Dueck, 2007 | N/A |
Contact for Reagent and Resource Sharing
Further information and requests for resources and reagents may be directed to and will be fulfilled by the Lead Contact, Rui Costa (rc3031@columbia.edu).
Experimental Model and Subject Details
All animal procedures were reviewed and performed in accordance with the Champalimaud Center for the Unknown Ethics committee guidelines and approved by the Portuguese Veterinary General Board (Direcção Geral de Veterinária, Ref. No. 0421/000/000/2014). Experimental mice were 3 to 5 month-old BAC transgenic males individually housed on a 12 hr light/dark cycle with ad libitum access to food and water. Transgenic mice expressed Cre recombinase under the control of the dopamine D1 receptor (D1-Cre, Tg(Drd1a-cre)FK150Gsat/Mmucd; MMRRC #029178-UCD) for targeting of direct-pathway SPNs, or the dopamine D2 receptor (D2-Cre, Tg(Drd2-cre)ER43Gsat/Mmucd; MMRRC #017268-UCD) or adenosine A2a receptor (A2a-Cre, B6.FVB(Cg)-Tg(Adora2a-cre)KG139Gsat/Mmucd; MMRRC #036158-UCD) for targeting of indirect-pathway SPNs. All lines have been backcrossed onto C57Bl6/J mice for at least 8 generations. Sample size is detailed in the Results or figure legends.
Method Details
Virus injection and chronic lens implantation
Surgeries were performed under sterile conditions and isoflurane (1%–3%, plus oxygen at 1-1.5 l/min) anesthesia on a stereotactic frame (David Kopf Instruments, Model 962LS). Throughout each surgery, mouse body temperature was maintained at 34°C using an animal temperature controller (ATC1000, World Precision Instruments) and afterward, each mouse was allowed to recover from the anesthesia in its homecage on a heating pad. The mouse head was shaved, cleaned with 70% alcohol and iodine, and a small incision from anterior to posterior was made on the skin to allow for aligning the head and drilling the hole for the injection site. Each animal was unilaterally injected with 300 nl of AAV5.CAG.Flex.GCaMP6f.WPRE.SV40 (University of Pennsylvania Vector Core) into the left dorsal striatum (AP: 0.5 mm, ML: 2.3 mm, DV: −2.3 mm) using a Nanojet II Injector (Drummond Scientific, USA) at a rate of 4.6 nl per pulse every 5 s. The injection pipette was left in place for 10 min post-injection before it was removed. After the injection, the skull was cleaned and the skin sealed with Vetbond tissue adhesive (3M, USA). Following the same surgical procedures, one week after viral injection, a 1-mm-diameter gradient index (GRIN) lens (Inscopix) was implanted in the left mouse striatum directly above the injection site after carefully aspirating ∼1.8-2 mm of the overlaying cortical tissue with a 30-gauge blunt needle. Care was taken to minimize bleeding. Once in place, the lens was secured to the skull using a combination of black Ortho-Jet powder and liquid acrylic resin (Lang Dental, USA) and covered with paper/tape to protect the lens surface. One week after the GRIN lens implantation, the microendoscope baseplate (Inscopix) was mounted onto the mouse head under visual guidance using the attached microscope to determine the best field of view. The imaging field of view was inspected and allowed to clear for several days prior to imaging and behavioral experiments. After completion of the behavioral experiments, mice were transcardially perfused with saline and 4% paraformaldehyde in PBS. Brains were removed for histological analysis and coronal slices were sectioned at 50 μm (Leica vibratome VT1000). Immunohistochemistry was performed for GCaMP-GFP expression by incubating the sections with a GFP antibody (GFP Tag polyclonal antibody, Alexa Fluor 488 conjugate, Molecular Probes #A-21311) diluted at 1:1000 in 0.4% Triton-PBS overnight at room temperature and counterstained with DAPI. Both placement of lens and spread of injection were confirmed using a Zeiss Lumar widefield fluorescence microscope (Figures 1B and S1A).
Behavior
Mice were placed in an open field arena (39.5 × 39.5 × 17.5 cm, length × width × height) inside a sound-attenuating chamber and imaged for 10-15 min every day for 5 days during the light cycle. Behavior was recorded using an overhead-mounted video camera (Flea3, Point Grey Research) at 15-30 frames per second (fps) and a head-mounted 3-axis accelerometer sampled at 1 kHz with a Cerebus acquisition system (Blackrock Microsystems). One-photon imaging of intracellular calcium activity was acquired at 7-10 fps using an nVista microendoscope [lens: 1 mm diameter, ∼4 mm length, 0.5 numerical aperture, product number 1040; excitation: blue light-emitting diode (LED); excitation filter: 475/10 nm, ∼0.24-0.6 mW/mm2; emission filter: 535/50 nm; Inscopix, Palo Alto, CA] and acquisition system with 12-bit resolution. The accelerometer was secured to the side of the microendoscope on the opposite side to the excitation LED. Mice were lightly anesthetized with isofluorane to facilitate mounting (and removal) of the microendoscope and accelerometer. Mice were allowed to wake up fully at least 15 min prior to image acquisition. Resulting calcium movies and acceleration data were analyzed as described below. Time stamps from the video camera, microendoscope and accelerometer were synchronized using the Cerebus recording system.
Calcium imaging analysis
All calcium movies were initially preprocessed in Mosaic (Inscopix) for spatial binning (4 × 4 pixels) and motion correction (Figure S1B) and subsequently analyzed using custom MATLAB scripts. One-photon imaging is known to contain significant background signals arising from out-of-focal plane light and neuropil (Zhou et al., 2017) due to the fluorescence excitation of a relatively large three-dimensional volume compared to, for example, two-photon imaging. Because out-of-focus background contains relatively low spatial frequencies (Zhou et al., 2017), appropriate methods can be used to estimate background signals from the soma surrounding and correct for it. Two independent methods were employed to correct somatic calcium transients: (1) local estimation of background and baseline for fluorescence correction (LBC; Klaus and Plenz, 2016), and (2) a constrained non-negative matrix factorization for endoscopic data (CNMF-E; Pnevmatikakis et al., 2016, Zhou et al., 2017).
LBC
The LBC method was based on the manual selection of somatic regions of interest (ROIs) and an automatic estimation of local background and baseline signals for fluorescence correction. A circular ROI template with diameter of 14 μm based on the half-width of the average soma shape (14.4 ± 1.0 μm, 1154 neurons from n = 10 recordings; example for single recording in Figure 1C, inset) was used. ROIs were selected using so-called ‘activity’ images (Figure 1C), which were derived pixel-wise by calculating the maximum deviation over time from the average (pixel-wise) fluorescence. To allow for the identification of neurons with very low baseline fluorescence and low firing rate, ‘activity’ images were calculated for consecutive periods of 10-15 s (detailed example views shown in Figure 1D, top) using the average fluorescence over the entire session. After manual selection of all neurons, individual background regions were determined within a 2-diameter radius around each ROI. The background region was the region with lowest average fluorescence in the ‘activity’ image with a linear penalty term for being too close to somatic ROIs. For each ROI, raw and background fluorescence (Fraw and Fbg, respectively) were extracted by averaging pixel intensities within the corresponding ROIs for each frame. To correct for out-of-focus background contamination, a fraction, r, of the background was subtracted from Fraw (Kerlin et al., 2010, Pinto and Dan, 2015). Because blood vessels only have small contributions of neuropil signals they allow for an estimation of r, which was defined as the ratio between fluorescence in a blood vessel versus the surrounding neuropil (i.e., background). We found no difference for direct- and indirect-pathway SPN recordings (D1-Cre: 0.91 ± 0.011, D2/A2a-Cre: 0.91 ± 0.009, two-sample t test, t(13) = 0.1, p = 0.92, 2-3 recordings per subject analyzed) and used r = 0.9 for all analyses if not stated otherwise. The relative change in fluorescence was calculated as
where F denotes the background-corrected fluorescence, F = Fraw - r⋅Fbg, and F0 denotes the baseline of F fluorescence estimated from a ± 15 s sliding window. Due to the sparse activity in SPNs, F0 was calculated from the baseline defined as the average of all values below the 80th percentile in F. The decay dynamics of intracellular calcium transients was τdecay = 299 ± 30 ms in direct-pathway SPNs and τdecay = 289 ± 20 ms in indirect-pathway SPNs in line with previous reports for GCaMP6f in pyramidal neurons of the visual cortex (Chen et al., 2013). Importantly, relative increases of the intracellular, somatic calcium concentration as quantified by ΔF/F have been shown to monotonically report the number of action potentials (Chen et al., 2013, Cui et al., 2013, Klaus and Plenz, 2016). Consequently, transient changes in ΔF/F are abolished when blocking active sodium currents using tetrodotoxin (Cui et al., 2013).
For some analysis, where indicated, we used time series of ΔF/F peak events to exclude possible influences of baseline fluctuations and the GCaMP6f decay dynamics. The values of the time series were set to the amplitudes of significant ΔF/F peaks at the corresponding peak times and were equal to zero otherwise. A significant ΔF/F peak event was defined by the time point and maximum value of ΔF/F during threshold crossings. The threshold was defined as mean plus three standard deviations (SDs) of the ΔF/F distribution (obtained by fitting a Gaussian function with mean and SD to the distribution of ΔF/F values individually for each neuron). Because successive (i.e., cumulative) increases in ΔF/F represent neuronal firing in successive bins, we also used, where indicated, the thresholding of the time derivative of ΔF/F, that is, the (ΔF/F(t+1)-ΔF/F(t))/Δt time series, where t represents the frame number (i.e., Δt = 1).
CNMF-E
Constrained non-negative matrix factorization is a recently proposed framework for simultaneously denoising, deconvolving and demixing of calcium imaging data (Pnevmatikakis et al., 2016). This framework identifies the cell locations and handles spatial overlaps between neurons. CNMF-E is one of its extensions specialized for processing microendoscopic data (Zhou et al., 2017). It can reliably deal with the large fluctuating background from multiple sources in the data, allowing the accurate source extraction of cellular signals. It includes four steps: (1) initialize spatial and temporal components of single neurons without the direct estimation of the background; (2) estimate the background given the estimated neurons’ spatiotemporal activity; (3) update the spatial and temporal components of all neurons while fixing the estimated background fluctuations; (4) iteratively repeat step 2 and 3. We briefly describe the algorithm used in our work, and more details can be found in the preprint of the CNMF-E paper (Zhou et al., 2017). In the initialization step, we first used a mean-subtracted two-dimensional Gaussian kernel to filter the raw video data. The parameters of this kernel are selected to resemble the distribution of soma diameters (μCNMF-E = 0, σCNMF-E = 6.9 μm, maximum soma diameter dCNMF-E = 35 μm). Filtering the data with this kernel acts as a template matching to find all morphological shapes similar to a soma. In the filtered data, the background is approximately removed because it is almost flat within the spatial range of the kernel, and the kernel integrates to zero. In contrast, soma shapes are preserved and become more visible because they match the template shape. As a result, we can accurately extract each neuron’s calcium activity from the fluorescence at its center pixels (so-called seed pixels) in the filtered data. Furthermore, we developed a method to detect seed pixels by choosing pixels with high local correlations and signal-to-noise ratio. Given a seed pixel, we initialize one neuron by estimating its temporal activity as the temporal trace of the pixel in the filtered data. To get its spatial component, we crop a small square with the size of 2 times larger than a cell body centered at the seed pixel from the raw data. Then we estimate the background fluctuation within the cropped area as the median in each frame. For each pixel within the selected square, we assume its fluctuations are from two sources: one is the initialized neuron and the other one is the background fluctuation. Since we have the temporal traces for all these two sources, we run linear regression to get the weights for each component and the weights corresponding to the neural activity lead to our initialization of the spatial footprints. Once we have both the spatial and temporal component of this neuron, we subtract its spatiotemporal activity from the raw video data and repeat the same procedure to initialize another neuron until the specified number of neurons has been detected or no more seed pixels can be found. This greedy initialization method is able to efficiently and accurately detect almost all neurons. In the next step, we estimate the background activity for each pixel individually. For each pixel, we first choose its neighbors with a distance larger than neuron size. Accordingly, these pixels do not share the same cellular activity but they share the same sources of the background. Then we use the projection of this pixel’s temporal trace on a linear span of its neighbors’ traces as the estimated background fluctuations. Finally, we subtract this estimated background from the raw video data and update all neuronal spatial and temporal components using alternating matrix factorization (Friedrich et al., 2017, Pnevmatikakis et al., 2016, Zhou et al., 2017). The temporal deconvolution step for denoising was used for the update of the temporal activity. The final temporal, neuronal components reported for CNMF-E were not denoised and are denoted with a capital letter C throughout the paper. Time series of significant C peak events were calculated as described for ΔF/F (see LBC above).
Analysis of ground truth data
We investigated whether LBC and CNMF-E were able to recover the underlying CC-distance relationship in simulated ground truth data (Figures S1C, S2D, and S2E). To simulate the strong background component in microendoscopic imaging data, we used the sum of 10 time-varying background frames with individual temporal profiles and added neuronal signals plus random noise to this image sequence. The following parameters were matched between simulated and experimental data: mean fluorescence intensity and standard deviation, average neuron diameter, number of neurons per session, neuron locations, GCaMP6f decay time constant, amplitudes of somatic fluorescence changes, and individual neuronal activity patterns obtained from the original calcium recordings (events were detected by thresholding ΔF/F > 3 SD of baseline, see description of significant ΔF/F peak events above). To obtain a flat CC-distance relationship, we randomized the neuron positions as described below in Calculation of spatially shuffled datasets. The resulting calcium movies were analyzed with LBC and CNMF-E as described above. For the LBC method, we re-applied the positions of the neuronal ROIs from the original dataset.
Calculation of CC
For the calculation of the CC between two time series x and y, we used Pearson’s correlation coefficient:
where E[·] denotes the expected operator and μ and σ denote the mean and standard deviation, respectively. Average CCs between neuronal activities were reported as the average across neuronal pairs. For the calculation of CCs between “action-related”/“other” SPNs (Figure 3), see “Definition of action-related neurons” below.
To exclude possible influences of baseline fluctuations and the GCaMP6f decay dynamics on the CC measure, we calculated, where indicated, CC on time series of significant peak events in ΔF/F (LBC) or C (CNMF-E), or their time derivatives. To determine whether average CCs were significantly larger than zero, we corrected the CC by chance-level correlations. That is, CCs obtained from significant events in the time derivative of ΔF/F were calculated and the CCs from temporally shuffled data preserving the inter-event interval distributions for each neuron were subtracted. We furthermore verified that our CC measure was not affected by the optical properties of the GRIN lens due to, for example, optical aberrations (Figure S2A).
For the quantification of the correlation between BA and neuronal activity in Figure 1G, ΔF/F was the average activity of all SPNs in the recording session. Time-shifted controls were obtained by randomly shifting the BA time series between ± (20-30) s. CCs for time-shifted traces were averaged over 1000 random instances per session.
Calculation of spatially shuffled datasets
Spatial shuffling of calcium activity was performed by randomizing the mapping between neuron position and activity. Specifically, for each neuron, a random neuron from the same session was selected, and the 2-dimensional positions were swapped. This approach preserved the distribution of pairwise distances between neurons as well as the precise temporal distribution of calcium events. The latter aspect is particularly relevant for continuous time series of ΔF/F (LBC) and C (CNMF-E), which contain temporal correlations due to the GCaMP6f decay dynamics that need to be preserved for the comparison to original data. We calculated 10 shuffled instances per session and used average values for further calculation. In addition, the spatial shuffling allowed us to study the influence of specific SPN ensemble configurations for the behavior decoding (Figure 5) without changing the average SPN activity during each behavior. Therefore, the magnitude reduction of the correlation between behavioral similarity and percentage of correct classification (Figures 5B and 5C) can be attributed solely to the randomization of the spatial SPN ensemble pattern.
Comparison to Barbera et al. (2016)
To cluster the neuronal activity, we applied a meta-clustering approach to the neuronal data that was recently proposed by Barbera et al. (2016). We used the same parameters as in their study. Specifically, we applied k-means clustering with k-means++ initialization to ΔF/F time series from randomly selected 30 s windows. The number of clusters was set to where N denotes the number of neurons. The clustering was repeated 100 times per 30 s window using different k-means++ initializations. This procedure was repeated for a total of 100 30 s windows resulting in an average overlap of ∼80% between windows. A N × N co-occurrence matrix, M, was built, which contained at position i,j the number of times neuron i and neuron j were clustered together. Accordingly, Mi,j = 0 if neurons i and j were never clustered together, and Mi,j = 10,000 if neurons i and j were always clustered together. From the final co-occurrence matrix, meta-clusters were obtained by applying a threshold, T, and determining the largest neuronal groups. T was chosen to maximize the ratio between number of meta-clusters and number of unclustered neurons. We performed this analysis on the neuronal (i.e., soma) signals, the raw data, and the background signal obtained with CNMF-E. All signals were baseline-corrected as described in LBC. For the calculation of average intra-cluster distance and CC, only clusters with at least 5 members were used.
As shown in Figures S2H–S2J, the above meta-clustering did result in spatially extended, non-compact neuronal clusters, which was in contrast to the compact clusters reported by Barbera et al. (2016). Because we used GCaMP6 ‘fast’ in the current study, in contrast to GCaMP6 ‘slow’ used in Barbera et al. (2016), we verified that the spatially extended, non-compact clusters in our data were not a result of a difference in the GCaMP6 decay dynamics. To this end, we convolved continuous ΔF/F and ΔF/F peak time series with an exponential kernel with different decay time constants (up to 2 s) and found spatially extended, non-compact clusters irrespective of the chosen decay time constant (data not shown). This result suggests that the discrepancy between the current study and Barbera et al. (2016) might be due to differences in the extraction of intracellular calcium time series from raw fluorescence data. As described above, fluorescence signals obtained with one-photon calcium imaging require proper background subtraction to correct for strong out-of-focus contributions from neuropil and other sources (Zhou et al., 2017) and baseline subtraction to correct for slow trends due to, for example, photobleaching. We note that the approach used by Barbera et al. to calculate relative fluorescence changes, ΔF/F, differs in two details from LBC, which previously has been shown to reliably report intracellular action potential firing (Klaus and Plenz, 2016). First, Barbera et al. perform baseline subtraction on soma and background fluorescence before background-correcting the somatic fluorescence. Second, they used the minimum value of the image stack for subtraction from the raw fluorescence. This latter step, however, is not suited to remove slow trends in raw fluorescence time series and could potentially affect CC measures.
Measurement and quantification of behavior
Behavior was quantified on time series of acceleration and video rotation. In the main analysis (Figures 3, 4, and 5), we used: (i) total body acceleration to distinguish movement versus rest (Figure 1A), (ii) gravitational acceleration along the rostro-caudal/anterior-posterior (AP) axis to extract postural changes (Figure S3B), and (iii) rotational information extracted from the video to measure head and whole-body orientation (Figures 3A–3D). Total body acceleration was defined as
where BAAP/ML/DV denote the body acceleration in the anterio-posterior, mediolateral, and dorsoventral axis, respectively, with respect to the animal’s head. The individual BA components were calculated by median-filtering the raw acceleration time series and by subsequent high-pass (0.5 Hz) filtering with a fourth-order Butterworth filter. Gravitational acceleration, GA, was obtained for each axis by median and subsequent low-pass filtering (0.5 Hz cutoff, fourth-order Butterworth filter). We used GAAP to quantify postural changes (i.e., vertical head position) in the open field during resting, locomotion and rearing (regression on the GAAP and vertical head-position time series: R2 = 0.72-0.76, p < 0.001 for n = 2 mice; Figure S3B). Head and body rotation angle of the animal was extracted from video as relative (i.e., frame-to-frame) change in body/head axis orientation. We then converted the time series into cumulative changes of head/body rotation (positive for left rotations, negative for right rotations) to remove small rotations and noise by considering only rotations with at least ± 20°/s of cumulative change before any change in direction. The angle, φ, for each rotation was then set to the maximum relative change between the beginning (±30-60°/s) and end (i.e., change in direction) of the rotation. This step improved the detection of left and right turns using the clustering algorithm described below compared to cumulative changes in head/body rotation. An example time series of φ is shown in Figures 3A and S3A.
Time series of all features were binned into 300 ms long, non-overlapping segments (Wiltschko et al., 2015), which were used for the following clustering analysis. For each 300-ms segment and per feature, values were discretized using one or two thresholds: For BA, a single threshold was used to separate moving from resting. The threshold was the same for all subjects and was set to the average value separating the bimodal distribution of BA (visualized in logarithmic scale; Figure S3A). For GAAP, 2 thresholds were used based on Otsu’s method (Figure S3A). For φ, we used 2 thresholds (±45-90°/s) separating left and right turns from straight and forward movements. The resulting histograms, that is, 3 per 300-ms segment, were individually normalized to obtain probability distributions and then used to calculate pairwise similarities between segments (Figure S3A). For a 600 s long recording and 300 ms long segments, this resulted in a 2000 × 2000 similarity matrix. Our measure of similarity, S, was based on the so-called “earth mover’s” (EM) distance (Rubner et al., 2000):
where DEM is the sum of the normalized EM distances for the 3 features (BA, GAAP, and φ) as defined below. The normalizations constrain the values of S to be within the range [-1,0], that is, −1 and 0 indicate the maximum dissimilarity and identity between the two probability distributions, respectively. For each single feature, the normalized EM distance between probability distributions and is calculated iteratively as follows:
where i iterates over the number of bins of the probability distributions, that is, for BA, and for GAAP and φ. The EM distance for a single feature is then defined as
and subsequently normalized by the number of bins minus 1. DEM is defined as the sum of the normalized EMDs.
The EM-similarity, S, has a unique advantage over other measures of similarity, such as the histogram intersection similarity (Zhang and Lu, 2003), or similarity based on the cross-validated Euclidean distance (Walther et al., 2016). Similar to intersection and Euclidean similarity, the EM-similarity S takes into account the pairwise differences between corresponding bins in the two distributions to be compared. The unique property of S is that it also considers the distance between the bins within the distribution. For example, the probability density for the rotation φ has three bins corresponding to ‘left’, ‘straight’, and ‘right’. While intersection and Euclidean similarity attribute the same distance to ‘left’ versus ‘straight’ and ‘left’ versus ‘right’, the EM-similarity considers the distance between ‘left’ versus ‘right’ to be bigger. This makes intuitively sense because movements are generally smooth, that is, φ will not jump from ‘left’ to ‘right’ but will be ‘straight’ in between. Despite this difference, the three similarity measures (i.e., EM-similarity, intersection similarity, and cross-validated Euclidean similarity) were correlated and gave highly similar results.
The obtained similarity measures (Figure S3A) were clustered using affinity propagation (Frey and Dueck, 2007) with the preference parameter set to −0.5 (similar results were obtained over a wide range tested; the particular value was chosen to maximize the accuracy of cluster separation, see Figure 3B, while maintaining a stable number of behavioral clusters). Using this method, we are able to generate a continuous unbiased classification of behavioral states (Figures 3A–3D; Movie S2). Based on this clustering, we finally calculated a matrix of similarities, (Figure 4A, left), using the average distribution over all 300-ms segments within behavioral clusters i and j, respectively (i and j range from 1 to the number of behavioral clusters within the session).
The analysis in Figures 4C–4F and 5 was restricted to clusters with movement (“move”). To this end, we excluded clusters with average BA less than 2 times the threshold used for behavioral clustering (see above). See Figures S4D and S4E for the summary of move plus rest behavioral clusters.
Visualization of behavioral similarity in two dimensions
For the visualization of behavioral time bins in two dimensions (Figure 3C), we used the non-linear dimensionality reduction technique t-SNE (van der Maaten and Hinton, 2008). We used the matrix of pairwise EM-distances (DEM, with 5% added, uniform noise) for all behavioral histograms (i.e., 300 ms time bins) as the input for the algorithm. We verified that the Euclidean distance in the two-dimensional projection appropriately reflected the true EM-distance (Figure S3C).
Definition of action-related neurons
To determine the statistical significance of action-related increases in activity at the single-neuron level (Figures 3 and S3F–S3H), we applied, for each neuron and behavioral cluster, a threshold to the average ΔF/F (LBC) or C (CNMF-E), and considered the neuron to be significantly modulated if the average during the behavioral cluster crossed the 99th percentile of shuffled data (i.e., the ‘baseline’ average during the entire recording session). The shuffled data for a given behavioral cluster was obtained by randomizing the start time stamp of each behavioral segment (i.e., preserving their durations) and calculating the average ΔF/F (LBC) and C (CNMF-E) during these randomized segments. 10,000 shuffled instances were used to calculate the ‘baseline’ average and its 99th percentile. In Figure 3, we restricted the analysis to neurons that showed significant positive modulations in activity (“action-related”). Figures S3G and S3H shows quantification for SPNs with significant decrease.
The calculation of pairwise measures (i.e., CC and inter-neuron distance; Figures 3E–3G and S3H) for “action-related” and “other” neurons was done for each behavioral cluster and final values were averaged across behavioral clusters within the same recording session. Thus, neurons considered “other” for one particular behavioral cluster, could be “action-related” for another behavioral cluster. CCs were calculated using the entire time series (ΔF/F for LBC; C for CNMF-E).
We note that for the analysis at the SPN ensemble level (Figures 4 and 5), we included all neurons imaged during the recording session.
Quantification of neuronal similarity
For each behavioral cluster, we extracted for all neurons, the time-averaged calcium activities, ΔF/F and C (for LBC and CNMF-E, respectively) during the cluster. This resulted in an n-dimensional vector, x, for each behavioral cluster that represents the SPN ensemble patterns during that behavior (n denotes the number of all recorded neurons during the imaging session). To quantify the similarity between those SPN ensemble patterns (Figure 4), we used a similarity measure based on the cross-validated Euclidean distance (Walther et al., 2016). To this end, we divided calcium activities into odd and even image frame numbers to obtain unbiased estimates of the similarity between SPN ensemble patterns (Figure 4A, right):
where xi and xj denote the SPN ensemble vectors for behavioral clusters i and j, respectively (i and j range from 1 to the number of behavioral clusters within the session). We note that dividing the dataset into first and second half for the above calculation of cross-validated measures, or similarity based on crosscorrelation between the SPN ensemble vectors, gave similar results. Because changes in the average SPN population activity (as evident in Figures 1F, 1G, and 3D) could contribute to the estimate of the Euclidean similarity between SPN ensemble patterns, we normalized the ensemble vector x to have a Euclidean norm equal to unity (Figure 4; similar results were obtained without normalization or normalization of the mean, i.e., average across SPNs equal to one).
To quantify the relationship between behavioral and neuronal similarity (Figures 4B–4F), we used the Spearman correlation coefficient ρ. ρ and corresponding p-values were calculated using MATLAB’s corr function. Behavioral clusters with less than 10 occurrences were excluded from the analysis. Furthermore, sessions with less than four data points for the calculation of ρ were excluded from the calculation of averages. To test the influence of movement versus resting on the relationship between behavioral and neuronal similarity, we performed two control measures. First, the analysis was, in addition to all clusters (moving and resting, Figure 4B, gray), performed only on clusters with strong movement (Figure 4B, red; Figures 4C–4F; see Measurement and quantification of behavior for the definition of the threshold separating moving from resting). Second, behavioral similarity was, in addition to the full features set (BA, GAAP, φ), performed only on the similarity in BA (i.e., the cross-validated difference in average BA during the behavioral clusters) (Figures 4D and 4F), or movement speed (i.e., cross-validated difference in average video pixel change during the behavioral clusters). For spatially shuffled control measures, the mapping between neuron position and neuronal activity (ΔF/F for LBC; C for CNMF-E) was randomized for each session and each behavioral cluster (see Calculation of spatially shuffled datasets).
Decoding of behavior from SPN ensemble activities
For the decoding analysis of behaviors from SPN ensemble activities, we used a linear support vector machine (SVM) for binary classification. The aim of the decoding was to predict the behavioral cluster membership obtained with affinity propagation (see above) based on the SPN ensemble activity at the timescale of the behavioral segments. Many behavioral segments were as short as 300 ms (the bin size for the behavioral clustering) but could range, in multiples of 300 ms, to many seconds (Figure S4C). For each behavioral segment obtained with our behavioral clustering approach, we first determined the corresponding SPN calcium activities, and averaged them during that segment. This resulted in n-dimensional vectors representing the SPN ensemble patterns, where n is equal to the number of all recorded neurons during the imaging session. The vectors representing the SPN ensemble patterns and the information about which behavioral cluster they belong to where then used to train and evaluate the SVM. Specifically, for each pair of behavioral clusters, a random set of 60% of the data was used for training the SVM, while the remaining data was used for evaluating the decoding accuracy quantified as the percentage of correct classifications (“percentage correct”; Figure 5). We averaged the “percentage correct” over 10 random training/evaluation datasets to obtain more reliable estimates. To account for sample number differences between behavioral clusters i and j and a possible classification bias, the percentage correct was calculated as the average between the percentage correct for behavioral cluster i and percentage correct for behavioral cluster j. The decoding analysis gave similar results for non-normalized and normalized SPN ensemble activity. Results in Figure 5 are shown for non-normalized SPN ensemble activity. The spatial shuffling (see above) in Figure 5 was done for each behavioral segment, thus preserving the average SPN activity within each behavioral cluster. This allowed attributing differences in the behavior decoding between original and spatially shuffled data solely to the precise configuration of the original SPN ensemble patterns and not the average SPN activity.
For the quantification of the relationship between “behavioral similarity” and “percentage correct” in Figure 5, we used the Spearman correlation coefficient ρ and followed the same approach as described in Quantification of neuronal similarity for Figure 4.
Quantification and Statistical Analysis
Mean ± standard error of the mean (SEM) was used to report statistics if not indicated otherwise. For all within-subject quantifications, we calculated the average across all 5 recording sessions. Statistical tests used and the sample size for each analysis is listed in the Results or figure legends. Both parametric and non-parametric tests were used wherever appropriate and are detailed in the Results and Table S1. Hypothesis testing was done at a significance level of α = 0.05. No statistical methods were used to pre-determine sample size. Where required, datasets were tested for normality using the Lilliefors test. All analysis and statistical tests were performed in MATLAB (MathWorks). Animals were excluded prior to the collection of experimental data based on imaging quality due to movement artifact, a lack of cells, or a bad focal plane.
Author Contributions
G.J.M. and R.M.C. designed the experiments. A.K., G.J.M., and R.M.C. conceptualized the analyses. V.B.P. developed the unsupervised behavioral clustering algorithm. P.Z. and L.P. developed the CNMF-E with feedback from A.K. P.Z. and L.P. provided the code for the simulated ground truth data. G.J.M. performed the surgeries, one-photon imaging experiments, and histological analysis. V.B.P. performed the behavioral clustering. A.K. performed all other analyses. A.K., G.J.M., V.B.P., and R.M.C. wrote the paper with the input from P.Z. and L.P. R.M.C. supervised and guided all aspects of the work.
Acknowledgments
We thank Ana Vaz and Mariana Correia for help with the animal care and genotyping, Joaquim Alves da Silva for technical advice and support, the Scientific Hardware Platform (Champalimaud Neuroscience Program) for the assembly of the accelerometer device, and members of the lab for useful discussions. We thank Vivek Jayaraman, PhD, Douglas S. Kim, PhD, Loren L. Looger, PhD, and Karel Svoboda, PhD from the Genetically-Encoded Neuronal Indicator and Effector (GENIE) Project, Janelia Research Campus, Howard Hughes Medical Institute for providing the AAV5.CAG.Flex.GCaMP6f.WPRE.SV40 used in this study. This work was funded by Simons Foundation (SFARI #294295), European Research Council Consolidator Grant (COG 617142), HHMI International Early Career Scientist (IEC 55007415), and ERA-Net NEURON grants to R.M.C. L.P. was supported by grants from the NIH (R01 EB22913) and DARPA (N66001-15-C-4032). P.Z. was supported by grants from the NIH (2R01MH064537 and R90DA023426) and IARPA (D16PC00007).
Published: August 30, 2017
Footnotes
Supplemental Information includes four figures, one table, and two movies and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2017.08.015.
Contributor Information
Andreas Klaus, Email: andreas.klaus@neuro.fchampalimaud.org.
Rui M. Costa, Email: rc3031@columbia.edu.
Supplemental Information
Statistical data presented per animal or comparison for each figure.
Top left: Raw fluorescence after motion correction imaged in direct-pathway SPNs (D1-Cre). ∼1 min of a single session is shown. Top right: Corresponding background estimated using CNMF-E. Bottom left: Background-subtracted raw fluorescence. Bottom right: Somatic fluorescence estimated using the spatial footprints and denoised temporal components for all 243 neurons during that session.
5 out of 14 clusters for a single session (D1-Cre) are shown (see also Figures 3C and 3D). These clusters largely correspond to left turning, right turning, forward movement, rearing, and resting (from left to right). Top row: for each cluster, the first 300 ms of all behavioral segments were merged into a single movie (Wiltschko et al., 2015). Bottom row: detailed view of the same movements as above aligned to the body center of mass and body orientation. For better visualization, pixel intensities were logarithmically scaled for the aligned sequences.
References
- Alexander G.E., Crutcher M.D. Functional architecture of basal ganglia circuits: neural substrates of parallel processing. Trends Neurosci. 1990;13:266–271. doi: 10.1016/0166-2236(90)90107-l. [DOI] [PubMed] [Google Scholar]
- Alexander G.E., DeLong M.R. Microstimulation of the primate neostriatum. II. Somatotopic organization of striatal microexcitable zones and their relation to neuronal response properties. J. Neurophysiol. 1985;53:1417–1430. doi: 10.1152/jn.1985.53.6.1417. [DOI] [PubMed] [Google Scholar]
- Bakhurin K.I., Mac V., Golshani P., Masmanidis S.C. Temporal correlations among functionally specialized striatal neural ensembles in reward-conditioned mice. J. Neurophysiol. 2016;115:1521–1532. doi: 10.1152/jn.01037.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbera G., Liang B., Zhang L., Gerfen C.R., Culurciello E., Chen R., Li Y., Lin D.-T. Spatially compact neural clusters in the dorsal striatum encode locomotion relevant information. Neuron. 2016;92:202–213. doi: 10.1016/j.neuron.2016.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellay T., Klaus A., Seshadri S., Plenz D. Irregular spiking of pyramidal neurons organizes as scale-invariant neuronal avalanches in the awake state. eLife. 2015;4:e07224. doi: 10.7554/eLife.07224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman G.J., Choi D.M., Bialek W., Shaevitz J.W. Mapping the stereotyped behaviour of freely moving fruit flies. J. R. Soc. Interface. 2014;11:20140672. doi: 10.1098/rsif.2014.0672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody C.D. Correlations without synchrony. Neural Comput. 1999;11:1537–1551. doi: 10.1162/089976699300016133. [DOI] [PubMed] [Google Scholar]
- Brown L.L. Somatotopic organization in rat striatum: evidence for a combinational map. Proc. Natl. Acad. Sci. USA. 1992;89:7403–7407. doi: 10.1073/pnas.89.16.7403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo-Reid L., Tecuapetla F., Tapia D., Hernández-Cruz A., Galarraga E., Drucker-Colin R., Bargas J. Encoding network states by striatal cell assemblies. J. Neurophysiol. 2008;99:1435–1450. doi: 10.1152/jn.01131.2007. [DOI] [PubMed] [Google Scholar]
- Chen T.-W., Wardill T.J., Sun Y., Pulver S.R., Renninger S.L., Baohan A., Schreiter E.R., Kerr R.A., Orger M.B., Jayaraman V. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui G., Jun S.B., Jin X., Pham M.D., Vogel S.S., Lovinger D.M., Costa R.M. Concurrent activation of striatal direct and indirect pathways during action initiation. Nature. 2013;494:238–242. doi: 10.1038/nature11846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czubayko U., Plenz D. Fast synaptic transmission between striatal spiny projection neurons. Proc. Natl. Acad. Sci. USA. 2002;99:15764–15769. doi: 10.1073/pnas.242428599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudman J.T., Krakauer J.W. The basal ganglia: from motor commands to the control of vigor. Curr. Opin. Neurobiol. 2016;37:158–166. doi: 10.1016/j.conb.2016.02.005. [DOI] [PubMed] [Google Scholar]
- Durieux P.F., Schiffmann S.N., de Kerchove d’Exaerde A. Differential regulation of motor control and response to dopaminergic drugs by D1R and D2R neurons in distinct dorsal striatum subregions. EMBO J. 2012;31:640–653. doi: 10.1038/emboj.2011.400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frey B.J., Dueck D. Clustering by passing messages between data points. Science. 2007;315:972–976. doi: 10.1126/science.1136800. [DOI] [PubMed] [Google Scholar]
- Friedrich J., Zhou P., Paninski L. Fast online deconvolution of calcium imaging data. PLoS Comput. Biol. 2017;13:e1005423. doi: 10.1371/journal.pcbi.1005423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerfen C.R., Engber T.M., Mahan L.C., Susel Z., Chase T.N., Monsma F.J., Jr., Sibley D.R. D1 and D2 dopamine receptor-regulated gene expression of striatonigral and striatopallidal neurons. Science. 1990;250:1429–1432. doi: 10.1126/science.2147780. [DOI] [PubMed] [Google Scholar]
- Grienberger C., Konnerth A. Imaging calcium in neurons. Neuron. 2012;73:862–885. doi: 10.1016/j.neuron.2012.02.011. [DOI] [PubMed] [Google Scholar]
- Hintiryan H., Foster N.N., Bowman I., Bay M., Song M.Y., Gou L., Yamashita S., Bienkowski M.S., Zingg B., Zhu M. The mouse cortico-striatal projectome. Nat. Neurosci. 2016;19:1100–1114. doi: 10.1038/nn.4332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunnicutt B.J., Jongbloets B.C., Birdsong W.T., Gertz K.J., Zhong H., Mao T. A comprehensive excitatory input map of the striatum reveals novel functional organization. eLife. 2016;5:e19103. doi: 10.7554/eLife.19103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isomura Y., Takekawa T., Harukuni R., Handa T., Aizawa H., Takada M., Fukai T. Reward-modulated motor information in identified striatum neurons. J. Neurosci. 2013;33:10209–10220. doi: 10.1523/JNEUROSCI.0381-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X., Tecuapetla F., Costa R.M. Basal ganglia subcircuits distinctively encode the parsing and concatenation of action sequences. Nat. Neurosci. 2014;17:423–430. doi: 10.1038/nn.3632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi Y., Wilson C.J., Emson P.C. Projection subtypes of rat neostriatal matrix cells revealed by intracellular injection of biocytin. J. Neurosci. 1990;10:3421–3438. doi: 10.1523/JNEUROSCI.10-10-03421.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerlin A.M., Andermann M.L., Berezovskii V.K., Reid R.C. Broadly tuned response properties of diverse inhibitory neuron subtypes in mouse visual cortex. Neuron. 2010;67:858–871. doi: 10.1016/j.neuron.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaus A., Plenz D. A low-correlation resting state of the striatum during cortical avalanches and its role in movement suppression. PLoS Biol. 2016;14:e1002582. doi: 10.1371/journal.pbio.1002582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kravitz A.V., Freeze B.S., Parker P.R.L., Kay K., Thwin M.T., Deisseroth K., Kreitzer A.C. Regulation of parkinsonian motor behaviours by optogenetic control of basal ganglia circuitry. Nature. 2010;466:622–626. doi: 10.1038/nature09159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parent A., Bouchard C., Smith Y. The striatopallidal and striatonigral projections: two distinct fiber systems in primate. Brain Res. 1984;303:385–390. doi: 10.1016/0006-8993(84)91224-1. [DOI] [PubMed] [Google Scholar]
- Pinto L., Dan Y. Cell-type-specific activity in prefrontal cortex during goal-directed behavior. Neuron. 2015;87:437–450. doi: 10.1016/j.neuron.2015.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Planert H., Szydlowski S.N., Hjorth J.J.J., Grillner S., Silberberg G. Dynamics of synaptic transmission between fast-spiking interneurons and striatal projection neurons of the direct and indirect pathways. J. Neurosci. 2010;30:3499–3507. doi: 10.1523/JNEUROSCI.5139-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pnevmatikakis E.A., Soudry D., Gao Y., Machado T.A., Merel J., Pfau D., Reardon T., Mu Y., Lacefield C., Yang W. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron. 2016;89:285–299. doi: 10.1016/j.neuron.2015.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prevedel R., Verhoef A.J., Pernía-Andrade A.J., Weisenburger S., Huang B.S., Nöbauer T., Fernández A., Delcour J.E., Golshani P., Baltuska A., Vaziri A. Fast volumetric calcium imaging across multiple cortical layers using sculpted light. Nat. Methods. 2016;13:1021–1028. doi: 10.1038/nmeth.4040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resendez S.L., Stuber G.D. In vivo calcium imaging to illuminate neurocircuit activity dynamics underlying naturalistic behavior. Neuropsychopharmacology. 2015;40:238–239. doi: 10.1038/npp.2014.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum R., Smith M.A., Kohn A., Rubin J.E., Doiron B. The spatial structure of correlated neuronal variability. Nat. Neurosci. 2017;20:107–114. doi: 10.1038/nn.4433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubner Y., Tomasi C., Guibas L.J. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vis. 2000;40:99–121. [Google Scholar]
- Sakata S., Harris K.D. Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron. 2009;64:404–418. doi: 10.1016/j.neuron.2009.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tecuapetla F., Matias S., Dugue G.P., Mainen Z.F., Costa R.M. Balanced activity in basal ganglia projection pathways is critical for contraversive movements. Nat. Commun. 2014;5:4315. doi: 10.1038/ncomms5315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tecuapetla F., Jin X., Lima S.Q., Costa R.M. Complementary contributions of striatal projection pathways to action initiation and execution. Cell. 2016;166:703–715. doi: 10.1016/j.cell.2016.06.032. [DOI] [PubMed] [Google Scholar]
- Tepper J.M., Koós T., Wilson C.J. GABAergic microcircuits in the neostriatum. Trends Neurosci. 2004;27:662–669. doi: 10.1016/j.tins.2004.08.007. [DOI] [PubMed] [Google Scholar]
- van der Maaten L., Hinton G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008;9:2579–2605. [Google Scholar]
- Walther A., Nili H., Ejaz N., Alink A., Kriegeskorte N., Diedrichsen J. Reliability of dissimilarity measures for multi-voxel pattern analysis. Neuroimage. 2016;137:188–200. doi: 10.1016/j.neuroimage.2015.12.012. [DOI] [PubMed] [Google Scholar]
- Wiltschko A.B., Johnson M.J., Iurilli G., Peterson R.E., Katon J.M., Pashkovski S.L., Abraira V.E., Adams R.P., Datta S.R. Mapping sub-second structure in mouse behavior. Neuron. 2015;88:1121–1135. doi: 10.1016/j.neuron.2015.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yttri E.A., Dudman J.T. Opponent and bidirectional control of movement velocity in the basal ganglia. Nature. 2016;533:402–406. doi: 10.1038/nature17639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D., Lu G. Evaluation of similarity measurement for image retrieval. IEEE Oper. Cent. 2003;II:928–931. [Google Scholar]
- Zhou, P., Resendez, S.L., Rodriguez-Romaguera, J., Jimenez, J.C., Neufeld, S.Q., Stuber, G.D., Hen, R., Kheirbek, M.A., Sabatini, B.L., Kass, R.E., et al. (2017). Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data. arXiv, arXiv:1605.07266v2, https://arxiv.org/abs/1605.07266. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Statistical data presented per animal or comparison for each figure.
Top left: Raw fluorescence after motion correction imaged in direct-pathway SPNs (D1-Cre). ∼1 min of a single session is shown. Top right: Corresponding background estimated using CNMF-E. Bottom left: Background-subtracted raw fluorescence. Bottom right: Somatic fluorescence estimated using the spatial footprints and denoised temporal components for all 243 neurons during that session.
5 out of 14 clusters for a single session (D1-Cre) are shown (see also Figures 3C and 3D). These clusters largely correspond to left turning, right turning, forward movement, rearing, and resting (from left to right). Top row: for each cluster, the first 300 ms of all behavioral segments were merged into a single movie (Wiltschko et al., 2015). Bottom row: detailed view of the same movements as above aligned to the body center of mass and body orientation. For better visualization, pixel intensities were logarithmically scaled for the aligned sequences.