A spatially resolved estimate of High Mountain Asia glacier mass balances, 2000-2016

Abstract

High Mountain Asia hosts the largest glacier concentration outside the polar regions. These glaciers are important contributors to streamflow in one of the most populated areas of the world. Past studies have used methods that can only provide regionally-averaged glacier mass balances to assess the High Mountain Asia glacier contribution to rivers and sea level rise. Here we compute the mass balance for about 92 % of the glacierized area of High Mountain Asia using time series of digital elevation models derived from satellite stereo-imagery. We calculate an average region-wide mass balance of -16.3 ± 3.5 Gt yr^-1 (-0.18 ± 0.04 m w.e. yr^-1) between 2000 and 2016, which is less negative than most previous estimates. Region-wide mass balances vary from -4.0 ± 1.5 Gt yr^-1 (-0.62 ± 0.23 m w.e. yr^-1) in Nyainqentanglha to +1.4 ± 0.8 Gt yr^-1 (+0.14 ± 0.08 m w.e. yr^-1) in Kunlun, with large intra-regional variability of individual glacier mass balances (standard deviation within a region ˜0.20 m w.e. yr^-1). Specifically, our results shed light on the Nyainqentanglha and Pamir glacier mass changes, for which contradictory estimates exist in the literature. They provide crucial information for the calibration of the models used for projections of future glacier response to climatic changes, models that presently do not capture the pattern, magnitude and intra-regional variability of glacier changes in High Mountain Asia.

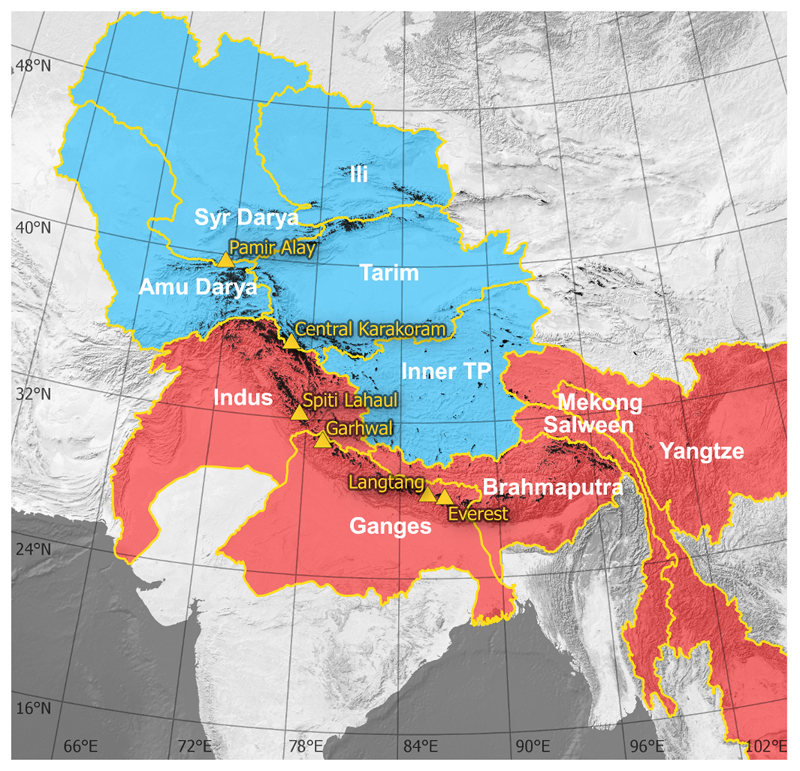
The recent global estimates of glacier contribution to sea level rise (SLR) stressed the need to better constrain High Mountain Asia (HMA) glacier mass change^1,2. Two main strategies have been used to estimate the glacier mass loss for the ca. 100,000 km² of glaciers covering the Tibetan Plateau (TP) and its surrounding mountain ranges including Himalaya, Karakoram, Pamir, and Tien Shan (Figure 1).

Figure 1. High Mountain Asia major drainage basins.

The endorheic basins are in blue and the exorheic basins in red. The yellow triangles show the validation sites (named after the region or a summit) where we evaluated the glacier mass balance obtained with the ASTER method (see Supplementary Information and Fig. S4-7). The glaciers from the GAMDAM glacier inventory²⁸ are shown in black.

(i) The first strategy consists in compiling all local observations of glacier mass changes, either from field measurements (glaciological method) or from local remote sensing analysis (geodetic method using digital elevation model (DEM) differencing), and extrapolating them to the rest of the mountain ranges. In HMA, this strategy suffers from the scarcity of local measurements in space and time³ and the consequent need to extrapolate to vast unsampled areas. This is problematic, given that the pattern of glacier mass change in HMA is now known to be strongly heterogeneous⁴. For example, only two discontinuous in-situ mass balance measurements (Muztagh Ata and Abramov glaciers) are available for subsets of the 2000-2015 period in the western part of HMA, hosting more than 40,000 km² of glaciers (GMBAL database, ref. 5). Geodetic DEM differencing provided mass balance estimates for areas smaller than a few thousand square kilometers only^6–13 and for varying periods. Earlier studies have demonstrated that these sub-regional measurements are not representative of the larger region². This is all-the-more problematic as such local measurements are needed to calibrate future projections of glacier evolution^14,15.

(ii) The second strategy consists in using large-scale satellite measurements, such as variations in the earth gravity field (GRACE mission¹) or laser altimetry (ICESat¹⁶). The difficulty of applying GRACE data at the scale of HMA is mainly due to the strong influence of terrestrial water storage on the GRACE signals – not least in the large endorheic basins (Figure 1), but also of underground water depletion, for instance from India, or monsoon intensity change^1,17–19. The ICESat laser altimeter, on the other hand, operated only from 2003 to 2009, and had a sparse spatial sampling leading to potential large bias²⁰.

In this study, we bridge the gap between these two strategies and compute the mass balance of 92 % of the glacierized area in HMA. Our results have high spatial resolution and extend the temporal coverage of previous studies. This provides new insights about the mass balance of controversial regions such as Pamir or Nyainqentanglha where previous studies disagree. Our study stresses the inability of existing region-wide glacier mass balance models to capture the pattern of glacier mass changes and provides highly resolved data useful to tune or validate these models. Another advantage is that our new spatially-detailed estimates can be directly evaluated or compared to numerous published local geodetic studies, which is not feasible with GRACE and ICESat estimates. This systematic evaluation increases the confidence in our revised estimates.

Glacier surface elevation changes

We apply a fully automated method to compute DEMs from the vast amount of freely available ASTER optical satellite stereo pairs. We use these DEMs to assess glacier volume changes over the entire HMA for the period 2000-2016. We fit a linear regression through time series of co-registered ASTER DEMs to estimate the rate of elevation change for each 30-m pixel (ref. ²¹ and Methods section). Inspired from previous studies^22–24, this methodology was further developed and validated on the Mont-Blanc area in the European Alps²¹. Contrary to earlier studies, we did not rely on DEMs available online (the so-called 14DMO product) but directly calculated more than 50,000 DEMs from L1A ASTER images using the Ames Stereo Pipeline²⁵. One strength of this method is that it relies exclusively on satellite optical data. Thus, it is not affected by signal penetration, which is a major source of uncertainty in DEMs derived from radar sensors (e.g., from Shuttle Radar Topography Mission; SRTM), for which the signal penetrates to a mostly unknown depth of up to many meters into snow and ice^16,21,26.

We integrate these elevation changes and use a mass to volume conversion factor of 850 ± 60 kg m^-3 (ref. ²⁷ and Supplementary Information). Our glacier mask for DEM co-registration and for integrating the glacier elevation change is derived from the GAMDAM inventory²⁸, as this is the only homogenous inventory covering the entire HMA. As a sensitivity test, we compare our GAMDAM-based estimates with those obtained using the ICIMOD inventory²⁹, the ESA CCI inventory³⁰ and the Randolph Glacier Inventory³¹ (Supplementary Information).

Over our study region, the method is evaluated using published estimates for individual glaciers or groups of several glaciers. Our volume change estimates are compared with Chhota Shigri glaciological mass balance during 2002-2014 (ref. ³²; the only series available in HMA validated against geodetic mass balance and covering almost the same time frame as our study) and independent geodetic estimates over 6 selected areas (Supplementary Information and Figures 1, S4, S5). For 60 individual glaciers larger than 2 km², we obtain a mean difference between the published values and our estimates of -0.07 m w.e. yr^-1 and a standard deviation of the residual of 0.17 m w.e. yr^-1.

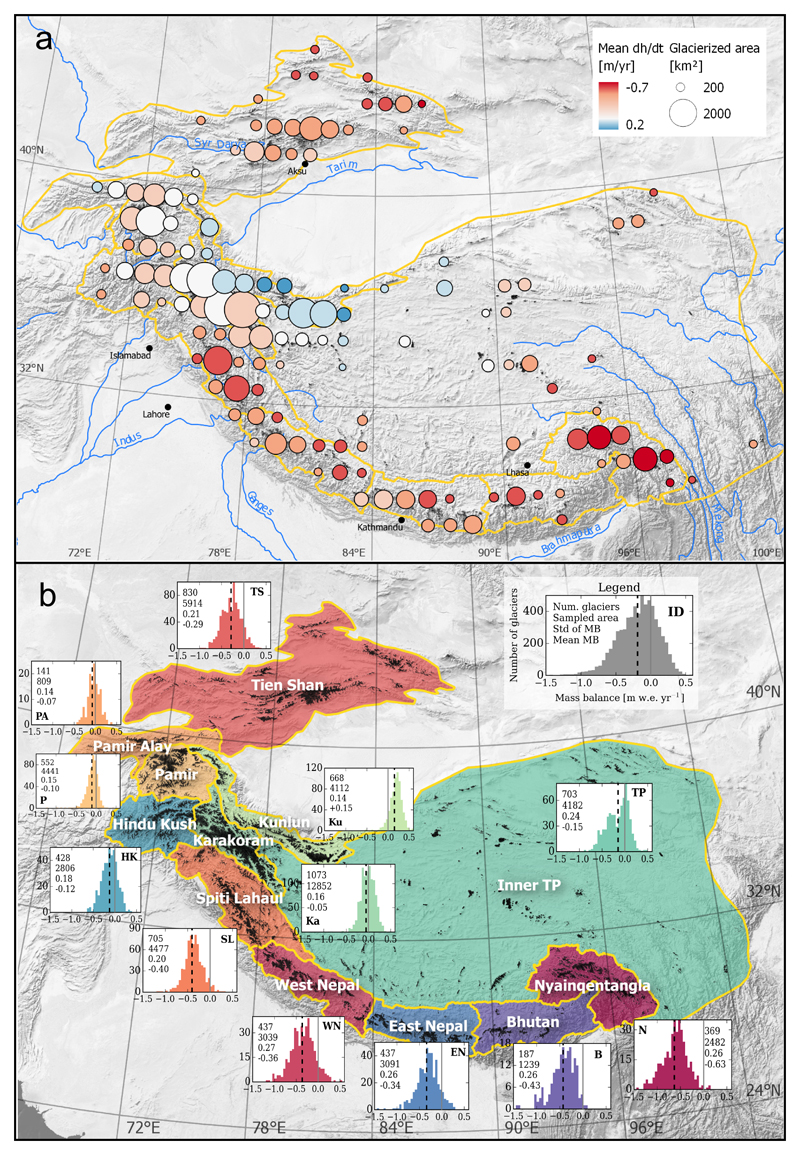
For visualization, we provide mass changes averaged over a 1×1 degree grid (Figure 2a) and aggregated them over the regions of ref. 4 for the sake of comparison (Figure 2b). Our total HMA glacier mass change is -16.3 ± 3.5 Gt yr^-1 (-0.18 ± 0.04 m w.e. yr^-1) between March 2000 and November 2016. This mass change is calculated on more than 92 % of the glacierized area of HMA (total area of 91,990 km² in the GAMDAM inventory²⁸). The remaining 8% correspond to the 1×1 degree tiles with less than 150 km² glacier area each. The latter were not processed and their glacier change signal was substituted by the regional averages. Our results confirm that the mass balance anomaly, first observed over the Karakoram and named the “Karakoram anomaly” (ref. ³³), is in fact also extending to the Kunlun and West Pamir regions (Figure 2). The most positive mass change of 0.26 ± 0.07 m w.e. yr^-1 is observed in the Kunlun (hypsometric average of the tile spanning between 35°N, 36°N, 82°E and 83°E). The glacier mass balance anomaly appears thus to be centered over Western Kunlun. According to our results, Pamir and Karakoram are both regions of transition from positive to negative mass balance⁴. The most negative changes are found for the eastern HMA in Nyainqentanglha with -0.62 ± 0.23 m w.e. yr^-1 (even as negative as -0.80 ± 0.25 m w.e. yr^-1 in for the hypsometric average of the tile spanning between 29°N, 30°N, 97°E and 98°E). The mass balance pattern is homogeneous in Tien Shan, with mass losses averaging at -0.28 ± 0.20 m w.e. yr^-1 for the entire region. Moderate mass losses are observed along the Himalayan range with values ranging from -0.42 ± 0.20 m w.e. yr^-1 in Bhutan to -0.33 ± 0.20 m w.e. yr^-1 in the East Nepal region.

Figure 2. Glacier elevation changes and mass balance for High Mountain Asia (2000-2016).

a- map of glacier mean elevation change on a 1°×1° grid. b- For each region in ref. 4, the distribution of glacier-wide mass balance for every individual glacier (> 2 km²) is represented in histograms of the number of glaciers (y-axis) as a function of MB (x-axis in m w.e. yr^-1). The black dashed line represents the area-weighted mean. The numbers denote the total number of individual glaciers (first), the corresponding total area (in km², second), the standard deviation of their mass balances (in m w.e. yr^-1, third) and the area weighted average mass balance (in m w.e. yr^-1, fourth). Initials of the respective regions are repeated in bold in the graphs.

Altitudinal distribution of thickness changes

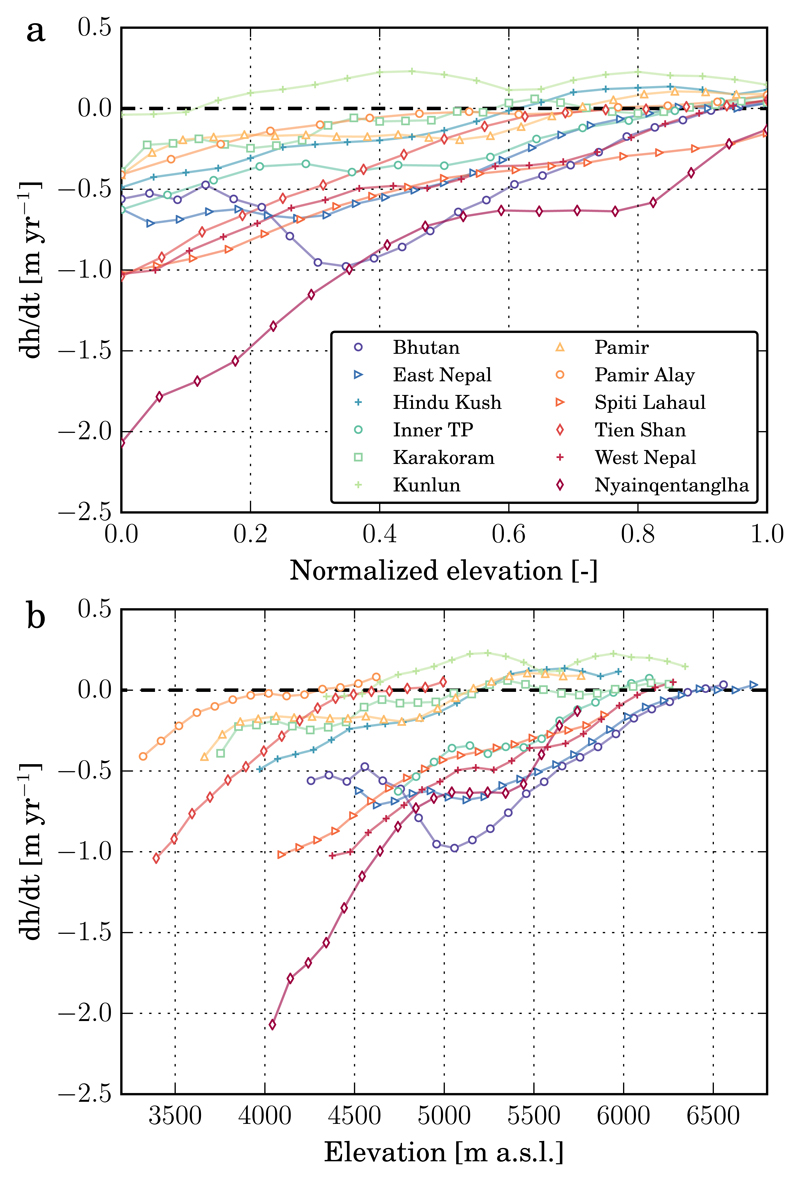
In addition to these regional averages, we compute the altitudinal distribution of surface elevation change within each region (Figure 3 and Figure S3). These curves highlight the potential of our method to understand the elevation behavior of glaciers over large regions, even in elevation zones that are otherwise hardly measured using optical satellite stereo due to the lack of image contrast on snow. Overall, we observe decreasing thinning rates with elevation, which is a commonly observed pattern^7,11. Exceptions are the glaciers in Bhutan, which exhibit a reduced thinning at their terminus, potentially due to the thick debriscover, and those in Kunlun, which show a rather constant thickening rate for all elevations. In Nyainqentanglha and Spiti Lahaul, significant thinning rates are observed even at high elevations. This finding stresses the importance of taking into account the changes occurring in the accumulation area of glaciers when computing geodetic mass balance estimates from optical stereo methods. The altitudinal distribution of elevation changes is the result of the combined effects of glacier dynamics and surface mass balance³⁴. In Nyainqentanglha and Spiti Lahaul, two regions with highly negative mass balances (Figure 2) and where field observations are also available³⁵, the thinning observed even at highest elevations reveals that the glaciers are losing large parts of their accumulation areas, with equilibrium line altitudes approaching the uppermost glacier elevations. A similar behavior is observed for Alpine glaciers²⁶, which are also in an advanced state of decline. In contrast, the thickening of high elevations in Kunlun could be a direct mass-balance signal, combined with a dynamic signal due to a delay of the glaciers to reach their balance velocities. The altitudinal dependency of thickness change is thus a valuable validation for glaciological models⁵.

Figure 3. Altitudinal distribution of glacier elevation change.

a- Rate of elevation change for the period 2000-2016 as a function of normalized elevation, which is defined as (z - z_2.5)/(z_97.5-z_2.5), where z is the elevation and z_2.5 and z_97.5 are the elevation of the 2.5 and 97.5 percentile of area, respectively. b- Rate of elevation change for the period 2000-2016 as a function of elevation (in m a.s.l.).

Spatial variability of individual glacier mass balances

To calculate the mass balance of individual glaciers, we restricted our analysis to the 6350 glaciers larger than 2 km² and with more than 70 % of valid data (i.e. pixel values within a conservative range of possible elevation changes, see method section). They represent 49,450 km² (about 54 % of the glacierized area of HMA). The glacier-wide mass balances for the period 2000-2016 are variable from glacier to glacier for regions with negative mass balance (Figure 2b), with a standard deviation of ˜0.25 m w.e. yr^-1. In contrast, balanced regions have a low variability of ˜0.15 m w.e. yr^-1. The very large Inner TP region is an aggregation of climatically heterogeneous sub-regions, which results in a bi-modal distribution of glacier mass balance, and a high dispersion. This is also the case to a lower extent for West Nepal and Tien Shan. Maybe counterintuitively, regions with a large number of surge-type glaciers such as Pamir, Pamir Alay and Karakoram³⁶ show a lower variability of ˜0.15 m w.e. yr^-1, perhaps related to the fact that these surge-clusters are mostly in regions with stable or slightly increasing glacier mass. The differences between regions in terms of individual glacier-wide mass balance variability should be taken into account when performing regional calibration of mass balance models¹⁴.

The intra-regional variability is well illustrated for three neighboring sub-regions (Everest, Langtang and Kanchenjunga) defined in Figure S8. Their sub-region-wide glacier mass balances are very similar (ranging from -0.35 to -0.42 m w.e. yr^-1), with strong similarities of their altitudinal pattern of elevation change (Figure S9d). By contrast, mass balances of individual glaciers larger than 2 km² differ considerably from these averages (Figure S9e), with standard deviations of 0.21, 0.23 and 0.28 m w.e. yr^-1 respectively for Everest, Kanchenjunga and Langtang. Our remote sensing analysis is in line with field measurements that showed also a strong mass balance variability for glaciers smaller than 2 km² in the Everest region³⁷. The most negative glacier-wide mass balance for each region (around -2 m w.e. yr^-1, -1.5 m w.e. yr^-1 and -1 m w.e. yr^-1 for Langtang, Everest and Kanchenjunga, respectively) correspond to glaciers terminating in proglacial lakes³⁸. Our new mass balance dataset can thus be used to assess the representativeness of single-glacier measurements and to complement them.

Comparison with other regional mass balance estimates

From previous studies, it is well established that the contrasted climatic setting of HMA³⁹ leads to a heterogeneous response of glaciers^2,7,16. The spatial pattern of glacier thickening and thinning from the present study over the period 2000-2016 is consistent with the pattern during 2003-2008 (ref. ⁴), underlying its temporal persistence. For seven regions out of twelve (Tien Shan, Karakoram, Kunlun, Spiti Lahaul, East Nepal, West Nepal and Inner TP), there is a good agreement between our glacier mass change and published values (Table S4).

The remaining five regions (each covering 1,900 to 7,000 km² of glaciers) are controversial (i.e. Pamir Alay, Pamir, Hindu Kush, Bhutan and Nyainqentanglha), as contradictory estimates of glacier mass changes have been published for the first decade of the 21^st century (Table S4). In particular, the Pamir region was reported to have a significantly negative rate of elevation change in ref. 4 (-0.48 ± 0.14 m yr^-1 for 2003-2008, in the following section, elevation change results are given in m yr^-1 to avoid uncertainty due to the volume to mass conversion), whereas it was less negative in ref. 2 (-0.13 ± 0.22 m yr^-1 for 2003-2008) and even positive in ref. 7 (+0.16 ± 0.15 m yr^-1 for 1999-2011). Similarly, the Nyainqentanglha region was reported to have a very negative rate of elevation change in ref. 4 (-1.34 ± 0.29 m yr^-1 for 2003-2008), whereas it was less negative in ref. 2 (between -0.30 and -0.40 m yr^-1 for 2003-2008) and in ref. 7 (-0.39 ± 0.16 m yr^-1 for 1999-2010). For these two regions, we find respectively -0.05 ± 0.08 m yr^-1 (Pamir) and -0.72 ± 0.27 m yr^-1 (Nyainqentanglha) between 2000 and 2016. We verify that the sparse sampling of ICESat is not the reason for these differences (Table 1, Supplementary Information and Table S1). Further, there is no consistent shift in ASTER mass balances between the sub-periods 2000-2008 and 2008-2016 that could explain the disagreement (Supplementary Information and Table S2). In contrast, we find that the inter-annual variability of the observed surface elevation is much higher for these five controversial regions than the others (Figure S10). Consequently, for such regions of large inter-annual variability, removing one year of acquisition from the trend fitting might impact the resulting ICESat-derived trend more than for other regions with low inter-annual variability (Figure S11c). This likely explains the contradictory results in the literature and stresses the need for caution when extrapolating in time ICESat trends of elevation change or other short-term glacier elevation of mass balance changes.

Table 1. region-wide mass balance from ASTER time series compared to ICESat estimates.

The glacierized areas are calculated from the GAMDAM glacier inventory²⁸. For the column “ASTER MB [2000 – 2016] with ICESat sampling” ASTER-derived trends have been sampled at ICESat footprint locations (Supplementary Information), these numbers should be considered as indicative and are not provided with an uncertainty. ICESat data are taken from ref. 4 except for Kunlun, Inner TP, Tien Shan and Pamir Alay, which were extended for this study using the same method.

Region	Glacier area	ASTER MB [2000 – 2016]	ASTER MB [2000 – 2016] with ICESat spatial sampling	ICESat MB [2003 – 2008]
	km2	m w.e. yr-1	m w.e. yr-1	m w.e. yr-1
Bhutan	2,291	-0.42 ± 0.20	-0.30	-0.76 ± 0.20
East Nepal	4,776	-0.33 ± 0.20	-0.33	-0.31 ± 0.14
Hindu Kush	5,147	-0.12 ± 0.07	-0.14	-0.42 ± 0.18
Inner TP	13,102	-0.14 ± 0.07	-0.12	-0.06 ± 0.06
Karakoram	17,734	-0.03 ± 0.07	-0.06	-0.09 ± 0.12
Kunlun	9,912	0.14 ± 0.08	0.17	0.18 ± 0.14
Nyainqentanglha	6,378	-0.62 ± 0.23	-0.51	-1.14 ± 0.58
Pamir Alay	1,915	-0.04 ± 0.07	+0.00	-0.59 ± 0.27
Pamir	7,167	-0.08 ± 0.07	-0.05	-0.41 ± 0.24
Spiti-Lahaul	7,960	-0.37 ± 0.09	-0.33	-0.42 ± 0.26
Tien Shan	10,802	-0.28 ± 0.20	-0.20	-0.37 ± 0.31
West Nepal	4,806	-0.34 ± 0.09	-0.27	-0.37 ± 0.15
Total	91,990	-0.18 ± 0.04	-0.15	-0.34 ± 0.06

The total difference between the HMA mass change estimate derived from ASTER and ICESat is 11.2 Gt yr^-1, in which 9.0 Gt yr^-1 originates from the controversial regions (Figure S10a, b and Table 1).

To complete the comparison with other mass balance estimates, we compare our results with ref. 2, based on Randolph Glacier Inventory³¹ glacier mask and regions (Table S6).

HMA glacier contribution to SLR and hydrology

We provide spatially resolved estimates for the potential contribution of HMA glaciers to SLR and changes in the downstream hydrology (Table 2), aggregated by major river basins. We find a total sea level contribution of 16.3 ± 3.5 Gt yr^-1 (14.6 ± 3.1 Gt yr^-1 when including only the exorheic basins), corresponding to 0.046 ± 0.009 mm yr^-1 SLE (0.041 ± 0.009 mm yr^-1 SLE when including only the exorheic basins). This estimate is in marked disagreement with the total estimate of 46 ± 15 Gt yr^-1 from ref. 5 and 40 commonly used in the sea level budget studies⁴¹. The model contribution estimates of ref. 5 and 40 for the period 2000-2013 are nearly four times larger than our estimate for Central Asia (22 Gt yr^-1 for the model versus 6 Gt yr^-1 for this study) and over twice as large for South Asia East and South Asia West (14 Gt yr^-1 for the model vs. 6 Gt yr^-1 for this study and 9 Gt yr^-1 for the model vs 4 Gt yr^-1 for this study for the two regions respectively; Randolph Glacier Inventory regions³¹ Table S5). These discrepancies can be explained by the lack of direct measurements to constrain both the interpolation method of ref. 5 and the model tuning and/or the high temporal smoothness of atmospheric models of ref. 40. In particular, these estimates attribute mass losses to Karakoram and Kunlun, two regions with a large glacierized area where we find only little mass loss or even mass gain (Figure S12).

Table 2. mass balance of the main river basins originating in HMA for 2000-2016.

Following ref. 42 and 43 the excess discharge is 0 for glaciers with balanced or positive mass budget (which is the case only for the Tarim basin). We added an extra significant digit for the Mekong basin, because the values were too small to be adequately represented otherwise. Excluding endorheic basins, the total contribution is -14.6 ± 3.1 Gt yr^-1 or 0.041 ± 0.009 mm yr^-1 SLE. The endorheic basins are noted with an asterisk.

Basin name	Glacierized area [km2]	Mass budget [Gt yr-1]	Annual excess discharge [m3 s-1]
Amu Darya*	10,784	-1.0 ± 0.8	-31 ± 24
Brahmaputra	9,513	-5.1 ± 2.1	-163 ± 66
Ganges	8,314	-2.7 ± 0.7	-84 ± 24
Ily*	4,316	-1.6 ± 0.9	-49 ± 27
Indus	24,698	-4.0 ± 2.0	-125 ± 63
Inner TP*	7,285	-0.4 ± 0.5	-12 ± 16
Mekong	221	-0.09 ± 0.04	-3 ± 2
Salween	1,195	-0.8 ± 0.3	-24 ± 9
Syr Darya*	2,336	-0.3 ± 0.2	-10 ± 5
Tarim*	18,409	0.4 ± 1.3	0 ± 41
Yangtze	1,422	-0.5 ± 0.3	-14 ± 9

The importance of glacier runoff to total river discharge refers to multiple concepts and definitions, especially when looking at seasonality of glacier runoff⁴². As we provide averages of annual mass balance, we can only calculate the annual “excess discharge”, which constitutes the additional water due to a reduction in the water stored by glaciers^42,43. According to this definition, glacierized catchments with a positive or balanced glacier mass balance have an excess discharge of zero (this is the case for Tarim basin only, Table 2). The largest contributions originate from Indus and Brahmaputra basins, each accounting for roughly a third of HMA’s total excess discharge. The Indus basin contributes largely because of its large glacierized area and Brahmaputra mostly because of the strongly negative mass balance (Table 2).

In this study we provide new and spatially resolved estimates of glacier mass change over the entire HMA for the period 2000-2016 and, additionally, for individual glaciers larger than 2 km², which represent ˜54 % of the glacierized area. On a regional basis, these estimates are in line with ICESat laser altimetry studies, indicating that the contrasted pattern of glacier mass change has been persistent during nearly two decades, except for five regions where the inter-annual variability in glacier mass balance is high. For the latter regions, the 5-year ICESat trends are strongly influenced by individual years (especially 2003 and 2008) due to the short sampling interval. Our new estimate of HMA glacier contribution to SLR for 2000-2016 (0.041 ± 0.009 mm yr^-1 SLE, when excluding endorheic basins) is slightly smaller than the values of ref. 4 (0.06 ± 0.01 mm yr^-1 SLE) and ref. 2 (0.07 ± 0.03 mm yr^-1 SLE), but much smaller than the model-based estimate of ref. 5 and 40 (0.13 ± 0.05 mm yr^-1 SLE), although the latter are widely used in the literature^41,44. Nevertheless, the increasing number of mass balance observations that are available to calibrate mass balance models will lead to an improvement of these models and will thus help to reconcile observed and modelled estimates.

Methods

Generation and adjustment of ASTER DEMs

ASTER DEMs were derived from AST_L1A data (freely available to download at http://reverb.echo.nasa.gov) using the open-source Ames Stereo Pipeline (ASP)²⁵. The correlation kernel size was set to 7 pixels and we used the void filled version of SRTM (SRTMGL1 V003) as a seed for the generation of the ASTER DEMs. No ground control point was used. The DEMs were corrected for planimetric and altimetric shifts⁴⁵ using SRTM as a reference. Then the across track, along track and curvature bias were corrected by fitting fifth order polynomials to the elevation difference on stable ground²¹, after excluding glaciers and water bodies. For that purpose, we used the GAMDAM glacier inventory²⁸ together with water bodies from the Global Lakes and Wetlands Database⁴⁶.

Extracting the rate of elevation change

For each 30-m DEM pixel, we first excluded all the elevation values from the time series that have an absolute difference larger than 150 m from the non-void filled SRTM or from the temporal median of all ASTER elevation values. As a first guess, we fitted a linear trend to the time series of SRTM and ASTER elevation values and subsequently excluded the data points that lay outside the 99 % confidence interval of this initial linear regression. We then fitted a final linear trend to ASTER elevation time series only. Further details are available in ref. 21. An example of the distribution of the rate of elevation change on stable terrain as a function of elevation, curvature, slope and aspect is shown on Figure S13.

From elevation changes to glacier mass-balance

We averaged the 30-m gridded elevation change rates on four distinctive spatial units: (i) individual glaciers, (ii) 1°×1° tiles, (iii) geographic regions and (iv) main river basins. For a given spatial unit, the elevation change rate on glaciers was calculated for each 100 m elevation band as the mean of all pixels belonging to this band. This means that for 1°×1° tiles, geographic regions and main river basins (ii-iv), the glacierized area was considered as one virtual contiguous ice body. For each elevation band, the pixels were filtered to the level of three normalized median absolute deviations (NMAD; ref. 47) with respect to the median of the elevation band. Pixels exceeding this threshold were considered not valid (Table S3, Figure S2). The total rate of volume change was calculated as the sum of the mean rate of elevation change multiplied by the area for each elevation band. If no data were available for an elevation band (e.g. for the uppermost reaches), a zero elevation change rate was assigned. This never happened when calculating the region-wide averages, but could happen for individual glacier mass balances. The rate of volume change was converted to rate of mass change assuming a volume to mass conversion factor of 850 ± 60 kg m^-3 (ref. ²⁷).

Uncertainty assessment

The total uncertainty of a given mass balance estimate (σ_ΔM,tot) can be calculated as the quadratic sum of a random (σ_ΔM,rdn) and a systematic (σ_ΔM,sys) error⁴⁵:

$${\sigma }_{\Delta M,tot}=\sqrt{{\sigma }_{\Delta M,rd{n}^2}+{\sigma }_{\Delta M,sy{s}^2}}$$

Uncertainty assessment – random error

The random error on mass balance has three main sources, which are assumed to be independent: the uncertainty on the rate of elevation change (σ_Δz), the uncertainty on glacierized area (σ_A) and the uncertainty on volume to mass conversion (σ_fΔV). The uncertainty on the rate of elevation change follows ref. 26 and 48:

$${\sigma }_{\Delta z}=\{\begin{array}{c}{\sigma }_{\Delta h}\sqrt{\frac{A_{cor}}{5A}},A<A_{cor}\\ {\sigma }_{\Delta h,}A\ge A_{cor}\end{array}$$

where σ_Δh is the standard deviation of the rate of elevation change on stable ground, A is the glacier area and A_cor = πL², with L being the decorrelation length, taken here as 500 m.

Assuming independence between the uncertainty on area and the uncertainty on the rate of elevation change, the total uncertainty on the rate of volume change (σ_ΔV) is:

$${\sigma }_{\Delta V}=\sqrt{{\left({\sigma }_{\Delta z}\left(p+5\left(1-p\right)\right)A\right)}^2+{\left({\sigma }_A\Delta z\right)}^2}$$

where ΔZ is the mean rate of elevation change for the glacierized area and ${\sigma }_A=\frac{10}{100}A$ (ref. ¹⁶) and p is the proportion of surveyed area. In the equation above, we conservatively assume a factor of 5 in the elevation change uncertainty in non-surveyed areas⁴⁹.

Assuming independence between the uncertainty on the rate of volume change and the volume to mass conversion factor, the random uncertainty on geodetic mass balance is:

$${\sigma }_{\Delta M,rdn}=\sqrt{{\left({\sigma }_{\Delta V}{f}_{\Delta V}\right)}^2+{\left({\sigma }_{f_{\Delta V}}\Delta V\right)}^2}$$

where f_ΔV = 850 kg m^-3 is a volume to mass conversion factor²⁷, σ_fΔV = 60 kg m^-3 is the uncertainty on the volume to mass conversion factor²⁷ and ΔV is the volume change.

Uncertainty assessment – systematic error

The systematic error is almost never evaluated in the literature⁴⁵. To assess this error, we studied the absolute value of the triangulation residual, noted r, between two sub periods:

$$r=\left|\Delta M_{2000-2016}-\frac{1}{2}\left(\Delta M_{2000-2008}+\Delta M_{2008-2016}\right)\right|$$

where ΔM_xxxx–yyyy is the annual mass balance (expressed in m w.e. yr^-1) for the period between the year xxxx and yyyy. We found that these residuals depended mostly on the mean number on DEMs used to calculate ΔM_2000–2016. Residuals calculated with less than 8 DEMs were higher than those calculated with more than 8 DEMs. Therefore, we assigned the value of the 67^th percentile of each of these populations to the systematic error. This gives σ_ΔM,sys equal to 0.07 m w.e. yr^-1 for mass balances calculated with more than 8 DEMs and 0.19 m w.e. yr^-1 for mass balances calculated with less than 8 DEMs.

The total uncertainty on HMA glacier mass change was calculated as the quadratic sum of the uncertainties in Gt yr^-1 for each region or basin. This results in a relative uncertainty of 21 %, which was transferred to the area weighted mean obtained in m w.e. yr^-1.