Abstract
Magnetic resonance (MR) nano-theranostic hyperthermia uses magnetic nanoparticles to target and accumulate at the lesions and generate heat to kill lesion cells directly through hyperthermia or indirectly through thermal activation and control releasing of drugs. Preclinical and translational applications of MR nano-theranostic hyperthermia are currently limited by a few major theoretical difficulties and experimental challenges in in vivo conditions. For example, conventional models for estimating the heat generated and the optimal magnetic nanoparticle sizes for hyperthermia do not accurately reproduce reported in vivo experimental results. In this work, a revised cluster-based model was proposed to predict the specific loss power (SLP) by explicitly considering magnetic nanoparticle aggregation in in vivo conditions. By comparing with the reported experimental results of magnetite Fe3O4 and cobalt ferrite CoFe2O4 magnetic nanoparticles, it is shown that the revised cluster-based model provides a more accurate prediction of the experimental values than the conventional models that assume magnetic nanoparticles act as single units. It also provides a clear physical picture: the aggregation of magnetic nanoparticles increases the cluster magnetic anisotropy while reducing both the cluster domain magnetization and the average magnetic moment, which, in turn, shift the predicted SLP toward a smaller magnetic nanoparticle diameter with lower peak values. As a result, the heating efficiency and the SLP values are decreased. The improvement in the prediction accuracy in in vivo conditions is particularly pronounced when the magnetic nanoparticle diameter is in the range of ~10–20 nm. This happens to be an important size range for MR cancer nano-theranostics, as it exhibits the highest efficacy against both primary and metastatic tumors in vivo. Our studies show that a relatively 20%–25% smaller magnetic nanoparticle diameter should be chosen to reach the maximal heating efficiency in comparison with the optimal size predicted by previous models.
Keywords: nano-theranostics, hyperthermia, magnetic resonance, magnetic nanoparticle, specific loss power
Introduction
Theranostics refers to the development of molecular diagnostics and targeted therapeutics in an interdependent, collaborative manner. Nano-theranostics takes advantage of the high capacity of nano-platforms to ferry cargo and load onto them both imaging and therapeutic functions. The resulting nanosystems, capable of diagnosis, drug delivery, and monitoring of therapeutic response, are expected to play a significant role in the dawning era of personalized medicine, and much research effort has been devoted toward that goal. For example, magnetic resonance (MR) nano-theranostics uses magnetic nanoparticles for cancer detection by MR molecular imaging and for cancer therapy by MR nano-medicine.1 Through active (e.g. antibody–antigen) and passive (e.g. enhanced permeability and retention effect) targeting mechanisms, the magnetic nanoparticles can serve as “molecular beacons” to enhance the MR image contrast for early lesion detection. Moreover, through interacting with external alternating magnetic fields produced by the MR hardware, these magnetic nanoparticles accumulated at the lesions can generate heat to serve as “molecular bullets” to kill cancer cells directly through hyperthermia or indirectly through thermal activation and control releasing of drugs.
MR nano-theranostic hyperthermia with magnetic nanoparticles has been an emerging field for the last decade, mainly for its promising applications to cancer treatment.2 In particular, a number of studies have shown that these magnetic fluids, or magnetic nanoparticle suspensions, are able to release heat through various relaxation mechanisms when exposed to a weak alternating magnetic field.3,4 The selective heating can be used to target cancer tissues, as abnormal growth is more susceptible to cell death under elevated temperatures. However, preclinical and translational applications of MR nano-theranostic hyperthermia with magnetic nanoparticles are limited by a few major theoretical difficulties and experimental challenges. For example, conventional theoretical models for MR nano-theranostic hyperthermia assume that the magnetic nanoparticles act independently as single units and are dispersed uniformly in the colloidal suspension, making the interaction among the nanoparticles negligible.5 However, in real biomedical in vivo applications, when magnetic nanoparticles have been injected into blood vessels or bound to cancer cells through the antibody–antigen interaction, individual nanoparticles are highly likely to aggregate and form clusters.6,7
Aggregation changes the physical and magnetic properties of the magnetic nanoparticles in tissues, such as magnetic susceptibility and specific loss power (SLP). Furthermore, aggregate formation and disruption were found to be affected by external magnetic field conditions.8,9 Consequently, a higher magnetic field strength is required to disrupt these aggregates, lowering the heating efficiency of the magnetic nanoparticles in tissues. Therefore, further understanding and formulation of the effect of magnetic nanoparticle aggregation on MR nano-theranostic hyperthermia becomes critical.
To understand and optimize MR nano-theranostic hyperthermia using magnetic nanoparticles, the SLP lays a constructive platform for calculating the heat generation per mass unit of dissipating material. SLP is shown to depend on magnetic nanoparticle properties and external alternating magnetic fields, specifically the mean particle size and size distribution, as well as the amplitude and frequency of the alternating magnetic fluids.10–12 Therefore, reaching a therapeutic temperature for cancer treatment while administering minimal amounts of magnetic nanoparticles, due to limited targeting efficiency, would thus depend greatly on manipulating magnetic-nanoparticle properties and external alternating magnetic fields to control the desired SLP and heat generated. Problematically, conventional models for estimating SLP do not accurately reproduce reported experimental results.13 This limitation may be alleviated by analyzing the magnetic nanoparticle composition and structure under experimental conditions.
The original model proposed by Rosensweig assumes magnetic nanoparticles act independently of one another in suspension.5 Morais et al and Castro et al found magnetic nanoparticles form clusters when in solution.14,15 Ganguly et al reported experimental observation on the micro- and meso-scale field-assisted self-assembly of magnetic nanoparticles due to interparticle electrostatic attraction, electrostatic repulsion, steric repulsion, and magnetic dipolar interactions.16 Interestingly, several groups have determined that magnetic nanoparticle aggregate formation is not sensitive to the solution composition, as magnetic nanoparticles were found to form aggregates in similar magnitudes when suspended in either water or glycerol.17,18 Furthermore, magnetic fluid characteristics and structures differ under varying alternating magnetic field strengths, such that the fraction of agglomerates changes the magnetization and susceptibility of the ferrofluid.19,20
In this work, we proposed a revised cluster-based model to more accurately estimate the SLP by considering magnetic nanoparticle aggregation. Under an alternating magnetic field, magnetic susceptibility is temperature dependent and can be conveniently described by the Langevin function. The fraction of monomeric and clustered magnetic nanoparticles in the ferrofluid can be characterized by a critical temperature, which is defined as the temperature at which magnetic nanoparticle aggregates completely dissociate into individual units.21 To account for dependence on this critical temperature, we proposed a modified Langevin function to redefine the magnetic susceptibility of the ferrofluid and developed an alternative SLP model based on the revised Langevin function. The proposed model, called “revised cluster-based model,” can account for the aggregate formation and the size distribution of the magnetic nanoparticles. Finally, the proposed model was compared with experimental results of magnetite Fe3O4 and cobalt ferrite CoFe2O4 magnetic nanoparticles.22–25 It is shown that the revised cluster-based model provides more accurate estimates of SLP and heating efficiency for MR nano-theranostic hyperthermia in cancer therapy.
Materials and methods
Fraction of monomers and clusters
The disruption of magnetic nanoparticle clusters follows a second-order phase transition at the critical temperature.14 Magnetic nanoparticle monomers and clusters coexist within the colloidal solution when the temperature of the ferrofluid is below the critical temperature. Correspondingly, clusters disrupt completely into monomeric units when the ferrofluid temperature is at or above the critical temperature. Therefore, the fraction of clusters (Pc) in the ferrofluid was chosen as an order parameter to describe this thermal-assisted cluster disruption, according to the Landau second-order phase transition theory, where Pc was expressed in terms of the suspension temperature, T, and the critical temperature, T*.21
| (1A) |
From the expression of Pc, it can be concluded that when the temperature is much lower than the critical temperature, T ≪ T*, monomers and clusters coexist in the ferrofluid system, and there are no clusters when the temperature is at or above the critical temperature. Consequently, the fraction of monomers (Pm) in the ferrofluid can be simply treated to be proportional to the temperature:
| (1B) |
Notice that Pm + Pc = 1 when it is at two limiting conditions: T ≪ T* and T ≅ T*.
Relaxation mechanisms
To calculate the SLP of colloidal magnetic nanoparticles as an interacting system in ferrofluid, we first need to describe two major relaxation mechanisms for magnetic nanoparticles dispersed in a fluid. The first relaxation mechanism is referred to as the Brownian relaxation and was first derived by Deby.26 It assumes the whole nanoparticle rotates toward the external field mechanically against the viscous drag in the suspending medium. Consequently, the change in the magnetization of a ferrofluid is due to the rotation of the magnetic nanoparticles with the internal magnetization remaining fixed with respect to the crystalline lattice. For this reason, it is also known as the “rigid dipole model.” Assuming that the viscosity of the ferrofluid solution, η, is temperature independent and the effect of the magnetic nanoparticle aggregation does not depend on the suspending solution, one can derive the characteristic zero-field Brownian relaxation time constant, τB, to be:
| (2) |
where the magnetic nanoparticle’s hydrodynamic volume Vh = (1 + δ/R)3V, kB is the Boltzmann constant, T is the temperature of the ferrofluid solution (the product kBT is the thermal energy), η is the viscosity of the carrier fluid, V is the volume of the magnetic nanoparticle, R is the radius of the magnetic nanoparticle, and δ is the surfactant thickness (a property of the ferrofluid).
The second relaxation mechanism, known as the Néel relaxation, describes a process where the magnetic nanoparticles do not mechanically rotate, but the magnetization rotates internally with respect to the crystalline lattice.27 Because of the nanoparticle’s magnetic anisotropy, the magnetization has usually two stable orientations antiparallel to each other, separated by an energy barrier. The stable orientations define the magnetic easy axis of the nanoparticle. Because the magnetization rotates away from the easy axis toward the external field in the Néel relaxation process, the mechanism is also known as the “soft dipole model.” The characteristic zero-field Néel relaxation time constant, τN, can be expressed as:
| (3) |
where , KaV is the energy barrier (a product of the magnetic anisotropy constant, Ka, and the volume of the magnetic nanoparticle, V), and τ0 is the attempt time (its reciprocal is called the attempt frequency). Typical values for τ0 are between 10−9 and 10−10 s.
Because both relaxation mechanisms occur simultaneously in the ferrofluid, the effective total relaxation time constant, τ, is given by:
| (4A) |
or, alternatively, by:
| (4B) |
When τB ≪ τN, τ ≈ τB. Similarly, when τB ≫ τN, τ ≈ τN. Hence, the total relaxation effect is dominated by the stronger relaxation mechanism with shorter relaxation time constant.
Since aggregation increases the magnetic anisotropy of clusters,28–30 in our proposed model, the magnetic anisotropy constant, Ka, has different values for monomers and clusters. If we denote the magnet anisotropy constants for monomers and clusters as Kam and Kac, respectively, then:
| (5A) |
| (5B) |
where the represents the increase in the average of the magnetic anisotropy constant due to the formation of clusters, and (1 − Pm) represents the fraction of monomers that comes from the disruption of clusters. It should be noted that when T is close to T*, the value of Kac is slightly higher than that of Kam, and when T ≪ T*, the complicated structure of clusters makes Kac significantly higher than Kam.
Equilibrium magnetization
In this work, we investigated the effect of magnetic nanoparticle aggregation on the magnetization and the magnetic susceptibility of ferrofluid. Considering the linear response of the magnetic susceptibility, one can rewrite the equilibrium magnetization of ferrofluid as a function of the temperature, M0(T), as:21
| (6) |
where and are the fractions of monomers and clusters, respectively, as shown in equation 1; ϕ is the volume fraction of the magnetic nanoparticles; H0 is the strength of the external alternating magnetic field; µ0 is the magnetic permeability in free space; Mdm and Mdc are the domain magnetization of monomers and clusters, respectively; and are the average magnetic moment of monomers and clusters, respectively; and L is the Langevin function with formula . The Langevin x function describes the dependency of the magnetization on the applied magnetic field in the classical limit, with the expression:
| (7A) |
| (7B) |
In equation 6, the first term in the parentheses indicates the contribution from monomers, while the second term in the parentheses indicates the contribution from clusters. Similar to the effect of magnetic nanoparticle aggregation on the magnetic anisotropy constant, the domain magnetization (Mdc) and the average magnetic moment of clusters are also different from those of monomers:
| (8A) |
| (8B) |
where Mdm and are the domain magnetization and the average magnetic moment of monomers, respectively. While aggregation increases the magnetic anisotropy constant for clusters, Kac (equation 5B), it decreases both the domain magnetization (Mdc) and the average magnetic moment for clusters (equations 8A and B), due to the minimization of internal energy.31 Consequently, in this work, the effect of the magnetic nanoparticle aggregation is modeled through a corrected expression for the actual magnetization using a revised Langevin function.
Magnetic susceptibility
In the presence of an alternating magnetic field of the form
| (9A) |
the magnetization, M(t), lags the magnetic field, H(t). Therefore, it is convenient to express the magnetization in terms of the complex magnetic susceptibility, χ = χ ′ − iχ″, resulting in:
| (9B) |
As can be derived from the Shilomis relaxation equations, when an alternating magnetic field is applied to the ferrofluid, the dynamics of the magnetization, M(t), is governed by:
| (10A) |
where the equilibrium magnetization, M0(t), under the alternating magnetic field can be expressed as:
| (10B) |
where χ0(T) is the equilibrium magnetic susceptibility. Substituting equations 9B and 10B into equation 10A yields:
| (10C) |
Comparing the corresponding coefficients, we can obtain the expression for both the real part and the imaginary part of the complex magnetic susceptibility, χ:
| (11A) |
| (11B) |
where the equilibrium magnetic susceptibility, χ0(T), can be derived from the expression for the equilibrium magnetization of ferrofluid (equation 6):
| (12) |
Power dissipation
Using the equilibrium magnetization, M0(T) from equation 6 and the equilibrium magnetic susceptibility, χ0(T), from equation 12, we are ready to calculate the adjusted power dissipation. For magnetic nanoparticles suspended in an alternating magnetic field, the energy dissipation is equal to the change in the internal energy, ∆U, or equivalently, the loss of the magnetic work5:
| (13A) |
| (13B) |
| (13C) |
Substituting equation 11B and ω = 2πf into equation 13C, we obtain the final expression for the change in the internal energy, ∆U:
| (13D) |
Using the change in the internal energy, ∆U, the volumetric power dissipation, P, can be expressed as:
| (14A) |
which is derived from the integration and multiplication of cyclic frequency, f, and internal energy change, ∆U. Substituting equation 13D into equation 14A, we can express the volumetric power dissipation, P, as:
| (14B) |
Finally, to obtain the modified power dissipation for magnetic nanoparticle aggregates, we substituted equation 12 for χ0(T) into equation 14B:
| (14C) |
Specific loss power
The SLP can be calculated as:
| (15A) |
where ρ denotes the mass density of the ferrofluid. The corresponding adjusted SLP accounting for cluster formation in the ferrofluid can then be expressed as:
| (15B) |
Comparison with experimental results
To determine the validity and accuracy of our revised cluster-based model, predicted SLP values based on the revised cluster-based model and the Rosensweig model were compared with available experimental results using magnetite Fe3O4 magnetic nanoparticle22,23 and cobalt ferrite CoFe2O4 magnetic nanoparticles reported in the previous literature.24,25 In comparison with the reported experimental results, we have taken into account different physical properties of magnetic nanoparticles such as magnetic anisotropy, surface chemistry, size distribution, and magnetic environment (e.g. applied magnetic field amplitude, applied magnetic field frequency). All the numerical calculations and nonlinear fitting were done using our custom-written program on MATLAB 2013b (The MathWorks, Natick, MA, USA). The experimental results and the parameters used in the theoretical calculation are summarized in Table 1 for magnetite Fe3O4 magnetic nanoparticles and in Table 2 for cobalt ferrite CoFe2O4 magnetic nanoparticles.
Table 1.
Experimental results and parameters used in the theoretical calculations of the SLP for magnetite Fe3O4 magnetic nanoparticles, to determine the validity and accuracy of the revised cluster-based model, as shown in Figures 3 and 4
| Magnetic nanoparticle | Magnetite Fe3O4 | ||||||
|---|---|---|---|---|---|---|---|
| Magnetic anisotropy constant, Ka (kJ/m3) | 21 | ||||||
| Domain magnetization of monomers, Mdm (kA/m) | 446 | ||||||
| Viscosity of the carrier fluid, η (kg/m/s) | 0.0007 (water) | ||||||
| Temperature, T (K) | 300 | ||||||
| Critical temperature, T* (K) | 358 | ||||||
| Alternating magnetic field | |||||||
| Frequency, f (kHz) | 80 | 168 | |||||
| Amplitude, H0(kA/m) | 32.5 | 21 | |||||
| Magnetic nanoparticle mean diameter (nm) | 7.5 | 13 | 4.5 | 6.7 | 10.9 | 16.0 | 35.4 |
| SLP (W/g) | |||||||
| Experiment22,23 | 15.6 | 39.4 | ~0 | 3 | 32 | 61 | 76 |
| Cluster-based model | 0.13 | 30.6 | ~0 | 0.14 | 6.87 | 76.1 | 9.38 |
| Rosensweig model | 0.11 | 10.1 | ~0 | 0.04 | 2.86 | 101 | 9.42 |
| Reference | Ma et al22 | Lartigue et al23 | |||||
| Figure number | Figure 3 | Figure 4 | |||||
Abbreviation: SLP, specific loss power.
Table 2.
Experimental results and parameters used in the theoretical calculations of the SLP for cobalt ferrite CoFe2O4 magnetic nanoparticles, to determine the validity and accuracy of the revised cluster-based model, as shown in Figures 5 and 6
| Magnetic nanoparticle | Cobalt ferrite CoFe2O4 | ||||||
|---|---|---|---|---|---|---|---|
| Magnetic anisotropy constant, Ka (kJ/m3) | 1,200 | ||||||
| Domain magnetization of monomers, Mdm (kA/m) | 425 | ||||||
| Viscosity of the carrier fluid, η (kg/m/s) | 0.0007 (water) | ||||||
| Temperature, T (K) | 300 | ||||||
| Critical temperature, T* (K) | 358 | ||||||
| Alternating magnetic field | |||||||
| Frequency, f (kHz) | 167 | 700 | |||||
| Amplitude, H0(kA/m) | 21 | 24.8 | |||||
| Magnetic nanoparticle size | |||||||
| Mean diameter (nm) | 5.5 | 5.9 | 6.0 | 6.2 | 6.7 | 3.9 | 9.1 |
| Standard deviation, σ | 0.19 | 0.18 | 0.19 | 0.23 | 0.21 | 0.40 | 0.22 |
| SLP (W/g) | |||||||
| Experiment24,25 | 76.7 | 105 | 153 | 188 | 250 | 40 | 360 |
| Cluster-based model | 140 | 183 | 199 | 235 | 294 | 33.1 | 361 |
| Rosensweig model | 151 | 198 | 215 | 255 | 318 | 35.8 | 387 |
| Reference | Baldi et al24 | Fortin et al25 | |||||
| Figure number | Figure 5 | Figure 6 | |||||
Abbreviation: SLP, specific loss power.
In vivo demonstration of magnetic nanoparticle aggregation in cancer tissues
In order to demonstrate the aggregation of magnetic nanoparticles in biomedical applications, we inspected MR T2-weighted imaging and the pathological iron stain of pancreatic cancers in in vivo xenograft mouse models, which were targeted and labeled by magnetic nanoparticles. To enhance targeting specificity and efficiency, anti-cancer-antigen 19-9 (anti-CA 19-9) antibodies (400 μg) were conjugated to NH2-PEG-coated magnetic nanoparticles (5 mg) utilizing reductive amination chemistry into a 900 μL solution. Conjugation was verified using dynamic light scattering for particle size determination and the Bradford protein assay. More details on the preparation, bioconjugation, and characterization of the anti-CA 19-9 antibodies–magnetic nanoparticles can be found in the “Supplementary Materials”.
The human pancreatic cancer cell line, BxPC-3, which reveals positive expression of CA19-9 antigen,32 was purchased from Bioresource Collection and Research Center (BCRC, Hsinchu, Taiwan), derived from American Type Culture Collection and cultured in Roswell Park Memorial Institute 1640 (RPMI-1640) medium (Sigma-Aldrich, St Louis, MO, USA) supplemented with 10% fetal bovine serum (Gibco, Gaithersburg, MD, USA) and 100 U/mL penicillin-streptomycin antibiotics (Sigma-Aldrich) and maintained in a 5% CO2 humidified incubator at 37°C. The antigen binding capacity to CA 19-9 overexpressing cell lines (BxPC3) was confirmed with in vitro MR cellular images. An NMR tube of 1 cm containing twelve 1-mm capillaries with BxPC3 cells labeled by various concentrations of magnetic nanoparticles was imaged. The relaxation rate, R2, parameter mapping of the 12 capillaries obtained from the axial T2-weighted spin-echo images showed quantitative agreement with the concentration of the magnetic nanoparticles.
Furthermore, two control experiments using mouse models bearing both CA19-9(+) and CA19-9(−) pancreatic cancers and mouse models bearing CA19-9(+) pancreatic cancers and no pancreatic cancers were used to additionally confirm specific, reliable targeting and binding. The subcutaneous xenograft pancreatic cancer was created with 3×106 CA19-9(+) BxPC-3 cells on the right flank of the mouse and 3×106 CA19-9(−) Mia PaCa-2 cells on the left flank. In both control experiments, magnetic nanoparticles could only be found in the CA19-9(+) pancreatic cancer tissues.
The MRI experiments were performed on Varian INOVA 7-T micro-imaging spectrometer (Varian Inc., Walnut Creek, CA, USA) at day 35 after tumor implantation. The multiple slice spin-echo T2-weighted images were acquired on the axial plane with TR =7.5 s, TE =10 ms, 30 ms, 50 ms, FOV =32×32 mm, thickness =0.5 mm, pixel size =128×128, number of slices =64, and number of scans =1. Prior to injecting 200 L CA19-9-magnetic nanoparticle (corresponding to 2.0 mg Fe/Kg mouse) to the tail vein of the mouse, we injected 100 g IgG (Immunoglobulin G, Sigma-Aldrich) to the tail vein of the mouse to suppress the immune response of the mouse. Administration of IgG to mice in combination with particulate antigen suppressed the immute response that was mediated by macromolecules found in extracellular fluids such as secreted antibodies, complement proteins, and certain antimicrobial peptides by masking B-cell epitopes.33
Results and discussion
In vivo demonstration of magnetic nanoparticle aggregation in pancreatic cancers
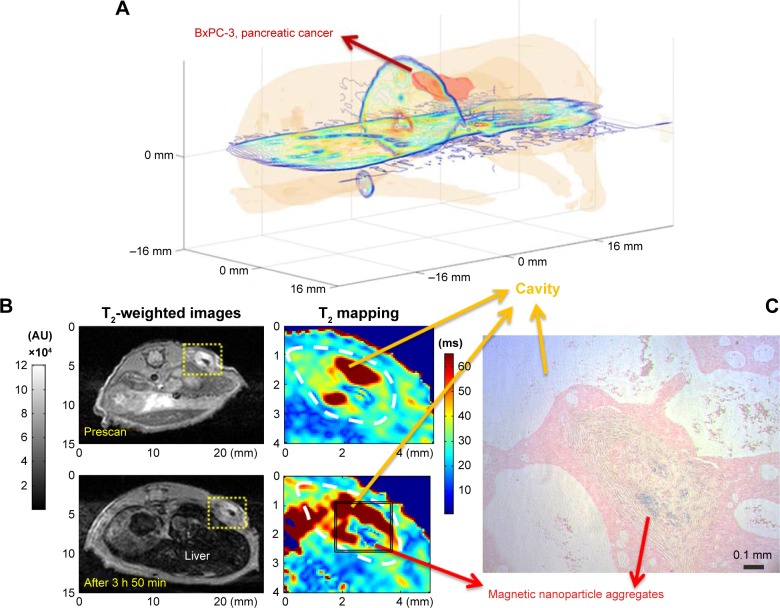
Pancreatic cancer, called the silent killer, is the fourth leading cause of cancer-related death in both men and women in the USA. Due to difficulties in diagnosis and therapy, pancreatic cancer patients’ 5-year survival rate is only about 1% in the USA. Nonetheless, hope for mitigating pancreatic cancers arises from the early detection and targeted thermo-chemotherapy through MR nano-theranostics. Figure 1 demonstrates the formation of magnetic nanoparticle aggregates in targeted pancreatic cancers, which motivated the authors to propose a revised cluster-based model to more accurately predict SLP and to optimize heating efficiency for future in vivo applications of MR nano-theranostic hyperthermia in cancer therapy.
Figure 1.
Formation of magnetic nanoparticle aggregates in targeted pancreatic cancer tissues.
Notes: In order to demonstrate the aggregation of magnetic nanoparticles in biomedical applications, we inspected MR T2-weighted imaging and the pathological iron stain of pancreatic cancers in in vivo xenograft mouse models, which are targeted and labeled by magnetic nanoparticles. To enhance targeting specificity and efficiency, anti-CA 19-9 antibodies were conjugated to NH2-PEG-coated magnetic nanoparticles. (A) A 3D reconstruction of the pancreatic cancer mouse model from 2D axial T2-weighted images. (B) T2-weighted images (left) and the T2 parameter mapping corresponding to the yellow dashed line box area (right) acquired before (top) and after (bottom) the pancreatic cancer tissues (circled by white dashed line) were targeted and labeled by anti-CA 19-9 antibodies–magnetic nanoparticles. (C) To confirm and visualize the magnetic nanoparticle aggregates in (B), Prussian blue staining was performed where magnetic nanoparticle aggregates to form an insoluble deep blue hydrated ferric ferrocyanide complex (i.e. Prussian blue dye).
Abbreviations: MR, magnetic resonance; anti-CA, anti-cancer-antigen.
Comparison with the Rosensweig model
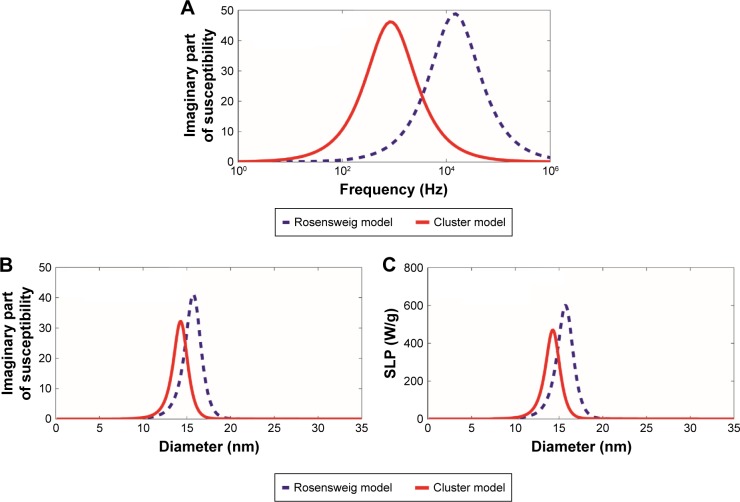
To investigate how the aggregation behavior of interacting magnetic nanoparticles affects the hyperthermia properties, the SLP was computed from the revised cluster-based model and then was compared with that from the original Rosensweig model.5 Because SLP is proportional to the volumetric power dissipation, which is, in part, determined by the imaginary part of the magnetic susceptibility as described in equations 14A and 15A, changes in the imaginary part of the magnetic susceptibility due to magnetic nanoparticle aggregation would be reflected on the resulting SLP. Experimental results reported by Hergt et al13 regarding the relationship between the frequency, f, and the imaginary part of the magnetic susceptibility of the ferrofluid, χ″, were shown to be significantly different from the predicted Rosensweig theoretical values. Specifically, experimental results for the colloidal-based ferrofluid suspension were shown to have a lower magnetic susceptibility peak value than predicted, implying the model suggested by Rosensweig alone cannot fully characterize the ferrofluid system. Our revised cluster-based model aims to explain the inconsistency between the original Rosensweig prediction and experimental results by considering cluster formation in the ferrofluid solution.
Using the experimental parameters previously reported by Hergt et al,13 we compared the differences between the Rosensweig model and the revised cluster-based model, as shown in Figure 2. The imaginary part of the magnetic susceptibility, χ″, was calculated as a function of the alternating magnetic field frequency, f (Figure 2A), where the magnetic nanoparticle diameter was set to 18 nm and the magnetic field amplitude to 11 kA/m. The imaginary part of the magnetic susceptibility, χ″, was also calculated as a function of the magnetic nanoparticle diameter (Figure 2B) to further illustrate the effect of magnetic nanoparticle aggregation, where the magnetic field amplitude was set to 11 kA/m and the frequency to 410 kHz. As a result, the revised cluster-based model shifts the curve of χ″ to lower frequency and smaller magnetic nanoparticle diameter, and decreases the maximum peak value. This is because magnetic nanoparticle aggregation increases the overall cluster magnetic anisotropy (Kac), as described in equation 5B, and decreases both the domain magnetization (Mdc) and the average magnetic moment of clusters due to the minimization of internal energy,31 as shown in equation 8. Particularly, the increase in cluster magnetic anisotropy is reflected in the effective relaxation time constant, τ, by affecting the Neel relaxation time constant, τN, as denoted in equations 3 and 4, while the decrease in both the domain magnetization and the average magnetic moment of the clusters is reflected in the equilibrium magnetic susceptibility, as shown in equation 12. These factors altogether contribute to the shift of the curve of χ″, resulting in the shifted theoretical SLP value, as shown in equation 15B. Therefore, the theoretical SLP based on equation 15B was plotted in Figure 2C as a function of the magnetic nanoparticle diameter using the same parameters as those in Figure 2B. The predicted SLP values reflect the variation in the imaginary part of the magnetic susceptibility, as these two parameters are linearly related to each other (equation 14A).
Figure 2.
Comparison with the Rosensweig model.
Notes: The imaginary part of the magnetic susceptibility, χ″, and the SLP were computed by our revised cluster-based model (red solid line) and the Rosensweig model (blue dashed line). (A) χ″ as a function of the alternating magnetic field frequency, f, for magnetic nanoparticle diameter =18 nm, alternating magnetic field amplitude H0=11 kA/m, and magnetic anisotropy constant Ka =15 kJ/m3. (B) χ″ as a function of the magnetic nanoparticle diameter for alternating magnetic field frequency f=410 kHz, alternating magnetic field amplitude H0=11 kA/m, and magnetic anisotropy constant Ka =15 kJ/m3. (C) The SLP, as a function of the magnetic nanoparticle diameter, using the same parameters as those in (B).
Abbreviation: SLP, specific loss power.
The main difference between the revised cluster-based model and the Rosensweig model is the consideration of magnetic nanoparticle interactions within the real ferrofluid. Because the Rosensweig model assumes that magnetic nanoparticles act as individual units independent of each other, the SLP value, as well as the optimal magnetic nanoparticle size, is overestimated. In biomedical applications, however, magnetic nanoparticles are not found simply in single units, but rather as aggregated clusters (Figure 1). Accurate theoretical models should, therefore, reflect the fraction of clusters in the real ferrofluid. By taking cluster formation into consideration, the revised cluster-based model predicts SLP values and the corresponding optimal magnetic nanoparticle diameter at the maximum SLP to be about 20%–25% smaller than those made by the Rosensweig model, as shown in Figure 2C.
Comparison with the experimental results of magnetite Fe3O4 magnetic nanoparticles
SLP were computed based on the revised cluster-based model and the Rosensweig model and then were compared with the experimental results of magnetite Fe3O4 magnetic nanoparticles reported by Ma et al22 and Lartigue et al23 as summarized in Table 1 and shown in Figures 3 and 4. Magnetite Fe3O4 is the most popular form of magnetic nanoparticles, as it is well tolerated by the human body. Although there are still some differences between our cluster-based prediction and the experimental results, our model offers relatively more accurate estimates of SLP in comparison with the Rosensweig model. Within the superparamagnetic size range (i.e. magnetic nanoparticle diameter 5–50 nm), the SLP values increase significantly with the increase of the nanoparticle size, mainly due to the onset of other heat generation mechanisms.10,13 However, aggregation of magnetic nanoparticle shifts the overall curve to the left (i.e. smaller magnetic nanoparticle diameter), predicting lower SLP values when compared with the predictions made by the Rosensweig model, in agreement with Figure 2. Notably, the revised cluster-based model works especially well within the magnetic nanoparticle diameter range of 10–20 nm, which is commonly chosen for MR nano-theranostics. On the other hand, neither theoretical model accurately predicts the SLP for magnetic nanoparticles with a diameter >20 nm (Figure 4). This divergence can be attributed to the availability of other heat generation mechanisms and nonlinear effect, such as hysteresis,10,13 associated with larger magnetic nanoparticle diameters.
Figure 3.
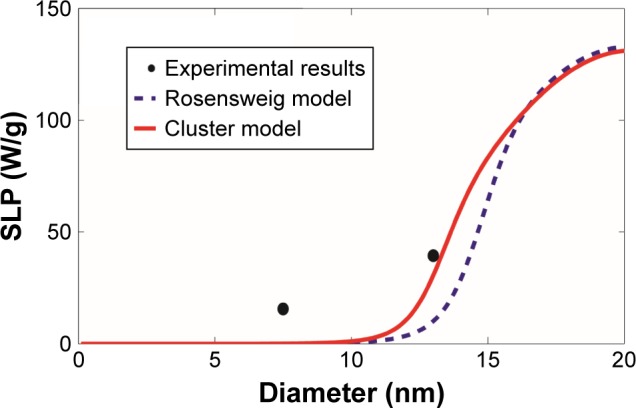
Comparison with the experimental results of magnetite Fe3O4 magnetic nanoparticles.
Notes: The SLP values were computed as a function of the magnetic nanoparticle diameter, based on our revised cluster-based model (red solid line) and the Rosensweig model (blue dashed line), using the experimental results and parameters reported by Ma et al22 (black filled circle). The experimental results and parameters used in the theoretical calculations are summarized in Table 1: magnetite Fe3O4, magnetic anisotropy constant Ka =21 kJ/m3, domain magnetization of monomers Mdm=446 kA/m, alternating magnetic field frequency f=80 kHz, alternating magnetic field amplitude H0=32.5 kA/m, viscosity of the carrier fluid (water) η=0.0007 kg/m/s, temperature T =300 K, and critical temperature T* =358 K.
Abbreviation: SLP, specific loss power.
Figure 4.
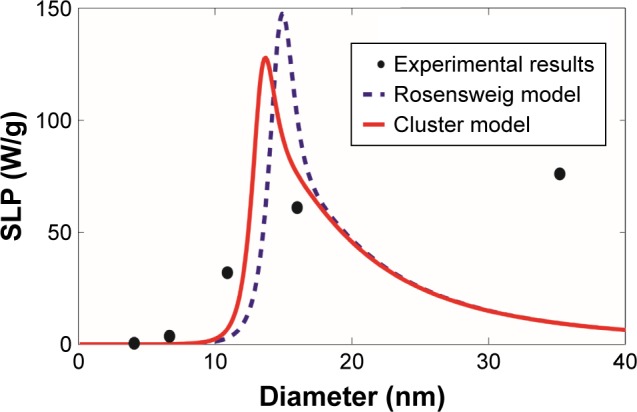
Comparison with the experimental results of magnetite Fe3O4 magnetic nanoparticles.
Notes: The SLP values were computed as a function of the magnetic nanoparticle diameter, based on our revised cluster-based model (red solid line) and the Rosensweig model (blue dashed line), using the experimental results and parameters reported by Lartigue et al23 (black filled circle). The experimental results and parameters used in the theoretical calculations are summarized in Table 1: magnetite Fe3O4, magnetic anisotropy constant Ka =21 kJ/m3, domain magnetization of monomers Mdm=446 kA/m, alternating magnetic field frequency f=168 kHz, alternating magnetic field amplitude H0=21 kA/m, viscosity of the carrier fluid (water) η=0.0007 kg/m/s, temperature T =300 K, and critical temperature T* =358 K.
Abbreviation: SLP, specific loss power.
Comparison with the experimental results of cobalt ferrite CoFe2O4 magnetic nanoparticles
Additional comparisons were made using experimental results of cobalt ferrite CoFe2O4 reported by Baldi et al24 and Fortin et al25 as summarized in Table 2 and shown in Figures 5 and 6, respectively. Similar to the previous comparison with the experimental results of magnetite Fe3O4 magnetic nanoparticles, the revised cluster-based model approaches the experimental results better than the Rosensweig model, as the maximum and overall SLP is reduced by the aggregation of magnetic nanoparticles. Again, SLP of magnetic nanoparticles with diameters between 10 and 20 nm was more accurately predicted by the revised cluster-based model. However, since cobalt ferrite CoFe2O4 possesses a relatively larger magnetic anisotropy constant than magnetite Fe3O4, the effect of aggregation on magnetic anisotropy becomes less significant, resulting in a smaller shift to the left (i.e. smaller magnetic nanoparticle diameter) by the revised cluster-based model, as portrayed in both Figures 5 and 6.
Figure 5.
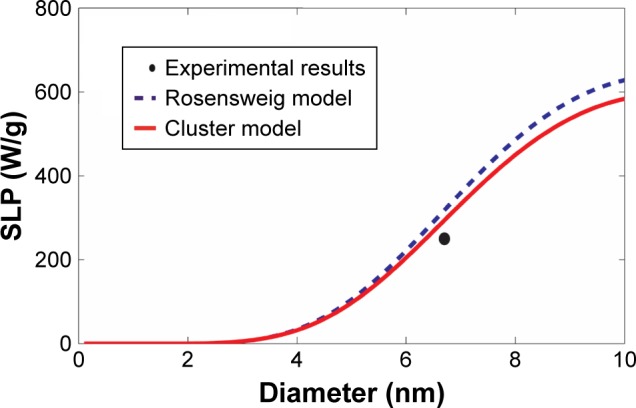
Comparison with the experimental results of cobalt ferrite CoFe2O4 magnetic nanoparticles.
Notes: The SLP values were computed as a function of the magnetic nanoparticle diameter, based on our revised cluster-based model (red solid line) and the Rosensweig model (blue dashed line), using the experimental results and parameters reported by Baldi et al24 (black filled circle). The experimental results and the parameters used in the theoretical calculations are summarized in Table 2: cobalt ferrite CoFe2O4, magnetic anisotropy constant Ka=1,200 kJ/m3, domain magnetization of monomers Mdm=425 kA/m, alternating magnetic field frequency f=167 kHz, alternating magnetic field amplitude H0=21 kA/m, viscosity of the carrier fluid (water) η=0.0007 kg/m/s, temperature T =300 K, critical temperature T* =358 K, and the mean (standard deviation σ) of the magnetic nanoparticle diameter =6.7 nm (σ=0.23 nm).
Abbreviation: SLP, specific loss power.
Figure 6.
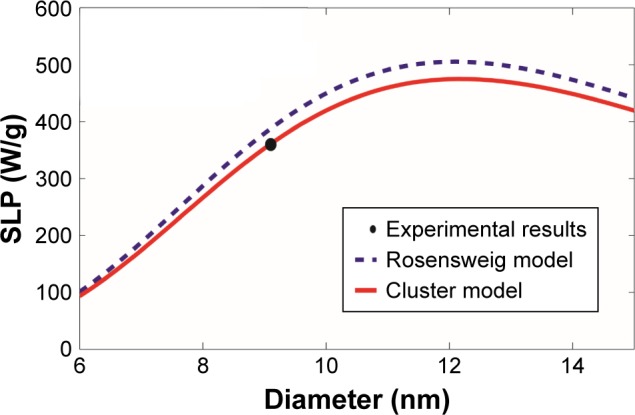
Comparison with the experimental results on cobalt ferrite CoFe2O4 magnetic nanoparticles.
Notes: The SLP values were computed as a function of the magnetic nanoparticle diameter, based on our revised cluster-based model (red solid line) and the Rosensweig model (blue dashed line), using the experimental results and parameters reported by Fortin et al25 (black filled circle). The experimental results and parameters used in the theoretical calculations are summarized in Table 2: cobalt ferrite CoFe2O4, magnetic anisotropy constant Ka=1,200 kJ/m3, domain magnetization of monomers Mdm=425 kA/m, alternating magnetic field frequency f=700 kHz, alternating magnetic field amplitude H0=24.8 kA/m, viscosity of the carrier fluid (water) η=0.0007 kg/m/s, temperature T =300 K, critical temperature T* =358 K, and the mean (standard deviation σ) of the magnetic nanoparticle diameter =9.1 nm (σ=0.22 nm).
Abbreviation: SLP, specific loss power.
Conclusion
MR nano-theranostic hyperthermia uses nontoxic, biocompatible magnetic nanoparticles to target and accumulate at the lesions to generate enhanced contrast for early lesion detection and generate heat to kill lesion cells directly through hyperthermia or indirectly through thermal activation and control releasing of drugs.34–38 By considering the effects of magnetic nanoparticle aggregation on MR nano-theranostic hyperthermia, our revised cluster-based model provides a more accurate prediction of experimental values, as shown in Figures 3–6 for magnetite Fe3O4 and cobalt ferrite CoFe2O4 magnetic nanoparticles. The aggregation of magnetic nanoparticles increases the cluster magnetic anisotropy while reducing both the cluster domain magnetization and the average magnetic moment, which, in turn, decreases the imaginary part of the magnetic susceptibility to shift the predicted SLP toward smaller magnetic nanoparticle diameter with lower peak values. The effect of magnetic nanoparticle aggregation can also be understood in terms of energy transfer. A portion of the energy provided by the magnetic field is absorbed by the magnetic nanoparticle aggregates to overcome inter-nanoparticle interactions, such as electrostatic attraction, electrostatic repulsion, steric repulsion, and magnetic dipolar interactions to disrupt the aggregates into monomers. As a result, the heating efficiency is decreased and the SLP values are less than the prediction made by the Rosensweig theory.
The improvement in the prediction accuracy provided by the revised cluster-based model is particularly pronounced when the magnetic nanoparticle diameter is in the range of ~10–20 nm or, equivalently, the resulting drug–nanoparticle–ligand conjugates in the range of ~30–50 nm. This happens to be an important size range for MR nano-theranostics, as recent studies showed that anticancer nano-medicine with 50-nm nanoparticle size provides the optimal combination of deep tumor tissue penetration, efficient cancer cell internalization, and slow tumor clearance, and therefore exhibits the highest efficacy against both primary and metastatic tumors in vivo.39 When the magnetic nanoparticle becomes larger, as seen in the case of magnetite Fe3O4 in Figure 4, the prediction becomes inaccurate even with the revised cluster-based model, mainly due to alternative heat generation mechanisms and nonlinear response of magnetic susceptibility,40–42 which motivates more sophisticated and accurate theoretical models in the future.
Finally, nanoparticle size plays a pivotal role in nano-theranostics, as it determines their biodistribution, tumor penetration, cellular internalization, clearance from blood plasma and tissues, as well as excretion from the body – all of which impact the overall therapeutic efficacy against cancers.39,43 Our studies show that, as far as MR nano-theranostic hyperthermia is concerned, a relatively 20%–25% smaller magnetic nanoparticle diameter should be chosen to reach the maximal heating efficiency in comparison with the optimal size predicted by previous models.
Supplementary materials
Orthotopic pancreatic cancer mouse models
The 4-week-old male BALB/c nude mice (N=4) were obtained from BioLASCO, Taipei, Taiwan. BALB/c is an albino, laboratory-bred strain of the house mouse from which a number of common substrains are derived. BALB/c mice are distributed globally and are among the most widely used inbred strains used in animal experimentation.
Orthotopic pancreatic cancer mouse models are preferred in this work, because they offer tissue site-specific pathology, allow studies of metastasis, and are generally deemed more clinically relevant. Orthotopic implantation of pancreatic cancer cells includes the following steps: 1) Make incision with sterile microscissors beside the splenic silhouette. 2) Expose the entire pancreas and spleen by using a pair of blunt-nose forceps. 3) Insert the needle with the human pancreatic cancer cells into the tail of the pancreas and pass into the pancreatic head area. Suture the abdominal muscle layer first as putting back the pancreas and spleen into the abdominal cavity and close the skin.
We waited until the volume of the subcutaneous xenograft pancreatic cancer reached 5 mm3. We first injected 100 g IgG (Immunoglobulin G) from the tail vein of the mouse to suppress the immune response of the mouse. Then we injected 200 L CA19-9-magneic nanoparticle (corresponding to 2.0 mg Fe/kg mouse) from the tail vein of the mouse. All injections were performed under anesthesia by isoflurane (Panion & BF Biotech Inc., Taipei, Taiwan), and all efforts were made to minimize suffering.
During the MRI acquisition, mice were anesthetized by inhalation of isoflurane (Panion & BF Biotech Inc.). A vaporizer specially calibrated for isoflurane was used to accurately control the anesthetic concentration during MRI scanning. The physiological status of the mice was kept under surveillance with a small animal monitoring system (SA Instruments Stony Brook, NY, USA). Mice were humanely sacrificed after experiments. All animal procedures were in accordance with the regulations approved by the Institution Animal Care and Utilization Committee at National Taiwan University (approval number NTU-103-EL-61).
Tissues were fixed in 10% formalin overnight, embedded in paraffin, and then sectioned. Tissues sections with a thickness of 5 μm were deparaffinized in xylene, rehydrated in a gradient ethanol series, and incubated in blocking buffer. To visualize nuclei and cytoplasm, H&E staining was performed according to the standard protocols. Images of the tissues were acquired using a wield-field scanner with a 40× objective and detected with a color microscope camera (DFC7000T, Leica, Wetzlar, Germany).
To visualize the magnetic nanoparticle aggregates, Prussian blue staining was performed according to the standard protocols. The staining is an optical method based on the binding of cellular ferric ions to the soluble ferrocyanide salt at low pH, forming an insoluble deep blue hydrated ferric ferrocyanide complex (i.e. Prussian blue dye). Therefore, in order to detect magnetic nanoparticle aggregates in tissue sections, the specimens were deparaffinized and treated with 20% aqueous solution of concentrated HCl to dissolve the magnetic nanoparticles to release ferric iron in the cells.
Preparation, bioconjugation, and characterization of the anti-CA 19-9 antibodies–magnetic nanoparticles
To oxidize the glycosylated anti-CA 19-9 antibodies, 400 μg of the antibody was mixed with 40 μL of 0.10 M sodium periodate solution and reacted for 45 min in dark at room temperature. Then 40 μL of 0.20 M Na2SO3 solution was immediately added into the mixture and allowed to react for another 10 min. The sample was then run through D-Salt Dextran Desalting Columns (Thermo Fisher Scientific, Waltham, MA, USA) to isolate the oxidized antibody from the mixture.
The oxidized antibody was quickly mixed with the amine-coated magnetic nanoparticles (0.054 nmole/mL) (Ocean Nanotech, Springdale, AR, USA) at a pH of 8.0 to reduce aggregation and maximize Schiff base formation while preventing the denaturation of the antibody. The reaction was then shaken at room temperature for 6 h. To stabilize the Schiff bases, 53 μL of 5.0 M sodium cyanoborohydride solution was added and reacted for 45 min to reduce the bond to a secondary amine linkage. Additionally, 268 μL of 1.0 M ethanolamine solution was added to the mixture to quench the unreacted aldehyde groups on the antibody. This reaction mixture was then purified by washing 5 times using Amicon Ultra Centrifugal Filters (Millipore, Carrigtwohill, Ireland) to remove the quenching reagents. Unbound antibody was also purified from conjugated magnetic nanoparticles through a separation magnet (Ocean Nanotech) overnight. The final solution was suspended in PBS at a concentration of 5 mg Fe/mL.
Dynamic light scattering (DLS) measurements were taken to verify the bioconjugation between the anti-CA 19-9 antibodies and the magnetic nanoparticles. DLS measurements were taken on a Zetasizer Nano using a disposable, low-volume cuvette. The standard protein method on the detector was utilized to generate a size distribution plot. The diameter of unconjugated magnetic nanoparticles was measured to be 25 nm, while that of the conjugated magnetic nanoparticles was 38 nm, as shown in Figure S1.
Dynamic light scattering measurements were taken to verify the bioconjugation between the anti-CA 19-9 antibodies and the magnetic nanoparticles.
Notes: The standard protein method on the detector was utilized to generate a size distribution plot. The diameter of unconjugated magnetic nanoparticles was measured to be 25 nm, while that of the bioconjugated magnetic nanoparticles was 38 nm.
Abbreviation: anti-CA, anti-cancer-antigen.
Acknowledgments
The authors thank Ms Tanya Kim for editorial assistance. This work was supported by the Camille and Henry Dreyfus Foundation (TC-05-053), National Science Foundation (DMS-0833863, CHE-1112574, and CHE-1416598), Hirshberg Foundation for Pancreatic Cancer Research, and Taiwan Ministry of Science and Technology (NSC 100-2113-M-002-008, NSC 101-2113-M-002-018, and MOST 103-2923-M-002-006).
Footnotes
Disclosure
The authors report no conflicts of interest in this work.
References
- 1.Cantillon-Murphy P, Wald LL, Zahn M, Adalsteinsson E. Proposing magnetic nanoparticle hyperthermia in low-field MRI. Concepts in Magn Reson A. 2010;36(1):36–47. [Google Scholar]
- 2.Gordon RT, Hines JR, Gordon D. Intracellular hyperthermia: a biophysical approach to cancer treatment via intracellular temperature and biophysical alterations. Med Hypotheses. 1979;5(1):83–102. doi: 10.1016/0306-9877(79)90063-x. [DOI] [PubMed] [Google Scholar]
- 3.Jordan A, Wust P, Fӓhling H, John W, Hinz A, Felix R. Inductive heating of ferrimagnetic particles and magnetic fluids: physical evaluation of their potential for hyperthermia. Int J Hyperthermia. 1993;9(1):51–68. doi: 10.3109/02656739309061478. [DOI] [PubMed] [Google Scholar]
- 4.Jordan A, Wust P, Scholz R, et al. Cellular uptake of magnetic fluid particles and their effects on human adenocarcinoma cells exposed to AC magnetic fields in vitro. Int J Hyperthermia. 1996;12(6):705–722. doi: 10.3109/02656739609027678. [DOI] [PubMed] [Google Scholar]
- 5.Rosensweig RE. Heating magnetic fluid with alternating magnetic field. J Magn Magn Mater. 2002;252:370–374. [Google Scholar]
- 6.Banobre M, Teijeiro A, Rivas J. Magnetic Nanoparticle-based hyperthermia for cancer treatment. Rep Prac Oncol Radiother. 2013;18(6):397–400. doi: 10.1016/j.rpor.2013.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guibert C, Dupuis V, Peyre V, Fresnais J. Hyperthermia of magnetic nanoparticles: experimental study of the role of aggregation. J Phys Chem C. 2015;199(50):28148–28154. [Google Scholar]
- 8.Xiang Q, Zhong J, Zhou M, Morais PC, Liu W. AC field dependence of cluster disruption in magnetic fluids. J Appl Phys. 2011;109(7):07B317. [Google Scholar]
- 9.Bordelon DE, Cornejo C, Grüttner C, Westphal F, DeWeese TL, Ivkov R. Magnetic nanoparticle heating efficiency reveals magneto-structural differences when characterized with wide ranging and high amplitude alternating magnetic fields. J Appl Phys. 2011;109(12):124904. [Google Scholar]
- 10.Hergt R, Dutz S, Röder M. Effects of size distribution on hysteresis losses of magnetic nanoparticles for hyperthermia. J Phys Condens Matter. 2008;20(38):385214. doi: 10.1088/0953-8984/20/38/385214. [DOI] [PubMed] [Google Scholar]
- 11.Li Z, Kawashita M, Araki N, Mistumori M, Hiraoka M. Effects of particle size of magnetite nanoparticles on heat generating ability under alternating magnetic field. Bioceram Dev Appl. 2011;1:D110128. [Google Scholar]
- 12.Khandhar AP, Ferguson RM, Simon JA, Krishnan KM. Enhancing cancer therapeutics using size-optimized magnetic fluid hyperthermia. J Appl Phys. 2012;111(7):07B306. doi: 10.1063/1.3671427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hergt R, Dutz S, Müller R, Zeizberger M. Magnetic particle hyperthermia: nanoparticle magnetism and materials development for cancer therapy. J Phys Condens Matter. 2006;18(38):S2919–S2934. [Google Scholar]
- 14.Morais PC, Gonçalves GRR, Bakuzis AF, Neto KS, Pelegrini F. Experimental evidence of dimer disruption in ionic ferrofluid: a ferromagnetic resonance investigation. J Magn Magn Mater. 2001;225(1–2):84–88. [Google Scholar]
- 15.Castro LL, da Silva MF, Bakuzis AF, Miotto R. Aggregate formation on polydisperse ferrofluids: a Monte Carlo analysis. J Magn Magn Mater. 2005;293(1):553–558. [Google Scholar]
- 16.Ganguly R, Zellmer B, Puri IK. Field-induced self-assembled ferrofluid aggregation in pulsatile flow. Phys Fluids. 2005;17(9):097104. [Google Scholar]
- 17.Minkowycz WJ, Sparrow EM, Abraham JP. Nanoparticle Heat Transfer and Fluid Flow. Boca Raton, FL: CRC Press; 2012. [Google Scholar]
- 18.Dennis CL, Jackson AJ, Borchers JA, et al. Nearly complete regression of tumors via collective behavior of magnetic nanoparticles in hyperthermia. Nanotechnology. 2009;20(39):395103. doi: 10.1088/0957-4484/20/39/395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu W, Zhong J, Xiang Q, Yang G, Zhou M. Discretization of magnetization curves and their application in size estimation of nanosized ferrofluid. IEEE Trans Nanotechnol. 2011;10(6):1231–1237. [Google Scholar]
- 20.Sherman SG, Wereley NM. Effect of particle size distribution on chain structures in magnetoheological fluids. IEEE Trans Magn. 2013;49(7):3430–3433. [Google Scholar]
- 21.Zhong J, Xiang Q, Massa LO, Qu F, Morais PC, Liu W. Second-order-like cluster-monomer transition within magnetic fluids and its impact upon the magnetic susceptibility. Nanoscale Res Lett. 2012;7(1):167. doi: 10.1186/1556-276X-7-167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ma M, Wu Y, Zhou J, Sun Y, Zhang Y, Gu N. Size dependence of specific power absorption of Fe3O4 particles in AC magnetic field. J Magn Magn Mater. 2004;268(1–2):33–39. [Google Scholar]
- 23.Lartigue L, Innocenti C, Kalaivani T, et al. Water-dispersible sugarcoated iron oxide nanoparticles: an evaluation of their relaxometric and magnetic hyperthermia properties. J Am Chem Soc. 2011;133(27):10459–10472. doi: 10.1021/ja111448t. [DOI] [PubMed] [Google Scholar]
- 24.Baldi G, Lorenzi G, Ravagli C. Hyperthermic Effect of magnetic nanoparticles under electromagnetic Field. PAC. 2009;3(1–2):103–109. [Google Scholar]
- 25.Fortin JP, Wilhelm C, Servais J, Menager C, Bacri JC, Gazeau F. Size-sorted anionic iron oxide nanomagnets as colloidal mediators for magnetic hyperthermia. J Am Chem Soc. 2007;129(9):2628–2635. doi: 10.1021/ja067457e. [DOI] [PubMed] [Google Scholar]
- 26.Debye P. Polar Molecules. New York: The Chemical Catalog Co. Inc; 1929. [Google Scholar]
- 27.Néel L. Theorie du trainage magnetique des ferromagnetiques en grains fins avec applications aux terres cuites. Geophysics. 1949;5:99–136. France. [Google Scholar]
- 28.Kumar C. Magnetic Nanomaterials. Hoboken, NJ: John Wiley & Sons; 2009. [Google Scholar]
- 29.Saville SL, Qi B, Baker J, et al. The formation of linear aggregate in magnetic hyperthermia: Implication on specific absorption rate and magnetic anisotropy. J Colloid Interface Sci. 2014;424:141–151. doi: 10.1016/j.jcis.2014.03.007. [DOI] [PubMed] [Google Scholar]
- 30.Mehdaoui B, Tan RP, Meffre A, et al. Increase of magnetic hyperthermia efficiency due to dipolar interactions in low-anisotropy magnetic nanoparticles: theoretical and experimental results. Phys Rev B. 2013;87(17):174419. [Google Scholar]
- 31.Feynman RP, Leighton RB, Sands M. The Feynman Lectures on Physics The Definitive and Extended Edition. Boston, MA: Addison Wesley; 2005. [Google Scholar]
- 32.McElroy M, Kaushal S, Luiken GA, et al. Imaging of primary and metastatic pancreatic cancer using a fluorophore-conjugated anti-CA19-9 antibody for surgical navigation. World J Surg. 2008;32(6):1057–1066. doi: 10.1007/s00268-007-9452-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cerottini JC, McConahey PJ, Dixon FJ. The immunosuppressive effect of passively administered antibody IgG fragments. J Immunol. 1969;102(4):1008–1015. [PubMed] [Google Scholar]
- 34.Chen KJ, Wolahan SM, Wang H, et al. A small MRI contrast agent library of Gadolinium(III)-encapsulated supramolecular nanoparticles for improved relaxivity and sensitivity. Biomaterials. 2011;32(8):2160–2165. doi: 10.1016/j.biomaterials.2010.11.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ho LC, Hsu CH, Ou CM, et al. Unibody core-shell smart polymer as a theranostic nanoparticle for drug delivery and MR imaging. Biomaterials. 2015;37:436–446. doi: 10.1016/j.biomaterials.2014.10.006. [DOI] [PubMed] [Google Scholar]
- 36.Li Z, Hsu CH, Dimitrov N, et al. Sensitive imaging of magnetic nanoparticles for cancer detection by active feedback magnetic resonance. Magn Reson Med. 2015;74(1):33–41. doi: 10.1002/mrm.25632. [DOI] [PubMed] [Google Scholar]
- 37.Yao J, Hsu CH, Li Z, et al. Magnetic resonance nano-theranostics for Glioblastoma Multiforme. Curr Pharm Des. 2015;21(36):5256–5266. doi: 10.2174/1381612821666150923103307. [DOI] [PubMed] [Google Scholar]
- 38.Wang C, Li Z, Lin YY. Optimizing magnetic nanoparticle hyperthermia effect in MR nanomedicine. Chinese Journal of Magnetic Resonance. 2015;32(2):248–260. [Google Scholar]
- 39.Li T, Yang X, Yin Q, et al. Investigating the optimal size of anticancer nanomedicine. PNAS. 2014;111(43):15344–15349. doi: 10.1073/pnas.1411499111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fannin PC, Charles SW, Oireachtaigh CM, Odenbach S. Investigation of possible hysteresis effects arising from frequency- and field-dependent complex susceptibility measurements of magnetic fluids. J Magn Magn Mater. 2006;302(1):1–6. [Google Scholar]
- 41.Oireachtaigh CM, Fannin PC. Investigation of the non-linear loss properties of magnetic fluids subject to large alternating fields. J Magn Magn Mater. 2008;320(6):871–880. [Google Scholar]
- 42.Fannin PC, Oireachtaigh CM. Investigating the isotropic properties of a magnetic fluid following the removal of a polarising field. J Magn Magn Mater. 2007;316(2):e802–e804. [Google Scholar]
- 43.Arami H, Khandhar A, Liggitt D, Krishnan KM. In vivo delivery, pharmacokinetics, biodistribution, and toxicity of iron oxide nanoparticles. Chem Soc Rev. 2015;44(23):8576–8607. doi: 10.1039/c5cs00541h. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Dynamic light scattering measurements were taken to verify the bioconjugation between the anti-CA 19-9 antibodies and the magnetic nanoparticles.
Notes: The standard protein method on the detector was utilized to generate a size distribution plot. The diameter of unconjugated magnetic nanoparticles was measured to be 25 nm, while that of the bioconjugated magnetic nanoparticles was 38 nm.
Abbreviation: anti-CA, anti-cancer-antigen.