High-resolution in vivo diffusion imaging of the human brain with Generalized SLIce Dithered Enhanced Resolution Simultaneous MultiSlice (gSlider-SMS)

Abstract

Purpose

To develop an efficient acquisition for high-resolution diffusion imaging and allow in vivo whole-brain acquisitions at 600–700μm isotropic resolution.

Theory and Methods

We combine blipped-CAIPI Simultaneous Multi-Slice with a novel slab RF-encoding (gSlider) to form an SNR-efficient volumetric Simultaneous Multi-Slab acquisition. Here, multiple thin-slabs are acquired simultaneously with controlled aliasing, and unaliased with parallel imaging. To achieve high-resolution in the “slice” direction, the slab is volumetrically encoded using RF-encoding with a scheme similar to Hadamard encoding. However, with gSlider, the RF-encoding bases are specifically designed to be highly independent and provide high image-SNR in each slab acquisition to enable self-navigation of diffusion’s phase corruption. Finally, the method is combined with zoomed imaging (while retaining whole-brain coverage) to facilitate low distortion single shot in-plane encoding with EPI at high resolution.

Results

A 10 slices-per-shot gSlider-SMS acquisition was used to acquire whole-brain data at 660 and 760μm isotropic resolution with b-values of 1500 and 1800 s/mm² respectively. Data were acquired on the Connectom 3T scanner with 64-channel head-coil. High quality data with excellent contrast were achieved at these resolutions, which enable the visualization of fine-scale structures.

Conclusion

gSlider-SMS provides a new approach for efficient acquisition of high-resolution diffusion data.

Introduction

Diffusion MRI (dMRI) has been widely used to study brain’s white-matter structures and connectivity. However, the current isotropic resolution of 1–2 mm is inadequate for detailed study of brain’s fine-scale structures, particularly the gray-white matter boundary and cortex (1). Sub-millimeter isotropic resolution dMRI is needed to improve surface and laminar analysis of fibers in the cortex (2,3), to study changes in diffusion properties such as Fractional Anisotopy (FA) in gray matter, and to potentially improve brain parcellation by using FA differences between gray matter regions (4,5).

A major hurdle in performing sub-millimeter isotropic resolution dMRI is its inherent low SNR. Recently, Simultaneous Multi-Slice (SMS) (6–11) and 3D Multi-Slab (12–15) acquisitions have been developed to improve dMRI’s SNR efficiency. Conventional slice-by-slice dMRI exhibits long TRs due to the lengthy diffusion encoding that is repeated for each imaging slice. With SMS and Multi-Slab acquisitions, data from a larger volume can share the same diffusion encoding and readout period, resulting in much shorter TRs and improved SNR efficiency when TR≫T₁. SMS acquisition with blipped-CAIPI (16) is now widely used to provide multiband (MB) speed up of 2–4× with minimal g-factor penalty for dMRI. Nonetheless, higher MB accelerations cannot be achieved without introducing significant g-factor noise, in particular when used in conjunction with in-plane acceleration. This limits the ability to achieve short TRs for very high-resolution dMRI with thin slices (note that unlike dMRI, fMRI can use much higher MB factors since physiological noise typically dominates over g-factor related noise (17)). These considerations have motivated the use of 3D Multi-Slab dMRI, where multiple thick slabs are excited sequentially in each TR, and Fourier encoding is performed in the slab direction for each slab across multiple TRs. This approach enables short TR acquisitions of high-resolution dMRI to provide higher SNR efficiency (18), but suffers from a few drawbacks. For example thick slabs introduce slab boundary artifacts, and only limited parallel imaging is possible in the slice-direction due to the small FOV in the slab direction. Moreover, Fourier encoding across each slab complicates the ability to self phase navigate the multiple shots, which is mandatory in diffusion to eliminate the shot-to-shot nuisance phase introduced from microscopic motion during the diffusion gradients. A number of innovative methods have been proposed to address these issues including slab profile encoding (19,20) to mitigate slab boundary artifacts, simultaneous multi-slab (21) to improve parallel imaging, and cardiac-reordered k-space acquisition (13) to reduce phase/motion artifacts that cannot be completely captured and corrected using 2D navigators.

Another major challenge in sub-millimeter dMRI is the need to perform all of the in-plane encoding in a single shot. This can cause large image distortion and blurring along the PE direction in EPI, and blurring in all directions in spiral. Finally, the long encoding window can reduce SNR by lengthening TE. A number of multi-shot approaches have been proposed to mitigate this issue for 2D acquisitions including interleaved-EPI (22–24), interleaved-Spiral quality dMRI with low distortion and low blurring, but have extensive phase navigator needs and can lead to lengthy acquisition times if multiple shots are needed for both in-plane and through-slab encoding. To mitigate this issue, readout segmented EPI has also been combined with SMS (25). Moreover, an alternative approach to shorten in-plane encoding without lengthening the acquisition has also been developed through the combinational use of in-plane parallel imaging and reduced FOV acquisition with outer volume suppression (OVS) (26,27). The ZOOPPA technique (ZOOmed imaging and Partially Parallel Acquisition) in this category, which utilizes “skewed” RF pulse (28,29) for OVS to provide sharp saturation edge, has also been combined with SMS (30) for faster imaging. This was further optimized to enable whole-brain imaging through sagittal acquisition with OVS of the neck and phase encoding applied in the head-foot direction (31). In addition to this approach, Saritas et al. have recently developed a 2D spatially selective RF pulse to limit the imaging FOV while simultaneously exciting two imaging slices of the spinal cord (32). Here the two slices are unaliased through Hadamard encoding, with cardiac gating and signal averaging across multiple repetitions to mitigate diffusion phase corruptions.

In this work, we developed a multi-shot acquisition for diffusion imaging which limits the multi-shot encoding to a partition direction within a thin slab (typically 5× thicker than the final resolution in the partition direction). Multiple thin slabs are excited simultaneously and reconstructed with the blipped-CAIPI SMS-EPI method. The partitions within the thin slab are reconstructed using a novel slab RF-encoding which we term gSLIDER (Generalized SLIce Dithered Enhanced Resolution). The result is a high-resolution multi-shot diffusion scan where the multi-shot encoding is entirely in the partition direction and is amenable to self-navigation. Efficiency improvements compared to traditional 2D EPI is achieved both through the SMS (typical MB = 2 or 3) and through the 3D encoding within the thin slabs (typically 5 encoding shots). To achieve low image distortion without lengthening the acquisition, gSlider-SMS is then further combined with zoom imaging using inferior saturation pulse in a sagittal acquisition to also retain whole-brain coverage as per (31). The gSlider-SMS acquisition was used to acquire whole-brain diffusion data at 660 and 760μm isotropic resolutions. Data were acquired on the Connectom 3T with 64-channel head-coil, where fine scale structures in gray matter, white matter and at the gray-white matter boundaries are observed.

Theory

Generalized SLIce Dithered Enhanced Resolution (gSlider)

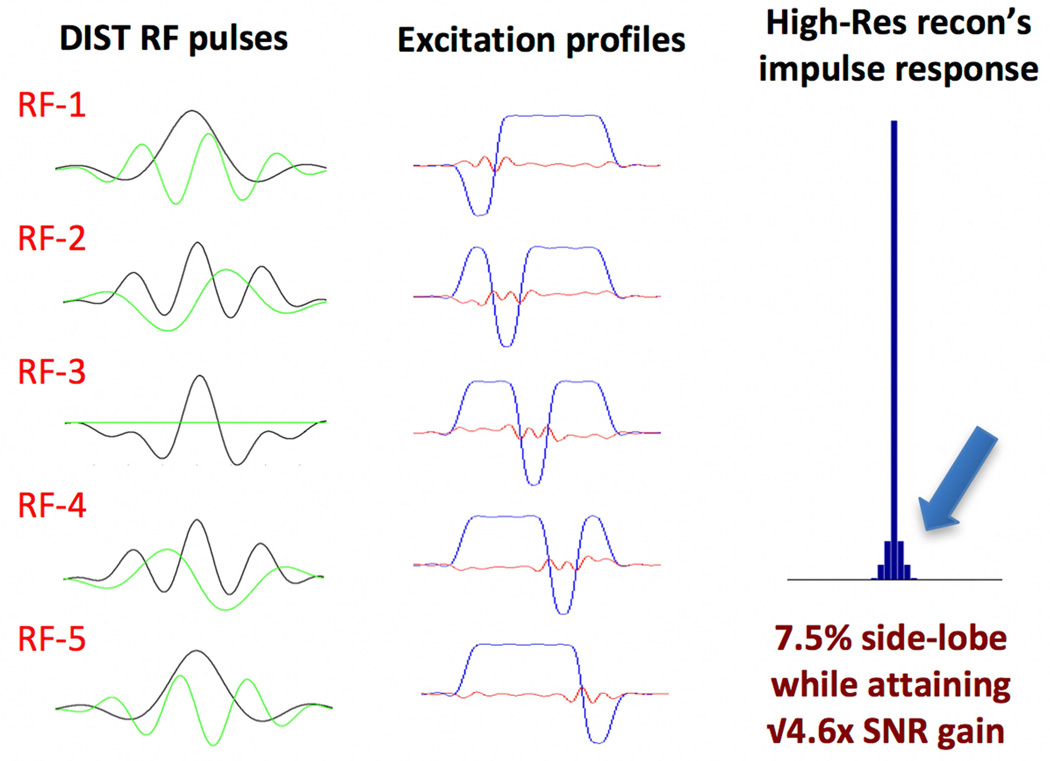
gSlider’s slab RF-encoding is similar to conventional Hardamard encoding in that multiple RF-encoded slab volumes are acquired in a sequential manner and combined to create high-resolution thin-slice reconstruction. However, a distinct feature of gSlider is that the RF-encoding bases are designed not only to be highly independent, but also so that each shot contains high image-SNR to allow robust estimation and removal of any phase corruption imparted by motion during the diffusion gradient. This self-navigation achieves this goal without lengthening the sequence with additional navigator acquisitions (33,34). The through-slab encoding method also enables the use of real rather than magnitude data to avoid large magnitude bias in the noise when reconstructing SNR-poor, thin-slice images. Figure 1 shows an exemplar basis used for the partition encoding of the thin slabs for 5×-gSlider. Here DIST RF pulses (35) with time-bandwidth-product (TBWP) of 12 are used to create 90° excitations with ‘slice-phase dithering’ (in conjunction with conventional 180° SLR refocusing at TBWP of 8). Shown on the left are the real (black) and the imaginary (green) components of the RF pulses, and in the middle the corresponding excitation profiles obtained via Bloch simulation. For each excitation, one sub-slice within each slab undergoes a π phase modulation. This ‘slice-phase dithering’ approach provides a highly independent basis, while maintaining high image-SNR in each thin-slab, at ~3× that of the standard thin-slice acquisition.

Figure 1.

5×-gSlider with ‘slice-phase dither’ encoding to provide highly independent basis, while maintaining high image-SNR in each individual slab acquisition. The DIST RF pulses are shown in the left column, with real and imaginary parts shown in black and green respectively. The corresponding slab profiles are shown in the middle column, each with a π phase dithering applied to a different sub-slice. The impulse response of the thin-slice high-resolution reconstruction with Tikhnonov regularization is shown in the right column.

To achieve thin-slice high-resolution reconstruction, data are first Fourier transformed into the image domain along the in-plane directions (x and y). The thin partitions are then resolved within the acquired thin-slabs using standard linear reconstruction with Tikhonov regularization:

$$z={(A^{T}A+\lambda I)}^{-1}{A}^{T}b=A_{\mathit{\text{inv\_tik}}}b$$

Here A contains the RF-encoding information obtained from the Bloch simulation, b is the concatenation of the acquired RF-encoded slab data (at a given x, y position), and z is the corresponding high slice-resolution reconstruction. By using the Bloch simulation of the slab profiles to create the forward model (A), the small cross-talk/coupling between adjacent slabs is captured and accounted for in the reconstruction. Here the slab’s cross-talk (as can be observed in the Bloch simulation results in Figure 1) is much smaller than the typical multi-slab acquisitions, where much thicker slabs are used, making it much harder to achieve sharp slab profiles.

With Tikhonov reconstruction, the regularization effect on the final image resolution can be characterized via impulse response analysis, where an impulse signal is passed through the forward model matrix (A) and reconstruction matrix (A_{inv_tik}).

$${\mathit{\text{Imp}}}_i=A_{\mathit{\text{inv\_tik}}}A{\delta }_i$$

Here, δ_i is an impulse vector at the i^th position along z, and Imp_i is the corresponding impulse response.

To calculate the SNR of the i^th voxel of the final image, the signal level is obtained by summing up the impulse response and the standard deviation is obtained by performing root-sum-of-square weighting of the values in i^th row of A_{inv_tik}.

$${\mathit{\text{SNR}}}_{\mathit{\text{highres}}(i)}=\frac{s_i}{{\sigma }_i}=\frac{{\Sigma }_j{\mathit{\text{Imp}}}_i(j)}{\sqrt{{\Sigma }_j{(A_{{\mathit{\text{inv}}}_{\mathit{\text{tik}}}}(i,j))}^2{\sigma }_{\mathit{\text{low\_res}}}^2}}$$

Here, SNR_highres(i) is the SNR of the high-resolution reconstruction at the i^th voxel along z, S_i is the reconstructed signal strength for the same voxel, and ${\sigma }_{\mathit{\text{low\_res}}}^2$ is the variance of the acquired slab data. Using the impulse response and SNR characterization outlined here along with an appropriate level of Tikhonov regularization (λ= 0.4), the 5×-gSlider of Figure 1 can achieve an SNR gain of √4.6 (close to the theoretical √5), while maintaining a sharp partition resolution at 7.5% side-lobes amplitude (Figure1-right), comparable to conventional 2D slice-by-slice imaging. A comparison of the image reconstruction performance with and without Tikhonov regularization is included in the supplemental material (Supporting Figure 1). Note that for accurate modeling/reconstruction, the small excitation side-lobes from the gSlider slab-encoding that leaks into the adjacent slabs are incorporated into the forward model and the reconstruction. As such, the reconstruction is coupled and is performed one whole-slice at a time (for each x, y position).

gSlider-SMS with zoom imaging

gSlider can be combined with blipped-CAIPI SMS to achieve efficient simultaneous multi-slab imaging with fast volumetric encoding and short TR. With each of the gSlider’s slabs being relatively thin in high-resolution dMRI at a slab thickness of 3–4 mm, the g_z gradient blips in the blipped-CAIPI EPI used to achieve controlled aliasing between the slabs will have minimal effect within each slab. This enables the use of a simple sequential reconstruction pipeline where leak-block slice-GRAPPA (36) is first employed to unalias the simultaneously acquired slabs. The background phase removal for each slab volume is then performed using the real-value diffusion algorithm (34). Here, real-valued data is obtained to avoid magnitude bias, first by utilizing the ‘SENSE1’ complex coil combination (37) and second by estimating and removing shot-to-shot background phase in each diffusion image (34). The processed data of the multiple RF-encoded slab volumes are then combined using the Tikhonov regularized reconstruction outlined above to achieve the final thin-slice high-resolution image.

To mitigate the lengthy in-plane k-space encoding at high-resolution, gSlider-SMS is combined with zoom imaging with inferior saturation pulse. By combining gSlider with SMS, shorter TRs can be achieved. By further combining it with zoom imaging, the long k-space encoding period can be reduced without a multi-shot approach that would increase the total acquisition time and the motion sensitivity, with longer period needed to acquire data for each high-resolution volume. With this approach, high-quality whole-brain data at 600–700μm isotropic resolution can be acquired with a total acquisition time per high-resolution volume of ~20s rather than multiple minutes.

Method

Data acquisition and reconstruction

To validate gSlider-SMS, data were acquired in vivo from two volunteers with institutionally approved protocol consent. Imaging was performed on the MGH-UCLA Skyra Connectom Scanner with a maximum gradient strength of 300mT/m and with a maximum slew rate of 200T/m/s. A custom built 64 channel phased array coil was employed for signal reception (38). For both subjects, data were acquired using a 10 simultaneous slice sagittal acquisition (gSlider×MB = 5×2), where OVS of the neck was employed for zooming (R_zoom×R_GRAPPA = 1.85×2 = 3.7). A monopolar diffusion acquisition was performed where DIST RF pulses with a duration of 11ms and TBWP of 12 were used for 90° excitations to provide ‘slice-phase dithered’ gSlider encoding, and a conventional 180° SLR RF pulse with TBWP of 8 and pulse duration of 7.5ms was used for refocusing. The RF pulses were VERSEd and multi-banded to achieve simultaneous multi-slab acquisition at MB-2. Fat saturation was achieved using vendor supplied spectrally selective RF pulse at 110 degree flip, while the asymmetric adiabatic full-passage “skewed” RF pulse as proposed in Hwang et al (28) and Pfeuffer et al (29) was used for OVS to provide sharp saturation edge. During the acquisition, the OVS pulse is applied first, following with the fat saturation pulse, after which the monopolar diffusion acquisition is performed. The use of EPI acquisition in the sagittal plane with head-foot phase encoding is seen to be more susceptible to nerve stimulation warnings. This was overcome by rotating the acquisition plane by 10–20% in the clock-wise direction (which also helps align the brain volume), and by using an echo-spacing that is slightly larger than the minimum value (by 3–5%) to reduce the gradient slew of the phase-encoding and g_z CAIPI blips.

For the first subject, data were acquired at 660μm isotropic using the following imaging parameters: FOV 220×118×151.8 mm³; Partial Fourier 6/8; TE/TR_effective = 80ms/22s (TR per slab volume = 4.4s); effective echo spacing = 0.32ms, 4 repetitions of 64 diffusion directions at b=1500 s/mm² with interspersed b0 every 10 volumes, total scan-time ~100 minutes. For the second subject, data were acquired at 760μm isotropic using the following imaging parameters: FOV 220×119×159.6 mm³; p.f. 6/8; TE/TR_eff = 77ms/21s (TR per thick-slice volume = 4.2s); effective echo spacing = 0.29ms, 1 repetitions of 128 diffusion directions at b=1800 s/mm² with interspersed b0 every 10 volumes, total scan-time ~50 minutes. Note that the g_z CAIPI blips used to create FOV/2 shift in these acquisitions, introduce only ~4° through-slab phase variation, resulting in <0.1% signal loss. For both subjects, data reconstruction was performed as outlined above. Eddy-current and motion correction were performed using FSL eddy-current toolbox, and DTI-fitting were also then accomplished using FSL (39,40).

Sensitivity Analysis of gSlider to non-idealities and confounds

B₀ and B₁ inhomogeneity

Simulations were performed to access the impact of B₁ and B₀ inhomogeneity onto the gSlider acquisition/reconstruction. The non-ideal RF encodings created by the gSlider and SLR RF pulses under non-ideal B₁ and B₀ conditions were simulated and incorporated into the forward model of the encoding (A_non-ideal). The reconstruction impulse response was then assessed under these non-ideal conditions (Imp_non-ideal,i), where it is assumed that standard reconstruction matrix (A_{inv_tik}), which do not account for these imperfections, will be used for the reconstruction. Specifically:

$${\mathit{\text{Imp}}}_{\mathit{\text{non-ideal,i}}}=A_{\mathit{\text{inv\_tik}}}{A}_{\mathit{\text{non-ideal}}}{\delta }_i$$

To assess the impulse response variations over a B₀ and B₁ variation range of up to 100Hz and 30%, simulations were performed at two extreme points within this range: (i) B₀ = +50Hz and B₁ = 85% and (ii) B₀ = −50Hz and B₁= 115%. VERSEd RF pulses with a 55% peak voltage reduction (used in the in vivo experiments) were used for this simulation. Since the degradation of the gSlider encoding profiles at off-resonance is spatially varied across the encoded slab, the reconstruction performance will varies across the sub-slices. As such the non-ideal impulse response was calculated for all sub-slice positions. These results were then compared to the impulse response under idealized conditions. We note that B₀ inhomogeneity will cause the RF encoding profile to both degrade and shift along z. The shift along z can cause the center of the impulse response in our analysis to stagger between two discretized z voxels, causing it to be difficult to visualize clearly. We therefore round the effective z shift to an integer position, which help overcome this issue but do not affect the validity of the overall analysis (for our constant B₀ offset cases with no spatial variation).

Motion

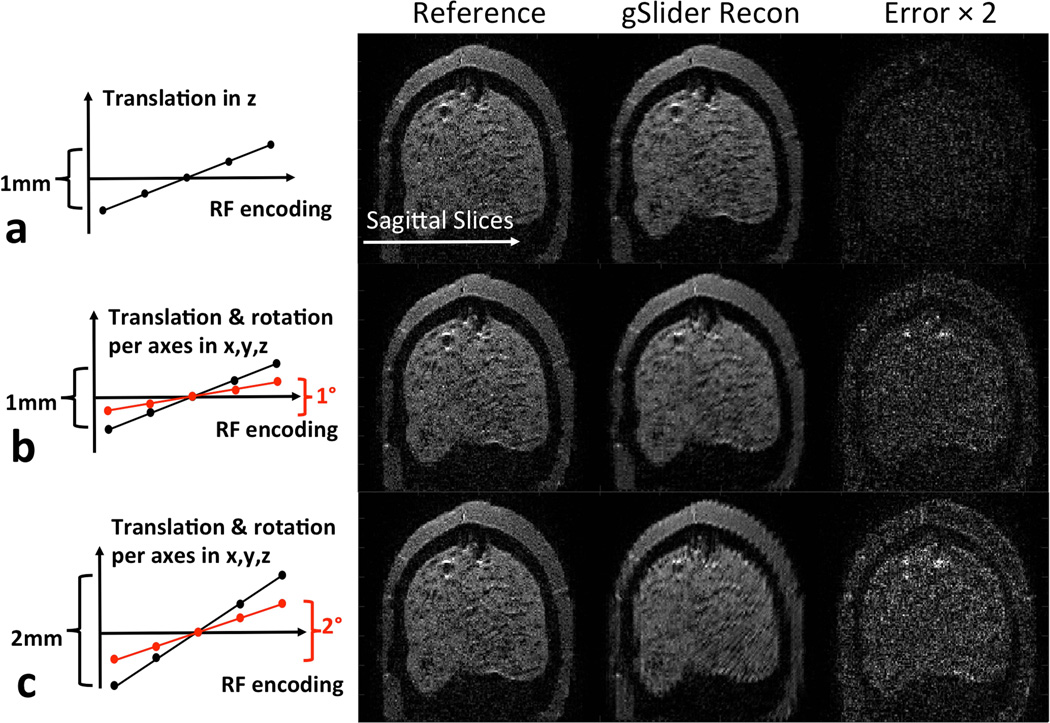
The proposed gSlider-SMS acquisition can acquire a 600–700μm whole-brain diffusion image in just over 20s, which is fast compare to current diffusion acquisition approaches. Nonetheless, significant motion can still occur during this ~20s timeframe. As such, simulations were performed to access the effect of such motion during the gSlider encoding. As a gold-standard dataset, gSlider data were collected on an anthropomorphic head phantom and reconstructed to high slice-resolution using the proposed reconstruction framework. gSlider slab-encoded data with motion were then simulated by adding motion to the high-resolution dataset and passing the resulting volume through the forward encoding model. The motion corrupted gSlider slab-encoded data were then reconstructed to high slice-resolution using the proposed reconstruction framework (without accounting for motion) and were then compared with the gold-standard dataset. Three motion cases were simulated: a) a linear translation of 1mm in the slice direction during the 5 gSlider encoding acquisition, b) a linear translation of 1mm and rotation of 1° in each of the slice, read and phase encode direction, c) a linear translation of 2mm and rotation of 2° in each of the slice, read and phase encode direction. The gold standard dataset was acquired at b=1500 s/mm² and 860μm resolution (This resolution was chosen to achieve a good SNR level in the gold-standard data. The minor difference in resolution to the in vivo datasets should not significantly affect the analysis).

Results

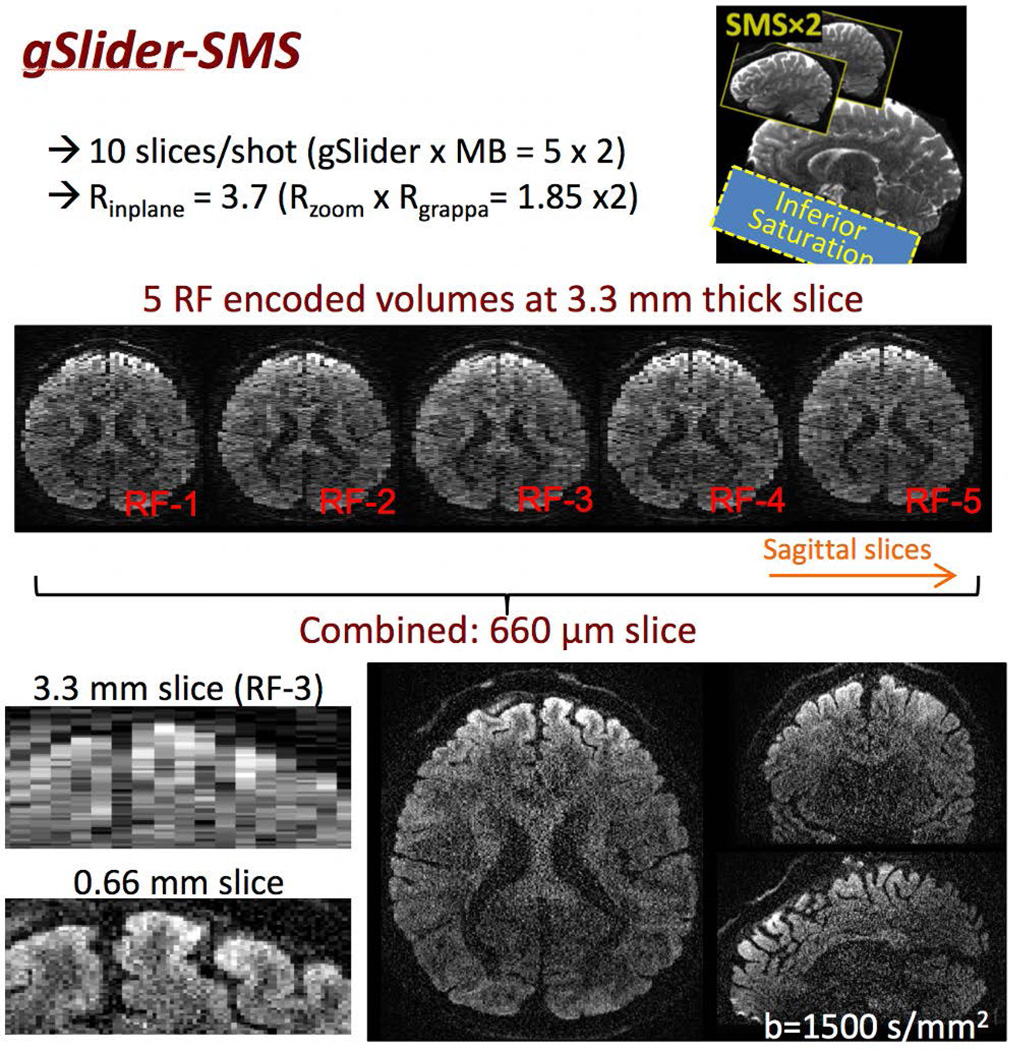
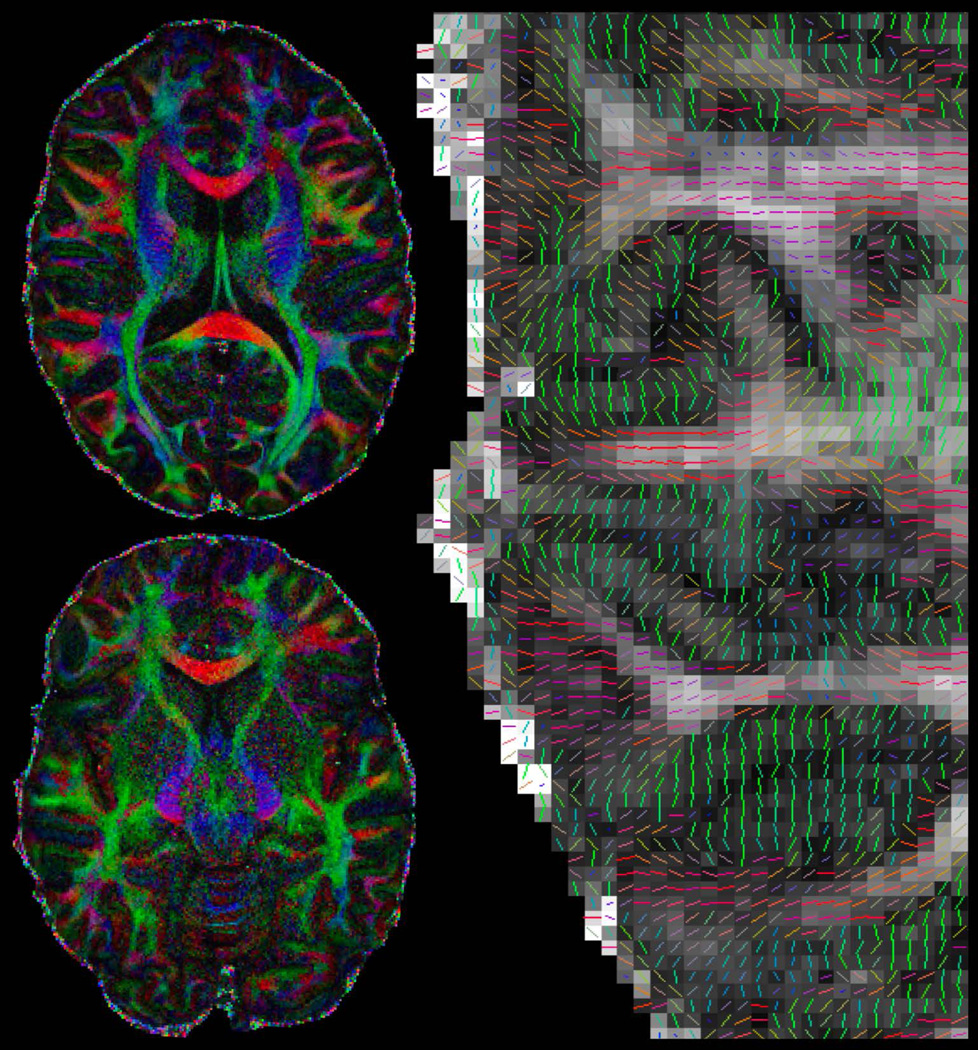
Figure 2 shows the overall image acquisition schematic of gSlider-SMS (top right), along with a representative 660μm diffusion data at b-value of 1500 s/mm² (center and bottom). Figure 2-center shows the 5 RF-encoded slab volumes, each at 3.3 mm sagittal slab thickness, each with high image-SNR to allow effective background phase estimation and removal. Figure 2-bottom shows 660μm isotropic reconstruction achieved from combining these RF-encoded volumes. Also, shown on the bottom left are the zoom-ins of the anterior region of the brain in the axial plane along the sagittal slice direction (running left-right) of (i) one of the RF-encoded slab volume (RF-3) and (ii) the final thin-slice high-resolution reconstruction. A large gain in resolution can be observed in the final reconstruction, where much more detailed information of the cortical folding can be resolved.

Figure 2.

A 10 simultaneous slice gSlider-SMS acquisition where two sagittal thin-slabs are acquired simultaneously, each at 5× the thickness of the final slice resolution. Here, zoom imaging with inferior saturation pulse in a sagittal acquisition is also used to achieve high in-plane acceleration while retaining whole-brain coverage. Five thin-slab volumes with different slice-phase dither encoding are acquired in total sequentially (middle row). These volumes are combined to create the final high-resolution image (bottom row). Also shown on the bottom row are the zoom-ins of the thin-slab axial image and the final high-resolution image, where the resolution gain can be clearly observed.

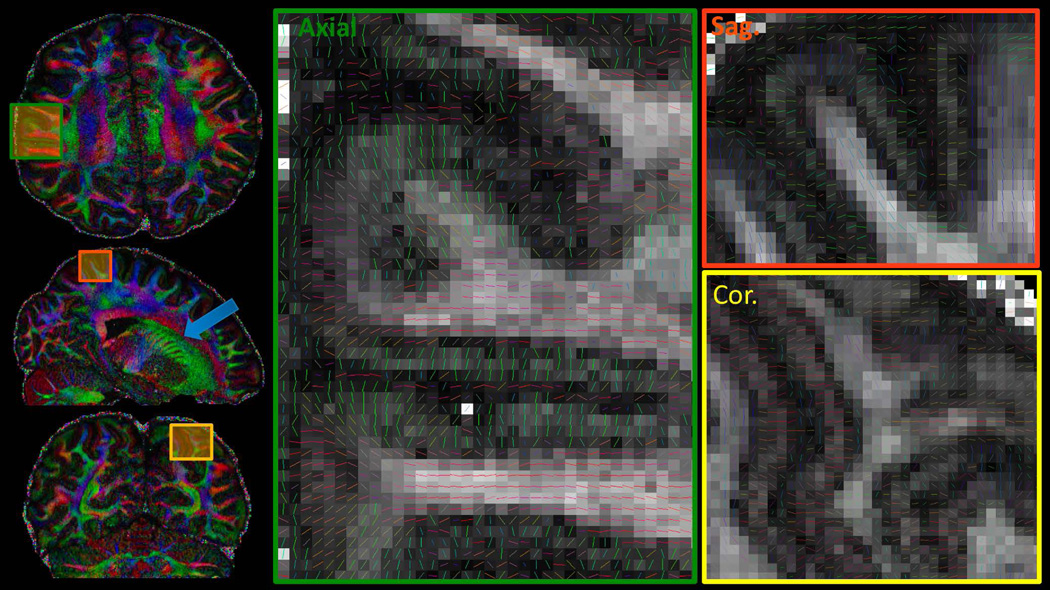
The DTI reconstruction of the 660μm gSlider-SMS data is shown in Figure 3, with color-FA results in three orthogonal planes on the left, and the zoomed-in tensor plot of each plane on the right. Fine-scale structures can be observed such as the striatum in the sagittal plane of the color FA map (blue arrow), which clearly depict the cell-bridge connecting between the Caudate and Putamen. The zoomed-in tensor plots demonstrate the ability of this high isotropic resolution data to aid in the detection of fine-scale structures in any spatial orientation, with multiple voxels across the cortical layers and expected dark bands of FA at gray-white tissue boundaries.

Figure 3.

Diffusion results of the 660μm isotropic data, with color-FA maps shown on the left and the zoom-ins of the tensor results shown on the right. Results are displayed in three orthogonal planes to highlight the ability of this high-resolution isotropic data in enabling the visualization of fine-scale structures in all spatial orientations.

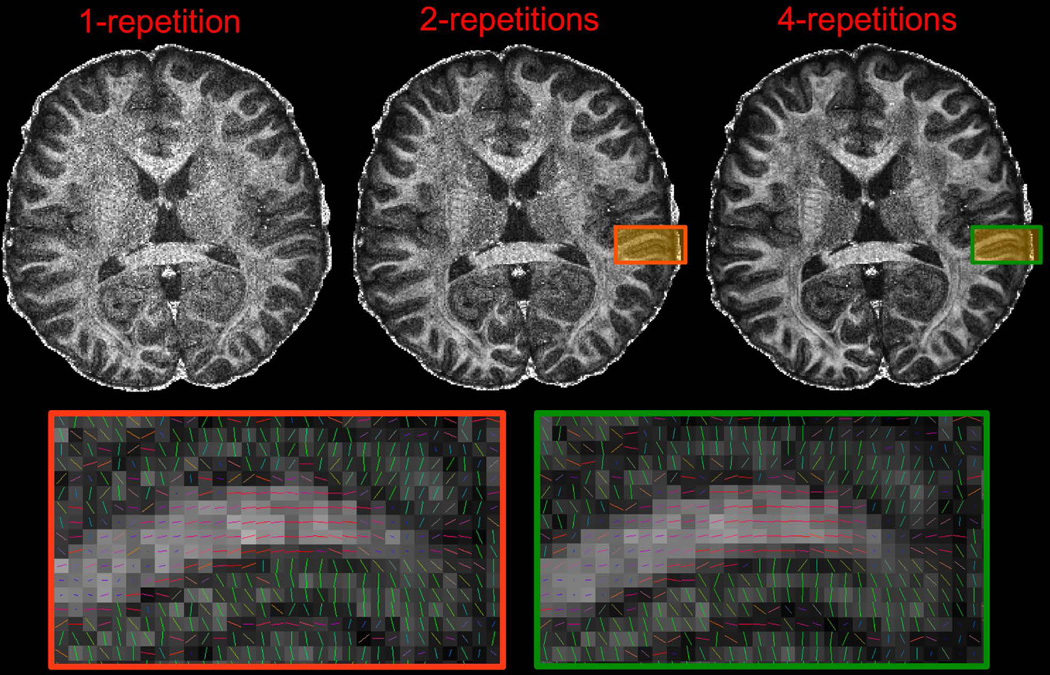
Figure 4 compares DTI reconstructions from using 1, 2 and 4 repetitions of the 64-direction 660μm data (25minutes/repetition). In moving from one to two repetitions, the FA map improves significantly, with lower noise level to provide reasonable tensor results (orange zoomed box) at this extreme resolution using a 50-minute scan. With 4 repetitions, the FA and tensor estimates further improve to provide robust diffusion estimates, with the zoomed-in tensor result shown in the green box.

Figure 4.

SNR and effect of averaging of the 660μm isotropic data. FA maps and zoom-in tensor results are shown, where each data repetition took 25 minutes to acquire. With two repetitions and 50-minute scan time, reasonable FA and tensor results can be achieved. These results improve with further data averaging to provide robust results with 4 data averaging.

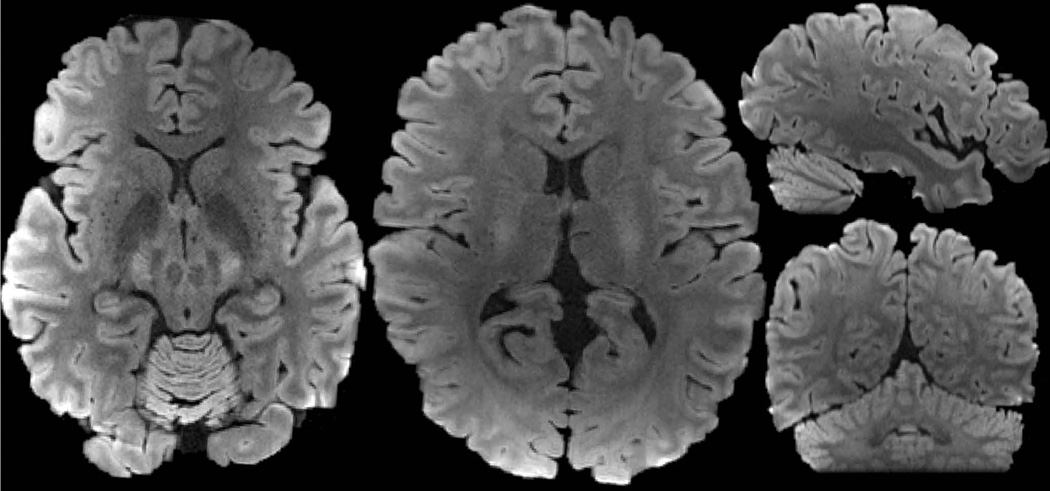
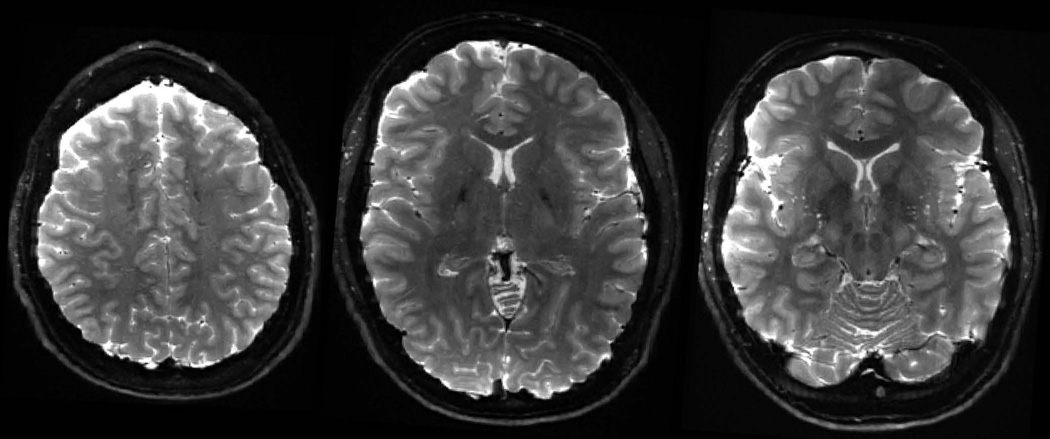
Diffusion reconstructions from subject 2’s data at 760μm isotropic resolution are shown in Figure 5, where the voxel size here is ~50% larger when compared to the 660μm isotropic resolution. At this resolution, robust FA and tensor results can be obtained from a single 50-minute scans of 128 directions at b 1800s/mm². Figure 6 shows the averaged DWI with high contrast and high level of anatomical detail, while Figure 7 shows the averaged-b0 image obtained through averaging across the 13 repetitions of b0 data that were acquired during the 50-minute scan.

Figure 5.

Diffusion results of the 760μm isotropic data at b = 1800s/mm². Color-FA maps are shown on the left and the zoom-in of the tensor results is shown on the right.

Figure 6.

Average DWI of the 760μm data obtained by averaging across the 128 diffusion direction dataset.

Figure 7.

b0 images at 760μm isotropic resolution obtained from averaging across 13 intersperse b0 data.

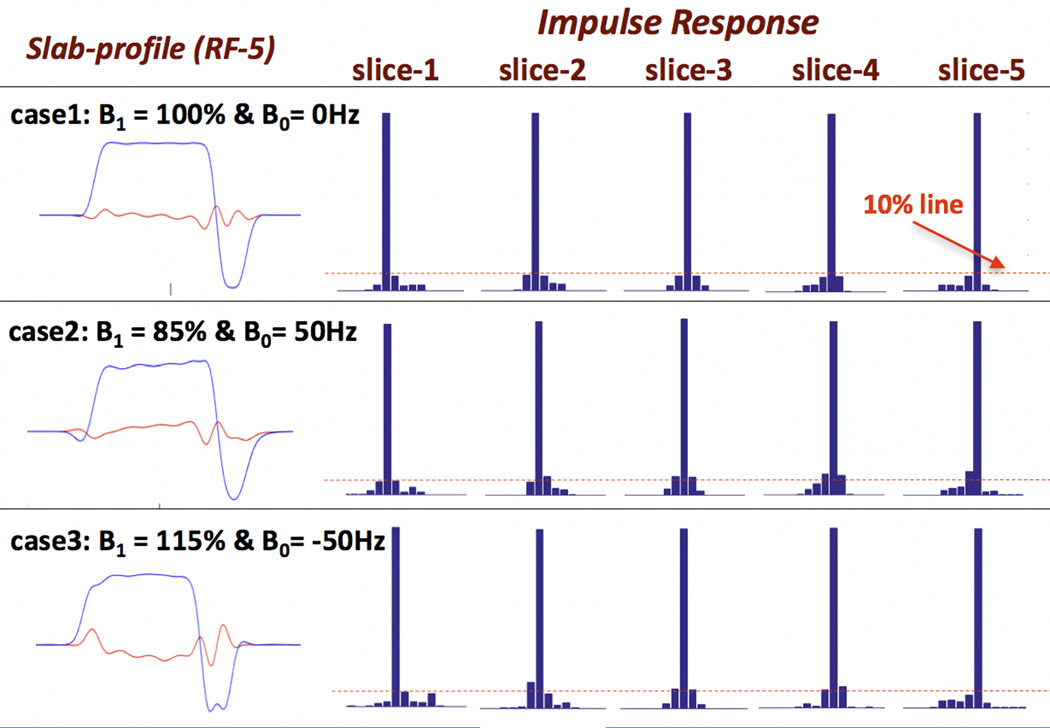
Figure 8 shows the effect of B₁ and B₀ inhomogeneity on gSlider acquisition/reconstruction. Shown are the slab-encoding profiles of one of the encoding basis (RF-5) along with the reconstruction’s impulse response for all of the 5 sub-slices, under three different B₁ and B₀ conditions. Under ideal conditions (case1, top row), good slab-encoding and impulse response (max side-lobe of 7.5%) were achieved. With non-ideal conditions in case 2 and 3 (B₁ and B₀ ranges of 100Hz and 30% respectively), some degradation in the slab-profile is observed along with some increase in the impulse response’s side-lobes. Overall, the impulse response deviation remains relatively small with the maximum side-lobe of ~13%.

Figure 8.

Sensitivity analysis of gSlider encoding and reconstruction to B₁ and B₀ inhomogeneity. The slab-encoding profiles of one of the encoding basis (RF-5) along with the reconstruction’s impulse responses for all of the sub-slices are shown for three different B₁ and B₀ cases. A relatively small amount of degradation in the impulse responses is observed in the non-ideal cases.

Figure 9 shows the effect of motion during the 5× gSlider RF-encoded acquisitions on the resulting high slice-resolution reconstruction. In case a (top-row), a linear translation of 1mm in the slice direction (z) results in some blurring in the reconstruction, with a relatively small error (error image shown on the right column at 2× scaling). With the addition of linear translations along the readout and phase encoding directions, and a 1° rotation on each of the three axes (case b), increased blurring and some edge artifacts are observed in the reconstruction. In case c, where these motions are then increased by a further two-fold, the image reconstruction artifacts becomes more pronounced, but such motions do not cause a catastrophic reconstruction failure.

Figure 9.

Simulation of gSlider reconstruction on an anthropomorphic head phantom in the present of motion between the 5×-gSlider slab-encoded acquisitions. Three different amount of motion were simulated, with more blurring and edge artifacts being observed in the reconstruction as the motion increases, but without catastrophic reconstruction failure.

Discussion and conclusion

gSlider-SMS was developed to provide efficient, self-navigated simultaneous multi-slab dMRI acquisition that can take advantage of volumetric encoding from both SMS and a Hadamard style encoding in the partition direction using simple self-navigation. This approach was further combined with zoom imaging to achieve low distortion ultra high-resolution dMRI. The combined acquisition approach was successfully used to acquire data at 660 and 760μm isotropic resolutions, where fine detailed brain structures were observed in gray and white matter areas, as well as at the gray-white matter boundaries.

In addition to the efficient acquisition sequence, these acquisitions also benefited from the increased SNR provided by the tight-fitting custom-built 64 head-only receive array and the TE reduction from using the high gradient strength of the custom Connectom scanner. However, at 660μm isotropic resolution, data averaging across four repetitions of 25-minute scan was still required to obtain robust diffusion results. At such resolution, the voxel size is ~6 fold smaller than the current high-end diffusion acquisitions at ~1.2 mm isotropic, and therefore would require 36 times longer scan to achieve the same SNR level if conventional methods were used (not accounting for SNR loss from increased T₂ decay of longer TE, which is mitigated here through zoom imaging). Increasing the voxel size to 760μm isotropic was shown to enable high quality data to be obtained in a single 50-minute scan with our efficient acquisition. With the relatively low b-value of 1500–1800 s/mm² that was used, the TE reduction of using the Connectom scanner over high-end clinical 3T scanners (with e.g. G_max=80mT/m) is only 6–8ms and therefore does not translate to a dramatic SNR benefit. Future work will therefore explore the deployment of our new acquisition strategy on clinical scanners, particularly in conjunction with our recently developed de-noising reconstruction (41) and Q-space compressed sensing (42) frameworks. The goal will be to achieve high-quality sub-millimeter dMRI on clinical scanners in a clinically relevant time frame.

In this work, 5×-gSlider encoding was achieved using the ‘slice-phase dithering’ approach, implemented through the DIST 90° excitation pulses. Here, the slice-phase dithering effectively spreads the RF energy of each excitation pulse across the real and imaginary components (see Figure 1), which reduces the peak power of the slab excitation (This is somewhat similar to the phase optimization scheme used to design low peak power MB pulses (43)). However, the standard SLR refocusing pulse used for refocusing still exhibits high peak-power, particularly at MB-2, requiring the use of VERSE to reduce peak power. The 90° excitation was similarly VERSEd to achieve off-resonance slice-profile shift (and degradation) similar to that of the refocusing pulse, thereby providing good slice refocusing performance. Simulations were performed to assess the degradation in the gSlider encoding and image reconstruction performance in the present of B₁ and B₀ inhomogeneity (range 100Hz and 30% respectively). Some degradation in the reconstruction’s impulse response was observed, but was in a reasonably small range. These simulations were performed for constant B₁ and B₀ offsets (not spatially varying), which should provide a good approximation to the slow spatially varying field cases, but not for the rapidly varying ones. Future work will include the analysis of more complex non-ideal cases. More importantly, to improve the reconstruction accuracy at spatial locations with large off-resonance and transmit field variations, B₀ and B₁ field maps will also be acquired and incorporated into the reconstruction model directly. A joint design strategy to share the gSlider RF-encoding load across both the 90° and 180° pulses to reduce peak power will also be pursued to reduce off-resonance sensitivity. This can be done by exploiting a similar approach to the design of low peak-power 90°and 180° slice-selective pulse pairs with varying through-slice phases that combine to provide a flat phase spin-echo excitation (44,45). This should reduce the need for VERSE and enable shorter RF pulses.

The gSlider acquisition provides a new approach for self-navigated multi-slab dMRI. The slice-phase dithering used in this work provides near orthogonal encoding basis for 5×gSlider acquisition, while achieve a high ~3× SNR level in the individual acquisitions to allow accurate estimate of the background phase corruption at our targeted resolution of 600–700μm. In addition to slice-phase dithering, other RF-encoding bases under this framework that can provide high-image SNR while being highly independent, should be explored to allow higher gSlider factors and/or shorter RF pulses. At higher gSlider factors, the TR of each slab volume acquisition will be shortened, leading to further improvements in SNR efficiency. Nonetheless, at these shorter TRs of 4s or less, the slab-cross talk would likely become more prominent even for our relatively thin-slab acquisition. Therefore, a correction approach similar to Nonlinear Inversion for Slab Profile Encoding (NPEN) (20) is likely to be needed to ensure high quality reconstruction. Additionally, with the gSlider slab-excitation, the transition regions between the sub-slices undergo no/partial excitation. As such, the spins at these locations would be inverted rather than refocused when the SLR 180 pulse is applied. At short TRs, this could lead to TR-related spin-history effects, as different gSlider encoding pulses with different transition profiles are used from one TR to the next. Future work includes the modeling of such effect and the development of mitigation approaches through improved RF pulse design and the incorporation of the spin-history information into the reconstruction.

The effect of motion during a set of five thick-slice gSlider acquisitions (~20s time-frame) on the image reconstruction was simulated. It was observed that such motions could lead to some image blurring and edge artifacts in the reconstruction, but they do not cause a catastrophic reconstruction failure. With gSlider acquisition, full imaging volumes (at thick-slice) are created at a high temporal rate (of ~4s in this work). Future work will explore the use of these imaging volumes for motion estimation, and to incorporate such information directly into the gSlider reconstruction framework to improve motion robustness. The incorporation of spin-history effects in relation to such motion into the reconstruction framework will also be examined.

In this work, zoom imaging was employed to provide high in-plane acceleration of 3.7×, without a large g-factor noise penalty or resorting to a multi-shot approach that would lengthen the acquisition and increase motion sensitivity. If higher in-plane acceleration is desired to achieve a further reduction in image distortion and blurring, a multi-shot approach can still be incorporated with zoom imaging. With the acceleration factors of these approaches adding multiplicatively, i.e. R_InPlane =R_zoom×R_GRAPPA×R_multishot, a low multi-shot factor of e.g. 2–3× would already enable a very high total in-plane acceleration.