Bayesian adaptive model selection for optimizing group sequential clinical trials

SUMMARY

This article presents a new approach to the problem of deriving an optimal design for a randomized group sequential clinical trial based on right-censored event times. We are motivated by the fact that, if the proportional hazards assumption is not met, then a conventional design’s actual power can differ substantially from its nominal value. We combine Bayesian decision theory, Bayesian model selection and forward simulation (FS) to obtain a group sequential procedure that maintains targeted false-positive rate and power, under a wide range of true event time distributions. At each interim analysis, the method adaptively chooses the most likely model and then applies the decision bounds that are optimal under the chosen model. A simulation study comparing this design with three conventional designs shows that, over a wide range of distributions, our proposed method performs at least as well as each conventional design, and in many cases it provides a much smaller trial.

1. INTRODUCTION

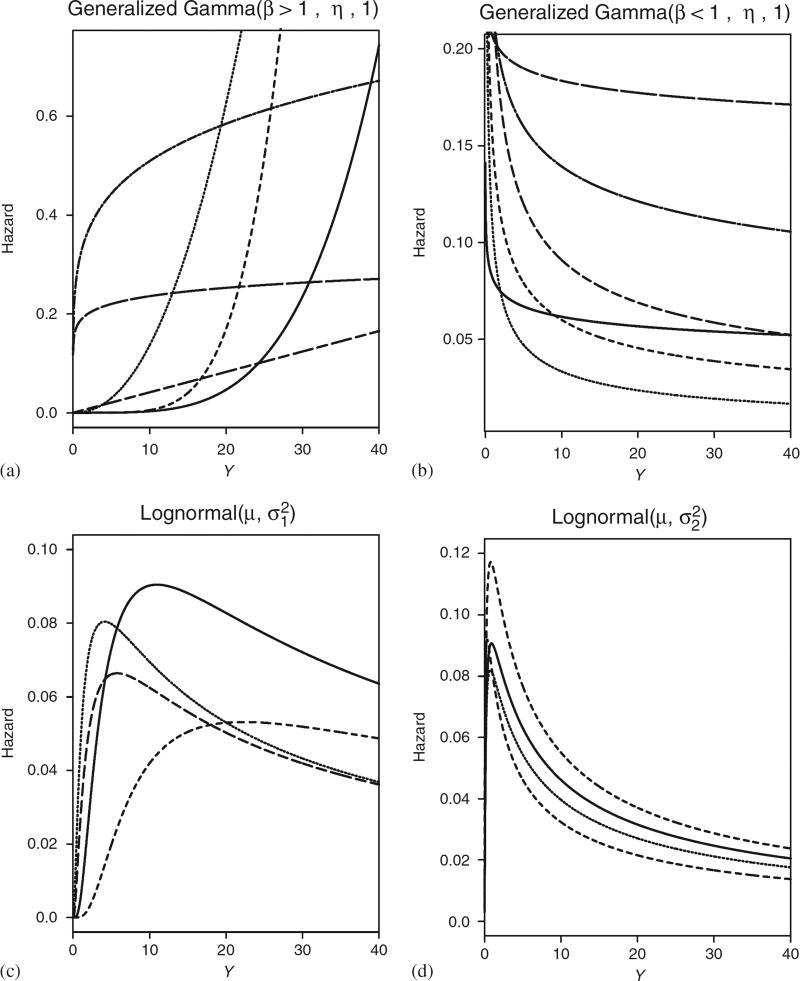
The use of group sequential designs has become routine in phase III clinical trials. Many authors have provided general group sequential methods [1–3] and approximately optimal group sequential procedures [4–9]. Each of these group sequential designs is derived by assuming a sequence of normally distributed test statistics with unknown mean and known variance, with proportional hazards usually assumed to accommodate right-censored event times. While these designs are used routinely in practice, if the proportional hazards assumption is not met, then the design’s actual power may differ substantially from its nominal value. For example, if the true event time distribution is lognormal with a hazard that initially increases and then decreases (Figure 1(d)), then the actual power achieved by the O’Brien and Fleming (OF) [1], Pocock [2] and optimal Hwang, Shih and De Cani (HSD) [5] designs with nominal power 80 per cent may be as low as 20–40 per cent (Tables I–III). Thus, the trial would be unlikely to identify a true treatment advance. In contrast, if the true event time distribution is Weibull with an increasing hazard (Figure 1(a)), then the actual power achieved by the OF, Pocock and HSD designs with nominal power 80 per cent may be as high as 99 per cent (Tables I–III). In this case, these designs each enroll 33 per cent to 50 per cent more patients than the optimal Bayesian design that we will present here.

Figure 1.

Summary of potential hazards in ℳ. ℳ₁ is generalized gamma(1, η, 1), equivalent to an exponential, which has constant hazard and thus is not shown: (a) ℳ₂; (b) ℳ₃; (c) ℳ₄; and (d) ℳ₅.

Table I.

Robustness simulation study results to compare Bayesian doubly optimal group sequential (BDOGS) with O’Brien–Fleming (OF) procedure when the assumption of proportional hazards is not met in a clinical trial with five analyses. The true median TTF is 12 months for A.

True hazard	Method	False pos.	Power	Sample size, δ =0 (δ=3)
				Mean	2.5 per cent	25 per cent	50 per cent	75 per cent	97.5 per cent
Proportional hazards assumption met
Exp	BDOGS	0.05	0.80	625 (651)	380 (395)	536 (669)	668 (716)	716 (716)	716 (716)
	OF	0.05	0.80	618 (658)	512 (449)	536 (573)	655 (698)	687 (716)	716 (716)
Robustness study-proportional hazards assumption not met
WI	BDOGS	0.04	0.90	371 (389)	347 (366)	363 (381)	371 (389)	380 (398)	398 (415)
	OF	0.04	0.99	585 (503)	478 (375)	500 (408)	613 (514)	638 (532)	716 (666)
PI	BDOGS	0.01	0.84	356 (374)	332 (353)	348 (366)	356 (375)	364 (384)	379 (402)
	OF	0.05	0.99	572 (409)	464 (354)	485 (370)	596 (381)	623 (482)	716 (519)
VS	BDOGS	0.05	0.95	369 (378)	335 (350)	350 (367)	359 (377)	369 (386)	492 (408)
	OF	0.05	0.99	578 (461)	463 (354)	487 (381)	599 (490)	626 (508)	716 (641)
LN2	BDOGS	0.05	0.40	481 (543)	381 (397)	403 (422)	418 (477)	573 (716)	716 (716)
	OF	0.05	0.38	655 (682)	550 (568)	580 (624)	716 (716)	716 (716)	716 (716)
WD	BDOGS	0.04	0.27	406 (458)	373 (388)	391 (408)	400 (421)	412 (447)	553 (716)
	OF	0.05	0.24	638 (675)	530 (546)	559 (678)	686 (716)	716 (716)	716 (716)
PD	BDOGS	0.05	0.26	473 (433)	398 (384)	420 (404)	433 (415)	538 (430)	680 (587)
	OF	0.05	0.36	637 (674)	545 (539)	580 (608)	680 (716)	680 (716)	680 (716)

Table III.

Robustness simulation study results to compare Bayesian Doubly Optimal Group Sequential (BDOGS) with HSD optimal procedure when the assumption of proportional hazards is not met in a clinical trial with five analyses. The true median TTF is 12 months for A.

True hazard	Method	False pos.	Power	Sample size, δ =0 (δ=3)
				Mean	2.5 per cent	25 per cent	50 per cent	75 per cent	97.5 per cent
Proportional hazards assumption met
Exp	BDOGS	0.05	0.80	639 (650)	505 (409)	638 (675)	675 (680)	680 (680)	680 (680)
	HSD	0.05	0.80	611 (627)	383 (398)	537 (566)	656 (680)	680 (680)	680 (680)
Robustness study—proportional hazards assumption not met
WI	BDOGS	0.03	0.90	375 (397)	346 (365)	363 (381)	371 (390)	381 (401)	483 (515)
	HSD	0.05	0.99	584 (473)	363 (369)	498 (390)	610 (427)	680 (522)	680 (680)
PI	BDOGS	0.01	0.84	357 (388)	334 (350)	349 (365)	357 (377)	364 (385)	380 (503)
	HSD	0.05	0.99	572 (389)	346 (352)	481 (368)	592 (377)	680 (388)	680 (506)
VS	BDOGS	0.05	0.98	384 (380)	335 (351)	351 (368)	362 (377)	382 (387)	488 (492)
	HSD	0.04	0.99	578 (429)	350 (354)	486 (373)	594 (388)	680 (490)	680 (624)
LN2	BDOGS	0.05	0.36	455 (501)	381 (395)	402 (418)	415 (436)	445 (591)	680 (680)
	HSD	0.05	0.36	629 (646)	398 (413)	579 (680)	680 (680)	680 (680)	680 (680)
WD	BDOGS	0.04	0.25	406 (460)	373 (388)	391 (408)	401 (421)	411 (535)	542 (680)
	HSD	0.05	0.20	629 (648)	394 (409)	572 (680)	680 (680)	680 (680)	680 (680)
PD	BDOGS	0.05	0.27	473 (436)	398 (385)	420 (404)	433 (415)	543 (431)	680 (590)
	HSD	0.05	0.36	637 (645)	417 (403)	593 (680)	680 (680)	680 (680)	680 (680)

Although Bayesian methods for randomized clinical trials have received increasing attention in recent years [10–12], the use of Bayesian rules in large-scale trials remains controversial. A central issue when using Bayesian methods in a group sequential setting is that of controlling the overall false-positive error rate, especially for registration trials. Spiegelhalter et al. [11], Pocock and Hughes [13] and many others feel that controlling the false-positive rate is crucial, and this is the policy of regulatory agencies such as the U.S. food and drug administration. We share this viewpoint, since any method that does not control type I error has little chance of being widely adopted.

In this paper, we present a Bayesian decision-theoretic approach to group sequential clinical trials, with rules for concluding either superiority or futility, that controls the overall false-positive rate and power. We focus on two-sided tests for two-arm trials with time-to-event outcomes, in settings where little prior information is available about the shapes of the hazard functions. A typical approach used in practice is to assume proportional hazards and employ a conventional group sequential design. In contrast, our proposed method requires one to first specify a small set of possible models for the event time distribution. Forward simulation (FS) is used to obtain optimal decision boundaries under each possible model. Each set of decision boundaries is optimal, in that it minimizes the equally weighted average of the null and alternative expected sample sizes under the assumed model, subject to conventional overall false-positive rate and power constraints. Since the true model is not known, and we do not wish to base our decisions on a single model chosen from prior data that may turn out to be suboptimal, we utilize the data at each interim analysis by applying Bayesian model selection [14] to adaptively choose the model having the largest posterior probability. The interim decision is then based on the optimal boundaries under the chosen model. Because the model having the largest posterior probability may change as the data accumulate during the trial, the boundaries used for a given interim decision may differ from those used at previous decisions. By combining Bayesian decision theory and Bayesian model selection in this way, we are able to maintain the specified overall false-positive rate and power under a broad set of possible models. Consequently, in many cases our method enrolls substantially fewer patients than conventional designs typically used in practice. Because the optimal boundaries are chosen for each model before the trial and stored, and the model is optimized adaptively during the trial, we call the method Bayesian doubly optimal group sequential (BDOGS). To assess the design’s performance, we provide a simulation study comparing BDOGS to the OF, Pocock and HSD designs. We compare each method with BDOGS under a proportional hazards model, and also under several alternative models where this assumption is not met. Our simulations show that BDOGS performs at least as well as the OF, Pocock, and HSD designs, and in many cases it provides a much smaller trial.

The remainder of the article is organized as follows. In Section 2, we provide the general decision-theoretic framework. Section 3 develops the FS procedure for obtaining optimal bounds and presents the decision rules. Section 4 describes the model selection algorithm used at each interim analysis. Section 5 presents the BDOGS procedure, with computational algorithms given in Section 6. Section 7 presents the results of the simulation study, and we conclude with a discussion in Section 8.

2. DECISION-THEORETIC FRAMEWORK

We consider trials that will be monitored group sequentially with up to K analyses with a maximum of N patients randomized fairly between two treatments, A and B. Denote the median event times by θ_A and θ_B, with δ = θ_B − θ_A and θ = (θ_A, θ_B). The goal of the trial is to test H₀ : δ = 0 versus H₁ : δ ≠ 0. To facilitate comparison to conventional group sequential designs and promote wide acceptability of our method, we restrict attention to designs with a maximum type I error rate α* under H₀ and minimum power β* when δ = δ*.

Our notation and decision-theoretic structure will be similar to Berger [15]. Denote the observed data of the first n_k patients enrolled by the kth analysis by X_nk = (X₁, X₂, …, X_nk) for k = 1, …, K. We refer to a decision made during the trial as an action, denoted by a, with 𝒜 the set of possible actions, the action space. At the kth interim decision, the utility function, u(θ, a_k, X_nk), is the gain from taking action a_k after observing data X_nk if θ is the true parameter. A decision rule, ϕ_nk (X_nk), is a function from 𝒳^n_k, the sample space of X_nk, into 𝒜, defining the action to be taken when X_nk is observed, e.g. claim superiority of one treatment over the other. A stopping rule is a function τ_nk(X_nk) = 1 if the trial is terminated, and τ_nk (X_nk) = 0 if the trial is continued. Since N is the maximum sample size, τ_N (X_N) = 1 for all possible X_N. The decision at the kth analysis is d_k = {τ_nk (X_nk), ϕ_nk (X_nk)}, and d_k = (d₁, d₂, …, d_k) is a sequential decision procedure. The random sample size when the trial is terminated is Z = min{n_k≥0: τ_nk (X_nk) = 1} and we denote by Ψ_nk the set of observations for which the trial stops at the kth analysis and Z = n_k. Thus, Ψ_nk is the set of all X_nk ∈𝒳^n_k such that τ_nk (X_nk) = 1 and τ_ni (X_ni) = 0 for all i <k.

We define the utility of d_K to be u(θ, ϕ_Z(X_Z), X_Z) = −Z, an approach similar to that of Lewis and Berry [16]. Since, in general, we do not know the true utility of d_k, we estimate the expected utility, U(π, d_K), with respect to the posterior distribution, π, on Θ. As a computational convenience for calculating U(π, d_K), we assume that the prior of θ satisfies the conditions Pr(θ_A = θ_B) = Pr(θ_B = θ_A + δ*) = 0.5, which says that the null and the targeted alternatives are equally likely. This prior is a practical compromise between what is reasonable and what will facilitate computation of the expected utility while yielding a design that satisfies the false-positive rate and power constraints. The expected utility of a sequential decision procedure d_k is

$$U(\pi ,{\mathbf{d}}_K)=E_{\mathrm{\Theta }}{E}_{{\mathrm{\Psi }}_Z}[u(\mathbf{\theta },{\varphi }_Z({\mathbf{X}}_Z),X_Z)]={\int }_{\mathrm{\Theta }}\sum _{z=0}^N{\int }_{{\mathrm{\Psi }}_z}u(\mathbf{\theta },{\varphi }_z({\mathbf{X}}_z),{\mathbf{X}}_z)f_z({\mathbf{X}}_z|\mathbf{\theta })\pi (\mathbf{\theta })\mathrm{d}{x}_z\mathrm{d}\mathbf{\theta }={\int }_{\mathrm{\Theta }}-\sum _{z=0}^N{\int }_{{\mathrm{\Psi }}_z}{\mathbf{X}}_z{f}_z({\mathbf{x}}_z|\mathbf{\theta })\pi (\mathbf{\theta })\mathrm{d}{x}_z\mathrm{d}\mathbf{\theta }=-{\int }_{\mathrm{\Theta }}{E}_{{\mathrm{\Psi }}_Z}(Z|\mathbf{\theta })\pi (\mathbf{\theta })\mathrm{d}\mathbf{\theta }=-\{\frac{1}{2}{E}_{{\mathrm{\Psi }}_Z}(Z|{\theta }_A={\theta }_B)+\frac{1}{2}{E}_{{\mathrm{\Psi }}_Z}(Z|{\theta }_B={\theta }_A+{\delta }^{\ast })\}$$ (1)

The sequential decision process is computationally complex since it requires repeated calculation of U(π, d_K) subject to the constraints that d_K must have type I error, α, and power, β, satisfying α≤α* and β≥β*. The following section explains how the computation of U(π, d_K) may be carried out efficiently to facilitate practical application.

3. OBTAINING OPTIMAL BOUNDS

Computational difficulties in implementing backward induction [17] impose severe practical limitations on Bayesian optimal designs. Consequently, most Bayesian optimal designs, using backward induction, assume simple models [16, 18]. To deal with this problem, Carlin, Kadane, and Gelfand (CKG) [19] proposed FS as a practical alternative to backward induction. With FS, an optimal design is obtained by first simulating the trial repeatedly and storing the results. A given sequential decision procedure, d_k, is applied to each simulated data set, and expected utilities using d_k are obtained empirically from the simulated data. Since the simulation results have been stored, different d_k may be evaluated and a suitable search algorithm can be used to find the d_k that maximizes U(π, d_K). This facilitates computation, since storing the simulated data and the results of any time-consuming calculations does away with the need to resimulate the trial. Thus, one needs to apply each d_k to obtain U(π, d_K). CKG use FS to obtain the 2K − 1 boundary points of their decision procedure to maximize the expected utility. In the case considered by CKG, the complexity of finding the optimal d_K grows linearly with K. For a fully sequential or group sequential trial with large K, however, FS may become very difficult, if not impossible.

To deal with this computational problem, we propose a decision procedure that uses FS but does not depend on K by defining the decision boundaries in terms of two monotone functions, each having three parameters. Let a_U, b_U, a_L, b_L≥0 and c_U, c_L>0 be decision boundary parameters and let N ⁺ (X_nk) denote the number of treatment failures (events) in X_nk. We define the boundary functions

$$P_{\mathrm{U}}({\mathbf{X}}_{n_k},a_{\mathrm{U}},b_{\mathrm{U}},c_{\mathrm{U}})=a_{\mathrm{U}}-b_{\mathrm{U}}{\left(\frac{N^{+}({\mathbf{X}}_{n_k})}{N}\right)}^{c_U}{P}_{\mathrm{L}}({\mathbf{X}}_{n_k},a_{\mathrm{L}},b_{\mathrm{L}},c_{\mathrm{L}})=a_{\mathrm{L}}+b_{\mathrm{L}}{\left(\frac{N^{+}({\mathbf{X}}_{n_k})}{N}\right)}^{c_{\mathrm{L}}}$$ (2)

with P_L(X_nk, a_L, b_L, c_L)≤P_U(X_nk, a_U, b_U, c_U). For K≥4, γ = (a_U, b_U, c_U, a_L, b_L, c_L) has smaller dimension than the 2K − 1 boundary points of CKG. In these boundary functions, a_U and a_L define the initial decision boundaries before any patients are enrolled, b_U and b_L determine the final boundaries when all events have been observed, and c_U and c_L determine the rate at which P_U decreases and P_L increases. To ensure that P_L≤P_U, for a given γ and k′, if $P_{\mathrm{L}}({\mathbf{X}}_{n_k^{\prime }},a_{\mathrm{L}},b_{\mathrm{L}},c_{\mathrm{L}})>P_{\mathrm{U}}({\mathbf{X}}_{n_k^{\prime }},a_{\mathrm{U}},b_{\mathrm{U}},c_{\mathrm{U}})$ then for all k≥k′ we set $P_{\mathrm{L}}({\mathbf{X}}_{n_k},a_{\mathrm{L}},b_{\mathrm{L}},c_{\mathrm{L}})=P_{\mathrm{U}}({\mathbf{X}}_{n_k^{\prime }},a_{\mathrm{U}},b_{\mathrm{U}},c_{\mathrm{U}})$.

Denote the Bayesian decision criteria by p_B>A (X_nk) = Pr(δ>δ* | X_nk) and p_A>B (X_nk) = Pr(δ<−δ* | X_nk). Using these criteria and the boundary functions in (2), the trial is conducted as follows:

1. Superiority: (a) If p_B>A (X_nk)>P_U(X_nk, a_U, b_U, c_U)>p_A>B (X_nk), then stop the trial and select B; that is, d_k = (1, B). (b) If p_A>B(X_nk)>P_U(X_nk, a_U, b_U, c_U)>p_B>A (X_nk), then stop the trial and select A; that is, d_k = (1, A).

2. Futility: If max{p_B>A (X_nk), p_A>B (X_nk)}<P_L(X_nk, a_L, b_L, c_L), then stop the trial and conclude that neither treatment is superior to the other; that is, d_k = (1, Neither).

3. Continuation: If either (a) P_L(X_nk, a_L, b_L, c_L)≤p_B>A (X_nk), p_A>B (X_nk)≤P_U(X_nk, a_U, b_U, c_U) or (b) min{p_A>B (X_nk), p_B>A(X_nk)}≥P_U(X_nk, a_U, b_U, c_U), then continue enrolling patients; that is, d_k = (0, C).

Part (b) of rule 3 is included to deal with cases where var(δ | X_nk) is large and both p_A>B (X_nk) and p_B>A (X_nk) are large, although in practice both values being ≥P_U occurs rarely. Thus, from the decision rules above, ϕ_nk(X_nk) = A, B, continue or neither, and τ_nk (X_nk) = 1 if the trial is terminated, 0 if continued. At the final analysis, if the superiority rule does not apply for either treatment then we conclude that the treatments are equivalent.

Together, γ and rules 1–3 determine d_K. Denote the optimal decision rule by ${\mathbf{d}}_K^{\text{OPT}}$ and let γ^OPT be the corresponding design parameter vector. Note that ${\mathbf{d}}_K^{\text{OPT}}$ maximizes the expected utility. To find γ^OPT, we first simulate the trial 10 000 times under each of the two cases θ_B = θ_A and θ_B = θ_A + δ*. For each simulated trial, we generate the accrual times and outcomes for the maximum N patients. At each interim analysis in each simulated trial, we calculate p_B>A (X_nk) and p_A>B (X_nk). The results of these calculations and all patients’ data are stored for later use. To calculate the expected utility U(π, d_K), we apply d_K to each simulated data set and obtain the expected sample size N_a (θ, d_K) for each of the cases θ_B = θ_A and θ_B = θ_A + δ*. The expected utility is the negative of the average of the expected samples sizes under θ_A = θ_B and θ_B = θ_A + δ. If the resulting design has α≤α* and β≥β*, then the expected utility is the sample mean of the utilities from the 10 000 simulated trials; otherwise we exclude d_K from the set of possible decision procedures. If the expected utility using γ is not the maximum, then another γ is tried. Because p_B>A(X_nk), p_A>B(X_nk), and the simulated data sets have been stored and do not depend on γ, there is no need to resimulate the trial or repeat any time-consuming calculations. Therefore, in the search for γ^OPT, we only need to apply the sequential decision procedures using each proposed γ and obtain the expected utility, which is extremely fast. By using FS, we have the ability to search over a very large set of γ in a relatively short amount of time. To find γ^OPT, we begin with a coarse grid of γ and refine the grid around potential γ^OPT. Using this general procedure, the particular method used to find γ^OPT is not critical, and any efficient grid search algorithm can be used.

4. MODEL SELECTION

Bayesian model selection and model averaging have been used extensively in many settings [20, 21]. However, Bayesian model selection has not been used in clinical trial design. We use posterior model probabilities based on the current data each time an interim decision is made to choose the most likely model empirically. Denote the set of J models under consideration, by ℳ = (ℳ₁, ℳ₂, …, ℳ_J). To simplify notation, we temporarily suppress treatment information and all subscripts on X. The posterior probability of ℳ_ℓ for ℓ = 1, 2, …, J is

$$f({ℳ}_{\ell }|\mathbf{X})=\frac{f(\mathbf{X}|{ℳ}_{\ell })f({ℳ}_{\ell })}{{\sum }_{r=1}^{J}f(\mathbf{X}|{ℳ}_r)f({ℳ}_r)}$$ (3)

where f (ℳ_ℓ) is the prior probability of ℳ_ℓ, f (X | ℳ_ℓ) = ∫ f (X | ψ_ℓ, ℳ_ℓ)π(ψ_ℓ | ℳ_ℓ)d ψ_ℓ is the marginal likelihood, ψ_ℓ is the parameter vector, and π (ψ_ℓ | ℳ_ℓ) is the prior density of ψ_ℓ under ℳ_ℓ.

Since computing f (X | ℳ_ℓ) can be very time-consuming, especially if the dimension of each ψ_ℓ is large, we use an approximation of the Bayes factor (BF) given in Raftery [14] to compute the posterior probability of each ℳ_ℓ given by (3). The BF for model ℳ_ℓ versus ℳ₁ is the ratio of the posterior to prior odds,

$$B_{\ell ,1}=\frac{f({ℳ}_{\ell }|\mathbf{X})/f({ℳ}_1|\mathbf{X})}{f({ℳ}_{\ell })/f({ℳ}_1)}=\frac{f(\mathbf{X}|{ℳ}_{\ell })}{f(\mathbf{X}|{ℳ}_1)}$$ (4)

with B_{1, 1} = 1. Let ℒ_ℓ (X | ψ_ℓ, ℳ_ℓ) denote the likelihood, ${\chi }^2=2[\text{log }{ℒ}_{\ell }(\mathbf{X}|\widehat{{\mathbf{\psi }}_{\ell }},{ℳ}_{\ell })-\text{log }{ℒ}_0(\mathbf{X}|\widehat{{\mathbf{\psi }}_{\ell }},{ℳ}_{\mathrm{\ell }})]$, n the number of observations, $\widehat{{\mathbf{\psi }}_{\ell }}$ the MLE of ψ_ℓ under ℳ_ℓ, and p_ℓ = dim(ψ_ℓ) Raftery [14] gives the approximation

$$2\text{log }{B}_{\ell ,1}\approx {\chi }^2-(p_{\ell }-p_1)\text{log }n$$ (5)

where the notation a_n ≈ b_n means that lim_n→∞ (a_n/b_n) = 1. To compute f (ℳ_ℓ | X), we express the posterior model probabilities in (3) in terms of BFs, and then exploit the method of Raftery [14] to obtain B_{ℓ, 1} for ℓ = 2, 3, …, J. Denote the prior odds ξ_ℓ = f (ℳ_ℓ)/f (ℳ₁) with ξ₁ = 1. Combining (3) and (4), the posterior probability of ℳ_ℓ is

$$f({ℳ}_{\ell }|\mathbf{X})=\frac{B_{\ell ,1}\times {\xi }_{\ell }}{{\sum }_{r=1}^J{B}_{r,1}\times {\xi }_r}$$ (6)

Substituting (5) into (6) gives an approximate value of f (ℳ_ℓ | X) for ℓ = 2, …, J. The main computational requirements are obtaining the MLEs of ψ₁, ψ₂, …, ψ_M under their respective models. While Raftery provides other approximations that are more accurate, since our method requires model selection to be done repeatedly during simulation, we require a fast method for calculating the posterior model probabilities in (6). We thus use the slightly less accurate approximation in (5) to gain speed.

5. THE BDOGS DESIGN

In this section, we combine the methods described in Sections 2–4 to obtain a BDOGS design. Intuitively, it may seem that a flexible model for the event time distribution should give a robust design. However, our preliminary simulations showed that this is not the case, since ${\mathbf{d}}_K^{\text{OPT}}$ depends heavily on the true model, specifically the shape of the hazard. Therefore, rather than finding a single ${\mathbf{d}}_K^{\text{OPT}}$ under one highly flexible model, we find ${\mathbf{d}}_K^{\text{OPT}}$ for each of J prespecified models (hazards), thus deriving J sets of optimal decision rules ( ${\mathbf{d}}_{K,1}^{\text{OPT}},{\mathbf{d}}_{K,2}^{\text{OPT}},\dots ,{\mathbf{d}}_{K,J}^{\text{OPT}}$), where ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ is the optimal sequential decision procedure under ℳ_ℓ for ℓ = 1, 2, …, J. Since an essential feature of our procedure is its ability to switch decision boundaries based on repeated adaptive model selection, this makes the method inherently robust (Section 7).

Theoretically, the optimal boundary should be computed at every interim analysis given the current data. However, this computation is impractical and thus we combine FS and model selection to obtain J sets of optimal decisions as an approximation. An important practical requirement is that J must be small enough to allow the necessary computations to be carried out within a reasonable time frame to facilitate application. However, ℳ must include a broad array of different hazard functions. After examining the behavior of our method using a wide variety of possible ℳ with varying J, we chose J = 5 specific models from the three-parameter-generalized gamma (GG) family, selected in terms of the shapes of their hazards. The GG distribution is characterized by pdf

$$f(y|\beta ,\eta ,\kappa )=\frac{\beta }{\mathrm{\Gamma }(\kappa )\eta }{\left(\frac{y}{\eta }\right)}^{\kappa \beta -1}\text{exp}\{-{\left(\frac{y}{\eta }\right)}^{\beta }\},\beta ,\eta ,\kappa >0$$ (7)

This distribution has survival function S(y) = 1 − Γ_I ({y/η}^β, κ) and median θ = ηθ_I (κ)^1/β, where Γ_I (a, κ) is the cdf and θ_I (κ) is the median of a Gamma (κ, 1) distribution with pdf Γ(κ) ⁻¹ z^κ−1 e^−z. We chose the GG family because its hazard function may take many shapes, and it contains the gamma, lognormal and Weibull as special cases. ℳ₁ was chosen to have a constant hazard, and Figure 1 displays possible forms of the hazards under models ℳ₂, …, ℳ₅, each of which was obtained by constraining (β, η, κ). ℳ₂ and ℳ₃ were chosen to have, respectively, a wide variety of increasing and decreasing hazards. ℳ₄ is lognormal with scale parameter, ${\sigma }_1^2$, chosen so that its hazard first increases then levels off or decreases slightly. In contrast, the scale parameter, ${\sigma }_2^2$, was chosen for the lognormal ℳ₅ to have an increasing hazard followed by a sharp decrease.

Denote the GG parameter vector under treatment t = A or B by ψ_t = (β_t, η_t, κ_t). At each interim analysis, the data for patient i are $X_i=(Y_i^0,C_i,t_i)$ where the observed time $Y_i^0$ is the minimum of the event time Y_i and the time of right-censoring, C_i = 1 if $Y_i^0=Y_i$ and C_i = 0 if $Y_i^0<Y_i$, and treatment t_i = A or B. We assume Y_i ~ GG (β_ti, η_ti, κ_ti). The likelihood at the kth interim analysis after enrolling n_k patients and observing X_nk is

$$ℒ({\mathbf{X}}_{n_k}|{\mathbf{\psi }}_A,{\mathbf{\psi }}_B)=\prod _{i=1}^{n_k}f{(y_l^o|{\mathbf{\psi }}_{t_i})}^{C_i}S{(Y_i^o|{\mathbf{\psi }}_{t_i})}^{1-C_i}$$ (8)

At each interim analysis, we calculate the posterior decision criteria p_B>A (X_nk) and p_A>B (X_nk) using the likelihood in (8). For priors, we assume β_ti ~ Gamma and η_ti, κ_ti ~ Inverse Gamma. Numerical prior hyperparameters values will be given in Section 7.1 in the context of the simulation study. Since the prior and likelihood are non-conjugate, obtaining the posterior probabilities needed for decision making requires time-consuming Markov chain Monte Carlo (MCMC) methods. Thus, the use of FS is crucial in order to examine even a small set of decision rules.

Using the current data at each analysis, we base our decision on ${\mathbf{d}}_{K,{\ell }^{\ast }}^{\text{OPT}}$ under the optimal model, denoted by ℳ_ℓ*. To find ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ for each ℳ_ℓ, we use FS described in Section 3. The ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ are then stored for later use. Specific computational details are provided in Section 6. Since we have five sets of optimal decision rules, one set for each model, we need the ability to switch ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ repeatedly based on the accumulating data. Therefore, we compute the posterior model probabilities, f (ℳ_ℓ | X_nk), ℓ = 1, …, 5, based on the current data each time an interim decision is made to choose the most likely model empirically, assuming that the five models are equally likely a priori.

6. COMPUTATIONAL ALGORITHMS

To determine how well our method performs, we must simulate the trial repeatedly to obtain its operating characteristics (OCs) under each of several different cases, varying the true model as well as δ. The BDOGS method is implemented using the following algorithm.

Algorithm 1

The first algorithm is used to compute ( ${\mathbf{d}}_{K,1}^{\text{OPT}},{\mathbf{d}}_{K,2}^{\text{OPT}},\dots {\mathbf{d}}_{K,J}^{\text{OPT}}$) the optimal bounds. The following steps are carried out for each ℳ_ℓ in ℳ.

• Step 1: Simulate one replication of the trial, and for each interim analysis calculate p_B>A(X_nk) and p_A>B(X_nk) using (8).

• Step 2: Store the simulated data and calculated values from Step 1.

• Step 3: Repeat steps 1 and 2 each 10 000 times.

• Step 4: Combine the results of the 10 000 replications.

• Step 5: Obtain ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ using the details described in Section 3.

• Step 6: Store ${\mathbf{d}}_{K,\ell }^{\text{OPT}}$ for use in Algorithm 2.

To calculate p_B>A(X_nk) and p_A>B(X_nk), we implement four MCMC chains and begin sampling with an initial burn-in of 5000 followed by an additional 30 000 samples. Convergence is monitored using the potential scale reduction method given in [22]. We use parallel processing for Steps 1–3 to obtain 10 000 replications within a reasonable time frame.

In order to conduct the simulation study reported here that examines the robustness of BDOGS and compares it with each conventional method, we employed the following computational algorithm. In practice, one may conduct a similar robustness study to determine how well the design will do in cases where the proportional hazards assumption is not met, although this is not strictly necessary when applying BDOGS.

Algorithm 2

• Step 1: Simulate one replication of the trial. For each interim analysis, compute p_B>A(X_nk) and p_A>B(X_nk) using (8) and the posterior model probability f(ℳ_ℓ | X) given in Section 4.

• Step 2: Store the simulated data and the calculated values from Step 1.

• Step 3: Repeat steps 1 and 2 each 5000 times.

• Step 4: Combine the results of the 5000 replications.

• Step 5: For the kth interim analysis, apply ${\mathbf{d}}_{k,{\ell }^{\ast }}^{\text{OPT}}$ from Algorithm 1 and store the sample size and the decision.

• Step 6: Average the results from Step 5 to obtain the OCs.

7. SIMULATION STUDIES

7.1. Group sequential design specifications

The conventional group sequential designs, used as a basis for comparison in the simulations, were chosen because they are used routinely in practice. To compare BDOGS to each of the three conventional methods, we specified all designs to test H₀ : δ = 0 versus H₁ : δ ≠ 0, with overall type I error rate α* = 0.05 and power β* = 0.80 to detect improvement δ* = 3, assuming median failure times ${\theta }_A^{\text{true}}={\theta }_B^{\text{true}}=12\text{ months}$ under H₀ and ${\theta }_B^{\text{true}}=15\text{ months}$ under H₁. For each method, a maximum of K = 5 analyses were conducted, with up to four interim tests and one final test. For all simulated trials, we assumed an accrual rate of 150 patients per year, simulated as a Poisson process.

For all methods, at each interim analysis, the trial could be terminated for superiority of either treatment, or because it was unlikely that either treatment would ultimately prove to be superior (futility). For each of the OF, Pocock, and HSD designs we obtained N, the monitoring times and boundaries from East Version 3.0 [23]. Since the boundaries for superiority and futility were based on spending functions and the details are complex and lengthy, we refer the reader to the East documentation [23] Appendix A.2, page 469 under the LD(OF), LD(PK), and Gamma(γ) subsections for the OF, Pocock, and HSD boundaries, respectively. To obtain the HSD optimal design, a custom Excel macro was written to perform a grid search over all possible combinations of the spending function parameters and N. For each combination, the macro called East to calculate the expected sample sizes under H₀ and H₁, and the HSD parameterization minimizing the equally weighted average of these values was chosen.

To compare the average behaviors of the different methods, we simulated 5000 trials using each design. Since the OF, Pocock, and HSD designs assume proportional hazards, we first simulated event times from an exponential distribution. Since, in general, one does not know the true hazard or if the assumption of proportional hazards is met, we also performed a sensitivity analysis to determine how the performance of each method was affected if the proportional hazard assumption is violated under particular alternative models. Specifically, we generated event times from each of nine different distributions, summarized graphically in terms of their hazards in Figure 2. These included six parametric distributions (a–f) as well as three non-parametric distributions, denoted by PI (piecewise-increasing), PD (piecewise-decreasing) and VS (vee-shaped). To ensure fair comparisons, we first simulated all patients’ accrual times and event times and presented all four methods with the same data.

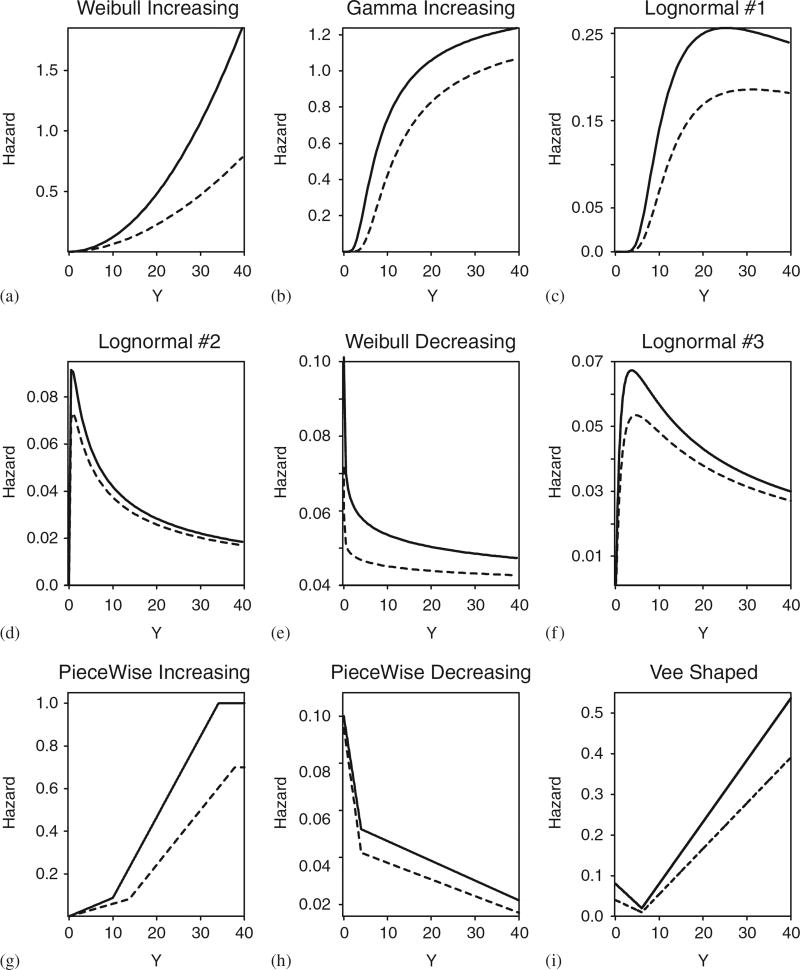
Figure 2.

Hazard functions used in the simulation study for A (solid line) and B (dashed line). The exponential (Exp) distribution has a constant hazard, and thus is not shown: (a) WI; (b) GI; (c) LN1; (d) LN2; (e) WD; (f) LN3; (g) PWI; (h) PWD; and (i) VS.

Because the three standard group sequential methods do not maintain the desired power in many cases, we provide two simulation studies. In the first simulation study, we calibrated BDOGS to match the achieved power of the design to which it was compared. In addition, since the three conventional designs have different interim test times and maximum sample sizes, N, to ensure that each comparison was fair the interim test times and the value of N for BDOGS were set to match those of the conventional design to which it was compared. Thus, for each pairing, BDOGS and the conventional method received the same data. In the second simulation study, since the maximum sample sizes under the conventional designs were not adequate to maintain the desired power in all cases, we allowed all methods to have an equal, larger maximum sample size and calibrated BDOGS to maintain the nominal power in all cases. The stopping boundaries for the conventional methods were derived assuming a piece-wise linear hazard.

7.2. Simulation study 1

In the first simulation study (Tables I–III), the OF method enrolled up to N = 716 patients with tests when 211,337,463,589, and 715 events are observed, corresponding outer Z-score test boundaries ± (3.61, 2.86, 2.49, 2.16, 1.96) for superiority and inner futility boundaries ± (0, 0.57, 1.14, 1.59, 1.96). For the Pocock method, N = 1058 with tests when 211, 423, 634, 846, and 1057 events are observed, and boundaries ± (2.33, 2.33, 2.33, 2.33, 2.33) for superiority and ± (0.33, 1.00, 1.52, 1.96, 2.33) for futility. For the HSD design, N = 680 with tests when 211, 328, 445, 562 and 679 events are observed, and boundaries ± (3.05, 2.87, 2.61, 2.33, 1.97) for superiority and ± (0.13, 0.27, 0.76, 1.37, 1.97) for futility. For OF, Pocock, and HSD, the trial is terminated for superiority of E(S) if the Z-sore is greater than (less than) the test boundaries for superiority, and stopped for futility if the Z-score falls within the futility boundaries. The initial look at 211 events was set to be the same for all methods, and subsequent analyses were equally spaced between 211 events and the maximum sample size for each given method. Thus, when comparing BDOGS to the OF, Pocock and HSD designs, BDOGS had maximum sample sizes 716, 1058, and 680, respectively, also matching the conventional method’s times of interim analysis, as noted earlier. BDOGS was calibrated to have nominal power 80 per cent, with the important exception that, in cases where the OF, Pocock, or HSD design had <80 per cent power, to ensure comparability BDOGS was calibrated to match the observed power of the respective design. An important difference between BDOGS and conventional designs is that BDOGS does not use Z-score boundaries. Rather, the six BDOGS decision parameters (a_U, b_U, c_U, a_L, b_L, c_L) are optimized under each of the five GG models given in Figure 1 and thus can be calibrated to have a different power for each of the five GG models.

The first simulation study is summarized in Tables I–III. When the event times are simulated from an exponential model, the assumptions for the OF, Pocock, and HSD designs are met and, as expected, all four methods maintain α* and β*. In addition, the sample size distributions are very similar for all four methods.

Since the results of the sensitivity analysis are extensive, and moreover the results for true hazards WI (Weibull-increasing), GI (gamma-increasing), and LN1 (lognormal 1) (Figure 2) are very similar, we only present the WI case. Similarly, because the results under the WD (Weibull-decreasing) and LN3 (lognormal 3) models are very similar we only present the WD case. To facilitate explanation, we provide a brief description of the key differences and direct the reader to Tables I–III for complete results.

In cases where the achieved power of the conventional methods is ≥ 0.80, BDOGS achieved power closer to the targeted 0.80 than OF, Pocock, or HSD. Consequently, BDOGS provides a substantial reduction in expected sample size compared to all three conventional methods, with the largest reduction when δ = 0.

In cases where the targeted power is not reached by the conventional methods, BDOGS obtains a slightly higher power. Specifically, the desired power is not maintained by any of the four methods in the PD case, and also is not maintained by OF or Pocock in the WD case. In general, if the targeted false-positive rate is maintained, BDOGS has at least the same power as the alternative method and has a much smaller expected sample size.

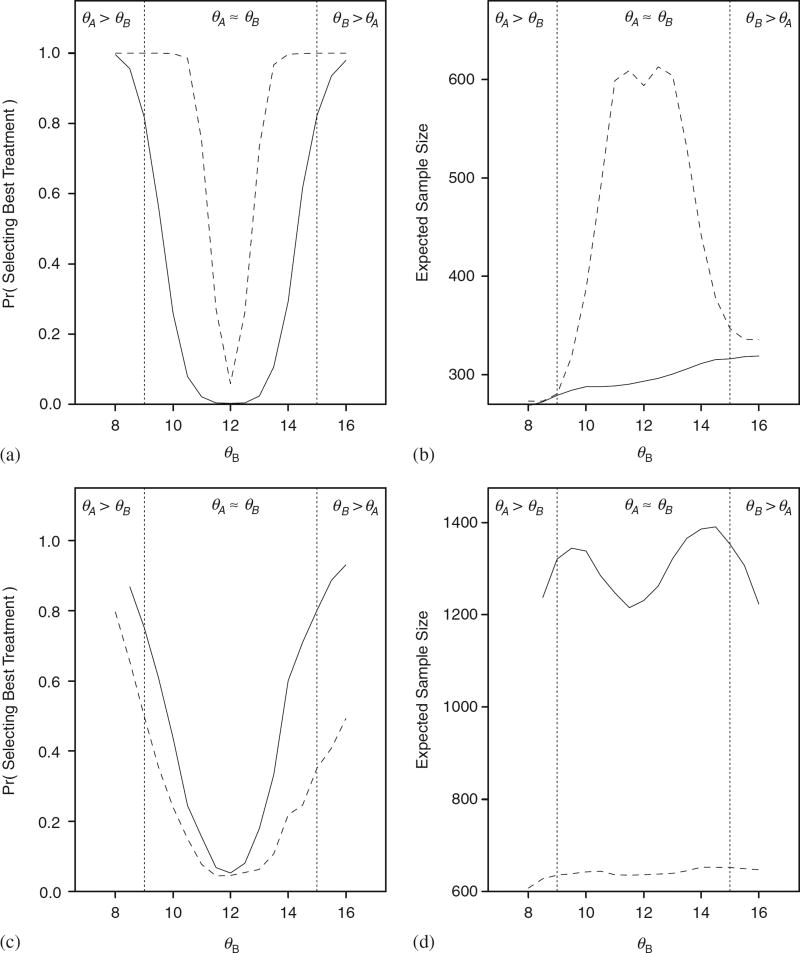
To assess the performance of BDOGS for values of δ other than 0 and 3, we performed additional simulations in which we set θ_A = 12 and varied θ_B over the range from 8 to 16. We did this in the case where the true hazards were either WI or lognormal with a hazard similar to LN2 with the specified median survival times. Figure 3 displays the probability of selecting the best treatment and expected sample size for BDOGS and HSD. The results for OF and Pocock are similar to those for HSD. For the Weibull case, OF, Pocock, and HSD are all overpowered at the expense of a much larger trial, on average. For the lognormal case, OF, Pocock, and HSD are all severely underpowered.

Figure 3.

Power curve and expected sample size when θ_A = 12 and the true event time distributions are Weibull with an increasing hazard (A and B) and lognormal with an increasing then decreasing hazard (C and D) for BDOGS (solid line) and HSD (dashed line). Results for Pocock and OF (not shown) are similar to those for HSD.

Decision making is most difficult, regardless of method, in cases where the hazard is initially high and then decreases quickly and remains low, such as WD. The difficulty arises since the information is accruing at a low rate and the majority of patients are enrolled before a treatment difference can be detected.

7.3. Simulation study 2

In the second simulation study (Table IV), we compared BDOGS with two designs that do not assume a constant hazard. Specifically, we compared BDOGS with an OF design obtained from East that assumes a piece-wise constant hazard that initially increases then decreases. We refer to this design as OF*. The second design assumes a GG likelihood with a single set of group sequential boundaries optimized under this model. We denote this design by GG*. Thus, the GG* design is a conventional group sequential procedure under one assumed general model, in contrast with the BDOGS design that adaptive selects among five particular GG models. For comparability, all three methods enrolled up to N = 1650 patients and the interim decision are conducted when 142, 423, 634, 946, and 1625 events are observed. For the second simulation study, we calibrated BDOGS to have power 80 per cent for all cases. This was in contrast with simulation study 1, where for each comparison the power of BDOGS was calibrated to match that of the design to which it was compared.

Table IV.

Simulation comparing BDOGS, O’Brien–Fleming (OF*), and generalized gamma (GG*) designs in a clinical trial with five analyses, size=0.05, and power=0.80. OF* decision boundaries were obtained using East assuming a piece-wise constant hazard. GG* assumes a GG likelihood and has one set of decision boundaries.

True hazard	Method	False pos.	Power	Sample size, δ =0 (δ=3)
				Mean	2.5 per cent	25 per cent	50 per cent	75 per cent	97.5 per cent
Proportional hazards assumption met
Exp	BDOGS	0.05	0.80	603 (671)	285 (300)	320 (334)	624 (651)	646 (865)	1167 (1204)
	OF*	0.05	0.99	1399 (1220)	836 (842)	1159 (902)	1650 (1187)	1650 (1650)	1650 (1650)
	GG*	0.01	0.65	806 (1465)	593 (633)	623 (1216)	645 (1650)	857 (1650)	1650 (1650)
Robustness study—proportional hazards assumption not met
WI	BDOGS	0.05	0.80	310 (336)	275 (292)	291 (308)	300 (317)	309 (328)	578 (609)
	OF*	0.05	0.99	1378 (731)	787 (582)	1106 (605)	1650 (794)	1650 (818)	1650 (1128)
	GG*	0.01	0.65	381 (1400)	276 (314)	294 (1132)	305 (1650)	570 (1650)	606 (1650)
PI	BDOGS	0.02	0.80	288 (329)	266 (281)	279 (297)	287 (307)	295 (318)	314 (506)
	OF*	0.05	0.99	1371 (593)	773 (562)	1090 (579)	1650 (587)	1650 (596)	1650 (785)
	GG*	0.01	0.56	301 (1406)	264 (301)	280 (1119)	288 (1650)	297 (1650)	570 (1650)
VS	BDOGS	0.05	0.96	365 (322)	264 (281)	280 (297)	291 (306)	556 (316)	585 (593)
	OF*	0.05	0.99	1378 (671)	773 (567)	1091 (586)	1650 (600)	1650 (794)	1650 (828)
	GG*	0.00	0.94	461 (1181)	267 (306)	288 (804)	558 (1120)	572 (1650)	599 (1650)
LN2	BDOGS	0.05	0.80	1311 (1463)	646 (319)	949 (1337)	1307 (1650)	1650 (1650)	1650 (1650)
	OF*	0.04	0.68	1459 (1515)	927 (949)	1292 (1335)	1650 (1650)	1650 (1650)	1650 (1650)
	GG*	0.05	0.80	1333 (1507)	669 (710)	954 (1350)	1310 (1650)	1650 (1650)	1650 (1650)
WD	BDOGS	0.05	0.80	1028 (1050)	315 (302)	665 (667)	895 (915)	1230 (1650)	1650 (1650)
	OF*	0.05	0.92	1409 (1350)	850 (860)	1176 (1188)	1650 (1217)	1650 (1650)	1650 (1650)
	GG*	0.01	0.67	911 (1468)	610 (643)	638 (1219)	850 (1650)	1166 (1650)	1650 (1650)
PD	BDOGS	0.05	0.80	1005 (1165)	298 (309)	666 (703)	905 (1273)	1248 (1650)	1650 (1650)
	OF*	0.05	0.98	1438 (1392)	891 (917)	1239 (1270)	1650 (1299)	1650 (1650)	1650 (1650)
	GG*	0.01	0.76	1124 (1480)	639 (679)	888 (1294)	1199 (1650)	1272 (1650)	1650 (1650)

For the priors on the GG parameters (β, η, κ) in (7) used in the BDOGS design, for both j = A and B we assumed β_j ~ Gamma(0.5, 2), which has mean 1 and variance 2, η_j ~ Inverse Gamma(2.03, 17.83) which has mean 17.312 and variance 10 000, and κ_j ~ Inverse Gamma(2.0001, 1.0001) which has mean 1 and variance 10 000. The mean of η_j was chosen to give median failure time 12 months if the data were exponentially distributed. The means of β_j and κ_j were set equal to 1 so that, if these parameters were replaced by their mean values, then the likelihood would be exponential with median 12 months. If the data were exponentially distributed, the information in this prior would correspond to observing two patients.

Since the results for true hazard WI, GI, or LN1 (Figure 2) in the second simulation study are very similar, we only present the WI case; similarly, because the results under the WD and LN3 models are very similar we only present the WD case. The results are summarized in Table IV in terms of the achieved type I error, power, and sample size distribution.

To facilitate explanation, we provide a brief description of the key differences and direct the reader to Table IV for complete results. By assuming a decreasing hazard, the maximum sample size was large enough for BDOGS to maintain the desired power in all cases. Because BDOGS adaptively switches between decision boundaries, it does not inflate the expected sample sizes in cases where a difference can be detected between the treatments early in the trial. In general, the achieved power figure for BDOGS is closer to the desired level, thus resulting in a substantially smaller trial. In some cases, the reduction in expected sample size is greater than 60 per cent when compare to OF*. The achieved power figure with the GG* design is typically lower than the desired power, illustrating the benefit of BDOGS’s adaptively model selection.

7.4. Illustrative trial

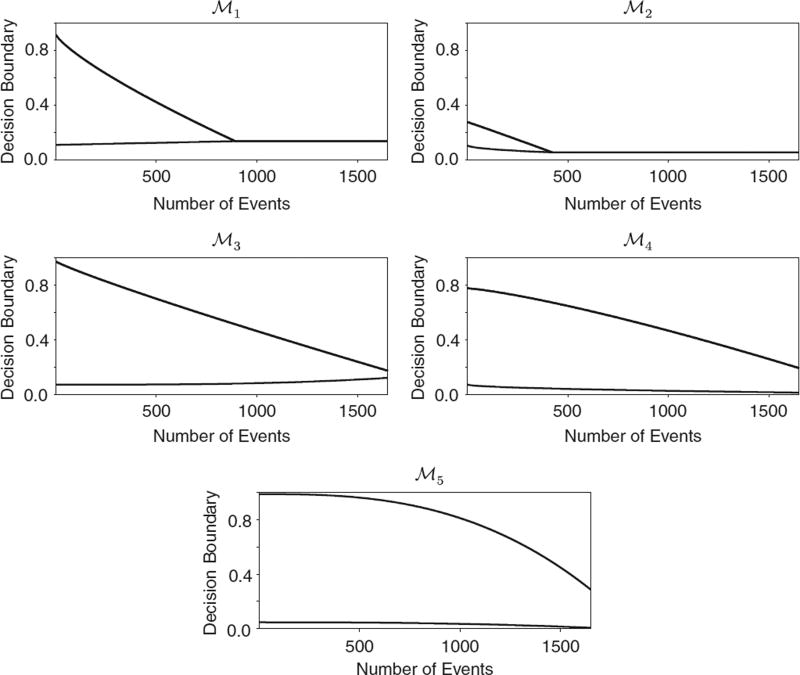
To illustrate how BDOGS works in practice, we simulated one data set in the case where the true hazard is WI and δ = δ* = 3 months, and applied both BDOGS and OF to the simulated data. The information needed for decision making by OF consists of the Z-score and the boundaries given in Section 7.1, while BDOGS requires p_A>B(X_nk) and p_B>A(X_nk) for k = 1, …, 5, ( ${\mathbf{d}}_{5,1}^{\text{OPT}},{\mathbf{d}}_{5,2}^{\text{OPT}},\dots ,{\mathbf{d}}_{5,5}^{\text{OPT}}$), shown in Figure 4, and the interim posterior model probabilities of (ℳ₁, …, ℳ₅). In the simulated data set, at the first evaluation, the Z-score was 2.9, p_A>B(X_nk) = 0.005, p_B>A(X_nk) = 0.51>0.48 = P_U(X_nk, a_U, b_U, c_U) and the interim posterior probability of ℳ₂ was 0.98. Since 0<2.9<3.61, OF would continue the trial to the second analysis and thus enroll more patients. However, based on the observed data, BDOGS would use the optimal boundaries under ℳ₂, and thus would stop the trial at the first analysis and conclude that B is superior to A. If the constant hazard model had been most likely then BDOGS, like OF, would have continued to the second analysis. Thus, the BDOGS adaptive model selection played a critical role in making the correct decision.

Figure 4.

The boundary functions, P_U(X_nk, a_U, b_U, c_U) (top curve) and P_L(X_nk, a_L, b_L, c_L) (bottom curve) under the optimal decision rules ${\mathbf{d}}_{5,1}^{\text{OPT}},{\mathbf{d}}_{5,2}^{\text{OPT}},\dots ,{\mathbf{d}}_{5,5}^{\text{OPT}}$.

8. DISCUSSION

We have presented a Bayesian adaptive decision-theoretic approach to designing a randomized group sequential clinical trial with time-to-event outcomes. An advantage of our computational procedure for finding optimal decision boundaries, when compared with the FS method of Carlin et al. [19], is that our approach does not increase in complexity with the number of interim analyses. We use Bayesian model selection to adaptively choose decision boundaries during the trial, since the optimal boundaries depend on the selected model. A critical component contributing to the performance of our method is the fact that, rather than using historical data to pick a single model at the start of the trial, we use the accumulating data to continually update our choice of the ‘best’ model. Our simulations show that, compared with standard group sequential designs, on average BDOGS provides a smaller trial and does a better job of maintaining the targeted power.

One important question is how often the model selection algorithm selects the correct model at the early evaluations. We found that, under most models, BDOGS had an 80–90 per cent chance of selecting the correct model at the initial evaluation. In the cases with a decreasing hazard, the model selection was only correct approximately 50 per cent of the time at the first evaluation. However, in the decreasing hazards case p_A>B(X_nk) and p_B>A(X_nk) typically were both large for the first three evaluations, so that the trial would continue under all models.

In our implementation of the BDOGS method, we included J = 5 possible different models, characterized in terms of their hazards. Initially, we investigated the method’s behavior for several larger values of J , and evaluated the OPs of the resulting designs. We removed models that resulted in optimal boundaries that were very similar to other models and then examined the OPs of the new design with a reduced J. Once the five models that we used here were determined, we found that the performance of BDOGS was substantially degraded when J <5. However, in practice, if substantial information is available about possible hazards one could use this information in building the set of potential models.

Although we have assumed that the event times follow a GG distribution, for the three cases that we examined where the true distribution follows a piece-wise hazard, including PI, PD, and VS, BDOGS was still superior to conventional methods. We also conducted simulations, not shown here, under many other distributions not in the GG family, and the results were very similar to those presented here. These simulations indicate that BDOGS is robust.

In our simulations, we formulated BDOGS using large prior variances so that the accumulating data would quickly overwhelm the prior. To assess the effects of a more informative prior, we multiplied each prior variance by 0.001 and reran all of the simulations. The results were very similar to what we have presented here.

Table II.

Robustness simulation study results to compare Bayesian Doubly Optimal Group Sequential (BDOGS) with Pocock procedure when the assumption of proportional hazards is not met in a clinical trial with five analyses. The true median TTF is 12 months for A.

True hazard	Method	False pos.	Power	Sample size, δ =0 (δ=3)
				Mean	2.5 per cent	25 per cent	50 per cent	75 per cent	97.5 per cent
Proportional hazards assumption met
Exp	BDOGS	0.05	0.80	614 (656)	371 (387)	398 (412)	623 (641)	652 (876)	1058 (1058)
	Pocock	0.05	0.80	631 (672)	373 (389)	410 (421)	626 (651)	811 (867)	1058 (1058)
Robustness study—proportional hazards assumption not met
WI	BDOGS	0.04	0.86	375 (403)	347 (365)	363 (381)	372 (391)	380 (401)	403 (606)
	Pocock	0.04	0.99	587 (444)	355 (366)	386 (384)	583 (395)	611 (416)	1014 (791)
PI	BDOGS	0.01	0.81	357 (393)	335 (350)	349 (368)	357 (377)	365 (388)	380 (594)
	Pocock	0.05	0.99	572 (409)	464 (354)	485 (370)	596 (381)	623 (482)	716 (519)
VS	BDOGS	0.03	0.97	373 (381)	333 (351)	349 (368)	358 (376)	368 (386)	577 (576)
	Pocock	0.05	0.99	574 (406)	340 (352)	369 (370)	567 (378)	760 (391)	1004 (608)
LN2	BDOGS	0.05	0.45	531 (637)	381 (397)	403 (422)	419 (678)	681 (739)	1058 (1058)
	Pocock	0.05	0.42	678 (759)	389 (403)	429 (461)	684 (716)	730 (974)	1058 (1058)
WD	BDOGS	0.02	0.45	504 (639)	374 (390)	395 (416)	409 (650)	648 (888)	930 (1058)
	Pocock	0.05	0.40	749 (814)	392 (405)	650 (676)	688 (891)	891 (911)	1058 (1058)
PD	BDOGS	0.05	0.40	595 (640)	401 (386)	427 (414)	661 (656)	693 (893)	1058 (1058)
	Pocock	0.05	0.45	768 (818)	411 (405)	677 (675)	707 (896)	921 (919)	1058 (1058)