Abstract
Purpose
To compare the accuracy of axial length vergence formulas versus refractive vergence formulas for secondary intraocular lens (IOL) implantation in pediatric aphakia.
Methods
This retrospective comparative study, evaluated 31 eyes of 31 patients aged ≤3.5 years, who had undergone secondary IOL implantation. The median absolute error (MedAE) was compared between axial length vergence formulas (Hoffer Q, Holladay I, SRK II, and SRK/T) and refractive vergence formulas (Lanchulev, Holladay R, Mackool, and Khan) as well as between formulas within the same vergence.
Results
There was a significant difference (P = 0.010) between MedAE for axial length vergence formulas [1.19 Diopter(D)] and MedAE for refractive vergence formulas (2.48 D). The MedAE of axial length vergence formulas were comparable as to Hoffer (1.59 D), Holladay (1.27 D), SRK/T (1.23 D), and SRK II (1.30 D). Among refractive vergence formulas, Lanchulev (5.00 D) and Holladay R (2.51 D) had significantly larger MedAE as compared to Khan (2.06 D) and Mackool (2.15 D).
Conclusion
Axial length vergence formulas performed significantly better than refractive vergence formulas; however, axial length vergence formulas were comparable within the same vergence.
Keywords: Axial length, Refractive, Intraocular lens, Pediatric, Aphakia, Intraocular lens power calculation
Introduction
In general, there are two types of intraocular lens (IOL) calculation formulas: axial length vergence formulas and refractive vergence formulas.1 IOL formulas such as Hoffer Q,2 Holladay I,3 SRK/T,4 and SRK II5, 6 require the measurement of axial length, keratometry, and an IOL constant. Alternately, refractive vergence formulas do not require axial length measurements; instead, they require the preoperative refraction and manufacturer's IOL constant to calculate IOL power. Refractive vergence formulas assume that the patient has clear media and that no power, e.g. lens, will be removed.1
Refractive vergence formulas are suitable for phakic IOLs, secondary IOLs for aphakia as in this study, and piggyback lenses for pseudophakia. A refractive formula that works well for phakic IOL, for example, will also work well for secondary IOL as well as piggyback IOL.1 Refractive vergence formulas include Lanchulev,7 Holladay R,8 Khan,9 and Mackool.10 This study compares mean absolute error (MAE) between vergences (Axial length vergence formulas versus refractive vergence formulas) and between formulas within same vergence to investigate the optimal formula for secondary IOLs in aphakic children.
Methods
This comparative, retrospective, non-randomized, observational study was approved by the Institutional Review Board and was compliant with the principles of the Declaration of Helsinki. A chart review was performed of pediatric patients who underwent secondary IOL implantation by two surgeons (K.E., L.J.) between the years 2006–2012. Inclusion criteria were patients aged ≤3.5 years old who were aphakic post-cataract extraction and then underwent posterior chamber IOL (PC IOL) implantation in the ciliary body's sulcus. The posterior capsule was removed and the anterior vitrectomy was done during cataract surgery. The soemmering ring, adhesion of the anterior and posterior capsules, was left during the secondary IOL implantation surgery to provide support to the sulcus IOL.
Data were collected on patient demographics, age at cataract surgery, gender, and the operated eye. Aphakic refraction (AR) over contact lenses was collected within 3 months prior secondary IOL implantation. Intraoperative data were collected on surgery date, axial length, keratometry, implanted IOL power, IOL material, IOL A-constant. Pseudophakic refraction was collected from 1 to 3 months postoperatively. For the purposes of this study, refraction denotes spherical equivalent. Tropicamide 1.0% was instilled in patient's eyes every 10 min three times for better visualization of retina reflex. Refraction was carried out after 45 min from initial drops in the clinic setting.
Axial length was measured with contact A-scan (Scan-1000; Ophthalmic Technology International, Toronto, Canada), and this device's built-in IOL calculator was used with Hoffer Q, Holladay I, SRK II, and SRK/T formulas. Keratometry was measured by the ARK-30 Auto-Keratometer/Refractor (NIDEK Co. Ltd., Gamagori, Japan) in the operating room under general anesthesia same time for secondary IOL implantation. All measurements of biometry and refraction were performed by experienced optometrists. The target refraction was calculated as 7 minus the age of the patient. The target refraction was set to make the eye hyperopic to compensate for myopic shift that will occur with elongation of the eye as the child ages.
Refractive vergence formulas as Holladay-R, Mackool, Khan, and Lanchulev calculated IOL power directly from AR when Khan estimated axial length from AR then used this estimated axial length in Holladay 1 formula with assumed keratometry of 43 D and 44 D respectively to calculate IOL power.
For accurate calculations, average keratometry of each eye was used in Khan formula instead of assumed keratometry of 43 D and 44 D, respectively, for all eyes. Last modification to Khan in this study was use of standard 12.0 mm vertex distance instead of Khan's assumed vertex of 10.0 mm. A term including predicted refraction of −1.25 * AR was linearly added to Mackool and Lanchulev formulas as these were primarily built to calculate emmetropic IOL, given that 1.00 D at glasses plane translated into 1.25 D at IOL plane. On the other hand, formulas of Holladay-R and Khan had term in their formulas for predicted refraction. In addition, Mackool and Lanchulev used A-constant of 118.84 and 118.4, respectively. In order to use different IOL with different A-constant, a term of (A-118.84) or (A-118.4) were added linearly to Mackool and Lanchulev formulas, respectively. Holladay IOL Consultant trial version 2013 was used to calculate predicted refraction for Holladay-R.
To compensate for sulcus IOL implantation, effective lens position (ELP) or lens constant was reduced by 0.50 mm which represented the distance between the bag and the sulcus.
Predicted refraction corresponding to the implanted IOL was noted and MAE and median absolute error (MedAE) were computed as mean and median of absolute difference between predicted refraction by formula corresponding to the implanted IOL and actual postoperative refraction for axial length vergence formulas namely Hoffer Q, Holladay 1, SRKT, and SRK II, and refractive vergence formulas namely Lanchulev, Holladay R, Khan, and Mackool, Prediction error might unveil if there was a systemic error (hyperopic/myopic shift). Absolute error was considered to avoid cancellation of positive and negative errors. For example, mean prediction error of +2, −2, +4, −4 was zero when mean absolute (prediction) error was six. However, absolute, by definition, made all values positive, so distribution curves for MAEs would be right-skewed which was confirmed by their histograms. Therefore, non-parametric tests of Wilcoxon signed-rank test for pair comparison of two MedAEs. Paired t-test with bootstrapping was performed to zero out prediction error. As IOL power comes in 0.50 D increment, MAE more than 0.50 D was considered clinically important. Statistical analysis was performed with statistical package for the social sciences (SPSS, v.20; IBM Corp., NY, USA). The significance level (Alpha (α)) was 0.05 for single comparison and 0.008 (0.05/6) for 6 multiple comparisons.
Results
The study group was comprised of 31 eyes (31 patients: 14 males, 17 females) with mean (range) age of 5.95 ± 3.90 (0.62–15.61) months at cataract surgery, and 23.15 ± 8.05 (7.62–39.33) months at secondary IOL implantation. Thirteen eyes underwent secondary IOL implantation by K.E. and eighteen by L.J., all patients were Arab. CP65T, a Polymethyl methacrylate (PMMA) IOL, was implanted in 10 eyes, and acrylate IOLs including SA60AT and MA60AC were implanted in 21 eyes. Biometry and refraction statistics are summarized in Table 1.
Table 1.
Summary of the study group biometry, keratometry, refraction, and implanted intraocular lens (IOL) power.
| Parameter | Median range | Mean ± SD | Standard errora | 95% Confidence intervala |
|
|---|---|---|---|---|---|
| Lower limit | Upper limit | ||||
| Axial length (mm) | 21.19 18.83 to 24.20 |
21.16 ± 1.38 | 0.25 | 20.65 | 21.67 |
| Keratometry (D) | 43.75 39.88 to 50.75 |
44.30 ± 2.56 | 0.43 | 43.46 | 45.17 |
| Preoperative refraction (D) | 17.00 8.50 to 21.57 |
16.73 ± 2.88 | 0.51 | 15.77 | 17.72 |
| IOL power (D) | 28.60 10.00 to 35.00 |
24.24 ± 5.35 | 0.93 | 22.37 | 26.10 |
| Postoperative refraction (D) | 1.50 −3.50 to 5.25 |
1.30 ± 2.24 | 0.42 | 0.52 | 2.14 |
mm: Millimeter; D: Diopter; IOL: Intraocular lens; a: Bootstrap output; SD: Standard deviation.
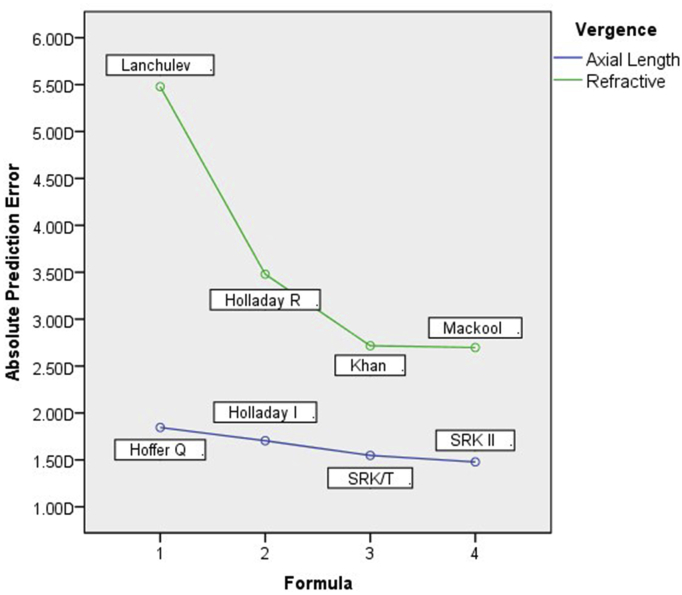
Axial length vergence formulas showed significantly (P = 0.010) lower MedAE than refractive vergence formulas as seen in Table 2. A summary of PEs, MAEs, MedAE for all formulas is summarized in Table 3. There was systemic myopic shift, minimal among axial vergence formulas and maximal among refractive vergence formulas. The MedAE and the MAE were comparable among Hoffer Q, Holladay R, SRK II, and SRK/T. Among refractive vergence formulas, Lanchuleve and relatively Holladay R had higher MAE and MedAE compared to Khan and Mackool formulas. All pair comparisons between formulas are summarized in Table 4. Also, these comparisons could easily be grasped by looking at Fig. 1.
Table 2.
Comparison of overall mean absolute error (MAE) between axial length and refractive vergence intraocular lens (IOL) power formulas.
| Vergence | PE ± SD | MedAE range | P-valueb | MAE ± SD | Standard errora | P-valuea | 95% Confidence intervala |
|
|---|---|---|---|---|---|---|---|---|
| Lower limit | Upper limit | |||||||
| Axial length (D) | −0.38 ± 2.01 | 1.19 0.31 to 4.05 |
– | 1.64 ± 1.20 | 0.22 | – | 1.25 | 2.04 |
| Refractive (D) | −2.89 ± 3.40 | 2.48 0.68 to 9.89 |
– | 3.59 ± 2.70 | 0.49 | – | 2.62 | 4.67 |
| Difference (D) | 2.52 ± 3.70 | 1.01 −1.74 to 9.33 |
<0.001 | 1.95 ± 2.93 | 0.52 | 0.010 | 0.98 | 3.04 |
MAE: Mean absolute error; MedAE: Median absolute error; D: Diopter; a: Bootstrap output; SD: Standard deviation; b: P-value from Wilcoxon signed rank test; PE: Prediction error.
P-value less than 0.05 was statistically significant.
Table 3.
Mean absolute error (MAE) of axial length and refractive vergence intraocular lens (IOL) power formulas.
| Vergence | Formula | PE ± SD | MedAE range | MAE ± SD | Standard errora | 95% Confidence intervala |
|
|---|---|---|---|---|---|---|---|
| Lower limit | Upper limit | ||||||
| Axial Length (D) | HofferQ | −0.71 ± 2.24 | 1.59 0.21 to 5.08 |
1.85 ± 1.42 | 0.26 | 1.34 | 2.35 |
| Holladay I | −0.49 ± 2.14 | 1.27 0.03 to 4.43 |
1.70 ± 1.35 | 0.24 | 1.22 | 2.15 | |
| SRK/T | −0.15 ± 1.95 | 1.23 0.07 to 3.86 |
1.55 ± 1.16 | 0.22 | 1.06 | 1.92 | |
| SRK II | −0.16 ± 1.84 | 1.30 0.01 to 3.82 |
1.48 ± 1.07 | 0.18 | 1.10 | 1.84 | |
| Refractive (D) | Lanchulev | −5.48 ± 3.55 | 5.00 0.33 to 12.72 |
5.48 ± 3.55 | 0.63 | 4.30 | 6.81 |
| Holladay R | −2.85 ± 3.60 | 2.51 0.10 to 10.43 |
3.48 ± 2.97 | 0.53 | 2.51 | 4.56 | |
| Khan | −1.66 ± 3.19 | 2.06 0.03 to 8.37 |
2.72 ± 2.32 | 0.42 | 1.96 | 3.58 | |
| Mackool | −1.59 ± 3.31 | 2.15 0.05 to 8.60 |
2.70 ± 2.46 | 0.45 | 1.91 | 3.66 | |
MAE: Mean absolute error; MedAE: Median absolute error; D: Diopter; a: Bootstrap output; SD: Standard deviation; PE: Prediction error.
P-value less than 0.05 was statistically significant.
Table 4.
Difference in mean absolute error between intraocular lens (IOL) formulas within the same vergence.
| Vergence | Formula (a) | Formula (b) | Difference (a−b) | Standard errora | P-valuea | 95% Confidence intervala |
P-valueb | |
|---|---|---|---|---|---|---|---|---|
| Lower limit | Upper limit | |||||||
| Axial Length (D) | Hoffer Q | Holladay I | 0.14 | 0.06 | 0.026 | 0.03 | 0.25 | 0.040 |
| SRK/T | 0.30 | 0.14 | 0.039 | 0.03 | 0.57 | 0.096 | ||
| SRK II | 0.37 | 0.16 | 0.030 | 0.08 | 0.69 | 0.064 | ||
| Holladay I | SRK/T | 0.16 | 0.09 | 0.087 | −0.01 | 0.33 | 0.096 | |
| SRK II | 0.23 | 0.12 | 0.064 | 0.00 | 0.45 | 0.085 | ||
| SRK/T | SRK II | 0.07 | 0.06 | 0.249 | −0.05 | 0.18 | 0.290 | |
| Refractive (D) | Lanchulev | Holladay R | 2.00 | 0.25 | 0.002 | 1.48 | 2.45 | <0.001 |
| Khan | 2.76 | 0.37 | 0.002 | 1.97 | 3.45 | <0.001 | ||
| Mackool | 2.78 | 0.41 | 0.001 | 1.88 | 3.48 | <0.001 | ||
| Holladay R | Khan | 0.76 | 0.18 | 0.001 | 0.39 | 1.12 | 0.001 | |
| Mackool | 0.78 | 0.21 | 0.002 | 0.37 | 1.21 | 0.002 | ||
| Khan | Mackool | 0.02 | 0.08 | 0.810 | −013 | 0.17 | 0.702 | |
D: Diopter; a: Bootstrap output; b: P-value from Wilcoxon signed rank test.
P-value less than 0.05 was statistically significant.
Fig. 1.
Mean absolute error (MAE) for intraocular lens (IOL) power formulas.
Discussion
As to refraction in aphakia, small changes in vertex distance will cause big changes in the power of correcting lens due to high refractive error in aphakic eye. Hence, it is recommended to perform refraction over contact lens.
When implantation is performed in the sulcus, ELP needs to be reduced by 0.50 mm. PMMA IOLs with an A-constant of 118.0 (ELP = 4.97) was adjusted to 117.15 (ELP = 4.47), and acrylic IOLs with A-constant of 118.4 (ELP = 5.20) was adjusted to 117.55 (ELP = 4.70) for sulcus implantation. This adjustment corrected myopic shift due to use of in the bag IOL power for in the sulcus IOL. This adjustment reduced IOL power by 0.50 D for IOL range (9 D < IOL ≤ 17 D), 1.00 D for IOL range (17 < IOL ≤ 28), and 1.50 D for IOL range (28 < IOL). In other words, an in-the-sulcus IOL with power less than that power of in-the-bag IOL by certain diopters as per IOL range would result in the same predicted refraction that would result from that in-the-bag IOL. For example, if refractive formula predicted +1.00 of refraction when implanting 23.00 D IOL in the bag, a 22.00 D in the sulcus IOL would result in same +1.00 D.
In the current study, axial length vergence formulas showed statistically significant and clinically important difference as compared to the refractive vergence formulas (Table 2). Similar difference of 0.8 D was found in the study of Abdel-Hafez.11 This outcome may be due to the lower precision of preoperative AR compared to the precision of axial length measurements and keratometry measurements. Another explanation may be the variation in data that was introduced by different optometrists who performed the refraction preoperatively and postoperatively.
Minimal myopic shift and maximal myopic shift were noticed in axial length vergence and refractive vergence, respectively. This could be due to postoperative lens position based on anterior chamber depth. A new formula that takes into account the anterior chamber depth in aphakia and consequently adjust the IOL power could perform better in children especially.12 Anterior chamber depth in aphakia could be estimated from the spike of anterior surface of the cornea to the posterior lens capsule spike or spike from the iris.
The SRK II,SRK/T, Holladay I formulas showed comparable errors that was lower compared to Hoffer Q formulas in the current study. This observation is similar to the results reported by Kekunnaya et al in their study of 128 eyes of 84 children less than two years.13 We found the refractive formulas showed the highest prediction error compared to axial length formulas. Lanchulev and relatively Holladay refractive showed heist prediction error compared to Khan and Mackool. Thus, in case axial length measurement is not possible when refraction is available, Mackool or Khan formula could be used.
The influences of IOL material might be negligible in the current study. This was likely because the variation was too small in lens material and design indicated by the A-constant (range, 118.0 to 118.4). Notably, limiting the age of patients in this study to 3 years or younger limited the variation in data making it homogenous. Shenoy found inverse relationship between age at surgery and MAE.14
In summary, development of a new regression or theoretical formulas for pediatric IOL implantation with optimized coefficients is recommended for future studies. The axial length vergence formulas showed greater precision than refractive vergence formulas due to the difference in precision between measurement methods for axial length versus refraction.
Footnotes
Peer review under responsibility of the Iranian Society of Ophthalmology.
References
- 1.Holladay J.T. Intraocular lens power calculations for the refractive surgeon. J Operat Tech Cataract Refract Surg. 1998;1(3):105–117. [Google Scholar]
- 2.Hoffer K.J. The Hoffer Q formula: a comparison of theoretic and regression formulas. J Cataract Refract Surg. 1993;19(6):700–712. doi: 10.1016/s0886-3350(13)80338-0. Erratum 1994; 20(6):677. [DOI] [PubMed] [Google Scholar]
- 3.Holladay J.T., Prager T.C., Chandler T.Y., Musgrove K.H., Lewis J.W., Ruiz R.S. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg. 1988;14(1):17–24. doi: 10.1016/s0886-3350(88)80059-2. [DOI] [PubMed] [Google Scholar]
- 4.Retzlaff J., Sanders D.R., Kraff M.C. Development of the SRK/T intraocular lens implantation power calculation formula. J Cataract Refract Surg. 1990;16(3):333–340. doi: 10.1016/s0886-3350(13)80705-5. Erratum 1990; 16(4):528. [DOI] [PubMed] [Google Scholar]
- 5.Sander D.R., Retzlaff J., Kraff M.C. Comparison of the SRK II formula and other second generation formulas. J Cataract Refract Surg. 1988;14:36–41. doi: 10.1016/s0886-3350(88)80087-7. [DOI] [PubMed] [Google Scholar]
- 6.Dang M.S., Raj P.P. SRK II formula in the calculation of intraocular lens power. Br J Ophthalmol. 1989;73:823–826. doi: 10.1136/bjo.73.10.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ianchulev T., Salz J., Hoffer K., Albini T., Hsu H., Labree L. Intraoperative optical refractive biometry for intraocular lens power estimation without axial length and keratometry measurements. J Cataract Refract Surg. 2005 Aug;31(8):1530–1536. doi: 10.1016/j.jcrs.2005.01.035. [DOI] [PubMed] [Google Scholar]
- 8.Holladay J.T. Refractive power calculations for intraocular lenses in the phakic eye. Am J Ophthalmol. 1993;116(1):63–66. doi: 10.1016/s0002-9394(14)71745-3. [DOI] [PubMed] [Google Scholar]
- 9.Khan A.O., AlGaeed A. Paediatric secondary intraocular lens estimation from the aphakic refraction alone: comparison with a standard biometric technique. Br J Ophthalmol. 2006 Dec;90(12):1458–1460. doi: 10.1136/bjo.2006.100834. Epub 2006 Aug 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mackool R.J., Ko W., Mackool R. Intraocular lens power calculation after laser in situ keratomileusis: aphakic refraction technique. J Cataract Refract Surg. 2006 Mar;32(3):435–437. doi: 10.1016/j.jcrs.2005.11.045. [DOI] [PubMed] [Google Scholar]
- 11.Abdel-Hafez G., Trivedi R.H., Wilson M.E., Bandyopadhyay D. Comparison of aphakic refraction formulas for secondary in-the-bag intraocular lens power estimation in children. J AAPOS. 2011;15(5):432–434. doi: 10.1016/j.jaapos.2011.05.021. [DOI] [PubMed] [Google Scholar]
- 12.Eom Y., Kang S.Y., Song J.S., Kim Y.Y., Kim H.M. Comparison of Hoffer Q and Haigis formulae for intraocular lens power calculation according to the anterior chamber depth in short eyes. Am J Ophthalmol. 2014 Apr;157(4) doi: 10.1016/j.ajo.2013.12.017. 818–824.e2. [DOI] [PubMed] [Google Scholar]
- 13.Kekunnaya R., Gupta A., Sachdeva V., Rao H.L., Vaddavalli P.K., Om Prakash V. Accuracy of intraocular lens power calculation formulae in children less than two years. Am J Ophthalmol. 2012;154(1) doi: 10.1016/j.ajo.2011.11.031. 13–19.e2. [DOI] [PubMed] [Google Scholar]
- 14.Shenoy B.H., Mittal V., Gupta A., Sachdeva V., Kekunnaya R. Refractive outcomes and prediction error following secondary intraocular lens implantation in children: a decade-long analysis. Br J Ophthalmol. 2013;97(12):1516–1519. doi: 10.1136/bjophthalmol-2012-302775. [DOI] [PubMed] [Google Scholar]