A Dirichlet-Tree Multinomial Regression Model for Associating Dietary Nutrients with Gut Microorganisms

Summary

Understanding the factors that alter the composition of the human microbiota may help personalized healthcare strategies and therapeutic drug targets. In many sequencing studies, microbial communities are characterized by a list of taxa, their counts, and their evolutionary relationships represented by a phylogenetic tree. In this article, we consider an extension of the Dirichlet multinomial distribution, called the Dirichlet-tree multinomial distribution, for multivariate, over-dispersed, and tree-structured count data. To address the relationships between these counts and a set of covariates, we propose the Dirichlet-tree multinomial regression model for which we develop a penalized likelihood method for estimating parameters and selecting covariates. For efficient optimization, we adopt the accelerated proximal gradient approach. Simulation studies are presented to demonstrate the good performance of the proposed procedure. An analysis of a data set relating dietary nutrients with bacterial counts is used to show that the incorporation of the tree structure into the model helps increase the prediction power.

1. Introduction

Next generation sequencing of DNA extracted from microbial communities has advanced our knowledge of the role of microbiota in human health and disease (Cho and Blaser, 2012). Researchers have found that changes in the human microbiota are associated with a number of pathological states such as obesity and inflammatory bowel disease (Clemente et al., 2012). It has also been found that microbiota populations are sensitive to genetic and environmental influences (Spor et al., 2011). Despite these progresses, we are still at the very beginning of fully understanding the factors regulating our microbiota and the impacts of microbiota on our health. In particular, our statistical methods for extracting meaningful information from microbiome studies have not been developed as quickly as experimental techniques.

To process raw data from either targeted amplicon or metagenomic sequencing studies (Kuczynski et al., 2011), Operational Taxonomic Units (OTUs), which are microbial genomic sequences clustered by sequence similarity, are commonly used to partition sequences into discrete groups in place of traditional taxonomic units. For each OTU, its abundance or count is defined as the number of sequences belonging to this OTU. Typically, the most abundant sequence in an OTU is chosen as the representative sequence, and representative sequences from all the OTUs are used to construct a phylogenetic tree among all the OTUs, and/or to map OTUs to a taxonomic reference database (Schloss et al., 2009; Navas-Molina et al., 2013). After these processing steps, a microbial community can be characterized by a list of OTUs and their counts, their phylogenetic relationships, and/or their taxonomy.

The data that motivated the statistical method in this article were part of a human gut microbiome study conducted at the University of Pennsylvania (Wu et al., 2011), where the investigators aimed to assess the effect of diet on gut microbiome composition. For this study, both gut microbiome data and nutrient intake data were available (see Section 6 for details). Using a distance-based analysis procedure, the authors identified a few gut microbiome-associated nutrients that are biologically interpretable. As noted by Chen and Li (2013), however, this method is based on distances between microbiome samples, and thus is unable to provide information on how dietary nutrients affect bacterial taxa. In order to identify key nutrients as well as the taxa they affect, Chen and Li (2013) adopted a regression-based approach, where they treated OTU-abundance data as multivariate count responses, and nutrients as covariates.

Let Y = (Y₁, …, Y_K)^⊤ denote the random vector of counts on K bacterial taxa or OTUs. The simplest distribution for multivariate count data is the multinomial distribution. Suppose y = (y₁, …, y_K)^⊤ is a draw from this distribution. Given ${\sum }_{k=1}^K{Y}_k={\sum }_{k=1}^K{y}_k$, the probability mass of Y at y is

$$f_M(y;p)=\frac{\mathrm{\Gamma }({\sum }_{k=1}^K{y}_k+1)}{{\prod }_{k=1}^K\mathrm{\Gamma }(y_k+1)}\prod _{k=1}^K{p}_k^{y_k},$$

where Γ(·) is the gamma function, and p = (p₁, …, p_K)^⊤ is the vector of probabilities such that ${\sum }_{j=1}^K{p}_j=1$. In the multinomial regression model, p is linked to the covariates via the multinomial-Poisson transformation.

Bacterial count data in microbiome studies are usually over-dispersed. The multinomial distribution is inappropriate, however, when more variation is observed than expected. In order to overcome this problem, Chen and Li (2013) assumed that p is random with some prior distribution. Denote by 𝒮^d the (d − 1)-dimensional simplex. Since the support of p is 𝒮^K−1, they used the Dirichlet distribution whose density at u = (u₁, …, u_K) ∈ 𝒮^K−1, parameterized by K positive values α₁ > 0, …, α_K > 0, is given by

$$f_D(u;\alpha )=\frac{\mathrm{\Gamma }\left({\sum }_{k=1}^K{\alpha }_k\right)}{{\prod }_{k=1}^K\mathrm{\Gamma }({\alpha }_k)}\prod _{k=1}^K{u}_k^{{\alpha }_k-1},$$

where α = (α₁, …, α_K)^⊤. The Dirichlet distribution is popular mainly because, as a prior distribution, it is conjugate to the multinomial distribution, leading to the Dirichlet multinomial distribution (Mosimann, 1962), also known as the Dirichlet compound multinomial distribution, with probability mass function

$$f_{\mathit{\text{DM}}}(y;\alpha )={\int }_{u\in {𝒮}^{K-1}}{f}_M(y;u)f_D(u;\alpha )\mathit{\text{du}}=\frac{\mathrm{\Gamma }({\sum }_{k=1}^K{y}_k+1)\mathrm{\Gamma }\left({\sum }_{k=1}^K{\alpha }_k\right)}{\mathrm{\Gamma }({\sum }_{k=1}^K{y}_k+{\sum }_{k=1}^n{\alpha }_k)}\prod _{k=1}^K\frac{\mathrm{\Gamma }(y_k+{\alpha }_k)}{\mathrm{\Gamma }(y_k+1)\mathrm{\Gamma }({\alpha }_k)}.$$

Using the Dirichlet multinomial distribution, Chen and Li (2013) considered a Dirichlet-multinomial regression model, and applied it to the analysis of gut microbiome and nutrient intake data.

The Dirichlet (multinomial) distribution has three limitations. First, all components must share a common variance parameter. Second, the components are mutually independent, up to the constraint that they must sum up to one (Mosimann, 1962). Finally, the distribution fails to take into account the special and inherent property of microbiome count data, namely, microbial taxa are not independent of each other, but are related evolutionarily in a phylogenetic tree. To address these limitations, we consider a generalization of the Dirichlet (multinomial) distribution. Assuming that the relationships among components of the count vector can be represented as a tree, the generalized distribution encodes the tree structure node-by-node as detailed in the next section. By construction, each component has an independent variance, and components are correlated at subtree levels. Based on this distribution, we propose a regression model to include the effects of covariates, and develop a regularized method for selecting covariates (e.g., nutrients) that are associated with the count responses (e.g., OTUs).

To circumvent the first two issues with the Dirichlet (multinomial) distribution, Billheimer et al. (2001) proposed an alternative distribution for over-dispersed multivariate count data, called the logistic normal multinomial distribution, by replacing the Dirichlet distribution for p with Aitchison’s logistic normal distribution (Aitchison, 1982). The corresponding regression model, which relates covariates to the count vector, was studied by Billheimer et al. (2001), and was recently applied to link dietary nutrients with bacterial counts by Xia et al. (2013). However, like the Dirichlet multinomial distribution, the logistic normal multinomial distribution cannot exploit the tree structure information, and unlike the Dirichlet multinomial distribution and the generalized version considered here, its density does not have a closed-form expression, making the regression estimation computationally intensive.

The rest of the article is organized as follows. We review the Dirichlet-tree multinomial distribution and its properties in Section 2. We then propose the Dirichlet-tree multinomial regression model in Section 3. Regularized likelihood estimation, including the algorithm and tuning, are considered in Section 4. Simulation studies and an application to a human gut microbiome data set, respectively in Sections 5 and 6, are used to evaluate the performance of our method. Finally, Section 7 contains some remarks.

2. Dirichlet-Tree Multinomial Distributions

Data on bacterial community structure can be compiled in a matrix of counts, where samples are represented as rows and taxa as columns. As in Chen and Li (2013) and Xia et al. (2013), we treat the total number of counts, which is determined by the sequencing depth, as an ancillary statistic, and conduct the analysis conditioning on this number. Now suppose we have available a tree T representing the hierarchical structure over the count responses (e.g., a phylogenetic tree of bacterial taxa). We seek to incorporate this structural information into the modeling process.

Denote by ℒ the set of leaf nodes and 𝒱 the set of internal nodes of T, respectively. For each internal node υ ∈ 𝒱, let 𝒞_υ be the set of child nodes of υ. For each υ and c ∈ 𝒞_υ, define δ_υc(l) to be 1, if the branch from υ to c leads to l ∈ ℒ, and 0, otherwise. For simplicity, write ℒ = {1, …, K}. Denote by y_υc = Σ_l∈ℒ δ_υc(l)y_l and p_υc = Σ_l∈ℒ δ_υc(l)p_l, respectively, the count and probability in the subtree indexed by c ∈ 𝒞_υ.

Let υ₀ be the root node of T. For each leaf node l ∈ ℒ, denote by

$${\upsilon }_0\equiv {\upsilon }_0^l\to {\upsilon }_1^l\to \cdots \to {\upsilon }_{D_l-1}^l\to {\upsilon }_{D_l}^l\equiv l$$

the path from υ₀ to l, where ${\upsilon }_d^l\in 𝒱$ for d = 0, …, D_l − 1, and D_l ≥ 1 is the number of branches in this path. Let b_υc = p_υc/Σ_s∈𝒞υ p_υs. Then Σ_c∈𝒞υ b_υc = 1, hence each branch of T is assigned a probability. A simple calculation shows that

$$p_l=b_{{\upsilon }_0{\upsilon }_1^l}\times b_{{\upsilon }_1^l{\upsilon }_2^l}\times \cdots \times b_{{\upsilon }_{D_l-1}^l}=\prod _{\upsilon \in 𝒱}\prod _{c\in {𝒞}_{\upsilon }}{b}_{\upsilon c}^{{\delta }_{\upsilon c}(l)}.$$

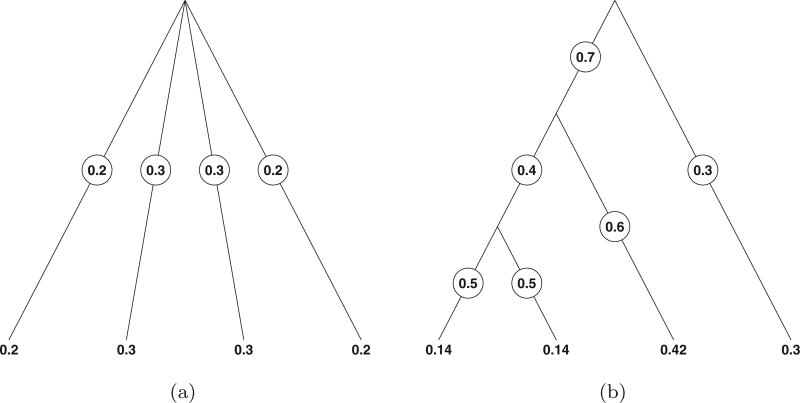
That is, p_l is the product of branch probabilities as we traverse from υ₀ to l. See Figure 1 for an illustration. Furthermore, we can write

$$f_M(y;p)=f_M(y;b_{\upsilon },\upsilon \in 𝒱)=\prod _{\upsilon \in 𝒱}\frac{\mathrm{\Gamma }({\sum }_{c\in {𝒞}_{\upsilon }}{y}_{\upsilon c}+1)}{{\prod }_{c\in {𝒞}_{\upsilon }}\mathrm{\Gamma }(y_{\upsilon c}+1)}\prod _{c\in {𝒞}_{\upsilon }}{b}_{\upsilon c}^{y_{\upsilon c}},$$

where b_υ = {b_υc, c ∈ 𝒞_υ}.

Figure 1.

Two trees, each with four leaf nodes. Shown are branch and leaf probabilities.

Instead of assuming one Dirichlet distribution for p, we can specify a separate Dirichlet distribution for b_υ, for each internal node υ ∈ 𝒱. Specifically, the joint density function of (b_υ, v ∈ 𝒱) has the form

$$\prod _{\upsilon \in 𝒱}{f}_D(u_{\upsilon };{\alpha }_{\upsilon })=\prod _{\upsilon \in 𝒱}\frac{\mathrm{\Gamma }\left({\sum }_{c\in {𝒞}_{\upsilon }}{\alpha }_{\upsilon c}\right)}{{\prod }_{c\in {𝒞}_{\upsilon }}\mathrm{\Gamma }({\alpha }_{\upsilon c})}\prod _{c\in {𝒞}_{\upsilon }}{u}_{\upsilon c}^{{\alpha }_{\upsilon c}-1},$$

where u_υ = (u_υc, c ∈ 𝒞_υ) ∈ 𝒮^K_υ−1, K_υ is the number of children of υ, and α_υ = (α_υc > 0, c ∈ 𝒞_υ) is a vector of positive scalars. This gives the Dirichlet-tree multinomial distribution (Dennis, 1996; Minka, 2004), which is a compound multinomial distribution with probability mass function

$$f_{\mathit{\text{DTM}}}(y;{\alpha }_{\upsilon },\upsilon \in 𝒱)=\prod _{\upsilon \in 𝒱}{\int }_{u_{\upsilon }\in {𝒮}^{K_{\upsilon }-1}}{f}_M(y;u_{\upsilon },\upsilon \in 𝒱)f_D(u_{\upsilon };{\alpha }_{\upsilon }){\mathit{\text{du}}}_{\upsilon }=\prod _{\upsilon \in 𝒱}\frac{\mathrm{\Gamma }({\sum }_{c\in {𝒞}_{\upsilon }}{y}_{\upsilon c}+1)\mathrm{\Gamma }\left({\sum }_{c\in {𝒞}_{\upsilon }}{\alpha }_{\upsilon c}\right)}{\mathrm{\Gamma }({\sum }_{c\in {𝒞}_{\upsilon }}{y}_{\upsilon c}+{\sum }_{c\in {𝒞}_{\upsilon }}{\alpha }_{\upsilon c})}\times \prod _{c\in {𝒞}_{\upsilon }}\frac{\mathrm{\Gamma }(y_{\upsilon c}+{\alpha }_{\upsilon c})}{\mathrm{\Gamma }(y_{\upsilon c}+1)\mathrm{\Gamma }({\alpha }_{\upsilon c})}.$$ (1)

Note that each component in the product Π_υ∈𝒱 corresponds to an internal node in the tree, which is described by a Dirichlet multinomial distribution based on the accumulated counts along branches of that node. In the special case where υ₀ is the only internal node, that is, 𝒱 = {υ₀}, this distribution reduces to the Dirichlet multinomial distribution.

It is not difficult to show that

$$E(p_l)=\prod _{\upsilon \in 𝒱}\prod _{c\in {𝒞}_{\upsilon }}{\{E(b_{\upsilon c})\}}^{{\delta }_{\upsilon c}(l)}=\prod _{\upsilon \in 𝒱}\prod _{c\in {𝒞}_{\upsilon }}{\left(\frac{{\alpha }_{\upsilon c}}{{\sum }_{c\in {𝒞}_{\upsilon }}{\alpha }_{\upsilon c}}\right)}^{{\delta }_{\upsilon c}(l)}.$$

Thus, given ${\sum }_{k=1}^K{Y}_k={\sum }_{k=1}^K{y}_k,E(Y_l)=E(p_l){\sum }_{k=1}^K{y}_k$. Other moments of the Dirichlet-tree distribution can be found in Dennis (1991). In particular, Dennis showed that when 𝒱 ≠ {υ₀}, each component p_l has an independent variance, and two components corresponding to the subtree indexed by υ ∈ 𝒱 are correlated, due to their dependence on the ancestors of υ.

3. A Dirichlet-Tree Multinomial Regression Model

The Dirichlet-tree distribution is often used as a prior in a Bayesian analysis (see, e.g., Tam and Schultz, 2007; Haffari and Teh, 2009). On the other hand, to our knowledge the Dirichlet-tree (multinomial) distribution is not thought of as a response distribution, while in practice it is frequent to find multivariate count data (such as counts of bacterial taxa) with observed covariates (such as measurements of dietary nutrients). In this section, we use the Dirichlet-tree multinomial distribution to develop a model for regressing the count vector Y on p covariates X₁, …, X_p.

To model the effects of covariates, for each υ ∈ 𝒱 and c ∈ 𝒞_υ we express log(α_υc) as a linear combination of the covariates. Specifically, we assume that

$$\text{log}({\alpha }_{\upsilon c})=X^{\top }{\beta }_{\upsilon c},$$ (2)

where X = (X₁, …, X_p)^⊤, and β_υc = (β_υc1, …, β_υcp)^⊤ is the vector of coefficients.

Let β_υ = (β_υc, c ∈ 𝒞_υ) and β = (β_υ, υ ∈ 𝒱). The standard way of estimating β is to use maximum likelihood. Let y_i = (y_i1, …, y_iK)^⊤ denote the observed vector of counts and x_i = (x_i1, …, x_ip)^⊤ the observed vector of covariates, for i = 1, …, n. Subject to a constant, the log-likelihood function for the observed data is

$$l_{\mathit{\text{DTM}}}(\beta )=\sum _{\upsilon \in 𝒱}{l}_{\upsilon }({\beta }_{\upsilon })$$ (3)

with

$$l_{\upsilon }({\beta }_{\upsilon })=\sum _{i=1}^n\left[\stackrel{\sim }{\mathrm{\Gamma }}\right(\sum _{c\in {𝒞}_{\upsilon }}{\alpha }_{i\upsilon c})-\stackrel{\sim }{\mathrm{\Gamma }}(\sum _{c\in {𝒞}_{\upsilon }}{y}_{i\upsilon c}+\sum _{c\in {𝒞}_{\upsilon }}{\alpha }_{i\upsilon c})+\sum _{c\in {𝒞}_{\upsilon }}\{\stackrel{\sim }{\mathrm{\Gamma }}(y_{i\upsilon c}+{\alpha }_{i\upsilon c})-\stackrel{\sim }{\mathrm{\Gamma }}({\alpha }_{i\upsilon c})\}],$$

where Γ̃(·) = log{Γ(·)}, ${\alpha }_{i\upsilon c}=\text{exp}(x_i^{\top }{\beta }_{\upsilon c})$, and y_iυc = Σ_l∈ℒδ_υc(l)y_il.

4. Regularized Likelihood Estimation

One can show that the number of parameters in the Dirichlet-tree multinomial regression model equals the number of covariates, p, times the number of branches, Σ_υ∈𝒱 K_υ, and thus it increases rapidly both as the dimension p grows and as the tree T expands. This makes the maximum likelihood estimation unappealing in terms of both accuracy and interpretability. In order to obtain a reliable and interpretable model, we propose a penalized (negative) log-likelihood method that estimates parameters and selects covariates simultaneously. Specifically, we consider the following objective function

$${\mathit{\text{pl}}}_{\mathit{\text{DTM}}}(\beta )\equiv {\mathit{\text{pl}}}_{\mathit{\text{DTM}}}(\beta ;{\lambda }_1,{\lambda }_2)=-l_{\mathit{\text{DTM}}}(\beta )+{\lambda }_1\sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_1+{\lambda }_2\sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_2,$$ (4)

where λ₁ and λ₂ are tuning parameters, and ‖·‖₁ and ‖·‖₂ are the usual l₁ and l₂ norms.

4.1. Algorithm

Since the penalty function is non-smooth, we adopt the accelerated proximal gradient method (see, e.g., Beck and Teboulle, 2009) to minimize pl_DTM(β). The algorithm alternates between two sequences {β^(t)} and {η^(t)}, where t is the index of iteration. At the (t + 1)-th iteration, we approximate −l_DTM(β) at η^(t) by

$$-{\stackrel{\sim }{l}}_{\mathit{\text{DTM}}}(\beta ;{\eta }^{(t)})=-l_{\mathit{\text{DTM}}}({\eta }^{(t)})-\langle \beta -{\eta }^{(t)},\nabla l_{\mathit{\text{DTM}}}({\eta }^{(t)})\rangle +\frac{C}{2}{\Vert \beta -{\eta }^{(t)}\Vert }_2^2,$$

where 〈·, ·〉 is the trace operator, ∇l_DTM(·) is the gradient of l_DTM(·), and C > 0 is a constant. Let

$$p{\stackrel{\sim }{l}}_{\mathit{\text{DTM}}}(\beta )=-{\stackrel{\sim }{l}}_{\mathit{\text{DTM}}}(\beta ;{\eta }^{(t)})+{\lambda }_1\sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_1+{\lambda }_2\sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_2.$$ (5)

We update β^(t+1) by solving

$${\beta }^{(t+1)}=\text{arg }\underset{\beta }{\text{min}}\{p{\stackrel{\sim }{l}}_{\mathit{\text{DTM}}}(\beta )\}.$$ (6)

We then update η^(t+1) as

$${\eta }^{(t+1)}={\beta }^{(t+1)}+\frac{1-a_t}{a_t}{a}_{t+1}({\beta }^{(t+1)}-{\beta }^{(t)}).$$ (7)

Here, a_t = 2/(t + 2). A simple calculation shows that the optimization problem (6) can be decomposed into a set of subproblems

$${\beta }_{\upsilon c}^{(t+1)}=\text{arg }\underset{{\beta }_{\upsilon c}}{\text{min}}[\frac{1}{2}{\Vert {\beta }_{\upsilon c}-\{{\eta }_{\upsilon c}^{(t)}-\frac{1}{C}\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})\}\Vert }_2^2+\frac{{\lambda }_1}{C}{\Vert {\beta }_{\upsilon c}\Vert }_1+\frac{{\lambda }_2}{C}{\Vert {\beta }_{\upsilon c}\Vert }_2]$$

for υ ∈ 𝒱 and c ∈ 𝒞_υ, where ∇l_υc(η_υ) is the gradient of l_υ(η_υ) with respect to η_υc. Let

$${\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}=\text{sgn }\{{\eta }_{\upsilon c}^{(t)}-\frac{1}{C}\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})\}\text{ max }\{0,|{\eta }_{\upsilon c}^{(t)}-\frac{1}{C}\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})|-\frac{{\lambda }_1}{C}\},$$

where sgn is the sign function, and the equality holds element-wise. The solution of ${\beta }_{\upsilon c}^{(t+1)}$ is easily shown to be

$${\beta }_{\upsilon c}^{(t+1)}=\frac{{\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}}{{\Vert {\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}\Vert }_2}\text{max }\{0,{\Vert {\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}\Vert }_2-\frac{{\lambda }_2}{C}\}.$$ (8)

Instead of using a constant step size C, we can use the backtracking rule to choose a suitable C at each iteration. In summary, the algorithm for each pair of (λ₁, λ₂) proceeds as follows.

S1 Initialize C = Συ∈𝒱 Kυ × p, a0 = 1, β0, and η0 = β0.

S2 Iterate until plDTM (β(t+1)) < pl̃DTM (β(t+1); η(t)).

S2.1 For all υ ∈ 𝒱 and c ∈ 𝒞υ, compute $\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})$ and $${\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}=\text{sgn }\{{\eta }_{\upsilon c}^{(t)}-\frac{1}{C}\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})\}\times \text{max }\{0,|{\eta }_{\upsilon c}^{(t)}-\frac{1}{C}\nabla l_{\upsilon c}({\eta }_{\upsilon }^{(t)})|-\frac{{\lambda }_1}{C}\}.$$

S2.2 Update $${\beta }_{\upsilon c}^{(t+1)}=\frac{{\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}}{{\Vert {\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}\Vert }_2}\text{max }\{0,{\Vert {\stackrel{\sim }{\beta }}_{\upsilon c}^{(t+1)}\Vert }_2-\frac{{\lambda }_2}{C}\}.$$

S2.3 Set C to be 2C.

S3 Update at+1 = 2/ (t + 3) and $${\eta }^{(t+1)}={\beta }^{(t+1)}+\frac{1-a_t}{a_t}{a}_{t+1}({\beta }^{(t+1)}-{\beta }^{(t)}).$$

S4 If the objective value converges, stop the algorithm. Otherwise, set t to be t + 1 and go to S2.

Three things are noteworthy. First, each of the two sequences is computed analytically, hence the algorithm is easy to implement. Second, the complexity of the algorithm scales well with both the number of covariates and the number of branches. Third, as l_DTM(β) is non-convex, convergence is not guaranteed. Generally, the algorithm converges to a local minimizer, since the objective value decreases over iterations. Empirically, based on our own experience in simulations, the algorithm is fast and efficient.

4.2. Tuning and Implementation

A key issue in the above penalized likelihood estimation is the choice of appropriate values for the tuning parameters. To this end, we consider a re-parametrization of λ₁ and λ₂ as follows. Let λ = λ₁ + λ₂ and γ = λ₂/(λ₁ + λ₂). We can write

$${\mathit{\text{pl}}}_{\mathit{\text{DTM}}}(\beta ;{\lambda }_1,{\lambda }_2)={\mathit{\text{pl}}}_{\mathit{\text{DTM}}}(\beta ;\lambda ,\gamma )=-l_{\mathit{\text{DTM}}}(\beta )+\lambda \{(1-\gamma )\sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_1+\gamma \sum _{\upsilon \in 𝒱}\sum _{c\in {𝒞}_{\upsilon }}{\Vert {\beta }_{\upsilon c}\Vert }_2\}.$$

Denote by β̂(λ, γ) the minimizer of pl_DTM(β; λ, γ). Two special cases are the lasso estimate β̂(λ, 0) and the group lasso estimate β̂(λ, 1). When 0 < γ < 1, we call β̂(λ, γ) a sparse group lasso estimate.

For each given γ, we use the Bayesian information criterion (Schwarz, 1978) to select λ. To be specific, we define

$$\text{BIC}(\lambda ,\gamma )=-2\times l_{\mathit{\text{DTM}}}\{\hat{\beta }(\lambda ,\gamma )\}+\text{log}(n)\times \text{df}\{\hat{\beta }(\lambda ,\gamma )\},$$

where df{β̂(λ, γ)} is the effective degrees of freedom implied by β̂(λ, γ). In this article, we approximate df{β̂(λ, γ)} by the number of nonzero components in β̂(λ, γ). We then select λ by minimizing BIC(λ, γ) over a set of candidate values. Note that cross validation is an alternative to BIC, but it tends to over-select spurious features (Wasserman and Roeder, 2009). Also, cross validation is computationally too intensive on large data sets.

It is now essential to specify an interval for the values of λ, for each given γ. Clearly, β̂(λ, γ) is exactly zero when λ is sufficiently large. To determine such a value, denoted by λ_max, we search for the smallest λ so that zero is a minimizer of

$$\frac{1}{2}{\Vert {\beta }_{\upsilon c}+\frac{1}{C}\nabla l_{\upsilon c}(0)\Vert }_2^2+\lambda (\frac{1-\gamma }{C}{\Vert {\beta }_{\upsilon c}\Vert }_1+\frac{\gamma }{C}{\Vert {\beta }_{\upsilon c}\Vert }_2)$$

for all υ ∈ 𝒱 and c ∈ 𝒞_υ. To obtain estimates over a grid of λ values, we start with λ_max for which β̂(λ, γ) = 0, decrease it on a log scale, and run the proposed algorithm to compute β̂(λ, γ). Then λ is decreased again and the process is repeated. To reduce the computing time, we use the estimate from the previous λ as a warm start, and to avoid over-fitting, we stop the process until the proportion of nonzero components in β̂(λ, γ) exceeds a certain threshold (e.g., 80%).

It might be cumbersome to interpret potentially tens of thousands of parameters in β̂(λ, γ). To partly overcome this problem, as we will do in the data analysis, we can proceed as follows. Note that for each leaf node l in the tree, which represents a count response, there is a path from the root node υ₀ to l. To see how a covariate (e.g., a dietary nutrient) affects this count response (e.g., a bacterial taxon), we can check whether this nutrient appears in the path from υ₀ to l. In other words, we look at the problem from the viewpoint of covariate selection and take advantage of the tree topology to summarize the information in β̂(λ, γ).

5. Simulation Studies

In this section, we use simulated data to examine the performance of our method. To mimic the association study between nutrient intake and OTU abundance that will be described in Section 6, we generate n = 75 samples, each with K = 28 count responses and p = 100 covariates, and we use the tree in Figure 2 to represent the relationship among the responses. For simplicity, the first 10 covariates are assumed to be relevant (i.e., each of them is associated with at least one response) and the rest redundant.

Figure 2.

The phylogenetic tree. Leaves (i.e., OTUs) are labeled as 1, …, 28, and internal nodes are labeled as 29, …, 55 and indicated by circles.

We first draw the covariate vector X = (X₁,…, X_p)^⊤ from a multivariate normal distribution with mean vector zero and covariance matrix Σ = (0.5^|i−j|) ∈ ℝ^p×p. We then generate the count vector Y = (Y₁, …, Y_K)^⊤ using the Dirichlet-tree multinomial model with parameters specified in Figure 3. Here, we choose nonzero coefficients to be of the same magnitude just for simplicity and for ease of illustration. The conclusions are qualitatively similar if they vary in magnitude.

Figure 3.

Coefficients of the 10 relevant covariates used in the Dirichlet-tree multinomial model. This figure appears in color in the electronic version of this article.

We generated 100 data sets in this way, and for each data set, we applied our method with the tuning parameter λ selected by BIC. Throughout this section, we considered four instances of γ: 0, 0.25, 0.5, and 1. To see how each competitor selected the covariates, we calculated the true positive rate and false positive rate at each tuning parameter value λ, and summarized them by the Receiver Operating Characteristic (ROC) curve that resulted from a grid of λ values. The average ROC curves over 100 data replications are shown in Figure 4. We can see that, for this simulation setup, the sparse group lasso (γ = 0.25 or γ = 0.5) performs better than the lasso (γ = 0) and the group lasso (γ = 1).

Figure 4.

Simulation studies. ROC curves for the four regularized estimators, all based on the Dirichlet-tree multinomial model. The colored triangles show the true positive rate (TPR) and false positive rate (FPR), when the tuning parameter λ was selected by the BIC criterion. (a) n = 75, and (b) n = 100.

For each data set, we further generated a separate set of size n* = 25, and computed the prediction error using the following cost function

$$\sum _{i=1}^{n^{\ast }}\frac{1}{y_{i·}^{\ast }}\sum _{k=1}^K\frac{{(y_{\mathit{\text{ik}}}^{\ast }-{\hat{y}}_{\mathit{\text{ik}}}^{\ast })}^2}{{\hat{y}}_{\mathit{\text{ik}}}^{\ast }},$$

where $\{{(y_{i1}^{\ast },\dots ,y_{\mathit{\text{iK}}}^{\ast })}^{\top },i=1,\dots ,n^{\ast }\}$ are test samples, $y_{i·}^{\ast }={\sum }_{k=1}^K{y}_{\mathit{\text{ik}}}^{\ast }$, and ${\hat{y}}_{\mathit{\text{ik}}}^{\ast }$ denotes a predicted value of $y_{\mathit{\text{ik}}}^{\ast }$. For comparison, we also evaluated the performance of the method of Chen and Li (2013), which was based on the Dirichlet multinomial model. The results are reported in Table 1. Our method had higher prediction accuracy than theirs. Furthermore, for this simulation setup, the performance of the sparse group lasso was better than that of the (group) lasso.

Table 1.

Means and standard deviations (in parentheses) of the prediction error, over 100 replications, are reported for the four regularized estimators based on the Dirichlet-tree multinomial (DTM) model, and those based on the Dirichlet multinomial (DM) model

		n = 75	n = 100
DTM	γ = 0	80 (28)	65 (24)
	γ=0.25	77 (24)	63 (20)
	γ=0.5	79 (23)	64 (19)
	γ=1	138 (34)	123 (33)
DM	γ=0	315 (653)	154 (160)
	γ=0.25	145 (95)	113 (35)
	γ=0.5	141 (34)	115 (25)
	γ=1	212 (37)	175 (51)

Finally, we increased the sample size from n = 75 to n = 100. From Figure 4 and Table 1 we see that the performance of our method improved, but the conclusions remain qualitatively similar.

Note that the Dirichlet-tree distribution reduces to the Dirichlet distribution, when the parameters in the former are chosen carefully. However, this nesting structure is lost in regression models: in the presence of predictors, the Dirichlet multinomial regression is not a sub-model of the Dirichlettree multinomial regression. This makes the direct comparison between these two models difficult, and is the reason for our use of prediction accuracy as a measure of performance. To make feasible the comparison of ROC curves between our method and that of Chen and Li (2013), we can calculate the true positive rate and false positive rate in terms of how each method identifies the relevant covariates. For the simulation example considered here, our method was shown to be superior to Chen and Li (2013)’s; see Web Appendix A for details.

6. Data Analysis

The human gut harbors trillions of microbes that play a fundamental role in human health and disease (Clemente et al., 2012). Some recent studies have suggested that diet is an important factor that underlies the gut microbiota composition (De Filippo et al., 2010; Wu et al., 2011; David et al., 2014). One important goal of microbiome studies is thus to identify which food constituents specifically promote/inhibit growth and functionality of which microorganisms in the human gut.

The data we consider come from a cross-sectional study associating nutrient intake with the human gut microbiota composition (Wu et al., 2011). In this study, the investigators used 16S rRNA sequencing to characterize fecal samples from 98 healthy volunteers. After processing the generated sequences using the QIIME pipeline with the default parameter settings (Navas-Molina et al., 2013), more than 3000 species-level OTUs were obtained, and the microbiome data was summarized by an OTU table (i.e., a matrix of OTU counts) including the taxonomy of each OTU, and a phylogenetic tree relating these OTUs. To link long-term dietary patterns with the microbiome composition, diet information of each subject was collected using a food frequency questionnaire, and was converted into nutrient intake profiles for more than 200 micro-nutrients.

In our analysis, we combined the species-level OTUs at the genus level, and considered 28 relatively prevalent genera that occurred in more than 25 of the 98 samples. Further, we considered a subset of 97 dietary nutrients (Wu et al., 2011) that were obtained by screening the nutrients using a distance-based nonparametric test (McArdle and Anderson, 2001). Our final data consisted of an OTU-count matrix Y ∈ ℝ^98×28, a phylogenetic tree T among 28 genus-levels OTUs, as shown in Figure 2, and a nutrient-intake matrix X ∈ ℝ^98×97. Each nutrient was standardized to have zero mean and unit variance.

In order to evaluate the performance, we randomly split the 98 samples into balanced training and test sets. Specifically, we set approximately 75% of the observations as training samples, and the rest as test samples. Our method was first applied to the training set, and its performance was then assessed by the test set using the same cost function defined in the previous section. We also compared our method with the method of Chen and Li (2013), which was developed for the Dirichlet multinomial model and thus failed to exploit the tree information. Three values of γ were explored to favor sparse solutions, 0, 0.25, and 0.5.

To reduce the variability, the splitting into training and test sets was repeated 100 times and the error estimates were averaged. The results are summarized in Table 2. We can see that the incorporation of the tree structure helped improve the prediction accuracy.

Table 2.

Means and standard deviations (in parentheses) of the prediction error, based on 100 random splits of 98 samples into training sets (75 samples) and test sets (23 samples), are reported for the three regularized estimators based on the Dirichlet-tree multinomial (DTM) model, and those based on the Dirichlet multinomial (DM) model.

DTM	γ = 0	170 (88)
	γ = 0.25	162 (77)
	γ = 0.5	149 (69)
DM	γ = 0	189 (112)
	γ = 0.25	169 (95)
	γ = 0.5	154 (76)

To see how dietary nutrients affected bacterial taxa, we set γ = 0.25 and concentrated on two genera, Bacteroides and Prevetella, that were previously used to define enterotypes of the human gut microbiome (Arumugam et al., 2011; Wu et al., 2011). For each genus-nutrient pair, we checked whether the nutrient appeared in the path from the root node to the leaf node corresponding to the genus. The top 10 nutrients, based on 100 random splits of the total samples into training and test sets, are listed in Table 3. The results are largely consistent with the findings of Wu et al. (2011), where they reported that the Bacteroides enterotype was associated with a number of amino acids and animal protein, while the Prevotella enterotype was associated with a carbohydrate-based diet. Comparing our method with that of Chen and Li (2013), the two subsets of identified nutrients were different. Nevertheless, the conclusions were similar, largely because some nutrients are highly correlated. In Web Appendix B, we provide a heatmap of selection frequencies of all dietary nutrients across 100 random splits.

Table 3.

The 10 most frequently appeared nutrients, respectively for Bacteroides and Prevetella, are reported based on 100 random splits of the total samples

Bacteroides	Prevotella
Cholesterol	Catechin, flavan-3-ol
Added Germ from wheats	Total Trans/Cis Trans Linoleic
Sucrose	Alcohol
Valine	Added Germ from wheats
Proline	Naringenin, flavanone
Methionine	Cholesterol
Maltose	Glycemic Index
Animal Protein	Sucrose
Serine	Maltose
Tyrosine	Valine

7. Discussion

We have considered a generalization of the Dirichlet multinomial distribution for describing multivariate, over-dispersed, and tree-structured count data, called the Dirichlet-tree multinomial distribution, and its associated regression model for relating a set of covariates to these counts. By introducing the l₁ + l₂ regularization, we have proposed a method for simultaneous parameter estimation and covariate selection. We have conducted simulation studies to demonstrate the efficacy of the new approach. When applied to analyze the motivating data set, our method was shown to improve the accuracy of prediction.

We have implemented the proposed method in R (R Core Team, 2014). Our experience suggests that the procedure works reasonably fast. For instance, for the simulation example in Section 5 where n = 100, K = 28, and p = 100, the average computing time (including tuning by BIC) was less than 1.5 minutes on the Yale Louise high performance cluster (Dell m620 system, 8-core processor, 48G of memory) using R version 3.1.0 and a single processer. Due to the incorporation of tree structure, our method is computationally more intensive than that of Chen and Li (2013). However, the complexity of the proposed algorithm increases linearly with the number of branches, and in the numerical studies our method was 2–4 times slower than Chen and Li’s. We also tried the block-coordinate descent algorithm of Chen and Li (2013), and found that this algorithm was much slower than ours, and that it occasionally broke down for a range of tuning parameters. We believe our method of coupling l₁ and l₂ regularizations with the Dirichlet-tree multinomial model would provide a useful data analysis tool for associating covariates (such as dietary nutrients) with multivariate, over-dispersed, and tree-structured count data (such as taxa counts).

In the literature, several schemes have been proposed to take advantage of the tree structure over either the covariates or responses (see, for example, Zhao et al., 2009; Jenatton et al., 2011; Kim and Xing, 2012; Garcia et al., 2014). However, these methods are mainly for univariate or multivariate continuous responses, while our method is for multivariate count responses. More importantly, our way of incorporating the tree information into the model is inherently different from the imposition of tree-guided penalties on the regression parameters for achieving structured sparsity. Indeed, our proposed Dirichlet-tree multinomial model is more flexible than the Dirichlet multinomial model in the sense that it allows the rich dependence structure among the count responses.

It might be reasonable to expect that non-zero regression coefficients are similar for phylogenetically related OTUs, and in this case some tree-based fused lasso regularization is preferable to sparse group lasso regularization. But, the resulting optimization is expected to be more challenging. Also, in reality it is possible that sister taxa can have very different metabolic pathways, ecologies, and interactions with the host. A comparison of our method and a tree-based fused lasso on multiple data sets would be an interesting area for future research.

In this article, we assume that the tree structure is known a priori. In the real data example, the tree is learned from 16S rRNA sequences using a fast and approximate maximum likelihood method (Price et al., 2010). Note that the Dirichlet-tree multinomial regression reduces to the Dirichlet multinomial regression, when the tree is a “comb” tree, that is, the root node of the tree is the only internal node (see Figure 1 for illustration). This, together with the simulation results in Section 5, implies that the correct specification of the tree structure is important. Indeed, tree mis-specification could be a major risk for shotgun sequencing data (Matsen et al., 2010). Another issue is that we exploit the topology of the phylogenetic tree, but ignores the branch lengths. Since each component l_υ of the log-likelihood function (3) corresponds to one internal node υ, direct incorporation of branch lengths is cumbersome. For each internal node υ, the distances of its child nodes from it (i.e., branch lengths) may be summarized and then used as the weight for l_υ. But, robustness against tree mis-specification could be a concern, since both tree topology and branch lengths are exploited. Also, we need to choose a summary statistic that is biologically meaningful. Alternatively, we may use a new model with new inference algorithms. These are beyond the scope of the present article.