Mechanisms of charge transfer and electronic properties of Cu₂ZnGeS₄ from investigations of the high-field magnetotransport

Abstract

Recent development of the thin film solar cells, based on quaternary compounds, has been focused on the Ge contain compounds and their solid solutions. However, for effective utilization of Cu₂ZnGeS₄, deeper investigations of its transport properties are required. In the present manuscript, we investigate resistivity, ρ (T), magnetoresistance and Hall effect in p-type Cu₂ZnGeS₄ single crystals in pulsed magnetic fields up to 20 T. The dependence of ρ (T) in zero magnetic field is described by the Mott type of the variable-range hopping (VRH) charge transfer mechanism within a broad temperature interval of ~100–200 K. Magnetoresistance contains the positive and negative components, which are interpreted by the common reasons of doped semiconductors. On the other hand, a joint analysis of the resistivity and magnetoresistance data has yielded series of important electronic parameters and permitted specification of the Cu₂ZnGeS₄ conductivity mechanisms outside the temperature intervals of the Mott VRH conduction. The Hall coefficient is negative, exhibiting an exponential dependence on temperature, which is quite close to that of ρ(T). This is typical of the Hall effect in the domain of the VRH charge transfer.

Introduction

Recent development of the solar cell science and technology, based on the I₂-II-IV-VI₄ quaternary chalcogenides, has been focused on their solid solutions with a partial cation substitution. The most promising results have been achieved with Cu₂ZnSn_xGe_1−x(S,Se)₄ belonging to this family of compounds^1–5. Herewith, even introduction of a small amount of Ge as dopant in the Cu₂ZnSnSe₄ layers (with Ge contents well below 10%) yields a significant increase of the solar cell efficiency^{4, 5}. Following this tendency, an incrementing amount of investigations of the Cu₂ZnSn_xGe_1-x(S,Se)₄ solid solutions has been published in recent time^6–12. On the other hand, an alternative way for a future development of the solar cells based on quaternary compounds is considered widely nowadays. It deals with tandem solar cells, where quaternary compounds are used in a top device with a higher band gap^13–15. Theoretical investigations predict an inverse dependence of the top device efficiency on the absorbing layer band gap¹³. Accordingly, an absorbing layer with the band gap, E _g, of 2 eV or higher requires less than 9% of efficiency for the top solar cell to ensure more than 25% of total efficiency of the tandem device. In this sense, Cu₂ZnGeS₄ (CZGeS) is a good candidate for utilization. Indeed, its band gap lies in the range of E _g ~2.1–2.3 eV^16–20, whereas the absorption coefficient exceeding 10⁴ cm^{-1 19} is an additional advantage. Besides of the photovoltaic applications, CZGeS shows promising results also for the hydrogen evolution of water²¹ and is regarded as a possible application in thermoelectric materials²². However, additional investigations of the fundamental properties of CZGeS should be performed, before its effective utilization in different optoelectronic devices would be possible, including a solid solution or the compound itself.

The main feature of CZGeS, distinguishing it from other quaternaries, is existence of the two different structural types, kesterite^{6, 10, 12, 23–26} and wurtzstannite^{17, 18, 20, 27, 28}, both observed experimentally. Along with the structural investigations^{17, 18, 23, 24, 27}, the optical^16–20 and vibrational^{10, 12, 25, 26, 28} properties of CZGeS have been studied extensively for both types. On the other hand, the electronic transport of CZGeS, which is important for any material utilization in optoelectronic devices, is still investigated quite insufficiently. There exist only a few articles, where the room temperature resistivity^{16, 17, 20}, and its behavior in the high temperature range of 450–550 K^{22, 29} have been observed, without any analysis of the data. Probably, the only exclusion is an explicit analysis of the resistivity and magnetoresistance in the kesterite type Cu₂ZnSn_xGe_1-xSe₄ solid solutions¹¹.

In the present work, the temperature dependence of the zero-field resistivity, ρ(T), and magnetotransport in CZGeS single crystals with wurtzstannite structure are investigated within a wide interval below 300 K. This permits identification of the conductivity mechanisms in different temperature ranges and determination of important electronic parameters, which are required to estimate efficiency of the material in optoelectronic devices. In particular, the joint analysis of the resistivity and magnetoresistance data has been widely demonstrated to be an effective method for such a purpose (see e. g. refs 30–38 and references therein), which has been already utilized recently in various kesterite type quaternary compounds^{11, 39}.

Results and Discussion

Experimental results

As can be seen in the top panel of Fig. 1, ρ(T) of all samples is similar, exhibiting a strongly activated behavior within the whole temperature range, available for the resistivity measurements.

Figure 1.

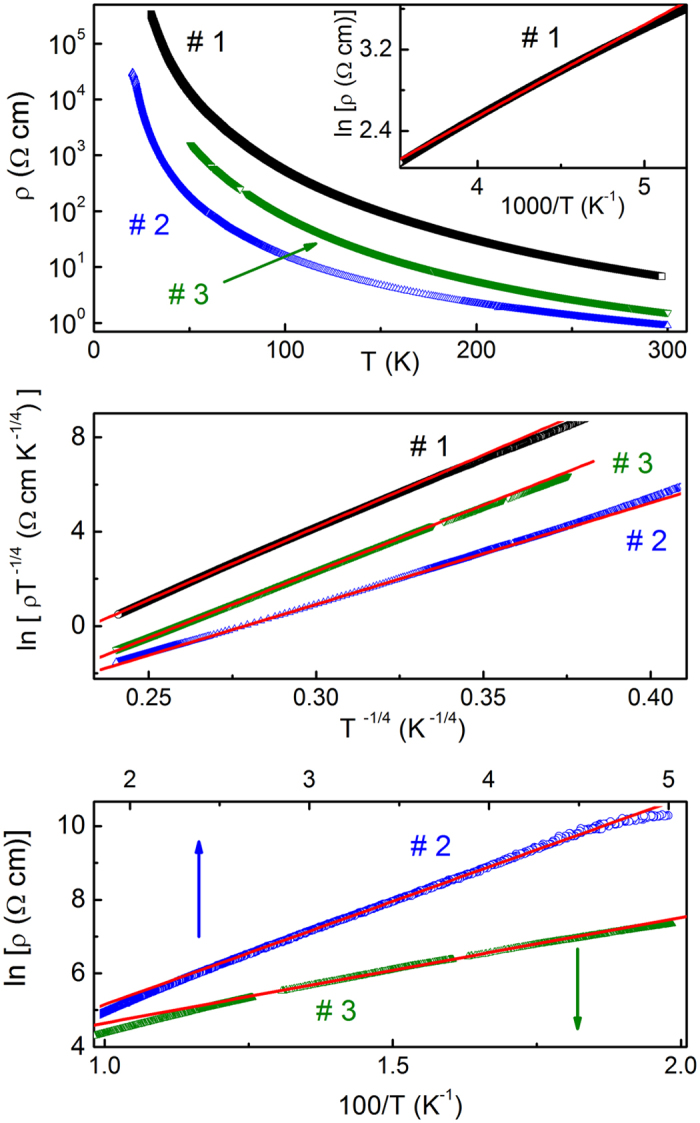
Temperature dependence of the resistivity (top panel), the plots of ln (ρ T ^−1/4) vs. T ^−1/4 (middle panel) and the plots of ln ρ vs. T ⁻¹ (inset to the top panel and bottom panel) for samples #1, #2 and #3. The lines are linear fits.

As follows from Fig. 2, magnetoresistance (MR) contains both the positive (pMR) and the negative (nMR) contributions within the whole temperature range of ~50–300 K. In particular, the relative MR, Δρ/ρ ≡ [ρ(B) − ρ(0)]/ρ(0), is negative almost at any B and T, excluding only the cases of T = 70 K in #1, and T = 50 K and 300 K in #3 at B > 18 T. The behavior of MR with increasing temperature is noticeable, having different temperature dependences within two different temperature intervals, addressed to the lower and higher T, as well as various shapes of the curves in Fig. 2 in the corresponding intervals. Namely, between T = 70–100 K, 60–80 K and 50–70 K in #1, #2 and #3, respectively, the MR effect increases with increasing T. The decay of MR with T, conventional for semiconductors, starts only with further increase of the temperature beyond the intervals above. In addition, such a transition is accompanied by a gradual flattening of the MR shape, showing different relations between temperature dependences of the nMR and pMR contributions in each of the temperature intervals, defined above.

Figure 2.

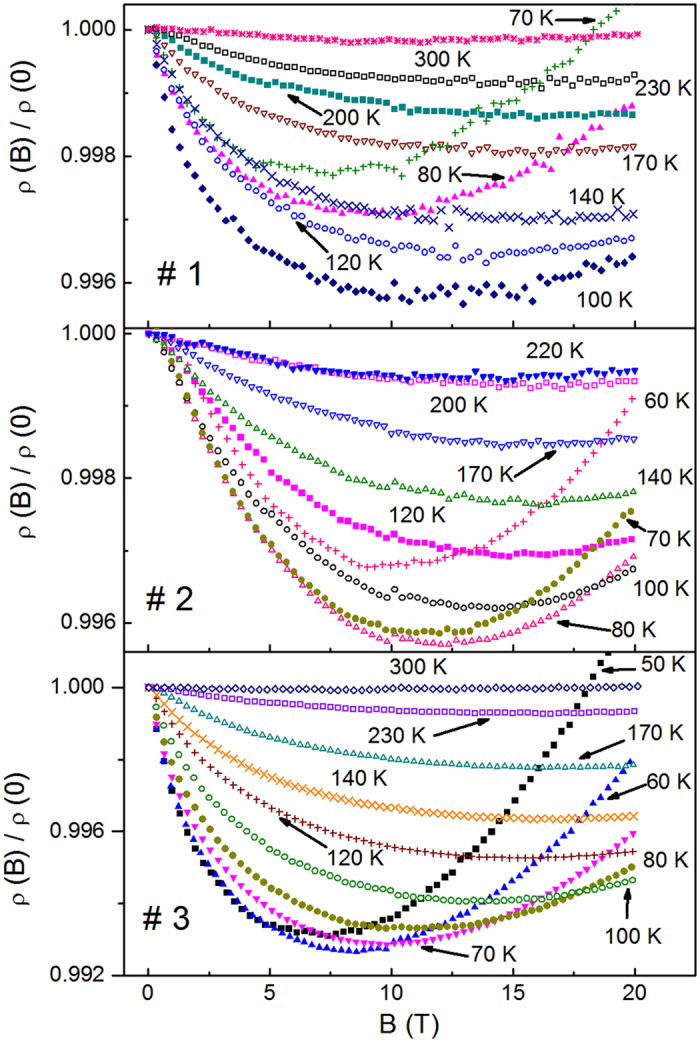
The dependence of the relative resistivity, ρ(B)/ρ(0), on B for the investigated samples at different temperatures.

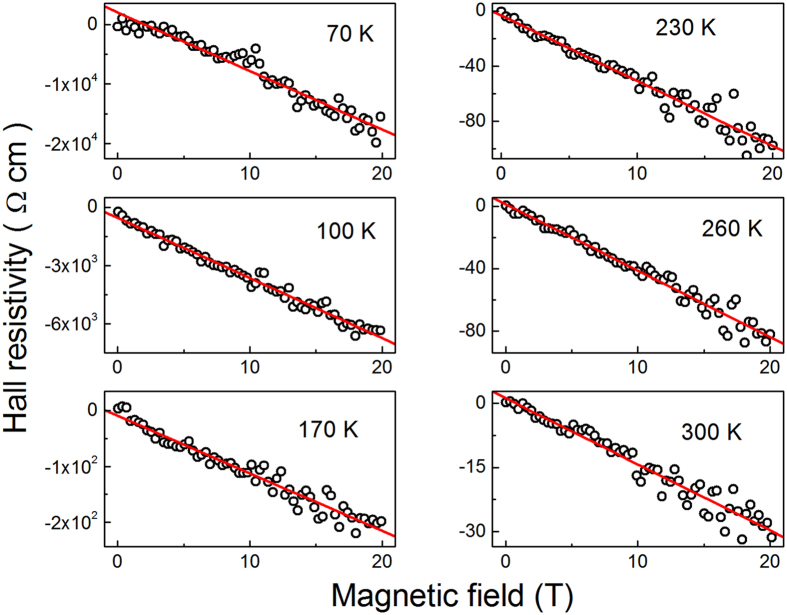
In Fig. 3 is evident, that the Hall resistivity, ρ_H, of sample #1 is negative at any T between 70–300 K, despite of the positive sign of the thermopower and the p-type conduction of our CZGeS samples. Note, that the hole conduction is typical of all Cu based quaternary compounds of this family of materials, although possessing the kesterite structure (see e. g. refs 11, 39 and references therein). One cannot observe distinguishable deviations of the ρ_H(B) function from linearity, which, however, may be connected partially to a rather high scattering of the data points in Fig. 3. On the other hand, a strong dependence of ρ_H(T) between T = 70 and 230 K is evident at any field, weakening substantially with further increase of T up to 300 K.

Figure 3.

The dependence of the Hall resistivity on the magnetic field for sample #1 at different temperatures. The lines are linear fits.

Temperature dependence of resistivity at B = 0

In the quaternary Cu based kesterite materials the hopping charge transfer, mainly the Mott variable-range hopping (VRH), has been reported for different chemical content, stoichiometry and macroscopic state, including single crystals^{11, 39–42}, thin polycrystalline films^43–48 and powder samples^{49, 50}. The temperature border of the hopping conduction is usually very high, stretching even up to the room temperature already in single crystals, whereas width of the defect acceptor band, W, vary from ~10 to ~100 meV and even higher^39–50. Both these features are quite uncommon for conventional semiconductors with shallow hydrogenic impurities, exhibiting usually W between ~1–10 meV and the hopping charge transfer at temperatures well below 300 K^{32–36, 51–54}. The point is that the energy of the main (most stable) acceptor level, E _A, connected to Cu_Zn antisites^55–60, in such materials is rather high (e.g. in Cu₂ZnSnS₄ and Cu₂ZnSnSe₄ the values of E _A ≈ 120–140 meV have been reported^{39, 55–58}), which favors the hopping charge transfer in general. On the other hand, domination of the Mott VRH conduction is connected with a high intrinsic lattice disorder, caused by formation of the disordered kesterite phase^61–63. In turn, the disorder can be effectively varied experimentally, as has been demonstrated by observations of considerable changes in W of the Cu₂ZnSnS₄ films after thermal annealing⁴⁴. At this point, the VRH conduction is quite expectable in CZGeS, too, supported by E _A = 140 meV⁶⁴ and by a complicated crystal structure^23–28 permitting similar reasons for the microscopic disorder, as in kesterites^61–63.

Therefore, it is reasonable to start the analysis of ρ(T) in our samples by searching the possible interval of the Mott VRH charge transfer, given by the resistivity law

$$\mathrm{\rho }(T)=D{T}^{1/4}\exp \left[{\left(\frac{T_0}{T}\right)}^{1/4}\right].$$ 1

Here, D is the VRH prefactor constant and

$$T_0=\mathrm{\beta }{\left[k_{\mathrm{B}}g(\mathrm{\mu })a^3\right]}^{-1}$$ 2

is the VRH characteristic temperature, where k _B is the Boltzmann constant, β = 21 is a numerical constant, g(μ) is the density of the localized states (DOS) at the Fermi level, μ, and a is the localization radius of charge carriers, scaling the space decay of the impurity wave functions^51–54. Generally, the VRH conduction sets in, when it is energetically more profitable for a carrier to jump beyond nearest centers, with levels with large energy difference, towards more distant centers with a smaller energy difference with respect to the initial center⁵². Therefore, the factors favoring the VRH charge transfer are connected to decreasing temperature and increasing degree of the disorder. Formally, the VRH conduction of Eq. (1) is expected at ε_m(T) < W, where ε_m(T) ≈ 0.5 k _B (T ³ T ₀)^1/2 is the mean hopping energy^{40, 53}. In addition, Eqs (1) and (2) have been obtained in refs 53 within a percolation approach for the shallow hydrogenic levels, satisfying the condition of E _A/E _g <<1. With the values of E _g ~2.1–2.3 eV and E _A = 140 meV, given above, one finds E _A /E _g ~0.06–0.07, in agreement with the condition above.

Indeed, the plots in the middle panel of Fig. 1 exhibit broad linear intervals, pertinent to the Mott VRH conduction according to Eq. (1). The values of T ₀ have been found with the slopes of these plots. The temperature intervals, ΔT _v, of the Mott VRH charge transfer, have been obtained with the linear intervals of the corresponding plots. The data of T ₀ and ΔT _v are collected in Table 1. In addition, W in Table 1 has been evaluated with the expression of W ≈ 0.5 k _B (T _v ³ T ₀)^{1/4  40, 53}, where T _v is the Mott VRH onset temperature on cooling (i. e. the right border of the intervals ΔT _v in Table 1).

Table 1.

The VRH conduction interval (ΔT _v), VRH characteristic temperature (T ₀), width of acceptor band (W), and MR coefficient (A ₀₄).

Sample	ΔT v K	T 0 107 K	W meV	A 04 10−3 T −2 K1/4
#1	95–210	1.43 ± 0.02	146 ± 6	1.11 ± 0.03
#2	90–195	0.343 ± 0.003	97 ± 4	1.10 ± 0.02
#3	95–185	1.00 ± 0.01	121 ± 5	1.73 ± 0.03

Density of the acceptor states

In order to proceed the analysis of the resistivity and MR, below we assume a conventional DOS of the Anderson type^{51, 52} in the acceptor band, exhibited in Fig. 4. It is considered to be symmetrical, centered at E _A = 0 and is characterized by a finite total width 2W. The parameters −E _c and E _c in Fig. 4 are the mobility edges, separating the delocalized acceptor states from the localized states of the acceptor band, which are hatched. Finally, a small overlap of the acceptor band with the states of the valence band, taking place for #1 (in Table 1, W = 146 meV exceeds slightly E _A = 140 meV⁶⁴) can be neglected in the analysis below. Indeed, the position of μ is expected to lie among the localized states, because otherwise the conductivity would be metallic^{51, 52} contradicting to the activated behavior of ρ(T) in Fig. 1. Such position should be chosen near the left edge of the DOS, as shown in Fig. 4. This corresponds to a sufficiently high degree of compensation, K = N _D/N _A, where N _A is the acceptor concentration and N _D is the concentration of the compensating donors. Therefore, the details of the energy spectrum on the right edge of the DOS, which is close to the valence band edge, are unimportant. In turn, this position of μ is connected with the high W values, which are comparable with the E _A value (see Table 1). This excludes the possibility of μ lying among the right-hand interval of the localized states in Fig. 4, because in this case the conductivity, connected to the activation of the holes from μ to the valence band states, would dominate at any T due to a small difference between W and E _A. Instead, another type of the resistivity^{51, 52},

$$\mathrm{\rho }(T)={\mathrm{\rho }}_0\exp \left[\frac{E_a}{k_{B}T}\right],$$ 3

Figure 4.

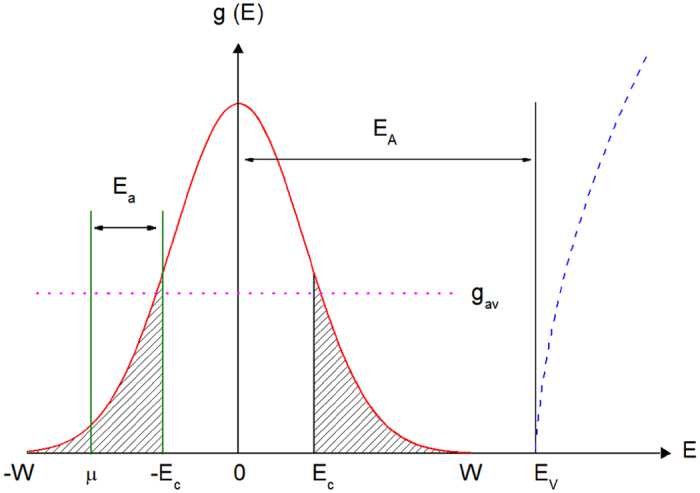
The DOS of the acceptor band (schematically). The localized states are hatched. E _v is the valence band edge (given by the dashed line). The dotted line is the average DOS value, g _av.

characterized by the constant prefactor ρ₀ and the activation energy

$$E_a=\left|\mathrm{\mu }-E_c\right|,$$ 4

has been predicted for the position of μ shown in Fig. 4. Namely, as outlined in Fig. 4, the charge transfer connected to Eq. (3) is determined by activation of the localized holes from μ to −E _c, or, more strictly, from the localized states below the Fermi level into the interval of delocalized states of the impurity band^{51, 52}. In turn, the temperature interval of Eq. (3), ΔT _a, may lie either above or below that of the VRH interval ΔT _v, depending on the distance between μ and –E _c according to Eqs (3) and (4). In particular, both cases of the position of ΔT _a with respect to ΔT _v have been observed in kesterites^{39, 41, 50}.

Analysis of magnetoresistance

In doped semiconductors pMR in the Mott VRH conduction regime is connected mainly with the shrinkage of the impurity wave functions by the magnetic field⁵³. In weak magnetic fields of λ(B)>> a, where λ(B) = [ħ/(eB)]^1/2 is the magnetic length (here, ħ is the Planck constant and e is the elementary charge), pMR of this mechanism can be expressed as⁵³

$$\ln \left[\frac{\mathrm{\rho }(T,B)}{\mathrm{\rho }(T,0)}\right]=A_4(T)B^2,$$ 5

where $A_4(T)=A_{04}{T}^{-3/4}$ and

$$A_{04}=t_4(e^2{a}^4/{\hslash }^2)T_0^{3/4}.$$ 6

Here, t ₄ = 5/2016 is a numerical constant⁵³. The most general mechanism of nMR, proposed for the Mott VRH charge transfer, is addressed to the quantum interference of the direct paths, arising from multiple scattering of the hopping charge carriers by the intermediate centers of the same nature as those involved in the hopping process (acceptors in the case of CZGeS)^65–69. This mechanism has been proposed initially for the VRH conduction at sufficiently low temperatures, where the inelastic collision frequency is expected to be also low, providing conservation of a carrier phase coherence during multiple scattering⁶⁵. However, in strongly disordered systems the constraint above may be weakened, which expands the temperature interval, where the interference effects are important. The point is that a higher disorder, being eventually a main reason of the interference effects^65–69, would lead to their stronger contribution to MR at the same T. Therefore, one can expect a corresponding increase of the upper temperature limit, where the interference effects still survive, when the disorder is increased. Indeed, nMR in the VRH regime, attributable to the interference mechanism above, has been observed at T up to 300 K in disordered polyaniline silicon nanocomposites⁷⁰ and highly disordered pregraphitic carbon nanofiber⁷¹, as well as up to 280 K in Cu₂Zn(Sn_xGe_1-x)Se₄ single crystals¹¹.

As mentioned above, CZGeS and related quaternary compounds are characterized, generally, by high intrinsic lattice disorder. In particular, such disorder leads to a considerable broadening of the impurity band, which exceeds substantially typical values of W in doped semiconductors. As can be seen in Table 1, large values of W characterize our CZGeS samples, too. This permits us to use tentatively the orbital interference mechanism^65–69 to interpret the nMR effect in our material.

For the weak scattering, given by the relation of

$$A_s\ll 1,$$ 7

where A _s ≈ πE _Aβ/(3k _B T ₀) × (T ₀/T)^{1/4  36, 68}, and below a critical field B _c, nMR can be expressed as Δρ/ρ = −a ₂(T)B ², whereas above B _c it is given by the expression Δρ/ρ = −a ₁(T)B ⁶⁸. Here, a ₂(T) ∝ T ⁻¹, a ₁(T) ∝ T ^−3/4 and

$$B_c\approx {(\Delta /E_A)}^{1/2}{B}_{\mathrm{q}},$$ 8

where Δ = k _B(T ³ T ₀)^1/4, B _q ≈ 2^2/3πħ(E _A k _B T)^1/2/(eJ ₀ a ²) × (T/T ₀)^1/4 and J ₀ is the prefactor of the overlap integral⁶⁸. Finally, at B > B _c′, where B _c′ is defined by the condition of λ²(B _c′) ≈ R _h a and R _h ≈ γ₄ a(T ₀/T)^1/4 is the mean hopping length (where γ₄ ≈ 0.357 is a constant⁷²), the nMR law of Δρ/ρ ∝ B ^1/2 has been predicted⁶⁹.

First, we estimate the value of B _c′ for our CZGeS samples. As evident in the top panel of Fig. 1, the strongly activated behavior of ρ(T) is consistent with the state of all the samples lying relatively far from the metal-insulator transition, meaning that the value of a should exceed only slightly the value of the Bohr radius, a _B = ħ²κ₀/(me ²). For evaluation of a _B, the theoretical values of the dielectric constant far from the metal-insulator transition, κ₀ = 6.8⁷³, and of the mean hole effective mass of a stannite CZGeS, m = 0.48m ₀ (where m ₀ is the free electron mass)⁷⁴ can be used, yielding a _B = 7.5 Å. This result is supported completely by the value of E _A = ħ²/(2ma _B ²) = 140 meV, coinciding with its value observed experimentally in ref. 64. Hence, taking e. g. a = 10 Å, we obtain with the direct expression of B _c′ = ħ/(a ² eγ₄) × (T/T ₀)^1/4, the values of B _c′ ≈ 100–140 T at T = 100 K and 110–160 T at T = 200 K. These data permit to exclude a possibility of the square-root dependence of nMR on B above from further consideration, meaning that B _c′ exceeds considerably the maximum applied field of B = 20 T irrespective the possible error of the a value used above. Similarly the magnetic field B ₂, addressed to violation of Eq. (5) and defined by the condition of λ(B ₂) ~ a, i. e. B ₂ ~ ħ/(ea ²), can be estimated to lie close to B ₂ ~600 T. This guarantees applicability of Eq. (5) for our samples, too.

Eventually, the data of A _s ≈ 0.040–0.049, 0.12–0.14 and 0.055–0.064 can be evaluated for #1, #2 and #3, respectively, with the expression of A _s, given below Eq. (7) directly, using E _A = 140 meV and the values of T ₀ and ΔT _v from Table 1. This guarantees the regime of the weak scattering in agreement with Eq. (7). However, the value of the critical field B _c dividing the field intervals of the quadratic and linear nMR dependences above cannot be estimated beforehand requiring the value of the parameter J ₀. On the other hand, as evident in Fig. 2, the field interval of Δρ/ρ ∝ B ² in our samples looks to be quite narrow and is shifted to the low fields (lying probably below B ~1–2 T), constituting only a negligible part of the investigated field interval, where the MR data are less confident than at higher B. Therefore, it is more consistent to concentrate the analysis of MR on the higher field interval of B > 10 T, where the linear field dependence of nMR and the quadratic dependence of the pMR on B are more expected to persist. Hence, taking into account the consideration of nMR above, Eq. (5) for pMR and the evident fact that the expression of ln[ρ (T, B)/ρ (T, 0)] ≈ Δρ/ρ is fulfilled with a high accuracy, provided that the relative MR does not exceed 1% anywhere (Fig. 2), we can use for the analysis of MR the expression

$$\mathrm{\Delta }\mathrm{\rho }/\mathrm{\rho }+a_{\mathrm{1}}(T)B=A_4(T)B^2.$$ 9

The values of a ₁ (T) are found by plotting the left-hand side of Eq. (9) vs. B ² and choosing a ₁(T) to obtain the best linearization of the plots. This is done by minimizing the standard deviation (SD), provided that all the plots should pass through the origin. Finally, the slope of these plots in Fig. 5 gives A ₄(T).

Figure 5.

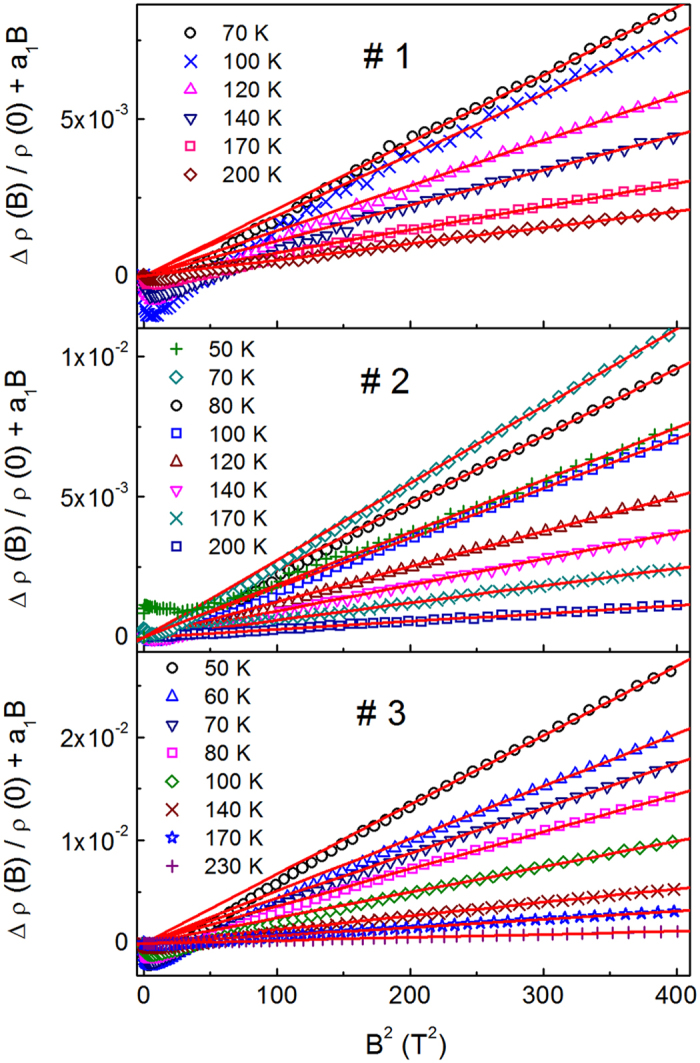
The plots of Δρ(B)/ρ(0) + a ₁ B vs. B ² for the investigated samples at different temperatures. The lines are linear fits according to Eq. (9).

As can be seen in Fig. 5, the procedure above can be done for the majority of the MR plots in Fig. 2, including those lying within the VRH interval ΔT _v (some of the data are not shown only for convenience), whereas the onset of the linear dependence, lying between B _ons ~5–12 T, can be found only approximately. However, the interval of linearity looks sufficient for a reasonably accurate determination of both parameters, a ₁(T) and A ₄(T), which are plotted in the top and middle panels of Fig. 6, respectively, as functions of T ^−3/4. One can see a good linearity of both functions within a whole temperature interval ~100–200 K of the Mott VRH conduction regime (cf. Table 1), deviating from such behavior only below 80 K. The values of A ₀₄ were obtained with linear fits of the plots in the middle panel of Fig. 6 according to the expression of A ₄(T), given below Eq. (5). They are collected in Table 1.

Figure 6.

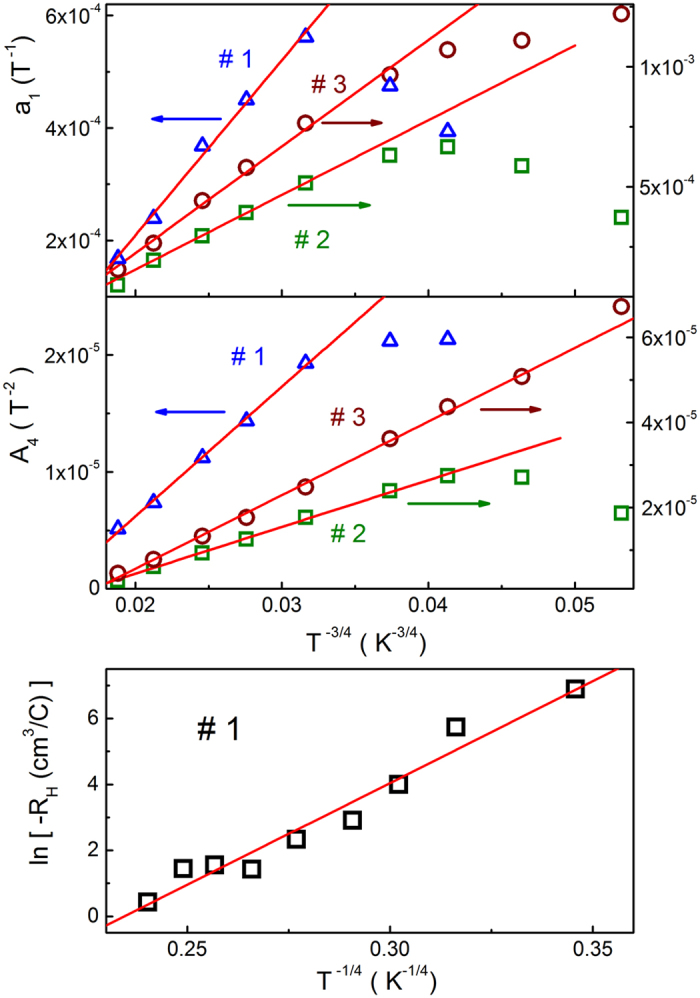
The plots of a ₁ vs. T ^−3/4 (top panel), A ₄ vs. T ^−3/4 (middle panel) and ln(−R _H) vs. T ^−1/4 (bottom panel). The lines are linear fits.

Finally, existence of other nMR mechanisms, probably less universal than that discussed above, should be mentioned for the sake of completeness. In particular, we have tested the nMR models based on the Zeeman effect⁷⁵ and on a possible sensitivity of DOS to the magnetic field⁷⁶, as well as the Khosla-Fischer model, taking into account both nMR and pMR contributions and addressing nMR to the scattering of charge carriers by the localized magnetic moments⁷⁷. Concerning the first two models^{75, 76}, their application could not reproduce correctly either the field or the temperature dependences of nMR in our samples. Formally, our MR data can be reproduced with the last out of the models above⁷⁷. However, this model requires a degeneracy of the carrier gas, which obviously does not take place in our samples contradicting to the strongly activated behavior of ρ(T) in Fig. 1. In addition, no evidence for existence of the localized magnetic moments (or any types of paramagnetic centers) have been obtained in CZGeS in any previous investigations. In particular, those of the magnetization^{78, 79} and the EPR⁷⁹ measurements have established only a weak diamagnetic response, which does not permit to consider any model of nMR, based on localized magnetic moments, to be substantiated sufficiently.

Determination of microscopic parameters

The first pair of the hole parameters, namely those of a and g(μ), can be found directly from the pair of Eqs (2) and (6). This is done using the data of T ₀ and A ₀₄ (which have been obtained from the slope of the plots in the middle panel of Fig. 6) collected in Table 1, irrespective to the details of the DOS model shown in Fig. 4. The values of a and g(μ) are collected in Table 2.

Table 2.

The absolute (a) and relative (a/a _B) values of the localization radius, the values of the DOS under different conditions [g(μ) and g _av], the absolute (N _A) and relative (N _A/N _C) values of the acceptor concentration.

Sample	a Å	a/a B	g(μ) 1016 meV−1 cm−3	g av 1016 meV−1 cm−3	N A 1018 cm−2	N A/N C
#1	9.6 ± 0.5	1.3 ± 0.1	2.0 ± 0.2	2.7 ± 0.3	7.8 ± 0.6	0.21 ± 0.02
#2	12.5 ± 0.6	1.7 ± 0.1	3.7 ± 0.3	7.6 ± 0.7	14.6 ± 0.7	0.40 ± 0.04
#3	11.4 ± 0.6	1.5 ± 0.1	1.6 ± 0.2	5.2 ± 0.5	12.6 ± 0.7	0.34 ± 0.03

However, further analysis designed for determination of such details of the hole spectrum, as positions of μ and E _c, as well as those of N _A, requires utilization of the DOS model, although without a detailed knowledge of its shape. At this point, the analysis above is valid for both possible positions of μ, namely, near −W and W, since a symmetrical DOS has been proposed. On the other hand, the arguments towards the strong compensation, formulated in Section “Density of the acceptor states”, still dictates the position of μ as shown in Fig. 4. Further argument for such a choice will be obtained below.

The general expression of the localization radius can be written in a form

$$a=a_B{(1-N_A/N_C)}^{-v},$$ 10

where ν ≈ 1 is the critical index of the correlation length and N _c is the critical acceptor concentration^51–54. The latter is connected to the Bohr radius with the universal Mott criterion, $N_C^{1/3}{a}_{\mathrm{B}}\approx 0.25$ ^{51, 52}. With the value of a _B = 7.5 Å, calculated above, we obtain N _C ≈ 3.7 × 10¹⁹ cm⁻³. Moreover, N _A can be found with the expression

$$N_A=N_C\left[1-{\left(\frac{k_{\mathrm{B}}{T}_{0}g(\mathrm{\mu })a_{\mathrm{B}}^3}{\mathrm{\beta }}\right)}^{1/(3\nu )}\right],$$ 11

obtained with Eq. (2) and (10). The data of N _A are collected in Table 2.

On the other hand, according to ref. 51, another expression of a, conformed with the energy scale of Fig. 4, can be written as

$$a=a_{\mathrm{B}}{\left(1-\frac{W+\mu }{W+E_c}\right)}^{-\nu },$$ 12

where

$$E_{\mathrm{c}}=-W+V_0^2/\left[4(z-1)J\right].$$ 13

In Eq. (13), V ₀ ≈ 2 W is a typical width of a carrier potential energy, expanded due to the disorder, z = 6 is the coordination number and J = J ₀ exp(−R/a _B) is the overlap integral⁵¹. Here, R = (4πN _A/3)^−1/3 is the half of the mean distance between acceptors, whereas the prefactor J ₀ for the case of the broad impurity (acceptor) band can be expressed as^{41, 51}

$$J_0=\frac{e^2}{{\mathrm{\kappa }}_0{a}_{\mathrm{B}}}\left[\frac{3}{2}\left(1+\frac{R}{a_B}\right)+\frac{1}{6}{\left(\frac{R}{a_B}\right)}^2\right].$$ 14

The values of μ and E _c are obtained with Eqs (12–14), using the value of κ₀ = 6.8 cited above, the value of a _B = 7.5 Å and those of N _A in Table 2, by variation of μ to fit the data of a in Table 2 with Eq. (6) explicitly for each sample. The data of W in Table 1 and N _A in Table 2 permitted evaluation of the average DOS values, g _av ≡ N _A/(2 W), which are collected also in Table 2. For convenience, the values of μ and E _c are displayed in a separate Table 3 below (see section “Discussion”). Finally, the data of E _a have been calculated with Eq. (4), using those of μ and E _c (Table 3), and are collected in Table 3, too.

Table 3.

The values of the Fermi energy (μ) and the mobility edge (E _c), the activation energies (calculated, E _a = |μ − E _c|, and experimental, E _a ^(ex)), and the interval of activated conduction (ΔT _a).

Sample	−μ meV	−E c meV	E a meV	E a (ex) meV	ΔT a K
#1	127 ± 8	55 ± 3	72 ± 8	78 ± 2	215–255
#2	88 ± 5	74 ± 4	14 ± 2	15.1 ± 0.5	20–40
#3	107 ± 6	81 ± 4	26 ± 3	25.6 ± 0.8	60–75

Hall coefficient

The Hall effect in the domain of the VRH conduction has different nature, than in the case of the band conductivity over the delocalized states (or drift conduction), connected to the Lorenz force. Therefore, the sign of the Hall resistivity, ρ_H, and of the Hall coefficient, R _H, should not be obligatory the same as that of the charge carriers. Namely, it can be opposite to the sign of the thermopower, which has been observed in the amorphous, as well as in the doped crystalline semiconductors^{54, 80–85}, including our case of CZGeS (see Fig. 3).

The early theories of the Hall effect under VRH conduction predicted the behavior of R _H (T) similar to ρ(T), given by Eq. (1), but with another (and much smaller) value of the characteristic temperature T _0H ≈ 0.15T ₀ due to the influence of the exponential dependence of the Hall mobility, μ_H(T) = R _H(T)/ρ(T). However, this prediction has not obtained a comprehensive experimental support, meaning observations of R _H(T) with T _0H both smaller than T ₀ and close to T ₀ (see ref. 54 and references therein). Moreover, it has been even suggested in investigations of CuInSe₂, that the dependence of R _H(T) is not exponential at all, whereas the resistivity-like behavior with the same value of T ₀ should be addressed only to the Hall mobility^{81, 82}.

On the other hand, further theoretical work, based on an explicit percolation approach to the treatment of the Hall effect^{80, 83–85}. has given the evidence for only a weak (power-law) temperature dependence of μ_H (T) and for the exponential dependence of R _H(T), same as that of ρ(T). Namely, according to the results of ref. 80, the temperature dependence of the Hall coefficient can be presented in the form

$$R_{\mathrm{H}}(T)=C(T)\exp \left[{\left(\frac{T_{0\mathrm{H}}}{T}\right)}^{1/4}\right],$$ 15

where T _0H = T ₀ and the dependence of C(T) is quite weak (logarithmic).

As can be seen in Fig. 3, some scattering of the data points does not permit to establish deviations of ρ_H(B) in # 1 from linearity unambiguously, excluding probably only the case of low fields at 70 K. Therefore, the plots in Fig. 3 have been fitted with the linear function within the whole interval of B to obtain R _H(T), and the plots of ln(−R _H) vs. T ^−1/4, neglecting the very weak dependence of C(T), are presented in the bottom panel of Fig. 6. The linear fit of the data yields the value of T _0H = (1.5 ± 0.4)×10⁷ K.

Discussion

The good linearity of the plots in Fig. 5, accompanied with the dependences of a ₁(T) and A ₄(T) in the top and middle panels of Fig. 6, respectively, provide a sufficient evidence of the interpretation of both nMR and pMR contributions to the total MR of our CZGeS samples, proposed in Section “Analysis of magnetoresistance”. In addition, the analysis given in previous Section permits a more straightforward evaluation of the critical field B _c according to Eq. (8), using the explicit values of a in Table 2, those of T ₀ in Table 1 and J₀ = 3.0, 2.4 and 2.5 eV for #1, #2 and #3, respectively, following from Eq. (14). So, one can obtain the values of B_c ≈ 3–9 T, which are comparable but smaller than those of B_ons ≈ 5–12 T marking the onset of the linear behavior in Fig. 5. Such a relation between B_c and B_ons is in a reasonable agreement with the linear contribution of nMR, as discussed in Section “Analysis of magnetoresistance”. On the other hand, the deviations from linearity of the plots of A₄ vs. T ^−3/4 and especially those of a₁ vs. T ^−3/4 (see the top and middle panels of Fig. 6) already close to the lower border of the VRH conduction (i. e. below ~80 K) look too strong. This requires a special discussion. At this point, only the orbital interference nMR mechanism may be insufficient to account for all details of the temperature dependence of nMR in our samples. Namely, the violation of the linearity of the plots in Fig. 6 with lowering T may be connected also to importance of the spin disorder and spin correlation effects of the hopping electrons with decreasing temperature^86–88. Indeed, the temperature dependence of nMR due to the spin effects above is determined by the ratio of τ/τ_s, where τ and τ_s are the characteristic hopping time and the spin relaxation time, respectively, having non-trivial and quite different dependences on T ^{87, 88}. Hence, the issue above is attributable also to the contribution of spin-disorder and spin-correlation effects, which are more important when T is decreased^86–88. A similar situation with the anomalous temperature behavior of the nMR contribution has been observed recently in the magnetotransport of Cu₂Zn(Sn_xGe_1-x)Se₄ single crystals¹¹.

For the next, as follows from the data in Table 2, the small values of the ratio of N _A/N _C ~0.2–0.4 agree completely with those of another ratio, a/a _B ~ 1.3–1.7 exceeding unity only slightly. As can be seen with Eq. (10), the values of both ratios above mean, that all the investigated CZGeS material lies relatively far from the metal-insulator transition. In addition, one can see in Table 2, that the values of g(μ) are comparable with the average DOS values, g _av, but are systematically smaller. The comparability of g(μ) and g _av supports the consistence of our analysis in general, whereas the smallness of g(μ) with respect to g _av is evident from Fig. 4, provided that the position of μ is shifted towards one of the DOS edges.

Eventually, the shift of μ towards the left DOS edge, or −W, suggests that the degree of the compensation in our samples is sufficiently strong. The arguments for such a situations have been already given in Section “Density of the acceptor states”. In addition, the values of E _a have been evaluated in Section “Determination of microscopic parameters” above (see Table 3). Such values of E _a suggest existence of the intervals ΔT _a of the activated ρ(T) behavior, given by Eq. (3), which is not connected to the Mott VRH behavior within the corresponding interval ΔT _v, but is due to the activation of the holes into the interval (−E _c, E _c) of the delocalized states of the acceptor band (see Section “Density of the acceptor states”, inset in the top panel and the bottom panel of Fig. 1). Namely, the relatively high value of E _a for #1 should shift ΔT _a above ΔT _v, whereas small values of E _a for #2 and #3 suggest that ΔT _a should lie below ΔT _v. The corresponding intervals ΔT _a have been found by the linearization of the plots in the inset to the top panel of Fig. 1 and in the bottom panel in Fig. 1, and are given in Table 3. The values of E _a ^(ex), obtained from the slopes of the linear fits of these plots, are displayed in Table 3, too. One can see that, indeed, ΔT _a for #1 lies above Δ T _v, while those for #2 and #3 lie below ΔT _v. Such behavior is accompanied with the experimental values, E _a ^(ex), lying quite close to those of E _a, evaluated in previous Section (see Table 3). This supports completely the position of μ in Fig. 3, as well as clarifies the nature of the charge transfer in CZGeS outside the Mott VRH interval, indicating a sufficiently strong degree of the compensation K in our material, as has been supposed above. On the other hand, the too strong compensation does not favor the nMR effect in general^{39, 65}, which in turn may limit the value of K from above.

Finally, one can see that the Hall coefficient (bottom panel of Fig. 6) vary with T sufficiently close to the law of Eq. (15). In addition, the value of T _0H = (1.5 ± 0.4) × 10⁷ K is close to that of T ₀ = 1.43 × 10⁷ K for #1, following from the ρ(T) dependence of Eq. (1). This suggests a reasonable agreement with the percolation model of the Hall effect in the domain of the Mott VRH conduction⁸⁰. However, some deviations from the model of ref. 80, including a possible exponential contribution to the Hall mobility, cannot be excluded due to a rather high error of T _0H.

From the presented results, it is evident that the charge transport mechanisms in CZGeS have a complicated nature. In particular, this leads to observations of the VRH conductivity at unusually high temperatures, including the nMR and the pMR contributions in non-zero magnetic field, as well as to the non-conventional Hall effect. All these findings, including the variation of the macroscopic and microscopic parameters from sample to sample, should be considered anyway during the production of CZGeS based optoelectronic devices. Particularly for the solar cell use, the key problem of this material is its high tolerance to the intrinsic defect formation. Confirmed deep position of defect acceptor levels, as well as their broadening into the quite wide acceptor bands, may have an important detrimental influence on the photo carriers recombination and the final device efficiency. Therefore, the growing conditions of the CZGeS absorber layer for the thin film solar cells should be optimized to prevent or at least minimize the formation of the deep defects. In addition, the non-conventional Hall effect, which does not have any direct connections to the hole concentration, should be taken into account with a certain cautions for the characterization of CZGeS materials.

Conclusions

We have investigated the resistivity, the magnetoresistance and the Hall effect in p-Cu₂ZnGeS₄ single crystals in pulsed magnetic fields up to 20 T. The dependence of ρ(T) in zero magnetic field is described by the Mott VRH charge transfer mechanism within a broad temperature interval of ~100–200 K. Magnetoresistance contains the positive and negative components, which are interpreted by the common reasons of doped semiconductors, including the shrinkage of the impurity wave functions by the magnetic field and the damping of the electron interference effects in the VRH hopping conduction regime, respectively. On the other hand, the joint analysis of the resistivity and MR data has yielded a series of important electronic parameters and permitted specification of the CZGeS conductivity mechanisms outside the temperature intervals of the Mott VRH conduction. The Hall coefficient is negative, exhibiting an exponential dependence on temperature, which is quite close to that of ρ(T), as typical of the Hall effect in the domain of the VRH charge transfer.

Materials and Methods

Single crystals of CZGeS were grown by a chemical vapor transport using iodine as a transport agent. The growing process was performed in the vertical two-zone furnace with 850 °C in the evaporation zone and 800 °C in the growth zone. More details of the crystal growth process could be found elsewhere²⁰.

Three CZGeS samples were selected for detailed investigations by a most convenient shape for electrical measurements. Chemical composition of the samples was determined by the X-ray fluorescence method, performed in three different points of each sample. The obtained data do not vary significantly from point to point, and the mean values are presented in Table 4. It can be seen, that all samples have the composition close to stoichiometry, exhibiting a slight Cu and Zn excess for #2 and some Cu and Zn deficient for #3 and #1. A part of the obtained material was grounded for the X-ray diffraction analysis, which showed the wurtzstannite structure of all the samples²⁰.

Table 4.

Chemical composition of the Cu₂ZnGeS₄ single crystals.

Sample	Cu at.%	Zn at.%	Ge at.%	Cu/(Zn + Ge)	Zn/Ge
#1	24.1	12.6	13.3	0.93	0.95
#2	25.4	13.0	11.6	1.03	1.12
#3	24.1	12.4	13.5	0.93	0.92

The hot point probe method, addressed to the thermopower measurements, showed p-type conductivity in all samples. Six indium contacts were made in each sample. The resistivity, ρ(T), was measured with a standard dc method, and MR was investigated in the pulsed magnetic field with B up to 20 T (see ref. 39 for the device details). The sample was fixed on the holder and inserted inside a cryostat. A filling helium cryostat was used to vary the sample temperature in the range of 20–300 K. A finger of the cryostat, containing the sample, was installed inside a pulsed solenoid. The main sample plate was oriented perpendicular to the direction of the magnetic field. A measurement at a certain T was performed by increasing and decreasing B from 0 up to the values between ~0.5–20 T, with subsequent changing of the field polarity. The results with the opposite polarities were averaged with a special software, to obtain the parallel (ρ) and the perpendicular (ρ_H) components and to avoid their mutual influences. Eventually, series of above measurements was integrated to obtain the dependence of ρ(B) and ρ_H(B) over the whole field diapason. Finally, it should be noted that the measurements at lower temperatures were hindered by the high sample resistance, which exceeded somewhat the installation limits.

Author Contributions

S.L. grown the single crystals. M.G. and I.Z. performed the resistivity and magnetoresistance measurements. M.A.S. supervised the experimental process and discussed the results. M.G. and E.H.-C. carried out the preliminary data analysis. K.G.L. performed the major part of analysis of experimental data and wrote the article. E.A. and E.L. supervised the whole work, discussed the results and commented on the manuscript. All authors reviewed the manuscript.

Competing Interests

The authors declare that they have no competing interests.