Abstract
To further our understanding of the complexity and genetic heterogeneity of rare diseases, it has become essential to shed light on how combinations of variants in different genes are responsible for a disease phenotype. With the appearance of a resource on digenic diseases, it has become possible to evaluate how digenic combinations differ in terms of the phenotypes they produce. All instances in this resource were assigned to two classes of digenic effects, annotated as true digenic and composite classes. Whereas in the true digenic class variants in both genes are required for developing the disease, in the composite class, a variant in one gene is sufficient to produce the phenotype, but an additional variant in a second gene impacts the disease phenotype or alters the age of onset. We show that a combination of variant, gene and higher-level features can differentiate between these two classes with high accuracy. Moreover, we show via the analysis of three digenic disorders that a digenic effect decision profile, extracted from the predictive model, motivates why an instance was assigned to either of the two classes. Together, our results show that digenic disease data generates novel insights, providing a glimpse into the oligogenic realm.
INTRODUCTION
Next Generation Sequencing (NGS) and in particular Whole Exome Sequencing (WES) have provided enormous amounts of information on human genetic variation (1,2), as well as on the relationship between this variation and disease (3,4). As many genetic disorders are caused by protein-coding variants (5), exome sequencing provides a cost-effective approach to capture the majority of the variants directly relevant for clinicians, which has led to the identification of more than 100 new disease-gene associations in the last few years (5,6). Nevertheless, for many disorders, the genetic component remains only partially known (e.g. Brugada syndrome (7) and neurodevelopmental disorders (8)). The identification of genes implicated in a disease is more difficult when a phenotype in a familial pedigree does not show a clear monogenic segregation pattern, exhibiting for instance genetic heterogeneity, incomplete penetrance and/or non-Mendelian inheritance mechanisms (9). Moreover, even when the segregation of the causal variant is clear, the disease can show high phenotypic variability, necessitating the consideration of additional effects in different genes (8,10). In addition, the concept of locus heterogeneity suggests that the causal relation between genes and diseases is far from univocal (11). Some examples of disease phenotypes being modified by variants on different loci, are Huntington disease, Bardet-Biedl syndrome or Hirschsprung disease (OMIM: #143100, #209900, #142623).
Oligogenic inheritance models are necessary in such cases to provide a more specific link between genotype and phenotype (11): relaxing the monogenic assumptions in favour of a digenic model in case of the Bardet-Biedl syndrome improved the comprehension of the disease and provided a clearer explanation for the observed segregation pattern (12–14). Although insufficient data are currently available to examine the more complex oligogenic diseases, there is already a sufficient amount of publications reporting on the digenic ones (15–18), allowing one to try to shed light on the specificities of digenic diseases.
Digenic inheritance may refer to different scenarios. In some cases the disease phenotype is caused by a combination of unique variants in two genes, while in others two different phenotypes caused by variants in different genes are combined together leading to a more complex phenotype, which includes both previous ones (18–20). The Digenic Diseases Database (DIDA) contains information on 44 digenic diseases, comprising 213 digenic combinations (16). It contains the details about digenic combinations of variants that cause disease, as well as annotated meta-information concerning variants and genes involved. DIDA defines a digenic combination as a combination of variants in two distinct genes, which together are causative for the patient’s phenotype (16). Given this novel resource, one can now examine each digenic combination and ask what synergistic mechanisms lead to specific phenotypes. An answer to this question can provide genetic and clinical insight into the causal relationships between variants mapped on the two genes and the disease phenotype they produce.
The majority of instances in DIDA are categorized into one of two classes that are a coarse-grained simplification of the original definition provided by Schäffer (15). The first class represents true digenic instances (currently labeled as ‘on/off’ in DIDA): variants at both loci are required for disease, variants at one of the two loci result in no phenotype (18). The second class we will refer to as the composite class as it includes different possibilities (currently labeled as ‘severity’ in DIDA): A composite instance in DIDA can refer to mendelizing variants plus modifiers, when a driver variant is necessary for the phenotype but rare variants in a second gene, usually related to the same pathway/organ system, may modify the phenotype (21)), or dual molecular diagnosis, wherein mendelizing variants at each of the two loci segregate independently and result in complementary (or blended) phenotypes (18)). Throughout this paper the true digenic class will be annotated by TD and the composite class by CO.
Further fine-tuning of these classes will become possible when more digenic diseases data become available. Yet for now we can limit ourselves to the current constraint, exploring the reason why a certain digenic combination belongs to the TD or CO class.
We hypothesise that genetic and biological properties regarding variants and genes linked to digenic combinations can be used to differentiate between the above mentioned digenic effect (DE) classes. The allelic state of the genes, the impact of all the variants involved, the ability of a gene to tolerate loss of function variants, and the relationship between genes involved are likely to determine the DE. To examine this hypothesis, we construct a classification model that employs features consisting of different variant-, gene- and pathway-related characteristics. Our results reveal that quantitatively relevant predictions can be obtained in stratified cross-validation settings, which are furthermore confirmed on an independent dataset that contains digenic combinations not yet present in DIDA.
Next to the prediction itself, an explanation on how the DE predictor arrives at its conclusion is also provided. Concretely, the binary classification into TD or CO is transformed into a clarification, representing every digenic combination in DIDA by a DE profile that provides an explanation of the decision process that assigns the combination to its class. Making this decision process explicit allows us to investigate the mechanisms related to DEs and to analyse the differences between similar cases. The analysis of three different digenic diseases reveals that relevant rules, which clarify the nature of the digenic combination, can be extracted.
MATERIALS AND METHODS
Datasets
The dataset used in this work is a subset of DIDA (16). We downloaded the 124 digenic combinations for which the DE information is available (68 TD, 56 CO). These instances are involved in 32 different diseases. In this dataset, 69% of the digenic combinations have heterozygous variants in both genes and, of these heterozygous cases, 62% belong to the TD class and 38% to CO class. The digenic combinations with homozygous or compound heterozygous variants are distributed as follows: 41% to the TD class and 59% to the CO class. An in depth analysis of this dataset is performed in the Results section.
In addition to this dataset, an independent dataset containing new digenic disease cases was constructed. We manually mined PubMed, retrieving data for digenic combinations published between July 2015 and April 2016. This new set contains 19 novel digenic combinations and is used as a validation set to examine the quality of the predictor. Based on the information in the articles, the DE of each digenic combination was identified, labeling them with either TD or CO. This dataset is composed of 11 unique gene pairs, none of which are present in the current DIDA dataset, divided over eight diseases (also not present in DIDA). Although the dataset is balanced in terms of DE classes (10 TD, 9 CO), there is an imbalance in terms of the diseases: 4/19 and 9/19 belong respectively to either the CANDLE syndrome (22) (OMIM: #256040) or the Alport syndrome (23) (OMIM: #104200). This new set of digenic combinations is available in Supplementary Material Table S1.
Feature definition
To construct the DE predictor, we identified different features relevant for discriminating between the two DE classes. We selected these features by integrating information from different biological levels of contextualization (24), conceptually differentiating between variant-oriented, gene-oriented and pathway-oriented features. The following sections define in detail the selected features.
Variant-oriented features
These features quantify the deleteriousness of each single variant. The possible number of allelic variants in a digenic combination ranges from two to four, depending on the zygosity of both genes (16). Therefore, variant-oriented features are encoded using four dimensions. Each dimension represents the pathogenicity value (calculated using DEOGEN (24)) of each allelic variant belonging to the digenic combination. The first two dimensions (DEOA1, DEOA2) represent variants in the first gene (GeneA) and the other two (DEOB1, DEOB2) variants in the second gene (GeneB). When a gene presents a variant in heterozygous state, only one allelic variant is present for that gene, since the second copy is the wild type allele. We encoded these cases as ‘silent’ variants by assigning a pathogenicity score of 0, to indicate a completely harmless effect. In this way, also the zygosity state of each gene is intrinsically represented, since the presence of a 0 for DEOA2 or DEOB2 expresses an heterozygous state respectively for gene A and gene B.
Approximately 80% of variants in the digenic combinations that are used here are either missense or in-frame indels, and thus their pathogenicity can be computed using DEOGEN. The remaining 20% correspond to several other types, which, as explained in the manuscripts from which they were obtained (16), are expected to be more detrimental than the former. This includes i) variants which alter a portion of the protein, for example nonsense and frameshift variants resulting in altered/truncated amino acid sequences (25), ii) variants that have been shown to prevent the correct splicing because they are near to a splicing site or in cryptic splice sites (26), producing non-functional isoforms, iii) nonsense and frameshift variants involved in nonsense-mediated mRNA decay (NMD), eliminating the mRNA transcripts that contain premature stop codons (27). DEOGEN score for missense variants and in-frame indels ranges from 0 (neutral) to 1 (deleterious), to differentiate the other types of effects described we assigned to them the score 2. No distinction was made between frameshift and nonsense variants likely leading to NMD (41 variants) or not (7 variants) according to the 50–55 nt rule (28). The arbitrary choice of the value 2 does not imply any proportional comparison with the DEOGEN score obtained for missense variants and indels, but is just a value that allows the RF model to identify a threshold to separate missense/indels from the 20%, usually stronger, effects. Altering the value to the maximum DEOGEN score or any other bigger value produces a predictive accuracy equivalent to what is reported in Table 1.
Table 1. Incremental contribution of the features used in our model for the predictive quality.
| Scheme | Sen. | Spe. | MCC | AUC (S.D.) |
|---|---|---|---|---|
| DEO | 0.63 | 0.68 | 0.31 | 0.64 (0.01) |
| DEO+ESS | 0.63 | 0.70 | 0.33 | 0.65 (0.01) |
| DEO+REC | 0.66 | 0.61 | 0.27 | 0.66 (0.01) |
| DEO+ESS+REC | 0.72 | 0.66 | 0.38 | 0.74 (0.01) |
| DEO+ESS+REC+PATH | 0.71 | 0.70 | 0.42 | 0.79 (0.01) |
Sen and Spe refer respectively to sensitivity and specificity. MCC and AUC are the Matthew correlation coefficient and Area Under the Curve results.
Gene-oriented features
Gene-level information has been included in the model using the ‘recessiveness index’ (REC (29)) and the ‘essentiality’ (ESS (30)) scores of the genes involved in the digenic combination. The recessiveness is the estimated probability that the gene will cause a recessive disease if homozygously lost, while the essential genes have been found to be critical for survival in knock-out experiments in mice. We refer as EssA and RecA to the annotations for the gene A and as EssB and RecB for gene B. We addressed the missing values by using the median values instead: 0.246 for REC and 0.392 for ESS.
Pathway-oriented features
Digenic diseases are often caused by variants in two genes which often have a physical or functional relationship (11,15). From DIDA (16), we extracted information about the possible interaction between the two genes involved in the digenic combination. A value of 1 is assigned when the two genes are known to share a common pathway (as evidenced from KEGG (31) or REACTOME (32)), 0 otherwise. We refer to this feature as Path.
The feature vectors for the DIDA dataset and the new dataset are available in Supplementary Material files TrainingDataset.csv and NewDataset.csv. Note that to avoid biases in the cross-validation study, we also made sure that each feature vector is unique in the dataset. This required us to remove five instances from the 124 digenic combinations, producing a non-redundant dataset of size 119 to construct the DE predictor.
Construction and evaluation of predictive models
In this study, the scikit-learn (33) implementation of the Random Forest (RF) algorithm (34) was used to create a classification model for DE classes. We fixed the size of the forest to 100 trees; to limit the flexibility of the model, we set the maximum trees depth to 10. We prevented random fluctuations from influencing the cross-validation results by repeating each cross-validation 100 times, averaging the obtained scores and measuring the standard deviation. This procedure has been used for the construction of Table 1. We evaluated the performances with the widely adopted scores sensitivity (SEN), specificity (SPE), Matthews Correlation Coefficient (MCC) and Area Under the Curve (AUC).
To control the risk of over-fitting, we assessed the significance of the observed performance with a permutation test (35). We stacked the feature vectors in a M × N matrix (where M is the number of samples and N the number of features) and we randomly shuffled the order of the elements within each column. In this way, the distribution of the values for each feature in the dataset remains the same, but the combinations of features representing each instance are permuted. We assessed the cross-validation performances after each permutation and we repeated this procedure 10 000 times, obtaining a distribution of AUCs. From this distribution, we used the Kernel Density Estimation function from scipy to compute the p-value for the model performance with respect to the distribution of permutations.
Stratification according to gene pairs is necessary to avoid bias in the prediction
A preliminary analysis of the features based on the Gini importance (34) indicates that RecA and RecB are the most important features. This may be related to the fact that many digenic combinations with variants mapped on the same gene pair lead to the same DE class. Nevertheless, this should not be considered as a definitive rule, since we can also observe digenic combinations involving the same pair of genes, but leading to different DE. To ensure the consistency and generalisability of the model, we performed a stratified cross-validation at the pair-of-gene level using the non-redundant dataset. Within each step of the cross-validation, we removed from the training dataset all digenic combinations sharing a specific pair of genes. The model is trained on the remaining data and the predictions are evaluated on those that were removed. The final performance is an average of the performance of these cross-validation steps. In this way, we ensure that the performance evaluation is less biased, obtaining a more robust predictor that avoids learning undesired pair-of-gene dependencies.
Analysis of the decision process using digenic effect profiles
For the visualization and the interpretation of the trained Random Forest (RF) model, we relied on the treeinterpreter python library (https://github.com/andosa/treeinterpreter) created by Ando Saabas (unpublished work).
Given a target feature vector x containing the values for the nine features discussed earlier, the library visits each tree t in the trained forest T and analyses which clauses are activated following the path of decisions leading from the root of t to the final leaf (corresponding to the prediction t(x)) for the feature values x. While traversing t, the algorithm records whether the features guarding the splitting nodes pushed the final prediction towards the TD or CO class. This method produces two major advances with respect to the classical ‘feature relevance’ computed during the training of the RF models (33,34). The first one is that the feature relevance is computed over the entire dataset while treeinterpreter acts on each feature vector x at a time, explaining why the model T made the particular decision T(x) ∈ [0, 1]. This explanation is represented by a vector of contributions (one for each of the k = 9 features used by the RF for the prediction, see Figure 1 as an example). We refer to this contribution vector as the DE profile, that we visualize by spider/radar plots in this paper. These contributions are obtained through a mathematical inspection and decomposition of the decision process within the RF: the final prediction can be recovered as:
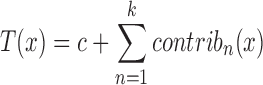 |
(1) |
where c is a dataset-dependent constant and contribk(x) is the contribution of the kth feature in the feature vector x (for full details, see http://blog.datadive.net/interpreting-random-forests/) Second, if the feature contributions are averaged over the entire dataset instead of just focusing on x, treeinterpreter tells, for each feature, not only its absolute relevance but also whether it is used to discriminate one class better than the other (see Supplementary Material Figure S1). The classical feature relevance scores focus necessarily on the entire dataset and give therefore little insight into how individual decisions are made, which is not the case for the treeinterpreter approach (see again https://github.com/andosa/treeinterpreter for the technical details).
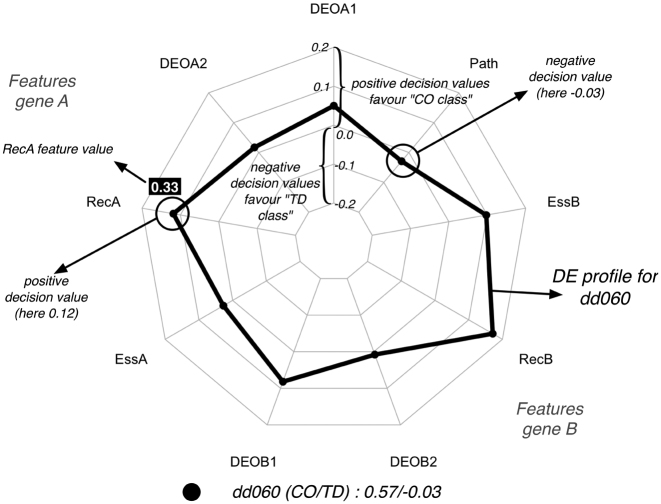
Figure 1.
Visualization of a DE profile for dd060 generated by treeinterpreter library using a radar (or spider) plot. The dd060 has the following feature vector x = (0.46, 0.46, 0.33, 0.0, 0.96, 0, 0.3, 1.0, 0), where the features are respectively DEOA1, DEOA2, RecA, EssA, DEOB1, DEOB2, RecB, EssB and Path. dd060 is an instance of the CO class. When analyzing this vector with the treeintepreter algorithm and our DE predictor, the following vector of contributions is produced: contrib(x) = (0.05, 0.017, 0.118, 0.027, 0.082, 0.008, 0.1718, 0.096, −0.029). Each separate contribution in contrib(x) is visualized as a filled circle on its corresponding spoke of the radar plot. The value of the contribution can range between a positive maximum (closer to the outside) to a negative minimum (closer to the center) decision value. The lines connecting the spokes mark the scale we use on the spokes and we added in black italic the value of those lines. The DE profile as a whole (black line) reveals how the combination of contributions favours a particular class. To explain differences between DE profiles we will sometimes add the actual feature values coming from x in a colored box with white lettering, as was done here for the feature RecA. The values next to the legend correspond to the sums of the positive and negative contributions respectively.
Of interest for the current work are the single contributions contribk(x) in the DE profile, which can either be positive or negative, and that all together (plus the constant c) constitute the final prediction. A positive contribution means that the feature pushes the decision towards the CO class and a negative contribution means it favors the TD class. To make this more clear, consider the digenic combination dd060 (CO instance) visualized in Figure 1. The digenic combination dd060 is represented by the feature vector x = (0.46, 0.46, 0.33, 0.0, 0.96, 0, 0.3, 1.0, 0). The treeintepreter algorithm in combination with our DE predictor will generate the following DE profile contrib(x) = (0.05, 0.017, 0.118, 0.027, 0.082, 0.008, 0.1718, 0.096, −0.029) and c = 0.45 for the data set. Only one feature has a negative contribution (i.e. Path) and the rest is either close to zero or positive. The class preference, which can be inferred also from the figure, is determined by how the positive and negative contributions alter c, making it either smaller or bigger than the prediction threshold (which is 0.5 in this paper). Comparing the impact of the positive contributions with the negative ones, while taking into account this constant, provides hence insight into the decision of the predictor. In the dd060 example, the sum of positive contributions equals 0.57 and the sum of negative contributions is equal to −0.03. Clearly, the sum of positive contributions (0.57) will tilt the decision in favor of the CO class, which cannot be countered by the sum of the negative ones (−0.03), confirming the assignment reported in DIDA (16). The DE profile itself (black line in Figure 1) reveals that RecB and then RecA are the most influential in assigning this instance to the CO class as the larger the contribution (in both directions) the stronger it will influence the final outcome. Path, the only one favouring the TD class, is not strong enough to change this decision. The contributions generated by the treeinterpreter library for each feature are not independent: an identical feature value in two digenic combinations may correspond to different contributions as the result of the influence of the other features on the decision process (see for instance the recessiveness scores for gene A in Figure 3). The DE profiles provide a bi-dimensional representation of the multi-dimensional decision boundary learned by the RF during training. Feature vectors and corresponding contribution vectors for dd060 are available in Supplementary Material (Tables S2 and S3).
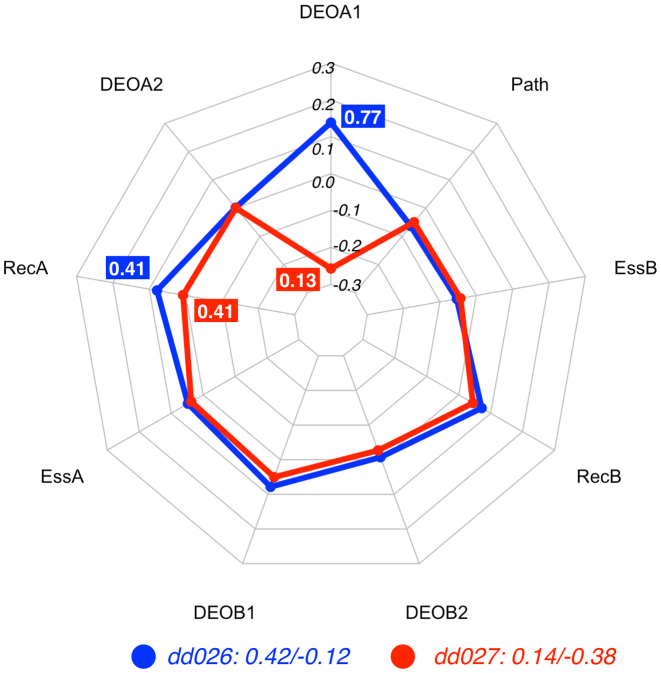
Figure 3.
Radar plot of the DE profiles for the digenic combinations dd026 (CO) and dd027 (TD), two instances related to autosomal glaucoma. The feature vectors of both digenic combinations are identical except for the DEOA1 score, making it the feature that decides to which class either instance is assigned : with all other features being equal, the high DEOA1 value (0.77 as opposed to 0.13) leads the DE predictor to decide in favour of the CO class. The plot also shows also that even when values in the feature vector x are identical the contributions contribn(x) may be different, as can be seen for the RecA feature. Feature vectors and corresponding decision vectors for dd026 and dd027 are available in Supplementary Material (Table S2 and Table S3).
RESULTS
Feature vector construction reveals the necessity to correctly define primary and secondary genes
From DIDA, we extracted 124 digenic combinations related to 32 different diseases, for which the DE classes were clearly determined by medical literature (16). These digenic combinations involve 206 variants mapped onto 95 different genes, mainly missense (65%) and frameshift (15%) variants, the remaining ones are in-frame indels, nonsense or splice variants. Among the dataset, 92 digenic combinations are di-allelic, 30 tri-allelic and two are tetra-allelic. The instances are reasonably balanced between the two DE classes, i.e. 68 TD and 56 CO instances.
Each of the 124 digenic combinations in this dataset, which will be used to train a RF predictor (34), is encoded by a feature vector (see Materials and Methods). These vectors are devised to contain information from different biological scales, providing a comprehensive contextualization of various aspects implicated in the disease mechanisms. Variant-level information is computed by DEOGEN (24). Gene-level information is represented by the essentiality (30) and recessiveness (29) scores of the two genes involved (see Materials and Methods). These gene-based scores evaluate the relevance of the mutated genes to the individual’s health. The highest-level feature incorporated in the feature vector is a binary pathway feature indicating whether both genes share a common pathway or not, as evidenced from REACTOME (32) and KEGG (31) (see Materials and Methods for more details).
While assembling the feature vectors, a conceptual issue was encountered: the ordering of the two genes participating in the digenic combination. The articles from which the data in DIDA were extracted often do not provide an ordering of the genes, or remain relatively vague about which gene should be considered the primary. As a consequence, the ordering of most digenic combinations in the database was done arbitrarily. In the medical literature, primary disease genes are considered those that ‘stand out’ in initial association and/or linkage studies (36), while secondary genes are detected later and they are supposed to be less detrimental, usually only contributing to the phenotype caused by variants in primary genes. Since this clinical annotation is not available for all the digenic combinations in DIDA and since the same gene may be involved in different digenic combinations, causing different diseases (with both a primary or secondary role depending on the specific case), we chose to adopt a consistent and reproducible definition for the gene order in the digenic combinations by using the Gene Damaging Index (GDI) (37). We assigned this score to each gene in our dataset and, within each digenic combination, we call ‘Gene A’ the one with lower GDI (least tolerant to variants) and ‘Gene B’ the other. As such, we expect the most detrimental characteristics to be observed for gene A in the data set. As we will show later on, this choice has an important role to play in the predictions.
Analysis of ordered gene features identifies classification potential
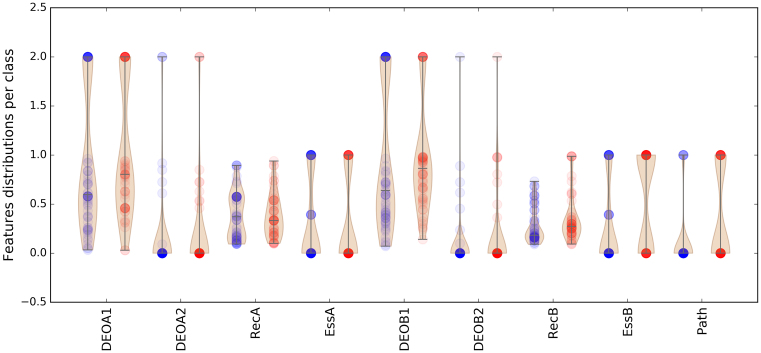
Applying the gene ordering discussed in the previous section, the feature value distributions among the dataset can be grouped per DE class, as shown in Figure 2. Red dots represent the TD class data points, while blue ones indicate the CO class. The feature vector has 9 dimensions: four of them are variant-based and are represented by DEOGEN scores for the two alleles of gene A (DEOA1, DEOA2) and gene B (DEOB1, DEOB2). DEOGEN scores range from 0 (neutral) to 1 (pathogenic), while the other variants (e.g. nonsense, frameshift and splicing) were assigned the value 2 (see subsection Feature Definitions). At the gene level, RecA, EssA and RecB, EssB represent respectively the recessiveness (29) and essentiality (30) scores of genes A and B. We handled the missing values by substituting them by the median values. Path is a binary feature which is 1 if genes A and B share a common pathway (31,32).
Figure 2.
Distribution of feature values for both classes: Red dots represent the TD class while blue ones indicate the CO class. The four DEO scores, obtained with DEOGEN (24) represent the variant-effect predictions for the two alleles of the first (DEOA1, DEOA2) and second (DEOB1, DEOB2) gene. RecA and RecB are the recessiveness scores for Gene A and B obtained from (29). EssA and EssB scores indicate when a gene is essential (1) or not (0) as evinced from knock-out experiments in mice (30). Finally the path feature represents whether both genes are part of the same pathway (1) or not (0).
The data in Figure 2 show that the TD class (red) tends to have slightly more deleterious variants on the first copy of gene B (DEOB1) than the CO class (blue) (Kolmogorov-Smirnov (KS) test p-value=0.03). It is also noticeable that many DEOGEN scores are equal to 0 for the variants in the second allele of gene A (DEOA2) and gene B (DEOB2), which is due to the fact that many digenic combinations in DIDA are heterozygous variants with the wild-type allele on the second copy of the gene.
A comparison of the RecB and EssB distributions between the two classes shows that in the composite cases, the gene B is generally less relevant than in the true digenic cases, both in terms of lower RecB (KS P-value = 0.00011) and lower EssB (KS P-value = 0.0059) scores. Furthermore, a comparison between RecA and RecB within each class shows that in the CO class, the distributions are more different compared to those of the TD class (KS test P-value of 0.0022 and 0.0045 for the TD and CO classes respectively). These former observations are interesting results as they are consistent with our separation in two digenic classes: in the CO case, the role of the gene B is minor when compared to gene A. In the case of the true digenic class, we can observe a less unbalanced state between the two genes, suggesting that they are equally contributing to the phenotype.
Figure 2 also reveals that the TD class generally has more genes sharing the same pathway (KS P-value = 0.017).
Cross-validated predictions are accurate
In Table 1, we show the incremental predictive contributions of the features used in our model. We start by adding the four DEOGEN scores (DEOA1, DEOA2, DEOB1, DEOB2), obtaining a performance significantly better than random predictions. DEOGEN was selected to predict the effects of missense and indel variants as it was shown to outperform other state of the art methods like SIFT, Polyphen2 and CADD (24), as motivated by Supplementary Table S4.
This first step indicates that the pathogenicity of the variants involved in the digenic combination is, to a certain extent, related to the DE. Adding gene-level features (such as Ess and Rec) improves the performances both in terms of MCC and AUC. When including all features, the classifier achieves 79% of AUC and 0.42 of MCC; >70% of the TD elements are correctly identified.
When machine learning methods are applied on a small dataset, the risk of over-fitting has to be taken into consideration. To control this problem, we computed the p-value of our performances using a permutation test (35) (see Methods). The performances reached by our model have a P-value of 8.6 × 10−11 computed over 10k column-wise random permutations of the feature values.
As already mentioned, the assignment of primary and secondary roles to the genes using GDI scores is crucial for the DE predictor development (see Methods for more details). Comparing the AUC obtained by the GDI-ordered model with a distribution of AUCs collected by training identical RF models using 1000 random assignments of gene A and B roles, reveals that this choice leads to significant differences in the result with a P-value <0.01 (0.00285, see Supplementary Material Figure S2).
Predictions remain robust on an independent dataset
To provide further validation for the predictive model, the performance of the model was also evaluated on a independent dataset of novel digenic combinations that are currently not present in DIDA (see Supplementary Material Table S1). This additional evaluation is especially meaningful given the risk for overfitting that always exists when training on small datasets. This set consists in newly collected digenic combinations published between July 2015 and April 2016 (see Methods). As the size of this independent set is very limited, the metrics used in Table 1 do not convey properly the quality of the predictions on this new set. For this reason we decided to show the actual classification results via the confusion matrix (see Table 2). The predictions for each instance are available in the Supplementary Table S1.
Table 2. Confusion matrix showing the prediction result on the independent dataset (19 instances). COact and TDact are the actual class labels, while COpred and TDpred are the predicted class labels. The combination COact and COpred correspond to the true positive predictions and the combination TDact and TDpred to the true negative predictions. The MCC is 0.41.
| COpred | TDpred | ||
|---|---|---|---|
| COact | 9 | 0 | 9 |
| TDact | 7 | 3 | 10 |
| 16 | 3 |
One can observe in Table 2 that although we identify all the new CO instances correctly, the majority of TD cases appear to be misclassified as CO. Examining the actual data (see Supplementary Table S1) we see that all four CANDLE syndrome cases were misclassified (22). This error affects the specificity of the predictor since half of the TD class members are misclassified. We hypothesize that this error may be due to missing information on the recessiveness of the genes PSMA3 and PSMB4 as well as the lack of essentiality information for genes PSMB8 and PSMB9. Similar information is missing for two other TD class instances, producing also a misclassification. Notwithstanding this issue, the results on this independent set are highly encouraging and the quality of the DE predictor will improve as new well-annotated digenic data become available.
Exploring disease instances using DE profiles
Although our model appears to be fairly accurate, understanding these predictions requires the support of an explanation, comprehensible for geneticists and clinicians. To achieve this goal, it is important to distill from the RF how decisions are made and represent this in a meaningful manner. The open source treeinterpreter library (see Materials and Methods) was used to perform this task. In summary, this method visualizes the propensity of each feature to vote for one of the two classes, expressing its contribution to the final decision of the RF model (see Materials and Methods and also Figure 1 for an explanation of the visualization). The bigger the absolute value of the feature’s contribution, the more important the corresponding feature is in pushing that decision in favor of a particular class. A negative contribution means that this feature voted in favor of the TD class, whereas a positive contribution pushed the decision toward the CO class. Each line shown in the figures corresponds to a decision profile, which we called in the Materials and Methods section a DE profile, for a specific digenic combination and the colors show to which class each profile belongs (red spectrum = true digenic, blue spectrum = composite). As explained in the Methods section, one can examine this DE profile for each digenic combination, as is done in the current section, or one can consider the distribution of contributions produced per feature (see Supplementary Material Figure S1), evaluating in this way their importance for a particular class.
In the following subsections a number of cases will be discussed, showing that the DE profiles are consistent when examining them in the light of the publications in which they were first identified.
For reasons of illustration, we will focus here on the DE profiles for cases where both classes are present, clarifying in this way how the decision process within the RF determines the outcomes. Essentially all instances in DIDA can be visualized and analyzed in a similar manner.
The impact of variants in MYOC are crucial in determining DE class for autosomal glaucoma
The first cases we show are the digenic combinations in DIDA with identifiers dd026 and dd027. Both lead to autosomal glaucoma (OMIM: #231300, #137750), an eye disease characterized by damage to the optic nerve. It is one of the major causes of bilateral blindness in the world, and interestingly it exhibits variable onset because of Mendelian or multifactorial traits (38). The digenic combinations dd026 and dd027 share a common variant (R368H) in the gene CYP1B1, but have different variants in MYOC, as shown in Table 3. These two instances were reported in two different studies (39,40).
Table 3. Digenic cases related to autosomal glaucoma available in DIDA.
| id | Gene A | Var. | Gene B | Var. | Cl. |
|---|---|---|---|---|---|
| dd026 | MYOC | G399V/+ | CYP1B1 | R368H/+ | CO |
| dd027 | MYOC | Q48H/+ | CYP1B1 | R368H/+ | TD |
‘Var’ refers to variants and ‘Cl’ to class, with ‘TD’ being the true digenic and ‘CO’ the composite class. For more information about dd026 and dd027, see Supplementary Table S5.
It was observed in (39) that the variant G399V in MYOC alone leads to the development of the disease. Yet, the variant Q48H discussed in (40) did not produce any phenotypic effect. Vincent et al. (39) hypothesized that the variant R368H in CYP1B1 may influence the mean age of onset of the disease. Individuals in the family of dd026, carrying both the CYP1B1 and the MYOC variants developed glaucoma with a mean age at onset of 27 years (range 23–38 years). Individuals with only the MYOC variant developed the disease with a mean age at onset of 51 years (range 48–64 years). Although this digenic combination is supported by one single pedigree, a two-tailed unpaired t-test analysis showed that the difference in age at onset between these two groups in the same family was statistically significant (39).
On the contrary, in the case of the patient represented by the combination dd027, the parents are each carrier of one variant in one of the two genes (40). They show no signs of the disease. Both variants in MYOC and CYP1B1 are hence necessary to develop glaucoma, which is in contrast with what was observed for the digenic combination dd026.
Following the initial definition of the DE categories (see Introduction), we consider dd026 as having a mendelizing variant in MYOC that segregates independently, and has a phenotype that can be modified by variants in CYP1B1. The instance dd027, for whom neither carrier parent has the disease, is considered to follow a digenic model of inheritance. Consequently, we labeled dd026 and dd027 as composite (CO) and true digenic (TD), respectively.
Since the features REC, ESS and Path are identical for both digenic combinations as they are related to the same gene pair and the variants for the gene CYP1B1 (DEOB1 and DEOB2) are identical in both cases, they have a similar DE profile, as shown in Figure 3. The essential difference is in the contribution for DEO1A, which is the pathogenicity prediction for the variant on the first allele of MYOC. In dd026, the missense variant G399V is predicted to be deleterious (DEOA1 value = 0.77).
The pathogenicity of the variant G399V may be enough for the development of the disease without the presence of variants in a second gene, justifying the CO label for dd026. Accordingly, the decision profile in Figure 3 shows how the DEOA1 feature is determinant for the prediction of the CO class.
In dd027, the DEOA1 value of variant Q48H is 0.13, indicating that the variant is much less detrimental, and in this case the feature pushes the decision to the TD class. As such our feature DE profile provides an interpretation coherent with the results in the literature.
It is interesting to note here that even though the feature values for the RecA are the same in both instances (0.41), the differences in DEOA1 induce a shift in their contributions. This example illustrates the non-linear effect that each feature has on the other ones in the decision process, as was discussed in Materials and Methods.
Biallelic and triallelic states cause a different phenotype in oculocutaneous albinism
Another interesting case is provided by the digenic combinations dd029 and dd121, recapped in Table 4, as it shows how the zygosity state can influence the decision process. The digenic combinations dd029 and dd121 cause the development of oculocutaneous albinism (OMIM: #203200), a condition that involves variants in the genes mediating melanin synthesis (41). This affects the pigmentation of the skin, hair, eyes and leads to other visual anomalies. The two combinations share a common pair of genes, but with different variants leading to different classes. The triallelic combination dd029 (25) leads to the composite class, the biallelic combination dd121 leads to the true digenic class (42).
Table 4. Digenic cases related to ocultaneous albinism available in DIDA.
| id | Gene A | Var. | Gene B | Var. | Cl. |
|---|---|---|---|---|---|
| dd029 | TYR | A490Cfs* | OCA2 | V443I/+ | CO |
| 20/R402Q | |||||
| dd121 | TYR | R116*/+ | OCA2 | A481T/+ | TD |
‘Var’ refers to variants and ‘Cl’ to class, with ‘TD’ being the true digenic and ‘CO’ the composite class. For more information about dd029 and dd121, see Supplementary Table S5.
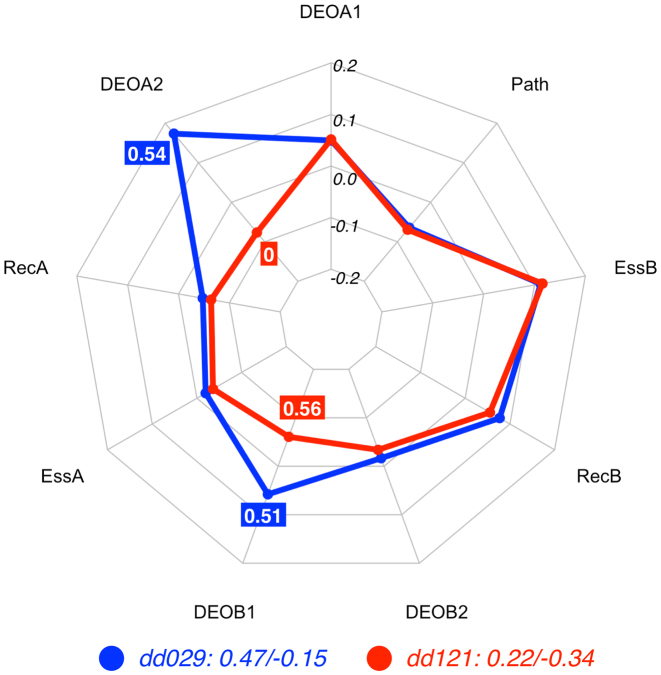
Comparing the DE profiles of the digenic combinations dd029 and dd121 in Figure 4, one can observe again that gene and pathway contributions are equal, with EssA and RecA favouring the TD class (negative contribution) and EssB and RecB favouring the CO class (positive contribution). The Path feature also votes in favour of the TD class. The differences in the variant effects in the second allele of gene A, i.e. DEOA2, and the first allele of gene B, i.e. DEOB1, are deciding the final class assignment: for dd029 (blue line), DEOA2 (DEOGEN value = 0.54) in combination with DEOB1 (DEOGEN value = 0.52) is decisive in voting for the CO class. In case of dd121 the second allele in gene A is harmless (DEOA2 = 0) and DEOB1 is slightly higher (DEOB1 = 0.56), leading the DE predictor to decide in favour of the TD class. Thus, even when the DEOB1 values are quite similar in both digenic combinations, their synergy with the larger difference in DEOA2 makes both features essential for the identification of the correct class.
Figure 4.
Radar plot for the decision process of the RF predictor for the digenic combinations dd029 (CO) and dd121(TD), two instances related to Oculocutaneous Albinism. The deciding factor in this example is due to the difference in allelic state between the two instances: On the one hand, the high feature value of DEOA2 in combination with the DEOB1 value leads the DE predictor to decide to put the dd029 in the CO class. On the other hand, the harmless state of the second allele in gene A (DEOA2 = 0) in combination with a similar feature value for the first allele of gene B leads the decision towards the TD class. See Methods for an explanation of the radar plot. Feature vectors and corresponding decision vectors for dd029 and dd121 are available in Supplementary Material (Table S2 and Table S3).
Unfortunately, for dd029 and dd121 no familial studies are available, making the interpretation of the influence of the variant in the second allele of the TYR gene more difficult. Nonetheless, a genetic explanation may arise from the monogenic inheritance model of this disease and the two associated genes. The mode of inheritance for oculocutaneous albinism is autosomal recessive for the TYR gene (OMIM: #203100), as well as for the OCA2 gene (OMIM: #203200). In dd029, compound heterozygous variants in TYR are enough for the development of the disease (25).
In digenic combination dd121, the heterozygous variants in TYR and OCA2 are by themselves not enough for developing the disease (42), which is supported by an autosomal recessive model for the two genes, but together they lead to the digenic TD effect. Interestingly, this DE profile difference is also relevant for other diseases in DIDA, as for instance haemochromatosis (OMIM: #235200).
Recessiveness determines the classification of combinations in Bardet-Biedl syndrome
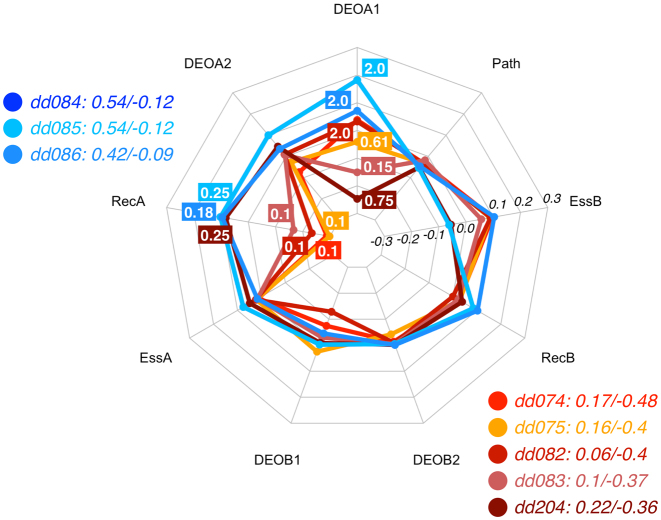
Bardet-Biedl syndrome (BBS) is a genetically heterogeneous disorder represented by various clinical phenotypes, for instance pigmentary retinal dystrophy, polydactyly, obesity, developmental delay, and renal defects (12). BBS genes and other genes involved in the development of the disease have an autosomal recessive inheritance pattern when interpreted via a monogenic model (e.g OMIM: *209901, *604896, *606151). Table 5 lists instances in DIDA leading to BBS for which it was possible to define the DE, reported in different studies (dd074 (12), dd075 (43), dd082 and dd083 (44), dd084 dd085 and dd204 (26), dd086 (45)) .
Table 5. Digenic cases related to Bardet-Biedl syndrome available in DIDA. In the Class column, ‘TD’ refers to the true digenic and ‘CO’ to the composite class. The symbol ‡ indicates that the variant enhances the use of a cryptic splice acceptor site, making it a severe variant. The gene CCDC28B is called MGC1203 in the reference publication (26). For more information about these digenic combinations, see Supplementary Table S5.
| id | Gene A | Variants | Gene B | Variants | Class |
|---|---|---|---|---|---|
| dd074 | BBS2 | Y24*/Q59* | MKKS | Q148*/+ | TD |
| dd075 | BBS2 | T558I/T558I | BBS4 | A364E/A364E | TD |
| dd082 | BBS2 | R413*/+ | BBS4 | P503L/+ | TD |
| dd083 | BBS2 | R643H/+ | BBS4 | K46R/+ | TD |
| dd204 | BBS1 | M390R/M390R | CCDC28B | splicing‡/+ | TD |
| dd084 | BBS1 | Y113*/M390R | CCDC28B | splicing‡/+ | CO |
| dd085 | BBS1 | E549*/M390R | CCDC28B | splicing‡/+ | CO |
| dd086 | BBS7 | G63R/+ | BBS4 | L114Wfs*28/+ | CO |
As there are multiple DE profiles here, we can try to infer more general rules that may be relevant to discriminate between the two types of DE in Bardet-Biedl syndrome. As can be inferred from Figure 5, the recessiveness scores, especially in the first genes, appear to be the determining factor. Additional influence is provided by the variant effects in the first allele of gene A (which is either BBS2, BBS1 or BBS7). When BBS2 is gene A, a low recessiveness (RecA = 0.1) drives the decision towards the TD class (dd074, dd075, dd082 and dd083). This provides the main difference with those favouring the CO class (dd084, dd085 and dd086), whose primary gene (gene A) is either BBS1 or BBS7. The only exception for the latter group is the case dd204, which involves BBS1 but is assigned to the TD class (26). In that case the milder variant effect in the first allele in the gene BBS1 is the determining factor, leading to a TD prediction, even when that gene has a similar recessiveness influence on the DE profile as the other CO classified pairs. Hence the DE predictor has learned to detect the differences between the instances dd084, dd085 and dd204.
Figure 5.
Radar plot for the decision process of the RF predictor for eight digenic combinations leading to Bardet-Biedl syndrome, i.e. three associated with the CO class (blue spectrum) and five related to the TD class (red spectrum). This visualization shows that the recessiveness in gene A (which can be either BBS2, BBS1 or BBS7) together with DEOA1 pushes the instances towards the TD class. Note that dd084 and dd085 have identical feature values and hence identical contributions, resulting in overlapping lines in the radar plot. See Methods for an explanation of the radar plot. Feature vectors and corresponding decision vectors for these digenic combinations are available in Supplementary Material (Tables S2 and S3).
The role of recessiveness, evidenced from the previous paragraph, is coherent with its definition: a very low REC means that a gene, even when presenting two mutated alleles, cannot alone cause the disease by itself. Additional variants in gene B are required, making it all true digenic instances. By contrast, higher REC score in gene A and the presence of strong variants in its alleles put the digenic combinations into the composite DE class. In conclusion for the Bardet-Biedl digenic combinations, we see that the contributions of DEOA1, RecA and RecB are the decisive factors in the classification.
DISCUSSION
The study of digenic diseases is an initial step towards the comprehension of oligogenic diseases. A peculiar aspect related to digenic disease is the DE, which concerns the possible digenic mechanisms causing the observed different phenotypic outcomes. To make this analysis treatable with the currently available data, we simplified the original Schäffer description (15) by grouping them into two main classes, i.e the true digenic (TD) and composite (CO) class, with the latter including mendelizing variants plus modifiers and dual molecular diagnosis.
The DE may be considered simply the sum of the effects of the variants involved, but it should be treated as an emergent property of digenic combinations. For this reason, the DE was studied considering the synergy between the impact of the variants, the role of the genes involved and their molecular relationship. We hypothesized that using this information one can distinguish between the two simplified DE types.
This hypothesis was confirmed through the construction of a machine learning model using the labeled data available in DIDA. The stratified cross-validation shows that the DE predictor is highly effective. To assess the robustness of the DE predictor further, we examined an independent dataset, containing digenic combinations and diseases not yet present in DIDA. Although the small size of this new dataset does not allow an exhaustive evaluation, the current results are encouraging. A limiting factor, which was revealed when analyzing the independent set, appears to be the availability of all relevant annotations: Missing values for gene-related features appear to lead to many erroneous predictions, i.e. assigning instances of the TD class to the CO class. As with any predictive method, more and better annotated data will improve the quality of the model.
In order to escape the black box nature of a RF predictor we introduced the notion of a DE profile that quantifies how the features are used internally by the RF to assign an instance to a class. The DE profile shows how each feature contributed to the final prediction, making the decision process explicit. The selected cases reported in this manuscript show that either single features or combinations of them push the decision in one or the other direction and that tie-breaking features are sometimes required to make the final decision. In this manner, DE profiles can be used to examine newly identified, hence unlabeled, digenic combinations, supporting clinicians and geneticists in the analysis of their newly generated data. This DE classification will also one day impact patient- and family counselling as it may be used to provide biological understanding as well as a way to assess the recurrence risk within the family. Genetic counselling about digenic combinations needs to integrate two type of information, the bi-locus mode of inheritance (true digenic or composite) and the variant allelic state at each locus (mono- or bi-allelic). The DE classification will help the counsellors at the locus level. Additionally, the DE profiles will be used in the context of a novel bioinformatics pipeline that aims to identify and rank novel digenic combinations as has been done for single genes (46).
We observed that some general properties of digenic combinations are distinctive for the two classes, and somehow reflect the underlying biological mechanisms. It emerges that in the TD class the recessiveness scores of the two genes are more similar, and this may be related to the fact that both genes are equally contributing to the phenotype. On the other hand, the lack of balance between the recessiveness of the two genes, which is common in those instances consisting in mendelizing variants plus modifiers (CO class), leads to an asymmetric situation. In this case the primary gene is indeed the main factor responsible for the disease and the secondary contributes less to the phenotype. We also noticed that the DE is often strongly influenced by the impact of the variants involved as well as their zygosity, which is implicitly encoded in the feature vector. In our model the final predictions depend on the combination of gene-based and variant-based features. For example, genes with high recessiveness in the primary gene and strong variants in both its alleles tend to the CO class, which is supported by the definition of a recessive gene in a monogenic inheritance model.
Apart from the novelty of the DE predictor and the profiles one can produce, our work underlines the importance of clearly identifying the primary and secondary genes in the digenic combination. The definition of the primary gene influences both the general performance and the DE profiles, making this ordering crucial. Our work reveals that the GDI provides a useful unbiased criterium to order the genes. Yet, while this simplification solves the problem of reproducibility of the vectors and it has a positive influence on performance, it is not an ideal solution. In fact, when two genes are highly recessive and one of them has homozygous or heterozygous compound strong variants while the other heterozygous variants, the first one should be consider as primary gene, even if it has a slightly lower GDI. Further analysis in this area is therefore required.
A limitation of the current study is the coarse-grained labeling of each digenic combination into true digenic and composite classes. As was recently also argued by Katsanis (47) the causality in human genetic disorders should be considered to be a continuum. We are convinced that true digenic and composite classes should be considered to be part of this continuous spectrum between monogenic and oligogenic diseases. Yet such an analysis is at this moment not feasible given the current limitations on the available data. Improvements in this issue are expected given the identification of 20 novel articles on digenic diseases within one year after the creation of DIDA and the observation that the Online Mendelian Inheritance in Man (OMIM) database introduced new inheritance categories ‘digenic recessive’ and ‘digenic dominant’ (e.g. OMIM: #209900, #220290), allowing for the further expansion of the data on digenic diseases.
In conclusion, the current research shows for the first time an analysis of digenic combinations and their effects, using a classification model. While the true digenic cases can be evidently considered as pure digenic, the composite ones constitute part of the boundary between monogenic and oligogenic diseases. We tried to extract generalisable observations regarding their differences, with the aim of elucidating one small piece of the complex puzzle of oligogenic diseases.
Supplementary Material
ACKNOWLEDGEMENTS
We thank all the members of the Interuniversity Institute for Bioinformatics in Brussels, especially the group of people interested in digenic and oligogenic diseases, for their comments and valuable suggestions. We thank the anonymous reviewers for their careful reading of our manuscript and their many insightful comments and suggestions for improvements.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
ARC project Deciphering Oligo- and Polygenic Genetic Architecture in Brain Developmental Disorders [to A.G. and T.L.]; European Regional Development Fund (ERDF) and the Brussels-Capital Region-Innoviris within the framework of the Operational Programme 2014–2020 through the ERDF-2020 project ICITY-RDI.BRU [27.002.53.01.4524 to T.L. and S.V.D.]; Agency for Innovation by Science and Technology in Flanders (IWT) [to D.R.]; Wetenschappelijk Fonds Willy Gepts - UMCOR (Vrije Universiteit Brussel, UZ Brussel) [to S.V.D. and D.D.]; Brussels Institute for Research and Innovation (Innoviris) [RBC/13-PFS EH-11 to D.D., G.S., S.V.D. and T.L.]. Funding for open access charge: European Regional Development Fund (ERDF) and the Brussels-Capital Region-Innoviris within the framework of the Operational Programme 2014–2020 through the ERDF-2020 project ICITY-RDI.BRU.
Conflict of interest statement. None declared.
REFERENCES
- 1. 1000 Genomes Project Consortium An integrated map of genetic variation from 1,092 human genomes. Nature. 2012; 491:56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Exome Sequencing Project (ESP) Exome Variant Server http://evs.gs.washington.edu/EVS/.
- 3. Stenson P.D., Ball E.V., Mort M., Phillips A.D., Shiel J.A., Thomas N.S., Abeysinghe S., Krawczak M., Cooper D.N.. Human gene mutation database (HGMD®): 2003 update. Hum. Mut. 2003; 21:577–581. [DOI] [PubMed] [Google Scholar]
- 4. Hamosh A., Scott A.F., Amberger J.S., Bocchini C.A., McKusick V.A.. Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res. 2005; 33(suppl. 1):D514–D517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Chong J.X., Buckingham K.J., Jhangiani S.N., Boehm C., Sobreira N., Smith J.D., Harrell T.M., McMillin M.J., Wiszniewski W., Gambin T. et al. . The genetic basis of Mendelian phenotypes: discoveries, challenges, and opportunities. Am. J. Hum. Genet. 2015; 97:199–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bamshad M.J., Ng S.B., Bigham A.W., Tabor H.K., Emond M.J., Nickerson D.A., Shendure J.. Exome sequencing as a tool for Mendelian disease gene discovery. Nat. Rev. Genet. 2011; 12:745–755. [DOI] [PubMed] [Google Scholar]
- 7. Gourraud J.-B., Barc J., Thollet A., Le Scouarnec S., Le Marec H., Schott J.-J., Redon R., Probst V.. The Brugada syndrome: a rare arrhythmia disorder with complex inheritance. Front. Cardiovasc. Med. 2016; 3:9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Gonzalez-Mantilla A.J., Moreno-De-Luca A., Ledbetter D.H., Martin C.L.. A cross-disorder method to identify novel candidate genes for developmental brain disorders. JAMA Psychiatry. 2016; 73:275–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Van Heyningen V., Yeyati P.L.. Mechanisms of non-Mendelian inheritance in genetic disease. Hum. Mol. Genet. 2004; 13:R225–R233. [DOI] [PubMed] [Google Scholar]
- 10. De Rubeis S., Buxbaum J.D.. Genetics and genomics of autism spectrum disorder: embracing complexity. Hum. Mol. Genet. 2015; ddv273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Robinson J.F., Katsanis N.. Oligogenic disease. Vogel and Motulsky’s Human Genetics. 2010; Springer; 243–262. [Google Scholar]
- 12. Katsanis N., Ansley S.J., Badano J.L., Eichers E.R., Lewis R.A., Hoskins B.E., Scambler P.J., Davidson W.S., Beales P.L., Lupski J.R.. Triallelic inheritance in Bardet-Biedl syndrome, a Mendelian recessive disorder. Science. 2001; 293:2256–2259. [DOI] [PubMed] [Google Scholar]
- 13. Abu-Safieh L., Al-Anazi S., Al-Abdi L., Hashem M., Alkuraya H., Alamr M., Sirelkhatim M.O., Al-Hassnan Z., Alkuraya B., Mohamed J.Y. et al. . In search of triallelism in Bardet-Biedl syndrome. Eur. J. Hum. Genet. 2012; 20:420–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. M’hamdi O., Ouertani I., Chaabouni-Bouhamed H.. Update on the genetics of bardet-biedl syndrome. Mol. Syndromol. 2014; 5:51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Schaffer A.A. Digenic inheritance in medical genetics. J. Med. Genet. 2013; 50:641–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Gazzo A.M., Daneels D., Cilia E., Bonduelle M., Abramowicz M., Van Dooren S., Smits G., Lenaerts T.. DIDA: A curated and annotated digenic diseases database. Nucleic Acids Res. 2016; 44:D900–D907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lupski J.R. Digenic inheritance and Mendelian disease. Nat. Genet. 2012; 44:1291–1292. [DOI] [PubMed] [Google Scholar]
- 18. Posey J.E., Harel T., Liu P., Rosenfeld J.A., James R.A., Coban Akdemir Z.H., Walkiewicz M., Bi W., Xiao R., Ding Y., Xia F. et al. . Resolution of disease phenotypes resulting from multilocus genomic variation. N. Engl. J. Med. 2017; 376:21–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Tarailo-Graovac M., Shyr C., Ross C.J., Horvath G.A., Salvarinova R., Ye X.C., Zhang L.-H., Bhavsar A.P., Lee J.J.Y., Drögemöller B.I. et al. . Exome sequencing and the management of neurometabolic disorders. N. Engl. J. Med. 2016; 374:2246–2255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Balci T.B., Hartley T., Xi Y., Dyment D.A., Beaulieu C.L., Bernier F.P., Dupuis L., Horvath G.A., Mendoza-Londono R., Prasad C. et al. . Debunking Occam’s razor: Diagnosing multiple genetic diseases in families by whole-exome sequencing. Clin. Genet. 2017; doi:10.1111/cge.12987. [DOI] [PubMed] [Google Scholar]
- 21. Gonzaga-Jauregui C., Harel T., Gambin T., Kousi M., Griffin L. B., Francescatto L., Ozes B., Karaca E., Jhangiani S.N., Bainbridge M.N. et al. . Exome sequence analysis suggests that genetic burden contributes to phenotypic variability and complex neuropathy. Cell Rep. 2015; 12:1169–1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Brehm A., Liu Y., Sheikh A., Marrero B., Omoyinmi E., Zhou Q., Montealegre G., Biancotto A., Reinhardt A., De Jesus A.A. et al. . Additive loss-of-function proteasome subunit mutations in CANDLE/PRAAS patients promote type I IFN production. J. Clin. Invest. 2015; 125:4196–4211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Mencarelli M.A., Heidet L., Storey H., van Geel M., Knebelmann B., Fallerini C., Miglietti N., Antonucci M.F., Cetta F., Sayer J.A. et al. . Evidence of digenic inheritance in Alport syndrome. J. Med. Genet. 2015; 52:163–174. [DOI] [PubMed] [Google Scholar]
- 24. Raimondi D., Gazzo A.M., Rooman M., Lenaerts T., Vranken W.F.. Multilevel biological characterization of exomic variants at the protein level significantly improves the identification of their deleterious effects. Bioinformatics. 2016; 32:1797–1804. [DOI] [PubMed] [Google Scholar]
- 25. Hutton S.M., Spritz R.A.. A comprehensive genetic study of autosomal recessive ocular albinism in Caucasian patients. Invest. Ophthalmol. Vis. Sci. 2008; 49:868–872. [DOI] [PubMed] [Google Scholar]
- 26. Badano J.L., Leitch C.C., Ansley S.J., May-Simera H., Lawson S., Lewis R.A., Beales P.L., Dietz H.C., Fisher S., Katsanis N.. Dissection of epistasis in oligogenic Bardet-Biedl syndrome. Nature. 2006; 439:326–330. [DOI] [PubMed] [Google Scholar]
- 27. Floeth M., Bruckner-Tuderman L.. Digenic junctional epidermolysis bullosa: mutations in COL17A1 and LAMB3 genes. Am. J. Hum. Genet. 1999; 65:1530–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Nagy E., Maquat L.E.. A rule for termination-codon position within intron-containing genes: when nonsense affects RNA abundance. Trends Biochem. Sci. 1998; 23:198–199. [DOI] [PubMed] [Google Scholar]
- 29. MacArthur D.G., Balasubramanian S., Frankish A., Huang N., Morris J., Walter K., Jostins L., Habegger L., Pickrell J.K., Montgomery S.B. et al. . A systematic survey of loss-of-function variants in human protein-coding genes. Science. 2012; 335:823–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Georgi B., Voight B.F., Bućan M.. From mouse to human: evolutionary genomics analysis of human orthologs of essential genes. PLoS Genet. 2013; 9:e1003484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kanehisa M., Goto S., Sato Y., Kawashima M., Furumichi M., Tanabe M.. Data, information, knowledge and principle: back to metabolism in KEGG. Nucleic Acids Res. 2014; 42:199–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Croft D., Mundo A.F., Haw R., Milacic M., Weiser J., Wu G., Caudy M., Garapati P., Gillespie M., Kamdar M.R. et al. . The Reactome pathway knowledgebase. Nucleic Acids Res. 2014; 42:D472–D477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. et al. . Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011; 12:2825–2830. [Google Scholar]
- 34. Breiman L. Random forests. Mach. Learn. 2001; 45:5–32. [Google Scholar]
- 35. Ojala M., Garriga G.C.. Permutation tests for studying classifier performance. J. Mach. Learn. Res. 2010; 11:1833–1863. [Google Scholar]
- 36. Rao D.C., Gu C.C.. Genetic Dissection of Complex Traits. 2008; 60:Academic Press. [Google Scholar]
- 37. Itan Y., Shang L., Boisson B., Patin E., Bolze A., Moncada-Velez M., Scott E., Ciancanelli M.J., Lafaille F.G., Markle J.G. et al. . The human gene damage index as a gene-level approach to prioritizing exome variants. Proc. Natl. Acad. Sci. U.S.A. 2015; 112:13615–13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Cascella R., Strafella C., Germani C., Novelli G., Ricci F., Zampatti S., Giardina E.. The genetics and the genomics of primary congenital glaucoma. BioMed. Res. Int. 2015; 2015:321291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Vincent A.L., Billingsley G., Buys Y., Levin A.V., Priston M., Trope G., Williams-Lyn D., Heon E.. Digenic inheritance of early-onset glaucoma: CYP1B1, a potential modifier gene. Am. J. Hum. Genet. 2002; 70:448–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Kaur K., Reddy A.B., Mukhopadhyay A., Mandal A.K., Hasnain S.E., Ray K., Thomas R., Balasubramanian D., Chakrabarti S.. Myocilin gene implicated in primary congenital glaucoma. Clin. Genet. 2005; 67:335–340. [DOI] [PubMed] [Google Scholar]
- 41. Que S. K.T., Weston G., Suchecki J., Ricketts J.. Pigmentary disorders of the eyes and skin. Clin. Dermatol. 2015; 33:147–158. [DOI] [PubMed] [Google Scholar]
- 42. Wei A.H., Yang X.M., Lian S., Li W.. Genetic analyses of Chinese patients with digenic oculocutaneous albinism. Clin. Med. J. 2013; 126:226–230. [PubMed] [Google Scholar]
- 43. Katsanis N., Eichers E.R., Ansley S.J., Lewis R.A., Kayserili H., Hoskins B.E., Scambler P.J., Beales P.L., Lupski J.R.. BBS4 is a minor contributor to Bardet-Biedl syndrome and may also participate in triallelic inheritance. Am. J. Hum. Genet. 2002; 71:22–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Fauser S., Munz M., Besch D.. Further support for digenic inheritance in Bardet-Biedl syndrome. J. Med. Genet. 2003; 40:e104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Bin J., Madhavan J., Ferrini W., Mok C.A., Billingsley G., Heon E.. BBS7 and TTC8 (BBS8) mutations play a minor role in the mutational load of Bardet-Biedl syndrome in a multiethnic population. Hum. Mutat. 2009; 30:E737–E746. [DOI] [PubMed] [Google Scholar]
- 46. Moreau Y, Tranchevent L.C.. Computational tools for prioritizing candidate genes: boosting disease gene discovery. Nat. Rev. Genet. 2012; 13:523–536. [DOI] [PubMed] [Google Scholar]
- 47. Katsanis N. The continuum of causality in human genetic disorders. Genome Biol. 2016; 17:233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.