Case-control data analysis for randomly pooled biomarkers

Abstract

Pooled study designs, where individual biospecimens are combined prior to measurement via a laboratory assay, can reduce lab costs while maintaining statistical efficiency. Analysis of the resulting pooled measurements, however, often requires specialized techniques. Existing methods can effectively estimate the relation between a binary outcome and a continuous pooled exposure when pools are matched on disease status. When pools are of mixed disease status, however, the existing methods may not be applicable. By exploiting characteristics of the gamma distribution, we propose a flexible method for estimating odds ratios from pooled measurements of mixed and matched status. We use simulation studies to compare consistency and efficiency of risk effect estimates from our proposed methods to existing methods. We then demonstrate the efficacy of our method applied to an analysis of pregnancy outcomes and pooled cytokine concentrations. Our proposed approach contributes to the toolkit of available methods for analyzing odds ratios of a pooled exposure, without restricting pools to be matched on a specific outcome.

1 Introduction

Pooling biospecimens prior to performing laboratory assays is a design strategy in which individual samples are grouped, either randomly or by some criteria, and then physically combined to create a set of pooled biological samples which are then assayed. This technique can be particularly advantageous in reducing lab costs, by reducing the number of tests required to obtain information from all available specimens. Pooling is commonly used as a cost-saving tool in screening for disease (e.g., screening donated blood for HIV), but also has utility when continuous biomarkers are assessed for epidemiological studies (Kacena et al., 1998; Pilcher et al., 2005). Strategic pooling designs have been shown to promote statistical efficiency, particularly when compared with similar designs that select the same number of individual assays for analysis (Weinberg and Umbach, 1999; Liu and Schisterman, 2003; Mumford et al., 2006; Ma et al., 2011; Schisterman et al., 2011; Malinovsky et al., 2012; Saha-Chaudhuri and Weinberg, 2013; Heffernan et al., 2014). In certain situations assays may require a minimum volume for analysis that is impractical or impossible to obtain from single specimens. Pooling multiple biospecimens increases the pooled sample volume to attain that minimum necessary quantity for the assay, yielding usable measurements where none would have been available by conventional strategies.

When pools are matched based on case status, application of common statistical tools such as logistic regression models or receiver operating characteristic curves is straightforward (Weinberg and Umbach, 1999; Schisterman et al., 2005; Saha-Chaudhuri et al., 2011; Whitcomb et al., 2012). However, few techniques are available for the analysis of pooled case-control data when pools are “mixed” based on case status (Zhang and Albert, 2011). Explicitly, a mixed pool is composed of specimens from individuals where at least one member is of each disease status. This scenario could occur, for instance, if pools are formed based on a primary outcome, but analysis is later conducted on a secondary outcome. In the secondary analysis, the existing pools are unlikely to be perfectly matched with respect to this secondary outcome.

In this study, we propose and examine the statistical properties of a technique for analyzing mixed pool data from a case-control study, specifically, assessing the relation between a continuous exposure and disease status. The development of methods to analyze such mixed pools is motivated by an ancillary study of the Collaborative Perinatal Project to assess the association between cytokine levels and pregnancy outcomes. Using specimens obtained from this study, pools of size g = 2 matched on spontaneous abortion (SA) status were formed and cytokines were measured, facilitating a cost-effective strategy to estimate the odds ratio of cytokines on SA status. However, there was additional interest in assessing the relation between cytokine levels and the secondary outcome of low birth weight (LBW). Since pooling was conducted without regard for LBW, a considerable proportion of mixed pools with respect to LBW were formed. We are unaware of any readily applicable methods for analyzing such mixed pools of a highly skewed biomarker, implying that these pools (approximately 50% in this example) might be rendered useless for assessing cytokine relations with LBW based on existing methodology.

In the next section, we summarize the theoretical basis for estimating the odds ratio of interest based on disease-specific gamma distributions of the exposure when pools are mixed. In Section 3, we assess the performance of our methods that utilize mixed pools and compare these estimates to those that would have been available from only matched pools or a random sample of the same size. Finally, we apply these methods to the Collaborative Perinatal Project ancillary study on the relation between maternal cytokine levels and LBW.

2 Methods

Let OR(x) denote the odds ratio of interest for a disease (D) corresponding to a 1-unit increase in the exposure (X), such that:

$$OR(x)=\frac{\text{Pr}(D|X=x+1)/\text{Pr}(D|X=x)}{\text{Pr}(\overline{D}|X=x+1)/\text{Pr}(\overline{D}|X=x)}.$$ (1)

When this odds ratio is assumed to be constant for all values of X, it can easily be estimated from the full, individual data by performing logistic regression. For pooled data, Weinberg and Umbach (1999) showed that when pools are matched by case status, it is relatively straightforward to estimate Eq. (1) via a set-based logistic regression model. When pools are mixed with respect to case status, these mixed pools cannot be accommodated under the existing set-based logistic regression model, and thus must be omitted from the analysis. When pools are formed initially based on a primary outcome, the status of the pools with respect to a secondary outcome is highly dependent on the correlation between the primary and secondary outcome. Figure 1 illustrates a pooling strategy in which individual samples are grouped in pools of g = 2 matched on a primary outcome (O1). It is easy to see that for a secondary outcome (O2), even one that is highly correlated with O1, these original groupings would lead to both matched and mixed pools for O2. Omitting the mixed pools and relying on existing matched pool methods would greatly reduce sample size, information, and our ability to investigate a relation between the biomarker and O2.

Figure 1.

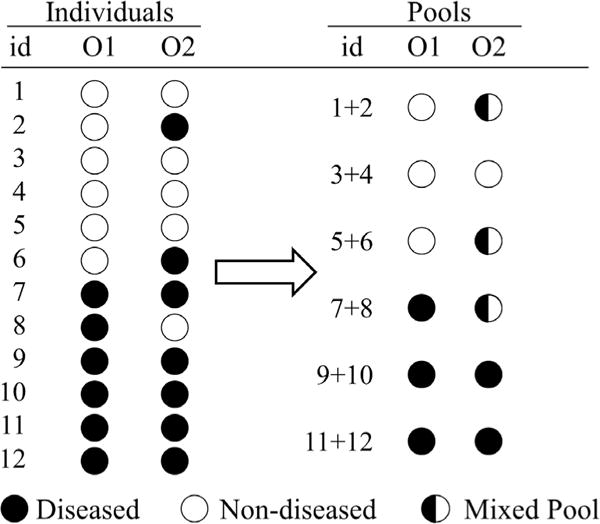
Example of case (black) and control (white) data where pools are formed based on a primary outcome (O1) and the potential effects regarding a secondary outcome (O2) on the same groupings of individuals.

Zhang and Albert (2011) developed a general method for performing binary regression with a pooled exposure, which can utilize pools of mixed case status; however, their methods assume an approximately normal distribution for the exposure, which may not apply to many highly skewed biomarkers. Whitcomb et al. (2012) proposed a flexible methodology for constant and nonconstant odds ratio estimates for individual specimens and matched pools, with particular focus on exposures that are well characterized by a gamma distribution. Here, we apply the convenient properties of the gamma distribution to develop an accessible and flexible procedure to estimate constant and nonconstant odds ratios, by extending the existing methods of Whitcomb et al. (2012) to incorporate all types of pools.

Let $Y_i=g_i^{-1}{\displaystyle {\sum }_{l=1}^{g_i}{X}_{il}}$ represent the measured value of the i-th pool, which may contain specimens from both case and control populations. Continuous measurements of the pool are considered the average of the measurements of the individual biospecimens in each pool. In other words, Y_i is assumed to be the average of the individual X_il, a reasonable assumption given that most assays are per unit of volume. Applying Bayes’ theorem, Eq. (1) can be rewritten as:

$$OR(x)=\frac{f(x+1|D,{\theta }_1)/f(x|D,{\theta }_1)}{f(x+1|\overline{D},{\theta }_0)/f(x|\overline{D},{\theta }_0)},$$ (2)

where f (x|D, θ₁) and $f(x|\overline{D},{\theta }_0)$ represent the exposure densities for cases (D) and controls $(\overline{D})$, respectively, that depend on some unknown parameters θ₀ and θ₁. Equation (2) can be evaluated by assuming conditional densities and estimating the unknown parameters θ₀ and θ₁. Since individual level measurements, x_il, of the exposure values are not available, maximum likelihood estimates of θ₀ and θ₁ must be obtained by maximizing the log-likelihood for the pooled exposures:

$$l({\theta }_0,{\theta }_1|Y)={\displaystyle \sum _{i=1}^n\text{log}{f}_Y(Y_i|{\theta }_0,{\theta }_1)},$$ (3)

where f_Y (Y_i|θ₀, θ₁) denotes the density of the measured value of the i-th pool. Suppose that the first m_i, m_i ≤ g_i, specimens contained in this pool are from cases, and the remaining g_i − m_i specimens are from controls. Then, f_Y (Y_i|θ₀, θ₁) is characterized by the multidimensional integral as follows:

$$f_Y(Y_i|{\theta }_0,{\theta }_1)={\displaystyle \int g_{i}I}\left({\displaystyle \sum _{l=1}^{g_i}{x}_{il}=g_i{Y}_i}\right){\displaystyle {\prod }_{i=1}^{m_i}f(x_{il}|D_i,{\theta }_1)}\times {\displaystyle {\prod }_{l=m_i\times 1}^{g_i}f(x_{il}|{\overline{D}}_i,{\theta }_0)}dX,$$ (4)

where dX indicates integrating sequentially with respect to each of the members of the i-th pool, the x_il, l = 1, …, g_i. Due to the complicated nature of this density function, calculating maximum likelihood estimator (MLEs) based on direct optimization of the log-likelihood can be highly impractical. Through prudent choice of f(x|θ), Eq. (4) can be greatly simplified. When the conditional density of the exposure given disease status is normal, for instance, the pool measurement retains a normal distribution due to summation properties of this distribution. Subsequent optimization of the log-likelihood would be straightforward, and closed-form OR estimates could be obtained using a minor variant of normal-theory discriminant function analysis (Hosmer et al., 2013).

Many biomarkers, however, exhibit a positive, right-skewed distribution, which may be better modeled by a lognormal or gamma distribution. Lognormal is often conveniently chosen in analysis of individual level data because of the resulting normality after a log transformation. Since the log of the average is not equal to the average of the logs, the log transformation is problematic with pooled data. Alternatively, the gamma distribution is particularly compelling in this situation since it requires no transformation and benefits from similar distributional preservation properties as the normal distribution.

Suppose the exposure is a gamma random variable such that X_D Gamma(α₁, β₁) for cases and $X_{\overline{D}}~\text{Gamma}({\alpha }_0,{\beta }_0)$ for controls, where α represents the shape parameter and β the rate. Then, as Whitcomb et al. (2012) showed, the odds ratio of interest Eq. (2) can be written as:

$$OR(x)=\text{exp}\left\{{\beta }_0-{\beta }_1+({\alpha }_1-{\alpha }_0)\text{log}\left(\frac{x+1}{x}\right)\right\}.$$ (5)

Note that the OR(x) in Eq. (5) is a function of x, when α₀ ≠ α₁, that reduces to a constant when α₀ = α₁.

To estimate MLEs for θ = {α₁, β₁, α₀, β₀}, let us partition our pooled measurements into three groups with respect to the disease status of the contributors: (i) matched pools of cases, $g{Y}_D={\displaystyle {\sum }_{l=1}^g{X}_{Dl}~\mathit{Gamma}(g{\alpha }_1,{\beta }_1)}$ (ii) matched pools of controls $g{Y}_{\overline{D}}={\displaystyle {\sum }_{l=1}^g{X}_{\overline{D}l}~\mathit{Gamma}(g{\alpha }_0,{\beta }_0)}$, (iii) mixed pools with m cases and g − m controls, $g{Y}_M=\left({\displaystyle {\sum }_{l=1}^m+X_{Dl}}+{\displaystyle {\sum }_{l=m+1}^g{X}_{\overline{D}l}}\right)$, where 0 < m < g. The distributions of gY_D and $g{Y}_{\overline{D}}$ have previously been exploited in the pooling literature (Schisterman et al., 2005; Whitcomb et al., 2012). Applying the same summation property of gamma distributions, we can reduce Eq. (4) to a much more manageable likelihood by collapsing the cases and controls within a mixed pool such that ${\displaystyle {\sum }_{l=1}^m{X}_{Dl}~\mathit{Gamma}(m{\alpha }_1,{\beta }_1)}$ and ${\displaystyle {\sum }_{l=m+1}^g{X}_{\overline{D}l}~\mathit{Gamma}([g-m]{\alpha }_0,{\beta }_0)}$. The density of gY_M can then be written as:

$$f_{g{Y}_M}(g{Y}_M|\mathit{\theta },m)={\displaystyle {\int }_0^{g{Y}_M}f(t|m{\alpha }_1,{\beta }_1)}f(g{Y}_M-t|(g-m){\alpha }_0,{\beta }_0)dt,$$ (6)

where f (t|α, β) = Γ(α)⁻¹β^αt^α−1 exp(−tβ) is the gamma density. Note that if β₀ = β₁, that is the rate parameters are identical for cases and controls, this density reduces further to $f_{g{Y}_M}(g{Y}_M|\theta ,m)=f(g{Y}_M|m{\alpha }_1+[g-m]{\alpha }_0,\beta )$, since equivalence of rate parameters is sufficient to preserve the gamma distribution. The likelihood in Eq. (3) can now be written as follows:

$$l({\alpha }_1,{\beta }_1,{\alpha }_0,{\beta }_0|Y,m,g)={\displaystyle \sum _{i=1}^n\text{log}{f}_Y(g_i{Y}_i|{\alpha }_1,{\beta }_1,{\alpha }_0,{\beta }_0,m_i)}={\displaystyle \sum _{i:m_i=g_i}\text{log}f(g_i{Y}_i|m_i{\alpha }_1,{\beta }_1)}+{\displaystyle \sum _{i:m_i=0}\text{log}f(g_i{Y}_i|m_i{\alpha }_0,{\beta }_0)}+{\displaystyle \sum _{i:0<m_i<g_i}\text{log}{\displaystyle \underset{0}{\overset{g_i{Y}_M}{\int }}f(t|m_i{\alpha }_1,{\beta }_1)f(g_i{Y}_i-t|(g_i-m_i){\alpha }_0,{\beta }_0)}}dt.$$ (7)

Since the contribution of each pool to the likelihood contains at most a one-dimensional integral, it is fairly straightforward to apply numerical integration and optimization techniques to Eq. (7) in order to estimate the MLEs θ = {α₁, β₁, α₀, β₀} that characterize the disease-specific distributions of the exposure. Once calculated, these MLEs can then be applied to Eq. (5) in order to estimate the odds ratio of interest.

A natural concern is the potential dependence in Y induced when the pools are created based on O1. In the Appendix, we develop the likelihood (A.1) given Y and disease status for O1 and O2 and show how the resulting parameter estimates can be used to estimate OR(x) similar to Eq. (5). We will continue to focus throughout on the simplified approach employing Eqs. (7) and (5) since it is consistent and comparatively more efficient for estimating OR(x) for O₂ than the fuller (A.1) and (A.3).

3 Simulation

Extensive simulation studies were conducted to evaluate the effects of mixed pooling on estimation of the odds ratio for a gamma-distributed exposure. Five thousand simulations were run in R for each scenario, where X_D was generated from a gamma distribution with various values of shape and scale parameters(α₁, β₁), and $X_{\overline{D}}$ was generated from a gamma distribution such that $X_{\overline{D}}~\mathit{Gamma}({\alpha }_0=1,{\beta }_0=1)$.

An equal number of diseased and nondiseased with respect to the primary outcome were simulated based on the total sample size (N). The number of diseased and nondiseased for the secondary outcome was then generated based on the specified proportions a and d (see Fig. 2). n pools were then formed with equal size g matched on the primary outcome, resulting in both matched and mixed pools with respect to the secondary outcome. Established methods are limited to using only the matched pools for data analysis (Weinberg and Umbach, 1999; Whitcomb et al., 2012). Log-odds ratio estimates for the secondary outcome corresponding to a 1-unit increase in exposure (X) were calculated based on these existing methods using only the matched pools (denoted “Matched Pools” in results tables). Since the gamma-distributed exposure can imply nonconstant odds ratios, logOR estimates are calculated at the first and third quartiles of X. We then compare these estimates to those that we can obtain from the entire set of pools (mixed and matched) based on our proposed analytical methods outlined in Section 2. Results from this analysis are subsequently labeled “Mixed Pools”.

Figure 2.

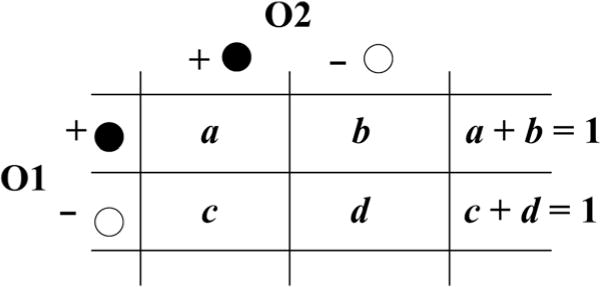
Conditional probabilities of case status for a secondary outcome (O2) given primary outcome (O1) status where cases are black and controls are white.

Log-odds ratio estimates were calculated from Eq. (5), where MLEs of θ = {α₁, β₁, α₀, β₀} were estimated by optimizing the log-likelihood Eq. (7) using R’s optim function. Each contribution to the likelihood was defined in accordance with the type of pooling or sampling, and the density for mixed pools was evaluated using R’s numerical integration function integrate. Standard errors for the Wald 95% confidence intervals (CIs) log(OR) were calculated in straightforward fashion based on components estimated in the Hessian matrix.

Various parameters could potentially impact the proportion of mixed pools, and subsequently, the performance of the proposed estimation procedure. In particular, a strong positive correlation between O1 and O2 can result in a greater number of pools matched with respect to O2, improving performance of the estimation procedure for the O2 odds ratio. A weak correlation or a large g, however, can result in mostly mixed pools, which will almost certainly reduce precision of estimates. Figure 2 provides a visualization of these potential correlations between the two outcomes, where the effect of various a and d are tested in the simulation studies. In addition, Table 1 gives the distribution of case pools, control pools, and mixed pools from each of the simulation studies. On average, when a = 0.2 and d = 0.9, only five case pools were available for analysis. Consequently, analytical methods that exclude mixed pools can be highly unstable due to the degree of partial separation.

Table 1.

Average number of case, control, and mixed pools for the simulation studies, N = 400, g = 2, n = 200, at various combinations of the concordance proportions, a and d.

aa	db	Average number
		Case pools	Control pools	Mixed pools
0.7	0.7	58	58	84
0.9	0.9	82	82	36
0.2	0.9	5	145	50

^aProportion of individuals with a primary outcome that also have the secondary outcome.

^bProportion of individuals negative for a primary outcome and the secondary outcome.

3.1 Nonconstant odds ratio

First, we consider the scenario when odds ratios are not constant across different values of the exposure. In this scenario, a nonconstant odds ratio has different shape parameters of the gamma distributions of the cases and controls, that is α₀ ≠ α₁. This characteristic has been shown to apply to the cytokine studied in the motivating example (Whitcomb et al., 2012). Relative bias, 95% CI coverage, and root mean square error (RMSE) of logOR estimates from these simulations are provided in Table 2 at various levels of a, d, and θ. Mixed and Matched columns of Table 2 display, respectively, the proposed method applied to mixed pools versus the method developed by Whitcomb et al. (2012) for matched pools. LogOR results are displayed at the first and third quartiles of the healthy population, $X_{\overline{D}}$, in each simulation, denoted by Q1 and Q3, respectively. As evidenced by these results, estimates from mixed pools calculated under the proposed method far outperform those from existing methodology for a nonconstant odds on only matched pools. Analysis using only matched pools performs particularly poorly when a = 0.2 and d = 0.9, due to the limited number of diseased matched pools (see Table 1). In fact, less than 62% of the simulations under this scenario contained enough matched pools of each type to provide reliable estimates. Analysis on mixed pools, however, was able to utilize all pools, not just those matching by chance on O2, providing reliable estimates for over 99% of the simulations (Table 3).

Table 2.

Relative bias, 95% CI coverage, and RMSE of log-odds ratio estimates evaluated from N = 400 individuals with exposures pooled in pairs, g = 2, matched on outcome status or pooled randomly, mixed, at the first and third quartiles of exposure, Q1 = 0.288 and Q3 = 1.39 of the healthy population^a.

A	d	α1	β1		Relative bias (95% CI coverage)		RMSE
					Mixed	Matchedb	Mixed	Matched
0.7	0.7	1.5	0.5	logOR(Q1) = 1.249	0.024 (95.0)	0.060 (95.3)	0.298	0.376
				logOR(Q3) = 0.772	0.042 (95.0)	0.056 (95.3)	0.146	0.157
		2	0.5	logOR(Q1) = 1.999	0.019 (95.4)	0.051 (95.3)	0.374	0.517
				logOR(Q3) = 1.043	0.038 (95.0)	0.054 (95.1)	0.160	0.189
0.9	0.9	1.5	0.5	logOR(Q1) = 1.249	0.030 (95.0)	0.043 (95.8)	0.279	0.304
				logOR(Q3) = 0.772	0.038 (95.3)	0.042 (95.4)	0.124	0.128
		2	0.5	logOR(Q1) = 1.999	0.021 (94.6)	0.035 (94.9)	0.369	0.426
				logOR(Q3) = 1.043	0.029 (95.0)	0.036 (95.3)	0.143	0.154
0.2	0.9	1.5	0.5	logOR(Q1) = 1.249	0.091 (94.5)	0.440 (96.5)	0.484	1.239
				logOR(Q3) = 0.772	0.039 (94.4)	0.337 (98.8)	0.137	0.746
		2	0.5	logOR(Q1) = 1.999	0.076 (94.6)	0.145 (96.4)	0.626	1.124
				logOR(Q3) = 1.043	0.046 (95.0)	0.436 (97.5)	0.179	0.923

^aHealthy population assumed gamma distribution with α₀ = 1 and β₀ = 1 for all simulations.

^bEstimators based on methods relying solely on matched pools after omitting mixed pools.

Table 3.

Percent of the total simulated iterations where estimation procedures converged using mixed and matched pooled data.

a	d	α1	β1	% Convergence
				Mixed	Matched
0.7	0.7	1.0	0.5	99.2	100.0
		1.5	0.5	99.8	100.0
		2.0	0.5	99.8	99.9
0.9	0.9	1.0	0.5	99.7	99.9
		1.5	0.5	99.9	99.9
		2.0	0.5	99.9	100.0
0.2	0.9	1.0	0.5	99.1	87.0
		1.5	0.5	99.8	76.0
		2.0	0.5	99.5	61.9

As expected, the RMSE under mixed pools (Table 2) is lowest when the correlation between O1 and O2 is strong (a = 0.9, d = 0.9), since this strong correlation results in a greater number of pools matched on the secondary outcome. When O1 and O2 are weakly correlated (a = 0.2, d = 0.9), RMSE for all methods is noticeably larger, due to a small number of matched pools with O2. Even in this scenario, however, the analysis under mixed pooling performs surprisingly well. In general, additional simulations suggested similar trends for various values of n, g, and N, where an increase in the number of assays (n) led to reduced bias and lower RMSE values.

3.2 Constant odds ratio

In some cases, the odds ratio may be constant across different values of the exposure, meaning that the shape parameters from the gamma distributions characterizing the cases and controls are equal, α₀ = α₁ (Whitcomb et al., 2012). In such cases, it will be more efficient to calculate a joint MLE for the shape parameter, instead of calculating this parameter separately for cases and controls. Tables 4 and 5 demonstrate the potential improvements in results when a constant odds ratio is correctly assumed. As evidenced by these results, correctly assuming equal shape parameters noticeably improves CI coverage and reduces RMSE for all situations. Note that assuming constant odds ratios and analyzing only matched pools can also be analyzed via the method proposed by Weinberg and Umbach (1999), column 2 of Tables 4 and 5. While their method is flexible in that it does not require distributional assumptions on the exposure, it is limited to analyzing only matched pools, reducing the available information and precision of the resulting estimates when a substantial number of pools are mixed.

Table 4.

Relative bias and 95% CI coverage of log-odds ratio estimates evaluated from N = 400 individuals with exposures pooled in pairs, g = 2, matched on outcome status or pooled randomly, mixed, when the true odds ratio is constant across all values of the exposure^a.

a	d		Relative bias (95% CI coverage)
			Constant oddsb		Nonconstant oddsc
			Mixed	Matchedd	Mixed	Matched
0.7	0.7	logOR(Q1) = 0.5	0.031 (94.8)	0.043 (95.1)	0.020 (90.5)	0.050 (95.8)
		logOR(Q3) = 0.5			0.051 (90.1)	0.061 (95.5)
0.9	0.9	logOR(Q1) = 0.5	0.029 (95.1)	0.030 (95.5)	0.028 (92.8)	0.039 (95.3)
		logOR(Q3) = 0.5			0.037 (92.8)	0.040 (95.4)
0.2	0.9	logOR(Q1) = 0.5	0.001 (95.7)	0.007 (98.4)	0.137 (91.3)	1.096 (96.6)
		logOR(Q3) = 0.5			0.003 (93.9)	−0.124(99.7)

^aHealthy and diseased populations assumed gamma distributions with α₀ = 1, β₀ = 1 and α₁ = 1, β₁ = 0.5 for all simulations with Q1 and Q3 denoting first and third quartiles of the healthy population.

^bMethods applied assume constants odds.

^cMethods applied allow for nonconstant odds.

^dMethod applied to only matched pools as developed by Weinberg and Umbach (1999).

Table 5.

RMSE of log-odds ratio estimates evaluated from N = 400 individuals with exposures pooled in pairs, g = 2, matched on outcome status or pooled randomly, mixed, when the true odds ratio is constant across all values of the exposure^a.

a	d		RMSE
			Constant oddsb		Nonconstant oddsc
			Mixed	Matchedd	Mixed	Matched
0.7	0.7	logOR(Q1) = 0.5	0.124	0.136	0.214	0.236
		logOR(Q3) = 0.5			0.142	0.148
0.9	0.9	logOR(Q1) = 0.5	0.104	0.110	0.188	0.197
		logOR(Q3) = 0.5			0.115	0.117
0.2	0.9	logOR(Q1) = 0.5	0.117	0.370	0.335	1.199
		logOR(Q3) = 0.5			0.124	0.681

^aHealthy and diseased populations assumed gamma distributions with α₀ = 1, β₀ = 1 and α₁ = 1, β₁ = 0.5 for all simulations with Q1 and Q3 denoting first and third quartiles of the healthy population.

^bMethods applied assume constants odds.

^cMethods applied allow for nonconstant odds.

^dMethod applied to only matched pools as developed by Weinberg and Umbach (1999).

To test the constant odds assumption, we apply a likelihood ratio (LR) test with null hypothesis α₀ = α₁. Table 6 gives the Type I Errors of the LR test for the simulation studies in this section. When the proposed analytical strategies for mixed pools are applied, nominal 5% and 1% error rates are exhibited. When only matched pools are included in the analysis, however, Type I Error rates can exceed the 5% and 1% nominal values as a decreases and d = 0.9, due to the smaller number of matched case pools. Specifically, a matched pools strategy results in nominal rates when d = 0.9 from a = 0.9 to 0.6, however, Type I Errors continually increase thereafter for a = 0.5 to almost doubling at a = 0.2. Thus, the ability to include all pools in the analysis can improve accuracy in identifying a constant odds ratio, which can subsequently result in more appropriate and efficient log-odds ratio estimates.

Table 6.

Type I Error Rates of likelihood ratio test to determine equivalence of shape parameters (i.e., constant odds ratio test).

a	d	LR test Type I Error Rate
		0.05		0.01
		Mixed	Matched	Mixed	Matched
0.7	0.7	0.050	0.048	0.009	0.009
0.9	0.9	0.047	0.048	0.010	0.009
0.8	0.9	0.043	0.044	0.008	0.008
0.7	0.9	0.053	0.053	0.013	0.012
0.6	0.9	0.051	0.056	0.012	0.013
0.5	0.9	0.055	0.059	0.014	0.014
0.4	0.9	0.052	0.062	0.011	0.015
0.3	0.9	0.048	0.071	0.010	0.020
0.2	0.9	0.054	0.087	0.010	0.018

4 Data analysis

Various cytokines were measured in stored samples from the Collaborative Perinatal Project to investigate associations with SA (Whitcomb et al., 2008). “Matched” pools of size g = 2 were formed within SA status. The Fluorokine MAP Multiplex Human Cytokine Panel A detection system (R&D Systems, Inc., Minneapolis, MN, USA) and the Luminex 100IS platform (Luminex Corporation, Austin, Texas) was used to measure cytokine levels in the pooled serum. Nonspecificity was accounted for with “blank” subtracted calibration curves and samples were randomly dispersed within the 96-well plates with respect to SA. The goal of our analysis is to investigate the relation between the secondary outcome LBW, defined by birth weight less than 2500 g, and the same cytokines. In particular, we are interested in the association between LBW and Interferon gamma-inducible protein (IP). In general, biomarkers, cytokines, and in this case IP, often have right-skewed distributions that can be well characterized by disease-specific gamma distributions (Whitcomb et al., 2012).

Since birth weight is an outcome conditional on live birth, only biospecimens from controls were available for the secondary analysis on LBW. Subsequently, IP measurements on 177 pools were available. One hundred and forty-six pooled biospecimens had both normal weight babies, 29 pooled biospecimens had a mixed outcome of a normal weight baby and an LBW baby, and two pooled biospecimens were from LBW babies. Since LBW was not considered in the initial formation of the pools and with a 9.3% prevalence in our sample (33 out of 354 women), only two of the pools in this sample were matched randomly with respect to LBW. The measurement of IP from the pooled specimens ranged from 0.0001 to 0.109, where these measurements are assumed to be the average of the measurements that would have been observed on the individual specimens. Figure 3 illustrates the distribution of the pooled measurements across each pool type.

Figure 3.

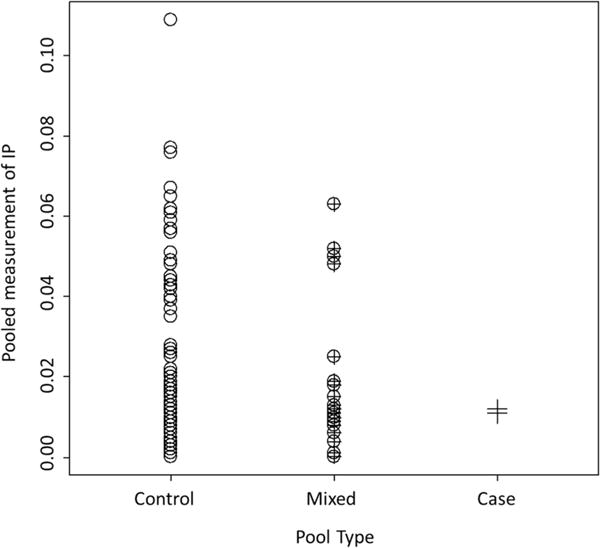
Scatterplot of pooled measurements of IP separated by pool type. “Control” refers to pools containing specimens from only controls, “Case” to those pools containing only specimens from cases, and “Mixed” refers to pools with one specimen from a case, and the other from a control.

Focusing on the columns of matched pools in Fig. 3, circles and crosses, it is easy to see that analysis excluding the middle column of mixed pools, circle-cross, greatly reduces the overall sample size. Moreover, such a small number of matched case pools preclude the estimation of ORs, constant or nonconstant, using existing analytical methods (logistic regression and MLEs, respectively) that can only accept matched pools.

Utilizing the mixed pools based in our proposed method can investigate IP’s relation with LBW. Assuming gamma distributions and maximizing Eq. (7), we estimated distribution parameters from the full set of pools, with and without the α₀ = α₁ constraint. Log-odds are calculated to reflect the logOR of a 0.01 unit increase in IP. Estimates and CIs of the constant and nonconstant logOR are provided in Table 7, at various quartiles (Q1–Q3). While neither result is significant, the nonconstant, ORs of 1.37, 1.19, and 1.10, are suggestive of a potential relation between IP and LBW at lower levels that can be further investigated if additional data become available. Alternatively, relying on previous methods and requiring matched pools considerably reduces sample size to $n_{\overline{D}}=146$ and n_D = 2. These analyses are unstable at best and surely unreliable.

Table 7.

Log-odds ratio estimates (95% confidence interval) for LBW infants, based on N = 354 women with specimens pooled in pairs prior to measurement of Interferon gamma-IP. Estimates are provided at quartiles of exposure, Q1–Q3.

IP level	logOR
	Constant	Nonconstant
Q1	0.000 (−0.045, 0.045)	0.312 (−0.208, 0.832)
Q2	0.000 (−0.045, 0.045)	0.173 (−0.128, 0.473)
Q3	0.000 (−0.045, 0.045)	0.097 (−0.084, 0.279)

5 Conclusions

In this study, we developed methods to estimate odds ratios when an exposure is measured on pools that are not matched on case status. We expanded on existing methods requiring matched pools and demonstrated the efficacy of our proposed analysis via a simulation study and an auxiliary study of the Collaborative Perinatal Project.

Pooling is an attractive design strategy to alleviate fiscal or practical limitations on analyzing individual level biospecimens while answering important research questions (Heffernan et al., 2014). Previous methods that focus on a primary outcome have been shown to be reliable and efficient when pools are matched based on this status (Weinberg and Umbach, 1999; Liu and Schisterman, 2003; Mumford et al., 2006; Saha-Chaudhuri et al., 2011; Whitcomb et al., 2012). The analytical procedures proposed here provide a reliable and effective method to alleviate the matched pool constraint and incorporate all pooled measurements, whether mixed or matched on outcome status, into calculation of gamma distribution parameters and constant or nonconstant OR estimates.

As illustrated in the simulation studies, the efficiency of the OR estimates of a secondary outcome will depend largely on the degree to which the pools are matched on the secondary outcome or the correlation with the primary outcome. Of course, OR estimates will generally gain efficiency when more assays are performed (n) relative to the total sample size (N). This potential precision gain is often limited, however, by budgetary constraints or other factors that initially motivated pooling on the primary outcome. Relying solely on matched pools also resulted in inflated Type I Error as prevalence of a secondary outcome decreased, while our mixed pool methodology performed nominally. As demonstrated in the data analysis, the proposed methods employing mixed pools was the only means to enable analysis of a secondary outcome because too few matched case pools were created to use either the existing approaches by Weinberg and Umbach (1999) or Whitcomb et al. (2012).

The gamma distributional assumption was the key in estimation of distribution parameters and the OR estimate when X is continuous and right-skewed in our developments. Additional distributions could have been assumed for X, such as a lognormal distribution, but subsequent analysis would be considerably more difficult for larger pool sizes (g > 2). The gamma distribution, in addition to enjoying much simpler computation, has previously been demonstrated to be effective at characterizing right-skewed variables (Firth, 1988; Whitcomb et al., 2012; Mitchell et al., 2015). For nonskewed continuous biomarkers where normality might be assumed on X, similar techniques can be adapted from the developments in Section 2. Another assumption of the strategies presented here is that the secondary outcome is conditionally independent of the primary outcome. Given the exposure of interest, a straightforward extension to the likelihood is provided in the Appendix that can help assess this assumption and facilitate additional analyses.

Regardless of motivation for the implementation of a pooling design, statistical techniques for pooled data must continually develop and attempt to mirror those for individual level data. As our example demonstrated, utilizing mixed pools, as a consequence of being a secondary outcome or otherwise, is vital to analysis of pooled data. The flexible framework of our extension of case-control methods to utilize the valuable information in pools of mixed outcome status is an important next step to the broader implementation of pooling designs in practice.

Appendix

Assume individual level biospecimens, X, are grouped into pools of size g based on the status of a primary binary outcome, O1, and then measured, Y. Then assume a known secondary outcome, O2, which may or may not be associated with O1 but was not considered in the creation of the pools. Let D₁ = j and D₂ = k be the disease status for O1 and O2, respectively, where j = 0,1, k = 0,1 and 1 and 0 indicating with and without the disease, respectively. Let the parameters governing the distribution of X given D₁ and D₂ be denoted by θ_jk. Also, let m₁ and m₂ be the number of individuals within a pool with diseases O1 and O2, respectively, noting that m₁ = 0 or g by design.

Under a Gamma distribution, the likelihood (similar to Eq. (7)), conditional on Y, m₁, and m₂, can now be written as:

$$l({\theta }_{11},{\theta }_{10},{\theta }_{01}.{\theta }_{00}|Y,m_1,m_2,g)={\displaystyle \sum _{i=1}^n\text{log}{f}_Y(g_i{Y}_i|{\alpha }_{j1},{\beta }_{j1},{\alpha }_{j0},{\beta }_{j0},m_{1i}=j,m_{2i})}={\displaystyle \sum _{i:m_{1i}=1}^n\text{log}{f}_Y(g_i{Y}_i|{\alpha }_{11},{\beta }_{11},{\alpha }_{10},{\beta }_{10},m_{2i})}+{\displaystyle \sum _{i:m_{1i}=0}^n\text{log}{f}_Y(g_i{Y}_i|{\alpha }_{01},{\beta }_{01},{\alpha }_{00},{\beta }_{00},m_{2i}),}$$ (A.1)

where log f_Y (g_iY_i|α₁₁, β₁₁, α₁₀, β₁₀, m_2i) is defined as in Eq. (7). Maximizing Eq. (A.1) yields MLEs for the shape and rate parameters θ = {α₁₁, β₁₁, ⋯, α₀₀, β₀₀} that characterize the four disease-specific distributions of the exposure. Once calculated, these MLEs can be applied to Eq. (5) in order to estimate the odds ratio for a given status for D₁ as follows:

$$OR(x|D_1=j)=\frac{f(x+1|D_1=j,D_2=1,{\theta }_{j1})/f(x|D_1=j,D_2=1,{\theta }_{j1})}{f(x+1|D_1=j,D_2=0,{\theta }_{j1})/f(x|D_1=j,D_2=0,{\theta }_{j1})}=\text{exp}\left\{{\beta }_{j0}-{\beta }_{j1}+\left({\alpha }_{j1}-{\alpha }_{j0}\right)\text{log}\left(\frac{x+1}{x}\right)\right\}.$$ (A.2)

Table A.1.

Relative bias and RMSE of log-odds ratio^a estimates evaluated from N = 400 individuals with exposures pooled in pairs, g = 2, matched on a primary outcome, O1, and pooled randomly on a secondary outcome, O2, at Q1 = 0.288 and Q3 = 1.39 of the healthy population^b.

a	d	α1	β1		Relative bias		RMSE
					With O1c	Without O1d	With O1c	Without O1d
0.7	0.7	1.5	0.5	logOR(Q1) = 1.249	0.026	0.018	0.352	0.306
				logOR(Q3) = 0.772	0.013	0.047	0.156	0.156
0.9	0.9	1.5	0.5	logOR(Q1) = 1.249	0.024	0.024	0.304	0.294
				logOR(Q3) = 0.772	0.015	0.040	0.132	0.135
0.2	0.9	1.5	0.5	logOR(Q1) = 1.249	0.080	0.077	0.521	0.473
				logOR(Q3) = 0.772	0.043	0.036	0.189	0.140

^alogOR(x) is the log-odds ratio of O2 based on change in exposure, x.

^bHealthy population assumed gamma distribution with α₀ = 1 and β₀ = 1 for all simulations.

^cEstimators based on Eq. (5), ignoring O1 and using information on O2.

^dEstimators based on Eq. (A.3), which uses information on O1.

To achieve the relation of interest, OR(x) for D₂ not conditioned on D₁, we simply sum over D₁

$$OR(x)=\frac{f(x+1|D_2=1,{\theta }_{11},{\theta }_{01})/f(x|D_2=1,{\theta }_{11},{\theta }_{01})}{f(x+1|D_2=0,{\theta }_{10},{\theta }_{00})/f(x|D_2=0,{\theta }_{10},{\theta }_{00})},$$ (A.3)

where

$$f(x|D_2=k,{\theta }_{1k},{\theta }_{0k})=f(x|D_1=1,D_2=k,{\theta }_{1k})\mathit{Prob}(D_1=1|D_2=k)+f(x|D_1=0,D_2=k,{\theta }_{0k})\mathit{Prob}(D_1=0|D_2=k).$$

While this formulation is not reducible in the way that resulted in Eq. (A.2), it is easy to calculate given parameter estimates and a cross tabulation of D₁ and D₂. Furthermore, note that if D₁ and D₂ are conditionally independent given X, then Eq. (A.2) reduces to Eq. (2) since

$$f(x|D_1=j,D_2=k)=\frac{\mathit{Prob}(D_1=j,D_2=k|x)f(x)}{\mathit{Prob}(D_1=j,D_2=k)}=\frac{\mathit{Prob}(D_1=j|x)\mathit{Prob}(D_2=k|x)f(x)}{\mathit{Prob}(D_1=j,D_2=k)}=\frac{f(x|D_1=j)\mathit{Prob}(D_1=j)f(x|D_2=k)\mathit{Prob}(D_2=k)}{\mathit{Prob}(D_1=j,D_2=k)f(x)}$$

and every component containing D₁ cancels. A brief simulation similar to that displayed in Table 2 demonstrates that estimating logOR(x) from Eq. (A.3) achieves similar relative bias (Table A1) to estimates from Eq. (5), which ignores O1 in the likelihood. Table A1 displays a simulated comparison of logOR(x) estimates for O2 from Eq. (A.3) (“with O1” column) and Eq. (5) (“without O1” column), corresponding to likelihoods which do and do not consider D₁ in the likelihood, respectively. Predictably, a loss of efficiency results from estimating the additional parameters in Eq. (A.1) versus Eq. (7).