New Predictive Equations for Serum Ionized Calcium in Hospitalized Patients

Abstract

Objective

To study a new and easy way to calculate equations to predict ionized calcium (Ca^2s+) for adult hospitalized patients with the usual laboratory and clinical parameters.

Subjects and Methods

This retrospective observational study was conducted in a third-level university hospital. An initial learning cohort (cohort L: 269 patients) was selected to derive the new equations. These equations were tested in a validation of another cohort (cohort V: 146 patients). Patients selected were hospitalized adults who had simultaneous determinations of Ca^2s+ and serum total calcium (CaTot). They were classified using their estimated glomerular filtration rate (GFRe) into normal function, moderate and severe kidney dysfunction. Demographic and biochemical parameters, in addition to comorbidities, were collected from hospital databases. Nine published equations to predict Ca^2s+ and 2 widely used equations to predict corrected CaTot were also selected to be compared to newer equations for accuracy in detecting serum calcium alterations. New equations were derived by a multiple linear-regression analysis from patients in cohort L.

Results

Three equations were derived containing the CaTot square root as the main independent variable. Equation 1: Ca^2s+ = 0.815 × CaTot^0.5. Equation 2: Ca^2s+ = 0.826 × CaTot^0.5 − 0.023 × renal function. Equation 3: Ca^2s+ = 0.813 × CaTot^0.5 − 0.006 × albumin^0.75 s+ 0.079. These equations performed better than published equations to predict Ca^2s+ when their error measures were analyzed in cohort V, even in special populations such as critically ill and very old patients.

Conclusions

Three new equations predicting Ca^2s+ were derived requiring easily available clinical and laboratory parameters. They could be valuable in predicting hypocalcemia but are of limited use in hypercalcemia.

Introduction

Calcium plays an essential role in many enzymes, membrane transporters and multiple physiological processes [1]. It is the most abundant mineral in the human body and mainly stored in the bones [2]. In serum, calcium exists in three forms: bound to proteins, predominantly albumin (40–50s%), forming complexes with anions such as citrate, lactate or phosphate (5–10s%), and in a free ionized form known as ionized calcium (Ca^2s+; 45–50s%) [2]. The Ca^2s+ is the biologically active form [3], and its measurement has been suggested as a reference test for calcium status [4,5,6,7]. However, serum total calcium (CaTot) determination is still the most used test in health centers [1,2] that needs subsequent correction by equations to obtain a ‘corrected calcium’ [1,2]. These equations are based on the fact that CaTot is lower in hypoalbuminemia than in normoalbuminemia, but being the calcium bound to albumin the only fraction decreased and not the Ca^2s+. ‘Corrected calcium’ equations try to deduce CaTot supposing normoalbuminemia. The Ca^2s+ test is viewed by many clinicians as neither practical due to technical reasons nor cost-effective for all patients [1,2], or, conversely, it is ordered excessively leading to increased costs [8]. Equations to predict Ca^2s+ could be an alternative when this value is not available, difficult to obtain or for deciding about further tests. However, predictive equations for Ca^2s+ have been considered complex, outdated and unadapted to patients, since many of them have been derived from laboratory tests or from a healthy population [1,2].

The objective of this study was to derive new equations to predict Ca^2s+ for adult hospitalized patients. These equations were intended to contain the usual laboratory or clinical parameters and to be easily calculable.

Subjects and Methods

Study Design and Setting

This was a retrospective observational study conducted in a third-level university hospital of 400 beds. The Clinical Research Ethics Committee of the institution approved the study.

Patients

An initial learning cohort (cohort L) was recruited to derive the equations (January 2007 to June 2008). It comprised 269 patients amongst 1,008 patients screened. Later, a validation cohort (cohort V) was recruited to test the new equations (December 2009 to December 2010). It comprised 146 patients amongst 877 patients screened.

During the two study periods, the computerized hospital records were screened for all patients admitted if they were adults (≥18 years old) and they had had a simultaneous blood determination of Ca^2s+ and CaTot. These initially selected patients were further screened for serum values of creatinine, sodium, potassium, phosphate, magnesium, total proteins (ProtTot), albumin (Alb) and glycemia obtained in a simultaneous blood drawing to the Ca^2s+ sample. Patients without these values were then excluded.

Laboratory Tests

Once obtained, venous blood samples were centrifuged and the supernatant serum separated. These serum samples were refrigerated to 0–4°C when determined immediately or they were frozen until delayed determination. Ca^2s+ was measured by ion selective electrode direct potentiometry and was adjusted for pH 7.4 by an analyzer-based equation (GEM Premier 3000, Instrumentation Laboratory-Werfen, Bedford, Mass., USA). CaTot was determined by automated spectrophotometry. The remaining parameters were determined by the usual automated laboratory techniques. All samples were analyzed by the same laboratory. The laboratory operates 24 h per day, 7 days per week. The majority of samples were processed within 2 h. When convenient, conventional units were converted to SI units.

Data Collected

Each patient contributed only with the first determination of Ca^2s+ during his/her admission. Normocalcemia was defined as a Ca^2s+ between 1.16 and 1.34 mmol/l. Lower values were considered as hypocalcemia and higher values as hypercalcemia. The CaTot normal range was 2.12–2.62 mmol/l. Additional data collected were department of admission, diagnosis and demographics. Patients were classified depending on their renal function (RF), estimated by the CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) equation [9] into normal function (estimated glomerular filtration rate, GFRe ≥60 ml/min/1.73 m²), moderate dysfunction (<60–30 ml/min/1.73 m²) and severe dysfunction (<30 ml/min/1.73 m²). Patients were also classified as hypoglycemic (glycemia <4.44 mmol/l), normoglycemic (4.44–6.11 mmol/l) and hyperglycemic (>6.11 mmol/l). Comorbidities affecting calcium metabolism were also recorded: acute and/or chronic kidney disease, heart failure, hypertension, diabetes, liver failure, chronic obstructive pulmonary disease, alcoholism, dyslipidemia, active neoplasm, hypo- or hyperthyroidism, hypo- or hyperparathyroidism, and bone diseases.

Published Calcium Predictive Equations

The medical literature was searched for predictive equations of Ca^2s+. Search results were limited to equations applied to adults, with variables easily obtainable, and not designed for specific diseases. Additional references were obtained screening the publications initially found. Widely used equations to calculate corrected CaTot were also selected to compare the accuracy in detecting calcium alterations. Ten equations were found that were used as comparators [10,11,12,13,14,15,16,17,18,19]. They are shown in table 1. For each patient in cohort V, predicted Ca^2s+ and corrected CaTot were calculated using all equations.

Table 1.

Published predictive equations for serum calcium

Equation	Year	Mathematical expression	Study characteristics	Ref.
General predictive equations for Ca2s+
McLean-Hastings	1935	Ca2s+ = CaTot − 0.122 × ProtTot − 0.006 s+ 0.5 × [(0.024 × CaTot) s+ (0.122 × ProtTot – CaTot s+ 0.006)2]0.5	In vitro model of frog heart; derived from an undetermined number of serum samples	10
Zeisler	1954	Ca2s+ = [(250.50 × CaTot) – (ProtTot × 0.375)]/[4.01 × ProtTot s+ 260.52]	Theoretical formula derived from McLean-Hastings nomogram; neither learning nor validation samples	11
Zeisler simplified	1954	Ca2s+ = [(240 × CaTot) – (ProtTot/3)]/[4 × ProtTot s+ 240]	Same as Zeisler equation	11
Hanna	1964	Ca2s+ = (118 × CaTot)/(118 s+ ProtTot)	Theoretical nomogram; derived partially from 100 patient samples; no validation cohort	12
Pottgen	1976	Ca2s+ = (721.5 × CaTot – K)/(120.24 × K s+ 721.5) K = (0.19 × ProtTot) s+ albumin	Corrected from Zeisler equation; derived from 44 inpatients; no validation cohort	13
Siggaard-Andersen	1983	Ca2s+ = 0.8333 × Ca2s+ calculated by the McLean-Hastings equation	Theoretical correction of McLean-Hastings equation; 24 undetermined samples to calculate accuracy	14
Butler	1984	Ca2s+ = 0.005 × albumin s+ 0.980	Derived from 111 inpatient s+ 48 normal-subject samples	19
Predictive equations for Ca2s+ in selected populations Forster	1985	For critically ill surgical patients: Ca2s+ = 0.225 s+ (0.55 × CaTot) – (0.007 × albumin)	Derived from 389 inpatient samples; no validation cohort	15
Pfitzenmeyer	2007	For patients of ≥80 years old: Ca2s+ = 0.592 − 0.00449 ProtTot s+ 0.410 × CaTot	Derived from 294 inpatient samples; validation cohort: 77 patient samples	16
General predictive equations for CaTot Payne	1973	CaAdj = CaTot − 0.025 × albumin s+ 1	Derived from 200 patient samples; no validation cohort	17
James	2008	CaAdj = CaTot s+ [0.012 × (39.9 – albumin)]	Derived from 4,613 outpatient samples; validation cohort: 1,538 outpatient samples	18

Equations were transformed to SI units when necessary. CaAdj = Adjusted total calcium.

Statistical Analysis

Patients with outlier values for Ca^2s+ were excluded. Quantitative variables were tested for normal distribution. Those without this condition were transformed by the box Cox transformation. Linear transformations were also applied to change a variable scale when considered appropriate. Serum variables, transformed when necessary, demographics, and comorbidities, as dichotomous variables, were tested initially as independent variables for univariate linear regression taking Ca^2s+ as the dependent variable. Independent variables resulting with a p value ≤0.15 were selected to perform a further multiple linear-regression analysis with a stepwise approach. Different sets of variables were manually selected to obtain the simplest equations. Reliability was measured by the intraclass concordance coefficient for a single measure. Values of s+1 denote perfect concordance, values of −1 perfect reverse concordance, and a value of zero absence. Accuracy was measured with mean error, mean absolute error, mean absolute percentage error and root mean square error. Agreement between equations in classifying calcemia as hypo-, hyper- or normocalcemia was measured by the weighted kappa coefficient for categorical variables. A kappa of 1 indicates perfect agreement, whereas a kappa of 0 indicates agreement by chance. Sensibility, specificity and likelihood ratios were calculated for detecting hypocalcemia. For a positive likelihood ratio, higher values indicate a larger increase in the change in probability of the disease. For a negative likelihood ratio, smaller values indicate a larger decrease in the change in probability of the disease. Comparisons of quantitative variables were performed by the Mann-Whitney U test and comparisons of qualitative variables by the Fisher exact test. The agreement between each predictive equation and the Ca^2s+ measured were plotted in a Bland-Altman plot. The limits of agreement for each comparison were set at an average difference ±1.96 SD of the difference.

Data were analyzed using IBM SPSS Statistics 19.0 (IBM Corporation, Armonk, N.Y., USA) and Microsoft Excel 2010 (Microsoft Corporation, Redmond, Wash., USA).

Results

Cohort L and cohort V differed in several parameters as shown in table 2. Cohort V included more males, presented worse GFRe and had more comorbidities. In contrast, it presented a lower neoplasm rate and less mortality. Admission departments differed also between cohorts. In cohort L, the range of Ca^2s+ was 0.78–1.56 mmol/l; 120 (44.6s%) patients were hypocalcemic and 26 (9.7s%) hypercalcemic. In cohort V, the range of Ca^2s+ was 0.59–1.60 mmol/l, and 87 (59.6s%) patients presented hypocalcemia and 7 (4.8s%) were hypercalcemic. Independent variables that initially entered the analysis were transformed age [log(100 – age)], sex, transformed CaTot (CaTot^0.5 or CaTot square root), ProtTot, transformed albumin (Alb^0.75 − 2.2), transformed creatinine (Creat^−0.87), sodium, transformed potassium (K^0.25), magnesium, phosphate, RF (normal function = 0; moderate dysfunction = 1; severe dysfunction = 2), glycemic status (hypoglycemia = −1; normoglycemia = 0; hyperglycemia = 1), and comorbidities shown in table 2.

Table 2.

Characteristics of cohorts L and V

	Cohort L	Cohort V	p value
Demographics
Patients, n	269	146
Age, years	71.0 [55.5 – 78.0]	70.0 [56.8 – 78.0]	0.889
Male/female sex	146/123 (54.3/45.7)	99/47 (67.8/32.2)	0.009
GFRea, ml/min/1.73 m2	60.5 [34.7 – 85.6]	38.3 [17.1 – 81.2]	<0.001
Ca2s+, mmol/l	1.18 [1.08 – 1.25]	1.13 [1.06 – 1.21]	0.003
CaTot, mmol/l	2.07 [1.87 – 2.27]	2.07 [1.92 – 2.20]	0.917
Type of patient medical/surgical/trauma	191/73/5 (71.0/27.1/1.9)	107/34/5 (73.3/23.3/3.4)	0.450
Critically ill patientsb	36 (13.4)	12 (8.2)	0.148
Comorbidities
Hypertension	151 (56.1)	106 (72.6)	0.001
Neoplasm	122 (45.4)	47 (32.2)	0.012
Acute renal impairment moderate/severe	75/56 (27.9/20.8)	33/66 (22.6/45.2)	<0.001
Diabetes mellitus	63 (23.4)	64 (43.8)	<0.001
Dyslipidemia	61 (22.7)	53 (36.3)	0.04
Chronic renal impairment	54 (20.1)	81 (55.5)	<0.001
Chronic liver disease	42 (15.6)	22 (15.1)	1.00
Chronic obstructive pulmonary disease	40 (14.9)	30 (20.5)	0.170
Chronic heart failure	33 (12.3)	26 (17.8)	0.141
Chronic alcoholism	26 (9.7)	16 (11.0)	0.734
Bone diseases	22 (8.2)	10 (6.8)	0.703
Hypothyroidism/hyperthyroidism	19/2 (7.1/0.7)	7/10 (4.8/6.8)	0.001
Hypoparathyroidism/hyperparathyroidism	1/25 (0.4/9.3)	32/7 (21.9/4.8)	<0.001
Initial department of admission
General surgery	53 (19.7)	17 (11.6)	0.040
Medical oncology	34 (12.6)	2 (1.4)	<0.001
Internal medicine	24 (8.9)	3 (2.1)	0.006
Nephrology	24 (8.9)	70 (47.9)	<0.001
Gastroenterology	18 (6.7)	10 (6.8)	1.000
Hematology	15 (5.6)	2 (1.4)	0.040
Intensive care unit	12 (4.5)	13 (8.9)	0.084
Other departments	89 (33.1)	29 (19.9)	–
Outcomes
Length of stay, days	18.0 [10.0 – 34.0]	16.0 [8.0 – 31.5]	0.204
Mortality	60 (22.3)	14 (9.6)	0.001

Values are expressed in medians with quartile 1 to quartile 3 in square brackets or alternatively in numbers with percentages in parentheses.

^aCalculated by the CKD-EPI 2009 equation.

^bAt the time of Ca^2s+ determination.

The univariate analysis found only 9 variables to affect Ca^2s+: transformed CaTot (F = 37,829.57, p < 0.001), ProtTot (F = 14.21, p < 0.001), transformed albumin (F = 10.27, p = 0.002), transformed potassium (F = 5.75, p = 0.018), RF (F = 3.74, p = 0.054), sodium (F = 3.07, p = 0.081), diabetes (F = 2.99, p = 0.085), transformed creatinine (F = 2.44, p = 0.119), and chronic obstructive pulmonary disease (F = 2.38, p = 0.124). The remaining variables were discarded for further analysis. In the multivariate analysis, several sets of variables had to be discarded for problems in multicollinearity, autocorrelation and independence. Diabetes and chronic obstructive pulmonary disease lost significance in all cases. Finally, 3 equations were selected to be tested in cohort V (units: Ca^2s+ in mmol/l, CaTot in mmol/l, Alb in g/l):

Equation 1: Ca^2s+ = 0.815 × CaTot^0.5

corrected R² = 0.993, F = 37,829.57, standard error of the estimate (SEE) = 0.395, p < 0.001

Equation 2: Ca^2s+ = 0.826 × CaTot^0.5 − 0.023 × RF

corrected R² = 0.993, F = 19,527.65, SEE = 0.389, p < 0.001

Equation 3: Ca^2s+ = 0.813 × CaTot^0.5 − 0.006 × Alb^0.75 s+ 0.079

corrected R² = 0.993, F = 16,073.40, SEE = 0.390, p < 0.001

The derived equations converted into conventional units were as follows (units: Ca^2s+ in mg/dl, CaTot in mg/l, Alb in g/dl):

Equation 1: Ca^2s+ = 1.629 × CaTot^0.5

Equation 2: Ca^2s+ = 1.651 × CaTot^0.5 − 0.093 × RF

Equation 3: Ca^2s+ = 1.631 × CaTot^0.5 − 0.144 × Alb^0.75 s+ 0.317

Table 3 presents the concordance and accuracy of the actual values of Ca^2s+ in cohort V with the predicted values for the new equations and for the published general equations. At the bottom of this table, values are shown for specific populations, critically ill or very old (≥80 years) patients.

Table 3.

Reliability and accuracy for the predictive equations

	ICC	ME, mmol/dl	MAPE, s%	MAE, mmol/dl	RMSE, mmol/dl
All patients
Equation 1	0.539 (0.373 to 0.663)	−0.04 (−0.05 to −0.02)	7.35 (6.17 to 8.53)	0.08 (0.07 to 0.09)	0.04 (0.03 to 0.06)
Equation 2	0.609 (0.480 to 0.709)	−0.03 (−0.04 to −0.01)	6.51 (5.43 to 7.59)	0.07 (0.06 to 0.08)	0.03 (0.02 to 0.05)
Equation 3	0.521 (0.347 to 0.651)	−0.04 (−0.06 to −0.02)	7.30 (6.10 to 8.50)	0.08 (0.07 to 0.09)	0.04 (0.03 to 0.06)
Published general predictive equations
McLean-Hastings	0.345 (−0.095 to 0.675)	−0.24 (−0.26 to −0.22)	21.72 (19.95 to 23.48)	0.24 (0.22 to 0.26)	0.30 (0.25 to 0.34)
Zeisler	0.496 (−0.070 to 0.766)	0.11 (0.10 to 0.13)	10.64 (9.61 to 11.68)	0.12 (0.11 to 0.13)	0.08 (0.07 to 0.10)
Zeisler simplified	0.506 (−0.051 to 0.766)	0.11 (0.09 to 0.12)	10.37 (9.33 to 11.41)	0.12 (0.11 to 0.13)	0.08 (0.07 to 0.10)
Hanna	0.264 (0.050 to 0.621)	−0.26 (−0.27 to −0.25)	23.65 (22.15 to 25.16)	0.26 (0.25 to 0.27)	0.30 (0.27 to 0.33)
Pottgen	0.508 (0.174 to 0.699)	−0.08 (−0.10 to −0.06)	9.67 (8.29 to 11.04)	0.11 (0.09 to 0.12)	0.08 (0.05 to 0.10)
Siggaard-Andersen	0.731 (0.646 to 0.799)	−0.01 (−0.03 to 0.01)	8.04 (7.04 to 9.04)	0.09 (0.08 to 0.10)	0.05 (0.04 to 0.06)
Butler	0.095 (−0.063 to 0.251)	0.02 (0 to 0.04)	8.48 (6.89 to 10.07)	0.09 (0.08 to 0.11)	0.06 (0.04 to 0.09)
Special populations
Critically ill patientsa
Equation 1	0.556 (0.054 to 0.844)	−0.04 (−0.08 to 0)	6.20 (3.91 to 8.50)	0.07 (0.04 to 0.09)	0.02 (0.01 to 0.04)
Equation 2	0.640 (0.16 to 0.879)	−0.03 (−0.07 to 0)	5.21 (2.79 to 7.63)	0.06 (0.03 to 0.08)	0.02 (0 to 0.04)
Equation 3	0.528 (−0.015 to 0.835)	−0.05 (−0.09 to −0.01)	6.44 (3.83 to 9.05)	0.07 (0.04 to 0.09)	0.03 (0.01 to 0.04)
Forster	0.623 (0.113 to 0.874)	−0.02 (−0.07 to 0.03)	8.73 (4.74 to 12.72)	0.07 (0.04 to 0.10)	0.03 (0.01 to 0.05)
Patients ≥80 years oldb
Equation 1	0.417 (0.008 to 0.699)	−0.06 (−0.08 to −0.03)	7.36 (5.43 to 9.30)	0.08 (0.06 to 0.10)	0.03 (0.02 to 0.05)
Equation 2	0.494 (0.108 to 0.743)	−0.04 (−0.07 to −0.02)	6.48 (4.75 to 8.21)	0.07 (0.05 to 0.08)	0.03 (0.01 to 0.04)
Equation 3	0.390 (−0.054 to 0.695)	−0.07 (−0.09 to −0.04)	7.81 (5.82 to 9.80)	0.08 (0.06 to 0.10)	0.04 (0.02 to 0.05)
Pfitzenmeyer	0.441 (−0.095 to 0.759)	−0.08 (−0.10 to −0.06)	5.94 (4.47 to 7.40)	0.09 (0.07 to 0.11)	0.04 (0.03 to 0.05)

ICC = Intraclass concordance coefficient, values of s+1 denote perfect concordance and 0 denotes absence of concordance; ME = mean error; MAPE = mean absolute percentage error; MAE = mean absolute error; RMSE = root mean square error, in all cases lower is better. 95s% CIs are given in parentheses.

^aFor 12 (8.2s%) critically ill patients.

^bFor 26 (17.8s%) patients ≥80 years old.

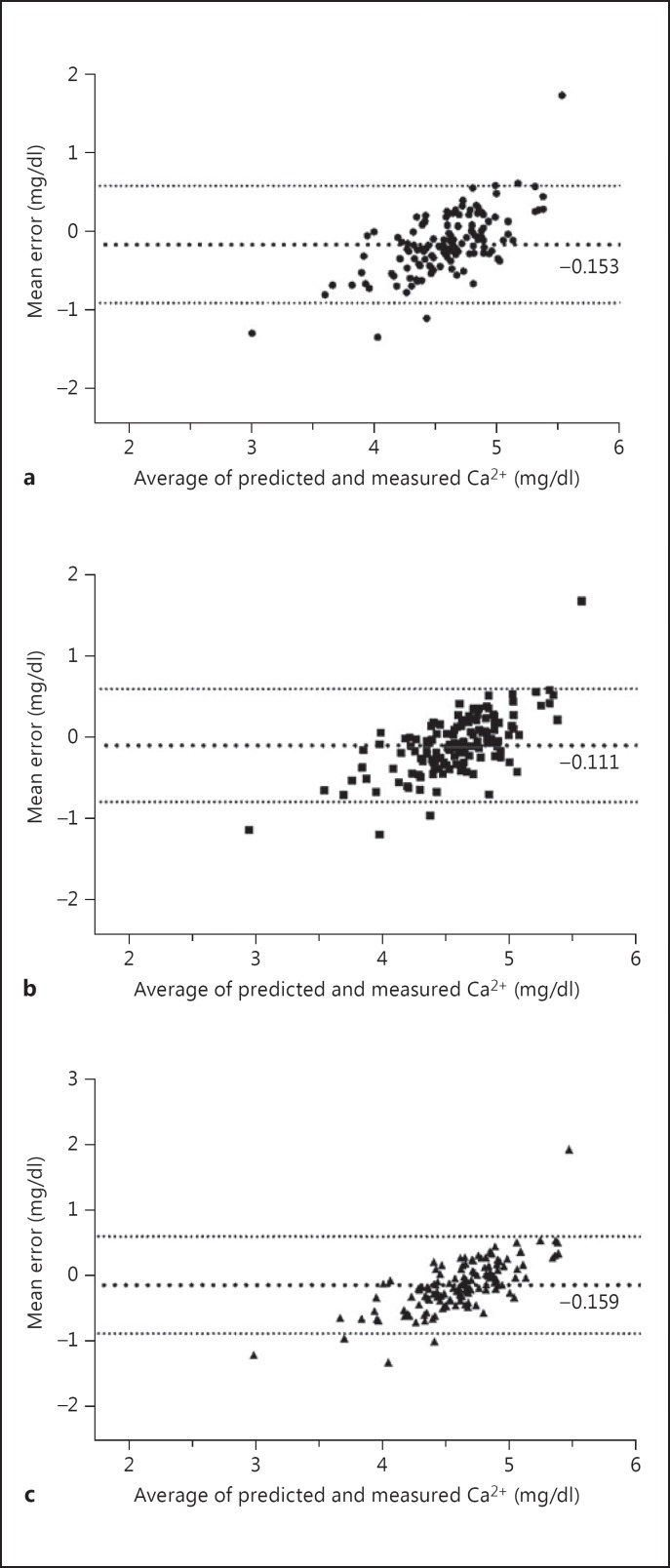
Figure 1 shows the Bland-Altman plots for equations 1, 2 and 3. The agreement on classification by calcemia status and the sensitivity, specificity and likelihood ratio for detection of hypocalcemia are presented in table 4. Values for hypercalcemia were not calculated since only 7 (4.8s%) patients presented it in cohort V.

Fig. 1.

Bland-Altman plots for equations 1 (a), 2 (b) and 3 (c).

Table 4.

Sensitivity, specificity and likelihood ratio for detecting hypocalcemia and agreement of equations to classify calcemia status

Equation	Sensitivity	Specificity	Positive likelihood ratio	Negative likelihood ratio	Agreementa	p value
Equation 1	0.564	0.797	2.780	0.547	0.303 (0.180 – 0.427)	<0.001
Equation 2	0.697	0.780	3.168	0.389	0.424 (0.296 – 0.551)	<0.001
Equation 3	0.552	0.831	3.266	0.539	0.310 (0.184 – 0.435)	<0.001
Published general predictive equations
McLean-Hastings	0.175	0.949	3.439	0.869	not calculableb	–
Zeisler	0.977	0.136	1.131	0.169	0.142 (0.030 – 0.254)	0.192
Zeisler simplified	0.977	0.153	1.153	0.150	0.176 (0.06 – 0.291)	0.046
Pottgen	0.423	0.831	2.503	0.694	0.290 (0.164 – 0.416)	<0.001
Siggaard-Andersen	0.683	0.661	2.014	0.480	0.387 (0.245 – 0.528)	<0.001
Hanna	0.089	1.000	–	0.911	not calculableb	–
Butler	1.000	0.051	1.054	0.000	0.071 (0.004 – 0.138)	0.035
General predictive equations for corrected calcium
Payne	0.259	0.949	5.074	0.781	0.247 (0.134 – 0.359)	<0.001
James	0.477	0.881	4.008	0.594	0.363 (0.236 – 0.489)	<0.001

Figures in parentheses are 95s% CI. The sensitivity value of 1 would denote perfect ability to detect hypocalcemia when hypocalcemia was present; the specificity value of 1 would denote perfect ability to exclude hypocalcemia when hypocalcemia was not present; a positive likelihood ratio value of <1 increases the probability that the equation confirmed hypocalcemia. Greater values increased the probability; a negative likelihood ratio value of <1 increases the probability that the equation discards hypocalcemia. Smaller values increased the probability.

^aWeighted kappa, a value of 1 denotes perfect agreement.

^bWeighted kappa smaller than mean chance concordance.

As equation 2 contained RF as a parameter, its concordance and accuracy were calculated for patients with renal dysfunction (GFRe <60 ml/min/1.73 m²): mean error −0.04 mmol/dl (95s% CI −0.05 to 0.02); mean absolute percentage error 6.41s% (95s% CI 5.00−7.82); mean absolute error 0.07 mmol/dl (95s% CI 0.05−0.08); root mean square error 0.03 mmol/dl (95s% CI 0.02−0.04). Evaluations for predicting hypocalcemia were sensitivity 0.736, specificity 0.811, positive likelihood ratio 3.895, negative likelihood ratio 0.325, agreement kappa 0.496 (95s% CI 0.245–0.807), p < 0.001.

Discussion

The new equations derived and validated in this study predicted better Ca^2s+, especially equation 2, than the equations published so far. They contained the usual clinical and laboratory parameters and could be easily calculated, especially equation 1. In addition, they predicted equally well as the published specific equations for critically ill or very old patients. The purpose of this study was not to obviate the determination of Ca^2s+ when necessary, but to obtain a reliable approximation when this parameter is not available. Ca^2s+ determination is not a routine test in several health settings [17,20], has increased costs concerning CaTot [8,21] and has technical difficulties in processing samples [20,22]. Ca^2s+ prediction is difficult. Blood calcium homeostasis depends on several factors such as blood proteins, pH, parathyroid hormone levels, calcitonin, 1,25-dihydroxyvitamin D status, intestinal calcium transport proteins, and the action of several organs and systems [2]. In addition, calcium complexes with several blood ligands such as albumin, globulin, bicarbonate, phosphate, lactate and citrate, and it is affected by the anion gap [23,24]. The variability of these fractions makes the accuracy of Ca^2s+ equations lower than equations predicting other biological parameters. Very accurate equations for Ca^2s+ should include many parameters, but this would be unpractical in a clinical setting.

In these new equations, the square root of CaTot was the main independent variable. This mathematical treatment differed from published equations that used the more intuitive CaTot plain value. The transformed albumin in equation 3 is more difficult to calculate. However, the exponent ³/₄ or 0.75· is one of the most frequent exponents found in allometric equations to predict numerous biological phenomena [25]. Albumin [13,15,16,18,19] and ProtTot [10,11,12,13,14,17] are found in several Ca^2s+-predicting equations. However, in this study, many equations containing them were discarded due to problems of multicollinearity and independence. In equation 2, RF classification was made using the CKD-EPI equation [9]. Other equations for estimating RF such as MDRD (modification of diet in renal disease) have not been tested, but they were not expected to change the accuracy in predicting. In another study, MDRD was highly correlated with the CKD-EPI equation [26].

The new equations tended to moderately overestimate Ca^2s+ as shown by the mean error in table 3. However, they were slightly more accurate than the Siggaard-Andersen equation [14], the most accurate amongst those published. This equation requires the initial calculation of the McLean-Hastings equation [10] and a further multiplication by a coefficient that represents a correction for complex-bound calcium. The need of an initial cumbersome calculation makes the Siggaard-Andersen equation less practical in a clinical setting.

The kappa coefficient is a statistic that takes into account the fact that predictors (equations in this case) will sometimes agree or disagree by chance in classifying the result of a test. It is more accurate than simple percent agreement calculation. In general, the agreement of published predictive equations is from slight to fair in detecting hypocalcemia (table 4). Equation 2 performed better than all of them and presented a moderate agreement. Considering specificity and sensitivity (table 4), again equation 2 performed better than the published predictive equations. The values of specificity and sensitivity found in this study were higher than those reported by Dickerson et al. [7], but patients in that study were critically ill trauma patients receiving specialized nutritional support. Performance in hypercalcemia could not be tested since few (<5s%) patients presented it in cohort V. Hypercalcemia is less frequent than hypocalcemia [17]. Prevalence of hypercalcemia has been reported in 0.7–8.8s% depending on numerous factors [5,7,15,27]. Thus, a learning cohort of around 1,000 patients with an additional validation cohort would be needed to derive an accurate predictive equation for hypercalcemia. Published equations have not an acceptable predictive power for hypercalcemia, and better equations are lacking [7].

This study had several limitations. It was retrospective, and the sample size is limited. Patients of special populations, with special conditions that alter calcium homeostasis or with hypercalcemia, have not been represented extensively. Obesity, which in some studies alters calcium homeostasis, was not evaluated as a possible variable. Also, they have not been tested in populations with alterations in calcium homeostasis, such as patients recently thyroidectomized or under renal replacement therapy.

Recently, Ca^2s+ adjusted for pH has been questioned as a good marker of calcium status [22]. However, this remains controversial due to possible technical artifacts [20,22] and the actual correlation with pH [28,29]. Ca^2s+ adjusted for pH is still recommended [30].

Conclusion

Three new equations requiring easily available clinical or laboratory parameters predicted Ca^2s+ better than the currently available equations. They could be valuable in predicting hypocalcemia but are of limited use in hypercalcemia. They could be useful as an initial approximate value for deciding further calcium tests or as an alternative when the adequate technology to determine Ca^2s+ is not available.

Disclosure Statement

There is no conflict of interest.