Glycemic Variability and Its Association With Demographics and Lifestyles in a General Adult Population

Abstract

Objective:

The objective was to investigate glycemic variability indices in relation to demographic factors and common environmental lifestyles in a general adult population.

Methods:

The A Estrada Glycation and Inflammation Study is a cross-sectional study covering 1516 participants selected by sampling of the population aged 18 years and over. A subsample of 622 individuals participated in the Glycation project, which included continuous glucose monitoring procedures. Five glycemic variability indices were analyzed, that is, SD, MAGE, MAG, CONGA1, and MODD.

Results:

Participants had a mean age of 48 years, 62% were females, and 12% had been previously diagnosed with diabetes. In the population without diabetes, index distributions were not normal but skewed to the right. Distributional regression models that adjusted for age, gender, BMI, alcohol intake, smoking status, and physical activity confirmed that all indices were positively and independently associated with fasting glucose levels and negatively with heavy drinking. SD, MAGE, and CONGA1 were positively associated with aging, and MAG was negatively associated with BMI. None of the GVI studied were influenced by physical activity. Age-group-specific reference values are given for the indices.

Conclusions:

This study yielded age-specific reference values for glucose variability indices in a general adult population. Significant increases were observed with aging. Heavy drinking of more than 140 g/week was associated with significant decreases in variability indices. No differences were found between males and females. These normative ranges provide a guide for clinical care, and may offer an alternative treatment target among persons with diabetes.

Glycemic variability (GV) is a physiologic phenomenon which refers to fluctuations in blood glucose (BG) levels over time. It can be described as within-day variability, with differences between fasting and postprandial BG values throughout a 24-hour period, and between-day variability.

GV is emerging as a measure of glycemic control, which may be a reliable predictor of complications. Results from a systematic literature review suggest that in type 2 diabetes, glucose variability is associated with development of microvascular complications.¹ Evidence is accumulating to indicate that high GV levels have deleterious effects beyond those of sustained chronic hyperglycemia, in terms of oxidative stress, diabetes complications, cardiovascular outcomes, and mortality,^2-7 though some contradictory reports also exist.^8,9

Determining the distribution of glycemic variability indices (GVI) in general populations is important for interpreting reference values. Almost all previously published data have come from patients with diabetes. Few studies into 24-hour BG profiles and glucose fluctuations have involved healthy subjects, and none have used subjects from a general population.^10-13 In addition, the standard guidelines for definition and determination of reference intervals note that partitioning should be considered in cases where there are significant differences among subgroups defined by age, sex, and common exposures such as smoking or alcohol consumption.¹⁴ Since the aim of treating diabetes is to restore glycemia to that of persons without diabetes, the generation of a metric of glycemic excursions should begin with an examination of the profiles of individuals without diabetes.¹⁵ It is also crucial to define the boundary beyond which GVI take on a pathological significance.¹⁶

Taken together, it is imperative to have valid comparative frameworks for the interpretation of individual values and population distributions of GVI. Hence, this adult population-based study investigated GVI levels in relation to demographic factors (age and sex) and common environmental lifestyles (physical activity, alcohol consumption, and smoking).

Methods

Study Design

The A Estrada Glycation and Inflammation Study (AEGIS) is a cross-sectional study which was performed in the municipality of A-Estrada, in Northwestern Spain. An age-stratified random sample of the population aged 18 years and older was drawn from Spain’s National Health System Registry.

Any subjects who could not provide written informed consent was deemed ineligible to participate in the study; this group included patients with dementia, mental retardation, cerebrovascular disease, terminal cancer, or inability to communicate.

A total of 1516 subjects agreed to participate in the study (overall participation rate, 68%), made up of 678 men (45%) and 838 women (55%). Participation was lower, not only among men (65%) versus women (71%), but also in the youngest and oldest age groups. There were no significant differences in terms of age or residence (rural/urban) between subjects who did and did not agree to participate in the study. From November 2012 through March 2015, all subjects were successively convened for 1 day at the Primary Care Center for evaluation, which comprised (1) an interviewer-administered structured questionnaire that included demographic and anthropometric data; (2) a lifestyle description, including physical exercise, alcohol consumption, and smoking; and (3) fasting venous blood sampling.

In addition, study participants were invited to participate in the glycation project, which included continuous glucose monitoring (CGM) procedures. Additional exclusion criteria in this group were inability to fulfill the protocol, eating out, allergy to adhesives, or any concomitant medical condition that would likely affect evaluation of the performance of a device. A total of 622 subjects consented to undergo a 6-day period of CGM. Study profiles are summarized in Figure 1.

Figure 1.

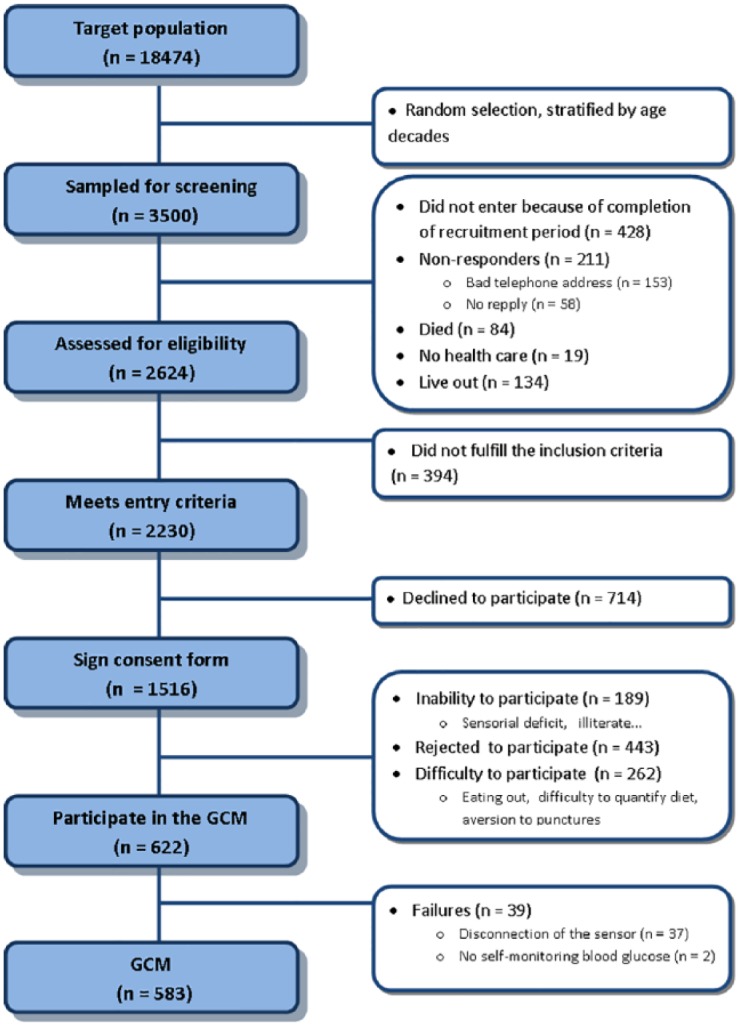
Study flowchart.

CGM Procedures

At the start of each monitoring period, a research nurse inserted a sensor (Enlite™, Medtronic, Inc, Northridge, CA, USA) subcutaneously into the abdomen, and instructed the participant in the use of the CGM device (iPro™, Medtronic, Inc, Northridge, CA, USA). This sensor measures subcutaneous tissue interstitial glucose levels continuously, recording values every 5 min, within a range of 40-400 mg/dL (2.2-22.2 mmol/L). Participants were provided with a conventional glucometer (OneTouch® Verio® Pro; LifeScan, Milpitas, CA, USA) as well as compatible lancets and test strips for calibrating the CGM. Subjects were asked to make at least 3 capillary BG measurements (usually before the main meals). The capillary BG readings were performed without checking the current CGM reading, and were also used for calibration of the iPro2 CGM system. On the 7th day the sensor was removed, and the data were downloaded and stored for further analysis. In any case where the number of data-acquisition “skips” per day totaled more than 2 hours, the entire day was discarded.

Of the 622 subjects enrolled in the study, 581 completed at least 2 days of monitoring. Forty-one subjects withdrew from the study due to noncompliance with protocol demands (n = 4), or difficulties in handling the device (n = 37). Itching was reported in 60 subjects and minor redness in 11. Swelling of the skin or bruises were never seen, and none of the patients reported pain at the sensor insertion site.

Classification of Alcohol Consumption and Smoking

Alcohol consumption was assessed using the standard drinking unit system,¹⁷ which sums the number of glasses of wine (~10g), bottles of beer (~10g), and units of spirits (~20g). Individuals with an habitual alcohol consumption of 1-140 g/week (n = 281, 48.4%) were considered light drinkers, and those with an alcohol consumption of >140 g/week (n = 71, 12.2%) were considered heavy drinkers: the remainder (n = 229, 39.4%), made up of alcohol abstainers and very occasional alcohol drinkers, were pooled and included in the same group.

Tobacco smoking was recorded as the number of cigarettes regularly consumed per day. Consumers of at least 1 cigarette per day were considered smokers, as were individuals who had quit smoking during the preceding year. Subjects were classified according to smoking status into the following 3 groups: (1) nonsmokers (n = 309, 53.2%), (2) ex-smokers (n = 154, 26.5%), and (3) current smokers (n = 110, 20.3%).

Physical Activity Assessment

Subjects completed the International Physical Activity Questionnaire (short form),¹⁸ from which we calculated metabolic equivalent of task and hours per week engaged in vigorous and moderate activities and walking, as described by Craig et al.¹⁹ We then classified them according to the 3 levels of physical activity: (1) “inactive” (n = 209, 36.0%), (2) “minimally active” (n = 223, 38.4%), and (3) “HEPA active” (health-enhancing physical activity; a high active category, n = 149, 25.6%).

Laboratory Determinations

The HbA1c was determined by high-performance liquid chromatography. All HbA1c values were converted to Diabetes Control and Complications Trial–aligned units.²⁰ Glucose was determined in fasting serum samples by the glucose oxidase peroxidase method.

Measures of Glycemic Variability

After downloading the recorded data, 4 GVI were analyzed, that is, standard deviation (SD),¹⁵ mean amplitude of glycemic excursions (MAGE),^15,21 mean absolute glucose (MAG) change per patient per hour,⁷ continuous overlapping net glycemic action at 1 h (CONGA1),²² and the mean of daily differences (MODD).²³ The mathematical formulae of the methods of assessment for glucose variability were taken from their original publications for inclusion in an R program, which is available free of charge for noncommercial use (Table 1).

Table 1.

Function in R to Extract Glycemic Variability Indices From csv Files.

# index(data, d, n)

# Arguments

# data is a database with covariates: id (identification), day (1, 2, 3, …), Glucose (mg/dl)

# d, time (in min) between two consecutive glucose measurements

# n, for CONGAn estimation (at 1, 2, … hours)

index <- function(data, d, n) {

glucosemg <- data$Glucose

day <- data$day

id <- unique(data$id)

glucose <- glucosemg/18

N <- length(glucose)

m <- length(table(day)) # number of monitoring days

Th <- 24*m # total time in hours

# number of observations in 1 hour

K <- dim(data[day = = 1, ])[1]

dat <- cbind(c(1:N), data)

colnames(dat)[1] <- “num” ; orden <- dat$num

sd <- tapply(dat$glucose, dat$day, sd) # SD for each day

IGV <- 120 # Ideal glucose value

MG <- mean(glucosemg)

SD <- sd(glucosemg)

CV <- 100*SD/MG

IQR <- IQR(glucosemg)

M <- mean(abs(10*log10(glucosemg/IGV))^3) +

(max(glucosemg)-min(glucosemg))/20 # M-value

J <- 0.001*(MG + SD)^2 # J-Index (mg/dl)

# J <- 0.324*(MG + SD)^2 # J-Index (mmol/l)

FG <- 1.509*((log(glucosemg))^1.084 - 5.381)

rl <- ifelse(FG < 0, 10*FG^2, 0)

rh <- ifelse(FG > 0, 10*FG^2, 0)

LBGI <- 1/N*sum(rl) # Low Blood Glucose Index

HBGI <- 1/N*sum(rh) # High Blood Glucose Index

LR = HR = NULL

for (i in 1:m) {

LR <- max(rl[day = = i])

HR <- max(rh[day = = i])

}

ADRR <- 1/m*sum(LR + HR) # Average Daily Risk Ratio

HYPO <- 100*mean((glucosemg < 70)) # Hypoglycaemia (%)

HYPER <- 100*mean((glucosemg > 140)) # Hyperglycaemia (%)

LI <- sum((glucose[1:N-1] - glucose[2:N])^2)/d # Lability Index

# Glycemia Risk Assessment Diabetes Equation Score

GRADE <- median(425*(log10(log10(glucose)) + 0.16)^2)

# Continuous Overall Glycemic Action

CONGA <- sd(glucose[(n+1):N] - glucose[1:(N-n)]

# Mean of Daily Differences

MODD <- sum(abs(glucose[(n+1):N] - glucose[(1+K):N])) / (K*m-1)

# Area under the curve

AUC <- (1/2*5*sum(glucosemg[1:N-1] + glucosemg[2:N])) / (m*24*60)

# Mean Amplitude of Glycemic Excursions

infl = maxi = mini = dif = downs = NULL

for (i in 2:(N - 1)) {

if ((glucosemg[i] - glucosemg[i - 1]) * (glucosemg[i + 1] - glucosemg[i]) < = 0) {

infl = c(infl, i)}

}

infl <- c(infl,N)

eps <- 8

n_infl <- length(infl)

for (j in 1:(n_infl)) {

I1 <- (infl[j] - eps):(infl[j] + eps)

I <- subset(I1, I1 < = max(infl) & 0 < I1)

if (max(glucosemg[I]) = = glucosemg[infl[j]] |

min(glucosemg[I]) = = glucosemg[infl[j]]) {

maxi = c(maxi, infl[j])

mini = c(mini, infl[j])

}

}

mm <- c(sort(c(maxi, mini)), infl[n_infl])

def <- ifelse(glucosemg[mm[1:(length(mm)-1)]] = = glucosemg[mm[2:length(mm)]],     NA, mm[1:length(mm)-1])

def <- c(subset(def, def ! = “NA”), infl[n_infl])

for (k in 1:m) {

ii <- day[def] = = k

deff = def[ii]

diff = NULL

for (j in 1:length(deff)) {

diff <- c(diff, glucosemg[deff[j]] - glucosemg[def[j + 1]])

}

downs <- c(downs, (subset(diff, diff > 0 & diff > sd(k)))

}

MAGE <- sum(downs)/length(downs)

values <- round(c(id, MG, SD, CV, IQR, M, AdM, J, LBGI, HBGI, ADRR,

HYPO, HYPER, LI, MAG, GRADE, MAGE, CONGA, MODD, AUC), 6)

return(values)

}

Ethical Considerations

The present study was reviewed and approved by the Clinical Research Ethics Committee from Galicia, Spain (CEIC2012-025). Written informed consent was obtained from each participant in the study, which conformed to the current Helsinki Declaration.

Statistical Analyses

The optimal GVI cut-off points for distinguishing subjects with and without diabetes were computed using the Youden J statistic.²⁴

Different distributions were fitted to the observed distribution of the different GVI, using Generalized Additive Models for Location Scale and Shape (GAMLSS).²⁵ GAMLSS allow for modeling, not only the mean response µ (ie, the location), but also other distribution parameters, such as standard deviation σ (ie, the scale) or skewness and kurtosis (ie, the shape parameters), as a function of a set of explanatory variables.

Goodness of fit was assessed by the Bayesian information criterion and Q-Q plots, to select the final model including the fitted distribution of GVI and the influence of covariates on the distribution parameters. Worm plots were used as a diagnostic tool to assess whether adjustment for kurtosis and/or skewness was required.²⁶

Percentile curves of GVI as a function of the covariate age were calculated on the basis of the GAMLSS regression models that displayed the best goodness of fit. To facilitate the clinical use of our percentile curve data, we defined cut points at the 90th, 95th, and 97.5th percentiles for GVI.

All statistical analyses were performed using the R statistical software environment (version 3.0.2; R Foundation, http://www.r-project.org) with the “gamlss” and “OptimalCutpoints” packages.

Results

Subject Characteristics

Participants had a mean age of 48 years (range 18 to 87), 62% were females and 70 (12%) had been previously diagnosed of diabetes. Among patients with diabetes, 69% took oral antidiabetics, 4% insulin alone, and 17% insulin plus oral drugs, and 10% were not taking insulin neither oral antidiabetics. Subjects with diabetes were older (61 ± 12 vs 46 ± 14 years; P < .001), contained a higher proportion of men (50% vs 36%; P < .001), and had a higher BMI (31.2 ± 5.1 vs 27.8 ± 5.1 kg/m²; P < .001) than those without diabetes. As expected, levels of fasting glucose and HbA1c were higher among subjects with diabetes than among those without diabetes (134 ± 35 vs 88 ± 11 mg/dL and 7.1 ± 1.2 vs 5.3 ± 0.3%, respectively).

Distribution of Glycemic Variability Indices in the Population

Figure 2 shows nonparametric kernel density estimates of the GVI distributions in populations with and without diabetes. GVIs were highly correlated, showing correlation coefficients that ranged from 0.74 (between MAG and MODD) to 0.96 (between SD and MAGE).

Figure 2.

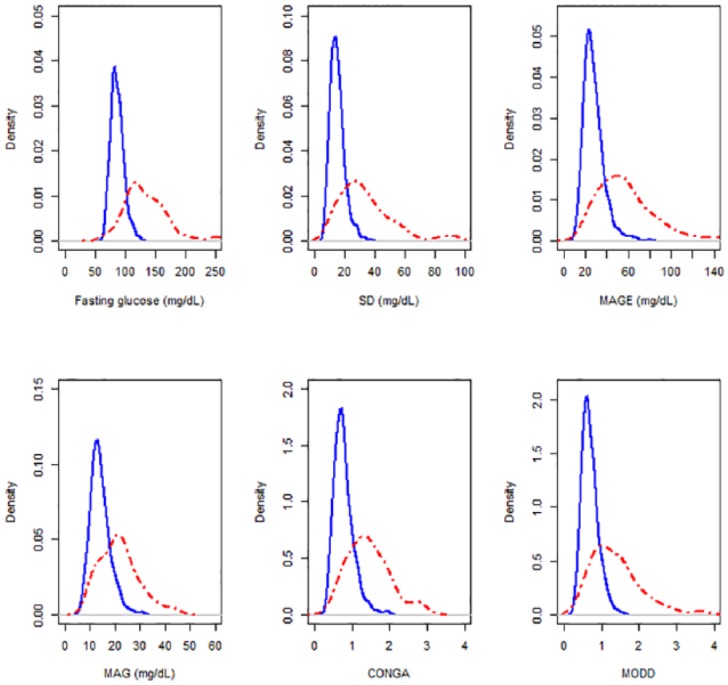
Univariate density distributions of fasting glucose and glycemic variability indices (fasting glucose, SD, MAGE, MAG, CONGA, and MODD) in subjects with diabetes (red lines) and without diabetes (blue dotted lines).

As expected, GVI were higher among subjects with diabetes than among those without diabetes. Table 2 also shows the distribution of cut-off values for all GVI, with their corresponding sensitivities, specificities and areas under the ROC curve (AUCs) for distinguishing between subjects with and without diabetes. All indices had a high discriminative ability for distinguishing individuals with and without diabetes, with values ranging from 0.80 to 0.89 for AUCs.

Table 2.

Glycemic Variability Indices in Individuals With and Without Diabetes, Cut-Off Levels (Youden Criterion) With Their Corresponding Sensitivity (Se), Specificity (Sp), and Area Under the ROC Curve for Distinguishing Individuals With and Without Diabetes.

	Nondiabetes	Diabetes	Optimal cut point	Se	Sp	Area under the ROC curve (95% CI)
SD, mg/dL	14 (9, 24)	30 (13, 87)	23	0.76	0.94	0.88 (0.83, 0.93)
MAGE, mg/dL	26 (16, 45)	55 (24, 144)	40	0.77	0.90	0.89 (0.85, 0.94)
MAG, mg/dL	14 (9, 22)	21 (11, 37)	19	0.64	0.90	0.80 (0.74, 0.87)
CONGA1	0.74 (0.45, 1.25)	1.38 (0.66, 2.71)	1.17	0.70	0.93	0.87 (0.82, 0.92)
MODD	0.67 (0.40, 1.11)	1.26 (0.54, 3.29)	0.93	0.74	0.86	0.87 (0.81, 0.92)

Data describing glycemic indices in subjects with and without diabetes are medians and 5th-95th percentile ranges (in brackets).

GVI distributions were not normal but skewed to the right (Figure 2). In the population without diabetes, the best fit in GAMLSS was obtained as follows: for SD and MAG, using the log-normal distribution with parameters log(μ) and log(σ) modeled linearly; for MAGE and CONGA1, using the reverse Gumbel distribution with parameters μ and log(σ) modeled linearly; and for MODD, using the inverse Gaussian distribution with parameters log(μ) and log(σ) modeled linearly.

Relation of Glycemic Variability Measures With Age, Gender, BMI, and Lifestyle in the Population Without Diabetes

The univariate distribution of GVI in the population without diabetes according to gender, age, BMI, smoking habit, alcohol consumption, and physical activity is shown in Table 3.

Table 3.

Glycemic Variability Indices (Univariate Analysis) in Relation to Age, Sex, Body Mass Index, and Lifestyle, in the Population Without Diabetes.

	n (%)	SD	MAGE	MAG	CONGA1	MODD
Age group (years)		[.002]	[.000]	[.429]	[.000]	[.291]
18-29	70 (14)	14 (8, 19)	23 (14, 40)	13 (8, 20)	0.68 (0.42, 1.13)	0.68 (0.42, 1.00)
30-39	101 (20)	15 (9, 23)	24 (17, 44)	13 (8, 22)	0.70 (0.44, 1.25)	0.65 (0.42, 1.08)
40-49	126 (24)	14 (9, 24)	26 (15, 45)	14 (8, 22)	0.74 (0.48, 1.29)	0.64 (0.39, 1.12)
50-59	102 (20)	15 (9, 23)	28 (17, 44)	14 (8, 22)	0.78 (0.43, 1.21)	0.68 (0.43, 1.15)
60 +	112 (22)	15 (9, 28)	28 (16, 49)	14 (9, 22)	0.80 (0.47, 1.44)	0.70 (0.38, 1.20)
Gender		[.359]	[.360]	[.701]	[.871]	[.969]
Female	326 (64)	15 (9, 26)	26 (17, 45)	14 (9, 22)	0.74 (0.46, 1.28)	0.66 (0.42, 1.13)
Male	185 (36)	15 (8, 23)	26 (15, 43)	14 (9, 22)	0.76 (0.44, 1.22)	0.67 (0.38, 1.09)
Body mass index		[.533]	[.429]	[.435]	[.451]	[.622]
Normal weight	159 (31)	15 (9, 23)	26 (16, 42)	14 (9, 21)	0.75 (0.44, 1.22)	0.66 (0.40, 1.08)
Overweight	194 (38)	15 (9, 25)	26 (16, 46)	13 (9, 22)	0.73 (0.44, 1.29)	0.66 (0.41, 1.12)
Obese	158 (31)	15 (9, 26)	26 (16, 49)	14 (9, 22)	0.76 (0.45, 1.33)	0.68 (0.39, 1.16)
Alcohol intake		[.052]	[.055]	[.058]	[.247]	[.086]
Abstainers	198 (39)	15 (9, 26)	27 (17, 43)	14 (9, 22)	0.74 (0.47, 1.21)	0.67 (0.44, 1.14)
Light drinkers	254 (50)	15 (9, 25)	26 (15, 48)	13 (9, 22)	0.74 (0.43, 1.32)	0.68 (0.42, 1.11)
Heavy drinkers	59 (11)	14 (8, 20)	25 (15, 40)	13 (8, 20)	0.75 (0.43, 1.03)	0.61 (0.37, 1.05)
Smoking		[.048]	[.198]	[.430]	[.209]	[.070]
Nonsmokers	271 (53)	15 (9, 26)	26 (16, 46)	14 (9, 22)	0.69 (0.44, 1.26)	0.69 (0.44, 1.17)
Ex-smokers	133 (26)	14 (8, 23)	26 (15, 45)	14 (8, 22)	0.74 (0.44, 1.32)	0.66 (0.37, 1.03)
Smokers	107 (21)	14 (9, 22)	25 (15, 41)	13 (9, 21)	0.72 (0.47, 1.14)	0.65 (0.38, 1.04)
Physical activity		[.292]	[.091]	[.292]	[.473]	[.551]
Inactive	183 (36)	15 (9, 26)	27 (17, 47)	14 (9, 22)	0.74 (0.46, 1.29)	0.67 (0.45, 1.17)
Minimally active	192 (37)	15 (9, 25)	27 (15, 46)	14 (9, 22)	0.74 (0.43, 1.23)	0.67 (0.40, 1.11)
HEPA active	136 (27)	14 (9, 23)	25 (15, 43)	14 (8, 21)	0.74 (0.43, 1.21)	0.67 (0.40, 1.11)

Data are medians and 5th-95th percentile ranges (in brackets), and P values [in square brackets]. Individuals with alcohol consumption of 1-140 g/week were considered light drinkers, and those with alcohol consumption > 140 g/week were considered heavy drinkers. Alcohol abstainers and very occasional alcohol drinkers were pooled in the same category. Normal weight, body mass index (BMI) < 25 kg/m²; overweight, BMI 25-30 kg/m²; obese, BMI > 30 kg/m². HEPA active, health enhancing physical activity, a high active category.

In the population without diabetes, no significant differences were found between men and women in any of the GVI. However, significant age-related differences were found in the SD, MAGE, and CONGA1 indices, though not in MAG and MODD.

Drinkers of more than 140 g/week had the lowest GVI when compared with other categories of alcohol consumption. Light drinkers had similar GVI to abstainers. Ex-smokers had the lowest SD levels when compared with other categories of tobacco consumption. No significant differences were found in any of the indices in terms of BMI or physical activity.

To further elucidate the influence of variables that might be associated both with BG levels and with GVI, a multivariate analysis was performed (See Table 4). Distributional regression models adjusted for age, gender, BMI, alcohol intake, smoking status, and physical activity confirmed that all indices were positively and independently associated with fasting glucose levels and negatively with heavy drinking. SD, MAGE, and CONGA1 were positively associated with aging, and MAG was negatively associated with BMI. None of the GVI studied were influenced by physical activity. Although MAG and MODD were not associated with age, age-specific reference values are given for all the studied indices (Table 5), and percentiles are shown in Figure 3.

Table 4.

Results of the Multivariate Distributional Analysis for Glycemic Variability Indices in Relation to Age, Sex, Body Mass Index, and Lifestyle, After Adjusting for Glucose Fasting Levels, in the Population Without Diabetes.

	SD	MAGE	MAG	CONGA1	MODD
	Coeff (SE) P value	Coeff (SE) P value	Coeff (SE) P value	Coeff (SE) P value	Coeff (SE) P value
Intercept	2.203 (0.117) .000	13.22 (2.844) .000	2.352 (0.106) .000	0.398 (0.097) .000	−0.840 (0.122) .000
Age, years	0.002 (0.001) .043	0.066 (0.026) .010	0.001 (0.001) .400	0.002 (0.001) .003	−0.001 (0.001) .518
BMI, kg/m2	0.001 (0.003) .685	−0.001 (0.074) .990	−0.006 (0.003) .017	−0.004 (0.002) .096	0.004 (0.003) .187
Gender (1. Men)	−0.008 (0.029) .779	−0.115 (0.741) .877	0.032 (0.027) .227	0.010 (0.021) .651	0.007 (0.030) .819
Smoking
Nonsmoker	Reference	Reference	Reference	Reference	Reference
Ex-smoker	−0.058 (0.031) .061	−0.721 (0.751) .337	−0.017 (0.028) .551	0.010 (0.021) .943	−0.088 (0.031) .005
Smoker	−0.011 (0.034) .739	−0.076 (0.836) .926	0.005 (0.031) .878	0.002 (0.023) .143	−0.014 (0.035) .679
Alcohol consumption
Abstainer	Reference	Reference	Reference	Reference	Reference
Light drinker	−0.031 (0.430) .283	−1.098 (0.698) .116	−0.038 (0.026) .144	−0.029 (0.019) .143	−0.002 (0.029) .949
Heavy drinker	−0.151 (0.047) .001	−2.944 (1.166) .012	−0.144 (0.043) .001	−0.081 (0.033) .014	−0.133 (0.047) .005
Physical activity
Inactive	Reference	Reference	Reference	Reference	Reference
Minimally active	−0.028 (0.030) .339	−0.771 (0.717) .283	−0.014 (0.027) .599	−0.022 (0.020) .264	−0.032 (0.030) .287
HEPA active	−0.031 (0.033) .356	−0.737 (0.804) .359	−0.016 (0.030) .605	−0.007 (0.023) .747	−0.029 (0.034) .400
Glucose, mg/dL	0.005 (0.001)a 0.000	0.107 (0.035)a 0.003	0.005 (0.001)a 0.000	0.004 (0.001)a 0.008	0.005 (0.001)a 0.000
Sigma intercept (log)	−1.252 (0.031) .000	1.921 (0.035) .000	−1.349 (0.031) .000	−1.658 (0.054) .000	−1.248 (0.049) .000
Mu link	Log	Identity	Log	Identity	Log
Distribution type	Log normal	Reverse Gumbel	Log normal	Reverse Gumbel	Inverse Gaussian

^aSplines used for parameter estimation.

Table 5.

Suggested Cut-Points for Glycemic Variability Indices Based on the Average Predicted Value Within Each Age Group and 90th, 95th, and 97.5th Percentiles.

Age, years			SD			MAGE		MAG			CONGA1			MODD
	90	95	97.5	90	95	97.5	90	95	97.5	90	95	97.5	90	95	97.5
20	20	22	25	37	42	49	19	21	22	1.05	1.20	1.38	0.95	1.05	1.20
25	20	22	25	38	42	49	19	21	22	1.06	1.21	1.39	0.96	1.06	1.21
30	20	23	26	38	43	50	19	21	23	1.08	1.23	1.40	0.97	1.07	1.21
35	21	23	26	39	43	50	19	21	23	1.09	1.24	1.41	0.97	1.08	1.22
40	21	23	27	39	44	51	19	21	23	1.10	1.25	1.42	0.98	1.09	1.23
45	21	23	27	40	44	51	19	21	23	1.11	1.26	1.44	0.99	1.10	1.24
50	22	24	27	40	45	52	19	21	23	1.12	1.27	1.45	0.99	1.11	1.25
55	22	24	28	40	45	52	19	21	23	1.14	1.29	1.46	1.00	1.11	1.26
60	23	25	28	41	46	53	20	22	24	1.15	1.30	1.47	1.01	1.12	1.27
65	23	25	29	41	46	53	20	22	24	1.16	1.31	1.49	1.01	1.13	1.28
70	23	26	29	42	47	53	20	22	24	1.17	1.32	1.50	1.02	1.14	1.29
75	24	26	30	42	47	54	20	22	24	1.19	1.33	1.51	1.03	1.15	1.30
80	24	26	31	43	48	54	20	22	24	1.20	1.35	1.52	1.04	1.16	1.31

Figure 3.

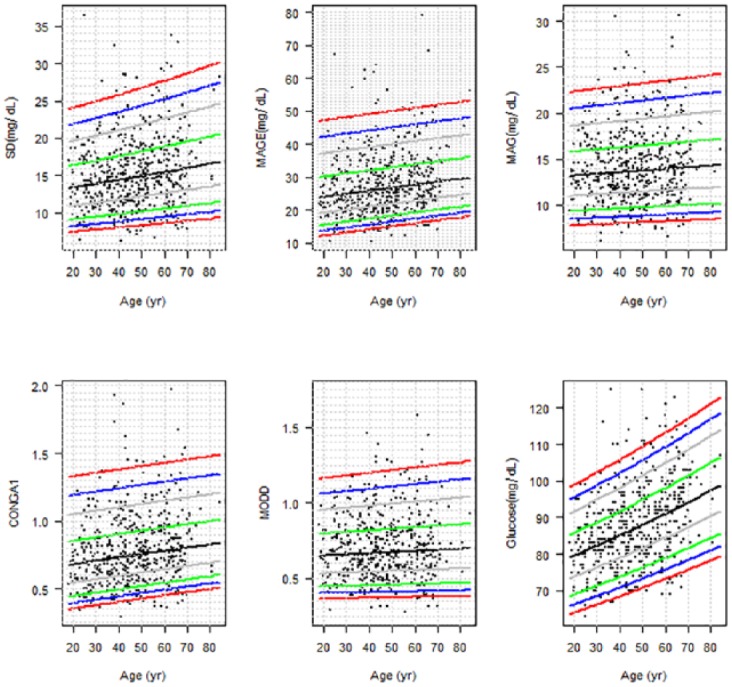
Percentile curves (2.5, 5, 10, 25, 50, 75, 90, 95, 97.5) for glycemic variability indices (SD, MAGE, MAG, CONGA1, and MODD) and fasting glucose levels in the population without diabetes.

Discussion

This article reports age-specific reference values for glucose variability indices drawn from a general adult population aged 18-90 years. According to our results, while GVI showed significant increases with aging and significant decreases in heavy drinkers of more than 140 g/week, no differences were found between males and females. These results show that age- and alcohol-related changes in GVI are independent of potential confounders, such as levels of fasting glucose, BMI, smoking, and physical activity.

As expected, GVI were also found to differ significantly between individuals with and without diabetes. In the population without diabetes, 90th percentile values for GVI were very close to the optimal cut-off points obtained by using the Youden criterion for discriminating between individuals with and without diabetes. AUCs registered values above 0.8, thus showing that GVI could be useful tools for distinguishing between subjects with and without diabetes.

Most studies investigating reference values for glucose variability have been conducted on patients with diabetes, with few having addressed healthy subjects, and none -at least to our knowledge- having addressed a representative sample of the general population. In the largest study published to date, which involved 434 healthy volunteers, Zhou et al found that SD and MAGE were non-normally distributed within the population and tended to increase with age, and that neither SD nor MAGE showed a significant difference between men and women.¹⁰ Median values for both parameters were 0.75 mmol/L (14 mg/dL) and 1.73 mmol/L (31 mg/dL),¹¹ similar to those obtained by us (SD 15 mg/dL, MAGE 26 mg/dL) and by the study conducted by the Juvenile Diabetes Research Foundation on 74 healthy individuals without diabetes (SD 14 mg/dL, MAGE 28 mg/dL).¹² In the latter, however, measures of glucose variability were not influenced by age. Similar results were also reported by Hill et al for MAGE but not for SD, in a study undertaken on adult subjects without diabetes in different ethnic groups.¹³ Unlike Zhou et al, who recommend a unified cut-off point for the normal reference values of the CGM parameters without differentiation by age or sex,¹⁰ our study indicates cut-off points that vary with aging.

Different indices have been proposed for assessing GV, and no consensus has yet been reached as regards which are clinically most useful. An US expert panel of diabetes specialists met in 2012 to discuss recommendations for standardization of analysis and presentation of glucose monitoring data. The majority (69%) of panel members indicated that SD was the most widely used and understood metric for assessing and reporting GV.²⁷

In addition to SD, MAGE is a popular metric to quantify glucose variability.^1,9-11,15 MAGE has been criticized on a number of grounds: (1) the qualifying limit of 1 SD is arbitrary; (2) its calculation is operator-dependent when a graphical approach is used; and (3) only the ascending or descending limb is used for its calculation.²⁸ Another criticism of MAGE found is its high correlation with SD, in this study 0.96. To exclude operator-dependent influences, we developed a computer software program for calculating MAGE values, based on the criterion that descending glucose excursions exceed 1 SD of the arithmetic mean of 24-hour periods. However, in a study evaluating software programs for the calculation of MAGE, Sechterberger et al found varying agreement among 4 available programs when applied to the same set of continuous glucose monitoring (CGM) traces, which would add other limitation to the previously reported.²⁹ CONGA was the first GV metric to be specifically designed for CGM data.²² As CONGA does not require arbitrarily defined glucose cut-offs or changes in glucose levels, this approach provides a more objective assessment of GV over short time intervals. The absolute mean of daily differences (MODD) was developed to evaluate interday variability;²³ this approach calculates the mean absolute value of the differences between glucose values on 2 consecutive days at the same time. However, the timing of meals can greatly affect MODD scores, making a strict dietary regimen essential for accurate monitoring.

As in the case of populations with diabetes, GVI are not symmetrically distributed: the larger values are further away from the mean than the smaller values, which means that the normal distribution might not be appropriate to fit GV data. Percentile curves were calculated using the so-called GAMLSS, developed by Rigby and Stasinopoulos.²⁵ This method is an extension of the least mean squares method for modeling age-dependent GVI distribution, while accounting for the dispersion, kurtosis and, in particular, skewness of this distribution.

An interesting finding of our study is that, in free living conditions, consumers without diabetes of more than 140 g of alcohol per week showed lower GVI than did abstainers without diabetes and light drinkers. Alcohol consumption is a recognized risk factor for hypoglycemia in individuals with type 1 diabetes,³⁰ and a recent meta-analysis showed that moderate alcohol consumption decreased fasting insulin concentrations among subjects without diabetes.³¹

Physical activity is widely recognized as an important component of a healthy lifestyle. In the present study, physical activity showed no association with any GVI. In a clinical trial on patients with type 1 diabetes, Kapitza et al³² found no differences in the glucose profiles with respect to the exercise challenge and some studies have shown that subjects with normal glucose tolerance do not improve insulin sensitivity, glucose regulation, or insulin release in response to exercise interventions.³³

Our study has several limitations. First, the fact that these curves were derived from a cross-sectional study means that they provide accurate GV values in a European population but no information about the evolution of GV over time. Second, at the present time, the reference value database does not contain outcome data. Whether the reference values should be used as cut-off values for treatment remains to be discussed. Prospective studies and clinical trials are needed to determine whether percentile-based GVI have a role in identifying patients at higher risk of developing cardiovascular complications. Taken together with the long time span of recruitment, this could increase the scattering of the reference values provided; on the other hand, however, it also improves the external validity of our results.

Conclusions

These age-specific reference values for GVI may well serve as an orientation of glucose variability values in adult populations without diabetes in the context of standard medical practice.