Abstract
The rate of photosynthesis depends on the CO2 partial pressure near Rubisco, Cc, which is commonly calculated by models using the overall mesophyll resistance. Such models do not explain the difference between the CO2 level in the intercellular air space and Cc mechanistically. This problem can be overcome by reaction-diffusion models for CO2 transport, production and fixation in leaves. However, most reaction-diffusion models are complex and unattractive for procedures that require a large number of runs, like parameter optimisation. This study provides a simpler reaction-diffusion model. It is parameterized by both leaf physiological and leaf anatomical data. The anatomical data consisted of the thickness of the cell wall, cytosol and stroma, and the area ratios of mesophyll exposed to the intercellular air space to leaf surfaces and exposed chloroplast to exposed mesophyll surfaces. The model was used directly to estimate photosynthetic parameters from a subset of the measured light and CO2 response curves; the remaining data were used for validation. The model predicted light and CO2 response curves reasonably well for 15 days old tomato (cv. Admiro) leaves, if (photo)respiratory CO2 release was assumed to take place in the inner cytosol or in the gaps between the chloroplasts. The model was also used to calculate the fraction of CO2 produced by (photo)respiration that is re-assimilated in the stroma, and this fraction ranged from 56 to 76%. In future research, the model should be further validated to better understand how the re-assimilation of (photo)respired CO2 is affected by environmental conditions and physiological parameters.
Introduction
The mesophyll of C3 plants can substantially constrain CO2 transport from the intercellular air space to Rubisco[1–4]. This results in a significant drawdown between the CO2 partial pressures in the intercellular air space (Ci) and near the binding sites of Rubisco (Cc) where CO2 is fixed. Cc is an input variable for the widely used Farquhar-von Caemmerer-Berry model [5] (abbreviated as “FvCB model”) that is used to predict the net rate of CO2 assimilation (AN) of a leaf. In order to calculate Cc, the mesophyll resistance (rm) to CO2 transport is commonly introduced as:
| (1) |
Fig 1A shows a schematic representation of this model. This approach has several limitations though. rm, or its inverse (mesophyll conductance gm), in Eq (1) needs to be estimated by one of the various gas exchange-based methods described in literature (see [6] and [7] for reviews). It has been shown that the mesophyll resistance is not constant, but possibly varies with light and CO2 levels [8], although there is also proof that part of the variation in rm with light and CO2 levels could be caused by measurement errors and statistical artefacts [9,10]. One way to incorporate this variability in Eq (1) is to use a Leuning-type phenomenological model [11] that describes the relation between Cc and gm [12,13]. However, this approach does not provide a mechanistic explanation for the variability of rm with light and CO2 levels.
Fig 1. Schematic representation for the different types of models for the resistance of CO2 transport in the mesophyll.
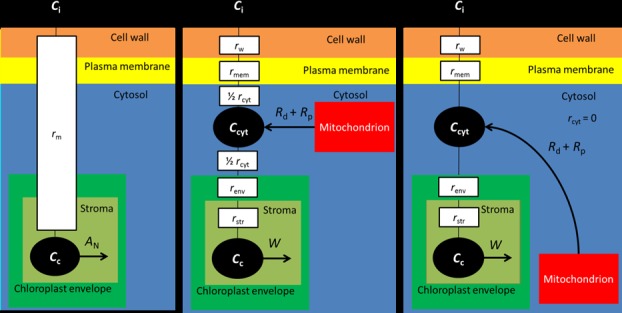
The Ci, Ccyt and Cc represent the CO2 partial pressure in the intercellular air space, the cytosol and the CO2 binding cites of Rubisco in the chloroplast stroma, respectively. In the model in Panel A), all structural barriers of the mesophyll for CO2 transport are lumped in a single resistance, called mesophyll resistance rm. The intracellular sinks and sources for CO2 are assumed to be at the same location, i.e. in the chloroplast stroma. The net flux of CO2 from the chloroplast stroma equals the net CO2 assimilation rate AN. In the model in Panel B) an additional cytosol compartment is added. The resistance components for CO2 transport between the air spaces and this compartment is the sum of resistances of the of the cell wall (rw), of the plasma membrane (rmem) and half the resistance of the cytosol (rcyt). The resistance components for CO2 transport between the cytosol compartment and Rubisco consists of the resistance of the chloroplast envelope (renv) and the CO2 diffusion path in the stroma (rstr). The rate of carboxylation by Rubisco (W) in the chloroplast stroma is the sink for CO2. The intracellular sources of CO2 are the rate of respiration in the light (Rd) and the rate of photorespiration (Rp). Both sources are located in the cytosol. This model places the source for CO2 between two cytosol resistance components and can, therefore, only be used to study C3 leaf photosynthesis if the mitochondrion are located in the outer cytosol layer. The model in Panel c) is largely similar to the model in Panel C), with the exception that the resistance of the cytosol is negligible. Consequently, the CO2 partial pressure is equal in any part of the cytosol and Ccyt is not affected by the location of the mitochondrion relative to the chloroplast. Therefore, this model cannot be used to study how the position of the mitochondria relative to the chloroplast affects C3 leaf photosynthesis.
Recently, a mathematical resistance-model framework [14] was presented to allow for the fact that CO2 fixation takes place in chloroplasts whereas respiratory and photorespiratory CO2 (hereafter, (photo)respired CO2) is released in mitochondria that are in the cytosol. Using this framework, the variability of rm with CO2 levels is shown to be at least partly explained by the difference in the diffusion pathway between the (photo)respired CO2 and the CO2 coming from the intercellular air space [15]. This model assumes that CO2 production by (photo)respiration takes place in a cytosol compartment between the plasma membrane and the chloroplast envelope and that there is CO2 influx from the intercellular air space into this compartment[15]. This implies that CO2 from the intercellular air space and CO2 produced by (photo)respiration share the diffusion pathway from the cytosol to Rubisco, where CO2 is fixed. However, the shared diffusion pathway of these two sources of CO2 can only occur if one of the following two conditions is met [7,16]. The first condition is that all mitochondria are located between the plasma membrane and the chloroplasts (instead of between the tonoplast and the chloroplasts), as is done in [17] (schematically drawn in Fig 1B). The second condition is that CO2 in the cytosol is completely mixed as is done in the model described in [14] (schematically Fig 1C). The authors of this model [18] commented on their earlier framework [14] that this latter assumption was made by surmising that the cytosol has a negligible resistance for CO2 transport. Complete mixture of CO2 from the atmosphere and CO2 produced by (photo)respiration implies that CO2 diffusion in the cytosol is much faster than that in the combined cell wall and plasma membrane and in the chloroplast. Physically, this means that under these assumptions the location of mitochondria does not affect Cc and that this framework cannot be used to investigate the effect of the placement of mitochondria. However, the position of mitochondria relative to the chloroplast may affect net CO2 assimilation rate. If most of the (photo)respired CO2 is produced between the chloroplast envelope and the tonoplast, the released CO2 will likely be re-assimilated. This is especially the case when the space between the chloroplasts is small[19,20]. The exposed mesophyll surface that is not covered by chloroplasts may provide a pathway for CO2 to escape to the intercellular air space. Overall, it is difficult to mechanistically explain and simulate the variation in rm with different light and CO2 levels, using a resistance-model approach.
In order to deal with most of the limitations of the concept of mesophyll resistance and to study the influence of several leaf structural and biochemical properties on leaf photosynthesis separately, reaction-diffusion models of a leaf have been produced. In one of the earliest studies, a leaf was modelled as a porous volume. Within this volume, CO2 transport and assimilation were simulated [21]. In later studies, the leaf structure was modelled more explicitly to study the effect of stomatal opening state and pore size, gradients of CO2 in the intercellular air space [22–24], and the effect of temperature dependency of carbon anhydrase activity, CO2 solubility and diffusion-related related parameters [23,25,26] on CO2 assimilation. A limitation of these models is that they assume that (photo)respiration and CO2 assimilation take place in the same compartments. More recent reaction-diffusion models [27,28] describe the structure in more detail in order to compartmentalize these processes, allowing mechanistic modelling of the contribution of (photo)respired CO2 to the calculated mesophyll resistance. There has also been a resistance model that tried to achieve this [17]. This model calculated the resistance of each mesophyll component by dividing the length of the diffusion path of these components by their diffusion coefficient as described in [29]. These lengths can be determined as the thickness of the compartment in the cases of the cell wall and the cytosol. However, this cannot be done to quantify the diffusion pathway length in the stroma, as CO2 is consumed along its diffusion path in the stroma. Therefore, the average diffusion path of a CO2 molecule in the stroma is shorter than the stroma thickness. This issue can be tackled by calculating the diffusion path length as the product of the stroma thickness and a fixed fraction, as previously described in [29]. However, the value of this fixed fraction is unknown and sensitivity analyses showed that the net CO2 assimilation rate calculated by this type of model is very sensitive to this parameter[17]. Compared with resistance models [17,29,30] that use anatomical properties to calculate rm and Cc, reaction-diffusion models do not require a predefined diffusion distance in the chloroplasts.
Recently, a 3-D reaction-diffusion model for CO2 and HCO3- transport was implemented into a detailed representation of a single mesophyll cell[27]. Another recent model [28] also described CO2 and HCO3- transport, but incorporated the geometry of leaf tissue based on synchrotron computed laminography images. The complexity of these computational domains has consequences. The model in [27] describes a very detailed cell microstructure. Therefore, it may become computationally expensive if a whole mesophyll tissue sample is modelled in this way. The computationally expensive models are unattractive to use for procedures that require a large number of model runs, like optimization or parameter estimation. When running this model (assuming a constant light absorption throughout the leaf) to simulate a CO2 response curve on a personal computer (Processor Intel(R) Xeon CPU W3550 @ 3.07 GHz 3.06 GHz, Installed memory: 24 GB RAM), it took us about 9 hours to simulate a single point in a CO2 response curve and several days to simulate the whole curve. Although this can be speeded up by the use of parallel computing, it still takes several hours before the simulation of a single curve is completed. Also, the 3-D leaf geometry in [28] is a direct reconstruction of a whole leaf section, which makes it impossible to change the structure of mesophyll cells for sensitivity analyses.
In the current study, we present a simple 2-D microstructural model of a leaf, in which CO2 transport, CO2 production by (photo)respiration, and CO2 consumption by carboxylation are modelled. The mesophyll microstructures in the model are very simple and flexible. This makes the model easy to apply to a wide range of C3 species within a reasonable computational time. The model will be parameterized from simultaneously measured data for gas exchange and chlorophyll fluorescence. We will demonstrate that the model can contribute to the understanding of how the position of the sites of mitochondria relative to the chloroplast stroma affects the re-assimilation of CO2 produced by (photo)respiration, and thus, the net rate of CO2 assimilation.
Results
Overall description of the model
The model consists of two main parts: a description of the geometry of the computational domain and a mathematical formulation, in the form of partial differential equations and boundary conditions, of the processes that are simulated within this geometry.
The computational domain consists of a rectangular section (Fig 2). This section contains a single rectangular chloroplast surrounded by a layer of cytosol. CO2 enters the domain by diffusing through the cell wall and plasma membrane into the outer cytosol. From there, it diffuses through the double-layered chloroplast membrane into the stroma. Part of the CO2 may diffuse through cytosol gaps between the chloroplasts and enter the inner cytosol. CO2 may be produced through (photo)respiration in the outer cytosol, or the inner cytosol or the cytosol gaps between the chloroplasts, depending on where mitochondria are located. (Photo)respired CO2 either escapes towards the intercellular space, or diffuses back into the chloroplasts, being re-assimilated. The construction and the parameterization of the computational domain (Fig 2) are described in S1 Text and S2 Text, respectively.
Fig 2. Schematic drawing of the computational domain and its position relative to the intercellular air space and the vacuole.
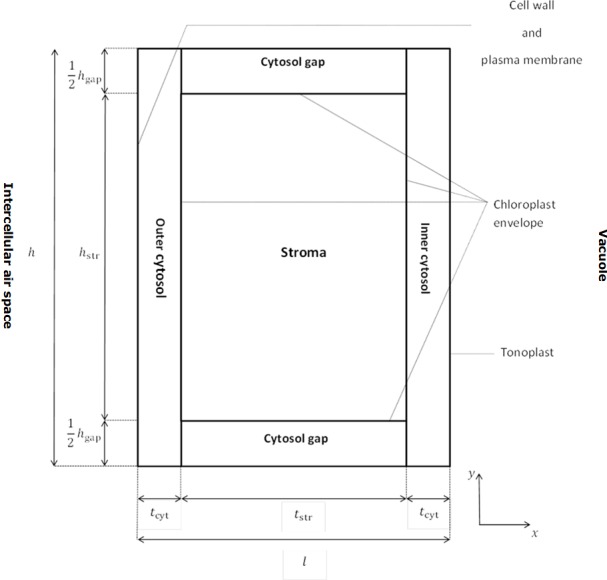
CO2 transport, CO2 production by (photo)respiration, and CO2 consumption by RuBP carboxylation were simulated by solving a reaction-diffusion model over this domain. The partial differential equations and the boundary conditions were parameterized by both leaf anatomical properties and simultaneous gas exchange and chlorophyll fluorescence measurements. Table 1 shows an overview of definitions and values of all model parameters and input variables. Thicknesses of the cell wall (twall), cytosol (tcyt), and the chloroplast stroma (tstr) were adopted from[17], in which they were measured from transmission electron microscopic photographs of tomato (Solanum lycopersicum) mesophyll cells. The ratios of the mesophyll surface area exposed to the intercellular air space to the leaf surface (Sm/S) and the chloroplast surface area facing the intercellular air space to the exposed mesophyll surface area (Sc/Sm) were adopted from measurements presented in the same study. The Michaelis-Menten constants for RuBP carboxylation (KmC) and for oxygenation (KmO) were adopted from[28], who estimated these parameters using data from simultaneously conducted gas exchange and chlorophyll fluorescence measurements on tomato leaves. Also, the diffusion coefficients and permeabilities of the various mesophyll components were adopted from this study.
Table 1. Values of parameters and variable input for the model.
| Symbol | Explanation | Value | Unit | Source |
|---|---|---|---|---|
| Ca | Ambient CO2 partial pressure near leaf surface | * | Pa | [17] |
| DCO2,water | Diffusion coefficient of CO2 in water at T = 298.13 K | 1.79·10−9 | m2 s-1 | [29] |
| gs | Stomatal conductance | ** | mol m-2 s-1 Pa-1 | [28] |
| Gmem | Plasma membrane permeability | 3.50·10−3 | m s-1 | [17] |
| Genv | Chloroplast envelope permeability | 1.75·10−3 | m s-1 | [28] |
| H | Henry’s constant for CO2 at T = 298.13 K | 2941 | Pa m3 mol-1 | [17] |
| Iinc | Irradiance | * | μmol m-2 s-1 | |
| KmC | Michaelis-Menten constant for RuBP carboxylation by Rubisco | 26.7 | Pa | [28] |
| KmO | Michaelis-Menten constant for RuBP oxygenation by Rubisco | 16.4 | kPa | [28] |
| O | Oxygen partial pressure | 21 | kPa | |
| peff,wall | Effective porosity of the cell wall | 0.2 | [17] | |
| q | Ratio of the height of a chloroplast to its thickness | 2.5 | [27] | |
| R | Universal gas constant | 8.314 | Pa m3 mol-1 K-1 | [17] |
| Rd | Rate of respiration in the light | *** | μmol m-2 s-1 | |
| s | Slope of the assumed linear relationship between J and IincΦ2/4 at low light levels and low O2 levels | 0.529 | ||
| Sm/S | Ratio of the area of the mesophyll cell surface, exposed to the intercellular air space, to the leaf surface area | 17.0 | [17] | |
| Sc/Sm | Ratio of the area of the chloroplast surface, facing the intercellular air space, to the mesophyll surface area, exposed to the intercellular air space | 0.919 | [17] | |
| SC/O | Rubisco specificity factor | 2.6 | mmol μmol-1 | [14] |
| twall | Cell wall thickness | 0.118 | μm | [17] |
| tcyt | Cytosol thickness | 0.243 | μm | [17] |
| tstr | Stroma thickness | 2.54 | μm | [17] |
| T | Leaf temperature | 298.13 | K | |
| Tp | Rate of triose phosphate utilization | *** | μmol m-2 s-1 | |
| Vcmax | Rate of RuBP carboxylation by Rubisco | *** | μmol m-2 s-1 | |
| ζcyt | Fraction of CO2 diffusion coefficient in cytosol to CO2 diffusion coefficient in water | 0.5 | [28] | |
| ζstr | Fraction of CO2 diffusion coefficient in stroma to CO2 diffusion coefficient in water | 0.5 | [28] | |
| Φ2 | Quantum yield of photosystem II | ** | mol mol-1 | [28] |
* Environmental conditions; during the gas exchange and chlorophyll fluorescence measurements, the leaf was exposed to various combinations of Ca, Iinc, and O.
** For each combination of Ca and Iinc, gs and Φ2 were measured.
*** These parameters were estimated by the model for different scenarios for the location of (photo)respiration.
Input FvCB parameters that represent partial pressure were converted from Pa to mol m-3. Input parameters that represent rates expressed in μmol m-2 s-1 were converted to mol m-3 s-1. After solving the model, the average rate of CO2 assimilation (mol m-3 s-1) in the chloroplast was calculated from the steady state CO2 distribution. It was used to calculate the rate of CO2 assimilation at the leaf level, expressed in μmol m-2 s-1. The Material and Methods section and S3 Text contain more information about these unit conversions.
Estimates of Rd, Tp, and Vcmax
We estimated s, which is the slope of the assumed linear relationship between J and IincΦ2/4 at low light levels and low O2 levels using the method described in[13]. We used this parameter, the average measured quantum yield of photosystem II, and the irradiance to calculate the rate of electron transport (Eq 8). After determination of s, the rate of respiration Rd and the maximum rate of RuBP carboxylation Vcmax were estimated by the 2-D model. Table 2 shows Rd and Vcmax and their standard errors estimated by our model. The estimate of s was 0.529. The estimates for Rd were 3.43 μmol m-2 s-1, 3.36 μmol m-2 s-1, and 3.41 μmol m-2 s-1 assuming the (photo)respired CO2 is released in the inner cytosol, the outer cytosol and the cytosol gap compartments, respectively. These Rd and the measured Aj values were used to calculate Tp, which was 13 μmol m-2 s-1 for each assumed location of (photo)respiration (Table 2). The estimates of Vcmax were 174 μmol m-2 s-1, 177 μmol m-2 s-1, and 227 μmol m-2 s-1 assuming (photo)respiratory CO2 release in the inner cytosol, the outer cytosol and the cytosol gaps, respectively. Those estimates of Rd are considerably higher than the ones reported in [7,28] for young cv. Admiro leaves. In both studies, the Yin method [13] was used to estimate Rd as the intercept of the correlation between AN and IincΦ2/4 for high atmospheric CO2 partial pressures and very low oxygen levels. Possibly, the differences between our and their estimates is that the Yin method, which, strictly speaking, applies to non-photorespiratory conditions [17], was used to estimate Rd under ambient oxygen levels in their study. In contrast, our model does not have such a restriction and the estimate by our model should better represent Rd under ambient O2 levels. In order to investigate to what extent our relatively high Rd estimates could have influenced our estimates for Vcmax, we estimated Vcmax for a range of Rd values varying from 1.0 μmol m-2 s-1 to 5.0 μmol m-2 s-1 (Table A in S9 Text). The estimate of Vcmax was not effected by Rd if (photo)respired CO2 is released in the outer cytosol and that the standard error of the estimate was very high relative to the estimate. In the other two scenarios, the standard error of the estimates was small relative to the estimate. The estimates of Vcmax increased with the assumed values of Rd. However, the relative increase of the estimated Vcmax with increasing Rd was relatively small as an increase of Rd by 500% only resulted in an increase of Vcmax by 18% and 24% for the scenarios that assume (photo)respiratory CO2 release in the inner cytosol and cytosol gaps, respectively.
Table 2. Estimated values of parameters of the FvCB model and their standard error for each scenario for (photo)respired CO2 release (it takes place in the inner cytosol, or in the outer cytosol, or in the cytosol gaps).
| Symbol |
Unit |
Explanation |
(Photo)respired CO2 release in: | ||
|---|---|---|---|---|---|
| Inner cytosol | Outer cytosol | Cytosol gaps | |||
| Rd | μmol m-2 s-1 | Rate of respiration | 3.44±0.36 | 3.36±0.36 | 3.41±0.36 |
| Tp | μmol m-2 s-1 | Rate of triose phosphate utilization | 13.39 | 13.38 | 13.38 |
| Vcmax | μmol m-2 s-1 | Rate of RuBP carboxylation by Rubisco | 174±29 | 177±251 | 227±29 |
In order to compare the estimates and the standard errors of Vcmax found by our model and by the FvCB model extended with mesophyll conductance, we estimated Vcmax using the estimation procedure described in[13], which assumes [11] that mesophyll conductance varies with Ci according to a Leuning-type phenomenological model[11]. The SAS 9.4 script (SAS Institute Inc., Cary, NC, USA) for this procedure can be found in Script A in S10 Text. We set in this analysis that Rd = 3.4 μmol m-2 s-1, which is the average of the estimated Rd across the three scenarios (Table 2). We used the same experimental data for those low CO2 levels as we used for the estimation of Vcmax using the 2-D model. This analysis resulted in an estimate of Vcmax = 130 ± 19 μmol m-2 s-1, which was simultaneously estimated with shape parameter δ (5.7486±3.4596)[11–13]. The standard error of Vcmax is of the same order of magnitude as the estimates by the 2-D model, which that assumes (photo)respired CO2 release in the inner cytosol and the cytosol gaps, but the estimate is smaller than any of the scenarios investigated by the 2-D model (Table 2). This lower estimated value may be explained by the fact that we had to estimate Vcmax simultaneously with shape parameter δ to take the variation of mesophyll conductance with Ci into account. In contrast, it was not necessary to estimate such an additional parameter with the 2-D model presented in this study.
Validation
Fig 3 shows a comparison between the simulated and measured net CO2 assimilation rates. Only the lower parts of the AN-Iinc curve (Iinc ≤ 200 μmol m-2 s-1) were used for the estimation of photosynthetic parameters of s and Rd. Only the measurements at Ca = 200 Pa in the AN-Ca curve were used to determine Tp. The model was validated by predicting AN for the remaining levels of Ca and Iinc that were used in the experiment. If (photo)respired CO2 is released in the inner cytosol, the model predictions of AN generally agree well with the measurements. The same is true if (photo)respired CO2 release is assumed to take place in the cytosol gap compartment, although the model tends to slightly underestimate AN for intermediate Ca levels in the AN-Ca curve. This underestimation is considerably higher if (photo)respired CO2 is assumed to take place in the outer cytosol (Fig 3B and 3C). Additionally, if Iinc ≥ 200 μmol m-2 s-1, the predicted AN is substantially lower than the measured AN, if (photo)respiratory CO2 release takes place in the outer cytosol (Fig 4).
Fig 3. Measured (symbols) and simulated (lines) AN-Ca (left) and AN-Iinc (right) curves for different scenarios for the location of (photo)respiratory CO2 release.
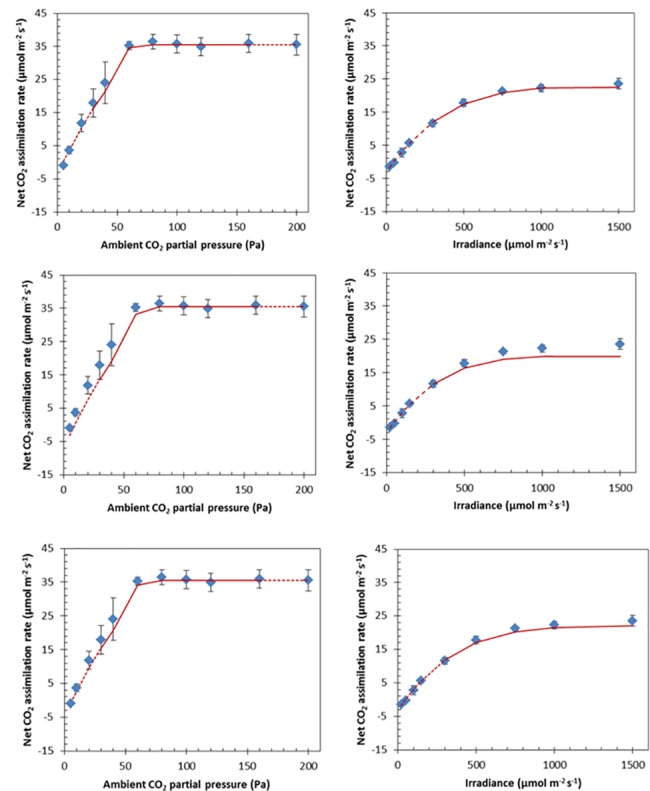
The error bars represent one standard deviation. In the simulated AN-Ca curves, (photo)respiration either takes place in the inner cytosol (A-B), in the outer cytosol (C-D) or in the cytosol gaps (E-F). The solid line represents the predicted net CO2 assimilation rates for values of Ca and Iinc that were neither used in the estimation procedure of Rd and Vcmax nor for the determination of Tp. The dashed lines connect the predicted net CO2 assimilation rates under the remaining values of Ca and Iinc with the solid curve.
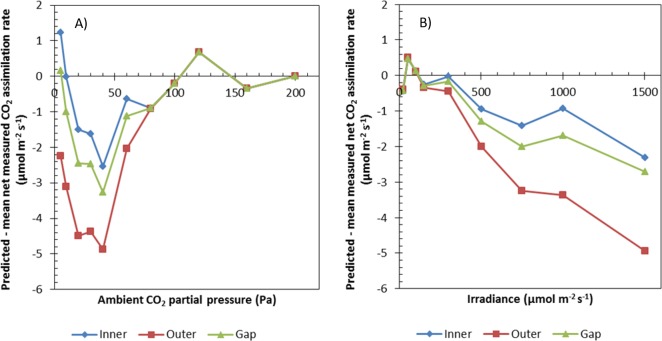
Fig 4. Differences between predicted and measured net CO2 assimilation rates.
Differences between the predicted net CO2 assimilation rate and the average measured net CO2 assimilation rate for different ambient CO2 partial pressures (A) and irradiances (B). In both figures, it is assumed in models that (photo)respired CO2 is released in the inner cytosol, or in the outer cytosol, or in the gaps between the inner and the outer cytosol.
CO2 concentration profiles
Figs 5–7 show CO2 concentration profiles at ambient CO2 levels (Ca = 40 Pa) and saturating light (Iinc = 1500 μmol m-2 s-1) for three scenarios. It is assumed that (photo)respiratory CO2 is released in the inner cytosol (Fig 5), in the outer cytosol (Fig 6) or in the cytosol gaps (Fig 7). If CO2 is released in the outer cytosol, the CO2 partial pressure decreases along the diffusion pathway from the cell wall to the tonoplast. If CO2 is released in the inner cytosol or in the cytosol gap, the CO2 partial pressure also decreases along the diffusion pathway from the cell wall to near the inner chloroplast envelope. However, in these two scenarios, it slightly increases again in the inner cytosol (Figs 5 and 7).
Fig 5. CO2 concentration profiles for (photo)respiratory CO2 release in the inner cytosol.
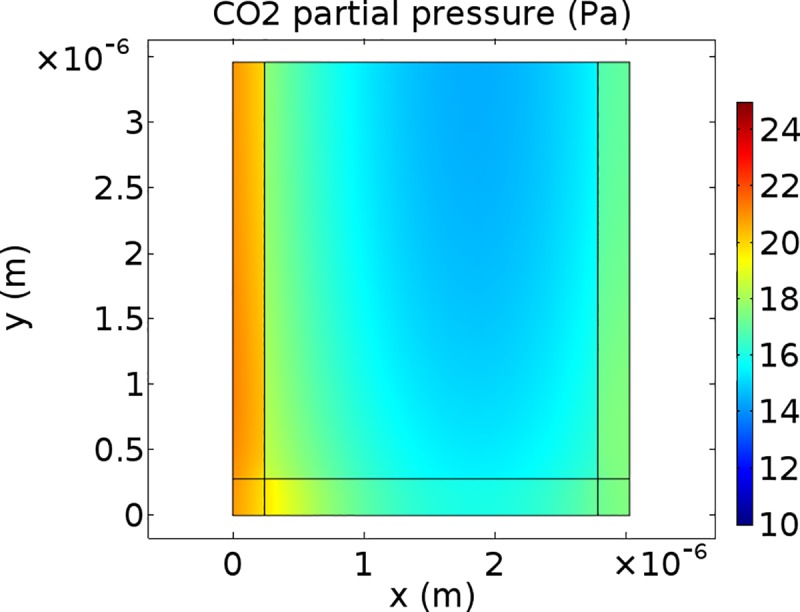
CO2 partial pressure profile within half the computational domain at Ci = 25 Pa levels and saturating light (Iinc = 1500 μmol m-2 s-1). The color bar displays CO2 partial pressures (Pa). (Photo)respired CO2 is produced in the inner cytosol.
Fig 7. CO2 concentration profiles for (photo)respiratory CO2 release in the cytosol gaps.
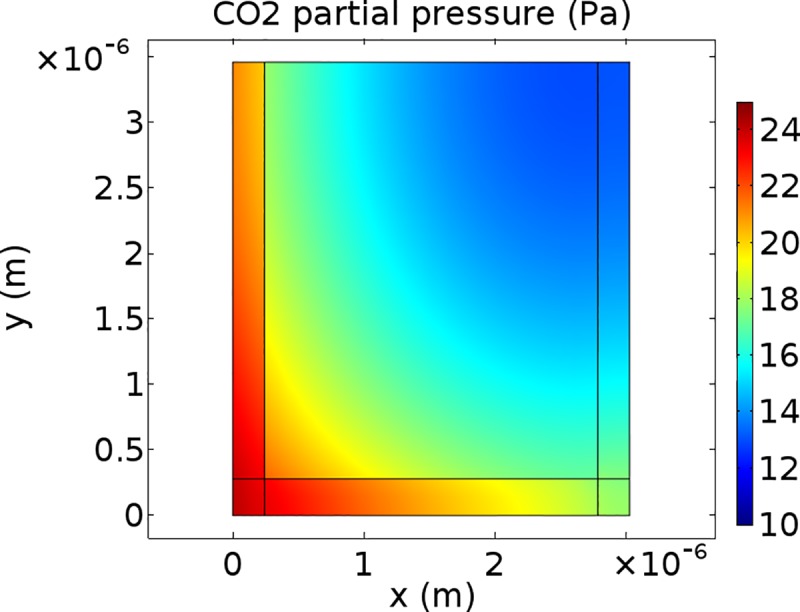
CO2 partial pressure profile within half the computational domain at Ci = 25 Pa levels and saturating light (Iinc = 1500 μmol m-2 s-1). The color bar displays CO2 partial pressures (Pa). (Photo)respired CO2 is produced in the cytosol gaps.
Fig 6. CO2 concentration profiles for (photo)respiratory CO2 release in the outer cytosol.
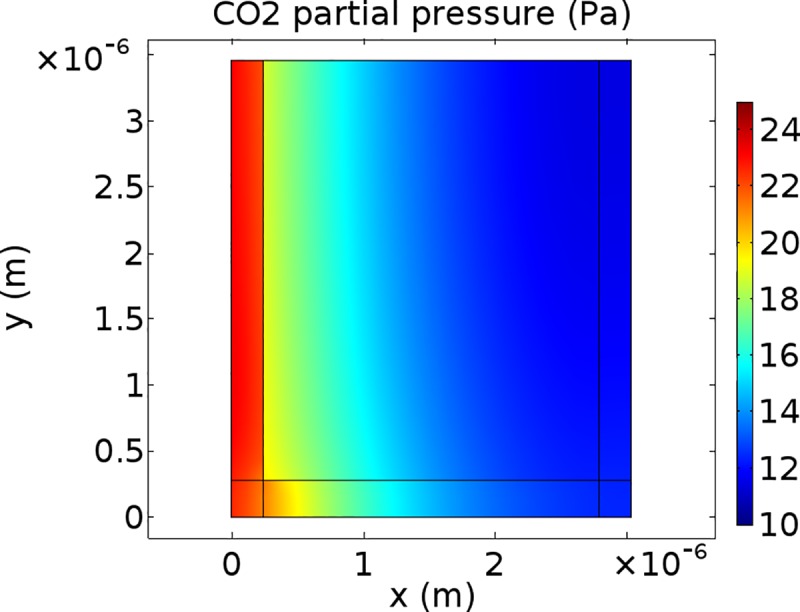
CO2 partial pressure profile within half the computational domain at Ci = 25 Pa levels and saturating light (Iinc = 1500 μmol m-2 s-1). The color bar displays CO2 partial pressures (Pa). (Photo)respired CO2 is produced in the outer cytosol.
Re-assimilation of CO2
The reaction-diffusion model was used to calculate the fraction of re-assimilation of CO2 produced by (photo)respiration, frec. It was calculated under ambient CO2 levels (Ca = 40 Pa) and saturating light (Iinc = 1500 μmol m-2 s-1). The highest values for frec were obtained if (photo)respired CO2 release took place in the inner cytosol (frec = 0.76), The lowest values of frec were obtained if it took place in the outer cytosol (frec = 0.56). If it took place in the cytosol gap, frec = 0.70. The reaction-diffusion model was also used to calculate the average CO2 partial pressure Cc in the stroma, expressed as a gas phase concentration, for each of the different scenarios. The highest value for Cc was found if (photo)respired CO2 release took place in the inner cytosol (Cc = 15.6 Pa), and the lowest value for Cc was found if (photo)respired CO2 release took place in the outer cytosol (Cc = 14.1 Pa). If (photo)respired CO2 release took place in the cytosol gaps, Cc was 15.1 Pa. The calculated values for the CO2 partial pressure in the intercellular air spaces were 26.0 Pa, 27.5, and 26.5 Pa for the three scenarios, respectively.
Discussion
In this study, a 2-D microstructural model for photosynthesis was developed based on a simplified geometry of a mesophyll cell consisting of four compartments (outer cytosol, chloroplasts, inner cytosol, cytosol gaps) (Fig 2). The microstructural model was parameterized by the measured leaf anatomical properties Sc/Sm, tcyt, and tstr (Table 1), which were determined from transmission electron microscopic images [17], and an assumed value for the aspect ratio of a chloroplast. Within the microstructural model, a reaction-diffusion model was solved for CO2. The model was used directly to estimate the parameters Rd and Vcmax for each scenario of (photo)respired CO2 release.
By estimating Rd with the model, the estimation method does not make the assumption that there is no re-assimilation of (photo)respired CO2, which is made implicitly in simpler models to estimate Rd [13,31–34]. Current models for mesophyll resistance models either made the implicit assumption that CO2 release by (photo)respiration takes place in the stroma itself [3,13,35,36], in the outer cytosol [17] or that there is no CO2 gradient in the cytosol[14,18]. By estimating Vcmax with the 2-D model, the estimation method also avoids the assumption that (photo)respiration and RuBP carboxylation take place in the same compartment or that the location of (photo)respiration is limited to the outer cytosol.
The model was validated by comparing the predicted AN with measurements for AN that were not used for estimation of Rd and Vcmax or the determination of Tp (Fig 3). The model described the data well for both the light and the CO2 response curves, if it was assumed that (photo)respiratory CO2 release takes place in the inner cytosol. In the other two simulated cases for the location of (photo)respiration (outer cytosol and cytosol gap), the model tended to predict lower values for the net CO2 assimilation rate for high light levels and/or low CO2 levels. The estimates of Rd did not differ among the scenarios for the localizations of (photo)respiration (Table 2). The estimate of Vcmax for the scenario that assumes release of (photo)respired CO2 in the cytosol gaps is higher than in the scenario that assumes release of (photo)respired CO2 in the inner cytosol (Table 2). An explanation for the difference between the Vcmax estimates is that the model in the latter scenario attempts to compensate the short diffusion path for (photo)respired CO2 with a more efficient RuBP carboxylation. This does not explain why the estimate of Vcmax in the scenario for (photo)respired CO2 release in the outer cytosol is lower than the estimate than in the scenario that assumes (photo)respired CO2 release in the cytosol gaps though. The very high standard error in the scenario of the model that assumes (photo)respired CO2 release in the outer cytosol suggests that the estimate of Vcmax in this scenario is very uncertain. This uncertainty can either be explained by the absence of Rubisco limited photosynthesis in the data range that was used to estimate Vcmax or by an inability of the model to compensate the short length of the diffusion path for (photo)respired CO2 by estimating a higher Vcmax value. Given the poorer performance of the scenario assuming (photo)respiratory release in the outer cytosol during the model validation compared to the other two scenarios (Fig 4), the latter explanation is more likely. These results suggest that CO2 release by (photo)respiration is more likely to take place in the inner cytosol or the cytosol gaps than in the outer cytosol.
Our results also show that the estimates of Rd are very little affected by the localization of (photo)respiration. This is in contrast with the results from the study in [37]. In that study, a slope-regression method was combined with the multiple resistance model from [14,18] to estimate Rd simultaneously with Γ*, while assuming different ratios of rw (serial resistance of cell wall and plasma membrane) and rc (serial resistance of the chloroplast envelope and the stroma). It was found in that study that changing the assumed ratio of rc and rw from 0 to 1 resulted in a decrease of the estimate of Rd by 30%. The fact that we did not find such a change in the estimate in our study may be explained by the fact that Rd was not estimated simultaneously with Γ*. We did find that the estimate of Vcmax was affected by the localization of (photo)respiratory CO2 release, as its estimates differed considerably among the scenarios. The results from [37] and our results show that it is possible that the assumptions about the localization of (photo)respiratory can affect the estimates of other parameters of the FvCB model and further research is needed to examine this.
After validation, the model was extended to allow simulating the transport, consumption and production of 12CO2 and 13CO2 simultaneously. This approach allowed us to implement in silico experiments to determine the percentage for re-assimilation of CO2 produced by (photo)respiration. Our results show that the re-assimilation percentage varied from 56% to 75%, depending on the scenario. The range of reported values for frec in literature is large. In one study, it is determined that 23%-29% of the (photo)respired CO2 is recycled [38]. However, this percentage is likely underestimated, because the authors assumed in their calculations that the ratio of the concentrations 12CO2 to 13CO2 in the intercellular air space is the same as in the chloroplasts, which is very unlikely[28]. In another study, a resistance model was used [14] to calculate that this percentage is between 25% and 40% in tobacco. However, in that study it was assumed that the CO2 concentration is completely mixed throughout the cytosol. Results from our study clearly show that this is not the case (Figs 5–7). It has also been reported that 100% of the (photo)respired CO2 is re-assimilated in tomato and over 80% is re-assimilated in a number of other species [39]. In another study, re-assimilation percentages were found to be between 14% and 18% in sunflower and rye and between 42% and 50% in wheat[35]. More recently, a somewhat higher re-assimilation percentage has been reported for wheat (45.9%) under an ambient CO2 level [20]. Under a lower CO2 level (200 μmol mol-1), this percentage was about the same (i.e. 46.8%). In the same study, it has been observed that 50.6% of the (photo)respired CO2 is re-assimilated in rice under ambient CO2 level. However, in contrast to wheat, the re-assimilation percentage was considerably higher under low CO2 levels in rice (58.7%). This literature overview shows that the range of possible values for frec is considerable, even within species, and that the use of different environmental conditions, and species and methods affects the calculated or measured value of frec and that frec can even be different within species. In future research, our model can be used to determine frec for different species or environmental conditions to examine how differences between re-assimilation fractions between species can be explained.
An advantage of the 2-D model presented in our study is that it does not require determining mesophyll resistances, because several factors that determine mesophyll resistance are explicitly modelled. However, the model requires a number of assumed values of diffusion coefficients and permeabilities of several mesophyll cell compartments. The permeability of both the plasma membrane and the chloroplast envelope was adopted from [17]. We assumed that this permeability lumps the permeability for CO2 of aquaporins and the phospholipid bilayer in these membranes [40]. We also assumed that the permeability of the chloroplast envelope is twice as low as the plasma membrane. Values for the effective porosity of the cell wall peff,wall were adopted from [41] and effective diffusion coefficients from the stroma and cell wall from [28]. Since there are only a very few measurements of these diffusive properties and permeabilities available [42], it can be argued that these uncertainties can result in large errors in the predicted net CO2 assimilation rate. Nevertheless, validation of the model showed that the model predicted the net CO2 assimilation rate reasonably well for both the case that (photo)respiration takes place in the inner cytosol (Fig 3A and 3B) and in the cytosol gap (Fig 3E and 3F). This suggests that even though each single assumed permeability or diffusion coefficient can be biased, the combination of these assumptions results in reasonable predictions of light and CO2 response curves.
Compared with other recent reaction-diffusion models for CO2 transport in leaves [27,28], we made a number of simplifications in both the modelled leaf structure and in the processes. These simplifications are as follows. (i) The compartment in which (photo)respiratory CO2 is released is a compartment in which mitochondria and cytosol are lumped, rather than modelling individual mitochondria as described in [27]. (ii) It is assumed that the resistance of the intercellular air space is negligible, rather than explicitly model the intercellular air space like in[28]. (iii) The leaf model is 2-D, instead of 3-D as was done in previous studies[27,28]. (iv) The leaf structure is reduced to simple geometrical shapes. (v) The light absorption gradient is not explicitly modelled like in [28,43]. (vi) The activity of carbonic anhydrases is lumped in the apparent diffusion coefficient of the stroma and the cytosol, rather than modelling its activity and HCO3- transport explicitly. We have made these simplifications, because adding more complexity requires additional assumed parameter values that are uncertain and cannot easily be measured. Adding complexity will also make the model less flexible and more computationally demanding, which makes the model cumbersome and unattractive to use. Nevertheless, any of these simplifications can potentially have a substantial impact on the predictions. We, therefore checked how these simplifications might affect the predicted net CO2 assimilation rate. We investigated simplification (i) in S4 Text where we presented a modified version of the model in which we modelled individual mitochondria explicitly and compared the predicted net CO2 assimilation rate and frec with the predictions of the default model. We found that modelling loose mitochondria hardly changed these predictions (Fig A in S4 Text). The assumption of no CO2 gradient in the intercellular air space (ii) is reasonable for tomato leaves. The intercellular air space in tomato leaves are highly interconnected[17]. This high interconnectivity, combined with the fact that the diffusion coefficient of CO2 in air is about 104 times as large as in water at room temperature[44], makes it very unlikely that there is a CO2 gradient in the intercellular air space in tomato leaves or any other homobaric leaf with highly interconnected air space. This was demonstrated in [23], where a 3-D model was used to simulate CO2 diffusion in both the intercellular air space and within mesophyll cells. There was only a stomatal pore modelled at the abaxial leaf surface. In [23] it was found that the CO2 concentration difference between the upper and lower boundary was less than 0.1%. In order to discuss the impact of modelling a 2-D leaf structure (iii), instead of 3-D leaf structure, we will first discuss potential problems of a 2-D approach and then how we dealt with these issues. If a digitized transversal section of a leaf is used as a 2-D computational domain [45–47], it is implicitly assumed that Sm/S equals the length ratio of the exposed mesophyll surface area to the length of the section Lm/L, measured from leaf transversal sections. This assumption will result in the underestimation of the exposed mesophyll surface available for CO2 uptake [48,49] and, thereby, the net CO2 assimilation rate. In our model, we dealt with this issue by modelling the leaf as a rectangular geometry in two dimensions and assuming that each of the leaf anatomical parameters (twall, tcyt, tstr, q, Sc/Sm, Sm/S) does not change in the direction of the third dimension. Another implicit assumption of a 2-D reaction model from a previous study [46] was that air spaces that seemed isolated in 2-D microscopic images from transversal leaf sections were also isolated in 3-D space. This makes the mesophyll surface exposed to these isolated air spaces unavailable for CO2 uptake, which lowers the net CO2 assimilation rate even more. In [46] study, the problem of assumed isolated intercellular air spaces and of the assumption that Lm/L was equal to Sm/S was solved by estimating the diffusion coefficients for CO2 in the epidermis and the cell wall from gas exchange measurement data. This resulted in effective diffusion coefficients for CO2 that were about 100 times as large as water. Although applying these effective diffusion coefficients resulted in a reasonable fit of gas exchange measurements with simulated AN-Ci and AN-Iinc curves, their concentration profiles show that the cell wall and the interface between the epidermal cells and the mesophyll cells are a major diffusion pathways for CO2, which is very unlikely. In our 2-D model, the issue of isolated air spaces is solved by assuming that the resistance for CO2 transport in the intercellular air space is negligible and by implementing stomatal conductance in the boundary conditions of the outer border of the computational domain. In S5 Text, we checked whether our other assumptions, namely, the reduction of the leaf structure to simple geometrical shapes (iv) and not explicitly modelling the light gradient (v) and carbonic anhydrase activity (vi), affect the predicted net CO2 assimilation rate. We did so by comparing simulated A − Ca curves modelled by a complex 3-D model that does not have any of these simplifications [28] with A − Ca curves modelled by the model from our study. The net CO2 assimilation rates were about the same. All these analyses above show that the simplifications in our model, at least for tomato, do not affect the predictions of the net CO2 assimilation rate.
There are analyses that cannot be done with the current version of the model, as they require more details on the description of the leaf geometry. Our previous study [28] examined to what extent C3 leaf photosynthesis can be optimized by optimizing the gradient of photosynthetic capacity parameters (Vcmax, Tp and the maximum rate of electron transport Jmax) between the upper and the lower epidermis. However, such an analysis requires huge computational times and a 3-D tomography of a leaf. In order to make such analyses less time and resource demanding, in future research it could be examined whether our simple 2-D model is capable of reproducing the results from[28]. This could be done, by instance, for defining the 2-D leaf geometry in the model, Iinc, Jmax, Vcmax, and Tp at different depths, solving the model at each depth and calculate the whole leaf net CO2 assimilation rate.
To the best of our knowledge, this study is the first attempt to directly assess how the localization of released CO2 produced by (photo)respiration could affect both the net rate of CO2 assimilation and re-assimilation. This is important, because previous resistance models [13,14,17,18,29,30] make implicit assumptions about the location of (photo)respiration or about the CO2 gradients in the cytosol. Our study showed that it is unlikely that (photo)respiratory CO2 release takes place in the outer cytosol and also that it is unlikely that there is no CO2 gradient in the cytosol. In our analyses, we limited the number of scenarios to two extreme situations (all (photo)respiratory CO2 release takes place in the outer cytosol or in the inner cytosol) and one intermediate situation. Recently, it has been shown that mitochondria can be present in both the inner and the outer half of the cytosol in C3 grasses [50], which could explain differences in photosynthetic capacity among species. In future research, one could use the model presented in this study as a tool to analyse how the distribution of mitochondria over different cytosol compartments affects leaf photosynthesis.
Additionally, none of the aforementioned models allows to model CO2 diffusion through the gaps between the chloroplasts. This can affect the predicted net CO2 assimilation rate and fraction of (photo)respired CO2 that is re-assimilated. Since the parameter estimates in our study are directly estimated by the model, for each estimate it is clear what the assumed location of (photo)respiration is. As far as the authors know, the only attempt in which a reaction diffusion model is directly used to estimate FvCB parameters is described in [26]. In that study, parameters for the FvCB model and parameters for the temperature response were estimated by both a 3-D model [23] and by a simple photosynthesis model [51]. In [26] it was found that the estimates can be quite different, because the 3-D model described in [23,26] is capable of partitioning the temperature response of photosynthesis due to physical (solubility of CO2 in the liquid phase, temperature response of the diffusion coefficient of CO2 in water) and biochemical (temperature dependency of kinetic constants of Rubisco) parameters.
Our model has the capability to distinguish how CO2 transport is affected by biochemical processes and leaf structural barriers. Therefore it can be interesting to use the model in future research to re-examine the temperature response of various photosynthetic parameters. As our model is also capable of calculating the fraction of (photo)respired CO2, it can also be used in further research to investigate how environmental conditions (Ca, Iinc, O, temperature) and stomatal conductance affect re-assimilation. It would further be interesting to further validate the model for other tomato cultivars and crop species and environmental conditions and subsequently investigate how this affects the re-assimilation of (photo)respired CO2 and the estimates of photosynthetic parameters. Finally, the results of the validation of our 2-D model suggest that it is possible to simplify both the structures and the processes, while the model still is capable of predicting the net CO2 assimilation well.
Material and methods
Description of the experimental data
We used experimental data described in[17]. This data set consisted of microscopic and ultramicroscopic leaf anatomical measurements as well as simultaneous gas exchange and chlorophyll fluorescence measurements on leaves of two ages in three tomato cultivars. The gas exchange measurements consisted of CO2 and light response measurements under both 21% O2 and 2% O2. For our present study, we only used the data for 15-days old leaves of cv. ‘Admiro’. Those data can be found in S7 Text.
Description of the geometry of the model
The 2-D computational domain consists of an l x h rectangular section of a mesophyll cell exposed to the intercellular space. The centre of this section contains a single rectangular chloroplast with dimensions tstr x hstr. The remaining part of the section consists of cytosol. This cytosol compartment was subdivided into inner cytosol (rectangular cytosol layer adjacent to tonoplast), outer cytosol (rectangular cytosol layer adjacent to plasma membrane), and two remaining rectangles called cytosol gaps. The lengths of the inner and outer cytosol are tcyt,inner and tcyt,outer. It is assumed (unless explicitly mentioned) that tcyt,in = tcyt,out = tcyt. For reasons of symmetry, the height of the cytosol gap at the bottom and the top of the computational domain was half of that of the total gap height (hgap). More details on the reconstruction of the geometry can be found in S1 Text. The chloroplast envelope was modelled as a thin film diffusion barrier. Since preliminary simulations showed that the presence of a vacuole did barely affect the net CO2 assimilation rate, we did not include a vacuole. An insulated boundary condition (net flux is zero) was applied over the tonoplast, which is the membrane between the inner cytosol and the vacuole.
In all simulations an assumption from [27] was adopted; namely, the aspect ratio q of the chloroplasts (in this study, ) was constant and equal to 2.5. The gap width hgap was varied in order to produce geometries with different values of Sc/Sm. It can be expressed as:
| (2) |
More details on the derivation of Eq (2) can be found in S2 Text. By applying this geometry, it is assumed that all anatomical parameters (Sc/Sm, tstr, tcyt, and q) are uniform in the paradermal direction.
Process description
Diffusion equation for CO2 transport
In a steady state, CO2 diffusion, consumption and production should be in balance as:
| (3) |
where the subscript ‘i’ denotes the medium (either a cytosol compartment or the stroma). is the diffusion coefficient of CO2 (m2 s-1) in compartment i. wi is the volumetric rate of carboxylation by Rubisco (mol CO2 m-3 s-1), which is only non-zero in the stroma. rp,i is the volumetric rate of photorespiration (mol CO2 m-3 s-1), which is only non-zero in the cytosol. rd is the volumetric rate of respiration (mol CO2 m-3 s-1) that is only non-zero in the cytosol and was taken as a constant. [CO2] is the CO2 concentration (mol m-3). ∇ (m-1) is the gradient operator. The diffusion coefficient for CO2 transport depends on the porosity and the viscosity of the medium. For the cytosol and the stroma, the diffusion coefficient for CO2 was calculated as[29]:
| (4) |
where peff is the effective porosity of the medium. It was assumed that the effective porosity of the cytosol and the stroma is 1.0. ζi is a reduction factor in the medium compared to pure water due to a higher viscosity of the media compared to water and was assumed to be 0.5 for the stroma and the cytosol and 1.0 for the cell wall[17,28]. Table 1 shows values and units of physical parameters used in this study.
Carboxylation rate
The FvCB model[5], expanded with triose phosphate utilization limited carboxylation[52], was used to quantify the rate of carboxylation by Rubisco w in the stroma:
| (5) |
where vcmax is the maximum volumetric rate of carboxylation by Rubisco (mol m-3 s-1); kmC and kmO are the Michaelis-Menten constants of Rubisco (mol m-3) for carboxylation and oxygenation, respectively; j is the volumetric rate of electron transport (mol m-3 s-1); tp is the volumetric rate of triose phosphate utilization (mol m-3 s-1); and γ* is the CO2 compensation point, the CO2 concentration (mol m-3) in the stroma at which the amount of CO2 consumed by carboxylation equals the amount of CO2 released by photorespiration.
Photorespiration rate
The rate of CO2 production due to photorespiration was modelled as[27]:
| (6) |
where “Stroma” is the stroma compartment in the computational domain, and “(Photo)respiration” is the location in the computational domain, in which CO2 release by (photo)respiration is assumed to take place. Three different scenarios for the location for CO2 release by (photo)respiration were considered: either (1) the inner cytosol, or (2) the outer cytosol, or (3) the cytosol gaps between the chloroplasts.
Unit conversions
The variables vcmax, rd, rp, tp, j and w in Eqs (3), (5) and (6) are rates per unit of volume. Their equivalents expressed in rate per unit of leaf area (mol m−2 s−1) are denoted here in capitals; Vcmax, Rd, Rp, Tp, J and W. In order to calculate j, vcmax, and tp, J, Vcmax and Tp are multiplied with the ratio S/Vstr, which is the ratio of the leaf area to the total volume of the stroma in a leaf. S2 Text and S3 Text explain how this term is derived mathematically; rd is calculated by multiplying Rd with S/Vcyt,inner, S/Vcyt,outerr, or S/Vcyt,gap, depending on the scenario. Table 3 shows mathematical expressions for these surface to volume fractions.
Table 3. Overview of surface to volume ratios and parameterizations.
| Symbol |
Unit |
Mathematical expression | Meaning of ratios |
|---|---|---|---|
| m-1 | Leaf area to total chloroplast volume | ||
| m-1 | Leaf area to total volume of the inner cytosol | ||
| m-1 | Leaf area to total volume of the outer cytosol | ||
| m-1 | Leaf area to total volume of the cytosol gaps |
There are also a number of parameters that represent concentrations (kmC, kmO, γ*, [O2], [CO2]) expressed in mol m-3. In most photosynthesis research, these parameters are expressed as partial pressures instead (here written as KmC, KmO, Γ*, O). The ideal gas law and Henry’s law were applied [53]to convert all mentioned CO2 partial pressure parameters, expressed in gas phase (KmC, KmO, Γ*), into concentrations in the liquid phase.
Quantification of parameters
Quantification of leaf anatomical parameters
Leaf anatomical parameters (tcyt, tstr, Sc/Sm, Sm/S, twall) for 15-day-old Admiro leaves were adopted from[17]. Sc/Sm, tcyt, and tstr were used to generate a unique geometry for this leaf, as described in S1 Text, S2 Text and S3 Text. The anatomical parameter values are listed in Table 1. The measured cytosol thicknesses are considerably smaller than the thickness of mitochondria assumed in[27]. To the best of our knowledge, there have been no systematic measurements of diameters of mitochondria and some sample images from a number of studies [20,54,55] suggest that this diameter can vary considerably. Due to lack of data, we assumed that the thickness is equal to the cytosol thickness measured on the TEM images in [17]. In S6 Text, we present a sensitivity analysis for tcyt,inner and tcyt,outer to show that these thicknesses have a very small effect on AN and frec.
Quantification of Rubisco kinetic parameters
We adopted the Michaelis-Menten constants for carboxylation (KmC) and oxygenation (KmO) by Rubisco from[28]. We further assumed that the specificity factor of Rubisco for CO2 and O2, SC/O, equals 2.6[14]. For SC/O, we calculated the CO2 compensation point Γ* as:
| (7) |
Determination of the rate of electron transport
We used AN − Iinc data measured at 2% O2 under limiting irradiance conditions (Iinc equal to 25, 50, 100, and 150 μmol m-2 s-1) to fit AN against by linear regression, where Φ2 is the quantum yield of Photosystem II derived from chlorophyll fluorescence measurements[56]. Based on the estimated slope of this regression (s), we calculated the rate of electron transport J for each combination of averages of the measured values for Iinc and Φ2 as in[13]:
| (8) |
Fig A in S8 Text shows the relationship between J and Iinc.
Boundary conditions
In the model, it is assumed that the resistance of the intercellular air space for CO2 transport is negligible. The cell wall and the plasma membrane were not modelled as separate domains, because they were very thin. Together with the stomata, they were incorporated in the boundary conditions of the combined cell wall and plasma membrane (Fig 2) instead. The following convection boundary conditions were thus assigned to these edges:
| (9) |
where ϕwp is the net flux of CO2 over the cell wall from the intercellular air space normal to the mesophyll surface; [CO2]a is the CO2 concentration at the leaf surface; [CO2]l is the local liquid phase CO2 concentration at the mesophyll surface; Gmem is the plasma membrane conductance (m s-1); twall is the cell wall thickness; peff is the effective porosity of the cell wall; R is the universal gas constant; T is the temperature; and H is Henry’s law constant for CO2 at temperature T and standard pressure. The term RT/H represents the dimensionless Henry’s law constant that is used to convert gas phase concentrations into liquid phase concentrations [29,53]. It is assumed that Gmem = 3.5·10−3 m s−1 [17] and peff,wall = 0.2. Gs represents the stomatal conductance expressed in m s−1. It was calculated from the measured stomatal conductance, expressed in mol m-2 s-1 Pa-1, as:
| (10) |
Since the chloroplast envelope is a double membrane, it was assumed that its conductance was half that of the plasma membrane. Therefore, the flux over the chloroplast envelope was modelled as a resistance with conductance . By applying Eqs (9) and (10), it was assumed that the resistance of the intercellular air space was negligible. All other boundaries of the computational domain were insulated as explained earlier. The formulation of the boundary conditions was equal for any of the scenarios for the location of mitochondria.
Estimation of leaf physiological parameters
We used the reaction-diffusion model directly to estimate the parameters Rd and Vcmax by minimizing the squared difference between the model and the data. For both estimation procedures, we used the MATLAB (The Mathworks, Natick, USA) lsqnonlin() function. We calculated the standard error of these estimates as , where ν is the squared norm of the residuals, J is the Jacobian matrix and JT is the transposed Jacobian matrix, and n is the number of data points[57]. The data that were used for the estimation of Rd and Vcmax can be found in S7 Text.
Estimation of Rd
We estimated Rd, based on the assumed location of (photo)respiratory CO2 release (inner cytosol, outer cytosol, or cytosol gaps between chloroplasts). For this estimation, we only used the AN and gs measurements from AN-Iinc curve measurements at Iinc set at 25, 50, 100, and 150 μmol m-2 s-1 at O = 21 kPa and Ca = 40 Pa. For this range of light levels, corresponding to limiting light levels commonly used to estimate Rd by conventional methods (12,38,40,41), we estimated Rd by minimizing the squared difference between average measured net rates of CO2 assimilation and the ones for each light level simulated by the reaction-diffusion model. For these light levels, the RuBP carboxylation rate is always limited by electron transport; so, Rd is expected to be estimated using J and Γ* as inputs.
Determination of Tp
In order to calculate Tp, we first determined the triose-phosphate-utilization-limited net CO2 assimilation rate Ap as the average measured net CO2 assimilation rate at Ca = 200 Pa, O = 21 kPa and Iinc = 1500 μmolm-2 s-1. From that average net CO2 assimilation rate, we calculated Tp as:
| (11) |
where we used the previously estimated values of Rd as input for Eq (11). By doing so, we made the assumption that, for these conditions of very high light and ambient CO2 levels, photosynthesis is limited only by triose-phosphate limitations throughout the chloroplast.
Estimation of Vcmax
For the estimation of Vcmax, we only used the AN and Ci measurements from AN-Ci curves measured at Iinc = 1500 μmol m-2 s-1, O = 21 kPa and Ca equal to 5, 10, 15, and 20 Pa. We estimated Vcmax by minimizing the squared difference between the average measured and simulated net CO2 assimilation rates at these ambient CO2 levels, assuming that the net CO2 assimilation rate is limited by Rubisco. During this procedure, we used the previously determined values for Rd and Tp as input variables. In order to do this estimation, we used COMSOL 5.2a with MATLAB livelink (COMSOL AB, Stockholm, Sweden) to convert the COMSOL model into a MATLAB 2014b (The Mathworks, Natick, USA) script to allow optimization. S11 Text contains scripts for the scenario that assumes (photo)respired CO2 release in the inner cytosol (Script A in S11 Text), the outer cytosol (Script B in S11 Text) and the cytosol gaps (Script C in S11 Text), respectively.
Validation
We did not use the measurements of the AN-Ci curves at ambient CO2 levels if the leaf was exposed to CO2 partial pressures between 40 Pa and 160 Pa for the estimation of s, Rd, Tp, and Vcmax. Neither did we use the AN-Iinc measurements at irradiances between 300 and 1500 μmol m-2 s-1. We used these remaining combinations of measured values for O, Iinc, and Ci to predict the net CO2 assimilation rate and compared these predictions with the experimental data. Those data can be found in S7 Text. We also checked whether a model with a single CO2 pool and two CO2 pools (12CO2 and 13CO2) would result in the same results. For each scenario, the calculated values for Cc, Ci and frec were the same.
Solving the model and post-processing
The model was implemented and solved in the finite element software COMSOL Multiphysics 5.1. After solving the model, the rate of CO2 production by RuBP carboxylation rate W, expressed as the rate per unit of leaf area per second, was calculated by multiplying the average volumetric rate of RuBP carboxylation by the total stroma volume and dividing this by the leaf surface area:
| (12) |
The rate of CO2 production per unit of leaf area by photorespiration was calculated as:
| (13) |
The net rate of CO2 assimilation was calculated as:
| (14) |
We used the calculated net CO2 assimilation rate and the simulated CO2 gradient in the chloroplast stroma to calculate the average CO2 partial pressure in the air spaces and the chloroplast stroma Cc, expressed in the gas phase, as:
| (15) |
| (16) |
Estimating re-assimilation of (photo)respired CO2
The model was used to calculate the fraction (frec) of CO2 produced by (photo)respiration that is re-assimilated. The method to achieve this is largely based on the method described in [28]. We used our model to conduct an in silico experiment mimicking the in vivo experiment described in[38]. In this experiment, a leaf was adapted to ambient CO2 levels and saturating light. Under ambient conditions, atmospheric CO2 mainly consists of 12CO2 isotopes. After adaptation, the leaf was exposed to air that contained 13CO2, but no 12CO2. The concentration of 13CO2 was the same as the concentration of 12CO2 under ambient conditions. The concentrations of 12CO2 and 13CO2 at the leaf surface reached new equilibrium concentrations after about 12 seconds. Although no atmospheric 12CO2 is taken up, the assimilates still contain mainly 12C isotopes, so all CO2 produced by (photo)respiration consists of 12CO2. It takes a longer period (20–30 s) than the 12-seconds adaptation time before measureable amounts of 13CO2 are released by (photo)respiration. The authors of this study [38] exploited this fact by stating that 12CO2 and 13CO2 are in quasi steady state during this period of 12 seconds. Since all (photo)respired CO2 consists of 12CO2, the measured net 13CO2 assimilation rate 13CAN equals the carboxylation rate W. Next they measured the 12CO2 and 13CO2 concentrations in the intercellular air space. The total CO2 concentration (12[CO2] + [13CO2]) is during the experiment. Since the discrimination of 13CO2 is very small (0.27‰) [58], they therefore assumed it to be negligible and stated that: .
The symbols [12CO2]i and [13CO2]i represent the concentrations of 12CO2 and 13CO2, respectively, in the intercellular air space. Since all assimilated CO2 produced by (photo)respiration consists of 12CO2, 12AN is also the rate of CO2 re-assimilation.
For the in silico experiment in this study, Eq (3) was replaced by separate reaction-diffusion equations for 12CO2 and 13CO2 transport. Since all CO2 production by (photo)respiration consists of 12CO2, the partial differential equations for 12CO2 and 13CO2 can be expressed as:
| (17) |
| (18) |
Since the total CO2 concentration does not change after 12CO2 in the air near the leaf surface was replaced by 13CO2, 12[CO2] + [13CO2] were substituted for [CO2] in Eqs (5) and (6). The volumetric consumption of 12CO2 and 13CO2 by RuBP carboxylation (w12 and w13) were expressed as:
| (19) |
| (20) |
It is assumed that the 12CO2 concentration at the leaf surface is zero and the following conditions were applied at the mesophyll cell surface, in analogy to Eq (9):
| (21) |
| (22) |
where and are the net fluxes of 12CO2 and 13CO2 respectively over the stomata, the intercellular air space, the cell wall and the plasma membrane; [13CO2]a is the concentration of 13CO2 at the leaf surface.
The re-assimilation rate was calculated, equivalent to the rate 12CO2 consumption due to RuBP carboxylation W12, as:
| (23) |
We validated the extension of the model with two CO2 isotopes by comparing Cc, frec and Ci calculated by this model and by the model that assumes only one CO2 pool for each scenario. The fraction of CO2 produced by (photo)respiration that is re-assimilated is calculated as[28]:
| (24) |
Note that our definition of re-assimilation is different from the one from[38]. In our study, we define the rate of re-assimilation as the rate of 12CO2 RuBP carboxylation W12. In contrast, in the definition of the rate of re-assimilation in [38] is , it is assumed that the rate of intracellular re-assimilation is negligible [20]. Therefore, this rate is called the rate of intercellular respiration in [20], which is the rate at which (photo)respired CO2 that enters the intercellular air spaces is re-assimilated. In this definition of intercellular respiration, it is implicitly assumed that RuBP carboxylation and (photo)respiration take place in the same compartment. As our model takes into account that (photo)respiration takes place in different compartments, this definition of intercellular re-assimilation cannot be used in our model. Therefore, we did not explicitly intercellular re-assimilation rates in our model.
Additional analyses
S4 Text contains the description of a sensitivity analysis for tcyt,in and tcyt,out to assess how these parameters may affect AN and frec. S4 Text also describes an analysis in which the mitochondria were modelled explicitly to assess to what extent modelling loose mitochondria may change the calculated values of AN and frec.
Supporting information
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Acknowledgments
The authors thank Ruud Börger (COMSOL BV, Zoetermeer, The Netherlands), Durk de Vries (COMSOL BV, Zoetermeer, The Netherlands) and dr. Tycho van Noorden (COMSOL Multiphysics BV, Zoetermeer, The Netherlands) for their advices to construct the model presented in this study. The authors also thank Dr. Steven Driever (Centre for Crop Systems Analysis, Wageningen University & Research, The Netherlands) for useful discussions on isotope discrimination and re-assimilation, and Dr. Alejandro Morales Sierra and Laurens Krah BSc for comments on an early version of the manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
Wageningen-based authors thank the BioSolar Cells programme (project C3B3) for financial support. Leuven-based authors thank the Research Council of the KU Leuven (project C16/16/002) for financial support. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Flexas J, Ribas-Carbo M, Diaz-Espejo A, Galmes J, Medrano H (2008) Mesophyll conductance to CO2: current knowledge and future prospects. Plant Cell and Environment 31: 602–621. [DOI] [PubMed] [Google Scholar]
- 2.Flexas J, Barbour MM, Brendel O, Cabrera HM, Carriqui M, et al. (2012) Mesophyll diffusion conductance to CO2: An unappreciated central player in photosynthesis. Plant Science 193–194: 70–84. doi: 10.1016/j.plantsci.2012.05.009 [DOI] [PubMed] [Google Scholar]
- 3.Harley PC, Loreto F, Dimarco G, Sharkey TD (1992) Theoretical considerations when estimating the mesophyll conductance to CO2 flux by analysis of the response of photosynthesis to CO2. Plant Physiology 98: 1429–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Niinemets U, Diaz-Espejo A, Flexas J, Galmes J, Warren CR (2009) Importance of mesophyll diffusion conductance in estimation of plant photosynthesis in the field. Journal of Experimental Botany 60: 2271–2282. doi: 10.1093/jxb/erp063 [DOI] [PubMed] [Google Scholar]
- 5.Farquhar GD, Caemmerer SV, Berry JA (1980) A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90. doi: 10.1007/BF00386231 [DOI] [PubMed] [Google Scholar]
- 6.Pons TL, Flexas J, von Caemmerer S, Evans JR, Genty B, et al. (2009) Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. Journal of Experimental Botany 60: 2217–2234. doi: 10.1093/jxb/erp081 [DOI] [PubMed] [Google Scholar]
- 7.Berghuijs HNC, Yin X, Ho QT, Driever SM, Retta MA, et al. (2016) Mesophyll conductance and reaction-diffusion models for CO2 transport in C3 leaves; needs, opportunities and challenges. Plant Science 252: 62–75. doi: 10.1016/j.plantsci.2016.05.016 [DOI] [PubMed] [Google Scholar]
- 8.Flexas J, Diaz-Espejo A, Galmes J, Kaldenhoff R, Medrano H, et al. (2007) Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant Cell and Environment 30: 1284–1298. [DOI] [PubMed] [Google Scholar]
- 9.Yin X, Struik PC (2009) Theoretical reconsiderations when estimating the mesophyll conductance to CO2 diffusion in leaves of C3 plants by analysis of combined gas exchange and chlorophyll fluorescence measurements. Plant Cell and Environment 32: 1513–1524. [DOI] [PubMed] [Google Scholar]
- 10.Gu LH, Sun Y (2014) Artefactual responses of mesophyll conductance to CO2 and irradiance estimated with the variable J and online isotope discrimination methods. Plant Cell and Environment 37: 1231–1249. [DOI] [PubMed] [Google Scholar]
- 11.Leuning R (1995) A critical-appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell and Environment 18: 339–355. [Google Scholar]
- 12.Gu JF, Yin X, Stomph TJ, Wang HQ, Struik PC (2012) Physiological basis of genetic variation in leaf photosynthesis among rice (Oryza sativa L.) introgression lines under drought and well-watered conditions. Journal of Experimental Botany 63: 5137–5153. doi: 10.1093/jxb/ers170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yin X, Struik PC, Romero P, Harbinson J, Evers JB, et al. (2009) Using combined measurements of gas exchange and chlorophyll fluorescence to estimate parameters of a biochemical C3 photosynthesis model: a critical appraisal and a new integrated approach applied to leaves in a wheat (Triticum aestivum) canopy. Plant Cell and Environment 32: 448–464. [DOI] [PubMed] [Google Scholar]
- 14.Tholen D, Ethier G, Genty B, Pepin S, Zhu XG (2012) Variable mesophyll conductance revisited: theoretical background and experimental implications. Plant Cell and Environment 35: 2087–2103. [DOI] [PubMed] [Google Scholar]
- 15.von Caemmerer S (2013) Steady-state models of photosynthesis. Plant Cell and Environment 36: 1617–1630. [DOI] [PubMed] [Google Scholar]
- 16.Yin X, Struik PC (2017) Simple generalisation of a mesophyll resistance model for various intracellular arrangements of chloroplasts and mitochondria in C3 leaves. Photosynthesis Research 132: 211–220. doi: 10.1007/s11120-017-0340-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Berghuijs HNC, Yin X, Ho QT, van der Putten PEL, Verboven P, et al. (2015) Modelling the relationship between CO2 assimilation and leaf anatomical properties in tomato leaves. Plant Science 238: 297–311. doi: 10.1016/j.plantsci.2015.06.022 [DOI] [PubMed] [Google Scholar]
- 18.Tholen D, Ethier G, Genty B (2014) Mesophyll conductance with a twist. Plant Cell and Environment 37: 2456–2458 [DOI] [PubMed] [Google Scholar]
- 19.Sage TL, Sage RF (2009) The functional anatomy of rice leaves:implications for refixation of photorespiratory CO2 and efforts to engineer C4 photosynthesis into rice. Plant and Cell Physiology 50: 756–772. doi: 10.1093/pcp/pcp033 [DOI] [PubMed] [Google Scholar]
- 20.Busch FA, Sage TL, Cousins AB, Sage RF (2013) C3 plants enhance rates of photosynthesis by reassimilating photorespired and respired CO2. Plant Cell and Environment 36: 200–212. [DOI] [PubMed] [Google Scholar]
- 21.Parkhurst DF (1977) A three-dimensional model for CO2 uptake by continuously distributed mesophyll in leaves. Journal of Theoretical Biology 67: 471–488. [DOI] [PubMed] [Google Scholar]
- 22.Parkhurst DF, Mott KA (1990) Intercellular diffusion limits to CO2 uptake in leaves. Plant Physiology 94: 1024–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Aalto T, Juurola E (2002) A three-dimensional model of CO2 transport in airspaces and mesophyll cells of a silver birch leaf. Plant Cell and Environment 25: 1399–1409. [Google Scholar]
- 24.Vesala T, Ahonen T, Hari P, Krissinel E, Shokhirev N (1996) Analysis of stomatal CO2 uptake by a three-dimensional cylindrically symmetric model. New Phytologist 132: 235–245. [Google Scholar]
- 25.Aalto T, Vesala T, Mattila T, Simbierowicz P, Hari P (1999) A three-dimensional stomatal CO2 exchange model including gaseous phase and leaf mesophyll separated by irregular interface. Journal of Theoretical Biology 196: 115–128. doi: 10.1006/jtbi.1998.0820 [DOI] [PubMed] [Google Scholar]
- 26.Juurola E, Aalto T, Thum T, Vesala T, Hari P (2005) Temperature dependence of leaf-level CO2 fixation: revising biochemical coefficients through analysis of leaf three-dimensional structure. New Phytologist 166: 205–215. doi: 10.1111/j.1469-8137.2004.01317.x [DOI] [PubMed] [Google Scholar]
- 27.Tholen D, Zhu XG (2011) The mechanistic basis of internal conductance: a theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plant Physiology 156: 90–105. doi: 10.1104/pp.111.172346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ho QT, Berghuijs HNC, Watte R, Verboven P, Herremans E, et al. (2016) Three-dimensional microscale modelling of CO2 transport and light propagation in tomato leaves enlightens photosynthesis. Plant, Cell and Environment 39: 50–61. doi: 10.1111/pce.12590 [DOI] [PubMed] [Google Scholar]
- 29.Tosens T, Niinemets U, Westoby M, Wright IJ (2012) Anatomical basis of variation in mesophyll resistance in eastern Australian sclerophylls: news of a long and winding path. Journal of Experimental Botany 63: 5105–5119. doi: 10.1093/jxb/ers171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tomas M, Flexas J, Copolovici L, Galmes J, Hallik L, et al. (2013) Importance of leaf anatomy in determining mesophyll diffusion conductance to CO2 across species: quantitative limitations and scaling up by models. Journal of Experimental Botany 64: 2269–2281. doi: 10.1093/jxb/ert086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kok B (1948) A critical consideration of the quantum yield of Chlorella photosynthesis. Enzymologia 13: 1–56. [Google Scholar]
- 32.Kok B (1949) On the interrelation of respiration and photosynthesis in green plates. Biochimica et Biophysica Acta 3: 625–631. [Google Scholar]
- 33.Laisk A (1977) Kinetics of photosynthesis and photorespiration in C3 plants (in Russian) Nauka Moscow. [Google Scholar]
- 34.Yin X, Sun ZP, Struik PC, Gu JF (2011) Evaluating a new method to estimate the rate of leaf respiration in the light by analysis of combined gas exchange and chlorophyll fluorescence measurements. Journal of Experimental Botany 62: 3489–3499. doi: 10.1093/jxb/err038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Parnik T, Keerberg O (2007) Advanced radiogasometric method for the determination of the rates of photorespiratory and respiratory decarboxylations of primary and stored photosynthates under steady-state photosynthesis. Physiologia Plantarum 129: 34–44. [Google Scholar]
- 36.Ethier GJ, Livingston NJ (2004) On the need to incorporate sensitivity to CO2 transfer conductance into the Farquhar-von Caemmerer-Berry leaf photosynthesis model. Plant Cell and Environment 27: 137–153. [Google Scholar]
- 37.Walker BJ, Skabelund DC, Busch FA, Ort DR (2016) An improved approach for measuring the impact of multiple CO2 conductances on the apparent photorespiratory CO2 compensation point through slope-intercept regression. Plant Cell Environ 39: 1198–1203. doi: 10.1111/pce.12722 [DOI] [PubMed] [Google Scholar]
- 38.Haupt-Herting S, Klug K, Fock HP (2001) A new approach to measure gross CO2 fluxes in leaves. Gross CO2 assimilation, photorespiration, and mitochondrial respiration in the light in tomato under drought stress. Plant Physiol 126: 388–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Loreto F, Delfine S, Di Marco G (1999) Estimation of photorespiratory carbon dioxide recycling during photosynthesis. Australian Journal of Plant Physiology 26: 733–736. [Google Scholar]
- 40.Terashima I, Hanba YT, Tazoe Y, Vyas P, Yano S (2006) Irradiance and phenotype: comparative eco-development of sun and shade leaves in relation to photosynthetic CO2 diffusion. Journal of Experimental Botany 57: 343–354. doi: 10.1093/jxb/erj014 [DOI] [PubMed] [Google Scholar]
- 41.Fanta SW, Vanderlinden W, Abera MK, Verboven P, Karki R, et al. (2012) Water transport properties of artificial cell walls. Journal of Food Engineering 108: 393–402. [Google Scholar]
- 42.Evans JR, Kaldenhoff R, Genty B, Terashima I (2009) Resistances along the CO2 diffusion pathway inside leaves. Journal of Experimental Botany 60: 2235–2248. doi: 10.1093/jxb/erp117 [DOI] [PubMed] [Google Scholar]
- 43.Watté R, Aernouts B, Van Beers R, Herremans E, Ho QT, et al. (2015) Modeling the propagation of light in realistic tissue structures with MMC-fpf: a meshed Monte Carlo method with free phase function. Optics Express 23: 17467–17486. doi: 10.1364/OE.23.017467 [DOI] [PubMed] [Google Scholar]
- 44.Nobel PS (2009) Physicochemical and Environmental Plant Physiology. Oxford, United Kingdom: Elsevier Inc. [Google Scholar]
- 45.Pachepsky LB, Haskett JD, Acock B (1995) A two-dimensional model of leaf gas exchange with special reference to leaf anatomy. Journal of Biogeography 22: 209–214. [Google Scholar]
- 46.Ho QT, Verboven P, Yin X, Struik PC, Nicolai BM (2012) A microscale model for combined CO2 diffusion and photosynthesis in leaves. Plos One 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Retta M, Ho QT, Yin X, Verboven P, Berghuijs HNC, et al. (2016) A two-dimensional microscale model of gas exchange during photosynthesis in maize (Zea mays L.) leaves. Plant Science 246: 37–51. doi: 10.1016/j.plantsci.2016.02.003 [DOI] [PubMed] [Google Scholar]
- 48.Evans JR, Von Caemmerer S, Setchell BA, Hudson GS (1994) The relationship between CO2 transfer conductance and leaf anatomy in transgenic tobacco with a reduced content of Rubisco. Australian Journal of Plant Physiology 21: 475–495. [Google Scholar]
- 49.Thain JF (1983) Curvature correction factors in the measurement of cell-surface areas in plant-tissues. Journal of Experimental Botany 34: 87–94. [Google Scholar]
- 50.Hatakeyama Y, Ueno O (2016) Intracellular position of mitochondria and chloroplasts in bundle sheath and mesophyll cells of C3 grasses in relation to photorespiratory CO2 loss. Plant Production Science 19: 540–551. [Google Scholar]
- 51.Aalto T, Juurola E (2001) Parametrization of a biochemical CO2 exchange model for birch (Betula pendula Roth.). Boreal Environment Research 6: 53–64. [Google Scholar]
- 52.Sharkey TD (1985) Photosynthesis in intact leaves of C3 plants—Physics, physiology and rate limitations. Botanical Review 51: 53–105. [Google Scholar]
- 53.Ho QT, Verboven P, Verlinden BE, Nicolai BM (2010) A model for gas transport in pear fruit at multiple scales. Journal of Experimental Botany 61: 2071–2081. doi: 10.1093/jxb/erq026 [DOI] [PubMed] [Google Scholar]
- 54.Gielwanowska I, Pastorczyk M, Kellmann-Sopyla W, Gorniak D, Gorecki RJ (2015) Morphological and ultrastructural changes of organelles in leaf mesophyll cells of the Arctic and Antarctic plants of Poaceae family under cold influence. Arctic Antarctic and Alpine Research 47: 17–25. [Google Scholar]
- 55.Moser T, Holzinger A, Buchner O (2015) Chloroplast protrusions in leaves of Ranunculus glacialisL. respond significantly to different ambient conditions, but are not related to temperature stress. Plant Cell and Environment 38: 1347–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Genty B, Briantais JM, Baker NR (1989) The relationship between the quantum yield of photosynthetic electron-transport and quenching of chlorophyll fluorescence. Biochimica et Biophysica Acta 990: 87–92. [Google Scholar]
- 57.Van Riel N Parameter estimation in non-equidistantly sampled nonlinear state space models; a Matlab implementation
- 58.Farquhar GD, Oleary MH, Berry JA (1982) On the relationship between carbon isotope discrimination and the inter-cellular carbon-dioxide concentration in leaves. Australian Journal of Plant Physiology 9: 121–137. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.