Abstract
In this paper, three non-parametric test statistics are proposed to design single-arm phase II group sequential trials for monitoring survival probability. The small-sample properties of these test statistics are studied through simulations. Sample size formulas are derived for the fixed sample test. The Brownian motion property of the test statistics allowed us to develop a flexible group sequential design using a sequential conditional probability ratio test procedure (Xiong, 1995). An example is given to illustrate the trial design by using the proposed method.
Keywords: Brownian motion, Interim analysis, Nelson-Aalen estimate, Single-arm phase II trial, Sample size, Survival probability
1 Introduction
Phase II trial evaluation is an important step in the development of new anti-cancer drugs and treatments. The goal of phase II cancer clinical trials is assessing the efficacy and toxicity of a new agent or treatment. Evidence of anti-cancer efficacy demonstrated in a phase II trial often determines whether the new agent or treatment warrants further study in a large and confirmatory randomized phase III trial. Phase II trials are often designed as single-arm studies with a limited number of subjects. Due to ethical concerns, interim monitoring rules are frequently used to terminate the trial early for futility, thereby reducing the number of subjects exposed to an ineffective therapy. The proportion of subjects achieving complete or partial response is often chosen as a surrogate endpoint of the study. Such trials with binary endpoints are often designed and monitored using Simon’s optimal or minimax two-stage design. However, for many phase II cancer trials, the probability of a subject surviving after some clinically meaningful landmark point x is the primary endpoint. Designing such trials with interim monitoring rules is challenging because of incomplete follow-up for some subjects at the time of the interim analyses. A naive approach is to estimate the survival probability as a simple proportion of all subjects surviving the required time at the interim analyses. There are several disadvantages to this approach. First, subjects who have not been followed for the required time will not contribute to the estimate of the survival probability, resulting in an inefficient estimate. Second, simply treating subjects who are lost to follow-up as treatment failures or excluding them from the analysis will result in a biased estimate. Finally, suspending accrual to wait for all the subjects to be followed up for the required length of time for an interim analysis is often impractical. Long trial suspensions can ruin a trial’s momentum, increase study length, and increase costs (Case and Morgan, 2003).
To design a trial with incomplete follow-up data, survival analysis can be used. There is much literature available to assist in the design of randomized phase III survival trials with multi-stage interim analyses, such as Jennison and Turnbull (2000) and references therein. However there are few such methods for the design of single-arm phase II survival trials with interim monitoring rules. Recently, several methods have been proposed for monitoring the survival probabilities at a fixed time point for single-arm phase II trials. For example, Case and Morgan (2003) proposed an optimal two-stage phase II design to minimize the expected sample size or expected study length under the null hypothesis. Huang et al. (2010) modified Case and Morgan’s approach to protect the type I error rate and improve the robustness of the design. Zhao et al. (2011) proposed a simulation based Bayesian decision theoretic two-stage design for a phase II clinical trial with survival endpoint. All these designs are restricted to a two-stage design only. Lin et al. (1996) developed a multi-stage sequential procedure for monitoring the survival probabilities, but it was developed for the purpose of testing a specific umbrella hypothesis of the National Wilms Tumor Study.
In phase II drug testing trials, it is also important to know as early as possible if the drug is highly promising. For this purpose and to allow more flexible monitoring of the trial, a sequential conditional probability ratio test (SCPRT) procedure (Xiong, 1995; Xiong et al., 2003) can be used to design a study with multi-stage interim analyses, and the trial can be monitored or stopped early for either futility or efficacy. The maximum sample size required for the SCPRT test is the same as for a fixed sample test, and the SCPRT boundaries have analytical solutions. Therefore, the proposed method can be easily applied to design a group sequential trial for monitoring the survival probability for a single-arm phase II study.
The rest of the paper is organized as follows: Section 2 discusses three non-parametric test statistics based on Nelson-Aalen estimate. Sample size formulas for a fixed sample test are derived in Section 3. A group sequential design using the SCPRT procedure is discussed in Section 4. The empirical type I error and power of the three test statistics are studied in Section 5 through simulations. An example is given in Section 6 to illustrate trial design using the proposed method. Section 7 is the concluding discussion.
2 Test Statistics
In a single-arm phase II trial with survival outcome, such as the time-to-failure (disease progression, relapse, or death) at some clinically meaningful landmark point x is often the primary interest. Let S(x) be the survival probability at x and S0(x) be the level of survival probability at x at which investigators are no longer interested in the treatment. Then the design of the single-arm phase II trial can be based on testing the following one-sided hypotheses:
for a given x; it is equivalent to test the hypotheses based on the cumulative hazard function Λ(x) = −logS(x)
| (1) |
where Λ0(x) = −logS0(x)
Suppose during the accrual phase of the trial, n subjects are enrolled in the study at calendar times Y1, ⋯, Yn which are measured from the start of the study. Let Ti and Ci denote, respectively, the failure time and censoring time of the ith subject, with both being measured from the time of study entry of this subject. We assume that the failure time Ti is independent of the censoring time Ci and entry time Yi, and {(Yi, Ti, Ci); i = 1, ⋯, n} are independent and identically distributed.
When the data are examined at calendar time t ≤ τ, where t is measured from the start of study and τ is the study duration, including the periods of enrollment and follow-up, we observe the time to failure Xi(t) = Ti∧Ci∧(t − Yi)+ and failure indicator Δi(t) = I(Ti ≤ Ci ∧ (t − Yi)+), i = 1, ⋯, n. Based on the observed data {Xi(t), Δi(t), i = 1, ⋯, n}, the Nelson-Aalen estimate for the cumulative hazard function is
| (2) |
where . It has been shown (Lin et al., 1996) that the process
converges weakly to a Gaussian process with time variable t and independent increments and variance
| (3) |
as a function of t, where π(u; t) = P(X1(t) ≥ u), and σ2(x; t) can be estimated by
| (4) |
(Lin et al., 1996; Breslow and Crowley, 1974; Fleming and Harrington, 1991).
However, the distribution of Λ̂(x; t) is often skewed, and it requires large sample sizes to maintain its type I error rate. This is partly because Λ̂(x; t) is restricted to nonnegative values. However, since a logarithmic transformation of the Nelson-Aalen estimate logΛ̂(x; t) takes the value over the entire real line, the asymptotic normality is expected to be more accurate. Therefore, Lin et al. (1996) suggested testing the hypothesis (1) using the following test statistic:
| (5) |
and showed that Z1(x; t) as a process in t can be approximated by a Gaussian process. Several other transformations have also been discussed in the literature (Klein et al., 2007), and the corresponding test statistics will be introduced as follows. The Nelson-Aalen estimate for the survival function is given as
| (6) |
which is asymptotically equivalent to the Kaplan-Meier estimator. The next test statistic is constructed based on an arcsine-square root transformation on Ŝ(x; t), which is given by
| (7) |
where
The third test statistic discussed in the paper is based on the logit transformation, which is given by
| (8) |
The small-sample properties of these three test statistics Z1 – Z3 will be studied and compared through simulations in Section 5.
3 Sample Size for Fixed Sample Test
A key step in designing a clinical trial is to calculate the required minimal sample size with constrained type I error and power. If the study is interested in testing hypotheses (1), then given type I error rate α and power 1 − β at the alternative Λ1(x)(< Λ0(x)) for a given x, the sample sizes for fixed sample tests can be derived as follows. The power of a test is the probability of rejecting the null hypothesis when the alternative is true. Hence, for a fixed sample test, the power of the test statistic Z1 = Z1(x; τ) under the alternative Λ(x) = Λ1(x) is determined by
where Φ(·) is the standard normal distribution function, and is the asymptotic variance of Λ̂(x; τ) for the alternative at the end of study duration t = τ. Thus, the sample size for a fixed sample test for test statistic Z1 is given by
| (9) |
Similarly, the sample size for Z2 is given by
| (10) |
where
and for Z3 is given by
| (11) |
To calculate the sample size n given in above formulas, we have to calculate the asymptotic variance under the alternative hypothesis, which is given by (3) with t = τ. Assuming subjects were recruited with a uniform distribution over the accrual period ta and followed for an additional period of length tf, then the study duration τ = ta + tf. We further assume that the survival function of censoring time is G1(u). Then under the alternative, π(u; t) = P(T1 ∧ C1 ∧ (t − Y1)+ ≥ u) = P(T1 ≥ u)P(C1 ≥ u)(P(Y1 < t − u) = S1(u)G1(u)min{(t − u)/ta, 1}, t > u. Thus from equation (3), we have
| (12) |
where λ1(·) and S1(·) are the hazard and survival distribution function at the alternative, respectively.
As a special case, if there is no loss to follow-up, then G1(u) = P(C1 ≥ u) = 1 and min{(ta + tf − u)/ta, 1} = 1 for any 0 < u ≤ x ≤ tf; hence equation (12) can be simplified as
| (13) |
This implies that if there is no loss to follow-up and x ≤ tf, then the sample size for a fixed sample test depends only on the single value S1(x), but not on the specification of the underlying survival distribution S1(·).
In traditional randomized oncology trials with survival as the endpoint, the study power is determined by the number of events (see, e.g., Collett, 2003). Similarly here, equation (12) showed that the variance depends on the survival probability and the censoring distribution. The more events in [0, x], the smaller is S(u) for u < x; the heavier is censoring, the smaller is G(u) for u < x; and then the larger is variance , which leads to larger sample size n. Therefore, even though the power of the test statistic is expressed explicitly in terms of sample size n, it is actually determined by the number of events. Unfortunately, there is no explicit formula available here to express the power in terms of number of events; however, the number of events is not as convenient as the sample size to be used for the design and operation of a planned study with survival data, in general.
4 Group Sequential Procedure
In this section, we will apply an SCPRT procedure (Xiong, 1995) to the test statistic Z1(x; t) as a sequential test statistic with time variable t based on its Brownian motion property (Lin et al., 1996; Breslow and Crowley, 1974). The SCPRT has some unique features: (1) the maximum sample size of the sequential test is the same as the sample size of the fixed sample test; (2) the probability of discordance, or the probability that the conclusion of the sequential test would be reversed if the experiment were not stopped according to the stopping rule but continued to the planned end, can be controlled to an arbitrarily small level; (3) the power function of the SCPRT is virtually the same as that of the fixed sample test (Xiong et al., 2007; Xiong, 1995). All these features make the SCPRT more practical and attractive to be used for designing a sequential trial.
Letting {Bt : 0 < t ≤ 1} be a Brownian motion Bt ~ N(θt, t) and B1 be the Bt at the final stage with full information t = 1, then the joint distribution of (Bt, B1) has a bivariate normal distribution with mean μ = (θt, θ) and variance matrix Σ = (σij)2×2 with σ11 = σ12 = σ21 = t and σ22 = 1. Therefore, according to multivariate normal conditional distribution theory (see, e.g., Anderson, 1958), the conditional density f(Bt|B1) is normal density of N(B1t, (1 − t)t). Let s0 = z1−α be the critical value of B1 to reject the null for the fixed sample test. Then the conditional maximum likelihood ratio for the stochastic process on information time t is (Xiong, 1995; Xiong, et al., 2003)
Taking the logarithm, the log likelihood ratio can be simplified as
which has a positive sign if Bt > z1−αt and a negative sign if Bt < z1−αt. This equation leads to lower and upper boundaries for Btk as
| (14) |
for k = 1, …, K, where K is the total number of looks, and t1, t2, ⋯, tK(= 1) are the information times of interim looks and the final look. The a in (14) is the boundary coefficient, and it is crucial to choose an appropriate a for the design such that the probability of conclusion by the sequential test being reversed by the test at the planned end is small but not unnecessarily small. The larger is a, the smaller is the discordance probability, and the wider apart are the upper and lower boundaries, making it harder for the sample path to reach boundaries and stop early and resulting in larger expected sample sizes. An appropriate a can be determined by choosing an appropriate discordance probability (Xiong, 1995; Xiong et al., 2003). As an illustration, the calculations of the operating characteristics of a multi-stage group sequential design are given in the Appendix.
We now apply the SCPRT to the test statistic Z1(x; t) in (5). Let
| (15) |
where . For a fixed x, U(x; t) is asymptotically a Brownian motion in the time scale of the information I(x; t), with mean E{U(x; t)} = δI(x; t) and covariance cov{U(x; t), U(x; s)} = I(x; t) for any t and s such that x < t < s < τ, where δ = n1/2(logΛ0(x) − logΛ1(x))Λ1(x) (Lin et al., 1996; Breslow and Crowley, 1974). Then we can transform this process into a process with time variable t* on [0, 1] by letting
| (16) |
be the information time, where is calculated by (3) or (12) or (13), depending on given conditions in the design, and letting
| (17) |
Then the sequential test statistic B(x; t*) ~ N(θt*, t*) is approximately a Brownian motion in information time t*, where the drift parameter . Based on the SCPRT procedure presented above, the lower and upper boundaries for at the kth look are given by
| (18) |
for k = 1, …, K, where is the information time at the kth look with calendar time tk. The nominal critical p-values for testing hypotheses (1) are
| (19) |
The observed p-value at the kth look is
The stopping rule for monitoring the trial can be executed by stopping the trial when, for the first time, (accept H0 and stop for futility) or (reject H0 and stop for efficacy). Since Z1(x; tk) and are asymptotically the same standard normal distribution under the null hypothesis, the observed p-value at k-stage can be calculated from the test statistic Z1(x; tk) by applying all observations up to stage k. The derived sequential boundaries (18) are also applied to the test statistics Z2 in (7) and Z3 in (8) because the two sequential test statistics obviously have the same Brownian process property based on arguments by Lin et al. (1996). The maximum sample sizes (n) for the three sequential test statistics Z1(x; t), Z2(x; t), and Z3(x; t) are same as the sample sizes for corresponding fixed test statistics and can be obtained by equations (9), (10), and (11), respectively. The operating characteristics of a multi-stage group sequential design can be calculated using computation methods illustrated in the Appendix.
For convenience, an SCPRT procedure can be summarized as follows: a) Compute the sample size n for a fixed sample test using the formulas given in Section 2. b) Given the number of looks, K, and the maximum conditional discordance probability ρ, determine the boundary coefficient a (Xiong et al., 2003). c) Given calendar times t1, …, tK, calculate information times using formulas (16) and (3) or (12) or (13), depending on the given conditions of the design. d) Calculate SCPRT boundaries using equation (18). e) Calculate the nominal critical p-values using formula (19).
5 Simulation Study
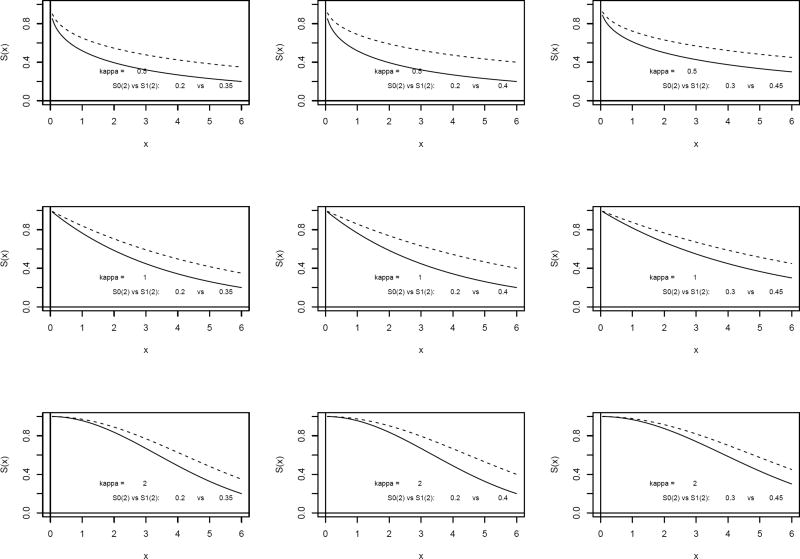
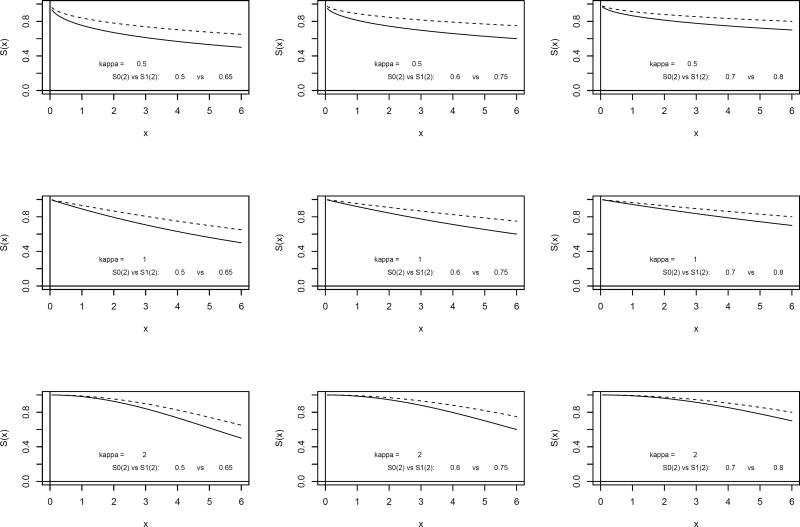
To show the small-sample properties of the three test statistics discussed in Section 2, we conducted simulation studies to compare the type I errors and powers for the three test statistics Z1, Z2, and Z3 under various scenarios. In simulation studies, the survival distribution was taken as S(x) = e−(ωx)κ, which is the Weibull distribution W(ω, κ) with scale parameter ω and shape parameter κ, where the shape parameter is set to be κ = 0.5, 1, and 2. The physical meaning of κ for the shape of the survival function by the Weibull distribution can be understood by observing plots of survival functions in Figure 1. The scale parameter ω is determined by the given values of S0(2) and S1(2) under null and alternative hypotheses, where x = 2 is the clinically meaningful landmark point (e.g., 2 months or 2 years) selected for the simulations. The simulations were performed for a variety of study designs of the fixed sample test and are shown in Table 1. The survival functions under null S0(x) and alternative S1(x) of the Weibull distribution with the various settings of simulation parameters in Table 1 are plotted in Figure 1 for illustration and for helping one to choose an appropriate shape parameter κ for sample size calculations in real applications. The null and alternative hypothesis value of survival probabilities S0(2) and S1(2) are set up to be in a normal hypothesis range 0.2–0.8 to detect a difference of 0.1–0.2 between S0(2) and S1(2).
Figure 1.
Survival functions for the Weibull distribution under the null and alternative hypotheses for different design scenarios.
Table 1.
Sample size and simulated empirical type I error (α) and power (1 − β) based on 100,000 simulation runs for Weibull and log-normal distributions with nominal level 0.05 and power of 80% for fixed test statistics Z1 − Z3
| Dist. | Design | 0.2 vs 0.35 | 0.2 vs 0.4 | 0.3 vs 0.45 | |||||||
|
| |||||||||||
| W(ω, κ) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 0.5 | Z1 | 63 | .055 | .837 | 38 | .056 | .849 | 77 | .051 | .840 | |
| Z2 | 59 | .058 | .825 | 35 | .060 | .834 | 70 | .056 | .821 | ||
| Z3 | 51 | .069 | .803 | 30 | .078 | .817 | 65 | .062 | .811 | ||
|
| |||||||||||
| 1 | Z1 | 65 | .054 | .837 | 40 | .055 | .854 | 79 | .051 | .839 | |
| Z2 | 61 | .058 | .825 | 36 | .061 | .833 | 72 | .057 | .821 | ||
| Z3 | 52 | .071 | .802 | 31 | .077 | .818 | 68 | .063 | .816 | ||
|
| |||||||||||
| 2 | Z1 | 67 | .056 | .838 | 41 | .055 | .854 | 82 | .051 | .841 | |
| Z2 | 63 | .057 | .823 | 37 | .059 | .831 | 74 | .057 | .820 | ||
| Z3 | 54 | .068 | .802 | 31 | .077 | .811 | 70 | .062 | .816 | ||
|
| |||||||||||
| LN(μ, σ2) | σ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 2 | Z1 | 63 | .056 | .837 | 39 | .056 | .855 | 77 | .051 | .838 | |
| Z2 | 59 | .056 | .821 | 35 | .059 | .832 | 70 | .058 | .820 | ||
| Z3 | 51 | .071 | .804 | 30 | .078 | .816 | 66 | .063 | .813 | ||
|
| |||||||||||
| 1 | Z1 | 65 | .053 | .834 | 40 | .055 | .854 | 80 | .051 | .839 | |
| Z2 | 62 | .056 | .827 | 36 | .060 | .831 | 73 | .057 | .822 | ||
| Z3 | 53 | .071 | .806 | 31 | .076 | .815 | 68 | .062 | .813 | ||
|
| |||||||||||
| 0.5 | Z1 | 67 | .054 | .836 | 41 | .054 | .852 | 82 | .052 | .838 | |
| Z2 | 63 | .057 | .823 | 37 | .059 | .828 | 75 | .056 | .823 | ||
| Z3 | 54 | .071 | .798 | 32 | .076 | .817 | 70 | .062 | .813 | ||
|
| |||||||||||
| Dist. | Design | 0.5 vs 0.65 | 0.6 vs 0.75 | 0.7 vs 0.8 | |||||||
|
| |||||||||||
| W(ω, κ) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 0.5 | Z1 | 86 | .048 | .856 | 82 | .048 | .869 | 152 | .045 | .857 | |
| Z2 | 72 | .058 | .817 | 65 | .060 | .825 | 124 | .058 | .816 | ||
| Z3 | 77 | .055 | .833 | 74 | .055 | .852 | 143 | .051 | .847 | ||
|
| |||||||||||
| 1 | Z1 | 89 | .049 | .838 | 85 | .049 | .869 | 157 | .046 | .857 | |
| Z2 | 75 | .058 | .820 | 67 | .058 | .825 | 128 | .059 | .815 | ||
| Z3 | 80 | .055 | .835 | 77 | .055 | .852 | 148 | .050 | .847 | ||
|
| |||||||||||
| 2 | Z1 | 92 | .048 | .854 | 87 | .048 | .866 | 162 | .046 | .856 | |
| Z2 | 77 | .057 | .819 | 69 | .058 | .823 | 132 | .058 | .815 | ||
| Z3 | 82 | .055 | .833 | 79 | .055 | .851 | 153 | .051 | .847 | ||
|
| |||||||||||
| LN(μ, σ2) | σ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 2 | Z1 | 88 | .048 | .856 | 84 | .047 | .872 | 156 | .047 | .858 | |
| Z2 | 74 | .058 | .822 | 66 | .059 | .822 | 127 | .058 | .815 | ||
| Z3 | 78 | .055 | .830 | 76 | .051 | .850 | 147 | .051 | .847 | ||
|
| |||||||||||
| 1 | Z1 | 91 | .048 | .855 | 87 | .047 | .869 | 162 | .047 | .855 | |
| Z2 | 76 | .057 | .818 | 68 | .061 | .825 | 132 | .058 | .815 | ||
| Z3 | 81 | .055 | .834 | 79 | .052 | .852 | 152 | .050 | .847 | ||
|
| |||||||||||
| 0.5 | Z1 | 93 | .048 | .852 | 89 | .046 | .869 | 166 | .047 | .857 | |
| Z2 | 78 | .057 | .818 | 70 | .059 | .825 | 135 | .057 | .813 | ||
| Z3 | 83 | .055 | .832 | 81 | .053 | .852 | 157 | .050 | .847 | ||
We assumed that subjects were recruited with a uniform distribution over the accrual period ta = 5 and followed for tf = 3, with the study duration τ = ta + tf = 8. By the definition of Xi(t) and equation (2), at the interim look time t, a subject was censored if his/her failure time was longer than either x = 2, or censoring time Ci or t − ui, where Ci follows an exponential distribution with hazard rate of 0.1 and ui is an uniform distributed entry time on interval [0, ta] for ith subject. The empirical type I error and power of the test statistics by simulation were evaluated at the end of the study τ = 8 for the fixed sample test and at t1 = 4 and t2 = 8 for the two-stage group sequential test. The fixed sample sizes for each design were calculated using formula (9), (10), and (11), respectively, for Z1(x; t), Z2(x; t), and Z3(x; t); the in these formulas was calculated by (12) with t = τ. For each parameter configuration of the corresponding design, 100,000 observed samples of censored failure times were generated from the Weibull distribution W(ω, κ) to calculate the test statistics under the null or alternative hypothesis. The nominal type I error and power were set to be 5% and 80%, respectively. The proportions rejecting the null under the true null hypothesis represent the estimated empirical type I error. The proportions rejecting the null under the alternative hypothesis represent the estimated empirical power. The simulated empirical type I errors and powers based on samples (excluding those with Ŝ(2; τ) = 0 and Ŝ(2; τ) = 1) are summarized in Tables 1–4 for Z1–Z3 in various scenarios.
Table 4.
Operating characteristics of the three-stage SCPRT design based on 100,000 simulation runs under Weibull distribution W(ω, κ) with nominal level 0.05 and power of 80% of the test Z1 for the example in Section 6
| At kth interim look | k = 1 | k = 2 | k = 3 | total |
|---|---|---|---|---|
| Type I error | ||||
| Nominal | 0.0026 | 0.0028 | 0.0452 | 0.0507 |
| Empirical | 0.0019 | 0.0025 | 0.0472 | 0.0516 |
|
| ||||
| Power | ||||
| Nominal | 0.1274 | 0.1554 | 0.5165 | 0.7993 |
| Empirical | 0.1174 | 0.1608 | 0.5297 | 0.8079 |
|
| ||||
| Probability of stopping under null | ||||
| Nominal | 0.2759 | 0.2585 | 0.4658 | 1.0000 |
| Empirical | 0.2472 | 0.2510 | 0.5017 | 1.0000 |
|
| ||||
| Probability of stopping under alternative | ||||
| Nominal | 0.1393 | 0.1712 | 0.6897 | 1.0000 |
| Empirical | 0.1244 | 0.1689 | 0.7067 | 1.0000 |
|
| ||||
| Expected stopping time and sample size | ET(0) | ET(θa)* | EN(0) | EN(θa) |
| Nominal | 0.7608 | 0.8659 | 77 | 87 |
| Empirical | 0.7791 | 0.8747 | 78 | 88 |
: θa = z1 − α + z1 − β is the drift parameter at the alternative hypothesis.
From Table 1, we may have following observations. First, under each hypothetical setting of the Weibull distribution, being the same for Z1–Z3, the calculated sample sizes of the three statistics could be quite different, with the largest for Z1; the empirical type I errors by simulation for the three statistics are slightly different but all close to the targeted goal (0.05), with the smallest for Z1; the empirical powers for the three statistics could be quite different, but all are above the targeted goal (0.80), with the largest for Z1. Second, for each test statistic (e.g., Z1) under the same hypothetical setting (e.g., 0.2 vs 0.35), the sample sizes under different values of κ are slightly different, increasing with the largest for κ = 2; for the same test statistic, the empirical type I errors and powers of this statistic under three values of κ are very close to one another. Third, for each test statistic (e.g., Z1) under the same value of κ setting (e.g., κ = 1), the sample sizes under different hypothetical settings (e.g., (0.2 vs 0.3) and (0.5 vs 0.65)) could be quite different; the sample size increases as the difference between S0(2) and S1(2) gets smaller.
In summary, the simulation results for empirical type I errors and powers showed that the test statistic Z1 is slightly liberal (e.g., α = 0.055) when the null survival probability S0(2) is set low (e.g., S0(2) = 0.2), and slightly conservative (e.g., α = 0.045) when S0(2) is set high (e.g., S0(2) = 0.7); whereas the empirical type I errors for Z2 and Z3 are liberal in most scenarios. The Z1 requires largest sample size and it is overpowered in all scenarios. Therefore, the sample size calculated based on Z1 is overestimated. Z2 and Z3 require relatively small sample size, but both have inflated type I error.
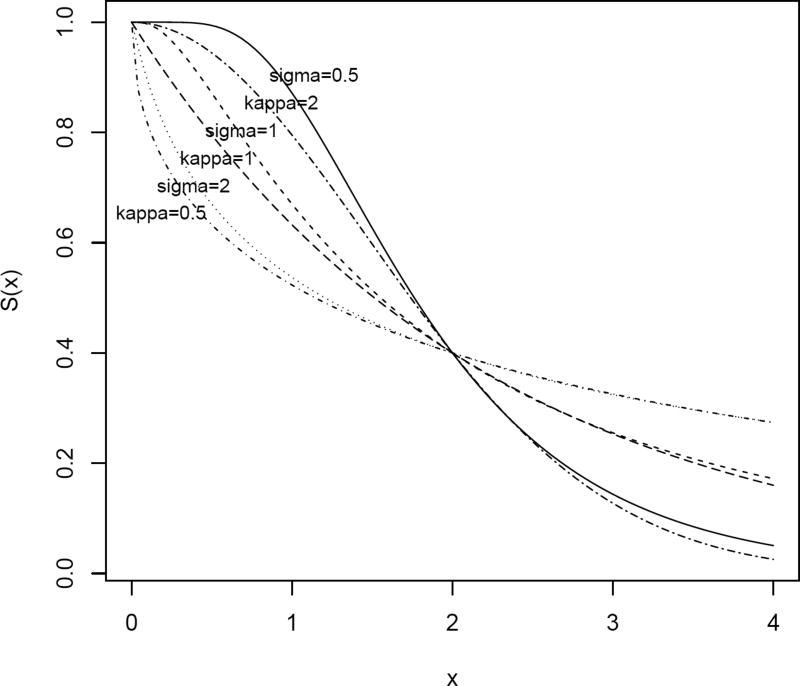
Sample size calculations and simulations were also done under the log-normal distribution LN(μ, σ2) using the same design scenarios as discussed above for the Weibull distribution. The sample sizes and simulation results under the log-normal are almost identical to those under the Weibull distribution when σ = 2, 1, and 0.5 for the log-normal distribution are set corresponding to κ = 0.5, 1, and 2 for the Weibull distribution. To help us understood this phenomenon, the Weibull distribution W(ω, κ) and log-normal distribution LN(μ, σ2) are plotted in Figure 2 with scale parameters (ω and μ) equal to survival probability under the null hypothesis (e.g., S0(2) = 0.4) and shape parameters (κ and σ) ranging from 0.5 to 2.
Figure 2.
Survival functions for the Weibull and log-normal distributions under the null hypothesis for different shape parameters.
To study the properties of the sequential tests with Z1–Z3, simulations were done for a two-stage SCPRT design under the Weibull distribution using the same fixed design scenarios as discussed above (Tables 3–4). The simulated empirical type I error of test Z1 were slightly liberal when the null hypothesis survival probability was set low, and slightly conservative when the null hypothesis survival probability was set high, in particular at the first stage with a small sample size, whereas the empirical type I error for Z2 and Z3 was liberal for most scenarios.
Table 3.
Simulated empirical type I error and power of the two-stage SCPRT design based on 100,000 simulation runs for Weibull distribution W(ω, κ) with nominal level 0.05 and power of 80% for fixed test statistics Z1 − Z3
| Type I error | Power | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Design | κ | Test | At kth interim look | k = 1 | k = 2 | total | k = 1 | k = 2 | total | ||
| 0.2 vs 0.35 | 0.5 | Z1 | Empirical | .0058 | .0511 | .0569 | .2883 | .5507 | .8384 | ||
| Z2 | Empirical | .0082 | .0512 | .0594 | .3118 | .5112 | .8230 | ||||
| Z3 | Empirical | .0149 | .0603 | .0752 | .3423 | .4659 | .8082 | ||||
|
|
|||||||||||
| Nominal | .0046 | .0462 | .0507 | .2091 | .5901 | .7992 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0050 | .0506 | .0557 | .2434 | .5957 | .8391 | |||
| Z2 | Empirical | .0082 | .0518 | .0599 | .2720 | .5542 | .8262 | ||||
| Z3 | Empirical | .0137 | .0625 | .0762 | .2988 | .5066 | .8054 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0046 | .0520 | .0566 | .2060 | .6307 | .8367 | |||
| Z2 | Empirical | .0067 | .0532 | .0599 | .2402 | .5840 | .8242 | ||||
| Z3 | Empirical | .0133 | .0622 | .0755 | .2706 | .5376 | .8082 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 0.2 vs 0.4 | 0.5 | Z1 | Empirical | .0060 | .0519 | .0579 | .2935 | .5556 | .8495 | ||
| Z2 | Empirical | .0103 | .0541 | .0643 | .3396 | .4955 | .8352 | ||||
| Z3 | Empirical | .0181 | .0653 | .0834 | .3675 | .4549 | .8224 | ||||
|
|
|||||||||||
| Nominal | .0046 | .0461 | .0507 | .2120 | .5871 | .7991 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0049 | .0524 | .0573 | .2473 | .6084 | .8557 | |||
| Z2 | Empirical | .0105 | .0542 | .0647 | .2960 | .5375 | .8334 | ||||
| Z3 | Empirical | .0171 | .0668 | .0839 | .3263 | .4961 | .8224 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0042 | .0530 | .0573 | .2037 | .6507 | .8543 | |||
| Z2 | Empirical | .0092 | .0542 | .0634 | .2621 | .5704 | .8325 | ||||
| Z3 | Empirical | .0149 | .0678 | .0827 | .2838 | .5286 | .8124 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 0.3 vs 0.45 | 0.5 | Z1 | Empirical | .0052 | .0483 | .0535 | .2712 | .5698 | .8411 | ||
| Z2 | Empirical | .0080 | .0502 | .0582 | .3073 | .5173 | .8246 | ||||
| Z3 | Empirical | .0100 | .0547 | .0647 | .3112 | .5046 | .8158 | ||||
|
|
|||||||||||
| Nominal | .0046 | .0461 | .0507 | .2145 | .5848 | .7992 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0044 | .0490 | .0534 | .2257 | .6137 | .8394 | |||
| Z2 | Empirical | .0078 | .0508 | .0586 | .2674 | .5565 | .8239 | ||||
| Z3 | Empirical | .0096 | .0563 | .0659 | .2744 | .5448 | .8192 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0034 | .0492 | .0525 | .1904 | .6504 | .8408 | |||
| Z2 | Empirical | .0073 | .0523 | .0596 | .2347 | .5880 | .8227 | ||||
| Z3 | Empirical | .0083 | .0574 | .0656 | .2412 | .5757 | .8169 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 0.5 vs 0.65 | 0.5 | Z1 | Empirical | .0035 | .0446 | .0481 | .2538 | .6013 | .8551 | ||
| Z2 | Empirical | .0085 | .0512 | .0605 | .3110 | .5102 | .8211 | ||||
| Z3 | Empirical | .0060 | .0504 | .0564 | .2780 | .5566 | .8366 | ||||
|
|
|||||||||||
| Nominal | .0047 | .0460 | .0507 | .2217 | .5756 | .7993 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0032 | .0464 | .0495 | .2008 | .6536 | .8544 | |||
| Z2 | Empirical | .0084 | .0530 | .0614 | .2690 | .5571 | .8261 | ||||
| Z3 | Empirical | .0053 | .0523 | .0576 | .2334 | .6031 | .8365 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0025 | .0451 | .0477 | .1633 | .6910 | .8543 | |||
| Z2 | Empirical | .0080 | .0529 | .0608 | .2359 | .5868 | .8227 | ||||
| Z3 | Empirical | .0052 | .0516 | .0568 | .1980 | .6349 | .8329 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 0.6 vs 0.75 | 0.5 | Z1 | Empirical | .0030 | .0451 | .0482 | .2403 | .6283 | .8686 | ||
| Z2 | Empirical | .0100 | .0524 | .0623 | .3239 | .5040 | .8280 | ||||
| Z3 | Empirical | .0049 | .0488 | .0536 | .2645 | .5879 | .8524 | ||||
|
|
|||||||||||
| Nominal | .0047 | .0459 | .0507 | .2275 | .5718 | .7993 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0026 | .0444 | .0470 | .1818 | .6883 | .8701 | |||
| Z2 | Empirical | .0100 | .0532 | .0632 | .2789 | .5477 | .8266 | ||||
| Z3 | Empirical | .0038 | .0495 | .0533 | .2069 | .6452 | .8521 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0017 | .0461 | .0478 | .1397 | .7285 | .8682 | |||
| Z2 | Empirical | .0097 | .0530 | .0627 | .2477 | .5783 | .8260 | ||||
| Z3 | Empirical | .0037 | .0498 | .0535 | .1671 | .6833 | .8504 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 0.7 vs 0.8 | 0.5 | Z1 | Empirical | .0033 | .0443 | .0477 | .2396 | .6174 | .8570 | ||
| Z2 | Empirical | .0087 | .0509 | .0596 | .3054 | .5128 | .8181 | ||||
| Z3 | Empirical | .0042 | .0474 | .0516 | .2531 | .5931 | .8462 | ||||
|
|
|||||||||||
| Nominal | .0047 | .0459 | .0506 | .2288 | .5705 | .7993 | |||||
|
| |||||||||||
| 1 | Z1 | Empirical | .0024 | .0457 | .0480 | .1857 | .6702 | .8559 | |||
| Z2 | Empirical | .0079 | .0520 | .0600 | .2609 | .5571 | .8180 | ||||
| Z3 | Empirical | .0032 | .0470 | .0502 | .2006 | .6461 | .8466 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
|
| |||||||||||
| 2 | Z1 | Empirical | .0021 | .0449 | .0470 | .1456 | .7083 | .8539 | |||
| Z2 | Empirical | .0085 | .0534 | .0619 | .2311 | .5881 | .8191 | ||||
| Z3 | Empirical | .0032 | .0480 | .0511 | .1676 | .6782 | .8458 | ||||
|
|
|||||||||||
| Nominal | .0043 | .0469 | .0512 | .1454 | .6534 | .7987 | |||||
Overall, the test statistic Z1 has a satisfactory type I error rate and hence is recommended for use in phase II trial design. However, the sample size calculated based on Z1 is overestimated. A further simulation (Table 2) showed that by reducing sample size by about 10%, the power of the test Z1 will stay at the nominal 80% level without inflating the type I error. The sample size calculation results also showed that even one misspecified κ value in design stage for the Weibull distribution or a misspecified underlying distribution from the Weibull to the log-normal had little impact on the study power or sample size.
Table 2.
Simulated empirical type I error (α) and power (1 − β) based on 100,000 simulation runs for the Weibull and log-normal distributions with the reduced sample size, adjusting the empirical power of Z1 to nearly 80%, for fixed tests with Z1 − Z3
| Dist. | Design | 0.2 vs 0.35 | 0.2 vs 0.4 | 0.3 vs 0.45 | |||||||
|
| |||||||||||
| W(ω, κ) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 0.5 | Z1 | 56 | .055 | .800 | 33 | .057 | .806 | 70 | .051 | .808 | |
| Z2 | 56 | .057 | .807 | 33 | .061 | .815 | 70 | .056 | .822 | ||
| Z3 | 56 | .070 | .830 | 33 | .073 | .841 | 70 | .062 | .833 | ||
|
| |||||||||||
| 1 | Z1 | 58 | .054 | .803 | 34 | .056 | .802 | 72 | .052 | .807 | |
| Z2 | 58 | .059 | .810 | 34 | .060 | .814 | 72 | .057 | .821 | ||
| Z3 | 58 | .072 | .831 | 34 | .075 | .843 | 72 | .063 | .831 | ||
|
| |||||||||||
| 2 | Z1 | 60 | .055 | .802 | 35 | .055 | .806 | 74 | .052 | .808 | |
| Z2 | 60 | .058 | .810 | 35 | .059 | .814 | 74 | .057 | .819 | ||
| Z3 | 60 | .069 | .833 | 35 | .074 | .842 | 74 | .062 | .833 | ||
|
| |||||||||||
| LN(μ, σ2) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 2 | Z1 | 56 | .055 | .801 | 33 | .055 | .804 | 70 | .052 | .806 | |
| Z2 | 56 | .057 | .807 | 33 | .060 | .815 | 70 | .058 | .820 | ||
| Z3 | 56 | .070 | .830 | 33 | .074 | .838 | 70 | .063 | .832 | ||
|
| |||||||||||
| 1 | Z1 | 58 | .054 | .799 | 34 | .056 | .802 | 72 | .051 | .805 | |
| Z2 | 58 | .058 | .810 | 34 | .059 | .812 | 72 | .057 | .817 | ||
| Z3 | 58 | .070 | .831 | 34 | .075 | .841 | 72 | .062 | .829 | ||
|
| |||||||||||
| 0.5 | Z1 | 60 | .055 | .802 | 35 | .057 | .804 | 74 | .051 | .805 | |
| Z2 | 60 | .056 | .809 | 35 | .058 | .811 | 74 | .057 | .817 | ||
| Z3 | 60 | .070 | .831 | 35 | .073 | .839 | 74 | .062 | .831 | ||
|
| |||||||||||
| Dist. | Design | 0.5 vs 0.65 | 0.6 vs 0.75 | 0.7 vs 0.8 | |||||||
|
| |||||||||||
| W(ω, κ) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 0.5 | Z1 | 75 | .048 | .805 | 68 | .046 | .806 | 132 | .047 | .807 | |
| Z2 | 75 | .058 | .830 | 68 | .059 | .839 | 132 | .058 | .837 | ||
| Z3 | 75 | .054 | .826 | 68 | .052 | .821 | 132 | .050 | .819 | ||
|
| |||||||||||
| 1 | Z1 | 77 | .048 | .805 | 70 | .047 | .804 | 136 | .046 | .801 | |
| Z2 | 77 | .057 | .830 | 70 | .059 | .837 | 136 | .058 | .833 | ||
| Z3 | 77 | .055 | .822 | 70 | .052 | .821 | 136 | .050 | .811 | ||
|
| |||||||||||
| 2 | Z1 | 80 | .048 | .808 | 72 | .046 | .801 | 139 | .046 | .801 | |
| Z2 | 80 | .058 | .830 | 72 | .058 | .835 | 139 | .058 | .833 | ||
| Z3 | 80 | .055 | .826 | 72 | .053 | .820 | 139 | .049 | .813 | ||
|
| |||||||||||
| LN(μ, σ2) | κ | Test | n | α | 1 − β | n | α | 1 − β | n | α | 1 − β |
|
| |||||||||||
| 2 | Z1 | 75 | .048 | .801 | 68 | .046 | .796 | 132 | .047 | .797 | |
| Z2 | 75 | .058 | .826 | 68 | .062 | .832 | 132 | .058 | .826 | ||
| Z3 | 75 | .056 | .821 | 68 | .053 | .814 | 132 | .050 | .808 | ||
|
| |||||||||||
| 1 | Z1 | 77 | .048 | .799 | 70 | .045 | .792 | 136 | .047 | .795 | |
| Z2 | 77 | .058 | .823 | 70 | .059 | .830 | 136 | .058 | .826 | ||
| Z3 | 77 | .055 | .814 | 70 | .052 | .813 | 136 | .050 | .805 | ||
|
| |||||||||||
| 0.5 | Z1 | 80 | .048 | .803 | 72 | .046 | .792 | 139 | .046 | .792 | |
| Z2 | 80 | .058 | .827 | 72 | .060 | .828 | 139 | .057 | .825 | ||
| Z3 | 80 | .055 | .819 | 72 | .053 | .812 | 139 | .051 | .807 | ||
6 An Example
The example is to design a single-arm phase II trial for patients with refractory metastatic colorectal cancer. The primary objective of the study was to evaluate overall survival at 6 months from enrollment (Huang, et al., 2010). The null overall survival probability at 6 months was 0.45 based on historical data. An alternative survival probability of 0.60 at 6 months was selected as a success rate warranting further development of the new treatment. Assume that overall survival time is exponentially distributed (i.e., Weibull with κ = 1) and during the trial patients could be censored exponentially with a hazard rate of 0.1 in addition to the administrative censoring. Under these assumptions, the sample size for the fixed sample test calculated based on the test Z1 is 112 patients with a nominal level α = 0.05 and power of 80% at the alternative. However, a simulation of 100,000 runs based on sample size 112 showed that the empirical type I error and power are 0.05 and 84.6%, respectively. Therefore, the study is overpowered. A further simulation showed that sample size of 100 for the fixed test would have 81% empirical power and type I error of 0.051. Hence the study with a sample size of 100 maintains the study power and does not inflate the type I error. If an average of 3.7 patients can be accrued per month, then the accrual period is ta = 27 months for 100 patients. Assuming a follow-up period tf = 6 months, then the study duration is τ = 33 months. The investigators are planning a three-stage group sequential design with two interim looks and a final look planned at calendar times t1 = 18, t2 = 24, and t3 = 33 months. Then the corresponding variances at interim look tk can be calculated by
where κ = 1 and ω is determined by the alternative S1(6) = 0.6. By numerical integration, and the information time t* = (0.445, 0.667, 1). Assuming a maximum conditional probability of discordance ρ = 0.02 (recommended by Xiong et al., 2003), we have a = 2.604 for K = 3 (Xiong et al., 2003). The lower boundary and upper boundary calculated by (6) are (a1, a2, a3) = (−0.402, 0.0216, 1.645) and (b1, b2, b3) = (1.866, 2.173, 1.645), respectively. The acceptance and rejection nominal critical significance levels are (0.727, 0.489, 0.05) and (0.0026, 0.0039, 0.05), respectively. Therefore, at the first interim look, if the observed p-value ≤ 0.0026, then reject the null (declaim or stop for efficacy), or if the observed p-value ≥ 0.727, then accept the null (stop for futility); otherwise, the trial continues to the second stage. At the second interim look, if the observed p-value ≤ 0.0039, then reject the null (declaim or stop for efficacy), or if the observed p-value ≥ 0.489, then accept the null (stop for futility); otherwise, the trial continues to the final stage. We performed 100,000 simulation runs under the exponential model to evaluate the operating characteristics of the proposed group sequential design. The empirical (nominal) type I error and power of the three-stage sequential test were 0.0516 (0.0507) and 0.8079 (0.799), respectively. The empirical (nominal) probabilities of stopping under null and alternative hypothesis were 0.247 (0.276) and 0.124 (0.139) at the first look; 0.251 (0.259) and 0.169 (0.171) at the second look, respectively. The details of the operating characteristics for the proposed group sequential design are shown in Table 4.
7 Conclusion
A single-arm phase II group sequential design is proposed for monitoring the survival probability at a fixed time point. A practical issue to design such a study is to select the time point at which the survival probability to be tested. First, because the trial is monitored to stop the futility and/or efficacy, therefore, the fixed time point can be chosen such that the survival probability at fixed time point should not be too high or too low so that there is a room to detect a specified effect size of the study design. Second, there is often a landmark time point for the survival probability of the historical data in a particular disease research area. Therefore, the survival probability at such a landmark time point can be chosen for the trial design. Third, the landmark time point could be obtained after careful deliberation as a compromising of accrual rate, urgency of investigation, expectation of improvement, and prevention of worst situation.
Three non-parametric test statistics for testing survival probability at a fixed time point are discussed in this paper. The sample size formulas for fixed sample tests are also derived. These test statistics are non-parametric and applicable to test any survival function; however, the sample size calculation may depend on the underlying failure time distribution, censoring distribution, and accrual distribution, as shown by equation (12). Simulation results showed that the underlying failure time distribution has little impact on the study power or sample size. However, the censoring distribution and accrual distribution could have large impacts on the study power. In this paper, we have studied the property of three test statistics under the assumption of an exponential censoring distribution and an uniform accrual distribution. It would be worth exploring the property of the test statistics under other censoring distribution and accrual distribution assumptions.
The common basis of the three test statistics is the cumulative hazard function Λ(x; t), and its estimate Λ̂(x; t) in equation (2) shows that any of the test statistics does include subjects who have not been followed for the required time x. This implies that these test statistics should be more efficient than the naive approach of estimating the survival probability as a simple proportion of all subjects surviving the required time at the interim analyses.
Among the three test statistics, test statistic Z1 is recommended. The sample size calculated based on Z1 is robust against the underlying distribution assumption; however, it is overestimated. Roughly a 10% sample size reduction could be appropriate to keep the study power at the design level but we recommend that a simulation study should be done to reduce the sample size while keeping the type I error and power at the nominal levels. The trial can be monitored by a multi-stage group sequential design based on the SCPRT procedure. A practically useful and unique feature of SCPRT is that the investigators may have freedom to ignore any predetermined interim stopping during the study without harming the integrity of study because the skipping does not change the overall significance level and power of the testing. This feature is useful when a study has reached significance or futility at an interim look but investigators wish to continue the study to the planned end for some reasons, e.g., either wanting to collect more data for later analysis or wanting to convince others (or even themselves) that the interim result can be trusted. For this situation, one may continue the study and take the result at the final end; they should ignore the interim result if there is contradiction between the two results. For an SCPRT design, the probability of this contradiction is very small, e.g., its maximum is ρmax = 0.0054 if the conditional discordant probability ρ = 0.02 is used for the design. Therefore, the proposed method can be easily used to design a single-arm phase II group sequential trial for monitoring survival probability.
Acknowledgments
The work was supported in part by National Cancer Institute (NCI) support grant CA21765 and the American Lebanese Syrian Associated Charities (ALSAC).
Appendix
Computation for the sequential test normalized with information time
Assumption
Let B(t) ~ N(θt, t) be a Gaussian process with the time variable t on interval [0, 1] and drift θ. Let 0 < t1 < ⋯ < tK = 1 be the information times of the looks for a sequential test with K looks. Let ak < bk be lower and upper boundaries for B(t) at time tk for k = 1, ⋯, K − 1, and aK = bK.
Function
Define as a function of s on interval (ak, bk), for k = 1, ⋯, K − 1; this series of functions can be determined recursively as follows. Let for s on (a1, b1); for k = 2, ⋯, K, for s in (ak, bk),
| (20) |
where ϕ(·) in (20) is the density function of the standard normal distribution.
Function ltk(·)
Define ltk(s) as a function of s on interval (−∞, ak)∪(bk, ∞), for k = 1, ⋯, K; this series of functions can be determined using functions defined in (20) as follows. Let lt1(s) = 1 for s on (−∞, a1) ∪ (b1, ∞); for k = 2, ⋯, K, for s in (−∞, ak) ∪ (bk, ∞), let
| (21) |
where ϕ(·) in (21) is the density function of the standard normal distribution.
Power Function
For testing H0 : θ ≤ 0 vs. Ha : θ > 0, with functions ltk(·) by (21), the power function P(θ) or the probability to reject H0 under true mean θ is
| (22) |
For the sequential test design, the significance level is α = P(0) and the power is 1 − β = P(θa), where θa is the value of θ under Ha.
Probability of Stopping
The probability of stopping at time tk is a function of θ as
| (23) |
with which the probability of stopping at tk is Ptk(0) for the null hypothesis and Ptk(θa) for the alternative hypothesis.
Expected Stopping Time
With the probability of stopping Ptk(θ) by (23), the expected stopping ET(θ) is a function of θ as
| (24) |
with which the expected stopping time is ET(0) for the null hypothesis and ET (θa) for the alternative hypothesis.
Expected Sample Size
Suppose the maximum sample size for the sequential test is n. The expected sample size for the sequential test is a function of θ and can be obtained as
| (25) |
with which the expected sample size is EN(0) for the null hypothesis and EN(θa) for the alternative hypothesis.
For SCPRT design
To test H0 : θ ≤ 0 vs. Ha : θ > 0 with significance level α and power 1 − β by an SCPRT design, the cutoff value at final stage tK = 1 is aK = bK = z1−α, the drift at the null hypothesis is θ0 = 0, and the drift at the alternative hypothesis is θa = z1−α + z1−β; which are the same as those for the fixed test at the final stage with information time t = 1. Including the cutoff value, θ0 and θa into equations (22), (24), (23), and (25), we can compute type I error, power, probability of stopping at given tk, and expected sample sizes under the null and alternative hypotheses for the SCPRT design.
For details of the derivation of these computational formulas, please refer to Xiong and Tan (1999, 2001) and Xiong et al. (2002).
References
- Anderson TW. An introduction to multivariate statistical analysis. New York: Wiley; 1958. [Google Scholar]
- Breslow N, Crowley J. A large sample study of the life table and product limit estimates under random censorship. The Annals of Statistics. 1974;2:437–453. [Google Scholar]
- Case LD, Morgan TM. Design of phase II cancer trials evaluating survival probabilities. BMC Medical Research Methodology. 2003;3:1–12. doi: 10.1186/1471-2288-3-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collett D. Modeling survival data in medical research. 2. London: Chapman and Hall; 2003. [Google Scholar]
- Fleming TR, Harrington DP. Counting processes and survival analysis. New York: John Wiley and Sons; 1991. [Google Scholar]
- Huang B, Talukder E, Thomas N. Optimal two-stage phase II designs with long-term endpoints. Statistics in Biopharmaceutical Research. 2010;2:51–61. [Google Scholar]
- Jennison C, Turnbull WD. Group sequential methods with applications to clinical trials. New York: Chapman & Hall; 2000. [Google Scholar]
- Klein JP, Logan B, Harhoff M, Andersen PK. Analyzing survival curves at a fixed point in time. Statistics in Medicine. 2007;26:4505–4519. doi: 10.1002/sim.2864. [DOI] [PubMed] [Google Scholar]
- Lin DY, Shen L, Ying Z, Breslow NE. Group sequential designs for monitoring survival probabilities. Biometrics. 1996;52:1033–1042. [PubMed] [Google Scholar]
- Tan M, Xiong X. A flexible multi-stage design for phase II oncology trials. Pharmaceutical Statistics. 2010;10:369–373. doi: 10.1002/pst.478. [DOI] [PubMed] [Google Scholar]
- Xiong X. A class of sequential conditional probability ratio tests. Journal of American Statistical Association. 1995;15:1463–1473. [Google Scholar]
- Xiong X, Tan M. Sufficiency-Based methods for evaluating sequential tests and estimations. ASA Proceedings, Biometrics Section. 1999:268–273. [Google Scholar]
- Xiong X, Tan M. Evaluating sequential tests for a class of stochastic processes. Computing Science and Statistics. 2001;33:30–34. [Google Scholar]
- Xiong X, Tan M, Boyett J. Sequential conditional probability ratio tests for normalized test statistic on information time. Biometrics. 2003;59:624–631. doi: 10.1111/1541-0420.00072. [DOI] [PubMed] [Google Scholar]
- Xiong X, Tan M, Boyett J. SCPRT: a sequential procedure that gives another reason to stop clinical trials early. Advances in Statistical Methods for the Health Sciences Statistics for Industry and Technology. 2007:419–434. [Google Scholar]
- Xiong X, Tan M, Kutner MH. Computation methods for evaluating sequential tests and post-estimations via sufficiency principle. Statistica Sinica. 2002;12:1027–41. [Google Scholar]