Combining List Experiment and Direct Question Estimates of Sensitive Behavior Prevalence

Abstract

Survey respondents may give untruthful answers to sensitive questions when asked directly. In recent years, researchers have turned to the list experiment (also known as the item count technique) to overcome this difficulty. While list experiments are arguably less prone to bias than direct questioning, list experiments are also more susceptible to sampling variability. We show that researchers need not abandon direct questioning altogether in order to gain the advantages of list experimentation. We develop a nonparametric estimator of the prevalence of sensitive behaviors that combines list experimentation and direct questioning. We prove that this estimator is asymptotically more efficient than the standard difference-in-means estimator, and we provide a basis for inference using Wald-type confidence intervals. Additionally, leveraging information from the direct questioning, we derive two nonparametric placebo tests for assessing identifying assumptions underlying list experiments. We demonstrate the effectiveness of our combined estimator and placebo tests with an original survey experiment.

1 Introduction

The prevalence of sensitive attitudes and behaviors is difficult to estimate using standard survey techniques due to the tendency of respondents to withhold information in such settings. In recent years, the list experiment has grown in popularity as a method for eliciting truthful responses to sensitive questions. Introduced as the “item count technique” by Miller (1984), the procedure has been used to study racial prejudice (Kuklinski, Cobb, and Gilens 1997a; Sniderman and Carmines 1997; Redlawsk, Tolbert, and Franko 2010), drug use (Biemer et al. 2005; Coutts and Jann 2011), risky sexual activity (LaBrie and Earleywine 2000; Walsh and Braithwaite 2008), vote buying (Gonzalez-Ocantos et al. 2012), and support for military occupation by foreign forces (Blair, Imai, and Lyall 2013). The standard list experiment proceeds by randomly partitioning respondents into control and treatment groups. Subjects in the control group receive a list of J non-sensitive items and report how many of the items apply to them. Subjects in the treatment group receive a list of J + 1 items comprised of the same J non-sensitive items plus one sensitive item. The list experiment estimate of the prevalence of the sensitive behavior is the difference-in-means between the treatment and control groups. The list experiment gives respondents cover to admit to engaging in the sensitive behavior – so long as the respondent reports between 1 and J items, the researcher cannot be certain whether an individual respondent engages in the sensitive behavior, but aggregate prevalence can be estimated.

List experiments may be useful because prevalence estimates based on direct questions are biased when some subjects tell the truth and others withhold information. In particular, the researcher cannot distinguish a respondent who does not engage in the sensitive behavior from one who does but is withholding: both types answer “No” to the direct question. Nevertheless, direct questions provide an important source of information when subjects admit to engaging in a sensitive behavior. Direct questions are biased but yield precise estimates of prevalence. Under some assumptions, list experiments provide unbiased estimates of prevalence, but these estimates can be quite variable. The method we detail below allows researchers to reap the benefits of both direct questions and list experiments: increased precision and decreased bias. The central intuition of our approach is that, given a Monotonicity assumption (no false confessions), the true prevalence is a weighted average of two subject types: those who admit to the sensitive behavior and those who withhold; we estimate the former with direct questions and the latter with list experiments.

A popular design for the list experiment is to randomly split the sample into three groups: those receiving the control list and no direct question, those receiving the treatment list and no direct question, and those receiving a direct question but no list at all (Brueckner, Morning, and Nelson 2005; Holbrook and Krosnick 2010; Heerwig and McCabe 2009). This design is often used so that direct and list experiment estimates can be compared within the same population. A variant of this design asks only subjects in the control group the direct question (Ahart and Sackett 2004; Gilens, Sniderman, and Kuklinski 1998). Our estimator requires that both treatment and control subjects receive a direct question. Examples of this more extensive measurement approach include Droitcour et al. (1991) and Gonzales-Ocantos et al. (2012). Echoing similar design advice given in Kramon and Weghorst (2012) and Blair and Imai (2012), we advocate asking the direct question whenever feasible and investigating any possible ordering effects.

When respondents are asked both direct and list questions, researchers can also test core assumptions underlying the list experiment: No Liars, No Design Effects, and ignorable treatment assignment (Imai 2011). The No Liars assumption requires that those who engage in the sensitive behavior do in fact include the sensitive item when reporting the number of list items that apply. The No Design Effects assumption requires that subjects’ responses to the non-sensitive items on the list are unaffected by the presence or absence of the additional sensitive item. The treatment ignorability assumption requires that assignment be independent of both list experiment and direct question potential outcomes. These tests complement the one proposed by Blair and Imai (2012), which assesses whether any identified proportions of respondent types are negative, which would imply a contradiction between the model and the observed data.

We propose two tests. The logic of the first test, which is formalized below, is as follows: under the core list experiment assumptions and a Monotonicity assumption, the treatment versus control difference-in-means is in expectation equal to 1 among those who answer “Yes” to the direct question. Failing to reject the null hypothesis that the true difference in means for this subset is equal to 1 is equivalent to failing to reject the null hypothesis that the assumptions hold. We also propose a test of a variant of the ignorable treatment assignment assumption by assessing the dependence between responses to the direct question and the experimental treatment. While not conclusively demonstrating that the assumptions hold, these test results may give researchers more confidence that their survey instruments are providing reliable prevalence estimates.

Previous methodological work on list experiments has largely been focused on two goals: decreasing the variance of list experiment estimates and modeling prevalence in a multivariate setting. Droitcour et al. (1991) propose the “Double List Experiment” design in which the prevalence of the same sensitive item is investigated by two list experiments conducted with the same subjects, thereby reducing sampling variability. Holbrook and Krosnick (2010) use multivariate regression with treatment-by-covariate interaction terms to explore prevalence heterogeneity. Glynn (2013) suggests constructing the non-sensitive items so that they are negatively correlated with one another, a design feature that simultaneously reduces baseline variability and avoids ceiling effects. Corstange (2009) modifies the standard list experiment design by asking the control group each of the non-sensitive items directly, so that responses to the non-sensitive items can be modeled and more precise estimates of the sensitive items can be calculated. Imai (2011) proposes a nonlinear least squares estimator and a maximum likelihood estimator to model responses with covariate data. Blair and Imai (2012) offer a detailed review of these techniques.

Our contribution to the list experiment literature is to show the ease with which the additional information yielded by direct questioning can be incorporated into existing techniques. We demonstrate our proposed estimator and placebo tests on data from an original survey experiment conducted on Amazon’s Mechanical Turk platform. We conclude with suggestions for the design and analysis of list experiments in scenarios where it is ethically feasible to ask direct questions as well.

2 Setting and Identification

Suppose we have a random sample of n subjects independently drawn from a large population. Let X_i = 1 if subject i engages in a sensitive behavior and X_i = 0 otherwise. We attempt to measure the behavior X_i using two methods: direct questioning and list experimentation. Our goal is to identify the prevalence of the sensitive behavior in the population, μ = Pr[X_i = 1]. Let Y_i be the report of subject i to the direct question. We assume that, under direct questioning, subjects may lie and claim that they do not engage in the behavior but will not lie and falsely claim that they do engage in the behavior.

Assumption 1 (Monotonicity)

There exist three latent classes of respondents under direct questioning: those who do not engage in the behavior and report truthfully (X_i = 0, Y_i = 0), subjects who engage and report truthfully (X_i = 1, Y_i = 1), and subjects who engage but report that they do not, i.e., withhold (X_i = 1, Y_i = 0).

Let p = Pr[Y_i = 1|X_i = 1] be the probability of a subject reporting truthfully to the direct question, given that he or she engages in the sensitive behavior. Then the response of subject i is

$$Y_i=\{\begin{array}{ll}0\hfill & \text{with}\text{probability}1-\mu +\mu (1-p)\hfill \\ 1\hfill & \text{with}\text{probability}\mu p.\hfill \end{array}$$

The response Y_i = 0 can be seen as a mixture of truthful negative reports and withholding. The probability that subject i engages in the behavior, given a negative response, is therefore

$$\mathrm{Pr}[X_i=1|Y_i=0]=\frac{(1-p)\mu }{1-\mu p}.$$

While direct questioning is sufficient to reveal Pr[Y_i = 1] = μp, it is not sufficient to identify Pr[Y_i = 0|X_i = 1] = 1 − p.

In contrast, the list experiment provides sufficient information to identify μ. Suppose we have a treatment Z_i ∈ {0, 1}. In the list experiment, treated subjects (Z_i = 1) receive a number of control questions and an additional question about the sensitive behavior. We denote the number of items that the subject states are applicable with V_i.

Assumption 2 (No Liars and No Design Effects)

Reframing Imai’s (2011) formulations, we observe V_i = W_i + X_iZ_i, where W_i is the baseline outcome (under control) for subject i for the list experiment.

We further require that the treatment assignment be independent of the actual behavior, direct question, and baseline response. This is a stricter variant of Imai’s (2011) ignorability assumption.

Assumption 3 (Treatment Independence)

(W_i, X_i, Y_i) ⫫ Z_i.

Assumption 3 would be violated if (i) we did not have random assignment of the treatment or (ii) there are additional design effects; e.g., the treatment assignment affects the response to the direct question. Given random assignment, only the latter is a concern.

To ensure that all target quantities are well-defined (and, later, to facilitate inference), we impose the mild regularity condition that all population variances be positive.

Assumption 4 (Non-degenerate Distributions)

Var [V_i|Z_i = z, Y_i = y] > 0, for z, y ∈ {0, 1}, Var [Z_i] > 0 and Var [Y_i] > 0.

We now turn to our primary identification result.

Lemma 1

Given Assumptions 1–4 (Monotonicity, No Liars, No Design Effects, Treatment Independence, and Non-degenerate Distributions), the prevalence may be represented as

$$\mu =\mathrm{E}\left[Y_i\right]+\mathrm{E}\left[1-Y_i\right](\mathrm{E}\left[V_i|Z_i=1,Y_i=0\right]-\mathrm{E}\left[V_i|Z_i=0,Y_i=0\right]).$$ (1)

Proof

By Assumptions 2 and 3,

$$\mathrm{E}\left[V_i|Z_i=1\right]-\mathrm{E}\left[V_i|Z_i=0\right]=W_i+\mu -W_i=\mu$$ (2)

Then expanding the left-hand side of (2) by marginalizing over Y_i, we represent the prevalence of the sensitive behavior as

$$\mu =\mathrm{E}\left[V_i|Y_i=0,Z_i=1\right]\mathrm{E}\left[1-Y_i\right]+\mathrm{E}\left[V_i|Y_i=1,Z_i=1\right]\mathrm{E}\left[Y_i\right]-(\mathrm{E}\left[V_i|Y_i=0,Z_i=0\right]\mathrm{E}\left[1-Y_i\right]+\mathrm{E}\left[V_i|Y_i=1,Z_i=0\right]\mathrm{E}\left[Y_i\right])=(\mathrm{E}\left[V_i|Y_i=1,Z_i=1\right]-\mathrm{E}\left[V_i|Y_i=1,Z_i=0\right])\mathrm{E}\left[Y_i\right]+(\mathrm{E}\left[V_i|Y_i=0,Z_i=1\right]-\mathrm{E}\left[V_i|Y_i=0,Z_i=0\right])\mathrm{E}\left[1-Y_i\right]=\mathrm{E}\left[X_i|Y_i=1\right]\mathrm{E}\left[Y_i\right]+(\mathrm{E}\left[V_i|Y_i=0,Z_i=1\right]-\mathrm{E}\left[V_i|Y_i=0,Z_i=0\right])\mathrm{E}\left[1-Y_i\right].$$

The result follows since E [X_i|Y_i = 1] = 1 by Assumption 2. □

Note that if Assumptions 2–4 hold, but Assumption 1 (Monotonicity) does not hold, then E [Y_i]+E [1−Y_i] (E [V_i|Z_i = 1, Y_i = 0] − E [V_i|Z_i = 0, Y_i = 0]) > μ, as then E [X_i|Y_i = 1] < 1.

3 Estimation, Inference and Efficiency

In this section, we propose a simple nonparametric estimator of μ based on (1) and provide a basis for inference using Wald-type confidence intervals under a normal approximation. We also prove that our estimator is asymptotically more efficient than the standard difference-in-means estimator for the list experiment alone.

Define the sample means

$$\overline{Y}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{Y}_i}$$

$${\overline{V}}_{1,0}=\frac{{\displaystyle \sum _{i=1}^n{V}_i{Z}_i(1-Y_i)}}{{\displaystyle \sum _{i=1}^n{Z}_i(1-Y_i)}}\text{and}{\overline{V}}_{0,0}=\frac{{\displaystyle \sum _{i=1}^n{V}_i(1-Z_i)(1-Y_i)}}{{\displaystyle \sum _{i=1}^n(1-Z_i)(1-Y_i)}}.$$

Define an estimator of μ based on (1),

$$\widehat{\mu }=\overline{Y}+(1-\overline{Y})({\overline{V}}_{1,0}-{\overline{V}}_{0,0}).$$

A preliminary Lemma will assist us in deriving the asymptotic variance of this estimator.

Lemma 2

${\overline{V}}_{1,0}$ and ${\overline{V}}_{0,0}$ are uncorrelated with $1-\overline{Y}$

A proof is given in Appendix B.

We can derive results on the sampling variance of $\widehat{\mu }$. Let γ = Pr(Z_i = 1) be the probability of receiving the treatment question in the list experiment.

Proposition 1

Given Assumption 4 (Non-degenerate Distributions), the asymptotic variance of $\widehat{\mu }$ is characterized by

$$\underset{n\to \mathrm{\infty }}{\mathit{plim}}n\text{Var}\left[\widehat{\mu }\right]=\frac{{(1-\mu )}^2}{1-\mu p}\mu p+(1-\mu p)\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=0]}{\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=0]}{1-\gamma }\right].$$ (3)

Proof is given in Appendix B. Under Assumptions 1–4, $\widehat{\mu }$ is root-n consistent and asymptotically normal, with a consistent estimator of the variance obtained by substituting sample analogues (i.e., sample means and sample variances) for population quantities. Namely, let

$$\widehat{\text{Var}}\left[\widehat{\mu }\right]=\frac{{(1-\widehat{\mu })}^2}{1-\overline{Y}}\overline{Y}+(1-\overline{Y})\left[\frac{{\widehat{\sigma }}^2(V_i|Z_i=1,Y_i=0)}{\widehat{\gamma }}+\frac{{\widehat{\sigma }}^2(V_i|Z_i=0,Y_i=0)}{1-\widehat{\gamma }}\right],$$

where ${\widehat{\sigma }}^2(\cdot )$ denotes the sample variance and $\widehat{\gamma }={\displaystyle {\sum }_{i=1}^n{Z}_i/n}$. These properties are sufficient for construction of Wald-type confidence intervals using $\widehat{\text{Var}}[\widehat{\mu }]$.

Corollary 1

If Assumptions 1–4 hold, then confidence intervals constructed as $\widehat{\mu }\pm z_{1-\alpha /2}\sqrt{\widehat{\text{Var}}[\widehat{\mu }]}$ will have μ 100(1 − α)% coverage for μ for large n.

A proof follows directly from asymptotic normality and Slutsky’s Theorem.

An estimator based upon Equation (1) will have efficiency gains relative to standard difference-in-means-based estimators. Consider the standard difference-in-means-based estimator for the list experiment,

$${\widehat{\mu }}_S={\overline{V}}_1-{\overline{V}}_0$$

where

$${\overline{V}}_1=\frac{{\displaystyle {\sum }_{i=1}^n{V}_i{Z}_i}}{{\displaystyle {\sum }_{i=1}^n{Z}_i}}\text{and}{\overline{V}}_0=\frac{{\displaystyle {\sum }_{i=1}^n{V}_i(1-Z_i)}}{{\displaystyle {\sum }_{i=1}^n(1-Z_i)}}$$

We now show that the combined estimator $\widehat{\mu }$ is asymptotically more precise than ${\widehat{\mu }}_S$.

Proposition 2

Under Assumptions 1–4 (Monotonicity, No Liars, No Design Effects, Treatment Independence, and Non-degenerate Distributions),

$$\underset{n\to \mathrm{\infty }}{\mathit{plim}}n\text{Var}[\widehat{\mu }]<\underset{n\to \mathrm{\infty }}{\mathit{plim}}n\text{Var}[{\widehat{\mu }}_S].$$

Proof is given in Appendix B.

4 Placebo Tests

In this section, we derive two placebo tests to assess the validity of the identifying assumptions.

4.1 Placebo Test I

It is possible to jointly test the Monotonicity, No Liars, No Design Effects, and Treatment Independence assumptions. Under these assumptions, for all t, Pr[V_i = t|Z_i = 0, Y_i = 1] = Pr[V_i = (t + 1)|Z_i = 1, Y_i = 1], thus tests of distributional equality are appropriate. Any valid test of distributional equality between V_i (under Z_i = 0, Y_i = 1) and V_i + 1 (under Z_i = 1, Y_i = 1) will permit rejection of the null.

However, since distributional equality implies that E [V_i|Z_i = 1, Y_i = 1] − E [V_i Z_i = 0, Y_i = 1] = 1, a simple test is available. Define β = E [V_i|Z_i = 1, Y_i = 1] − E [V_i|Z_i = 0, Y_i = 1]. Consider estimators

$$\widehat{\beta }={\overline{V}}_{1,1}-{\overline{V}}_{0,1}$$

and

$$\widehat{\text{Var}}[\widehat{\beta }]=\frac{{\widehat{\sigma }}^2(V_i|Z_i=1,Y_i=1)}{{\displaystyle {\sum }_{i=1}^n{Z}_i{Y}_i}}+\frac{{\widehat{\sigma }}^2(V_i|Z_i=0,Y_i=1)}{{\displaystyle {\sum }_{i=1}^n(1-Z_i)Y_i}}.$$

Proposition 3

Under the null hypothesis that Assumptions 1–4 (Monotonicity, No Liars, No Design Effects, and Treatment Independence) hold, β = 1. For large n, if Assumption 4 (Non-degenerate Distributions) holds, then a two-sided p-value is given by

$$2\mathrm{\Phi }\left(-|\widehat{\beta }-1|/\sqrt{\widehat{\text{Var}}[\widehat{\beta }]}\right),$$

where Φ(.) is the normal CDF.

A proof for Proposition 3 follows directly from calculations analogous to those for Proposition 1.

We also explore the power of Placebo Test I using a series of Monte Carlo simulations. We vary a number of factors, including: the number of subjects answering “Yes” to the direct question, the proportions of false confessors, liars, and the design-affected, and the variance of responses to the control list. The placebo test does not always have high power. For example, if 20% of 200 subjects responding “Yes” to the direct question are false confessors, the placebo test only has about 30% power. But when 20% of 800 subjects answering “Yes” are falsely confessing, the test has approximately 80% power. In general, the power of placebo test depends both on the number of subjects answering “Yes” and the proportion of subjects violating the assumptions. These results are presented in Appendix C.

4.2 Placebo Test II

We can probe the validity of the Treatment Independence assumption with a second placebo test. Treatment Independence is violated if the answer to the direct question is systematically related to treatment assignment (i.e, $Y_i\cancel{\text{⫫}}{Z}_i$). Define δ = E [Y_i|Z_i = 1] − E [Y_i|Z_i|= 0]. Consider the estimators

$$\widehat{\delta }=\frac{{\displaystyle {\sum }_{i=1}^n{Y}_i{Z}_i}}{{\displaystyle {\sum }_{i=1}^n{Z}_i}}-\frac{{\displaystyle {\sum }_{i=1}^n{Y}_i(1-Z_i)}}{{\displaystyle {\sum }_{i=1}^n(1-Z_i)}}$$

and

$$\widehat{\text{Var}}[\widehat{\delta }]=\frac{{\widehat{\sigma }}^2(Y_i|Z_i=1)}{{\displaystyle {\sum }_{i=1}^n{Z}_i}}+\frac{{\widehat{\sigma }}^2(Y_i|Z_i=0)}{{\displaystyle {\sum }_{i=1}^n(1-Z_i)}}.$$

Proposition 4

Under the null hypothesis that Assumption 3 holds, δ = 0. For large n, if Assumption 4 (Non-degenerate Distributions) holds, then a two-sided p-value is given by

$$2\mathrm{\Phi }\left(-|\widehat{\delta }|/\sqrt{\widehat{\text{Var}}[\widehat{\delta }]}\right).$$

A proof for Proposition 4 again follows directly from calculations analogous to those for Proposition 1. When the treatment is randomly assigned, Placebo Test II is simply a test of whether Z_i has a causal effect on Y_i. When Z_i is randomly assigned and the list experiment treatment is presented after the direct question, Assumption 3 holds by design.

5 Application

We tested the properties of our estimator with a pair of studies carried out on Amazon’s Mechanical Turk service, an internet platform where subjects perform a wide variety of tasks in return for compensation. Our main purpose was to assess the properties of our estimator by investigating an array of different behaviors, some of which may be considered socially sensitive. The relative anonymity of internet surveys provides a favorable environment for list experiments precisely because we expect subjects to withhold less often than they might in face-to-face or telephone settings.

5.1 Experimental Design

We conducted five list experiments that paralleled five direct questions. The exact wording of the list experiments and direct questions is given in Appendix A. In three list experiments, we chose topics that are not socially sensitive: preferences over alternative energy sources, neighborhood characteristics, and news organizations. Two of the five list experiments dealt with racial and religious prejudice, topics where we would expect some withholding of anti-Hispanic and anti-Muslim sentiment.

We recruited a convenience sample of 1,023 subjects from Mechanical Turk. We offered subjects $1.00 to complete our survey, which is equivalent to a $15.45 hourly rate – a comparatively high wage by the standards of Mechanical Turk (Berinsky, Huber, and Lenz 2012). In order to defend against the potential for subjects to supply answers without reading or considering our questions, we included an “attention question” that required subjects to select a particular response in order to continue with the survey. Two subjects failed this quality check, and we exclude them from the main analysis. An additional seven subjects failed to respond to one or more of our questions, so we exclude them from the main analysis as well. The resulting sample size is n = 1, 014.

Subjects were first assigned at random to either Study A or Study B. In Study A, direct questions were posed before the list questions, whereas in Study B, list questions were asked first. Subjects in both studies were then assigned to either the treatment or control conditions of each of the five list experiments. Table 1 displays the number of subjects in each treatment condition for each study, as well as every pairwise crossing of conditions. All randomizations used Bernoulli random assignment with equal probability 0.5. Consistent with our randomization procedure, each cell in the table (with the exception of the diagonal) contains approximately one-quarter of the subjects.

Table 1.

Number of Subjects in Each Treatment Condition

		Study A or B		List 1		List 2		List 3		List 4		List 5
		A	B	T	C	T	C	T	C	T	C	T	C
Study A or B	A	500	0	255	245	262	238	225	275	257	243	268	232
	B	0	514	242	272	255	259	261	253	243	271	254	260
List 1	T			517	0	251	266	273	244	269	248	273	244
	C			0	497	246	251	255	242	245	252	219	278
List 2	T					497	0	253	244	246	251	240	257
	C					0	517	275	242	268	249	252	265
List 3	T							528	0	269	259	263	265
	C							0	486	245	241	229	257
List 4	T									514	0	256	258
	C									0	500	236	264
List 5	T											492	0
	C											0	522

Before being randomized into treatment groups, subjects answered a series of background demographic questions. Table 2 shows balance statistics across age, gender, political ideology, education, and race across the treatment and control groups for the first list experiment in both studies. Our subject pool is more likely to be white, male, liberal, well-educated, and young than the general population. This pattern is consistent with the demographic description of Mechanical Turk survey respondents given by Mason and Suri (2011).

Table 2.

Covariate Balance: List Experiment 1

	Study A		Study B
	Treat	Control	Treat	Control
18 to 24	24.49	25.49	23.53	32.64
25 to 34	40.82	43.92	41.18	40.91
35 to 44	20.00	15.29	17.28	14.88
45 to 54	8.16	10.98	10.66	6.20
55 to 64	4.90	3.92	5.88	3.72
65 or over	1.63	0.39	1.47	1.65
Female	46.12	47.45	46.32	42.98
Male	53.88	52.16	53.31	57.02
Prefer not to say – Gender	0.00	0.39	0.37	0.00
Liberal	50.61	42.35	50.37	51.65
Moderate	28.16	34.51	26.84	28.51
Conservative	18.37	19.22	20.59	14.46
Haven’t thought much about this	2.86	3.92	2.21	5.37
Less than High School	0.41	0.78	0.74	1.24
High School/GED	11.02	11.76	10.66	7.44
Some College	42.45	42.75	40.44	40.91
4-year College Degree	33.47	33.73	35.29	36.36
Graduate School	12.65	10.98	12.87	14.05
White, non Hispanic	79.18	77.65	79.78	80.17
African-American	7.76	10.98	6.62	4.55
Asian/Pacific Islander	5.71	4.71	5.15	9.92
Hispanic	4.90	3.92	6.25	4.13
Native American	0.82	0.78	1.10	0.83
Other	1.22	1.18	1.10	0.41
Prefer not to say – Race	0.41	0.78	0.00	0.00
n	245	255	272	242

5.2 Study A (Direct Questions First)

In Study A, subjects were presented with the five direct questions before receiving the five list experiments. Table 3 presents three estimates of the prevalence in our subject pool. The first is a naive estimate computed by taking the average response to the direct question, $\overline{Y}$ (Direct). The remaining two estimates are ${\widehat{\mu }}_S$ (Standard List) and $\widehat{\mu }$ (Combined List). For example, the direct question estimate $\overline{Y}$ of the percentage agreeing that Muslims should not be allowed to teach in public schools¹ is 11%, the list experiment estimate ${\widehat{\mu }}_S$ is 17%, and the combined estimate $\widehat{\mu }$ is 19%. Of particular note are the standard errors associated with the standard list experiment as compared with those associated with the combined estimate: the reductions in estimated sampling variance are dramatic, ranging from 14% to 67%. As expected, reductions tend to be larger when a larger number of subjects respond “Yes” to the direct question. Figure 1 presents these results graphically: the estimates generally agree (providing confidence that the list experiments and the direct questions are measuring the same quantities), and the 95% confidence intervals around the combined estimate are always tighter than those around the standard estimate.

Table 3.

Study A (Direct First): Three Estimates of Prevalence

	Direct		Standard List		Combined List		% Reduction in Sampling Variance
	$\overline{Y}$	SE	${\widehat{\mu }}_S$	SE	$\widehat{\mu }$	SE
Nuclear Power	0.656	0.021	0.748	0.084	0.666	0.049	66.8
Public Transportation	0.538	0.022	0.513	0.072	0.627	0.049	54.0
Spanish-speaking	0.102	0.014	0.035	0.079	0.042	0.074	14.0
Muslim Teachers	0.110	0.014	0.166	0.081	0.187	0.074	15.4
CNN	0.444	0.022	0.338	0.105	0.533	0.070	55.3

n = 500 for all estimates

Figure 1.

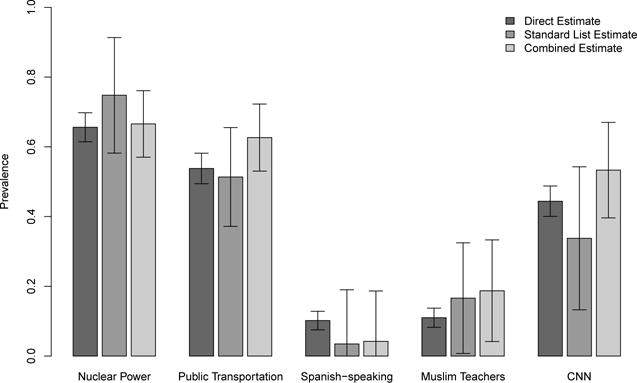
Study A (Directs First): Three Estimates of Prevalence

Table 4 presents the results of Placebo Test I. If these assumptions hold, the standard list experiment difference-in-means estimator will recover estimates that are in expectation equal to one among the subsample that answers “Yes” to the direct question. In two cases, we reject the joint null hypothesis of Monotonicity, No Liars and No Design Effects: Public Transportation (p = 0.02) and CNN (p = 0.03). We speculate that some subjects may have felt that claiming to watch CNN was socially desirable, thereby violating Monotonicity.

Table 4.

Study A (Directs First): Placebo Test I

	$\widehat{\beta }$	SE	p-value	n
Nuclear Power	1.054	0.095	0.568	328
Public Transportation	0.790	0.091	0.021	269
Spanish-speaking	0.848	0.279	0.585	51
Muslim Teachers	1.008	0.237	0.973	55
CNN	0.696	0.143	0.034	222

Since we employed random assignment and the experimental treatment comes after the administration of the direct question, we expect to pass Placebo Test II, which seeks to verify that the treatment does not affect direct question responses. Indeed, the Placebo Test II results show no significant differences in mean responses to the direct questions by the list experimental treatment assignments.

5.3 Study B (List Experiments First)

Study B reverses the order of the direct questions and list experiments: subjects participated in all five list experiments before answering the direct questions. This design choice risks priming subjects in the treatment group in ways that might alter their responses to subsequent direct questions. For example, treated subjects may be prone to misreport if subjects suspect that a particular topic is being given special scrutiny.

All three prevalence estimates for Study B are presented in Table 6 and Figure 2. The direct question estimates are very similar between Study A and Study B – none of the differences between the estimates is significant at the 0.05 level. The standard list experiment estimates differ between Studies A and B, suggesting a question order effect. The combined estimator produces tighter estimates in Study B as well, with estimated sampling variability reductions in a very similar range. Appendix E presents formal tests of the differences in estimates across the studies.

Table 6.

Study B (Lists First): Three Estimates of Prevalence

	Direct		Standard List		Combined List		% Reduction in Sampling Variance
	$\overline{Y}$	SE	${\widehat{\mu }}_S$	SE	$\overline{Y}$	SE
Nuclear Power	0.603	0.022	0.499	0.089	0.624	0.052	65.3
Public Transportation	0.539	0.022	0.578	0.073	0.608	0.051	51.8
Spanish-speaking	0.113	0.014	0.144	0.083	0.149	0.076	16.3
Muslim Teachers	0.103	0.013	0.107	0.083	0.123	0.074	20.1
CNN	0.496	0.022	0.645	0.101	0.587	0.065	59.4

n = 514 for all estimates

Figure 2.

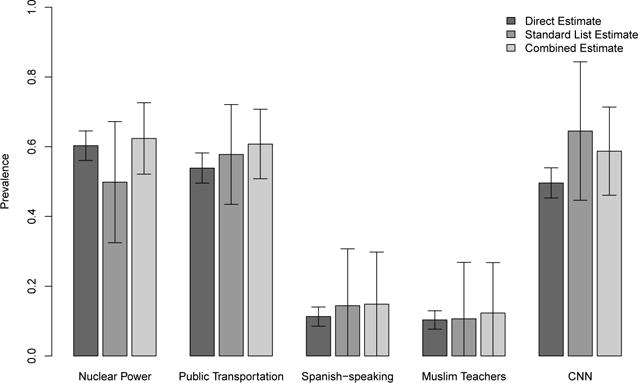
Study B (Lists First): Three Estimates of Prevalence

The results of Placebo Test I for Study B are presented in Table 7. Among the subgroup of respondents who answer “Yes” to the direct question, the list experiment difference-in-means estimate β should be equal to 1, under Assumptions 1–4 (Monotonicity, No Liars, No Design Effects, and Treatment Independence). None of the values of β are statistically significantly different from 1 using the placebo test, and a joint test via Fisher’s method is insignificant as well.

Table 7.

Study B (Lists First): Placebo Test I

	$\widehat{\beta }$	SE	p-value	n
Nuclear Power	0.881	0.113	0.294	310
Public Transportation	0.913	0.091	0.339	277
Spanish-speaking	0.767	0.229	0.309	58
Muslim Teachers	0.700	0.285	0.293	53
CNN	0.847	0.135	0.256	255

As described in section 4.2, the combined estimator relies in part on the assumption that a subject’s response to the direct question is unaffected by the list experimental treatment assignment. Violations of this assumption are directly testable using Placebo Test II. In study B, subjects were exposed to either a treatment or a control list before answering the direction question. Table 8 below presents the effect the treatment lists may have had on answers to the direct questions. In two of the five cases, direct questions were significantly affected by the treatment list: Treated subjects were 8.6 percentage points less likely to declare their support for Nuclear power and were 13.2 percentage points more likely to report watching CNN. These findings indicate that the Treatment Independence assumption is most likely violated for these questions, rendering the Study B combined list estimates for these two questions unreliable.

Table 8.

Study B (Lists First): Placebo Test II

	$\widehat{\beta }$	SE	p-value	n
Nuclear Power	−0.086	0.043	0.046	514
Public Transportation	0.034	0.044	0.436	514
Spanish-speaking	0.027	0.028	0.339	514
Muslim Teachers	0.016	0.027	0.550	514
CNN	0.132	0.044	0.003	514

5.4 Replication Study

We conducted a replication study following the identical design with 506 new Mechanical Turk subjects in a replication of Study A and 506 in a replication of Study B. Full results of this replication study are presented in Appendix F, but the findings are strikingly similar to the first investigation. The list experimental estimates vary somewhat between the original experiments and the replication, but none of these differences are significant (p > 0.05). One of five placebo tests was significant in Study A and three of five were significant in Study B. Perhaps surprisingly, the effect of the treatment list on direct answers to the CNN question presented in Table 8 was also replicated.

6 Discussion

Social desirability effects may bias prevalence estimates of sensitive behaviors and opinions obtained using direct questioning, but that does not mean that direct questions are useless. Under an assumption of Monotonicity (subjects who do not engage in the sensitive behavior do not falsely confess), direct questions reveal reliable information about those who answer “Yes.” Among those who answer “No,” we cannot directly distinguish those who withhold from those who do not engage in the sensitive behavior – for these subjects, list experiments may provide a workaround. Combining these two techniques into a single estimator yields more precise estimates of prevalence, and employing direct and list questions in tandem also enables the researcher to test crucial identifying assumptions.

A few caveats are in order with respect to empirical applications. First, Monotonicity is not guaranteed to hold, especially when social desirability cuts in opposite directions for different subgroups. For example, moderates in liberal areas may feel pressure to support Muslim teachers, whereas moderates in conservative areas may feel pressure to oppose them. Second, list experiments are often employed when the safety of respondents would be compromised if they admitted to sensitive opinions or behaviors (e.g., Pashtun respondents admitting support for NATO forces, Blair, Imai, and Lyall 2013). We do not take these concerns lightly, and in such cases would not recommend the use of our method. Third, the order in which direct questions and list experiments are asked appears to matter. Unfortunately, the empirical results of Placebo Test I fail to provide clear guidance with respect to ordering: we reject the joint null hypothesis of Monotonicity, No Liars and No Design Effects for two of the experiments in Study A, but fail to reject it for any of the five experiments in Study B. Our replication study saw the opposite pattern: one rejection in Study A, and three rejections in Study B. Placebo Test II, on the other hand, suggests that, at least in our application, asking the direct question second induced a violation of the Treatment Independence assumption. In sum, we recommend randomizing the order in which the list experiment and the direct question are presented, so that a) question-order effects can be contained and b) the relevant tests of the assumptions can be performed. Finally, the power of Placebo Test I varies with the prevalence rate, and is consequently less useful when the goal of the list experiment is to estimate the prevalence of a rare attitude or behavior – a common circumstance if one imagines that sensitive behaviors also tend to be low-prevalence. Nevertheless, Placebo Test I detected many instances of violated assumptions (six of twenty opportunities), suggesting that caution is warranted when interpreting list experimental estimates of prevalence.

We have combined direct question estimates with the simplest of the various list experiment estimators: difference-in-means. This work could be extended straightforwardly to the multivariate settings discussed by Corstange (2009), Holbrook and Krosnick (2010), and Imai (2011). One such approach would involve regression estimation (Särndal, Swensson, and Wretman 1992, Lin 2013) or, equivalently, post-stratification (Holt and Smith 1979, Miratrix, Sekhon and Yu 2013) for computing covariate adjusted means. Such an approach would improve asymptotic efficiency without any parametric assumptions, and a consistent variance estimator may be derived by substituting residuals from the regression fit. Finally, we note that other methods for eliciting truthful responses to sensitive questions, such as randomized response (Warner 1965) and endorsement experiments (Bullock, Imai, and Shapiro 2011; Lyall, Blair, and Imai forthcoming), could also be combined with direct questioning to improve precision.

Table 5.

Study A (Directs First): Placebo Test II

	$\widehat{\beta }$	SE	p-value	n
Nuclear Power	0.066	0.043	0.120	500
Public Transportation	−0.000	0.045	0.994	500
Spanish-speaking	0.016	0.027	0.561	500
Muslim Teachers	−0.030	0.028	0.286	500
CNN	−0.056	0.045	0.207	500

Appendix A: Survey Text

	List Question (sensitive item in bold)	Direct Question
Nuclear Power (L1 & D1)	Here is a list of four (five) alternative energy sources that some people think the United States should be developing. Please read all four (five) and select how many of them you think the United States should be developing. We do not want to know which ones, just how many.	Some people think nuclear power is an alternative energy source that the United States should be developing. How about you? Do you think nuclear power is an alternative energy source that the United States should be developing?
	Wind Solar Nuclear Power Natural Gas Ethanol	Yes No
Public Transportation (L2 & D2)	Here is a list of three (four) things some people consider important when choosing a neighborhood to live in. Please read all three (four) and select how many of them you consider important when choosing a neighborhood. We do not want to know which ones, just how many.	Some people consider access to public transportation important when choosing a neighborhood to live in. How about you? Do you consider access to public transportation important when choosing a neighborhood to live in?
	Proximity to shops and restaurants Quality of local schools Neighbors who share my values Access to public transportation	Yes No
Spanish-speaking (L3 & D3)	Here is a list of four (five) things that sometimes make people angry or upset. Please read all four (five) and select how many of them upset you. We do not want to know which ones, just how many.	Sometimes people are angry or upset when a Spanish-speaking family moves in next door. How about you? Would a Spanish-speaking family moving in next door upset you?
	The federal government increasing the tax on gasoline Professional athletes earning large salaries A Spanish-speaking family moving in next door Requiring seat belts be used when driving Large corporations polluting the environment	Yes No
Muslim Teachers (L4 & D4)	Here is a list of three (four) groups that some people think should be prohibited from teaching in public schools. We do not want to know which ones, just how many.	Sometimes people think that Muslims should be prohibited from teaching in public schools. How about you? Do you think that Muslims should be prohibited from teaching in public schools?
	18–21 year olds Muslims People without a Masters degree in education People who earn a 2.0 GPA or lower	Yes No
CNN (L5 & D5)	Here is a list of four (five) news organizations. Please read all four (five) and select how many you read or watch in the course of an ordinary month. We do not want to know which ones, just how many.	In the course of an ordinary month, do you watch CNN?
	The New York Times CNN The Huffington Post Fox News Politico	Yes No

Appendix B: Proofs

Proof of Lemma 2

Proof

To show that ${\overline{V}}_{1,0}$ and ${\overline{V}}_{0,0}$ are uncorrelated with $1-\overline{Y}$, we demonstrate that the expected values of these variables are invariant to conditioning on $1-\overline{Y}$. Suppose that exactly k direct responses are zero, so $1-\overline{Y}=k/n$. Then

$$\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^n{V}_j{Z}_j(1-Y_j)}}{{\displaystyle {\sum }_{j=1}^n{Z}_j(1-Y_j)}}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^k{V}_j{Z}_j}}{{\displaystyle {\sum }_{j=1}^k{Z}_j}}|Y_j=0\text{for}j=1,\dots k\right],$$ (4)

where we have re-ordered the indices so that Y₁ = ⋯ = Y_k = 1. Then applying the law of iterated expectation, we have

$$\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}=\frac{k}{n}\right]={\mathrm{E}}_Z\left[\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^k{V}_j{Z}_j}}{{\displaystyle {\sum }_{j=1}^k{Z}_j}}|Y_j=0\text{for}j=1,\dots ,k,{\displaystyle \sum _{j=1}^k{Z}_j}=i\right]\right]={\displaystyle \sum _{i=1}^k\frac{{\displaystyle {\sum }_{j=1}^i\mathrm{E}\left[V_j|Z_j=1,Y_j=0\right]}}{i}}\mathrm{Pr}\left({\displaystyle {\sum }_{j=1}^k{Z}_j=i}\right)$$ (5)

where we have again re-ordered the indices so that Z₁ = ⋯ = Z_i = 1. Since E[V_j|Z_j = 1; Y_j = 0] is the same for every j = 1, …, i,

$$\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[V_1|Z_1=1,Y_1=0\right]{\displaystyle \sum _{i=1}^k\mathrm{Pr}\left({\displaystyle \sum _{j=1}^k{Z}_j=i}\right)}=\mathrm{E}\left[V_1|Z_1=1,Y_1=0\right].$$ (6)

Then since the last line does not depend on k, we conclude that

$$\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}=\frac{k^{\prime }}{n}\right]$$

for k ≠ k′. It follows that the expectation of ${\overline{V}}_{1,0}$ is invariant to conditioning on $1-\overline{Y}$ and so $\mathrm{E}\left[{\overline{V}}_{1,0}|1-\overline{Y}\right]=\mathrm{E}\left[{\overline{V}}_{1,0}\right]$.

A similar argument holds for ${\overline{V}}_{0,0}$:

$$\mathrm{E}\left[{\overline{V}}_{0,0}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^n{V}_j}(1-Z_j)(1-Y_j)}{{\displaystyle {\sum }_{j=1}^n(1-Z_j)(1-Y_j)}}|1-\overline{Y}=\frac{k}{n}\right]=\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^k{V}_j}(1-Z_j)}{{\displaystyle {\sum }_{j=1}^k(1-Z_j)}}|Y_j=0\text{for}j=1,\dots k\right]={\mathrm{E}}_Z\left[\mathrm{E}\left[\frac{{\displaystyle {\sum }_{j=1}^k{V}_j}(1-Z_j)}{{\displaystyle {\sum }_{j=1}^k(1-Z_j)}}|Y_j=0\text{for}j=1,\dots ,k,{\displaystyle \sum _{j=1}^k(1-Z_j)=i}\right]\right]={\displaystyle \sum _{i=1}^k\frac{{\displaystyle {\sum }_{j=1}^i\mathrm{E}[V_j|Z_j=0,Y_j=0]}}{i}}\mathrm{Pr}\left({\displaystyle \sum _{j=1}^k(1-Z_j)=i}\right)=\mathrm{E}[V_1|Z_1=0,Y_1=0]{\displaystyle \sum _{i=1}^k\mathrm{Pr}\left({\displaystyle \sum _{j=1}^k(1-Z_j)=i}\right)}=\mathrm{E}[V_1|Z_1=0,Y_1=0].$$

Since the expectations of both ${\overline{V}}_{1,0}$ and ${\overline{V}}_{0,0}$ are unchanged by conditioning on $1-\overline{Y}$, these variables are uncorrelated with $1-\overline{Y}$, as claimed.□

Proof of Proposition 1

Proof

The proof proceeds by working with linearized variances.

$$\text{Var}[\widehat{\mu }]=\text{Var}[1+(1-\overline{Y})({\overline{V}}_{1,0}-{\overline{V}}_{0,0}-1)]=\text{Var}[(1-\overline{Y})({\overline{V}}_{1,0}-{\overline{V}}_{0,0}-1)]$$ (8)

By Lemma 2, ${\overline{V}}_{1,0}$ and ${\overline{V}}_{0,0}$ are uncorrelated, so the variance of the product in (8) decomposes as follows:

$$\text{Var}[\widehat{\mu }]={(\mathrm{E}[1-\overline{Y}])}^2\text{Var}[{\overline{V}}_{1,0}-{\overline{V}}_{0,0}]+\text{Var}[1-\overline{Y}]{(\mathrm{E}[{\overline{V}}_{1,0}-{\overline{V}}_{0,0}-1])}^2+\text{Var}[1-\overline{Y}]\text{Var}[{\overline{V}}_{1,0}-{\overline{V}}_{0,0}]={(1-\mu p)}^2\text{Var}[{\overline{V}}_{1,0}-{\overline{V}}_{0,0}]+\frac{\mu p(1-\mu p)}{n}{\left(\frac{1-\mu }{1-\mu p}\right)}^2+\frac{\mu p(1-\mu p)}{n}\text{Var}[{\overline{V}}_{1,0}-{\overline{V}}_{0,0}]+O(n^{-2})=\frac{\mu p{(1-\mu )}^2}{n(1-\mu p)}+{(1-\mu p)}^2\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=0]}{(1-\mu p)n\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=0]}{(1-\mu p)(n-n\gamma )}\right]+O(n^{-2})=\frac{\mu p{(1-\mu )}^2}{n(1-\mu p)}+(1-\mu p)\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=0]}{n\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=0]}{n-n\gamma }\right]+O(n^{-2}),$$ (9)

where γ is the probability of receiving treatment, so $n\gamma ={\displaystyle {\sum }_{i=1}^n{Z}_i}$. Multiplying by n yields the desired result.□

Proof of Proposition 2

Proof

We begin by expressing the asymptotic variance of ${\widehat{\mu }}_S$:

$$\begin{gathered} \underset{n\to \mathrm{\infty }}{\text{plim}}n\text{Var}[{\widehat{\mu }}_S]=(1-\mu p)\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=0]}{\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=0]}{1-\gamma }\right] \\ +\mu p\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=1]}{\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=1]}{1-\gamma }\right] \\ +(1-\mu p)\left[\frac{{\text{(E}[V_i|Z_i=1,Y_i=0]-\mathrm{E}[V_i|Z_i=1])}^2}{\gamma }\right] \\ +(1-\mu p)\left[\frac{{\text{(E}[V_i|Z_i=0,Y_i=0]-\mathrm{E}[V_i|Z_i=0])}^2}{1-\gamma }\right] \\ +\mu p\left[\frac{{\text{(E}[V_i|Z_i=1,Y_i=1]-\mathrm{E}[V_i|Z_i=1])}^2}{\gamma }\right] \\ +\mu p\left[\frac{{\text{(E}[V_i|Z_i=0,Y_i=1]-\mathrm{E}[V_i|Z_i=0])}^2}{1-\gamma }\right] \\ =(1-\mu p)\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=0]}{\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=0]}{1-\gamma }\right] \\ +\mu p\left[\frac{\text{Var}[V_i|Z_i=1,Y_i=1]}{\gamma }+\frac{\text{Var}[V_i|Z_i=0,Y_i=1]}{1-\gamma }\right] \\ +\mu p(1-\mu p)\left[\frac{{\text{(E}[V_i|Z_i=1,Y_i=0]-\mathrm{E}[V_i|Z_i=1,Y_i=1])}^2}{\gamma }\right] \\ +\mu p(1-\mu p)\left[\frac{{\text{(E}[V_i|Z_i=0,Y_i=0]-\mathrm{E}[V_i|Z_i=0,Y_i=1])}^2}{1-\gamma }\right]. \end{gathered}$$

By Assumptions 1 and 2 (Monotonicity, No Liars and No Design Effects), E [V_i|Z_i = 1, Y_i = 1] = E [V_i|Z_i = 0, Y_i = 1] + 1. Then

$$\underset{n\to \mathrm{\infty }}{\text{plim}}n\text{Var}\left[{\widehat{\mu }}_S\right]=(1-\mu p)\left[\frac{\text{Var}\left[V_i|Z_i=1,Y_i=0\right]}{\gamma }+\frac{\text{Var}\left[V_i|Z_i=0,Y_i=0\right]}{1-\gamma }\right]+\mu p\left[\frac{\text{Var}\left[V_i|Z_i=1,Y_i=1\right]}{\gamma }+\frac{\text{Var}\left[V_i|Z_i=0,Y_i=1\right]}{1-\gamma }\right]+\mu p(1-\mu p)\left[\frac{{(\frac{\mu -1}{1-\mu p}+\mathrm{E}\left[V_i|Z_i=0,Y_i=0\right]-\mathrm{E}\left[V_i|Z_i=0,Y_i=1\right])}^2}{\gamma }\right]+\mu p(1-\mu p)\left[\frac{{(\mathrm{E}\left[V_i|Z_i=0,Y_i=0\right]-\mathrm{E}\left[V_i|Z_i=0,Y_i=1\right])}^2}{1-\gamma }\right].$$

Applying the first order condition, ${\text{plim}}_{n\to \mathrm{\infty }}n\text{Var}\left[{\widehat{\mu }}_S\right]$ is minimized when E [V_i|Z_i = 0, Y_i = 0] − E [V_i|Z_i = 0, Y_i = 1] = [γ − 1][(μ − 1)/(1 − μp)]. Substituting terms, it follows that

$$\underset{n\to \mathrm{\infty }}{\text{plim}}n\text{Var}\left[{\widehat{\mu }}_S\right]\ge (1-\mu p)\left[\frac{\text{Var}\left[V_i|Z_i=1,Y_i=0\right]}{\gamma }+\frac{\text{Var}\left[V_i|Z_i=0,Y_i=0\right]}{1-\gamma }\right]+\mu p\left[\frac{\text{Var}\left[V_i|Z_i=1,Y_i=1\right]}{\gamma }+\frac{\text{Var}\left[V_i|Z_i=0,Y_i=1\right]}{1-\gamma }\right]+\mu p(1-\mu p){\left(\frac{1-\mu }{1-\mu p}\right)}^2\ge \underset{n\to \mathrm{\infty }}{\text{plim}}n\text{Var}\left[\widehat{\mu }\right].$$ (10)

Assumption 4 (Non-degenerate Distributions) ensures that the inequality holds strictly. □