This study describes the development of a survey grounded in expectancy-value theory, providing multiple forms of validity evidence to support its use as a measure of students’ interest in using math to understand biology, the usefulness of math for one’s life science career, and the perceived cost of using math in biology courses.
Abstract
In response to calls to improve the quantitative training of undergraduate biology students, there have been increased efforts to better integrate math into biology curricula. One challenge of such efforts is negative student attitudes toward math, which are thought to be particularly prevalent among biology students. According to theory, students’ personal values toward using math in a biological context will influence their achievement and behavioral outcomes, but a validated instrument is needed to determine this empirically. We developed the Math–Biology Values Instrument (MBVI), an 11-item college-level self-report instrument grounded in expectancy-value theory, to measure life science students’ interest in using math to understand biology, the perceived usefulness of math to their life science career, and the cost of using math in biology courses. We used a process that integrates multiple forms of validity evidence to show that scores from the MBVI can be used as a valid measure of a student’s value of math in the context of biology. The MBVI can be used by instructors and researchers to help identify instructional strategies that influence math–biology values and understand how math–biology values are related to students’ achievement and decisions to pursue more advanced quantitative-based courses.
INTRODUCTION
While the field of biology is becoming increasingly quantitative, undergraduate biology education has been comparatively slow to incorporate quantitative skills into the curriculum (American Association for the Advancement of Science [AAAS], 2011). This, in part, has led to a number of national calls to improve the quantitative training undergraduate biology students receive (National Research Council, 2003, 2009; Steen, 2005; AAAS, 2011). In response to these calls, there have been efforts to better integrate math into biology curricula. Such reforms include incorporating the teaching of quantitative skills (e.g., via modules or in-class research experiences) into biology courses (Robeva et al., 2010; Speth et al., 2010; Thompson et al., 2010; Colon-Berlingeri and Burrowes, 2011; Madlung et al., 2011; Wightman and Hark, 2012; Makarevitch et al., 2015; Hoffman et al., 2016), redesigning mathematics courses for biology majors to include biology examples (Edelstein-Keshet, 2005; Metz, 2008; Chiel et al., 2010; Duffus and Olifer, 2010; Watkins, 2010; Rheinlander and Wallace, 2011; Thompson et al., 2013), and designing fully integrated math–biology courses and majors (Depelteau et al., 2010; de Pillis and Adolph, 2010; Duffus and Olifer, 2010; Hoskinson, 2010; Usher et al., 2010; Thompson et al., 2013; Hester et al., 2014). The goal of such reforms is to ensure that students develop quantitative skills that will prepare them for careers in the field of modern biology.
However, one challenge to quantitative biology education reform is negative student attitudes toward math (Colon-Berlingeri and Burrowes, 2011; Thompson et al., 2013). For example, if students have a negative attitude toward math, they may resist learning math or avoid professors who emphasize math or courses in which more math is incorporated (Colon-Berlingeri and Burrowes, 2011). Negative math attitudes are thought to be particularly prevalent among biology students relative to other science students. Indeed, many reform efforts have incorporated elements specifically to promote positive math attitudes in biology students, such as the use of humor (Thompson et al., 2010) or the use of real-world problems (Matthews et al., 2009, 2010).
From a theoretical perspective, math attitudes are important for the development of students’ quantitative skills because they are posited to influence student motivation. According to expectancy-value theory of achievement motivation, students’ performance (e.g., achievement on quantitative tasks) depends on how well they expect to do on a task and the value they place on the task (Eccles et al., 1983; Wigfield and Eccles, 2000; Eccles and Wigfield, 2002). Students who are confident they can successfully do a task are motivated to persist and complete the task (Wigfield and Cambria, 2010). However, even if students are confident in their ability to complete a task, they will not necessarily be motivated to engage in the task unless there is some value in it for them (Wigfield and Cambria, 2010).
The personal values a student places on a task, called task values, comprise four different constructs: 1) the intrinsic or interest value of the task, 2) the utility value of the task, 3) the attainment value of the task, and 4) the perceived cost of the task (Wigfield and Eccles, 2000). Interest value is the enjoyment a student experiences from engaging in a task (Eccles et al., 1983; Wigfield and Eccles, 2000). Utility value is the usefulness of a task for a student’s future goals (Eccles et al., 1983; Wigfield and Eccles, 2000). Attainment value is the importance of doing well on a task for one’s identity (Eccles et al., 1983; Wigfield and Eccles, 2000). For example, if being good at math is an important part of a student’s identity, then the student will have high attainment value for quantitative tasks, because successful completion of these tasks will affirm the student’s self-identity. Finally, perceived cost involves the negative aspects of engaging in a task. Cost includes 1) extra effort required for a task, 2) the loss of opportunities that result from engaging in a task, and 3) the emotional toll of a task (Eccles et al., 1983; Wigfield and Eccles, 2000). These four constructs of task values are predicted by expectancy-value theory to affect a student’s performance on a task and the courses a student chooses to take (Eccles et al., 1983; Wigfield and Eccles, 2000).
Indeed, in K–12 environments, task values have been shown to affect achievement (Berndt and Miller, 1990; Simpkins et al., 2006; Lee et al., 2014), course enrollment intentions (Eccles et al., 1984; Meece et al., 1990), academic aspirations (Korhonen et al., 2016), and plans to attend college (Eccles et al., 2004). While postsecondary environments are less studied, there is also evidence linking college students’ task values to achievement (Bong, 2001; Zusho et al., 2003; Hulleman et al., 2010), course enrollment intentions (Bong, 2001), plans to attend graduate school (Battle and Wigfield, 2003), and career plans (Jones et al., 2010). Thus, it is likely that college students’ personal values of math in a biological context (i.e., math–biology task values) will influence their performance on quantitative tasks in biology courses and their intentions to further pursue quantitative biology, through either additional undergraduate course work, graduate study, or a job in a quantitative biology field. To determine this empirically, however, there is a need for a validated instrument to measure college students’ personal values toward the use of math in the context of biology, as no such instrument currently exists.
Although an instrument does exist to measure college students’ general math task values (Mathematics Value Inventory [MVI]; Luttrell et al., 2010), students’ values toward using math in the context of biology are likely different from their general math task values. Students can have difficulties applying math skills to new contexts (Britton, 2002; Hester et al., 2014), which may contribute to differing costs associated with engaging in general math tasks compared with engaging in math tasks in the context of biology. Additionally, students may not understand the specific relevance of math to biology, particularly given that few have had experiences using math in biology, which may lead to differences in the perceived utility of general math versus the utility of math in biology.
We describe here the development of an 11-item college-level self-report instrument, which we call the Math–Biology Values Instrument (MBVI), intended to measure the values undergraduate life science majors place on using math in the context of biology. This instrument uses expectancy-value theory as a theoretical framework and is adapted from the existing MVI (Luttrell et al., 2010). The MBVI is composed of three components of math–biology task values: interest, utility value, and perceived cost. In the context of math–biology, interest refers to the enjoyment one gets from using math to understand biology, utility value refers to the usefulness of math for one’s life science career, and perceived cost refers to negative aspects of using math in biology courses. Consistent with the recommendations of Reeves and Marbach-Ad (2016), we used a process that integrates multiple forms of validity evidence to support the use of the MBVI as a measure of undergraduate life science majors’ math–biology task values. We believe the MBVI can be used by instructors and researchers to help identify instructional strategies that influence math–biology values and how math–biology values are related to students’ achievement and their decisions to pursue more advanced quantitative-based courses.
METHODS
The MBVI was modeled after the MVI developed and validated by Luttrell and colleagues (2010) as a measure of undergraduates’ math task values. The MVI consists of four subscales, each containing seven Likert-type response items, that correspond to each of the four task values of expectancy-value theory: interest, utility value, attainment value, and perceived cost (Luttrell et al., 2010). Validity evidence was gathered using undergraduate non–math majors, and each subscale was shown to have high internal consistency (α = 0.91–0.95; Luttrell et al., 2010).
We created the initial item pool for the MBVI by modifying each of the MVI items in three of the subscales (interest, utility value, and perceived cost) to reflect the use of math specifically within a biological context (Table 1). Attainment value was conceptualized by Eccles and colleagues (1983) as the importance to one’s identity of doing well on a task, but it did not make sense that a student would have a mathematical biology identity, especially given that many students have had few, if any, experiences using math in biology courses. Instead, we developed items to measure both math attainment value and biology attainment value, as we thought both may impact students’ achievement on interdisciplinary mathematical biology tasks. We created math attainment items rather than use the attainment value subscale of the MVI, because the MVI items did not necessarily reflect the importance of doing well in math specifically for a student’s identity. We developed eight attainment value items that would measure the importance of doing well in math for a student’s math identity (e.g., Being good at math is an important part of who I am). We also developed seven attainment value items that would measure the importance of doing well in biology for a student’s biology identity (e.g., Being good at biology is an important part of who I am). Our initial pool of survey items, therefore, consisted of nine interest items, seven utility value items, seven cost items, eight math attainment value items, and seven biology attainment value items for a total of 38 items.
TABLE 1.
Sample items from the MVI and their corresponding modifications to reflect math–biology task valuesa
| Construct | Math–biology definition | Item from MVI | Modified item |
|---|---|---|---|
| Interest | Enjoyment one gets from using math to understand biology | It is fun to do math. | It is fun to use math to explore biology. |
| Utility value | The usefulness of math for one’s life science career | After I graduate, an understanding of math will be useless to me. | After I graduate, an understanding of math will be useful to me in a life science career. |
| Perceived cost | Negative aspects of using math in biology courses | Taking math classes scares me. | Taking biology courses that incorporate math scares me. |
aSample MVI items from Luttrell et al. (2010). The modified items were subsequently sent out for expert review.
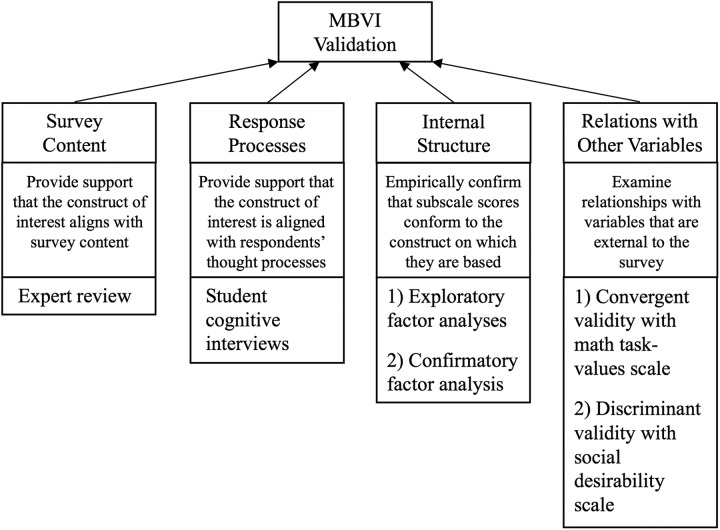
Once we developed the initial items for the MBVI, we used a multistep process in line with the recommendations of Reeves and Marbach-Ad (2016), who describe five forms of validity evidence: evidence based on 1) survey content, 2) response processes, 3) internal structure, 4) relations with other variables, and 5) the consequences of testing. Here we provide initial validity evidence based on the first four forms of evidence (Figure 1). We used expert review to provide evidence that the construct measured (e.g., math–biology interest) and the content of the survey (e.g., the specific math–biology interest items on the survey) were aligned (validity evidence based on survey content; Reeves and Marbach-Ad, 2016). Think-aloud interviews with students were conducted to ensure that students’ interpretation of each item on the survey aligned with our definition of the item’s construct (validity evidence based on response processes; Reeves and Marbach-Ad, 2016). To confirm empirically that the items indeed represented the constructs they are intended to represent (evidence based on internal structure; Reeves and Marbach-Ad, 2016), we used exploratory and confirmatory factor analyses (EFA and CFA) to show that the items for each math–biology task-value construct are highly correlated with each other but weakly correlated with items from the other constructs. Finally, we provide validity evidence based on relations with other variables by showing that survey scores are significantly related to similar constructs (convergent validity) and are unrelated to dissimilar constructs (discriminant validity; Reeves and Marbach-Ad, 2016).
FIGURE 1.
Validity evidence framework described by Reeves and Marbach-Ad (2016) and the corresponding approaches used to validate the MBVI as a measure of life science majors’ values of math in the context of biology.
Content Validity: Expert Review
To provide evidence for validity based on survey content, we sent our initial items, representing five constructs (interest, utility value, and perceived cost of math in a biology context; attainment value in math; and attainment value in biology), to six experts in the field of quantitative biology and one expert in assessment. Experts were provided with definitions of each of the five constructs and were asked to rate the relevance of each item to the construct and the clarity of each item as either low, medium, or high. Experts could also provide comments on each item or suggest additional items that would be useful for measuring a particular construct. On the basis of the comments and suggestions from the expert reviewers, we compiled 45 items to test with students.
Response Process Validity: Student Cognitive Interviews
To provide evidence for validity based on response processes, we tested the 45 items created from the expert reviewer comments through in-person think-aloud interviews with undergraduate life science majors, based on guidance by Willis (1999). We split the 45 items into two smaller sets of 22–23 items; both sets contained similar numbers of items from each of the five constructs. This smaller set of items was presented to undergraduates in order to avoid student fatigue from answering all 45 items. Two researchers interviewed a total of 20 undergraduate life science majors, 10 using the first set of items and 10 using the second set of items (see Supplemental Material A for additional details). Students were compensated with a $25 gift card for participating in the 30- to 60-minute-long interviews. This study was approved by the IRB at the University of Texas at Austin (#2015-03-0005).
Validity Evidence Based on Internal Structure and Relations with Other Variables: Pilot Survey
Once we refined and narrowed down the MBVI items based on expert review and student cognitive interviews, we created a pilot survey to gather validity evidence based on internal structure and relations with other variables. The purpose of the pilot survey was threefold: 1) to verify that the items used to measure the four constructs are interrelated in expected ways (as described earlier) via EFA, 2) to establish convergent validity using a scale that measures similar constructs, and 3) to demonstrate discriminant validity using a social desirability scale.
Participants.
Survey invitations were distributed via course listservs to introductory biology and upper-level biology courses at four institutions (two research universities, one comprehensive university, and one primarily undergraduate institution) and one community college system in the United States (three in the Northeast, one in the Southwest, and one in the South Central region). The anonymous survey was administered online through Qualtrics. Only students who were at least 18 years old and life science majors were eligible to take the survey; students self-identified with these criteria to enter the survey. Students who completed the survey were compensated with a $10 gift card. This study was approved by the IRB at the University of New Hampshire (#6389). In total, 228 students responded, representing ∼30 different life science majors. Of these 228 respondents, we removed 19 from the data set because they had missing data; using a missing-data technique (i.e., imputation or full information maximum likelihood) did not provide additional useful information for the exploratory analysis. We also removed two students because they provided the same response to all items on the survey, including positively and negatively worded items (e.g., “It is/would be fun to use math to understand biology” and “Trying to use math to understand biology causes/would cause me anxiety”). This resulted in a final sample of 207 students (see Table 2 for complete demographics).
TABLE 2.
Demographics of the life science majors used in the EFA (n = 207) and CFA (n = 206)a
| Description | EFA n (%) | CFA n (%) |
|---|---|---|
| Gender | ||
| Male | 49 (24) | 46 (22) |
| Female | 154 (74) | 157 (76) |
| Other | 1 (<1) | 3 (1) |
| Race | ||
| American Indian or Alaska Native | 6 (3) | 2 (1) |
| Asian | 18 (9) | 26 (13) |
| African American or Black | 9 (4) | 21 (10) |
| Native Hawaiian or other Pacific Islander | 4 (2) | 1 (0.5) |
| White | 165 (78) | 152 (74) |
| Other | 9 (4) | 6 (3) |
| Ethnicity | ||
| Hispanic or Latinx | 35 (17) | 13 (6) |
| Not Hispanic or Latinx | 157 (76) | 183 (89) |
| Year in college | ||
| First year | 55 (27) | 128 (62) |
| Second year | 31 (15) | 37 (18) |
| Third year | 45 (22) | 34 (16) |
| Fourth year | 63 (30) | 3 (1) |
| Fifth year or greater | 11 (5) | 4 (2) |
| Honors status | ||
| Honors | 33 (16) | 27 (13) |
| Not in honors | 170 (82) | 173 (84) |
| Institution type | ||
| Research university | 112 (54) | 151 (73) |
| Comprehensive | 43 (21) | 55 (27) |
| Primarily undergraduate institution | 11 (5) | |
| Community college system | 27 (13) |
aStudents could select “Prefer not to respond” to any question and could select more than one race, thus percentages might not sum to 100%.
Measures.
The pilot survey contained the following measures: the MBVI, a math task-values survey (Eccles et al., 1983; Fredricks and Eccles, 2002), the Marlowe-Crowne Social Desirability Scale (MCSDS; Crowne and Marlowe, 1960), and a demographic questionnaire, each of which is described in detail.
The MBVI was prefaced by a definition of math (“For the purposes of this survey, math includes arithmetic, algebra, calculus, and statistics”) and contained a total of 25 Likert-type items related to four constructs: interest in using math to understand biology, utility value of math for a life science career, cost of incorporating math into biology courses, and attainment value of math (Supplemental Table B1). Each item had a seven-point response scale ranging from “strongly disagree” to “strongly agree.” Each item also contained options for “I don’t know” and “Prefer not to respond.” We intentionally included several items that were similar to one another to see whether there were empirical differences between the item performances. That is, we wanted to see whether the items, although similar in wording and/or meaning, functioned differently in practice.
A math task-values instrument developed by Eccles and colleagues (1983) was included to establish convergent validity. This instrument was chosen because it contains measures of interest, utility value, and attainment value in a similar domain. The math task-values instrument has been used extensively on K–12 students and has been shown to be a valid measure of task values (Eccles et al., 1993; Wigfield et al., 1997; Fredricks and Eccles, 2002). It is composed of seven Likert-type items measuring students’ personal values toward math: three items measuring interest, two items measuring utility value, and two items measuring attainment value (Eccles et al. 1983, Fredricks and Eccles 2002; Supplemental Table B2). All items were on a seven-point scale with an option to select “Prefer not to respond.” Each subscale showed high internal consistency (interest: n = 207, α = 0.94; utility value: n = 205, α = 0.88; attainment value: n = 206, α = 0.83).
To determine whether students’ responses were affected by social desirability bias (a tendency to give responses that present themselves in a more favorable light) and establish discriminant validity, we used Crowne and Marlowe’s (1960) Social Desirability Scale (MCSDS). The MCSDS is a 33-item, true–false scale designed to assess whether respondents are answering truthfully (low score) or in a more socially desirable way (high score; Supplemental Table B3). Students could also select “Prefer not to respond.” Internal consistency and validity evidence for the use of the MCSDS as a measure of social desirability bias has been established in many studies (Beretvas et al., 2002; for a review, see Paulhus, 1991) and is commonly used to support discriminant validity of self-report measures (Lent et al., 2003; Luttrell et al. 2010; Reysen et al., 2013; Bhalla et al., 2016; Doran et al., 2016). The MCSDS showed good internal consistency (n = 152; α = 0.80).
The final portion of the survey consisted of 13 items on students’ demographic characteristics (gender, race, and ethnicity) and their academic backgrounds (institution, year in college, major, pre-professional status, number of college math courses taken, number of college biology courses taken, current college grade point average [GPA], honors program status, and career aspirations). Students were not required to complete open-ended questions, and for all multiple-choice questions, students had the option to select “Prefer not to respond.”
Validity Based on Internal Structure.
A series of EFAs were conducted in the statistical program R (R Core Team, 2016) to determine the relationships among the MBVI items. Although our sample size might be considered small for EFA, smaller sample sizes (<300) may be adequate if there are at least four items per factor and factor loadings are greater than |0.60| (Worthington and Whittaker, 2006). In our pilot survey, the interest, utility value, and cost factors each had at least four items, and the factor loadings were generally greater than |0.60| (Supplemental Table C1). The EFAs were performed using principal axis factoring with an oblimin rotation (“psych” R package; Revelle, 2016). We used this approach to identify the least number of common factors to explain the covariance among the items while still allowing the items to load on all the potential factors.
Validity Based on Relations with Other Variables.
Students’ values of math in the context of biology should be similar to their values of math in general. Therefore, we used a math task-values instrument (Eccles et al. 1983; Fredricks and Eccles, 2002) to establish convergent validity. We used Pearson’s correlations to examine the relationship between the interest subscales of the MBVI and the math task-values instrument and the utility value subscales of the MBVI and the math task-values instrument. We ended up dropping all of the attainment value items from the MBVI based on the results of the EFA (see Results); thus we did not use the attainment value subscale of the math task-values instrument. We expected there to be strong positive correlations between the MBVI and math task-value interest and utility subscale scores, which would indicate that they are measuring similar constructs and provide evidence for convergent validity (Reeves and Marbach-Ad, 2016). The math task-value instrument did not contain a cost subscale. However, cost has been shown to have a negative relationship with both interest and utility value; correlations between cost and interest are strong and negative, whereas those between cost and utility value are more moderate and negative (Trautwein et al., 2012; Gaspard et al., 2015). Therefore, we calculated the correlation between the cost subscale of the MBVI and the interest and utility value subscales of the math task-values instrument to establish validity of the cost subscale. Subscale scores were created by summing the scores of all items on each subscale.
We used the MCSDS (Crowne and Marlowe, 1960) to establish discriminant validity. Socially desirable responses were coded as “1” and summed to create a total MCSDS score. The cost items on the MBVI were reverse scored, and all items were subsequently summed to create a total MBVI score for each student. We used Pearson’s correlation to examine the relationship between students’ MCSDS total scores and their MBVI total scores. A nonsignificant correlation between the MBVI and the MCSDS would indicate that the MBVI is not confounded with social desirability bias and would provide evidence of discriminant validity (Paulhus, 1991).
Additional Validity Based on Internal Structure: CFA
As an additional step to provide validity evidence based on internal structure, we performed CFA on the final MBVI survey, consisting of 11 items on three subscales (interest, utility value, and perceived cost), using a second, independent sample of students. This is a prudent step in instrument validation to ensure that the initial EFA results were not sample dependent. In addition, we wanted to ensure that the final 11 items on the MBVI functioned similarly in isolation as they had when administered alongside the 14 culled MBVI items. The sample for this follow-up study consisted of 206 life science majors from three universities (one research university from the Northeast, one research university from the Mid-Atlantic region, and one comprehensive university from the Mid-Atlantic region; see Table 2 for demographic information of participants); these data are the first time points in a larger, longitudinal study examining change in math–biology values. Students were recruited through survey invitations sent to introductory biology course listservs and compensated with a $5 gift card for completion of the survey. This study was approved by the IRB at the University of New Hampshire (#6507).
The CFA was conducted using the “lavaan” R package for structural equation modeling (Rosseel, 2012) with maximum-likelihood robust estimation to correct for any nonnormality in the data. Additionally, full information maximum likelihood was used to handle any missing responses to the 11 MBVI items. Although our sample size is small, the guidelines provided by Wolf and colleagues (Wolf et al., 2013) suggest that only 150 participants are needed for a three-factor model with three or four indicators per factor with average standardized factor loadings of 0.80 (the average from our championed EFA model was 0.88).
RESULTS
Validity Based on Internal Structure: EFA
We hypothesized that a four-factor solution would appropriately fit the data in accordance with item development. We used several different measures to determine the number of factors presented in the data: the Kaiser-Guttman criterion (also known as the “eigenvalues-greater-than-one” criterion), parallel analysis, optimal coordinates, and the acceleration factor, all from the “nFactors” R package (Raiche and Magis, 2015). The last two criteria are based on mathematical characteristics of the implied scree plot, and all four statistics aim to provide a suggested number of factors based on nonvisual analysis of the data. The Kaiser-Guttman, parallel analysis, and optimal coordinates criterion all indicated that a three-factor solution would best describe the data. The only dissenting information was provided by the acceleration factor, which indicated that only one factor was necessary, but this criterion has been demonstrated to consistently provide underfactored solutions (Ruscio and Roche, 2012).
On the basis of these results and our theoretical development of the MBVI, we examined solutions for one-factor, two-factor, three-factor, and four-factor EFA solutions. While we were mainly interested in examining the multidimensional solutions, it is prudent to examine more parsimonious explanations of the data to see whether theoretically defensible factor solutions emerge that adequately explain the variance in the observed items.
The results from the one-factor EFA showed that all items had generally strong loadings (Supplemental Table C1; also see Supplemental Table C2 for the correlation matrix of all items used in the EFA). The perceived cost items all had negative loadings, which is consistent with their theoretical relationship to the other items (i.e., a high score for perceived cost represents a negative attitude, while a high score for interest, utility value, and math attainment value represents a positive attitude). While the one-factor solution had generally acceptable factor loadings above traditional cutoff values of 0.32 (Tabachnick and Fidell, 2001) or 0.50 (Osborne and Costello, 2009), we felt that interpreting the scale as a single dimension masked more nuanced and fine-grained constructs responsible for the item responses. In addition, the one-factor solution only extracted 50% of the variance in the items, and we felt that more item variance could be explained by the inclusion of additional factors.
The two-factor solution revealed more of this nuanced relationship between the items, as all (and only) perceived cost items strongly positively loaded on the second identified factor (Supplemental Table C1). The first factor was characterized by the interest, utility value, and math attainment value items, with the math attainment value items loading less strongly (0.58–0.63) than the rest of the items on the first factor (0.67–0.82). All perceived cost items loaded strongly on the second factor (0.68–0.90). This solution offered a more interpretable and meaningful result (interest–utility value–math attainment value and perceived cost) and was also able to explain more of the variance in the items, with 63% of the variance explained, but we thought that the first factor could be further divided to provide more information to researchers about the constructs underlying the observed responses.
The three-factor solution was similar to the two-factor solution in that perceived cost constituted the second factor (loadings of 0.67–0.94; Supplemental Table C1). The third factor now consisted of all of the utility value items (loadings of 0.66–0.88), with the math attainment value items hanging together with the interest items on the first factor. While these two constructs constituted the first factor, there were distinct differences in their factor loadings. The loadings for interest remained high (0.78–0.95), but the loadings for math attainment value were lower than all other items (0.53–0.60). Again, the three-factor solution accounted for more variance in the observed items (70%) than the two-factor solution.
The four-factor solution mirrored the three-factor solution apart from the math attainment value items now constituting their own factor (Supplemental Table C1). The factor loading for the third math attainment value item (Atn3) was very high (0.94), with the other two items loading less strongly (0.62, 0.73). The strength of all other factor loadings in the four-factor solution were nearly identical to the three-factor solution (most changed by no more than |0.02|), except for four interest items (Int1–Int3 and Int5), which changed by no more than |0.07|. The inclusion of the fourth factor accounted for an additional 3% of the variance in the items (for a total of 73%).
After examining all the factor solutions, we proceeded with scale refinement, considering only items from the first three dimensions: interest, utility value, and perceived cost. While the math attainment value items represented an interesting aspect of the MBVI, they were developed to assess students’ math identity (as opposed to math–biology), and thus did not function as well as the other items. The third math attainment item (Atn3 in Supplemental Table C1) loaded strongly on the fourth factor in the four-factor solution but did not load as strongly in any of the other solutions. Importantly, while Atn3 had a high factor loading in the four-factor solution, the other math attainment items only had moderately strong loadings, suggesting that the math attainment factor was primarily defined by Atn3 and the other math attainment items did not correlate as strongly as desired with that item (Supplemental Table C1). Retaining only Atn3 was not adequate for construct representation, and we did not wish to develop additional math attainment items to pilot for scale inclusion, so we chose not to pursue including information about math attainment value on the MBVI.
We now had an indication that all items selected to represent the constructs of interest, utility value, and perceived cost functioned well in practice, as evidenced by their high factor loadings on their respective factors and extremely low cross-factor loadings. With the exclusion of the math attainment value items, we now had 22 items in total, some of which were extremely similar to one another. As such, we decided to choose those items for each construct that were most representative of that construct and eliminate the items that were less representative. Doing so would also reduce the overall number of items for the MBVI, making it less burdensome on the survey taker. We did not select the items for the final MBVI by choosing those items that loaded most strongly on their respective factors. Instead, the theory behind the item development and construct representation were used as the guiding principles for scale refinement. This resulted in a final set of 11 items: four representing interest, four representing utility value, and three representing perceived cost (Table 3; bolded items in Supplemental Table B1). The solution for this final three-factor EFA showed high loadings for all three factors; the lowest loading was 0.77 (Uty3), with an average factor loading of 0.88 across all items (Table 3). This solution accounted for 79% of the variance in the final 11 scale items. Additionally, all three factors demonstrated good reliability, with Cronbach’s alpha values ranging from 0.91 (utility value) to 0.95 (interest; Table 3).
TABLE 3.
Factor loadings from the final three-factor solution from the EFA (n = 207)a
| Factorc | ||||
|---|---|---|---|---|
| Itemb | I | II | III | Mean (SD) |
| I. Interest | ||||
| Int2: Using math to understand biology intrigues/would intrigue me. | 0.88 | 0.05 | 0.05 | 4.76 (1.78) |
| Int6: It is/would be fun to use math to understand biology. | 0.83 | −0.01 | −0.07 | 4.33 (1.82) |
| Int7: Using math to understand biology appeals/would appeal to me. | 0.95 | −0.01 | −0.01 | 4.62 (1.82) |
| Int8: Using math to understand biology is/would be interesting to me. | 0.96 | −0.01 | 0.01 | 4.75 (1.80) |
| II. Utility value | ||||
| Uty3: Math is valuable for me for my life science career. | 0.07 | 0.77 | −0.03 | 5.75 (1.26) |
| Uty4: It is important for me to be able to do math for my career in the life sciences. | 0.02 | 0.87 | 0.00 | 5.76 (1.28) |
| Uty5: An understanding of math is essential for me for my life science career. | −0.04 | 0.89 | 0.02 | 5.54 (1.44) |
| Uty6: Math will be useful to me in my life science career. | −0.02 | 0.85 | −0.01 | 5.76 (1.17) |
| III. Perceived cost | ||||
| Cst6: I have/would have to work harder for a biology course that incorporates math than for one that does not. | 0.06 | 0.07 | 0.91 | 4.63 (1.93) |
| Cst7: I worry/would worry about getting worse grades in a biology course that incorporates math than one that does not. | 0.02 | −0.06 | 0.93 | 4.20 (2.05) |
| Cst8: Taking a biology course that incorporates math intimidates/would intimidate me. | −0.14 | −0.03 | 0.79 | 3.81 (2.03) |
| Mean factor scored | 4.61 | 5.70 | 4.21 | |
| Mean factor SD | 1.69 | 1.15 | 1.86 | |
| PVEe | 0.31 | 0.26 | 0.22 | |
| CVEe | 0.31 | 0.57 | 0.79 | |
| Cronbach’s alpha | 0.95 | 0.91 | 0.92 | |
| Factor correlations | ||||
| I | — | |||
| II | 0.62 | — | ||
| III | −0.51 | −0.27 | — | |
aSee Supplemental Table B1 for items on the initial survey that were not retained.
bItem abbreviations (e.g., Int2) correspond to the CFA factor model in Figure 2.
cFactor loadings greater than |0.50| are bolded; loadings less than |0.50| are in italics.
dMean factor score (and associated SD) is the mean score of all observed responses for the items on that factor.
ePVE, proportion of variance explained by the factor; CVE, cumulative variance explained.
Convergent and Discriminant Validity
The MBVI utility value subscale had a strong positive correlation with the math task-value utility items (r = 0.52, p < 0.001, n = 205). An even stronger correlation was observed between the interest items on the two scales (r = 0.69, p < 0.001, n = 207). Cost scores from the MBVI were strongly negatively correlated with math interest scores (r = −0.61, p < 0.001, n = 205) and moderately negatively correlated with math utility value scores (r = −0.33, p < 0.001, n = 205). These results demonstrate that the MBVI interest and utility value items are positively related to items of a similar type in a less specific context, and the MBVI cost items are negatively correlated with interest and utility value as predicted, thus providing evidence of convergent validity.
The correlation between MCSDS total scores and MBVI total scores was low and not significant (r = 0.05, p = 0.51, n = 152). This indicates that students’ responses to the MBVI were not confounded by social response bias and provides evidence of discriminant validity.
CFA
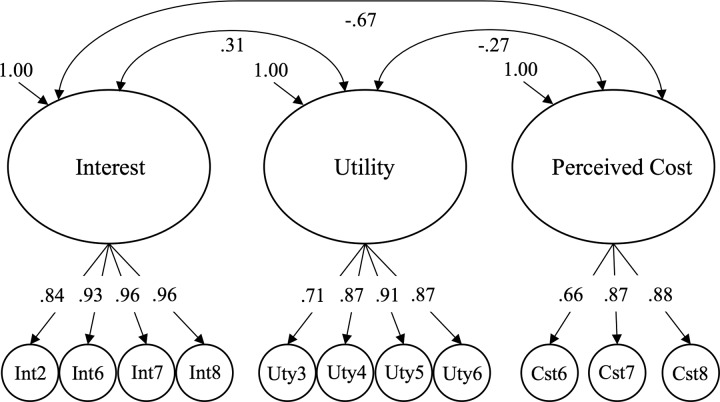
The chi-square test of model fit was significant (χ2(41) = 79.34, p = 0.003), but this test is known to reject correct models with sample sizes as low as 200 (Jöreskog and Sörbom, 1993). Thus, we consulted four supplemental fit indices to determine whether our hypothesized model was a plausible explanation of the relationships observed in the data. All of these fit indices indicated acceptable model fit. The confirmatory fit index (0.98) and the Tucker-Lewis index (0.97) were both above the suggested cutoff values of 0.95 (Hu and Bentler, 1999). Additionally, the root-mean-square error of approximation (Steiger and Lind, 1980; Steiger, 1990) was 0.07, and the standardized root-mean-square residual (Jöreskog and Sörbom, 1981; Bentler, 1995) was 0.06, both of which were at or below their suggested cutoffs (0.07 and 0.08, respectively; Hu and Bentler, 1999; Steiger, 2007). Because the model had adequate fit, the model parameters could then be meaningfully interpreted. As can been seen in Figure 2, the standardized factor loadings were similar (within ± |0.06|) to what was observed in the EFA. The only exceptions were Int6, which increased from 0.83 to 0.93, Cst6, which decreased from 0.91 to 0.66, and Cst8, which increased from 0.79 to 0.88. Given that the CFA model had acceptable model fit and that the factor loadings were generally the same in the CFA result as the EFA result, this provides additional supporting validity evidence for the internal structure of the MBVI.
FIGURE 2.
Standardized factor loadings of the CFA on the second, independent sample of students (n = 206). The factor variances were set to 1.00 to identify each model. Abbreviations (e.g., Int2) correspond to the items in Table 3.
DISCUSSION
The field of biology is becoming increasingly quantitative, leading to major reform efforts geared toward increasing the quantitative skills of undergraduate biology majors. Expectancy-value theory suggests that students’ personal values toward a task are an important predictor of achievement (Eccles et al., 1983; Wigfield and Eccles, 2000; Eccles and Wigfield, 2002). Thus, understanding students’ values toward the use of math in the context of biology is an important step in the process of developing effective quantitative reforms. While instruments exist to measure undergraduates’ math task values (e.g., Luttrell and colleagues’ [2010] MVI), and some researchers have measured students’ math–biology or math–science attitudes with single items (Elliott et al., 2001; Matthews et al., 2009, 2010; Thompson et al., 2010), there is no validated instrument designed to measure multiple constructs of undergraduate students’ values toward math in the context of biology specifically. Our goal was therefore to develop such an instrument to measure undergraduate life science majors’ personal values toward using math in the context of biology. A multistep approach to survey development and validation resulted in the 11-item MBVI that can be used to measure three constructs of math–biology task values: interest, utility value, and perceived cost. We believe that the MBVI can be used by instructors and researchers to help identify instructional strategies that influence math–biology task values and to help understand how math–biology task values relate to students’ achievement and behavioral outcomes, such as the decision to pursue more advanced quantitative-based courses.
Math–Biology Task-Value Constructs
The MBVI has strong validity evidence in support of its use to measure three math–biology task values: interest, utility value, and perceived cost. In addition, each of these factors was shown to have strong internal consistency via Cronbach’s alpha. We provided evidence for content validity of the MBVI by grounding the development of our initial math–biology task-value items for the MBVI in expectancy-value theory (Eccles et al., 1983), adapting them from a carefully validated existing inventory of math task values (MVI; Luttrell et al., 2010), and subjecting them to expert and student review. A series of EFAs combined with qualitative refinement grounded in theory resulted in a three-factor version of the MBVI that showed high factor loadings and extremely low cross-factor loadings. CFA on an independent sample of students indicated that this three-factor model was acceptable. Thus, although some studies have found that interest and utility value factor as a single construct in their surveys (e.g., Eccles et al., 1984; Perez et al., 2014), our survey is able to differentiate between interest and utility value as well as perceived cost.
The interest subscale of the MBVI measures the enjoyment one gets from using math to understand biology. Interest is related to intrinsic motivation (Eccles et al., 1983; Eccles and Wigfield, 2002); that is, the motivation to engage in a task is derived from within, rather than from external pressures or rewards (Ryan and Deci, 2000). This type of motivation is posited to lead to deep-level learning (Ryan and Deci, 2000). Indeed, research has demonstrated that students with an interest in a topic are more likely to answer higher-order cognitive skill questions correctly (Schiefele, 1991), take a mastery goal approach to learning (Harackiewicz et al., 2008), and engage in deep-level learning strategies (Schiefele, 1991; Krapp, 1999). Thus, it is likely that interest in using math to understand biology would promote achievement on quantitative biology tasks, but future research is needed to understand the nature of this relationship.
The utility value subscale of the MBVI measures the usefulness of math specifically for a student’s life science career. This aligns with the conceptualization of utility value as the usefulness of a task for a future goal (Eccles et al., 1983). Although we considered framing utility value in terms of the usefulness of math for a students’ life science major, there was little variability in student responses to these items in the cognitive interviews. Students viewed math as important to their life science majors simply because they were required to take math courses to fulfill their major requirements. However, if utility value is framed within the context of a student’s life science career, students are more likely to consider the personal relevance of math, which can act as a source of extrinsic motivation. Interestingly, we found high mean scores for utility value (5.70 on a seven-point scale) among biology majors. In studies that have used a single item to measure students’ utility value toward math in the context of science, others have also found that undergraduates tend to believe that math is useful for biology (Thompson et al., 2010) or science in general (Elliott et al., 2001, Matthews et al., 2009, 2010). Though past studies have found utility value influences student performance (Bong, 2001; Cole et al., 2008; Hulleman et al., 2010), it is unclear the extent to which math–biology utility value positively affects biology students’ performance on quantitative tasks.
Three items on the MBVI measure the perceived cost of using math in biology courses. Item Cst6 asks students about extra effort required for biology courses that incorporate math, and items Cst7 and Cst8 measure students’ negative emotions about using math in biology courses. Thus, the perceived-cost subscale incorporates two of the three dimensions that make up cost according to Eccles and colleagues (1983): extra effort required for a task and the psychological cost of a task. However, the MBVI does not distinguish between these different dimensions within the construct of cost. Recent research has raised a concern that items intended to measure the cost of extra effort may not adequately distinguish between general effort, which may have positive connotations (e.g., some students thrive on and appreciate “hard work”), and true cost, which is perceived negatively (Flake et al., 2015). Although item Cst6 focuses on working harder rather than on “too much work,” as suggested by Flake and colleagues (2015), it loads strongly on the factor with both cost items that use negative language (e.g., “worry” and “intimidate”; Table 3 and Figure 2). High positive correlations between item Cst6 and items Cst7 and Cst8 (0.81 and 0.73, respectively; Supplemental Table C2) demonstrate that students worried about using math in biology courses also perceive doing math in biology courses will take extra effort. However, future research could explore the possibility of testing the addition of more perceived cost items that are framed with negative language to better align with the negative connotation of cost.
We found a strong correlation between our math–biology interest and utility value constructs (Table 3), similar to other studies (Luttrell et al., 2010; Gaspard et al., 2015). However, a high appreciation for the usefulness of math to biology is not necessarily enough to promote interest in math. For example, Matthews and colleagues (2009) found that students with low GPAs were often frustrated when they could not understand the math used in an interdisciplinary science course, which led to boredom and disinterest (“cycle of disengagement”), even if they understood the importance of math in science. While the authors did not measure perceived cost directly, the feelings of frustration and being overwhelmed by the workload and fast pace of the course described by students suggest that cost was a factor (Matthews et al., 2009). In the current study, perceived cost was negatively correlated to both math–biology interest and utility value. While correlation does not equal causation, this does suggest that minimizing the cost experienced by students could lead to increased interest in and utility of math–biology. Taken together, these data highlight the value of an instrument that can be used to measure multiple constructs of math–biology task values.
Limitations
Although we have made an effort to thoroughly validate the use of the MBVI as a measure of life science majors’ math–biology values, there are some limitations to this study. Participants in both surveys were mostly white (78 and 74%, respectively), non-Hispanic (76 and 89%, respectively), female (74 and 76%, respectively), and enrolled in a research university (54 and 73%, respectively). The low numbers of male students and Hispanic/Latinx, Black, and other underrepresented minority (URM) students in our populations did not allow us to test the validity of the math–biology task-value constructs on students from a diverse range of backgrounds. Thus, while understanding the math–biology task values of people with diverse backgrounds is critical for designing quantitative biology courses that meet the needs of diverse learners, we caution readers against interpreting MBVI scores obtained from populations not represented by the research presented here without first gathering validity evidence from those populations (e.g., by performing CFA). This will be particularly vital for readers intending to use the MBVI in conjunction with measuring behavioral outcomes (e.g., performance or persistence in quantitative biology). As survey validation is a continuous process, we believe that this is an excellent opportunity for further research that would build upon the work presented here and help accumulate additional validity evidence.
Another limitation is that our definition of math encompassed arithmetic, algebra, calculus, and statistics. Owing to this all-encompassing definition, the MBVI is unable to tease apart potentially different attitudes toward different types of math. For example, students might believe that statistics and data-interpretation skills are very useful to their careers in the life sciences but might not understand how calculus is relevant. The cost associated with applying basic arithmetic to a biological context is also likely to be different from the cost associated with applying calculus in a biological context, particularly for students who did not take calculus in high school. Modifications to the definition of math given at the beginning of the MBVI could be made to focus on a particular type of math, such as statistics; alternatively, the word “math” in each item could be replaced with a particular type of math (e.g., Statistics is valuable for me for my life science career). However, any modifications to the MBVI would require evidence that the resulting survey functions as a valid measure of undergraduates’ value of that math subdiscipline in the context of biology.
In addition to these theoretical considerations, further work is needed to demonstrate that the MBVI is predictive of student achievement (e.g., performance on quantitative tasks). Prior research has shown that math task values can affect college students’ achievement (Bong, 2001; Zusho et al., 2003; Hulleman et al., 2010). While it is therefore likely that students’ math–biology task values may similarly influence their performance on quantitative tasks in biology courses, explicitly linking task values and achievement was beyond the scope of this study. Thus, we caution readers against use of the MBVI as a proxy for predicting students’ achievement on quantitative tasks. However, we are currently in the process of investigating the extent to which students’ math–biology task values relate to their achievement by administering the MBVI to introductory biology students and collecting grades on quantitative assignments. Collecting such information on the predictive nature of the MBVI will help establish criterion-related validity evidence (i.e., consequences of testing as discussed by Reeves and Marbach-Ad, 2016) and provide additional information relevant to the use of the MBVI.
Implications for Educators and Researchers
The MBVI can be a useful tool for both educators and researchers. Instructors of courses with significant quantitative components could give the MBVI to students early in the semester to gauge their attitudes toward math; scores could then be used to inform the approach taken to incorporating quantitative skills into the course. For example, if student scores on the interest subscale are low, instructors could focus on providing students with novel, challenging quantitative tasks and allowing students to interact with each other as they solve these tasks to generate interest (Renninger and Hidi, 2011). Additionally, humor has been found to increase the interest of students in a task if they have low interest in the subject matter (Matarazzo et al., 2010). Similarly, instructional strategies to reduce math anxiety, such as expressive writing (Park et al., 2014) or the activities being developed through the Biology Students Math Attitudes and Anxiety Program (https://qubeshub.org/groups/biomaap), can be incorporated into courses in which student cost scores are high. If utility value scores are low, instructors could think creatively about how to frame quantitative skills in contexts that would be relevant for students pursuing particular life science careers. For example, data and results from clinical trials could be used to teach statistics to pre-medicine students. Alternatively, utility value interventions, in which students write about how course material is personally relevant (e.g., Hulleman et al., 2010), could be employed; these short interventions have been shown to increase students’ perceptions of the usefulness of a course, their interest in a course, and their performance in a course (Hulleman and Harackiewicz, 2009; Hulleman et al., 2010; Harackiewicz et al., 2016).
Educators and researchers can also use the MBVI to assess the efficacy of quantitative biology reforms. Reforms should aim to engender more positive attitudes toward math, in addition to developing students’ quantitative skills (Aikens and Dolan, 2014), especially given that students will continue to encounter math in their college biology course work. Changes in values could be assessed through pre- and posttests with the MBVI. Additionally, understanding the specific roles of interest, utility value, and cost in student achievement, as well as how malleable each of these constructs is over a semester, would provide insight into which values to focus curricular materials around to maximize gains in student performance. Because the MBVI contains only 11 items and can be completed in less than 10 minutes, it can easily be administered to address both curricular assessment questions or more complex research questions aimed at determining why an intervention works.
This study serves as the initial validation for the use of the MBVI to investigate undergraduate life science majors’ math–biology task values. The survey measures students’ interest in using math to understand biology, the perceived usefulness of biology to their life science careers, and the cost of using math in biology courses, which are predicted to influence students’ performance on quantitative tasks and their decisions to enroll in quantitative courses (Eccles et al., 1983; Wigfield and Eccles, 2000). Future research should aim to provide additional validity evidence, particularly for use with populations not represented by the research presented here (e.g., URM students). Additionally, combining the MBVI with an existing math attainment scale (e.g., Fredricks and Eccles, 2002; Conley, 2012) and a measure of students’ expectancies of success on quantitative biology problems would help determine the relationship of each of these attitudes to student performance on quantitative tasks and decisions to enroll in quantitative courses.
Supplementary Material
Acknowledgments
We thank Tiffany Whittaker for valuable discussions related to instrument development and Jade Caines Lee for her thoughtful review of an early version of this article. Comments from two anonymous reviewers also greatly improved this paper. We also thank Hannah Callender, Carrie Diaz Eaton, Lisa Elfring, Arietta Fleming-Davies, Lou Gross, Alison Hale, and Becca Runyon for their feedback on the initial set of survey items. Finally, we thank the faculty who distributed our survey invitation and reminders to their classes. Support for this work was provided by a grant from the National Science Foundation (NSF DUE-1640347). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
REFERENCES
- Aikens M. L., Dolan E. L. Teaching quantitative biology: Goals, assessments, and resources. Molecular Biology of the Cell. 2014;25(22):3478–3481. doi: 10.1091/mbc.E14-06-1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- American Association for the Advancement of Science. Vision and change in undergraduate biology education: A call to action. Washington, DC: 2011. [Google Scholar]
- Battle A., Wigfield A. College women’s value orientations toward family, career, and graduate school. Journal of Vocational Behavior. 2003;62:56–75. [Google Scholar]
- Bentler P. M. EQS structural equations program manual. Encino, CA: Multivariate Software; 1995. [Google Scholar]
- Beretvas S. N., Meyers J. L., Leite W. L. A reliability generalization study of the Marlowe-Crowne Social Desirability Scale. Educational and Psychological Measurement. 2002;62(4):570–589. [Google Scholar]
- Berndt T. J., Miller K. E. Expectancies, values, and achievement in junior high school. Journal of Educational Psychology. 1990;82(2):319–326. [Google Scholar]
- Bhalla A., Durham R. L., Al-Tabaa N., Yeager C. The development and initial psychometric validation of the eHealth readiness scale. Computers in Human Behavior. 2016;65:460–467. [Google Scholar]
- Bong M. Role of self-efficacy and task-value in predicting college students’ course performance and future enrollment intentions. Contemporary Educational Psychology. 2001;26:553–570. doi: 10.1006/ceps.2000.1048. [DOI] [PubMed] [Google Scholar]
- Britton S. Are students able to transfer mathematical knowledge? In: Vakalis I., editor. Proceedings of the 2nd international conference on the teaching of mathematics. New York: Wiley.; 2002. Retrieved February 2, 2017, from http://users.math.uoc.gr/~ictm2/Proceedings/ICTM2_Presentations_by _Author.html. [Google Scholar]
- Chiel H. J., McManus J. M., Shaw K. M. From biology to mathematical models and back: Teaching modeling to biology students, and biology to math and engineering students. CBE—Life Sciences Education. 2010;9:248–265. doi: 10.1187/cbe.10-03-0022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole J. S., Bergin D. A., Whittaker T. A. Predicting student achievement for low stakes tests with effort and task value. Contemporary Educational Psychology. 2008;33(4):609–624. [Google Scholar]
- Colon-Berlingeri M., Burrowes P. A. Teaching biology through statistics: Application of statistical methods in genetics and zoology courses. CBE—Life Sciences Education. 2011;10:259–267. doi: 10.1187/cbe.10-11-0137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conley A. M. Patterns of motivation beliefs: Combining achievement goal and expectancy-value perspectives. Journal of Educational Psychology. 2012;104(1):32. [Google Scholar]
- Crowne D. P., Marlowe D. A new scale of social desirability independent of psychopathology. Journal of Consulting Psychology. 1960;24(4):349–354. doi: 10.1037/h0047358. [DOI] [PubMed] [Google Scholar]
- Depelteau A. M., Joplin K. H., Govett A., Miller H. A., Seier E. SYMBIOSIS: Development, implementation, and assessment of a model curriculum across biology and mathematics at the introductory level. CBE—Life Sciences Education. 2010;9:342–347. doi: 10.1187/cbe.10-05-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Pillis L., Adolph S. C. Mathematical biology at an undergraduate liberal arts college. CBE—Life Sciences Education. 2010;9:417–421. doi: 10.1187/cbe.10-08-0099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doran J. M, Safran J. D., Muran J. C. The alliance negotiation scale: A psychometric investigation. Psychological Assessment. 2016;28(8):885–897. doi: 10.1037/pas0000222. [DOI] [PubMed] [Google Scholar]
- Duffus D., Olifer A. Introductory life science mathematics and quantitative neuroscience courses. CBE—Life Sciences Education. 2010;9:370–377. doi: 10.1187/cbe.10-03-0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles J., Adler T. F., Futterman R., Goff S. B., Kaczala C. M., Meece J. L., Midgley C. Expectancies, values, and academic behaviors. In: Spence J. T., editor. Achievement and achievement approaches. San Francisco, CA: Freeman; 1983. pp. 75–146. [Google Scholar]
- Eccles J., Adler T., Meece J. L. Sex differences in achievement: A test of alternate theories. Journal of Personality and Social Psychology. 1984;46(1):26–43. [Google Scholar]
- Eccles J. S., Vida M. N., Barber B. The relation of early adolescents’ college plans and both academic ability and task-value beliefs to subsequent college enrollment. Journal of Early Adolescence. 2004;24(1):63–77. [Google Scholar]
- Eccles J. S., Wigfield A. Motivational beliefs, values, and goals. Annual Review of Psychology. 2002;53:109–132. doi: 10.1146/annurev.psych.53.100901.135153. [DOI] [PubMed] [Google Scholar]
- Eccles J., Wigfield A., Harold R. D., Blumenfeld P. Age and gender differences in children’s self- and task perceptions during elementary school. Child Development. 1993;64(3):830–847. [PubMed] [Google Scholar]
- Edelstein-Keshet L. Adapting mathematics to the new biology. In: Steen L. A., editor. Math & Bio 2010: Linking undergraduate disciplines. Washington, DC: Mathematical Association of America; 2005. pp. 63–73. [Google Scholar]
- Elliott B., Oty K., McArthur J., Clark B. The effect of an interdisciplinary algebra/science course on students’ problem solving skills, critical thinking skills, and attitudes towards mathematics. International Journal of Mathematical Education in Science and Technology. 2001;32(6):811–816. [Google Scholar]
- Flake J. K., Barron K. E., Hulleman C., McCoach B. D., Welsh M. E. Measuring cost: The forgotten component of expectancy-value theory. Contemporary Educational Psychology. 2015;41:232–244. [Google Scholar]
- Fredricks J. A., Eccles J. S. Children’s competence and value beliefs from childhood through adolescence: Growth trajectories in two male-sex-typed domains. Developmental Psychology. 2002;38(4):519–533. [PubMed] [Google Scholar]
- Gaspard H., Dicke A. L., Flunger B., Schreier B., Häfner I., Trautwein U., Nagengast B. More value through greater differentiation: Gender differences in value beliefs about math. Journal of Educational Psychology. 2015;107(3):663–667. [Google Scholar]
- Harackiewicz J. M., Canning E. A., Tibbetts Y., Priniski S. J., Hyde J. S. Closing achievement gaps with a utility-value intervention: Disentangling race and social class. Journal of Personality and Social Psychology. 2016;111(5):745–765. doi: 10.1037/pspp0000075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harackiewicz J. M., Durik A. M., Barron K. E., Linnenbrink-Garcia L., Tauer J. M. The role of achievement goals in the development of interest: Reciprocal relations between achievement goals, interest, and performance. Journal of Educational Psychology. 2008;100(1):105–122. [Google Scholar]
- Hester S., Buxner S., Elfring L., Nagy L. Integrating quantitative thinking into an introductory biology course improves students’ mathematical reasoning in biological contexts. CBE—Life Sciences Education. 2014;13:54–64. doi: 10.1187/cbe.13-07-0129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman K., Leupen S., Dowell K., Kephart K., Leips J. Development and assessment of modules to integrate quantitative skills in introductory biology courses. CBE—Life Sciences Education. 2016;15 doi: 10.1187/cbe.15-09-0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoskinson A. M. How to build a course in mathematical biological modeling: Content and processes for knowledge and skill. CBE—Life Sciences Education. 2010;9:333–341. doi: 10.1187/cbe.10-03-0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu L., Bentler P. M. Cutoff criteria for fit indices in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling—A Multidisciplinary Journal. 1999;6(1):1–55. [Google Scholar]
- Hulleman C. S., Godes O., Hendricks B. L., Harackiewicz J. M. Enhancing interest and performance with a utility value intervention. Journal of Educational Psychology. 2010;102(4):880–895. [Google Scholar]
- Hulleman C. S., Harackiewicz J. M. Promoting interest and performance in high school science classes. Science. 2009;326(5958):1410–1412. doi: 10.1126/science.1177067. [DOI] [PubMed] [Google Scholar]
- Jones B. D., Paretti M. C., Hein S. F., Knott T. W. An analysis of motivation constructs with first-year engineering students: Relationships among expectancies, values, achievement, and career plans. Journal of Engineering Education. 2010;99(4):319–336. [Google Scholar]
- Jöreskog K. G., Sörbom D. LISREL V: Analysis of linear structural relationships by the method of maximum likelihood. Chicago, IL: National Educational Resources; 1981. [Google Scholar]
- Jöreskog K., Sörbom D. LISREL 8: Structural equation modeling with the SIMPLIS command language. Chicago, IL: Scientific Software International; 1993. [Google Scholar]
- Korhonen J., Tapola A., Linnanmäki K., Aunio P. Gendered pathways to educational aspirations: The role of academic self-concept, school burnout, achievement and interest in mathematics and reading. Learning and Instruction. 2016;46:21–33. [Google Scholar]
- Krapp A. Interest, motivation and learning: An educational-psychological perspective. European Journal of Psychology of Education. 1999;14(1):23–40. [Google Scholar]
- Lee W., Lee M.-J., Bong M. Testing interest and self-efficacy as predictors of academic self-regulation and achievement. Contemporary Educational Psychology. 2014;39:86–99. [Google Scholar]
- Lent R. W., Hill C. E., Hoffman M. A. Development and validation of the counselor activity self-efficacy scales. Journal of Counseling Psychology. 2003;50(1):97–108. [Google Scholar]
- Luttrell V. R., Callen B. W., Allen C. S., Wood M. D., Deeds D. G., Richard D. C. S. The Mathematics Value Inventory for general education students: Development and initial validation. Educational and Psychological Measurement. 2010;70(1):142–160. [Google Scholar]
- Madlung A., Bremer M., Himelblau E., Tullis A. A study assessing the potential negative effects in interdisciplinary math-biology instruction. CBE—Life Sciences Education. 2011;10:43–54. doi: 10.1187/cbe.10-08-0102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makarevitch I., Frechette C., Wiatros N. Authentic research experience and “big data” analysis in the classroom: Maize response to abiotic stress. CBE—Life Sciences Education. 2015;14 doi: 10.1187/cbe.15-04-0081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matarazzo K. L., Durik A. M., Delaney M. L. The effect of humorous instructional materials on interest in a math task. Motivation and Emotion. 2010;34(3):293–305. [Google Scholar]
- Matthews K. E., Adams P., Goos M. Putting it into perspective: Mathematics in the undergraduate science curriculum. International Journal of Mathematical Education in Science and Technology. 2009;40(7):891–902. [Google Scholar]
- Matthews K. E., Adams P., Goos M. Using the principles of BIO2010 to develop an introductory, interdisciplinary course for biology students. CBE—Life Sciences Education. 2010;9:290–297. doi: 10.1187/cbe.10-03-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meece J. L., Wigfield A., Eccles J. S. Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology. 1990;82(1):60–70. [Google Scholar]
- Metz A. M. Teaching statistics in biology: Using inquiry-based learning to strengthen understanding of statistical analysis in biology laboratory courses. CBE—Life Sciences Education. 2008;7:317–326. doi: 10.1187/cbe.07-07-0046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Research Council (NRC) BIO2010: Transforming undergraduate education for future research biologists. Washington, DC: National Academies Press; 2003. [PubMed] [Google Scholar]
- NRC. A new biology for the 21st century: Ensuring the United States leads the coming biology revolution. Washington, DC: National Academies Press; 2009. [PubMed] [Google Scholar]
- Osborne J. W., Costello A. B. Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Pan-Pacific Management Review. 2009;12(2):131–146. [Google Scholar]
- Park D., Ramirez G., Beilock S. L. The role of expressive writing in math anxiety. Journal of Experimental Psychology: Applied. 2014;20(2):103–111. doi: 10.1037/xap0000013. [DOI] [PubMed] [Google Scholar]
- Paulhus D. L. Measurement and control of response bias. In: Robinson J. P., Shaver P. R., Wrightsman L. S., editors. Measures of personality and social psychological attitudes. San Diego, CA: Academic; 1991. pp. 17–59. [Google Scholar]
- Perez T., Cromley J. G., Kaplan A. The role of identity development, values, and costs in college STEM retention. Journal of Educational Psychology. 2014;106(1):315–329. [Google Scholar]
- Raiche G., Magis D. nFactors: Parallel analysis and non graphical solutions to the Cattell Scree Test (Version 2.3.3) Montreal, QC, Canada: Universite du Quebec a Montreal; 2015. Retrieved February 2, 2017, from https://CRAN.R-project.org/package=nFactors. [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2016. Retrieved March 1, 2017, from www.R-project.org/ [Google Scholar]
- Reeves T. D., Marbach-Ad G. Contemporary test validity in theory and practice: A primer for discipline-based education researchers. CBE—Life Sciences Education. 2016;15 doi: 10.1187/cbe.15-08-0183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renninger K. A., Hidi S. Revisiting the conceptualization, measurement, and generation of interest. Educational Psychologist. 2011;46(3):168–184. [Google Scholar]
- Revelle W. psych: Procedures for psychological, psychometric, and personality research (Version 1.6.12) Evanston, IL: Northwestern University; 2016. Retrieved February 2, 2017, from https://CRAN.R-project.org/package =psych. [Google Scholar]
- Reysen S., Katzarska-Miller I., Nesbit S. M., Pierce L. Further validation of a single-item measure of social identification. European Journal of Social Psychology. 2013;43(6):463–470. [Google Scholar]
- Rheinlander K., Wallace D. Calculus, biology, and medicine: A case study in quantitative literacy for science students. Numeracy. 2011;4(1):art3. [Google Scholar]
- Robeva R., Davies R., Hodge T., Enyedi A. Mathematical biology modules based on modern molecular biology and modern discrete mathematics. CBE—Life Sciences Education. 2010;9:227–240. doi: 10.1187/cbe.10-03-0019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosseel Y. lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software. 2012;48(2):1–36. Retrieved February, 2, 2017, from www.jstatsoft.org/v48/i02/ [Google Scholar]
- Ruscio J., Roche B. Determining the number of factors to retain in an exploratory factor analysis using comparison data of known factorial structure. Psychological Assessment. 2012;24(2):282. doi: 10.1037/a0025697. [DOI] [PubMed] [Google Scholar]
- Ryan R. M., Deci E. L. Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemporary Educational Psychology. 2000;25(1):54–67. doi: 10.1006/ceps.1999.1020. [DOI] [PubMed] [Google Scholar]
- Schiefele U. Interest, learning, and motivation. Educational Psychologist. 1991;26(3–4):299–323. [Google Scholar]
- Simpkins S. D., Davis-Kean P. E., Eccles J. S. Math and science motivation: A longitudinal examination of the links between choices and beliefs. Developmental Psychology. 2006;42(1):70–83. doi: 10.1037/0012-1649.42.1.70. [DOI] [PubMed] [Google Scholar]
- Speth E. B., Momsen J. L., Moyerbrailean G. A., Ebert-May D., Long T., Wyse S., Linton D. 1, 2, 3, 4: Infusing quantitative literacy into introductory biology. CBE—Life Sciences Education. 2010;9:323–332. doi: 10.1187/cbe.10-03-0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steen L. A, editor. Math & Bio 2010: Linking undergraduate disciplines. Washington, DC: Mathematical Association of America; 2005. [Google Scholar]
- Steiger J. H. Structural model evaluation and modification: An interval estimation approach. Multivariate Behavioural Research. 1990;25(2):173–180. doi: 10.1207/s15327906mbr2502_4. [DOI] [PubMed] [Google Scholar]
- Steiger J. H. Understanding the limitations of global fit assessment in structural equation modeling. Personality and Individual Differences. 2007;42(5):893–898. [Google Scholar]
- Steiger J. H., Lind J. M. Statistically based tests for the number of factors. Paper presented at: Annual Meeting of the Psychometric Society (Iowa City, IA) 1980.
- Tabachnick B. G., Fidell L. S. Using multivariate statistics. Boston, MA: Pearson; 2001. [Google Scholar]
- Thompson K. V., Cooke T. J., Fagan W. F., Gulick D., Levy D., Nelson K. C., Presson J. Infusing quantitative approaches throughout the biological sciences curriculum. International Journal of Mathematical Education in Science and Technology. 2013;44(6):817–833. [Google Scholar]
- Thompson K. V., Nelson K. C., Marbach-Ad G., Keller M., Fagan W. F. Online interactive teaching modules enhance quantitative proficiency of introductory biology students. CBE—Life Sciences Education. 2010;9:277–283. doi: 10.1187/cbe.10-03-0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trautwein U., Marsh H. W., Nagengast B., Lüdtke O., Nagy G., Jonkmann K. Probing for the multiplicative term in modern expectancy–value theory: A latent interaction modeling study. Journal of Educational Psychology. 2012;104(3):763–777. [Google Scholar]
- Usher D. C., Driscoll T. A., Dhurjati P., Pelesko J. A., Rossi L. F., Schleiniger G., White H. B. A transformative model for undergraduate quantitative biology education. CBE—Life Sciences Education. 2010;9:181–188. doi: 10.1187/cbe.10-03-0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins J. C. On a calculus-based statistics course for life science students. CBE—Life Sciences Education. 2010;9:298–310. doi: 10.1187/cbe.10-03-0035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wigfield A., Cambria J. Students’ achievement values, goal orientations, and interest: Definitions, development, and relations to achievement outcomes. Developmental Review. 2010;30(1):1–35. [Google Scholar]
- Wigfield A., Eccles J. S. Expectancy-value theory of achievement motivation. Contemporary Educational Psychology. 2000;25:68–81. doi: 10.1006/ceps.1999.1015. [DOI] [PubMed] [Google Scholar]
- Wigfield A., Eccles J. S., Yoon K. S., Harold R. D., Arbreton A. J. A., Freedman-Doan C., Blumenfeld P. C. Change in children’s competence beliefs and subjective task values across the elementary school years: A 3-year study. Journal of Educational Psychology. 1997;89(3):451–469. [Google Scholar]
- Wightman B., Hark A. T. Integration of bioinformatics into an undergraduate biology curriculum and the impact on development of mathematical skills. Biochemistry and Molecular Biology Education. 2012;40(5):310–319. doi: 10.1002/bmb.20637. [DOI] [PubMed] [Google Scholar]
- Willis G. B. Cognitive interviewing: A “how to” guide. Paper presented at: Meeting of the American Statistical Association (Research Triangle Park, NC) 1999.
- Wolf E. J., Harrington K. M., Clark S. L., Miller M. W. Sample size requirements for structural equation models: An evaluation of power, bias, and solution propriety. Educational and Psychological Measurement. 2013;73(6):913–934. doi: 10.1177/0013164413495237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worthington R. W., Whittaker T. A. Scale development research: A content analysis and recommendations for best practices. Counseling Psychologist. 2006;34(6):806–838. [Google Scholar]
- Zusho A., Pintrich P. R., Coppola B. Skill and will: The role of motivation and cognition in the learning of college chemistry. International Journal of Science Education. 2003;25(9):1081–1094. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.