Undergraduate life science majors are reputed to have negative attitudes toward mathematics, yet little empirical evidence supports this belief. The adaptation and initial findings of a semantic differential measure of science and math majors’ emotional satisfaction with math are reported here.
Abstract
Undergraduate life science majors are reputed to have negative emotions toward mathematics, yet little empirical evidence supports this. We sought to compare emotions of majors in the life sciences versus other natural sciences and math. We adapted the Attitudes toward the Subject of Chemistry Inventory to create an Attitudes toward the Subject of Mathematics Inventory (ASMI). We collected data from 359 science and math majors at two research universities and conducted a series of statistical tests that indicated that four AMSI items comprised a reasonable measure of students’ emotional satisfaction with math. We then compared life science and non–life science majors and found that major had a small to moderate relationship with students’ responses. Gender also had a small relationship with students’ responses, while students’ race, ethnicity, and year in school had no observable relationship. Using latent profile analysis, we identified three groups—students who were emotionally satisfied with math, emotionally dissatisfied with math, and neutral. These results and the emotional satisfaction with math scale should be useful for identifying differences in other undergraduate populations, determining the malleability of undergraduates’ emotional satisfaction with math, and testing effects of interventions aimed at improving life science majors’ attitudes toward math.
INTRODUCTION
Despite the fact that life science researchers regularly use quantitative methods and undergraduate life science degrees universally require one or more math courses, biology continues to be perceived as the field of choice for science-interested but math-disinterested students. Yet little if any empirical evidence exists to support the idea that biology majors as a group hold negative attitudes toward math (Aikens and Dolan, 2014). Attitudes, which are defined as “predispositions that consistently affect actions” (Allport [1967] as cited by Richardson, 1996, p. 103), are known to play an important role in explaining students’ academic and career development. For example, Ajzen’s theory of planned behavior predicts that students will be more likely to engage in math pursuits, such as enrolling in optional math courses or completing more quantitative degrees, if they hold positive attitudes toward math, if they believe that having positive attitudes toward math is “normal,” and if they perceive that their decision to do math and be successful at it is within their control (Ajzen, 1985, 1991). Furthermore, students’ attitudes have been shown to significantly affect their willingness to engage in learning activities, take additional courses in a discipline, persevere when they face difficulties, and persist in certain educational or career paths (Feierabend, 1960; Aiken, 1970; Steiner and Sullivan, 1984; Meece et al., 1990; Glynn et al., 2007; Rheinlander and Wallace, 2011; Matthews et al., 2013; Poladian, 2013). Given the influences of attitudes, it is important to determine whether biology majors differ from other science majors in their attitudes toward math and whether biology majors themselves vary in their attitudes toward math. The life science community can then use this knowledge to design curricula, programs, and interventions to recruit, retain, and train biologists with the quantitative skills necessary to solve 21st-century problems (National Research Council [NRC], 2003).
McLeod proposed a three-dimensional model of attitude toward mathematics that comprised students’ emotional disposition toward math, their vision of math, and their perceived competence in math (McLeod, 1992). We focus here on emotions, given the long-standing recognition that students may view math negatively (Buxton, 1981) and the documented interplay between cognition and affect in mathematics (Zan et al., 2006). Specifically, Mandler, McLeod, and others describe the emotional experience of mathematics as being initiated by the demands of an activity leading to physiological arousal, resulting in an emotion that reduces cognitive capacity for problem solving (Mandler, 1989; McLeod, 1992; Zan et al., 2006).
To understand the role of emotions about mathematics in the educational experiences of life science majors in particular, we needed a measure of undergraduate science majors’ emotions about mathematics. We wanted a practical tool that could be used by instructors, program designers and evaluators, and administrators to diagnose these emotions in large populations of students and capture shifts that occur over time. There appeared to be few if any quantitative measures useful for documenting undergraduate science majors’ emotions about math. One of the first, robust examples of a math attitudes measure was developed by Fennema and Sherman (1976). The 48-item Fennema-Sherman Attitudes Scale consists of four subscales intended to measure four attitude-related constructs: students’ confidence in their ability to do and learn math, views of the usefulness of math, perceptions of math as a male domain, and perceptions of math teachers’ attitudes toward them as math learners. However, this scale has a number of features that limit its widespread use and usefulness. As language has changed, the scale has become outdated, although an updated version is available (Mohamed and Waheed, 2011). Its length makes it time-consuming to administer and likely to result in survey fatigue, especially if it is administered repeatedly over time, further limiting its utility. The item wording is more appropriate for K–12 students than undergraduates, restricting its application in higher education contexts. In addition, the items measure constructs beyond students’ attitudes toward the discipline of math, such as respondents’ confidence in their math abilities (i.e., math self-efficacy) and their perceptions of math teachers. Although there are other measures of math-related attitudes, they focus on math anxiety or self-efficacy or views of the utility of math (i.e., math value; Chipman et al., 1992; McGinnis et al., 2002; Tapia and Marsh, 2004) rather than emotions about the subject per se.
In our search, we determined that the semantic differential technique (Osgood et al., 1957) had been widely and successfully used to measure emotions in a variety of contexts, including other science, technology, engineering, and mathematics disciplines (e.g., Friborg et al., 2006; Bauer, 2008; Koga and Iwasaki, 2013; Torija et al., 2013). Semantic differential scales typically include eight to 20 adjective pairs (e.g., exciting–boring) that are positioned on either end of a seven-point scale. This technique is thought to be highly generalizable because it relies on common, easily understood words, and it is straightforward to implement and brief to administer. Moreover, semantic differentials are thought to reduce response bias due to social desirability, meaning they are useful for measuring whether respondents do or do not like the attitudinal object (e.g., the subject of math), rather than whether they should or should not like it (Fowler, 1995; Bauer, 2008; DeVellis, 2012).
Bauer (2008) used this approach to measure chemistry attitudes by developing a 20-item semantic differential instrument, titled Attitudes toward the Subject of Chemistry Inventory (ASCI). Xu and Lewis (2011) refined the instrument based on results of additional psychometric analyses, which resulted in a two-factor structure with four items measuring students’ views about the “intellectual accessibility” of chemistry and four items measuring students’ “emotional satisfaction” with chemistry. This refinement not only shortened the scale to eight items, it also improved model fit statistics over the original instrument. We decided to adapt this shortened form by substituting “mathematics” for “chemistry” to generate an Attitudes toward the Subject of Math Inventory (ASMI). We then collected data from undergraduate students majoring in a range of science and math disciplines, including students enrolled in life science majors that require various levels of mathematics course work. We included a prompt “Mathematics is…” at the beginning of the inventory to collect data that would help determine the validity of our approach of adapting an existing chemistry attitudes scale rather than developing a scale de novo. We then used a series of statistical techniques to test the quality of the scale and conducted a preliminary “landscape assessment” of undergraduate science and math majors’ attitudes toward mathematics, highlighting salient features and differences among student groups.
METHODS
Participants
The participants in this study were 362 undergraduate students enrolled in diverse science and math majors at two large research universities in the southern United States. Students were recruited by emails forwarded to listservs for science and math majors. No incentive was offered. The study was determined exempt from institutional review board review at the University of Georgia (2013-10946-0) and the University of Texas Austin (2014-06-0029). For the following analyses, only complete cases were analyzed (i.e., no missing data; N = 359, Table 1), as missing data were assumed to be missing at random, and very few cases (n = 3) were eliminated by dropping students whose responses were incomplete.
TABLE 1.
Study participants
| Gender | Year in school | Race/ethnicity |
|---|---|---|
| 193 female | 108 freshmen | 196 white |
| 132 male | 46 sophomores | 60 Asian |
| 34 other/no response | 44 juniors | 58 URM |
| 125 seniors | 45 no response | |
| 36 other/no response |
Data Collection
The ASMI was adapted from the shortened ASCI (Xu and Lewis, 2011), which included eight items from Bauer’s original (2008) 20-item instrument. These items fit a two-factor structure, measuring “intellectual accessibility” and “emotional satisfaction.” Similar to the data-collection procedures used for the shortened ASCI, students were instructed to “Rate how well these words describe your feelings about mathematics. Think carefully and try not to include your feelings toward mathematics teachers or mathematics courses. For each line, choose a position between the two words that describes exactly how you feel. Select that number. The middle position (4) is if you are undecided or have no feelings related to the terms on that line”:
| MATHEMATICS IS… | |||||||||
| 1 | Easy | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Hard |
| 2 | Complicated | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Simple |
| 3 | Confusing | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Clear |
| 4 | Comfortable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Uncomfortable |
| 5 | Satisfying | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Frustrating |
| 6 | Challenging | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Not challenging |
| 7 | Pleasant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Unpleasant |
| 8 | Chaotic | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Organized |
We employed the same physical design features used in the ASCI and its short form to encourage students to focus carefully on the adjectives and make use of the range of the scales. This was done to take advantage of respondents’ ability to draw distinctions, namely,
Adjectives and choices were presented on a single line (e.g., “easy” at one end, “hard” at the other end, with numbers 1–7 in between);
Some pairs were listed with the positive adjective on the left side, and others with the positive adjective on the right (as depicted) to discourage respondents from selecting a single response across the entire scale; and
“Mathematics is…” was presented in all capitals to keep students focused on the discipline as the object of their attitudes.
Students were asked to report demographic data, including year in school, gender, race, and ethnicity. Students had the option to indicate that they preferred not to respond for all items. Items with the “positive” term on the left (1, 4, 5, 7) were reverse scored before analyses were performed.
Qualitative Data Analysis and Results
The eight ASMI items were preceded by a free-response prompt: “Please complete the following sentence to explain your definition of ‘mathematics.’ MATHEMATICS IS…” This was intended to prime the students’ feelings toward the subject and to gather information that could be used to determine whether it was reasonable to adapt an existing chemistry attitudes scale to mathematics. Because this aspect of the work is primarily for validation purposes for the quantitative data collection and analysis, we present both the analysis and results of this qualitative component here.
Of the 359 students who provided quantitative responses, 224 also provided text (i.e., qualitative) responses to the “Mathematics is…” prompt. We conducted content analysis of students’ responses as follows. One researcher (E.L.D.) read student responses and generated the following initial set of codes, which included the semantic pairs from the ASCI that were evidenced by the responses of students in our sample (indicated with an asterisk*), as well as any other attitudes they expressed:
Beautiful–ugly
Creative–algorithmic
Difficult–easy*
Fun or interesting–boring*
Good–bad
Important–unimportant
Intuitive–nonintuitive
Logical–illogical
Objective–subjective
Precise–vague
Relevant–irrelevant
Simple–complicated*
Scary–comforting
Useful–useless
Warm–cold
Then, another researcher (L.P.W.) used this codebook to de novo code the same responses independently. Responses were double coded if applicable. For example, if a student indicated mathematics is both interesting and challenging, the response was coded as both “interesting” and “challenging.” Thus, the numbers of responses total to more than 100%.
Even though the introductory text prompted students to think about their feelings about mathematics, students’ responses fit three overarching categories: emotions about math (n = 48), views regarding the utility of math (n = 14), and thoughts about the nature of math (e.g., “numerical analysis,” “using numbers to solve problems”; n = 154) as well as comments we considered to be vague or off-topic, such as “everything” (n = 9). We did not consider the responses related to the utility or nature of math or the off-topic responses further in this analysis.
The researchers agreed 100% on coding of all of the emotion-related responses (n = 48) at the level of the codes in the codebook. The researchers then grouped the codes into the following bipolar categories:
Easy/doable (n = 4) versus challenging/difficult (n = 19) or frustrating (n = 2)
Fun (n = 11) or interesting (n = 10) versus boring (n = 2)
Simple (n = 1) versus complicated (n = 1)
Additional codes that we could not clearly categorize included: beautiful (n = 3), creative (n = 3), scary (n = 1), good (n = 1), precise (n = 1), and cold (n = 1). The “easy versus difficult/challenging” and “simple versus complicated” are represented in the ASCI scales, which provides some justification for adapting the ASCI scales rather than developing items de novo. “Fun” or “interesting versus boring” are not directly represented in the ASCI scales, but may be captured in the “pleasant versus unpleasant” or “comfortable versus uncomfortable” scales. Future studies should consider testing additional scales that may measure this emotion about mathematics more directly, such as interesting versus uninteresting, agreeable versus disagreeable, or enjoyable versus unenjoyable.
Quantitative Data Analysis
Given that the qualitative results provided support for adapting the ASCI to create the ASMI, we used exploratory factor analysis (EFA) to explore the dimensionality of students’ responses to the ASMI. We chose to use EFA instead of confirmatory factor analysis (CFA) because we did not assume a priori that the ASMI would have the same model fit as the shortened ASCI for two reasons. First, there was no empirical or theoretical support to suggest that these semantic differential items would function the same way for mathematics as they did for chemistry. For example, work from psychology suggests that activities may be enjoyable at least in part because they are challenging (Csikszentmihalyi, 2014), even though results from the ASCI indicate that students’ perceptions of chemistry being “satisfying” and “challenging” factor separately, with satisfaction reflecting emotion and challenge reflecting intellectual accessibility (Xu and Lewis, 2011). Second, the students in our study might have more varied experiences with mathematics depending on their degree program and thus might represent a more heterogeneous population than participants in the validity studies of both forms of the ASCI (Bauer, 2008; Brandriet et al., 2011; Xu and Lewis, 2011). In addition, Xu and colleagues found it necessary to calculate the intellectual accessibility subscale score of the ASCI without the “challenging/not challenging” item for Saudi Arabian students due to concerns about their interpretation of the item (Xu et al., 2015).
We performed EFA using R, version 3.3.0 (R Core Team, 2016) with the “psych” (Revelle, 2016) and “nFactors” (Raîche, 2010) packages. Best practice with testing instrument validity is to randomly split a sample into two samples, with an EFA performed on the first sample and the factor structure confirmed via CFA on the second sample. However, doing so in the present study would decrease the sample size to ∼180 in each sample. Thus, we opted to retain all 359 participants in the EFA to maximize statistical power. We extracted factors using the principal axis factoring (PAF). We selected PAF rather than principal component analysis because we sought to identify the number of latent variables responsible for producing the observed responses to the items and wanted to appropriately model the unreliability represented in each item to do so (Matsunaga, 2015). We made use of oblimin rotation because we believed that the factors were correlated based on theoretical considerations of the scale and the observed correlations of the ASCI (Brandriet et al., 2011; Xu and Lewis, 2011). We analyzed the pattern of factor loadings for one-, two-, and three-factor solutions. We deemed further factor solutions to be prima facie inadmissible due to the limited number of items that would be representing each factor. We also consulted the results of a parallel analysis (Horn, 1965; Hayton et al., 2004), the acceleration factor and optimal coordinates (Raîche et al., 2013), and the Kaiser (1960) rule (eigenvalue > 1) for additional nongraphical solutions for analyzing the scree plot to determine the appropriate number of factors.
RESULTS
Undergraduate Science and Math Students’ Attitudes about Mathematics
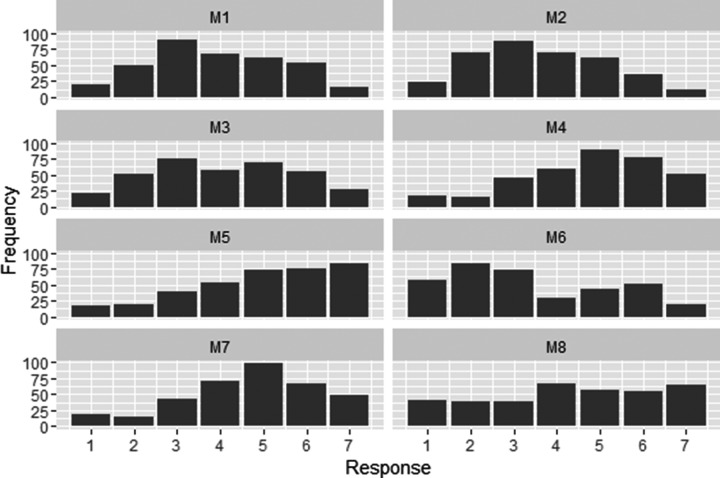
Students in our sample reported a fairly symmetric distribution of responses with item means near the midpoint, reflecting no opinion/undecided (Figure 1). Generally, students’ responses trended toward characterizing math as a subject that was “complicated” and “challenging.” Students also indicated some level of comfort with math in that their responses skewed toward describing math as “satisfying,” “pleasant,” and “organized.” Table 2 presents the interitem correlations, item means, and item standard deviations for the ASMI items.
FIGURE 1.
Response frequencies to each item. These response frequencies are for the raw data (i.e., before recoding items 1, 4, 5, and 7 to account for reverse wording).
TABLE 2.
Descriptive statistics for the ASMI items (N = 359)a
| 1 Easy–hard | 2 Simple–complicated | 3 Clear–confusing | 4 Comfortable–uncomfortable | 5 Satisfying–frustrating | 6 Not challenging–challenging | 7 Pleasant–unpleasant | 8 Organized–chaotic | |
|---|---|---|---|---|---|---|---|---|
| 1 | — | |||||||
| 2 | 0.17 | — | ||||||
| 3 | 0.18 | 0.36 | — | |||||
| 4 | 0.55 | 0.03 | 0.26 | — | ||||
| 5 | 0.47 | 0.05 | 0.25 | 0.67 | — | |||
| 6 | 0.20 | 0.41 | −0.12 | −0.02 | 0.03 | — | ||
| 7 | 0.40 | 0.10 | 0.30 | 0.70 | 0.70 | 0.01 | — | |
| 8 | 0.05 | −0.05 | 0.44 | 0.14 | 0.15 | −0.48 | 0.18 | — |
| Mean | 3.91 | 3.65 | 4.05 | 4.75 | 4.95 | 3.42 | 4.67 | 4.34 |
| SD | 1.57 | 1.56 | 1.68 | 1.62 | 1.73 | 1.87 | 1.59 | 1.96 |
aSemantic differential terms are presented with the “negative term” = 1 and “positive” term = 7 (i.e., order has been reversed so means of responses to items can be compared), such that ratings less than 4 indicate positive attitudes (top word), ratings greater than 4 indicate negative attitudes (bottom word), and ratings equal to 4 represent the midpoint (no feelings one way or the other, or undecided).
Exploratory Factor Analysis
When conducting EFA to determine the factor structure of the ASMI, the one- and three-factor solutions converged without any problems. The two-factor solution produced a warning, indicating that some of the estimated factor scores were “probably incorrect” and that a Heywood case was detected. A Heywood case is when the maximum-likelihood estimation method converges on a solution that is inadmissible because one of the estimated values is beyond the logical scope of plausible values. An investigation of the two-factor solution suggested that items 1 (factor loading = 0.57), 4 (0.84), 5 (0.80), and 7 (0.82) defined one factor. However, the most salient problem with the second factor was that the estimated standardized factor loading for item 6 (challenging–not challenging) was 1.09—an inadmissible solution, suggesting that a two-factor model is misspecified and is a not a plausible model for the data (Chen et al., 2011). Factor loadings for all three solutions can be found in Table 3.
TABLE 3.
Factor loadings for the one-, two-, and three-factor solutionsa
| One-factor solution | Two-factor solution | Three-factor solution | ||||
|---|---|---|---|---|---|---|
| Factor 1 | Factor 1 | Factor 2 | Factor 1 | Factor 2 | Factor 3 | |
| 1. Easy–hard | 0.57 | 0.57 | 0.18 | 0.58 | 0.20 | 0.05 |
| 4. Comfortable–uncomfortable | 0.84 | 0.84 | −0.02 | 0.88 | −0.01 | −0.05 |
| 5. Satisfying–frustrating | 0.80 | 0.80 | 0.01 | 0.82 | 0.01 | −0.02 |
| 7. Pleasant–unpleasant | 0.82 | 0.82 | −0.01 | 0.80 | −0.01 | 0.05 |
| 6. Not challenging–challenging | 0.03 | 0.02 | 1.09H | 0.07 | 0.83 | 0.08 |
| 8. Organized–chaotic | 0.22 | 0.25 | −0.48 | 0.07 | −0.62 | 0.36 |
| 2. Simple–complicated | 0.14 | 0.14 | 0.29 | −0.07 | 0.42 | 0.65 |
| 3. Clear–confusing | 0.38 | 0.38 | −0.16 | 0.13 | −0.24 | 0.72 |
aBold type indicates acceptable factor loadings, which are above the recommended cutoff values of |0.32| (Tabachnick and Fidell, 2007); factor loadings are bound between −1.00 and 1.00. Superscript “H” indicates a Heywood case, signifying an inadmissible solution because a factor loading is out of bounds; such a case invalidates the entire solution.
The one-factor solution was deemed not to be an adequate solution, as two of the items (2 and 6) had low factor loadings (0.14 and 0.03, respectively), and items 3 (0.38) and 8 (0.22) only minimally loaded on the only factor. This suggested that one factor was not adequate to explain the variance in these items. The three-factor solution produced a theoretically uninterpretable solution. The first factor in the three-factor solution mirrored the results from both the one-factor solution and the first factor in the two-factor solution. The second factor in the three-factor solution was primarily defined by item 6 (0.83) and item 8 (−0.62), with item 2 (0.42) also moderately loading on the factor. The third factor was defined most strongly by item 2 (0.65) and item 3 (0.72). The loading of item 2 (complicated–simple) on the two factors, the negative loading of item 8 on factor 2, and general pattern of loadings across factors two and three made the factor interpretations difficult.
These results indicate that there is likely to be a single factor represented by items 1, 4, 5, and 7, which reflects emotional satisfaction with math. However, none of the solutions are reasonable interpretations of the responses to data from the entire scale. Notably, item 8, which factored with other emotion-related items for the chemistry scale (ASCI), did not factor with emotion-related items for the ASMI. In addition, item 1 factored with other items related to the intellectual accessibility of chemistry on the ASCI, but factored with emotion-related items on the ASMI.
Exploratory Latent Profile Analysis
The lack of a clear solution to the EFA could be due to variation in students’ understanding of mathematics. To gain some insight into these results, we performed a latent profile analysis (also called a factor mixture analysis) using the “mclust” R package (Fraley and Raftery, 2002; Fraley et al., 2012). A latent profile analysis is a person-centered analysis that attempts to decompose the variance in the data by hypothesizing that several subpopulations exist within with the sample. Person-centered analyses aim to understand the observed variance across a set of items with the individual as the unit of analysis. This is distinct from the standard variable-centered analytic techniques, in which the focus of the analysis is on the interaction between the variables themselves. In other words, if science and math majors, or even subpopulations of life science majors, have distinct attitudes toward math, the similarity of responses within subpopulations could explain the overall observed variance in the data. (For a comparison of person-centered and variable-centered analytic techniques, see Bauer and Shanahan [2007] or Pastor et al. [2007].)
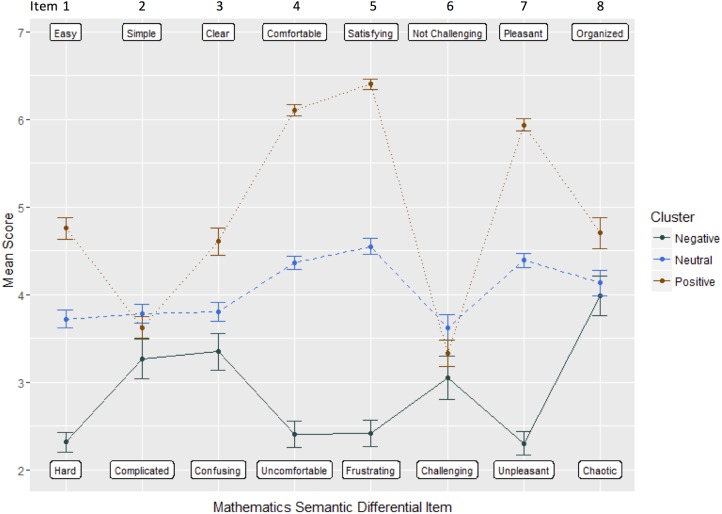
Results from the latent profile analysis suggested that three clusters, or subpopulations, were present in the data. Figure 2 displays a graph of cluster means for each item, which provides some support that there are interesting patterns of responses to the items across the scale. For example, all three clusters responded similarly on items 2, 3, 6, and 8, but varied widely in their responses to items 1, 4, 5, and 7. Given that items 1, 4, 5, and 7 factored together in all of the EFA solutions and appear to represent emotions about math, it is likely that there are three subpopulations represented in our sample: those who have strongly favorable emotions about math, those who have strongly unfavorable emotions about math, and those who are neutral. In addition, students’ emotions about math seem unrelated to whether they find math intellectually challenging.
FIGURE 2.
Item means for each cluster from the latent profile analysis. Item numbers are displayed at the top, and cluster means are displayed on the y-axis. These results suggest that three subpopulations, or clusters, are represented in our sample: those who have strongly favorable emotions about math, those who have strongly unfavorable emotions about math, and those who are neutral. In addition, students’ emotions about math seem unrelated to whether they find math intellectually difficult, i.e., all three clusters show similar responses to items 2 (simple–complicated), 3 (clear–confusing), and 6 (challenging–not challenging).
Comparison of Math Attitudes among Subgroups of Students
To identify student characteristics that might explain the three clusters of respondents, we conducted Welch’s t test, which adjusts the degrees of freedom to account for unequal group variances (Welch, 1947). We also conducted one-way analysis of variance (ANOVA) to test for significant differences in ASMI scores between subpopulations of students who might reasonably differ in their attitudes toward math. We compared both the summed scores on the total ASMI and the summed scores for the four items that factored together in the two- and three-factor EFA solutions (i.e., factor 1). We were confident in using this factor for comparisons for two reasons. First, the factor 1 item loadings in the two-factor solution were not substantially different from those in the one- and three-factor solutions. Second, results of the latent profile analysis indicated that the items comprising factor 1 (1, 4, 5, and 7) fully captured group differences. We chose to use the conservative Bonferroni adjustment to the usual α = 0.05 to control for our experiment-wise type I error rates, with α = 0.05/10 = 0.005. We also report effect sizes—either Cohen’s d for t tests or partial eta-squared (ηp2) for ANOVA—to provide a measure of practical importance to supplement the results regarding statistical significance (Cohen, 1988; Fan, 2001; Nakagawa and Cuthill, 2007; Maher et al., 2013).
We first compared responses of students from majors traditionally considered life sciences (i.e., biology and biochemistry majors; n = 187) versus physical sciences and math (i.e., applied mathematics, astronomy, chemistry, computer science, mathematics, and physics majors; n = 93).1 Our aim was to test the hypotheses that 1) life science majors hold more negative attitudes toward math than physical science and math majors (i.e., astronomy, chemistry, physics, applied mathematics, and mathematics majors); and 2) physical science and math majors hold similar attitudes toward math. Indeed, we found evidence that physical science and math majors reported similar attitudes toward math (t(87.293) = 0.93, p = 0.36, d = 0.11). We also found that their attitudes were not significantly more favorable than the attitudes of life science majors based on their responses to both the factor 1 items (t(169.16) = 2.41, p = 0.017, d = 0.37) and the total scale (t(147.26) = 2.07, p = 0.040, d = 0.31). However, the standardized mean differences were larger than 0.3 in both of the latter comparisons, which is considered a small to moderate effect in behavioral studies (Cohen, 1988; Fan, 2001). This suggests that the current analysis may be underpowered to detect significance and that there may be some differences between the life science majors and physical sciences/math majors (Cohen, 1992).
We compared responses of students according to their gender (female vs. male2) because previous research has shown that women hold less favorable attitudes toward mathematics than men (Hyde et al., 1990; Nosek et al., 2002; Frenzel et al., 2007). The results of this analysis were inconclusive because male students did not hold significantly more favorable attitudes toward math than female students (t(313.12) = 2.34, p = 0.020, d = 0.25), but the effect size again suggests that differences may exist between the two groups. We also compared responses of students according to their race/ethnicity (white, Asian, and underrepresented minority [URM],3 which included students identifying as African American or Black, Hispanic or Latina/o, Native Hawaiian, and Pacific Islander). Previous research is equivocal regarding whether students with different racial or ethnic identities differ in their attitudes toward mathematics (Matthews, 1984; Rech, 1994), and most of this work has been done at the precollege rather than undergraduate level. Finally, we compared students’ responses by year in school (lower division = freshmen and sophomores; upper division = juniors and seniors). We observed no significant differences by race/ethnicity (p = 0.17, (ηp2) = 0.01) or by year in school (p = 0.70, d = 0.04) and little to no effect of race/ethnicity or year in school (i.e., near-zero effect sizes). As a final check to make sure that no important relationships in the data were being overlooked, we regressed the math attitude scores on year in school, race, and gender, including all two-way interactions and the three-way interaction. None was significant, although these analyses were most likely underpowered.
DISCUSSION
Although no clear factor structure emerged for the ASMI, items 1, 4, 5, and 7 grouped together consistently in the solutions we examined, suggesting that these items comprise a reasonable measure of undergraduate science and math majors’ emotional satisfaction with math. This set of items is similar to the emotional satisfaction subscale of the ASCI, with two key differences. First, item 8 (organized–chaotic) did not factor with the other emotion-related items in the ASMI, but did for the chemistry scale. This difference, in addition to the fact that students on average viewed math as more organized than chaotic, may indicate something about students’ views of the nature of math as procedural or algorithmic (Kloosterman, 2002) versus views of the nature of science as more conceptual, dynamic, and messy. This hypothesis could be explored further by comparing students’ responses to this item with their views of the nature of math. Second, item 1 (easy–hard) factored with other items related to the intellectual accessibility of chemistry on the ASCI, but factored with emotion-related items on the ASMI. This suggests that the extent to which undergraduates view math as easy or hard may be more emotionally laden than viewing chemistry as easy or hard. Math instruction is a main component of formal education starting in grade school, while chemistry is not a formal part of K–12 curricula in the United States until middle school or later (NRC, 2013). Perhaps students form emotional inclinations or disinclinations to the math early on, and less personal, more general impressions of chemistry. Although the effects of early exposure to math on undergraduate attitudes toward math has not been explored, research has shown that early exposure to an attitudinal object leads to more stable and consistent attitudes toward that object.
The results of our latent profile analysis support the use of items 1, 4, 5, and 7 as a measure of emotional satisfaction with math because responses to these items appear to distinguish among groups of students. Responses of students within each group indicate that one group is emotionally satisfied with math, another group is emotionally dissatisfied with math, and the third group is neutral in their emotions about math. Given the preliminary nature of the results reported here, much more research is needed to confirm that students can reasonably be categorized into three groups with respect to their emotional satisfaction with math and to determine the usefulness of this characterization for tailoring instruction.
On the basis of our results, we recommend that students representing diverse science and math majors, including life science majors, be interviewed to further explore how they are interpreting and responding to the current set of emotional satisfaction items and to identify and characterize any additional math-related emotions they have. The results of these interviews should be used to expand on and improve the current emotional satisfaction scale. We also recommend that the current emotional satisfaction items as well as any future improvements on this measure be used to collect data from a larger sample of students. These students should represent a more diverse set of institutions and the range of undergraduate science and math students’ sociodemographics (gender, race/ethnicity, etc.). A larger, more diverse, and nationally representative sample would allow for more powerful tests of the significance and effect size of relationships between students’ major, gender, and race/ethnicity and their emotional satisfaction with math, as well as any interactions among them. Both effect sizes and confidence intervals should be calculated in these analyses to yield insight into the practical importance of any differences and to facilitate future meta-analyses (Nakagawa and Cuthill, 2007). Finally, we recommend that further research on undergraduate science and math students’ emotional satisfaction with math be coupled with research in other attitudinal domains such as life science students’ value of math. Andrews and colleagues have recently developed the Math-Biology Values Instrument (MBVI) for measuring life science majors’ math values from the perspective of expectancy value theory (Wigfield and Eccles, 1992, 2000; Andrews et al., 2017). Conceiving attitudes more broadly and with stronger theoretical grounding would allow for greater insight into the factors that influence life science students’ pursuit of, experiences with, and outcomes in math learning.
Ultimately, instructors may find this information useful for tailoring instruction to suit students with different attitudes. For example, students who report higher emotional satisfaction may find mathematical work inherently satisfying or intrinsically motivating (Ryan and Deci, 2000a, 2000b). Students who report neutral or lower levels of emotional satisfaction may need mathematical work to be framed in terms of its personal relevance or utility to find the work satisfying (Walkington et al., 2013; Walkington and Bernacki, 2014), an idea that could be tested using the MBVI (Andrews et al., 2017) and emotional satisfaction scale in concert. Because there are only four emotional satisfaction items and the MBVI has 11 items, these small scales may provide a starting point for instructors to examine their students’ attitudes toward math. Brief and easy to administer, the scales could be used to begin testing ideas about the malleability of students’ emotional satisfaction with math and values of math, as well as the effects of particular interventions.
The factors we identified did not match those reported for both the short and long forms of the ASCI (Bauer, 2008; Xu and Lewis, 2011). This result indicates that undergraduate science and math students’ attitudes toward mathematics are composed of elements other than intellectual accessibility and emotional satisfaction. Importantly, the intellectual accessibility of math is not being captured by items 2, 3, 6, and 8, and thus should be reconsidered. To address this, groups of undergraduate science and math majors who hold generally positive, negative, or neutral attitudes toward math could be identified and interviewed as a starting point for identifying the constructs underpinning these attitudinal differences. In addition, from a more technical perspective, it is somewhat worrisome that the two- and three-factor solutions suggested by the EFA corresponded to whether the items were reverse scored or not. It is possible that the effect of the valence of the items alone could explain their groupings. In other words, the three-cluster solution from the latent profile analysis could represent groups of students who noticed that the valence of the items changed (positive cluster in Figure 2), did not notice that valence of the items changed (negative cluster in Figure 2), or were confused by or indifferent about the structure of the semantic differential (neutral cluster in Figure 2). Future studies should present the items using a common valence (i.e., none reversed) or with differing valence (i.e., different items reverse scored) and with larger and more nationally representative samples of students to determine whether the results support or refute the idea that students can be classified according to their positive, negative, or neutral emotions about math.
We used the emotional satisfaction with math scale and the entire ASMI to examine the attitudes of undergraduates majoring in traditional life science majors versus non–life science majors to determine empirically whether life science majors do indeed have less favorable attitudes toward math. Our comparison of the emotional satisfaction with math of life science majors’ versus non–life science majors (i.e., astronomy, chemistry, computer science, mathematics, physics) was inconclusive because it was underpowered to detect significant differences but revealed a small to moderate effect of major (d ∼ 0.3) (Cohen, 1988; Nakagawa and Cuthill, 2007). As noted earlier, more data from a larger and more nationally representative pool of students are needed to confirm this effect. If the effect is observed in future studies, it may be due to non–life science majors having more exposure to math and developing more positive emotions about math as a result (Hidi and Renninger, 2006), although our analyses reveal no relationship between time in college (i.e., being upper vs. lower division) and students’ emotional satisfaction with math. This result is consistent with the interpretation that positive emotions about math influence students’ choices to major in math-intensive disciplines, rather than increased math exposure leading to the development of more favorable attitudes. The relationship between attitudes about a subject and future school-related behavior such as course enrollment has repeatedly been demonstrated (Maltese and Tai, 2011; Alexander et al., 2012). However, more longitudinal research is needed to characterize undergraduate life science majors’ emotional satisfaction with math over time in programs that require various levels of math course work to determine whether attitudes predict enrollment, enrollment predicts attitudes, or both.
Our test of whether women and men differed in their emotional satisfaction with math was also inconclusive because it was underpowered to detect significant differences but revealed a small effect of gender on students’ emotional satisfaction with math (d = 0.25), with women being less emotionally satisfied with math. Again, more data from a larger and more nationally representative pool of students are needed to confirm this effect. It would also be prudent for future analyses to perform EFA on men and women separately to see whether the pattern of results is equal across these two genders (as well as across other subgroups of interest); we were unable to do so with the present analyses due to sample size (i.e., power) considerations. If confirmed, this result would be consistent with findings from many studies and meta-analyses, namely, that on average women hold more negative attitudes toward math than men (e.g., Hyde et al., 1990). Women’s negative attitudes about math have been attributed to cultural beliefs about gender and mathematics, such as the belief that women are less competent at math or that math is not a “feminine” task (Correll, 2001). Women’s negative attitudes have also been attributed to their confidence in their ability to do math (e.g., Ellis et al., 2016) and their anxiety about math (e.g., Stoet et al., 2016). The higher enrollment of women in life science majors may exacerbate the perception that biology majors hold negative attitudes toward math.
Future research should repeat our test of differences between lower- and upper-division students’ emotional satisfaction with math to determine whether the lack of effect we observed holds for a larger and more diverse sample. Our observation of a near-zero effect of year in school on students’ emotional satisfaction with math raises questions of whether students’ levels of emotional satisfaction with math are set by the time they reach college or remain malleable during college. It is important to note that we made use of a cross-sectional data set. Thus, the attitudes of students in our sample may be subject to bias at the upper-division level because students with less favorable attitudes may have transferred to majors outside science or math or may have left college altogether. Tracking students’ levels of emotional satisfaction with math over time would also be useful for determining the malleability of their attitudes within and across college. The fact that the emotional satisfaction with math scale includes only four items will help minimize the burden associated with repeated measures for both students and researchers.
Acknowledgments
Support for this work was provided by a grant from the National Science Foundation (DBI-1156707). The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of the National Science Foundation. We thank the university personnel who helped to distribute our study invitation and our participants for their responses.
Footnotes
The sample sizes for all of these comparisons does not sum to the total of 359 respondents because the distinction between the groups was not always wholly inclusive (e.g., a major was not part of either grouping) or the requisite information was not provided by students.
We acknowledge that gender is a spectrum, but the population in our study primarily identified as males and females. We did not have a sufficient sample size to draw inferences about students who identified as other than male or female.
We recognize that students who identify as Asian or URM have a spectrum of experiences and more careful analysis by specific identity is needed to understand their experiences. Owing to sample size constraints, we made the decision to group nonwhite students into two categories: Asian and URM. This pooling may mask patterns distinct to each population, but broadly gives us information on patterns shared across these groups.
REFERENCES
- Aiken L. R. Attitudes toward mathematics. Review of Educational Research. 1970;40(4):551–596. https://doi.org/10.3102/00346543040004551. [Google Scholar]
- Aikens M. L., Dolan E. L. Teaching quantitative biology: Goals, assessments, and resources. Molecular Biology of the Cell. 2014;25(22):3478–3481. doi: 10.1091/mbc.E14-06-1045. https://doi.org/10.1091/mbc.E14-06-1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ajzen I. From intentions to actions: A theory of planned behavior. In: Kuhl P. D. J., Beckmann D. J., editors. Action control. Berlin: Springer; 1985. pp. 11–39. https://doi.org/10.1007/978-3-642-69746-3_2. [Google Scholar]
- Ajzen I. Theories of cognitive self-regulation: The theory of planned behavior. Organizational Behavior and Human Decision Processes. 1991;50(2):179–211. https://doi.org/10.1016/0749-5978(91)90020-T. [Google Scholar]
- Alexander J. M., Johnson K. E., Kelley K. Longitudinal analysis of the relations between opportunities to learn about science and the development of interests related to science. Science Education. 2012;96(5):763–786. https://doi.org/10.1002/sce.21018. [Google Scholar]
- Andrews S. E., Runyon C., Aikens M. L. The Math-Biology Values Instrument: Development of a tool to measure life science majors’ task values of using math in the context of biology. CBE—Life Sciences Education. 2017:ar45. doi: 10.1187/cbe.17-03-0043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer C. F. Attitude toward chemistry: A semantic differential instrument for assessing curriculum impacts. Journal of Chemical Education. 2008;85(10):1440. https://doi.org/10.1021/ed085p1440. [Google Scholar]
- Bauer D. J., Shanahan M. J. Modeling complex interactions: Person-centered and variable-centered approaches. In: Little T. D., Bovaird J. A., Card N. A., editors. Modeling contextual effects in longitudinal studies. Mahwah, NJ: Erlbaum; 2007. pp. 255–283. [Google Scholar]
- Brandriet A. R., Xu X., Bretz S. L., Lewis J. E. Diagnosing changes in attitude in first-year college chemistry students with a shortened version of Bauer’s semantic differential. Chemistry Education Research and Practice. 2011;12(2):271–278. https://doi.org/10.1039/C1RP90032C. [Google Scholar]
- Buxton L. Do you panic about maths? Coping with maths anxiety. London: Heinemann Educational; 1981. [Google Scholar]
- Chen M., Zaas A., Woods C., Ginsburg G. S., Lucas J., Dunson D., Carin L. Predicting viral infection from high-dimensional biomarker trajectories. Journal of the American Statistical Association. 2011;106(496):1259–1279. doi: 10.1198/jasa.2011.ap10611. https://doi.org/10.1198/jasa.2011.ap10611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipman S. F., Krantz D. H., Silver R. Mathematics anxiety and science careers among able college women. Psychological Science. 1992;3(5):292–295. https://doi.org/10.1111/j.1467-9280.1992.tb00675.x. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Cohen J. A power primer. Psychological Bulletin. 1992;112(1):155–159. doi: 10.1037//0033-2909.112.1.155. https://doi.org/10.1037/0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Correll S. J. Gender and the career choice process: The role of biased self-assessments. American Journal of Sociology. 2001;106(6):1691–1730. https://doi.org/10.1086/321299. [Google Scholar]
- Csikszentmihalyi M. Flow and the foundations of positive psychology. Dordrecht, Netherlands: Springer; 2014. Toward a psychology of optimal experience; pp. 209–226. https://doi.org/10.1007/978-94-017-9088-8_14. [Google Scholar]
- DeVellis R. F. Scale development: Theory and applications. Thousand Oaks, CA: Sage; 2012. [Google Scholar]
- Ellis J., Fosdick B. K., Rasmussen C. Women 1.5 times more likely to leave STEM pipeline after calculus compared to men: Lack of mathematical confidence a potential culprit. PLoS ONE. 2016;11(7):e0157447. doi: 10.1371/journal.pone.0157447. https://doi.org/10.1371/journal.pone.0157447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan X. Statistical significance and effect size in education research: Two sides of a coin. Journal of Educational Research. 2001;94(5):275–282. https://doi.org/10.1080/00220670109598763. [Google Scholar]
- Feierabend R. L. Review of research on psychological problems in mathematics education. Cooperative Research Monograph. 1960;3:3–46. www.worldcat.org/title/cooperative-research-monograph/oclc/1585963. [Google Scholar]
- Fennema E., Sherman J. A. Fennema-Sherman mathematics attitudes scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for Research in Mathematics Education. 1976;7(5):324. https://doi.org/10.2307/748467. [Google Scholar]
- Fowler F. J. Improving survey questions: Design and evaluation. Thousand Oaks, CA: Sage; 1995. [Google Scholar]
- Fraley C., Raftery A. E. Model-based clustering, discriminant analysis and density estimation. Journal of the American Statistical Association. 2002;97:611–631. [Google Scholar]
- Fraley C., Raftery A. E., Murhpy T. B., Scrucca L. 2012. mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation (Technical Report No. 597), Department of Statistics, University of Washington.
- Frenzel A. C., Pekrun R., Goetz T. Girls and mathematics—A “hopeless” issue? A control-value approach to gender differences in emotions towards mathematics. European Journal of Psychology of Education. 2007;22(4):497. https://doi.org/10.1007/BF03173468. [Google Scholar]
- Friborg O., Martinussen M., Rosenvinge J. H. Likert-based vs. semantic differential-based scorings of positive psychological constructs: A psychometric comparison of two versions of a scale measuring resilience. Personality and Individual Differences. 2006;40(5):873–884. https://doi.org/10.1016/j.paid.2005.08.015. [Google Scholar]
- Glynn S. M., Taasoobshirazi G., Brickman P. Nonscience majors learning science: A theoretical model of motivation. Journal of Research in Science Teaching. 2007;44(8):1088–1107. https://doi.org/10.1002/tea.20181. [Google Scholar]
- Hayton J. C., Allen D. G., Scarpello V. Factor retention decisions in exploratory factor analysis: A tutorial on parallel analysis. Organizational Research Methods. 2004;7(2):191–205. https://doi.org/10.1177/1094428104263675. [Google Scholar]
- Hidi S., Renninger K. A. The four-phase model of interest development. Educational Psychologist. 2006;41(2):111–127. https://doi.org/10.1207/s15326985ep4102_4. [Google Scholar]
- Horn J. L. A rationale and test for the number of factors in factor analysis. Psychometrika. 1965;30(2):179–185. doi: 10.1007/BF02289447. https://doi.org/10.1007/BF02289447. [DOI] [PubMed] [Google Scholar]
- Hyde J. S., Fennema E., Ryan M., Frost L. A., Hopp C. Gender comparisons of mathematics attitudes and affect. Psychology of Women Quarterly. 1990;14(3):299–324. https://doi.org/10.1111/j.1471-6402.1990.tb00022.x. [Google Scholar]
- Kaiser H. F. The application of electronic computers to factor analysis. Educational and Psychological Measurement. 1960;20:141–151. https://doi.org/10.1177/001316446002000116. [Google Scholar]
- Kloosterman P. Beliefs about mathematics and mathematics learning in the secondary school: Measurement and implications for motivation. In: Leder G. C., Pehkonen E., Törner G., editors. Beliefs: A hidden variable in mathematics education? Dordrecht, Netherlands: Springer; 2002. pp. 247–269. https://doi.org/10.1007/0-306-47958-3_15. [Google Scholar]
- Koga K., Iwasaki Y. Psychological and physiological effect in humans of touching plant foliage—Using the semantic differential method and cerebral activity as indicators. Journal of Physiological Anthropology. 2013;32:7. doi: 10.1186/1880-6805-32-7. https://doi.org/10.1186/1880-6805-32-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maher J. M., Markey J. C., Ebert-May D. The other half of the story: Effect size analysis in quantitative research. CBE—Life Sciences Education. 2013;12(3):345–351. doi: 10.1187/cbe.13-04-0082. https://doi.org/10.1187/cbe.13-04-0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maltese A. V., Tai R. H. Pipeline persistence: Examining the association of educational experiences with earned degrees in STEM among U.S. students. Science Education. 2011;95(5):877–907. https://doi.org/10.1002/sce.20441. [Google Scholar]
- Mandler G. Affect and learning: Causes and consequences of emotional interactions. In: McLeod D. B., Adams V. M., editors. Affect and mathematical problem solving. New York: Springer; 1989. pp. 3–19. https://doi.org/10.1007/978-1-4612-3614-6_1. [Google Scholar]
- Matsunaga M. How to factor-analyze your data right: Do’s, don’ts, and how-to’s. International Journal of Psychological Research. 2015;3(1):97–110. https://doi.org/10.21500/20112084.854. [Google Scholar]
- Matthews K. E., Hodgson Y., Varsavsky C. Factors influencing students’ perceptions of their quantitative skills. International Journal of Mathematical Education in Science and Technology. 2013;44(6):782–795. https://doi.org/10.1080/0020739X.2013.814814. [Google Scholar]
- Matthews W. Influences on the learning and participation of minorities in mathematics. Journal for Research in Mathematics Education. 1984;15(2):84–95. https://doi.org/10.2307/748884. [Google Scholar]
- McGinnis J. R., Kramer S., Shama G., Graeber A. O., Parker C. A., Watanabe T. Undergraduates’ attitudes and beliefs about subject matter and pedagogy measured periodically in a reform-based mathematics and science teacher preparation program. Journal of Research in Science Teaching. 2002;39(8):713–737. https://doi.org/10.1002/tea.10042. [Google Scholar]
- McLeod D. B. In Handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics. New York: Macmillan; 1992. Research on affect in mathematics education: A reconceptualization; pp. 575–596. [Google Scholar]
- Meece J. L., Wigfield A., Eccles J. S. Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology. 1990;82(1):60–70. https://doi.org/10.1037/0022-0663.82.1.60. [Google Scholar]
- Mohamed L., Waheed H. Secondary students ‘ attitude towards mathematics in a selected school of Maldives. International Journal of Humanities and Social Science. 2011;1(15):277–281. [Google Scholar]
- Nakagawa S., Cuthill I. C. Effect size, confidence interval and statistical significance: A practical guide for biologists. Biological Reviews. 2007;82:591–605. doi: 10.1111/j.1469-185X.2007.00027.x. [DOI] [PubMed] [Google Scholar]
- National Research Council (NRC) BIO2010: Transforming undergraduate education for future research biologists. Washington, DC: National Academies Press; 2003. http://www.nap.edu/catalog/10497/bio2010-transforming-undergraduate-education-for-future-research-biologists. [PubMed] [Google Scholar]
- NRC. Next generation science standards. 2013. Retrieved April 20, 2017, from www.nextgenscience.org. [Google Scholar]
- Nosek B. A., Banaji M. R., Greenwald A. G. Math = male, me = female, therefore math ≠ me. Journal of Personality and Social Psychology. 2002;83(1):44–59. https://doi.org/10.1037/0022-3514.83.1.44. [PubMed] [Google Scholar]
- Osgood C. E., Suci G. J., Tannenbaum P. H. The measurement of meaning. University of Illinois Press; 1957. [Google Scholar]
- Pastor D. A., Barron K. E., Miller B. J., Davis S. L. A latent profile analysis of college students’ achievement goal orientation. Contemporary Educational Psychology. 2007;32(1):8–47. https://doi.org/10.1016/j.cedpsych.2006.10.003. [Google Scholar]
- Poladian L. Engaging life-sciences students with mathematical models: Does authenticity help? International Journal of Mathematical Education in Science and Technology. 2013;44(6):865–876. https://doi.org/10.1080/0020739X.2013.811301. [Google Scholar]
- Raîche G. An R package for parallel analysis and non graphical solutions to the Cattell scree test (Version R package version 2.3.3) 2010. Retrieved June 1, 2016, from http://CRAN.R-project.org/package=nFactors. [Google Scholar]
- Raîche G., Walls T. A., Magis D., Riopel M., Blais J.-G. Non-graphical solutions for Cattell’s scree test. Methodology: European Journal of Research Methods for the Behavioral and Social Sciences. 2013;9(1):23–29. https://doi.org/10.1027/1614-2241/a000051. [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2016. Retrieved June 1, 2016, from www.R-project.org/ [Google Scholar]
- Rech J. F. A comparison of the mathematics attitudes of Black students according to grade level, gender, and academic achievement. Journal of Negro Education. 1994;63(2):212–220. https://doi.org/10.2307/2967384. [Google Scholar]
- Revelle W. psych: Procedures for psychological, psychometric, and personality research (Version R package version 1.6.12) Evanston, IL: Northwestern University; 2016. Retrieved June 1, 2016, from https://CRAN.R-project.org/package=psych. [Google Scholar]
- Rheinlander K., Wallace D. Calculus, biology and medicine: A case study in quantitative literacy for science students. Numeracy. 2011;4(1) https://doi.org/http://dx.doi.org/10.5038/1936-4660.4.1.3. [Google Scholar]
- Richardson V. The role of attitudes and beliefs in learning to teach. In: Sikula J., Buttery T., Guyton E., editors. Handbook of research on teacher education. New York: Simon & Schuster Macmillan; 1996. pp. 102–119. [Google Scholar]
- Ryan R. M., Deci E. L. Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemporary Educational Psychology. 2000a;25(1):54–67. doi: 10.1006/ceps.1999.1020. https://doi.org/10.1006/ceps.1999.1020. [DOI] [PubMed] [Google Scholar]
- Ryan R. M., Deci E. L. Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. American Psychologist. 2000b;55(1):68–78. doi: 10.1037//0003-066x.55.1.68. https://doi.org/10.1037/0003-066X.55.1.68. [DOI] [PubMed] [Google Scholar]
- Steiner R., Sullivan J. Variables correlating with student success in organic chemistry. Journal of Chemical Education. 1984;61(12):1072. https://doi.org/10.1021/ed061p1072. [Google Scholar]
- Stoet G., Bailey D. H., Moore A. M., Geary D. C. Countries with higher levels of gender equality show larger national sex differences in mathematics anxiety and relatively lower parental mathematics valuation for girls. PLoS ONE. 2016;11(4):e0153857. doi: 10.1371/journal.pone.0153857. https://doi.org/10.1371/journal.pone.0153857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabachnick B. G., Fidell L. S. Using multivariate statistics. 5th ed. Boston: Allyn and Bacon/Pearson Education; 2007. [Google Scholar]
- Tapia M., Marsh G. E. An instrument to measure mathematics attitudes. Academic Exchange Quarterly. 2004;8(2):16–22. [Google Scholar]
- Torija A. J., Ruiz D. P., Ramos-Ridao A. F. Application of a methodology for categorizing and differentiating urban soundscapes using acoustical descriptors and semantic-differential attributes. Journal of the Acoustical Society of America. 2013;134(1):791–802. doi: 10.1121/1.4807804. https://doi.org/10.1121/1.4807804. [DOI] [PubMed] [Google Scholar]
- Walkington C., Bernacki M. L. Motivating students by “personalizing” learning around individual interests: A consideration of theory, design, and implementation issues. In: Karabenick S. A., Urdan T. C., editors. Motivational Interventions (Advances in Motivation and Achievement. Vol. 18. Bingley, UK: Emerald Group; 2014. pp. 139–176. https://doi.org/10.1108/S0749-742320140000018004. [Google Scholar]
- Walkington C., Petrosino A., Sherman M. Supporting algebraic reasoning through personalized story scenarios: How situational understanding mediates performance. Mathematical Thinking and Learning. 2013;15(2):89–120. https://doi.org/10.1080/10986065.2013.770717. [Google Scholar]
- Welch B. L. The generalization of ‘student’s’ problem when several different population variances are involved. Biometrika. 1947;34(1/2):28–35. doi: 10.1093/biomet/34.1-2.28. https://doi.org/10.2307/2332510. [DOI] [PubMed] [Google Scholar]
- Wigfield A., Eccles J. S. The development of achievement task values: A theoretical analysis. Developmental Review. 1992;12(3):265–310. https://doi.org/10.1016/0273-2297(92)90011-P. [Google Scholar]
- Wigfield A., Eccles J. S. Expectancy–value theory of achievement motivation. Contemporary Educational Psychology. 2000;25(1):68–81. doi: 10.1006/ceps.1999.1015. https://doi.org/10.1006/ceps.1999.1015. [DOI] [PubMed] [Google Scholar]
- Xu X., Alhooshani K., Southam D., Lewis J. E. Gathering psychometric evidence for ASCIv2 to support cross-cultural attitudinal studies for college chemistry programs. In: Kahveci M., Orgill M., editors. Affective dimensions in chemistry education. Berlin: Springer; 2015. pp. 177–194. https://doi.org/10.1007/978-3-662-45085-7_9. [Google Scholar]
- Xu X., Lewis J. E. Refinement of a chemistry attitude measure for college students. Journal of Chemical Education. 2011;88(5):561–568. https://doi.org/10.1021/ed900071q. [Google Scholar]
- Zan R., Brown L., Evans J., Hannula M. S. Affect in mathematics education: An introduction. Educational Studies in Mathematics. 2006;63(2):113–121. [Google Scholar]