Thermodynamic properties of amyloid fibrils in equilibrium

Abstract

In this manuscript we use a two-dimensional coarse-grained model to study how amyloid fibrils grow towards an equilibrium state where they coexist with proteins dissolved in a solution. Free-energies to dissociate proteins from fibrils are estimated from the residual concentration of dissolved proteins. Consistent with experiments, the concentration of proteins in solution affects the growth rate of fibrils but not their equilibrium state. Also, studies of the temperature dependence of the equilibrium state can be used to estimate thermodynamic quantities, e.g., heat capacity and entropy.

Graphical abstract

INTRODUCTION

The self-assembly of proteins into amyloid-like fibrils is a ubiquitous process that arises for seemingly unrelated amino acid sequences when subjected to the right conditions [1, 2]. Segments of proteins incorporated into these fibrils adopt extended conformations, i.e., β-strands, which are hydrogen bonded to neighboring proteins forming a β-sheet. Stacking of β-sheets through side chain interactions accounts for the common pattern of amyloid fibrils, also known as cross-β structure [3, 4]–see Fig. 1a. Proteins that form fibrils at physiological conditions were found to be either functional, e.g., silk fibrils that are used by spiders to capture their prey, or related to plaque formation in amyloid diseases that include Alzheimer’s and Parkinson’s [5, 6]. Fibril formation proceeds through a nucleation phase followed by growth [7–9]. In the nucleation phase, some proteins form a disordered aggregate [10, 11] from which the fibril nucleates while in the growth phase proteins are added to the fibril increasing its length. Important questions regarding the pathway of fibril formation [12–14] as well as the structure of the disordered aggregates remain open [11]. Also, understanding the equilibrium of mature fibrils in solution is of great interest as it could enable the development of a thermodynamic framework to study these structures. In analogy with protein folding [15], thermodynamics may provide insights into the stability of fibrils and their underlying molecular mechanisms [16].

FIG. 1.

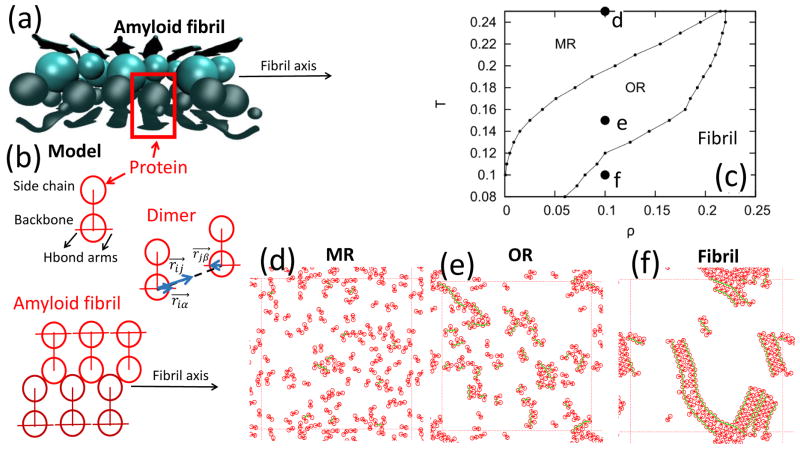
(a) Structure of a fibril made from residues 16–21 of the amyloid-β protein (PDB ID: 3OW9). Backbone and side chains of proteins are depicted using cartoon-like and bead representations, respectively. (b) Schematic representation of a protein in the model. Side chain and backbone beads are highlighted as well as Hbond arms. The representation of a dimer depicts the vectors (blue arrow) used in Eq. 3 to account for Hbonds. The representation of an amyloid fibril shows two β-sheets made of three peptides each stack on top of each other. The fibril axis is also shown. (c) Phase diagram showing monomeric (MR), oligomeric (OR) and fibrillar states as well as representative snapshots of the system at these states computed at the same density 0.1 and temperatures (d) 0.25, (e) 0.15, and (f) 0.1.

Equilibrium thermodynamic properties of amyloid fibrils are challenging to measure using conventional experimental methods. For example, heat capacities measured as a function of temperature in calorimetric experiments were found to be irreversible for most fibrils precluding the use of analytic frameworks to compute free-energies [17, 18]. Moreover, it is difficult to deconvolute contributions from molecular interactions between proteins and fibrils from these calorimetric heat capacities that depend on the overall morphology of the fibrillar network. Overcoming these limitations, recent “amyloid assembly equilibrium measurements” have shown that at least for some protein sequences mature fibrils can exist in equilibrium with dissolved proteins, i.e., monomers [19–23]. This equilibrium has been explored to measure free-energies required to dissociate a protein from a fibril, i.e., ΔG. Studies of the temperature dependence of this equilibrium can also provide insights of other thermodynamic quantities, i.e., change in enthalpy (ΔH), entropy (ΔS), and heat capacity (ΔC_p). These quantities played a key role in determining the molecular driving forces of protein folding [24, 25] but they remain mostly unknown for amyloid fibrils. Only few experiments have estimated ΔC_p for amyloid fibrils finding both positive and negative values [18, 26–28]. Currently, it is unknown how the magnitude and sign of ΔC_p relate to the peptide sequence, fibril structure, and/or condition of the solvent. Notice that unfolding of proteins accounts for a large and positive (never negative) change in heat capacity [24, 29–36]. Timescales to equilibrate fibrils and proteins in a solution are of the order of hours and days which is beyond reach of all-atom computer simulations [20, 23, 37]. Thus, models to study these equilibrium reaction require a coarse-grained approach [38–40].

Here, we develop an off-lattice coarse-grained model to study how amyloid fibrils grow towards an equilibrium state wherein free-energies ΔF to add or dissociate a protein from a fibril can be measured. The initial density of proteins in a solution affects the kinetics of aggregation and the time required for mature fibrils to form. However, we show that mature fibrils that were generated from different densities of proteins can reach the same fibril-monomer equilibrium state defined by ΔF. Moreover, ΔH, ΔS, and ΔC_p can be obtained by studying the temperature dependence of this equilibrium. We discuss how the greater stability of fibrils with respect to temperature when compared to native protein structures implies a small ΔC_p (close to zero). Despite its small value, we show that ΔC_p can be measured in our model. We also study ΔC_p for the honeycomb lattice model of amyloid fibrils which has recently been developed to study fibril solubility [41]. We find that changes in the thickness of the fibril in the honeycomb lattice accounts for an increase in the magnitude of ΔC_p. This suggests that measurements of ΔC_p for amyloid fibrils might provide insights into the residues that are buried in the fibril core.

METHODOLOGY

Our coarse grained model accounts for the two length scales that are characteristic of amyloid fibrils and which emerge from backbone hydrogen bonding and side chain interactions. Proteins are described by two-dimensional dimers, i.e., two beads separated by a fixed distance l. Beads mimic side chain and backbone atoms (see Fig. 1b) and they interact with beads from neighboring proteins through a Lennard-Jones potential defined by ε_ΦΨ (binding energy) and σ (distance parameter):

$${\mathrm{U}}_{\text{LJ}}(r_{i\mathrm{\Phi }j\mathrm{\Psi }})=4{\epsilon }_{\mathrm{\Phi }\mathrm{\Psi }}\left[{\left(\frac{\sigma }{r_{i\mathrm{\Phi }j\mathrm{\Psi }}}\right)}^{12}-{\left(\frac{\sigma }{r_{i\mathrm{\Phi }j\mathrm{\Psi }}}\right)}^6\right],$$ (1)

where r_iΦjΨ is the distance between bead Φ of protein i and bead Ψ of protein j.

In addition to Lennard-Jones interactions, backbone beads can also form two hydrogen bonds (Hbonds). The directionality of Hbonds in fibrils is accounted for by two arms separated by an angle of 180° and which are perpendicular to the line joining backbone and side chain beads–see Fig. 1b. If r⃗_ij is the distance vector between centers of mass of backbone beads of proteins i and j, and r̂_iα is the unit vector along arm α of backbone bead i (see Fig. 1b), then the Hbond energy in the Ben-Naim’s framework is [42–44]:

$$\begin{array}{l}{U}_{\text{HB}}(r_{ij},\{{\widehat{r}}_{i\alpha }\},\{{\widehat{r}}_{j\beta }\})={\epsilon }_{\text{HB}}exp\left(-\frac{{(r_{ij}-R_{\text{HB}})}^2}{2{\sigma }_{\text{HB}}^2}\right)\\ \times \left[\sum _{\alpha =1}^{2}exp\left[-{\left(\frac{{\widehat{r}}_{i\alpha }{\overrightarrow{r}}_{ij}}{r_{ij}}-1\right)}^2\frac{1}{2{\sigma }_{\text{HB}}^2}\right]\right]\\ \times \left[\sum _{\beta =1}^{2}exp\left[-{\left(\frac{{\widehat{r}}_{j\beta }{\overrightarrow{r}}_{ij}}{r_{ij}}+1\right)}^2\frac{1}{2{\sigma }_{\text{HB}}^2}\right]\right],\end{array}$$ (2)

where ε_HB = −1 and R_HB = 1 are the binding energy and equilibrium distance of the Hbond. The constant σ_HB = 0.085 R_HB is the attenuation parameter of the interaction. Equation 2 favors configurations where the distance between backbone beads of molecules i and j is R_HB, one arm of molecule i is aligned with the line joining the centers of mass of backbone beads, and the same for one arm of molecule j. Distances and energies in this work are given in units of R_HB and ε_HB, respectively, and the Boltzmann constant k_b is defined as one. In terms of these reduced units, the Lennard-Jones potential is defined by σ = 0.75 (same distance parameter for all beads) and ε_ΦΨ = 0.1, 0.2, or 0.141 if beads Φ and Ψ correspond both to side chain, backbone, or a mixture of side chain and backbone beads, respectively. This set of binding energies for the Lennard-Jones potential was chosen by trial-and-error to account for fibril formation. In particular, a same ε_ΦΨ value for pairs of side chain and backbone beads resulted in circular aggregates instead of linearly elongated fibrils. The binding energy for the interaction between side chain and backbone (i.e., ε_ΦΨ =0.141) beads was obtained from the standard Lorentz-Berthelot rule. The fixed distance between beads is l = 1.

Here, we perform Monte Carlo (MC) simulations in the canonical (NVT) ensemble [45]. Periodic boundary conditions is used to mimic an infinite system. Initial conditions are chosen randomly. At each time-step, we tried to translate, rotate and switch (180° rotation) in random order a randomly chosen protein. A MC cycle which corresponds to N time-steps is used as our unit of time. Average densities are computed from 10⁶ MC cycle simulations that are performed after an equilibration period of 10⁵ cycles. Cluster analysis is used to classified the overall bonding state of the system. It uses an energy criteria wherein proteins are considered bonded when their potential energy is less than −0.05. Small variations of this energy cutoff did not account for significant differences in the bonding state of the system. The different states of the system are: the monomeric state when more than 50% of proteins are non-bonded, the fibril state when at least 50% of the proteins are bonded to one big cluster, and the oligomeric state which comprises all other situations, i.e., when less than 50% of proteins are non-bonded and less than 50% are not part of a big cluster.

RESULTS

In Fig. 1c we show the phase diagram of a system comprising N = 120 proteins. This diagram was obtained from simulations carried out at different temperatures (from 0.08 to 0.26 in steps of 0.01) and densities (from 0.01 to 0.25 in steps of 0.01). Characteristic configurations are shown in Fig. 1d–f [46]. The monomeric state occur for conditions of high temperature and low density which are unfavorable to bond formation. Accordingly, proteins in Fig. 1d are mostly dispersed in the simulation box. Conversely, the fibrillar state is favored by conditions of low temperature and high density. Under these conditions, proteins are mostly bonded to each other and fibrils in Fig. 1f are characterized by β-sheet structures, i.e., extended regions of Hbonded proteins stacked on top of each others via side chain interactions. In the oligomeric state, which occurs for intermediate values of temperature and density in Fig. 1c, Hbonded proteins do not form ordered β-sheets which is required for fibril formations.

In Fig. 2, we study how systems evolve towards equilibrium. Starting from a random initial conditions, the fraction of monomeric proteins f_o in the system is shown as a function of time for systems with low and high protein concentrations. Notice that in this figure equilibrium is reached in about 4,000 MC cycles. For the low concentration system, the fraction of non-bonded proteins in equilibrium is greater than 50% and, therefore, the system is considered to be in the monomeric state–see Fig. 1c. Evolution towards equilibrium is a fast process which is fitted in Fig. 2 by a single exponential with a characteristic decay time of 30 MC cycles. The high concentration system reaches equilibrium in the oligomer state and a characteristic configuration is shown in Fig. 1e. The evolution of this system towards equilibrium proceeds in two steps: a very fast bonding process in which dimers and trimers are formed by local rearrangements of proteins, e.g., rotation, followed by a slower addition of proteins to β-sheets accounting for the extended but disordered Hbonded regions visible in Fig. 1e. The time dependence of this system is fitted by a double exponential with characteristic decay times of 1200 and 14 MC cycles.

FIG. 2.

Time dependence of the fraction of monomers f_o in the system. Only a fraction of the whole trajectory is shown. Dashed and full lines correspond to systems in the monomeric (i.e., ρ = 0.02) and oligomeric (ρ = 0.1) states, respectively. The thermal energy of the system is 0.15 and each point in the figure is an average over 10 MC cycles. Lines correspond to exponential fits of the data.

Fig. 2 shows that systems evolve toward an equilibrium condition in which bonded and monomeric proteins coexist. Assuming that these two species interconvert, first-order rate equations predict a linear dependence of the equilibrium density of monomers ${\rho }_o^{\ast }$ on the overall density of proteins ρ [47]:

$${\rho }_o^{\ast }=\left(\frac{k_{bo}}{k_{bo}+k_{ob}}\right)\rho ,$$ (3)

where k_ob and k_bo are the rate constants for binding a monomer and dissolving a bonded protein, respectively. This equation is valid in the monomeric states of the phase diagram where all bonded proteins can be interconverted into monomers. However, in the fibril state interconvertion occurs only at the extremities of the fibril. This process is best described by a fibril dissociation reaction in which a protein bonded to the extremity of a fibril dissociates becoming a monomer. A first order rate equation for this reaction for detachment and second order for attachment of monomer predicts

$${\rho }_o^{\ast }=\left(\frac{k_{fo}}{k_{of}}\right).$$ (4)

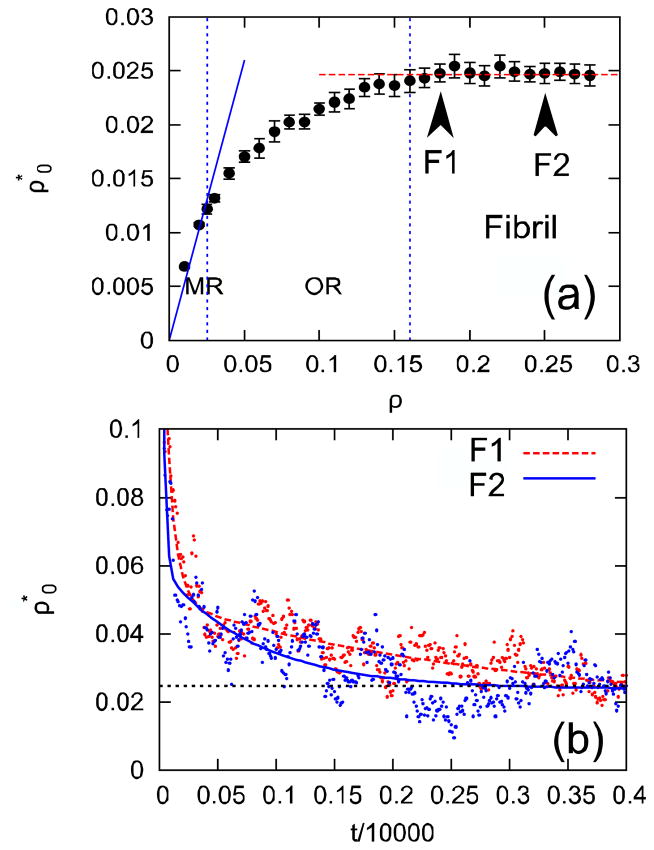
In Fig. 3a, we observe a constant density of monomers ( ${\rho }_o^{\ast }=0.0247$) in the fibril region of the phase diagram [39]. Experiments aiming to study equilibrium properties of fibrils are performed with seeded fibrils for which ρ_f is a constant [19]. Thus, in our simulations and for seeded fibril experiments, ρ_o is independent of ρ in the fibril region of the phase diagram. The oligomeric phase provides cross-over for the dependence of ρ_o on ρ in monomeric (Eq. 3) and fibril (Eq. 4) regions. Fig. 3b shows that the kinetics of fibril formation for two fibril states (labeled F1 and F2 in Fig. 3a) is not the same despite both systems reaching the same density of monomers in equilibrium. Equilibrium is reached faster for the system (F2) with higher protein concentration [14].

FIG. 3.

(a) Dependence of the equilibrium density of monomers ${\rho }_o^{\ast }$ on the density of proteins ρ in the system at the reduced temperature 0.15. Vertical dashed lines separate monomeric (MR), oligomeric (OR), and Fibril regions. The full line corresponds to the fit of ${\rho }_o^{\ast }$ to Eq. 3 for data points in the monomeric region. The horizontal dashed line shows that the equilibrium density of monomers in the fibril state is independent of ρ. Error bars were estimated using block average in which simulations were divided in 20 blocks. (b) Time dependence of ρ_o compute at ρ = 0.17 (dashed line) and ρ = 0.25 (full line). Only a fraction of the whole trajectory is shown. The horizontal dashed line shows the equilibrium density of monomers.

The stability of mature fibrils can be quantified by measuring the free-energy ΔF required to dissociate a protein from a fibril. ΔF can be written in terms of the equilibrium dissociation constant K_d:

$$K_d=\frac{[F][M]}{[F]}=[M],$$ (5)

where [F] is the equilibrium concentrations of fibrils and $[M]={\rho }_o^{\ast }/{\rho }_s$ where the standard concentration ρ_s = 1 (given in units of $R_{\text{HB}}^{-2}$) [48]. Accordingly, $\mathrm{\Delta }\mathcal{F}=-k_{b}Tln{K}_d=-k_{b}Tln{\rho }_o^{\ast }$, where the equilibrium density of monomer ${\rho }_o^{\ast }$ is accessible both experimentally and in our simulations [49]. In experimental studies, ΔF was measured to unravel how mutations of the protein sequence and conditions of the solvent affect the stability of fibrils [19]. Here, we are interested in the temperature dependence of ΔF which, according to thermodynamics, can described by [15, 30, 50, 51]:

$$\mathrm{\Delta }\mathcal{F}=\mathrm{\Delta }{U}_o-T\mathrm{\Delta }{S}_o+\mathrm{\Delta }{C}_o\left[(T-T_o)-Tlog\left(\frac{T}{T_o}\right)\right]$$ (6)

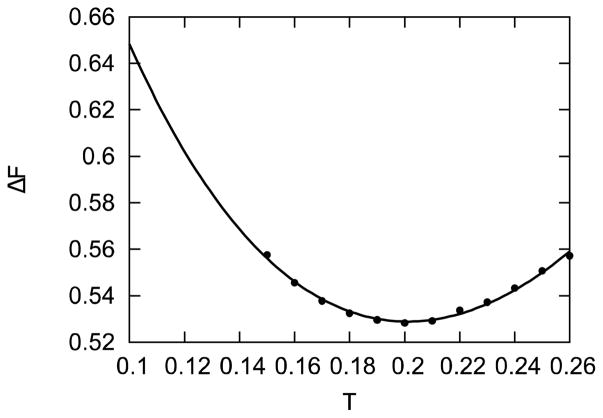
where ΔU_o, ΔS_o, and ΔC_o are the change in energy, entropy, and heat capacity related to the dissociation of a protein from a fibril computed at temperature T_o. The temperature dependence of ΔF from our simulations is shown in Fig. 4 and the best fit of this dependence to Eq. 6 using T_o = 0.15 gives ΔU_o = 0.740 ± 0.006, ΔS_o = 1.22 ± 0.03, and ΔC_o = −4.29 ± 0.14. While our model does not have enough detail to account for the magnitude and sign of these quantities in real proteins, it is interesting to observe that the free-energy is dominated by ΔU_o close to T_o, i.e., ΔU_o ≫ T_oΔS_o. This behavior is expected since fibrils are highly stable, i.e., more stable than native protein conformations [52], and internal energy (or enthalpy) favors the fibrillar state while entropy opposes it [51].

FIG. 4.

Dependence of the free-energy ΔF to dissociate a protein from a fibril on temperature. The best fit of the data point to Eq. 6 is shown.

In Eq. 6, ΔC_o which is related to the curvature of ΔF is expected to be small (close to zero) for amyloid fibrils [51] on the basis that the stability of these structures is not strongly dependent on temperature. This justifies the use of van’t Hoff equation:

$$ln{K}_d=-\frac{\mathrm{\Delta }{U}_o}{k_{b}T}+\frac{\mathrm{\Delta }{S}_o}{k_b}$$ (7)

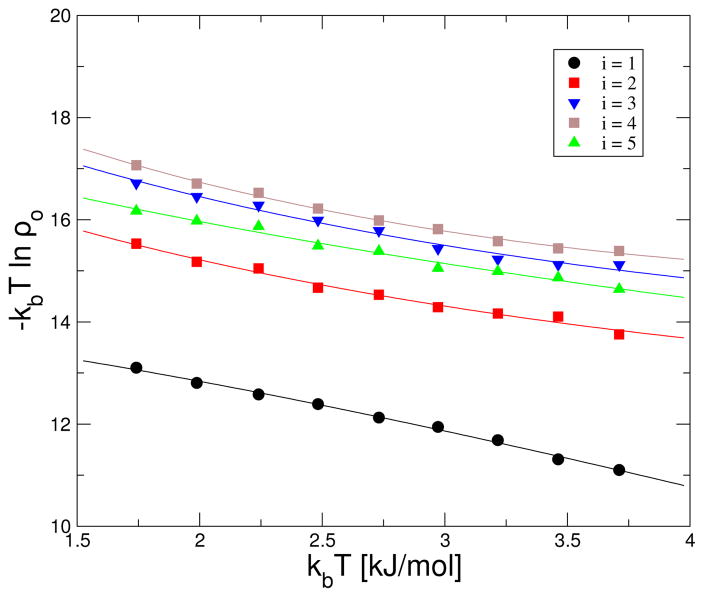
to study amyloid fibrils as it can be derived from Eq. 6 in the limit $\mathrm{\Delta }{U}_o-T\mathrm{\Delta }{S}_o\gg \mathrm{\Delta }{C}_o\left[(T-T_o)-Tlog\left(\frac{T}{T_o}\right)\right]$. According, Eq. 7 has recently been used to study the honeycomb-peptide lattice model of fibril formation [41]. In this model, peptides are represented by hexagons in a two-dimensional triangular lattice which can bind to each other along a straight line to form a β-sheet. Also, stacking of β-sheets account for fibrils with different thickness. Here, we show that despite the small value of ΔC_o for the honeycomb lattice model, this quantity can be computed for amyloid fibrils. Symbols in Fig. 5 are results from Fig. 6b of reference [41] where i represents the thickness of the fibril, i.e., the number of β-sheet layers in the fibril. Results in reference [41] were obtained from Monte Carlo simulations. In particular, an initial fibril with fixed thickness and isolated peptides in solution (i.e., honeycombs) were placed in the simulation box. Allowed Monte Carlo moves were translation and rotation of peptides. Depending on the initial concentration of peptides, the fibril elongated or shrunk until a residual concentration of peptides (i.e., ρ_o in Fig. 6) in solution was reached. Lines in this figure are fits to Eq. 6 using T_o = 2 kJ/mol and ρ_s = 1. Quantities obtained from these fits, i.e., ΔU_o, ΔS_o, and ΔC_o, are shown in Table 1. ΔU_o and ΔS_o increase with the thickness i of the fibril as more bonds need to break to dissociate peptides accounting for a greater dissociation entropy. ΔC_o which is positive for i = 1 (i.e., ΔC_o =0.36 kJ/mol/K) becomes increasingly more negative with increasing i implying that “thicker” fibrils are more stable to both high and low temperatures. In the honeycomb model, an increase in the thickess of the fibrils (i.e., an increase in i) accounts for more hydrophobic interactions between side chains. Accordingly, this interaction was shown to be responsible for the dependence of ΔU_o on i [41] and it can also be expected to account for changes in ΔC_o in the model.

FIG. 5.

Dependence of ΔF on temperature for the honeycomb peptide lattice model of fibril formation [41]. Lines correspond to best fit of the data point to Eq. 6.

TABLE I.

Changes in internal energy ΔU_o, entropy ΔS_o, and heat capacity ΔC_o obtained from fits in Fig. 5 using T_o=2 kJ/mol. Errors were obtained from analysis of the fitting

i	ΔUo kJ/mol	ΔSo kJ/mol/K	ΔCo kJ/mol/K
1	14.62 ± 0.16	0.89 ± 0.07	0.36 ± 0.23
2	17.37 ± 0.26	1.08 ± 0.12	−0.79 ± 0.32
3	17.79 ± 0.25	0.91 ± 0.11	−0.42 ± 0.38
4	18.75 ± 0.30	1.15 ± 0.14	−0.90 ± 0.45
5	19.15 ± 0.15	1.21 ± 0.06	−1.16 ± 0.22

CONCLUSION

In conclusion, we provide computational proof of principle that fibrils can exist in equilibrium with proteins dissolved in solution and this equilibrium can be used to compute free-energies ΔF to dissociate a protein [40]. We show that conditions of density accounting for different fibril growth rates can lead to the same ΔF and studies of the temperature dependence of ΔF can be used to extract thermodynamic quantities of the system. These quantities remain mostly unknown but they have the potential to provide important insights into molecular mechanisms underlying fibril stability. For example, compensation between ΔH_o and ΔS_o in protein folding provides rationalization for the marginal stability of the native state [53]. This compensation is being explored in strategies to design drugs that target protein conformations [54, 55]. Thus, understanding enthalpy-entropy compensations in fibrils may be valuable to design more specific drugs for amyloid diseases. Also, ΔC_o for protein unfolding depends linearly on the number of non-polar residues in the protein core [15]. It provides, therefore, insights into the position of non-polar amino acids in the native state. Similarly, if ΔC_o for fibrils is found to be related to the position of residues, it may be used to complement other techniques to resolve the structure of fibrils. ΔC_o may also be used to predict the stability of fibrils as a function of temperature [56]. Therefore, measurements of thermodynamic quantities will be a valuable addition to our understanding of amyloid fibrils.