Collaborative targeted maximum likelihood estimation for variable importance measure: Illustration for functional outcome prediction in mild traumatic brain injuries

Abstract

Standard statistical practice used for determining the relative importance of competing causes of disease typically relies on ad hoc methods, often byproducts of machine learning procedures (stepwise regression, random forest, etc.). Causal inference framework and data-adaptive methods may help to tailor parameters to match the clinical question and free one from arbitrary modeling assumptions. Our focus is on implementations of such semiparametric methods for a variable importance measure (VIM). We propose a fully automated procedure for VIM based on collaborative targeted maximum likelihood estimation (cTMLE), a method that optimizes the estimate of an association in the presence of potentially numerous competing causes. We applied the approach to data collected from traumatic brain injury patients, specifically a prospective, observational study including three US Level-1 trauma centers. The primary outcome was a disability score (Glasgow Outcome Scale – Extended (GOSE)) collected three months post-injury. We identified clinically important predictors among a set of risk factors using a variable importance analysis based on targeted maximum likelihood estimators (TMLE) and on cTMLE. Via a parametric bootstrap, we demonstrate that the latter procedure has the potential for robust automated estimation of variable importance measures based upon machine-learning algorithms. The cTMLE estimator was associated with substantially less positivity bias as compared to TMLE and larger coverage of the 95% CI. This study confirms the power of an automated cTMLE procedure that can target model selection via machine learning to estimate VIMs in complicated, high-dimensional data.

1 Introduction

Variable importance measures (VIM) are used to rank the importance of each of a set of explanatory variables (e.g. competing causes) in predicting an outcome. Standard estimation methods rely on ad hoc techniques such as multivariate regressions and associated stepwise procedures,¹ penalized regression (e.g. lasso²), recursive partitioning methods³ or random forest.⁴ Most of these methods are constrained by assuming parametric models, while others such as the random forest produce VIM that are not typically robust nor directly interpretable by clinicians. Moreover, none of these methods is “targeted” to estimate specifically variable importance, but such importance measures are simply byproducts of a prediction algorithm. The approach we advocate defines VIM by analogous causal parameters, such as the average treatment effect (ATE), and then estimates this parameter for each variable separately.⁵ Under a set of causal assumptions, this approach has the virtue of estimating causal variable importance rather than associations. In addition, it offers the possibility to use data-adaptive machine learning methods for the relevant prediction models.

Targeted maximum likelihood estimation (TMLE) is a general multistep procedure to produce substitution estimators with robust inference and optimal asymptotic properties.⁵ TMLE estimates for variable importance analysis tend to be stable at large sample sizes.⁶ However, if there are practical positivity violations (that is, for some sets of individuals defined by values of covariates, there is little to no experimentation in the variable of interest⁷), TMLE performance can be dismal. We hypothesize that collaborative targeted maximum likelihood estimation (cTMLE), which is an important modification of the TMLE procedure particularly well-suited to finite samples, might help to overcome this problem and thus provide a true automated machine for variable importance.^8–10 cTMLE, for each variable of interest (one at a time), automatically selects the set of adjustment variables using appropriate dimension reductions, so that the bias-variance trade-off for estimating variable importance is optimal.¹¹ The purpose of our study was to evaluate the performance of cTMLE for analyzing high-dimensional data and return a ranked list of variable importance estimates with associated robust inference. For this purpose, we analyzed a prospectively collected dataset of patients suffering from traumatic brain injury (TBI),¹² with the goal of finding the most important variables among pre-injury, injury-related factors, routine clinical, biological and radiological factors, to predict global functional recovery, as measured by the Glasgow Outcome Scale – Extended (GOSE) disability instrument,¹³ following mild TBI.

2 Variable importance measure

The goal of the methodology is to define variable importance as a parameter that can be estimated data-adaptively, but maintains both relevant clinical interpretations, and also desirable asymptotic statistical properties. Thus, we start with discussing formalities regarding the data-generating model and definitions of our proposed VIM. Then, we discuss straightforward substitution methods, as well as important modifications of these (TMLE and cTMLE) resulting in a fully automated, data-adaptive (machine learning) procedure.

2.1 Defining a variable importance measure as a substitution estimator

Consider our data to be (Y, X), where Y is the outcome and X is a vector of predictors, X=X₁,.…,X_p. Start by defining $X_j^{\ast }=I(X_j\in S_j)$ and X_−j =(X₁, X₂,…, X_j−1, X_j+1,…, X_p) that is $X_j^{\ast }$ is the indicator that the variable X_j in some subset S_j (for which we are willing to estimate the VIM) and X_−j simply includes all the remaining covariates in their original form. Note that in the case of a model that defines a time-ordering $(X_{-j}\to X_j^{\ast }\to Y)$, then the VIM based on adjustment association of $X_j^{\ast }$ and Y has particular causal interpretation.¹⁴

We define our VIM parameter to be

$$VI{M}_j=E_{X-j}\left\{E\left(Y|X_j^{\ast }=1,X_{-j}\right)-E\left(Y|X_j^{\ast }=0,X_{-j}\right)\right\}$$ (1)

Note that if one assumes the above time ordering, along with other assumptions (e.g. positivity), equation (1) identifies the causal parameter E(Y(1)−Y(0)), where Y(a) is the so-called counterfactual outcome had everyone in the population been set to $X_j^{\ast }=a$. Note that if some of the X_-j’s precede $X_j^{\ast }$, whereas others are after, then equation (1) might still identify a causal parameter, but a more complicated one. Given we are not asserting a time ordering among the X’s, we do not emphasize the correspondence with causal effect estimation, but the VIM above is still an interesting variable importance parameter, which can be identified in a nonparametric model, that is, without constraints on how we estimate the regression of Y versus X.

If ${\widehat{Q}}_j(X_j^{\ast },X_{-j})=\widehat{E}(Y|X_j^{\ast },X_{-j}.)$ is the estimated regression of Y versus the covariates, then a simple substitution estimator is defined as

$$V\widehat{I}{M}_j=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Q}}_j(1,X_{-j,i})-{\widehat{Q}}_j(0,X_{-j,i})}$$ (2)

with subscript i referring to the observations and j refers to the predictor.

To make the analogy to standard methods, such as simple linear regression of Y versus X, note that if $Q_j(X_j^{\ast },X_{-j})={\beta }_0+\alpha .X_j^{\ast }+{\beta }_1.X_1+\cdots$, then VIM_j =α. Our goal is to avoid such biased parametric assumptions, use procedures much more powerful for fitting the data, but still result in a relatively interpretable VIM for which the estimation can be automated. In the next section, we discuss an optimal data-adaptive method for fitting the regression model Q_j.

2.2 Super learner

The algorithm used to estimate the regression plugged into equation (2) should be estimated based on some principles of optimality, and should be flexible enough to allow for very simple or very complex models. The Super Learner (SL) is such an algorithm, which has been proposed as a method to select an optimal regression algorithm from among a set of candidates (or library) using cross-validation.^15–17 We used the SL (available in R¹⁸) with 10 splits for the V-fold cross-validation step and the following parametric and non-parametric algorithms were included in the Super Learner library: logistic regression both including only main terms for each covariate and also including interaction terms¹⁹; Stepwise logistic regression using a variable selection procedure based on the Akaike Information Criterion²⁰; Bayesian generalized linear model²¹, Random Forest⁴ and Neural Networks.²² The risks associated with the different estimators were evaluated using the cross-validated mean squared error (MSE).

The next step is to determine the importance of each variable to predicting the outcome. This is a particular challenge because although the SL has optimality properties with regards to prediction, it offers no direct way of interpreting the model to determine which variables are most important in prediction. Substitution estimators^23–25 are based on using such “black box” algorithms to predict the distribution of the outcome at different levels of the current variable of interest, while keeping the others fixed at their observed values. Specifically, the SL can be used to estimate $E(Y|X_j^{\ast }=1,X_{-j})$ and $E(Y|X_j^{\ast }=0,X_{-j})$ for each individual. Then, the difference in the mean predicted outcome at different levels of the prediction variable could be used as a summary of its independent association with the outcome as in equation (2). However, even if SL is optimal at estimating $E(Y|X_j^{\ast }=1,X_{-j})$ and $E(Y|X_j^{\ast }=0,X_{-j})$, there is no guarantee that it will be optimal at estimating the difference between the two, which is precisely our quantity of interest. This needs an additional targeting step, which may be realized by using targeted maximum likelihood estimators as detailed in the next section.

2.3 TMLE and cTMLE

The TMLE approach involves fluctuating the initial estimate of Q_j into an updated estimate Q_j*, in order to make a bias/variance tradeoff targeted towards the parameter of interest. TMLE is consistent and asymptotically normally distributed under regularity conditions, when either one of these two factors of the likelihood is correctly specified, and it is efficient if both are correctly specified.^8,9

Practically, TMLE in this context is a two-step procedure: first running an initial regression to fit $Q_j(X_j^{\ast },X_{-j})$ i.e. the expected value of the outcome given the covariate of interest (i.e. the candidate risk factor in our situation) and adjusting for all other covariates. We emphasize Super Learning for this step. The next step is an update of the initial regression by (a) getting the predicted value from the initial estimator, which will be used as an offset, (b) deriving a so-called clever covariate $h_j(X_j^{\ast },X_{-j})=\left[\frac{I(X_j^{\ast }=1)}{g_j(X_{-j})}-\frac{I(X_j^{\ast }=0)}{1-g_j(X_{-j})}\right]$ where $g(X_{-j})\equiv P(X_j^{\ast }=1|X_{-j})$ and (c) regressing the outcome against this covariate and the offset: ${\widehat{Q}}_j^{\ast }(X_j^{\ast },X_{-j})=\widehat{Q}(X_j^{\ast },X_{-j})+\widehat{\epsilon }h(X_j^{\ast },X_{-j})$ or $\mathit{\text{logit}}[{\widehat{Q}}_j^{\ast }(X_j^{\ast },X_{-j})]=\mathit{\text{logit}}[\widehat{Q}(X_j^{\ast },X_{-j})]+\widehat{\epsilon }h(X_j^{\ast },X_{-j})$ if a logistic model is fit, e.g. for a binary Y. Note that one must fit a model for g(X_−j) as well, and this can also involve Super Learning; we discuss how to automate variable selection in this model below as it can have serious consequences for efficiency in finite samples. The TMLE estimator of the parameter of interest is then estimated, just as equation (2), but with the updated regression of Y versus the covariates

$$V\widehat{I}{M}_j^{\mathit{\text{TMLE}}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Q}}_j^{\ast }(1-X_{-j,i})-{\widehat{Q}}_j^{\ast }(0,X_{-j,i})}$$ (3)

In the situation of variable importance measure, this parameter must be estimated for each variable in the subset $X_j^{\ast }$ of X. Hence, a separate procedure/estimate is conducted for each $X_j^{\ast }$, considering this $X_j^{\ast }$ as the exposure and the others X_−j as covariates. Standard errors are calculated using the influence curve, and the central limit theorem⁵ can be applied to derive the typical measures of uncertainty (p-values, confidence intervals, etc.).

2.4 Finite sample performance and practical positivity

If all datasets had “sufficient” sample sizes, then this TMLE for VIM results in a potentially automated procedure. However, for such ambitious parameters (particularly when there are many covariates), the machine learning fits of the required regressions can result in TMLE estimators that behave poorly in finite samples (significant bias, non-normal sampling distributions, etc). One of the most important causes of non-robust performance is practical violation of the positivity assumption.⁷ The positivity assumption requires that all possible combinations of covariates X_−j must be observable for all levels of $X_j^{\ast }$; concisely, it is required that $0<g_j(X_{-j})\equiv P(X_j^{\ast }=1|X_{-j})<1$ over the distribution of X_−j. In the situation of finite samples, and especially when the set of $X_j^{\ast }$ is large, there is likely to be some “practical” positivity assumption, meaning that in the sample, there are groups of subjects defined by close values of X_−j, that have little to no experimentation in the covariate of interest, $X_j^{\ast }$. Given that we are estimating the VIM separately for each variable of interest, it is likely that, for some of them, the practical positivity assumption will not hold. In this case, the updating step of the TMLE procedure, which relies on estimating g_j to calculate the clever covariate, may fail to produce consistent, robust estimators. Note that this would be true for alternative estimators based on g_j, i.e. inverse probability of treatment weighted (IPTW) and the doubly robust versions (DR-IPTW^26,27). Thus, one would need a procedure that automatically adjusts the “complexity” of the estimator to optimize the variance-bias trade-off, based upon the information in the data for the parameter of interest.

The best bias/variance tradeoff for g_j might not coincide with the optimal final estimate especially when X is of high dimension. Thus, there is a need for an automated procedure that would tailor the fit of g_j to optimize the final estimate. Such a procedure has only recently been proposed and is called collaborative targeted maximum likelihood estimation (cTMLE).¹⁰

The cTMLE is an extension of the TMLE methodology.^10,11 It also involves a targeted model selection step for the nuisance parameter portion of the likelihood g_j in order to get the most efficient estimate of variable importance. A cTMLE estimator is constructed by building a family of candidate estimators, then choosing the “best” among them, using the cross-validated risk of the resulting augmented model ${\widehat{Q}}_j^{\ast }$. The template for construction of the cTMLE estimator is described in detail in Chapter 19 of Van der Laan and Rose.⁵ This procedure creates an entire sequence of candidate TMLE based on an initial estimate for $Q_j(X_j^{\ast },X_{-j})$ coupled with a succession of increasingly non-parametric estimates for $g(X_{-j})\equiv P(X_j^{\ast }|X_{-j})$. The evolution with TMLE where g_j may be estimated data-adaptively is that cTMLE estimates of g_j are constructed based on a loss function for the TMLE of the relevant factor Q_j that uses the nuisance parameter to carry out the fluctuation, instead of a loss function for the nuisance parameter itself. Likelihood-based cross-validation is used to select the best estimator among all candidate TMLE estimators of Q_j in this sequence. Theoretical results have demonstrated that the cTMLE is consistent and asymptotically normally distributed even when Q_j and g_j are both misspecified, provided that g_j solves a specified score equation implied by the difference between the Q_j and the true Q_j.^10,11

In summary, combining an initial SL fit with cTMLE results in a “machine” that may be used for robust estimation of our VIM parameter. Similarly to TMLE, inference is also based on the influence curve and the confidence intervals are constructed by applying the central limit theorem. In this case, one not only does not need re-sampling based inference procedures such as the bootstrap (which can dampen the performance of such an intensive data-adaptive procedure), but in fact conditions for the consistency of bootstrap are much more restrictive and often fails in practice. Thus, deriving inference, given it only relies on calculation of the influence curve once after estimation is completed, is essentially computationally free.

In our example, the statistical analysis consisted of examining the relative influence of each explanatory variable on the GOSE at three months (i.e. variable importance measure). For both Q and g_j, we used Super Learner.¹⁵ Such predictions were used to derive the TMLE and the cTMLE estimators for variable importance measure. All analyses were run on R 2.15.2 statistical software running on a Mac OsX platform (The R Foundation for Statistical Computing, Vienna, Austria), using the packages Super Learner,¹⁸ cvAUC,²⁸ and TMLE.²⁹

2.5 Estimator performance

We defined the bias in the VIM estimator as Bias(VIM_j) = E(VIM_j) − VIM_0,j where VIM_0,j is the true value of the particular variable importance measure. Bias in an estimator can arise due to a range of causes. Among them, we focused on the bias related to the positivity assumption violation (positivity bias). Our objective was to quantify the positivity bias associated with each estimator (TMLE and cTMLE).

The variables for which the TMLE was potentially biased were identified by comparing the TMLE and cTMLE estimates, any important discrepancy between the two estimates indicating that one of the two estimators has to be biased. For those variables with strong differences, we quantified the extend to which such difference could be explained by the positivity bias. To quantify the bias related to positivity violation, we used a simulation procedure proposed by Petersen et al.⁷ that relies on parametric bootstrap. This procedure does not rely on some arbitrary data-generating distribution but instead aims at recreating samples from a distribution as close as possible to the actual data-generating distribution. The bias as quantified by the parametric bootstrap can be written as Bias(VIM_j) = E_Pboot(VIM_b,j) − VIM_j repeated where ${\widehat{P}}_{\mathit{\text{boot}}}$ is the bootstrap distribution (defined by draws from empirical distribution), and VIM_b,j are the estimates from each of the b = 1,…,B bootstrap samples. The candidate estimators (in our case, the TMLE and the cTMLE estimators) are applied to each bootstrapped dataset. In the bootstrap samples, the bias is defined as the difference between the mean of the resulting estimates across datasets and the true parameter value for the bootstrap data generating distribution. Specifically, one first estimates both Q and g from the data as discussed above. Then, using these estimates, one generates new random data sets in same way the original data set was assembled (e.g. random draws). By using the same estimation procedure as in the original sample, one can examine the sampling distribution of competing estimators in a world where one treats the estimated Q and g as the true distributions. Given that one estimates the models in these random parametric bootstrap draws assuming the same algorithms used to construct the “true” distribution, the estimators are guaranteed to be consistent unless g fails to satisfy the positivity assumption. As a result, the parametric bootstrap provides an optimistic estimate of finite sample bias, in which bias due to model misspecification other than truncation is eliminated.

Bootstrap-based simulations were also used to compute the coverage of the 95% confidence intervals (95% CI) for each estimator, defined as the proportion of time the confidence interval contained the true value set by simulation. In addition, in order to quantify to extend to which the coverage was affected by the bias in the point estimates rather than the variance estimator performance, we computed the bias-adjusted coverage of the 95% CI as the area under N(0,1) density between $-1.96-{\widehat{b}}_n$ and $1.96-{\widehat{b}}_n$, with b_n being the normalized bias defined as $b_n=\frac{\mathit{\text{Bias}}(VI{M}_j)}{SE(VI{M}_j)}$, that is the estimated bias divided by the standard error.

In order to explore whether the benefit associated with cTMLE in case of positivity violation was dependent of the sample size, we reran the parametric bootstrap to simulated new datasets with decreasing sample size (n = 1000; 500; 100; 50). The positivity bias was recalculated for each sample size. Because such simulations are computationally intensive, they were only performed for a single variable, the one associated with the largest positivity bias.

3 Application on TRACK-TBI data

3.1 TRACK-TBI

The Transforming Research and Clinical Knowledge in Traumatic Brain Injury Pilot (TRACK-TBI Pilot) study aimed to prospectively examine the influence of pre-injury factors, injury-related factors, and some routine clinical, biological and radiological factors on the functional outcome following TBI, as evaluated by the GOSE at three months.¹³ This study is a prospective, multicenter, observational cohort study including patients referred to the emergency department (ED) of three Level-I trauma centers in the USA (San Francisco General Hospital, University of Pittsburgh, and University Medical Center Brackenridge) for TBI. Institutional review boards of the three participating centers approved all study protocols, and all patients or their legal representatives gave written informed consent. Inclusion criteria for TRACK-TBI Pilot were acute external force trauma to the head, presentation to the ED within 24 h of injury, and sufficient indications for a clinical head CT to assess for traumatic intracranial injury using the American College of Emergency Physicians/Centers for Disease Control (ACEP/CDC) evidence-based joint practice guideline.³⁰ Exclusion criteria were pregnancy, comorbid life-threatening disease, incarceration, or serious psychiatric and neurologic disorders that would interfere with outcome assessment. Non-English speakers were not enrolled due to inability to participate in outcome assessments, which are normed and administered in English. As our analysis is focused on mild TBI, we included only patients with complete three-month GOSE, and mild TBI as defined by the clinical standard of ED admission GCS of 13 to 15. For clinical relevance, three different populations had to be considered separately: (1) the overall population (n = 365); (2) the population of patients with genetic information (n = 261); and (3) the population of patients without any PTSD six months after injury (n = 188). Thus, though a large study of its kind, the questions of interest, and numbers of variables involved, were relatively large for such modest sample sizes. Therefore, relying on data-adaptive procedures might be misleading, inspiring procedures that could adjust the estimation/inference for the available sample size.

3.2 Outcome measures and covariates

The primary outcome measure for this study was the eight-point GOSE at three months post-injury, obtained through structured interview with each participant by research assistants trained to uniformly assess the GOSE. The GOSE is a well-validated, widely employed summary assessment of global function after TBI suitable for clinical trials.¹³ Secondary outcome measures included GOSE at six months, mortality at hospital discharge and three-month outcome, as well as presence of post-traumatic stress disorder (PTSD) symptoms measured by the PTSD Checklist (civilian version, PCL-C) and classified by the Diagnostic and Statistical Manual of Mental Disorders, 4th Edition (DSM-IV) PTSD criteria at six months.³¹

The goal was to estimate VIM with potential relevant clinical interpretations for many potential competing causes of the outcome which can be categorized as (1) pre-injury factors (e.g. age, gender, medical history, prior anticoagulant drugs, psychiatric history, previous TBI, educational level, marital status, and employment status), (2) injury-related factors (e.g. trauma mechanism, PTA, loss of consciousness), (3) clinical factors (e.g. GCS, injury severity score,³² heart rate, blood pressure, oxygen saturation, and temperature), (4) biological factors (e.g. hemoglobin, platelet count, and blood glucose); and (5) radiological factors (Marshall score³³ and Rotterdam score³⁴). Information concerning some genotypic single nucleotide polymorphisms such as the ankyrin repeat and kinase domain containing 1 (ANKK1) candidate gene (rs1800497) involved in dopamine transmission of the dopamine D2 receptor and the Apolipoprotein E (ApoE) gene (rs7412, rs429358) was available for 270 patients. The variables explored as potential risk factors had to be dichotomized as follows: Marshall grade = 1 vs. >1; Rotterdam grade ≤2 vs. >2; GCS = 15 vs. <15; systolic blood pressure <90 mmHg vs. ≥90 mmHg; heart rate <100 bpm vs. ≥100 bpm; respiratory rate >18 cpm vs. ≤18 cpm; oxygen saturation <94% vs. ≥94%; ApoE polymorphism E2/E4, E3/E4, E4/E4 vs. others; and ANKK1 polymorphism T/T vs. others.

3.3 Results

A total of 485 mild TBI patients have been included in the TRACK-TBI Pilot study, of whom 125 patients with missing three-month GOSE were excluded from the analysis. The remaining 365 patients were included in the analysis (Figure 1): 107(40.1%) were females and the median age was 44.^27–59 Clinical, demographic, and socioeconomic characteristics of study participants are described in the Table 1. Most patients (363, 99%) were alive at hospital discharge (Table 1). All these 363 patients were alive at three months post-injury and their median GOSE was 7.^6–8 The presence of PTSD was assessed in 256 patients. Sixty-eight (27% of the 256; 19% of the overall cohort) had symptoms of PTSD at six months after injury. The three-month GOSE in patients diagnosed with a PTSD was lower than the GOSE in patients without PTSD [6 (5; 7) vs. 7(7; 8), p < 0.001].

Figure 1.

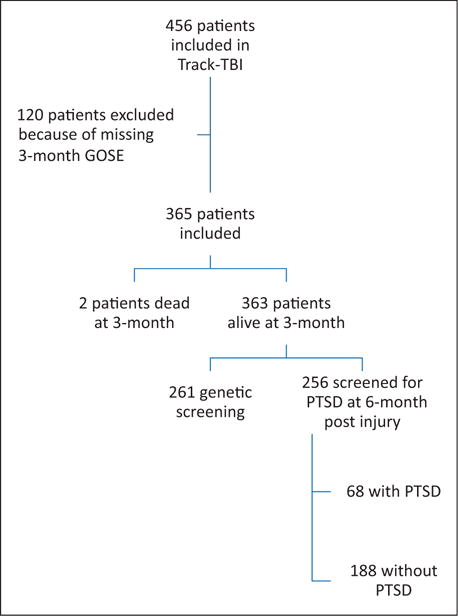
Flowchart.

Table 1.

Clinical, demographic, and socioeconomic characteristics of the 365 study participants.

Characteristic	Value
Age (years)	44 (27–59)
Gender (female)	107 (40%)
Race
Caucasian	302 (83%)
African-American Black	32 (8%)
Asian	18 (5%)
Other	11 (3%)
Unknown	2 (1%)
LOC	245 (67%)
PTA	226 (65%)
Employment status at time of TBI (active)	200 (55%)
Marital Status at time of TBI (married/living together)	125 (34%)
Prior TBI	186 (51%)
History of psychiatric disease	115 (31%)
Prior anticoagulant use	54 (15%)
GCS	15 (14–15)
ISS	9 (0–17)
Heart rate (bpm)	86 (76–100)
Systolic blood pressure (mmHg)	138 (127–155)
Respiratory rate (cpm)	18 (16–19)
Oxygen saturation (%)	99 (97–100)
Body temperature (°C)	36.6 (36.1–36.8)
Hemoglobin (g/dl)	14 (13–14.9)
Platelet count (×1000/mm3)	242 (193–301)
Prothrombine time (s)	13.6 (12.9–14.2)
Blood glucose (g/L)	1.1 (1.0–1.3)
CT-Marshall category	213/132/8/4/6/2
CT-Rotterdam category	5/271/76/8/3/2
GOSE at three months post-injury	6/7/9/42/63/117/121
GOSE at six months post-injury	8/4/4/37/53/83/107
PTSD at six months post injury	68 (19%)
Three-month survival	363 (99%)

LOC: loss of consciousness; PTA: post-traumatic amnesia; GCS: Glasgow Coma Scale; ISS: injury severity score.

3.4 cTMLE-based variable importance measure

Based on cTMLE, two characteristics concerning patients’ medical history were associated with a poor functional outcome (Table 2): history of hepatic disease [VIM: −0.176 (−0.215; −0.136), p < 0.001] and history of psychiatric disease [VIM = −0.103 (−0.156; −0.050), p < 0.001]. Unemployment at the time of trauma was also associated with a lower value of the three-month post-injury GOSE [VIM = −0.066 (−0.113; −0.019), p = 0.010]. Being married or living together at the time of injury associated with a better outcome [VIM = 0.040 (−0.005; 0.084), p = 0.080]. At hospital admission, a tachycardia as defined by a heart rate >100 bpm [VIM = −0.045 (−0.083; −0.006), p < 0.001] was associated with the three-month post-injury GOSE. CT scan abnormalities, as evaluated by the Marshall [VIM = −0.107 (−0.153; −0.062), p < 0.001] and the Rotterdam [VIM = −0.081 (−0.127; −0.036), p < 0.001] classifications, were found to be significantly associated with the three-month post-injury GOSE.

Table 2.

Variable importance measure (VIM; equation (1)) results based on cTMLE.

Characteristic	VIM (95% CI)
History of hepatic disease	−0.176 (−0.215; −0.136)a
History of psychiatric disease	−0.103 (−0.156; −0.050)a
Prior TBI	−0.037 (−0.078; 0.003)
Prior treatment with anticoagulants	0.024 (−0.024; 0.072)
Employment status at time of TBI (inactive vs. active)	−0.066 (−0.113; −0.019)a
Marital Status at time of TBI (Married/living together vs. alone)	0.040 (−0.005; 0.084)
Hypotension (SBP < 90 mmHg)	−0.062 (−0.131; 0.070)
Tachycardia (HR > 100 bpm)	−0.045 (−0.083; −0.006)a
Tachypnea (RR > 18 cpm)	−0.020 (−0.069; 0.028)
Hypoxia (SpO2 < 94%)	0.010 (−0.018; 0.037)
GCS (<15 vs. 15)	−0.017 (−0.065; 0.031)
Positive drug screening	−0.009 (−0.085; 0.067)
Rotterdam classification (>2 vs. ≤2)	−0.081 (−0.127; −0.036)a
Marshall classification (>1 vs. 1)	−0.107 (−0.153; −0.062) a
ANKK1 polymorphism: T/T vs. others	−0.467 (−0.879; −0.056)a
ApoE polymorphism: E2/E4, E3/E4, E4/E4 vs. others	0.001 (−0.307; 0.308)

Note: The estimates are adjusted for all measures confoundings and obtained using collaborative targeted maximum likelihood estimation; 95% CI: 95% confidence intervals; Apo E: Apolipoprotein E; ENT: ear, nose, throat.

^aStatistical significance (p<0.05).

The same analysis was performed in the subsample of patients without PTSD at six months post-injury. This led to similar results for the Marshall grade [VIM = −0.205 (−0.275; −0.135), p < 0.001], the Rotterdam grade [VIM = −0.150 (−0.198; −0.103), p < 0.001] and the history of hepatic disease [VIM = −0.107 (−0.162; −0.052), p < 0.001], which remained the most important predictors for the three-month post-injury GOSE. However, when only considering the patients without PTSD at six months post-injury, the impact of marriage status [VIM 0.017 (−0.038; 0.071), p = 0.545], employment status [VIM = −0.063 (−0.130; 0.003), p = 0.063] as well as psychiatric history [VIM = −0.045 (−0.114; 0.024), p = 0.200) on the three-month GOSE were no longer significant.

Eventually, of the 270 patients with genetic information, the ANKK1 polymorphism T/T was found to be negatively associated with the three-month post-injury GOSE [VIM = −0.467 (−0.879; −0.056), p = 0.026]. No significant association was found between the polymorphism of the ApoE gene and the neurological outcome [VIM = 0.001 (−0.307; 0.308), p = 0.997) (Table 2).

3.5 Parametric bootstrap

The relative contribution of each variable on the outcome was also evaluated using TMLE. Four variables for which the TMLE and the cTMLE estimates substantially differed were considered at risk of positivity assumption violation: gender, history of musculoskeletal disease, of pulmonary disease and hypotension at hospital admission (Table 3).

Table 3.

Variables with high suspicion of positivity violation.

Characteristic	VIM(TMLE)	VIM(cTMLE)
History of musculoskeletal disease	−0.156 (−0.194; −0.118)	−0.031 (−0.078; 0.016)
History of pulmonary disease	0.009 (−0.021; 0.039)	0.045 (−0.008; 0.097)
Hypotension (SBP < 90 mmHg)	−0.323 (−0.372; −0.272)	−0.062 (−0.131; 0.070)
Gender	0.123 (0.086; 0.159)	0.035 (−0.014; 0.084)

3.6 Positivity bias

Table 4 summarizes the bias related to positivity violation for the four variables as determined by the parametric bootstrap as described above (again, we note since the data-generating distribution in this case is known, we can directly determine the true value of the parameter). As expected, the variable for which the difference in the estimates was the most pronounced is the one where the TMLE was associated with the largest positivity bias: history of pulmonary disease (positivity bias = 0.369). The cTMLE estimator was associated with substantially less positivity bias as compared to TMLE. For instance, the positivity bias decreased from 0.369 to 0.001 for history of pulmonary disease.

Table 4.

Experimental treatment assignment-related bias and 95% CI coverage associated with TMLE and cTMLE estimators.

Characteristic	TMLE		cTMLE
	Positivity bias	Coverage	Positivity bias	Coverage
History of musculoskeletal disease	0.020	0.262	0.005	0.782
History of pulmonary disease	0.369	0.055	0.001	0.766
Hypotension (SBP < 90 mmHg)	0.026	0.609	0.005	0.833
Gender	0.096	0.135	0.008	0.838

3.7 Coverage of the 95% CI

Consistently, the variable with the largest positivity bias was also associated with the smallest 95% CI coverage (history of pulmonary disease: 0.055) (Table 4). As expected, the positivity bias reduction achieved with cTMLE lead to larger coverage of the 95% CI (history of pulmonary disease: 0.766). However, it was still below the nominal value of 95%. To assess whether this lack of coverage was due to the influence curve-based variance estimator and/or to the remaining amount of bias, we computed the bias corrected coverage as describe above. As reported in Table 5, for the four variables, bias correction lead to coverage values close to the expected 95%, suggesting that the influence curve based variance estimator for cTMLE is valid in this context. In any case, the automated variable selection method and use of cross-validation for selecting model for clever covariate shows much better performance in estimation and inference.

Table 5.

95% CI coverage and bias-corrected 95%CI coverage for cTMLE estimates.

	Coverage	Bias corrected Coverage
Gender	0.838	0.946
Musculoskeletal disease	0.782	0.947
Pulmonary disease	0.766	0.949
Hypotension	0.833	0.947

4 Discussion

Based on a prospectively collected dataset of patients suffering from TBI (12), we were able to show that TMLE for variable importance measure is associated with substantial bias when the positivity assumption is not fully fulfilled. In this context, the use of cTMLE was associated with substantial bias reduction and better coverage.

These results are in line with the underlying theory. Indeed, the targeting step of TMLE relies on a clever covariate, which is a function of the inverse of the propensity score. Therefore, when the estimated propensity score is close to zero or one (i.e. when the practical positivity assumption is nearly violated), the clever covariate can blow up and cause great instability in the targeting step. Hence, despite nice asymptotic properties such as consistency, linearity and double robustness, TMLE estimators may be biased in finite samples when the positivity assumption is nearly violated. For five variables, we were able to show using parametric bootstrap that the positivity-related bias was substantial, resulting in coverage of the 95% CI close to zero. cTMLE represents a further advance over standard TMLE.¹⁰ Previous work by Gruber et al.^10,11 have demonstrated that the collaborative targeted maximum likelihood estimator is asymptotically linear and consistent even when Q and g are both misspecified, providing that g solves a specified score equation implied by the difference between the Q and the true Q₀. This marks an improvement over the current definition of double robustness in the estimating equation literature, and specifically over standard targeted maximum likelihood estimators. Our results emphasize that this properties are particularly interesting when dealing with causal parameters and positivity issues. In this situation, likelihood-based cross-validation targeting the best estimator among all candidate TMLE estimators of Q₀ guaranties to avoid the inclusion in the model for g, any explanatory variable for which there is no contrast in A. Hence, choosing the best g, i.e. the one associated with the most consistent estimate for our parameter of interest, will in turn limit the impact of positivity violation. We were able to confirm these theoretical results by quantifying the positivity bias using parametric bootstrap. Consistently, cTMLE was less prone to positivity bias than TMLE.

These results were reinforced by the clinical findings obtained with cTMLE, which are in line with the known pathophysiology and consistent with those previously published concerning the prognosis of mild TBI patients. We are able to identify several risk factors associated with the three-month post-injury GOSE. First, certain components of the patient medical history may contribute to functional disability at three months post-injury. It is indeed not surprising to find that psychiatric history is associated with a poorer three-month GOSE. Consistently with our results, Ponsford et al.³⁵ report that prior history of psychiatric disorders is associated with post-concussive symptoms three months after mild TBI. Interestingly, history of hepatic disease was found to be associated with worse prognosis. This may be, at least partially, explained by the coagulation abnormalities frequently associated with liver diseases and the higher incidence of liver disease in chronic alcoholism. We also looked at the relationship between the three-month post-injury GOSE and the genotypic polymorphisms ANKK1 (rs1800497) and ApoE. The T allele of rs1800497 has indeed been implicated in addiction disorders and has also been reported to be a risk factor for depression, childhood behavior and learning problems.³⁶ Interestingly, veterans with PTSD who carried the T allele had more symptoms of anxiety, depression and social dysfunction than C/C homozygotes.³⁷

Some limitations should be highlighted. First, the cTMLE-based VIM as implemented in the present study required to dichotomize the covariates. However, some extensions have been developed to pursue VIM for continuous variables.^38,39 Second, although derived from causal inference, the parameters estimated for VIM using TMLE or cTMLE may only be interpreted causal if the usual underlying causal assumptions hold. In the context of VIM, this may be true for some variables but not for others. Third, despite substantial decrease in positivity bias with cTMLE, the coverage of the 95% confidence intervals were still far from the nominal value in case of strong positivity bias. Finally, it should be emphasized that computational feasibility may sometimes be an issue with cTMLE. Multicore parallel computing is strongly recommended to speed up the procedure when analyzing large dataset and wealthy Super Learner library.

This study confirms that cTMLE holds promise as a fully automated procedure that can harness the power of any machine learning algorithm, to return estimates of variable importance optimized for specific clinically relevant parameters. It has the power to reduce the arbitrariness of typical statistical exercises with high dimensional data, while not sacrificing the ability to target certain associations. Most importantly, these estimates will all derived from an automated procedure, a variable importance machine.