Flat building blocks for flat silicene

Abstract

Silicene is the silicon equivalent of graphene, which is composed of a honeycomb carbon structure with one atom thickness and has attractive characteristics of a perfect two-dimensional π-conjugated sheet. However, unlike flat and highly stable graphene, silicene is relatively sticky and thus unstable due to its puckered or crinkled structure. Flatness is important for stability, and to obtain perfect π-conjugation, electron-donating atoms and molecules should not interact with the π electrons. The structural differences between silicene and graphene result from the differences in their building blocks, flat benzene and chair-form hexasilabenzene. It is crucial to design flat building blocks for silicene with no interactions between the electron donor and π-orbitals. Here, we report the successful design of such building blocks with the aid of density functional theory calculations. Our fundamental concept is to attach substituents that have sp-hybrid orbitals and act as electron donors in a manner that it does not interact with the π orbitals. The honeycomb silicon molecule with BeH at the edge designed according to our concept, clearly shows the same structural, charge distribution and molecular orbital characteristics as the corresponding carbon-based molecule.

Introduction

Silicene is the silicon equivalent of graphene, which is a famous material composed of a honeycomb layer of carbon just one atom thick^1–3. If applied to electronic devices, these silicene layers would enable the semiconductor industry to achieve ultimate miniaturization^{4, 5}. However, unlike flat and highly stable graphene (Fig. 1a), silicene is relatively sticky and unstable due to its puckered or crinkled structure (Fig. 1b)⁶. To produce silicene, the hot vapor of silicon atoms is condensed onto crystalline blocks of silver^7–16 or other materials^17–19. However, the substrate can affect the π conjugated system. Recent twisted silicene multilayers have proved the two-dimensional (2D) nature of silicene and was a major progress toward flat silicene²⁰, but interlayer interactions still perturb the electronic structure of 2D materials.

Figure 1.

2D sheets of carbon and silicon and their building blocks. Graphene (a), silicene (b), benzene and a C₆ cluster (c), and hexasilabenzene and a Si₆ dianion cluster (d).

The building blocks of graphene are benzene and/or C₆ clusters (Fig. 1c), both of which are flat^{21, 22}. In contrast, hexasilabenzene, which is a building block of silicene, is not flat but instead has a chair form (Fig. 1d)²³. Benzene is an archetypical aromatic hexagon composed of carbon with delocalized π electrons. The 2D aromaticity of flat monocyclic systems is governed by the Hückel 4 N + 2 rule, where N is the number of π electrons. The outstanding properties of C₆ clusters include double aromaticity²⁴ with an orthogonal Hückel framework (an out-of-plane p_π orbital and an in-plane radial-type orbital contributing to σ-aromaticity in a single molecule). We previously discovered a similar flat silicon hexagon with double aromaticity, i.e., the dianion of the Si₆ cluster (Fig. 1d)^{25, 26}. This finding encouraged us to design the present flat silicene building blocks using electron-donating substituents. A pioneering work recently reported the formation of flat silicene via doping with calcium as an electron donor²⁷, and attempts to make flat hexasilabenzene and Si₆ clusters were carried out earlier with Zintl anions^{28, 29}. In either case, the Si₆ hexagon is surrounded by an electron donor, creating a three-dimensional crystal but not a pure 2D crystal.

To realize a perfect and stable π-conjugated 2D sheet of silicene, the sheet must be flat and have no electron-donating atoms or molecules interacting with the π electrons. The only way to donate electrons without disturbing the out-of-plane π orbital is to modify the in-plane edges. A theoretical study of silicene molecules (large polycyclic molecules consisting of six-membered silicon rings) from Si₁₃H₉ to Si₆₀H₂₄ showed that silicene molecules with hydrogen atoms at the edge are not flat but have a low-buckled structure³⁰. This indicates that, as described above, electron-donating substituents are good candidates for the formation of flat silicene molecules and hydrogen atoms are not suitable. Although a theoretical attempt to use an electron-donating metal, such as lithium, at the in-plane edge gave the D _6h planar structure of hexasilabenzene^31–33, the lithium atoms were not attached to one silicon atom but instead attached between two adjacent silicon atoms due to the ability of silicon to form three-center bonds with lithium. Furthermore, the bicyclic chain is no longer flat when lithium is used as the electron donor but is puckered with a zigzag chain. A completely different concept is necessary for the design of a flat polycyclic molecule consisting of silicon hexagons as flat silicene building blocks. Here, we report the successful design of flat 2D molecules composed of six-membered silicon rings with modifications at the in-plane edges using density functional theory (DFT) calculations.

Results

Basic concept

Our basic concept for the design of flat polycyclic molecules consisting of silicon hexagons is to use sp-hybrid orbitals (Fig. 2b) with electron-donating ability. We first considered the differences between C-H and Si-H interactions. Notably, the energies of the interacting orbitals are different. That is, the energy difference between the H 1s and Si 3p orbital is larger than that between the H 1s and C 2p orbital. The use of a lithium 2s orbital instead of a hydrogen 1s orbital is a straightforward way to compensate for the energy difference (Fig. 2a). However, unlike hydrogen, the empty 2p orbital (Fig. 2b) of lithium interacts with the silicon 3p orbital and forms a three-center bond with two adjacent silicon atoms of the silicon ring. Eventually, we decided to use linear sp-hybrid orbitals and selected BeH as the substituent. First-year chemistry textbooks state that BeH₂ has a linear shape due to its sp-hybrid orbital. Figure 2b shows the molecular orbital of an Li atom and BeH radical for comparison. The difference between the two singly occupied molecular orbitals (SOMOs) is that the SOMO of the BeH radical points to the Si₆ ring (Fig. 2b). Silicon equivalents 1, 2, 3, 4 and 5 of benzene (6), naphthalene (7), anthracene (8), pyrene (9) and coronene (10), respectively, were selected as building blocks and substituted with BeH at the ring edge (Fig. 3).

Figure 2.

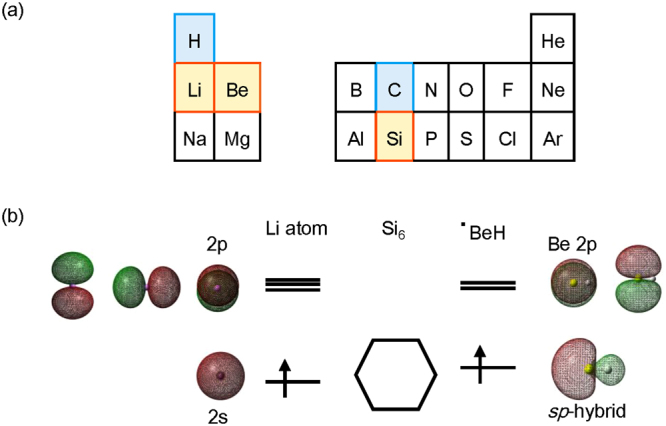
(a) The periodic table of elements H–Ar. (b) The molecular orbitals of an Li atom and BeH radical. The orbitals were calculated at the B3LYP/cc-pVTZ level and are depicted at the 0.02 isovalue.

Figure 3.

Calculated molecules. 1–5: X = Si, R = BeH; 6–10: X = C, R = H. The notation r1–r5 represents the bond length between the adjacent X atoms.

Optimized structure

The five silicon-based molecules 1–5 with BeH at the ring edge show the same structural, charge distribution and molecular orbital features as the corresponding carbon-based molecules 6–10, where BeH is used according to the above concept. All of the calculated molecules 1–10 have a flat structure as their minimum with no imaginary frequencies. Electron donation stabilizes the flat structure of the six-membered silicon ring and further provides the stable flat structure of polycyclic silicon molecules. The lowest vibrational frequency modes (ν ₁), given in Table 1, are the out-of-plane motion of the terminal BeH moiety (3) and the out-of-plane ring deformation (1, 2, 4–10), respectively. The calculated silicon-silicon bond length (2.22 to 2.28 Å) is between the silicon-silicon single and double bond length (the bond lengths of H₃Si–SiH₃ and H₂Si = SiH₂ at the B3LYP/cc-pVTZ level are 2.355 Å and 2.166 Å, respectively), which is similar to the structure of aromatic benzene having a bond length between the carbon-carbon single and double bond. The silicon-silicon bond lengths are equal in hexasilabenzene 1 due to its D _6h symmetry but differ at most by 0.06 Å in the other molecules 2–5. The carbon-based structures 6–10 show the same behavior. Benzene 6 has the same carbon-carbon bond lengths throughout the ring, while the others 7–10 have slightly different bond lengths, with the difference being at most 0.08 Å. Notably, the terminal BeH is not located between the two silicon atoms in the minimized structures of 1–5, which is markedly different from the lithium-terminated six-membered ring Si₆Li₆ ³¹.

Table 1.

Optimized geometry, charge (Q_ring), frequency (ν ₁) and HOMO-LUMO gap of molecules 1–10 at the B3LYP/cc-pVTZ level.

Molecule	Bond lengtha/Å	Qring b	ν 1 c /cm−1	H-L gapd/eV
1	2.252/r1	−2.2	47.57	1.90 (2.60)
2	2.267/r1, 2.234/r2, 2.267/r3, 2.266/r4	−3.0	22.22	1.61 (1.94)
3	2.274/r1, 2.229/r2, 2.274/r3, 2.250/r4, 2.274/r5	−3.8	13.41	1.21 (1.51)
4	2.248/r1, 2.252/r2, 2.280/r3, 2.222/r4, 2.263/r5	−3.8	15.26	1.39 (1.58)
5	2.231/r1, 2.268/r2, 2.255/r3, 2.263/r4	−4.6	14.80	1.24(1.71)
6	1.391/r1	−1.2	413.94	5.47 (6.70)
7	1.412/r1, 1.370/r2, 1.416/r3, 1.428/r4	−1.6	173.54	4.39 (4.79)
8	1.421/r1, 1.363/r2, 1.425/r3, 1.395/r4, 1.440/r5	−2.0	91.43	3.22 (3.57)
9	1.388/r1, 1.399/r2, 1.433/r3, 1.355/r4, 1.423/r5	−2.0	99.20	3.68 (3.84)
10	1.366/r1, 1.419/r2, 1.416/r3, 1.423/r4	−2.4	88.27	3.22 (4.03)

^aThe notation r1−r5 represents the bond length between the X atoms (X = Si, C) shown in Fig. 3. ^bQ_ring: Summation of the NPA charges on the ring. ^c ν ₁: The lowest vibrational frequency. ^dHOMO-LUMO gap from the first excitation energies obtained by TDDFT/B3LYP. HOMO-LUMO gap from the Kohn-Sham eigenvalues of the ground state DFT/B3LYP calculation is given in parentheses.

Charge distribution

As shown in Table 1, the total NPA charges on the silicon rings (Q_ring) of 1–5 are all negative, indicating electron donation from the terminal BeH to the ring moiety. Figure 4 compares the charge distribution in molecules 1–5 to that of 6–10. The charge of the ring-edge silicon, at which BeH is directly bound, is strongly negative (red), while that of the silicon inside the ring is nearly neutral (black). The charge of the Be atom is strongly positive (green), while that of the hydrogen in BeH is strongly negative (red). These trends are the same as those in 6–10, but the contrast between the negative and positive charges is slightly enhanced in the silicon-based molecules 1–5. The total NPA charge on the carbon ring (Q_ring) of 6–10 is negative, and the ring is surrounded by positively charged hydrogen atoms. The edge carbon is negatively charged, and the inside of the ring is nearly neutral. The neutrality of the charge inside the ring is more evident in larger molecules. The charge distribution indicates that BeH terminates the silicon equivalents 1–5 as well as the hydrogen atoms of 6–10.

Figure 4.

Charge distribution of molecules 1–10. Each atom is colored according to the charge, and the number indicates the charge.

Molecular orbitals

Pure π-conjugation is a key property of flat silicene as well as flat graphene. The highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) are shown in Fig. 5. The HOMO and LUMO of 1–5 are all confirmed to be π orbitals. Their shapes are similar to the HOMO and LUMO of 6–10, but slightly delocalized on the Be atoms. Thus our design using a linear sp-hybrid orbital at the terminus is expected to successfully provide the building blocks for flat and stable π-conjugated silicene. The HOMO-LUMO gap of all the proposed precursor molecules are listed in Table 1.

Figure 5.

HOMO and LUMO of molecules 1–10. The molecular orbitals were calculated at the B3LYP/cc-pVTZ level and are depicted at the 0.01 and 002 isovalues for 1–5 and 6–10, respectively.

Other hexagons and isomers

Several other hexagons X₆R₆ (X = Si, Ge) were calculated to investigate which R substituents, other than Si₆(BeH)₆, can be used for the design of flat hexagons (Table 2). Since our aim is to obtain a six-membered ring with D _6h symmetry, we optimized the structure under the constraint of D _6h symmetry. In case of metal substitution at ring edge, two types of structures have the symmetry of D _6h (Fig. 6): benzene-like (A) and Si₆Li₆-like where metal moves between two silicon atoms (B). For comparison, the results of Si₆H₆ and Si₆Li₆ of structure A at the same level of calculations as our present work are also listed in Table 2. As is well known, our results also showed benzene-like structure of Si₆H₆ and Si₆Li₆ did not give a minimum.

Table 2.

Optimized hexagonsX ₆R₆ with D _6h symmetry.

X	R	Stationary pointa	Imaginary Mode of 1st TS	Structureb
Si	Na	3rd TS		B
Si	K	1st TS	Our-of-plane motion of K	B
Si	Mg	2nd TS		B
Si	Ca	6th TS		B
Si	Cu	1st TS	Out-of-plane ring deformation	A
Si	Zn	1st TS	Our-of-plane motion of Zn	B
Si	C≡N	1st TS	Out-of-plane ring deformation	A
Si	MgH	MIN		A
Si	CaH	6th TS		A
Ge	BeH	MIN		A
Ge	MgH	1st TS	Our-of-plane motion of MgH	A
Ge	CaH	17th TS		A
Si	H	1st TS	Out-of-plane ring deformation	A
Si	Li	6th TS		A

Full geometry optimizations were performed at the B3LYP/6-311++ G(3df,3pd) level for K, Ca, Cu, Zn and CaH substitution, and at the B3LYP/cc-pVTZ level for H, Li, Na, Mg, C≡N, BeH and MgH substitution. ^aMIN: minimum, TS: transition state. ^bTwo D _6h structures A and B are shown in Fig. 6. More stable structure between the two D _6h structures is listed for the terminal substituent of metals (R = Na, K, Mg, Ca, Cu, Zn). For comparison, the results of Si₆H₆ and Si₆Li₆ of structure A are listed.

Figure 6.

Two D _6h structures. A: benzene-like, B: Si₆Li₆-like where metal moves between two silicon atoms.

Among the optimized hexagons in Table 2, a flat D _6h ring was obtained as the minimum for only the MgH-terminated six-membered silicon ring and the BeH-terminated six-membered germanium ring. In both hexagons, MgH and BeH have an sp-hybrid orbital and acts as an electron donor. In the optimized structure, BeH and MgH do not migrate to between the silicon atoms or germanium atoms. The optimized silicon-silicon and germanium-germanium bond lengths are 2.264 Å and 2.350 Å, respectively. Although the minimized geometry of the MgH-terminated six-membered silicon ring has a flat structure, the planar hexagon is not the minimum of the MgH-terminated six-membered germanium ring but is instead its 1^st order transition state (TS). Furthermore, with CaH substitution, both the six-membered silicon and germanium rings become considerably higher order TS. Therefore, light metals are better for the design of flat hexagons. The imaginary mode of MgH-terminated six-membered germanium ring is the out-of-plane motion of MgH, which leads to a nonplanar structure. This motion does not cause MgH to migrate between two germanium atoms. The lowest vibrational frequency of BeH-terminated six-membered germanium ring is 22.24 cm⁻¹, which is much smaller than that of BeH-terminated six-membered silicon ring (47.57 cm⁻¹). This makes it difficult to design flat building blocks for flat germanene. A proper substituent at the ring edge is required to tune the charge on the ring and the bond strength between Ge and the substituent.

Several monovalent and divalent metals with electron-donating ability were examined as substituents (R = Na, K, Mg, Ca, Cu, Zn), but these did not produce flat D _6h hexagons as the minimum. Table 2 lists more stable structure between the two D _6h structures, benzene-like (A) and Si₆Li₆-like (B). Three are 1^st order TSs, and the others are higher order TSs. The imaginary modes of the 1^st order TSs are the out-of-plane motion of the metal (R = K and Zn) and out-of-plane ring deformation (R = Cu), leading to a nonplanar minimum. As mentioned before, the lithium-terminated six-membered silicon ring has a D _6h planar structure^31–33, and the lithium atom is not attached to one silicon but between two adjacent silicon atoms. Cu showed a benzene-like structure (A), while the other metals migrated between two silicon atoms (B) similar to lithium. Thus, simple electron donation is insufficient for the design of flat hexagons. Next, for the substituent with an sp-hybrid orbital (R = (C≡N)), the D _6h structure was obtained as the 1^st order TS. The imaginary mode is out-of-plane ring deformation, leading to a nonplanar minimum. Therefore, a simple sp-hybrid orbital without electron donation is also insufficient for the design of flat hexagons.

Hexasilabenzene is known to be less stable than many of its isomers. For example, synthetically accessible hexasilaprismane^34–36 is more energetically stable. To examine the relative stability between the isomers of our system, we calculated the six valence isomers^{37, 38} of Si₆(BeH)₆ and obtained the silicon equivalent of benzvalene³⁹, prizmane⁴⁰ and bicyclopropenyl⁴¹ in addition to benzene (1) as a minimum. Among the four, BeH-terminated hexasilabenzvalene is the most stable at the B3LYP/cc-pVTZ level of calculation. Since BeH-terminated hexasilabenzene is not the most stable isomer, the step-by-step manufacture of flat silicene from BeH-terminated hexasilabenzene is not recommended. It would be better to prepare zigzag silicene and then terminate it with BeH.

Discussion

Here, we designed flat building blocks 1–5 to construct flat silicene using DFT calculations. We used substituents with sp-hybrid orbitals that act as electron donors. The minimum structure of all the obtained silicon polycyclic molecules 1–5 is flat. The charge is nearly neutral inside the ring and strongly negative at the ring edge due to the terminal BeH substituent. The HOMO and LUMO of 1–5 are π-orbitals. The designed molecules 1–5 could act as building blocks for flat silicene, which is a π-conjugated 2D sheet composed of six-membered silicon rings. The difference between the silicene constructed here and graphene is that BeH must be present at the terminal to stabilize the flat structure. In this sense, the molecules presented here are building blocks of silicene ribbons due to the existence of a terminal substituent. Flat six-membered silicon rings have long been desired in silicon chemistry and 2D silicon materials. In this study, flat hexasilabenzene was realized, and it was confirmed that the extended ring molecules are also flat. The flatness of these building blocks opens the way to flat silicene ribbons or films constructed by them, but at present it does not guarantee the flatness of silicene ribbons or films. Further theoretical and experimental studies with careful design of the edge structure are required to realize flat silicene.

Methods

DFT calculations

DFT calculations were performed with the Gaussian 09 software package⁴². We utilized a hybrid Becke-type three-parameter exchange functional⁴³ paired with the gradient-corrected Lee, Yang, and Parr correlation functional (B3LYP)^{44, 45} and the cc-pVTZ basis set^46–50 unless otherwise noted. The geometric parameters were fully optimized, and the minimized structures were confirmed to have no imaginary frequencies. To investigate the charge at each atom, natural population analysis (NPA)^51–56 charges were calculated, as NPA charges are less basis-set dependent. Time-dependent density functional theory (TDDFT) calculations were carried out to obtain the HOMO-LUMO gap using the optimized ground state geometries⁵⁷. In all molecules studied here, the first excitation is mainly contributed by the HOMO-LUMO transition, although some of them are forbidden with zero oscillator strength. In Table 1, we list the first excitation energies as the HOMO-LUMO gap.

Author Contributions

M.T. performed all DFT calculations and prepared the manuscript.

Competing Interests

The authors declare that they have no competing interests.