Global Dynamics and Exchange Kinetics of a Protein on the Surface of Nanoparticles Revealed by Relaxation-Based Solution NMR Spectroscopy

Abstract

The global motions and exchange kinetics of a model protein, ubiquitin, bound to the surface of negatively charged lipid-based nanoparticles (liposomes) are derived from combined analysis of exchange lifetime broadening arising from binding to nanoparticles of differing size. The relative contributions of residence time and rotational tumbling to the total effective correlation time of the bound protein are modulated by nanoparticle size, thereby permitting the various motional and exchange parameters to be determined. The residence time of ubiquitin bound to the surface of both large and small unilamellar liposomes is ∼20 μs. Bound ubiquitin undergoes internal rotation about an axis approximately perpendicular to the lipid surface on a low microsecond time scale (∼2 μs), while simultaneously wobbling in a cone of semiangle 30–55° centered about the internal rotation axis on the nanosecond time scale. The binding interface of ubiquitin with liposomes is mapped by intermolecular paramagnetic relaxation enhancement using Gd³⁺-tagged vesicles, to a predominantly positively charged surface orthogonal to the internal rotation axis.

Many biological processes involve transient interactions of proteins with very large macromolecular assemblies or cell surfaces. Recent NMR developments, involving the application of lifetime line broadening (ΔR₂) and dark state exchange saturation transfer (DEST) spectroscopy, have allowed quantitative study of the dynamics of interaction of NMR visible molecules with very large (>1 MDa) NMR invisible species such as protofibrils and molecular machines at atomic resolution.¹ In our previous studies,¹ however, the transverse relaxation rates $\left(R_2^{\text{bound}}\right)$ of the bound species were treated phenomenologically, i.e., not interpreted in the framework of a particular motional model for the bound (“dark”) state. Here, we show that global dynamics and exchange kinetics of a model protein on the surface of large nanoparticles can be quantitatively described by analysis of differential ΔR₂ effects for particles of varying size.

The focus of the current work is the interaction of ubiquitin with lipid-based nanoparticles (liposomes). Liposomes have been extensively used as drug carriers and vehicles for studying biological membranes and their interactions with proteins.² The interaction of ubiquitin with a wide variety of small-to-medium sized carbon, gold and silver nanoparticles has been the subject of recent investigations.³ However, no information is currently available on the dynamic behavior of ubiquitin on the surface of any nanoparticle.

Negatively charged and zwitterionic liposomes were made using 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (POPG) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocho-line (POPC), respectively (see SI). Liposomes were prepared as large (LUV) and small (SUV) unilamellar vesicles with mean diameters of 103 and 27 nm, respectively, and corresponding polydispersity indices of 0.1 and 0.2 (Figure S1A,B). The molecular tumbling correlation time (τ_R) of LUV and SUV nanoparticles, calculated using the Stokes–Einstein equation, is 100 and 1.8 μs, respectively.

The ¹⁵N–ΔR₂ profiles (measured in the rotating frame to suppress chemical exchange line broadening; see SI) for U-[¹⁵N/²H]-ubiquitin in the presence of LUVs and SUVs are shown in Figure 1A,B, respectively. Substantial ΔR₂ values are observed in the presence of negatively charged POPG vesicles but not zwitterionic POPC particles, indicating that ubiquitin interacts only with negatively charged liposomes. There are no observable exchange induced chemical shifts, and the ΔR₂ effect can be entirely attributed to line broadening caused by rapid decay of transverse relaxation during the lifetime of the bound state that is transferred by exchange to the observable free state.^1d The ¹⁵N–ΔR₂ values are weakly dependent upon the static magnetic field (Figures 1 and S2): the average ratio of ΔR₂ values at 800 to 500 MHz is ∼1.3 for LUVs (Figure 1C) and SUVs (Figure 1D), very close to the expected ratio of 1.3 from a relaxation mechanism based on the one-bond ¹H–¹⁵N dipolar interaction and a −170 ppm ¹⁵N chemical shift anisotropy (for a slowly tumbling particle in the absence of exchange), and much smaller than any contribution from chemical exchange line broadening, which scales as the square of the magnetic field (800²/500² = 2.56). Thus, one can conclude that the exchange rate constant $k_{\text{ex}}=k_{\text{off}}+k_{\text{on}}^{\text{app}}$, where k_off and $k_{\text{on}}^{\text{app}}$ are the dissociation and apparent first order association rate constants, respectively, for the binding of ubiquitin to liposomes, is higher than $R_2^{\text{bound}}$ for ubiquitin and that $k_{\text{on}}^{\text{app}}$ is larger than $\Delta R_2^{\text{max}}$.^1b,d

Figure 1.

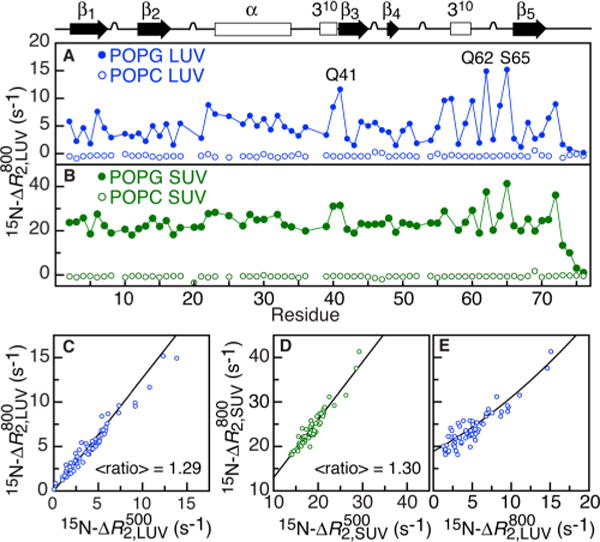
¹⁵N–ΔR₂ profiles for 0.8 mM U-[¹⁵N/²H] ubiquitin (dissolved in H₂O) in the presence of a 1:2 ratio (mol/mol on a lipid molecule basis) negatively charged (POPG, filled symbols) and zwitterionic (POPC, open symbols) liposomes of differing size: (A) LUVs (blue) and (B) SUVs (green). ¹⁵N–ΔR₂ dependence on magnetic field strength for (C) LUVs and (D) SUVs, and (E) on nanoparticle size. The black lines in C–E represent simulated correlations derived from global best-fitting of all LUV and SUV ¹⁵N–ΔR₂ data (see text, Figure 2 and SI). Experimental temperature = 25 °C.

The ¹⁵N–ΔR₂ data for LUVs and SUVs (Figure 1A,B) reveal two unexpected features. First, the ΔR₂ values for SUVs are 3–15-fold (average ∼4-fold) higher than those for LUVs (Figure 1E), even though the lipid monomer and ubiquitin concentrations are the same in both samples. This can be attributed to the larger concentration of SUV particles owing to their smaller size, hence the larger fraction of bound ubiquitin, and implies that the overall effective correlation time, τ_C = (1/τ_R+ k_ex)⁻¹, of bound ubiquitin is dominated, at least in the case of LUVs, not by τ_R but by the lifetime (τ_ex = 1/k_ex) of the complex. Note if τ_ex >> τ_R (∼100 μs) for LUVs, ${ }^{15}\text{N-}{R}_2^{\text{bound}}$ would be limited by the static ¹H–¹⁵N dipolar coupling of ∼20 kHz $\left(\text{corresponding}\text{to}{R}_2^{\text{bound}}\approx 6\times {10}^4{\mathrm{s}}^{-1}\right)$, and no sequence variation would be observed. Second, the ΔR₂ values would be expected to be uniform for the binding of a rigid protein to a large particle, yet their range spans over a factor of ∼8 for LUVs (Figure 1A,C) and ∼2 for SUVs (Figure 1B,D) (excluding the disordered C-terminal tail comprising residues 73–76). In contrast, the ¹⁵N–R₂ values for free ubiquitin, excluding the C-terminal tail and a small number of residues undergoing chemical exchange,⁴ are close to uniform with only minor variations owing to a very small degree of diffusion anisotropy.⁵ The experimental variation in ¹⁵N–ΔR₂ values cannot therefore be ascribed to local motion at the individual N–H bond vector level but rather to a global motional phenomenon involving the whole ubiquitin molecule on the surface of the nanoparticles.

The $R_2^{\text{bound}}$ values are related to molecular motion through the spectral density function J(ω) at a finite number of frequencies ω. Rotation of ubiquitin on the surface of the nanoparticle about an internal axis (Figure 2A) will result in a [P₂(cos α)]² = (3 cos² α − 1)²/4 dependence⁶ of $R_2^{\text{bound}}$ with a double-dip minimum at the magic angle (α = 54.74° and 180° − 54.74° = 125.26°) and a saddle point at α = 90°, where α is the angle between a given N–H bond vector (obtained from the molecular coordinates) and the axis of internal rotation. Internal rotation can therefore be described by an order parameter S_r², given by the square of the second-order Legendre polynomial P₂(cos α), and an internal rotation correlation time τ_r. $R_2^{\text{bound}}$ can be further modulated by a faster motion described by an order parameter S_w² and a correlation time τ_w. Assuming separation of time scales (τ_r > 5τ_w), J(ω) can be expressed, using the extended Lipari–Szabo formalism,⁷ as

$$J(\omega )=S_{\mathrm{w}}{ }^2{S}_{\mathrm{r}}{ }^2\frac{{\tau }_C}{1+{(\omega {\tau }_{\mathrm{C}})}^2}+S_{\mathrm{w}}{ }^2(1-S_{\mathrm{r}}{ }^2)\frac{{{\tau }^{\prime }}_{\mathrm{r}}}{1+{\left(\omega {{\tau }^{\prime }}_{\mathrm{r}}\right)}^2}+(1-S_{\mathrm{w}}{ }^2)\frac{{{\tau }^{\prime }}_{\mathrm{w}}}{1+{\left(\omega {{\tau }^{\prime }}_{\mathrm{w}}\right)}^2}$$ (1)

where τ_r′ = (1/τ_C + 1/τ_r)⁻¹ and τ_w′ = (1/τ_C + 1/τ_w)⁻¹, and the overall order parameter S² is given by S_w²S_r² (see SI for further details). The time scale τ_r is expected to be intermediate between the nanosecond time scale applicable for free ubiquitin and the low-microsecond time scale for transmembrane proteins;⁹ the faster motion can be considered as wobbling in a cone of semiangle β₀ (with S_w² = [cos β₀(1 + cos β₀)]²/4),⁷ which is equivalent to restricted rotational diffusion centered about the internal axis of rotation, and is expected to take place on a nanosecond time scale.⁹

Figure 2.

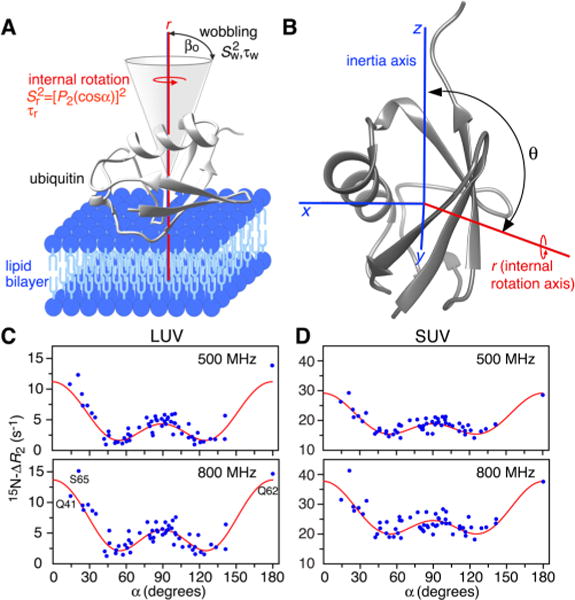
Global dynamics of ubiquitin on the surface of liposome nanoparticles. (A) Ubiquitin (gray ribbon, PDB 1UBQ⁸) rotates about an internal rotation axis (denoted as r and displayed in red), shown as perpendicular to the surface of the lipid bilayer (blue) while wobbling in a cone of semiangle β₀. (B) Relationship between the axis r (red) and the x, y, and z axes of the inertia tensor (blue, used as an arbitrary internal reference frame): θ is the angle between the r and z axes; and φ the angle (not shown) between the x axis and the projection of the r axis on the x–y plane. Dependence of ¹⁵N–ΔR₂ in the presence of (C) LUVs and (D) SUVs on the angle α between the N–H bond vectors and the internal rotation axis: experimental data are shown as blue circles; the best-fit curves, from global fitting to all LUV and SUV data, are in red (S_w² = 0.5 and τ_w = 300 ns; see text and SI).

Binding of ubiquitin to liposomes is fast on the relaxation time scale $\left(k_{\text{ex}}>R_2^{\text{bound}}-R_2^{\text{free}}\right)$ and for LUVs τ_ex < τ_R. Consequently, if the LUV and SUV ¹⁵N–ΔR₂ data are treated independently, direct characterization of the binding equilibrium is impossible without some simplifying assumptions (see SI for details). Since τ_C is dramatically different for LUVs and SUVs (as manifested by the much smaller variation in ¹⁵N–ΔR₂ for SUVs than LUVs; cf. Figure 1A,B) the solution to this problem lies in combined analysis of the LUV and SUV ¹⁵N–ΔR₂ data with the reasonable assumption that the parameters describing the global dynamics of ubiquitin on the nanoparticle surface (i.e., τ_r, τ_w, S_w², and the polar angles θ and φ defining the orientation of the internal rotation axis in the molecular frame of the inertia tensor; cf. Figure 2B) and the dissociation rate constant k_off are independent of nanoparticle size.

Even if the LUV and SUV data are analyzed simultaneously, not all global dynamics parameters can be reliably extracted because only the product of S_w² and τ_C enters into the first term of the spectral density (eq 1). Hence, only a range of possible values for the fast motional parameters, S_w² and τ_w, can be determined. Numerical analyses of the LUV and SUV data separately on a grid of S_w² and τ_w values for a set of fixed values of k_off (Figure S3) define realistic bounds of 0.7 > S_w² > 0.2, corresponding to wobbling within a cone of semiangle β₀ ≈ 30° to 55°, and 0 < τ_w < 500 ns (see SI).

Simultaneous nonlinear least-squares fitting of the LUV and SUV ¹⁵N–ΔR₂ data at multiple fields using the above assumptions, with S_w² = 0.5 and τ_w = 300 ns, results in excellent fits to the ΔR₂ data (Figures 2C,D and S2B) and yields values of k_off = 51(±16) × 10³ s⁻¹, τ_r = 2.0 ± 0.4 μs, and (θ, φ) = (108 ± 1°, −4.5 ± 1°). $k_{\text{on}}^{\text{app}}=65\pm 30$ and 1140 ± 410 s⁻¹ for LUVs and SUVs, respectively, corresponding to liposome-bound ubiquitin populations of 0.13 and 2.2%. The τ_C values for LUVs and SUVs thus differ by an order of magnitude (16 versus 1.6 μs, respectively) with the former being dominated by 1/k_off (∼20 μs) and the latter by the SUV molecular tumbing time τ_R (∼1.8 μs) The values of the various parameters are only slightly dependent on the choice of S_w² and τ_w values, and remain within the reported uncertainties for τ_w < 500 ns. At 800 MHz, the calculated ${ }^{15}\mathrm{N}-R_2^{\text{bound}}$ values range from ∼2000 to 14,000 s⁻¹ for LUVs and ∼1000 to 1600 s⁻¹ for SUVs (Figure S4). The dependence of ¹⁵N–ΔR₂ on the angle α subtended by each N–H bond vector and the internal rotation axis is shown in Figure 2C,D (and Figure S2B). A similar dependence of the amide proton ¹H_N–ΔR₂ values on α is also observed (Figure S5). Although ¹⁵N–ΔR₂ and ¹H_N–ΔR₂ values are correlated (Figure S5B), the ¹H_N–ΔR₂ values are “contaminated” by dipolar interactions between spatially close labile protons in U-[¹⁵N/²H] ubiquitin dissolved in H₂O and are therefore less suitable for quantitative analysis.

The lipid monomer concentration used in the NMR samples is 1.6 mM resulting in nanoparticle concentrations of 16 and 230 nM for LUVs and SUVs, respectively. The calculated bimolecular association rate constant for the binding of ubiquitin to both LUVs and SUVs is therefore ∼4 × 10⁹ M⁻¹ s⁻¹, which compares reasonably well with predicted values of 1 to 5 × 10¹⁰ M⁻¹ s⁻¹ for a nonspecific diffusion limited process (see SI).

Analysis of the global dynamics of ubiquitin bound to liposomes defines the orientation of the internal rotation axis in the molecular frame (Figure 2B) but not relative to the lipid bilayer. The latter can be inferred using intermolecular transverse (Γ₂) paramagnetic relaxation enhancement (PRE) measurements¹⁰ with Gd³⁺-paramagnetically tagged LUVs (see SI) to map the ubiquitin binding surface. The backbone amide and methyl proton (of Leu, Val, Ile-δ₁) Γ₂ PRE profiles are shown in Figure 3A. An approximately uniform ¹H-Γ₂ PRE background of ∼40 s⁻¹ arises from diffusion of ubiquitin in the magnetic field generated by the Gd³⁺-tagged LUVs, an effect analogous to the blood-oxygen-level dependent (BOLD) effect in functional MRI.¹¹ Superimposed on the background are regions with enhanced intermolecular PRE effects, which reach a maximal value of Γ₂ ≈ 70 s⁻¹ (with background subtracted) that is limited under the current exchange conditions by the value of $k_{\text{on}}^{\text{app}}$_. The intermolecular PRE effects are also manifested by wider paramagnetic ¹H-DEST profiles (Figure S6).

Figure 3.

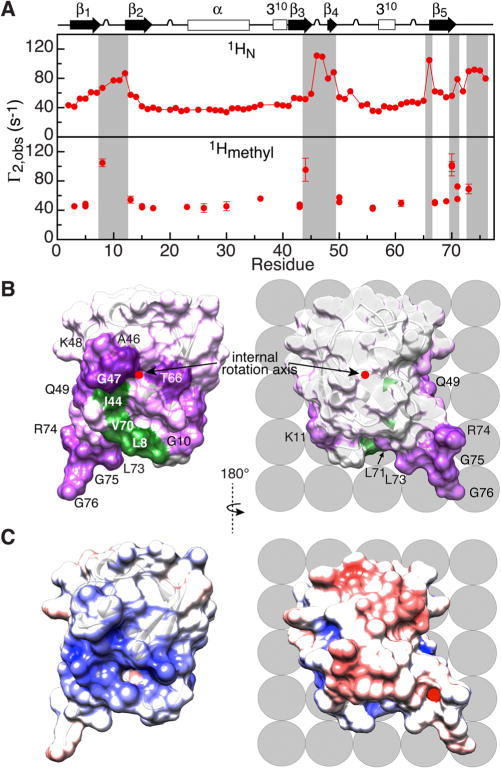
Proton intermolecular transverse PREs (Γ₂) observed for U-[¹⁵N/²H]/[¹H_methyl/¹³C_methyl-ILV] ubiquitin in the presence of negatively charged Gd³⁺-tagged POPG LUVs. (A) ¹H-Γ₂ profiles for backbone amide (top) and Ile/Leu/Val methyl (bottom) protons. (B) PRE mapping of the interaction surface of ubiquitin. The internal rotation axis (red dot) is perpendicular to the plane of the figure and orthogonal to the view shown in Figure 2A. ¹H_N-Γ₂ PREs are color-coded from purple (110 s⁻¹) to white (background = 40 s⁻¹), and residues with ¹H_N-Γ₂ ≥ 77 s⁻¹ are labeled; residues with large (>80 s⁻¹) ¹H_methyl-Γ₂ values are colored in green. (C) Molecular surface of ubiquitin (same views as in panel B) color-coded according to electrostatic potential (±5 kT with blue, positive; white, neutral; and red, negative). Lipid molecules on the nanoparticle surface are shown schematically as gray spheres.

Although the complexity of the paramagnetic labeling pattern (multiple Gd³⁺ tags on the surface of LUVs separated by average distances that exceed protein dimensions by more than a factor of 2) and the dynamics of the bound state preclude quantitative interpretation of the intermolecular PRE data, it allows one to map the preferential mode of interaction of ubiquitin with POPG LUVs (Figure 3B). For comparison, the molecular surface of ubiquitin color-coded according to electrostatic potential is shown in Figure 3C. The predominant interaction of ubiquitin with the negatively charged surface of POPG LUVs involves only a single face of the protein, comprising a central hydrophobic region surrounded by a ring of positive charges, orthogonal to the internal axis of rotation (Figure 3B). This same face has also been implicated in the interaction of ubiquitin with negatively charged silver,^3c Ln-doped SrF₂^3e, and hydroxylated C60 fullerenol^3d nanoparticles.

In summary, we have shown that it is possible to quantitatively characterize the global dynamics and exchange kinetics of an interaction occurring on the microsecond time scale between an NMR visible species (ubiquitin) and large lipid-based macromolecular assemblies (nanoparticles) with molecular tumbling times (τ_R) in the microsecond range. This was achieved by exploiting the different contributions of τ_R and lifetime (τ_ex) of the complex to the total effective correlation time (τ_C) of ubiquitin bound to the surface of nanoparticles of drastically differing sizes (τ_ex < τ_R for LUVs and >τ_R for SUVs). Ubiquitin rotates on the low microsecond time-scale around an internal axis approximately normal to the nanoparticle surface while undergoing faster rocking motions within a cone centered about the internal rotation axis (Figure 2A). In addition, the interaction surface on the protein can be delineated qualitatively from intermolecular PRE measurements using paramagnetically tagged liposomes (Figure 3B).