Hybrid Approaches to Structural Characterization of Conformational Ensembles of Complex Macromolecular Systems Combining NMR Residual Dipolar Couplings and Solution X-ray Scattering

Abstract

Solving structures or structural ensembles of large macromolecular systems in solution poses a challenging problem. While NMR provides structural information at atomic resolution, increased spectral complexity, chemical shift overlap, and short transverse relaxation times (associated with slow tumbling) render application of the usual techniques that have been so successful for medium sized systems (<50 kDa) difficult. Solution X-ray scattering, on the other hand, is not limited by molecular weight but only provides low resolution structural information related to the overall shape and size of the system under investigation. Here we review how combining atomic resolution structures of smaller domains with sparse experimental data afforded by NMR residual dipolar couplings (which yield both orientational and shape information) and solution X-ray scattering data in rigid-body simulated annealing calculations provides a powerful approach for investigating the structural aspects of conformational dynamics in large multidomain proteins. The application of this hybrid methodology is illustrated for the 128 kDa dimer of bacterial Enzyme I which exists in a variety of open and closed states that are sampled at various points in the catalytic cycles, and for the capsid protein of the human immunodeficiency virus.

Graphical abstract

1. INTRODUCTION

Biological macromolecules sample a range of conformational states (or microstates).^1,2 The distribution of this ensemble of microstates is dynamic and highly sensitive to changes in external conditions such as binding state,³ ligand concentration,⁴ pH,^5–7 ionic strength,⁸ and post-translational modifications.⁹ Important biological processes, including enzymatic catalysis,^10–15 ligand binding,^16,17 allostery,¹⁸ and signaling,^9,19 depend on the exact composition of the ensemble and on interconversion rates between microstates. Understanding the delicate balance between structure and dynamics that governs biological function represents a new frontier in modern structural biology and molecular biophysics and has driven several technical and conceptual advances in the field over the past few years.

Traditionally, high-resolution structures of conformational microstates have been obtained through the application of NMR and X-ray crystallographic studies in which the experimental conditions are adjusted to select one member, or a small subset of closely related members, of the conformational ensemble.^5,6 Although this approach allows determination of very precise structural models, trapping all different microstates accessed by a biopolymer can be a time-consuming and often impractical endeavor. More recently, computational strategies have been developed for interpreting structural data from highly heterogeneous systems, such as multidomain and intrinsically disordered proteins. Common aspects of these methods are the use of an ensemble-based representation for the system of interest, and the interpretation of experimental observables as a property of the overall ensemble instead of the individual microstates. Currently, structural ensembles are generated using one of two major approaches. The first calculates the ensemble by simulated annealing driven by the experimental data. Experimental restraints can be applied in either an ensemble-or time-average manner. The second involves first generating a large pool of possible structures and then selecting among these the most appropriate ensemble that fulfills the desired experimental observables. The computational strategies for generating dynamic structure ensembles have been extensively reviewed^20,21 and will not be discussed here.

There are a number of experimental methods that can provide structural and dynamical information to describe conformational ensembles. X-ray diffraction is affected by multiple sources of disorder (e.g., protein dynamics and crystal-lattice distortions) and has been used to model conformational heterogeneity in the crystal state.^10,22 Other methods, such as Förster resonance energy transfer (FRET)²³ and double electron–electron resonance (DEER) EPR spectroscopy,^24,25 have been used to investigate the structure and dynamics of biopolymers in solution. However, both FRET and DEER require covalent labeling of the molecule under investigation with fluorophores or paramagnetic centers, respectively, and, most importantly, only provide a single distance restraint per sample. These limitations have hampered the widespread use of FRET and DEER-derived distance restraints in calculations of conformational ensembles.

Undoubtedly, the most powerful experimental technique to investigate conformational ensembles is NMR spectroscopy. Indeed a large variety of NMR parameters can be measured that report on the structure and dynamics of biopolymers over a wide range of time scales and amplitudes of motion, and there are a number of methods to treat several types of NMR-derived restraints in ensemble calculations, including chemical shifts,²⁶ nuclear Overhauser enhancement (NOE) distance restraints,^27–31 generalized order parameters (S²),^30,32,33 scalar three-bond J couplings,^34,35 residual dipolar couplings (RDC),^36–40 chemical shift anisotropy (CSA),³⁷ paramagnetic relaxation enhancement (PRE),^41–43 and hydrogen/deuterium exchange protection factors.⁴⁴ The biggest advantage of NMR over other solution techniques is that it provides structural restraints for hundreds to thousands of individual atoms, or small groups of atoms, per sample per experiment.⁴⁵ However, when investigating high molecular weight systems, such as large complexes and multidomain proteins, line broadening (due to increases in rotational correlation time) and resonance overlap (due to the increased number of NMR-active nuclei) can drastically reduce the number of analyzable cross-peaks in multidimensional NMR spectra, resulting in sparse data sets. In such cases, hybrid methods that couple sparse NMR data with structural information from other lower-resolution techniques, such as cryo-electron microscopy⁴⁶ or small/wide-angle X-ray scattering (SAXS/WAXS),^47,48 have been shown to be very powerful in solving the structure of complex molecular systems.

Here we review the use simulated annealing driven by experimental NMR and SAXS/WAXS data for the quantitative investigation of the structure and dynamics of complex macromolecules at atomic resolution.

2. OVERVIEW OF THE USE OF SAXS/WAXS IN STRUCTURAL BIOLOGY

In structural biology, the term low resolution often has negative implications. Most instrumental techniques strive for the highest resolution possible with the gold standard being atomic resolution. Techniques such as crystallography and NMR easily achieve this goal but often come up short when looking at complex systems such as protein assemblies, nucleic acids, and transmembrane proteins. Additionally, analyses of highly flexible systems, such as intrinsically disordered proteins, suffer greatly or may even be impossible using only crystallography or NMR. Lower-resolution techniques such as atomic force microscopy, cryoelectron microscopy, and SAXS/WAXS are emerging as extremely useful tools for structural investigation of these difficult systems.^49–51

SAXS/WAXS is a solution state technique where a highly collimated X-ray beam is scattered by an incident sample containing the analyte of interest. This is a contrast technique that is very sensitive to changes in electron density. Because the analyte is tumbling in solution, its three-dimensional (3D) structure is reduced to a one-dimensional (1D) set of spherical shells and is represented as a one-dimensional plot of scattering intensity I against the momentum transfer vector q, given by

$$q=4\pi \text{sin}(\theta )/\lambda$$ (1)

where 2θ is the scattering angle and λ the wavelength of the incident X-ray beam.

3D structure envelopes can be calculated through ab initio modeling, but the resulting solution is not necessarily the correct one as the information content contained within a 1D data set is necessarily limited (see “Computational Modeling” section). Nevertheless, there are several powerful verification techniques that can be used to evaluate structural hypotheses.^52–54

In this section of the review we focus on the basics of sample preparation and requirements, instrumental design and operation, the theoretical basis of electromagnetic radiation scattering, data analysis, and finally 3D modeling of molecular structure. While this paper covers only SAXS/WAXS, small angle neutron scattering (SANS) is very closely related and useful but will not be discussed here. There are many informative reviews on SANS in the literature.^55,56

2.1. Sample Preparation for SAXS/WAXS

For a SAXS experiment to yield high quality data, a correspondingly high quality sample is required. The analyte of interest must be monodisperse and of the highest possible purity (>95%). Including size exclusion chromatography as a final step in purification is required to ensure purity and check for aggregation.⁵⁷ In addition, the use of techniques such as multiangle light scattering combined with size exclusion chromatography can be useful for checking sample quality. Even a small degree of aggregation present in the sample can skew the results of analysis. This necessitates collecting data at multiple concentrations to determine the ideal conditions for each individual analyte. For proteins, the ideal concentration is generally between 1 and 10 mg/mL. A more in-depth discussion of this will be given in the Data Analysis section.

As with many other popular spectroscopic methods, SAXS/WAXS is a contrast technique. The data resulting from these experiments (I_total) are defined as the sum of the intensities of scattering due to the buffer (I_b) and the analyte (I_a):

$$I_{\text{total}}=I_{\mathrm{b}}+I_{\mathrm{a}}$$ (2)

In most cases this is not an issue as it is fairly straightforward to produce a second sample with an identical buffer system, just excluding the protein to be studied. These two samples are run under identical conditions and their corresponding data subtracted from one another:

$$I_{\mathrm{a}}=I_{\text{total}}-I_{\mathrm{b}}$$ (3)

There are, however, some other important considerations that need to be taken into account. The contrast between the analyte and bulk solvent is dependent upon differences in electron density.⁵⁸ Water, with low concentrations of salts, has an electron density of ~0.33 e/Å whereas proteins have a slightly higher electron density of ~0.44 e/Å.⁵⁹ Thus, salt concentration should be kept below 1 M and ideally less than 100 mM. In addition to signal from bulk solvent and analyte, scattering by ordered layers of solvent around the analyte must be taken into account. This implies that the presence of detergents would be detrimental to data quality, in terms of adherence to proteins and in formation of bicelles/micelles, and must be used at very low to null concentrations.⁶⁰ Overall the signal collected in these experiments (I_total) is the sum of scattering intensities due to the buffer (I_b), protein (I_a), and ordered water layer around the protein (I_w).

$$I_{\text{total}}=I_{\mathrm{b}}+I_{\mathrm{a}}+I_{\mathrm{w}}$$ (4)

Finally, because the sample is subjected to high energy X-rays, radiation damage can occur. Radical species scatter light very strongly and so it is particularly important to minimize radiation damage.⁶¹ This is usually achieved in one of two ways. The X-ray source can be pulsed so as to let the sample recover from each exposure or a unidirectional constant flow cell can be utilized.⁶² Flowing the solution through the exposure area will limit the amount of radiation any given portion of the sample receives but require much more material. A static cell may require as little as 1 μL whereas a flow cell may require up to 100 μL.

2.2. Data Collection: Instrument Setup

The main components of a SAXS instrument are the X-ray source, the collimator, the sample holder, and the detector (Figure 1).⁶³ X-rays from the source, whose energy is around the 1 Å range, are focused by the collimator. The spatially coherent beam interacts with the sample and is scattered by an angle 2θ, and then travels toward the detector.⁶⁴ The gathered data is sent to a computer for storage and analysis.

Figure 1.

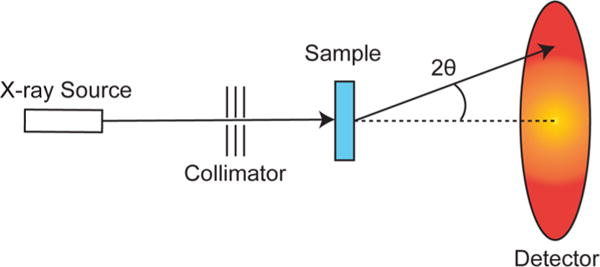
Schematic representation of a SAXS instrument (see main text).

X-rays can be generated from a variety of sources. Historically, high voltage vacuum tubes were used but are not the best choice because of energy inefficiencies and the relatively low energy photons they produce.⁶⁵ The most common sources today are synchrotron beamlines that produce high energy photons by accelerating electrons in a magnetic field.⁶⁶ These are particularly useful because many different instruments can be set up to use the same radiation source simultaneously.

Focusing X-rays using lenses is near impossible and reflective focusing is only a little better.⁶⁷ Instead, collimation is used as a subtractive means of colinearizing photons in the beam.⁶⁸ This is ideal because even with a focused photon source there will be changes in the diameter of the beam, as a function of distance from the lens, which would interfere with the resulting data. A perfectly collimated photon source is one with no divergence; that is all photons travel a parallel path with respect to the others. In this way, the only signal on the detector outside of the beam’s radius is due to scattering from the sample and not due to imperfections in the photon source.

The beam interacts with the sample (whose general criteria has been covered above) and is scattered (as described below) by an angle 2θ. The sample holder must either interact minimally with the incident photons both in terms of scattering and absorbance,⁶⁹ or must do so in a very predictable and reproducible way so that its effect can be subtracted out of the data.

2.3. Data Analysis

The data from a SAXS/WAXS experiment consist of a plot of scattering intensity over reciprocal space. As discussed above, the scattering intensity of the analyte, I(q), is the difference between the scattering of the analyte in the sample matrix and the matrix itself. The independent variable q is defined by eq 1. Occasionally in the literature, the variables s and h are used for q or q/2π, respectively, so one must be careful to note the definition of the momentum transfer variable. q has units of Å⁻¹ which roughly translates to 2π times the inverse resolution, being that I(q) is the Fourier transform of the electron density function ρ(r).

The curve I(q) can generally thought to be broken into three regions; low q, medium q, and high q (Figure 2a). Low and medium q data are collected at a small angle (hence SAXS), while high q data are collected at wide angle (hence WAXS)

Figure 2.

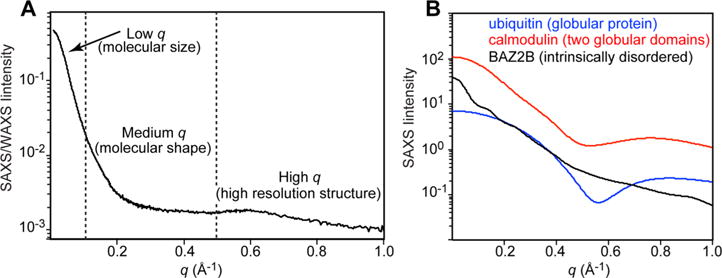
(A) SAXS/WAXS curve acquired for Enzyme I of the bacterial phosphoenolpyruvate:sugar phosphotransferase system. Vertical dashed lines separate the low, medium and high q regions. (B) SAXS curves acquired for ubiquitin (blue), calmodulin (red), and the bromodomain of protein 2B (BAZ2B – black). Data displayed in (B) were downloaded from the Small Angle Scattering Biological Data Bank (SASBDB).¹⁷²

Low q refers to the range q < 0.1 Å⁻¹ and reflects the size of the particle of interest. This metric is called the radius of gyration, R_gyr (defined as the root-mean-square distance of all atoms from their relative location to the particle’s center of mass). R_gyr is a good indicator of overall size and can be calculated by regression to I(0) using either the Guinier⁷⁰ or Debye^71,72 approximations:

$$\text{Guinier}:\text{ln}I(q)=\text{ln}I(0)-\frac{q^2{R_{\text{gyr}}}^2}{3}$$ (5)

$$\text{Debye}:I(q)=\frac{2I(0)}{q^4{R_{\text{gyr}}}^4}(q^2{R_{\text{gyr}}}^2-1+e^{-q^2{R_{\text{gyr}}}^2})$$ (6)

R_gyr can also be calculated by other methods that will be covered below.

The medium q range (0.1 < q < 0.5 Å⁻¹) is important for defining the shape of the particle. In Figure 2b we show a few examples of particle shapes and their corresponding I(q) curve. It is relatively difficult to determine the shape of a particle just based on visual inspection, but luckily there are computational procedures to aid in this respect (see below).

The high q range of the curve (q > 0.5 Å⁻¹) is dominated by the atomic resolution structure of the particle of interest, and is usually characterized by a lower signal-to-noise ratio.

While it is difficult to access the quality of SAXS data by a cursory glance at I(q), there is one important thing to consider. I(q) is the product of a form factor,⁷³ F(q), that describes the shape of the scattering particle, and a structure factor, S(q), that describes the interaction between different particles in the sample.⁷⁴

$$I(q)=F(q)·S(q)$$ (7)

Ideally S(q) equals unity for every value of q, and I(q) only reflects the particle shape. At low q, S(q) is very sensitive to oligomerization state and the presence of aggregation, and therefore it is usually good practice to check the early points of the SAXS profile to assess the aggregation state of the sample. In particular an increase in I(q) is diagnostic of an aggregated sample,⁷⁵ while, in contrast, a dip in the I(q) curve indicates repulsion between molecules.⁷⁶ A more quantitative way of evaluating the aggregation state is by using the Guinier plot. For S(q) = 1, the Guinier transformation (eq 5) yields a straight line for 0.65/R_gyr < q < 1.3/R_gyr.⁷⁷ Curvature in this plot can be attributed to sample imperfections and a residual plot can help identify such errors (Figure 3).

Figure 3.

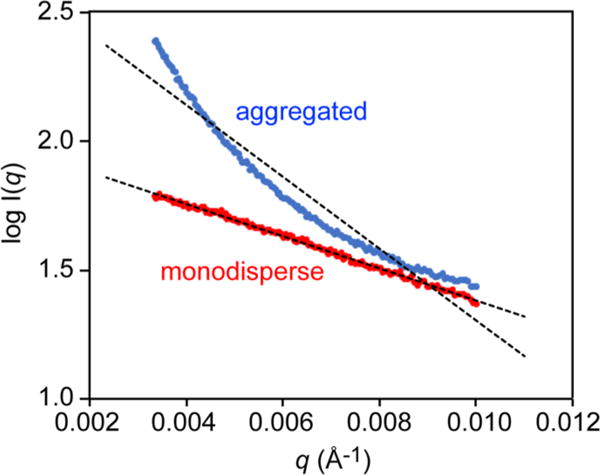
Examples of Guinier plots for monodisperse (red) and aggregated (blue) samples.

SAXS/WAXS experiments are limited in their information richness relative to similar instrumental techniques such as X-ray crystallography because of solution state tumbling which averages out the three-dimensional electron density map to a one-dimensional set of spherical shells. In crystallography, the Patterson function is an autocorrelation function that shows all atom pairs (including self-pairs) and provides the best solution to crystal structures without solving the phase problem.⁷⁸ The SAXS analog is the pair-distribution function,⁷⁹ P(r), the interpretation of which is a histogram of all atom–atom correlations plotted against the distance between the atoms (Figure 4). P(r) is calculated by an indirect Fourier transform of I(q) over 0 < r < D_max:⁸⁰

$$P(r)=\frac{r}{2{\pi }^2}{\displaystyle {\int }_0^{\text{∞}}qI(q)\text{sin}(qr)\mathrm{d}q}$$ (8)

where r is the distance between scattering elements (atoms in the case of a protein) and D_max is the maximum diameter of the particle. Because the value of D_max may not be known prior to calculation of P(r), iterative optimization can be used to define the ideal bounds for the integral. The pair-distribution function is useful for determining the shape of the analyte as well as its size. Spherical proteins will give a symmetrical, bell-shaped P(r) distribution while increasing deviations will result in tailing of the peak shape to higher values of r. When P(r) = 0, r = D_max as this is the point where there are no larger atom–atom pairwise distances. Once D_max has been determined, another method of approximating R_gyr can be calculated using the equation

$${R_{\text{gyr}}}^2=\frac{{\displaystyle {\int }_0^{D_{max}}{r}^{2}P(r)\mathrm{d}r}}{{\displaystyle {\int }_0^{D_{max}}P(r)\mathrm{d}r}}$$ (9)

Figure 4.

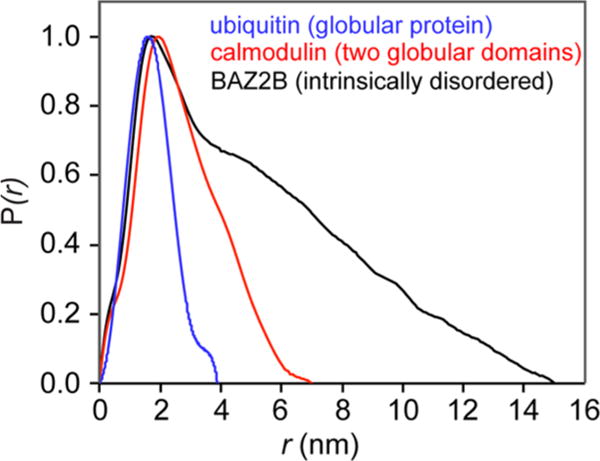
Pair-distribution functions, P(r), obtained from the SAXS curves acquired for ubiquitin (blue), calmodulin (red), and the bromodomain of protein 2B (BAZ2B – black). The experimental SAXS data were obtained from the SASBDB.¹⁷²

2.4. Computational Modeling

Noncomputational SAXS analysis is useful for basic characterization of macromolecules, but the real value lies in computational modeling. It is possible to define molecular envelopes that describe the low-resolution shape of a protein or complex as well as carry out hypothesis testing to differentiate between discrepant models.^81,82 However, one needs to take care when considering possible envelopes calculated from SAXS data. 1D SAXS data cannot be used to directly calculate a 3D envelope. Extrapolating into higher dimensional space requires some level of “guess and check” and it is possible (and likely) to come up with many different envelopes that fit the SAXS curve quite well. No matter the quality of the SAXS data, an envelope can still be calculated! This is not to say that computational modeling of SAXS data is unreliable; on the contrary, it has been successfully used to resolve differences between solid and solution state structures, and to model missing residues in crystal structures.^83,84 In addition, the chance of accidentally misinterpreting data is almost eliminated when SAXS is used in combination with other techniques such as NMR or crystallography (see below). But it is important to keep in mind the limitations and dangers of overanalyzing results derived from SAXS.

The SAXS curve is back-calculated from a structural model using the equation

$$I(q)={\langle |A(q){|}^2\rangle }_{\mathrm{\Omega }}$$ (10)

where 〈 〉_Ω denotes the average over solid angle Ω (the average due to molecular tumbling in solution) and A(q) is given by

$$A(q)={\displaystyle \sum _j{f}_j^{\text{eff}}(q){\mathrm{e}}^{iq{x}_j}+{\displaystyle \sum _k{f}_k^{\text{sph}}(q){\mathrm{e}}^{iq{y}_k}}}$$ (11)

where q is the reciprocal space scattering vector with amplitude q; j sums over all atoms; $f_j^{\text{eff}}(q)$ is the effective atomic scattering form factor; x_j is the position of atom j; k sums over points representing boundary-associated solvent; and $f_k^{\text{sph}}(q)$ and x_k are, respectively, the positions and scattering form factors of these points. In eq 11 the first sum describes the scattering from each solute atom, while the second sum describes scattering from ordered solvent molecules bound to the surface of the macromolecule.⁸⁵ Details about back-calculation of SAXS profiles, as well as of the mathematical tricks implemented for speeding up computation, are reviewed elsewhere.^86–88

In the context of analyzing conformational ensembles, the experimental SAXS curve is a population-weighted average of the SAXS profile of each conformer.⁴⁷ Therefore, given known structures for distinct conformational states, relative populations can be determined by simple linear combination of back-calculated scattering curves to maximize agreement with the experimental I(q).

3. OVERVIEW OF THE USE OF RESIDUAL DIPOLAR COUPLINGS IN STRUCTURAL BIOLOGY

Of the various types of data that can be obtained by solution state NMR, residual dipolar couplings (RDCs) are very useful for structure refinement because they yield long-range orientational information.^89,90 RDCs describe the orientation of bond vectors relative to the static magnetic field.⁹¹ To observe RDCs, the molecule under investigation must tumble anisotropically in solution so that the RDCs are not averaged out to zero. Weak alignment (of the order of 10⁻³) can be readily achieved using various dilute alignment media.⁹² This section of the paper will focus on the theoretical basis for RDCs, alignment media, alignment tensor prediction, and use of RDC restraints in structure calculation.

3.1. Theoretical Background

Dipolar couplings are through space interactions between magnetic nuclei. The dipolar interaction between two spins (D_AB) of gyromagnetic ratios γ_A and γ_B at a given distance, r, is given by

$$D_{\text{AB}}(\vartheta )=D_{max}\langle \frac{3{\text{cos}}^2\vartheta -1}{2}\rangle$$ (12)

where ϑ is the angle between the internuclear bond vector and the external magnetic field (Figure 5) and D_max is the maximum value of the dipolar coupling, given by

$$D_{max}=-\frac{({\mu }_0{\gamma }_{\mathrm{A}}{\gamma }_{\mathrm{B}}h)}{(8{\pi }^3{r}^3)}$$ (13)

where μ₀ is the magnetic permeability in a vacuum and h is Planck’s constant.⁹³ ⟨⟩ in eq 12 denotes the average over all possible orientations of the internuclear bond vector relative to the external magnetic field. In isotropic solution all orientations are possible, and D_AB averages to zero. Addition of an alignment medium breaks the orientational symmetry and results in nonzero values of D_AB.

Figure 5.

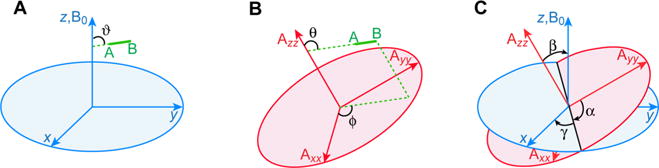
Relationship between the bond vector A–B, the alignment tensor and the external magnetic field (B₀). (A) The angle ϑ describes the orientation of the bond vector relative to B₀; (B) the angles θ and ϕ define the orientation of the bond vector relative to the alignment tensor; and (C) the relationship between the alignment tensor and the external magnetic field is given by the Euler angles α, β and γ. The A-B vector is displayed green; the alignment tensor is colored red. The magnetic field B₀ is taken parallel to an external reference frame (blue).

Eq 12 can be recast in terms of a molecular coordinate frame, called the alignment tensor, that describes the relative orientation of the molecule with respect to the alignment medium:

$$D_{\text{AB}}(\theta ,\varphi )=D_a^{\text{AB}}\left[(3{\text{cos}}^2\theta -1)+\frac{3}{2}({\text{sin}}^2\theta \text{cos}2\varphi )\right]$$ (14)

where θ is the angle between the internuclear bond vector and the z axis of the alignment tensor, ϕ the angle between the xy plane projection of the internuclear bond vector and the x axis (Figure 5), $D_a^{\text{AB}}$ the magnitude of the axial component of the alignment tensor, and η the rhombicity.⁹⁴

3.2. Alignment Media

The maximum strength of a dipolar coupling for completely aligned samples is of the order of 20 kHz for ¹H–¹⁵N and 40 kHz for ¹H–¹³C dipolar interactions. This would cause the NMR spectrum to be so complex and broad that it would be uninterpretable. To circumvent this problem, dilute alignment media are used resulting in an ordering of ~10⁻³ with maximum residual dipolar couplings (RDC) of about 20 Hz.^95,96 There are many different alignment media and these have been extensively reviewed.^97–103 Here we give a brief outline of the most popular media employed in structural biology applications.

Bicelles were the first media to be used for RDC measurements.⁹⁵ They are relatively easy to prepare and alignment is somewhat tunable based on the concentration of lipids. Most commonly, dimyristoylphosphatidylcholine (DMPC) and dihexanoylphosphatidylcholine (DHPC) are used to make bicelles. At low temperatures, bicelles are isotropically oriented but at temperatures greater than 30 °C they transition to a nematic liquid crystalline phase. The normal vector of the bicelles is oriented perpendicular to the applied magnetic field. Using DMPC and DHPC results in purely steric alignment but trace amounts of charged lipids can be incorporated to produce varying degrees of electrostatic alignment.⁹⁷ This makes bicelles quite useful because multiple RDC data sets can be acquired under similar solution conditions.

The second alignment medium to be described comprised rod-shaped, filamentous bacteriophages and viruses.^96,104 A commonly used phage is pf1 that is approximately 20 000 Å long and 60 Å in diameter.⁹⁸ These virus particles, which are commercially available, spontaneously align in a magnetic field making them especially convenient for NMR. Their surface is covered in negative charges so proteins are aligned through both steric and electrostatic interactions. This can cause problems with positively charged proteins because they may align too much. The extent of alignment can be tuned by varying the concentration of phage and salt. Typically, the concentration of phage employed is 10–20 mg/mL with 100 mM or less NaCl at pH 6.5 to 8.

Polyacrylamide gel can be used for alignment of a protein when the gel is mechanically stressed.^105,106 The pores in the gel become elongated when compressed which allows for steric alignment. First the acrylamide is polymerized using 0.1% w/v ammonium persulfate and 0.5% w/v tetramethylethylenediamine in a tube, generally, with an inner diameter between 3.5 mm to 8 mm. The gel is then washed and dehydrated. The gel is rehydrated in an NMR tube using the protein solution and then compressed using the plunger of a Shigemi NMR tube. Alternatively, radial compression can be achieved by pushing a gel with a diameter larger than the NMR tube through a funnel into the NMR tube. The alignment tensors of radially and axially compressed samples are of opposite sign and do not provide new data. Electrostatic alignment using negative or positive charges is also possible if 2-acrylamido-2-methyl-1-propanesulfonic acid or diallyldimethylammonium chloride, respectively is substituted for acrylamide during polymerization.¹⁰⁷ Either dialysis or dissolving the gel and centrifuging readily accomplish sample recovery.

3.3. Measuring RDCs

Measurement of RDCs is based on various common J scalar coupling experiments as well as some more sophisticated pulse schemes. RDCs appear in NMR spectra much in the same way that J-couplings do (Figure 6). The RDC between two nuclei is additive with that of the corresponding J coupling (Figure 6). To determine the magnitude of an RDC, one must know the sum of the dipolar and J coupling as well as the J coupling by itself, as shown in the equation below:

$$T=J+D$$ (15)

where J and D are the size, in Hz, of the J coupling and RDC, respectively, and T is the observed splitting.¹⁰⁸ This constitutes the basis of measuring RDCs in all of the available types of experiments. To determine the value of J, the experiment is carried out on a sample of the macromolecule under isotropic conditions. Using the same conditions, save for the inclusion of an alignment medium to produce anisotropy, the experiment is repeated to observe the new splitting that is equal to T. Subtraction of the splitting T from J yields the value of D.

Figure 6.

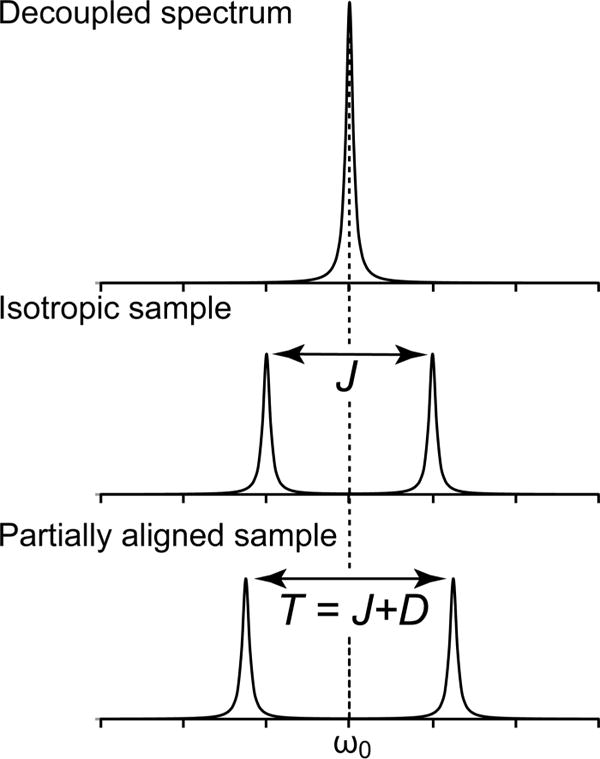
Comparison between a NMR peak measured in the (A) absence of coupling (i.e., decoupled), (B) presence of scalar (J) coupling (isotropic sample), and (C) presence of scalar (J) and dipolar (D) coupling (partially aligned sample).

The most commonly collected RDC for proteins is the ¹H–¹⁵N backbone amide set because of its sensitivity and spectral resolution even for large, slow tumbling proteins. However, many other nuclei pairs provide useful structural information including ¹H_N-¹H_α, ¹H_N-¹³C_α, ¹H_α-¹³C_α, ¹⁵N-¹³C_α, ¹⁵N–³C′, ¹³C_α-¹³C′, ¹³C_methyl-¹³C, ¹H_methyl-¹³C_methyl, and ¹H–¹H.^{104,109–114} It is generally more straightforward to collect and analyze data from nuclei pairs that have a relatively large J-coupling, such as ¹H–¹⁵N and ¹H–¹³C, because there is almost no possibility of an unresolved doublet. However, there is a greater chance of spectral overlap with other signals due to the larger J-coupling. With smaller J-coupled systems, such as ¹³C–¹³C and ¹⁵N–¹³C, there is less of a problem with signals interfering with one another and more of a problem with unresolved doublets.¹⁰²

There are two main techniques for collecting RDC data: IPAP and quantitative J-modulation.^115,116 Of these, there are important extensions that apply to various challenges. IPAP stands for in-phase/antiphase, and as the name implies, this experiment allows for the collection of the in-phase doublet spectrum, and then subsequently in an interleaved manner, the antiphase doublet spectrum.¹⁰⁹ The most commonly used example of this strategy is in the ¹⁵N-IPAP heteronuclear single quantum coherence (HSQC) experiment, where the spectrum yields data just as a regular ¹H–¹⁵N HSQC but includes the ¹J_HN splitting in the nitrogen dimension. This data collection scheme is unique in that it allows for the differentiation between the upper and lower components of a doublet. When the two spectra are summed together, the low field component of the doublet is added together while the high field component is canceled out. Likewise, the difference of the spectra results in canceling the lower field component, while adding the higher component. This technique is particularly useful when there is concern of spectral overlap due to doubling the number of peaks in the coupled spectrum.

The quantitative J-correlation experiment measures the J coupling between two nuclei by exploiting differences in signal intensities due to evolution of the scalar coupling.¹¹⁷ Two experiments are acquired in an interleaved fashion. The first is a decoupled reference spectrum. The second spectrum allows the coupling to evolve during a spin-echo period. The ratio of the peak intensities is proportional to the J coupling between the nuclei. Alternatively, the time delay during the spin–echo period can be varied through a series of experiments so as to collect multiple peaks of varying intensities.¹¹⁸ These intensities are fit to a trigonometric function to obtain the value of the coupling constant. The second method is generally more accurate, mostly by virtue of using more data points. The results of either method are resilient to signal loss effects, such as relaxation, that might skew peak integrations because each spectrum is normalized to a reference experiment that is identical to the attenuated experiment. More sophisticated versions of the basic quantitative J experiment have been developed and are primarily focused on expanding the applicability to larger systems. ARTSY (amide RDC by TROSY spectroscopy) is one such experiment based on a two-dimensional ¹H–¹⁵N transverse relaxation optimized (TROSY) HSQC.¹¹⁹ Here, the normal interleaved reference/attenuated data collection scheme is utilized. The main difference is that in the reference experiment the ¹H signal is allowed to dephase for half of the spin-echo period and in the attenuated experiment it dephases for the entire spin-echo period. As was the case before, taking the ratio of the attenuated to reference peak intensities will allow for the calculation of J or J + D in isotropic and aligned media, respectively.

When dealing with large systems, transverse (R₂) relaxation and spectral crowding becomes a considerable problem when measuring RDCs. One method to surmount both of these issues simultaneously is selective isotope labeling of methyl groups. During the production of the protein of interest, precursors are used to selectively label methyl groups of the side chains of isoleucine (I), leucine (L), valine (V), and alanine residues.^120–123 Spectra of these selectively labeled proteins are much less crowded than their uniformly labeled counterparts and, additionally, the relaxation characteristics of ¹³CH₃ methyl groups are particularly ideal.^124,125 This enables high resolution measurement of RDC data in large systems that might otherwise suffer from very poor spectral quality. For ILV-selectively labeled proteins it is possible to collect ¹H_methyl-¹³C_methyl and ¹³C_methyl-¹³C RDCs in spectra that are extended to a third dimension (¹³C^β/γ) to further increase resolution of crowded spectra.¹²⁶ This experiment is again based on the quantitative J methodology and yields best results using multiple delay values during J evolution and curve fitting to obtain the coupling constant.

3.4. Data Analysis

To utilize RDCs as restraints in structure refinement, the alignment tensor must be determined. The alignment tensor comprises 5 terms: the magnitude of the axial component of the tensor (D_a), the rhombicity η of the tensor, and three parameters describing the orientation of the tensor. In simulated annealing refinement, the three orientation parameters can be represented by an orthogonal axis system that is treated as a rigid body and allowed to rotate during the course of the calculation. D_a and η can be determined directly from a histogram of the measured RDCs by noting that the maximum of the distribution (corresponding to D_zz) for a fixed distance interaction is given by $2D_a^A$, the minimum (corresponding to D_yy) by −D_a(1 + 1.5η), and the mode (corresponding to D_xx) by −D_a(1−1.5η), with the additional constraint that the sum of D_xx + D_yy + D_zz = 0 (Figure 7).¹²⁷ The robustness of this simple approach can be enhanced by application of maximum likelihood methods.^30,128 Alternatively, the values of D_a and η can also be optimized during simulated annealing.³⁰

Figure 7.

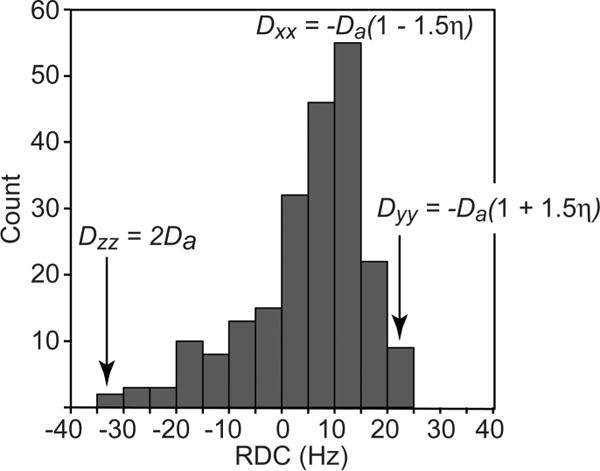
Deriving the magnitude of the axial component and rhombicity of the alignment tensor from a histogram of normalized RDCs. The data are taken for the protein cyanovirin,¹⁷³ and the backbone Cα-Hα and Cα-C′ RDCs are normalized relative to the backbone N–H RDCs. The maximum, minimum and mode of the distribution correspond to D_zz = 2D_a, D_yy = −-D_a(1 + 1.5η), and D_xx = −D_a(1 – 1.5η), where D_a (scaled for N–H bond vectors) is the magnitude of the axial component of the alignment tensor and η the rhombicity. The sum of the three orthogonal components of the alignment tensor is equal to zero (D_zz + D_yy + D_xx = 0).

If a structure has already been determined, its quality can be assessed using singular value decomposition (SVD) to obtain the best-fit alignment tensor that minimizes the difference between the observed RDCs and those back-calculated from the structure.⁹³

The quality of the RDC fit to the coordinates is assessed using an R-factor (spanning from 0 indicating no agreement to 1 for perfect agreement) that can be expressed as

$$R={\{\langle {(D_{\text{obs}}-D_{\text{calc}})}^2\rangle /(2\langle {D_{\text{obs}}}^2\rangle )\}}^{1/2}$$ (16)

where D_obs and D_calc are the observed and calculated RDCs, respectively.¹²⁹ 〈D_obs²〉 can either be the experimental value or can be calculated exactly by 2(D_a)²(4 + 3η²)/5.¹²⁹ The latter, however, is not suitable for an ensemble of structures since each ensemble member will have different values of D_a and η.

The manner in which the protein transiently interacts with the alignment medium is determined by steric and electrostatic effects (see above). The degree to which these two factors affect the orientation of the macromolecule under investigation varies from one alignment medium to the next, and also depends on the shape and charge distribution of the protein. For primarily steric alignment, the orientation can be approximated very well by obstruction theory.¹³⁰ The probability to find the molecule in a certain orientation Ω = (α, β, γ) is given by

$$P(\mathrm{\Omega })=\frac{L-l(\mathrm{\Omega })}{4\pi L-{\displaystyle \int l(\mathrm{\Omega })\mathrm{d}\mathrm{\Omega }}}\cong \frac{L-l(\mathrm{\Omega })}{4\pi L}$$ (17)

where L is the distance between two parallel planes, l(Ω) is the length of the molecule in the direction orthogonal to the planes, and α, β, and γ are Euler angles that describe the orientation of the alignment tensor.¹³¹ From this equation, it is immediately obvious that molecules will preferentially align with their long axis parallel to the planes. There are common programs to carry out this calculation such as PALES/SSIA¹³² and Xplor-NIH.³⁰ Xplor-NIH can also readily carry out this calculation during simulated annealing which is extremely useful when refining a structure ensemble.

It is much more difficult to predict the orientation of a protein in an alignment media that is dominated by electrostatic interactions because the surface charge distribution of the molecule plays a big role in alignment. The alignment tensor of macromolecules that have a very uniform charge distribution, such as DNA, can be accurately described in electrostatic aligning media while most proteins suffer due to their nonuniform surface charge.¹³³

Recently, it has been shown that it is also possible to perform structure calculations incorporating RDCs without using an alignment tensor.^134,135 The technique, dubbed the “ϑ method”, gets around the necessity of the alignment tensor by using eq 12 directly in the refinement protocol (i.e., without recasting into eq 14). When using the ϑ method, the orientation of the molecule relative to the external magnetic field is optimized to maximize the linear correlation between experimental RDCs and the dipolar couplings back-calculated from the structure using eq 12. Therefore, even though the ϑ method eliminates the need for calculating the alignment tensor, it still requires optimization of four variable parameters (three rotational degrees of freedom and an RDC scaling factor) to describe the alignment of the molecule in the external magnetic field.

4. COMBINED USE OF SAXS AND RDC DATA FOR STRUCTURE DETERMINATION OF COMPLEX MOLECULAR SYSTEMS

Traditionally, NMR structure determination of macromolecules requires close to complete resonance assignments and acquisition of extensive data sets of NMR-derived structural restraints. In particular, short (up to ~6 Å) distance restraints, which are obtained by the analysis of NOE data, and restraints on the backbone torsion angles from three-bond scalar couplings and backbone chemical shifts, have been extensively employed to solve the 3D structures of globular proteins.¹³⁶ More recently, introduction of orientational restraints from RDC data measured in a dilute liquid crystalline media has enormously expanded the complexity of protein folds and assemblies amenable to structure determination by NMR.^95,137,138 Once local geometries are defined by NOE and dihedral angle restraints, RDC data can be used to orient rigid groups of atoms (such as secondary structure elements and domains) relative to one another. The beauty of this approach is that, if the structural domains can be treated as rigid bodies, only a small number of RDCs is required to orient the domains relative to one another.¹³⁹

The main limitation of using RDCs to derive orientational information is the 4-fold degeneracy for orienting the alignment tensor that results in multiple solutions.¹⁴⁰ Ideally, NOE distance restraints¹³⁹ or a second noncolinear alignment tensor¹⁴¹ can be used to resolve this ambiguity. However, these methods require measurements of interdomain NOEs or acquisition of an orthogonal set of RDC data, and are usually not applicable to larger systems for which only a very restricted set of NOEs may be measurable, and that may only be compatible with a single alignment medium. In such cases, an alternative strategy using hybrid methodology is required.

The most generally applicable hybrid method combines RDC data with SAXS/WAXS and treats structural domains as rigid bodies. RDCs provide orientational restraints and, in purely steric alignment media, shape information as well (see above), while SAXS provides complementary information on size and shape.⁴⁷ Conjoined rigid body/torsion angle simulated annealing driven by the RDC and SAXS data is then used to obtain structural solutions that are consistent with the experimental data. To use such a hybrid approach, the structures of the individual domains must be known. This can be achieved either by experimental techniques (i.e., X-ray crystallography or NMR) or, under limited circumstances, by homology modeling when the degree of sequence similarity is very high (>60%) and there are no gaps or insertions between the experimental structure and the domain being modeled. In any case, before their use in the simulated annealing protocol, the quality of the structures must be carefully assessed by comparison of the RDCs measured on the multidomain molecule with those back-calculated from the high-resolution structures of the building blocks. It is worth mentioning that inconsistencies between experimental and back-calculated RDCs do not necessarily mean that the structures of the isolated domains are of poor quality. Indeed they can simply be the result of a conformational change induced by interdomain interactions that are absent under the experimental conditions used to determine the 3D structures of the building blocks. Rigid-body simulated annealing driven by SAXS and sparse RDC data has been used to solve the structures of large multidomain proteins,^47,48,142 complex nucleic acids,^143–145 and protein oligomers.¹⁴⁶ Recently, the technology has been expanded to the refinement of conformational ensembles.¹⁴⁷

4.1. Combined Use of SAXS and RDCs for Generation of Conformational Ensembles

A crucial step in setting up a structure calculation protocol is to decide whether to represent the molecule under investigation using a single structure or a conformational ensemble. As a general rule, an ensemble representation can only be invoked if the experimental data cannot be explained by refinement of a single structure. In addition, in the case of multidomain proteins, the presence of large amplitude interdomain motion can be confirmed by NMR relaxation measurements (sensitive to ps-ns time scale motions)^148,149 or by the analysis of experimental RDC data (sensitive to motions up to the ms time scale).^150,151

When using a conformational ensemble the experimental data are considered as a global average representation of the system. Thus, at each step of the refinement protocol the RDC and SAXS data are back-calculated from the conformational ensemble as population-weighted averages over the ensemble members. This means that the relative populations of the ensemble members (also referred to as ensemble weights) must be optimized during the refinement. Broadly speaking, there are two ways to optimize ensemble weights. In several applications all ensemble members are given equal populations throughout the simulations.^20,21 These protocols rely on the fact that if a particular conformation is prevalent in the experimental sample, it will also be prevalent in the computational ensemble. The main limitation of such approach is that to properly describe relative populations between clusters of conformations, large ensemble sizes must be used. An alternative approach is to use a limited number of ensemble members and optimize their relative populations directly in the simulated annealing calculation.^142,147

If interconversion between conformational states is in the fast-to-intermediate exchange regime (nano- to millisecond range), each ensemble member has its own alignment tensor.^142,147 Letting the alignment tensors float during refinement would add five variable parameters to the fit per ensemble member (see above), and would result in ill-defined and unstable fits. This fundamental problem can be circumvented by using a purely steric alignment medium so that the alignment tensor for each ensemble member can be directly calculated from its molecular coordinates at each step of the simulated annealing protocol.^131,142,147 We should also note that the tensor-free ϑ method¹³⁴ only reduces the number of parameters required to describe alignment from five to four per ensemble member (see above) and therefore does not provide a suitable alternative.

The optimal ensemble size (N_e) is usually determined empirically by searching for the smallest ensemble size that satisfies the experimental data.²⁰ To avoid data overfitting (for example by using an unreasonably large ensemble size), parameters for evaluating agreement between experimental and back-calculated data must be carefully chosen, and, where possible, additional data sets should be collected and reserved for cross-validation of the calculated conformational ensemble. In the context of ensemble refinement against RDC and SAXS data, the agreement between the structural ensemble and experimental RDCs is conveniently evaluated in terms of an R-factor (see above).¹²⁹ The target global R-factor value is given by the weighted average of the R-factors of the individual structural domains:

$$\text{global}{R}_{\text{target}}={\displaystyle \sum _i\frac{R_i{N}_i}{N}}$$ (18)

where R_i is the R-factor determined from the known structure of the ith structural domain using SVD, N_i is the number of RDCs measured for the ith structural domain, and N is the total number of experimental RDCs measured for the multidomain protein. Agreement between experimental and back-calculated SAXS data, is evaluated in terms of χ² with a target value of ~1.¹⁵² Final R-factor and χ² values that are smaller than the corresponding target value are indicative of overfitting the data.

In the following sections the successful application of rigid-body ensemble refinement driven by RDC and SAXS data to the challenging cases of the 128 kDa dimer of bacterial Enzyme I and the HIV-1 capsid protein will be discussed.

4.2. Solution Structure and Dynamics of Bacterial Enzyme I

Enzyme I (EI) is the first protein in the phosphoenolpyruvate (PEP):sugar phosphotransferase system (PTS),¹⁵³ a key signal transduction pathway involved in the regulation of central carbon metabolism in bacteria. EI is responsible for both activation and regulation of the overall PTS.^19,154,155 EI is a large, dynamic protein that presented a real challenge to structural biologists. In this section we will analyze how only the integrated analysis of data from multiple techniques allowed for characterization of the structure and dynamics of EI.

From the structural point of view, EI is a 128 kDa dimer of identical subunits (Figure 8). Each subunit comprises two structural domains.¹⁵⁶ The N-terminal domain (EIN) is further divided in two subdomains, named EIN^α and EIN^α/β, respectively. EIN^α/β contains the active site residue (His189) that is autophosphorylated by phosphoenolpyruvate (PEP). EIN^α provides the binding site for HPr (the second protein in the PTS pathway).^157,158 The C-terminal domain (EIC) is responsible for protein dimerization and contains the binding site for PEP.^17,159

Figure 8.

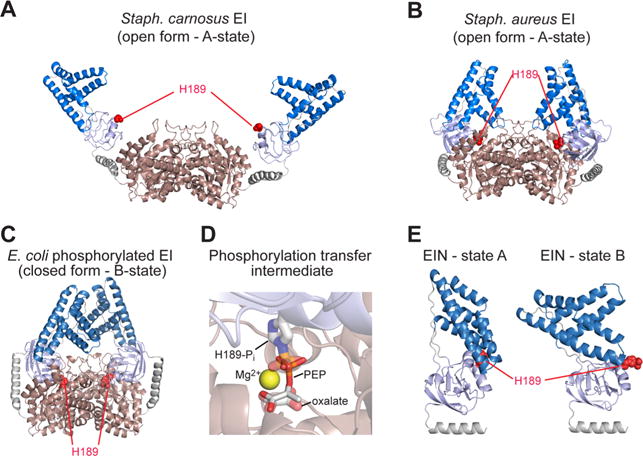
X-ray structures of bacterial Enzyme I (EI). (A) EI from Staph. carnosus (2HRO);¹⁶¹ (B) EI from Staph. aureus (2WQD);¹⁶⁰ (C) phosphorylated EI from E. coli (2HWG).¹⁶² The C-terminal dimerization domain (EIC) is colored pink; the EIN^α and EIN^α/β subdomains of the N-terminal domain (EIN) are colored blue and light blue, respectively; the active site His189, located in the EIN^α/β subdomain, is shown as red spheres. (D) Structural model of phosphoenolpyruvate (PEP) bound to the active site of the E. coli EI structure. PEP is shown as solid sticks, and the Mg²⁺ ion is displayed as a yellow sphere. The phosphorylated His189 and the oxalate molecule in the X-ray structure of the phosphoryl transfer intermediate in the closed state (2HWG) are displayed as transparent sticks. (E) A^157,174 and B¹⁶² conformations of the EIN domain seen in the open and closed states of EI, respectively.

Several X-ray structures of EI have been solved showing that the enzyme can adopt different conformations (Figure 8). Indeed, the free EI from Staphylococcus aureus¹⁶⁰ and Staphylococcus carnosus¹⁶¹ display two distinct open states in which the His189 is positioned more than 20 Å away from the PEP binding site on EIC, and the EIN domain adopts a conformation, named the A-state, in which the EIN^α and EIN^α/β subdomains form extensive contacts with one another. On the other hand, the X-ray structure of a trapped phosphorylated intermediate of Escherichia coli EI,¹⁶² solved by crystallizing EI from a solution containing PEP and Mg²⁺ and quenching the autophosphorylation reaction using oxalate, shows the enzyme in a closed conformation. In the closed state His189 is inserted into the PEP binding pocket on EIC and is positioned for in-line phosphoryl transfer from PEP to EIN. The open-to-closed transition is coupled to a conformational change in the EIN domain that involves a ~90° reorientation of EIN^α relative to EIN^α/β (Figure 8). The EIN conformation observed in closed EI is referred to as B-state. Interestingly these rearrangements do not affect the local fold of the structural domains (EIN^α, EIN^α/β and EIC) that display the same structure in all the crystal structures. However, an analysis of the EI structures on the basis of experimental SAXS data acquired for free EI indicates that none of these crystal structures corresponds to the solution structure of the enzyme (χ² for the fits to the SAXS data is >30 for all three crystal structures).^47,163

To solve the solution structure of free EI, a conjoined rigid body/torsion angle/Cartesian coordinate simulated annealing refinement protocol driven by the experimental RDC and SAXS was employed in which the structural domains were treated as rigid bodies, the backbone of the linkers were given Cartesian degrees of freedom, and side chains were allowed torsion degrees of freedom.⁴⁷ Due to the large size of the enzyme, assignment of the NMR spectra was achieved by transferring the assignments of the isolated EIN domain onto the spectra of the full-length protein. At the time this work was performed, no assignments were available for EIC. Therefore, the structure calculation used only 58 backbone ¹H–¹⁵N RDCs from the EIN domain (29 for EIN^α and 29 for EIN^α/β). These RDCs are fully consistent with the NMR and X-ray structures of isolated EIN in the A conformation but incompatible with the B conformation found in the structure of the closed state of EI; hence the EIN domain was held fixed to the NMR structure of free EIN. As mentioned earlier, the structure of the EIC dimer is the same in all the X-ray structures of EI; therefore, the EIC portion of the enzyme was kept fixed to the X-ray coordinates throughout the calculation. Given that one of the principal axes of the alignment tensor must coincide with the C₂ symmetry axis of the dimer,^164,165 the orientation of the EIN domains relative to the EIC dimer can be determined from sparse RDCs located only in the EIN domain. The results of the conjoined RDC/SAXS refinement revealed a new open structure for EI that is consistent with the experimental data (Figure 9). Interestingly, the data were fully satisfied by a single conformation, suggesting that the closed state, if at all present, is populated to a very minor extent (<5%).

Figure 9.

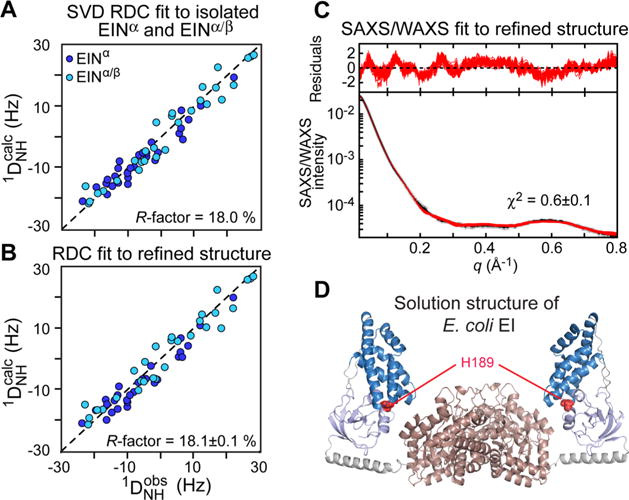
Combined SAXS/RDC refinement of the E. coli EI structure. (A) Comparison of the observed and calculated RDCs obtained by SVD fits to the individual EIN^α (blue circles) and EIN^α/β (light blue circles) subdomains. (B) Comparison of the observed and calculated RDCs for the refined structure of the EI dimer. The resulting RDC R-factor is the same (within experimental error) as the RDC R-factor obtained from the SVD fits to the individual subdomains. (C) Agreement between the experimental and back calculated SAXS/WAXS curve. (D) Solution structure of unliganded E. coli EI obtained by combined SAXS/RDC refinement (2KX9)⁴⁷ Color coding as in Figure 8. Adapted from Schwieters et al. (2010).⁴⁷

More recently, a study combining NMR relaxation dispersion measurements and SAXS confirmed that the closed structure is sampled at detectable populations only in the presence of PEP.¹⁶³ Indeed, PEP-binding suppresses conformational exchange in two loops of EIC that are part of the EIN/EIC interface in closed EI. This structural stabilization of the EIC domain by PEP binding activates the open-to-closed transition that allows EI to access the catalytically competent closed state. In addition, systematic analysis of SAXS profiles acquired for wild type EI (EI^WT) and two active site mutants on the basis of the solution structure of open EI and of the crystallographic closed state, revealed that the closed state of the enzyme is largely prevalent (best fit population ~60%) in the complex between PEP and the H189A (EI^A) mutant of the enzyme,¹⁶³ opening the way to structural characterization of closed EI in solution.¹⁴² 23, 20, and 25 backbone 1H–¹⁵N RDCs were measured for the EIN^α, EIN^α/β, and EIC, respectively, by aligning the EI^A-PEP complex in neutral bicelles, and were used together with SAXS data to restrain a simulated annealing refinement calculation in which EIN^α, EIN^α/β and EIC were treated as rigid bodies with the linkers given Cartesian degrees of freedom. Refinement against the RDC or SAXS data individually converges to a single structure representation of EI^A-PEP that reproduces the experimental data set used in the refinement but not the omitted data set (Figure 10). A two-member ensemble, however, is required to simultaneously satisfy the RDC and SAXS data (Figures 10 and 11). The two conformations are approximately equally populated and correspond to the crystallographic closed state, which is competent for phosphoryl transfer from PEP to the EIN domain, and a partially closed state that likely represents an intermediate between the fully closed state, which is only transiently sampled in the EI^WT-PEP complex, and the fully open apo state.¹⁴² The partially closed state revealed by the hybrid RDC/SAXS approach is likely involved in substrate-binding and product-release steps, and eluded characterization by other crystallographic and solution techniques.

Figure 10.

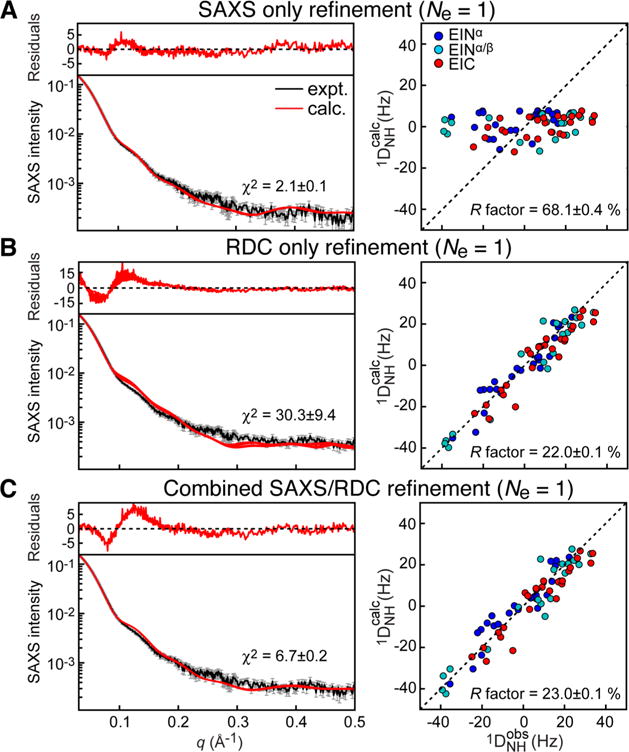
Comparison between experimental and back-calculated SAXS (left) and RDC (right) data for a single-structure refinement of the EI^A-PEP complex. (A) Refinement using only SAXS data. (B) Refinement using only RDC data. (C) Combined SAXS/RDC refinement. Adapted from Venditti et al. (2015).¹⁴²

Figure 11.

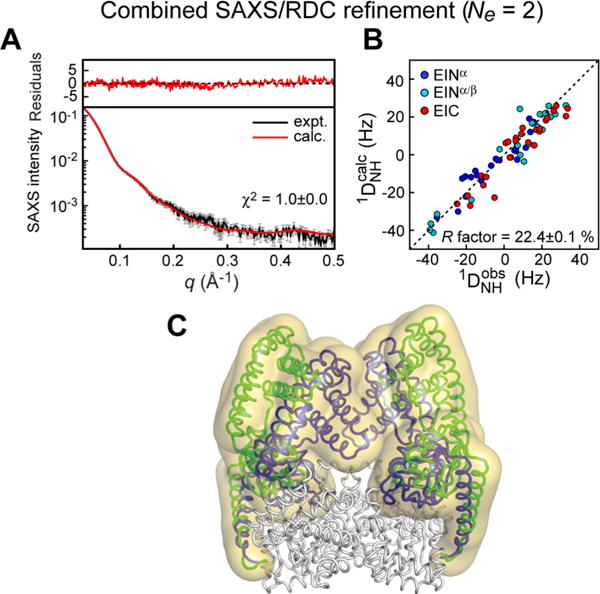
Combined SAXS/RDC refinement of the EI^A-PEP complex using a two-member ensemble representation. (A) Agreement between experimental and back calculated SAXS curve. (B) Comparison of observed and calculated RDCs. (C) Structural ensemble obtained for EI^A-PEP complex. The overall distribution of EIN relative to EIC is shown as a reweighted atomic probability map¹⁷⁵ plotted at 2% of maximum (transparent yellow surface). Representative structures for the closed and partially closed EI conformations (PDB code 2N5T) are shown as blue and green ribbons, respectively. Adapted from Venditti et al. (2015).¹⁴²

4.3. Solution Structure and Dynamics of the HIV-1 Capsid Protein

The human immunodeficiency virus (HIV-1) capsid protein assembles into a cone that encloses viral RNA.^166–168 The full-length capsid protein (CA_FL) consists of an arrow-shaped N-terminal domain (NTD) and a globular C-terminal domain (CTD) that undergoes a monomer/dimer equilibrium (dimer dissociation constant, K_D, ~40 μM at 25 °C) in solution (Figure 12). The N- and C-terminal domains are separated by a short, flexible linker (Figure 12). In the context of the mature HIV capsid, the N-terminal domains assemble into ~250 hexameric¹⁶⁹ and 12 pentameric¹⁶⁶ rings that form the exterior of the capsid. The N-terminal domain rings are connected to one another by symmetric C-terminal domain dimers (Figure 12). Although assembly of the HIV-1 capsid plays a crucial role in the virus lifecycle and infectivity, obtaining a comprehensive structural characterization of full length capsid protein prior to assembly has been hampered by the fact that the system is highly dynamic and heterogeneous. Indeed, large amplitude motions between the N- and C-terminal domains, as well as the presence of a dynamic monomer/dimer equilibrium, result in severe line-broadening of the NMR resonances of the linker and dimer-interface regions, making the study of full length capsid protein by conventional NMR techniques impossible.

Figure 12.

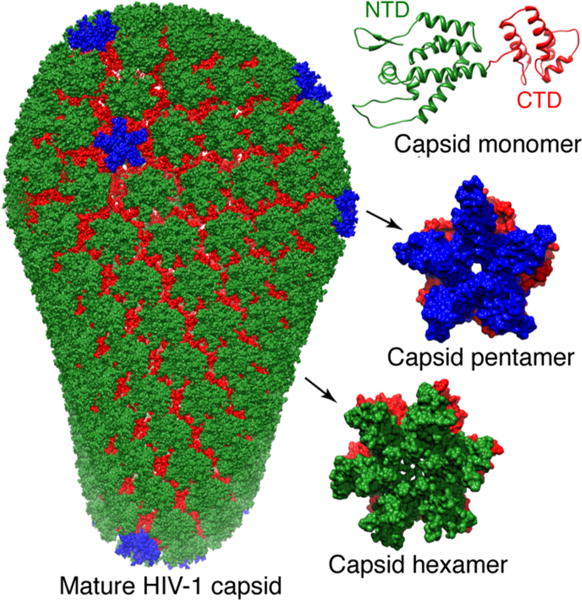
HIV-1 capsid assembly. The capsid protein comprises N (green) and C (red) terminal domains (top right).¹⁷⁶ The N-terminal domains associate to form either pentamers¹⁶⁶ (middle right with N-terminal domains in blue) or hexamers¹⁶⁹ (bottom right with N-terminal domains in green) which assemble via the C-terminal domain dimers to form a cone comprising ~250 hexamers and exactly 12 pentamers (left).¹⁶⁶ Adapted from Deshmukh et al.¹⁴⁷

By using the hybrid approach described here, Deshmukh et al. quantitatively determined the conformational space spanned by the N-terminal domain relative to the C-terminal domain in both monomeric and dimeric capsid protein.¹⁴⁷ The RDC and SAXS data were acquired for the full-length capsid protein at different concentrations (ranging from 50 μM to 260 μM) and used simultaneously to refine a conformational ensemble that include both monomeric and dimeric species. In the calculation the relative populations of monomer and dimer were fixed based on the protein concentration and dimer K_D’s (determined independently by analytical ultracentrifugation at the same temperatures as those used in the RDC and SAXS measurements), and an equal number of ensemble members was used to describe the monomeric and dimeric species (i.e., $N_{\mathrm{e}}^{\text{monomer}}=N_{\mathrm{e}}^{\text{dimer}}$). The optimal ensemble size $(N_{\mathrm{e}}=N_{\mathrm{e}}^{\text{monomer}}=2N_{\mathrm{e}}^{\text{dimer}})$ was determined empirically to be 10. Indeed, further increases in ensemble size did not result in any significant improvements in agreement with the experimental RDC and SAXS data (Figure 13). The results show that the conformational space sampled by the N-terminal domain relative to the C-terminal domain is different in the monomer and dimer with a distinct pattern of transient interactions between the two domains (Figure 14). This is due to the fact that much of the conformational space sampled by the N-teminal domain in the monomer is no longer accessible in the dimer due to steric clash with the C-terminal domain dimer. The conformational ensembles derived for the dimer and monomer are characterized by six (Figure 14A) and three (Figure 14B) main structural clusters, respectively. Interestingly, one of the clusters obtained for the protein dimer (cluster 6, which account for ~5% of the conformational ensemble of dimeric full length capsid protein) closely resembles the configuration sampled in both pentameric and hexameric capsid assemblies (Figure 14C).¹⁴⁷ These results suggest that the HIV-1 capsid assembles via conformational selection of a sparsely populated species and that stabilization of other clusters relative to cluster 6 may partially inhibit capsid assembly. In this regard the transient interactions between the N and C-terminal domains observed in cluster 2 of the dimer would be predicted to be enhanced by mutation of Pro38, Arg132 and Lys203 to a hydrophobic residue (alanine) consistent with the experimentally observed reduced capsid assembly rates for these three mutants.

Figure 13.

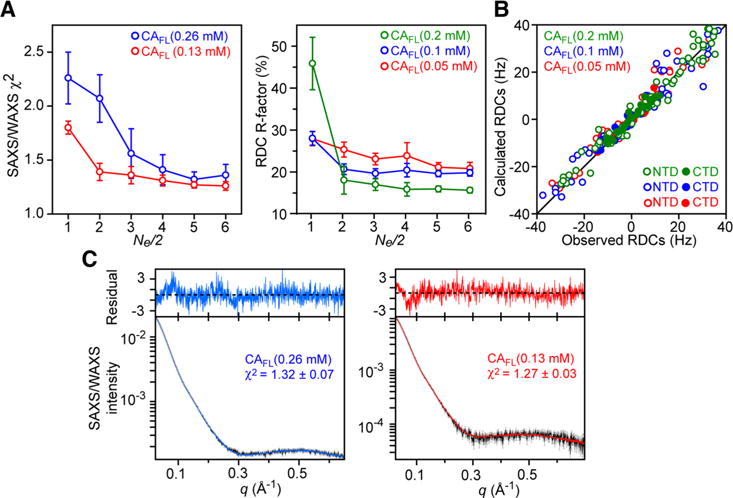
RDC and SAXS/WAXS driven ensemble simulated annealing refinement of the HIV-1 capsid protein. Both monomer and dimer are included in the calculations and are represented by an equal number of ensemble members (N_e/2). RDC and SAXS/WAXS data at several different concentrations are treated simultaneously. (A) SAXS/WAXS χ² and RDC R-factor as a function of ensemble size. (B) Correlation between observed and back-calculated RDCs based on molecular shape at three concentrations of capsid protein. (C) Agreement between observed (black) and calculated SAXS/WAXS curves at two capsid protein concentrations. The residuals, given by $(I_i^{\text{calc}}-I_i^{\text{obs}})/I_i^{\text{err}}$, are plotted above the curves. Error bars: ± 1 standard deviation. Adapted from Deshmukh et al.¹⁴⁷

Figure 14.

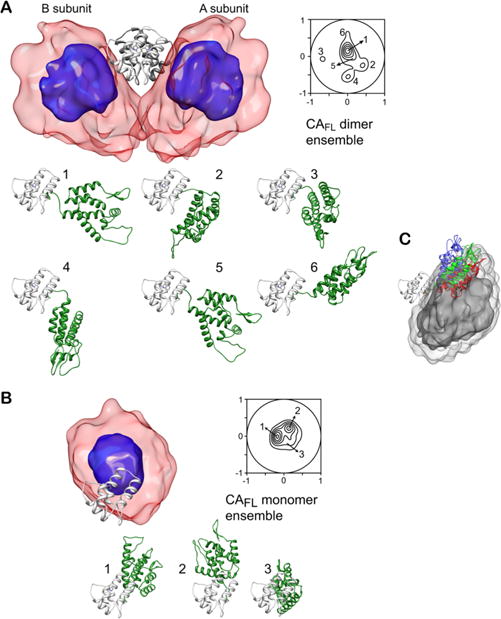
Structural ensembles calculated for full-length wild type HIV-1 capsid protein. The dimer and monomer ensembles are shown in (A) and (B), respectively. The overall distribution of the N-terminal domain relative to the C-terminal domain (gray ribbon) is displayed as a reweighted atomic probability density map plotted at 50% (blue) and 10% (red transparent) of maximum. Projection contour maps showing the distribution of the position of the centroid of the N-terminal domain relative to the C-terminal domain are also shown. The dimer and monomer ensembles are characterized by six and three main clusters, respectively. (For clarity only a single subunit is shown for the six dimer clusters; the orientation of the C-terminal domain is the same throughout). (C) Position of the N-terminal domain in cluster 6 (red) of the capsid protein dimer ensemble compared to that in the pentamer (green) and hexamer (blue) with the C-terminal domain shown as a gray ribbon, and the atomic probability density map of the N-terminal domain in the capsid dimer plotted at 10% (dark gray) and 2% (light gray) of maximum. Adapted from Deshmukh et al.¹⁴⁷

5. CONCLUDING REMARKS

An atomic level understanding of protein conformational dynamics is crucial to modem structural biology and holds the promise to address unanswered questions on the functioning of important biological molecules such as enzymes, molecular machines, and allosteric systems.¹⁷⁰ This goal, however, is challenging as the great majority of biologically relevant, dynamic systems are large and multimeric and, therefore, elude structural characterization by conventional techniques. In this context the use of integrative approaches that combine structural data from multiple techniques have been shown to be very useful in determining 3D structural models of large and complex molecular systems.¹⁷¹ Here, we have reviewed the application of a hybrid method that uses conjoined rigid body/torsion angle/Cartesian simulated annealing refinement driven by SAXS and NMR-derived RDC data to model conformational states in large multidomain proteins. This hybrid approach is streamlined because, once the high resolution structures of the rigid domains used as building-blocks are known from experimental or computational studies, only sparse RDC data complemented by SAXS data are required to reliably calculate conformational ensembles. This hybrid strategy has been successfully employed to obtain a quantitative description of the magnitude and distribution of interdomain motions in the HIV-1 capsid protein¹⁴⁷ and the complex between bacterial Enzyme I and PEP.¹⁴² The methodology described here is readily transferred to the study of many other challenging systems, especially those involving large multidomain proteins and their complexes. Moreover, not only can this approach characterize the conformational space sampled by one domain relative to another as in the case of the HIV-1 capsid protein,¹⁴⁷ but it can also detect the simultaneous existence of distinct conformations and characterize their structures as in the case of the 128 kDa complex of Enzyme I (H189A) with PEP.¹⁴² Further, in the case of the HIV-1 capsid protein the simultaneous existence of monomer and dimer can readily be handled.¹⁴⁷ In this regard it is worth noting that it would be impossible to characterize a mixture of coexisting states by crystallography as the crystallization procedure would only allow one state to crystallize out, and the probability of obtaining crystals of the various states is likely to be very small. Similarly, the coexistence of multiple conformational states renders interpretation of cryoelectron microscopy images extremely difficult if not impossible. Of course, any structural approach involving solution NMR does place certain limits on molecular size but, with deuteration and appropriate methyl-specific labeling, systems up to 200–300 kDa can potentially be tackled.

Biographies

Vincenzo Venditti is currently an Assistant Professor in the Department of Chemistry and in the Roy J. Carver Department of Biochemistry, Biophysics and Molecular Biology at Iowa State University (2015 to present). He received his Ph.D. degree from the Università degli Studi di Siena and was a postdoctoral fellow in the Laboratory of Chemical Physics at the NIH (2009–2014). His current interests lie in the use of NMR spectroscopy to study structure, dynamics, and interactions in large, multidomain systems.

Timothy K. Egner is currently a graduate student in the Department of Chemistry at Iowa State University. He received his B.S. in Biochemistry and Mathematics from North Central College in 2014. His current research focuses on the use of NMR spectroscopy for structural characterization of biological macromolecules.

G. Marius Clore is currently an NIH Distinguished Investigator in the Laboratory of Chemical Physics at the National Institute of Diabetes and Digestive and Kidney Disease, NIH. He received a B.Sc. (1st class honors) in Biochemistry from University College London (1976), an M.D. from University College Hospital Medical School (1979), and a Ph.D. from the National Institute for Medical Research, London (1982). He was a member of the Scientific Staff of the MRC National Institute for Medical Research, London (1980–1984); Head of the Biological NMR Group at Max Planck Institute for Biochemistry, Martinsried, Germany (1984–1988); and Senior Investigator (1988–2011), Chief of the Protein NMR Section (1991 to present), and NIH Distinguished Investigator (2011–present) in the Laboratory of Chemical Physics, NIDDK, at the National Institutes of Health. He is an elected Member of the United States National Academy of Sciences, a Fellow of the American Academy of Arts and Sciences, and a Foreign Member of the Academia Europeae. Among the prizes he has been awarded are the Royal Society of Chemistry Centenary Prize (2011) and the Biochemical Society Centenary Award and Francis Gowland Hopkins Memorial Lecture (2013).