Abstract
This study examined the power production differences between weightlifting derivatives through a comparison of power-time (P-t) curves. Thirteen resistance-trained males performed hang power clean (HPC), jump shrug (JS), and hang high pull (HHP) repetitions at relative loads of 30%, 45%, 65%, and 80% of their one repetition maximum (1RM) HPC. Relative peak power (PPRel), work (WRel), and P-t curves were compared. The JS produced greater PPRel than the HPC (p < 0.001, d = 2.53) and the HHP (p < 0.001, d = 2.14). In addition, the HHP PPRel was statistically greater than the HPC (p = 0.008, d = 0.80). Similarly, the JS produced greater WRel compared to the HPC (p < 0.001, d = 1.89) and HHP (p < 0.001, d = 1.42). Furthermore, HHP WRel was statistically greater than the HPC (p = 0.003, d = 0.73). The P-t profiles of each exercise were similar during the first 80-85% of the movement; however, during the final 15-20% of the movement the P-t profile of the JS was found to be greater than the HPC and HHP. The JS produced greater PPRel and WRel compared to the HPC and HHP with large effect size differences. The HHP produced greater PPRel and WRel than the HPC with moderate effect size differences. The JS and HHP produced markedly different P-t profiles in the final 15-20% of the movement compared to the HPC. Thus, these exercises may be superior methods of training to enhance PPRel. The greatest differences in PPRel between the JS and HHP and the HPC occurred at lighter loads, suggesting that loads of 30-45% 1RM HPC may provide the best training stimulus when using the JS and HHP. In contrast, loads ranging 65-80% 1RM HPC may provide an optimal stimulus for power production during the HPC.
Key points.
The JS and HHP exercises produced greater relative peak power and relative work compared to the HPC.
Although the power-time curves were similar during the first 80-85% of the movement, the JS and HHP possessed unique power-time characteristics during the final 15-20% of the movement compared to the HPC.
The JS and HHP may be effectively implemented to train peak power characteristics, especially using loads ranging from 30-45% of an individual’s 1RM HPC.
The HPC may be best implemented using loads ranging from 65-80% of an individual’s 1RM HPC.
Key words: Hang power clean, jump shrug, hang high pull, mechanical work, time normalization
Introduction
Power output is a common variable used to characterize the performance of athletes (Baker and Newton, 2008; Barker et al., 1993; Young et al., 2005). In the case of human movement, mechanical power is defined as the rate at which work is performed. When it comes to athletic movements, a given task requires a certain amount of work to be performed. Thus, it could be argued that athletes who perform the work necessary to complete a task faster may have an advantage. While most team sports require a number of tasks to be performed throughout a competition (e.g. soccer, football, etc.), some individual competitions may be decided based on the ability to perform a given task’s work faster than their opponents (e.g. 100 meter dash). Considering that strong relationships have been identified between many fundamental movements such as sprinting (Weyand et al., 2000; 2010), jumping (Hori et al., 2008; Newton et al., 1999), change of direction tasks (Nimphius et al., 2010; Spiteri et al., 2012), and power, it should come as no surprise that the development of power is often a primary focus of many resistance training programs.
While a number of resistance training strategies have been identified for improving power (Cormie et al., 2011), several studies have indicated that weightlifting movements may provide a superior training effect compared to traditional resistance training (Hoffman et al., 2004), jump training (Teo et al., 2016; Tricoli et al., 2005), and kettlebell training (Otto III et al., 2012). Traditionally, if practitioners elect to implement weightlifting movements in training, they typically prescribe the full movements (e.g. clean, snatch, and jerk) or their catching derivatives (e.g. hang power clean (HPC), power snatch, etc.) where the full squat catch is omitted (Suchomel et al., 2017). While weightlifting catching derivatives may improve an athlete’s strength and power as evidenced above, weightlifting pulling derivatives that omit the catch phase may provide several advantages including decreased movement complexity, easier to learn/teach movements, and greater ability to provide an force or velocity overload stimulus (Suchomel et al., 2015b; 2017; Suchomel and Sato, 2013). In fact, previous literature has indicated that weightlifting pulling derivatives may provide a training stimulus that is comparable (Comfort et al., 2011a; 2011b) or greater (Kipp et al., 2016; Suchomel and Sole, 2016; Suchomel et al., 2014d; 2014e) than weightlifting catching derivatives.
A growing body of literature has shown the value of examining the differences in force-time and power-time (P-t) curve analyses as a means of comparing resistance training exercises (Suchomel and Sole, 2016), performance levels (Sole et al., 2017), exercise intensities (Cormie et al., 2008), and adaptations to different training modalities (Cormie et al., 2009). These types of analyses benefit sport scientists and practitioners by providing not only instantaneous values along the force-time or P-t curve, but also providing a greater mechanistic understanding of performance. Although previous comparisons between weightlifting catching and pulling derivatives have examined power (Comfort et al., 2011b; Kipp et al., 2016; Suchomel et al., 2014d), no study to date has investigated the P-t curves of weightlifting derivatives. Because maximal power is never applied instantaneously during sport or training, an analysis of power production with respect to time between weightlifting derivatives would provide a greater understanding of how power is developed during each exercise and how best to implement each exercise. Thus, the purpose of this study was to examine power production between the HPC, jump shrug (JS), and hang high pull (HHP) through an analysis of P-t curves of each movement. Based on previous research, it was hypothesized that the JS and HHP would produce greater power magnitudes and possess unique power-time characteristics compared to the HPC.
Methods
Design
A repeated measures design was used to compare the characteristics of the P-t curves of the HPC, JS, and HHP performed at several relative loads. Each participant performed repetitions of the HPC, JS, and HHP at 30, 45, 65, and 80% of their one repetition maximum (1RM) HPC. Relative peak power (PPRel), relative work (WRel), and profiles of normalized P-t curves were compared between exercises and loads.
Participants
The participants in the current study included thirteen resistance-trained men (age = 21.2 ± 1.1 years; body mass = 86.1 ± 17.7 kg; height = 1.81 ± 0.06 m; 1RM HPC = 110.2 ± 22.4 kg; relative 1RM HPC = 1.3 ± 0.2 kg·kg-1). Each participant competed in either NCAA Division III track and field (sprints, jumps, or throws) or collegiate club/intramural sports and had at least two years of previous training experience with weightlifting movements. All of the participants performed their testing during their preseason phase of training. Each participant read and signed an informed consent document in accordance with the University’s Institutional Review Board.
Procedures
All data were collected during four separate testing sessions. The first testing session was to determine each participant’s 1RM HPC and to familiarize them with the technique of the JS and HHP exercises. Prior to performing 1RM attempts, participants completed a standardized warm-up that consisted of stationary cycling, lower body dynamic stretches, and submaximal HPC sets at 30, 50, 70, and 90% of their self-estimated 1RM HPC (Suchomel et al., 2014a). Heavier loads were attempted until the participant failed a single load twice. The participants were given 3-5 minutes of rest in between each maximal attempt and the heaviest load lifted was recorded as their 1RM. A minimum increase of 2.5 kg was required between 1RM attempts. After a self-selected rest period, each participant performed submaximal exercise JS and HHP sets with 30% of their 1RM HPC to familiarize participants with each movement and ensure proper technique.
Each participant completed three subsequent testing sessions following their 1RM testing session. During the remaining testing sessions, each participant performed exercise sets of either the HPC, JS, or HHP at 30, 45, 65, and 80% of their 1RM HPC. These loads were examined based on previous literature (Suchomel and Sole, 2016; Suchomel et al., 2014d) and the findings of additional literature that displayed unique force-velocity characteristics of between several lower body exercises across various loads (Cormie et al., 2007; Soriano et al., 2015; Thomas et al., 2007). The technique and cues used for each exercise have been discussed in previous literature (Suchomel et al., 2014a; 2014b; 2014c). All exercises started with the participants in a standing position, knees slightly bent, and the bar positioned at the mid-thigh (DeWeese et al., 2013). Participants began the exercises by performing a countermovement by flexing at the hip while maintaining a constant knee angle and lowering the barbell to a position just above their patella. Following the countermovement, participants immediately transitioned back to the mid-thigh by flexing their knees and extending their hips to bring the torso to an upright position. Participants then performed the second pull movement by aggressively extending their hip, knee, and ankle joints. Using instructional cues from the above literature, each participant 1) “drove their elbows upward”, rotated their elbows around the barbell rapidly, driving them “forward and up”, and caught the barbell across their shoulders in a semi-squat position during the HPC, 2) “jumped as high as possible” while simultaneously shrugging their shoulders during the JS, or 3) “drove their elbows upward” and elevated the barbell to chest height during the HHP.
Each participant performed the standardized warm-up described above and an exercise specific warm-up which included submaximal sets of the exercise that was to be performed that day (i.e. HPC, JS, or HHP) with 30 and 50% of their 1RM HPC before performing testing repetitions. Following the exercise specific warm-up sets, participants performed two repetitions with maximum effort of the testing exercise at each load (30, 45, 65, and 80% 1RM HPC) with one minute of rest between each repetition and two minutes between each load. The exercise order was randomized over the final three testing sessions and participants had 2-7 days between sessions. The load order was also randomized during the first exercise testing session in an attempt to prevent a fatigue or potentiation order effect. As a result, the randomized load order for participants may have required them to perform their first testing repetitions at either 30, 45, 65, or 80% 1RM HPC following the specific warm-up. The load order that was performed during the first testing session was kept constant for each participant during the remaining testing sessions. Participants maintained their normal training regimen and the testing sessions were incorporated into their training and class schedules. The testing sessions were scheduled on the same day that participants completed their resistance training sessions; however, the testing sessions were completed prior to any training. Finally, each exercise testing session was performed at the same time of day in order to minimize the influence of circadian rhythms.
Data analyses
The HPC, JS, and HHP repetitions were performed on a 92 x 92 cm portable force platform (Type 9290AD, Kistler, Winterthur, Switzerland) sampling at 500 Hz. Based on previous methods (Suchomel and Sole, 2016), the onset of the concentric phase of each exercise was defined as the time point at which the system (lifter + external load) velocity changed from a negative to positive value. The end of the concentric phase was then determined as the point where force fell 10 N below system weight following peak concentric force. Power-time data were calculated as the product of force and velocity at each time point. The greatest magnitude of power during the concentric phase (i.e. peak power) was determined and subsequently divided by the participant’s body mass (i.e. peak power · participant body mass-1) to calculate the PPRel for each repetition. The WRel performed during each HPC, JS, and HHP repetition was calculated through integration of the positive portion of the P-t curve and was expressed relative to the participant’s body mass (i.e. [power · time] · participant body mass-1). Finally, propulsion duration was defined as the length of time where the system (participant + load) velocity changed from negative to positive to the time point where force fell 10 N below system weight. To represent a more true score and reduce random error (Henry, 1967), the average PPRel and WRel between the two repetitions at each load were used for statistical analysis. A computer re-sampling technique described in previous research (Suchomel and Sole, 2016) was used to perform a point-by-point visual comparison between the P-t curves of each lift. Each P-t curve was time normalized by equalizing the number of samples contained in each curve by adjusting the time delta between samples and then resampling the signal. Upon completion, the P-t curves could be expressed as a percentage (0-100% of the movement) and comparisons could be made between curves. Resampling was performed based on the repetition with the fewest samples. In the present study, all repetitions across all loads were normalized to 231 samples. Following the resampling procedure, the new mean sampling frequency was 329 ± 66 Hz. It should be noted that the normalized curves were used only to compare P-t profiles. The instantaneous variables PPRel and WRel were calculated from the raw P-t data of each repetition.
Statistical analyses
Normality of the data was examined using the Shapiro-Wilks test. The test-retest reliability of PPRel and WRel was determined using two-way random effects mixed model intraclass correlation coefficients (ICC) and typical error expressed as a coefficient of variation percentage. Two, 3 x 4 (exercise x load) repeated measures ANOVA were used to examine the statistical differences of the PPRel and WRel produced during each HPC, JS, and HHP repetition. Greenhouse-Geisser values were reported if the assumption of sphericity was violated. When necessary, Bonferroni post hoc comparisons were used to identify main effect differences between exercises and loads. Statistical power (c) was calculated for all main effect comparisons while 95% confidence intervals (CI) were calculated for all pairwise comparisons. Furthermore, Cohen’s d effect sizes were used to display the practical significance between exercises and were interpreted as trivial, small, moderate, large, very large, and nearly perfect when effect sizes were 0.00-0.19, 0.20-0.59, 0.60-1.19, 1.20-1.99, 2.00-3.99, and ≥ 4.00, respectively (Hopkins, 2014). In order to determine likely differences between normalized average P-t curves, upper and lower 95% confidence limits were calculated for each average curve and then plotted to form upper and lower control limits. All statistical analyses were completed using SPSS 24 (IBM, Armonk, NY). Statistical significance for all analyses was set at p ≤ 0.05.
Results
The ICC and typical error results for PPRel and WRel during the HPC, JS, and HHP repetitions are displayed in Table 1 and the descriptive statistics for each exercise and load are displayed in Table 2.
Table 1.
Intraclass correlation coefficient (ICC) and typical error (TE) statistics for relative peak power and relative work for the hang power clean, jump shrug, and hang high pull.
| Exercise | Load (% 1RM hang power clean) | Relative Peak Power | Relative Work | ||
|---|---|---|---|---|---|
| ICC | TE (CV%) | ICC | TE (CV%) | ||
| Hang power clean | 30% | .93 | 7.2% | .85 | 17.3% |
| 45% | .98 | 6.1% | .93 | 13.8% | |
| 65% | .99 | 3.6% | .91 | 17.7% | |
| 80% | .94 | 6.7% | .73 | 18.7% | |
| Jump shrug | 30% | .99 | 2.1% | .95 | 9.2% |
| 45% | .98 | 3.9% | .98 | 7.3% | |
| 65% | .95 | 11.0% | .95 | 12.3% | |
| 80% | .97 | 5.4% | .82 | 19.4% | |
| Hang high pull | 30% | .98 | 4.4% | .90 | 10.9% |
| 45% | .99 | 3.4% | .92 | 10.4% | |
| 65% | .96 | 6.3% | .71 | 19.1% | |
| 80% | .96 | 6.8% | .70 | 17.5% | |
1RM = one repetition maximum
Table 2.
Descriptive power-time characteristics for the hang power clean, jump shrug, and hang high pull performed at 30, 45, 65, and 80% 1RM hang power clean. Data are means (±SD).
| Exercise | Load (% 1RM hang power clean) | PPRel (W · kg-1) |
WRel (J · kg-1) |
Repetition Duration (ms) | Propulsion Duration (ms) |
|---|---|---|---|---|---|
| Hang power clean | 30% | 37.4 (7.1) | 2.7 (.6) | 660.5 (154.2) | 205.1 (61.3) |
| 45% | 43.6 (7.7) | 3.4 (.7) | 682.5 (120.4) | 217.5 (48.9) | |
| 65% | 46.0 (7.1) | 4.1 (1.0) | 751.2 (111.4) | 241.8 (44.0) | |
| 80% | 45.1 (6.8) | 4.7 (.9) | 786.4 (112.1) | 269.9 (52.9) | |
| Jump shrug | 30% | 69.9 (6.7) | 5.7 (.8) | 678.2 (146.2) | 213.7 (44.3) |
| 45% | 69.3 (7.3) | 6.2 (1.0) | 715.5 (157.4) | 246.7 (73.9) | |
| 65% | 60.4 (5.9) | 5.4 (1.0) | 769.0 (154.1) | 257.1 (63.4) | |
| 80% | 55.8 (5.7) | 5.7 (1.2) | 805.3 (153.8) | 290.5 (75.1) | |
| Hang high pull | 30% | 49.7 (4.1) | 4.2 (.6) | 682.3 (138.6) | 221.8 (48.7) |
| 45% | 51.4 (5.0) | 4.4 (.8) | 701.0 (129.9) | 230.5 (56.0) | |
| 65% | 47.4 (5.2) | 4.6 (.8) | 752.8 (118.3) | 255.7 (46.6) | |
| 80% | 44.9 (5.5) | 4.6 (1.0) | 803.1 (147.1) | 274.5 (54.2) |
IRM = one repetition maximum; PPRel = relative peak power; WRel = relative positive work; Repetition Duration = entire movement time; Propulsion Duration = concentric movement time
Relative peak power
Statistically significant exercise (p < 0.001, c = 1.00), load (p < 0.001, c = 0.99), and interaction effects (p < 0.001, c = 1.00) existed for PPRel. Post hoc analysis indicated that the PPRel produced during the JS was statistically greater than the PPRel produced during the HPC (p < 0.001, d = 2.53, CI = 16.49 – 25.18) and HHP (p < 0.001, d = 2.14, CI = 11.48 – 19.57). In addition, HHP PPRel was statistically greater than HPC PPRel (p = 0.008, d = 0.79, CI = 1.41 – 9.21).
Relative work
Statistically significant exercise (p < 0.001, c = 1.00), load (p = 0.001, c = 0.96), and interaction effects (p < 0.001, c = 0.99) existed for WRel. Post hoc analysis indicated that the WRel produced during the JS was statistically greater than the WRel produced during the HPC (p < 0.001, d = 1.89, CI = 1.36 – 2.65) and HHP (p < 0.001, d = 1.42, CI = 0.69 – 1.91). In addition, HHP WRel was statistically greater than HPC WRel (p = 0.003, d = 0.73, CI = 0.26 – 1.15).
Power-time curve comparisons
Several areas of the HPC, JS, and HHP P-t curves displayed non-overlapping confidence limits (Figure 1 Figure 2 Figure 3 Figure 4). At 30% 1RM, JS PPRel was greater than the HPC and HHP from 80.9-100% and 85.2-100% of normalized time, respectively, while the HHP exceeded the HPC from 80.4-100%. At 45% 1RM, JS PPRel was greater than the HPC and HHP from 80.4-100% and 83.9-100% of normalized time, respectively, while the HHP exceeded the HPC from 82.1-89.1%. At 65% 1RM, JS PPRel was greater than the HPC and HHP from 83.0-98.7% and 84.3-90.3% of normalized time, respectively, while no differences were observed between the HHP and HPC normalized P-t curves. Finally, at 80% 1RM, JS PPRel was greater than the HPC and HHP from 81.7-97.3% and 83.4-96.9% of normalized time, while no differences were observed between the HHP and HPC normalized P-t curves.
Figure 1.
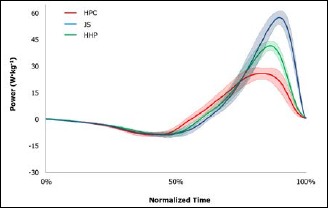
Normalized re-sampled power-time curves of the HPC, JS, and HHP performed at 30% 1RM HPC. Note: shaded areas represent 95% upper and lower confidence limits.
Figure 2.

Normalized re-sampled power-time curves of the HPC, JS, and HHP performed at 45% 1RM HPC. Note: shaded areas represent 95% upper and lower confidence limits.
Figure 3.
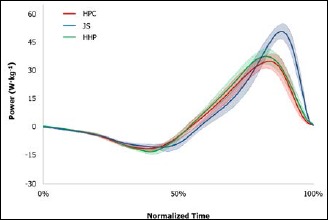
Normalized re-sampled power-time curves of the HPC, JS, and HHP performed at 65% 1RM HPC. Note: shaded areas represent 95% upper and lower confidence limits.
Figure 4.
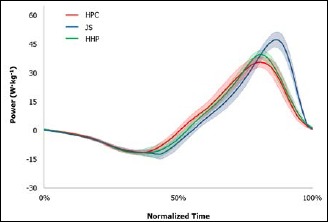
Normalized re-sampled power-time curves of the HPC, JS, and HHP performed at 80% 1RM HPC. Note: shaded areas represent 95% upper and lower confidence limits.
Discussion
This study examined the differences in PPRel, WRel, and P-t curve profiles between three weightlifting derivatives performed across a spectrum of loads. The primary findings of this study indicate that the JS produced statistically greater PPRel and WRel compared to the HPC and HHP across loads, while the HHP also produced statistically greater PPRel and WRel compared to the HPC. Furthermore, the JS displayed unique P-t differences compared to the HPC and HHP, while the HHP P-t characteristics were also unique compared to the HPC at several loads. Specifically, the JS produced greater power magnitudes during the final 15-20% of the movement.
The greatest PPRel was produced by the JS and followed in order by the HHP and HPC. Large practical significance, as indicated by effect sizes, was present when comparing JS PPRel and the PPRel produced during the HPC and HHP. In contrast, only moderate effects were present between the HHP and HPC. These findings are in line with previous research that examined absolute (Suchomel et al., 2014d) and joint-level (Kipp et al., 2016) power production between the HPC, JS, and HHP. It should be noted however that each exercise maximized PPRel at different loads, suggesting that each exercise possesses unique force-velocity characteristics. This notion is supported by a recent review (Suchomel et al., 2017) and additional literature that displayed similar PPRel during weightlifting derivatives that use various force-velocity strategies and those within in the current study (Haff and Stone, 2015). In line with previous research (Kipp et al., 2016; Suchomel et al., 2013; 2014a; 2015a), PPRel was maximized at 65%, 30%, and 45% 1RM HPC during the HPC, JS, and HHP, respectively. It is interesting to note that JS PPRel at every load was still greater than the greatest PPRel of both the HPC and HHP. With the exception of 80% 1RM HPC, the HHP also produced greater PPRel at every load compared to the HPC. Although all weightlifting movements are ballistic in nature, pulling derivatives may offer unique opportunities to manipulate the intent of the movement to potentially enhance the training stimulus. For example, athletes performing the JS should be cued to ‘jump as high as possible’ (Suchomel et al., 2014c), while this cue is not typically used when coaching the HPC. By being cued to jump as high as possible during the JS, the current participants likely accelerated throughout the entire triple extension movement compared to the HPC and HHP, which allowed them to produce greater PPRel magnitudes. From a practical standpoint, the greatest differences in power production between the pulling derivatives (i.e. JS and HHP) and catching derivative (i.e. HPC) were produced at the lighter loads of 30 and 45% 1RM HPC. These findings are in line with previous literature that has indicated that lighter loads maximize performance during the JS and HHP (Kipp et al., 2016; Suchomel et al., 2016b; 2014d), while moderate-heavy loads may maximize performance for the HPC (Kawamori et al., 2005; Kilduff et al., 2007; Suchomel et al., 2014a).
As noted above, power may be defined as the rate at which work is performed. While previous analyses only provided instantaneous values of power production (Comfort et al., 2011b; Kipp et al., 2016; Suchomel et al., 2014d), the current study examined continuous variables to provide a more thorough mechanistic understanding power production during weightlifting derivatives. Only one of the previously listed studies examined WRel during weightlifting derivatives, albeit the joint work performed on one side of the body (Kipp et al., 2016). Their results indicated that the load-averaged hip and knee positive joint work of the JS was greater than that of the HPC. The current study supports these findings with the results indicating that the greatest WRel was produced by the JS and was followed in order by the HHP and HPC. Large practically significant differences were present when comparing the WRel performed during the JS compared to the HPC and HHP, while moderate practical effects were present between the HHP and HPC. The current findings indicate that the participants spent more time performing positive work during the JS and HHP compared to the HPC, ultimately resulting in greater power production. This notion is supported by the P-t analyses, average duration and propulsion duration of each repetition in the current study, as well as the force production characteristics of each exercise. For example, Suchomel and Sole (2016) indicated that the second pull (i.e. triple extension of the hips, knees, and ankles) of the HPC may have been cut short, thus preventing greater force and impulse from being produced. The current study may also provide further evidence of this. It is interesting to note that propulsion duration increased with load in a similar manner between the exercises. While only trivial-small effect sizes existed between the exercise propulsion durations at each load, it is important to remember that the intent in which the propulsion phase is performed will dictate the performance outcomes (Lake et al., 2012; Newton et al., 1996). However, it is clear that further research examining phase characteristics of weightlifting derivatives is warranted.
To the authors’ knowledge no other study has compared time normalized P-t curves between weightlifting derivatives. The results of the current study indicated that the PPRel produced during the HPC, JS, and HHP was similar through the first 80-85% of the movement. This should not be surprising considering the mid-thigh starting position and mechanics of the countermovement and transition back to the mid-thigh prior to the second pull. In contrast, depending on the load, the PPRel produced during the final 15-20% of the time normalized movements displayed visible differences between exercises. The current analysis indicated that the JS produced greater relative power earlier during the second pull movement compared to the HPC and HHP. In addition, greater magnitudes of power were maintained over a longer duration, confirming that more positive WRel was performed. Although smaller practical differences existed, the HHP also produced unique P-t characteristics compared to the HPC. These findings are similar to a recent analysis of force-time differences between weightlifting derivatives (Suchomel and Sole, 2016). Because the current study examined P-t differences between several weightlifting derivatives performed across the loading spectrum, it is important to note that the greatest differences between the movements occurred at the lighter loads examined (i.e. 30 and 45% 1RM HPC). As noted above, these findings support previous literature that indicated that the JS and HHP may be best implemented using lighter loads (Kipp et al., 2016; Suchomel et al., 2013; 2015a), while the HPC may be best prescribed at moderate to heavy loads (Kawamori et al., 2005; Kilduff et al., 2007; Suchomel et al., 2014a).
Potential limitations to the current study should be acknowledged. The current study used loads based on the 1RM HPC for each exercise. However, it may be impractical to perform a 1RM for weightlifting pulling derivatives because there is currently a lack of criteria for what determines a successful repetition (Suchomel et al., 2016a). A second potential limitation may have been the randomization of loads. The current study attempted to prevent an order effect (fatigue or potentiation) through the randomization of loads; however, it may be possible that an order effect occurred due to the number of load order combinations. Thus, future research may consider examining the power production differences between weightlifting derivatives progressing from lighter loads to heavier loads. From a practical standpoint, this method may be desirable as it may mimic realistic resistance training practices.
Conclusions
The results of this study indicate that the JS and HHP possess unique P-t characteristics compared to that of the HPC. Specifically, the JS and HHP may produce greater PPRel and WRel as well as notable P-t differences during the second pull movement. The greatest differences in each variable were displayed at lighter loads of 30 and 45% 1RM HPC, suggesting that lighter loads may provide a greater overall training stimulus when implementing the JS and HHP exercises. In contrast, practitioners should prescribe moderate to heavy loads (65-80% 1RM) to maximize power output during the HPC.
Acknowledgements
The experiments comply with the current laws of the country in which they were performed. The results of this study do not constitute endorsement of the product by the authors or the journal. The authors report no conflicts of interest. There are no professional relationships with companies or manufacturers who will benefit from the results of the present study for either author.
Biographies

Timothy J. SUCHOMEL
Employment
Assistant professor and strength and conditioning coach at Carroll University in Waukesha, Wisconsin, USA.
Degree
PhD
Research interest
Weightlifting movements and their derivatives, postactivation potentiation, athlete monitoring, and adaptations to strength and power training.
E-mail: tsuchome@carrollu.edu

Christopher J. SOLE
Employment
Assistant professor at The Citadel – The Military College of South Carolina in Charleston, South Carolina, USA.
Degree
PhD
Research interest
Training monitoring, biomechanical analysis of resistance training exercise, adaptation to strength and power training, and relationships between training, performance, and injury in sport.
E-mail: csole@citadel.edu
References
- Baker D., Newton R.U. (2008) Comparison of lower body strength, power, acceleration, speed, agility, and sprint momentum to describe and compare playing rank among professional rugby league players. Journal of Strength and Conditioning Research 22, 153-158. [DOI] [PubMed] [Google Scholar]
- Barker M., Wyatt T.J., Johnson R.L., Stone M.H., O’Bryant H.S., Poe C., Kent M. (1993) Performance factors, psychological assessment, physical characteristics, and football playing ability. Journal of Strength and Conditioning Research 7, 224-233. [Google Scholar]
- Comfort P., Allen M., Graham-Smith P. (2011a) Comparisons of peak ground reaction force and rate of force development during variations of the power clean. Journal of Strength and Conditioning Research 25, 1235-1239. [DOI] [PubMed] [Google Scholar]
- Comfort P., Allen M., Graham-Smith P. (2011b) Kinetic comparisons during variations of the power clean. Journal of Strength and Conditioning Research 25, 3269-3273. [DOI] [PubMed] [Google Scholar]
- Cormie P., McBride J.M., McCaulley G.O. (2008) Power-time, force-time, and velocity-time curve analysis during the jump squat: impact of load. Journal of Applied Biomechanics 24, 112-120. [DOI] [PubMed] [Google Scholar]
- Cormie P., McBride J.M., McCaulley G.O. (2009) Power-time, force-time, and velocity-time curve analysis of the countermovement jump: impact of training. Journal of Strength and Conditioning Research 23, 177-186. [DOI] [PubMed] [Google Scholar]
- Cormie P., McCaulley G.O., Triplett N.T., McBride J.M. (2007) Optimal loading for maximal power output during lower-body resistance exercises. Medicine and Science in Sports and Exercise 39, 340-349. [DOI] [PubMed] [Google Scholar]
- Cormie P., McGuigan M.R., Newton R.U. (2011) Developing maximal neuromuscular power: part 2 - training considerations for improving maximal power production. Sports Medicine 41, 125-146. [DOI] [PubMed] [Google Scholar]
- DeWeese B.H., Serrano A.J., Scruggs S.K., Burton J.D. (2013) The midthigh pull: Proper application and progressions of a weightlifting derivative. Strength and Conditioning Journal 35, 54-58. [Google Scholar]
- Haff G.G., Stone M.H. (2015) Methods of developing power with special reference to football players. Strength and Conditioning Journal 37, 2-16. [Google Scholar]
- Henry F.M. (1967) “Best” versus “average” individual scores. Research Quartly 38, 317-320. [Google Scholar]
- Hoffman J.R., Cooper J., Wendell M., Kang J. (2004) Comparison of Olympic vs. traditional power lifting training programs in football players. Journal of Strength and Conditioning Research 18, 129-135. [DOI] [PubMed] [Google Scholar]
- Hopkins W.G. (2014) A scale of magnitude for effect statistics. Available from URL: http://sportsci.org/resource/stats/effectmag.html [Accessed May 15, 2017].
- Hori N., Newton R.U., Andrews W.A., Kawamori N., McGuigan M.R., Nosaka K. (2008) Does performance of hang power clean differentiate performance of jumping, sprinting, and changing of direction? Journal of Strength and Conditioning Research 22, 412-418. [DOI] [PubMed] [Google Scholar]
- Kawamori N., Crum A.J., Blumert P.A., Kulik J.R., Childers J.T., Wood J.A., Stone M.H., Haff G.G. (2005) Influence of different relative intensities on power output during the hang power clean: identification of the optimal load. Journal of Strength and Conditioning Research 19, 698-708. [DOI] [PubMed] [Google Scholar]
- Kilduff L.P., Bevan H., Owen N., Kingsley M.I., Bunce P., Bennett M., Cunningham D. (2007) Optimal loading for peak power output during the hang power clean in professional rugby players. International Journal of Sports Physiology and Performance 2, 260-269. [DOI] [PubMed] [Google Scholar]
- Kipp K., Malloy P.J., Smith J., Giordanelli M.D., Kiely M.T., Geiser C.F., Suchomel T.J. (2016) Mechanical demands of the hang power clean and jump shrug: A joint-level perspective. Journal of Strength and Conditioning Research, Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- Lake J.P., Lauder M.A., Smith N.A., Shorter K.A. (2012) A comparison of ballistic and non-ballistic lower-body resistance exercise and the methods used to identify their positive lifting phases. Journal of Applied Biomechanics 28, 431-437. [DOI] [PubMed] [Google Scholar]
- Newton R.U., Kraemer W.J., Hakkinen K. (1999) Effects of ballistic training on preseason preparation of elite volleyball players. Medicine and Science in Sports and Exercise 31, 323-330. [DOI] [PubMed] [Google Scholar]
- Nimphius S., McGuigan M.R., Newton R.U. (2010) Relationship between strength, power, speed, and change of direction performance of female softball players. Journal of Strength and Conditioning Research 24, 885-895. [DOI] [PubMed] [Google Scholar]
- Otto W.H., III, Coburn J.W., Brown L.E., Spiering B.A. (2012) Effects of weightlifting vs. kettlebell training on vertical jump, strength, and body composition. Journal of Strength and Conditioning Research 26, 1199-1202. [DOI] [PubMed] [Google Scholar]
- Sole C.J., Mizuguchi S., Sato K., Moir G.L., Stone M.H. (2017) Phase characteristics of the countermovement jump force-time curve: A comparison of athletes by jumping ability. Journal of Strength and Conditioning Research, Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- Soriano M.A., Jiménez-Reyes P., Rhea M.R., Marín P.J. (2015) The optimal load for maximal power production during lower-body resistance exercises: a meta-analysis. Sports Medicine 45, 1191-1205. [DOI] [PubMed] [Google Scholar]
- Spiteri T., Nimphius S., Wilkie J. (2012) Comparison of running times during reactive offensive and defensive agility protocols. Journal of Australian Strength and Conditioning 20, 73-78. [Google Scholar]
- Suchomel T.J., Beckham G.K., Wright G.A. (2013) Lower body kinetics during the jump shrug: impact of load. Journal of Trainology 2, 19-22. [Google Scholar]
- Suchomel T.J., Beckham G.K., Wright G.A. (2014a) The impact of load on lower body performance variables during the hang power clean. Sports Biomechanics 13, 87-95. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Beckham G.K., Wright G.A. (2015a) Effect of various loads on the force-time characteristics of the hang high pull. Journal of Strength and Conditioning Research 29, 1295-1301. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Comfort P., Lake J.P. (2017) Enhancing the force-velocity profile of athletes using weightlifting derivatives. Strength and Conditioning Journal 39, 10-20. [Google Scholar]
- Suchomel T.J., Comfort P., Stone M.H. (2015b) Weightlifting pulling derivatives: Rationale for implementation and application. Sports Medicine 45, 823-839. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., DeWeese B.H., Beckham G.K., Serrano A.J., French S.M. (2014b) The hang high pull: A progressive exercise into weightlifting derivatives. Strength and Conditioning Journal 36, 79-83. [Google Scholar]
- Suchomel T.J., DeWeese B.H., Beckham G.K., Serrano A.J., Sole C.J. (2014c) The jump shrug: A progressive exercise into weightlifting derivatives. Strength and Conditioning Journal 36, 43-47. [Google Scholar]
- Suchomel T.J., Nimphius S., Stone M.H. (2016a) The importance of muscular strength in athletic performance. Sports Medicine 46, 1419-1449. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Sato K. (2013) Baseball resistance training: Should power clean variations be incorporated? Journal of Athletic Enhancement 2(2). [Google Scholar]
- Suchomel T.J., Sole C.J. (2016) Force-time curve comparison between weightlifting derivatives. International Journal of Sports Physiology and Performance 11, 61-65. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Taber C.B., Wright G.A. (2016b) Jump shrug height and landing forces across various loads. International Journal of Sports Physiology and Performance 11, 61-65. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Wright G.A., Kernozek T.W., Kline D.E. (2014d) Kinetic comparison of the power development between power clean variations. Journal of Strength and Conditioning Research 28, 350-360. [DOI] [PubMed] [Google Scholar]
- Suchomel T.J., Wright G.A., Lottig J. (2014e). Lower extremity joint velocity comparisons during the hang power clean and jump shrug at various loads. In: XXXIInd International Conference of Biomechanics in Sports Eds: Sato K., Sands W.A., Mizuguchi S. Eds Johnson City, TN, USA.. 749-752. [Google Scholar]
- Teo S.Y., Newton M.J., Newton R.U., Dempsey A.R., Fairchild T.J. (2016) Comparing the effectiveness of a short-term vertical jump versus weightlifting program on athletic power development. Journal of Strength and Conditioning Research 30, 2741-2748. [DOI] [PubMed] [Google Scholar]
- Thomas G.A., Kraemer W.J., Spiering B.A., Volek J.S., Anderson J.M., Maresh C.M. (2007) Maximal power at different percentages of one repetition maximum: influence of resistance and gender. Journal of Strength and Conditioning Research 21, 336-342. [DOI] [PubMed] [Google Scholar]
- Tricoli V., Lamas L., Carnevale R., Ugrinowitsch C. (2005) Short-term effects on lower-body functional power development: weightlifting vs. vertical jump training programs. Journal of Strength and Conditioning Research 19, 433-437. [DOI] [PubMed] [Google Scholar]
- Weyand P.G., Sandell R.F., Prime D.N.L., Bundle M.W. (2010) The biological limits to running speed are imposed from the ground up. Journal of Applied Physiology 108, 950-961. [DOI] [PubMed] [Google Scholar]
- Weyand P.G., Sternlight D.B., Bellizzi M.J., Wright S. (2000) Faster top running speeds are achieved with greater ground forces not more rapid leg movements. Journal of Applied Physiology 89, 1991-1999. [DOI] [PubMed] [Google Scholar]
- Young W.B., Newton R.U., Doyle T.L.A., Chapman D., Cormack S., Stewart C., Dawson B. (2005) Physiological and anthropometric characteristics of starters and non-starters and playing positions in elite Australian Rules football: a case study. Journal of Science and Medicine in Sport 8, 333-345. [DOI] [PubMed] [Google Scholar]


