Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Aug 17;8(17):4177–4182. doi: 10.1021/acs.jpclett.7b01905

Surface Reaction Barriometry: Methane Dissociation on Flat and Stepped Transition-Metal Surfaces

Davide Migliorini †, Helen Chadwick ‡, Francesco Nattino †, Ana Gutiérrez-González ‡, Eric Dombrowski §, Eric A High §, Han Guo ∥, Arthur L Utz §, Bret Jackson ∥, Rainer D Beck ‡,*, Geert-Jan Kroes †,*
PMCID: PMC5592645  PMID: 28817773

Abstract

graphic file with name jz-2017-01905r_0004.jpg

Accurately simulating heterogeneously catalyzed reactions requires reliable barriers for molecules reacting at defects on metal surfaces, such as steps. However, first-principles methods capable of computing these barriers to chemical accuracy have yet to be demonstrated. We show that state-resolved molecular beam experiments combined with ab initio molecular dynamics using specific reaction parameter density functional theory (SRP-DFT) can determine the molecule-metal surface interaction with the required reliability. Crucially, SRP-DFT exhibits transferability: the functional devised for methane reacting on a flat (111) face of Pt (and Ni) also describes its reaction on stepped Pt(211) with chemical accuracy. Our approach can help bridge the materials gap between fundamental surface science studies on regular surfaces and heterogeneous catalysis in which defected surfaces are important.

Heterogeneous catalysis plays a key role in the production of most chemicals, and quantitatively accurate predictions of the rates and pathways of elementary steps can guide catalyst design and optimization. With the theoretical toolbox now available, it is possible to predict trends in transition-metal catalysis, and identify which materials should constitute good catalysts for making particular chemicals.1 However, theory still struggles to compute reaction rates reliably, with errors in the rate of ammonia production over Ru still being approximately 1–2 orders of magnitude.2

Several factors complicate the calculation of rates of heterogeneously catalyzed processes.3 These processes typically consist of sequences of elementary surface reactions, as illustrated by the Haber-Bosch production of NH3 in work that contributed to Ertl winning the 2007 Nobel Prize in chemistry.4 Typically, only one or a few reactions are “rate-controlling”, so one can focus on these reactions.5 However, the exponential dependence of reaction rate on activation energy places severe demands on the accuracy of reaction barrier heights calculated for the associated rate-controlling transition states.3,6 These barrier heights cannot be measured directly, and are best determined through a close comparison of molecular beam experiments and dynamics calculations reproducing the reaction probabilities measured therein.7 On the theory side, first-principles methods capable of computing the electronic energies of these states with chemical accuracy (1 kcal/mol) have yet to be demonstrated, and efforts to develop databases of reaction barriers for surface reactions are in their infancy:7 Presently, chemically accurate barriers are available only for four systems, in which a molecule reacts with a flat, low index metal surface.7−10

While a semiempirical density functional theory (DFT) approach10,11 for computing barriers on flat surfaces has been demonstrated, it has long been known12 that catalyzed reactions proceed mainly over sites usually called “defects”, such as kinks and steps.13−16 Simulations of catalyzed reactions often attempt to take this into account by computing the energies of the relevant states for model “defected surfaces” using standard density functionals.6,17,18 Here, by defected surface we mean a surface containing line defects (such as steps or edges) or point defects (such as kinks or corners), even though such a surface might be a regular crystal surface definable through Miller indices. Unfortunately, such simulations cannot yet be expected to capture the important effects of point and extended surface defects and of multifaceted surfaces.3 Furthermore, standard density functionals (i.e., the classes of nonempirical functionals based on constraints and semiempirical functionals fitted to a range of chemical and/or material properties3) only yield semiquantitative results for barrier heights of surface reactions on metals.7

Here, we test the accuracy of a joint theoretical–experimental approach (which we call reaction barriometry) that uses results from a flat, low index metal surface to obtain the minimum barrier for a molecule (CHD3) reacting on a stepped Pt(211) surface. We apply a surface science approach to derive a semiempirical functional that accurately describes a reaction on a flat metal surface (CHD3 + Pt(111)), and then rely on the transferability of that functional to describe the reaction on the defected surface (Pt(211); note that (211) surfaces of face-centered cubic (fcc) metals consist of 3-atom wide (111) terraces and (100) steps). For catalysis by Pt-particles, the molecule–surface reaction we address is the rate-limiting step of the steam-reforming process,19 which is widely used for industrial hydrogen production. Microkinetic simulations of steam reforming on Ni (the commercial catalyst) and Pt often use the (211) surface to simulate step site reactivity.6,18 Dissociation of methane on transition metal surfaces is also of fundamental interest, as a benchmark system exhibiting several interesting dynamical features,20−22 including selective bond breaking of partially deuterated methane.23

Our approach for determining barriers for molecules reacting at defected surfaces can be summarized in five steps (see ref (10) for details of the first 4 steps): (i) Perform conventional (“laser-off”) molecular beam experiments on the molecule (here: CHD3) reacting on a flat surface (here: Pt(111), top view in Figure 1A) to determine the reaction probability as a function of average incident kinetic energy, Ei. In these experiments, the Ei, the nozzle temperature Tn, and the surface temperature Ts should be taken such that the applicability of classical mechanics is ensured (see Supporting Information (SI): Joint Experimental–Theoretical Strategy). (ii) Fit a candidate specific reaction parameter (SRP) functional to the measured reaction probabilities (S0) using ab initio molecular dynamics (AIMD) calculations. (iii) Measure the initial state-resolved reaction probabilities (here: for CHD3(ν1 = 1)), and (iv) validate the candidate SRP functional by showing that AIMD calculations using this functional also reproduce the initial state-resolved experiments. The new finding presented here is that, in the final step (v), the SRP density functional derived for the molecule interacting with the flat surface can be used to derive the barrier height for the molecule reacting on the defected (stepped) surface, as we will show here for CHD3 + Pt(211) (top and side views in Figure 1B,C). The underlying assumption, which has been argued before,10,11 is this: if an SRP functional provides chemically accurate predictions of S0 for measurements made near the energy threshold and for multiple combinations of Ei and vibrational excitation (laser-off or ν1 = 1 reaction), it will also provide a chemically accurate description of the height of the minimum barrier, and accurately describe its geometry. All experiments and calculations reported here were done for normal incidence. As the dissociation of methane on transition metal surfaces like Ni(111)24 and Pt(111)25 typically follows normal energy scaling, this samples the initial conditions, which have the most significant effect on the reactivity.

Figure 1.

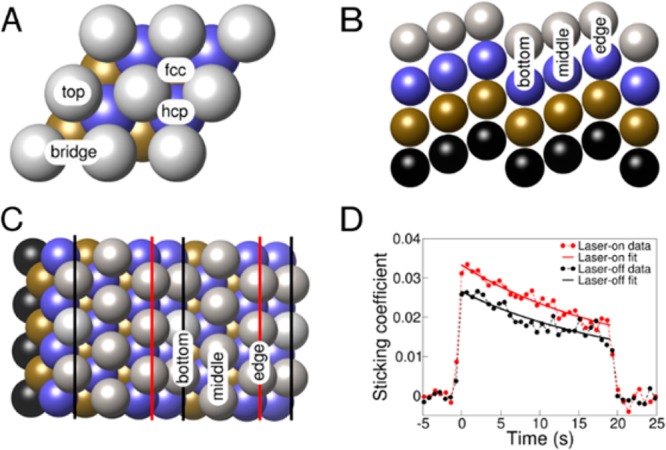
Figure 1

Open in a new tab

Views of the (111) and the (211) faces of fcc metals (like Ni and Pt), and experimental Kings and Well trace. (A) Top view of the (111) face. (B,C) Perspective and top views of the (211) face. (D) Kings and Wells trace of a measurement on CHD3 + Pt(111) at Ei = 82 kJ/mol.

In modeling the reaction of methane with transition metal surfaces, we compute reaction probabilities with AIMD, which allows modeling of the effects of surface atom vibrations and Ts, as required.26 The calculations use the ab initio total energy and AIMD program VASP.27,28 The SRP functional derived previously10 for CHD3 + Ni(111) is

graphic file with name jz-2017-01905r_m001.jpg 1

In eq 1 (for detailed justification, see ref (10) and the SI: SRP Density Functional Approach), EXRPBE and EX are the exchange parts of the RPBE29 and PBE30 functionals, and ECvdW is a correlation functional that provides an approximate description of the attractive van der Waals interaction.31 Adjusting the fit parameter x allows one to reproduce reactivity,10 while the use of well-constrained exchange and correlation functionals ensures the functional’s robustness for other system properties, e.g., crystal lattice structure. As before,10 molecular beam reflectivity experiments32 are used to determine CHD3 sticking coefficients, with typical data shown in Figure 1D. Laser preparation of the incident CHD3 in a specific rovibrationally excited quantum state (ν1 = 1, J = 2, K = 1) yields state-resolved reaction probabilities of CHD3(ν1 = 1). For further methodological details, see the SI: Experimental Methods, and Theoretical Methods.

To enable us to make an important point regarding the transferability of our approach, reaction probabilities computed and measured earlier for CHD3 + Ni(111) are presented in Figure 2A.

Figure 2.

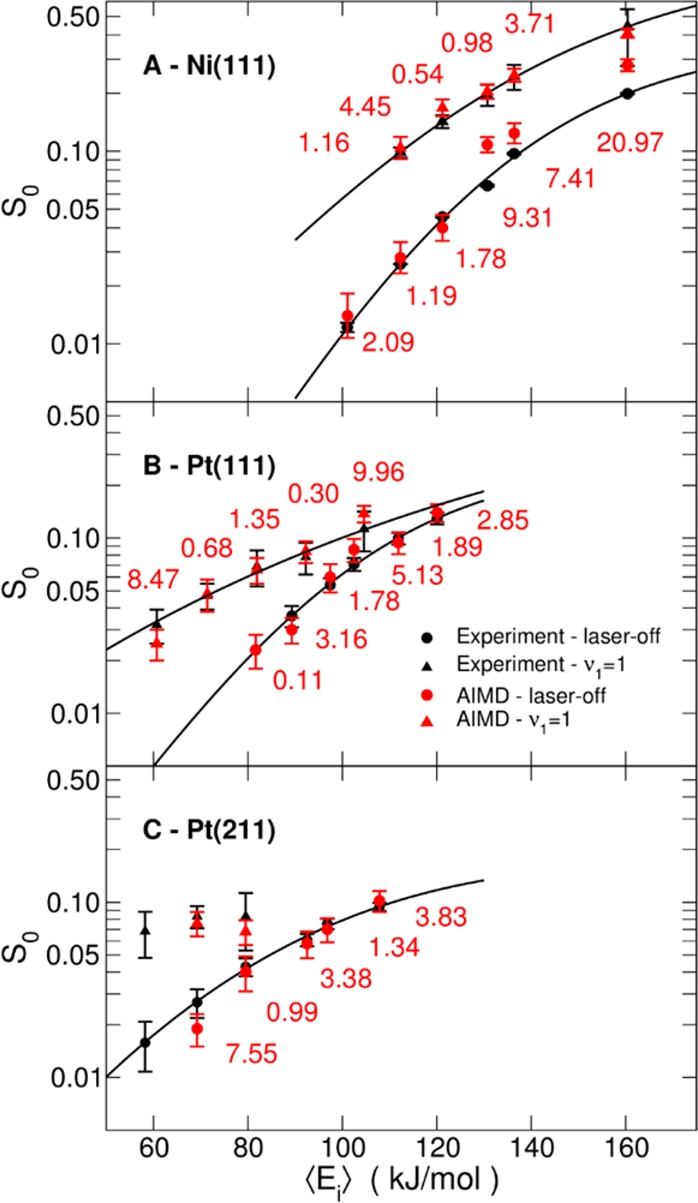
Figure 2

Open in a new tab

Comparison of theory with experiments for CHD3 + Ni(111), Pt(111), and Pt(211): Reaction probabilities as a function of Ei. (A) Reaction probabilities calculated with AIMD and measured in molecular beam experiments for CHD3 + Ni(111). Black symbols and lines: experimental results and fits to experiment. Red symbols: AIMD results. Circles are for laser-off conditions, triangles for ν1 = 1 CHD3. Numbers show the distance of the computed reaction probability to the fitted experimental curve along the incidence energy axis, in kJ/mol. Results reproduced with permission from ref (10). Copyright 2016 American Chemical Society. (B,C) Same, but with results from this work for CHD3 + Pt(111) and Pt(211).

For CHD3 + Ni(111), the value of x (0.32) was fitted with AIMD calculations modeling laser-off experiments with Ei = 112 and 121 kJ/mol (Tn = 600 and 650 K). Using that x-value, AIMD calculations predicted S0 for CHD3(ν1 = 1) with chemical accuracy, confirming the quality of the SRP functional (Figure 2A). For Ei > 130 kJ/mol calculations slightly overestimated laser-off reactivity. This was attributed to quasi-classical mechanics overestimating the reactivity of excited CD vibrational states, which become increasingly populated at higher Tn (≥700 K). Under these conditions AIMD calculations overestimate the fraction of CHD3 molecules dissociating via CD-bond cleavage.10

Here, new experiments and AIMD calculations are performed for CHD3 + Pt(111). In the fitting of x in eq 1, we could take a shortcut as the value of x derived for CHD3 + Ni(111) also provided excellent agreement between experiment and theory for CHD3 + Pt(111) (Figure 2B). For the laser-off reaction, chemical accuracy is obtained over the entire range of Ei: on average, the distance between the computed reaction probabilities and the fitted experimental curve along the energy axis is less than 4.2 kJ/mol (1 kcal/mol). The minimum barrier height to reaction, calculated with the surface frozen in its relaxed 0 K configuration, on Pt(111) (Eb = 79 kJ/mol, Table 1) is considerably lower than on Ni(111) (98 kJ/mol, Table 1). Therefore, laser-off experiments with Ei ≤ 120 kJ/mol (Tn ≤ 650 K) sample the full reactivity range of interest on Pt(111), and the complications associated with excited CD vibrational states at higher Tn seen for Ni(111) are avoided. The AIMD results also show chemical accuracy for CHD3(ν1 = 1) + Pt(111), a result that is not achieved using the PBE functional33 despite the transition state being similar to the SRP functional, as shown in Table 1. We attribute the observation of larger individual deviations to statistical fluctuations in the calculated reaction probabilities, and we note that in two of the three cases, computed probabilities are compared to an extrapolated (ν1 = 1) experimental curve. The comparison of the AIMD results to the molecular beam data also meets a statistical accuracy test (see Table S1 and SI sections: Statistical Test Based on Stouffer’s Z-Score, and AIMD Results).

Table 1. Computed Barrier Heights Eb, CH Distance of the Dissociating Bond rb, Distance from the C-Atom to the Surface Zb, and the Angle the Dissociating Bond Makes with the Surface Normal (θCH) in the Minimum Barrier Geometry for the SRP Functionala.

metal surface Eb (kJ/mol) rb (Å) Zb (Å) θCH
Ni(111) 97.9 (104.2) 1.61 (1.60) 2.18 (2.12) 136° (133°)
Pt(111) 78.7 (77.8) 1.56 (1.50) 2.28 (2.25) 133° (134°)
Pt(211) 52.6 (46.0) 1.53 (1.48) 2.27 (2.24) 133° (134°)
Open in a new tab
a

PBE results (from ref (34) for Ni(111), ref (35) for Pt(111), and from this work for Pt(211)) are shown in brackets for comparison.

The good agreement observed here for CHD3 + Pt(111) using an SRP functional developed for CHD3 + Ni(111) suggests that SRP functionals are transferable among chemically related systems (here: systems in which the same molecule reacts on the same low index surface of group 10 metals). We take this as additional proof of the sound physical basis of the SRP-DFT approach.

We now proceed to CHD3 reacting on the stepped Pt(211) surface. Again, the agreement between theory and experiment is excellent (Figure 2C). The theory using x = 0.32 describes the measured laser-off reactivity with chemical accuracy. Not enough data were available to make a fit of the experimental data for ν1 = 1 reaction, but the theoretical reaction probabilities agree with the experimental values within error bars. Again, the comparison of the AIMD results to the molecular beam data also meets our statistical accuracy test (Table S1). Note that we were not able to compare experiment with AIMD calculations at the lowest Ei for which experimental results were available. For this condition, large calculated trapping probabilities precluded an accurate comparison of the AIMD results with the experiments (see Figure S1 and the SI: AIMD Results). The Eb value extracted for CH4 + Pt(211) (53 kJ/mol, Table 1) is much lower than that for Pt(111) (79 kJ/mol).

The AIMD calculations also yield insights into reaction dynamics. Figure 3 shows that even vibrationally pre-excited CHD3 reacts preferentially at the steps (near the under-coordinated Pt atoms labeled “edge” in Figures 1B and 1C). This prediction can be tested with reflection absorption infrared spectroscopy.36 While approaching the surface at normal incidence, the molecules hardly change their projection on the surface (Figure 3). This result simplifies high-dimensional quantum dynamics calculations, because the dimensionality can be reduced using the “sudden” approximation to the molecule’s motion along the surface. This amounts to averaging over calculations performed for fixed projections of the molecule on the surface.37−39 Finally, calculations on CHD3 + Pt(111) using the reaction path Hamiltonian (RPH) method37 reveal how the molecular physisorption well affects reactivity. As discussed in the SI, according to RPH calculations, the use of the SRP functional yields a larger promoting effect on the reaction of pre-exciting the CH- and CD-stretch vibrations than the use of the PBE functional (see Figure S2 and the SI: Quantum Scattering Calculations). Model calculations attribute this to the molecule’s acceleration in the physisorption well, which leads to increased energy transfer from these vibrations to motion along the reaction path (see Figure S3).

Figure 3.

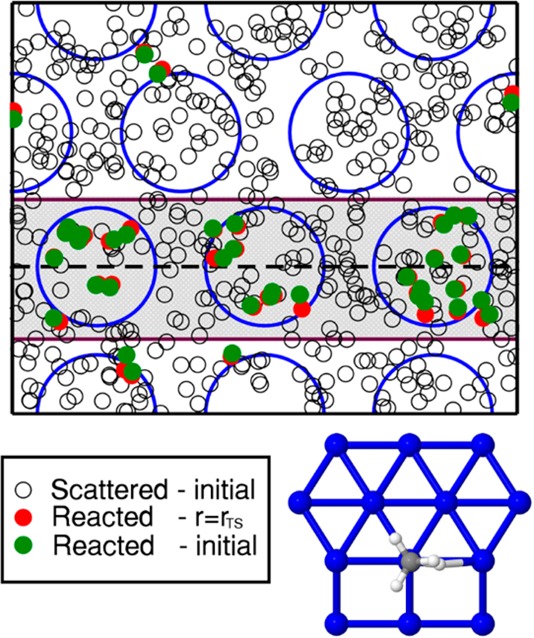
Figure 3

Open in a new tab

Points of impact of CHD3(ν1 = 1) molecules that react on Pt(211) for Ei = 69 kJ/mol, at time zero (green circles) and at the time of reaction (red circles), and initial points of impact of the molecules that scatter (white circles). The gray zone consists of the step edge atoms where the molecules react predominantly. The minimum barrier geometry, which is located on a step edge atom, is reported as an inset.

Our results point to the following promising approach to simulating heterogeneously catalyzed processes where elementary dissociative chemisorption reactions are rate controlling. First, perform AIMD calculations and molecular beam measurements of dissociative chemisorption on a low index face of the catalyst metal to derive an SRP functional. Next, exploit the transferability of the SRP functional demonstrated here (between Pt(111) and Pt(211)) to simulate the overall reaction proceeding on multifaceted catalyst particles on which point and extended surface defects are also present. The SRP functional is then used to also compute barriers (or activation energies) at these defects, and at other low index facets (the transferability of SRP functionals among low index faces of metals was already demonstrated for H2 + Cu(111) and Cu(100)8). Such an approach can help bridge the materials gap between surface science (which deals with smooth surfaces) and catalysis (with reactions typically proceeding over nanoparticles exhibiting defects).40,41 The present research describes a test-case of transferability in which a single σ-bond is broken, for which the transition state typically occurs over a surface atom, and surface defects promote the reaction by decreasing the coordination of the surface atoms.42 While the transferability is here demonstrated for only one example, arguments based on the dependence of the molecular adsorption energy on the coordination of the metal atom adsorbed to, experiments, and transition-state scaling relations suggest that the demonstrated transferability should hold more generally for σ-bond breaking (see SI: Implications for Simulating Heterogeneous Catalysis).

An additional structural requirement (high coordination of the transition state42) needs to be met for defect sites at which double or triple π-bonds are broken. Further investigations will therefore have to test whether the transferability found here for σ-bond breakage also holds when double and triple π-bonds are broken, as we believe. This belief can be supported on the basis of transition-state scaling relations also holding for the breaking of double and triple bonds (see also the SI: Implications for Simulating Heterogeneous Catalysis). Future investigation might also test whether our approach can be extended to deal with direct support effects on the catalysis (i.e., other than the effect that the support may alter the size distribution and the shape of the supported nanonparticles), and the presence of dopant atoms and additives.3 Finally, on the basis of accurate quantum Monte Carlo (QMC) calculations on H2 + Cu(111),43 we anticipate that it will soon be possible to fit accurate SRP functionals to reliable QMC calculations on molecules reacting on surfaces. This will put SRP-DFT on a first-principles basis, and will yield a method that is easier to apply than the combined experimental/theoretical approach presented.

We have demonstrated a joint theoretical–experimental approach (which we call reaction barriometry) that uses results from a reaction on a flat, low index metal surface to obtain a chemically accurate barrier for the same reaction on a stepped surface of the metal. We have applied a surface science approach to derive a semiempirical functional that accurately describes the dissociation of CHD3 on Pt(111), and then have shown the transferability of this functional to describe its dissociation on the stepped Pt(211) surface. Our approach can help bridge the materials gap between fundamental surface science studies on regular surfaces and real-life heterogeneous catalysis where reactions often proceed over defected metal nanoparticles.

Acknowledgments

This work was supported financially by the European Research Council through an ERC2013 advanced grant (Nr. 338580), by the Nederlandse organisatie voor Wetenschappelijk onderzoek (NWO-CW), by the Swiss National Science Foundation (Nrs. P300P2-171247 and 159689/1), by the Ecole Polytechnique Fédérale de Lausanne, by the US National Science Foundation (Nr. 1465230), and with computer time granted by NWO-EW.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b01905.

  • Experimental methods, theoretical methods, construction of the SRP functional, AIMD calculations, AIMD results, quantum scattering calculations, comparison of SRP and PBE results CHD3 + Pt(111), implications for heterogeneous catalysis, supporting figures, and supporting tables (PDF)

Author Present Address

# Present address: Leiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands.

Author Contributions

⊥ These authors have contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

jz7b01905_si_001.pdf (9.8MB, pdf)

References

  1. Medford A. J.; Vojvodic A.; Hummelshøj J. S.; Voss J.; Abild-Pedersen F.; Studt F.; Bligaard T.; Nilsson A.; Nørskov J. K. From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis. J. Catal. 2015, 328, 36–42. 10.1016/j.jcat.2014.12.033. [DOI] [Google Scholar]
  2. Medford A. J.; Wellendorff J.; Vojvodic A.; Studt F.; Abild-Pedersen F.; Jacobsen K. W.; Bligaard T.; Nørskov J. K. Assessing the Reliability of Calculated Catalytic Ammonia Synthesis Rates. Science 2014, 345, 197–200. 10.1126/science.1253486. [DOI] [PubMed] [Google Scholar]
  3. Sabbe M. K.; Reyniers M.-F.; Reuter K. First-Principles Kinetic Modeling in Heterogeneous Catalysis: An Industrial Perspective on Best-Practice, Gaps and Needs. Catal. Sci. Technol. 2012, 2, 2010–2024. 10.1039/c2cy20261a. [DOI] [Google Scholar]
  4. Ertl G. Primary Steps in Catalytic Synthesis of Ammonia. J. Vac. Sci. Technol., A 1983, 1, 1247–1253. 10.1116/1.572299. [DOI] [Google Scholar]
  5. Stegelmann C.; Andreasen A.; Campbell C. T. Degree of Rate Control: How Much the Energies of Intermediates and Transition States Control Rates. J. Am. Chem. Soc. 2009, 131, 8077–8082. 10.1021/ja9000097. [DOI] [PubMed] [Google Scholar]
  6. Wolcott C. A.; Medford A. J.; Studt F.; Campbell C. T. Degree of Rate Control Approach to Computational Catalyst Screening. J. Catal. 2015, 330, 197–207. 10.1016/j.jcat.2015.07.015. [DOI] [Google Scholar]
  7. Kroes G. J. Toward a Database of Chemically Accurate Barrier Heights for Reactions of Molecules with Metal Surfaces. J. Phys. Chem. Lett. 2015, 6, 4106–4114. 10.1021/acs.jpclett.5b01344. [DOI] [PubMed] [Google Scholar]
  8. Sementa L.; Wijzenbroek M.; van Kolck B. J.; Somers M. F.; Al-Halabi A.; Busnengo H. F.; Olsen R. A.; Kroes G. J.; Rutkowski M.; Thewes C.; et al. Reactive Scattering of H2 from Cu(100): Comparison of Dynamics Calculations Based on the Specific Reaction Parameter Approach to Density Functional Theory with Experiment. J. Chem. Phys. 2013, 138, 044708. 10.1063/1.4776224. [DOI] [PubMed] [Google Scholar]
  9. Nour Ghassemi E.; Wijzenbroek M.; Somers M. F.; Kroes G.-J. Chemically Accurate Simulation of Dissociative Chemisorption of D2 on Pt(111). Chem. Phys. Lett. 2017, 683, 329–335. 10.1016/j.cplett.2016.12.059. [DOI] [Google Scholar]
  10. Nattino F.; Migliorini D.; Kroes G. J.; Dombrowski E.; High E. A.; Killelea D. R.; Utz A. L. Chemically Accurate Simulation of a Polyatomic Molecule-Metal Surface Reaction. J. Phys. Chem. Lett. 2016, 7, 2402–2406. 10.1021/acs.jpclett.6b01022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Díaz C.; Pijper E.; Olsen R. A.; Busnengo H. F.; Auerbach D. J.; Kroes G. J. Chemically Accurate Simulation of a Prototypical Surface Reaction: H2 Dissociation on Cu(111). Science 2009, 326, 832–834. 10.1126/science.1178722. [DOI] [PubMed] [Google Scholar]
  12. Taylor H. S. A. Theory of the Catalytic Surface. Proc. R. Soc. London, Ser. A 1925, 108, 105–111. 10.1098/rspa.1925.0061. [DOI] [Google Scholar]
  13. Zambelli T.; Wintterlin J.; Trost J.; Ertl G. Identification of The “Active Sites” of a Surface-Catalyzed Reaction. Science 1996, 273, 1688–1690. 10.1126/science.273.5282.1688. [DOI] [Google Scholar]
  14. Hammer B. Bond Activation at Monatomic Steps: NO Dissociation at Corrugated Ru(0001). Phys. Rev. Lett. 1999, 83, 3681–3684. 10.1103/PhysRevLett.83.3681. [DOI] [Google Scholar]
  15. Gee A. T.; Hayden B. E.; Mormiche C. E.; Kleyn A. W.; Riedmüller B. The Dynamics of the Dissociative Adsorption of Methane on Pt(533). J. Chem. Phys. 2003, 118, 3334–3341. 10.1063/1.1538184. [DOI] [Google Scholar]
  16. Abild-Pedersen F.; Lytken O.; Engbæk J.; Nielsen G.; Chorkendorff I.; Nørskov J. K. Methane Activation on Ni(111): Effects of Poisons and Step Defects. Surf. Sci. 2005, 590, 127–137. 10.1016/j.susc.2005.05.057. [DOI] [Google Scholar]
  17. Honkala K.; Hellman A.; Remediakis I. N.; Logadottir A.; Carlsson A.; Dahl S.; Christensen C. H.; Nørskov J. K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. 10.1126/science.1106435. [DOI] [PubMed] [Google Scholar]
  18. Xu Y.; Lausche A.; Wang S.; Khan T.; Abild-Pedersen F.; Studt F.; Nørskov J.; Bligaard T. In Silico Search for Novel Methane Steam Reforming Catalysts. New J. Phys. 2013, 15, 125021. 10.1088/1367-2630/15/12/125021. [DOI] [Google Scholar]
  19. Wei J.; Iglesia E. Mechanism and Site Requirements for Activation and Chemical Conversion of Methane on Supported Pt Clusters and Turnover Rate Comparisons among Noble Metals. J. Phys. Chem. B 2004, 108, 4094–4103. 10.1021/jp036985z. [DOI] [Google Scholar]
  20. Smith R. R.; Killelea D. R.; DelSesto D. F.; Utz A. L. Preference for Vibrational over Translational Energy in a Gas-Surface Reaction. Science 2004, 304, 992–995. 10.1126/science.1096309. [DOI] [PubMed] [Google Scholar]
  21. Beck R. D.; Maroni P.; Papageorgopoulos D. C.; Dang T. T.; Schmid M. P.; Rizzo T. R. Vibrational Mode-Specific Reaction of Methane on a Nickel Surface. Science 2003, 302, 98–100. 10.1126/science.1088996. [DOI] [PubMed] [Google Scholar]
  22. Yoder B. L.; Bisson R.; Beck R. D. Steric Effects in the Chemisorption of Vibrationally Excited Methane on Ni(100). Science 2010, 329, 553–556. 10.1126/science.1191751. [DOI] [PubMed] [Google Scholar]
  23. Killelea D. R.; Campbell V. L.; Shuman N. S.; Utz A. L. Bond-Selective Control of a Heterogeneously Catalyzed Reaction. Science 2008, 319, 790–793. 10.1126/science.1152819. [DOI] [PubMed] [Google Scholar]
  24. Lee M. B.; Yang Q. Y.; Ceyer S. T. Dynamics of the Activated Dissociative Chemisorption of CH4 and Implication for the Pressure Gap in Catalysis: A Molecular Beam–high Resolution Electron Energy Loss Study. J. Chem. Phys. 1987, 87, 2724–2741. 10.1063/1.453060. [DOI] [Google Scholar]
  25. Luntz A. C.; Bethune D. S. Activation of Methane Dissociation on a Pt(111) Surface. J. Chem. Phys. 1989, 90, 1274–1280. 10.1063/1.456132. [DOI] [Google Scholar]
  26. Nave S.; Jackson B. Methane Dissociation on Ni(111): The Role of Lattice Reconstruction. Phys. Rev. Lett. 2007, 98, 173003. 10.1103/PhysRevLett.98.173003. [DOI] [PubMed] [Google Scholar]
  27. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  28. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  29. Hammer B.; Hansen L. B.; Nørskov J. K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 7413–7421. 10.1103/PhysRevB.59.7413. [DOI] [Google Scholar]
  30. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  31. Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van Der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
  32. King D. A.; Wells M. G. Reaction Mechanism in Chemisorption Kinetics: Nitrogen on the {100} Plane of Tungsten. Proc. R. Soc. London, Ser. A 1974, 339, 245–269. 10.1098/rspa.1974.0120. [DOI] [Google Scholar]
  33. Nattino F.; Ueta H.; Chadwick H.; van Reijzen M. E.; Beck R. D.; Jackson B.; van Hemert M. C.; Kroes G. Ab Initio Molecular Dynamics Calculations versus Quantum-State-Resolved Experiments on CHD3 + Pt(111): New Insights into a Prototypical Gas–Surface Reaction. J. Phys. Chem. Lett. 2014, 5, 1294–1299. 10.1021/jz500233n. [DOI] [PubMed] [Google Scholar]
  34. Nave S.; Tiwari A. K.; Jackson B. Dissociative Chemisorption of Methane on Ni and Pt Surfaces: Mode-Specific Chemistry and the Effects of Lattice Motion. J. Phys. Chem. A 2014, 118, 9615–9631. 10.1021/jp5063644. [DOI] [PubMed] [Google Scholar]
  35. Nattino F.; Migliorini D.; Bonfanti M.; Kroes G.-J. Methane Dissociation on Pt(111): Searching for a Specific Reaction Parameter Density Functional. J. Chem. Phys. 2016, 144, 044702. 10.1063/1.4939520. [DOI] [PubMed] [Google Scholar]
  36. Chen L.; Ueta H.; Bisson R.; Beck R. D. Quantum State-Resolved Gas/surface Reaction Dynamics Probed by Reflection Absorption Infrared Spectroscopy. Rev. Sci. Instrum. 2013, 84, 053902. 10.1063/1.4803933. [DOI] [PubMed] [Google Scholar]
  37. Jackson B.; Nave S. The Dissociative Chemisorption of Methane on Ni(100): Reaction Path Description of Mode-Selective Chemistry. J. Chem. Phys. 2011, 135, 114701. 10.1063/1.3634073. [DOI] [PubMed] [Google Scholar]
  38. Jiang B.; Liu R.; Li J.; Xie D.; Yang M.; Guo H. Mode Selectivity in Methane Dissociative Chemisorption on Ni(111). Chem. Sci. 2013, 4, 3249–3254. 10.1039/c3sc51040a. [DOI] [Google Scholar]
  39. Shen X.; Zhang Z.; Zhang D. H. Communication: Methane Dissociation on Ni(111) Surface: Importance of Azimuth and Surface Impact Site. J. Chem. Phys. 2016, 144, 101101. 10.1063/1.4943128. [DOI] [PubMed] [Google Scholar]
  40. Somorjai G. A.; York R. L.; Butcher D.; Park J. Y. The Evolution of Model Catalytic Systems; Studies of Structure, Bonding and Dynamics from Single Crystal Metal Surfaces to Nanoparticles, and from Low Pressure (<10–3 Torr) to High Pressure (>10–3 Torr) to Liquid Interfaces. Phys. Chem. Chem. Phys. 2007, 9, 3500–3513. 10.1039/B618805B. [DOI] [PubMed] [Google Scholar]
  41. Freund H.-J.; Kuhlenbeck H.; Libuda J.; Rupprechter G.; Bäumer M.; Hamann H. Bridging the Pressure and Materials Gaps between Catalysis and Surface Science: Clean and Modified Oxide Surfaces. Top. Catal. 2001, 15, 201–209. 10.1023/A:1016686322301. [DOI] [Google Scholar]
  42. Van Santen R. A. Complementary Structure Sensitive and Insensitive Catalytic Relationships. Acc. Chem. Res. 2009, 42, 57–66. 10.1021/ar800022m. [DOI] [PubMed] [Google Scholar]
  43. Doblhoff-Dier K.; Meyer J.; Hoggan P. E.; Kroes G.-J. Quantum Monte Carlo Calculations on a Benchmark Molecule-Metal Surface Reaction: H2 + Cu(111). J. Chem. Theory Comput. 2017, 13, 3208–3219. 10.1021/acs.jctc.7b00344. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b01905_si_001.pdf (9.8MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES