Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Aug 16;8(17):4113–4121. doi: 10.1021/acs.jpclett.7b01740

Behavior of Methylammonium Dipoles in MAPbX3 (X = Br and I)

Sharada Govinda †, Bhushan P Kore †, Menno Bokdam ‡, Pratibha Mahale †, Abhinav Kumar †, Somnath Pal †, Biswajit Bhattacharyya †, Jonathan Lahnsteiner ‡, Georg Kresse ‡, Cesare Franchini ‡, Anshu Pandey †, D D Sarma †,*
PMCID: PMC5592646  PMID: 28812901

Abstract

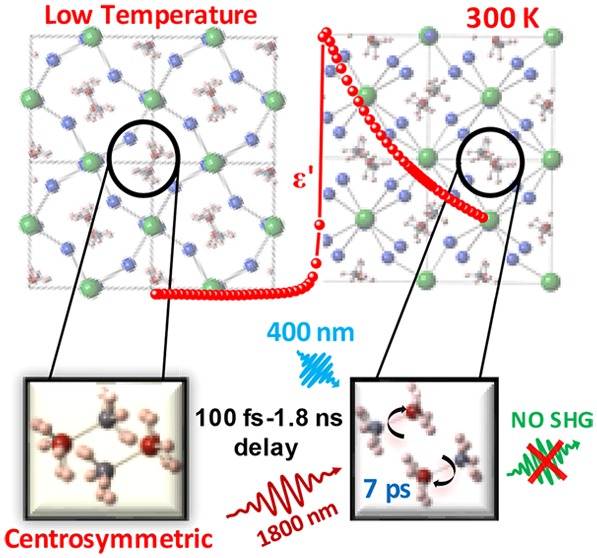
graphic file with name jz-2017-01740u_0006.jpg

Dielectric constants of MAPbX3 (X = Br, I) in the 1 kHz–1 MHz range show strong temperature dependence near room temperature, in contrast to the nearly temperature-independent dielectric constant of CsPbBr3. This strong temperature dependence for MAPbX3 in the tetragonal phase is attributed to the MA+ dipoles rotating freely within the probing time scale. This interpretation is supported by ab initio molecular dynamics simulations on MAPbI3 that establish these dipoles as randomly oriented with a rotational relaxation time scale of ∼7 ps at 300 K. Further, we probe the intriguing possibility of transient polarization of these dipoles following a photoexcitation process with important consequences on the photovoltaic efficiency, using a photoexcitation pump and second harmonic generation efficiency as a probe with delay times spanning 100 fs–1.8 ns. The absence of a second harmonic signal at any delay time rules out the possibility of any transient ferroelectric state under photoexcitation.

Interest in solution-processable organic–inorganic hybrid perovskites based on lead halides has shown a huge surge as potential photovoltaic materials, with efficiency crossing 22% within a few years.1−4 The most widely used active material is methylammonium lead iodide (MAPbI3) with a near-ideal band gap of about 1.5 eV, while the bromide and chloride analogues have larger band gaps.5−7 These compounds are characterized by the presence of an asymmetric and positively charged organic unit, methylammonium ion (CH3NH3)+, with a permanent dipole, at the center of a lead halide cage. These perovskite materials have a low-temperature orthorhombic phase and high/room-temperature cubic phase depending on the specific halide ion, with an intermediate tetragonal phase8 that is relevant to its photovoltaic properties. Though the low-temperature structure is more or less understood,9,10 where the methylammonium (MA+) dipoles order in an antiferroelectric arrangement,9 the behavior of these units and their possible roles in determining material properties in the-high temperature phases have remained controversial, as discussed later. The room-temperature structure of MAPbI3 is, on average, centrosymmetric, as shown by space- and time-averaged XRD, P–E loop, as well as second harmonic generation (SHG) efficiency measurements.11 However, this time-averaged description is consistent with many different dynamic behaviors, such as MA+ units (i) rotating freely and independently, (ii) rotating in a correlated manner, and (iii) not rotating at all but being frozen in an uncorrelated/random manner giving rise to a glassy state. Thus, it becomes crucial to understand the time scale of rotations of these dipoles and the extent of correlation between different MA+ units.

Several attempts have been made in the past to address these important issues, but, unfortunately, there is no clear consensus, with claims of ordered/locally ordered as well as dynamically disordered structures of various forms having been reported in the literature. For example, there are several publications suggesting reorientation of dipoles with reported relaxation times scattered over 0.1–28 ps.8,12−19 There are also several spectroscopic measurements that suggest dynamic disorder20−22 in MAPbX3 without the mention of any specific time scale. Then, there are also claims that the dipoles are in fact ferroelectrically ordered,23−41 in contrast to any description based on statically or dynamically disordered dipoles. On the theoretical front, several calculations using molecular dynamics (MD) and other techniques report rotations of these dipoles with time scales of a few picoseconds.27,42−47 One of these calculations, however, suggests that there is a collective behavior of these dipolar MA+ units, where they rotate as microscopic ferroelectric domains.44 In contrast, another calculation suggests no spatial correlation between individual dipoles.47 Another large supercell calculation46 shows that there is dynamical correlation present between neighboring MA+ units in the tetragonal phase, which is mediated by the Pb–I cage and reaches its maximum at room temperature. Interestingly, in this case, the calculations are interpreted to evince an underlying long-range antiferroelectric ordering of the MA+ units, which is smeared out at elevated temperature.46 This discussion makes it clear that the important issue of the behavior of dipoles on the MA+ units, both in the ground and photoexcited states, is still not clear, while the relevance of this in determining physical properties, specifically those influencing its function as the active photovoltaic material, is self-evident.

Since the dipoles and their behavior have a direct bearing on the dielectric constant of the material, we have performed dielectric measurements on MAPbX3 with X = Br and I as a function of temperature. In order to clearly identify the contribution from the dipoles, we have also measured dielectric properties of the related compound, CsPbBr3, where the dipole on the MA+ ion is replaced by the monopolar Cs+ ion with no dipole on it. Therefore, a comparison of the dielectric properties of MAPbBr3 and CsPbBr3 is expected to make the contribution from the dipoles obvious. This comparison of the MA system with the corresponding Cs system indicates a strong temperature dependence of the dielectric constant in MAPbX3 only in the tetragonal and cubic phases and not in the low-temperature orthorhombic phase. This strong temperature dependence in the two high-temperature phases can be clearly attributed to dipoles rotating well below the time scale of measurement. An antiferroelectric ordering of the dipoles in the lowest-temperature phase9 is responsible for the absence of any signature of these dipoles rotating, leading to the relatively temperature-independent dielectric properties, similar to what is observed for CsPbBr3 over the entire temperature range. We extend the time domain to smaller time scales with the help of extensive MD calculations and find that the dipoles indeed rotate in a time scale of 1–10 ps with little, if any, intersite correlation.

Recently, there has also been a claim39 of ferroelectric switching induced by photoexcitation leading to the generation of electron–hole pairs. In order to investigate the possibility of a photoabsorption-induced even transient ferroelectric alignment of dipoles, we have carried out a pump–probe experiment to probe the SHG efficiency as a function of time delays after an electron–hole excitation induced by a sufficiently high energy 100 fs laser pulse, down to the subpicosecond regime and up to a nanosecond, which is on the order of the lifetime of the excited state. We found no evidence of any transient ferroelectric behavior even in the excited state, suggesting other origins of its spectacular photovoltaic properties.

Dielectric constants of MAPbBr3, CsPbBr3, and MAPbI3 were measured from about 10 to 300 K over the frequency range of 1 kHz–1 MHz, as shown in Figure 1 for selected frequencies. The comparison of dielectric constants of MAPbBr3 and CsPbBr3 as a function of temperature is shown in Figure 1a. MAPbBr3 is known to have a crystallographic phase transition8 at about 237 K from the higher-temperature cubic phase to a tetragonal phase. It undergoes a further phase transition at 155 K to a second tetragonal phase, and finally, it enters the low-temperature orthorhombic phase upon lowering the temperature below 145 K.

Figure 1.

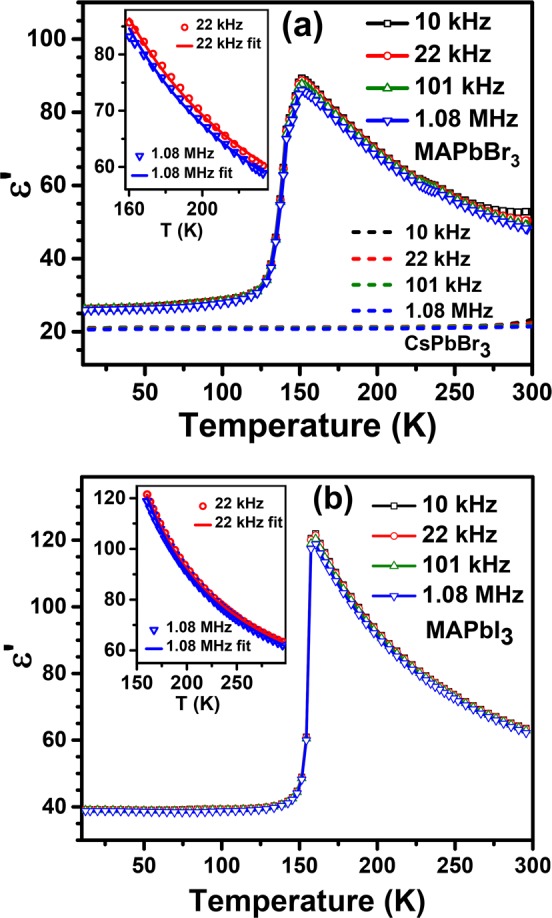
Figure 1

Open in a new tab

Dielectric constant, ε′, versus temperature for selected frequencies measured on MAPbBr3 (symbol and solid lines) and CsPbBr3 (dashed lines) (a) and MAPbI3 (b). The insets in (a) and (b) show the fit to the experimental data of the dielectric constant vs temperature in the tetragonal phase of MAPbBr3 and MAPbI3, respectively.

The dielectric constant of MAPbBr3 increases monotonically as the temperature decreases from 300 to 155 K, as seen in Figure 1a, for all frequencies. A small kink is seen in the dielectric constant at ∼237 K on an expanded scale, corresponding to the phase transition from the cubic to tetragonal (I) phase. Upon lowering the temperature further, it undergoes another transition at ∼155 K into a second tetragonal phase where the dielectric constant drops markedly. At the tetragonal to orthorhombic transition at ∼142 K, the dielectric constant drops sharply and a nearly temperature-independent dielectric constant is seen in the orthorhombic phase. The low-frequency dielectric constant is seen to slightly increase with an increase in the temperature above 240 K; this is attributed to extrinsic contributions to the dielectric constant.

The dielectric constant of CsPbBr3, shown as dashed lines in Figure 1a, exhibits only a slight temperature dependence, increasing from 20.5 to about 22 for a temperature variation from 11 to 300 K. Thus, the dielectric constants of CsPbBr3 and MAPbBr3 in the orthorhombic phase resemble each other closely in their temperature and frequency dependence. This is not altogether surprising because the PbBr3 cages in both compounds are similar.48 Moreover, the dipoles on MA+ units are expected to be ordered antiferroelectrically within the orthorhombic phase.9 Therefore, we do not expect any large thermal effects on contributions to the dielectric constant from these dipoles within the orthorhombic phase, explaining the qualitative as well as quantitative similarities of dielectric constants of these two compounds for T < 120 K. By the same logic, it is clear that the drastic increase of the dielectric constant for T > 120 K and its pronounced temperature dependence between 155 and 300 K in the case of MAPbBr3, compared to that of CsPbBr3, must arise from a prominent contribution of the dipoles on the MA+ units to the dielectric constant, distinguishing MAPbBr3 clearly from CsPbBr3 with no dipoles. The dielectric constant of MAPbI3, shown in Figure 1b, shows qualitatively similar behavior to MAPbBr3. MAPbI3 is orthorhombic below 162 K, with a single tetragonal phase between 162 and 331 K and a cubic phase beyond 331 K. The corresponding Cs analogue, namely, CsPbI3 cannot be stabilized long enough in the relevant structure type because it transforms readily to a nonperovskite structure type.49 However, comparing the dielectric data of MAPbI3 in Figure 1b with those of MAPbBr3 and CsPbBr3, we easily identify the orthorhombic phase in the low-temperature range as the one that is relatively less influenced by the temperature dependence of the dipoles on the MA+ units. This can be attributed to the dipoles ordered antiferroelectrically because there has been no evidence of a P–E loop within this low-temperature phase to suggest a ferroelectric state and the crystal structure has been shown in the past to be centrosymmetric.11 There is clear evidence of a large temperature-dependent contribution from dipoles within the tetragonal phase of MAPbI3 over the temperature range of 162–300 K in Figure 1b, similar to what is found in the case of MAPbBr3. Further, the dielectric constant in MAPbI3 does not show any discontinuous or even any significant change across the tetragonal to cubic phase transition (similar to ref (20)), indicating a smooth behavior of the dipoles across this phase transition, consistent with our interpretation, as discussed later, of essentially freely rotating dipoles already in the tetragonal phase (see Figure S2 in the Supporting Information).

The measured temperature dependence of the dielectric constant for MAPbBr3 and MAPbI3 reported here agree well with the previous reports.20,50−52 The comparison with the closely related CsPbBr3 with no dipole, not reported earlier, makes it clear that the dipoles in MAPbX3 (X = Br and I) contribute significantly to the dielectric constant in the tetragonal phase and this contribution is strongly temperature dependent, unlike in the orthorhombic phase, where the dipoles are ordered in an antiferroelectric manner, thereby suppressing any strong dynamical effects. In order to explore what kind of dynamical descriptions of these dipoles is consistent with its dielectric properties (Figure 1a,b), we examine the Debye theory of dipole relaxation that provides a description of free dipoles in a dielectric medium.

Within the Debye theory, the dielectric constant, ε′, can be expressed as8

graphic file with name jz-2017-01740u_m001.jpg 1

where ε∞ is the high-frequency dielectric constant, T is the temperature, ω the frequency of the applied electric field to measure the dielectric constant, and τ(T) is the relaxation time of the dipoles. C is a system-dependent parameter containing information on the dipole moment, symmetry of the lattice and so forth. This constant is related to the microscopic parameters as follows8

graphic file with name jz-2017-01740u_m002.jpg

where the number of dipoles per unit volume is N = n/V (n, number of dipoles in unit cell of volume V), μ is the dipole moment, η is the correction factor due to the Lorentz local field, k is the Boltzmann’s constant, and ε0 is the permittivity of free space. For tetragonal and cubic symmetry8

graphic file with name jz-2017-01740u_m003.jpg

Thus, the frequency dependence of ε′ comes from the 1/(1 + ω2τ2) term. As is evident from the data in the Figure 1a,b and already discussed earlier in this work, there is very little frequency dependence of ε′ in MAPbX3 (X = Br and I) in the measured frequency range (kHz–MHz), except for a slight increase with decreasing frequency at the high-temperature end in Figure 1a, attributed to slight extrinsic contributions. This, then, implies that ωτ ≪ 1 as this leads to an ε′ nearly independent of the frequency. Noting that the highest frequency of the probe electric field employed here is 1 MHz, clearly τ is several orders of magnitude smaller than 1 μs to fulfill the above requirement. This is consistent with earlier reports8,12,13,15−19 of the relaxation time of MA+ units in the range of ps within the tetragonal phase. Thus, we may safely ignore the ω2τ2, thereby reducing the Debye expression (eq 1) to

graphic file with name jz-2017-01740u_m004.jpg 2

The temperature dependence of ε′ arises from the 1/T term and is qualitatively consistent with the increasing value of ε′ for both MAPbBr3 and MAPbI3 in the tetragonal phase with a decrease in temperature (Figure 1a and b). However, a detailed analysis in terms of plots of (ε′ – ε∞) as a function of 1/T for various choices of ε∞ shows that this expression is unable to provide a proper quantitative description of the dielectric properties, suggesting a limitation intrinsic to the assumption of noninteracting dipoles in deriving eq 1. Since the dipolar interactions cannot be avoided, we account for it by replacing T with (T – T*), as has been invoked in the past literature,20,52 with the T* providing an energy scale of the (dipolar) interactions in close analogy to the Curie–Weiss law description of interacting paramagnetic system. This is reasonable also in view of the fact that both systems undergo a transition to a long-range ordered state at reasonably high ordering temperatures of 145 and 162 K for X = Br and I, respectively, indicating sufficient interactions between the dipoles that would naturally be present also in the disordered paraelectric state.

In order to provide a quantitative description of the dielectric constant as a function of temperature and frequency, we need to include extrinsic contributions because we see evidence of extrinsic contributions in terms of slight frequency dependence, for example, in the case of MAPbBr3 near 300 K in Figure 1a. Such extrinsic contributions are well described by the Maxwell–Wagner expression53 for ε′, which when coupled with the above equation leads to

graphic file with name jz-2017-01740u_m005.jpg 3

where β varies between 0 and 1 and εsext and ε∞ are the static and high-frequency dielectric constants contributed by external factors. The Maxwell–Wagner relaxation generally corresponds to the relaxation of grain boundaries and other such extrinsic contributions to the dielectric constant, which mostly dominate at low frequencies and high temperatures. The dielectric data within the tetragonal phase for both MAPbBr3 and MAPbI3 have been fitted for the frequency range of 22 kHz–1.08 MHz using eq 3, and these plots are shown in insets of Figure 1a,b for two extreme frequencies, namely, 22 kHz and 1.08 MHz. Clearly, eq 3 provides a good description of the dielectric constants in the tetragonal phase for the compounds over the entire range of frequencies and temperatures. It is to be noted that these analyses suggest a minor contribution from the Maxwell–Wagner part arising from extrinsic parts in both cases, namely, less than 0.5% for MAPbI3 and 1.2% for MAPbBr3 to the total dielectric constant. Various parameters in eq 3 determining the intrinsic contributions to the dielectric constants, obtained from the fit, are given in Table 1.

Table 1. Parameters Obtained from Fitting the Dielectric Data in the Tetragonal Phase.

  MAPbI3 MAPbBr3
C (K) 9221 7080
ε∞ 22 20
T* (K) 66.2 50.4
μ (C m) 10.23 × 10–30 8.51 × 10–30
Open in a new tab

The constant, C, obtained from fits to our dielectric data is very similar to that obtained by dielectric measurement8 at 90 GHz for both MAPbBr3 and MAPbI3. Unit cell volume reported in ref (8) has been used to estimate the dipole moment. The ε∞ values obtained by the fits are in the same range as the ε∞ values reported by similar measurements, for example,8,20 between ∼23–29 for MAPbI3 and ∼26–29 for MAPbBr3. The estimate of the dipole moment from the slope or the fitting is found to be close to the dipole moment of single MA+ units. Thus, we see that the dipoles on the MA+ units can be described as essentially free dipoles with relaxation time much shorter than the probing time scale down to μs, thereby establishing the intrinsic paraelectric state of the dipoles in the tetragonal phase.

In order to probe the dynamical behavior of individual dipoles down to a much shorter time scale and to obtain a microscopic understanding of dynamical or local correlations, if any, between dipoles beyond what can be probed by any type of dielectric measurements, we have performed large scale ab initio MD calculations at finite temperatures. For these calculations, we constructed supercells of MAPbI3 containing n × n × n unit cells with n = 2, 4, and 6. From the trajectory, we extract the orientation of all MA+ units. We define the time-dependent molecular polarization as the vectorial average of all dipole moments of the molecules

graphic file with name jz-2017-01740u_m006.jpg 4

Since the MA+ is chemically decoupled from the Pb–I framework,7 it is a reasonable assumption that the time evolution of the intrinsic dipole moment vector (p̂i) of each molecule is largely controlled by its direction, while the magnitude of the dipole moment remains essentially unchanged.

In order to understand the behavior of these dipoles within the tetragonal phase, we first started with a fully ferroelectrically polarized structure by aligning all dipoles at the start of our MD calculations at 300 K; the time evolution of the molecular polarization of this aligned structure, A, is shown in Figure 2 by the red dash–dot line. We find that the initial, fully polarized value of unity for Pmol(t = 0) rapidly decreases to approach a depolarized state within the first ∼20 ps of the MD trajectory at 300 K for the 64 unit cell (A) structure. This rapid depolarization of a starting polarized state within the MD provides a clear argument against a ferroelectric state being present within the tetragonal phase. It also suggests that the opposite limit of totally randomized dipoles is a better starting point for the MD steps, so that computationally heavy MD calculations over a large time window are not required only to equilibrate a starting structure far from the equilibrium.

Figure 2.

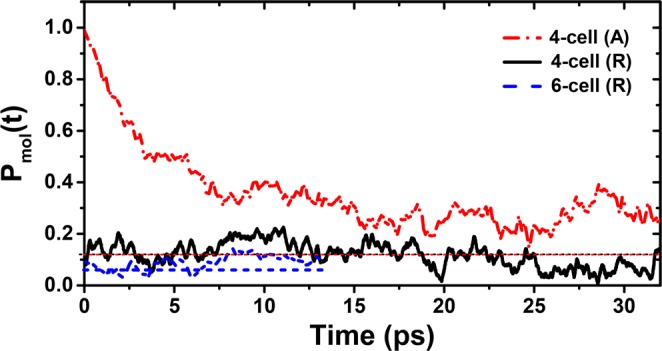
Figure 2

Open in a new tab

Molecular polarization Pmol(t) in the 64 and 216 unit cell, called 4-cell and 6-cell, respectively, at 300 K starting from an unpolarized-random (R) structure and from a polarized-aligned (A) starting structure. Average values for independent-random dipoles for the same system size are indicated by the dashed lines.

Therefore, for all subsequent calculations, all molecules in the supercells have been randomly rotated over three axes to generate an unbiased, not polarized starting structure (R) with 64 and 216 unit cells. After the initial equilibration time, both calculations show a fluctuating behavior with variance (σmol2) around a mean value P̅mol. This mean value depends on the size of the supercell employed, as evident in Figure 2. In order to understand the significance of these mean values and to serve as a reference, we have calculated Pmol(t) for random uncorrelated dipoles. This is calculated by assigning a new random orientation to the dipoles at every time step (fs scale) and determining values for (P̅rand, σrand2). All of these results are compiled in Table 2, and the P̅rand levels are shown as dashed lines in Figure 2. The average total molecular polarization (P̅mol) from the MD simulation does not differ that much from P̅rand, thereby establishing that the equilibrated structure is as effectively randomized as possible within a given system size. It is also seen that with increasing supercell size, P̅mol decreases systematically. Extrapolating this behavior to even larger supercells indicates the absence of any macroscopic molecular spontaneous polarization at 300 K. Figure 2 shows that the dipoles are dynamic in nature, fluctuating perceptibly, as evidenced by the instantaneous deviations of the Pmol(t) from P̅mol at various time steps. This is also reflected in the fact that the variance in the MD is about one order larger than in the random reference system (see Table 2). We have estimated the typical relaxation time τmol of these dipoles from their autocorrelation functions averaged over all dipoles and found it to be ∼7 ps at 300 K, which is in agreement with the values (4–15 ps) reported by other ab initio MD calculations.42−44,46,47 Lowering or raising the temperature within the tetragonal phase lowers or raises τmol and σmol, respectively. The value of P̅mol is, however, almost unaffected. The ps rotational mobility explains why these dipoles, when probed for their dielectric properties with a frequency of MHz, appear to be essentially free dipoles with no perceivable frequency dependence and explains the absence of simple 1/T dependence in ref (8), where a 90 GHz field was used.

Table 2. Average Molecular Polarization (P̅mol), the Variance of Pmol (t) (σmol2), and the Relaxation Time (τmol) for a n Cell at 300 K Starting from a Polarized-Aligned (A) and an Unpolarized-Random (R) Structurea.

system P̅mol σmol2 τmol (ps) P̅rand σrand2
2 × 2 × 2 (R) 0.31 0.11 7 0.33 2 × 10–2
4 × 4 × 4 (A) 0.27 0.05 8 0.12 2 × 10–3
4 × 4 × 4 (R) 0.15 0.03 7 0.12 2 × 10–3
6 × 6 × 6 (R) 0.07 0.02 5 0.06 7 × 10–4
Open in a new tab
a

The last two columns list the reference values for uncorrelated random dipoles.

Our conclusion that the room-temperature structure of MAPbI3 has free dipoles with essentially no correlation is in agreement with other ab initio MD calculations.46,47 In ref (44), a spontaneous microscopic polarization of the MA molecules is found, while refs (46) and (47) conclude the contrary, in agreement with our findings. This apparent discrepancy is most probably due to the limited system size used in ref (44), as already hinted by the authors there. If the coupling between neighboring dipoles is weak and they are able to rotate, the sum of their dipole moments (eq 4, also used in ref (44)) is not zero for finite-sized systems. Our results in Table 2 suggests that the net polarization, decreasing with an increasing system size, approaches zero asymptotically. Thus, most of the data presented in refs (44), (46), and (47) are in qualitative agreement with each other as well as with our results presented above.

Though the above results establish a free dipole-like behavior of MA+ molecules in the ground state for all practical time scales of relevance for its photovoltaic properties, it does not eliminate the possibility of local ferroelectric ordering of these dipoles following creation of the photoexcited state with an electron and a hole. The presence of additional charge carriers in the system, such as after photoexcitation, can alter the behavior of dipoles significantly. It is conceivable that the electron and the hole, particularly with a small excitonic binding energy, migrate to opposite ends of the dipole, thereby inhibiting the rotational dynamics and enhancing the possibility of dipole ordering at the same time. This is indeed an interesting possibility that merits careful investigation, which appears feasible because there are already claims of photoinduced ferroelectric switching in such materials,39 indicative of strong coupling between the exciton and the local polarization field. If true, such effects can significantly alter photovoltaic properties of the material by generating an internal local field during the lifetime of the excited electrons and holes. In order to examine this possibility, one necessarily needs a time-resolved experiment, capable of probing the system many times over within the photoexcited state lifetime, which is in the range of ns. Therefore, we have performed pump–probe experiments to probe the possibility of a transient ferroelectric state generated by the primary step of an electron–hole excitation.

We have performed pump–probe experiments on polycrystalline pellets of MAPbI3, MAPbBr3, and CsPbBr3 using a pump of 400 nm (3.1 eV), which was obtained by frequency doubling of a primary source at 800 nm (1.55 eV) for the photoexcitation step. A probe of 1800 nm (0.69 eV) with various delay times was used in an attempt to excite the SHG signal at 900 nm (1.38 eV) as a signature of a noncentrosymmetric structure, which is a necessary condition for any (even transient) ferroelectric state. The choice of the pump wavelength is of course dictated by the requirement that it is more energetic than the band gaps5,54,55 1.51, 2.2, and 2.25 eV of MAPbI3, MAPbBr3, and CsPbBr3, respectively. The probe wavelength was carefully chosen so as to avoid any absorption of the SHG signal by keeping it energetically below the band gap for each case.

The time delay for the probe was varied from 100 fs to 1.8 ns; spectra recorded for a few selected values of the time delay are shown in Figure 3a–c for MAPbI3, MAPbBr3, and CsPbBr3 samples, respectively. The normal SHG spectrum of urea, a common standard for SHG, recorded at the same laser power is shown in each panel for comparison. It can be seen that the spectra of samples at each delay time overlap. In MAPbI3, the decaying tail of intense photoluminescence (PL) at ∼805 nm is observed over the entire range of the plot, while in MAPbBr3 and CsPbBr3, a gently sloping background of much lower intensity is observed, which arises from the tail of the primary source at 800 nm used to generate the 400 nm pump. However, it is clear that in all three cases there is essentially no SHG signal that should appear, if present, as a peak at around 900 nm. In order to be more quantitative, we have analyzed the recorded signal after removing background contributions, including the tail of the PL signal in the case of MAPbI3 (see the Supporting Information), to estimate the upper limit of any possible signal at the second harmonic for each delay time for all three samples. The relative SHG efficiency has been calculated as the ratio of the area under the Gaussian of the SHG signal of the sample to that of urea and is plotted as a function of the delay time in Figure 4.

Figure 3.

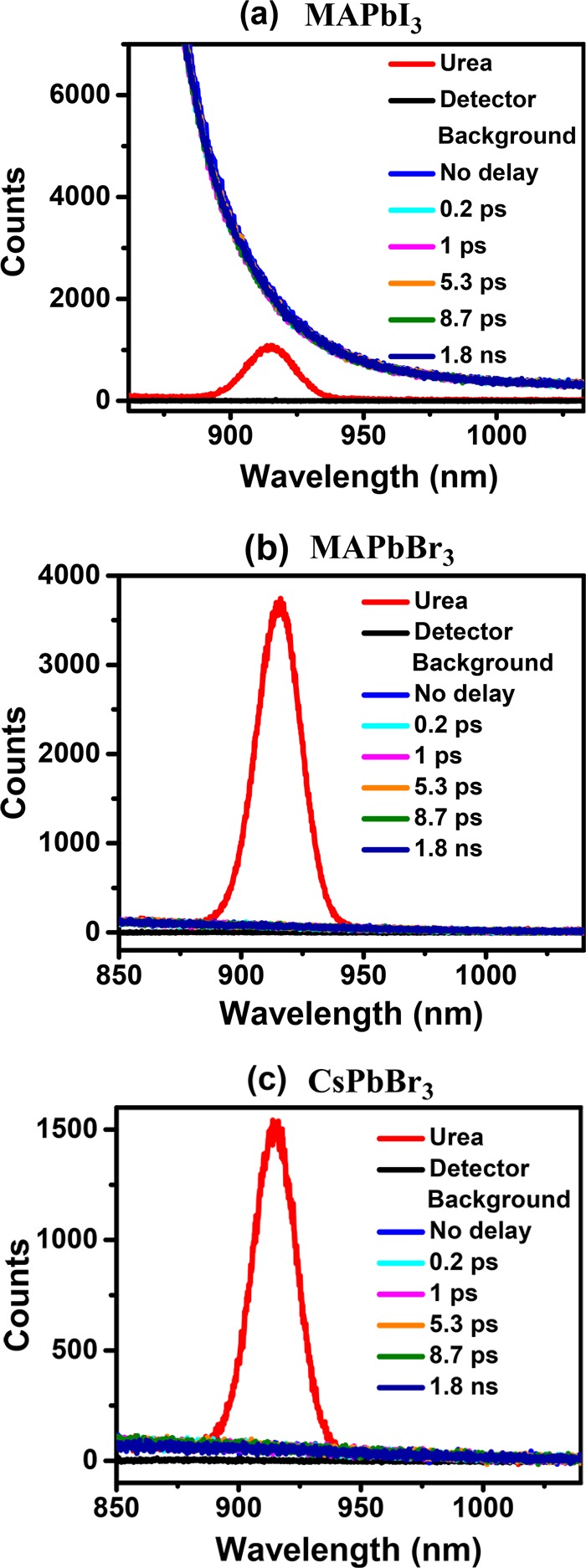
Figure 3

Open in a new tab

Spectra of the second harmonic generated at 900 nm with an incident 1800 nm laser measured on (a) MAPbI3 and urea with a pump power of 2.84 mW, (b) MAPbBr3 with a pump power of 2.62 mW, and (c) CsPbBr3 with a pump power of 2.60 mW at a few selected delay times indicated in the legend. It can be seen that all of the spectra at different delay times overlap.

Figure 4.

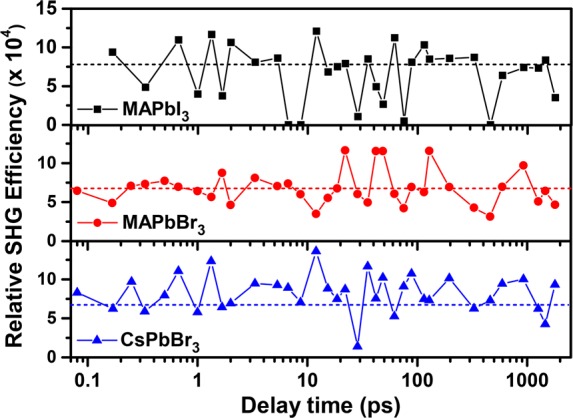
Figure 4

Open in a new tab

SHG efficiency of MAPbI3, MAPbBr3, and CsPbBr3 with respect to urea plotted against the delay time between the 400 nm pump and 1800 nm probe. The dashed lines drawn for reference in each panel represent the average SHG efficiency calculated for spectra before the arrival of the pump pulse. The pump powers were 2.84, 2.62, and 2.60 mW for MAPbI3, MAPbBr3, and CsPbBr3, respectively.

In order to understand the influence of the primary photoexcitation on the efficiency of SHG in these materials, we have indicated with a dashed line in each of the three panels the estimated upper limit of any relative SHG efficiency from these compounds in the absence of any photoexcitation. The results for CsPbBr3, shown in the lowest panel of Figure 4, provides us with an estimate of limits of significance of the SHG signal extracted from our experiments because, in the absence of any permanent dipolar unit, CsPbBr3 is centrosymmetric in its ground state and, therefore, cannot have any SHG signal in the absence of any photoexcitation. While it is not impossible, it is improbable that the photoexcited state of CsPbBr3 would adopt a noncentrosymmetric structure. This is clearly supported by the measured SHG signal of the photoexcited CsPbBr3 with various time delays in the lowest panel of Figure 4, exhibiting random, insignificant fluctuations around the base level (dashed line) defined by the SHG signal intensity from the ground-state CsPbBr3.

This base level, essentially defining the zero of the SHG signal, is essentially determined by the detector background. Comparing the data shown in the other two panels for MAPbBr3 and MAPbI3, it becomes clear at once that these also exhibit no detectable SHG activities either in the ground states or in the photoexcited state at any instant of time between the photoexcitation and the lifetime of the photoexcited state. It is important to note that we have explored over a delay time spanning four decades; specifically, the longest delay time recorded here is on the order of the lifetime of the excited state. Moreover, at this end, the delay time employed is more than 2 orders of magnitude larger than the dipole rotational time scale of ∼7 ps.

Therefore, if the creation of an electron–hole pair were to induce reorientations of the dipoles to give rise to a locally polar state, there would be enough time for the dipoles to achieve such a “ferroelectric” excited state within the time scale of the probe. Therefore, the complete absence of any SHG activity at any time point over this wide window of delay time is strong evidence for the absence of any collective orientation of dipoles in the photoexcited state.

In conclusion, careful dielectric measurements comparing CsPbBr3 with MAPbX3 (X = Br and I) suggest that the dipoles on MA+ units behave like free dipoles on the time scale of measurements down to 1 μs within the tetragonal phase, though they are ordered in the low-temperature orthorhombic phase. Extending our investigation down to the ps regime with the help of extensive MD calculations, we find that the characteristic rotational time scale of these dipoles is ∼7 ps in the tetragonal phase, and the dipoles undergo rotational relaxation with little correlation between them. Time-resolved pump–probe experiments over four decades of time delays, from <100 fs to >1 ns, establish that the photoexcited state does not lead to a transient polarized state at any stage within the lifetime of the electron–hole excited state.

Experimental Section

Synthesis. Polycrystalline MAPbI3 and MAPbBr3 were synthesized from PbX2 and MAX precursors, according to the methods outlined in earlier reports,5,54,56 with slight modifications.

Synthesis of Precursors.(5,57) MAI was prepared by reacting methylamine (40% in water) with hydroiodic acid at 0 °C for 2 h. The reaction mixture was distilled to obtain MAI as precipitate. This was washed with diethyl ether several times to remove unreacted HI and dried and stored in vacuum. MABr was prepared similarly by reacting methylamine with HBr.

MAPbI3 was prepared from a 1 M solution of MAI and PbI2 (99%, Sigma-Aldrich) in γ-butyrolactone. This solution was heated with constant stirring for 1 h at 60 °C. This solution was then drop-cast on glass slides at 100 °C. After 15–20 min, when the solvent evaporated completely, dark gray powder and small crystals of MAPbI3 were scratched off from the glass slides and then ground into powder and stored in vacuum.

MAPbBr3 was prepared from a 1 M solution of MABr and PbBr2 (98%, Alfa Aeser) in N,N-dimethylformamide (DMF). This solution was stirred constantly at room temperature for 1 h and then drop-cast on glass slides at 120 °C. After the solvent evaporated completely in about 15–20 min, the orange powder and small crystals of MAPbBr3 were collected and powdered and stored in vacuum.

CsPbBr3 was prepared by a method reported in ref (58), with some modifications, using a 0.5 M solution of CsBr and PbBr2 in dimethyl sulfoxide (DMSO). This solution was stirred constantly at 80 °C for 1 h and then drop-cast on glass slides at 185 °C. After all of the solvent evaporated, the powder of CsPbBr3 was collected and stored in vacuum.

Powder X-ray Diffraction. All samples were prepared just before the experiments, and the powder XRD pattern was collected in order to check the purity of the samples. Typical powder XRD patterns of each sample recorded before experiment are shown in Figure S1 in the Supporting Information.

Dielectric Measurements. Polycrystalline samples of MAPbI3, MAPbBr3, and CsPbBr3 were ground to fine powder in a mortar and pressed into pellets of 6 mm diameter in a steel die with a pressure of 0.15 kN/cm2. The pellets were annealed at ∼90 °C for 1 h in argon gas flow. The XRD pattern of the pellet was checked after the pellet cooled down to room temperature. Silver paste was used to make electrodes on each face of flat pieces of the pellet (about 0.5 mm thick).

Dielectric measurements were performed with the sample inside of a closed-cycle He cryostat (Sumitomo) using a Keysight E4990A impedance analyzer. Capacitance-loss (Cp-D) measurements were performed at each temperature in the frequency range of 1 kHz–1 MHz with an applied peak voltage of 0.5 V. The data were collected in a cooling cycle from 300 to 10 K with a step of 5 K otherwise and 3 K near phase transitions. The sample was cooled with a ramp rate of 0.5 K/min (controlled using a temperature controller, Lakeshore 332) between two temperature points and allowed to stabilize for sufficient time at each temperature. Data were also collected during ramping, and measurements made during ramping matched very well with the measurements after temperature stabilization. Cp-D measurements were also done while heating the sample from 10 to 300 K, and it was found that they matched well with the cooling cycle, except for some hysteresis in the transition temperature. Further, the measurements were also performed with a DC voltage applied across the sample, at various temperatures, and it was found that the data matched exactly with those with zero applied voltage, hence ruling out the possibility of a contribution due to space charge and similar effects.

Second Harmonic Generation. A pump–probe experiment to measure SHG was performed using a 100 fs pump of wavelength 400 nm and probe of wavelength 1800 nm. The details of the experimental setup are described elsewhere.11 Polycrystalline samples of MAPbI3, MAPbBr3, CsPbBr3, and urea were ground into fine powder and pressed into pellets for this measurement. A time delay stage was used to change the delay between the pump and probe pulses. The second harmonic spectra were recorded by a cooled CCD (Andor IDUS) in the range of 850–1050 nm. SHG was measured on urea, a standard sample used for SHG, before each sample to confirm that SHG is indeed observed. The probe power used was between 1.3 and 1.8 mW for all samples, focused at a spot of 0.95 mm diameter. The pump power was ∼1.5 and 2.5 mW for two different measurements on each sample, with a spot of 4.8 mm diameter.

Computational Method

For the first-principles MD calculations, we used a plane-wave basis and the projector augmented wave (PAW) method59 as implemented in the VASP code.60−62 The PBEsol63 functional was used. Relatively shallow pseudopotentials were used; for Pb the (6s26p2), for I the (5s25p5), for C the (2s22p2), and for N the (2s22p3) orbitals were included in the valence. This made it possible to set a relatively low energy cutoff of 250 eV to form the plane-wave basis. Gaussian smearing with σ = 0.05 eV was used to broaden the one-electron levels. The Brillouin zone was sampled by the Γ point only for the large 4- and 6-cell and by the Γ and R points for the 2-cell. The Kohn–Sham orbitals were updated in the self-consistency cycle until an energy convergence of 10–4 eV was obtained. A Langevin thermostat64 was applied to simulate a canonical ensemble. The trajectory was formed by propagating the structure with the calculated Hellmann–Feynman forces with time steps of 0.7/2.0/3.0 fs and increased hydrogen masses of 2/4/8 au for the 2/4/6-cells, respectively. The hydrogen masses were increased to allow for a larger time step for the large cell sizes. Additionally, in the 6-cell, the Pb and I masses were decreased to 20 au supercells (n × n × n, with n = 2, 4, 6), which were constructed out of pseudocubic unit cells (12 atoms) with experimental lattice constants (a, b = 6.3115 Å, c = 6.3161 Å),23 as described in ref (7). In the supercell, all atoms were allowed to move while keeping the lattice vectors fixed. The relaxation time was obtained by calculating the average autocorrelation function of all molecules. More details can be found in ref (46).

Acknowledgments

The authors thank the Department of Science and Technology, Government of India for support and Mr. Guru Pratheep. R. for help with SHG measurements. S.G. thanks Dr. Sumanta Mukherjee for useful discussions and acknowledges CSIR for a student fellowship. B.P.K. acknowledge UGC, India for a D.S. Kothari Postdoctoral Fellowship. M.B. and J.L. acknowledge funding by the Austrian Science Fund (FWF): P 30316-N27.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b01740.

  • Powder XRD patterns, dielectric data up to higher temperature, polynomial fits to SHG spectra, and residuals of polynomial fits (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz7b01740_si_001.pdf (249.1KB, pdf)

References

  1. Bi D.; Tress W.; Dar M. I.; Gao P.; Luo J.; Renevier C.; Schenk K.; Abate A.; Giordano F.; Correa Baena J.-P.; et al. Efficient luminescent solar cells based on tailored mixed-cation perovskites. Sci. Adv. 2016, 2, e1501170. 10.1126/sciadv.1501170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. McMeekin D. P.; Sadoughi G.; Rehman W.; Eperon G. E.; Saliba M.; Hörantner M. T.; Haghighirad A.; Sakai N.; Korte L.; Rech B.; et al. A mixed-cation lead mixed-halide perovskite absorber for tandem solar cells. Science 2016, 351, 151–155. 10.1126/science.aad5845. [DOI] [PubMed] [Google Scholar]
  3. Saliba M.; Matsui T.; Seo J.-Y.; Domanski K.; Correa-Baena J.-P.; Nazeeruddin M. K.; Zakeeruddin S. M.; Tress W.; Abate A.; Hagfeldt A.; et al. Cesium-containing triple cation perovskite solar cells: improved stability, reproducibility and high efficiency. Energy Environ. Sci. 2016, 9, 1989–1997. 10.1039/C5EE03874J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Yoon H.; Kang S. M.; Lee J.-K.; Choi M. Hysteresis-free low-temperature-processed planar perovskite solar cells with 19.1% efficiency. Energy Environ. Sci. 2016, 9, 2262–2266. 10.1039/C6EE01037G. [DOI] [Google Scholar]
  5. Baikie T.; Fang Y.; Kadro J. M.; Schreyer M.; Wei F.; Mhaisalkar S. G.; Graetzel M.; White T. J. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 2013, 1, 5628–5641. 10.1039/c3ta10518k. [DOI] [Google Scholar]
  6. Butler K. T.; Frost J. M.; Walsh A. Band alignment of the hybrid halide perovskites CH3NH3PbCl3, CH3NH3PbBr3 and CH3NH3PbI3. Mater. Horiz. 2015, 2, 228–231. 10.1039/C4MH00174E. [DOI] [Google Scholar]
  7. Bokdam M.; Sander T.; Stroppa A.; Picozzi S.; Sarma D. D.; Franchini C.; Kresse G. Role of polar phonons in the photo excited state of metal halide perovskites. Sci. Rep. 2016, 6, 28618. 10.1038/srep28618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Poglitsch A.; Weber D. Dynamic disorder in methylammoniumtrihalogenoplumbates (II) observed by millimeter-wave spectroscopy. J. Chem. Phys. 1987, 87, 6373–6378. 10.1063/1.453467. [DOI] [Google Scholar]
  9. Swainson I. P.; Hammond R. P.; Soullière C.; Knop O.; Massa W. Phase transitions in the perovskite methylammonium lead bromide, CH3ND3PbBr3. J. Solid State Chem. 2003, 176, 97–104. 10.1016/S0022-4596(03)00352-9. [DOI] [Google Scholar]
  10. Chi L.; Swainson I.; Cranswick L.; Her J.-H.; Stephens P.; Knop O. The ordered phase of methylammonium lead chloride CH3ND3PbCl3. J. Solid State Chem. 2005, 178, 1376–1385. 10.1016/j.jssc.2004.12.037. [DOI] [Google Scholar]
  11. G S.; Mahale P.; Kore B. P.; Mukherjee S.; Pavan M. S.; De C.; Ghara S.; Sundaresan A.; Pandey A.; Guru Row T. N.; et al. Is CH3NH3PbI3 polar?. J. Phys. Chem. Lett. 2016, 7, 2412–2419. 10.1021/acs.jpclett.6b00803. [DOI] [PubMed] [Google Scholar]
  12. Wasylishen R. E.; Knop O.; Macdonald J. B. Cation rotation in methylammonium lead halides. Solid State Commun. 1985, 56, 581–582. 10.1016/0038-1098(85)90959-7. [DOI] [Google Scholar]
  13. Knop O.; Wasylishen R. E.; White M. A.; Cameron T. S.; Oort M. J. M. V. Alkylammonium lead halides. Part 2. CH3NH3PbX3 (X = Cl, Br, I) perovskites: cuboctahedral halide cages with isotropic cation reorientation. Can. J. Chem. 1990, 68, 412–422. 10.1139/v90-063. [DOI] [Google Scholar]
  14. Onoda-Yamamuro N.; Matsuo T.; Suga H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II). J. Phys. Chem. Solids 1990, 51, 1383–1395. 10.1016/0022-3697(90)90021-7. [DOI] [Google Scholar]
  15. Bakulin A. A.; Selig O.; Bakker H. J.; Rezus Y. L. A.; Müller C.; Glaser T.; Lovrincic R.; Sun Z.; Chen Z.; Walsh A.; et al. Real-time observation of organic cation reorientation in methylammonium lead iodide perovskites. J. Phys. Chem. Lett. 2015, 6, 3663–3669. 10.1021/acs.jpclett.5b01555. [DOI] [PubMed] [Google Scholar]
  16. Chen T.; Foley B. J.; Ipek B.; Tyagi M.; Copley J. R. D.; Brown C. M.; Choi J. J.; Lee S.-H. Rotational dynamics of organic cations in the CH3NH3PbI3 perovskite. Phys. Chem. Chem. Phys. 2015, 17, 31278–31286. 10.1039/C5CP05348J. [DOI] [PubMed] [Google Scholar]
  17. Leguy A. M. A.; Frost J. M.; McMahon A. P.; Sakai V. G.; Kockelmann W.; Law C.; Li X.; Foglia F.; Walsh A.; O’Regan B. C.; et al. The dynamics of methylammonium ions in hybrid organic-inorganic perovskite solar cells. Nat. Commun. 2015, 6, 7124. 10.1038/ncomms8124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Létoublon A.; Paofai S.; Rufflé B.; Bourges P.; Hehlen B.; Michel T.; Ecolivet C.; Durand O.; Cordier S.; Katan C.; et al. Elastic constants, optical phonons, and molecular relaxations in the high temperature plastic phase of the CH3NH3PbBr3 hybrid perovskite. J. Phys. Chem. Lett. 2016, 7, 3776–3784. 10.1021/acs.jpclett.6b01709. [DOI] [PubMed] [Google Scholar]
  19. Selig O.; Sadhanala A.; Müller C.; Lovrincic R.; Chen Z.; Rezus Y. L. A.; Frost J. M.; Jansen T. L. C.; Bakulin A. A. Organic cation rotation and immobilization in pure and mixed methylammonium lead-halide perovskites. J. Am. Chem. Soc. 2017, 139, 4068–4074. 10.1021/jacs.6b12239. [DOI] [PubMed] [Google Scholar]
  20. Onoda-Yamamuro N.; Matsuo T.; Suga H. Dielectric study of CH3NH3PbX3 (X = Cl, Br, I). J. Phys. Chem. Solids 1992, 53, 935–939. 10.1016/0022-3697(92)90121-S. [DOI] [Google Scholar]
  21. Quarti C.; Grancini G.; Mosconi E.; Bruno P.; Ball J. M.; Lee M. M.; Snaith H. J.; Petrozza A.; Angelis F. D. The Raman spectrum of the CH3NH3PbI3 hybrid perovskite: interplay of theory and experiment. J. Phys. Chem. Lett. 2014, 5, 279–284. 10.1021/jz402589q. [DOI] [PubMed] [Google Scholar]
  22. Brivio F.; Frost J. M.; Skelton J. M.; Jackson A. J.; Weber O. J.; Weller M. T.; Goñi A. R.; Leguy A. M. A.; Barnes P. R. F.; Walsh A. Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 144308. 10.1103/PhysRevB.92.144308. [DOI] [Google Scholar]
  23. Stoumpos C. C.; Malliakas C. D.; Kanatzidis M. G. Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 2013, 52, 9019–9038. 10.1021/ic401215x. [DOI] [PubMed] [Google Scholar]
  24. Frost J. M.; Butler K. T.; Brivio F.; Hendon C. H.; van Schilfgaarde M.; Walsh A. Atomistic origins of high-performance in hybrid halide perovskite solar cells. Nano Lett. 2014, 14, 2584–2590. 10.1021/nl500390f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kutes Y.; Ye L.; Zhou Y.; Pang S.; Huey B. D.; Padture N. P. Direct observation of ferroelectric domains in solution-processed CH3NH3PbI3 perovskite thin films. J. Phys. Chem. Lett. 2014, 5, 3335–3339. 10.1021/jz501697b. [DOI] [PubMed] [Google Scholar]
  26. Wei J.; Zhao Y.; Li H.; Li G.; Pan J.; Xu D.; Zhao Q.; Yu D. Hysteresis analysis based on the ferroelectric effect in hybrid perovskite solar cells. J. Phys. Chem. Lett. 2014, 5, 3937–3945. 10.1021/jz502111u. [DOI] [PubMed] [Google Scholar]
  27. Quarti C.; Mosconi E.; De Angelis F. Interplay of orientational order and electronic structure in methylammonium lead iodide: implications for solar cell operation. Chem. Mater. 2014, 26, 6557–6569. 10.1021/cm5032046. [DOI] [Google Scholar]
  28. Chen H.-W.; Sakai N.; Ikegami M.; Miyasaka T. Emergence of hysteresis and transient ferroelectric response in organo-lead halide perovskite solar cells. J. Phys. Chem. Lett. 2015, 6, 164–169. 10.1021/jz502429u. [DOI] [PubMed] [Google Scholar]
  29. Zheng F.; Takenaka H.; Wang F.; Koocher N. Z.; Rappe A. M. First-principles calculation of the bulk photovoltaic effect in CH3NH3PbI3 and CH3NH3PbI3–xClx. J. Phys. Chem. Lett. 2015, 6, 31–37. 10.1021/jz502109e. [DOI] [PubMed] [Google Scholar]
  30. Chen B.; Shi J.; Zheng X.; Zhou Y.; Zhu K.; Priya S. Ferroelectric solar cells based on inorganic-organic hybrid perovskites. J. Mater. Chem. A 2015, 3, 7699–7705. 10.1039/C5TA01325A. [DOI] [Google Scholar]
  31. Dang Y.; Liu Y.; Sun Y.; Yuan D.; Liu X.; Lu W.; Liu G.; Xia H.; Tao X. Bulk crystal growth of hybrid perovskite material CH3NH3PbI3. CrystEngComm 2015, 17, 665–670. 10.1039/C4CE02106A. [DOI] [Google Scholar]
  32. Kim H.-S.; Kim S. K.; Kim B. J.; Shin K.-S.; Gupta M. K.; Jung H. S.; Kim S.-W.; Park N.-G. Ferroelectric polarization in CH3NH3PbI3 perovskite. J. Phys. Chem. Lett. 2015, 6, 1729–1735. 10.1021/acs.jpclett.5b00695. [DOI] [PubMed] [Google Scholar]
  33. Liu S.; Zheng F.; Koocher N. Z.; Takenaka H.; Wang F.; Rappe A. M. Ferroelectric domain wall induced band gap reduction and charge separation in organometal halide perovskites. J. Phys. Chem. Lett. 2015, 6, 693–699. 10.1021/jz502666j. [DOI] [PubMed] [Google Scholar]
  34. Rashkeev S. N.; El-Mellouhi F.; Kais S.; Alharbi F. H. Domain walls conductivity in hybrid organometallic perovskites and their essential role in CH3NH3PbI3 solar cell high performance. Sci. Rep. 2015, 5, 11467. 10.1038/srep11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Stroppa A.; Quarti C.; De Angelis F.; Picozzi S. Ferroelectric polarization of CH3NH3PbI3: a detailed study based on density functional theory and symmetry mode analysis. J. Phys. Chem. Lett. 2015, 6, 2223–2231. 10.1021/acs.jpclett.5b00542. [DOI] [PubMed] [Google Scholar]
  36. Seol D.; Han G. S.; Bae C.; Shin H.; Jung H. S.; Kim Y. Screening effect on photovoltaic performance in ferroelectric CH3NH3PbI3 perovskite thin films. J. Mater. Chem. A 2015, 3, 20352–20358. 10.1039/C5TA06190C. [DOI] [Google Scholar]
  37. Zhao P.; Xu J.; Ma C.; Ren W.; Wang L.; Bian L.; Chang A. Spontaneous polarization behaviors in hybrid halide perovskite film. Scr. Mater. 2015, 102, 51–54. 10.1016/j.scriptamat.2015.01.030. [DOI] [Google Scholar]
  38. Hermes I. M.; Bretschneider S. A.; Bergmann V. W.; Li D.; Klasen A.; Mars J.; Tremel W.; Laquai F.; Butt H.-J.; Mezger M.; et al. Ferroelastic fingerprints in methylammonium lead iodide perovskite. J. Phys. Chem. C 2016, 120, 5724–5731. 10.1021/acs.jpcc.5b11469. [DOI] [Google Scholar]
  39. Wang P.; Zhao J.; Wei L.; Zhu Q.; Xie S.; Liu J.; Meng X.; Li J. Photo-induced ferroelectric switching in perovskite CH3NH3PbI3 films. Nanoscale 2017, 9, 3806–3817. 10.1039/C6NR09310H. [DOI] [PubMed] [Google Scholar]
  40. Rakita Y.; Bar-Elli O.; Meirzadeh E.; Kaslasi H.; Peleg Y.; Hodes G.; Lubomirsky I.; Oron D.; Ehre D.; Cahen D. Tetragonal CH3NH3PbI3 is ferroelectric. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E5504–E5512. 10.1073/pnas.1702429114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rohm H.; Leonhard T.; Hoffmann M. J.; Colsmann A. Ferroelectric domains in methylammonium lead iodide perovskite thin-films. Energy Environ. Sci. 2017, 10, 950–955. 10.1039/C7EE00420F. [DOI] [Google Scholar]
  42. Mosconi E.; Quarti C.; Ivanovska T.; Ruani G.; De Angelis F. Structural and electronic properties of organo-halide lead perovskites: a combined IR-spectroscopy and ab initio molecular dynamics investigation. Phys. Chem. Chem. Phys. 2014, 16, 16137–16144. 10.1039/C4CP00569D. [DOI] [PubMed] [Google Scholar]
  43. Carignano M. A.; Kachmar A.; Hutter J. Thermal effects on CH3NH3PbI3 perovskite from ab initio molecular dynamics simulations. J. Phys. Chem. C 2015, 119, 8991–8997. 10.1021/jp510568n. [DOI] [Google Scholar]
  44. Goehry C.; Nemnes G. A.; Manolescu A. Collective behavior of molecular dipoles in CH3NH3PbI3. J. Phys. Chem. C 2015, 119, 19674–19680. 10.1021/acs.jpcc.5b05823. [DOI] [Google Scholar]
  45. Mattoni A.; Filippetti A.; Saba M. I.; Delugas P. Methylammonium rotational dynamics in lead halide perovskite by classical molecular dynamics: the role of temperature. J. Phys. Chem. C 2015, 119, 17421–17428. 10.1021/acs.jpcc.5b04283. [DOI] [Google Scholar]
  46. Lahnsteiner J.; Kresse G.; Kumar A.; Sarma D. D.; Franchini C.; Bokdam M. Room-temperature dynamic correlation between methylammonium molecules in lead-iodine based perovskites: An ab initio molecular dynamics perspective. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 214114. 10.1103/PhysRevB.94.214114. [DOI] [Google Scholar]
  47. Meloni S.; Moehl T.; Tress W.; Franckevičius M.; Saliba M.; Lee Y. H.; Gao P.; Nazeeruddin M. K.; Zakeeruddin S. M.; Rothlisberger U.; et al. Ionic polarization-induced current–voltage hysteresis in CH3NH3PbX3 perovskite solar cells. Nat. Commun. 2016, 7, 10334. 10.1038/ncomms10334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Kulbak M.; Gupta S.; Kedem N.; Levine I.; Bendikov T.; Hodes G.; Cahen D. Cesium enhances long-term stability of lead bromide perovskite-based solar cells. J. Phys. Chem. Lett. 2016, 7, 167–172. 10.1021/acs.jpclett.5b02597. [DOI] [PubMed] [Google Scholar]
  49. Eperon G. E.; Paterno G. M.; Sutton R. J.; Zampetti A.; Haghighirad A. A.; Cacialli F.; Snaith H. J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A 2015, 3, 19688–19695. 10.1039/C5TA06398A. [DOI] [Google Scholar]
  50. Gesi K. Effect of hydrostatic pressure on the structural phase transitions in CH3NH3PbX3 (X = Cl, Br, I). Ferroelectrics 1997, 203, 249–268. 10.1080/00150199708012851. [DOI] [Google Scholar]
  51. Maeda M.; Hattori M.; Hotta A.; Suzuki I. Dielectric Studies on CH3NH3PbX3 (X = Cl and Br) Single Cystals. J. Phys. Soc. Jpn. 1997, 66, 1508–1511. 10.1143/JPSJ.66.1508. [DOI] [Google Scholar]
  52. Chen Y.-F.; Tsai Y.-T.; Bassani D. M.; Hirsch L. Experimental evidence of the anti-parallel arrangement of methylammonium ions in perovskites. Appl. Phys. Lett. 2016, 109, 213504. 10.1063/1.4968579. [DOI] [Google Scholar]
  53. Ang C.; Yu Z.; Youn H. J.; Randall C. A.; Bhalla A. S.; Cross L. E.; Nino J.; Lanagan M. Low-temperature dielectric relaxation in the pyrochlore (Bi3/4Zn1/4)2(Zn1/4Ta3/4)2O7 compound. Appl. Phys. Lett. 2002, 80, 4807–4809. 10.1063/1.1486045. [DOI] [Google Scholar]
  54. Noh J. H.; Im S. H.; Heo J. H.; Mandal T. N.; Seok S. I. Chemical management for colorful, efficient, and stable inorganic–organic hybrid nanostructured solar cells. Nano Lett. 2013, 13, 1764–1769. 10.1021/nl400349b. [DOI] [PubMed] [Google Scholar]
  55. Stoumpos C. C.; Malliakas C. D.; Peters J. A.; Liu Z.; Sebastian M.; Im J.; Chasapis T. C.; Wibowo A. C.; Chung D. Y.; Freeman A. J.; et al. Crystal growth of the perovskite semiconductor CsPbBr3: a new material for high-energy radiation detection. Cryst. Growth Des. 2013, 13, 2722–2727. 10.1021/cg400645t. [DOI] [Google Scholar]
  56. Saidaminov M. I.; Abdelhady A. L.; Murali B.; Alarousu E.; Burlakov V. M.; Peng W.; Dursun I.; Wang L.; He Y.; Maculan G.; et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 2015, 6, 7586. 10.1038/ncomms8586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Im J. H.; Lee C. R.; Lee J. W.; Park S. W.; Park N. G. 6.5% Efficient perovskite quantum-dot-sensitized solar cell. Nanoscale 2011, 3, 4088–4093. 10.1039/c1nr10867k. [DOI] [PubMed] [Google Scholar]
  58. Kulbak M.; Cahen D.; Hodes G. How important is the organic part of lead halide perovskite photovoltaic cells? Efficient CsPbBr3 cells. J. Phys. Chem. Lett. 2015, 6, 2452–2456. 10.1021/acs.jpclett.5b00968. [DOI] [PubMed] [Google Scholar]
  59. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  60. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  61. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  62. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  63. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  64. Allen M. P., Tildesley D. J.. Computer Simulation of Liquids; Oxford University Press, 1991. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b01740_si_001.pdf (249.1KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES