Subzero water permeability parameters and optimal freezing rates for sperm cells of the southern platyfish, Xiphophorus maculatus

Abstract

This study reports the subzero water transport characteristics (and empirically determined optimal rates for freezing) of sperm cells of live-bearing fishes of the genus Xiphophorus, specifically those of the southern platyfish Xiphophorus maculatus. These fishes are valuable models for biomedical research and are commercially raised as ornamental fish for use in aquariums. Water transport during freezing of X. maculatus sperm cell suspensions was obtained using a shape-independent differential scanning calorimeter technique in the presence of extracellular ice at a cooling rate of 20 °C/min in three different media: (1) Hanks’ balanced salt solution (HBSS) without cryoprotective agents (CPAs); (2) HBSS with 14% (v/v) glycerol, and (3) HBSS with 10% (v/v) dimethyl sulfoxide (DMSO). The sperm cell was modeled as a cylinder with a length of 52.35 μm and a diameter of 0.66 μm with an osmotically inactive cell volume (V_b) of 0.6V₀, where V₀ is the isotonic or initial cell volume. This translates to a surface area, SA to initial water volume, WV ratio of 15.15 μm⁻¹. By fitting a model of water transport to the experimentally determined volumetric shrinkage data, the best fit membrane permeability parameters (reference membrane permeability to water at 0 °C, L_pg or L_pg [cpa] and the activation energy, E_Lp or E_Lp [cpa]) were found to range from: L_pg or L_pg [cpa] = 0.0053–0.0093 μm/min atm; E_Lp or E_Lp [cpa] = 9.79–29.00 kcal/mol. By incorporating these membrane permeability parameters in a recently developed generic optimal cooling rate equation (optimal cooling rate, $B_{\text{opt}}=1009.5{\exp }^{(-0.0546E_{\text{Lp}})}\left(L_{\text{pg}}\right)\left(\frac{\text{SA}}{\text{WV}}\right)$ where the units of B_opt are °C/min, E_Lp or E_Lp [cpa] are kcal/mol, L_pg or L_pg [cpa] are μm/min atm and SA/WV are μm⁻¹), we determined the optimal rates of freezing X. maculatus sperm cells to be 28 °C/min (in HBSS), 47 °C/min (in HBSS + 14% glycerol) and 36 °C/min (in HBSS + 10% DMSO). Preliminary empirical experiments suggest that the optimal rate of freezing X.maculatus sperm in the presence of 14% glycerol to be ~25 °C/min. Possible reasons for the observed discrepancy between the theoretically predicted and experimentally determined optimal rates of freezing X. maculatus sperm cells are discussed.

Live-bearing fishes of the genus Xiphophorus are valuable models for biomedical research. In the 1920s, Myron Gordon published a report showing that hybrids between the southern platyfish Xiphophorus maculatus and the green swordtail Xiphophorus helleri developed cancers virtually identical to malignant melanomas in man [40]. This animal model was one of the first to prove that certain cancers were inherited diseases. Since then, species of this genus are widely used in diverse areas of contemporary scientific research [14,26]. In addition to their value as experimental models for biomedical research, swordtails and platyfish are also valued as ornamental fish because of vibrant body coloration and a long sword-like tail. To keep up with the demand for new varieties, scientists and commercial farmers constantly develop new strains [34]. However, deforestation and urban expansion in Mexico and South America are resulting in loss of Xiphophorus habitat. Current stocks held in captivity may no longer exist in their natural habitats. Despite the study of sperm cryopreservation in some 200 species of freshwater and marine fishes [29], sperm cryopreservation in live-bearing fishes as a group has only recently been explored with X. helleri [11–13,36]. More than 22 species and more than 67 pedigreed lines of Xiphophorus are currently maintained only as live animal stocks, perpetuated by labor-intensive breeding regimes.

The focus of the present study was to measure a biophysical response (water transport) in X. maculatus sperm cells during freezing using a differential scanning calorimeter (DSC) [3–6,10,35,36]. In the DSC technique, two heat releases from the same cell suspension are measured: (i) during freezing of osmotically active (live) cells in suspension and (ii) during freezing of osmotically inactive (dead) cells in the same suspension. The difference in heat release measured between the two cooling runs from the same experiment is correlated to water transport. This has been demonstrated in a variety of sperm cells suspensions including murine [5], equine [6], canine [35], and recently in the Pacific oyster Crassostrea gigas [10] and the green sword tail X. helleri [36], and independently verified by Yuan and Diller [41] and Diller [7]. As described elsewhere, knowledge of the water transport (cellular dehydration) during freezing of a cell suspension can be used to predict a priori the optimal rates of freezing [4–6,10,30,35]. Briefly, the loss of post-thaw viability is either due to intracellular ice formation [21,23] or prolonged exposure to freeze-concentrated extracellular solution [19]. Differences in membrane permeability to water and the probability of intracellular ice formation (IIF) result in different optimal cooling rates for different cells [15,22,24,30,37–39]. Therefore, to biophysically determine an optimal cooling rate a priori it is important to measure the cell membranes permeability to water.

The aim of this project was to establish the water transport (and consequently the membrane permeability parameters) of X. maculatus sperm during freezing using a DSC technique at a cooling rate of 20 °C/min in three different media: Hanks’ balanced salt solution (HBSS) without cryoprotectants, HBSS with 14% glycerol and HBSS with 10% dimethyl sulfoxide (DMSO). The experimentally determined membrane permeability parameters were incorporated into a recently developed generic optimal cooling rate equation [37] and used to predict the optimal cooling rates for X. maculatus sperm cryopreservation. Additionally, the accuracy of the predicted optimal cooling rates was determined by comparing the post-thaw motility of X. maculatus sperm cells frozen at three different cooling rates (5, 25, and 45 °C/min) in HBSS with 14% glycerol.

Materials and methods

Sperm collection and sample preparation

A total of 32 male X. maculatus were used in this study. Fish were shipped by overnight delivery from the Xiphophorus Genetic Stock Center (XGSC) of Texas State University (San Marcos, TX, USA) to the Aquaculture Research Station of the Louisiana State University Agricultural Center in September 2004. Within 2–3 days of arrival at the ARS, fish were anesthetized in 0.01% tricaine-methane sulfonate (Western Chemical, Ferndale, WA, USA) for 2 min, and sperm were collected by surgical removal of the testis. Adherent tissue was dissected away and testes were pooled and placed in tared resealable plastic bags (NASCO whirl-pak, MBCOCT, New Haven, CT, USA) and weighed. Hanks’ balanced salt solution (HBSS) at 300 mOsmol/kg was added before crushing of the testis to release sperm. Concentrated sperm suspensions were diluted with HBSS to achieve the final concentrations of approximately 1 × 10⁹ cells/mL. Motility of fresh sperm were above 90% for all samples. The samples were transported chilled to the LSU bioengineering laboratory for DSC experiments. Note that the concentration of the cells was such that the product of initial intracellular cell water (~7 μm³), the latent heat of fusion of water (335 mJ/mg), the density of intracellular water (1000 kg/m³) and the number of cells in a DSC sample pan (~10⁹ cells/mL) translated to a value that could be measured by a DSC-7 machine (Perkin-Elmer Corporation, Norwalk, CT) which is approximately 1–3 mJ/mg of sample (see Devireddy et al. [3] for a more detailed description for the expected value of the DSC heat release).

DSC experiments

The DSC experiments were carried out in the absence and presence of CPAs. Nine separate DSC experiments were conducted in the absence of any CPA, and in the presence of two CPAs glycerol (14% v/v) and DMSO (10% v/v). Approximately 10 μL of the sperm suspension was loaded in a DSC standard aluminum sample pan (Perkin-Elmer Corporation) with ~0.5 mg Pseudomonas syringae (ATCC, Rockville, MD). The DSC dynamic cooling protocol used to measure the water transport out of the sperm cells was the same as reported in earlier studies on mammalian [5,6,35] and aquatic [10,36] sperm cells and will not be repeated here in the interest of brevity. Since we found that the X. maculatus sperm cells lose motility very rapidly, within 20 h interval, motility decreased by 50% and completely ceased at day 5 (unpublished data), all water transport (DSC) experiments were completed within 3–6 h of sperm collection.

Translation of heat release to water transport data

The heat release measurements of interest are q_dsc and q(T)_dsc which are the total and fractional difference between the heat releases measured by integration of the heat flows during freezing of osmotically active (live) cells in media and during freezing of osmotically inactive (dead) cells in media. This difference in heat release has been shown to be related to cell volume changes in several biological systems [3–6,10,35,36] as

$$V(T)=V_{\mathrm{i}}-\frac{\mathrm{\Delta }q{(T)}_{\text{dsc}}}{\mathrm{\Delta }{q}_{\text{dsc}}}(V_{\mathrm{i}}-V_{\mathrm{f}}).$$ (1)

Note that the DSC measured heat release readings q_dsc and q(T)_dsc are obtained separately both in the absence and presence of CPAs [3–6,10,35,36]. The unknowns required in Eq. (1) apart from the DSC heat release readings are V_i (the initial cell volume) and V_f (the final cell volume). The initial volume of the sperm cells in the HBSS solution was assumed to be the isotonic cell volume, V₀ (~18 μm³) (see Fig. 1 and Table 1) and from this the initial cell volume, V_i, was calculated to be 1.25 V₀ in HBSS with 14% glycerol and 1.18 V₀ in HBSS with 10% DMSO. Similarly, the final volume in HBSS was assumed to be the osmotically inactive cell volume, V_b (=0.6 V₀ or ~10.8 μm³) and from this the final volume V_f, was calculated to be 0.66 V_i in HBSS with 14% glycerol and 0.64 V_i in HBSS with 10% DMSO. These calculations, a detailed description of which is provided elsewhere [15,30], were performed assuming that both DMSO and glycerol are completely permeable to the X. maculatus sperm cell membrane and at equilibrium the concentrations of DMSO and glycerol inside the X. maculatus sperm cell are equal to the extracellular concentration.

Fig. 1.

(Left) Representative scanning electron micrographs (SEM) of sperm from X. maculatus showing the relationship of sperm head and tail in alignment with model used to calculate the cell volumes and surface areas shown on the right. (Right) A schematic of the model used to calculate the X. maculatus sperm cell volumes and surface areas from the SEM images shown on the left (see Table 1). Note that in the “geometric” model the head, mid-piece and tail of the X. maculatus sperm cell are all assumed to be cylinders.

Table 1.

Measurements, and calculated volumes, surface areas and ratios of surface area to volume (S:V) for head, mid-piece, tail and combined total of a sperm cell from Xiphophorus maculatus (n = 15)

Sperm cell geometry	Diameter (μm)	Length (μm)	Mean volume (V) (μm3)	Mean surface area (S) (μm2)	S:V (μm−1)
Heada	1.2 ± 0.08	3.7 ± 1.2	4.2	14.0	3.33
Mid-piecea	0.86 ± 0.1	7.1 ± 0.4	4.1	19.2	4.68
Taila	0.51 ± 0.2	45.9 ± 0.8	9.4	73.5	7.82
Totalb	0.66	52.35	17.7	106.7	6.03

^aThe volumes of the head, mid-piece and tail are all assumed to be cylinders.

^bSum of the volumes and surface areas of the head, the mid-piece and the tail. Note that as long as the values of available surface area, the cell volume and the S:V are maintained as close to the original values as possible, any geometry can be used to model the sperm cell. For simplicity we assumed the X. maculatus can be modeled as a thing long cylinder of length 52.35 μm and a diameter of 0.66 μm (which results in a surface area of 108.55 μm², a cell volume of 17.9 μm³ and a surface area to cell volume ratio of 6.06).

To ensure the accuracy and repeatability of the experimental data, a set of calibration and control experiments were performed as detailed previously for this instrument [3,4]. One of these tests was to compare the heat release measured during the final cooling run, q_final, with the DSC measured heat release from a separate control experiment composed of osmotically inactive (lysed) X. maculatus spermatozoa; the magnitude (~220 mJ/mg) of the heat releases were found to be within ±1%. This indicated that after the fast cooling in the DSC protocol (200 °C/min to −150 °C) the X. maculatus spermatozoa were osmotically inactive.

Water transport model and numerical methods

Kedem and Katchalsky [16] proposed a model for water and solute transport in response to chemical potential gradients based on irreversible thermodynamics. If the flux of CPA is negligible in comparison to the water flux, then the Kedem–Katchalsky model reduces to a model which assumes only water transport, as proposed by Mazur [20] and later modified by Levin et al. [18]. The water transport model of Mazur was further modified to incorporate the presence of CPAs on the volumetric shrinkage response of cells during freezing as [15,30]

$$\frac{\mathrm{d}V}{\mathrm{d}T}=-\frac{L_{\mathrm{p}}{A}_{\mathrm{c}}RT}{B_{v_{\mathrm{W}}}}\times \left[\ln \frac{(V_0-V_{\mathrm{b}}-n_{\text{cpa}}{v}_{\text{cpa}})/v_{\mathrm{w}}}{(V_0-V_{\mathrm{b}}-n_{\text{cpa}}{v}_{\text{cpa}})/v_{\mathrm{w}}+({\phi }_{\mathrm{s}}{n}_{\mathrm{s}}+n_{\text{cpa}})}-\frac{\mathrm{\Delta }{H}_f{v}_{\mathrm{w}}\rho }{R}\left(\frac{1}{T_{\mathrm{R}}}-\frac{1}{T}\right)\right]$$ (2)

with L_p, the sperm cell membrane permeability to water defined by Levin et al. [18] as

$$L_{\mathrm{p}}=L_{\text{pg}}[\text{cpa}]\exp \left(-\frac{E_{\text{Lp}}[\text{cpa}]}{R}\left(\frac{1}{T}-\frac{1}{T_R}\right)\right),$$ (3)

where, L_pg [cpa] is the reference membrane permeability at a reference temperature, T_R (=273.15 K); E_Lp [cpa] is the apparent activation energy or the temperature dependence of the cell membrane permeability; V is the sperm cell volume at temperature, T; A_c is the effective membrane surface area for water transport, assumed to be constant during the freezing process; V₀ and V_b are the isotonic (initial) and osmotically inactive sperm cell volumes, respectively; R is the universal gas constant; B is the constant cooling rate; n_cpa is the number of moles of salt; v_cpa is the partial molar volume of CPA; v_w is the molar volume of water; φ_s is the disassociation constant for salt; n_s is the number of moles of salt (=C_i(V₀ − V_b), where C_i is the initial cell osmolality); ΔH_f is the latent heat of fusion of water; ρ is the density of water. Note that when n_cpa is zero (i.e., no CPA is present), Eqs. (2) and (3) reduce to the “water transport” model as described by Mazur [20] and Levin et al. [18] and L_p is an Arrhenius function of L_pg and E_Lp. The two unknown membrane permeability parameters of the model either L_pg [cpa] and E_Lp [cpa] in the presence of CPA or L_pg and E_Lp in the absence of CPA, are determined by curve-fitting the water transport model to experimentally obtained volumetric shrinkage data during freezing. The various assumptions made in the development of Mazur’s model of water transport are discussed in detail elsewhere [15,18,24,30].

Numerical methods

A nonlinear least squares curve fitting technique was implemented using a computer program to calculate the membrane permeability parameters that best fit the volumetric shrinkage data as previously described by Bevington and Robinson [1]. The optimal fit of Eq. (3) to the experimental data was obtained by selecting a set of parameters which minimized the residual variance, χ², and maximized a goodness of fit parameter, R² [25]. All the curve fitting results presented have an R² value greater than or equal to 0.98 indicating that there was a good agreement between the experimental data points and the fit calculated using the estimated membrane permeability parameters.

Theoretical prediction of optimal cooling rates

Traditionally, the optimal rate of freezing is determined by analyzing the simulated biophysical (water transport) response of sperm cells at various cooling rates (5–100 °C/min). To simulate the biophysical response of sperm cell the best fit parameters were substituted in the water transport equation, which was then numerically solved using a fourth order Runge–Kutta method using a custom written FORTRAN code on a workstation [3–6,10,30,35,36]. Recently, Thirumala and Devireddy [37] report that for a variety of biological systems a comparison of the published experimentally determined values of B_opt (in °C/min) agreed quite closely with the value obtained using a generic optimal cooling rate equation that defines

$$B_{\text{opt}}=1009.5{\exp }^{(-0.0546E_{\text{Lp}})}(L_{\text{pg}})\left(\frac{\text{SA}}{\text{WV}}\right).$$ (4)

In this equation, L_pg and E_Lp (or L_pg [cpa] and E_Lp [cpa]) represent the membrane permeability parameters (in μm/min atm and kcal/mol, respectively), while the term SA/WV (in μm⁻¹) represents the ratio of the available surface area for water transport to the initial volume of intracellular water (with an assumed osmotically inactive cell volume of 0.6 V₀ this ratio has a value of 15.15 μm⁻¹ for X. maculatus sperm cells). Once the cell level parameters L_pg and E_Lp (or L_pg [cpa] and E_Lp [cpa]) are determined using the curve-fitting procedure described above, we propose to utilize Eq. (4) to predict the optimal rates of freezing X. maculatus sperm cells. Although, the use of Eq. (4) greatly simplifies the prediction of an optimal cooling rate, there are several limitations/assumptions made in the development of Eq. (4) that preclude it from being universally valid [37]. These assumptions include: (a) the cooling rate which optimizes the freeze/thaw response of any cellular system can be defined as the fastest cooling rate in a given media without forming damaging intracellular ice; (b) Mazur [22] defined intracellular ice as damaging and lethal if >10–15% of the initial intracellular water is involved. We defined the optimal cooling rate as the cooling rate at which 5% of the initial water volume is trapped inside the cells at −15 °C [37]. It is also important to note that, in the development of Eq. (4) the dynamics and kinetics of IIF have not been included [38,39], as no experimental techniques are currently available to make these measurements in sperm cells.

Empirical determination of optimal cooling rates

Aliquots (80 μL) of sperm suspensions with cryoprotectant (14% glycerol) were drawn into 0.25-ml French straws (IMV International, Minneapolis, MI, USA) and held (equilibrated) for 8 min at room temperature (23–25 °C) and 2 min at 4 °C before cooling in a controlled-rate freezer (Kryo 10 Series II; Planer Products, Sunbury-on-Thames, UK) at 5, 25, and 45 °C per min from 5 to −80 °C. The straws were transferred to a liquid nitrogen storage dewar after the temperature reached −80 °C. After a minimum of 12 h, the straws were thawed for 7 s in a 40 °C water bath (Model 1141, VWR Scientific, Niles, IL, USA). Post-thaw sperm motility was estimated visually at 200× magnification using darkfield microscopy (Optiphot 2, Nikon, Garden City, NY, USA) and was expressed as the percentage of cells (in increments of 2% when motility was less than 10%, otherwise in increments of 5%) actively moving in a forward direction. Sperm vibrating in place were not considered to be motile.

Results

Membrane permeability parameters and predicted optimal cooling rates

The water transport data and simulation using the best fit parameters in Eq. (2) were measured at a cooling rate of 20 °C/min in HBSS (Fig. 2A), in HBSS with 14% glycerol (Fig. 2B) and in HBSS with 10% DMSO (Fig. 2C). Water transport cessation was observed in the DSC heat release data as an overlap of the thermograms from the heat release signature obtained using osmotically active (initial) and inactive (final) cells. The dynamic portion of the cooling curve (where the thermograms were distinct) was found to be between −0.6 and −10 °C with HBSS, between −4.1 and −22 °C with HBSS and 14% glycerol, and between −3.2 and −25 °C with HBSS and 10% DMSO. The membrane permeability parameter values that best fit the 20 °C/min water transport data in the absence and presence of CPAs were calculated (Table 2). The theoretically predicted optimal cooling rate values obtained using the Eq. (4) for freezing X. maculatus sperm cells ranged from 28 °C/min in HBSS, 47 °C/min in HBSS with 14% glycerol, and 36 °C/min in HBSS with 10% DMSO (Table 2). The model-simulated equilibrium cooling response was generated by setting the left hand side (LHS) of Eq. (2) = 0 and balancing the intracellular and extracellular unfrozen chemical activity of water on the right hand side (RHS) at a particular subzero temperature (shown as a dashed line in Fig. 2).

Fig. 2.

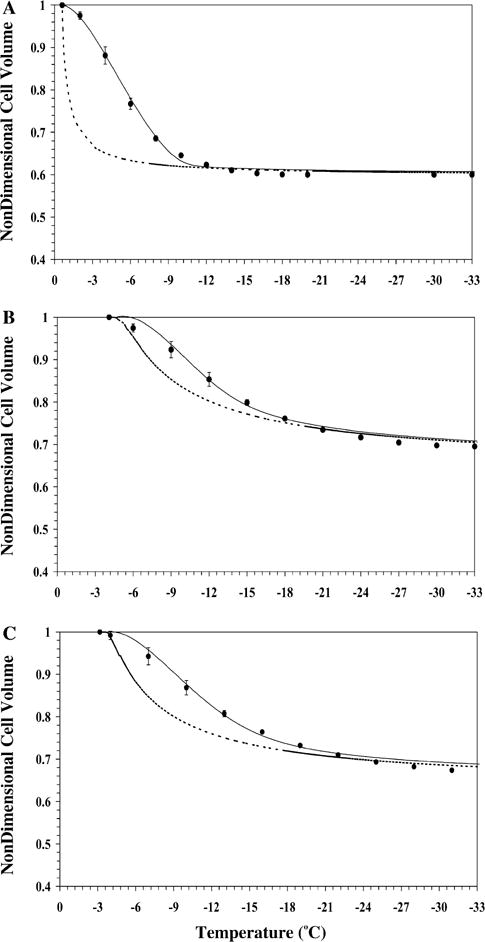
Volumetric response of X. maculatus sperm cells as a function of sub-zero temperatures obtained using the DSC technique in the presence of extracellular ice (A), in the presence of extracellular ice and glycerol (B) and in the presence of extracellular ice and DMSO (C). The filled circles represent the experimentally obtained water transport (volumetric shrinkage) at a cooling rate of 20 °C/min. The dynamic cooling response at 20 °C/min is shown as a solid line and was obtained by using the “best fit” membrane permeability parameters (L_pg and E_Lp or L_pg [cpa] and E_Lp [cpa]) (Table 2) in the water transport equation (Eqs. (2) and (3)). The model simulated equilibrium cooling response obtained is shown as a dotted line in all the figures. The non-dimensional cell volume is plotted along the y-axis and the sub-zero temperatures are shown along the x-axis. The error bars represent the standard deviation for the mean values of nine separate DSC experiments (n = 9).

Table 2.

Predicted sub-zero membrane permeability parameters (L_pg or L_pg[cpa] and E_Lp or E_Lp [cpa]) and the optimal rates of freezing for Xiphophorus maculatus sperm cells in the presence and absence of cryoprotective agents (CPAs)

Assumed inactive cell volume (Vb)	Concentration of CPA (v/v)	Lpg or Lpg [cpa] ×1015 m3/Ns (μm/min atm)	ELp or ELp [cpa] kJ/mol (kcal/mol)	Predicted optimal cooling ratea (°C/min)
0.6 V0	No CPA	1.59 (0.0093)	121.2 (29.0)	28
	14% glycerol	0.91 (0.005)	40.9 (9.8)	47
	10% DMSO	0.99 (0.006)	67.3 (16.1)	36
0.4 V0	No CPA	2.63 (0.015)	134.9 (32.3)	26
	14% glycerol	1.33 (0.008)	40.8 (9.8)	47
	10% DMSO	1.45 (0.009)	66.0 (15.8)	36
0.8 V0	No CPA	1.20 (0.007)	175.6 (42.0)	21
	14% glycerol	0.68 (0.004)	66.9 (16.0)	50
	10% DMSO	0.48 (0.003)	65.6 (15.7)	36

Note that the goodness of fit, R² value was always greater than >0.98.

^aThe optimal cooling rate was predicted using Eq. (4) in which E_Lp or E_Lp [cpa] are in kcal/mol, L_pg or L_pg [cpa] are in μm/min atm and SA/WV is 15.15 μm⁻¹.

To further understand the range of L_pg and E_Lp (or L_pg [cpa] and E_Lp [cpa]) values that best fit the experimental data, we generated contour plots as shown in Fig. 3 or L_pg [cpa] and E_Lp [cpa] space that corresponds to the water transport data at 20 °C/min in HBSS, in HBSS with 14% glycerol, and in HBSS with 10% DMSO. Any combination of L_pg and E_Lp (or L_pg [cpa] and E_Lp [cpa]) shown to be within the contour correlates to the water transport data in that media with a goodness of fit parameter R² value of >0.98. Note that the contours for the media containing 14% glycerol and 10% DMSO enclose a significantly smaller values of the activation energies than those enclosed by corresponding contour for the media containing no cryoprotective agents.

Fig. 3.

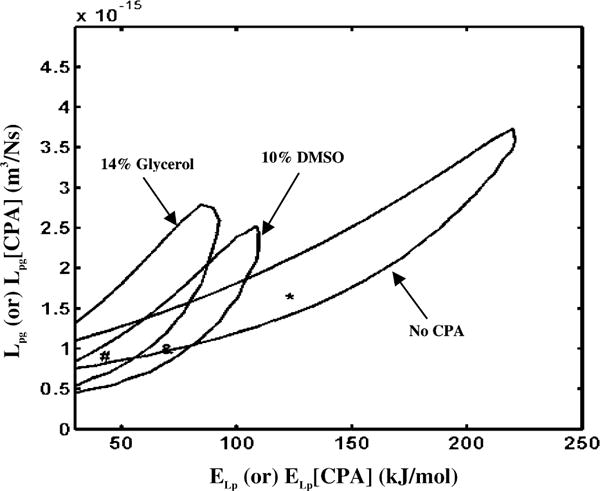
Contour plots of the goodness of fit parameter R² (=0.98) for water transport response in X. maculatus sperm cells in three different media: HBSS with no CPAs, HBSS with 14% glycerol and HBSS with 10% DMSO. Note that the best fit parameters (Table 2) are represented within the contours by a “*” (absence of CPAs), “#” (with 14% glycerol) and “ &” (with 10% DMSO). The membrane permeability at 0 °C, L_pg (or L_pg [cpa]) (m³/Ns) is plotted on the y-axis while the apparent activation energy of the membrane, E_Lp (or E_Lp [cpa]) (kJ/mol) is plotted on the x-axis.

Parameter sensitivity analysis—effect of varying V_b

The value of the osmotically inactive cell volume, V_b of mammalian sperm cells has been reported to be 0.6 V₀ (the value used in this and other studies) and to range from as low as 0.23 V₀ to as high as 0.75 V₀ [3–6,35–37]. To estimate the effect of varying the osmotically inactive cell volume on the measured membrane permeability parameters (L_pg and E_Lp or L_pg [cpa] and E_Lp [cpa]), the value of V_b was increased to 0.8 V₀ and decreased to 0.4 V₀. The DSC data were correspondingly modified (using Eq. (1)) and the modified DSC water transport data were curve fitted to the water transport model (Eqs. (2) and (3)) using the nonlinear least squares curve fitting technique described previously. The predicted values of the membrane permeability parameters (L_pg and E_Lp) using a value of 0.4 V₀ and 0.8 V₀ as the osmotically inactive cell volume are also shown in Table 2. Although, the predicted membrane permeability parameters using V_b of 0.4 V₀ and 0.8 V₀ were different from each other and the values obtained using V_b of 0.6 V₀ (Table 2), the predicted rates of optimal freezing are not that different and are within ±10% of one another. Thus, the variation in the value of V_b did not alter our model predicted optimal rates of freezing X. maculatus sperm cell across a broad range of V_b values.

To further illustrate the effect of varying the osmotically inactive cell volume on the predicted membrane permeability parameters, contour plots (similar to those shown in Fig. 3) were generated for an assumed V_b values of 0.8 V₀ and 0.4 V₀. A comparison of contour space for the three different values of V_b (0.4 V₀, 0.6 V₀, and 0.8 V₀) are shown in Fig. 4A (for HBSS with no CPAs), Fig. 4B (HBSS with 14% glycerol), and Fig. 4C (HBSS with 10% DMSO). The contour plots shown in Fig. 4 suggest that no precise conclusions could be drawn on the effect of assumed V_b on predicted X. maculatus sperm cell membrane permeability parameters, although there seems to be a trend towards lowering the range of best fit reference membrane permeability value (L_pg) with increasing V_b.

Fig. 4.

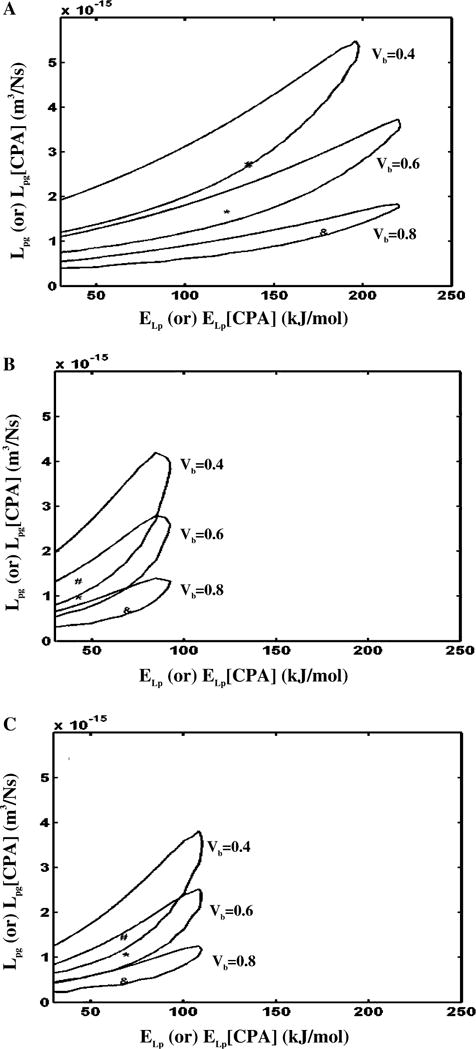
Contour plots of the goodness of fit parameter R² (=0.98) for water transport response in X. maculatus sperm cells in three different media: HBSS with no CPAs (A), HBSS with 14% glycerol (B) and HBSS with 10% DMSO (C). Within each figure, the three contour correspond to the three assumed values of osmotically inactive cell volume, V_b (0.4 V₀, 0.6 V₀, and 0.8 V₀). Note that the best fit parameters (Table 2) are represented within the contours by a “#” (V_b = 0.4 V₀), “*” (V_b = 0.6 V₀), and “&” (V_b = 0.8 V₀). The membrane permeability at 0 °C, L_pg (or L_pg [cpa]) (m³/Ns) is plotted on the y-axis while the apparent activation energy of the membrane, E_Lp (or E_Lp [cpa]) (kJ/mol) is plotted on the x-axis.

Independent verification of predicted optimal cooling rates

The predicted optimal rates of freezing X. maculatus sperm cells obtained in the present study ranged from 21 to 28 °C/min in HBSS, 47–50 °C/min in HBSS with 14% glycerol, and 36 °C/min in HBSS with 10% DMSO (Table 2). Fresh controls without the addition of 14% glycerol and freezing showed a rapid decline of motility from initial 90–60% at 5 h later. With 14% glycerol as the cryoprotectant, the highest post-thaw motility after thawing was obtained with the cooling rate of 25 °C/min (32 ± 6%; means ± SD; number of replicates = 3), and was significantly better than the post-thaw motility at either 5 °C/min (16 ± 4%) or 45 °C/min (21 ± 2%) (P = 0.0002).

Discussion

A DSC technique was used to obtain water transport data and water permeability parameters (L_pg or L_pg [cpa] and E_Lp or E_Lp [cpa]) of X. maculatus sperm cells in three different cryoprotective media. There was a significant decrease (~40–70%) in the measured values of reference membrane permeability, L_pg (or L_pg [cpa]) and activation energies E_Lp (or E_Lp [cpa]) obtained in the presence CPAs when compared with the corresponding values obtained in their absence [5,6,35]. The relative reduction in the values of L_pg (or L_pg [cpa]) and E_Lp (or E_Lp [cpa]) was relatively unaffected by the choice of assumed osmotically inactive cell volume, V_b. The best fit permeability parameters were incorporated into Eq. (4) to predict the optimal rates of freezing X. maculatus sperm cells (Table 2).

As stated earlier, in the development of Eq. (4) the dynamics and kinetics of IIF have not been included [15,38,39]. Thus, if IIF occurs by a heterogeneous or a surface catalyzed nucleation mechanism [15,38,39] (generally between −5 and −20 °C for a variety of single cells), which our model does not predict, then potentially even more water will be trapped in the sperm cells than predicted by water transport alone. Thus, the optimal cooling rates obtained using Eq. (4) are probably over estimated. And finally, although the predicted optimal rates using Eq. (4) agreed quite closely (±10%) with the experimentally determined optimal rates of freezing for several cell types, including mouse spermatozoa, yeast, lymphocytes, mouse oocytes and X. helleri sperm cells, the associated error (difference between theoretically predicted and experimentally determined) with the use of Eq. (4) was as high as 318% for AT-1 prostate tumor cells and 56% for canine sperm cells (a tabulated listing is provided in [37]). Clearly, the predicted optimal rates of freezing obtained using Eq. (4) need to be used with extreme circumspection.

As shown in Table 2, the optimal rates in the presence of 14% glycerol or 10% DMSO were higher (~30–70%) than the predicted optimal values in their absence. This result is not surprising, as the presence of CPAs are expected to increase the ability of the cell membrane to dehydrate at faster cooling rates as shown previously for several cell suspensions [5,9,22,30]. And finally, earlier empirical studies of X. helleri (swordtails) and X. couchianus (platyfish) indicated that optimal cooling rates ranged from 20 to 25 °C/min for both species [11–13]. These values are comparable to those obtained in the present study for X. maculatus sperm cells. Additional simulations also showed that errors and uncertainties in the measured X. maculatus sperm cell dimensions (i.e., changes in the S:V ratio by as much as 50%) did not significantly (±20%) alter the predicted optimal cooling rates (data not shown).

A comparison of the membrane permeability parameters reported earlier for C. gigas sperm cells in the presence of calcium-free HBSS (1000 mOs-mol/kg) and 8% DMSO [10] with the values obtained in the present study for X. maculatus sperm cells in the presence of HBSS (300 mOs-mol/kg) and 10% DMSO reveals the following differences: the apparent activation energies (different by a factor of two) and the reference membrane permeability (different by a factor of four) were higher for X. maculatus sperm cells. Additionally, the reported theoretical optimal rates of freezing of C. gigas haploid and diploid sperm cells (~53 and ~44 °C/min) with 8% DMSO [10] were higher than the corresponding values with 10% DMSO for X. maculatus sperm cells (36 °C/min), obtained in the current study.

Similarly, a comparison of the membrane permeability parameters reported earlier for X. helleri sperm cells [36] with the values obtained in the present study for X. maculatus sperm cells in the same freezing media also revealed several differences: both the activation energy and the reference membrane permeability (higher by a factor of two) for X. maculatus sperm cells in the absence of any CPAs and the corresponding optimal rates of cooling were significantly lower (28 °C/min for X. maculatus vs. 89 °C/min for X. helleri). However in the presence of 14% glycerol, the reference membrane permeability was essentially unchanged (0.0053 μm/min atm in X. maculatus vs. 0.0063 μm/min atm in X. helleri) while the activation energy was significantly lowered (9.8 kcal/mol in X. maculatus vs. 20.0 kcal/mol in X. helleri) and the corresponding optimal rates of cooling were significantly higher (47 °C/min for X. maculatus vs. 29 °C/min for X.helleri). And finally in the presence of 10% DMSO, both the reference membrane permeability and activation energies were lower (by ~30 to 50%) in X. maculatus and the corresponding cooling rates were essentially the same (36 °C/min for X. maculatus vs. 32 °C/min for X. helleri). Clearly, the relative importance of the effect of extracellular ice and concentration of CPAs on the predicted membrane permeability parameters (L_pg or L_pg [cpa] and E_Lp or E_Lp [cpa]) and on the optimal rates of cooling is dependent on the cell type and the choice of freezing media.

Empirically, the optimal cooling rate for X. maculatus (25 °C/min) is in agreement with those for X. helleri (20–25 °C/min) and X. couchianus (20–30 °C/min) [11–13], although it did not agree in the present study with the optimal cooling rate predicted using the water permeability parameters obtained using the DSC technique (47 °C/min). This is in contrast with the DSC prediction for sperm of X. helleri (20–30 °C/min) [36], which is in close agreement with the empirical value. The inconsistency of DSC prediction with these two Xiphophorus species could be due to several reasons. The most probable cause being the optimal amount of intracellular water (or the formation if intracellular ice, which we do not account for) that needs to be trapped inside the X. maculatus sperm cells to survive the freezing process. The theoretically predicted values are calculated assuming that ~5% of the initial intracellular water being trapped inside the cell is ideal. Should the % of initial intracellular water trapped inside the X. maculatus sperm cell be lowered to ~2% (or should intracellular ice form within the cells), the observed discrepancy between the theoretically predicted and experimentally observed cooling rates can be reconciled. It is as yet unclear if this result for X. maculatus sperm cells is independent of the freezing media composition (additional empirical experiments in the presence of DMSO and other CPAs are warranted and will be pursued in the near future). Another possibility could be that the time period from the sperm collection to initiation of experiments altered the DSC results. Sperm from X. maculatus retained motility less effectively after collection compared with X. helleri and X. couchianus. Sperm motility of X. maculatus decreased from >90 to 60% within 5 h after collection, by 50% after 20 h and completely ceased at day 5 (unpublished data), and thus a time duration of 3–6 h could have had, as yet, undetermined effects on the membrane properties of X. maculatus sperm cells. Although the same collection technique (crushing of testis) was used in both cases by the same researchers, inclusion of cells other than mature sperm was unavoidable, and the proportion of those cells can vary with testis maturity, species, or strains of the same species. Given the fact that all sperm suspensions used for experiments had motility of 80–90%, testis maturity of fish used for empirical and DSC experiments was constant. On the other hand, the rapid decline of motility after collection for sperm from X. maculatus may suggest that sperm from this species are more sensitive to handling than X. helleri although they are similar in morphology. The response to cryopreservation is also different. When cooled at 25 °C/min, the highest post-thaw motility in the presence of 14% glycerol in HBSS for X. maculatus was only 32 ± 6%, while the same conditions yielded 71 ± 7% for X. helleri, and 78 ± 3% for X. couchianus.

Although sperm quality may vary with species, different strains of the same species may also exhibit different sensitivity to cryopreservation. Clear evidence comes from recent studies of mouse sperm cryopreservation. Differences in freezing sensitivity were reported among various inbred and outbred strains of mice [27,31–33]. Interestingly, sperm cryopreservation of X. maculatus could be analogous to mouse with those species having various strains developed for biomedical studies, and with some of those strains being highly inbred. Thus, it is possible the discrepancy between empirical data and DSC prediction may due to differences in fish strains. In addition, male variations within the same strain could also contribute to this discrepancy. Sperm of different males were found to have different responses to the same freezing protocols in mammals and other aquatic species [8,17,28]. Empirical data for examining optimal cooling rates of sperm from X. maculatus should be collected on more individuals. Most strains of X. maculatus in XGSC are highly inbred; therefore it would be informative to investigate the effects of inbreeding. Stocks of Xiphophorus maintained in the laboratory differ significantly in breeding performance, with some strains remaining equal to wild fish after more than 60 generations of full-sib mating, but others becoming characterized by poor breeding performance [2]. In the future it would be important to examine the sperm behavior among different species, different strains, different individuals within the same strain, and more fundamentally of wildtype fish.