Behaviorally-selective engagement of short-latency effector pathways by motor cortex

SUMMARY

Blocking motor cortical output with lesions or pharmacological inactivation has identified movements that require motor cortex. Yet when and how motor cortex influences muscle activity during movement execution remains unresolved. We addressed this ambiguity using measurement and perturbation of motor cortical activity together with electromyography in mice during two forelimb movements that differ in their requirement for cortical involvement. Rapid optogenetic silencing and electrical stimulation indicated that short-latency pathways linking motor cortex with spinal motor neurons are selectively activated during one behavior. Analysis of motor cortical activity revealed a dramatic change between behaviors in the coordination of firing patterns across neurons that could account for this differential influence. Thus, our results suggest that changes in motor cortical output patterns enable a behaviorally-selective engagement of short-latency effector pathways. The model of motor cortical influence implied by our findings helps reconcile previous observations on the function of motor cortex.

eTOC Blurb

Miri et al. measured and perturbed motor cortical activity during simultaneous electromyography to reveal behavioral selectivity in the engagement of short-latency effector pathways by motor cortex. Changes in the correlation among output firing patterns appear to mediate this selectivity.

INTRODUCTION

Muscle contractions are readily evoked by stimulation of the motor cortex, indicating its capacity to drive movement (Leyton and Sherrington, 1917; Penfield and Boldrey, 1937; Van Acker et al., 2016). Although forms of movement that require motor cortical involvement have been identified, the influence of motor cortex on muscles during movement execution, and its underlying neural mechanisms, remain unresolved.

The behavioral consequences of inactivating motor cortex suggest it plays a limited role in motor control. After lesions to motor cortex or the corticospinal tract, mammals exhibit persistent deficits in grasping movements but regain the ability to perform many motor behaviors (Alaverdashvili and Whishaw, 2008; Farr et al., 2006; Lawrence and Kuypers, 1968; Metz et al., 1998; Piecharka et al., 2005). Similarly, pharmacological inhibition of neural activity in the primary motor cortex of cats induces deficits in the ability to step over obstacles, yet leaves basic treadmill walking essentially unaltered (Beloozerova and Sirota, 1993; Drew et al., 1996). Such findings have given rise to the view that motor cortex contributes to movements that require sensory-guided adaptation or that involve novel muscle activation patterns (Lemon, 1993; Shmuelof and Krakauer, 2011).

The specificity of deficits following inactivation, however, offers only limited insight into the influence of motor cortex during movement execution. The deficits that follow lesions or pharmacological inactivation change over time (Martin and Ghez, 1993; Passingham et al., 1983), implying the existence of compensatory mechanisms that modify motor control circuits (Nudo, 1999; Shadmehr and Krakauer, 2008) and obscure the normal role of motor cortical output. The specificity of inactivation deficits could reflect a role for motor cortex in driving muscle activity similarly across behaviors, with other motor areas compensating for the loss of motor cortical output during certain movements. Thus it remains unclear whether deficit specificity reflects a selective motor cortical influence on the execution of particular movements.

Electrical recording and stimulation of motor cortex have not thus far revealed a behavioral selectivity in motor cortical influence that can account for the specificity of inactivation deficits. The firing patterns of motor cortical neurons correlate with patterns of muscle activity across diverse behaviors, including those that survive motor cortical inactivation (Armstrong and Drew, 1984a; Beloozerova et al., 2010; Dombeck et al., 2009), indicating that motor cortex could drive muscle activity similarly across behaviors. In principle, during certain behaviors the impact of motor cortical output on downstream effector pathways could be negated by changes intrinsic to these pathways (Dyson et al., 2014; Schieber, 2011). However, electrical stimulation of motor cortex perturbs muscle activity at short latency during behaviors that endure after motor cortical inactivation (Armstrong and Drew, 1985; Bretzner and Drew, 2005; Otchy et al., 2015). Though the effects of electrical stimulation vary during and across behaviors, the results are inconsistent with a downstream attenuation of the influence of motor cortex. If movements that require motor cortical involvement feature a specialized influence of motor cortex on muscle activity, its uniqueness likely arises from structure in the patterns of motor cortical output that determines whether certain downstream effector pathways are modulated.

Here, we aimed to clarify the influence of motor cortex on the execution of movement. We first probed for a selective influence of motor cortex during movements that require motor cortical involvement. We compared the impact of motor cortical output on muscle activity during a trained reaching task that requires motor cortex, and treadmill walking, which persists after eliminating motor cortical output. We used rapid optogenetic silencing of motor cortex (Guo et al., 2014b) to reveal a short-latency influence on muscle activity that is specific to the trained reach behavior. The latency of this influence matched that at which muscle activity responds to electrical stimulation of motor cortex, indicating that relatively direct effector pathways are engaged by motor cortical output selectively during the trained behavior.

We then analyzed the structure of motor cortical firing patterns to assess how selective pathway engagement is mediated. Since the synaptic inputs to a neuron can be approximated as a weighted sum of the activity in presynaptic neurons, we examined whether motor cortical activity could be approximated by different weighted sums of neuronal firing patterns during the two behaviors (Druckmann and Chklovskii, 2012; Elsayed et al., 2016; Kaufman et al., 2014). We found this was the case, a consequence of changes in the correlations between neuronal firing patterns. Thus it appears that short-latency pathways used to drive muscle activity during the trained behavior are only responsive to particular patterns of motor cortical output. Collectively, our results support a model of motor cortical influence which can account for the specificity of deficits following motor cortical inactivation, as well as the pervasive nature of muscle-correlated motor cortical activity and stimulation-induced muscle activation.

RESULTS

Mouse forelimb movements that differ in their motor cortical dependence

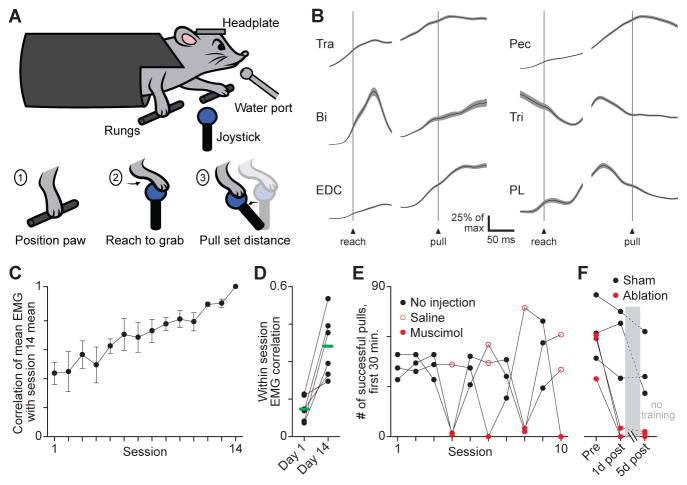
To elicit movements in mice that require the motor cortex, we developed a paradigm in which head-fixed mice learn to pull a joystick a fixed distance with precision (Farr and Whishaw, 2002; Guo et al., 2015; Kawai, 2014). In this task, mice place their right forepaw on a bar, then reach to a joystick and attempt to pull it a short distance (~5mm) that falls within an acceptable range to earn a reward (Figure 1A, Figure S1A, Movie S1). Training for this precision pull task involved behavioral shaping over twice daily training sessions, during which the acceptable range was adaptively changed to maintain the fraction of rewarded trials at 25–40% (Figure S1B; Kawai et al., 2015). Trials were initiated by the rapid motorized positioning of the joystick, which prompts trained mice to begin reaching. The median duration from reach initiation to pull initiation in trained mice was 176 ms, and the median duration of joystick pulling was 119 ms (n = 659 trials across 3 mice). To quantify muscle activity during limb movement, we performed chronic electromyographic (EMG) recordings from three pairs of antagonist muscles arrayed proximo-distally along the forelimb (Figure 1B; Figure S1C–E; Akay et al., 2006).

Figure 1. The precision pull task.

(A) Schematic depicting the precision pull task and its 3 stages. (B) Trial-averaged EMG (black) ± SEM (gray, n = 103) for trapezius (Tra), pectoralis (Pec), biceps (Bi), triceps (Tri), extensor digitorum communis (EDC), and palmaris longus (PL) during precision pull. Scale bar indicates a percentage of maximum in each average; averages normalized by this maximum. (C) Mean ± SEM (n = 6 mice) correlation between trial-averaged EMG from 6 forelimb muscles for individual sessions and their trial averages for the last session plotted (session 14), excluding unrewarded trials. (D) Mean correlation between muscle activation on individual rewarded trials within sessions on the 1^st and 14^th days of training. Green bars show means (6 mice). (E) Performance in terms of successful (rewarded) pulls over several training sessions for 3 mice. Unilateral injections of muscimol or saline alone into the caudal forelimb region occurred 90 minutes before training. Because sessions vary in length, successes were totaled over the first 30 minutes. (F) Performance before and after unilateral ablation of the caudal forelimb area or sham ablations. Mice were not trained between sessions 1 and 5 days after surgery. See also Figure S1.

Measurements of muscle activity during the precision pull task exhibited two hallmarks of motor behaviors learned through practice (Shmuelof and Krakauer, 2011). First, the correlation between trial-averaged muscle activation patterns for individual training sessions revealed a gradual change in mean activity patterns across sessions (Figure 1C). Second, the correlation between muscle activation patterns on individual trials within sessions showed an increase in the degree of stereotypy over time (Figure 1D).

The precision pull task was found to require motor cortex. Unilateral injection of the GABA_A agonist muscimol (74 nl of 1 ng/nl), but not saline alone, into contralateral primary motor cortex greatly diminished motor performance as assessed by the incidence of rewarded pulls (Figure 1E). Muscimol injection profoundly disturbed task execution: the frequency at which mice contacted and deflected the joystick to any degree was reduced by 85 ± 6% (mean ± standard error of the mean (SEM), n = 3 mice). Second, unilateral ablation of contralateral primary motor cortex caused a similar behavioral impairment, both 1 and 5 days after surgery (Figure 1F).

For comparison with the precision pull task, we had mice walk on a motor-driven treadmill (Movie S2). This behavior requires no training – mice placed on the treadmill without restraint walked naturally at speeds ranging from 10 to 20 cm/s, without prior exposure. Critically, interruption of motor cortical output via lesion or pharmacological inactivation did not impede the ability of mice to perform this task (Figure S1F, G). Thus, the precision pull and treadmill walking tasks exhibit a markedly different dependence on motor cortex, with the execution of precision pull selectively disrupted by motor cortical inactivation.

Behavioral selectivity of fast timescale motor cortical influence

We next asked whether motor cortical activity influences muscle activation in a behaviorally-selective manner. To avoid compensation from other motor control circuits, we rapidly silenced motor cortical output and analyzed the immediate effects on muscle activity during both the precision pull task and treadmill walking (Figure 2). Unilateral silencing was achieved by activating channelrhodopsin2 expressed in vGAT^on cortical inhibitory interneurons using a 2 mm-diameter spot of 473 nm light projected onto the surface of the caudal forelimb area in one hemisphere (upper left inset in Figure 2A, Figure S2A). We used a light intensity (10 mW/mm²) sufficient to cause nearly complete cessation of firing among putative vGAT^off neurons throughout motor cortical layers (Figure S2B–E; Guo et al., 2014b).

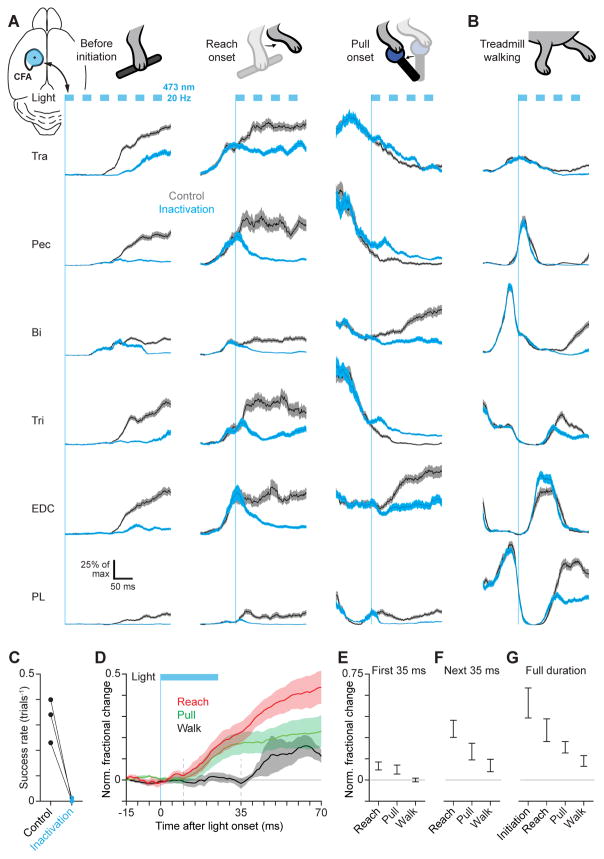
Figure 2. Fast timescale motor cortical influence is behavior-specific.

(A) Mean ± SEM EMG for trapezius (Tra), pectoralis (Pec), biceps (Bi), triceps (Tri), extensor digitorum communis (EDC), and palmaris longus (PL) during trials with and without 20 Hz blue light stimulation (blue rectangles) starting prior to movement initiation, at reach onset, or at pull onset. Upper left inset shows light stimulus position on the caudal forelimb area (CFA). Vertical blue lines indicate light onset. (B) Same as (A), but for inactivation triggered at a fixed phase of the step cycle during treadmill walking. The biphasic activation of Pec with a larger activation more aligned with that of flexor muscles seen here was present in a minority of mice (2/14). The more common monophasic, extensor-aligned Pec activation pattern during locomotion is seen in Figures S1E–G. (C) Success rate with or without light stimulation prior to movement initiation. (D) Mean ± SEM normalized fractional change in muscle activity between control and inactivation initiated during reaching (n = 4 mice), joystick pulling (n = 4), and treadmill walking (n = 8). (E)–(G) Mean ± SEM normalized fractional change in muscle activity between control and inactivation trials summed over the first 35 ms (E), the next 35 ms (F), or the full duration (G) of light stimulation. See also Figure S2.

Light-induced inactivation demonstrated the involvement of motor cortical activity throughout the precision pull task. A 500 ms inactivation (20 Hz, 50% duty cycle) beginning immediately before trial initiation dramatically altered movement (Figure 2A, left column, and G) and essentially abolished reward attainment (1 trial rewarded out of 293 inactivation trials, versus 181 rewarded out of 701 control trials, n = 3 mice; Figure 2C). Inactivation lasting 200 ms triggered at the onset of reaching or joystick pulling also had a dramatic effect on movement (Figure 2A, middle and right columns, and G), prolonging the time to reward by a comparable duration (n = 4 mice; Figure S2F, G). In both of these cases the effect of inactivation during ongoing movement began rapidly: muscle activation diverged from control patterns about 10 ms after the onset of light stimulation (Figure 2D–G). These results indicate that the output of motor cortex during precision pull rapidly influences muscle activation.

During treadmill walking, the influence of motor cortical output on muscle activation was markedly different. As mice walked on the treadmill for the first time, 200 ms inactivations were triggered sporadically (minimum interval of 5s, mean interval of 15s) at a constant phase within the step cycle, just after the peak activation of biceps. During the first 35 ms after stimulation onset, the divergence from control activation patterns was not significantly different from 0 (mean fractional change ± SEM = −0.000 ± 0.013, p = 0.516, one-tailed t-test, n = 8 mice), and was significantly less than that for inactivation at reach onset (mean ± SEM = 0.099 ± 0.029, p = 0.002) and at pull onset (mean ± SEM = 0.073 ± 0.031, p = 0.015; Figure 2B, D, E). However at later times after stimulation onset, divergence from controls that appeared to vary across muscles could be seen during walking, such that significant divergence from controls was detected in the next 35 ms epoch (mean ± SEM = 0.102 ± 0.044, p = 0.023; Figure 2B, D, F, G). Recordings of motor cortical neurons during 20 Hz light stimulation revealed no neurons (0/104) that fired in response to light pulse offsets throughout 200 ms of stimulation (Figure S2C), indicating that the timing of muscle activity divergence here does not reflect a response to light extinction.

To address how the latency of perturbation responses during treadmill walking depended on the locomotor phase of inactivation, we sporadically inactivated motor cortex for 200 ms during walking regardless of the current phase. Trials were divided into ten groups based on the phase of light stimulation onset. At all phases, the divergence from control muscle activation was not significantly different from 0 during the first 35 ms after stimulation onset (p > 0.05 with Bonferroni correction, one-tailed t-test, n = 4 mice; Figure S2H). Divergence from controls was apparent at later times, though it was not prominent during the next 35 ms epoch at all phases (Figure S2I–K). Thus, the short-latency control of muscle activation evident during precision pull is absent during treadmill walking, suggesting that in this context relatively direct effector pathways are not activated by motor cortical output.

We then used electrical stimulation in motor cortex to address two issues raised in interpreting the findings from fast timescale inactivation. First, we assessed how the ~10 ms latency of muscle activity perturbation following optogenetic silencing compares to the shortest latency response following electrical stimulation, which is believed to reflect the fastest pathway linking motor cortex to spinal motor neurons (Lemon, 2008; Woolsey et al., 1972). Second, we attempted to distinguish two potential explanations for the differential influence of motor cortical output between behaviors. Changes intrinsic to downstream circuits could attenuate the impact of this output during treadmill walking, or downstream circuits are capable of being engaged during walking but motor cortical output fails to do so. The former possibility is not consistent with previous observations in cat (Armstrong and Drew, 1985; Bretzner and Drew, 2005), but we used electrical stimulation to test whether motor cortical output induces short-latency muscle activation throughout treadmill walking in mice.

We stimulated the caudal forelimb area with different current levels as mice stood still, with minimal muscle activity in most forelimb muscles (Figure 3A, B). The latency of response initiation in EMG recordings was measured at each current level (Figure 3C). As current level increased, latencies decreased but then plateaued. To estimate the shortest response latency, we then fit a decaying exponential with a variable asymptote to the relation between latency and current level (Figure 3D). The mean ± SEM latency was 9.6 ± 0.2 ms (n = 3 mice), which is comparable to previous estimates made in anesthetized mice using a different estimation procedure (Ayling et al., 2009). Our latency estimate also matches closely with the latency at which motor cortical inactivation disturbs muscle activity during precision pull (Figure 2D). This implies that motor cortex influences muscles during precision pull via short-latency pathways that link cortical projections with spinal motor neurons.

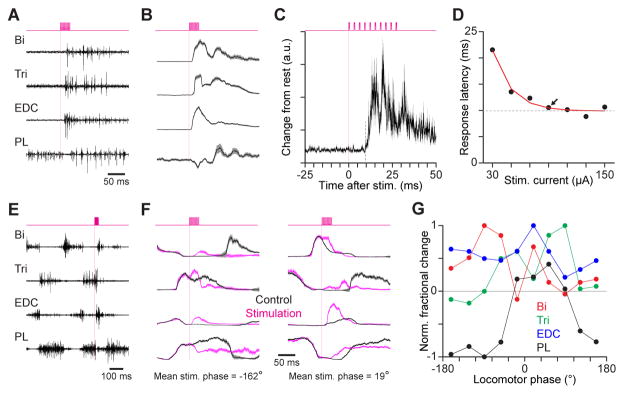
Figure 3. Motor cortical stimulation perturbs muscle activity at short latency.

(A) EMG from biceps (Bi), triceps (Tri), extensor digitorum communis (EDC), and palmaris longus (PL) in response to electrical stimulation (top) in the caudal forelimb area as a mouse stood still. Vertical magenta lines indicate stimulation onset. (B) Mean ± SEM EMG for muscles in (A) (n = 25 trials). (C) Mean ± SEM absolute change in activity from resting level (n = 25), summed across all four muscles. Current was 90 μA. Dotted line marks the initiation of divergence. (D) Relation between stimulus current and response latency for 1 mouse (circles) fit by an exponential function (red) with a variable asymptote (dotted). Arrow indicates the current level chosen for subsequent stimulation in this mouse. (E) EMG from Bi, Tri, EDC and PL in response to stimulation (top) during walking. (F) Mean ± SEM EMG for muscles in (E) during trials with and without stimulation. Stimulation averages used trials for which stimulation onset fell within a window spanning 1/10^th of the step cycle, and the mean stimulation phase for each trial group is given (bottom). (G) Normalized fractional change in EMG during the 50 ms following stimulation onset versus locomotor phase at which stimulation began in 1 mouse. Trials were grouped according to onset phase, and data are plotted along the x axis according to the mean phase for each group. Values are normalized by the maximum absolute change for the given muscle.

To test whether the motor cortical influence on downstream effector pathways is attenuated during treadmill walking, we electrically stimulated motor cortex as mice performed this task. We first identified an appropriate level of stimulation current from responses measured as mice stood still. For each mouse, we identified a current level that was just large enough reliably to evoke responses at the shortest observed latency (e.g. arrowhead in Figure 3D; range = 70–90 μA). Stimulation at these current levels during treadmill walking perturbed activity in forelimb muscles at all phases of the step cycle (Figure 3E, F; n = 3 mice).

Importantly, though the latencies of muscle activity disturbance after silencing were longer during treadmill walking, responses to electrical stimulation were as rapid as those seen when mice stood still (Figure 3F). As has been observed in cats (Bretzner and Drew, 2005), stimulation effects varied across muscles and changed as a function of the locomotor phase at which stimulation occurred (Figure 3F, G). Thus, results from electrical stimulation of motor cortex in mice are similar to those obtained in cats and argue against downstream attenuation of motor cortical influence during treadmill walking.

Motor cortical activity during precision pull and treadmill walking

The above results indicate that short-latency pathways linking motor cortex with spinal motor neurons are activated during precision pull but not treadmill walking, but that this is not because such pathways are unable to respond to motor cortical output during walking. This implies that structure in the patterns of motor cortical output dictates how downstream effector pathways are modulated. To resolve how such pathways can be engaged differentially, we examined neural activity in primary motor cortex.

We monitored the activity of motor cortical neurons during precision pull and treadmill walking using chronically implanted microwire tetrodes initially targeted 500μm below the pial surface. After three weeks of precision pull training, recordings were made over 45min during behavioral sessions, and for 15min immediately afterwards as mice walked along the treadmill. Tetrodes were lowered by 50μm after each recording session, permitting the isolation of ~300 single units in cortical output layers V and VI of each mouse over 11 days of recording (mean = 297 units, n = 3).

We first verified that neural activity in mouse motor cortex shares features observed in other mammals. Neuronal firing rates averaged across trials of precision pull behavior and across individual step cycles exhibited a wide array of patterns (Figure 4A, B; Figure S3A–I, K, M) that showed substantial correlations with muscle activity. For nearly all neurons, firing rate time series during both the precision pull behavior and during walking were significantly correlated with the activity of at least one forelimb muscle, after accounting for false discovery (Figure 4C, Figure S3J, L, N). Among neurons firing above 1 Hz on average, correlation magnitudes were substantial during both behaviors (Figure 4D), though there was a small, significant increase seen during precision pull (pull median = 0.708, walk median = 0.641; p = 0.00003, Wilcoxon rank-sum test). These findings are consistent with results from other mammals during behaviors that vary in their requirement for motor cortical involvement (Armstrong and Drew, 1984a; Drew et al., 1996; Kargo and Nitz, 2004).

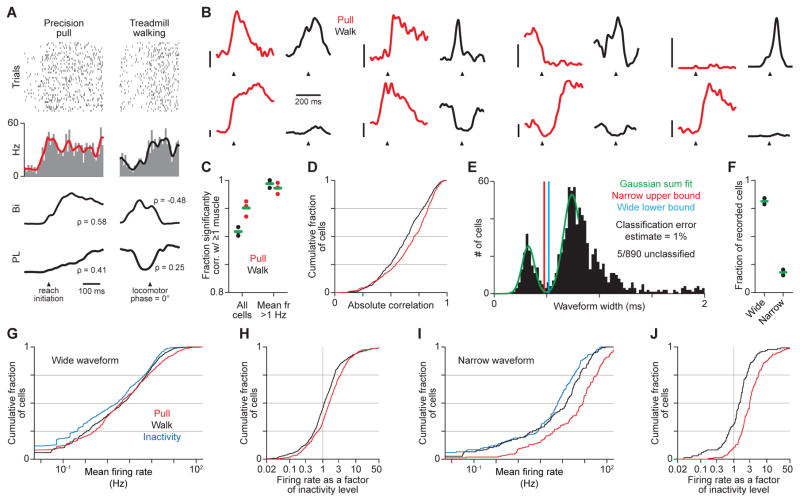
Figure 4. Muscle-correlated motor cortical firing during precision pull and treadmill walking.

(A) Spike rasters and histograms (top, trial-averaged firing rates overlaid) for 1 neuron and the trial-averaged activation (bottom) of biceps (Bi) and palmaris longus (PL), with correlation scores (ρ) for each EMG trial average with the corresponding neuronal firing rate. (B) Trial-averaged firing rates for 8 neurons during pull and walk. Scale bars are 20 Hz, and their bases indicate 0 Hz along the vertical. Arrowheads indicate muscle activation onset during pull, and a step cycle phase of 0°. (C) Fractions of recorded neurons with firing rates significantly correlated with the activity of at least 1 muscle. Fractions were also computed after ignoring neurons with very low firing rates, which may be poorly estimated. (D) Histograms of the maximum absolute correlation of neuronal firing rates with muscle activity during pull and walk, measured using trial averages. Neurons with mean firing rates < 1 Hz, which may be poorly estimated, were excluded. (E) Waveform widths, with values from 0 to 0.8 ms fit by a sum of two Gaussians, and boundaries for assigning narrow- and wide-spiking subtypes. (F) Fractions of neurons assigned to each subtype. Green bars show means (3 mice). (G)–(J) Histograms of mean firing rates (G),(I) during pull, walk and inactivity, and of firing rates as a factor of their level during inactivity (H),(J) during pull and walk, for wide- (G),(H) and narrow-spiking (I),(J) neurons. Means are measured as the mean of the trial-averaged time series. See also Figures S3, S4.

Despite observed correlations between motor cortical and muscle activity, previous reports have also noted deviation between the activity patterns of individual motor cortical neurons and those of particular muscles (Churchland and Shenoy, 2007; Schieber and Rivlis, 2007). This is true even for neurons that directly contact spinal motor neurons innervating the muscles in question (Cheney and Fetz, 1980; Muir and Lemon, 1983). Despite this deviation, correlation between motor cortical and muscle activity en masse has been demonstrated. In particular, certain weighted sums of neuronal firing rates can be found that strongly resemble the activity of muscles (Morrow and Miller, 2003; Oby et al., 2013; Schieber and Rivlis, 2007).

We searched for similar correlation between motor cortical and muscle activity in mice, using canonical correlation analysis (CCA; Hotelling, 1936; Sussillo et al., 2015) to compare the set of trial-averaged neuronal firing rates with the set of trial-averaged muscle activations for individual mice (Figure S4). Starting with two sets of variables, CCA finds weighted sums of each set (“canonical variables”) that are maximally correlated, and then iteratively repeats this process to find additional canonical variables uncorrelated with all previous ones. For both pull and walk, CCA identified canonical variables that are strongly correlated and account for a substantial fraction of the variance in neural and muscle data. This indicates substantial correlation between motor cortical and muscle activity en masse, as observed in primates. Nevertheless, such correlations imply little about the downstream influence of motor cortical output.

To further compare mouse motor cortical activity to previous observations, we took advantage of the relationship between spike width and neuronal identity to assess activity specifically in narrow-spiking, putative inhibitory interneurons and wide-spiking neurons expected to be primarily pyramidal neurons (Bartho et al., 2004; McCormick et al., 1985). Histograms of trough-to-peak spike widths appeared well-fit by a sum of two Gaussians for widths ranging from 0 to 0.8 ms (Figure 4E). We thus used this fit to assign neurons to either narrow- or wide-spiking groups. We set boundaries for assignment that were expected to yield a rate of misclassification of 1% of neurons under the assumption that each group shows a Gaussian distribution of waveform widths (see Methods). Using this assignment scheme, 81 ± 2% of neurons were wide-spiking, 18 ± 1% of neurons were narrow-spiking and 5/890 were unassigned (Figure 4F). These fractions are similar to those seen previously in mice (Guo et al., 2014b) as well as those observed histologically in rats (Beaulieu, 1993).

Consistent with previous observations across mammals, activity among both neuronal groups was increased on average during movement, as compared with periods of no muscle activity that fell between precision pull trials (“inactivity”; Figure 4G–J). Mean firing rates divided by their corresponding means during inactivity were on average 3.47 for wide- and 6.61 for narrow-spiking neurons during pull, and 3.11 for wide- and 2.85 for narrow-spiking neurons during walk. In particular, as has been recently described for primates (Kaufman et al., 2013), narrow-spiking neurons did not appear to decrease in firing when movement began during the precision pull, countering the idea that cortical inhibition gates voluntary movements. Interestingly, our observations contrast with recent reports of activity in rat vibrissa motor cortex (Ebbesen et al., 2017), where firing rates tend to increase during movement suppression. Collectively, our observations show that activity in the mouse caudal forelimb area shares basic features with that seen in the forelimb motor cortices of other mammals.

Probing the mechanism of differential influence on downstream pathways

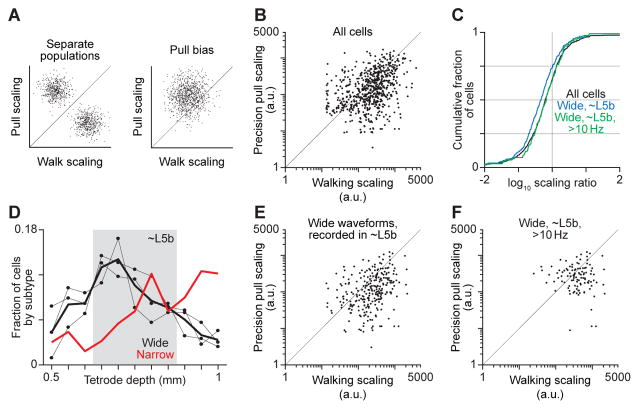
One possible mechanism for behavior-specific engagement of short-latency effector pathways is that separate neuronal populations are predominantly active during each behavior, and only the population that is highly active during precision pull engages such pathways (Dombeck et al., 2009; Hayashi-Takagi et al., 2015). To test this possibility, we calculated a ‘scaling’ index for each neuron that measures how the degree of change in its firing rate compares to the degree of change in muscle activity, during the two behaviors. This was computed by dividing the range of a neuron’s trial-averaged firing rate time series for a given behavior by the mean of the ranges of the trial-averaged EMG time series for the simultaneously recorded muscles. If separate neuronal populations exist, plots of scaling values computed for precision pull against those for walking would show groups of neurons with scaling values much larger for one of the two behaviors (Figure 5A, left). We did not observe this outcome (Figure 5B), providing evidence against the existence of separate neuronal populations active during individual behaviors.

Figure 5. Scaling between motor cortical firing and muscle activity.

(A) Schematics of the scaling between firing rates and muscle activity during pull plotted versus that during walk in hypothetical scenarios. (B),(E),(F) Scaling between firing rates and muscle activity during pull plotted versus that during walk for all cells (B), wide-spiking cells recorded in layer 5b (E), and wide-spiking cells recorded in layer 5b with mean firing rates > 10 Hz during at least 1 behavior (F) for 3 mice. Scaling was only calculated for neurons having mean firing rates > 1 Hz during at least 1 of the 2 behaviors. (C) Histograms of the log of the ratio between pull and walk scaling for all cells, wide-spiking cells recorded in layer 5b, and wide-spiking cells recorded in layer 5b having mean firing rates > 10 Hz during at least 1 behavior. (D) Mean fractions of recorded wide- and narrow-spiking neurons versus tetrode depth (thick lines, 3 mice). Connected black dots are for individual mice.

We also considered the possibility that, during precision pull, short-latency effector pathways could be engaged only by activity levels above those seen during treadmill walking (Beloozerova et al., 2010; Hosp et al., 2013). If this were the case, variation in neuronal firing would be larger relative to variation in muscle activity during precision pull, assuming firing generally increases with muscle activity. This quantitative difference would have to be substantial, because neural activity during the weakest movement involving short-latency pathway engagement would have to be higher than the activity during the strongest movement lacking this engagement. In this scenario, plots of precision pull scaling versus walking scaling would display a preponderance of points above the line where pull scaling = walk scaling (Figure 5A, right). However, this feature was not observed (Figure 5B). Indeed, the ratio of the pull scaling to walk scaling for each neuron has a distribution centered below 1 (log10 median = −0.21; Figure 5C), indicating more points below the line where pull scaling = walk scaling. This finding does not support the possibility that short-latency effector pathways are engaged only by modulation in motor cortical activity beyond the levels seen during treadmill walking.

We further tested the two above-stated hypotheses by repeating analyses on subsets of recorded neurons that may be particularly relevant to the downstream influence of motor cortex. Among wide-spiking neurons, we analyzed specifically those recorded between 650 and 850 μm below the pia, where the cell bodies of most subcerebral projection neurons reside in cortical layer 5b (S. Fageiry, personal communication). The vagaries of electrical recording do preclude assigning neurons recorded in this depth range to layer 5b. However, consistent with an overrepresentation of subcerebral projection neurons among our recorded populations, the number of wide-spiking units isolated per recording session was on average 72% higher when tetrodes were located in this range compared with other depths, while a similar trend was not seen for narrow-spiking units (Figure 5D). The distribution of scaling values for wide-spiking neurons recorded in this range was similar to that seen for the full population (Figure 5C, E). To focus on those neurons that may exert the strongest influence downstream, we further excluded neurons that did not fire above 10 Hz on average during at least one of the two behaviors. The distribution of scaling values changed only minimally (Figure 5C, F). Collectively, these results argue against both of the above-stated hypotheses.

Behavioral selectivity in the correlation of firing patterns across motor cortical neurons

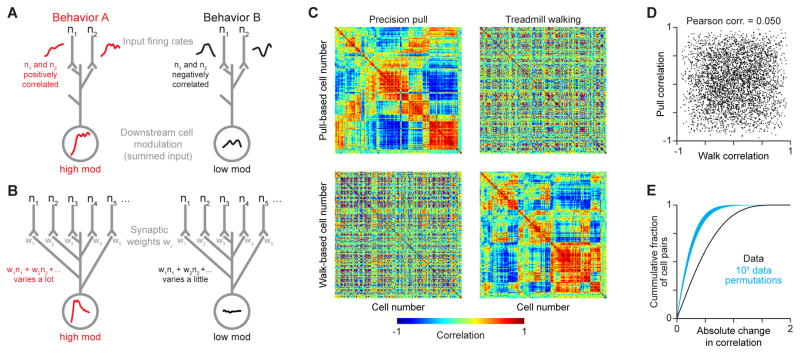
We next probed for behavior-dependent changes in the correlation between the firing patterns of motor cortical neurons. To see how this could account for differential engagement of short-latency pathways, consider first a downstream neuron within such a pathway that receives input from two motor cortical neurons (Figure 6A). During one behavior, the input neurons’ firing patterns are positively correlated, so their activities add cumulatively and the downstream neuron is strongly modulated. But during a second behavior, the firing patterns are negatively correlated, diminishing their impact on the downstream neuron.

Figure 6. Changes in firing rate correlations can modulate downstream influence.

(A) Schematic depicting how changes in firing rate correlations for two input neurons n₁ and n₂ can change their modulation of a downstream neuron. Activity depicted in the downstream cell is the sum of input firing rates. (B) Schematic depicting an analogous scenario in which weighted sums of neural activity are modulated differently between behaviors, which could enable behavior-specific effects. (C) Matrices of firing rate correlations in one mouse during precision pull (left) and treadmill walking (right) ordered to cluster neurons with similar correlation patterns during pull (top) and walk (bottom). Each row and the equivalently numbered column correspond to one neuron. Neurons having mean firing rates < 1 Hz during either behavior were excluded. (D) Firing rate correlation for neuron pairs during pull plotted versus their correlation during walk. Every tenth pair plotted from three mice. (E) Histogram of firing rate correlation changes between behaviors, and 10⁵ iterations of the same histogram calculated after data permutation. See also Figure S5.

Similarly, we can envisage a downstream neuron that receives direct and/or indirect input from motor cortex that is effectively a weighted sum of the firing patterns of motor cortical neurons (Figure 6B). If the correlations between the firing patterns of motor cortical neurons change between behaviors, weighted sums of these firing patterns that show particularly strong modulation during one behavior will show weaker modulation during the other. So if firing pattern correlations change such that a weighted sum of motor cortical output that matches the effective weighting of inputs to the downstream neuron varies strongly during only one behavior, then the downstream neuron may be strongly influenced by motor cortex during only one behavior. Thus, this neuron can respond in a behaviorally-selective manner, even if upstream neurons are active during both behaviors.

To assess the plausibility of such a mechanism, we calculated correlations between trial-averaged firing rate time series for each pair of neurons from individual mice, separately for each behavior. Matrices of the resulting correlation scores were ordered to reveal groups of similarly active neurons (Figure 6C, upper left and lower right). This structure largely disappeared in identically-ordered matrices constructed using correlation scores from the alternate behaviors (Figure 6C, upper right and lower left), indicating that groups of similarly active neurons during one behavior are less similarly active during the other behavior. Indeed, the fact that two neurons were similarly active during one behavior implied little about whether they were similarly active during the other behavior (Figure 6D).

The change in correlation scores between behaviors was large. We computed a null distribution using data permuted under the assumption that correlations were similar in both behaviors, but differences in observed correlations arise from the use of separate sets of trials. The actual median correlation score was more than 56 standard deviations beyond the median of the resulting null distribution (p < 10⁻⁵, one-tailed Monte Carlo test; Figure 6E). The change in correlation did not appear to be an artifact of the behavioral event chosen for aligning trials, nor of the inclusion of neurons with low firing rates that may have been poorly estimated given the number of trials used (Figure S5A–F). Moreover, we observed a similar change in correlation specifically among wide-spiking neurons recorded within layer 5b (Figure S5G–I). Thus, correlations among neuronal firing patterns change markedly between precision pull and treadmill walking.

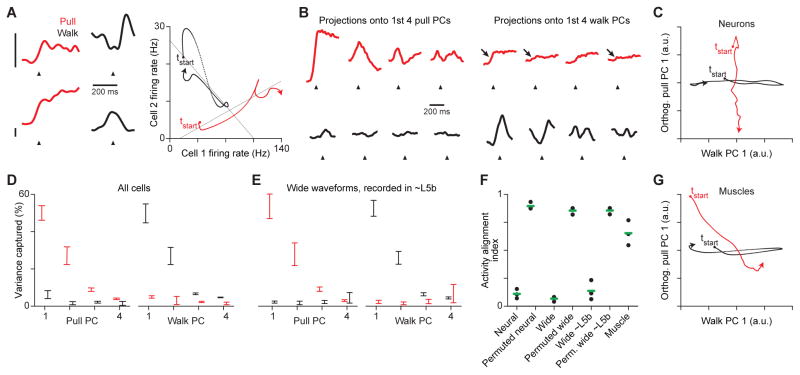
We used principal component analysis to quantify the resulting changes between behaviors in the modulation of weighted sums of neuronal firing patterns that vary strongly during one behavior. The first several principal components of firing patterns here define weighted sums of those patterns that account for a large fraction of firing rate variation across the population. The first four principal components during either of the two behaviors account for ≥ 90% of firing rate variation during the given behavior (mean ± SEM pull variance capture: 95 ± 1%, walk variance capture: 90 ± 0.3%). Because the correlations between firing rates change between behaviors (Figure 7A), each set of top principal components accounted for only a small fraction of firing rate variation during the other behavior (Figure 7B–D). Here again, the same held true specifically for wide-spiking neurons recorded within layer 5b (Figure 7E; Figure S6A). Thus the top principal components define weighted sums of firing rates that each vary strongly during only one behavior.

Figure 7. Behaviorally-selective variation in weighted sums of motor cortical firing patterns.

(A) Left: Trial-averaged firing rates for 2 neurons during pull and walk. Scale bars are 20 Hz, and their bases indicate 0 Hz along the vertical. Arrowheads in (A) and (B) indicate muscle activation onset during pull, and a step cycle phase of 0°. Right: Relations between the firing rates over the first 350 ms of the averages for pull and walk, with best-fit lines (solid black). To highlight trends, firing rates for this panel were computed with a 20 ms, rather than a 10 ms, Gaussian. (B) Projection of neuronal population activity from 1 mouse during pull (red) and walk (black) onto the top 4 principal components for the activity during pull (left) and walk (right). (C) Relation between neuronal population activity from 1 mouse during pull and walk projected onto the first principal component for activity during walk and the first principal component for activity during pull minus its projection onto the first axis (Orthogonalized). (D),(E) Mean ± SEM variance captured from pull and walk firing rates by the top principal components for pull and walk, using all neurons (D) or wide-spiking neurons recorded in layer 5b (E). (F) Alignment of firing rates, permuted firing rates, and muscle activity during pull and walk. Green bars show means (3 mice). (G) Relation between the activity of all recorded muscles from 1 mouse during pull and walk projected onto the first principal component for their activity during walk and the first principal component for their activity during pull minus its projection onto the first axis (Orthogonalized). See also Figures S6, S7.

To quantify the difference between behaviors in the firing rate variation accounted for by each set of top principal components, we measured the ratio between the small fractions of variance accounted for during the other behavior and the fractions of variance accounted for during the behavior for which the components were computed (alignment index, Figure 7F; Elsayed et al., 2016). The mean ± SEM alignment index for neural activity during pull and walk was 0.11 ± 0.02. As a control, we computed the alignment index after permuting data as above under the assumption that correlations were similar in both behaviors. The resulting alignment index was 0.89 ± 0.02 (p < 10⁻⁵, one-tailed t-test). Among wide-spiking neurons, alignment was 0.07 ± 0.01, and among those recorded within layer 5b, it was 0.14 ± 0.05. Changes in alignment were not primarily due to a small subset of recorded neurons, and so reflect a general feature of population activity (Figure S6B). Thus, weighted sums that account for the vast majority of variation in motor cortical firing patterns are much more strongly modulated during one behavior, which could enable downstream pathways to be engaged in a behavior-specific manner.

Most critically here, the fraction of firing rate variation during walking that is accounted for by the pull principal components is uniformly low (Figure 7D, E). This indicates that the motor cortical firing patterns associated with engagement of short-latency effector pathways during pull are weakly represented in the activity during walking. This could ensure that those pathways are not activated during walking.

We next addressed whether the changes in neural activity correlations between behaviors merely reflect changes in muscle activity patterns. If motor cortical and muscle activity are correlated, and correlations between the activity of different muscles change between the two behaviors, then we might expect some degree of difference in the correlations between the firing patterns of motor cortical neurons. However, the difference between behaviors in the modulation of weighted sums defined by prominent principal components for muscle activity was smaller than it was for neural activity (Figure 7G), and the alignment index for muscle activity was much higher (0.65 ± 0.06) than that seen for neural activity (Figure 7F). We note here though that this difference does not imply that activity among small groups of neurons of a size similar to the number of recorded muscles also show much less alignment than muscles. Nor do our claims require this to be true. These results suggest that the changes in the weighted sums that account for motor cortical activity do not merely reflect differences in the patterns of muscle activation between behaviors.

Lastly, variation in the weighted sums of motor cortical activity defined by principal components revealed another feature that is consistent with a difference in downstream pathway engagement between behaviors. We observed that while the weighted sums defined by walk principal components varied minimally after the onset of muscle activation during precision pull, these weighted sums varied much more so immediately before muscle activation onset (arrows in Figure 7B). We investigated this further by calculating principal components for motor cortical activity after muscle activation onset during precision pull, in order to focus on weighted sums prominent during movement (Figure S6C). We found that while the weighted sums defined by these components varied prominently both before and after muscle activation onset (Figure S6D, E), weighted sums defined by walk components varied most prominently prior to onset (Figure S6F, G). Moreover, the degree of variation just prior to onset in the weighted sums defined by walk components was comparable to that seen throughout walking (Figure S6H, I), and 56% as great as variation of the weighted sums defined by pull components during the equivalent epoch (arrows in Figure S6E, G). Since muscle activity is minimal during this epoch, these results are consistent with the view that the weighted sums of motor cortical activity prominent during walking are not involved in driving muscle activity through short-latency effector pathways.

DISCUSSION

We have examined the influence of motor cortex on muscle activity during movement execution and its underlying neural mechanisms. Rapid silencing and stimulation of motor cortex demonstrated that relatively direct effector pathways are engaged by motor cortical output during a trained precision pull behavior but not treadmill walking. Downstream effector pathways therefore respond to motor cortical output in a behaviorally-selective manner.

We then probed motor cortical activity for evidence of how this behaviorally-selective influence is mediated. Between behaviors we observed a dramatic change in the correlations among neuronal firing patterns, and accordingly a change in weighted sums of firing patterns that vary strongly. This structure in motor cortical activity represents a plausible strategy for behavior-specific influence of motor cortex, in which downstream neurons respond to particular weighted sums of activity in motor cortical output neurons (Figure 6A, B). Thus our results suggest that changes in the correlations between neuronal firing patterns permit a behaviorally-selective engagement of short-latency effector pathways.

Differential influence of motor cortex on downstream pathways

Our findings argue that motor cortical output does not drive muscle activity similarly across different behaviors. Muscle activation was disrupted at very different latencies when we rapidly silenced motor cortical output. Disturbance began about 10 ms after light stimulation onset during the precision pull behavior, matching the latency at which forelimb EMG responses are first detectable following electrical stimulation. Yet during treadmill walking, disturbance started with a delay of >35 ms. This variation in motor cortical influence suggests that the specificity of behavioral deficits following lesions or pharmacological inactivation that eliminate motor cortical output does not merely reflect an inability of other motor areas to compensate during a subset of movements. Moreover, the agreement between the latencies of silencing effects during precision pull and of stimulation responses implies a direct influence of motor cortical output on muscle activity in rodents, contrary to recent claims (Lopes et al., 2016).

Though basic treadmill walking survives the elimination of motor cortical output (Figure S1F, G), our results indicate that motor cortical output can influence treadmill walking. The increased latency of the disturbance in muscle activation could reflect activity perturbation in a neuronal pathway comprised of a larger number of neurons and synapses that lead to spinal motor neurons. The longer latency would result from delays due to conduction and synaptic transmission along such a pathway. One possibility is that motor cortical output is monitored by circuits that depend on the information about movement this output provides, and can influence movement at longer latency when motor cortical output is disturbed. Even when muscle activity is not directly driven through short-latency pathways, motor cortical output could still convey information about movement since afferent sensory pathways drive responses in motor cortex and can modulate its output (Armstrong and Drew, 1984b; Hatsopoulos and Suminski, 2011).

The model of motor cortical influence supported by our results can resolve the ambiguity posed by the specificity of deficits following motor cortical inactivation (Drew et al., 1996; Kawai et al., 2015; Passingham et al., 1983) despite the pervasive nature of muscle-correlated motor cortical activity and stimulation-induced muscle activation (Armstrong and Drew, 1984a, 1985; Griffin et al., 2011; Kargo and Nitz, 2004; Otchy et al., 2015). The circumscribed deficits seen from blocking motor cortical output with lesions or pharmacological inhibition could result from the inability of other motor areas to compensate for the engagement of short-latency effector pathways. Because electrical stimulation in motor cortex will induce broad changes in activity that should modulate almost any possible weighted sum of that activity, any given downstream pathway could readily be activated. Muscle activity is likely then to be modulated at short latency regardless of behavioral context, consistent with prior observations (Armstrong and Drew, 1985; Bretzner and Drew, 2005). And the observation of muscle-correlated motor cortical activity during a broad range of behaviors does not contradict behavior-specific engagement, because correlation between neural and muscle activity does not by itself imply direct control of muscle activity.

Here we have employed methodology that may be generally useful in assessing functional influence in the motor system. Certain observations have cast doubt on the capacity of pharmacological and optogenetic perturbations to elucidate motor circuit operation (Martin and Ghez, 1993; Otchy et al., 2015). Of particular concern is the possibility for delusive effects of perturbations to pathways normally unimportant for the behavior in question. Our results demonstrate that such concerns can be allayed by combining optogenetic perturbation with the millisecond precision readout EMG provides and with electrical stimulation of relevant pathways. The muscle activity perturbations we observed following optogenetic silencing during precision pull matched the latency of relevant pathways, were reproducible across animals, and were not observed during another behavior. Such criteria may be applicable when assessing the direct influence of neuronal populations during circuit operation.

Interpreting the downstream influence of cortical output

Findings from analysis of our entire recorded population held specifically for wide-spiking neurons and the subset thereof recorded within layer 5b. Still, the degree of difference between behaviors in firing rate correlations among subcerebral projection neurons themselves is not directly specified by our results. We note however that subcerebral projection neurons may be overrepresented in our recorded populations, as the number of wide-spiking units isolated in a given recording session was 72% higher when tetrodes were located within layer 5b. Moreover, the very limited similarity in neuronal correlations we observed between behaviors (Figure 7D–F) suggests that such correlations will vary within any substantial fraction of recorded motor cortical neurons.

Our findings do not preclude that changes intrinsic to downstream effector circuits also influence the manner in which they respond to motor cortical output. Indeed, previous studies using electrical stimulation show that responses in spinal circuits to descending input vary across movements and during different phases of particular movements (Bretzner and Drew, 2005; Drew and Rossignol, 1984; Dyson et al., 2014). Moreover, previous measurements of spike-triggered average muscle activity indicate that the impact of individual motor cortical neurons on muscle activity can vary across different movement types (Schieber, 2011), though such variation is not prominent in certain contexts (Buys et al., 1986). Our observation that electrical stimulation during treadmill walking perturbs muscle activity does however indicate that the behavioral selectivity of motor cortical influence on downstream effector pathways is not attributable to a negation of motor cortical influence by changes intrinsic to those pathways. Thus there should be structure in the patterns of motor cortical output that at least partly determines whether downstream effector pathways are modulated.

Behavior-specific responses in downstream neurons do not necessarily require that most all of the firing rate variation during a given behavior is captured by weighted sums of motor cortical output that are minimally modulated during other behaviors. Rather, specificity would merely require that some fraction of motor cortical output is captured by weighted sums that vary sufficiently to modulate downstream pathways only during certain behaviors. A downstream neuron sensitive to only this fraction of output could then respond in a behavior-specific manner. Here we show that the top principal components for motor cortical activity during precision pull capture only ~10% of the firing rate variation during walking. Though much of the variance captured by these weighted sums during pull may not be involved in engaging downstream pathways, large fractions of the variance during pull are at least available for this purpose without the consequence of much downstream pathway modulation during walking.

The changes in neural activity correlations we see do not appear to be a simple consequence of the fact that we recorded from many neurons. Because our weighted sums of activity have one term for each neuron in the recorded populations, the weights from each individual sum constitute a vector that represents a direction in a neural activity space – a high-dimensional space in which each cardinal dimension represents the firing of one neuron. We might imagine our sets of principal components during pull and walk define two small sets of randomly selected vectors in such a space and so are expected to be mostly orthogonal, consistent with our findings. However, if we assume that there are static neuronal correlations across behaviors so that any observed correlation changes only reflect chance variation, we would have expected the principal components we found to define vectors that were much less orthogonal (Sadtler et al., 2014). This is indicated by the alignment indices we calculated for permuted data sets, which assume static neuronal correlations yet showed much more similarity than the actual neural data (Figure 7F).

Implications of the variation in motor cortical activity correlations

Much of the structure in motor cortical firing patterns can be explained by a role in driving muscle activity and in helping generate the requisite output commands (Churchland et al., 2012; Evarts, 1968; Oby et al., 2013; Todorov, 2000). However, a corollary of our results is that correlations between the activities of motor cortical neurons and muscles can vary substantially across different movement types (Figure S7). This is implied by the marked difference between behaviors in the correlations among neuronal firing patterns that far exceeds the difference in correlations among muscle activity patterns. This extends previous reports of dissimilarity in primates between the activities of individual muscles and individual motor cortical neurons, even those that synapse onto spinal motor neurons (Morrow and Miller, 2003; Schieber and Rivlis, 2007). These previous studies have been used to argue that meaningful descending commands emerge at the level of the motor cortical population (Churchland and Shenoy, 2007; Kaufman et al., 2014), a point that is underscored by our results.

The finding of changes in the downstream influence of motor cortical output paired with changes in correlation between motor cortical and muscle activity also helps to reconcile certain other observations. A recent study in cats reported substantial similarity in the correlation of motor cortical and muscle activity during forelimb reach and obstacle avoidance (Yakovenko and Drew, 2015), though a previous study had noted substantial differences in such correlations between obstacle avoidance and generic treadmill walking (Drew et al., 1996). In this earlier study, both the motor cortical dependence and the muscle activation patterns differed between movements, whereas in the more recent study, both movements are known to require motor cortex and involve similar muscle activation patterns. Thus, the apparent discrepancy between studies may reflect the fact that forelimb reach and obstacle avoidance require motor cortical involvement and so rely on engagement of specific downstream effector pathways by motor cortical output. The particular patterns of activity required for this engagement could in turn change the correlations between motor cortical and muscle activity.

The view that certain weighted sums of neuronal firing patterns serve distinct functions (Druckmann and Chklovskii, 2012; Seung, 1996) is supported by other characterizations of firing dynamics in motor areas. Motor cortical neurons are active during both the planning and execution of movement but different weighted sums of their activities vary strongly during each phase (Elsayed et al., 2016), potentially ensuring that muscles are inactive during planning (Kaufman et al., 2014). Weighted sums of motor cortical firing patterns that are predictive of a decision-making behavior show preferential recovery following transient activity perturbations (Li et al., 2016). And in the oculomotor system, different weighted sums of firing patterns in the oculomotor neural integrator encode eye position during different types of eye movement (Daie et al., 2015). These movement-related neural dynamics exhibit parallels to those in other systems, such as the remapping of spatial representation across place cells in the CA1 region of hippocampus when the surrounding environment changes (Leutgeb et al., 2005). Functional distinctions between weighted sums of neuronal firing patterns may therefore prove broadly valuable in defining principles of neural system function.

STAR METHODS

CONTACT FOR REAGENTS AND RESOURCE SHARING

Further information and requests for reagents should be directed to, and will be fulfilled by the Lead Contact Andrew Miri (andrewmiri@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experiments and procedures were performed according to NIH guidelines and approved by the Institutional Animal Care and Use Committee of Columbia University.

Experimental Animals

A total of 52 adult male mice were used, including those in early experimental stages to establish methodology. Strain details and number of animals in each group are as follows: 16 VGAT-ChR2-EYFP line 8 mice (B6.Cg-Tg(Slc32a1-COP4*H134R/EYFP)8Gfng/J; Jackson Laboratories stock # 014548); and 34 C57BL/6J mice (Jackson Laboratories stock #000664).

All mice used in experiments were individually housed under a 12 hr light/dark cycle. At the time of the measurement reported, animals were 10–20 weeks old. Animals weighed approximately 23–28 g. All animals were being used in scientific experiments for the first time. This includes no previous exposures to pharmacological substances or altered diets.

METHOD DETAILS

Precision pull task

Male mice were trained via a behavioral shaping procedure to perform a precision pull task in which they first place their right forepaw in a particular spot on a rung, then reach out to grab a joystick, and finally pull the joystick a set but short distance (Figures 1A and S1A, B; Movie S1). The shaping procedure involved three phases: a first phase in which mice learned to turn a 60 mm diameter wheel with their right forepaw, a second phase in which they learned to reach towards and pull a joystick positioned further away during each successive training session, and a third phase during which the position of the joystick is fixed.

Apparatus

The training apparatus was housed inside a sound attenuating chamber (H10-24A, Coulbourn). Head-fixed mice were positioned within an enclosure constructed from Delrin tubing (1.5″ OD, 1.25″ ID, McMaster-Carr). Enclosures had sections removed to allow the mouse’s headplate to be fixed to a headplate holder. Enclosures also had a bottom section removed to allow the right forepaw access to a small custom-designed wheel during the early stages of training (60 mm diameter, 11.5 mm wide; Shapeways) or a rung outfitted with a copper foil electrode connected to capacitive touch sensor during later stages (SEN-12041, Sparkfun; the AT42QT1010 chip was replaced with a AT42QT1011, Newark). Enclosures also had a rung for the left forepaw and a divider below the mouse’s chest to prevent the left forepaw from gaining access to the wheel or joystick.

Experimental control was performed using the MATLAB Data Acquisition Toolbox and the NI PCIe-6323 DAQ. The wheel was affixed to an 8 in. stainless steel shaft mounted on bearings (8600N1, McMaster-Carr). An angular encoder amounted around the shaft (A2K-A-125-H-M, U.S. Digital) measured shaft position. A ratchet mechanism was used to ensure the wheel could only rotate toward the mouse. The joystick, which was mounted on a disk, was also affixed to a shaft similarly, except that one end of the shaft was coupled to a DC motor (DCM-375, All Electronics). Joystick position was controlled by the motor and a linear actuator (L12-30-50-12-I, Firgelli). The disk on which the joystick was mounted had a short bar attached that was parallel to the shaft. Prior to each trial, the linear actuator was used to position a plastic guard in the rotational path of this bar. To rapidly set the position of the joystick to initiate each trial, the DC motor would quickly rotate the shaft until the bar hit the guard, stopping its rotation and the rotation of the joystick. After a movement of the joystick by the mouse was detected via the angular encoder, the actuator was retracted to rotate the joystick out of the reach of the mouse. A one-dimensional laser displacement sensor was positioned in front of the mouse and aimed just above the right forepaw rung to enforce the proper initial position of the paw. Water rewards were dispensed with a solenoid valve (161T012, NResearch) attached to a lick tube (01-290-12, Fisher). A speaker was used to play a 5 kHz tone for 200 ms whenever rewards were achieved on a given trial or white noise for 200 ms whenever reward criteria were not met.

Training

Under anesthesia induced with isoflurane (1–3%; Henry Schein), mice were outfitted with titanium head plates (25 × 9 × 0.8mm) affixed to the skull using dental cement (Metabond, Parkell). Headplates had an open center that enabled subsequent access to the skull, which was covered with dental cement. During headplate implantation, the position of bregma relative to marks on either side of the headplate was measured to facilitate the positioning of craniotomies during later surgeries. After recovery from headplate implantation surgery, mice were placed on a water schedule in which they received 1 ml of water per day.

At least 4 days after the start of the water schedule, mice were acclimated to handling by the experimenter following established procedures (Guo et al., 2014a). After two daily sessions of acclimation to handling, mice were acclimated to head-fixation over two daily sessions (first 15 minutes, then 30 minutes) during which they were head-fixed in the wheel-turning apparatus and provided water rewards (3 μl per reward) at regular intervals. During acclimation, the wheel was locked in place to prevent its rotation by the right forepaw.

Following acclimation, mice underwent twice daily 40-minute training sessions of the precision pull task. The behavioral shaping procedure involved an initial stage aimed at training mice to perform a basic reach and pull behavior in order to receive rewards. During the first training session, the wheel was freed to allow it to rotate toward the mouse and rewards were triggered by an experimenter’s keypress whenever the mouse performed any slight rotation of the wheel in the desired direction (toward his body). Over the course of this session, mice generally learned to associate rotation with reward and began iteratively rotating the wheel. In the uncommon case a mouse failed to learn this pairing, sessions of this sort were repeated.

During the next ~10 sessions, mice were gradually trained to pull the wheel with increasing rapidity. During these sessions, the distance of wheel rotation was integrated in software until a certain threshold distance was achieved, the time to reach the threshold distance was calculated, and the integrated distance was reset to 0. On the first ten instances during a training session when the threshold distance was met, mice automatically received a water reward. On each subsequent instance, the time to reach threshold was compared to those from the previous 10 instances. If the time was below the 75^th percentile value from these 10, one water reward was dispensed. If it was below the 40^th percentile value, 2 rewards were dispensed. And if it was below the 10^th percentile value, 4 rewards were dispensed. Otherwise, no rewards were dispensed. The threshold distance was adaptively updated every minute to keep the reward rate at a level that ensures a mouse received about 0.5 ml of water over each training session. Accordingly, if the recent reward rate was too high, the threshold distance was raised; if the recent reward rate was too low, the distance threshold was lowered. The absolute number of rewards a mouse received during a given session was not capped, but the second training session of a given day was stopped once mice reached their daily water allotment. Once mice were turning the wheel frequently and rapidly enough to complete ~250 rotations within one 40-minute session, they progressed to the next stage of training.

During the next ~10 training sessions, mice were gradually trained to perform a precision pull behavior that involved an increasingly long reach component. For this training, the wheel was replaced with a joystick mounted to the shaft, and a rung on which the right forepaw could rest between reaches was mounted. Trials began with the motorized positioning of the joystick. During the first session, the joystick was positioned just a few mm beyond the rung. When mice reached out attempting to rotate the wheel as they had previously learned to do, they came in contact with the joystick and displaced it, leading to reward. In order to receive a reward on a given trial, the initial position of the paw measured by the laser displacement sensor had to be below an allowed absolute distance away (“paw error threshold”) from a target position and the movement of the joystick had to fall below an allowed absolute distance (“pull error threshold”) away from a target distance of 5mm. For the first session, these error thresholds were set to be liberal enough that any joystick movement from any initial paw position would garner a reward. During subsequent sessions, the error thresholds were each set to the 60^th percentile value of the errors from the previous training session. This updating procedure was intended to lead to roughly 30–40% of trials being rewarded. After 10 trials had elapsed in a session, the mouse could then earn additional rewards on a given trial: moving the joystick a distance closer than the 60^th percentile pull error for the previous 10 trials earned 2 rewards, while moving it a distance closer than the 20^th percentile pull error earned 4 rewards. If mice received at least 80 rewards in a given session, the initial position of the joystick was moved 2 mm further away from the rung for the subsequent session. Once the initial position of the joystick reached 18 mm away from the rung, the initial position was no longer updated. Training continued with updating of the error thresholds as before.

Treadmill walking

Mice were placed on a custom-built motor-driven rodent treadmill (Model 802, University of Cologne electronics lab). Optogenetic and electrical stimulation was performed as mice walked at 20 cm/s. Neural recording was performed as mice walked at 10 cm/s, allowing them to better accommodate the weight introduced by the neural headstage and cabling.

Electromyographic recordings

Electromyographic (EMG) electrodes were fabricated for forelimb muscle recording (Figure S1C–E) using a modification of established procedures (Akay et al., 2006; Pearson et al., 2005). Each set consisted of six pairs of electrodes. Each electrode pair was comprised of two 0.001″ braided steel wires (793200, A-M Systems) knotted together. On one wire of each pair, insulation was removed from 1 to 1.5 mm away from the knot; on the other, insulation was removed from 2 to 2.5 mm away from the knot. The ends of the wires on the opposite side of the knot were soldered to a 12-pin miniature connector (11P3828, Newark). Different lengths of wire were left between the knot and the connector depending on the muscle a given pair of electrodes would be implanted within: 2 cm for trapezius, 3.5 mm for biceps and triceps, 4.5 cm for extensor digitorum communis and palmaris longus, and 5.5 cm for pectoralis. The ends of wires with bared regions had their tips stripped of insulation then were twisted together and crimped inside of a 27-gauge needle that facilitated insertion into muscle.

Mice were implanted with EMG electrodes during the surgery in which headplates were attached. The neck and right forelimb of the mouse was shaved and incisions were made above the muscle to be implanted. Electrode pairs were led under the skin from the incision on the scalp to the incision at the site of implantation. Using the needle, electrodes were inserted into muscle, and the distal portion of the electrodes was knotted. The needle and excess wire was then cut away. Incisions were sutured and the connector was affixed with dental cement to the posterior edge of the headplate (Figure S1D).

Recordings were amplified and bandpass filtered (250–20,000 Hz) using a differential amplifier (MA102 with MA103S preamplifiers, University of Cologne electronics lab). Data was digitized and acquired at 40 kHz using the Omniplex64 and PlexControl software (Plexon). We used the presence of spike-like transients in records together with alternating activation and quiescence during treadmill walking to verify that EMG measurements reflected muscle activity rather than motion artifact. We note though that we are not able to rule out that EMG signals for certain muscles were influenced by the activity of adjacent, synergist muscles.

Movement strategies employed during precision pull varied across animals, as was reflected in a variation in muscle activation patterns seen across animals. Muscle activation patterns during locomotion were largely consistent across animals, with one exception. A biphasic activation of pectoralis with a larger activation more aligned with flexor muscle activation was seen in a minority of mice (2/14), and is exemplified in Figure 2B. The more common monophasic, extensor-aligned pectoralis activation pattern during locomotion is exemplified in Figure S1E–G. This variation may be due to differences in the activation patterns of motor units most strongly reflected in pectoralis EMG measurements, perhaps as a consequence of variation in the insertion position of the EMG electrode.

Muscimol injection

One day before injections were to begin, dental cement above the skull was removed and a 1 mm diameter craniotomy was made above the left caudal forelimb area. After the craniotomy was made, and following each round of injections, craniotomies were sealed with Kwik-Cast (WPI). Injections were performed between the two training sessions on a given day, 90 minutes prior to the latter session. We used a Nanoject II (Drummond) to inject 1 ng/nl muscimol hydrobromide (G019-5MG, Sigma) in saline (DPBS with CaCl₂ and MgCl₂, Gibco) through pulled glass capillaries. Injections were positioned 1.5 mm left and 0.25 mm rostral of bregma, aligned with the center of the caudal forelimb area as previously delineated (Tennant et al., 2011). Two extrusions of 36.8 nl were performed: one 700 μm below pia, and one 400 μm below pia. Extrusion was verified immediately before and immediately after capillary insertion into the brain. Injections of saline alone were performed identically.

Cortical ablation

Here we followed methods described by Asante and colleagues (2010). Dental cement was removed from the skull and a 2 mm diameter craniotomy was made above the left caudal forelimb area. The dura was removed with forceps. Brain tissue was then slowly aspirated away through iterative removal of ~100 μm of tissue depth at a time in a circular region spanning 0.5 to 2.5 mm left and 0.75 mm posterior to 1.25 mm anterior of bregma. Bleeding was controlled using Gelfoam (Pfizer) and the depth of tissue removal was continually measured. In each mouse, a total of between 800 and 1000 μm of tissue depth was removed. The cavity was then filled with Gelfoam and the exposed brain surface was covered in Kwik-Cast. A fresh layer of dental cement was then applied to cover the Kwik-Cast and any exposed skull. Sham ablations were performed identically, except no brain tissue was aspirated away.

On the day following surgery, precision pull performance was assayed during a training session (“1d post” in Figure 1F). Behavior was then assayed again 96 hours later (“5d post”) without any intervening training. Ablation had a marked effect on performance at both 1 and 5 days after surgery compared to sham surgeries (Figure 1F). Training was not performed between time points because the ablated animals could not perform the task after surgery and so could not practice. Thus to enable a legitimate comparison at the 5 day time point, no training of ablated or sham animals was performed. Because a lack of intervening training causes only a limited erosion of performance in the sham animals (Figure 1F), we do not attribute the effects of ablation to an acute effect of tissue removal at 1 day post-surgery and then a prolonged effect at 5 days from a lack of practice.

Optogenetic inactivation

After several days of performing the precision pull task at the full reach distance in VGAT-ChR2-EYFP mice, dental cement above the skull was removed and a 2–2.5 mm diameter craniotomy was made above the left caudal forelimb area. A thin layer of Kwik-Sil (WPI) was applied over the dura and a 3 mm diameter #1 thickness cover glass (64-0720, Warner Instruments) was placed on the Kwik-Sil before it cured. The gap between the skull and the cover glass was then sealed with dental cement around the circumference of the glass. A custom stainless steel ferrule guide (Ziggy’s Tubes and Wires; Figure S2A) was then cemented to the headplate a certain distance above the surface of the brain. This distance was set to ensure that the cone of light emanating from a 200 μm core, 0.39 NA optical patch cable terminating in a 2.5 mm ceramic ferrule (M81L01, Thorlabs) would project a spot of light 2 mm in diameter onto the surface of the brain. The ferrule guide enabled quick and reliable positioning of the ferrule above the brain surface so that a large expanse of cortex could be illuminated.

To attenuate firing throughout motor cortical layers, we used a 473 nm laser (CL473-075-O, CrystaLaser) to apply pulses of light at an intensity of 10 mW/mm² to the brain surface. The pulse frequency was 20 Hz and the duty cycle was 50%. Intensity and duty cycle were set to match those in experiments calibrating the relation between light power and the cessation of firing (Guo et al., 2014b).

To inactivate motor cortex during trial initiation, a 500 ms light pulse train was triggered in software immediately before the command to the DC motor to quickly position the joystick, ~70–100 ms before muscle activation began. To inactivate motor cortex near the outset of reaching, a 200 ms train was triggered when the standard deviation of biceps EMG activation over a 16 ms window reached a threshold set at the 90^th percentile value from the distribution of such measurements over time during repetitive reaching. To inactivate motor cortex at the outset of pulling, a 200 ms train was triggered when the rate of change in the position of the shaft’s optical sensor reached a threshold set to be ~6 standard deviations above the mean of this rate of change when the shaft is motionless. In each of the above three types of trials, light was applied during a random third of the trials on which the stimulation conditions were met. Unstimulated trials were then used as controls.

To inactivate motor cortex at a consistent phase during treadmill walking, a 200 ms light pulse train was triggered when the standard deviation of biceps EMG activation over a 16 ms window reached a threshold set at the 98^th percentile value from the distribution of such measurements during walking. After each detected threshold crossing, at least 5 seconds elapsed before a subsequent crossing could be detected. Light stimuli were applied on a random third of detections and unstimulated trials were used as controls. To verify that disturbances in EMG did not result from retinal responses to light stimulation, identical experiments were performed during treadmill locomotion in wildtype mice. Quantitative comparison of effects in wild types and VGAT-ChR2-EYFP mice, discussed below, demonstrate that perturbation effects cannot be attributed to retinal responses to light stimulation.

For experiments looking at the relation between locomotor phase and EMG disturbance following optogenetic inactivation, 200 ms light pulse trains were triggered at random times during treadmill walking. Inactivations were never performed less than 15 s apart.

Electrical stimulation

Stimulation electrodes were fabricated by soldering an ~5 mm length of insulated steel wire (790700, A-M Systems) to a male connector pin (520200, A-M Systems). To implant stimulation electrodes, dental cement was removed from the skull and a 2 mm diameter craniotomy was made above the left caudal forelimb area. Two electrodes were inserted to a depth of 700 μm below the pial surface roughly 1 mm apart surrounding the center of the caudal forelimb area at 1.5 mm left and 0.25 mm rostral of bregma (Tennant et al., 2011). The craniotomy was covered in Kwik-Cast (WPI) and then dental cement (Metabond, Parkell). A #000 screw (B000FN0J58, Amazon) with the top half of a male connector pin soldered on its head was inserted above the contralateral posterior parietal cortex for grounding.

Stimulation was performed in head-fixed mice sitting still in the enclosure used for the precision pull task, and in mice walking freely on the treadmill regardless of phase. Current pulse trains (10 400 μs pulses at 333 Hz, 10–150 μA) were generated using a function generator (33522A, Agilent) driving a stimulus isolator (A365D, WPI). Stimulations were never performed less than 15 s apart.

Neural recording

Tetrode microdrives were assembled using VersaDrive components (Neuralynx) but the microdrive design was modified to be better suited for targeting cortical neurons within forelimb motor cortex. Microdrive bases were outfitted with a 4.5 mm stainless steel cannula (20 gauge, 660 μm I.D., Amazon) into which 4 0.008″ polyimide tubes (Neuralynx) were positioned. Each drive housed 4 independently moveable tetrodes made from twisted 18 μm Pt-Ir wire (CFW0011173, California Fire Wire) plated with Platinum Black solution (Neuralynx) to achieve final impedances of 80–200 kΩ at 1 kHz. Microdrives were wrapped in aluminum tape (McMaster-Carr). Conductive silver epoxy (M.E. Taylor Engineering) was used to attach steel wires coming from the drive ground pin to both the cannula and the aluminum tape to ground them during recording. An 0.002″ insulated Pt-Ir wire was run from the reference pin of the microdrive and affixed to the side of the cannula with regular epoxy so that upon implantation, the stripped tip of the wire would protrude ~1 mm into the cortex, about 1 mm caudal or lateral to the recording electrodes.

To implant microdrives, dental cement above the skull was removed and a 2 mm diameter craniotomy was made above the left caudal forelimb area. Two small holes were drilled above the right posterior parietal and occipital cortex. A #000 screw (B000FN0J58, Amazon) was inserted into each hole, and wires were run from the ground pin of the microdrive to each one. The microdrive was positioned on the brain surface with the cannula in contact with dura and centered at 1.5 mm left and 0.25 mm rostral of bregma, unless large superficial blood vessels clearly obstructed the path of the tetrodes into the cortex. In this case, the microdrive was translated 100–200 μm to allow tetrodes a clear path. The interface between the cannula and the brain was sealed with Kwik-Cast, and dental cement was used to fix the microdrive in place. Tetrodes were slowly lowered down to 500 μm below pia and then raised to 250 μm below pia during implantation surgery. Over the subsequent two weeks, tetrodes were lowered ~30 μm every three days. Recording commenced at least 14 days after implantation with tetrodes positioned 500 μm below pia. Recording from sites spaced by 50 μm intervals between 500 and 1000 μm below the pia was done to focus recordings within layer 5, and ensure that electrode tips resided in or near layers 5 and 6 during all recordings (Tennant et al., 2011). Recordings were made using a 20x gain analog headstage (HST/16v-g20, Plexon). Data was digitized and acquired at 40 kHz using the Omniplex64 and PlexControl software (Plexon).

Acute recordings using a 32-site silicon probe (A1x32-Poly3-5mm-25s-177, NeuroNexus) were performed to gauge the efficacy of light stimulation on motor cortical output in VGAT-ChR2-EYFP mice. To implant bone screws, the dental cement above the skull was removed and 2 ~0.7 mm diameter craniotomies were drilled in the skull above the right parietal and occipital cortex. A #000 screw (B000FN0J58, Amazon) with attached male connector pin was positioned in each hole and rotated until in contact with the brain surface. The screws and surrounding skull were covered in dental cement, leaving the male connector pins exposed. To expose the recording area, dental cement above the skull was removed and a 2 mm diameter craniotomy was made over the left caudal forelimb area. The exposed brain tissue was sealed with Kwik-Cast. Male connector pins (520200, A-M Systems) were soldered to the probe’s ground and reference sites. During recording, female connector pins (520100, A-M Systems) soldered to either end of 2-stranded 28 gauge ribbon wire (10647, SparkFun) connected the probe’s male connectors to the bone screws.

Before recording, the animal was head-fixed, the Kwik-Cast was removed, and the silicon probe was slowly inserted at a 45° angle to vertical depths of 800, 1000, or 1200 μm from dura. Once the probe was in place, the tissue was allowed to relax for 20 minutes before recording began. Recordings were made using a digital headstage (Cereplex M64, Blackrock Microsystems). Data was acquired at 30 kHz using the Cerebus 128-channel and Central software (Blackrock Microsystems).

Spike sorting

Putative spikes were detected and sorted with KlustaKwik (Rossant et al., 2016). For each animal and each session, recordings made during the precision pull task and treadmill walking were concatenated and spike sorting was carried out as if they formed a single, continuous recording. Thus the cluster of waveforms assigned to an individual unit could involve spikes occurring during either behavior, and no matching of units between behavioral epochs was necessary. This allowed us to analyze the activity of the same unit during both behaviors, though the usual caveats in interpreting individual units as individual neurons still apply. Clusters of waveforms were deemed to correspond to well-isolated units if their spike autocorrelograms indicated an absolute refractory period of at least 1 ms and a firing rate far less than the unit’s mean firing rate for at least 2 ms before and after spikes occurred. Clusters that did not meet these criteria were discarded. If inspection revealed that the cluster contained activity from more than one unit, as shown by the presence of dissimilar waveforms or refractory period violations, the cluster was manually split. If multiple clusters contained spikes from the same unit, as shown by the presence of similar waveforms across clusters and the absence of refractory period violation in their cross-correlograms, those clusters were merged.

QUANTIFICATION AND STATISTICAL ANALYSIS

All analysis was completed in MATLAB v.8.0 or 9.0 (MathWorks).

EMG processing and analysis

With certain exceptions discussed below, EMG measurements were downsampled to 1 kHz, high-pass filtered at 40 Hz, rectified, and convolved with a Gaussian having a 10 ms standard deviation.

EMG during precision pull behavior

To define trials and identify the associated EMG segments for this analysis, we used the time at which the onset of joystick pulling was detected by the experiment control program from the angular encoder signal. This method used the mean change in the encoder signal over 8 ms epochs, detecting a joystick pull when this value rose to ~6 standard deviations above the mean value when the joystick was at rest. The analysis depicted in Figure 1C and D used EMG segments spanning 250 ms before to 200 ms after the onset of joystick pull. Correlations between time series segments were measured using Pearson correlation.

To compute the duration from the initiation of reaching to the initiation of pulling and the duration of pulling, we used a more involved method to detect the precise onset and offset of pulling. We first took the derivative of the angular encoder signal and smoothed it with a Savitzky–Golay filter (MATLAB function smooth, span = 10, order = 3). Joystick pulls were then detected as time points at which the resulting filtered time series rose to ~6 standard deviations above the mean value when the joystick was at rest. The filtered time series was then additionally smoothed by replacing each value by the median of the values spanning from 5 ms before to 5 ms after it. For each detected pull, the onset and offset of pulling were identified as the last value before and the first value after each detected pull at which this doubly filtered time series fell below 0. The onset of reaching was identified from the activation of biceps (Bi) and extensor digitorum communis (EDC), by first rectifying the raw EMG measurements and smoothing them with a Savitzky–Golay filter (MATLAB function smooth, span = 10, order = 3). We then identified the onset of reaching as the time point at which the sum of the resulting traces first rose above a threshold set ~6 standard deviations above the mean level during inactivity.

EMG during optogenetic inactivation

For optogenetic inactivation, we chose a method for smoothing EMG that used causal filtering to enable precise assessment of perturbation latencies. Thus, in this case EMG time series were high-pass filtered at 40 Hz, rectified, and convolved with a 10 ms Gaussian, except the Gaussian filter kernel had amplitudes for times < 0 – its “backwards in time” side – set uniformly to zero. The modal EMG value from periods of quiescence was then subtracted off each measurement to set the baseline to 0. Segments surrounding inactivation or control detections were aligned by the time at which the laser command pulse was initiated after detection (though on control trials this pulse was only sent to the acquisition system and not to the laser itself).

Before EMG trial averages were assembled, outliers were removed. Separately for either inactivation or control trials, we found the mean EMG array (time points x muscles) for the first half of trials. We then found the distance of each and every trial array – not just those in the first half – from this mean (MATLAB function pdist), generating distributions of distances from which we computed the standard deviation. We then eliminated those trial arrays that were more than 2 standard deviations away from the mean EMG array. This procedure was then repeated using the mean EMG array for the second half of trials, eliminating those trials more than 2 standard deviations away from this mean. This method was aimed at ensuring that individual outlying trials would be compared to mean EMG arrays to which they did not contribute. This prevents the inclusion of outlying trials because they skewed a mean EMG array used for comparison. We note that no outliers were removed when calculating the success rate (rewarded trials/total trials; Figure 2C) or the latency to pull or to reward (Figure S2F, G).

To calculate the normalized fractional change following inactivation (Figures 2D), we found for each muscle the difference between the means for EMG time series from control and inactivation trials. All values in the resulting matrix (time x muscles) were squared, the mean across muscles at each time point was taken, and the square root of each value in the resulting time series was found. Each time point in the resulting time series was then divided by the corresponding time point in a similarly constructed time series computed using EMG time series from control trials without subtracting values from inactivation trials. We then corrected these fractional change time series for the difference expected by chance due to the use of separate sets of trials. On 1000 different iterations, we divided the control trials into random halves and similarly calculated a fractional change time series using the two halves in place of the control and inactivation trial sets. The mean fractional change time series across these 1000 iterations was computed, and this mean was subtracted from the fractional change time series computed with the actual data. Lastly, we subtracted the mean value across the 25 ms preceding stimulus onset time from the resulting time series. The result was what we refer to as the normalized fractional change time series. The mean normalized fractional change was computed over the following epochs: 1 to 35 ms from light onset, 36 to 70 ms from light onset, and the full duration of light stimulation.

The normalized fraction change in VGAT-ChR2-EYFP mice over the full duration of light stimulation during locomotion was significantly different from that attributable to retinal responses or other unintended behavioral effects of stimulation seen in wild type mice (one-tailed t-test, p = 0.0068). The mean normalized fractional change during locomotion in VGAT-ChR2-EYFP mice was 0.224 ± 0.05 (n = 4), which was 28x as large in magnitude as the mean normalized fractional change in wild types (−0.0079 ± 0.003, n = 3).

To analyze EMG following inactivation at variable locomotor phases (Figure S2H–K). Locomotor phase was defined from EMG time series using the Phaser algorithm (Revzen and Guckenheimer, 2008), which computes a one-dimensional phase variable (range: −π to π) from multidimensional time series. To ensure that locomotor phase was defined in an equivalent manner across sessions, we trained the algorithm’s phase classifier only once for each animal, using data from just one session. Phase assignment appeared consistent across animals, in terms of the relation of particular phase values to particular muscle activation features.

Trials were divided into ten groups based on the locomotor phase at which the light stimulus began and were aligned by stimulus onset time. The phase boundaries between groups were defined to ensure approximately equal numbers of trials in each group, but the same boundaries were used for all animals. Outlying trials were removed from each group using the distance from mean EMG arrays for the first and last half of trials as above. A mean EMG array across trials was computed for each trial group.

An equivalently-sized number of EMG arrays identified from the time series intervening between inactivations served as controls for each group of trials. This set was identified as follows. First, all the time series samples at which the locomotor phase reached the mean stimulus onset phase for the given group were identified. Second, samples were eliminated if the length of the current step was more than 50 ms different from the mean step length for the full data set. Third, a random subset of ~1000 of the remaining samples was identified. From this set, 50,000 different random subsets of a size equal to that of the given trial group were taken. For each subset, we computed the sum squared difference between the mean EMG array over the preceding 300 ms and the trial group’s mean EMG array over the 300 ms preceding stimulus onset. We defined our control trials using the subset for which this sum squared difference was lowest.

Normalized fractional change was then computed as described above for each trial group, with one difference. Here, in order to correct fractional change time series for the difference expected by chance due to the use of separate sets of trials, we needed to use groups of control trials selected using the same method we used to find control trials for each trial group. Thus on each of 25 iterations, we selected a random subset with a size equal to that of the trial group from the ~1000 samples found based on the length of the current step above. From the remaining samples, we identified 50,000 different random subsets of the same size, computed the sum squared difference between the mean EMG array over the preceding 300 ms and the mean EMG array over the 300 ms preceding the samples in the first random subset, and found the subset for which this difference was lowest. On each of the 25 iterations, time series of the fractional change between EMG arrays for this subset and EMG arrays for the first random subset were found, the mean time series across the 25 iterations was computed, and this mean was subtracted from the fractional change time series computed with the actual data to yield the normalized fractional change time series for the given trial group.

EMG during electrical stimulation

Analysis of EMG data during electrical stimulation experiments utilized the same filtering and smoothing procedures as were used for optogenetic inactivation. However, the latency of stimulation response onset was measured using time series that were rectified but not smoothed and were subsampled only to 10 kHz. Latency measurements for a given stimulation current level were made with data only from muscles inactive as mice stood still, and utilized the following procedure. First, rectified time series for a given muscle surrounding the time of stimulation onset were subtracted by the mean value during the epoch from 100 to 10 ms prior to onset. Second, time series were normalized by dividing by their standard deviation during this same epoch. Third, each time series element was squared. Fourth, the resulting time series were summed across simultaneously recorded muscles. Fifth, the mean across trials (n ≥ 25) was taken, and the mean during the epoch from 100 to 10 ms prior to onset was again subtracted. Sixth, the first time point following onset at which the resulting time series rose above a threshold set to be 7 times the standard deviation of the time series from 100 to 10 ms prior to onset was determined. Lastly, the last time point at which the time series was below zero prior to this threshold crossing was defined to be the time of response onset for the given current level.

The relation between stimulation current level, s, and latency, L, was then fit with the following equation for a decaying exponential with a variable asymptote:

$$L=a+b{e}^{-\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}.$$

The constants a, b and c were fit using the simplex method implemented by MATLAB’s fminsearch function. The fit result for a was taken to be the response latency for a given animal.

Electrical stimulation responses during treadmill walking were quantified as follows. Locomotor phase was again defined from EMG time series using the Phaser algorithm. To ensure that phase was defined in an equivalent manner across sessions, we again trained the algorithm’s phase classifier only once for each animal, using data from just one session. Our analysis procedures then followed those of Bretzner et al. (2005) who used data collected in cats. Stimulation trials were divided into ten groups based on the locomotor phase of stimulation onset and were aligned by onset time. Outlying trials were removed from each group using the distance from mean EMG arrays for the first and last half of trials as above. A mean EMG array across trials was computed for each trial group. The response magnitude for a given muscle for each trial group was computed as the integral over the 50 ms following stimulation onset, of the difference of the across-trial mean time series and a mean of control trials aligned on the mean stimulation onset phase for the given trial group. These control trials were identified from time series intervening between stimulations. Response magnitudes were then normalized by the largest response across groups.

EMG during neural recording

All comparison between neural and muscle activity used EMG high-pass filtering at 40 Hz, rectified, and convolved with a symmetric 10 ms Gaussian. For analysis of trial-averaged neuronal firing rates, trial segments were defined using EMG measurements. To define precision pull trials, two types of events were detected for each instance of the behavior: the activation of biceps (Bi) and extensor digitorum communis (EDC) at the onset of reaching, and the onset of joystick movement during pulling. The activation of Bi and EDC was determined as described above. To identify the onset of joystick pulling, we first took the derivative of the angular encoder signal and smoothed it with a Savitzky–Golay filter (MATLAB function smooth, span = 10, order = 3). We then identified the onset of pulling during each trial as the time point at which the resulting trace rose above a threshold set ~6 standard deviations above the mean level when the shaft is motionless. Epochs for trials aligned to reach onset were set to span 150 ms before to 350 ms after onset. Epochs for trials aligned to pull onset were set to span 400 ms before to 100 ms after onset. In both cases, these definitions ensure that epochs begin with a period of quiescence prior to task initiation.

We defined sets of precision pull trials in a manner meant to maximize the similarity between the muscle activation across trials both within a given recording session and also across different recording sessions. For each animal, we therefore employed a two-step process: first, we defined a template for the activation of each muscle during the pull task using data from all recording sessions, then we found the 40 trials from each session in which the EMG activation was most similar to these templates. Templates were defined separately for trials aligned to reach onset and pull onset. To construct EMG templates, we first identified, separately for each recording session, sets of EMG arrays aligned to either reach onset or pull onset. We next smoothed EMG measurements as described above. EMG measurements were next baseline subtracted as above. We then aimed to identify the subset of size ≥ 25 in which trials were maximally similar in terms of the Euclidean distance between time series arrays. The task of identifying a maximally similar subset is known as the clique problem, and we solved it here using a routine available on the MATLAB file exchange (Bron-Kerbosch maximalCliques, downloaded 11/21/2013). After the clique problem was solved yielding trial subsets of each type, we found the mean EMG array across each subset. To compute across-session EMG templates, we then took the mean across sessions of these mean arrays for individual sessions. After identifying templates, we then went back through all trials from each session and identified the 40 for which EMG arrays had the smallest distance from the template.

To delineate steps from EMG recordings during treadmill walking, we used the Phaser algorithm to define a one-dimensional phase variable from the multidimensional EMG recordings, as above. Here again, to ensure that locomotor phase was defined in an equivalent manner, we trained the algorithm’s phase classifier only once for each animal, using data from just one session. For animals C20 and C31, the algorithm defined 0 radians to be a phase just before the onset of triceps activity. This phase occurred at 0.94 radians (54°) after the peak in biceps activity for C20, and 0.82 radians (47°) after the peak in biceps activity for C31. For animal C32, the algorithm set 0 radians much later in the step cycle, so we applied an offset to phase measurements so that 0 radians occurred 0.89 radians (51°) after the peak in biceps activity.

We applied the algorithm to data from each session, identified each instance when this phase variable reached π and defined the intervals between these instances as individual step cycles. We found the median step cycle duration across sessions, discarded step cycles less than half this duration or more than twice this duration, and calculated the median duration again (377 ms for C20, 387 ms for C31 and 363 ms for C32). We then defined an ideal phase variable time series as one cycle running from −π to π at a constant rate of change over a duration equal to the median cycle duration, followed by a second cycle of the same form. For every instance at which the phase variable reached π, we took the phase variable segment from one median step cycle duration before to one median step cycle duration after the instance and computed its distance from the ideal time series. For each session we found the 50 segments that had the shortest distance from the ideal and found the corresponding EMG array for each spanning the epoch from one half the median step cycle duration before to one half the median step cycle duration after the instance. From these 50, we then removed a small number (4–12%) using the EMG outlier removal procedure outlined above for optogenetic inactivation and electrical stimulation experiments.

To identify time series segments during which muscles were inactive between precision pull trials, full EMG time series from precision pull behavior sessions were divided into successive 500 ms segments. For each segment, we measured the summed muscle activity as the sum of the integrals of the EMG time series for each muscle. The 40 segments having the lowest summed muscle activity were used for subsequent analysis of neuronal firing during inactivity. Visual inspection determined that such segments involved no discernable movement related EMG activity.

Firing rate calculation

Firing rate time series were computed at 1 kHz for each isolated unit by defining for each identified spike a time series approximating a Gaussian function with a mean at the time of the spike and a standard deviation of 10 ms, and which was normalized so that it had a temporal integral equal to 1. These Gaussian time series were then summed to form a smoothed firing rate time series. All plotting and analysis of firing rates used these smoothed firing rate time series. Trial averages were assembled using smoothed firing rate segments from the epochs corresponding to those of trials identified using EMG measurements (see above). All analysis discussed in the paper or depicted in figures was performed using precision pull trials aligned to reach onset unless otherwise noted. Mean firing rates were computed as the mean value of trial-averaged firing rates, separately for precision pull and treadmill walking. The lower median values we find across neuronal mean firing rates compared to other published accounts may result from the spike sorting procedures we employed, which could have enabled us to better resolve lower firing rate units from multiunit recordings.

Pearson correlations between firing rates and EMG activation for individual muscles were computed (MATLAB function corr) both using time series from all individual trials (Figures 4C) and from trial averages (Figure 4D). When using all trials, trial segments for either firing rate or EMG were concatenated. P values for the significance of these correlations used all individual trials. Because there were multiple muscles recorded, p value thresholds for statistical significance were adjusted to account for the multiple comparisons. Instead of setting the threshold at α = 0.05, we used α = 0.05^{1/_{#of muscles}}.

To estimate the fraction of all neurons whose firing rates were significantly correlated with at least one muscle, we had to account for the rate at which these significance tests would fall below the adjusted threshold by chance (“false discovery”). As expected, histograms of p values were roughly flat above p = 0.5. To estimate the rate of false discovery for the correlation of neuronal firing rates with the activation of each muscle, we assembled histograms for the p values resulting from the correlation calculation having a bin size equal to the adjusted α. We then defined the number of expected false discoveries for that muscle to be the mean of the counts within bins starting above p = 0.5, rounding the mean to the nearest integer. To then estimate the number of neurons that will be correctly assigned as significant with at least one muscle after accounting for the rate of false discovery, we used a simulation-based approach. For 1,000 different iterations, we took the p values for all neurons for a given muscle and selected a random subset of p values < α, with the subset having a size equal to the number of expected false discoveries for that muscle, and set those p values equal to 1. After doing this for all muscles on a given iteration, we then calculated the percentage of cells that still had p values < α for at least one muscle, and returned the p values to their original values. The percentage of neurons whose firing was significantly correlated with at least one muscle was the mean percentage across all iterations.

Waveform-based subtype assignment

For each isolated unit, the electrode on which spike-related voltage transients were largest in amplitude was identified. The mean spike waveform was then computed as the mean voltage time series on the identified electrode from 1 ms before spike time to 2 ms afterwards for the first 300 recorded spikes. If less than 300 spikes were identified for a given unit, then all spikes were used. Trough-to-peak spike widths were measured as the duration between the mean spike waveform’s minimum and its subsequent maxima.

Histograms of waveform widths appeared well-fit (MATLAB function fminsearch) by a sum of two Gaussians for widths ranging up to 0.8 ms (Figure 4E). We then assumed that two groups of neurons, one with relatively narrow and one with relatively wide waveforms, each show a Gaussian distribution of waveform widths over this range of widths. This allowed us to identify width boundaries such that the expected rate of misclassification as narrow or wide was below a proscribed level. That is, we could find a width boundary so that among those neurons with smaller widths, we would expect only a proscribed fraction to come from the distribution of wide waveform neurons. And similarly, we could find a width boundary so that among those neurons with larger widths, we would expect only a proscribed fraction to come from the distribution of narrow waveform neurons.

We thus used the means (μ_N and μ_W) and standard deviations (σ_N and σ_W) for the narrow and wide waveform distributions resulting from the fit to calculate these two boundaries using the following equations:

$$\begin{array}{c}\text{erf}(x)=\frac{1}{\sqrt{\pi }}{\int }_{-x}^x{e}^{-t^2}dt\\ {\mathit{cdf}}_W(x)=\frac{1}{2}\left(1+\text{erf}\left(\frac{x-{\mu }_W}{{\sigma }_W\sqrt{2}}\right)\right)\\ {\mathit{cdf}}_N(x)=\frac{1}{2}\left(1+\text{erf}\left(\frac{x-{\mu }_N}{{\sigma }_N\sqrt{2}}\right)\right)\end{array}$$

Using these, than the expected fraction of neurons classified as wide-spiking that are actually narrow-spiking for a given width boundary b, m_W(b), is given by the following:

$$m_W(b)=\frac{1-{\mathit{cdf}}_N(b)}{\left(1-{\mathit{cdf}}_N(b)\right)+\left(1-{\mathit{cdf}}_W(b)\right)}$$

And the fraction of neurons classified as narrow-spiking that are actually wide-spiking for a given width boundary b, m_N(b), is given by the following:

$$m_N(b)=\frac{{\mathit{cdf}}_W(b)}{{\mathit{cdf}}_W(b)+{\mathit{cdf}}_N(b)}$$

Using these equations, we found boundaries that yield an expected rate of misclassification of 1% of assigned neurons. The width boundary below which neurons were classified as narrow-spiking was 0.475 ms. The width boundary above which neurons were classified as wide-spiking was 0.519 ms. These boundaries left 5 out of our 890 recorded neurons unclassified.

Canonical correlation analysis

Canonical correlation analysis (MATLAB function canoncorr) was applied to sets of all trial-averaged firing rate and smoothed EMG time series from a given animal after reducing the dimensionality of each set to four. The choice of four was based on the fact that plots of neural variance capture versus dimensionality quickly flattened out above 4. Four dimensions also captured essentially all EMG variance (~99%). Dimensionality was reduced by performing principal component analysis (MATLAB function princomp) and retaining the projection of the data onto the first four principal component vectors.

We next identified a temporal offset, ranging from the muscle activation being offset 0 to 60 ms forward in time relative to neural activity, at which the quality of agreement between the canonical variables that result from canonical correlation analysis was maximized. The parameter we maximized was computed as follows: for each pair of canonical variables, we took the product between their correlation, the amount of additional variance captured by the muscle variable, and the amount of additional variance captured by the neural variable. We then took the mean of this product across all pairs and all animals, arriving at a single scalar value for each lag tested. There was a reasonable agreement between the lag at which this parameter reached a peak – 31 ms for pull and 36 ms for walk. We thus used a lag of 34 ms, the median of the two values. Similar results were obtained when excluding the fourth and last pair of canonical variables from these calculations.

To provide a baseline for comparing the quality of agreement between canonical variables, we also performed canonical correlation analysis on neural and muscle activities after reformulating the neural data to change its structure. In one case, each neuron’s averaged firing rate was replaced by a trial average recomputed after randomly shuffling the sequence of interspike intervals for the given neuron. Since firing rates are much higher during movement, we only shuffled the intervals occurring during trials of the task. In a second case, each neuron’s averaged firing rate was replaced by one recomputed after replacing that neuron’s full firing rate time series with one generated by simulating a Poisson process having an event rate equal to the mean of the trial-averaged firing rate for the given neuron.

We note here that the canonical variables resulting from this analysis are not constrained to be orthogonal. To compute the additional variance capture by each canonical variable, we then orthogonalized the sets of neural or muscle canonical variables via the Gram-Schmidt process. The additional variance captured by a given canonical variable is then the fraction of the variance captured by the corresponding orthogonalized variable. We also note here that in Figure S4D and G, we plot the neural variance captured as a fraction of that of the dimensionally reduced data, not the full neural data set. This is necessary for comparison with the results from the comparator data sets made by reformulating the neural data, in which cases the relation between variance capture and dimensionality differs substantially compared to the actual data.

Scaling

For each neuron, we computed a scaling index to measure how much changes in the firing of that neuron scale with changes in muscle activation during either of the two behaviors. This was computed by dividing the range of a neuron’s trial-averaged firing rate for a given behavior by the mean of the ranges of the trial-averaged EMG activity. Scaling values were calculated for neurons having mean firing rates > 1 Hz during at least one of the two behaviors to exclude neurons with very low firing rates, which may be poorly estimated.

Correlation differences

Correlation matrices (Figure 6C, S5A, D, G) were computed by finding the Pearson correlation between each possible pair of trial-averaged firing rates having means > 1 Hz during both behaviors to exclude neurons with very low firing rates, which may be poorly estimated. We note here that Pearson correlation is insensitive to relative magnitude of data series values; no normalization of firing rates was performed prior to these calculations. Correlation scores for walking used the full trial averaged firing rate, which comprised one step cycle (363 to 387 ms, depending on the animal). For precision pull, segments of trial-averaged firing rates from 150 to 50 ms prior to the onset of movement were omitted for these calculations, as they reflect to a lesser extent the neural activity during the movement. Segments of the firing rate time series starting from 50 ms before movement and lasting for a time equal to the duration of the step cycle in the given animal were used. Row and column orderings based on correlations for pull or walk data used the symmetric approximate minimum degree permutation (MATLAB function symamd).

Correlation difference values (Figure 6E, S5C, F, I) were computed for each pair of neurons as the absolute value of the difference between the correlation scores for the two behaviors. We also computed the distribution of such differences that could be expected under a null hypothesis that the neuronal correlations are the same between behaviors and estimates from data vary merely because the trials used to compute trial averages for pull and walk are distinct. We computed this distribution by taking the firing rate segments for each neuron for the two sets of trials and assembling two new sets. One set was comprised of the firing rate segments from a random half of the trials for one behavior and the segments from a random half of the trials from the other. The second set was then assembled from the remaining half of trials from each behavior. Trial averages were then computed for each new set of trials for each neuron, and absolute correlation differences were calculated. A cumulative distribution of these differences was computed from the permuted firing rates for each of 100,000 different permutations. Monte Carlo-based tests were performed to probe the differences between the medians of these null distributions and those of the observed data. P values signifying differences were calculated as (1 + # of permutations for which the median was higher than that of the observed data)/100,001.

Analysis of weighted sums defined by principal components

Principal components were computed separately for each behavior using matrices of trial-averaged neuronal firing rates, D, each having rows corresponding to different time points and columns to different neurons. Projections onto individual principal components were computed by multiplying D by the column vector comprised by the weight on each cardinal neural dimension for a given component.

To plot changes in the projection across all dimensions from one set of components (Figure S6D, F, H), the vectors resulting from projecting onto individual components were collected in matrices having 4 columns. Each row of these matrices corresponds to a point in a four-dimensional space in which the principal components serve as cardinal dimensions. For each successive point in these matrices, the Euclidean distance from the first point was calculated, yielding the distance from the activity at time = 0.

To compute the normalized variance in individual epochs (Figure S6E, G, I), data matrices D were first divided temporally into 10 equally sized segments and then the dimensionality of each segment was reduced to 4 by projecting it onto the sets of components for the full data matrices, as above. Normalized variance for each segment was then computed as the trace of the covariance matrix for each of these projected segments, normalized by the trace of the covariance matrix for the full projection matrix of activity during precision pull. Normalizing by the total variance during the precision pull permits comparison of magnitudes across the two behaviors.

The alignment index (Figure 7E) measuring alignment between neural activity during pull and walk was computed for sets of trial-averaged firing rates, muscle activations, and for 1000 different sets of trial-average firing rates computed after regrouping trials as was done above for correlation score changes. Here again, permuted data reflects a null hypothesis that underlying neuronal correlations are the same between behaviors. For each of the 3 types of data here, we begin with two data sets, one from each behaviors, comprised by matrices D₁ and D₂ with each row corresponding to a different time point and each column to a different neuron or muscle. For each matrix, we then compute matrices P₁ and P₂ comprised of principal component vectors. Here we used matrices with four such vectors as columns. We then computed the alignment index a using

$$a=\frac{\mathit{trace}(P_1^T·\mathit{cov}(D_2)·P_1)}{\mathit{trace}(P_2^T·\mathit{cov}(D_2)·P_2)}.$$

Segments of trial-averaged firing rates from 150 to 50 ms prior to the onset of movement were omitted for these calculations. In each case, the alignment index was computed a second time after reversing the identities of behaviors 1 and 2, and the mean of both resulting values was used.

Regression

Ridge regression was used to fit two types of models in which the activation of each muscle is determined by neuronal firing rates. In the first type (“static model”), the trial-averaged activation of each muscle was fit by a linear combination of the trial-averaged firing rates. For matrices N of firing rates and M of muscle activations in which each row corresponds to a different time point and each column to a different neuron/muscle, this model has the form M = NW where W is a matrix of weights. Results plotted in Figure S7 were obtained using no temporal offset between neural and muscle activity. Similar results were obtained though when imposing temporal offsets ranging from the muscle activation being offset 10 to 50 ms forward in time relative to neural activity.

In the second type (“dynamic model”), the trial-averaged muscle activations were fit by a linear combination of trial-averaged neuronal firing rates at several different time lags ranging from 0 ms to 50 ms in 5 ms increments. Regressors were the neuronal firing rate time series at all 11 time lags, corresponding to 11n variables, where n is the number of neurons. This model is equivalent to one in which muscle activity is fit by a linear combination of the outputs from a linear dynamical system that has neuronal firing rates as inputs (Kailath, 1980).

For both model types, the ridge parameter was selected via a three-fold cross-validation procedure. Sets of trials were partitioned into three subsets. The training set was obtained by averaging across trials in two of the three partitions, and a test set was obtained by averaging across trials in the remaining partition. The ridge parameter was selected as the one that minimized mean squared error on the test sets. A different ridge parameter was calculated for each day of recordings, since each day corresponded to different sets of neurons.

For the fits to each muscle, the difference between behaviors was computed by subtracting the two vectors of weights, taking the norm of the resulting difference vector, and dividing it by the sum of the norms of the original two weight vectors. These normalized differences then can range from 0 to 1. To test the null hypothesis that the underlying relationship between firing rates and muscle activation was the same between behavioral contexts, models were also fit using 1000 different sets of trial-average firing rates computed after regrouping trials as was done above for correlation score changes. Here again, Monte Carlo-based tests were performed to probe the differences between the medians of these null distributions and those of the observed data. P values were calculated as (1 + # of permutations for which the median was higher than that of the observed data)/1,001.

To compute the variance captured by the weight matrices for each model, we orthogonalized each set of weight vectors using the Gram-Schmidt process, computed the projection of the firing rate matrices N onto the resulting vectors, computed the covariance matrix for this projection, and then took the trace of that covariance matrix. For the dynamic model, the weights on a given neuron’s activity at each different lag were summed, resulting in one matrix the same size as W for the static model, before the Gram-Schmidt process was applied. This ensured that neural dimensions used at each time lag were reflected equally in measurements of variance captured.

DATA AND SOFTWARE AVAILABILITY

Custom software are available. See Key Resources Table above for details.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Muscimol hydrobromide	Sigma	Cat. #: G019-5MG
Experimental Models: Organisms/Strains
Mouse: C57BL/6J	The Jackson Laboratory	JAX stock #: 000664; RRID: IMSR_JAX:000664
B6.Cg-Tg(Slc32a1-COP4*H134R/EYFP) 8Gfng/J	The Jackson Laboratory	JAX stock #: 014548; RRID: IMSR_JAX:014548
Software and Algorithms
MATLAB v.8.0 or 9.0	MathWorks	https://www.mathworks.com/products/MATLAB/
KlustaKwik	Rossant et al., 2016	http://klusta.readthedocs.io/en/latest/
Phaser algorithm	Revzen and Guckenheimer, 2008	N/A
Bron-Kerbosch maximal cliques	MATLAB file exchange	https://www.mathworks.com/matlabcentral/fileexchange/30413-bron-kerbosch-maximal-clique-finding-algorithm
Other
Sound attenuating chamber	Coulbourn	Cat. #: H10-24A
Omniplex64 neural acquisition system	Plexon	Cat. #: OmniPlex/64
4-channel EMG amplifier	University of Cologne Electronics Lab	Model #: MA 102S
PCIe-6323 DAQ	National Instruments	Cat. #: 781045-01
Stimulus Isolator	WPI	Cat. #: SYS-A365D
Function generator	Agilent	Cat. #: 33522A
Pt-Ir wire for tetrodes	California Fine Wire	Cat. #: CFW0011173
Tetrode drive components	Neuralynx	Cat. #: VersaDrive-4

HIGHLIGHTS.

• In mice, motor cortex is required for a trained forelimb task but not walking

• Motor cortex activates short-latency effector pathways only during the trained task

• Distinct weighted sums of motor cortical firing patterns vary strongly in each task

• This change could permit motor cortex to engage short-latency pathways differentially