Extraction of dynamic functional connectivity from brain grey matter and white matter for MCI classification

Abstract

Brain functional connectivity (FC) extracted from resting‐state fMRI (RS‐fMRI) has become a popular approach for diagnosing various neurodegenerative diseases, including Alzheimer's disease (AD) and its prodromal stage, mild cognitive impairment (MCI). Current studies mainly construct the FC networks between grey matter (GM) regions of the brain based on temporal co‐variations of the blood oxygenation level‐dependent (BOLD) signals, which reflects the synchronized neural activities. However, it was rarely investigated whether the FC detected within the white matter (WM) could provide useful information for diagnosis. Motivated by the recently proposed functional correlation tensors (FCT) computed from RS‐fMRI and used to characterize the structured pattern of local FC in the WM, we propose in this article a novel MCI classification method based on the information conveyed by both the FC between the GM regions and that within the WM regions. Specifically, in the WM, the tensor‐based metrics (e.g., fractional anisotropy [FA], similar to the metric calculated based on diffusion tensor imaging [DTI]) are first calculated based on the FCT and then summarized along each of the major WM fiber tracts connecting each pair of the brain GM regions. This could capture the functional information in the WM, in a similar network structure as the FC network constructed for the GM, based only on the same RS‐fMRI data. Moreover, a sliding window approach is further used to partition the voxel‐wise BOLD signal into multiple short overlapping segments. Then, both the FC and FCT between each pair of the brain regions can be calculated based on the BOLD signal segments in the GM and WM, respectively. In such a way, our method can generate dynamic FC and dynamic FCT to better capture functional information in both GM and WM and further integrate them together by using our developed feature extraction, selection, and ensemble learning algorithms. The experimental results verify that the dynamic FCT can provide valuable functional information in the WM; by combining it with the dynamic FC in the GM, the diagnosis accuracy for MCI subjects can be significantly improved even using RS‐fMRI data alone. Hum Brain Mapp 38:5019–5034, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Alzheimer's disease (AD) is the most prevalent form of dementia in elderly, accounting for about 50% to 80% of age‐related dementia cases [Association, 2012]. It has been estimated that 1 out of 85 will be suffering from this disease by 2050 [Brookmeyer et al., 2007]. AD is an irreversible neurodegenerative disease causing progressive cognitive and memory deficits, which severely interfere with daily life and may eventually cause death. Currently, there are no effective clinical treatments for AD. Therefore, accurate diagnosis of AD at its early stage may have pivotal importance in preventing progression of detrimental symptoms. Mild cognitive impairment (MCI), a prodromal stage of AD, has gained much attention recently since MCI subjects tend to progress to clinical AD at an annual conversion rate of 10% to 15%, compared with normal controls (NC) who develop to AD at much lower annual conversion rate of approximately 1% to 2% [Petersen et al., 2001]. Thus, identifying MCI subjects has played an important role in helping reduce the risk of developing AD by appropriate pharmacological treatments and behavioral interventions. However, it is very challenging to identify MCI subjects from those undergoing normal aging, because of mild cognitive impairment symptoms.

In the past decade, various advanced imaging techniques, such as structural magnetic resonance imaging (MRI) [McEvoy et al., 2009; Suk et al., 2015; Suk et al., 2013, Wee et al., 2013], functional MRI (fMRI) [Chen et al., 2016; Wee et al., 2012a, 2012b, 2015], diffusion tensor imaging (DTI) [Nir et al., 2013; Wee et al., 2011], and positron emission tomography (PET) [Coleman, 2007; Mosconi et al., 2010], have provided efficient and noninvasive ways to acquire structural and functional imaging data of the human brain. Different imaging techniques can reveal different valuable information and help us better understand the brain [Li et al., 2011]. For example, fMRI [Machulda et al., 2009; Wee et al., 2015] is able to detect hemodynamic changes related to neural activities based on the blood oxygenation level‐dependent (BOLD) signals in grey matter (GM) regions. DTI [Haller et al., 2010; Lee et al., 2013; Wee et al., 2012a, 2012b] quantifies the anisotropy of water molecule's diffusion process occurring in white matter (WM) tracts, thus providing a feasible way to analyze nerve fibers in WM and characterize structural connectivity in the brain. PET [Silveira and Marques, 2010] can be used to observe metabolic processes and indirectly measure brain function.

For the purpose of MCI classification, constructing brain functional connectivity (FC) networks [Rubinov and Sporns, 2010] based on the resting‐state fMRI (RS‐fMRI), which is acquired without explicit tasks, has become one of the most promising methods since MCI and AD are generally believed to be associated with a disconnection syndrome within brain networks. The FC is often measured by correlation between RS‐fMRI BOLD signals (indirectly measuring spontaneous neuronal activities) of different brain regions, which exhibits how structurally segregated and functionally specialized brain regions, interact with each other [Friston et al., 1993; Greicius, 2008]. Nowadays, the FC has been recognized as a crucial imaging biomarker for diagnosing numerous neurodegenerative diseases, including AD/MCI, and for understanding pathophysiological mechanisms, as FC may be altered in both topological structure and strength of connectivity due to pathological disruptions [Liang et al., 2015; Qiao et al., 2016; Zhang et al., 2016a]. Numerous methods have been proposed to characterize FC between brain regions based on the BOLD signals of RS‐fMRI, such as Pearson's correlation [Zhang et al.,2016a], partial correlation [Jie et al., 2014b], and sparse representation [Suk et al., 2015; Wee et al., 2015; Wright et al., 2009; Yu et al., 2017].

Conventionally, FC is assumed to be temporally stationary, indicating that the interaction patterns between different brain regions are fixed across time. However, this assumption may underestimate the complex and dynamic interaction patterns between different brain regions, which has been confirmed by many recent works [Chen et al., 2016; Damaraju et al., 2014; Hutchison et al., 2013; Leonardi et al., 2013; Li et al., 2015; Wee et al., 2015]. From this perspective, exploiting the rich temporal information contained in dynamic FC (dFC) is a promising way to improve the performance of MCI classification. In this article, we adopt a sliding window strategy [Chen et al., 2016; Leonardi et al., 2013; Wee et al., 2015] to partition the whole BOLD signals into multiple overlapping segments, which is considered a popular approach for exploring dFC. Specifically, on each BOLD signal segment, FC is calculated for measuring the functional relationships between different brain regions during a specific time period. In such a way, it can yield dFC for each pair of brain regions that represents variations of FC throughout time, which then can be used as new features for early AD diagnosis.

Besides RS‐fMRI data, diffusion‐weighted imaging (DWI, often called DTI, when analyzed by using the tensor model) is also used for disease diagnosis. DTI is a conventional in vivo imaging modality to investigate structural connectivity information in the WM [Jin et al., 2015, 2017]. It measures the anisotropic movement of water molecules in the brain by using multiple diffusion‐weighted gradient fields. Based on the DTI, the major WM fiber bundles can be delineated using a tractography approach. DTI is often used to characterize structural connectivity (SC), rather than FC, in the WM according to the voxel‐wise diffusion tensors. It should be emphasized that when we refer to SC, it is commonly believed to be static, i.e., the connectivity strength is not changing in a short period of time. Some works [Wee et al., 2012a, 2012b; Zhu et al., 2014] intended to combine the FC information from RS‐fMRI data and the SC information from DTI data, since the relationship between functional and structural connectivity of the brain is vital in understanding and interpreting neurophysiological findings.

However, in numerous clinical application studies, it is impractical to acquire both DTI and RS‐fMRI data due to the significant increase in total scanning time. Thus, many studies on the brain FC (or the FC‐based brain functional networks) do not acquire DTI data for WM abnormality detection. Meanwhile, in some disease‐related studies, e.g., early detection of AD, the brain FC has been shown to be more sensitive to pathological changes than SC [Das et al., 2013; Querbes et al., 2009]. Moreover, previous studies have also indicated that abnormalities in FC from RS‐fMRI can be detected earlier than abnormalities in SC acquired through DTI. Therefore, we are aiming to extract more FC‐based features from RS‐fMRI data. A possible solution is to extract FC information from the WM regions, in addition to the FC features usually extracted from the GM regions.

It has been argued that there exist putative and meaningful BOLD fMRI signals in the WM [Gawryluk et al., 2014]. Previous studies have indicated a large possibility of having BOLD signals in the WM. For example, task activation was found in the genu of the corpus callosum, which connects the GM activation areas [Tettamanti et al., 2002]. Besides the corpus callosum, fMRI activations have also been observed in other task‐related WM structures, such as the internal capsule during a swallowing task [Mosier et al., 1999] and a finger‐tapping task [Gawryluk et al., 2011]. These findings together suggest that the BOLD fMRI signals do exist in WM regions. The underlying biologically microscopic mechanism may be due to the existence of the vasculature and the detectability of cerebral blood flow (CBF) and cerebral blood volume (CBV) in the WM. Nevertheless, the commonly accepted theory is that the BOLD signals in the WM are much weaker (with lower signal‐to‐noise ratio) than those in the GM, i.e., with only one‐third of the GM BOLD signal change percentage in the WM [Gawryluk et al., 2014]. Because the task‐evoked response is absent and subject's state is largely unconstrained in the RS‐fMRI studies, deriving meaningful functional information from the WM is even more difficult.

Fortunately, in a series of pioneering studies, Ding et al. [2013, 2016] have proposed a novel concept of “functional correlation tensor (FCT),” by using a simple and intuitive way to quantify functional information in the WM based on a tensor model of each voxel's local spatiotemporal BOLD signal correlations. Besides an interesting overall coherence between the FCT from RS‐fMRI and the diffusion tensor (DT) from DWI in many major WM structures, it was also found that different functional statuses could modulate such FCTs in the related WM fibers during visual stimulation [Ding et al., 2016]. These are the first studies indicating that the FC based on the RS‐fMRI BOLD signals in the WM also carries meaningful functional information. Several follow‐up studies have further validated such findings [Marussich et al., 2017; Wu et al., 2017, 2016].

Therefore, the FCT can spatially convey static and anatomical connectivity information, but more importantly, it can measure dynamic and functional information that DTI cannot provide. In this way, we take a step further to make bold assumptions and propose in this study that: (1) the structurally anisotropic FCTs exist in the major WM fiber bundles; (2) these spatially constrained FCTs carry informative functional information; and (3) such functional information can be characterized by dynamic FCT changes captured by dynamics analysis of the time‐varying fractional anisotropy (FA) based on FCT. Because of the unneglectable effects of physiological and other sources of noise on the computation of FCT, we propose a noise‐robust way for computing the dynamic FCT metric by weighted averaging of the voxel‐wise WM fiber tract probability and the voxel‐wise FA across all voxels in each main WM fiber bundle. We hypothesize that the dynamic FCT (dFCT), as quantified by the root‐mean‐square (RMS), can be used as features from the WM, together with the RMS of dFC from the GM, which will help early diagnosis of AD. Our experimental result shows that these two types of (WM and GM) FC‐based features can be jointly used to provide complementary information for training a strong classification model for MCI diagnosis. It is worth noting that this is the first time using FCT in the WM (based on RS‐fMRI) for disease diagnosis.

MATERIALS

Preprocessing of RS‐fMRI Data for FC Analysis

In this study, the publically available Alzheimer's Disease Neuroimaging Initiative [ADNI, 2017] database (http://adni.loni.ucla.edu) is used to provide neuroimaging data. ADNI was launched in 2003 by research organizations and companies, such as the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and the Food and Drug Administration, among others. The goal of ADNI is to define biomarkers for use in clinical trials, find the best way to measure the treatment effects of AD therapeutics, and diagnose AD at a predementia stage.

In this work, 54 MCI patients and 54 NC subjects, which were age‐ and gender‐matched, were selected from ADNI database. The images of each subject were acquired using a 3.0T Philips scanners at centers in different places. The voxel size is 3.13 × 3.13 × 3.13 mm³. SPM8 software package (http://www.fil.ion.ucl.uk/spm/software/spm8) was applied to preprocess the RS‐fMRI data. The first three volumes of each subject were discarded to ensure magnetization equilibrium. Rigid‐body transformation was then used to correct subject's head motion, but the subjects with large head motion (i.e., larger than 2 mm or 2°) were discarded. Next, the fMRI images were normalized to the Montreal Neurological Institute (MNI) space and spatially smoothed with a Gaussian kernel with full width at half maximum (FWHM) of 6 × 6 × 6 mm³. We did not perform scrubbing to data with a frame‐wise displacement larger than 0.5 mm, as it would introduce additional artifacts. Subjects who had more than 2.5 min RS‐fMRI data with large (>0.5) frame‐wise displacement were excluded from further analysis. The BOLD signals were further band‐pass filtered (0.015 ≤ f ≤ 0.15 Hz) to avoid the physiological noises and measurement errors.

Generating Major WM Fiber Probability Template

To measure connectivity within WM, we generated WM major fiber masks, within which we calculated pair‐wise connectivity based on specific fiber tracts. Currently, there are several brain WM templates available [Mori et al., 2006], such as JHU DTI‐based atlas created by hand segmentation of a standard‐space average of DTI images of 81 subjects. However, only 48 WM tract labels were given in this template, which was not compatible with our regions of interest (ROI)‐based connectivity analysis. Therefore, in this work, we generated WM atlas using an independent dataset for our specific need. Concretely, DTI data of 60 subjects were selected from the Human Connectome Project (HCP) (http://www.humanconnectomeproject.org/) dataset in order to construct the major WM fiber probability template. HCP was started in 2010 and aims to share knowledge about the structural and functional connectivity of the healthy human brain. By using advanced imaging instruments, analysis tools, and informatics techniques to construct a human connectome map, it has served as a foundation for researching changes in brain networks that occur with age and neurodegenerative diseases, like AD. After preprocessing DTI data using FSL [Woolrich et al., 2009], dtifit function in FSL was used to calculate DT for each voxel. PANDA was then used to generate whole brain tractography within the brain tissue using FACT algorithm using the following parameters: minimal seed voxel FA = 0.1, angle threshold = 35, and the number of seed at each voxel = 4. Automated Anatomical Labeling (AAL) atlas [Tzourio‐Mazoyer et al., 2002] which contains 116 brain regions (or ROIs, regions of interest) was projected back to each individual's native space using a deformable DTI registration algorithm. If two ROIs were connected with more than 200 streamlines, this pathway was considered as a major fiber pathway. All of these processes were conducted at each subject's native space. All the corresponding major fibers were transformed to the MNI space and further averaged across all subjects to generate a probability template for each major fiber. Of all the major fibers, we also counted how many subjects have the same fibers, and those shared by over 50% subjects were finally chosen as “putative” major fiber tracts. As a result, we identified a total of 359 putative major WM fiber tracts.

METHOD

The flowchart of the proposed method is shown in Figure 1. In summary, it consists of the following steps: (1) generating dFC from grey matter and also dynamic FCT (dFCT) from white matter, (2) extracting statistical features based on root‐mean‐square of dFC and dFCT, (3) selecting a few crucial features based on a two‐stage feature selection method, and (4) classifying subjects based on the ensemble support vector machine (SVM). The detail of each of these four steps is described in the following subsections.

Figure 1.

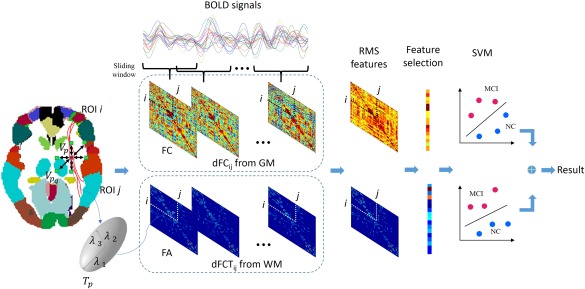
Framework of the proposed method. [Color figure can be viewed at http://wileyonlinelibrary.com]

Generating Dynamic FC from GM

The RS‐fMRI data of each subject was parcellated using the AAL atlas with 116 ROIs [Tzourio‐Mazoyer et al., 2002]. In order to capture the nonstationary interactions between different ROIs, the RS‐fMRI BOLD signal from each voxel was partitioned into multiple overlapping segments with a sliding window approach. Specifically, let $M$ be the total length of image volumes, $N$ be the length of sliding window, and $s$ be the step size between two successive windows. Then, the total number of segments is $K=⌊\left(M-N\right)/s⌋$. On each segment, within the GM, a regional mean BOLD signal can be calculated by averaging the BOLD time series over all voxels inside each ROI, reflecting the regional neural activity occurring during a relatively short period. Suppose the Pearson's correlation coefficients (PCC) between ROI $i$ and ROI $j$ on the $k$th sliding window is denoted as $C_{ij}^k$. Then, we can get interregional dFC, denoted as ${\mathrm{d}\mathrm{F}\mathrm{C}}_{ij}=\left[C_{ij}^1,\cdots ,C_{ij}^k,{\cdots ,C}_{ij}^K\right]$, which measures the dynamics of FC between ROI $i$ and ROI $j$. An illustration of ${\mathrm{d}\mathrm{F}\mathrm{C}}_{ij}$ from GM is shown in Figure 1. Note that, due to the symmetry of Pearson's correlation, the number of dFC is 6670, equaling to the total number of ROI pairs.

Generating Dynamic FCT From WM

To compute FCT, we focused on the voxels in WM. In parallel to the case above, a sliding window approach was first used to partition the BOLD signal from each voxel into $K$ overlapping segments. For a voxel $V_p$ in WM, its 3 × 3 × 3 neighborhood, comprising a total of 26 first‐tier neighboring voxels $\left\{V_{p_1},\cdots ,V_{p_q},\cdots ,V_{p_{26}}\right\}$, was defined. Based on the BOLD signal segments within the $k$th sliding window, the PCC $C_{p,p_q}^k$ between voxel $V_p$ and its neighboring voxel $V_{p_q}\left(q=\mathrm{1,2},\cdots ,26\right)$ was calculated, which together characterized the local profile of 26 temporal correlations along their respective directions during a short period. Define a 3 × 3 dyadic tensor ${\mathit{D}}_{p,p_q}$ as

$${\mathit{D}}_{p,p_q}=n_{p,p_q}{n}_{p,p_q}^T$$

where $n_{p,p_q}$ is a 3 × 1 unit vector, such that ${\mathit{D}}_{p,p_q}$ contains only one nonzero eigenvalue with the corresponding eigenvector pointing to the direction from $V_p$ to $V_{p_q}$. Then, a 3 × 3 FCT ${\mathit{T}}_p^k$ is defined for $V_p$ as a weighted combination of all ${\mathit{D}}_{p,p_q}$ [Ding et al., 2016]:

$${\mathit{T}}_p^k=\sum _{q=1}^{26}{C}_{p,p_q}^k{\mathit{D}}_{p,p_q}$$

Geometrically, FCT ${\mathit{T}}_p^k$ amounts to a three‐dimensional ellipsoid where three mutually‐orthogonal axes characterized the directions and magnitudes of FC around $V_p$. By performing eigen‐decomposition on ${\mathit{T}}_p^k$, we obtained its eigenvalues ${\lambda }_1,{\lambda }_2,{\lambda }_3$ and eigenvectors, which represented the dominant directions of 26 temporal correlations. To statistically summarize local anisotropy of temporal correlations, similar to the case of FA calculation based on DT in DTI studies, a FA value was calculated for $V_p$:

$${\mathrm{F}\mathrm{A}}_p^k=\sqrt{\frac{3}{2}}\frac{\sqrt{{\left({\lambda }_1-\overline{\lambda }\right)}^2+{\left({\lambda }_2-\overline{\lambda }\right)}^2+{\left({\lambda }_3-\overline{\lambda }\right)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$

where $\overline{\lambda }$ denotes the mean value of all eigenvalues. The above procedure is shown in Figure 1. By repeating the FCT and FA computation for all voxels in WM, we obtained a FA map of FCT on the $k$th sliding window. Next, for each pair of ROIs $i$ and $j$ in 359 major fiber probability templates constructed in Generating Major WM Fiber Probability Template section, we calculated a weighted mean FA value ${\mathrm{F}\mathrm{A}}_{ij}^k$ by combining the fiber probability map with the FA map, representing an overall anisotropy of the FCT in the WM tracts linking the two GM ROIs. For each subject, repeating the above process for each sliding window generated 359 time series, each of which was referred to as dFCT in this work and denoted by ${\mathrm{d}\mathrm{F}\mathrm{C}\mathrm{T}}_{ij}=\left[{\mathrm{F}\mathrm{A}}_{ij}^1,{\cdots ,\mathrm{F}\mathrm{A}}_{ij}^k,{\cdots ,\mathrm{F}\mathrm{A}}_{ij}^K\right]$. Similar to the ${\mathrm{d}\mathrm{F}\mathrm{C}}_{ij}$ in the above section, ${\mathrm{d}\mathrm{F}\mathrm{C}\mathrm{T}}_{ij}$ characterized the temporal dynamics of the FA values in the WM tracts linking ROI $i$ and ROI $j$. An illustration of dFCT is also shown in Figure 1.

Feature Extraction

In this study, we treated both dFC and dFCT as two types of discrete signals extracted from different pairs of ROIs. These signals formed bases for further diagnosis. To extract features from these signals, we calculated the RMS for each signal, which defined a statistic to measure the magnitude of varying metrics. Specifically, the RMS feature for a discrete signal ${\mathrm{d}\mathrm{F}\mathrm{C}}_{ij}=\left[C_{ij}^1,\cdots ,C_{ij}^k,{\cdots ,C}_{ij}^K\right]$ was given by

$$\mathrm{R}\mathrm{M}\mathrm{S}\left({\mathrm{d}\mathrm{F}\mathrm{C}}_{ij}\right)=\sqrt{\frac{{\sum }_{k=1}^K{{(C}_{ij}^k)}^2}{K}}$$

RMS value, also known as the quadratic mean in mathematics, represented the fluctuation level of the signals because its power was directly proportional to the square of RMS value [Altahat et al., 2012; Dey, 2014]. As a result, for dFC of each subject, a total of 6670 RMS features, which form a high‐dimensional feature representation, was generated. Similarly, for dFCT of each subject, a total of 359 RMS features was generated.

Feature Selection and Classifier Learning

The number of RMS features is much larger than that of subjects, especially for dFC; and more importantly, many features may be irrelevant to the classification task. Directly training a machine‐learning model on high‐dimensional small sample data tends to yield poor generalization performance because of the overfitting phenomenon [Chen et al., 2013, Zhang et al., 2017]. In addition, it also makes interpretation of the results quite difficult. To overcome the problems above, feature selection [Jie et al., 2014a; Ye et al., 2012] is necessary for reducing the number of features before building a classification model.

In this work, a two‐stage feature selection procedure was developed to select a subset of the original features, which was crucial for classification. Specifically, in the first stage, a two‐sample t‐test, which had been applied widely in the neuroimaging pattern analysis, was performed between MCI subjects and NC subjects for each original feature. Then, the features were ranked according to their individual discriminative capability indicated by corresponding p‐values. Only the features with p‐values smaller than a given threshold were retained, while the remaining were screened out. The resulting features after the t‐tests, although highly relevant to the class label, may still have contained redundant information. Therefore, in the second stage, LASSO regression was used to further optimize the feature subset. Different from the t‐test performed on each feature individually, LASSO regression [Tibshirani, 1996; Zhang et al., 2016b], which accounts all features jointly, keeps only the most discriminative features, while discarding the redundant ones. Let $X\in R^{m\times n}$ be the sample matrix, where $m$ is the number of samples and $n$ is the number of features selected by the t‐tests, and $y\in R^m$ be the label vector of samples, where $y_i=1$ if the ith subject is MCI and $y_i=-1$ if the ith subject is NC. Then, the LASSO regression was formulated as the following cost function:

$${\min }_{(w,b)}\frac{1}{2}\times {\parallel Xw+b-y\parallel }^2+\lambda \times {\parallel w\parallel }_1$$

where $w={\left[w_1,\cdots ,w_i,\cdots ,w_n\right]}^T\in R^n$, and $w_i$ is the weight for the ith feature, b is a bias term. $\lambda$ is a balance parameter controlling the model sparsity based on the $l_1$‐norm regularization. The larger the value of $\lambda$, the sparser the model [Zhang et al., 2017]. Finally, only those features with non‐zero weights $w_i$ were eventually retained.

Considering different characteristics of the features extracted from GM and WM regions, two SVM classifiers were constructed based on the respective feature subsets. SVM seeks a separation plane between training samples of different classes by maximizing the margin, meanwhile minimizing the classification errors. Balance between empirical risk and model complexity improved the generalization performance on unseen samples. To generate a final classification, the two SVMs were integrated at the decision level, that is, the scores from SVMs were fused by linear combination with a weight reflecting the importance of dFC.

EXPERIMENTS

To evaluate the effectiveness of the proposed method, we performed experiments by comparing with some related methods, including static functional connectivity (sFC), static functional correlation tensor (sFCT), dFC, dFCT, and two integrated methods, such as (1) combined sFC and sFCT (sComb) and (2) combined dFC and dFCT (dComb). For static cases, i.e., sFC and sFCT, there were two main differences from their dynamic counterparts. One was that the whole BOLD signal from each voxel in RS‐fMRI was employed, without using any sliding window approach. The other was that we directly calculated a single PCC value and a single FA value for each of all possible connections between any two ROIs. Note that, for such sFC and sFCT analyses, we could not produce any dynamic time series for these metrics, and thus could not extract RMS features. Specifically, the pairwise FC value based on the whole BOLD signals from each pair of the ROIs were used as the sFC feature; and we followed the same computation procedures of FCT (in Feature Extraction section) based on the whole BOLD signals and then calculated a weighted mean FA value for each pair of the ROIs from the resulting FCT maps as a sFCT feature. Note that sFC and dFC were constructed from GM regions, while sFCT and dFCT were from WM. For the subsequent feature selection and classification, all methods followed the same flowchart, so that different methods could be compared fairly.

In the experiments, due to limited samples, a leave‐one‐out (LOO) cross‐validation was applied to benchmark the generalization performance of different methods. Specifically, given a total of $L$ subjects, $L-1$ subjects were used as training data in order to obtain a model, which was subsequently evaluated by the rest subject in terms of the classification accuracy. The procedure above was repeated $L$ times, where at each time a different subject was used as a test data, and the averaged classification result across $L$ times was finally reported. The parameters in each method were tuned based on the $L-1$ training subjects by a nested LOO cross‐validation. The parameter $\lambda$ in LASSO regression was chosen by grid search from the set of $\left\{\mathrm{0.1,0.2},\cdots ,0.8\right\}$. All methods were implemented in MATLAB environment. For sFCT and dFCT, we only performed the LASSO‐based feature selection because many ROI pairs without notable anatomical connections were already screened out during the whole‐brain streamline fiber tractography and only 359 ROI pairs were retained. For sFC and dFC, we performed a two‐stage feature selection where the two‐sample paired t‐test with a significance of p = 0.05 was applied in the first stage. This was because for sFC and dFC, all 6670 pairs of ROIs were considered, which generated a much higher dimensionality. SLEP toolbox [Liu et al., 2009] was used to implement LASSO‐based feature selection. LIBSVM library [Chang and Lin, 2011] was used to implement SVM classification by using the default parameter value (i.e., $C=1$). For the sliding window approach, we simply allowed the window length be 30 and step size 1. Note that both feature selection and SVM training were carried out within the LOO cross‐validation stage for fair comparison.

Comparison of Classification Performance

To evaluate the performance of different methods, we employed the following five indices: accuracy (ACC), sensitivity (SEN), specificity (SPE), area under the receiver operating characteristic (ROC) curve (AUC), and F‐score [Sokolova et al., 2006]. Let TP, TN, FP, and FN to denote true positive, true negative, false positive, and false negative, respectively, where the controls were considered as the null distribution. On the other hand, the definitions of ACC, SEN, SPE, and F‐score are given as follows:

$$\mathrm{A}\mathrm{C}\mathrm{C}=\frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}$$

$$\mathrm{S}\mathrm{E}\mathrm{N}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$$

$$\mathrm{S}\mathrm{P}\mathrm{E}=\frac{\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}$$

$$F-\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=2\times \frac{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\times \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}$$

where $\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P} + \mathrm{F}\mathrm{P}}$, and $\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P} + \mathrm{F}\mathrm{N}}$. As we can see, ACC measures the proportion of subjects correctly classified among all subjects, SEN and SPE represent the proportions of MCI patients and NC correctly classified, respectively, and F‐score considers both precision and recall together. The ROC curve is a plot of SEN versus 1‐SPE over all possible values of discrimination threshold. The classification performance of the proposed method and other related methods are summarized in Table 1, where the best scores are highlighted in bold. Figure 2 plots the ROC curves for different methods.

Table 1.

Performance of different methods in MCI classification

Method	ACC	SEN	SPE	AUC	F‐score
sFC	62.04	61.11	62.96	0.6529	61.68
sFCT	66.67	62.96	70.37	0.6896	65.38
sComb	69.44	68.52	70.37	0.6954	69.16
dFC	74.07	70.37	77.78	0.7746	73.08
dFCT	71.30	70.37	72.22	0.7397	71.03
dComb	78.70	77.78	79.63	0.8449	78.50

Figure 2.

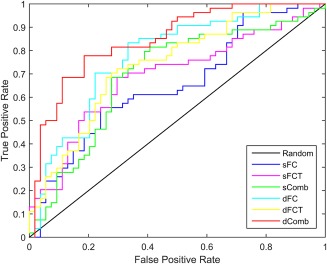
ROC curves of different methods for MCI classification. [Color figure can be viewed at http://wileyonlinelibrary.com]

As shown in Table 1, in static cases, FCT achieved higher accuracy than FC. It may be because the available functional correlation information from GM is limited in such a case, while FCT, in contrast, can incorporate valuable functional information from WM to assist the diagnosis of MCI. Moreover, the combination of both achieves superior performance than either sFC or sFCT individually. It indicates that the FC information from GM and WM regions can provide complementary information in MCI diagnosis. More interestingly, we can observe that, in dynamic case, FC gains larger performance improvement and eventually outperforms FCT. This verifies that the time‐varying correlation between ROIs can provide rich information compared with the static case. This phenomenon has been observed in many recent studies, e.g., in Chen et al. [2016] and Wee et al. [2015]. Furthermore, the integration of dFC and dFCT has achieved the best performance in terms of all indices. For instance, it outperformed individual dFC by 4% and individual dFCT by 7% in diagnosis accuracy. In order to implement a nonparametric statistical significance test, we followed DeLong's test [DeLong et al., 1988], which allowed for the comparison of the two AUCs calculated on the same dataset. The pairwise test results under the 95% confidence interval are shown in Table 2, where the p values less than 0.05 are highlighted in bold. As we can see from Table 2, our proposed dComb, which combines dFC and dFCT, significantly outperforms all other methods under 95% confidence interval. This demonstrates that the incorporation of the dynamic FC information in the WM is also helpful for improving the classification performance.

Table 2.

Nonparametric statistical significance test based on DeLong's test

Method	sFC	sFCT	sComb	dFC	dFCT	dComb
sFC	—	—	—	—	—	—
sFCT	0.6364	—	—	—	—	—
sComb	0.5103	0.9035	—	—	—	—
dFC	0.0343	0.2288	0.1766	—	—	—
dFCT	0.2014	0.2818	0.3775	0.6119	—	—
dComb	0.0003	0.0056	0.0006	0.0088	0.0365	—

In addition to the LOO cross‐validation, we also evaluated all methods by using 20‐fold cross‐validation, which had been widely adopted in previous studies [Salvatore et al., 2015]. To reduce the influence of randomness in data partition, we repeated this 20‐fold cross‐validation 10 times, and reported average accuracy and standard deviation in Figure 3. Consistent with the results from LOO cross‐validation, using 20‐fold cross‐validation also shows that the combination of dFC and dFCT features achieved the best performance. Thus, this study has certain practical significance in future clinical studies, as it brings significant performance improvement without acquiring DTI data. As a result, total scanning time and imaging costs can also be reduced.

Figure 3.

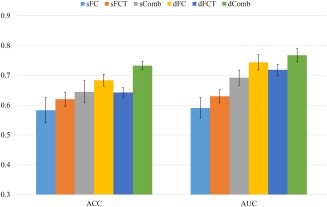
Performance comparison using 20‐fold cross‐validation. [Color figure can be viewed at http://wileyonlinelibrary.com]

Note that the RS‐fMRI based MCI diagnosis has attracted increasing interest from the neuroimaging community, with many research works presented in the literature. For example, Challis et al. [2015] applied Bayesian Gaussian process logistic regression (GP‐LR) as classifier to the diagnosis of MCI and AD subjects, which achieved a similar accuracy as our method. However, in addition to FC information, the above article also used age and mini mental state examination (MMSE) scores as features in classification. In contrast, our method did not use such features, instead only used RS‐fMRI data. We also noticed that many other studies dealt with similar problems as our study. However, in contrast to those methods, our study simultaneously considered both the dynamic variations of the conventional FC from the GM and the anisotropic local FC patterns, i.e., FCT, from the WM.

Figure 4 shows the temporal variations of FC and the weighted mean FA values associated with the left anterior cingulate gyrus (ACG.L) and the left posterior cingulate gyrus (PCG.L), as well as the left posterior cingulate gyrus (PCG.L) and the right posterior cingulate gyrus (PCG.R) for one subject, when using the sliding window approach. As demonstrated, the interregional interaction actually undergoes a large variation over the entire duration of the RS‐fMRI scan. For example, not only the magnitude but also the direction of the interregional correlation had changed for PCG.L‐PCG.R pair. This indicates a rather complex interaction relationship between ROIs, which should be modeled elaborately and leveraged for the diagnosis.

Figure 4.

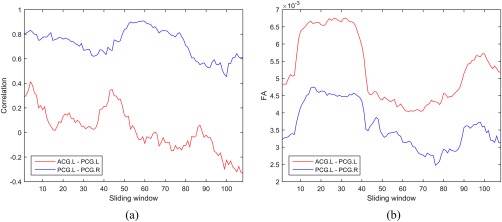
Dynamic variation of (a) FC and (b) weighted mean FA for connections ACG.L‐PCG.L and PCG.L‐PCG.R. [Color figure can be viewed at http://wileyonlinelibrary.com]

Most Discriminative Connections

In this subsection, we present the discriminative connections associated with ROI pairs revealed by our method. The feature selection process evaluates the relevance of each connection with respect to classification, and selects a few connections contributing to the linear classification model. Note that, due to the different training sets in LOO cross‐validation, different sets of discriminative connections might be selected in each evaluation procedure. Therefore, we computed the total frequencies of each connection across all LOO cross‐validations and sorted the results according to the resulting total frequencies. Similar to Wee et al. [2016], the connections with the highest frequencies during the LOO cross‐validation were selected as the most discriminative connections. The reported results are based on the original AAL atlas (with 116 ROIs) for illustration [Fox et al., 2005]. Figure 5 shows some most frequently selected connections, as well as the associated ROI pairs, from dFC and dFCT. The node represents ROI, and the edge represents connection, i.e., a pair of ROIs contributing to classification.

Figure 5.

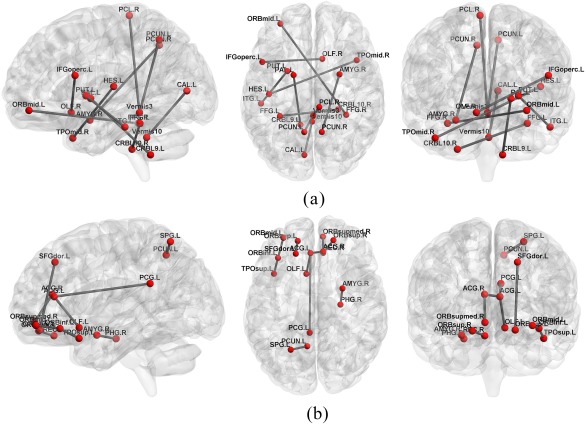
Illustration of top 10 ROI pairs selected with the highest frequencies. (a) dFC, and (b) dFCT. [Color figure can be viewed at http://wileyonlinelibrary.com]

As implicated from these experimental results, many connections of the default mode network (DMN) are selected, such as the precuneus, posterior cingulate cortex, middle temporal gyrus, middle orbitofrontal cortex, superior orbitofrontal cortex, and parahippocampal gyrus. It is generally accepted that the DMN plays an important role in high‐level cognitive functions, while abnormality of the DMN can be observed across a range of neurological disorders [Buckner et al., 2008]. Besides the DMN, other selected regions that may be important for early AD diagnosis are mainly the frontal areas, including the inferior orbitofrontal cortex, opercular inferior frontal gyrus, olfactory cortex, precentral gyrus, and paracentral lobule, thus indicating the importance of the frontal lobe for early diagnosis of AD.

Another main brain lobe suggested by our study to have potential diagnostic values is the temporal lobe, including the Heshl's gyrus, the superior and middle temporal pole, the amygdala and the parahippocampus, thus indicating that the temporal lobe could be another important brain lobe that is attacked by AD pathology [Echávarri et al., 2011; Poulin et al., 2011; Wee et al., 2015].

Other regions with potential diagnostic values include: the middle occipital gyrus, fusiform gyrus, the calcarine sulcus in the occipital lobe, and the putamen in subcortical regions, as well as several cerebellar areas, including the cerebellum lobules IX and X, lobule III of vermis, and lobule X of vermis. Most of these selected ROIs are consistently shown to be related to AD pathology in the previous studies [Adriaanse et al., 2014; De Jong et al., 2008].

Next, we discuss the potential biomarkers for future studies as indicated by our results from two aspects: dFC and dFCT analysis.

Based on the dFC analysis, several connections between the cerebral and cerebellar regions are suggested as important features. The cerebellum is often involved in motor learning, reflex adaptation, and other cognitive functions. AD pathology could not only lead to synaptic alterations [Baloyannis et al., 2000] in some cerebellar regions and cerebral regions (mostly in the frontal areas) [Braak and Braak, 1991] in MCI subjects, but also alter the indirect (via the relay of the thalamus and/or pons) long‐range pathway between the cerebral and cerebellar regions, thus resulting in abnormal cognitive function (see the review in Egidio and Stefano [2012] for more details). However, few previous studies have shown such a long‐range cerebrocerebellar functional connectivity abnormality in the early stage of AD, especially for the subjects without observable structural difference [Hanyu et al., 1993; Meoded et al., 2015]. Our result suggests that, by using dFC, we can detect subtle changes in the large‐scale cerebrocerebellar functional integration for MCI subjects. However, by using traditional static FC, such changes can be difficult to detect during early stages.

From dFCT analysis, our results show some noticeably clustered connections with aberrant dynamic FCT profiles in the prefrontal cortex (mostly in the orbitomedial prefrontal areas), which coincides with pathological signatures of AD. For example, in the prodromal stage of AD, the neurofibrillary tangles and amyloid plaque deposition are localized mostly in the entorhinal cortex and the orbitomedial prefrontal areas [Braak and Braak, 1991]. This AD pathology‐based staging model, in its very beginning, is quite consistent in the spatial pattern with our most discriminative dynamic FCT features (see Fig. 5b). It is well known that the prefrontal cortex plays an important role in decision making, attention control, and other high‐level cognitive functions [Grady et al., 2001]. We speculate that this result is mainly because the FCT is computed from the WM and could reflect local‐range FC pattern. The local FC changes may be more sensitive to the local pathological changes caused by the progression of AD. Therefore, we propose that the dFCT might be better suitable for serving as an effective early biomarker for diagnosis of AD, specifically in the prodromal stage.

Figure 6a,b shows the distributions of RMS features in MCI and NC subjects associated with a single connection selected from dFC and dFCT, respectively. For dFC, this connection is between the left inferior frontal gyrus (opercular) (IFGoperc.L) and right olfactory cortex (OLF.R), while for dFCT, this connection is between the left orbitofrontal cortex (middle) (ORBmid.L) and left orbitofrontal cortex (inferior) (ORBinf.L). As evident from Figure 6, although dFC shows slightly better separability than dFCT, a single connection either from dFC or from dFCT merely provides limited discriminating capability, while multiple connections chosen together through feature selection procedure can achieve better diagnosis accuracy for MCI, as verified by the experimental results shown in Table 1 and Figure 3.

Figure 6.

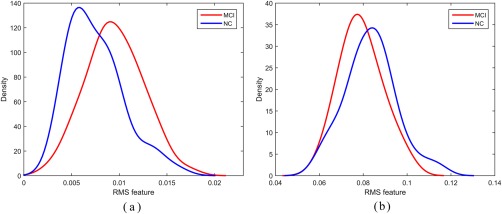
Distributions of RMS features selected from (a) dFC(IFGoperc.L‐OLF.R) and (b) dFCT(ORBmid.L‐ORBinf.L) in MCI and NC subjects, respectively. [Color figure can be viewed at http://wileyonlinelibrary.com]

In summary, these findings show that the disruptions of functional connectivity are widespread across the brain of MCI subjects even at its preclinical stage. The dFC and dFCT both reveal interesting and complementary information for clinical diagnosis.

Balance Between FC and FCT in Ensemble Classification

In ensemble classification, the weight for FC determines its contribution compared to FCT. A larger weight indicates the larger contribution of FC to the classification and vice versa. Thus, we investigate the variation of classification accuracy with respect to weights in both dynamic and static situations. The classification accuracy and AUC value of the proposed method are shown in Figure 7.

Figure 7.

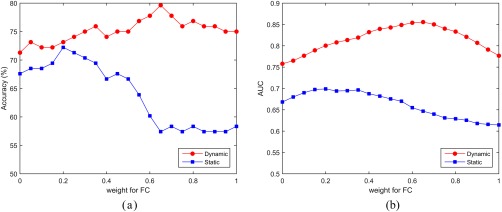
Performance of the proposed method with respect to the weight for FC. (a) Accuracy and (b) AUC. [Color figure can be viewed at http://wileyonlinelibrary.com]

It can be observed that, for static and dynamic cases, FC and FCT shows different importance. In the static case, higher classification accuracy is achieved when using small weights. A similar trend can be observed for the AUC values. This implies that the FCT constructed from WM regions plays a more important role than the FC constructed from GM regions. In contrast, in the dynamic case, a large weight can lead to better performance, indicating the dominance of information carried by FC from GM regions in the classification.

Computation Time

After training the classification model offline, the most discriminative features as well as the weights in SVM model can be determined. As a result, we only need to compute these selected features, instead of checking all ROI pairs or all major WM tracts. For a new subject, the total computational time is about 80 min. However, we should notice that the computations on each sliding window and at each WM voxel are essentially independent and thus are parallelizable. For example, if all computations on 108 sliding windows are performed in parallel, the computational time for a new subject will be about 100 times shorter than the unparalleled situation. After efficient optimization of our method, it can possibly be applied to disease diagnosis in the clinical setting.

DISCUSSION

Evaluation of Connection Importance

There are many dedicated ways [Haufe et al., 2014] to reveal the importance of connections in multivariate analysis models, such as the product measure, dominance analysis, proportion marginal variance decomposition, relative weight, as well as bootstrapping. Different methods may generate different results due to different implications of “importance.” In this study, we follow a widely adopted method in the MCI diagnosis related literature [e.g., Jie et al., 2016; Wee et al., 2015], by calculating the frequency of each connection chosen by the feature selection process across all the LOO cross‐validation iterations. The more frequently selected, the more reliable and robust are those selected connections. Therefore, the reliability and robustness can be regarded as one of the measurements of the feature importance in diagnosis. Furthermore, the connections can be sorted according to their frequencies being selected, with the most frequently selected connections shown in Figure 5 for illustration. Note that these frequently selected connections are determined in a data‐driven way based on feature selection and the label information of all subjects. Before feature extraction, we did not arbitrarily choose any features from any predefined brain regions based on any hypothesis– that is, the biomarker detection is conducted in an exploratory manner.

On the other hand, the bootstrapping method can be used to define another type of “importance” based on each feature's contribution to the final classification performance. In this method, by randomly changing the subjects' labels, we can conduct another round of “classification” (under the null hypothesis) based on the randomized labels, from which the weight (and also the frequency of being selected) for each feature can be derived. By including randomization and classification of multiple times, we were able to generate a null hypothesis of each feature's weight and also a null hypothesis of each feature's selection frequency. Then, we can obtain a p‐value for each feature according to the comparison with the null distribution. Since there are multiple comparisons, the p‐values can be further corrected based on multiple comparison correction (e.g., Bonferroni correction) in order to find out those significantly important features.

Biomarkers and Longitudinal Study

In order to discover potential biomarkers, many previous studies utilized the conventional mass‐univariate analysis methods, such as general linear modeling, two‐sample t‐test [Zhang et al., 2015, 2016a], and correlation analysis, to evaluate one feature by another feature independently. Although these types of methods can reveal features that are correlated with the disease, it can potentially ignore the nontrivial interactions among these features, which may lead to a group of weighted features or a pattern with higher sensitivity to disease detection. In contrast, our study is based on the multivariate analysis method, which investigates all features together and utilizes advanced machine learning algorithms to automatically determine the relationships between the combination weights among different features, as well as their relevance to the disease. In addition, our study is for individualized detection, while most of the previous mass‐univariate analysis derived only the group‐level statistical inference, which could not be applied directly to individualized detection. This is another difference between our study and traditional group‐level statistical analysis methods, and also one of the motivations of our work.

Cortical thickness is another important biomarker for detecting AD‐related brain morphometric changes. Its calculation is simple, robust, reliable and requires only a T1‐weighted image, which usually has the highest priority compared to all other imaging modalities scanned during MRI data acquisitions. In an AD patient's brain, the brain regions that are responsible for memory, language, problem‐solving, and other high‐level cognitive functions may appear smaller in volume and thinner in cortical thickness because of the neuronal death, when compared to normal aging subjects. Previous studies have already shown various effective cortical morphological features, such as cortical thickness, sulci depth, surface area, grey matter volume and mean curvature, for MCI classification [Li et al., 2014]. However, there are also many studies [Das et al., 2013; Querbes et al., 2009] suggesting that the changes in functional connectivity may occur even earlier than those detectable changes in the above‐mentioned anatomical, geometric and morphometric features [Zhang et al., 2016d]. With this commonly accepted hypothesis in mind during the design of the current study, we decided to use the features of various FC metrics for early diagnosis of AD, with higher detection sensitivity. Besides the conventional FC metric in the GM, we also explored the discriminative ability of FCT, computed from the WM beneath the brain cortex, where AD pathological changes could also occur.

Many studies [Misra et al., 2009; Lo et al., 2011] have focused on the trajectory modeling of longitudinal functional and structural imaging data in order to better understand the relationship between imaging‐based biomarkers and cognitive or behavioral decline in AD/MCI populations. In contract to longitudinal studies, we attempt to classify MCI from NC subjects based on their cross‐sectional RS‐fMRI data. In particular, this work emphasizes the roles of dFC as well as dFCT as the potential biomarkers for accurate diagnosis of MCI subjects. Note that several of these potential biomarkers detected by our study are shared by the biomarkers suggested by previous longitudinal studies [Yang et al., 2012], such as the frontal lobe and paracentral lobule. More importantly, the dFC and dFCT biomarkers suggested by our study can be used as the potential biomarker candidates in the future hypothesis‐orientated longitudinal studies for more comprehensive characterization of the trajectory of the neurodegeneration. Of note, several features detected by our study are new to the field, since the dFCT features in the WM structures are completely new in early AD detection.

Another useful implication of our study is that we use brain FC dynamics as features, whereas previous studies usually used static FC (calculated based on the whole BOLD signals). We argue that the functional dynamics‐based features can be more sensitive to AD pathological changes than the traditional static FC, since in the early stage the FC may not show detectable differences between MCI and NC subjects [Zhang et al., 2016c]. Therefore, our proposed features can also be applied to longitudinal studies for detecting abnormal degenerative trajectory. One of our ongoing works is to apply the FC dynamic information into a model of AD progression. Thus, we will be able to investigate brain functional changes at different stages of AD, and then differentiate the stable MCI from the progressive MCI.

Preprocessing and Reliability

Head motion during the RS‐fMRI scan is a confounding factor that could have significantly influenced both the functional connectivity measurement and the complex brain functional network measurement, which may lead to drastic changes or spikes in the BOLD signals across the entire brain. There are many works focusing on the influence of the head motion on FC estimation, as well as necessary preprocessing procedure to reduce such an effect [Power et al., 2012; Van Dijk et al., 2012]. In our work, the rigid‐body transformation was used to correct subject's head motion, and the subjects with large head motion (i.e., larger than 2 mm or 2°) were discarded in order to reduce potential influences. We did not perform data scrubbing to remove or resample the frames with frame‐wise displacement larger than 0.5 mm, as scrubbing itself will interrupt the temporal structure of the data and probably introduce artifacts into the subsequent dynamic analysis [Hutchison et al., 2013]. However, we only included the subjects who had more than 90 frames with acceptable micro‐head motion (frame‐wise displacement < 0.5), as suggested by previous studies [Wu et al., 2015].

On the other hand, band‐pass filtering is also an important preprocessing step that may influence FC analysis. In our work, the BOLD signals were band‐pass filtered (0.015 ≤ f ≤ 0.15Hz) to reduce the potential effect of the physiological noises. However, there are some studies [Salvador et al., 2008] showing that neuronal oscillations at distinct frequency bands have different physiological properties, and such inherent frequency‐specific property of BOLD spectrums contributes differently to FC estimation. Therefore, a straightforward extension of this work is to consider multiple frequency bands, instead of a single one, as well as to include FC or FCT features from different frequency bands.

Other imaging acquisition and preprocessing factors contain spatial resolution, flip angle, global signal regression, etc. A thorough exploration of all these factors and their combinations, as well as their influences on the classification results, is complicated and beyond the scope of this article. Additionally, data across studies may have different noise levels and artificial sources, thus making the problem even harder to investigate. Future studies should focus on optimizing strict preprocessing steps in order to provide homogenous parameters between disparate studies.

Test‐retest reliability is also an important issue that deserves further dedicated study. There are many test‐retest reliability studies on the static FC. For example, it has been suggested that the test‐retest reliability of the static FC is fair‐to‐good when examined in both region‐ [Wang et al., 2011] and voxel‐wise manners [Shehzad et al., 2009; Somandepalli et al., 2015], and the static FC‐based brain network properties are still satisfactorily reliable [Andellinia et al., 2015]. However, there are few test‐retest reliability studies on dynamic FC or dynamic FCT. Abrol et al. [2016] are of the few that have evaluated the reproducibility of properties of functional network connectivity (FNC) dynamics using the sliding window approach across different data sets. As the fMRI data used in our study was acquired during the resting state, there was no explicit task conducted and the subjects' statuses were unconstrained. Therefore, the dynamic FC and FCT profiles cannot be directly compared across subjects due to the absence of phase locking. In addition, considering that the used RS‐fMRI data in the current study does not incorporate repeated scans, we cannot conduct test–retest reliability assessment to investigate whether the RMS of the dynamic FC and FCT is reliable or not across the scanning sessions. Nevertheless, test‐retest reliability will be investigated in our future study.

Future Directions

In this article, RMS serves as a feature reduction way, although other methods of generating features from each sliding window will produce much more features for each subject. However, in this article, RMS is mainly selected based on the two considerations. First, RMS is able to characterize the overall activity level of dynamic FC and dynamic FCT. Second, RMS is invariant to the chronological order of sliding windows as temporal information collapses based on the definition of RMS. Using features from each sliding window could initiate the problem of phase mismatching across different subjects due to inclusion of temporal information. In this case, utilization of temporal features becomes another difficult problem. One possible solution is to further extract time‐invariant high‐level features based on sliding‐window features, such as distribution‐ and frequency‐spectrum‐based or status‐transformation‐probability‐based features. Besides RMS, other statistics can also be used to extract features from the time series, such as entropy, Hurst index, kurtosis, etc. Since different features characterize the same signal from different viewpoints, combining them appropriately is likely to further improve the outcomes.

CONCLUSIONS

In this article, we have presented a novel framework to integrate temporal correlation information extracted from both GM and WM regions for automatic MCI diagnosis. On one hand, dynamic functional connectivity between brain regions is estimated based on the regional mean BOLD signals in the GM regions. On the other hand, dynamic functional correlation tensor between brain regions is built based on functional anisotropy of the voxels lying on the WM fiber tract linking brain regions. Root‐mean‐square features are used as feature representation, while a two‐stage feature selection, as well as a classifier ensemble approach, may also be developed for classification. The experimental results show better diagnostic power by integrating connectivity information from both GM and WM regions. This work suggests the RS‐fMRI BOLD signals observed within WM, although weaker than those observed within GM, can provide complementary information for MCI classification.