Significance
Today’s lifeforms are based on informational polymers, namely proteins and nucleic acids. It is thought that simple chemical processes on the early earth could have polymerized monomer units into short random sequences. It is not clear, however, what physical process could have led to the next level—to longer chains having particular sequences that could increase their own concentrations. We study polymers of hydrophobic and polar monomers, such as today’s proteins. We find that even some random sequence short chains can collapse into compact structures in water, with hydrophobic surfaces that can act as primitive catalysts, and that these could elongate other chains. This mechanism explains how random chemical polymerizations could have given rise to longer sequence-dependent protein-like catalytic polymers.
Keywords: origin of life, HP model, biopolymers, autocatalytic sets
Abstract
It is not known how life originated. It is thought that prebiotic processes were able to synthesize short random polymers. However, then, how do short-chain molecules spontaneously grow longer? Also, how would random chains grow more informational and become autocatalytic (i.e., increasing their own concentrations)? We study the folding and binding of random sequences of hydrophobic () and polar () monomers in a computational model. We find that even short hydrophobic polar (HP) chains can collapse into relatively compact structures, exposing hydrophobic surfaces. In this way, they act as primitive versions of today’s protein catalysts, elongating other such HP polymers as ribosomes would now do. Such foldamer catalysts are shown to form an autocatalytic set, through which short chains grow into longer chains that have particular sequences. An attractive feature of this model is that it does not overconverge to a single solution; it gives ensembles that could further evolve under selection. This mechanism describes how specific sequences and conformations could contribute to the chemistry-to-biology (CTB) transition.
Among the most mysterious processes in chemistry is how the spontaneous transition occurred more than 3 billion years ago from a soup of prebiotic molecules to living cells. What was the mechanism of the chemistry-to-biology (CTB) transition? In this paper, we develop a model to explore how prebiotic polymerization processes might have produced long chains of protein-like or nucleic acid-like molecules (1, 2). What polymerization processes are autocatalytic? How could they have produced long chains? Also, how might random chain sequences have become informational and self-serving? Our questions here are about physical spontaneous mechanisms, not about specific monomer or polymer chemistries.
CTB Requires an Autocatalytic Process
Early on, it was recognized that the transition from simple chemistry to self-supporting biological behavior requires autocatalysis (i.e., some form of positive feedback or bootstrapping, in which the concentrations of some molecules become amplified and self-sustaining relative to other molecules) (3–8). That work has led to the idea of an autocatalytic set, a collection of entities in which any one entity can catalyze another.
We first review some of the key results. A class of models called Graded Autocatalysis Replication Domain (GARD) (9–11) predicts that artificial autocatalytic chemical kinetic networks can lead to self-replication, with a corresponding amplification of some chemicals over others. Such systems display some degree of inheritance and adaptability. GARD model is a subset of metabolism first models, which envision that small molecule chemical processes precede information transfer and precede the first biopolymers. Focusing on polymers, Wu and Higgs (12) developed a model of RNA chain-length autocatalysis. They envision that some of the RNA chains can spontaneously serve as polymerase ribozymes, leading to autocatalytic elongation of other RNAs. A related model asserts that autocatalytic chain elongation arises from template-assisted ligation and random breakage (13). Autocatalytic templating of the self-replication of peptides has also been shown (14, 15). These are models of the “preinformational” world before heteropolymers begin to encode biological sequence–structure relationships.
Another class of models describes a “postinformational” heteropolymer world, in which there is already some tendency of chains to evolve. In one such model, it is assumed that polymers serve as their own templates because of the ability of certain heteropolymers to concentrate their own precursors (16–19). It supposes an ability of molecules to recognize “self,” although without specifying exactly how. In another such model (20), chains undergo sequence-independent template-directed replication. It indicates that functional sequences can arise from nonfunctional ones through effective exploration of sequence space. These postinformational models predict that template-directed replication will enhance sequence diversity (19). These are abstract models of principle that do not specify what particular molecular structures and mechanisms might be autocatalytic. Also, they do not address the heteropolymeric or sequence-dependent informational aspects of the chains.
There has also been much experimental work leading, for example, to the creation of artificial autocatalytic sets in the laboratory (21–23). Such systems are designed so that pairs of molecules can catalyze each other (i.e., autocatalysis), leading to exponential growth of the autocatalytic members. For example, mixtures of RNA fragments are shown to self-assemble spontaneously into self-replicating ribozymes that can form catalytic networks that can compete with others (24). One limitation, however, is that these are fragments taken from existing ribozymes, and therefore, they do not explain the origins from more primitive random beginnings.
Here, we describe a dynamical mechanism that seeks to bridge from the pre- to postinformational world across the CTB transition. We describe a physical basis for how short chains could have spontaneously led to longer chains, how random chains led to specific sequences, and a structural basis and plausible kinetics for a prebiotic autocatalytic transition.
“Flory Length Problem”: Polymerization Processes Produce Mostly Short Chains
Prebiotic polymerization experiments rarely produce long chains. It is generally assumed that the prebiotic proteins or nucleic acids that initiated the transition to biology must have been at least 30- to 60-monomers long (25). Both amino acids and nucleotides can polymerize under prebiotic conditions without enzymes, but they produce mostly short chains (26–30). Leman et al. (29) showed that carbonyl sulfide, a simple volcanic gas, brings about the formation of oligopeptides from amino acids under mild conditions in aqueous solution in minutes to hours. However, the products are mainly dimers and trimers. Longer chains can sometimes result through adsorption to clays (31, 32) or minerals (33, 34), from evaporation from tidal pools (35), from concentration in ice through eutectic melts (36), or from freezing (37) or temperature cycling. Even so, the chain-length extensions are modest (38).
For example, mixtures of Gly and Gly2 grow to about 6-mers after 14 d (39, 40) on mineral catalysts, such as calcium montmorillonite, hectorite, silica, or alumina. Or, in the experiments of Kanavarioti et al. (36), polymers of oligouridylates are found up to lengths of 11 bases long, with an average length of 4 after samples of phosphoimidazolide-activated uridine were frozen in the presence of metal ions in dilute solutions. Similar results are found in other polymers: a prebiotically plausible mechanism produces oligomers having a combination of ester and amide bonds up to length 14 (38).
It is puzzling how prebiotic processes might have overcome what we call the Flory Length Problem (i.e., the tendency of any polymerization process to produce a distribution in which there are more short chains and fewer long chains). Standard polymerization mechanisms lead to the Flory or Flory–Schulz distribution of populations , whereby short chains are exponentially more populated than longer chains (41):
| [1] |
where is the chain length, and is the probability that any monomer addition is a chain termination. The average chain length is given by (Fig. 1A).
Fig. 1.
Polymerization processes lead to mostly short chains. (A) Spontaneous polymerization processes typically lead to a Flory distribution of chain lengths. Green line gives , and blue line corresponds to (B) Fitted distributions from experiments on prebiotic polymerization: red, Kanavarioti et al. (36); cyan, Ding et al. (46); magenta, Ferris (47).
Prebiotic monomer concentrations are thought to have been in the range of micromolar to millimolar (36, 42–45). Given micromolar concentrations of monomers and given , the concentration of 40-mers would be mol/L. Fig. 1B shows that, where the chain-length distributions are known for prebiotic syntheses, they are well fit by the Flory distribution [or exponential law constantl] (16, 19).
Foldamer Autocat Mechanism: Short Hydrophobic Polar Chains Fold and Catalyze the Elongation of Other Hydrophobic Polar Chains
We propose the hypothesis that the CTB transition occurred through foldable polymers (“foldamers”). Today’s biological foldamers are predominantly proteins [although RNA molecules and synthetic polymers can also fold (48–50)]. Many foldamers adopt specific native conformations, mainly through a binary solvation code of particular sequence patterns of the hydrophobic () and polar () monomers (51). We call these hydrophobic polar () copolymers.
Since today’s biocatalysts are proteins, it is not hard to imagine that early proteins could have been primitive catalysts. Precision and complexity are not required for peptides to perform biological functions. Proteins generated from random libraries can sustain the growth of living cells (52), and binding and catalysis from random peptides are not unusual (53) (refs. 11–14 and 54 and references therein and refs. 55–59). Even so, the sorts of actions suggested here are currently more in the realm of speculation than proven fact. Below, we describe results of computer simulations that lead to the conclusion that short random HP chains carry within them the capacity to autocatalytically become longer and more protein-like.
Here are the premises of the model.
-
i)
Some random HP sequences can fold into compact structures.
-
ii)
Some of those foldamers will have exposed hydrophobic “landing pad” surfaces.
-
iii)
Foldamers with landing pads can catalyze the elongation of other HP chains.
-
iv)
These foldamer catalysts form an autocatalytic set.
Here is evidence for these premises.
-
i)
Nondesigned random sequences are known to fold. polymers have been studied extensively as a model for the folding and evolution of proteins (51, 60–73). Those studies show that unique folded structures can be encoded simply in the binary patterning of polar and hydrophobic residues, with finer tuning by specific interresidue contacts. This binary encoding of unique folding is confirmed by experiments (74–77). Subsequently, the HP model has contributed several notable insights and advances, including sequence space superfunnels (64), the nonrandomess of uniquely encoding sequences (65), the determination of all uniquely encoding sequences of chain length 25 (66), recombination (67), homology-like comparative modeling features (68), and evolutionary switches (69). A comprehensive review is in the work by Sikosek and Chan (70).
-
ii)
Exposed hydrophobic clusters and patches are common on today’s proteins. A study of 112 soluble monomeric proteins (78) found patches ranging from to , averaging around ; they are often binding sites for ligands or other proteins. Modern proteins have many sites of interaction with other proteins, typically nearly a dozen partners. Almost three-quarters of protein surfaces have geometrical properties that are amenable to interactions, and those sites are enriched in hydrophobes (79).
-
iii)
Surface hydrophobic patches on proteins are often sites of catalysis (78, 80–82). For example, hydrophobic clusters on the surface of lipases serve as initiation sites, where the hydrophobic tail of a surfactant interacts with the patch first (81). A hydrophobic cluster on Cytochrome-c Oxidase is known to increase (82).
-
iv)
Primitive proteins might have catalyzed peptide chain elongation. Of course, today’s cells synthesize proteins using ribosomes, wherein the catalysis is carried out by RNA molecules. However, there are reasons to believe that peptide chain elongation might alternatively be catalyzable by proteins. First, peptide chain elongation entails a condensation step and the removal of a water molecule (ref. 83, chap. 3, p. 82). Dehydration reactions can occur in water if carried out in nonpolar environments (84, 85), such as protein surfaces. Second, a major route of protein synthesis in simple organisms, such as bacteria and fungi, uses nonribosomal peptide synthetases, which do not involve mRNAs (86, 87).
Modeling the Process of HP Chain Growth and Selection
The Dynamics of the Model.
We assume that chain polymerization takes place within a surrounding solution that contains a sufficient supply of activated and monomers. Since living systems—past or present—must be out of equilibrium, this assumption is not very restrictive. In our model, activated and monomers are supplied by an external source at rate . A given chain elongates by adding a monomer at rate . Just to keep the bookkeeping simple, we consider a steady-state process, in which molecules are removed from the system by degradation or dilution at a certain rate . We assume that chains can undergo spontaneous hydrolysis because of interaction with water; any bond can be broken at a rate . Without loss of generality, we define the unit rate by setting . All other rates are taken relative to this chain growth rate.
Chain Folding in the Model.
In addition, our model also allows for how the collapse properties of the different HP sequences affect the populations that polymerization produces. A standard way to study the properties of HP sequence spaces is using the 2D HP lattice model (51, 60). In this model, each monomer of the chain is represented as a bead. Each bead is either H or P. Chains have different conformations represented on a 2D square lattice. The free energy of a given chain in a given conformation equals (the number of HH noncovalent contacts) (the energy of one HH interaction). Some HP sequences have a single lowest free energy structure, which we call native, having native energy :
| [2] |
where is the number of HH contacts in the native structure of that particular sequence.
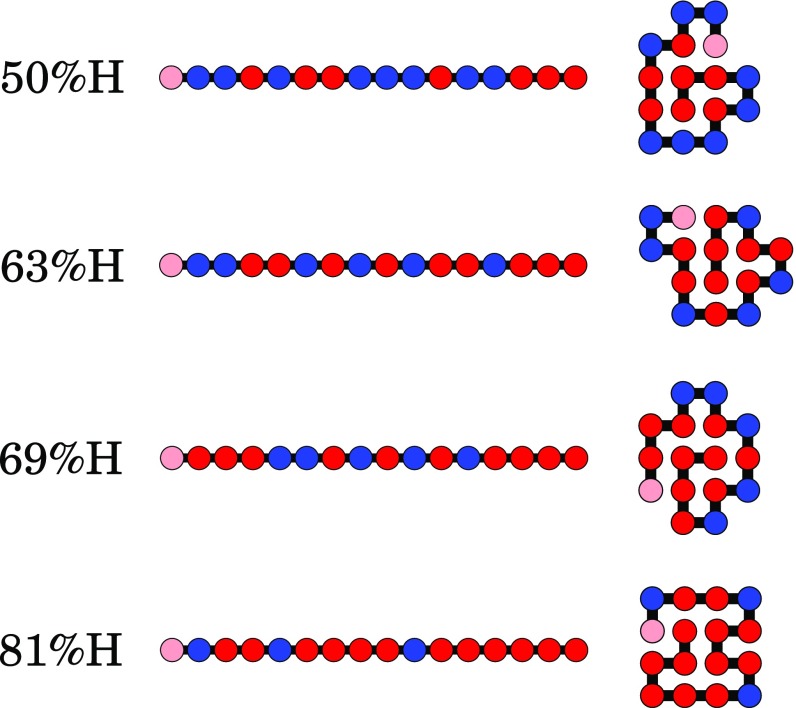
A virtue of the HP lattice model is that, for chains shorter than about 25-monomers long, every possible conformation of every possible sequence can be studied by exhaustive computer enumeration. Thus, folding and collapse properties of whole-sequence spaces can be studied without bias or parameters. Prior work shows that the HP lattice model reproduces many of the key observations of protein sequences, folding equilibria, and folding kinetics of proteins (88). A main conclusion from previous studies is that a nonnegligible fraction of all possible HP sequences can collapse into compact, structured, and partially folded structures resembling native proteins (60) (Fig. 2). The reason that the 2-dimensionality adequately reflects properties of 3D proteins is because the determinative physics is in the surface to volume ratios (because the driving force is burial of H residues). Also, it is convenient that the 10- to 30-mers that can be studied in 2D have the same surface to volume ratios as typical 3D proteins, which are 100- to 200-mers (89).
Fig. 2.
Examples of HP sequences that fold to unique native structures in the HP lattice model. Red (or pink if in the beginning of the sequence) corresponds to monomers, and blue corresponds to .
We assume that folded states behave differently from unfolded states, as they do in modern proteins. We suppose that a folded chain is prevented from additional growth and also, is protected from hydrolysis. This simply reflects that open chains are much more accessible to degradation from the solvent or adsorption onto surfaces than are folded chains. We suppose that unique folders are better protected than other compact chains, since oil drop-like chains have more core exposure to the solvent. We take folding to be reversible, as it is for natural small proteins. Therefore, some small fraction of the time, even folded chains are unfolded, and in that proportion, our model allows additional growth or degradation. For this purpose, we estimate the folding and unfolding rate coefficients for any HP sequence as (90)
| [3] |
where is the number of rotational df per peptide bond.*
The Catalysis Step in the Model.
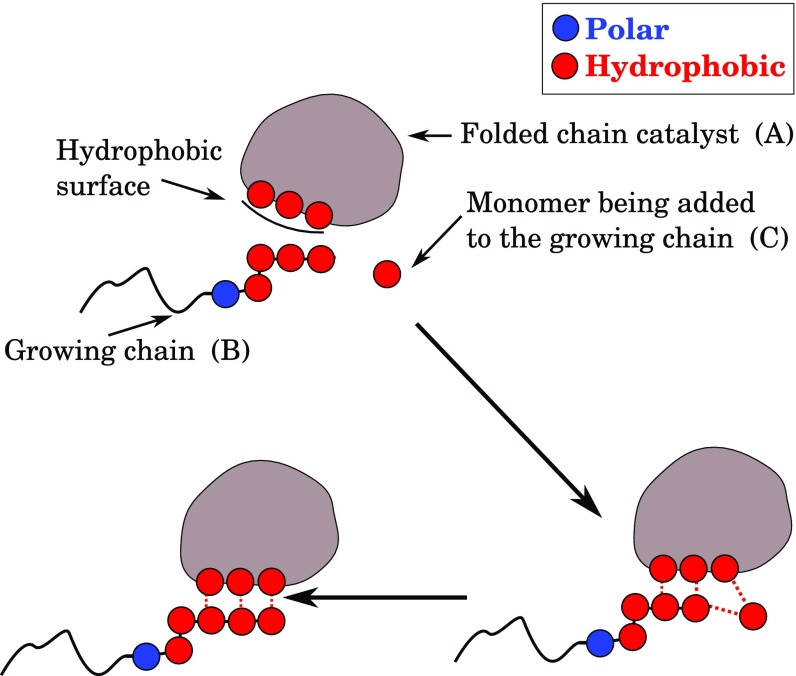
Some HP sequences will fold to have exposed hydrophobic surfaces. These surfaces could act as primitive catalysts, as modern proteins do more optimally today. Fig. 3 illustrates a standard elementary mechanism of catalysts, namely translational localization of the reacting components. A protein (the catalyst molecule) has a hydrophobic landing pad to which a growing reactant chain and a reactant hydrophobic monomer will bind, localizing them long enough to form a bond that grows the chain. It is important to notice here that the hydrophobic landing pad can facilitate only the addition of the hydrophobic monomer to a hydrophobic end of a chain, since polar residues will not interact with hydrophobic landing pad.
Fig. 3.
Some HP foldamers have hydrophobic patches, which serve as landing pads that can catalyze the elongation of other HP chains. Chain folds and exposes a hydrophobic sticky spot, or landing pad, where another molecule as well as a hydrophobic monomer can bind. This localization reduces the barrier for adding monomer to the hydrophobic end of the growing chain .
How much rate acceleration could such a localization give? Here is a rough estimate. For chain elongation, the catalytic rate will increase if the polymerization energy barrier is reduced by hydrophobic localization by a factor , where is the number of H monomers in the landing pad (see Fig. 6). The free energy of a typical hydrophobic interaction is 1–2. We take the minimum size of a landing pad to be three. For a landing pad size of three to four hydrophobic monomers, this binding and localization would reduce the kinetic barrier by 3–8kT, thus increasing the polymerization rate by one or more orders of magnitude. Of course, this rate enhancement is much smaller than the -fold of modern ribosomes (91), but even small rate accelerations might ultimately become amplified. The challenge in experimental tests here is that the initial signals being sought are likely to be small, be in the noise, and involve much sequence heterogeneity. Also, we do not mean to imply a belief that the true prebiotic mechanism was necessarily hydrophobic contacts and localization. Rather, it is intended to show the plausibility of getting few barrier reductions from simple undesigned surfaces.
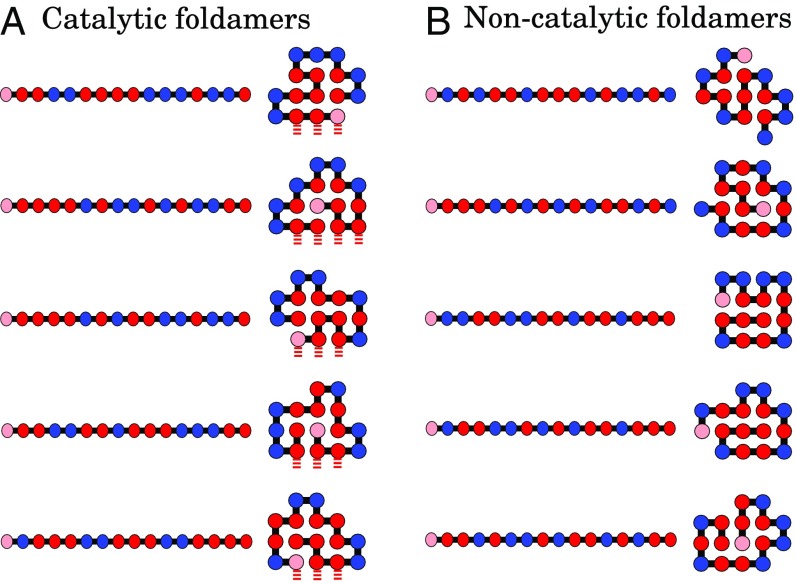
Fig. 6.
(A) HP lattice chains that fold and are autocatalytic. They fold into unique structures and have landing pads that can catalyze the elongation of each other. (B) HP chains that fold but are not catalytic. Most chains are not catalysts, but the size of the autocatalytic set is nonnegligible (Fig. 8).
To simulate this dynamics, we run stochastic simulations. For this purpose, we used the Expandable Partial Propensity Method (92). It is an exact stochastic simulation algorithm that improves on computational performance of the Gillespie method (93) for systems in which the number of potential species is much larger than the number of species actually present in the system. Also, we have shown that it gives probability distributions of molecule counts that are identical to those of the Gillespie algorithm (92). In Gillespie-like simulations, the time between reactions is stochastic and can be extracted from the simulations. In our simulations, one step is the time between two reactions, equal to 1/(rate of spontaneous monomer addition) s. In a single time step, one catalyst molecule can support only one growing chain plus one monomer unit. The growth rate of every single unfolded polymer is one. Only polymers which have come into contact with a catalyst have higher growth rate for this particular time step. They also can grow spontaneously with a rate of one.
The description and corresponding C++ library can be found at https://github.com/abernatskiy/epdm.
Results and Discussion
Folding Alone Does Not Solve the Flory Length Problem, but Folding Plus Catalysis Does.
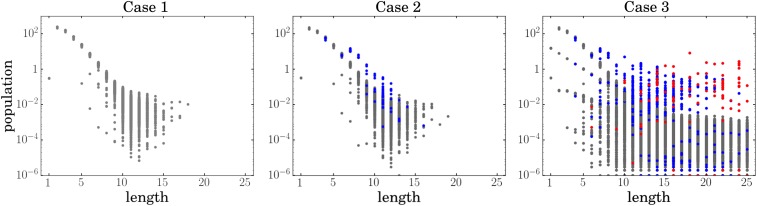
We compare three cases. Case 1 is a reference test, in which sequences grow and undergo hydrolysis, but no other factors contribute. Case 2 allows for chain folding but not for catalysis, and case 3 allows for both chain folding and catalysis. Case 1 simply recovers the Flory distribution, as expected, with exponentially decaying populations with chain length (Fig. 4, gray lines). In case 2, when chains can fold, they can bury some monomers in their folded cores. Thus, chains that are compact or folded degrade more slowly than chains that do not fold. Fig. 5, case 2 shows that folded polymers have higher populations than unfolded ones. Given a strong enough evolutionary pressure, even small advantages (as in case 2) could result in the selection of foldable structures. This conclusion is in the agreement with the work of Shakhnovich and coworkers (94), which showed that compact structures are favored by selection under conditions of aggregation and hydrolysis.
Fig. 4.
Chains become elongated by foldamer catalyst HP sequences. Case 1 (gray): a soup of chains has a Flory-like length distribution in the absence of folding and catalysis. Case 2 (blue): a soup of chains still has a Flory-like length distribution in the absence of catalysis (but allowing now for folding). Case 3 (red): a soup of chains contains considerable populations of longer chains when the soup contains HP chains that can fold and catalyze. We run 30 simulations for every case. To produce each line, we took a time average over time points in the steady-state interval, then counted molecules for each length, and divided it by the total molecular count.
Fig. 5.
The distributions over individual sequences are highly heterogeneous. We show the populations (molecule counts of individual sequences) for the three cases. In case 1, we do not allow folding or catalysis. In case 2, we allow folding but not catalysis, and in case 3, both folding and catalysis are allowed. For all of the cases, gray dots represent populations of the sequences that cannot fold, blue dots represent sequences that fold but cannot catalyze, and red dots represent sequences which act as catalysts and for which at least one elongation reaction has been catalyzed. For cases 1 and 2, populations of the sequences of the given length are distributed exponentially. Thus, we can take mean or median population for the given length as a faithful representation of the behavior of average sequence of that length. Case 3 is drastically different: the populations of the sequences of the given lengths are distributed polynomially. While most of the sequences have very low population for the longer chains, several sequences (mostly autocatalytic ones) have very high ones and constitute most of the biomass. For case 3, neither mean nor median is a good representation of the behavior of the chains; as we can see from the figure, all of the chains basically separate into two groups with different distributions, and this information cannot be shown in the mean or median. Every point is a time average over time points in the steady-state interval. Lower limit of is because of computational precision.
However, folding alone does not solve the Flory Length Problem (Figs. 4, blue lines and 5, case 2). Folding does increase the populations of some foldamer sequences relative to others, but the effects are too small to affect the shape of the overall distribution (Fig. 4, blue lines). It has been previously shown (94) that sequences capable of collapsing into compact structures can be prebiotically selected under just the forces of hydrolysis and aggregation alone. Our work is not necessarily in disagreement. That prior work posits a postbiotic mechanism driven by a selective force toward an optimization goal, whereas this mechanism is prebiotic and emergent, where sequence space is searched randomly with no preferential selection. A few iterations of this prebiotic mechanism could amplify small advantages.
Case 3 gives considerably larger populations of longer chains than cases 1 or 2 give (red lines in Fig. 4). When chains can both fold by themselves and also catalyze the elongation of others, such polymerization processes will “bend” the Flory distribution. This effect is robust over an order of magnitude of the hydrolysis and dilution parameters. The result is that some HP chains can fold, expose some hydrophobic surface, and reduce the kinetic barrier for elongating other chains. These enhanced populations of longer chains occur, although the degree of barrier reduction is relatively small.
Case 3 is qualitatively different from cases 1 and 2. Although cases 1 and 2 have substantial variances, they have well-defined mean values that diminish exponentially with chain length. Case 3 has much bigger variances and a polynomial distribution of chain lengths, and therefore, neither the mean nor median is a good representation of the behavior of the chains (Fig. 5, case 3).
The Foldamer Catalyst Sequences Form an Autocatalytic Set.
This model makes specific predictions about what molecules constitute the autocatalytic set—which HP sequences and native structures are in it and which ones are not. Fig. 6 shows a few of the HP sequences that fold to single native structures. Fig. 6A shows those foldamers that are catalysts, whereas Fig. 6B shows those foldamers that are not catalysts.
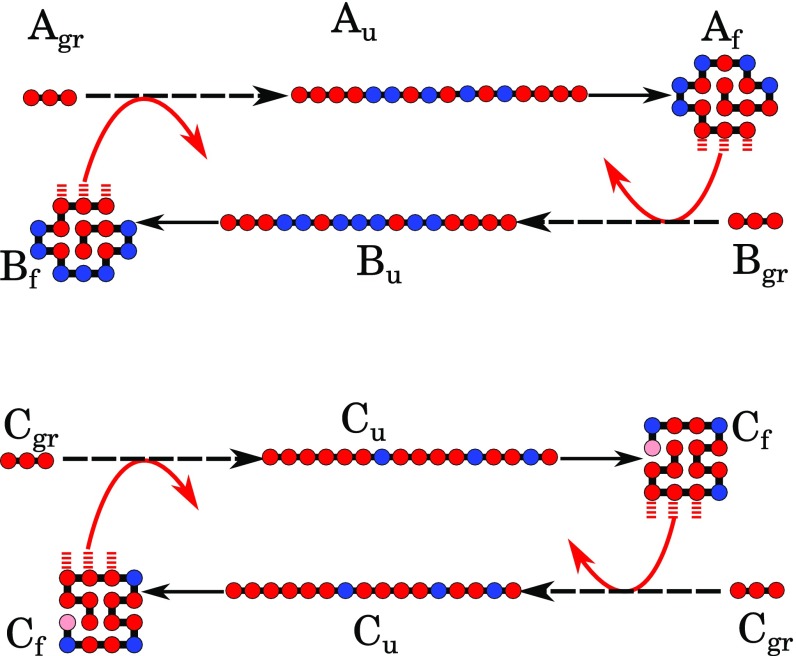
In short, all HP sequences that are foldamer catalysts are members of the autocatalytic set: any two HP foldamer catalyst sequences are autocatalytic for each other. Fig. 7 shows two examples of autocatalytic paired chain elongations. Fig. 7, Upper shows cross-catalysis: a polymer elongates a polymer , while is also able to elongate . Fig. 7, Lower shows autocatalysis: one molecule elongates another molecule in solution.
Fig. 7.
(Upper) Cross-catalysis of two different sequences. (Lower) Autocatalysis of two copies of an identical sequence. Dashed arrows represent multiple reactions of chain growth. Among them, there are both catalyzed reactions and spontaneous chain elongations. Catalysis is represented by red solid arrows. Solid black lines are folding reactions. Chains, which we call “autocatalytic,” experience catalysis during one (or more often, several) of the steps of elongation. Then, when they reach the length at which they can fold (), they fold and serve as catalysts themselves (). Mutual catalysis can happen between different sequences (here, A and B) and between different instances of the same sequence (here, C).
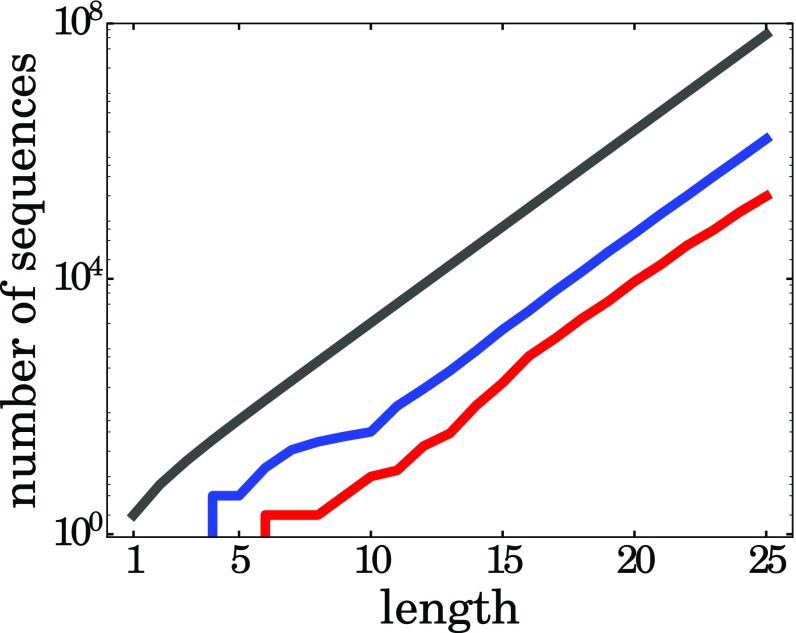
The Size of the Autocatalytic Set Grows with the Size of the Sequence Space.
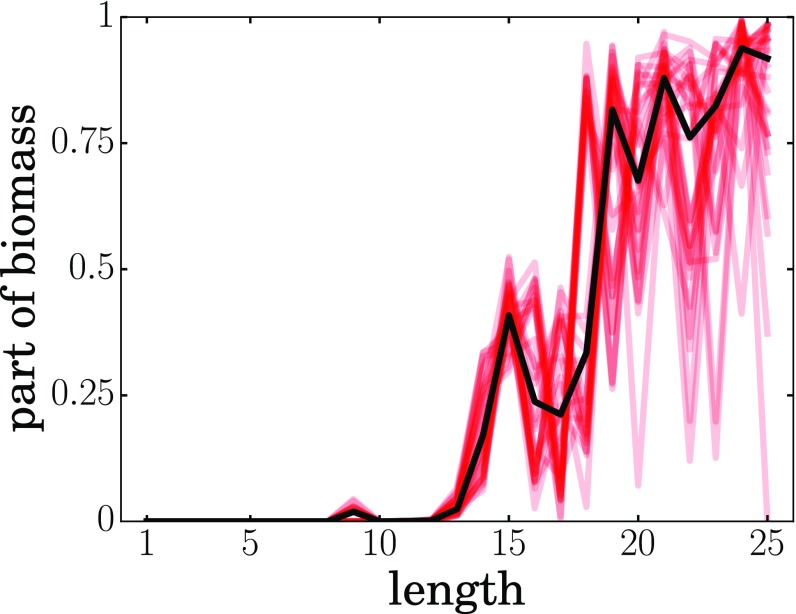
An important question is how the size of an autocatalytic set grows with the size of the sequence space. Imagine first the situation in which the CTB transition required one or two “special” proteins as autocatalysts. This situation is untenable, because sequence spaces grow exponentially with chain length. Therefore, those few particular special sequences would wash out as biology moves into an increasingly larger sequence space sea. In contrast, Fig. 8 shows that this mechanism resolves this problem. On the one hand, the fraction of HP sequences that are foldamers is always fairly small (about of the model sequence space), and the fraction of HP sequences that are also catalysts is even smaller (about of sequence space). On the other hand, Fig. 8 shows that the populations of both foldamers and foldamer cats grow in proportion to the size of sequence space. The implication is that the space of autocats in the CTB might have been large. Fig. 9 makes a closely related point. It shows that, for longer chains, the fraction of biomass that is produced by autocatalysts completely takes over and dominates the polymerization process relative to just the basic polymerization dynamics itself, although the catalytic enhancements are quite modest. This is caused by two factors: (i) the number of autocatalysts grows longer sequences (Fig. 8), and (ii) folding alone is not sufficient to populate longer chains. We find that the hydrophobicities of the dominant sequences ranges from 50 to 80%, with an average of .
Fig. 8.
Different sequence spaces grow exponentially with chain length: gray, the space of all HP sequences; blue, the space of foldamers; red, the space of foldamer catalysts.
Fig. 9.
The longer the chains, the bigger the contribution of the autocatalysts. Each red line shows how the contribution of autocatalytic chains to the biomass of the given length grows with chain length. Different red lines correspond to different simulation runs. The black line shows the median over 30 simulations.
Evolvability of HP Ensembles.
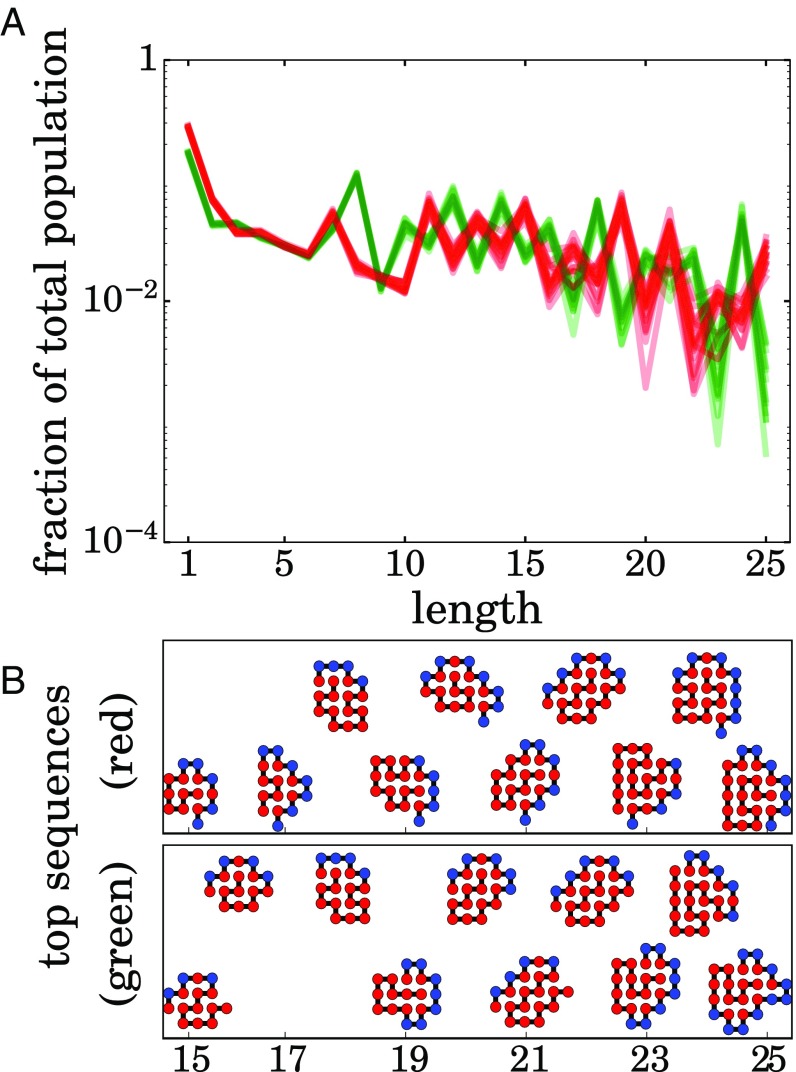
A key challenge in models of the CTB transition is “winner take all.” Suppose one type of molecule is better than others by some criterion. It will tend to win out. This is an undesirable feature of a CTB model, because it means that no additional evolvability or selection is possible (for example, discussions are in refs. 19 and 95). Early origins processes are more likely to have led to ensembles that are further evolvable. For a complex system that has many attractors, a perturbation can move the system over a threshold to the basin of another attractor. This allows for exploration of the sequence space and additional evolvability.
Fig. 10 shows that this model is not winner take all. Different initial seed conditions for the simulations lead to different dynamical attractors, with no stable switching between them. Fig. 10B shows some of the sequences and folded states in each of the respective autocatalytic sets for the green vs. red distributions. Each of the two attractors has its own signature ensemble of HP sequences that is an emergent property of the dynamics. We expect that there will be many such dynamical attractors in more refined models (20 monomer types rather than 2, allowing for longer chains, etc.). Moreover, because this model generates many different folds, it should generate many other types of catalytic functions other than chain elongation. These too will lead to additional dynamic attractors. Our goal here has not been to consider the evolution of functionalities beyond “ribosome-like chain elongation,” but ensemble models, such as this one, would lead to many other potential functionalities. Also, simulating chains longer than , it is likely to give richer and more complex behavior, as is true of real amino acid sequences.
Fig. 10.
Sequences can evolve to different autocatalytic sets. (A) catalytic system has at least two attractors. The lines are length distributions from case 3. Again, each line represents distribution of length in the steady state for one simulation run. It is clear that there are two kinds of distribution which get realized during the simulations. The system bifurcates either to a state represented by a green line or to one represented by a red one. These are the same lines as in Fig. 5A but separated in two sets by the clustering algorithm k-means. (B) Structure of the sequences which most often are main contributors into the total population of the polymers of their length. Upper corresponds to the macrostate shown in red in A, and Lower corresponds to the one shown in green.
At this point, we note what our model is and what it is not. First, it aims to capture a few principles in a coarse-grained way. This model only looks at the prebiotic question of how polymerizing random peptide-like molecules could collapse, partially fold, and catalyze the elongation and sequence differentiation of other sequences. It does not address how the genetic code evolved or how other protein functionalities evolved. Second, its catalytic mechanism is simply a translational localization in this case of the two reactants, polymer and monomer , in a chain extension reaction. It indicates how foldamer surfaces could give a nonnegligible (but probably small) reduction in the barrier to polymerization. Other binding and catalysis mechanisms are possible in foldamers; here, we simply show that this physics is plausible. Third, the mechanism is based on the same principle that today’s enzyme catalysts exploit: folded polymers can catalyze reactions, because the folded state is a miniature solid, having interatomic positions relatively fixed over timescales that are long enough for reactants to see a fixed potential surface. Unfolded polymers fluctuate too rapidly and are not good catalysts.
Fourth, the sequence evolution in this mechanism is not toward trivial states, such as the all H sequence, because those states do not have unique and stable folded states. The all H sequence is like an oil droplet, with a fluctuating ensemble of ground states that spends little time in any one and therefore, has more exposure to hydrolysis than unique folders have. How much more? The main point here is a qualitative one. Unfolded chains are most susceptible to degradation (they have no core), compact structures are less susceptible (they have cores but fluctuating ones), and unique folds are even less susceptible still (their cores are relatively stable). What is most important is not where the boundary is drawn but that there is some distinction among those three states. All H sequences would also tend to aggregate, and therefore, discriminating between oil drops and unique folds also gives a simple way to avoid confounding effects of aggregation. (Although aggregation is interesting in its own right as a possible mechanism of CTB, it is not the focus of this work.)
Why should we believe a simple lattice model, particularly a 2D one? The 2D HP lattice model is among the most canonical models for studying sequence spaces of foldamers. The reason for the reliance on this model is that, because it is studied by computational exhaustive enumeration, it is unbiased by any preconceptions about the nature of sequence space or arbitrary choices of energy parameters. This approach is the only unbiased, complete, and practical way to explore plausibilities of physical hypotheses, such as this one. Also, previous studies have shown that this model captures many important principles of folding and sequence-to-structure relationships. The principal value of such modeling is that it generates hypotheses that can be tested.
We note that this model is not necessarily exclusive to proteins. Nucleic acid molecules are also able to fold in water, indicating differential solvation. Although our model focuses on hydrophobic interactions, it is simply intended as a concrete model of solvation that could more broadly include hydrogen bonding or other interactions. Therefore, although our analysis here is only applicable to foldamers, that does not mean that it is limited to proteins. The unique power that foldable molecules have for catalyzing reactions—in contrast to other nonfoldable polymeric structures—is that foldamers lead to precisely fixing atomic interrelationships in relatively stable ways over the folding time of the molecule. It resembles a microscale solid, with the capability that substrates and transition states can recognize, bind, and react to those stable surfaces. For example, serine proteases use a catalytic triad of three amino acids. Therefore, foldability in some type of prebiotic polymer could conceivably have had a special role in allowing for primitive catalysis. Here, we use a toy model to capture that simple idea, namely that a folded polymer can position a small number of residues in a way that can catalyze a reaction.
Finally, we comment on the spirit of this model. In much of biological modeling, experiments come first, providing the premises for a model that can supply the rest of the chain of logic from premises to conclusions. However, this type of model serves a different goal, more in the spirit of other models in physics. In this predictions first approach, theory precedes and motivates subsequent experiments that can prove or disprove it. In predictions first modeling, the experimental premises are more an outcome than an input. Predictions first modeling is especially crucial for murky problems of science, such as in the origins of life, where even the basic premises are not all yet in plain sight. Our hope here is that this modeling can guide new experiments.
Conclusions
It has been recognized that life’s origins require some form of autocatalysis (5, 6, 8). However, what molecular structural mechanism might explain it? Here, we find that autocatalysis is inherent in the following process (Fig. 7). HP polymers are synthesized randomly. A small fraction of those HP polymers folds into relatively stable compact states. A fraction of those folded structures provides relatively stable landing pad hydrophobic surfaces. Those surfaces can help to catalyze the elongation of other HP molecules having foldable sequences.
The HP model allows for unbiased counting of sequences that do fold, do not fold, or fold and have a potentially catalytic hydrophobic landing pad. A nonnegligible fraction of all possible HP sequences folds to unique structures ( for lengths up to 25-mers). The fraction of all possible HP sequences that have catalytic surfaces (as defined above) is of foldable sequences or of the whole-sequence space. These ratios remain relatively constant with chain length, at least up to 25-mers (Fig. 8). This and successful designs of foldable, biologically active proteins based on the HP folding rule (96) suggest that folding in HP polymers is not rare. This model can suggest testable predictions for what early polymer sequences could be autocatalytic and provides a structural and kinetic mechanism for their action.
SI Text
Simulations.
To perform our stochastic simulations, we first needed to develop appropriate simulation code because of the large numbers of different molecular species that must be treated here. A description of the method, called the Expandable Partial Propensity Method (EPDM), and the corresponding C++ library can be found at https://github.com/abernatskiy/epdm (92). The challenge is to keep track of all of the molecular species and to search the full conformational spaces of each chain. This is nondeterministic-polynomial hard. We use the HP Sandbox algorithm (60, 97),* which is limited to maximum chain lengths of 25 monomers. To handle computational limitations, we restricted the total number of species to the level of a few thousands. We impose this limit by introducing a dilution parameter : molecules are randomly removed from the system with probability . Physically, it represents molecules that diffuse out of the reaction volume. The total numbers of molecules within the reaction volume vary in the range of . We start our simulations with a small pool of monomers, usually fewer than 100 molecules. Here are the dynamical steps.
-
•Polymerization happens when monomers react with other monomers or polymers at a rate :
[S1] -
•New monomers are imported into the system at high rate . From the point of view of the system, molecules appear out of nothing ():
[S2] -
•We assume that a fully unfolded chain can break at any internal site by hydrolysis. This happens with rate per chain bond:
[S3] -
•
Typical values for the half-time for the hydrolysis of a bond under neutral conditions and room temperature are on the order of hundreds of years.†. Here, we explored a range of hydrolysis rates that are about of the polymerization rate. Hence, our model polymerization rates are on the order of days to years.
-
•We assume that the system becomes diluted at rate . This has the practical purpose of limiting the total population of polymer in the system. We explored values of from . Given the values of that we used, it results in chains in the simulation volume
[S4] -
•Folding and unfolding reactions happen much faster than the polymerization processes, with corresponding rate coefficients of . The model considers folding to be a two-state process and does not take into account partially folded sequences because of the complexity of accounting for them:
[S5] - •
-
•where is the number of rotational dfs per peptide bond. To account for the difference between the 2D model and real 3D proteins, we calibrated the parameters taken from the literature to yield unfolding/folding rates that are meaningful in the context of the other rates in our model: folding is much faster than growth and for any of the sequence in our pool (100, 101) for 3D proteins. Because the literature models are only mean field, averaged over sequences, and to retain sequence dependence here, we set the unfolding rate of all sequences to the average for their lengths and assigned all of the sequence dependence to . Therefore, we used
[S7] -
•
The model is not sensitive to varying these parameters over a wide range. We use kT, and therefore, , which leads to a range of unfolding rates from one unfolding per hour to one unfolding per day. Folding rates vary from a reaction per hour to a reaction per fraction of a second.
-
•The catalytic step is (only monomers can be added to the sequences catalytically)
[S8] -
•
The rate enhancement is , where hydrophobic sticking energy is , and the number of contacting hydrophobes is , which varies in the range from three to six. With the hydrophobic energies of kT, this gives catalysis rates around hours to days per reaction. Because the EPDM supports only binary reactions, we divided the reaction above into two steps: interaction of catalyst with a monomer with rate and the reaction of this complex with a polymer that has the rate .
For each trajectory, we collected statistics only after the system reached an unchanging steady state. To explore the stochasticity, we repeated every simulation for 30 times for every experiment. We ran all of the simulations for of internal simulation time, during which individual reactions had occurred. We took measurements every For all of the trajectories, steady-state behavior was reached no longer than after the start of a simulation. Thus, we considered only the last (1 million recordings) for each simulation. All of the data points that we used in the figures are averages over these recordings.
For all of the experiments below, we used the following parameters:
-
i)
.
-
ii)
.
-
iii)
.
-
iv)
.
Values of are problematic, having numbers of sequences or populations either too high to calculate or too low to draw conclusions.
-
i)
.
When , hydrolysis dominates, and without catalysis, there is an explosion of short sequences.
When , hydrolysis is unphysically small, and therefore, nothing limits the growth of longer sequences, even in the absence of catalysis.
When , the forces of dilution and hydrolysis are relatively balanced, and populations are neither too small nor too large.
In Silico Experiments.
The simulations were performed on the Laufer Center’s computing cluster of central processing units. We performed the following computational experiments:
Experiment 1: Does our bare polymerization reproduce the Flory distribution?
We started simulations with a small pool of chains up to 3-mers. To calculate the length distributions, we calculated for each trajectory the average population of every sequence over time over all recordings after 40 s, resulting in 1 million time steps. Then, we summed all of the populations of a given length, obtained total populations for all -mers , and then, computed every population as
| [S9] |
giving probability of finding an -mer of a randomly chosen molecule in the system.
Experiment 2: What is the effect on the distribution of just HP folding?
We started with the same initial population as in experiment 1. However, now, we introduce the hydrophobic energy . To calculate the result in length distribution, we computed the average population of every sequence for each trajectory over time over all of the recordings after 40 s, resulting in 1 million time steps.
Experiment 3: What is the effect on the distribution of both folding and catalysis?
In addition to folding in this in silico experiment, we also accounted for the pairwise contact interactions between two proteins, with the parameters as indicated above. We explored ranges of parameters. We observed significant stability of the length distribution toward change of and in the range . The distributions that we observe are quite sensitive to the choice of hydrophobic energy, as expected for chemical reactions, since this enters into the exponent of the rate expression. In the generally physical range of , we observe a bending of the Flory distribution, as noted in the text.
Acknowledgments
We thank Nick Hud, Li Guo, Adam de Graff, Sam Gellman, Andrew Pohorille, and Miha Lukšic for their insights and Anton Bernatskiy for fruitful discussions and help with software. We received support from the Laufer Center and National Science Foundation Grant MCB1344230. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under Contract DE-AC02-05CH11231.
Footnotes
The authors declare no conflict of interest.
*In principle, we could also specifically exclude sequences that are too hydrophobic on the grounds that they would aggregate and exit the system. However, in practice, those highly hydrophobic sequences do not contribute anyway, because they do not fold uniquely. Therefore, we do not treat that process explicitly to keep the model simple.
*A Python implementation and description can be found at hp-lattice.readthedocs.org/en/latest/.
†The hydrolysis rate constants of oligopeptides in neutral conditions are of the order of : for benzoylglycylphenylalanine () (98), () for glycylglycine, and for glycylvaline (99).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1620179114/-/DCSupplemental.
References
- 1.Joyce G. Nonenzymatic template-directed synthesis of informational macromolecules. Cold Spring Harb Symp Quant Biol. 1987;52:41–51. doi: 10.1101/sqb.1987.052.01.008. [DOI] [PubMed] [Google Scholar]
- 2.Abel DL, Trevors JT. Three subsets of sequence complexity and their relevance to biopolymeric information. Theor Biol Med Model. 2005;2:29. doi: 10.1186/1742-4682-2-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eigen M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- 4.Eigen M, Schuster P. A principle of natural self-organization. Naturwissenschaften. 1977;64:541–565. doi: 10.1007/BF00450633. [DOI] [PubMed] [Google Scholar]
- 5.Eigen M, Schuster P. The hypercycle. Naturwissenschaften. 1978;65:7–41. doi: 10.1007/BF00450633. [DOI] [PubMed] [Google Scholar]
- 6.Dyson F. Origins of Life. Cambridge Univ Press; Cambridge, UK: 1985. [Google Scholar]
- 7.Prigogine I, Nicolis G. Exploring Complexity. St. Martin's Press; New York: 1989. [Google Scholar]
- 8.Kauffman SA. Autocatalytic sets of proteins. J Theor Biol. 1986;119:1–24. doi: 10.1016/s0022-5193(86)80047-9. [DOI] [PubMed] [Google Scholar]
- 9.Segré D, Lancet D, Kedem O, Pilpel Y. Graded autocatalysis replication domain (GARD): Kinetic analysis of self-replication in mutually catalytic sets. Orig Life Evol Biosph. 1998;28:501–514. [PubMed] [Google Scholar]
- 10.Segré D, Ben-Eli D, Lancet D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc Natl Acad Sci USA. 2000;97:4112–4117. doi: 10.1073/pnas.97.8.4112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Markovitch O, Lancet D. Excess mutual catalysis is required for effective evolvability. Artif Life. 2012;18:243–66. doi: 10.1162/artl_a_00064. [DOI] [PubMed] [Google Scholar]
- 12.Wu M, Higgs PG. Origin of self-replicating biopolymers: Autocatalytic feedback can jump-start the RNA world. J Mol Evol. 2009;69:541–54. doi: 10.1007/s00239-009-9276-8. [DOI] [PubMed] [Google Scholar]
- 13.Tkachenko AV, Maslov S. Onset of autocatalysis of information-coding polymers 2014 [Google Scholar]
- 14.Lee DH, Granja JR, Martinez JA, Severin K, Ghadri MR. A self-replicating peptide. Nature. 1996;382:525–528. doi: 10.1038/382525a0. [DOI] [PubMed] [Google Scholar]
- 15.Rubinov B, Wagner N, Rapaport H, Ashkenasy G. Self-replicating amphiphilic -sheet peptides. Angew Chem Int Ed Engl. 2009;48:6683–6686. doi: 10.1002/anie.200902790. [DOI] [PubMed] [Google Scholar]
- 16.Nowak MA, Ohtsuki H. Prevolutionary dynamics and the origin of evolution. Proc Natl Acad Sci USA. 2008;105:14924–14927. doi: 10.1073/pnas.0806714105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ohtsuki H, Nowak MA. Prelife catalysts and replicators. Proc Biol Sci. 2009;276:3783–3790. doi: 10.1098/rspb.2009.1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen IA, Nowak MA. From prelife to life: How chemical kinetics become evolutionary dynamics. Acc Chem Res. 2012;45:2088–2096. doi: 10.1021/ar2002683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Derr J, et al. Prebiotically plausible mechanisms increase compositional diversity of nucleic acid sequences. Nucleic Acids Res. 2012;40:4711–4722. doi: 10.1093/nar/gks065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walker SI, Grover MA, Hud NV. Universal sequence replication, reversible polymerization and early functional biopolymers: A model for the initiation of prebiotic sequence evolution. PLoS One. 2012;7:e34166. doi: 10.1371/journal.pone.0034166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.von Kiedrowski G. A self-replicating hexadeoxynucleotide. Angew Chem Int Ed Engl. 1986;25:932–935. [Google Scholar]
- 22.Lincoln TA, Joyce GF. Self-sustained replication of an RNA enzyme. Science. 2009;323:1229–1232. doi: 10.1126/science.1167856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vaidya N, et al. Spontaneous network formation among cooperative RNA replicators. Nature. 2012;491:72–77. doi: 10.1038/nature11549. [DOI] [PubMed] [Google Scholar]
- 24.Robertson MP, Joyce GF. Highly efficient self-replicating RNA enzymes. Chem Biol. 2014;21:238–245. doi: 10.1016/j.chembiol.2013.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Szostak JW, Ellington AD. In Vitro Selection of Functional Nucleic Acids in the RNA World. Cold Spring Harbor Lab Press; Plainview, NY: 1993. pp. 511–533. [Google Scholar]
- 26.Shock EL. Stability of peptides in high-temperature aqueous solutions. Geochim Cosmochim Acta. 1992;56:3481–3491. [Google Scholar]
- 27.Martin RB. Free energies and equilibria of peptide bond hydrolysis. Biopolymers. 1998;45:351–353. [Google Scholar]
- 28.Paecht-Horowitz M, Berger J, Katchalsky A. Prebiotic synthesis of polypeptides by heterogeneous polycondensation of amino-acid adenylates. Nature. 1970;228:636–639. doi: 10.1038/228636a0. [DOI] [PubMed] [Google Scholar]
- 29.Leman L, Orgel LE, Ghadiri MR. Carbonyl sulfide-mediated prebiotic formation of peptides. Science. 2004;306:283–286. doi: 10.1126/science.1102722. [DOI] [PubMed] [Google Scholar]
- 30.Orgel LE. Prebiotic chemistry and the origin of the RNA world. Crit Rev Biochem Mol Biol. 2004;39:99–123. doi: 10.1080/10409230490460765. [DOI] [PubMed] [Google Scholar]
- 31.Rao M, Odom DG, Oró J. Clays in prebiological chemistry. J Mol Evol. 1980;15:317–331. doi: 10.1007/BF01733138. [DOI] [PubMed] [Google Scholar]
- 32.Lambert JF. Adsorption and polymerization of amino acids on mineral surfaces: A review. Orig Life Evol Biosph. 2008;38:211–242. doi: 10.1007/s11084-008-9128-3. [DOI] [PubMed] [Google Scholar]
- 33.Bernal JD. The physical basis of life. Proc Phys Soc B. 1949;62:597–618. [Google Scholar]
- 34.Ferris JP, Hill AR, Liu R, Orgel LE. Synthesis of long prebiotic oligomers on mineral surfaces. Nature. 1996;381:59–61. doi: 10.1038/381059a0. [DOI] [PubMed] [Google Scholar]
- 35.Nelson KE, Robertson MP, Levy M, Miller SL. Concentration by evaporation and the prebiotic synthesis of cytosine. Orig Life Evol Biosph. 2001;31:221–229. doi: 10.1023/a:1010652418557. [DOI] [PubMed] [Google Scholar]
- 36.Kanavarioti A, Monnard PA, Deamer DW. Eutectic phases in ice facilitate nonenzymatic nucleic acid synthesis. Astrobiology. 2001;1:271–281. doi: 10.1089/15311070152757465. [DOI] [PubMed] [Google Scholar]
- 37.Bada JL. How life began on earth: A status report. Earth Planet Sci Lett. 2004;226:1–15. [Google Scholar]
- 38.Forsythe JG, et al. Ester-mediated amide bond formation driven by wet-dry cycles: A possible path to polypeptides on the prebiotic earth. Angew Chem Int Ed Engl. 2015;54:9871–9875. doi: 10.1002/anie.201503792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rode BM, Son HL, Suwannachot Y, Bujdak J. The combination of salt induced peptide formation reaction and clay catalysis: A way to higher peptides under primitive earth conditions. Orig Life Evol Biosph. 1999;29:273–286. doi: 10.1023/a:1006540101290. [DOI] [PubMed] [Google Scholar]
- 40.Rode BM. Peptides and the origin of life. Peptides. 1999;20:773–786. doi: 10.1016/s0196-9781(99)00062-5. [DOI] [PubMed] [Google Scholar]
- 41.Flory PJ. Principles of Polymer Chemistry. Cornell Univ Press; Ithaca, NY: 1953. p. 688. [Google Scholar]
- 42.Stribling R, Miller SL. Energy yields for hydrogen cyanide and formaldehyde syntheses: The HCN and amino acid concentrations in the primitive ocean. Orig Life Evol Biosph. 1987;17:261–273. doi: 10.1007/BF02386466. [DOI] [PubMed] [Google Scholar]
- 43.Huber C, Wächtershäuser G. Peptides by activation of amino acids with CO on (Ni,Fe)S surfaces: Implications for the origin of life. Science. 1998;281:670–672. doi: 10.1126/science.281.5377.670. [DOI] [PubMed] [Google Scholar]
- 44.Aubrey AD, Cleaves HJ, Bada JL. The role of submarine hydrothermal systems in the synthesis of amino acids. Orig Life Evol Biosph. 2009;39:91–108. doi: 10.1007/s11084-008-9153-2. [DOI] [PubMed] [Google Scholar]
- 45.Lazcano A, Miller SL. The origin and early evolution of life: Prebiotic chemistry, the pre-RNA world, and time. Cell. 1996;85:793–798. doi: 10.1016/s0092-8674(00)81263-5. [DOI] [PubMed] [Google Scholar]
- 46.Ding PZ, Kawamura K, Ferris JP. Oligomerization of uridine phosphorimidazolides on montmorillonite: A model for the prebiotic synthesis of RNA on minerals. Orig Life Evol Biosph. 1996;26:151–171. doi: 10.1007/BF01809853. [DOI] [PubMed] [Google Scholar]
- 47.Ferris JP. Prebiotic synthesis on minerals: Bridging the prebiotic and RNA worlds. Biol Bull. 1999;196:311–314. doi: 10.2307/1542957. [DOI] [PubMed] [Google Scholar]
- 48.Gellman SH. Foldamers: A manifesto. Acc Chem Res. 1998;31:173–180. [Google Scholar]
- 49.Lee BC, Zuckermann RN, Dill KA. Folding a nonbiological polymer into a compact multihelical structure. J Am Chem Soc. 2005;127:10999–11009. doi: 10.1021/ja0514904. [DOI] [PubMed] [Google Scholar]
- 50.Capriotti E, Marti-Renom MA. RNA structure alignment by a unit-vector approach. Bioinformatics. 2008;24:i112–i118. doi: 10.1093/bioinformatics/btn288. [DOI] [PubMed] [Google Scholar]
- 51.Chan HS, Dill KA. “Sequence space soup” of proteins and copolymers. J Chem Phys. 1991;95:3775–3787. [Google Scholar]
- 52.Ma Fisher, McKinley KL, Bradley LH, Viola SR, Hecht MH. De novo designed proteins from a library of artificial sequences function in Escherichia Coli and enable cell growth. PLoS One. 2011;6:e15364. doi: 10.1371/journal.pone.0015364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cherny I, Korolev M, Koehler AN, Hecht MH. Proteins from an unevolved library of de novo designed sequences bind a range of small molecules. ACS Synth Biol. 2012;1:130–138. doi: 10.1021/sb200018e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hilvert D. Design of protein catalysts. Annu Rev Biochem. 2013;82:447–470. doi: 10.1146/annurev-biochem-072611-101825. [DOI] [PubMed] [Google Scholar]
- 55.Giuliano MW, Miller SJ. Site-selective reactions with peptide-based catalysts. Top Curr Chem. 2016;372:157–201. doi: 10.1007/128_2015_653. [DOI] [PubMed] [Google Scholar]
- 56.Duschmalé J, Kohrt S, Wennemers H. Peptide catalysis in aqueous emulsions. Chem Commun (Camb) 2014;50:8109–8112. doi: 10.1039/c4cc01759e. [DOI] [PubMed] [Google Scholar]
- 57.Rozinov MN, Nolan GP. Evolution of peptides that modulate the spectral qualities of bound, small-molecule fluorophores. Chem Biol. 1998;5:713–28. doi: 10.1016/s1074-5521(98)90664-0. [DOI] [PubMed] [Google Scholar]
- 58.Rodi DJ, et al. Screening of a library of phage-displayed peptides identifies human bcl-2 as a taxol-binding protein. J Mol Biol. 1999;285:197–203. doi: 10.1006/jmbi.1998.2303. [DOI] [PubMed] [Google Scholar]
- 59.Adamala K, Szostak JW. Competition between model protocells driven by an encapsulated catalyst. Nat Chem. 2013;5:495–501. doi: 10.1038/nchem.1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lau KF, Dill KA. A lattice statistical mechanics model of the conformational and sequence spaces of proteins. Macromolecules. 1989;22:3986–3997. [Google Scholar]
- 61.Miller DW, Dill KA. A statistical mechanical model for hydrogen exchange in globular proteins. Protein Sci. 1995;4:1860–1873. doi: 10.1002/pro.5560040921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Yue K, Dill KA. Forces of tertiary structural organization in globular proteins. Proc Natl Acad Sci USA. 1995;92:146–150. doi: 10.1073/pnas.92.1.146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Agarwala R, et al. Local rules for protein folding on a Triangular lattice and Generalized hydrophobicity in the HP model. J Comput Biol. 1997;4:275–296. doi: 10.1089/cmb.1997.4.275. [DOI] [PubMed] [Google Scholar]
- 64.Bornberg-Bauer E, Chan HS. Modeling evolutionary landscapes: Mutational stability, topology, and superfunnels in sequence space. Proc Natl Acad Sci USA. 1999;96:10689–10694. doi: 10.1073/pnas.96.19.10689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Irbäck A, Sandelin E. On hydrophobicity correlations in protein chains. Biophys J. 2000;79:2252–2258. doi: 10.1016/S0006-3495(00)76472-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Irbäck A, Troein C. Enumerating designing sequences in the HP model. J Biol Phys. 2002;28:1–15. doi: 10.1023/A:1016225010659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Cui Y, Wong WH, Bornberg-Bauer E, Chan HS. Recombinatoric exploration of novel folded structures: A heteropolymer-based model of protein evolutionary landscapes. Proc Natl Acad Sci USA. 2002;99:809–814. doi: 10.1073/pnas.022240299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Moreno-Hernández S, Levitt M. Comparative modeling and protein-like features of hydrophobic-polar models on a two-dimensional lattice. Proteins. 2012;80:1683–1693. doi: 10.1002/prot.24067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sikosek T, Chan HS, Bornberg-Bauer E. Escape from adaptive conflict follows from weak functional trade-offs and mutational robustness. Proc Natl Acad Sci USA. 2012;109:14888–14893. doi: 10.1073/pnas.1115620109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sikosek T, Chan HS. Biophysics of protein evolution and evolutionary protein biophysics. J R Soc Interface. 2014;11:20140419. doi: 10.1098/rsif.2014.0419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Yue K, Dill Ka. Inverse protein folding problem: Designing polymer sequences. Proc Natl Acad Sci USA. 1992;89:4163–4167. doi: 10.1073/pnas.89.9.4163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Xiong H, Buckwalter BL, Shieh HM, Hecht MH. Periodicity of polar and nonpolar amino acids is the major determinant of secondary structure in self-assembling oligomeric peptides. Proc Natl Acad Sci USA. 1995;92:6349–6353. doi: 10.1073/pnas.92.14.6349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lipman DJ, Wilbur WJ. Modelling neutral and selective evolution of protein folding. Proc R Soc B. 1991;245:7–11. doi: 10.1098/rspb.1991.0081. [DOI] [PubMed] [Google Scholar]
- 74.Lim WA, Sauer RT. The role of internal packing interactions in determining the structure and stability of a protein. J Mol Biol. 1991;219:359–376. doi: 10.1016/0022-2836(91)90570-v. [DOI] [PubMed] [Google Scholar]
- 75.Kamtekar S, Schiffer JM, Xiong H, Babik JM, Hecht MH. Protein design by binary patterning of polar and nonpolar amino acids. Science. 1993;262:1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
- 76.Wei Y. Stably folded de novo proteins from a designed combinatorial library. Protein Sci. 2003;12:92–102. doi: 10.1110/ps.0228003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Brisendine JM, Koder RL. Fast, cheap and out of control – insights into thermodynamic and informatic constraints on natural protein sequences from de novo protein design. Biochim Biophys Acta. 2016;1857:485–492. doi: 10.1016/j.bbabio.2015.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lijnzaad P, Berendsen HJC, Argos P. Hydrophobic patches on the surfaces of protein structures. Proteins. 1996;25:389–397. doi: 10.1002/(SICI)1097-0134(199607)25:3<389::AID-PROT10>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 79.Tonddast-Navaei S, Skolnick J. Are protein-protein interfaces special regions on a protein’s surface? J Chem Phys. 2015;143:243149. doi: 10.1063/1.4937428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Mitchell Guss J, Freeman HC. Structure of oxidized poplar plastocyanin at 1·6 Å resolution. J Mol Biol. 1983;169:521–563. doi: 10.1016/s0022-2836(83)80064-3. [DOI] [PubMed] [Google Scholar]
- 81.van Ee JH, Onno M. In: Enzymes in Detergency. van Ee JH, editor. CRC; Boca Raton, FL: 1997. p. 408. [Google Scholar]
- 82.Witt H. Tryptophan 121 of subunit II is the electron entry site to cytochrome-c oxidase in paracoccus denitrificans. Involvement of a hydrophobic patch in the docking reaction. J Biol Chem. 1998;273:5132–5136. doi: 10.1074/jbc.273.9.5132. [DOI] [PubMed] [Google Scholar]
- 83.Nelson DL, Cox MM. Lehninger Principles of Biochemistry. 5th Ed Freeman; New York: 2008. [Google Scholar]
- 84.Manabe K, Sun XM, Kobayashi S. Dehydration reactions in water. Surfactant-type brønsted acid-catalyzed direct esterification of carboxylic acids with alcohols in an emulsion system. J Am Chem Soc. 2001;123:10101–10102. doi: 10.1021/ja016338q. [DOI] [PubMed] [Google Scholar]
- 85.Manabe K, Iimura S, Sun XM, Kobayashi S. Dehydration reactions in water. Brønsted acid-surfactant-combined catalyst for ester, ether, thioether, and dithioacetal formation in water. J Am Chem Soc. 2002;124:11971–11978. doi: 10.1021/ja026241j. [DOI] [PubMed] [Google Scholar]
- 86.Stachelhaus T, Mootz HD, Bergendahl V, Marahiel MA. Peptide bond formation in nonribosomal peptide Biosynthesis. J Biol Chem. 1998;273:22773–22781. doi: 10.1074/jbc.273.35.22773. [DOI] [PubMed] [Google Scholar]
- 87.Marahiel MA. Working outside the protein-synthesis rules: Insights into non-ribosomal peptide synthesis. J Pept Sci. 2009;15:799–807. doi: 10.1002/psc.1183. [DOI] [PubMed] [Google Scholar]
- 88.Dill KA. Polymer principles and protein folding. Protein Sci. 1999;8:1166–1180. doi: 10.1110/ps.8.6.1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Giugliarelli G, Micheletti C, Banavar JR, Maritan A. Compactness, aggregation, and prionlike behavior of protein: A lattice model study. J Chem Phys. 2000;113:5072–5077. [Google Scholar]
- 90.Ghosh K, Dill KA. Computing protein stabilities from their chain lengths. Proc Natl Acad Sci USA. 2009;106:10649–10654. doi: 10.1073/pnas.0903995106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Sievers A, Beringer M, Rodnina MV, Wolfenden R. The ribosome as an entropy trap. Proc Natl Acad Sci USA. 2004;101:7897–7901. doi: 10.1073/pnas.0402488101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Bernatskiy AV, Guseva EA. 2016. Exact rule-based stochastic simulations for the system with unlimited number of molecular species. arXiv:1609.06403v2.
- 93.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. 1976;22:403–434. [Google Scholar]
- 94.Abkevich VI, Gutin AM, Shakhnovich EI. How the first biopolymers could have evolved. Proc Natl Acad Sci USA. 1996;93:839–844. doi: 10.1073/pnas.93.2.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Vasas V, et al. Primordial evolvability: Impasses and challenges. J Theor Biol. 2015;381:29–38. doi: 10.1016/j.jtbi.2015.06.047. [DOI] [PubMed] [Google Scholar]
- 96.Murphy GS, Greisman JB, Hecht MH. De novo proteins with life-sustaining functions are structurally dynamic. J Mol Biol. 2015;428:399–411. doi: 10.1016/j.jmb.2015.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Dill KA, et al. Principles of protein folding - a perspective from simple exact models. Protein Sci. 2008;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Bryant RAR, Hansen DE. Direct measurement of the uncatalyzed rate of hydrolysis of a peptide bond. J Am Chem Soc. 1996;118:5498–5499. [Google Scholar]
- 99.Smith RM, Hansen DE. The pH-rate profile for the hydrolysis of a peptide bond. J Am Chem Soc. 1998;120:8910–8913. [Google Scholar]
- 100.Ghosh K, Dill KA. Cellular proteomes have broad distributions of protein stability. Biophys J. 2010;99:3996–4002. doi: 10.1016/j.bpj.2010.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Dill KA, Ghosh K, Schmit JD. Physical limits of cells and proteomes. Proc Natl Acad Sci USA. 2011;108:17876–17882. doi: 10.1073/pnas.1114477108. [DOI] [PMC free article] [PubMed] [Google Scholar]