Significance
When a person is at wakeful rest, not paying particular attention to the environment, his/her brain activity will not drift into random noise. Instead, it maintains robust dynamical structures to support ongoing cognition. Previous studies on the resting state have focused on either connectivity features across brain regions or local activity features within regions. Here, we show that the interactions between regions are dynamic and covary with local activity. This covariation provides insights into the neural underpinnings of ongoing cognition that is driven by the brain’s intrinsic network interactions.
Keywords: default-mode network, resting state, fMRI, MEG, functional connectivity
Abstract
Segregation and integration are distinctive features of large-scale brain activity. Although neuroimaging studies have been unraveling their neural correlates, how integration takes place over segregated modules remains elusive. Central to this problem is the mechanism by which a brain region adjusts its activity according to the influence it receives from other regions. In this study, we explore how dynamic connectivity between two regions affects the neural activity within a participating region. Combining functional magnetic resonance imaging (fMRI) and magnetoencephalography (MEG) in the same group of subjects, we analyzed resting-state data from the core of the default-mode network. We observed directed influence from the posterior cingulate cortex (PCC) to the anterior cingulate cortex (ACC) in the 10-Hz range. This time-varying influence was associated with the power alteration in the ACC: strong influence corresponded with a decrease of power around 13–16 Hz and an increase of power in the lower (1–7 Hz) and higher (30–55 Hz) ends of the spectrum. We also found that the amplitude of the 30- to 55-Hz activity was coupled to the phase of the 3- to 4-Hz activity in the ACC. These results characterized the local spectral changes associated with network interactions. The specific spectral information both highlights the functional roles of PCC–ACC connectivity in the resting state and provides insights into the dynamic relationship between local activity and coupling dynamics of a network.
A fundamental feature of large-scale human brain activity is concurrent segregation and integration (1–4). Different brain regions can be activated by subcomponents of a cognitive process, forming distributed neural representations. These segregated regions interact with each other through network connectivity, leading to an integrated outcome that determines behavior. This dual feature sets two major paradigms in cognitive neuroimaging (3, 5–8): one investigates the localized activity that represents cognitive subprocesses; the other investigates the cross-regional coupling that reflects integration across functional modules.
While the neuroimaging field advances on both topics, gaps remain between findings. The biological basis of the integration across segregated modules remains poorly understood. Central to this question is the mechanism by which one region adjusts its local activity under the influence of other regions, a necessary step for the network to reach a downstream output. However, existing literature has focused on either localized activity or cross-region connectivity, but rarely the relationship between the two.
The difficulty lies in studying connectivity and local activity at the same time. Such an approach would require data with high spatial and temporal resolution, which is difficult to achieve with current imaging techniques (5, 9, 10). Recently, many in the field have attempted to bridge these gaps. One approach is to put sliding windows on functional magnetic resonance imaging (fMRI) data, adding temporal information to the spatial patterns of connectivity (for a review of the methods, see, for example, ref. 11, but also see ref. 12). Another approach is to compare magnetoencephalography (MEG)-based connectivity with those measured from fMRI, verifying the identities of dynamically interacting regions (10, 13–17). These new methods retrieve the spatial and temporal information of a network, making it possible to study correspondent changes in both connectivity and local activity.
Here, we investigate the relationship between cross-region connectivity and within-region activity in the default-mode network (DMN). We chose the DMN for two reasons. First, the DMN is known to activate in the resting state (18, 19), and resting state avoids the mixture of network- and stimulus-driven activity. Second and most important, the DMN is an excellent candidate for studying ongoing cognition (19, 20). Its resting-state activity is closely associated with higher functions such as autobiographic memory and self-referential thoughts. Therefore, the biological meaning of the activity–connectivity association in the DMN is within the context of cognitive processing, regardless of the absence of a task.
We recorded fMRI and MEG data in the same group of subjects and focused the analysis on two core regions of the DMN (19, 20): the anterior and the posterior cingulate cortex (ACC and PCC, respectively). We quantified short-time Granger causality (GC) between the ACC and PCC in the MEG source space under the guidance of fMRI. This dynamic measure allowed us to examine within-region spectral changes of neural activity, and at the same time, how they correspond to the change of cross-region connectivity.
The results characterized how interactions between brain regions affect the within-region activity in a real-time manner. In particular, we found that the influence from the PCC in one frequency band was associated with local spectral changes in the ACC in multiple frequency bands. Moreover, the local frequency bands held a phase–amplitude relationship that reveals the possible functional consequence of the PCC–ACC interactions.
Results
We first verified that GC reliably captured the ACC–PCC connectivity in the MEG source space. The procedure consisted of two steps: (i) we used functional-connectivity MRI (fcMRI) as a guide to locate the MEG frequency range that contributed the most to the ACC–PCC connectivity; (ii) we used that frequency range to compute seed-based GC maps, which independently replicated the connectivity pattern between the ACC and PCC.
Next, we investigated whether the temporal change of GC was associated with a local power alteration of the MEG source signal. We compared the power spectral density (PSD) between the time periods when GC to a region was strong and when GC was weak. For the frequency components of the source signal that showed a PSD difference, we also tested for cross-frequency coupling to see whether the modulated activity carried functionally meaningful structures.
The 10-Hz Neural Activity as a Major Contributor to the fMRI-Based Connectivity.
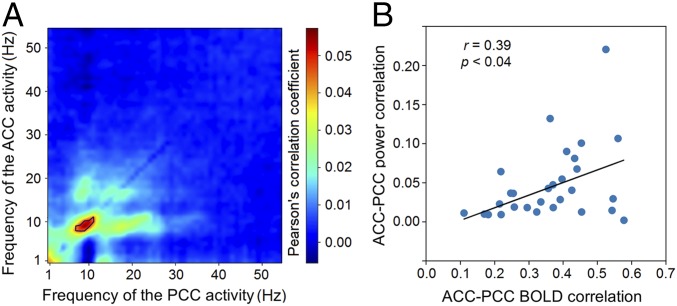
We computed the temporal correlations of power between MEG sources in the ACC and PCC as a measure of overall MEG connectivity across time. The source signals were first orthogonalized to remove spurious zero-lag correlation caused by crosstalk (refs. 10 and 15, and Materials and Methods). Narrow-band power envelopes were then extracted from the ACC and PCC sources to compute cross-region correlations for different frequency combinations between 1 and 56 Hz. The strongest correlation was found with the 10-Hz power envelopes (Fig. 1A), which survived the permutation test (Materials and Methods).
Fig. 1.
MEG connectivity around 10 Hz is associated with fMRI-based connectivity. (A) Heatmap of the temporal correlation between the leakage-corrected power envelopes of MEG sources in the ACC and PCC. Color represents the mean Pearson’s r scores across subjects at each frequency pair. The black line marks significant r scores within the contour that passed the permutation test. (B) Scatter plot of the MEG connectivity around 10 Hz against the fcMRI. Each dot represents a subject, and the regression line is shown in black.
We also computed fcMRI between the ACC and PCC using the blood oxygenation level-dependent (BOLD) signal. The 10-Hz power envelope connectivity and fMRI connectivity showed a significant cross-subject correlation (Pearson’s r = 0.39, P < 0.04, Fig. 1B), suggesting that individuals with stronger fcMRI also have stronger MEG connectivity at 10 Hz. Thus, we consider the 10-Hz-range neural activity to be a major contributor to the functional connectivity between the ACC and PCC.
Spatially Specific GC Between the ACC and PCC in the Seed-Based Maps.
Since the highest cross-subject correlation was found with activity near 10 Hz, we computed GC in the 10-Hz range for each interheartbeat time segment, as a sliding-window type of measurement for the dynamic MEG connectivity. Before testing the association between connectivity and local activity, we checked the spatial specificity of the GC measurement. This step was both to verify that GC effectively captured the connectivity, and to rule out a potential bias due to preselection of the ACC and PCC regions in the previous analysis. To do so, we used seed-based maps: when one region was set as seed, the GC measurement should show large clustered values around the other region and random small values in the rest of the cortex.
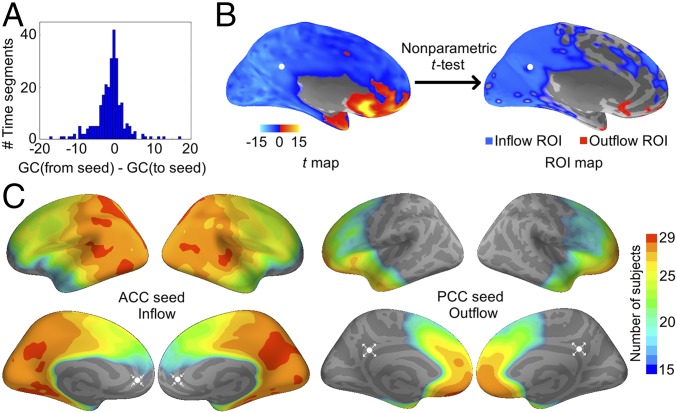
Due to technical concerns (Discussion), we used the difference score between the from-seed and to-seed GC (Fig. 2A) instead of the raw GC value. Positive scores were marked as “outflow” and negative scores “inflow.” A nonparametric cluster-level test was performed across time segments to determine the significance of GC-flow at each vertex (Materials and Methods). Significant vertices were marked as regions of interest (ROIs), representing regions of large GC-flow values (Fig. 2B). ROIs were first drawn in each subject and then overlaid across subjects to derive a group-level estimation (Fig. 2C). For the inflow to the ACC seed, the PCC appeared to be an ROI that sent out GC influence in all 29 subjects. For the outflow from the PCC seed, the ACC appeared to be an ROI that received GC influence in 28 subjects. We did not find a PCC ROI in the ACC outflow map or an ACC ROI in the PCC inflow map (Figs. S1 and S2). The results consistently showed that the GC influence was specifically directed from the PCC to the ACC.
Fig. 2.
Seed-based maps of GC-flow in the 10-Hz range. (A) Histogram from one subject as an example of the GC-flow between the seed and an arbitrary vertex over the interheartbeat time segments. The mean centered at zero, indicating no GC-flow in either direction. (B) Example from one subject illustrating the significance test for the GC-flow of a PCC seed. Positive t scores indicate outflow, and negative t scores, inflow. (C) Group-level estimation of the significant inflow to the ACC (Left) and outflow from the PCC (Right). Cross-subject conjunction scores are shown in color. Scores below 15 (i.e., consistency of less than one-half of the subjects) are not displayed. White dots indicate the seed locations, and arrows, the flow direction.
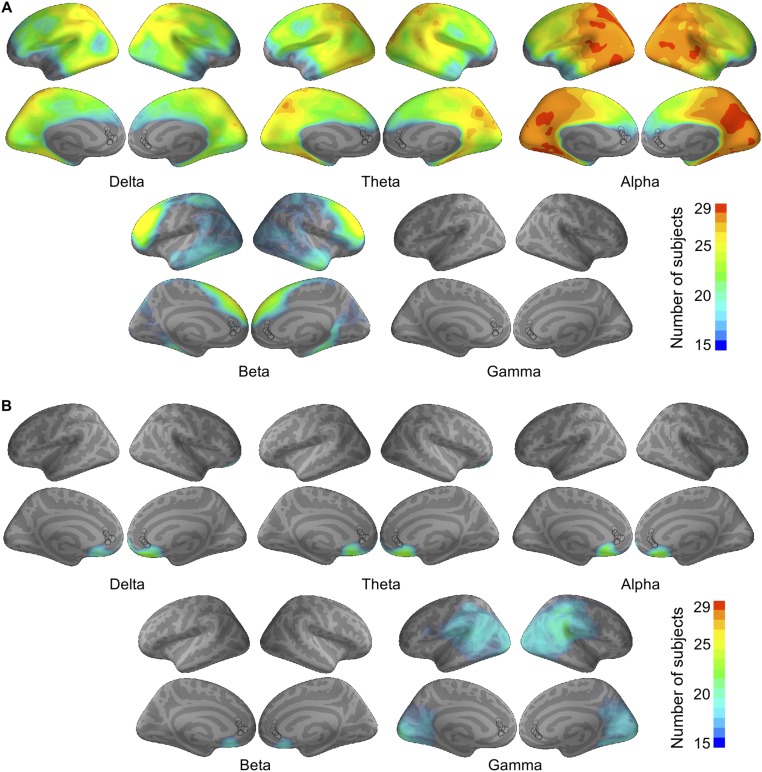
Fig. S1.
Overlay of significant (A) inflow and (B) outflow ROIs in all of the subjects with ACC seeds, shown separately for each frequency. Black circles label the locations of the five sampled seeds, across which the results were averaged.
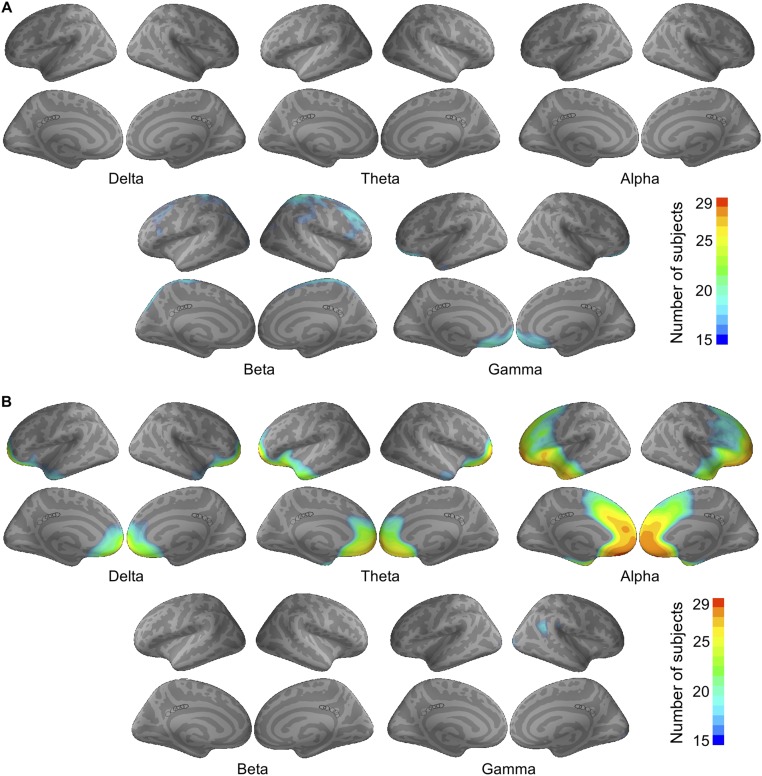
Fig. S2.
Overlay of significant (A) inflow and (B) outflow ROIs in all of the subjects with PCC seeds, shown separately for each frequency. Black circles label the locations of the five sampled seeds, across which the results were averaged.
GC-Associated Power Spectral Changes Within the ACC.
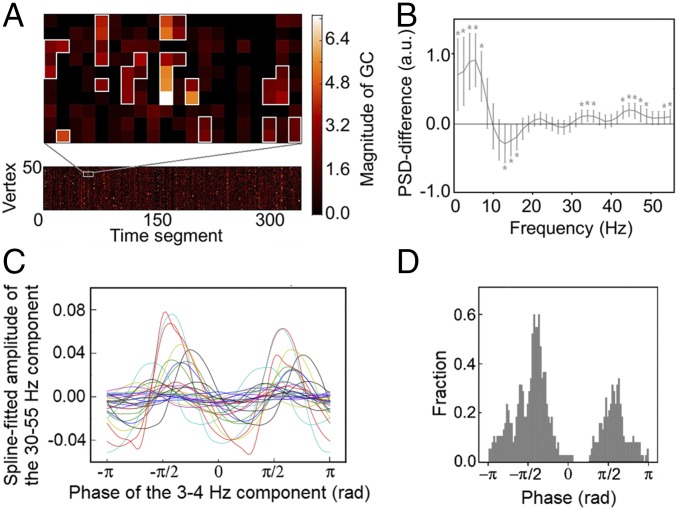
The seed-based GC maps not only verified the spatial specificity of the ACC–PCC interactions but also suggested directional asymmetry. Since stronger GC was directed from the PCC to the ACC than vice versa, we examined how local activity in the ACC changes according to GC influence from the PCC. Specifically, we measured the intensity of PSD in the ACC under different GC strengths. GC and PSD were estimated at each vertex of the ACC for each interheartbeat time segment (Fig. 3A). We grouped the vertices and time segments into spatiotemporal clusters according to their GC values (Materials and Methods). A cluster represented a spatiotemporal pattern that was stable in time (>20 s) and/or robust in space (>20 adjacent vertices). Depending on whether the data segment of a vertex belonged to a GC cluster, the power spectrum was marked as inside or outside cluster.
Fig. 3.
Systematic local activity changes associated with the 10-Hz GC fluctuation. (A) Example from one subject showing the spatiotemporal GC clusters within the ACC. The lower plot shows the alpha-band GC from the PCC to each vertex in the ACC across time segments. The plot above is a magnified view showing the spatiotemporal clusters from the chosen part of the lower plot. The vertices are arranged such that those in the clusters are spatially consecutive in the cortical surface. (B) Power difference of the activity inside and outside the clusters, shown as mean ± SEM across subjects. Asterisks denote the significant deviation from zero (*P < 0.05, Bonferroni corrected for 37 comparisons; Table S1). (C) Spline-fitted gamma amplitude over the 3- to 4-Hz phase in the ACC showing peaks around ±π/2. Each line represents one subject. (D) Histogram of the phase angles whose corresponding gamma amplitudes ranked in the top 5%. All subjects were pooled together. The count was standardized by dividing the total counts.
The data segments inside the clusters showed consistently less power in the 13- to 16-Hz range, but greater power in the lower (1–7 Hz) and higher ends (30–55 Hz) of the spectrum compared with those outside the cluster (Fig. 3B). A complete list of all of the difference scores and their significance can be found in Table S1. These results provided a spectral fingerprint for the relationship between the directed influence from the PCC to the ACC and the power changes within the ACC.
Table S1.
Statistics for the inside-cluster vs. outside-cluster power differences
| Frequency | t | P* |
| 1.48 | 4.42 | 1.32e-3 |
| 2.96 | 4.98 | 2.92e-4 |
| 4.44 | 7.15 | 1.00e-6 |
| 5.93 | 7.77 | 2.15e-7 |
| 7.41 | 6.14 | 1.34e-5 |
| 8.89 | 2.64 | 0.12 |
| 10.37 | −0.33 | 1.00 |
| 11.85 | −2.51 | 0.17 |
| 13.33 | −3.31 | 0.02 |
| 14.81 | −3.43 | 0.02 |
| 16.30 | −3.29 | 0.02 |
| 17.78 | −1.50 | 1.00 |
| 19.26 | 0.02 | 1.00 |
| 20.74 | 2.16 | 0.36 |
| 22.22 | 2.75 | 0.09 |
| 23.70 | 1.12 | 1.00 |
| 25.18 | −0.05 | 1.00 |
| 26.67 | −1.25 | 1.00 |
| 28.15 | −1.49 | 1.00 |
| 29.63 | −0.10 | 1.00 |
| 31.11 | 1.92 | 1.00 |
| 32.59 | 3.70 | 0.01 |
| 34.07 | 4.57 | 0.09e-3 |
| 35.55 | 4.13 | 2.97e-3 |
| 37.04 | 2.62 | 0.13 |
| 38.52 | 1.20 | 1.00 |
| 40.00 | 1.79 | 1.00 |
| 41.48 | 3.36 | 0.02 |
| 42.96 | 5.61 | 0.55e-4 |
| 44.44 | 6.74 | 2.84e-6 |
| 45.92 | 5.50 | 0.75e-4 |
| 47.41 | 4.02 | 3.89e-3 |
| 48.89 | 3.27 | 0.02 |
| 50.37 | 2.90 | 0.07 |
| 51.85 | 2.97 | 0.06 |
| 53.33 | 3.21 | 0.03 |
| 54.81 | 3.41 | 0.02 |
Bonferroni corrected for 37 comparisons.
Finally, we tested whether cross-frequency coupling existed between the lower and higher ends of the spectrum. This idea stemmed from the literature showing that, during particular cognitive processing, the phase of a slow activity component (typically in the theta band) can modulate the amplitude of a fast component (typically in the gamma band) (21, 22). If this pattern existed between the theta and gamma components found in Fig. 3B, it would provide evidence that the spectral fingerprint was not random but carried functional information.
Following the procedure in ref. 23, we found a coupling pattern between the 3- to 4-Hz and the 30- to 55-Hz components of the ACC activity: the estimated gamma amplitude peaked around ±π/2 of the 3- to 4-Hz phase (Fig. 3C). χ2 tests confirmed the significance of this observation (Fig. 3D). Specifically, if there was no coupling, the phase angles corresponding to the top 5% of the gamma amplitudes would distribute evenly over the [−π, π] interval. By contrast, the χ2 test was found significant (χ992 = 141.1, P < 0.01), demonstrating deviation from a uniform distribution (Fig. 3D). No significant coupling was found for the other lower-frequency components in the 1- to 7-Hz band.
Discussion
We investigated the relationship between dynamic connectivity and localized neural activity in the two core regions of the DMN. Combining fcMRI and MEG, we identified spatially specific, directionally asymmetric GC influence from the PCC to the ACC in the 10-Hz range. The time-varying strength of this GC influence was associated with power alterations in the ACC: strong GC corresponded to a decrease of power around 13–16 Hz and an increase of power in the lower (1–7 Hz) and higher (30–55 Hz) ends of the spectrum. There was also significant coupling between the phase of the lower-frequency and the amplitude of the higher-frequency components in the ACC. These findings highlight an approach for studying the integration and segregation of brain activity under a unified framework, shedding light on dynamic cross-region interactions in the DMN.
Functional Connectivity and Local Neural Activity May Be Interdependent.
Functional connectivity between cortical regions and localized activity within regions have been studied in separate bodies of literature (5–8). Here, we show that the two characteristics are interdependent in a real-time manner. It is worth noting that this relationship should not be interpreted as causal. It is possible that network interactions resulted in the local power fluctuation; it is also possible that changes in local dynamics affected the network coupling. The current analysis cannot disambiguate the two cases. Nonetheless, this regional activity–network interaction association may elucidate how functional specialty is preserved within regions that are coupled together.
Functional Connectivity Between PCC and ACC Is Dominated by the 10-Hz Oscillations.
In previous studies, the search for neural correlates of functional connectivity in the DMN has uncovered a wide spectrum of oscillatory components, among which the alpha/low-beta frequency range was the most commonly reported (13–16, 24–27). Here, consistently, we found that the alpha oscillation is the major contributor to ACC–PCC connectivity (Fig. 1). This conclusion is not based solely on the dominant carrier frequency observed in the power correlation but also the cross-subject correlation between fcMRI and the power correlation.
The subsequent results also supported this conclusion. First, the GC analysis demonstrated that there is directed influence from the PCC to the ACC (Fig. 2C) beyond their power cofluctuation. Also, the ACC power–GC association in the theta and gamma bands (Fig. 3B) indicates that not all network-related power fluctuations contribute to the cross-region correlation. While caution must be taken using the power envelope to measure MEG connectivity (27), the cross-validating evidence here suggests that the 10-Hz oscillations are the major contributors to ACC–PCC interactions.
Directional GC Asymmetry Supports the Role of the PCC as a Network Hub.
We have shown that the GC influence from the PCC to the ACC is stronger than that in the opposite direction (Fig. 2). This asymmetry is consistent with the recent finding that the information flow from posterior to anterior brain regions is mainly in the alpha/beta band (28). This asymmetry is also consistent with the role of the PCC as a structural (29) and functional (25) hub in the cortex. Especially in ref. 25, the PCC was found to transiently coordinate the interaction between resting-state networks. Here, the directional influence on the ACC may be part of the PCC’s coordinating activity carried out in the DMN. If so, the associated spectral changes in the ACC may help elucidate the neurophysiological consequences of the network coordinating activity.
In the literature, theta-band activity was reported to dominate the directed information flow from anterior to posterior regions (28). We did not observe this theta dominance in the GC from the ACC to the PCC. One possibility is that the interheartbeat segments contain too few theta cycles to reach the statistical power for GC estimation. This problem may be further explored in the future by extending the GC time periods while carefully excluding the heartbeat artifacts.
A potential concern is that the asymmetry of influence may be an artifact of different signal-to-noise ratios (SNRs) in the ACC and the PCC (30). While the exact noise level is unmeasurable, there are some observations that may alleviate this concern. First, although the occipital cortex is known to exhibit strong resting-state alpha oscillations, it did not show up as a consistent ROI in the GC maps (Fig. 2C). Second, although systematic SNR differences may also exist in the other frequency bands, no consistent ROI was observed in the GC maps of the other frequencies (Figs. S1 and S2). Third, while surface sources tend to have a higher SNR than deep sources in MEG, the surface GC-flow did not show systematic larger values than the deep GC-flow (Figs. S1 and S2).
The Cross-Frequency Coupling Suggests the ACC’s Role in Cortical Excitability Regulation.
Although both being core regions of the DMN, the ACC is functionally heterogeneous from the PCC (31). In task-based behavioral studies, the ACC has been considered a major region related to executive functions and goal-directed behavior (32, 33). Here, the phase–amplitude relationship we found between the theta and gamma frequencies is known as a neurophysiological reflection of cortical excitability (22, 34–36). It seems plausible to have an executive function-related region constantly modulated for its excitability during the resting state, so that the brain can flexibly switch from passive to active behavioral states. This has been proposed by work from a theoretical perspective (34, 37), but neurophysiological evidence remains scarce. Our finding may provide a test ground for further investigations on this hypothesis.
Insight for Future Investigation on Task Data.
Simultaneous EEG–fMRI studies have reported task-introduced increases of theta/gamma power and decreases of alpha/beta power, in correspondence with the increase of BOLD activity (38). This spectral pattern seems to mirror the GC-associated power fluctuation shown in Fig. 3B. Given that the DMN has elevated BOLD activity in the resting state (18, 19), this spectral pattern may reveal a common neurophysiological correlate of increased BOLD activity. It may be interesting to revisit some of the task data and see whether any of the spectral changes were induced by network interactions.
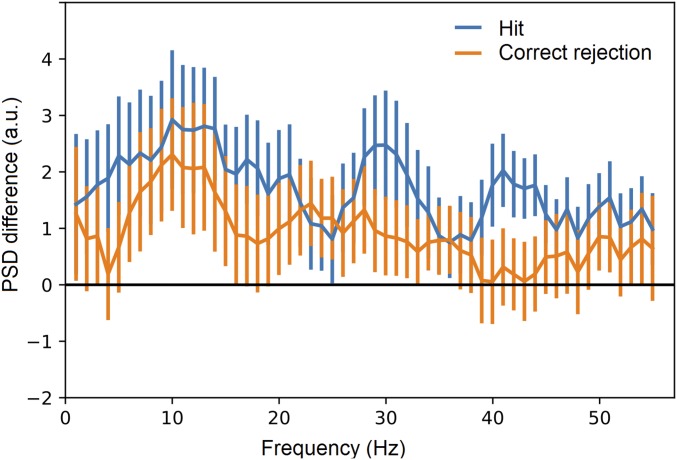
Importantly, revealing brain activity during “resting state” may lead to a better understanding of brain activity during specific cognitive tasks. The highly structured resting-state dynamics indicate a nonflat “baseline” for various tasks. For example, the ACC power–GC association can be observed from the same set of subjects during episodic memory retrieval (SI Results and Fig. S3). The power–GC association during resting state (Fig. 3B) can provide critical information about how memory-related processes modulate the ongoing neural dynamics (SI Results).
Fig. S3.
ACC power changes associated with the 10-Hz GC fluctuation in episodic memory retrieval, as a comparison with Fig. 3B.
Technical Considerations.
A common concern with MEG recordings has been the low SNR often seen in deep sources (39). Here, several methodological considerations were taken to reduce the influence of noise. First, we used a multimodal imaging approach to validate functional connectivity. The fcMRI and the MEG connectivity were measured from different imaging modalities. The fact that they correlate across subjects (Fig. 1B) helps validate the MEG results. Second, we used a data-driven approach to identify connectivity between regions. The seed-based maps did not use preselected ROIs but still identified spatially specific connectivity between the ACC and the PCC (Fig. 2C). This was a cross-validation of the 10-Hz-range connectivity in Fig. 1A. Third, we used the interheartbeat data segments to reduce heartbeat noise and provide multiple samples of GC. Sufficient samples allowed us to create conjunction maps and examine consistency across individuals, gaining greater statistical power than using the mean values of a group result.
The choice of GC in measuring connectivity is out of the concern for “crosstalk” (10, 40). Crosstalk refers to the spurious zero-lag correlation among the source signals, an unavoidable consequence of the MEG inverse solution. In the current study, we took advantage of the fact that GC measures time-lagged interaction between sources. Moreover, taking the difference score of the to-seed and from-seed GC (i.e., GC-flow) helps cancel the artifact if crosstalk affects both directions equally. Nevertheless, we note that the zero-lag correlation can still bias the GC measure (41, 42). Crosstalk is a special case of the additive noise problem in GC measurement (42). Interested readers can refer to Supporting Information for a simulated demonstration of this issue (SI Results, Table S2, and Figs. S4 and S5). In summary, GC is affected by the level of crosstalk, but its true value can be recovered by orthogonalizing the source signals. Our GC result proved to be robust using orthogonalized ACC and PCC sources (Fig. S6). Given the lack of literature on this topic, we hope this work can bring future interest to the related research.
Table S2.
Parameter settings for the GC simulation
| a = c = d = 0.4 | a = c = d = 0.8 | ||||
| True influence | Nonzero leakage | Zero leakage | True influence | Nonzero leakage | Zero leakage |
| b = 0.2 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 | b = 0.2 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 |
| b = 0.4 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 | b = 0.4 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 |
| b = 0.6 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 | b = 0.6 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 |
| b = 0.8 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 | b = 0.8 | h = [0.15, 0.3, 0.45, …, 1.5] | k = 0 |
| b = 0.2 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 | b = 0.2 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 |
| b = 0.4 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 | b = 0.4 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 |
| b = 0.6 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 | b = 0.6 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 |
| b = 0.8 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 | b = 0.8 | k = [0.15, 0.3, 0.45, …, 1.5] | h = 0 |
Fig. S4.
GC of the weakly autocorrelated source activity with (A) leakage between two sources x and y and (B) leakage from a third source z into both x and y. All plots share a common legend shown at the Top of the figure. GC was measured by an F score defined in the study by Geweke (49). Each plot shows how F changes with the level of leakage under a single parameter setting. Parameter b controls the strength of the true influence from y to x, while the true influence from x to y was held constantly at zero. Parameter h controls the leakage between x and y, and k controls the leakage from z to x and y. Each curve is an average over 200 runs with the SE across runs.
Fig. S5.
GC of the strongly autocorrelated source activity with (A) leakage between two sources x and y and (B) leakage from a third source z into both x and y. All plots share a common legend shown at the Top of the figure. GC was measured by an F score defined in the study by Geweke (49). Each plot shows how F changes with the level of leakage under a single parameter setting. Parameter b controls the strength of the true influence from y to x, while the true influence from x to y was held constantly at zero. Parameter h controls the leakage between x and y, and k controls the leakage from z to x and y. Each curve is an average over 200 runs with the SE across runs.
Fig. S6.
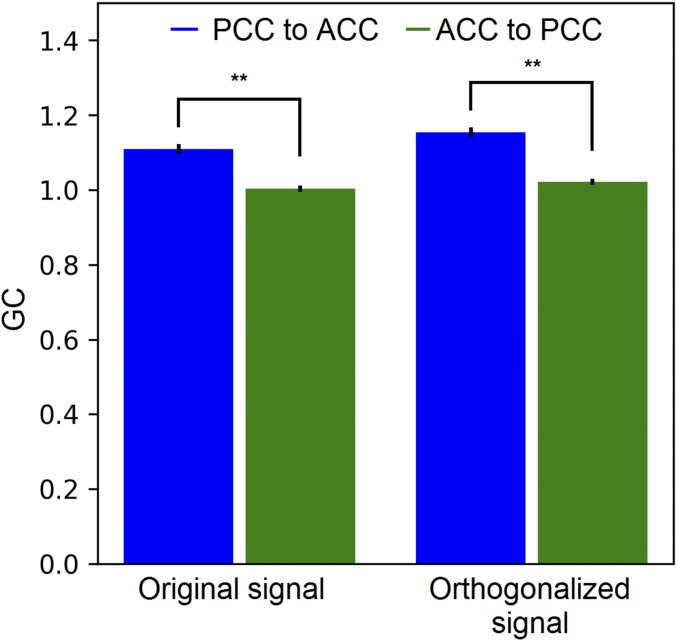
GC between the MEG source activity of the ACC and PCC. The orthogonalized signal was obtained using the multivariate regression method in ref. 53, treating the sources of each ROI as one vector. GC was calculated for paired sources between the ROIs, separately for each interheartbeat segment. Each bar is an average across source pairs, segments, and subjects. The error bars represent the SE across subjects. Asterisks represent the significance level of paired t test across subjects (**P < 0.01).
Finally, we note that the “hidden-node” problem (43) inherent to GC also applies here. The influence from the PCC to the ACC may go through a third region that was not captured in the GC map. Since the mapping covered all vertices in the cortex, the hidden influence, if present, would be likely coming from subcortical structures. This issue could not be resolved from the current data due to a lack of subcortical recordings.
Materials and Methods
Subjects and the Resting-State Experiment.
Twenty-nine subjects (20 females; mean age, 21.4 y) were seated in the upright position, facing a screen with cross hairs shown at the center. The subjects were asked to maintain fixation on the cross hair and refrain from blinking as much as they could during the experiments. These instructions were given in both the MEG and fMRI sessions. All subjects successfully followed the instructions, and no data were discarded due to excessive blinking. This study was approved by the institutional review board at Massachusetts General Hospital, and all subjects gave signed informed consent.
Structural and Functional MRI Recordings.
Anatomical images were acquired on the same day as the MEG experiment for each subject (SI Materials and Methods). FreeSurfer was used to reconstruct the cortical surface and downsample it to 8,192 vertices. The fMRI and MEG analyses were based on signals from the same vertices on the decimated surface. Functional recordings of the BOLD signal used the same resting-state experiment setup (SI Materials and Methods). Each subject’s BOLD data were then coregistered to the individual’s structural MRI and underwent commonly used preprocessing (SI Materials and Methods).
MEG Recording and Preprocessing.
MEG was continuously recorded in a magnetically shielded room with a 306-channel whole-head system at a sampling rate of 1,037 Hz (SI Materials and Methods). All preprocessing steps used the MNE-Python toolbox (ref. 44 and SI Materials and Methods).
Source Estimation.
The gain matrix needed for source estimation was computed using a single-compartment boundary element model (45). The source time courses were estimated using a cortically constrained minimum L2-norm estimate (MNE) (46), with noise covariance computed from empty-room recordings on the same day. The source current density was then normalized by an estimate of projected noise to generate the dynamic statistical parametric map (dSPM) (47). The dSPM was treated as the source activity and estimated at each time point.
Definition of the ACC and PCC Regions.
The regions of the ACC and PCC for the fcMRI and MEG power correlation analyses were defined according to a DMN atlas from ref. 48. The DMN atlas defines labels of the ACC and PCC on the fsaverage template brain surface (FreeSurfer 5.4). The labels were then morphed into each subject’s native space and used as subject-specific ROIs.
Power Correlation of the MEG Source Signal and the Permutation Test.
In each subject, the 5-min time courses of the ACC and PCC sources were bandpass filtered into 55 narrow bands of 1-Hz width, which evenly divided up the 1- to 56-Hz interval. The filtered signals from each vertex of the ACC were paired up with those from each vertex of the PCC. For each pair, a phase-orthogonalized power envelope correlation was calculated using the method in ref. 15. Envelope correlations were obtained for all 55 × 55 frequency combinations, and vertex pairs of the same frequency combination were averaged together, resulting in a 55 × 55 connectivity spectrogram for each subject.
To test the robustness of the envelope correlation, the temporal order of the envelopes was permuted 1,000 times, and a connectivity spectrogram was calculated for each cohort of permuted samples. For each frequency pair, the veridical correlation was considered significant if its value exceeded the 95% quantile of the 1,000 permutated correlation scores.
fMRI-Based Connectivity.
Pearson’s correlation was calculated between the BOLD time series for each ACC–PCC vertex pair, and then averaged across vertex pairs to generate one fcMRI score for each subject.
Seed-Based MEG GC Maps.
Heartbeat events were removed from the preprocessed signal (SI Materials and Methods), resulting in ∼300 short segments of MEG data in each subject. GC maps were computed for each interheartbeat segment between a seed chosen from the ACC/PCC and the rest of the cortex. Five different seeds were used for each region, and the results were averaged across the five runs. The seeds surrounded the center of the ACC and PCC labels defined by the DMN atlas. Each seed was a cortical region with a diameter of 1 cm.
For each time segment, source activities within the seed region were averaged across vertices to yield the seed time series Xt. The seed was paired with all vertices in the other region (denoted Yt), and a bivariate autoregressive (AR) model was fitted to each pair:
| [1a] |
| [1b] |
The ensemble mean of Xt and Yt were removed beforehand. Here, p denotes the model order, aij,k with i, j ∈ {1,2} and k = 1, 2, …, p are model coefficients, and E1t and E2t are uncorrelated white noise. The model was fitted using the Levinson–Wiggins–Robinson algorithm with a fixed model order P = 8 for each vertex pair (SI Materials and Methods and Figs. S7 and S8).
Fig. S7.
Histograms of the percentage of zero-PACF source time series.
Fig. S8.
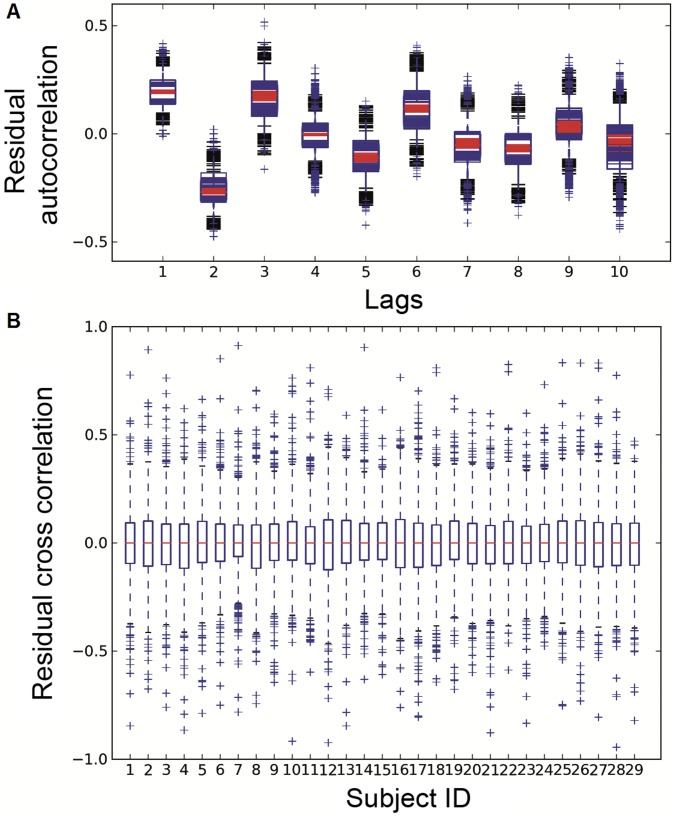
Residual whiteness tests for model validity. For computational efficiency, we sampled 1,000 models (10% of the total number of possible models) between the seed and randomly drawn vertices from the cortex. (A) Residual autocorrelation box plot with 29 subjects superimposed. At each lag value for each subject, the box plot shows the median (line inside the box), upper quantile (upper side of the box), lower quantile (lower side of the box), and outliers (crosses outside the black boundary) of the autocorrelation score distribution over the 1,000 models. (B) Residual cross-correlation box plot, separate for each subject, produced from the distribution over the 1,000 models.
Based on the fitted model coefficients, Geweke’s frequency-domain GC (49) was estimated in the range of 2–45 Hz with a resolution of 1.5 Hz. Values in the 8- to 12-Hz interval were summed to yield the alpha-band GC. The model fitting and GC computation were done using the Python toolbox nitime, which follows closely the procedure described by ref. 50.
Nonparametric Cluster-Level Significance Test for Defining ROIs.
For each pair of the seed–target vertex combinations, a GC difference was calculated for each interheartbeat segment, and a t score was used to summarize the difference over segments, which quantified the overall asymmetry of the influences between the seed and the target vertex. The significance of the t scores was determined by a nonparametric cluster-level test (51), which corrected for the family-wise error through a Monte-Carlo permutation that took into account the spatial correlation of nearby vertices. Test statistics with a P value lower than 0.05 were considered significant. The test was carried out in each subject’s native space, and the results were morphed into the fsaverage space for group average and conjunction analysis.
Spatiotemporal Clustering of the GC Values.
Spatiotemporal clusters of alpha-band GC values over adjacent vertices and time segments were identified. A threshold was set to two times the interquartile distance above the median across all vertices and time segments. Above-threshold GC values from more than 20 adjacent vertices and/or time segments were marked as spatiotemporal clusters. The number 20 was chosen so that the marked clusters were extensive enough in space (20 vertices covered an area ≈2 cm in diameter) or lasted long enough in time (20 time segments covered ≈20 s), which indicated robust GC influence that was unlikely driven by transient random fluctuations of noise in the signal.
Comparison of Power Inside and Outside the GC Clusters.
The PSD of the vertices and time segments inside the spatiotemporal clusters were compared with those outside the clusters. The test followed ref. 52. Briefly, the PSD S(f) was averaged across vertices and time segments and transformed to obtain Gaussianity:
| [2] |
where m equals one-half the number of Slepian sequences multiplied by the number of samples, and ψ is the digamma function. Once the mean power spectra x1(f) and x2(f) of two different groups were computed, the PSD-difference score was calculated as follows:
| [3] |
where m1 and m2 are the number of samples averaged in x1(f) and x2(f), and ψ′ is the trigamma function. assimilates the statistic of a paired t test in representing the difference between x1(f) and x2(f).
Estimation of the Cross-Frequency Phase–Amplitude Coupling.
The entire time course (5 min) of the source activity of each seed was filtered into six narrow-band lower-frequency components (1–2, 2–3, 3–4, 4–5, 5–6, and 6–7 Hz). The phase angle at each time point was obtained via Hilbert transform. The amplitudes of the gamma band (30–55 Hz) from the same signal were extracted across the same time points. Thus, the lower-frequency phase and gamma-frequency amplitude were paired across time. The coupling was estimated following a spline-fitting procedure (23). Briefly, the gamma amplitude was modeled as a function of the lower-frequency phase over 100 equally spaced phase bins dividing the [−π, π] interval. The function was fitted with cardinal spline basis using 20 control points that evenly divided the phase interval. The estimated function represents the distribution of gamma amplitudes over [−π, π].
SI Results
The Power–GC Association in Episodic Memory Retrieval.
We examined the power–GC association in the ACC on the same set of subjects performing an episodic memory task (SI Materials and Methods). We calculated the PSD-difference profile of the ACC by contrasting the GC it received from the PCC during memory retrieval (SI Materials and Methods and Fig. S3). The ACC showed increased alpha power in the trials with strong GC, as opposed to those with weak GC. This power–GC pattern differed from what was observed in the resting state (Fig. 3B), suggesting the modulation of DMN dynamics by the task. This modulation is likely sensitive to the retrieval conditions, showing an observable difference between correct recognition (“hit”) and correct rejection trials (Fig. S3).
This preliminary result is to illustrate the importance of resting-state analysis for understanding task data. Existing evidence (e.g., refs. 19 and 20), as well as the results of this study (Fig. 3B), have suggested that the resting state is not pure randomness. Instead, it reflects intrinsic brain dynamics that are structured and constrained by anatomy. Each task posts stimulus-specific modulation on the ongoing brain dynamics, and assumptions of the latter can fundamentally affect the interpretation of the former. For example, if one assumes a flat baseline for Fig. S3, unaware of the actual dynamics in Fig. 3B, one may postulate that the alpha power–GC association is task exclusive. However, we have observed a preexisting pattern of the alpha power–GC association in the resting state. Therefore, we believe that a careful examination of the resting state is necessary before delving into any specific task.
The Effect of Crosstalk on GC.
Simulation demonstration of the crosstalk artifact.
Time courses of three source signals , and were generated using an order-one vector autoregression model:
| [S1] |
| [S2] |
| [S3] |
with the simplification a = c = d. Two estimated sources and were modeled as linear mixtures of , , and :
| [S4] |
| [S5] |
with the simplification h1 = h2 and k1 = k2.
GC from to was calculated following Geweke’s definition (49) by comparing two nested regressions:
| [S6] |
| [S7] |
| [S8] |
Here, and are the sample parameters, and and are the sample prediction errors. quantifies GC from to . GC from to was calculated accordingly.
GC between the estimated sources was calculated in the same manner:
| [S9] |
| [S10] |
| [S11] |
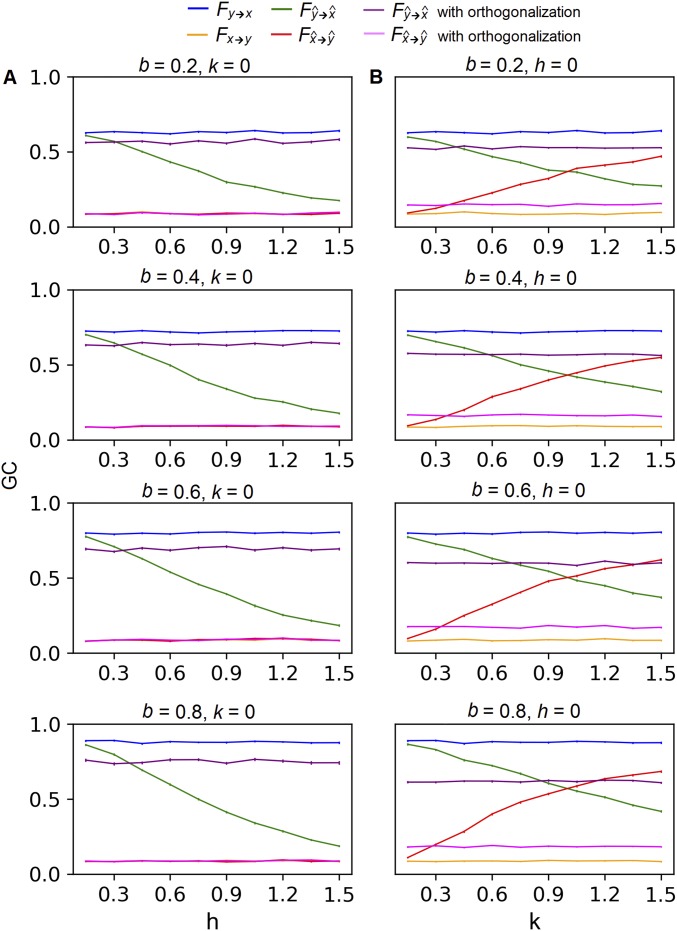
We computed , , , and under different parameter settings (Table S2). Specifically, we set a = c = d = 0.4 and then a = c = d = 0.8 to represent signals that are weakly or strongly autocorrelated. For each autocorrelation setting, we varied b to simulate different strengths of time-lagged influence from to . For each level of influence, we varied h while keeping k = 0 to test the effect of leakage between and , and then varied k while keeping h = 0 to test the effect of leakage from into both and .
The results showed that < for all parameter combinations. For different levels of signal leakage, decreases when either h or k increases (Figs. S4 and S5). In cases of severe leakage, can get close to zero (e.g., when b = 0.4 in Fig. S5). Interestingly, becomes spuriously positive for relatively large k values (Figs. S4B and S5B), even though is not set to influence in the model. This false positive causes directional asymmetry to flip when the leakage is severe (e.g., when k > 1 in Figs. S4B and S5B).
In summary, the simulation suggests that crosstalk diminishes GC when true time-lagged interaction exists; crosstalk also causes falsely positive GC between two noninteracting signals when a third signal leaks into both.
Correction for the biased GC using signal orthogonalization.
To correct for the bias, we orthogonalized the signals so that they contained minimal common components. For the case of leakage between and (k = 0), we regressed out and from each other, and recalculated GC using the residuals. For the case of leakage from into both and (h = 0), we regressed out from both and and recalculated GC using the residuals. The orthogonalization in both cases successfully reduced the bias (Figs. S4 and S5). The correction completely recovered the true GC with weakly autocorrelated sources (Fig. S4), but only partially recovered it with strongly autocorrelated sources (Fig. S5). Nonetheless, for both cases the directional asymmetry was recovered.
These results suggest that orthogonalization is effective in correcting the cross-talk–induced bias in GC. The correction is in both directions: when true interaction exists, orthogonalization increases GC back to the true values; when no interaction exists, orthogonalization decreases GC to eliminate the false positives.
Validation of the GC-flow between the ACC and PCC with signal orthogonalization.
Finally, we applied orthogonalization to the MEG data to validate the GC-flow between the ACC and PCC. We used the multivariate method in ref. 53 to orthogonalize the multiple sources from the ROIs of the ACC and PCC. We then computed pairwise GC between all vertices from the two ROIs for all interheartbeat intervals. Fig. S6 shows the preorthogonalization and postorthogonalization results, averaged across vertex pairs, subjects, and time. The GC with the orthogonalized signal slightly increased in both directions. Based on the simulation in the previous section, the increase of GC indicates the probable true interaction (because the orthogonalization will likely deflate the false positives). Importantly, the asymmetry between the two directions was preserved.
SI Materials and Methods
Episodic Memory Task.
Subjects performed an old/new recognition memory task in the MEG scanner after a study session involving deep incidental encoding performed approximately 1 h before the scan. During the study session, subjects were instructed to determine whether each of 50 words represented an animate (giraffe) or inanimate object (window).
Each word was presented on a computer screen for 2 s with a 1.6-s interstimuli interval (ISI). The subjects indicated their decisions by pressing the designated keys on the keyboard. The stimuli were then repeated in random order, and the subjects were instructed to rate them based on how much they liked the objects. The two-stage study procedure was conducted to maximize the level of elaboration and encoding for each item.
In the memory retrieval session, 100 words were presented on the screen for 1 s with 3-s ISI. Fifty words were old (encoded during the study session), and 50 were new. The subjects’ task was to determine whether each item was old or new using a right-hand key press. Instructions were to respond accurately and quickly. Old and new words were counterbalanced across subjects.
Structural and Functional MRI Recordings.
Anatomical images (magnetization-prepared rapid acquisition with gradient echo) were acquired on the same day as the MEG experiment for each subject (repetition time, 2,000 ms; echo time, 3.37 ms; flip angle, 100; field of view, 256; voxel size, 1 × 1 × 1 mm3; 160 volumes). FreeSurfer was used to reconstruct the cortical surface from each individual’s T1-weighted volume. The reconstructed surface was then downsampled to 8,192 vertices. The fMRI and MEG analyses were based on signals from the vertices on the decimated surface.
BOLD data were collected following the anatomical images, using the same resting-state experiment setup and an echo-planar imaging sequence (repetition time, 5,000 ms; echo time, 30 ms; flip angle, 900; field of view, 128; voxel size, 2 × 2 × 2 mm3; 76 volumes; 6.3-min acquisition). Two runs, in total ≈13 min of data, were collected. Each subject’s BOLD data were then coregistered to the individual anatomical images.
Preprocessing of the fMRI Data.
The BOLD data underwent commonly used preprocessing (48), namely (i) discarding the first four volumes of each run to ascertain T1-equilibrium, (ii) slice timing correction, (iii) head motion correction, (iv) removal of constant offset and linear trend per run, (v) low-pass filtering to 0.08 Hz, and (vi) regressing out of six motion parameters, signal of the ventricles and white matter. The volumetric images were then projected onto the cortical surface in each subject, after which a Gaussian smoothing kernel (FWHM = 6 mm) was applied.
MEG Recording.
MEG was continuously recorded in a magnetically shielded room with a 306-channel whole-head system (Elekta-Neuromag) and at a sampling rate of 1,037 Hz. Vertical and horizontal electro-oculograms were acquired simultaneously for off-line eye movement artifact rejection. Head position relative to the MEG sensors were recorded from four head position indicator coils attached to the scalp. Landmark points of the head were digitized using a 3D digitizer (Polhemus FASTRAK).
Preprocessing of the MEG Data.
Preprocessing for the GC analysis followed five steps: (i) bad channel rejection, (ii) eye movement artifact removal via Signal Space Projection (SSP), (iii) bandpass filtering to 2–45 Hz, (iv) downsampling with a decimate factor of 8, and (v) discarding 100-ms segments of signal centered at each heartbeat event. For step iii, the lower cutoff frequency at 2 Hz was chosen to diminish the artifact from heartbeats, given that step v would not completely remove the effect; the higher cutoff at 45 Hz was to avoid aliasing when downsampling. The purpose of downsampling was to reduce computational expense.
Preprocessing for the spectral analysis followed the same procedure except for steps iii and iv. Here, the signal was low-pass filtered to 55 Hz to span the frequency range free of line noise (60 Hz) as much as possible. No downsampling was applied.
Preprocessing for the spectral analysis took the same procedure except for steps iii and iv. Here, the signal was low-pass filtered to 55 Hz to span the frequency range free of line noise (60 Hz) as much as possible. No downsampling was applied.
Autoregressive Model Order Selection.
The model order p of the autoregressive (AR) model (Eq. 1) was selected using partial autocorrelation functions (PACF) (54). We did not apply the commonly used Akaike information criterion (AIC) (55, 56), due to the 1/f spectrum of the resting-state signal. The 1/f spectrum would in theory require an infinite-order AR model; thus, the AIC would not reach minimum at a reasonable lag. Alternatively, we followed another generally suggested procedure (54), choosing p to be the lag beyond which the PACF was not significantly different from zero. In this way, we obtained a finite-order model that was sufficient to capture the temporal structure of the signal.
For each data epoch and each vertex, we computed the source PACF up to lag 20 according to the following equation:
| [S12] |
where and are residuals from the regressions of yt and yt−k onto {1, yt−1, yt−2, …, yt−k+1}. Then, for each vertex, we computed the mean and SE of the PACF over time segments. If the absolute difference between the mean and zero was less than two times the SE, then the PACF was considered zero. At lag 8, all subjects had more than 75% of the vertex-wise PACFs at zero (Fig. S7). The data going into an eighth-order model were about 10 times the unknown parameters, an acceptable ratio for model fitting. The fitted eighth-order models produced white-noise residuals (Fig. S8), verifying the model validity. Therefore, we considered the eighth-order model to be a good balance between the PACF criterion and the request for statistical power.
GC Test for the Episodic Memory Task Data.
The task data went through the same preprocessing and source estimation steps as that of the resting data. The GC modeling followed the same bivariate AR-based procedure, and pairwise GC was calculated the same way between the PCC seed and each ACC vertex. The only difference in the task analysis was the preselection of stationary trials. We discarded trials with prominent evoked responses in both the ACC and PCC, under the assumption that stationary trials mostly contain task-modulated ongoing activity, driven by network interactions. We assumed that the ongoing activity was present in parallel to the stimulus-locked evoked response. More sophisticated methods exist for separating the ongoing activity from the evoked response in the same trial, but here, for illustration purposes, we simplified the procedure by choosing only the stationary trials.
To identify and discard trials with prominent evoked response, we used an empirical screening for nonstationarity. We measured piecewise temporal variance throughout each trial and discarded trials with strongly fluctuating variance. Specifically, we slid a 200-ms window through the 1-s poststimulus period at a 50-ms step and calculated the temporal variance for each window. Trials with the largest variance two times greater than the smallest were discarded. About one-third of the 200 trials passed the screening in each subject.
The GC clustering and PSD-difference calculation followed the same procedure used in the resting-state analysis.
Acknowledgments
We thank Dr. Kyle Lepage for his advice on the power spectral analysis and Dr. Martin Luessi for his help with MEG preprocessing. This work was supported by the Cognitive Rhythms Collaborative Grant (NSF-DMS-1042134) and jointly with NIH Grants R01NS091604, P50MH106435, R01NS0699696, P41EB015896, S10RR014978, R01NS095369, and MH099765 and Beijing Municipal Science and Technology Commission Z161100002616009.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702027114/-/DCSupplemental.
References
- 1.Mesulam MM. Large-scale neurocognitive networks and distributed processing for attention, language, and memory. Ann Neurol. 1990;28:597–613. doi: 10.1002/ana.410280502. [DOI] [PubMed] [Google Scholar]
- 2.Tononi G, Edelman GM. Consciousness and complexity. Science. 1998;282:1846–1851. doi: 10.1126/science.282.5395.1846. [DOI] [PubMed] [Google Scholar]
- 3.Sporns O. Networks of the Brain. MIT Press; Cambridge, MA: 2010. [Google Scholar]
- 4.Bressler SL, Menon V. Large-scale brain networks in cognition: Emerging methods and principles. Trends Cogn Sci. 2010;14:277–290. doi: 10.1016/j.tics.2010.04.004. [DOI] [PubMed] [Google Scholar]
- 5.Baillet S, Mosher JC, Leahy RM. Electromagnetic brain mapping. IEEE Signal Process Mag. 2001;18:14–30. [Google Scholar]
- 6.Poldrack RA. Region of interest analysis for fMRI. Soc Cogn Affect Neurosci. 2007;2:67–70. doi: 10.1093/scan/nsm006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 8.Friston KJ. Functional and effective connectivity: A review. Brain Connect. 2011;1:13–36. doi: 10.1089/brain.2011.0008. [DOI] [PubMed] [Google Scholar]
- 9.Logothetis NK. What we can do and what we cannot do with fMRI. Nature. 2008;453:869–878. doi: 10.1038/nature06976. [DOI] [PubMed] [Google Scholar]
- 10.Brookes MJ, et al. Measuring functional connectivity using MEG: Methodology and comparison with fcMRI. Neuroimage. 2011;56:1082–1104. doi: 10.1016/j.neuroimage.2011.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hutchison RM, et al. Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage. 2013;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Laumann TO, et al. On the stability of BOLD fMRI correlations. Cereb Cortex. September 2, 2016 doi: 10.1093/cercor/bhw265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.de Pasquale F, et al. Temporal dynamics of spontaneous MEG activity in brain networks. Proc Natl Acad Sci USA. 2010;107:6040–6045. doi: 10.1073/pnas.0913863107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brookes MJ, et al. Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proc Natl Acad Sci USA. 2011;108:16783–16788. doi: 10.1073/pnas.1112685108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK. Large-scale cortical correlation structure of spontaneous oscillatory activity. Nat Neurosci. 2012;15:884–890. doi: 10.1038/nn.3101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marzetti L, et al. Frequency specific interactions of MEG resting state activity within and across brain networks as revealed by the multivariate interaction measure. Neuroimage. 2013;79:172–183. doi: 10.1016/j.neuroimage.2013.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baker AP, et al. Fast transient networks in spontaneous human brain activity. eLife. 2014;3:e01867. doi: 10.7554/eLife.01867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shulman GL, et al. Common blood flow changes across visual tasks: II. Decreases in cerebral cortex. J Cogn Neurosci. 1997;9:648–663. doi: 10.1162/jocn.1997.9.5.648. [DOI] [PubMed] [Google Scholar]
- 19.Raichle ME, et al. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Buckner RL, Andrews-Hanna JR, Schacter DL. The brain’s default network: Anatomy, function, and relevance to disease. Ann N Y Acad Sci. 2008;1124:1–38. doi: 10.1196/annals.1440.011. [DOI] [PubMed] [Google Scholar]
- 21.Schröeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Canolty RT, Knight RT. The functional role of cross-frequency coupling. Trends Cogn Sci. 2010;14:506–515. doi: 10.1016/j.tics.2010.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kramer MA, Eden UT. Assessment of cross-frequency coupling with confidence using generalized linear models. J Neurosci Methods. 2013;220:64–74. doi: 10.1016/j.jneumeth.2013.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M. Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci USA. 2007;104:13170–13175. doi: 10.1073/pnas.0700668104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.de Pasquale F, et al. A cortical core for dynamic integration of functional networks in the resting human brain. Neuron. 2012;74:753–764. doi: 10.1016/j.neuron.2012.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jerbi K, et al. Exploring the electrophysiological correlates of the default-mode network with intracerebral EEG. Front Syst Neurosci. 2010;4:27. doi: 10.3389/fnsys.2010.00027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Foster BL, et al. Spontaneous neural dynamics and multi-scale network organization. Front Syst Neurosci. 2016;10:7. doi: 10.3389/fnsys.2016.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hillebrand A, et al. Direction of information flow in large-scale resting-state networks is frequency-dependent. Proc Natl Acad Sci USA. 2016;113:3867–3872. doi: 10.1073/pnas.1515657113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hagmann P, et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6:e159. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Newbold P. Feedback induced by measurement errors. Int Econ Rev. 1978;19:787–791. [Google Scholar]
- 31.Vogt BA, Finch DM, Olson CR. Functional heterogeneity in cingulate cortex: The anterior executive and posterior evaluative regions. Cereb Cortex. 1992;2:435–443. doi: 10.1093/cercor/2.6.435-a. [DOI] [PubMed] [Google Scholar]
- 32.Bush G, Luu P, Posner MI. Cognitive and emotional influences in anterior cingulate cortex. Trends Cogn Sci. 2000;4:215–222. doi: 10.1016/s1364-6613(00)01483-2. [DOI] [PubMed] [Google Scholar]
- 33.Carter CS, et al. Anterior cingulate cortex, error detection, and the online monitoring of performance. Science. 1998;280:747–749. doi: 10.1126/science.280.5364.747. [DOI] [PubMed] [Google Scholar]
- 34.He BJ, Raichle ME. The fMRI signal, slow cortical potential and consciousness. Trends Cogn Sci. 2009;13:302–309. doi: 10.1016/j.tics.2009.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lisman JE, Jensen O. The theta-gamma neural code. Neuron. 2013;77:1002–1016. doi: 10.1016/j.neuron.2013.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hyafil A, Giraud AL, Fontolan L, Gutkin B. Neural cross-frequency coupling: Connecting architectures, mechanisms, and functions. Trends Neurosci. 2015;38:725–740. doi: 10.1016/j.tins.2015.09.001. [DOI] [PubMed] [Google Scholar]
- 37.Deco G, Jirsa VK, McIntosh AR. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat Rev Neurosci. 2011;12:43–56. doi: 10.1038/nrn2961. [DOI] [PubMed] [Google Scholar]
- 38.Scheeringa R, et al. Neuronal dynamics underlying high- and low-frequency EEG oscillations contribute independently to the human BOLD signal. Neuron. 2011;69:572–583. doi: 10.1016/j.neuron.2010.11.044. [DOI] [PubMed] [Google Scholar]
- 39.Hillebrand A, Barnes GR. A quantitative assessment of the sensitivity of whole-head MEG to activity in the adult human cortex. Neuroimage. 2002;16:638–650. doi: 10.1006/nimg.2002.1102. [DOI] [PubMed] [Google Scholar]
- 40.Schoffelen JM, Gross J. Source connectivity analysis with MEG and EEG. Hum Brain Mapp. 2009;30:1857–1865. doi: 10.1002/hbm.20745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nolte G, et al. Robustly estimating the flow direction of information in complex physical systems. Phys Rev Lett. 2008;100:234101. doi: 10.1103/PhysRevLett.100.234101. [DOI] [PubMed] [Google Scholar]
- 42.Vinck M, et al. How to detect the Granger-causal flow direction in the presence of additive noise? Neuroimage. 2015;108:301–318. doi: 10.1016/j.neuroimage.2014.12.017. [DOI] [PubMed] [Google Scholar]
- 43.Pearl J. Causality. Cambridge Univ Press; Cambridge, UK: 2009. [Google Scholar]
- 44.Gramfort A, et al. MNE software for processing MEG and EEG data. Neuroimage. 2014;86:446–460. doi: 10.1016/j.neuroimage.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hämäläinen MS, Sarvas J. Feasibility of the homogeneous head model in the interpretation of neuromagnetic fields. Phys Med Biol. 1987;32:91–97. doi: 10.1088/0031-9155/32/1/014. [DOI] [PubMed] [Google Scholar]
- 46.Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: Minimum norm estimates. Med Biol Eng Comput. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- 47.Dale AM, et al. Dynamic statistical parametric mapping: Combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron. 2000;26:55–67. doi: 10.1016/s0896-6273(00)81138-1. [DOI] [PubMed] [Google Scholar]
- 48.Yeo BT, et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Geweke J. Measurement of linear dependence and feedback between multiple time series. J Am Stat Assoc. 1982;77:304–313. [Google Scholar]
- 50.Ding M, Chen Y, Bressler SL. Granger causality: Basic theory and application to neuroscience. In: Schelter B, Winterhalder M, Timmer J, editors. Handbook of Time Series Analysis. Wiley; Hoboken, NJ: 2006. pp. 437–460. [Google Scholar]
- 51.Maris E, Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J Neurosci Methods. 2007;164:177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- 52.Bokil H, Purpura K, Schoffelen J-M, Thomson D, Mitra P. Comparing spectra and coherences for groups of unequal size. J Neurosci Methods. 2007;159:337–345. doi: 10.1016/j.jneumeth.2006.07.011. [DOI] [PubMed] [Google Scholar]
- 53.O’Neill GC, et al. Dynamic recruitment of resting state sub-networks. Neuroimage. 2015;115:85–95. doi: 10.1016/j.neuroimage.2015.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chatfield C. The Analysis of Time Series. CRC Press; Boca Raton, FL: 2003. p. 64. [Google Scholar]
- 55.Akaike H. Second International Symposium on Information Theory. Akademiai Kiado; Budapest: 1973. Information theory as an extension of the maximum likelihood principle; pp. 267–281. [Google Scholar]
- 56.Pardey J, Roberts S, Tarassenko L. A review of parametric modelling techniques for EEG analysis. Med Eng Phys. 1996;18:2–11. doi: 10.1016/1350-4533(95)00024-0. [DOI] [PubMed] [Google Scholar]