Significance
When a particle diffuses in a corrugated channel, the channel’s boundaries have a twofold effect of limiting the configuration space accessible to the particle and increasing its hydrodynamic drag. Analytical and numerical approaches well-reproduce the former (entropic) effect, while ignoring the latter (hydrodynamic) effect. Here, we experimentally investigate nonadvective colloidal diffusion in channels with periodically varying width. While validating the current theory for channels much wider than the particle radius, we show that, in narrow channels, hydrodynamic and entropic effects can be equally strong and that hydrodynamic effects can be incorporated into existing descriptions by using an experimentally measured diffusivity. These results significantly advance our understanding of diffusive transport in confined geometries, such as in ionic channels and nanopores.
Keywords: diffusion, colloid, confinement, hydrodynamics, entropic effects
Abstract
In the absence of advection, confined diffusion characterizes transport in many natural and artificial devices, such as ionic channels, zeolites, and nanopores. While extensive theoretical and numerical studies on this subject have produced many important predictions, experimental verifications of the predictions are rare. Here, we experimentally measure colloidal diffusion times in microchannels with periodically varying width and contrast results with predictions from the Fick–Jacobs theory and Brownian dynamics simulation. While the theory and simulation correctly predict the entropic effect of the varying channel width, they fail to account for hydrodynamic effects, which include both an overall decrease and a spatial variation of diffusivity in channels. Neglecting such hydrodynamic effects, the theory and simulation underestimate the mean and standard deviation of first passage times by 40% in channels with a neck width twice the particle diameter. We further show that the validity of the Fick–Jacobs theory can be restored by reformulating it in terms of the experimentally measured diffusivity. Our work thus shows that hydrodynamic effects play a key role in diffusive transport through narrow channels and should be included in theoretical and numerical models.
Diffusive transport occurs prevalently in confined geometries (1, 2). Notable examples include the dispersion of tracers in permeable rocks (3), diffusion of chemicals in ramified matrices (4), and the motion of submicrometer corpuscles in living tissues (5, 6). The subject of confined diffusion is of paramount relevance to technological applications and for this reason, has been generating growing interest in the physics (1, 2), mathematics (7), engineering (3), and biology communities (5, 6, 8).
Spatial confinement can fundamentally change equilibrium and dynamical properties of a system via two different effects: limiting the configuration space accessible to its diffusing components (1) and increasing the hydrodynamic drag (9) on them. The former (entropic effect) has been extensively studied analytically and numerically in the case of quasi-1D structures, such as ionic channels (10), zeolites (4), microfluidic channels (11, 12), and nanopores (13). In these systems, transport takes place along a preferred direction, with the spatial constraints varying along it. Focusing on the transport direction, Jacobs (14) and Zwanzig (15), in the absence of advective effects, assumed that the transverse dfs equilibrate fast and proposed to eliminate them adiabatically by means of an approximate perturbation scheme. In first order, they derived a reduced diffusion equation, known as the Fick–Jacobs (FJ) equation, reminiscent of an ordinary 1D Fokker–Planck equation in vacuo, except for two entropic terms (2, 16–19). Predictions of the FJ equation have been extensively checked against Brownian dynamics (BD) simulations in different types of channels (16, 19–27). Using the FJ theory and BD simulations, researchers have predicted a variety of novel entropy-driven transport mechanisms, such as drive-dependent mobilities (2, 18, 20), stochastic resonance (28, 29), absolute negative mobilities (30), entropic rectification (31, 32), and particle separation (33). Several of these predictions are presently recognized as being of both fundamental and technological importance.
While these previous studies (2, 14–33) significantly improved our understanding of the entropic effects of confining boundaries, they largely ignored the hydrodynamic effects, which are notoriously difficult to treat analytically and in simulations (9, 34). How will hydrodynamic effects change the established entropic picture? To address this important question, we turn to laboratory experiments (12, 35–39) and measure the diffusive dynamics of micrometric colloidal particles through channels with systematically modulated cross-sections. Contrasting the experimental results with predictions obtained by FJ approximation and from BD simulation, we discover that, as the channel’s width shrinks toward the particle’s diameter, hydrodynamic effects (9, 34, 40–43) grow in strength and become comparable with the predicted entropic effects, thus indicating an unexpected breakdown of the standard FJ theory and BD simulation in narrow channels. We further show that hydrodynamic effects can be incorporated by using an experimentally measured local diffusivity. With such a phenomenological modification, the FJ theory and BD simulation accurately predict the experimental data.
Results
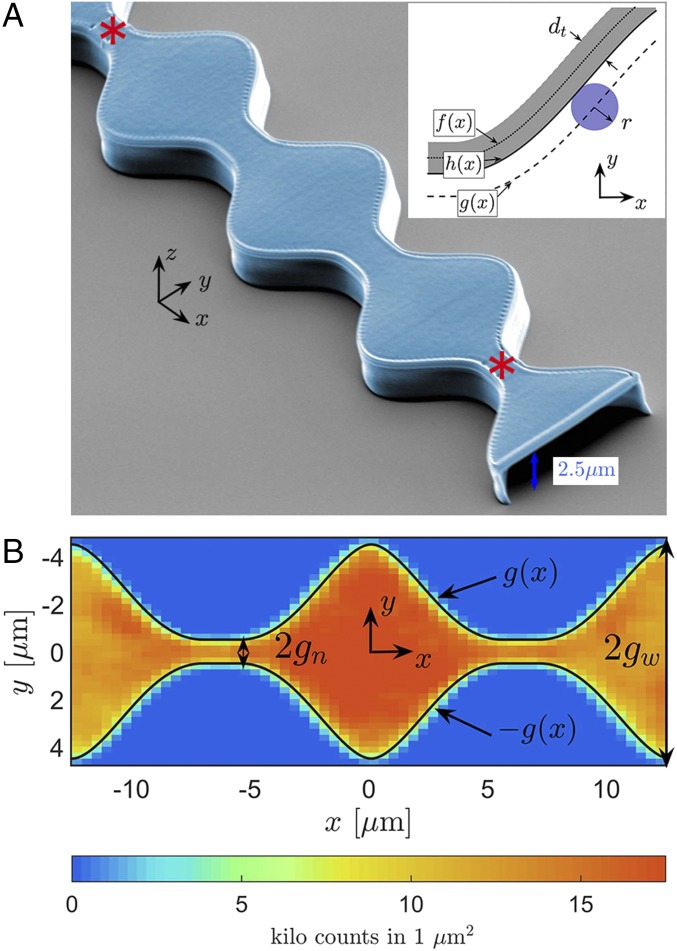
Our channels were fabricated on a coverslip by means of a two-photon direct laser writing system, which solidifies polymers according to the preassigned channel profile, , with a submicromicrometer resolution. As shown in Fig. 1A, the quasi-2D channel has a uniform height of 2.5 μm ( direction). The curved side walls are 0.7 -μm thick, and their inner side walls are a distance away from the channel’s axis ( direction).
Fig. 1.
(A) Scanning electron image of a channel of inner height m. Narrow openings at the two ends are marked by red asterisks. Inset illustrates the channel’s geometry: the laser-scanning contour, , the wall inner boundary, , and the effective boundary of the space accessible to the particle center, ; m and m are the wall thickness and the particle radius, respectively. (B) Spatial distribution of particle counts in a typical 20-h-long experiment. The effective channel boundary is marked by black lines and is denoted by (Eq. 1); here, m, and m.
After fabrication, channels were immersed in water with fluorescently labeled Polystyrene spheres of radius m. A holographic optical tweezer was used to drag a particle into the channel through a narrow entrance (red asterisks in Fig. 1A). The entrances are barely wider than the particle diameter so as to create insurmountable entropic barriers (2), which prevent the particle inside the channel from escaping. Particle motion in the quasi-2D channel was recorded through a microscope at rate of 30 frames per second for up to 20 h (see Movie S1 for a short segment of typical data). The projected particle trajectory in the plane was extracted from the recorded videos by standard particle-tracking algorithms; particle diffusion perpendicular to the imaging plane was not resolved in our measurements.
Inside the channels, the particle diffuses in a flat energy landscape. To show that, we quantized the measured particle coordinates into small bins (0.4 0.25 ) and counted the number of times that the particle enters each bin. As shown in Fig. 1B, particle counts are uniformly distributed with a standard deviation (SD) of about 12% of the mean. Regions where the particle counts drop sharply to zero are inaccessible to the particle’s center and in Fig. 1B, are delimited by the black curves (Fig. 2A, Inset). The effective channel’s boundary [denoted by ] is a periodic function; in the central region, the boundary was given the form of a cosine, which then tapers off to a constant in correspondence with the bottlenecks, that is
| [1] |
The length of the channel unit cell was kept fixed in all experiments, m, while the parameters and , representing its minimum and maximum half-width, respectively, were varied. For the channel shown in Fig. 1B, m, and m.
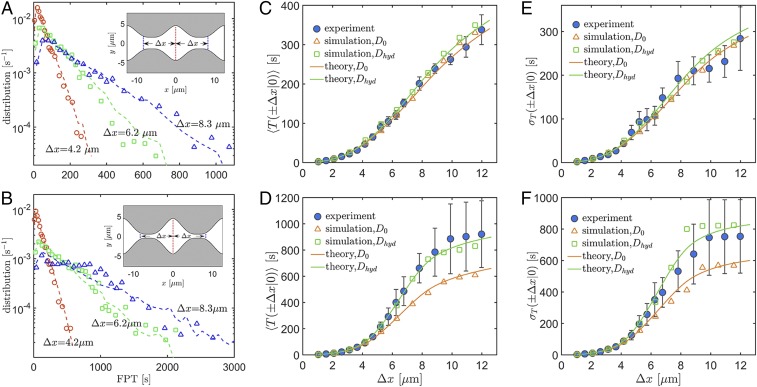
Fig. 2.
(A and B) Probability distributions, (C and D) averages, and (E and F) SDs of the FPTs in (A, C, and E) wide (m) and (B, D, and F) narrow (m) channels with the same maximum half-width, m. In A and B, experimental data (symbols) are compared with the outcome of BD simulations (curves) for the spatially modulated diffusivity, . The relevant channel profiles, , are shown in A, Inset and B, Inset; vertical dashed segments mark the starting (red: ) and ending (blue: ) positions of the first passage events. In C–F, experimental, numerical, and theoretical results are shown as solid symbols, open symbols, and solid curves, respectively. Numerical and theoretical results with constant and varying diffusivity are color-coded orange and green, respectively.
First Passage Time Statistics.
From acquired particle trajectories, we measured the first passage times (FPTs) (7, 44, 45). As in the FJ theory, we focus on the particle motion along the channel direction and measure the duration of the unconditional first passage events that start at (red segment in Fig. 2A, Inset) and end at (blue segments in Fig. 2A, Inset), with no restriction on the transverse coordinate . Distributions of experimentally measured unconditional FPTs, also denoted by , are plotted in Fig. 2 A and B; all distributions (for three values in two channels of different bottleneck half-width, ) exhibit an exponential tail, similar in spirit with the narrow escape problem (7). From these measured FPT distributions, we extract the means, , and the SDs, ; our results are plotted in Fig. 2 C–F against the diffusing distance, . A decrease of the bottleneck width, , from m in Fig. 2C to m in Fig. 2D sharply increases the diffusion time. For instance, the mean FPT to the center of the adjacent cells, , nearly triples from 300 s in Fig. 2C to 900 s in Fig. 2D. A similar increase can be observed in the SDs, , depicted in Fig. 2 E and F. To this regard, we notice that, for both channels, the experimental curves and almost overlap, which is to be expected in view of the exponential decay of the relevant FPT distributions (45). We note that the long-time channel diffusion coefficient (1) can be estimated in terms of an appropriate mean FPT: that is (45), . In periodically corrugated channels, has been estimated within the FJ formalism by means of the Lifson–Jackson formula for diffusivity (46).
We next compare our experimental data with the predictions of the standard FJ theory and BD simulations. The channel geometry renders our experimental system effectively 2D; analytical and numerical studies were carried out in the same dimension. Following the FJ scheme and taking advantage of symmetry properties of our experiments, we calculate the analytical expression,
| [2] |
for the mean FPT. Here, is the effective local diffusivity containing the entropic corrections that result from the adiabatic elimination of the transverse coordinate, . Among the (slightly) different functions proposed in the recent literature (21), we adopted the Reguera–Rubì heuristic expression (16), that is,
| [3] |
where is the slope of the channel’s profile , and is the particle’s diffusivity away from side walls. We also calculated the second FPT moment,
| [4] |
where reads like in Eq. 2, except that the outer integral runs here from to . The derivation of Eqs. 2 and 4 can be found in SI Appendix.
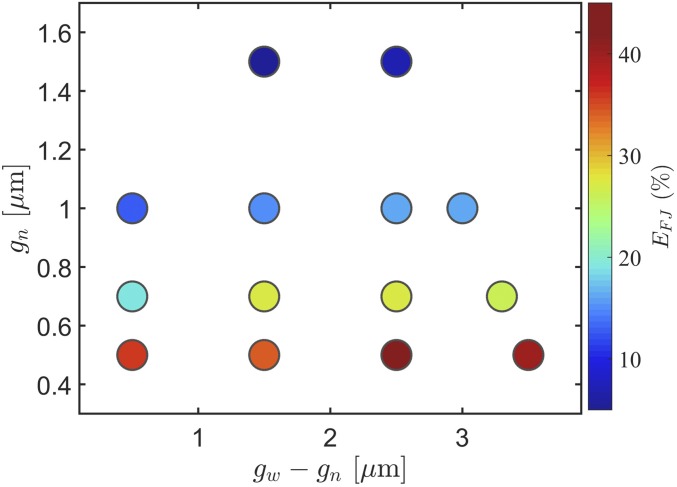
To use Eqs. 2 to 4, one needs to know the diffusivity . In an unbounded space, the diffusivity of a sphere coincides with the Stokes–Einstein value, . However, a general expression for the diffusivity of a colloidal particle in a confined geometry is not available. Hence, we experimentally measured by monitoring the diffusion of the particle about the center of a channel’s cell, where the entropic effects are minimal, and for displacements smaller than one particle radius. Eqs. 2 and 4 were then computed explicitly for the measured value of and the actual channel geometry (namely, the parameters , , and ). For the sake of a comparison, 2D BD simulations were also performed for the same model parameters. Theoretical and numerical results (orange symbols and curves in Fig. 2 C–F) agree closely with each other for both the wide and narrow channels. The comparison with the experimental data, instead, is satisfactory only in the case of the wide channel (Fig. 2 C and E). For the narrow channel in Fig. 2 D and F, the experimental data with are as much as 40% larger than the predicted values. To further investigate this discrepancy, we carried out experiments in channels with different width parameters, and ; the discrepancy is quantified in Fig. 3 by the relative mean–FPT difference at (bottleneck midpoints), . For narrow channels, the experimental values are consistently larger than the corresponding theoretical and numerical predictions. The discrepancy depends weakly on the amplitude of the channel modulation, , but increases significantly with decreasing bottleneck half-width, .
Fig. 3.
Deviation of theoretical predictions from experimental results, (definition in the text), increases with decreasing the bottleneck half-width, , and weakly depends on the modulation amplitude, , of the channel.
Diffusivity Measurements.
The theoretical and numerical predictions discussed so far assume a constant particle diffusivity, , throughout the channel, which is a reasonable approximation for particle diameters much smaller than the channel width. However, this assumption is doomed to fail for small bottleneck widths (when the FJ approach is supposed to work best), because the proximity of no slip side walls in the neck regions is known to increase the hydrodynamic drag on a finite-sized particle and therefore, suppress its local diffusivity (40–43, 47, 48).
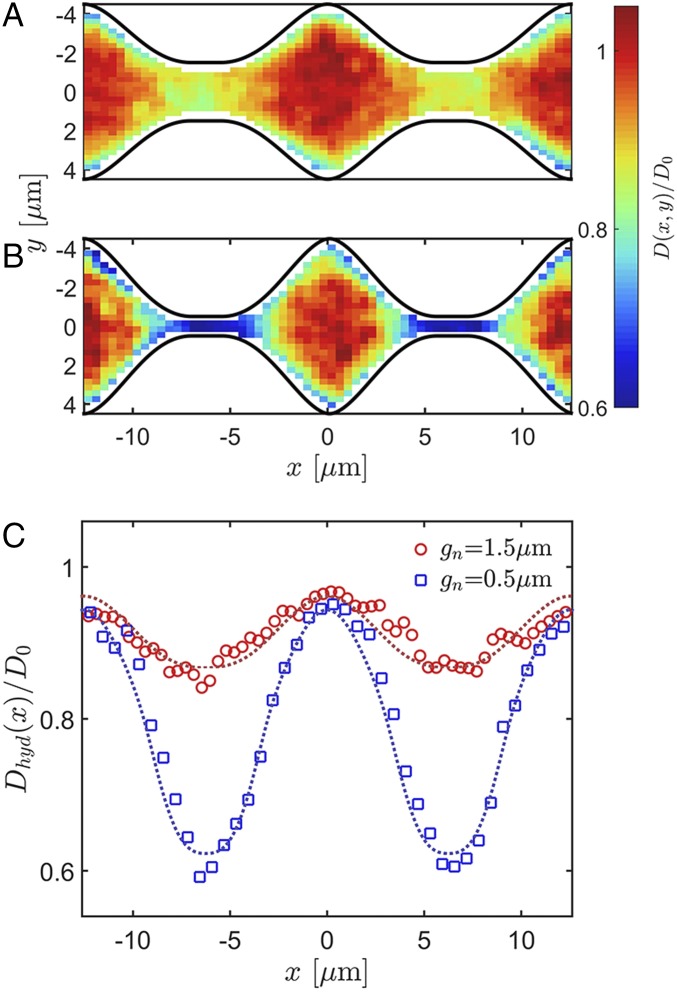
To show such a hydrodynamic effect in our device, we measured the particle diffusivity inside the channel. At any given location, , we recorded the particle mean-squared displacement in the direction, , for a time interval s and estimated the local diffusivity through Einstein’s law, . As shown in SI Appendix, the value chosen for is long enough to ensure good statistics for our measurements of ; during , particle displacements are smaller than m, so that channel corrugation does not affect diffusivity measurements (46). Measurements of in the wide and narrow channels are shown in Fig. 4 A and B. In both, is largest in the open regions at the center of the unit cells and strongly suppressed in the bottlenecks. In the spirit of the FJ theory, we average along the transverse direction
| [5] |
and plot as a function of in Fig. 4C. The spatial variabilities of are about 10 and 40% for the wide and narrow channels, respectively.
Fig. 4.
(A and B) Normalized local diffusivity from experiments, , measured in the wide and narrow channels of Fig. 2. (C) Normalized diffusivity, , vs. . Experimental data and results from finite element calculations are represented by symbols and curves, respectively. Experimentally measured values are and m2/s for wide and narrow channels, respectively; the Stokes–Einstein equation predicts a sphere diffusivity of m2/s in an unbounded space.
We corroborate the local diffusivity measurements with full hydrodynamic computations. The hydrodynamic friction coefficient in the direction was computed by means of a finite element package (COMSOL); the local diffusivity was calculated via the fluctuation–dissipation theorem, , and the result is averaged over the coordinate to obtain . Results from finite element calculations are shown in Fig. 4C as curves and are in excellent agreement with the experimental data.
Hydrodynamic Correction.
Fig. 4 depicts that particle diffusion through narrow bottlenecks can be significantly slower than in the wide region; moreover, the spatial modulation of the local particle diffusivity increases with decrease in the bottleneck width, which explains the results in Fig. 3. This spatial modulation is in clear contrast with the assumption of constant diffusivity that we adopted above when implementing the FJ formalism and the BD simulation code. To appreciate the effect of the spatial dependence of the local diffusivity, we replace the constant diffusivity, , with the experimental measurement, , reported in Fig. 4C, both in the theoretical treatment and in the numerical code. The analytical and numerical predictions are plotted in Fig. 2 C–F as green curves and symbols, respectively. Their agreement with the experimental data is excellent. Furthermore, we used the improved BD code to also compute, other than the first two FPT moments, the FPT distributions displayed in Fig. 2 A and B. Again, the close comparison obtained with the experimental data confirms the validity of our phenomenological approach.
Discussion
The coincidence of approximate analytical predictions and simulation results occurs for any choice of the local diffusivity [i.e., or ] as illustrated in Fig. 2. This means that the FJ theory well-describes the entropic effects of particle transport in weakly corrugated channels with (21). However, assuming constant particle diffusivity, as is common practice in the current literature, can lead to large discrepancies between theoretical predictions and experimental observations. Indeed, to correctly analyze the diffusion of finite-sized particles in narrow channels, one needs to account for the hydrodynamic effects as well. Because there is no general analytical solution for particle diffusivity in a corrugated confinement, we substituted the constant diffusivity, , with an empirical function from experimental measurements, . The substitution in Eq. 3 suggests a phenomenological factorization of entropic and hydrodynamic effects, with validity that is justified a posteriori by the reported close comparison with the experimental data. In conclusion, we have shown that, by making use of the measured diffusivity in Fig. 4C, the FJ theory can be improved to accurately predict the FPT statistics of Fig. 2; the FJ approach thus remains a powerful analytical tool to investigate diffusion in complex channels.
As shown in Fig. 4 A and B, the local diffusivity, , displays a rich 2D structure, which cannot be analytically predicted. The comparison with a more tractable geometry helps illustrate the phenomenon of the hydrodynamic diffusivity suppression advocated above. For a spherical particle of a radius diffusing along the axis of a relatively long cylinder (34, 49), the particle diffusivity is approximated by
| [6] |
where denotes the cylinder radius. According to Eq. 6, particle diffusivity in confined geometries is generally smaller than in an unbounded space. In our channels, the maximum diffusivity is about 60% of the Stokes–Einstein predicted value, (Fig. 4). Diffusivity also tends to decrease as the confinement grows tighter (i.e., for larger ); this qualitatively explains why diffusivity is smaller in the necking regions of our channel. In certain applications, such as the entropic splitters (33), one has recourse to tight confinement to generate high entropic barriers; we expect hydrodynamically suppressed diffusion to play an important role in these situations and possibly boost the separation efficiency.
In this work, we focused on the nonadvective diffusion of a single particle, although technological applications often involve many suspended particles driven by external fields (12, 35–38). Particle transport is certainly complicated by excluded volume and hydrodynamic interactions between nearby particles in dense suspensions. Moreover, external driving may prevent the system from equilibrating in the transverse directions and produce even more complex transport patterns (20); it can also cause additional hydrodynamic effects (36, 37, 50). The experimental setup and the data analysis methods presented here provide a promising framework for future systematic investigations of these important and challenging problems.
Materials and Methods
Channel Fabrication and Imaging Procedure.
Microchannels were fabricated with a two-photon direct laser writing system (FAB3D from Teem Photonics). This system uses a microscope objective lens (Zeiss Fluar 100, N.A. 1.3) to focus pulsed laser (Nd:YAG microchip laser with 532-nm wavelength, 750-ps pulse width, and 40-kHz repetition rate) into a droplet of photoresist resin that is mounted on a piezo-nanopositioning stage (Physik Instrumente model P-563.3CL). We used a polymer resin ORMOCOMP (Micro Resist Technology GmbH) with a photoinitiator [1,3,5-Tris(2-(9-ethylcabazyl-3)ethylene)benzene]. Photopolymerization occurs and solidifies the resin at the focal point; the piezo stage scans the resin relative to the focal point along a preassigned trajectory [ in Fig. 1A, Inset] to fabricate the desired structure. After the scanning is finished, the remaining liquid resin was removed by washing the structure with 4-methyl-2-pentanone and then acetone for 5 min. Then, channels were thoroughly cleaned with distilled water to prevent particles from sticking to the channel boundaries.
Fluorescently labeled Polystyrene particles were purchased from Invitrogen (catalog no. F13080). Particle motion was recorded through a 60× oil objective (N.A. 1.3) in an inverted fluorescent microscope (Nikon Ti-E). With the help of an autofocus function (Nikon Perfect Focus), we imaged the diffusion of a colloidal particle in the channel for up to 20 h at room temperature (27 °C).
BD Simulation.
The motion of a colloid particle is governed by a 2D overdamped Langevin equation in simulations. The particle diffusivity varies spatially when the diffusivity function is used; for thermodynamic consistency, we adopted the transport (also known as kinetic or isothermal) convention (51–54) to compute the stochastic integral (51, 55). The channel boundary was represented by a string of fixed particles, which interact with the colloidal particle via a short-range repulsive force. Particle trajectories from simulation were analyzed in the same way as their experimental counterpart to extract the effective volume of the channel’s unit cell and the FPTs. SI Appendix has more details.
Finite Element Calculation.
We solved the Stokes equations in a typical setup shown in SI Appendix, Fig. S2A. No slip boundary conditions were imposed on the side walls, floor, and ceiling, and open boundary conditions were imposed at the channel openings. The geometry of the side wall was set to reproduce the inner channel boundary measured in the experiments (Fig. 1A, Inset). A sphere was driven with a constant speed, , in the direction; at different points, is on a horizontal plane. We measured the drag force, , and computed the hydrodynamic drag coefficient, . SI Appendix has more details.
Supplementary Material
Acknowledgments
We thank Mingcheng Yang and Xiaqing Shi for useful discussions. We acknowledge the financial support of National Natural Science Foundation of China Grants 11422427 and 11505128 and Program for Professor of Special Appointment at Shanghai Institutions of Higher Learning Grant SHDP201301.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1707815114/-/DCSupplemental.
References
- 1.Hänggi P, Marchesoni F. Artificial brownian motors: Controlling transport on the nanoscale. Rev Mod Phys. 2009;81:387–442. [Google Scholar]
- 2.Burada PS, Hänggi P, Marchesoni F, Schmid G, Talkner P. Diffusion in confined geometries. ChemPhysChem. 2009;10:45–54. doi: 10.1002/cphc.200800526. [DOI] [PubMed] [Google Scholar]
- 3.Berkowitz B, Cortis A, Dentz M, Scher H. Modeling non-fickian transport in geological formations as a continuous time random walk. Rev Geophys. 2006;44:RG2003. [Google Scholar]
- 4.Kärger J, Ruthven DM. Diffusion in Zeolites and Other Microporous Solids. John Wiley; New York: 1992. [Google Scholar]
- 5.Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bressloff PC, Newby JM. Stochastic models of intracellular transport. Rev Mod Phys. 2013;85:135–196. [Google Scholar]
- 7.Benichou O, Voituriez R. From first-passage times of random walks in confinement to geometry-controlled kinetics. Phys Rep. 2014;539:225–284. [Google Scholar]
- 8.Hofling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys. 2013;76:046602. doi: 10.1088/0034-4885/76/4/046602. [DOI] [PubMed] [Google Scholar]
- 9.Deen WM. Hindered transport of large molecules in liquid-filled pores. AIChE J. 1987;33:1409–1425. [Google Scholar]
- 10.Hille B. Ion Channels of Excitable Membranes. Sinauer; Sunderland, MA: 2001. [Google Scholar]
- 11.Kettner C, Reimann P, Hänggi P, Müller F. Drift ratchet. Phys Rev E. 2000;61:312–323. doi: 10.1103/physreve.61.312. [DOI] [PubMed] [Google Scholar]
- 12.Matthias S, Müller F. Asymmetric pores in a silicon membrane acting as massively parallel brownian ratchets. Nature. 2003;424:53–57. doi: 10.1038/nature01736. [DOI] [PubMed] [Google Scholar]
- 13.Wanunu M, et al. Rapid electronic detection of probe-specific micrornas using thin nanopore sensors. Nat Nanotechnol. 2010;5:807–814. doi: 10.1038/nnano.2010.202. [DOI] [PubMed] [Google Scholar]
- 14.Jacobs M. Diffusion Processes. Springer; New York: 1967. [Google Scholar]
- 15.Zwanzig R. Diffusion past an entropy barrier. J Phys Chem. 1992;96:3926–3930. [Google Scholar]
- 16.Reguera D, Rubi JM. Kinetic equations for diffusion in the presence of entropic barriers. Phys Rev E. 2001;64:061106. doi: 10.1103/PhysRevE.64.061106. [DOI] [PubMed] [Google Scholar]
- 17.Kalinay P, Percus JK. Corrections to the Fick-Jacobs equation. Phys Rev E. 2006;74:041203. doi: 10.1103/PhysRevE.74.041203. [DOI] [PubMed] [Google Scholar]
- 18.Reguera D, et al. Entropic transport: Kinetics, scaling, and control mechanisms. Phys Rev Lett. 2006;96:130603. doi: 10.1103/PhysRevLett.96.130603. [DOI] [PubMed] [Google Scholar]
- 19.Berezhkovskii AM, Pustovoit MA, Bezrukov SM. Diffusion in a tube of varying cross section: Numerical study of reduction to effective one-dimensional description. J Chem Phys. 2007;126:134706. doi: 10.1063/1.2719193. [DOI] [PubMed] [Google Scholar]
- 20.Burada PS, Schmid G, Reguera D, Rubi JM, Hänggi P. Biased diffusion in confined media: Test of the Fick-Jacobs approximation and validity criteria. Phys Rev E. 2007;75:051111. doi: 10.1103/PhysRevE.75.051111. [DOI] [PubMed] [Google Scholar]
- 21.Berezhkovskii AM, Dagdug L, Bezrukov SM. Range of applicability of modified Fick-Jacobs equation in two dimensions. J Chem Phys. 2015;143:164102. doi: 10.1063/1.4934223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ai BQ, Liu LG. Current in a three-dimensional periodic tube with unbiased forces. Phys Rev E. 2006;74:051114. doi: 10.1103/PhysRevE.74.051114. [DOI] [PubMed] [Google Scholar]
- 23.Dagdug L, Berezhkovskii AM, Makhnovskii YA, Zitserman VY, Bezrukov SM. Communication: Turnover behavior of effective mobility in a tube with periodic entropy potential. J Chem Phys. 2011;134:101102. doi: 10.1063/1.3561680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Borromeo M, Marchesoni F. Particle transport in a two-dimensional septate channel. Chem Phys. 2010;375:536–539. [Google Scholar]
- 25.Bradley RM. Diffusion in a two-dimensional channel with curved midline and varying width: Reduction to an effective one-dimensional description. Phys Rev E. 2009;80:061142. doi: 10.1103/PhysRevE.80.061142. [DOI] [PubMed] [Google Scholar]
- 26.Dagdug L, Pineda I. Projection of two-dimensional diffusion in a curved midline and narrow varying width channel onto the longitudinal dimension. J Chem Phys. 2012;137:024107. doi: 10.1063/1.4733394. [DOI] [PubMed] [Google Scholar]
- 27.Bauer M, Godec A, Metzler R. Diffusion of finite-size particles in two-dimensional channels with random wall configurations. Phys Chem Chem Phys. 2014;16:6118–6128. doi: 10.1039/c3cp55160a. [DOI] [PubMed] [Google Scholar]
- 28.Burada PS, et al. Entropic stochastic resonance. Phys Rev Lett. 2008;101:130602. doi: 10.1103/PhysRevLett.101.130602. [DOI] [PubMed] [Google Scholar]
- 29.Ding H, Jiang HJ, Hou ZH. Entropic stochastic resonance without external force in oscillatory confined space. J Chem Phys. 2015;142:194109. doi: 10.1063/1.4921372. [DOI] [PubMed] [Google Scholar]
- 30.Hänggi P, Marchesoni F, Savelèv S, Schmid G. Asymmetry in shape causing absolute negative mobility. Phys Rev E. 2010;82:041121. doi: 10.1103/PhysRevE.82.041121. [DOI] [PubMed] [Google Scholar]
- 31.Marchesoni F, Savelèv S. Rectification currents in two-dimensional artificial channels. Phys Rev E. 2009;80:011120. doi: 10.1103/PhysRevE.80.011120. [DOI] [PubMed] [Google Scholar]
- 32.Malgaretti P, Pagonabarraga I, Rubi JM. Confined brownian ratchets. J Chem Phys. 2013;138:194906. doi: 10.1063/1.4804632. [DOI] [PubMed] [Google Scholar]
- 33.Reguera D, et al. Entropic splitter for particle separation. Phys Rev Lett. 2012;108:020604. doi: 10.1103/PhysRevLett.108.020604. [DOI] [PubMed] [Google Scholar]
- 34.Happel J, Brenner H. Low Reynolds Number Hydrodynamics. Prentice Hall; Englewood Cliffs, NJ: 1965. [Google Scholar]
- 35.Marquet C, Buguin A, Talini L, Silberzan P. Rectified motion of colloids in asymmetrically structured channels. Phys Rev Lett. 2002;88:168301. doi: 10.1103/PhysRevLett.88.168301. [DOI] [PubMed] [Google Scholar]
- 36.Huang LR, Cox EC, Austin RH, Sturm JC. Continuous particle separation through deterministic lateral displacement. Science. 2004;304:987–990. doi: 10.1126/science.1094567. [DOI] [PubMed] [Google Scholar]
- 37.Loutherback K, Puchalla J, Austin RH, Sturm JC. Deterministic microfluidic ratchet. Phys Rev Lett. 2009;102:045301. doi: 10.1103/PhysRevLett.102.045301. [DOI] [PubMed] [Google Scholar]
- 38.Mathwig K, Müller F, Gösele U. Particle transport in asymmetrically modulated pores. New J Phys. 2011;13:033038. [Google Scholar]
- 39.Pagliara S, et al. Diffusion coefficients and particle transport in synthetic membrane channels. Eur Phys J Spec Top. 2014;223:3145–3163. [Google Scholar]
- 40.Volpe G, Helden L, Brettschneider T, Wehr J, Bechinger C. Influence of noise on force measurements. Phys Rev Lett. 2010;104:170602. doi: 10.1103/PhysRevLett.104.170602. [DOI] [PubMed] [Google Scholar]
- 41.Chen SB. Drag force of a particle moving axisymmetrically in open or closed cavities. J Chem Phys. 2011;135:014904. doi: 10.1063/1.3606394. [DOI] [PubMed] [Google Scholar]
- 42.Dettmer SL, Pagliara S, Misiunas K, Keyser UF. Anisotropic diffusion of spherical particles in closely confining microchannels. Phys Rev E. 2014;89:062305. doi: 10.1103/PhysRevE.89.062305. [DOI] [PubMed] [Google Scholar]
- 43.Skaug MJ, Wang L, Ding YF, Schwartz DK. Hindered nanoparticle diffusion and void accessibility in a three-dimensional porous medium. ACS Nano. 2015;9:2148–2156. doi: 10.1021/acsnano.5b00019. [DOI] [PubMed] [Google Scholar]
- 44.Goel NS, Richter-Dyn N. Stochastic Models in Biology. Academic; New York: 1974. [Google Scholar]
- 45.Hänggi P, Talkner P, Borkovec M. Reaction-rate theory: Fifty years after kramers. Rev Mod Phys. 1990;62:251–341. [Google Scholar]
- 46.Verdel R, Dagdug L, Berezhkovskii AM, Bezrukov SM. Unbiased diffusion in two-dimensional channels with corrugated walls. J Chem Phys. 2016;144:084106. doi: 10.1063/1.4942470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Eral HB, Oh JM, van den Ende D, Mugele F, Duits MHG. Anisotropic and hindered diffusion of colloidal particles in a closed cylinder. Langmuir. 2010;26:16722–16729. doi: 10.1021/la102273n. [DOI] [PubMed] [Google Scholar]
- 48.Cervantes-Martinez AE, Ramirez-Saito A, Armenta-Calderon R, Ojeda-Lopez MA, Arauz-Lara JL. Colloidal diffusion inside a spherical cell. Phys Rev E. 2011;83:030402. doi: 10.1103/PhysRevE.83.030402. [DOI] [PubMed] [Google Scholar]
- 49.Misiunas K, Pagliara S, Lauga E, Lister JR, Keyser UF. Nondecaying hydrodynamic interactions along narrow channels. Phys Rev Lett. 2015;115:038301. doi: 10.1103/PhysRevLett.115.038301. [DOI] [PubMed] [Google Scholar]
- 50.Martens S, Straube AV, Schmid G, Schimansky-Geier L, Hänggi P. Hydrodynamically enforced entropic trapping of Brownian particles. Phys Rev Lett. 2013;110:010601. doi: 10.1103/PhysRevLett.110.010601. [DOI] [PubMed] [Google Scholar]
- 51.Hänggi P. Stochastic processes. I. Asymptotic behaviour and symmetries. Helv Phys Acta. 1978;51:183–201. [Google Scholar]
- 52.Sokolov IM. Itô, Stratonovich, Hänggi and all the rest: The thermodynamics of interpretation. Chem Phys. 2010;375:359–363. [Google Scholar]
- 53.Farago O, Gronbech-Jensen N. Langevin dynamics in inhomogeneous media: Re-examining the Itô-Stratonovich dilemma. Phys Rev E. 2014;89:013301. doi: 10.1103/PhysRevE.89.013301. [DOI] [PubMed] [Google Scholar]
- 54.Bruti-Liberati N, Platen E. Strong predictor–corrector Euler methods for stochastic differential equations. Stochastics Dyn. 2008;8:561–581. [Google Scholar]
- 55.van Kampen NG. Itô versus Stratonovich. J Stat Phys. 1981;24:175–187. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.