Neural signature of hierarchically structured expectations predicts clustering and transfer within and across rule sets

Abstract

Often the world is structured such that distinct sensory contexts signify the same abstract rule set. Learning from feedback thus informs us not only about the value of stimulus-action associations but also about which rule set applies. Hierarchical clustering models suggest that learners discover structure in the environment, clustering distinct sensory events into a single latent rule set. Such structure enables a learner to transfer any newly acquired information to other contexts linked to the same rule set, and facilitates re-use of learned knowledge in novel contexts. Here, we show that humans exhibit this transfer, generalization and clustering during learning. Trial-by-trial model-based analysis of EEG signals revealed that subjects’ reward expectations incorporated this hierarchical structure; these structured neural signals were predictive of behavioral transfer and clustering. These results further our understanding of how humans learn and generalize flexibly by building abstract, behaviorally relevant representations of the complex, high-dimensional sensory environment.

1. Introduction

How do we take actions that maximize the potential to obtain desired outcomes? Reinforcement-learning (RL) models successfully account for many aspects of human learning behavior and neural activity, by defining a process mechanism that integrates reinforcement history for well-specified stimuli and actions (1,2). However, in real life, stimuli are not so well defined: their features are nearly infinite, but only a small subset of them matter for determining how to act. While humans are adept at learning in complex novel situations, RL models in real world settings suffer from the curse of dimensionality. An approach to facilitate learning in complex environments would be to simplify the representation of the environment: for example, to recognize when different sensory states actually should be considered as equivalent, because interaction with them leads to similar outcomes. Doing so would afford generalization and transfer, obviating the need to learn for every single sensory state: given the same goal, any information gathered for one situation may also serve to inform other sensorily distinct, but behaviorally equivalent situations. This “learning to learn” functionality requires building a state and action space that is abstracted away from pure sensory/motor components, but instead comprises functionally relevant states/actions over which RL operates. Computational models of this structure learning process predict that learners cluster together contexts that are indicative of the same latent task set, and further, that such clustering also allows them to construct best guesses of the appropriate set of behaviors in novel contexts (3). Here, we investigate how the brain constructs, clusters and generalizes these types of structured rule abstractions in the course of learning.

As a real-world example, consider having a laptop with one operating system, and a desktop computer with another. Here, the current sensory context (laptop or desktop) cues a higher-order representation of an abstract context (Mac or Linux), which then determines the lower-order set of rules for behavior (specific actions to reach specific goals). The higher order context defines a rule-set that is “latent” or not tied to a specific context: in this case the observable context is the computer used, but the rule-set is more abstract and can be generalized to other contexts when appropriate, allowing for rapid learning and transfer of new actions. Thus, you may learn that your work desktop is also associated with the “Mac” rule-set. When you learn a new shortcut on that desktop, you can immediately assume that it will have the same effect on your laptop (but not on your home PC) even if you’ve never tried it before. Similarly, if you try a new computer and the shortcuts typically used on your PC produce desired effects, you may infer that it has the same OS and generalize your knowledge of that OS to other actions on that new machine. Clustering models further predict that the shortcuts you try in the first place are more likely to be the ones that have worked across a variety of machines – even if they’re not the machines (and hence shortcuts) you’ve used most frequently.

We recently showed that humans build structure a priori – subjects do not only discover structure when it exists in the task, but apply structure to learning problems that could be described more simply without structure and in which it is not directly beneficial to learning (3). Nevertheless, EEG markers of PFC function predicted subjects’ tendency to create structure and later use it to generalize previously learned rules to new contexts (4). Computational models captured this structured learning using Bayesian hierarchical clustering (5,6) of task-set rules, which could be approximately implemented in a hierarchical PFC-BG neural network (3). However, these previous studies were designed to test whether subjects tended to create structure even when no such structure was needed. Here, we develop a paradigm to assess whether subjects discover the form of structure that maximizes their ability to generalize, and whether they do so in a manner predicted by clustering models. In particular, these models predict that subjects should treat a particular dimension of the stimulus to be “higher-order” indicative of the rule-set if distinct elements of that dimension can be clustered together, that is, if they signify the same set of mappings between lower order stimulus features and actions. We test whether subjects can indeed identify the appropriate dimension that affords generalization, and further assess the implications of such clustering in novel contexts. We recorded EEG to assess evidence for such hierarchical clustering in the neural signal.

Specifically, our experimental paradigm (Fig. 1) assesses whether subjects abstract over multiple features that are perceptually distinct (e.g., different colors) but which all signify the same rule in terms of how they condition the contingencies between other features (e.g., shapes), actions and outcomes. Our model predicts that if one feature dimension (e.g. color) allows such clustering of lower level rules, then subjects will treat this feature as higher-order context indicative of an abstract latent task set (3), while treating the other features (shapes) as lower level stimuli. Because this structure separates the latent rule-set from the contexts (colors) that cue it, it endows a learner with the ability to append any newly encountered lower order stimulus-action associations to an existing rule-set, and thus to immediately generalize it to all contexts indicative of the same set.

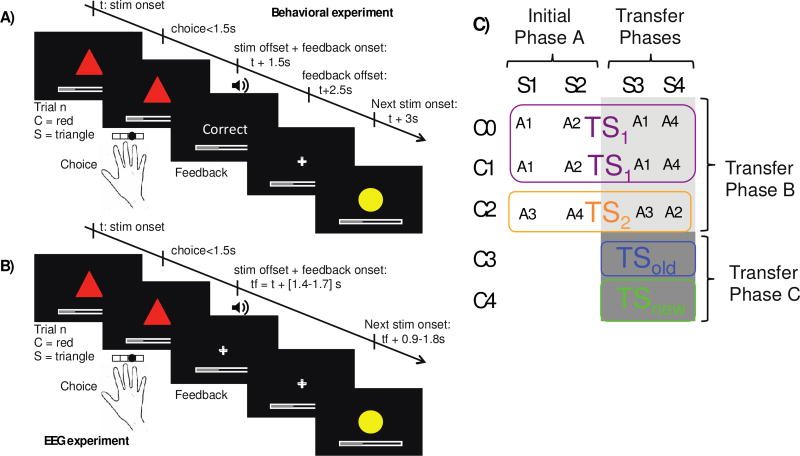
Figure 1. Experimental protocol.

A): Single trial structure for the behavioral experiment. B): Single trial structure for the EEG experiment. C) The table indicates correct (rewarded) action (A) contingencies for each context-stimulus (C-S) pair in initial phase A, and transfer phases B and C. “TS” indicates a task-set of stimulus-action contingencies that can be selected in a given context. If subjects learn that C0 and C1 cue the same TS1 in phase A, then they should more easily acquire new S-A associations that are shared across those contexts in phase B. In phase C, TS_old indicates that the valid TS in new context C3 corresponds to one of the previously learned TS1 or TS2, whereas TS_new denotes that a new set of S-A associations needs to be learned for context C4.

Our clustering model makes more specific predictions regarding how subjects treat new contexts in which they are uncertain about which existing rule-set (if any) should apply. Clustering implies not only that contexts indicative of the same rule can be grouped together, but also the number of such contexts in a cluster is indicative of the popularity of that structure, and hence affects the probability that this structure is selected in a new context (technically, we use a non-parametric prior called the Chinese Restaurant Process (CRP)(5,7)). Note, however, that the most popular rule may not be the one that has been experienced most often: clustering occurs as a function of number of distinct contexts and not the number of trials (as assumed in other clustering models (8)). (In the computer example, our model predicts that one’s expectation for the operating system of a new computer would be based on the relative proportion of computers that had used Mac OS in the subject’s experience, even if they had spent 95% of the time on a single PC). Thus in our design (Fig. 1, 2A,B) we equate trial frequency across different rule structures but assess whether subjects show evidence of context popularity-based clustering.

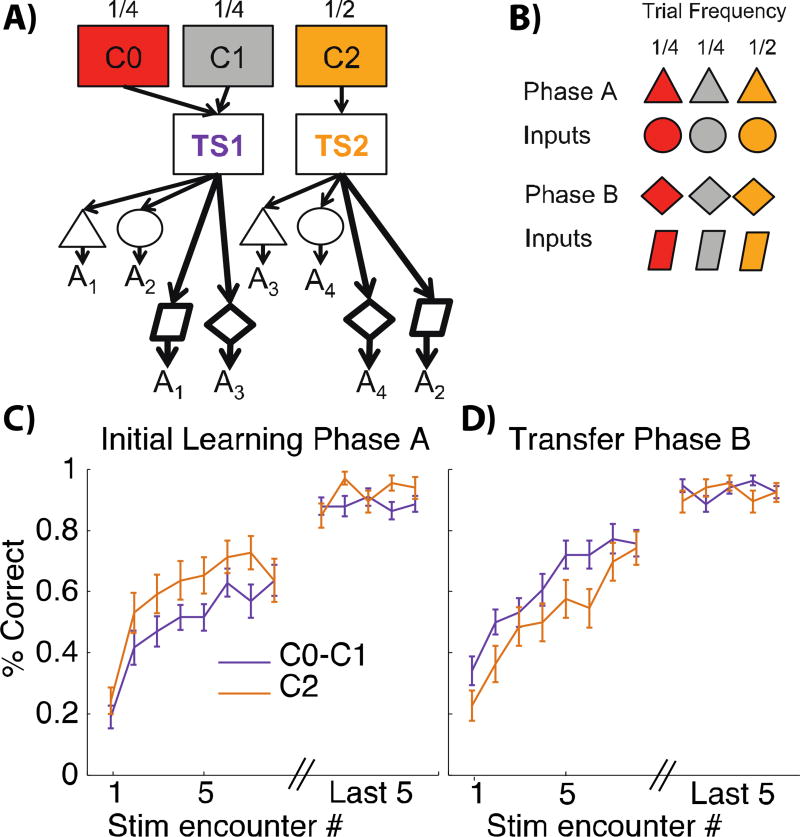
Figure 2. Initial learning phase A and transfer phase B.

A): Hierarchically-structured representation of phase A (light arrows) and new S-A associations to be learned in phase B (bold arrows). Subjects can learn in phase A to cluster C0 and C1 together to indicate the same abstract latent rule TS1. They can also expand the content of that TS (shared across contexts) in phase B to append new S-A mappings to it. B) Example of stimuli presented in initial phase A and transfer phase B of the experiments. Note that red and grey shapes are half as frequent as yellow shapes, such that TS1 and TS2 are both equally frequent. C–D): learning curves for initial phase A and transfer phase B, plotting the proportion of correct trials as a function of number of encounters of a given colored-shape, averaged over CO/C1 colored shapes (purple) and C2 colored-shapes (yellow). Within-cluster transfer is evident by faster learning of new S-A associations for C0/C1 than for C2 in phase B, despite slower initial learning in phase A.

EEG is sensitive to reward expectations (9–14). We use trial-by-trial model-based analysis (15–17) to investigate whether EEG signals are better accounted for by information processing that includes structure-learning, and whether these signals are predictive of generalization and clustering.

2. Material and Methods

2.1 Subjects

Behavioral experiment

34 subjects participated (20 female, ages 18–30), and one was excluded for outlier low performance. Analyses were performed on 33 subjects, including 18 in the TS1 as old TS in phase C group, and 15 in the TS2 group.

EEG experiment

We collected data for 39 subjects (26 female, ages 18–30). 7 subjects were excluded for poor participation (more than 50 no response trials) and a further 3 for poor performance (3 standard deviations under overall group mean performance), so that behavioral analysis was performed on 29 subjects. Due to technical problems with the EEG cap, 3 additional subjects were excluded from EEG analysis, leaving 26 subjects.

2.2 Experimental Protocol

Structure

Subjects performed a learning experiment in which they used reinforcement feedback to figure out which key to press for each presented visual input. The experiment was divided into three phases (see Fig. 1C). In all phases, visual input patterns comprised a novel set of colored shapes. After stimulus presentation, subjects selected one of 4 keys to press with their right hand. Simultaneous visual and auditory feedback indicated truthfully whether they had selected the correct action. See “trials” section below for more details.

Phases

The three phases of the experiment were designed to test whether subjects learned hierarchical structure and leveraged it to transfer and generalize knowledge in new contexts. We describe here the protocol in which color acts as “high level” context (Fig. 1A), but the role of color and shape was counterbalanced across subjects. Phase A included 6 different visual stimuli combining one of 3 colors (C0, C1 or C2) and one of two shapes (S1 or S2) (Fig 1C, Fig. 2A,B). We selected colored-shape action associations such that they were identical for C0 and C1 but different for C2. As shown in Fig. 2A, this provides an opportunity for structuring learning such that C0 and C1 can be clustered on a single task-set. Phase B included another 6 different visual stimuli combining one of the same 3 colors (C0, C1 or C2) with one of two new shapes (S3 or S4), Fig. 1, 2A,B. The associations to be learned in this transfer phase B respected the previous grouping of C0 and C1 into a single task-set (Fig. 2A), such that even though subjects still needed to learn de novo the correct actions for the new shapes, we could test whether they could use the structure acquired in phase A to more rapidly learn these associations that are shared between C0 and C1 by generalizing learning from one to the other. Phase C added novel contexts (colors C3 or C4) with one of two old shapes (S3 or S4) (Fig. 1, Fig. 3 top). Subjects could learn to re-use one of the previously learned task-sets (TS1 or TS2) for one context C3, but would need to create a new TS for C4. This transfer phase C thus allowed us to test whether, and how well, subjects could transfer a learned rule to a new context.

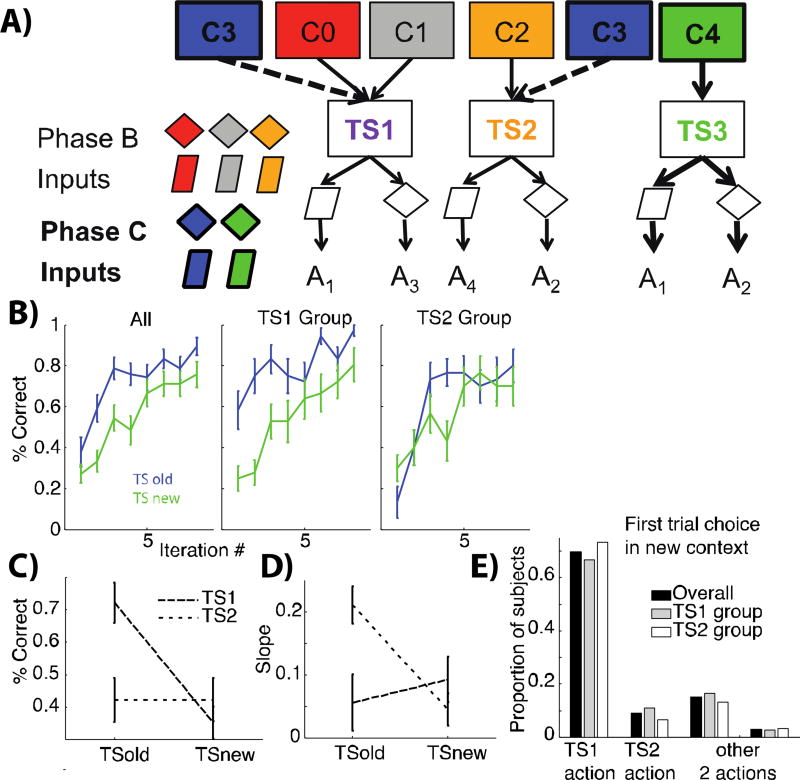
Figure 3. Transfer to novel contexts and clustering priors.

A): Hierarchically structured representation of phase B and C. If subjects applied structure to learning in phase A/B, they can then recognize that C3 points to one of the previously learned latent rules (either TS1 or TS2, dotted arrows) and hence generalize their learned S-A mappings. In contrast they would need to create a new TS3 for context C4. B) learning curves for transfer phase C. Learning is speeded for TS that were previously valid in old contexts. This effect is particularly evident for those subjects for whom the old TS was the more popular TS1 (clustered across two contexts; middle graph) compared to the less popular TS2 (right). C, D) summary measure over first 3 trials for each condition (TS_old or TS_new): mean performance (C), slope (D). E) Action choice for first trial in phase C. Proportion of subjects who chose the action prescribed by TS1 for that stimulus, by TS2, or either of the other two actions. There is a strong bias towards TS1, prior to any information in the new phase, despite equal TS and action frequencies.

In phase A and B, the sequence of visual input patterns was pseudo randomized such that C0-Si, and C1-Si appeared half as frequently as C2-Si (Fig. 2B). This allowed us to ensure that the two task-sets (TS1 and TS2) were equally frequent and that any benefit of context popularity could not be explained by overall TS frequency. In phase C, all input patterns were equally frequent. The correct action for a given shape was always identical for C0 and C1, and different from C2 (see Fig. 1, 2A). Phase A and B included at least 40 and at most 120 trials or up to a criterion of 4 out of 5 last trials correct for each stimulus, followed by 60 additional asymptotic trials. Phase C included 80 trials.

Trials

Stimuli were presented centrally on the black background screen (approximate visual angle of 8°) for 1.5s, during which time subjects were instructed to answer by pressing one of four keys (see Fig. 1A). This was immediately followed by feedback presentation for 1s: word “correct” or “incorrect”, tone (ascending 200ms tone for “correct” [frequencies 400–800Hz], a descending 200ms tone (same frequencies) for incorrect, and a [100Hz] low 200ms tone for missed trials) and filling/emptying of a cumulative reward bar. Failure to answer within 1.5s was indicated by a “too slow” message. Feedback was followed by a .5s fixation cross before next trial onset. For the EEG experiment, stimulus presentation was uniformly jittered (1.4–1.7s), but subjects still needed to respond within 1.5s (Fig. 1B). Feedback followed stimulus offset immediately, but did not include “correct/incorrect” words, it only included the tones, the cumulative reward bar, with a central fixation cross. Next stimulus onset occurred after a uniform jitter in [0.9–1.8]s.

2.3 Computational modeling

We contrast two kinds of models by which the task could be learned. The classic “flat” reinforcement learning (FRL) model makes the assumption that subjects learn to estimate stimulus-action values for each input pattern (e.g. red triangle C1S2, yellow circle C2S1, etc.) independently. Conversely, our structure-learning model (SRL) makes the assumption that subjects learn the latent task state space representing the structure of the environment, and that we perform reinforcement learning operating in this latent space. Thus actions to be learned are not tied to individual C or S or their conjunction, but to a latent task representation to be learned (e.g. where C0 and C1 cue the same set of stimulus-action associations). The latter is similar to our previously published hierarchical learning model (3).

The FRL model relies on standard delta rule learning for estimating expected reward Q(C_t,S_t,a_t) for a given color (C_t), shape (S_t) and action on each trial t. If the reward obtained is r_t (0 or 1), the estimate is updated by incrementing by α×δ, where α is the free learning rate parameter, and δ is the prediction error:

$$\mathrm{\delta }(\mathrm{t})=\mathrm{r}-\mathrm{Q}({\mathrm{C}}_{\mathrm{t}},{\mathrm{S}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}).$$ (Eq 1)

Value estimates are initialized at chance expectation Q₀ = ¼ (since there are four responses). Action choice is presumed to proceed from an epsilon-softmax policy such that for any action a = {1,2,3,4},

$$\mathrm{P}(\mathrm{a}|\mathrm{C},\mathrm{S})=\mathrm{\epsilon }/4+(1-\mathrm{\epsilon })\ast \text{exp}(\mathrm{\beta }\mathrm{Q}(\mathrm{C},\mathrm{S},\mathrm{a}))/\sum \text{ exp}(\mathrm{\beta }\mathrm{Q}(\mathrm{C},\mathrm{S},{\mathrm{a}}_{\mathrm{i}})).$$ (Eq 2)

Here, β is the gain of the softmax logistic function such that higher values imply more deterministic choice with greater differences in Q values, and ε reflects irreducible noise (i.e. to fit a proportion of trials due to attentional lapses etc). Two additional model-free learning mechanisms (decay, and within-dimension bleed-over) improved fit despite added complexity, and are thus integrated in the FRL. See Appendix for details.

Structure-learning model SRL

Our structure model assumes that, instead of learning to estimate values of actions for the specific shapes and colors, subjects create a latent state space that better reflects the structure of the environments. A latent state can be thought of as a task-set: it conditions the value of a shape-action-outcome association; and more than one color can be associated to this latent task-set. We call structure building the process of creating the space of latent variables over which learning is performed. We make the assumption that these latent variables represent clusters of input features (such as colors). Our model allows for building of structure using either input dimension (which features could be clustered into latent variables that conditioned action-outcome likelihoods): indeed, subjects cannot know in advance which (if any) input dimension needs to be clustered, so the model incorporates this uncertainty. The approximate inference process can thus infer clusters on both dimensions jointly, defining a new, more abstract factorized state space on which to perform learning.

The cluster membership of a color is tracked probabilistically in P(Zc|C). For a new color, this is initialized with the following prior (Eq 3):

• -for existing clusters Z_i, P(Z_i|C_new) = (1/K) × Σ_j=1:NP(Z_i|C_j), where {1,…,N} are the indices of N previously encountered contexts and K is a normalizing factor
• -for a new cluster, P(Z_c|C_new) = α /K (where α is a concentration parameter).

This prior is similar to the non-parametric “Chinese-Restaurant process” distribution (5,7)¹, and has the important properties that 1) the number of clusters is unconstrained 2) there is a parsimony bias such that the model attempts to assign new contexts to clusters that were most popular across multiple contexts. After an action is selected and a reward is obtained, P(Z_i|C_t) is updated via Bayes rule, with the likelihood of the observed outcome estimated from the Q-value table:

$$\mathrm{P}({\mathrm{Z}}_{\text{Ci}}|{\mathrm{C}}_{\mathrm{t}})\leftarrow \mathrm{P}({\mathrm{Z}}_{\text{Ci}}|{\mathrm{C}}_{\mathrm{t}})\times \mathrm{P}(\mathrm{r}|{\mathrm{Z}}_{\text{Ci}},{\mathrm{Z}}_{\text{St}},{\mathrm{a}}_{\mathrm{t}})/[{\sum }_{\text{Cj}}\mathrm{P}({\mathrm{Z}}_{\text{Cj}}|{\mathrm{C}}_{\mathrm{t}})\times \mathrm{P}(\mathrm{r}|{\mathrm{Z}}_{\text{Cj}},{\mathrm{Z}}_{\text{St}},{\mathrm{a}}_{\mathrm{t}})]$$ (Eq 4)

In this equation, the likelihood is estimated by the Q-table Q(Zc_i,Zs_t,.). The same process occurs independently for shapes.

At each trial, P(Z_Ci|C_t) and P(Z_Si|S_t) are used to infer the most likely cluster Zc_t, Zs_t for current color and shape C_t and S_t. This corresponds to a maximum a priori approximation for action selection, using the prior probability; and a maximum a posteriori approximation for learning, using the posterior probability.

The model uses reinforcement learning to estimate outcomes for different actions on the clustered input space, rather than directly on the original sensory state-space: if this trial’s context C and stimulus S were inferred a priori to belong to color cluster (Zc_t) and shape cluster (Zs_t) the model updated cluster estimates:

$$\mathrm{Q}({\text{Zc}}_{\mathrm{t}},{\text{Zs}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}})\leftarrow \mathrm{Q}({\text{Zc}}_{\mathrm{t}},{\text{Zs}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}})+\mathrm{\eta }\times \mathrm{\delta },$$ (Eq 5)

using prediction error δ = r_t − Q(Zc_t,Zs_t,a_t) as increment modulated by learning rate η. Similar to FRL, action selection was modeled using a noisy softmax logistic function over Q(Zc_t,Zs_t,.), where color cluster (Zc_t) and shape cluster (Zs_t) are inferred a posteriori to be the most likely relevant ones for the current color and shape.

As in FRL, we also included two mechanisms in SRL that account for forgetting and low level biases (see details in appendix).

We tested other models including various combinations of the mechanisms included in FRL and SRL, but we focus on these two models because they offered best fits within the flat and structured RL model classes, respectively, accounting for complexity. Parameter fitting was performed with constrained optimization function from matlab (fmincon), with 25 randomly chosen starting points. We penalized models for added parameter complexity with Akaike Information Criterion (18).

2.4 EEG

2.4.1 System

EEG was recorded from a 64-channel Synamps2 system (0.1–100 Hz band-pass; 500Hz sampling rate).

2.4.2 Data Preprocessing/Cleaning

EEG was recorded continuously with hardware filters set from 0.1 to 100 Hz, a sampling rate of 500 Hz, and an online vertex reference. Continuous EEG was epoched around the feedback onset (−1500 to 2500 ms). We used previously identified data cleaning and preprocessing method (4,19) facilitated by the EEGlab toolbox (20): data was visually inspected to identify bad channels to be interpolated and bad epochs to be rejected. Blinks were removed using independent component analysis from EEGLab. The electrodes were referenced to the average across channels.

2.4.3 ERPs

For event-related potentials (ERP) and multiple regression analysis, data were bandpass filtered from 0.5 to 20 Hz and down-sampled to 250Hz. For each subject, we performed a multiple regression at each electrode and time point within 0–800ms (200 time points). Because there were many less error than correct trials, we included only correct trials in the analysis, and restricted it to phase A and B. Scalp voltage was z-scored before being entered into the multiple regression analysis. There were three regressors. The first one was the FRL model prediction error (FPE; eq1), extracted for each subject from the model with their fit parameters. For the second regressor, we extracted the SRL model prediction error (SPE; eq 5) with the same procedure; but since SPE and FPE are strongly correlated, we orthogonalized SPE against FPE to obtain unique variance to SPE (note that in contrast, the FPE regressor contains both unique variance to FPE and shared variance with SPE). Last, we included one regressor of non-interest, indicating which phase of the experiment (A or B), the trial is part of, so as to control for this as a potential confound in SPE vs. FPE effects. We analyze regression weights for the first two regressors, β_FPE and β_SPE, obtained for each subject, time-point, and electrode.

2.4.4 Statistical analysis of GLM weights

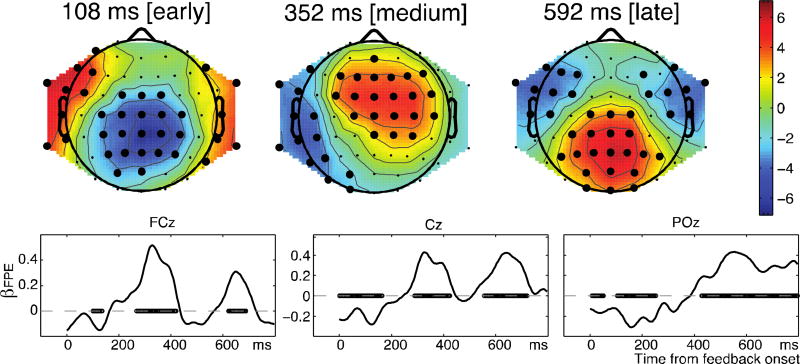
we tested the significance of β_FPE against 0 across subjects for all electrodes and time-points. To correct for multiple comparisons, we performed cluster-mass correction by permutation testing with custom-written matlab scripts, following the method described (21). Cluster formation threshold was for a ttest significance level of p=0.001². Cluster mass was computed across space-time, and only clusters with greater mass than maximum cluster mass obtained with 95% chance permutations were considered significant, with 1000 random permutations. We obtained 5 positive and 4 negative clusters with a significant effect of FPE. They spanned three time periods separated by time points with no significant electrodes. We thus grouped the clusters based on their time overlap into three regions of interest described in main text (see Fig. S4B, movie S1).

To analyze the supplementary effect of SPE, we computed the average β_SPE within each ROI (weighted by β_FPE t-score; such that a negative SPE weight in a negative FPE ROI would contribute positively, as would a positive SPE weight in a positive FPE ROI). We obtain similar results when weighing by the sign of the t-score only, or when looking at non-weighted averaged beta weights within clusters. Averaged betas for the three ROIs were then tested against 0 across subjects.

3. Results

As indicated in methods (2.2), subjects underwent three contiguous learning phases, each presenting different visual input patterns consisting of two features (colored shapes) in pseudo-randomized order. Subjects had 1.5s to select one of 4 actions (button presses with their dominant hand). Feedback followed indicating whether their choice was correct. In the initial phase (A, Fig. 2A,B), subjects learned to select correct action choices for each of 6 input patterns, comprising 3 colors and 2 shapes (or vice-versa; the role of color vs. shape was counterbalanced across subjects). Crucially, two contexts (colors C0 and C1) were linked to the same rule-set or task-set (TS1) signifying stimulus shape-action (S-A)-outcome contingencies, while the other (C2) signified a different task set (TS2). That is, for context C2, a different set of actions was rewarded for the same shapes. C0 and C1 were each presented on half as many trials as C2, such that TS1 and TS2, and each motor action, were equally frequent across trials.

3.1 Behavioral results

3.1.1 Within-Cluster Transfer of Newly Learned Rules

In phase B (Fig. 1, light grey, 2A bold arrows), 6 new input patterns corresponding to two new stimuli (in this example, shapes) but in previously seen contexts (colors) were presented; subjects had to learn novel arbitrary stimulus-action associations. Shape-action to be learned associations were again identical across C0 and C1, but different for C2. If subjects had learned in phase A to cluster together C0 and C1 into a single latent task set, then in phase B they should be able to append novel S-A mappings in either of these contexts to that TS structure rather than directly to the contexts themselves. As such, our model predicts that subjects transfer novel S-A mappings acquired in C0 immediately to C1 (linked to the same TS), and vice-versa, and hence learn faster in C0/C1 than in C2. Specifically, subjects should require less encounters of any single colored-shape to reach a given performance level for colors C0/C1 than they would in C2 (Fig. 4B for model predictions). Indeed, there was clear evidence for this transfer (t(32)=2.71, p=0.01; Fig. 2D). This finding implies that subjects appended new stimulus-action associations to existing latent structures, such that they can be immediately transferred to contexts linked to those structures.

Figure 4.

Model simulations from structure learning model with parameters fitted to individual subjects’ behavior in the EEG experiment. Learning curves show mean and standard error (error bars) across subjects, and represent proportion of correct trials for the xth presentation of each individual input pattern. A–B): phase A/B simulations account for the empirically observed transfer, with greater performance in C0/C1 than C2 in phase B, and the opposite counter-intuitive pattern in phase A. C) Phase C shows transfer of old task-set to a new context. D) Proportion of chosen TS1, TS2 or other actions taken for first 2 iterations of every input pattern of phase C shows a generalization bias to select previous TS1 more than TS2 (“context popularity-based clustering”), which was in turn more likely than other actions.

Note, however, that this transfer requires that subjects had already learned in phase A which contexts could be clustered together (and indeed, which dimension should be treated as higher order). Accordingly, there was no such transfer between C0 and C1 during phase A before this structure had been learned: indeed, performance during initial early learning (first 8 iterations of C0–C1 stimuli) was significantly lower than that for C2 stimuli (t(32)= −2.95, p=0.006; interaction between TS and phase t(32)=4.16, p=0.0002, Fig. 2C). This apparent counterintuitive finding is accounted for by the fact that by design (see above) C0 and C1 were presented half as often as C2, thus increasing the delay between two successive presentations of the same visual input and allowing for more forgetting (22). Once subjects discovered the structure, this disadvantage was reversed, leading to transfer in phase B despite the fact that delays between visual inputs were still longer. Fig. 4A–B shows that our computational model can reproduce this qualitative pattern of results. Our interpretation is supported by logistic regression analysis showing that the probability of correct choice was significantly impacted by delay in phase A (t=− 5.03, p<10−4; see SI). In contrast, we expected that once structure was learned, subjects should abstract away the specific perception of C0 and C1 into a single abstract TS1. Indeed, in phase B, once subjects observed the correct outcome for a choice in either C0 or C1, they were significantly more likely to make the same choice for the other context, as compared to phase A (t(30)= 2.4, p=0.02, see SI).

3.1.2 Generalization of Clusters to Novel Contexts

The above findings show that subjects reliably clustered contexts indicative of the same rule-set, allowing them to append novel stimulus-action associations to existing sets and to transfer them across contexts that cue them. We next investigated whether subjects could transfer these clustered rule-sets to novel contexts, and in particular, whether they would show evidence for context popularity-based clustering in their initial responses. In phase C (Fig. 1, dark grey, Fig. 3A), subjects learned about four new input patterns corresponding to two new contexts (eg. colors), one of which (C3) corresponded to an old rule-set (either the more popular TS1 or less popular TS2), while the other (C4) corresponded to a novel rule (TSnew). In a first behavioral experiment, subjects were assigned to either of two groups, with C3 mapping to either TS1 or TS2. In a second experiment, a separate group of subjects performed the same task twice in a row, once with TS1 and once with TS2 (with non-overlapping stimuli) while we measured EEG. We report the behavioral experiment results that were replicated in the EEG experiment (see appendix).

We first confirmed previous observations (3,4) that overall, subjects learned significantly faster for novel context C3 associated with an old rule, than for context C4, for which they needed to form a new set of stimulus-action associations (Fig. 3B, left, t(32)=3.29, p=0.002). Further, the design here allowed us to test a novel prediction of our clustering model: that a priori (i.e., without having any information on which TS applies), subjects should be more likely to try to transfer TS1, which was more popular across contexts during phases A/B than TS2, despite their equal frequency across trials. Indeed, subjects for whom the old TS to reapply in C3 was TS1 (n=18) exhibited very strong transfer (Fig. 3B, middle, t(17)=4.48, p=0.0004), while subjects in the TS2 group (n=15) did not (Fig. 3B, right; group effect on transfer, t(31)=2.94, p=0.006). Moreover, subjects in the TS2 group exhibited below chance performance in their initial trials, as expected if they had a prior to try TS1 first, but then subsequently showed significantly steeper learning for C3 than C4 (Fig. 3 D, t(15)=3.87, p=0.002). Thus, overall patterns of learning in phase C are consistent with an attempt to transfer the most popular TS1, with preserved ability to nevertheless transfer TS2 and rapidly detect when it applies, relative to a novel TS.

3.1.3 Context Popularity-Based Priors

Note that the model’s prediction relates to subjects’ priors in a new context, and thus this prior bias for TS1 vs. TS2 should be observed on the very first trial of phase C, before subjects have acquired any information, and independently of their group assignment. We tested this by looking at action choice for the very first trial of phase C, and whether it matched the action prescribed by either of the old task-sets (or neither). Subjects exhibited a strong bias for selecting the action prescribed by TS1 for that specific stimulus, as opposed to the action prescribed by TS2 or either other action (Fig. 3E; test against uniform: chi2(3)=35, p=10⁻⁷; binomial test TS1 action against any other: p=0.035), strongly supporting the popularity prior interpretation. As expected, this original bias decreased rapidly with experience, but was still present when looking at the first two iterations of each new input (TS1>TS2: t=1.92, p=0.06; TS1>other actions, t=2.26, p=0.03).

3.1.4 Model fitting

We fitted subjects’ trial-by-trial behavior with a modified version of our structure-learning model (see methods 2.3, appendix). The structure learning model fit significantly better than all other models. In particular, the SRL provided significantly better fit than FRL (lower AIC: t(28) = 4.4, p = 10−4), and the fit was better for a significant number of subjects (sign test, p<0.001; Fig. S3). Furthermore, simulations with fit parameters qualitatively replicated the main behavioral findings (Fig. 4), validating the use of this model for model-based analysis of trial-by-trial EEG data.

We hypothesized that, if subjects learn latent structure and use it for transfer and generalization, we should be able to see evidence for this structure in their neural encoding of reward expectations and violation thereof (prediction error). For example, if the brain treats the task hierarchically, with e.g., the color dimension at the top of the hierarchy because it facilitates TS clustering of S-A associations then we should be able to see evidence of that structure in the nature of their brain response to surprise (prediction errors). Thus, the EEG signals of surprise should be diminished for outcomes within a given structure when that same outcome had already been linked to that structure in a different context. Our model allows us to quantify each trial’s reward prediction error, and how it differs from a non-structured RL model (in which each context and stimulus is treated as its own state; see methods). We thus extracted for each subject the sequence of prediction errors inferred by our structure model SRL, and further label them SPE. We also extracted the prediction errors inferred by the best-fitting non-structure “flat” reinforcement-learning model FRL, and further denote them FPE.

3.2 EEG: effect of reward expectations

We next investigated subjects’ brain activity during learning, focusing on feedback-locked event-related potentials. Specifically, we investigated with a multiple regression the effect of reward expectation SPE and FPE on the EEG signal (correct trials of phases A–B; see methods 2.4.4). We predicted that subjects’ expectations for reward should be influenced by structure-building and information integration within clustered contexts. Thus, structure-learning model’s SPE should explain trial-by-trial neural variations better than classic prediction error FPE.

There was robust activity correlating with FPE across time and electrodes (see Fig. 5, p<.05 cluster corrected; Fig. S4 and movie S1 for complete pattern of PE-related activity). To investigate the additional effect of structure learning SPE, we first identified time-space regions of interest (ROIs) that were sensitive to classic prediction-error FPE: an early region (negative effect at Cz; see Fig. 5 at 108ms); a medium region (positive effect at FCz and Cz; see Fig. 5 at 352ms); and a late region (t>450ms), essentially centrally positive (see methods). We then tested whether these three ROIs showed additional sensitivity to unique variance of structured learning prediction error (SPE), averaging its regression weights across corresponding time-electrode pairs (weighted by t-values of FPE effect). The effect of SPE was significant over the grouped ROI (t(26)=2.9, p=0.007), as well as separately within the early (t=3.19, p=0.004) and medium (t=2.28, p=0.03) ROIs (Fig. 6A), but only trending within the late cluster (t=1.61, p=0.12). This indicates that SPE accounted for supplementary variance within areas sensitive to FPE, supporting the notion that neural markers of expectation are sensitive to structured information that could support generalization. A symmetric analysis of additional FPE effects within SPE ROIs found very similar ROI’s (as expected from the high correlation between the SPE and PE; see Fig. S4), but did not show evidence of added variance attributed to FPE (see SI; Fig. S5), supporting the special importance of structure learning for subjects in this experiment.

Figure 5. EEG effect of prediction error.

Top: scalp maps at representative time points of t-statistic of β_FPE across subjects, corresponding to the three cluster-groups identified as ROIs. Bold black dots indicate for visualization purpose corrected p<0.05 significant effects. Bottom: average across subjects of flat prediction error regressor β_FPE, for electrodes FCz, Cz and POz. Circles indicate significance against 0 at p<.05 (cluster-based permutation tested).

Figure 6. SPE effects in EEG.

A): average regression weight for unique structure RL variance in each group ROI shows that SPE accounts for additional variance beyond flat PE (Error bars indicate standard error). B) early+ medium SPE effect predicts behavior. We separate subjects into “high” and “low” SPE effect groups, by median-split. Left: “High” group showed stronger “within cluster” transfer, as indicated by increase in TS1 vs. TS2 performance difference between phase A and B. Middle: “high” group showed a stronger bias to select previously more clustered action (TS1 action). Right: “High” group shows significantly more generalization of old task-sets to new context in phase C.

We further tested whether the degree of neural sensitivity to SPE predicted behavioral evidence of structure. We pooled those ROIs sensitive to SPE (early and medium), and measured the SPE effect size as the weighted average of SPE beta values on this pooled ROI. We then investigated its link to the three main indicators of structure in behavior: transfer – within existing clusters, phase B, and to novel contexts, phase C – and clustering, as indicated by the degree to which initial actions show evidence for generalizing those TS that were most popular across contexts.

We first investigated whether the SPE effect in phases A and B predicted transfer of learned structure in early trials of phase C. Indeed, we found a significant correlation between the β_SPE and the early bias in selecting old TS actions (Spearman ρ=0.38, p=0.05). To further investigate this link, we separated subjects into “low” and “high” SPE effect groups by median split. The “high” group exhibited significant behavioral effects of transfer, including significant within cluster (phase B) transfer (t=2.6, p=0.02; Fig. 6B left) and across context (phase C) generalization (t=2.35, p=0.036; Fig. 6B right). In contrast, the low group showed neither effect (t=−0.3, t=−0.16, ns), although the effect of group on generalization did not reach significance (t=1.63, p=0.12; t=−0.16 ns). Additionally, the distribution of first trial choices (“clustering prior”) was significantly different across groups (chi2(2)=24; p=6.10-6; Fig. 6B middle), indicating that the “low” SPE group subjects were more likely to pick other actions and less likely to try the more popular TS1 actions, compared to the high SPE group (t=2.9; p=0.007). Taken together, these results support the hypothesis that subjects showing more evidence of structured learning in the EEG representation of expectations also exhibited more robust evidence of structure learning and generalization in behavior. Further, neural evidence of structured SPE was predictive of subsequent transfer and clustering priors in phase C (Fig. 6B), despite the fact that this phase was not included in the EEG analysis.

4. Discussion

These findings, replicated across two behavioral experiments, provide novel and strong support for the notion that subjects build latent rule structure during simple learning tasks, consistent with our computational model of hierarchical clustering. The degree of such structured behavior was also related to markers of hierarchical structure learning in EEG. Our results imply that subjects do not simply learn to predict outcomes for the given perceptual state and motor action spaces. Instead, they create latent variables that cluster together contexts corresponding to the same lower level rules. These latent rule pointers condition stimulus-action outcome predictions, and thus choice, indicating that learning occurs on the structured, latent state space, rather than on the sensory input variables. Such structure learning affords two levels of generalization. First, new stimuli, and their action-outcome consequents, do not need to be disembodied from existing knowledge, but can instead be appended onto existing latent rule-sets, rather than attached to a specific context. This provides potential immediate transfer to all contexts cuing this rule-set, regardless of which context was active when the new information was gathered. (As a real world example, consider a language as a rule-set. If one learns a new word label for a new object in a given language spoken by a particular person (context), one can then immediately use that word oneself to other people known to speak the language). This is evidenced by faster learning in phase B for contexts that have provided an opportunity for clustering. Such a result was predicted by our model (3) but had not yet been tested empirically.

Second, new contexts can be recognized as cueing to an existing cluster if they condition the same stimulus-action-outcome predictions. This allows for immediate transfer of an entire known latent rule to new contexts, even for as yet unencountered stimuli. We observe this in phase C where subjects learn faster for a new context corresponding to an old rule than a new one (3,4). Moreover, our findings show for the first time that their prior tendencies to select rule structures are consistent with a context-popularity based clustering. A principled way to cluster an unknown number of contexts into latent states that point to the same abstract rule can be achieved by a nonparametric Bayesian framework. Our model used the “Chinese restaurant prior”, building on existing models of conditioning (8). However, while those models use this prior to cluster experiences (trials) indicative of the same latent cause, we cluster the number of discrete contexts rather than individual trials. We thus predicted that even with equal popularity of rules across time, subjects would be a priori more likely to try out rules that were more popular across contexts. (In the language example, our model predicts that one’s expectation for the language of a new speaker would be proportional to the relative number of speakers of that language they had encountered, and not simply the relative number of words they had heard in each language, which could be biased by an inordinate number of experiences with a given foreign speaker). This prediction was confirmed both by comparing the overall degree of transfer of old popular vs. less popular rules, and by showing a biased action selection pattern at the very first trial in a new context, prior to having collected any information about that new context.

It is remarkable that subjects build structure despite the fact that they don’t benefit from it immediately, as indicated by the lower performance for the two contexts linking to the same rule during the initial learning phase (before the nature of the structure could be known). This study hints as an explanation for this prior tendency to build structure, as it affords two kinds of advantages in terms of long-term flexible generalization and transfer of learned knowledge.

As expected from published literature. we found that the ERP signal is sensitive trial-by-trial to reward expectation (9–11,13,14,17). We tested whether this signal included only purely model-free RL information, or whether it integrated expectations gathered via structure learning that provided transfer of information across context clusters. EEG results support the fact that the brain represents this latent structure RL expectation, rather than a simpler one. Furthermore, the degree to which the structure expectation was represented predicted observed behavioral transfer. This supports previous fMRI findings showing that the prediction error signal may include complex knowledge (14,23,24), and recent studies showing that frontocentral EEG signals reflect cognitive control rather than model-free learning (25) extending these to the domain of structure learning. Indeed, our neural model of structure learning (3) involves similar cognitive control mechanisms to prevent motor action selection until uncertainty about the currently valid latent rule is resolved. Note that we are agnostic as to the source of the EEG signals, given the limited research into how standard ERP components are implicated in hierarchically structured tasks with multiple dimensions. Thus our findings are limited in their ability to inform us of the underlying neural sources (26), but nevertheless facilitate characterization of the cognitive representations involved (beyond those inferred via indirect behavioral measures associated with RT switch costs and transfer) by assessing reward expectations (and violations thereof) associated with structured vs. non-structured learning.

Our structure-learning model complements a growing literature on hierarchical reinforcement-learning, state-space or structure learning. Related literature on acquired equivalence(27,28) shows that humans can link together stimuli that never appear together but which similarly predict subsequently appearing stimuli. Our finding of transfer within rule-sets extends this type of association to stimuli within hierarchical task-sets, and explores the nature of the clustering link. Other models have investigated how subjects find a relevant smaller state space on which to perform RL (8,29), even in a context-dependent way (30,31). However, these models learned to ignore irrelevant dimensions entirely, essentially relating them to attentional processes. In contrast, here all dimensions and features are relevant, but latent variables are created that abstract away some features of input dimensions, but not others. Furthermore, this latent variable is an abstract object in itself, rather than being equated to the sensory contexts it is selected in –providing the two generalization possibilities: extending the content of the object, and selecting it in new contexts. This property is similar to some of our previous work where structures are cued by episodic contexts (32,33), but is extended to building this structure even in the absence of a temporal shaping process. Other modeling work has proposed abstract representation of latent hierarchical task-rules or abstract task-relevant states, implicating OFC or ACC (34,35). Critically, contrary to our model, they did not provide a mechanism for the creation of these abstract representations, nor for the ability to append novel associations to these structures, which is crucial to the ability to transfer knowledge and cluster together contexts in a behaviorally, rather than perceptually, relevant manner.

These findings show that subjects were able to build structure that afforded strongest potential for future generalization – even though they did not benefit from it immediately. Two separable kinds of transfer were observed: the ability to reselect an abstract rule in a new context, in proportion to its popularity; and the ability to expand an abstract rule for all members of the cluster. EEG analysis confirmed that structure-dependent expectations were represented in the neural signal to an extent that predicted behavior. These results indicate the crucial importance played by building abstract structure, even in simple learning environments.

Highlights.

• Humans create latent hierarchical rule structure when learning from reinforcement

• They cluster such rules according to their popularity across contexts

• This allows immediate generalization of new information to equivalent contexts

• It also facilitates transfer of rules to new contexts

• EEG signals reflect hierarchically structured expectations and predict transfer