Using Machine Learning to Identify Air Pollution Exposure Profiles Associated with Early Cognitive Skills among U.S. Children

Abstract

Data-driven machine learning methods present an opportunity to simultaneously assess the impact of multiple air pollutants on health outcomes. The goal of this study was to apply a two-stage, data-driven approach to identify associations between air pollutant exposure profiles and children's cognitive skills. Data from 6,900 children enrolled in the Early Childhood Longitudinal Study, Birth Cohort, a national study of children born in 2001 and followed through kindergarten, were linked to estimated concentrations of 104 ambient air toxics in the 2002 National Air Toxics Assessment using ZIP code of residence at age 9 months. In the first-stage, 100 regression trees were learned to identify ambient air pollutant exposure profiles most closely associated with scores on a standardized mathematics test administered to children in kindergarten. In the second-stage, the exposure profiles frequently predicting lower math scores were included within linear regression models and adjusted for confounders in order to estimate the magnitude of their effect on math scores. This approach was applied to the full population, and then to the populations living in urban and highly-populated urban areas. Our first-stage results in the full population suggested children with low trichloroethylene exposure had significantly lower math scores. This association was not observed for children living in urban communities, suggesting that confounding related to urbanicity needs to be considered within the first-stage. When restricting our analysis to populations living in urban and highly-populated urban areas, high isophorone levels were found to predict lower math scores. Within adjusted regression models of children in highly-populated urban areas, the estimated effect of higher isophorone exposure on math scores was -1.19 points (95% CI -1.94, -0.44). Similar results were observed for the overall population of urban children. This data-driven, two-stage approach can be applied to other populations, exposures and outcomes to generate hypotheses within high-dimensional exposure data.

Graphical abstract

Introduction

There is growing evidence that early-life exposure to ambient air pollution may affect neurodevelopment in children. Epidemiologic studies have shown that prenatal and/or early-life exposures to ambient air pollutants are associated with measures of neurodevelopment and behavior in infants and young children(Edwards et al., 2010; Freire et al., 2010; Guxens et al., 2012; Lin et al., 2014; Perera et al., 2009; Perera et al., 2006), autism diagnoses(Becerra et al., 2013; Jung et al., 2013; Kalkbrenner et al., 2010; Roberts et al., 2013; Volk et al., 2014; Volk et al., 2013; Windham et al., 2006) and attention-deficit/hyperactivity disorder(Newman et al., 2013). There is also evidence that air pollutants contribute to deficits in neurodevelopment that persist into later childhood(Suglia et al., 2008), affecting cognitive outcomes such as academic achievement. Although ambient air is a complex mixture of multiple pollutants, most of this previous research has focused on associations between individual pollutants and children's cognitive health(Becerra et al., 2013; Edwards et al., 2010; Freire et al., 2010; Guxens et al., 2012; Jung et al., 2013; Lin et al., 2014; Newman et al., 2013; Perera et al., 2009; Perera et al., 2006; Roberts et al., 2013; Suglia et al., 2008; Volk et al., 2014; Volk et al., 2013; Windham et al., 2006). Environmental epidemiology is now transitioning from single-pollutant approaches to more holistic investigations of the exposome and environment's collective effect on health. The recent availability of datasets containing exposure estimates for multiple air pollutants, population demographics and health outcomes on large cohorts of children provides an opportunity to leverage methods for “big data” to advance environmental epidemiology.(Bellazzi, 2014)

In a 2014 review, Oakes et al identified fifty-seven distinct studies that focused on developing multi-pollutant metrics of exposure for a variety of outcomes.(Oakes et al., 2014a) The authors noted a lack of consensus on which multi-pollutant metrics were recommended for a given research question. They identified that a key limitation is that most metrics assume pure additivity of effects with no potential for synergistic or antagonistic interactions. This can be a major limitation, since pollutants vary spatially and can combine with each other to create distinct mixtures that may have different effects on exposed populations than the individual pollutants. Identification of these spatially-varying exposure profiles may allow researchers to pinpoint affected communities and target more in-depth research into sources and potential health effects. For example, Coker et al used Bayesian profile regression to identify exposure profiles associated with adverse birth outcomes in Los Angeles.(Coker et al., 2016) That study examined only three pollutants in conjunction with contextual neighborhood factors that could simultaneously impact birth outcomes.

Machine learning (ML) methods can be used to identify the exposures relevant to health outcomes of interest within high-dimensional exposure data, as well as the potential interactions between those exposures.(Patel, 2017) A recent application of ML methods, specifically classification and regression tree (CaRT)(Lemon et al., 2003), in air pollution epidemiology by Gass et al. examined the relationship of a small number of pollutants to asthma emergency department (ED) visits.(Gass et al., 2014) In that study, the typical CaRT objective of predicting the dependent variable (here, use of the ED) was replaced by identifying statistically significant combinations of (discrete) pollutant levels that best capture the risk of asthma ED visits as compared to referent levels of the pollutants. Although a promising step forward, this work confounds the goals of prediction using CaRT methods and estimation of effect sizes of the contributing pollutant combinations. It may be more appropriate to use CaRT methods as an initial screening tool to identify combinations of interest and then use a second analytic method to estimate the effect size, as suggested by Sun et al. in their recent review.(Sun et al., 2013) Using CaRT as a first-stage method allows for the examination of continuous exposure variables, as opposed to arbitrary discretization of the exposures. Additionally, this method can provide a more stable picture of the association between a pollutant profile and the outcome of interest than a single tree by learning multiple trees and then examining the occurrence frequency of the pollutant profile within slightly different samples from the study population. The pollutant profiles identified in the first-stage can then be investigated in more depth in the second-stage by using well-established epidemiologic methods to control for confounding, assess effect measure modification and investigate various exposure contrasts.

The goal of our study was to apply a data-driven approach to identify early-life exposure profiles associated with measures of cognitive skills and school readiness in a nationally-representative cohort of 6,900 U.S. children.(Najarian et al., 2010) This two-stage approach incorporates machine learning into environmental health research by first using CaRT methods to identify pollutant profiles associated with test scores. Then, epidemiologic methods for effect estimation and assessment of interaction were used to quantify the magnitude of the combined effect of these pollutant profiles on the children's math scores. We applied this approach in combination with stratification based on urbanicity levels, which were expected to confound the relationship between air pollution exposure and early cognitive skills.

Materials and Methods

Study Population

Conducted by the National Center of Education Statistics, the Early Childhood Longitudinal Study, Birth cohort (ECLS-B) is a longitudinal study of a nationally representative, random selection of children born in 2001 and followed from the age of 9 months through kindergarten entry.(Najarian et al., 2010) Women and children were recruited from birth certificate data and contacted for study visits at 9 months, 2 years, 4 years, and during kindergarten. At each visit, children participated in neurodevelopmental assessment activities and mothers participated in interviews. At later study points, childcare providers and teachers also participated in interviews. All sample sizes mentioned subsequently in this article are rounded to the nearest 50 to comply with ECLS-B privacy guidelines. Approximately 74% of eligible women and children (N=10,700) agreed to participate at study entry. Of these children, approximately 83% completed the preschool and kindergarten assessments at 4 and 5 years of age (N=8,900). For this study, children were limited to singleton births, whose mother provided a residential address at study entry and who completed the study assessments during Kindergarten, resulting in a cohort of 6,900 children.

Outcome Assessment: Mathematics Standardized Tests

At the kindergarten study visit, each child completed a variety of standardized tests aimed at assessing their basic math and verbal skills, as appropriate for school-entry. Because math scores may be less prone to confounding from language spoken in the child's home(Roberts and Bryant, 2011), our study utilized math scores as the primary outcome. The 58-item mathematics assessment was derived from standardized instruments, including the Test of Early Mathematics Ability (TEMA-3) and mathematics assessments from other NCES childhood studies. The concepts covered in the assessment included number sense, properties, operations, measurement, geometry, spatial sense, data analysis, statistics, probability, patterns, algebra, and functions.(Najarian et al., 2010) An adaptive two-stage design was used to adjust the test-difficulty based on the number of correct responses during the initial stage of the assessment. As the goal of our study was to assess the association between math scores and exposure to ambient air toxics, the raw scale score was used in all analyses, as suggested by NCES analytic guidelines.

Exposure Assessment: Estimated Concentrations of Ambient Air Toxics

Exposure to air toxics was assigned using data derived from the U.S. Environmental Protection Agency's National Air Toxics Assessment (NATA).(EPA, 2013) Air toxics, also known as hazardous air pollutants, are listed in the Clean Air Act and thought to be associated with cancer, birth defects, and other adverse health effects, but are not regulated by the U.S. National Ambient Air Quality Standards. Conducted periodically (i.e. 1996i.e. 1999i.e. 2002i.e. 2005i.e. 2011), each NATA assessment estimates the annual average concentration of each air toxic for each census-tract in the U.S. using emissions inventories and complex simulation models. In our study, data from the 2002 NATA assessment were used, as they were the closest in time to the ECLS-B study visit at 9 months. Each child was assigned concentrations of 104 different air toxics using the residential address provided at the 9-month assessment to capture early-life exposures. Since the ECLS-B only recorded residential ZIP code, and the NATA assessments provide census-tract specific estimates, we constructed weighted average exposures for each ZIP code based on the percent of each ZIP Code's population that resides in a specific census-tract. This method is consistent with previous research using ECLS-B data.(Stoner et al., 2013) Of the 187 air toxics listed in the 2002 NATA data, we considered the ones that had no more than 5% missing values across the whole cohort for our analyses, resulting in 104 pollutants for our analysis (Supplemental Table 1).

Construction of datasets

To determine if confounding would affect the pollutant profiles identified by CaRT, the population was stratified by the urbanicity of the ZIP Code of the child's residence. Urbanicity was considered explicitly as a stratification factor as it might serve as a proxy for socio-demographic profiles that could confound the association of interest between air toxics and test scores. As a confounder, urbanicity is hypothesized to be associated with both the air toxics that make-up potential air pollution profiles and school readiness skills in mathematics. Using the 2003 U.S.D.A Economic Research Service Rural-Urban Continuum Codes, each child was assigned an urbanicity code based on their county of residence at 9 months of age.(USDA, 2003) All the children who lived in counties designated as metropolitan (codes 1-3) were considered to be living in an urban community. All the children who lived in counties designated as a metropolitan area with a population of 1 million or more (code 1) were considered to be living in a highly-populated urban community. The two-stage approach was then applied to the full ECLS-B population and then repeated using only children who lived in urban communities and again using the subset of the children who lived in highly-populated urban communities. The populations are not mutually-exclusive, but were intended to investigate the hypothesis that finer levels of stratification would reduce residual confounding.

Data Analysis

Stage I, CaRTs

CaRTs are predictive models represented as trees consisting of nodes and edges. The internal nodes of a tree denote decision points based on values of the selected features, and the associated edges denote actions to be taken depending on the decision made at these nodes.(Lemon et al., 2003) Leaf nodes at the end of paths starting from the root node indicate the value of the outcome (class label or regression values) of the examples that satisfy the decision points on these paths. Root-to-leaf paths are referred to as branches or combinations constituting the tree, each of which can be represented as a decision rule with the internal node decision(s) as the antecedent(s) and the leaf node outcome as the consequent. While many algorithms could have been used for automatically deriving CaRTs from high-dimensional data sets, we focused on using the algorithm implemented in the widely used rpart R package.(Therneu and Atkinson, 2015) The rpart() function in this package was used to infer the regression trees in our study, with the response set to math scores, (predictor) data set to the pollutant levels, method set to “anova” and all the other parameters of the function set to their default values. With these basic settings, the rpart() function evaluates each exposure and a corresponding threshold to find the (exposure, threshold) combination that separates the full set of subjects into two more homogeneous subsets based on whether their exposure level was higher or lower than the threshold. The same algorithm is then applied recursively to these subsets to find progressively more predictive/discriminative (exposure, threshold) combinations, resulting in the root-to-leaf paths described above. To prevent overfitting of each of these trees, i.e. the trees becoming too specific to the training data, a ten-fold cross-validation procedure was run to optimize the parameters and sizes of the trees.(Arlot and Celisse, 2010) This was accomplished by setting the control parameter of the rpart() function to rpart.control(cp=0.0,xval=10).

CaRT models, including those inferred using rpart, offer several advantages, such as (i) easy interpretability in terms of understandable trees and/or rules, (ii) ability to identify nonlinear relationships between the features (exposures) and the outcome(s) (math scores), (iii) possibility of identifying interaction(s) among the features (exposures), (iv) making no/minimal assumptions about data distributions, (v) tolerance to missing values and outliers in the data, and (vi) implicit outcome-specific feature (exposure) prioritization/selection during tree inference. However, CaRT methods suffer from several potential limitations as well, such as (i) being prone to overfitting the (training) data, and (ii) being sensitive to small perturbations in the data and/or model/algorithm parameters. To address these potential limitations of individual decision trees, we followed an approach similar to a random forest, where a large number of trees were learnt on multiple partitions of the data instead of a single tree from the full dataset. This allowed us to more reliably identify pollutants or their combinations that are found to influence math scores across multiple decision trees, instead of just one.

Specifically, the full ECLS-B dataset was randomly partitioned 100 times in an 80:20 ratio into different training and test sets. The regression trees inferred from each of the training sets were then evaluated on the corresponding test sets to assess their predictive performance in term of the coefficient of determination (R²) between the predicted and true math scores. For downstream analyses, the trees were then decomposed into their constituent branches (combinations of pollutant(s)), and their frequencies counted across the 100 trees. Finally, in order to assess the significance of the above R² and pollutant combination frequency statistics, we assessed them in 10,000 random counterparts of the trees inferred from the true math scores. For this, these scores were randomly permuted 100 times, and the tree inference and statistics collection process was repeated 100 times (training-test splits) for each of these sets of permuted scores. R code for the developed approach can be obtained by contacting the corresponding author.

Stage II: Assessment of Interaction and Effect Size

Statistical interactions between pollutants within pollutant profiles identified in Stage I were assessed by including interaction terms between pollutants within multivariable linear regression models and conducting Wald tests, using an a priori alpha level of 0.1. Pollutants were modeled as dichotomous variables using the median threshold calculated across all branches where the pollutant profile appeared. All models were adjusted for confounders identified from the existing literature and directed acyclic graph analysis using DAGitty software (Supplemental Figure 1).(Greenland et al., 1999; Textor et al., 2011) The confounders identified as part of the minimally sufficient adjustment set and included in the second-stage models were maternal age at the time of the child's birth, maternal marital status at baseline, child's race/ethnicity, a socioeconomic index derived from maternal and paternal occupation, education and household income, a neighborhood deprivation index derived from census variables, and the primary language spoken in the home. The effect of pollutant profiles on math scores were estimated by restricting to subpopulations defined by the trees learned in Stage 1. For example, a pollutant profile in Stage 1 could identify a population with lower math scores that had greater exposure to pollutant A, pollutant B, and pollutant C. The modelling strategy was to restrict to the population with greater levels of exposure to pollutant A and B and then determine the effect of exposure to pollutant C by comparing those with greater exposure to pollutant C to those individuals in the subpopulation who had lower exposure to pollutant C. Implementing this strategy, multivariable linear regression models, adjusted for the same set of confounders listed above, were constructed to estimate the magnitude of the association between subpopulation-average math scores and pollutant exposure. However, the approach is flexible enough to accommodate other regression strategies, such as comparing those with the complete pollutant profile to all others within the full population. Because the primary goal of this manuscript was methods development, the complex sampling design of the ECLS-B was ignored in the analysis.

To illustrate how the results can be used to conduct more targeted research on the populations affected by these pollutant profiles, U.S. Census data from 2000 were compiled and used to construct a demographic profile of impacted communities. Impacted communities were defined by ZIP Codes in the United States that matched the identified pollutant profiles, i.e., had concentrations of the constituent pollutants greater than the identified thresholds.

Results

Demographic characteristics of the study populations are provided in Table 1. Approximately 6800 children in the full population had data on their address at 9 months of age, participated in the study through kindergarten entry and completed the mathematics assessment. The majority of children lived in urban communities (n=5550) and more than half lived in very highly-populated urban communities, defined as having more than 1 million residents (n=3650). Children living in urban communities have a different demographic profile than the full population. Urban children were more likely to be non-White, have a language other than English spoken at their home and live in a household with a slightly higher SES Index than the full population. Mothers in urban communities were more likely to be married and were slightly older at the time of their child's birth than mothers in the full study population. These differences were even more pronounced when comparing children in highly-populated urban communities to the full population. Average math score varied by urbanicity as children in the highly-populated urban communities had slightly higher average scores than the full population and the total urban population.

Table 1. Demographic Characteristics (%) of the Early Childhood Longitudinal Study, 2002 Birth Cohort Stratified by Target Population^*.

	Full Population N=(6800)**	Population in Urban Communities N=(5550)**	Population in Highly-populated Urban Communities N=(3650)**
Child Sex
Male	50.3	50.7	50.7
Female	49.7	49.3	49.3
Child Race
White, non-Latino/a	44.5	41	35.1
Black/African-American, non-Latino/a	17.1	17.6	18.1
Latino/a	21.8	24.2	26.9
Asian, non-Latino/a	12.4	14.8	18.7
Other	4.3	2.4	1.2
Primary Language Spoken in Home
Non-English Language	20.3	24.2	30.3
English Language	79.7	75.8	69.7
Socioeconomic Status Index***
First Quintile	18.6	17.3	17
Second Quintile	18.8	17.6	16.3
Third Quintile	19.1	18.5	16.3
Fourth Quintile	19.6	20.2	20.5
Fifth Quintile	23.8	26.4	30
Maternal Marital Status
Married	67.7	69.8	72.4
Separated/Divorced/ Widowed	6	5.5	4.6
Never Married	26.3	24.7	23
Maternal Age at Child's Birth
Less than 20 years of age	7	6.1	5.1
20-29 years of age	46.8	44.6	40.5
30-37 years of age	36.7	38.8	42.7
38 years of age and older	9.6	10.5	11.7
Math Score in Kindergarten****	44.1 (10.5)	44.5 (10.5)	45.1 (10.5)

^*Missing data now shown so some columns do not equal 100%

^**Frequency counts rounded to the nearest 50 per publishing guidelines of the National Center of Education Statistics

^***Socioeconomic Status Index is a composite index, provided in the ECLS-B dataset, derived from maternal and paternal information on education, occupations and household income.

^****Mean (Standard deviation)

First-Stage Analysis: Regression Trees

One hundred regression trees consisting of pollutant combinations that correlated with math scores of children in different segments of the target populations were learnt using a systematic machine learning methodology. Illustrative examples of these trees are shown in Figure 1. Across all populations, the learned regression trees were substantially more predictive than their random counterparts, thus indicating the ability of the first-stage regression trees to capture relationships that existed within the data. Specifically, for the total population, urban and very highly-populated urban populations, the trees learnt from true outcomes (math scores) are more predictive those learnt from the randomly permuted versions of the true outcomes (R²=0.067 vs. 6.6×10^-4, R²=0.074 vs. 1.1×10^-3 and R²=0.088 vs. 1.4×10^-3 respectively). Within the full, urban and highly-populated urban populations, the first-stage analysis identified 11, 10 and 9 pollutant profiles respectively that predicted math scores lower than the population average, and were found in at least 10% of the learned trees (Supplemental Table 2). Thresholds of pollutant concentrations that dictated node splits within the trees were relatively consistent across trees.

Figure 1.

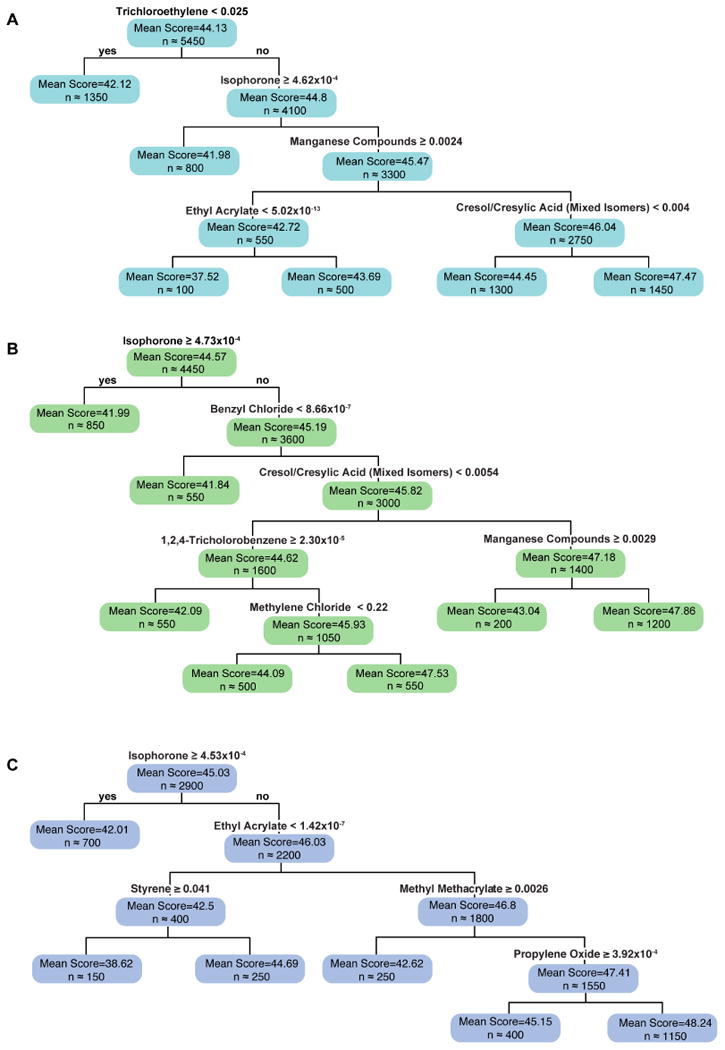
Representative regression trees from first-stage analysis of air toxics and child's math scores, Early Childhood Longitudinal Study Birth Cohort 2001. A) Full Study Population; B) Subset of Population living in Urban Communities; C) Subset of Population living in Highly-Populated Urban Communities. Each internal node in these trees indicates an (exposure, threshold) combination that separates the current sample of subjects (approximate size shown within the node) into two more homogeneous subpopulations based on whether their levels for the exposure are higher or lower than the threshold. Following these nodes from the root of the tree to the terminal/leaf nodes defines both the candidate pollution profiles as well as the populations subjected to them that are analyzed in Stage 2 of our approach.

Within the total population, the solvent trichloroethylene was the root node (most predictive pollutant) for a majority of the trees (63%), with children living in communities with ambient trichloroethylene less than 0.02505 μg/m³ having lower than average math scores. Among children exposed to trichloroethylene at or greater than 0.02505 μg/m³, higher concentrations of isophorone or manganese also emerged from the tree-based analysis as predicting lower than average math results. Other pollutant profiles were also identified, but in fewer than 15% of trees. Within the urban population, trichloroethylene was no longer identified as a predictor of math scores and the most common root node (65% of trees) associated with lower math scores was isophorone with a threshold concentration of greater than 0.00047 μg/m³. Among children with exposure to lower ambient isophorone, different pollutants emerged within the pollutant profiles, most commonly benzyl chloride, either alone or in combination with other pollutants. When the population is restricted further to children living in very highly populated urban communities, isophorone remains the most common root node (73% of trees), with similar thresholds of exposure indicating lower than average math scores. However, among children exposed to low isophorone levels, different combinations of air pollutants, including manganese and ethyl acrylate, begin to identify those with lower than average math scores.

Second-Stage Analysis: Multivariable Regression Models

Table 2 shows the adjusted betas and 95% confidence intervals resulting from the second-stage analysis of examining the identified combinations within linear regression models adjusting for confounders. Adjusting for confounders eliminated some of the associations identified in the first-stage analysis. However, among the pollutant profiles identified in more than 50% of the trees, the pollutant profiles remained associated with lower math scores, even after adjusting for confounders. Isophorone was the most consistent pollutant profile associated with low math scores observed across populations. Within the full population, among children with exposure to higher levels of trichloroethylene, higher exposure to isophorone was associated with slightly more than a 1 point decrement on the mathematics assessment (-1.31, 95% CI -2.01, -0.61). A similar magnitude of association was observed between isophorone and math scores in both the urban and highly-populated urban populations (a decrement in average math score of -1.12 and -1.19 points respectively). Among the children living in areas with lower isophorone levels, lower levels of other pollutants, such as ethyl acrylate and benzyl chloride, were also associated with lower than average math scores.

Table 2.

Adjusted betas^* and 95% confidence Intervals for the effect of air toxics on math scores in kindergarten children within subpopulations defined by tree results, Early Childhood Longitudinal Study, Birth-Cohort 2001-2007.^**

Full Population (N=6100)			Population living in Urban Communities (N=5050)			Population living in Urban Communities with > 1 million people (N=3350)
Pollutant Combination Identified within Regression Trees***	Number of Children Exposed to Entire Pollutant Combination / Number of Children in Subpopulation defined by all but last pollutant within the combination	Beta**** and 95% CI	Pollutant Combination Identified within Regression Trees***	Number of Children Exposed to Entire Pollutant Combination / Number of Children in Subpopulation defined by all but last pollutant within the combination	Beta and 95% CI	Pollutant Combination Identified within Regression Trees***	Number of Children Exposed to Entire Pollutant Combination / Number of Children in Subpopulation defined by all but last pollutant within the combination	Beta and 95% CI
TRICHLOROETHYLENE < 0.02505	1450/ 6100	-1.36 (-1.95, -0.77)	ISOPHORONE >= 0.00047	1000/5050	-1.12 (-1.79, -0.46)	ISOPHORONE >=0.00047	800/3350	-1.19 (-1.94, -0.44)
TRICHLOROETHYLENE >= 0.02505 AND ISOPHORONE >= 0.000462	900/4650	-1.31 (-2.01, -0.61)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE < 1.2e-6	750/4050	-1.79 (-2.54, -1.05)	ISOPHORONE <0.00047 AND MANGANESE COMPOUNDS < 0.002474 AND ETHYL ACRYLATE <1.8e-07	400/2050	-2.1 (-3.06, -1.11)
TRICHLOROETHYLENE >= 0.02505 AND MANGANESE COMPOUNDS >= 0.002447	900/4650	-1.01 (-1.73, -0.29)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE >= 1.2e-6 AND CRESOL/CRESYLIC ACID (MIXED.ISOMERS) < 0.0054 AND 1,2,4-TRICHLOROBENZENE >= 2.3e-5	600/1700	-1.63 (-2.60, -0.67)	ISOPHORONE < 0.00047 AND ETHYL ACRYLATE >= 1.8e-07 AND MANGANESE COMPOUNDS >=0.0024	400/2050	-0.97 (-2.04, 0.09)
TRICHLOROETHYLENE >= 0.02505 AND MANGANESE COMPOUNDS < 0.002447 AND ISOPHORONE >= 0.000472	650/3750	-1.54 (-2.37, -0.70)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE >= 1.1 e-6 AND CRESOL/CRESYLIC ACID (MIXED ISOMERS) < 0.0054 AND ALLYL CHLORIDE >= 4.6e-6	650/1700	-0.97 (-1.98, 0.04)	ISOPHORONE < 0.00047 AND MANGANESE COMPOUNDS >=0.002474	500/2550	-1.08 (-2.03, -0.13)
TRICHLOROETHYLENE < 0.02505 AND ARSENIC COMPOUNDS < 0.000243	750/1450	-0.52 (-1.76,0.72)	ISOPHORONE< BENZYL CHLORIDE>= CRESOL/CRESYLIC ACID (MIXED ISOMERS) >= MANGANESE COMPOUNDS>=	250/1600	-0.19 (-1.65, 1.25)	ISOPHORONE < 0.00047 AND ETHYL ACRYLATE < 1.8e-07	500/2550	-2.45 (-3.32, -1.59)
TRICHLOROETHYLENE >= 0.02505 AND ISOPHORONE < 0.000462 AND MANGANESE COMPOUNDS >= 0.002447 ETHYL ACRYLATE < 5.0 e-13	100/650	-5.19 (-7.18, -3.2)	ISOPHORONE >= 0.00047 AND ETHYLENE DICHLORIDE (1,2-DICHLOROETHANE) < 0.00424	700/3800	-1.54 (-2.35, -0.72)	ISOPHORONE < 0.00046 AND ETHYL ACRYLATE < 1.4e-07 AND STYRENE < 0.04093	300/500	0.97 (0.67, 2.62)
TRICHLOROETHYLENE < 0.02505 AND ARSENIC COMPOUNDS >= 0.000243	700/1450	0.52 (-0.72, 1.76)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE < 1.2 e-6 AND MANGANESE COMPOUNDS >= 0.0020	50/750	-2.50 (-4.97, -0.03)	ISOPHORONE < 0.00046 AND ETHYL ACRYLATE < 1.4e-07 AND STYRENE >= 0.04093	200/500	-0.97 (-2.62, 0.67)
TRICHLOROETHYLENE >= 0.02505 AND MANGANESE < 0.002447 AND CRESOL/CRESYLIC ACID >= 0.00528 AND DIMETHYL FORMAMIDE >= 0.0045	550/1850	-1.98 (-3.02,-0.93)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE < 1.2e-6 AND VINYL ACETATE >= 0.00125	250/750	-3.87 (-6.85, -0.88)	ISOPHORONE < 0.00045 AND ETHYL ACRYLATE >= 1.4e-07 AND METHYL METHACRYLATE >=0.00264	250/2000	-1.12 (-2.32, 0.08)
TRICHLOROETHYLENE >= 0.02505 AND MANGANESE COMPOUNDS >=0.002447 AND ETHYL ACRYLATE < 5.0e-13	100/900	-4.87(-6.84,-2.89)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE < 1.2 e-6 AND MANGANESE COMPOUNDS < 0.0020	700/750	2.58 (0.84, 4.33)	ISOPHORONE < 0.00047 AND MANGANESE COMPOUNDS >= 0.00247 AND ETHYL ACRYLATE< 2.128e-07	100/500	-3.81 (-5.74, -1.87)
TRICHLOROETHYLENE >= 0.02505 AND ISOPHORONE < 0.000458 AND MANGANESE COMPOUNDS >= 0.002447 AND ETHYL ACRYLATE >= 1.4e-13	600/650	5.36 (2.97, 7.76)	ISOPHORONE < 0.00047 AND BENZYL CHLORIDE >= 1.2 e-6 AND CRESOL/CRESYLIC ACID (MIXED.ISOMERS) < 0.0054 AND 1,2,4-TRICHLOROBENZENE < 2.3e-5 AND METHYLENE CHLORIDE < 0.20	400/1100	-1.62 (-2.78, -0.47)
TRICHLOROETHYLENE >= 0.02505 AND LEAD COMPOUNDS >= 0.003918	1450/4450	-0.81 (-1.45, -0.17)

^*Betas and 95% confidence intervals result from a linear regression model adjusted for the following covariates: child race, maternal age, maternal marital status, socioeconomic index, language spoken in the home, and neighborhood deprivation index.

^**All numbers rounded to the closest 50 in accordance with publication guidelines of the National Center of Education Statistics

^***Pollutant thresholds used to define exposure combinations represent the median threshold found in combinations observed across trees

^****Beta represents the average effect of the full pollutant combination among the subpopulation identified by all but the last pollutant within the combination

Statistical Interaction between Pollutants

The only evidence of statistical interaction between pollutants within pollutant profiles was between ethyl acrylate and manganese in children living in highly-populated urban areas exposed to lower isophorone levels (Wald-test on the interaction term p-value=0.08). The estimated association of higher manganese exposure with math scores was greater when ethyl acrylate was lower. Among children with lower exposure to both isophorone and ethyl acrylate, the average math score was 2.4 points lower among children who had higher manganese exposure (95%CI -4.52, -0.28). The association between manganese and test scores was attenuated among the children with low exposure to isophorone but high exposure to ethyl acrylate (-0.97 95%CI -2.04, 0.09).

Demographic Characteristics of Identified Subpopulations

Using this two-stage method identified that children living in areas with low levels of trichloroethylene and higher levels of isophorone had lower than average math scores. Within the full study population, lower trichloroethylene exposure was associated with rural neighborhoods, while higher isophorone exposure was associated with living in urban areas. When we restricted the study population to those living within urban communities to account for confounding by community levels of urbanicity, children living in areas with greater isophorone exposure continued to have lower than average math scores and trichloroethylene exposure was no longer associated with math scores.

Identifying pollutant profiles associated with lower than average math scores can facilitate more detailed research focused on the populations exposed to those pollutants. For example, looking beyond the study population to the broader US population revealed that 9% of ZIP codes in highly-populated urban areas have isophorone levels at or greater than the threshold observed in this study (0.47 ng/m³). In this context, Table 3 presents an illustrative example of the type of demographic analysis that can be done to facilitate subsequent studies and research on environmental justice issues that may be associated with health disparities. Examining communities with higher isophorone levels reveals that these communities are more likely to be in the Northeastern United States and have greater proportions of residents who are Black, non-Hispanic, living in poverty, and renting, as opposed to owning, their housing (Table 3).

Table 3.

Selected demographic characteristics^a of highly-populated urban ZIP codes, by ambient isophorone level.

	ZIP Code's Estimated Ambient ≥0.47 ng/m3	Concentration of Isophorone <0.47ng/m3
Geographic Region
Northeast	36.3	20.0
Southern/Southeastern	28.1	33.5
Central	23.2	27.2
Western	12.5	19.3
Community Demographics
Average Proportion of Residents with Less than a HS Education	22.0	19.7
Average Proportion of Residents who are unemployed	3.5	4.4
Average Proportion of Residents who are living in poverty	8.8	11.8
Average Proportion of Residents who are Black, non-Hispanic	19.2	7.8
Average Proportion of Residents who Rent their Homes	42.7	25.9
Average Proportion of Male Residents who have Professional Occupations	16.8	14.1
Average Proportion of Female Residents who have Professional Occupations	23.5	23.0
Average Proportion of Residents who lived in the same community for the previous five years	54.6	58.4

^aDemographic data from the 2000 US Census.

Discussion

Using a two-stage data analysis approach, we were able to identify air pollutant profiles associated with lower math test scores in kindergarten children. Implementation of machine learning as a first-stage approach to identify potentially relevant pollutant profiles allowed for informed hypothesis generation. This is shown by the fact that the regression trees learned from the real data were substantially more predictive than those learnt from randomized data. Another advantage of using regression trees is that complex combinations of pollutants can be relatively easily visualized and subsequently analyzed in the second stage of our approach. By assessing these pollutant combinations identified from the trees within epidemiologic models and after adjusting for potential confounders, we were able to detect isophorone as a potential marker of an early-life pollutant exposure profile associated with lower math scores in kindergarten children. Although a single pollutant, isophorone is commonly used in industrial processes and is likely related to a distinct pollutant profile that arises from these processes.

The occupational health literature suggests that exposure to isophorone at high levels can have adverse health effects(ATSDR, 1998; Samimi, 1982), and a recent review listed isophorone has a potentially neurotoxic agent (Grandjean and Landrigan, 2006). However, ambient monitoring data for air toxics are sparse, and there are limited data on the health effects of pollutants like isophorone at ambient levels. Thus, it can be difficult to interpret results suggesting that ambient isophorone exposure is associated with lower math scores in kindergarten. A widely-used solvent in multiple industries, isophorone is highly reactive and likely to be oxidized by reaction with hydroxyl radicals and ozone within the ambient air.(ATSDR, 1998) Evaporation of solvents containing isophorone is considered one of the primary sources of inhalatory exposure in urban communities. Because of its relatively short half-life in ambient air, air monitoring is especially limited and the biological plausibility of inhalation of isophorone as a causal contributor to adverse neurodevelopment is unclear. It is possible that communities with higher estimated isophorone levels are near sources of exposure that also contaminate water or soil with isophorone. As stated above, it is also possible that isophorone could be a marker for (mixtures of) other pollutants with a similar source, as isophorone is common in many manufacturing industries, including printing and metal-coating. Future, more targeted research in areas with elevated isophorone levels should attempt to decipher the more detailed pollutant profile associated with elevated levels of isophorone. Using more targeted study designs to conduct research within the subpopulations of exposed communities identified by our approach can help address these unanswered questions regarding the relationship between isophorone and children's neurodevelopmental outcomes.

As mentioned earlier, there have been a number of methods developed to identify pollutant profiles within ambient air and/or associate them with health outcomes in the population. Prior approaches have utilized self-organizing maps, a form of unsupervised learning (Pearce et al., 2016), multipollutant indicators that combine measured pollutant concentrations with emissions data (Oakes et al., 2014b), k-means and hierarchical clustering (Austin et al., 2012), and Bayesian clustering techniques that account for the uncertainty in the identification of the pollutant profiles (Molitor et al., 2016). All of these approaches have been shown to identify and estimate the health effects of air pollutant profiles. However, they have not been used in the context of high-dimensional exposure data. Most have been implemented while examining less than ten air pollutants at a time. The goal of the data-driven approach presented here is to identify pollutant profiles within the context of over one hundred air pollutants. Our data-driven approach could be used as a first method within high-dimensional exposure data before other, more targeted and refined methods for estimating the effects of pollutant profiles (after accounting for confounding) are applied within the smaller subset of identified pollutants.

Notably, although our data-driven approach holds potential for making relevant discoveries in environmental health and exposome research, it is also important to acknowledge the possible limitations. First, it's important to consider the quality of the data used with a data-driven methodology, such as the one proposed here. For example, the NATA air pollution data we used consist of model-derived estimates of ambient air pollutant concentrations rather than of actual monitoring data. There is a greater level of uncertainty associated with this kind of exposure estimate due to both the estimation process and the representativeness of the individual's exposure experience.(EPA, 2002) Additionally, this uncertainty varies by individual pollutant. Such uncertainty poses a challenge for most data-driven methods, such as the use of regression trees in our approach, since they don't explicitly take this uncertainty into account (Tsang et al., 2011). Due to this issue, our trees may identify a profile consisting of pollutants with highly uncertain measurements as associated with lower math scores. Although we hope that the second stage of our approach is able to eliminate some of these potentially spurious associations, the possibility of this uncertainty affecting the final results of our approach can not be ignored. One way of addressing the issue of uncertainty in the estimated air pollution data is to repeat the application of our approach using actual air monitoring data. This can be difficult since many air toxics are not monitored, but there are local areas within the United States and Canada with availability of air toxics monitoring data, although not at the scale modeled by the NATA assessments (Galarneau et al., 2016; Myers et al., 2015; Propper et al., 2015).

We focused on early-life as a critical window of exposure, and assigned exposure to air toxics using only the residential location at 9 months. This timepoint was within the critical window of brain development, prior to the age of 2, when the brain undergoes rapid growth and development(Gao et al., 2009; Gilmore et al., 2007; Knickmeyer et al., 2008). It is possible that exposure after this time period may also contribute to a child's neurodevelopment and eventual school readiness. Within this population, approximately 59% of children moved to at least once between the 9 month study visit and the school readiness assessments at age 5. This suggests that the results we see, such as the association between isophorone and math scores, could be due to a later exposure that is correlated with the exposure, e.g. isophorone, at 9 months. Since our approach currently only considers static exposures, future work should address how exposure to mixtures during different windows of development impact children's cognitive outcomes.

Additionally, the dataset(s) to which such approaches are applied should be representative of the source population(s). For instance, our dataset includes approximately 7000 children living throughout the U.S., which strengthens our ability to draw inferences for general populations. However, there is great spatial variability in exposure profiles, demographics and contextual characteristics of a nationally-representative population. This leads to the issues of confounding that we observed when running the first-stage models on the full population. We were able to use stratification by urbanicity to remove some confounding and identify relevant exposure profiles. Future applications of this approach will need to consider alternative methods to account for confounding prior to implementation of the first-stage CaRT models if stratification is not a reasonable option, such as due to sample size limitations. Additionally, it is possible that there is some spatial clustering of test scores that we are not accounting for in our models. The sampling scheme of the ECLS-B and its geographic scope of representing the entire country effectively limits the number of children in any given ZIP code or geographic area to be a small percentage of the population. However, some of the pollutant profiles identified are found in only a very small proportion of the population and could be due to the regression trees in the first-stage identifying a few spatially-correlated geographic areas. In these instances, it's possible that some other factor that is associated with the pollutant profile and varies spatially is confounding our results. Our second-stage models adjust for the demographic factors that often vary spatially. However, other unmeasured environmental factors that co-vary with the air pollutant profiles and/or differences in how well the NATA estimates represent actual exposures could be contributing to our results. Finally, to draw robust conclusions about specific populations, it will be beneficial to collect higher-granularity data from specific locations, such as high-density urban areas where we observed larger effect estimates. Overall, we recommend investigating data-quality related issues such as the above as a part of (Barrett et al., 2013)data-driven exposome/epidemiological research to ensure the robustness of the conclusions drawn.

Within the second-stage regression modelling, we chose to estimate the effect of pollutant profiles on math scores by restricting to subpopulations defined by the first-stage trees. For example, in multiple trees learned from the highly-populated urban population, it was observed that higher manganese exposure in areas of low isophorone was predictive of lower math scores. Therefore, in the second-stage regression modelling, we limited to the subpopulation with low isophorone exposure and then estimated the effect of manganese exposure, while adjusting for confounders. This strategy provides interpretable measures of effect among the exposed populations, but leads to models with different referent groups and populations of varying size. Thus, it is possible that some of the observed relationships between pollutant profiles and math scores is due to these variations. However, a strength of our approach, is that any modelling strategy can be implemented within the second stage. So, if researchers wanted to use the same referent group across models for all identified pollutant profiles, that could be easily implemented within the framework of this approach.

In conclusion, our approach can be applied in similar ways to other populations, exposures and outcomes for hypothesis generation and investigation of statistical interaction within the context of high-dimensional pollutant data, such as those representing environmental mixtures and multiple exposures.

Highlights.

1. Ambient air is a complex mixture but research has examined pollutants one by one.

2. Machine learning can identify relevant exposure profiles in high-dimensional data.

3. We propose a two-stage approach of machine learning followed by etiologic models.

4. Our approach found exposure profiles associated with cognitive skills in children.

5. Relevant exposure profiles found can enable future research and interventions.