Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids

Abstract

Additive force fields are designed to account for induced electronic polarization in a mean-field average way using effective empirical fixed charges. The limitation of this approximation is cause for serious concerns, particularly in the case of lipid membranes, where the molecular environment undergoes dramatic variations over microscopic length scales. A polarizable force field based on the classical Drude oscillator offers a practical and computationally efficient framework for an improved representation of electrostatic interactions in molecular simulations. Building on the first-generation Drude polarizable force field for the dipalmitoylphosphatidylcholine 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) molecule, the present effort was undertaken to improve this initial model and expand the force field to a wider range of phospholipid molecules. New lipids parameterized include dimyristoylphosphatidylcholine (DMPC), dilauroylphosphatidylcholine (DLPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), dipalmitoylphosphatidylethanolamine (DPPE), 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), and 1,2-Dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE). The iterative optimization protocol employed in this effort led to lipid models that achieve a good balance between reproducing quantum mechanical data on model compound representative of phospholipids and reproducing a range of experimental condensed phase properties of bilayers. A parameterization strategy based on a restrained ensemble - maximum entropy methodology was used to help accurately match the experimental NMR order parameters in the polar headgroup region. All the parameters were developed to be compatible with the remainder of the Drude polarizable force field that includes water, ions, proteins, DNA and selected carbohydrates.

Graphical Abstract

1. Introduction

The molecular force fields typically used to generate classical molecular dynamics (MD) simulations represent the electrostatic interactions as a sum of pairwise additive interactions between simple point charges with fixed constant values. These additive fixed charged models are designed to mimic the interaction between molecules in a polar aqueous environment and to account for induced polarization in a mean-field average way.¹ The overall correctness of this approximation is an issue of broad importance for the accuracy of molecular simulations. The issue is even more acute in the case of biological membranes, where the molecular environment undergoes dramatic variations over microscopic length scales. For instance, the lack of induced polarization in fixed charge models of hydrocarbons has a significant impact on the dipole potential at the membrane water interface, a property that strongly affects the permeation of charged species.^2,3

Accurate force field models of phospholipids are important, as those molecules are a major component of biological membranes—a fundamental architectural element of the living cell. The membranes serve as a barrier to help control the flow of information and material in and out of cells. They provide a specialized physical environment to support a wide range of transport and signaling proteins whose function requires a dynamical fluid environment allowing rotational and translational diffusion of the proteins.⁴ To correctly model these and other phenomena it is critically important that force fields used to carry out MD simulations of membrane systems be as accurate as possible.

In the last decade, polarizable force fields for modeling bimolecular systems have been receiving increasing attention. ^5–7 A polarizable force field based on the classical Drude oscillator has been shown to be an efficient tool for more accurately describing electrostatic interactions in MD simulation.^2,3,8–11 By virtue of its particle-based structure, the Drude force field can be efficiently parallelized and implemented in high performance molecular simulation programs.^12,13 By using an extended Lagrangian with a dual thermostat to closely approximate the self-consistent field (SCF) condition,⁸ stable trajectories can be generated using a timestep of 1 fs, making the computational cost not significantly larger than that of conventional additive force fields. This allows for MD simulation timescales of 100s of nanoseconds into microseconds, allowing for direct comparison between simulation results and experimental data for a range of structural and dynamic observables.^7,14

In 2013 we reported a polarizable model for dipalmitoylphosphatidylcholine(1,2-dipalmitoyl-sn-glycero-3-phosphocholine) (DPPC) based on the classical Drude oscillator.³ The results from this initial DPPC model comparable favorably well with both experimental data and the non-polarizable additive CHARMM36 (C36) force field.^15–17 The present study was undertaken to improve this initial DPPC model and to enable studies of a wider diversity of biological membranes by expanding the number of lipids supported by the Drude force field. To this end, two types of neutral zwiterionic head groups were considered, namely, the large phosphatidylcholine (PC), and the relatively smaller phosphatidylethanolamine (PE) head groups. In addition, both saturated and mono-unsaturated hydrocarbon chains were considered to increase the diversity of hydrophobic tail groups. While the change in head group has a considerable impact on the area per lipid, the presence of double bonds introduces kinks along the hydrocarbon tails, affecting the dynamics and fluidity of the membrane¹⁸ and shifting the gel to liquid-crystalline phase transition temperature within a physiological range.¹⁹ In the present study we provide new models for DPPC, dimyristoylphosphatidylcholine (DMPC), dilauroylphosphatidylcholine (DLPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), dipalmitoylphosphatidylethanolamine (DPPE), 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), and 1,2-Dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), which were chosen because of their abundance in biological membranes.²⁰ All the parameters presented in this study were developed to be compatible with the remainder of the Drude polarizable force field that includes water,^21,22 ions,^10,23 proteins,^7,11 nucleic acids,^24–26 and selected carbohydrates.^27–29

The paper is organized as follows. The Methods section provides a general overview of the protocol for developing the Drude model for lipid molecules, the set of model compounds used, and the step-by-step procedure for optimizing non-bonded and intramolecular dihedral parameters. The Results and Discussion section provides a detailed description on how properties calculated with the developed force field parameters compare with quantum mechanical (QM) and experimental data. This includes several properties of the lipid bilayers in condensed phase, including the area per lipid head group, the surface tension and the drop in the dipole potential across the membrane. The Conclusion summarizes the main points and puts the present results in the perspective of future research.

2. Methods

2.1 General parameterization protocol

A complete description of the functional form of the polarizable force field based on classical Drude oscillators and its associated parameters employed can be found in previous studies.^8,9,11,21 The polarizable Drude force field for a complex molecule such as a phospholipid comprises a large number of parameters. Using a systematic protocol for developing the force field for such complex molecules is essential to help avoid internal inconsistency among the molecules. A widely accepted protocol for developing force field parameters for a family of “target molecules” was introduced by MacKerell and co-workers.^1,14,30,31 In the present study, we briefly review the main elements of this protocol with respect to the Drude polarizable model.

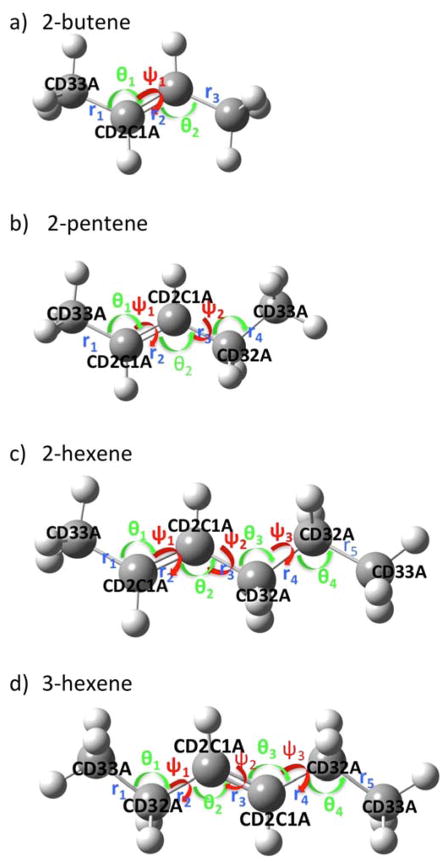
Based on the chemically important functional groups in the target molecule, a number of representative small compounds containing similar functional groups were selected to serve as elementary molecular building blocks for the optimization. Structural and energetics properties of the molecules based on ab initio QM calculations of the model compounds are then employed to generate target data for the initial stages of force field parametrization. Let us consider the DOPC molecule as an example. A complete DOPC molecule is comprised of a total of 138 atoms. It is impractical to characterize the conformations and energies of such a large molecule using an approach purely based on QM. Instead, we select a set of small representative model compounds to probe the relevant functionalities present in DOPC. For the hydrophilic head group and linkage region, the set includes dimethylphosphate (DMP) and tetramethylammonium (TMA). For the hydrophobic tail groups the set includes alkenes, 2-butene, 2-pentene, 2-hexene, and 3-hexene (Figure 1), building upon the previously optimized alkane parameters.³² Intramolecular degrees of freedom at the interface between functional groups were further characterized with the larger model compounds phosphoroglycerol (GLYP), and phosphatidylcholine (PC). Model compounds associated with the PC head group were treated in our previous study.³

Figure 1.

Model compounds employed to develop the parameters of the hydrophobic tail groups of mono-unsaturated carbon-carbon bond. (a) 2-butene, (b) 2-pentene, (c) 2-hexene, and (d) 3-hexene. Carbon and hydrogen atoms are represented as grey and white spheres, respectively. The colored labels indicate important internal degree of freedoms (bonds, angles, and dihedrals). Their values were employed as the targets of parameter optimization. The carbon atom types in the model compounds used in the Drude force filed are indicated.

As a first step, the parameters affecting the non-bonded interaction terms were optimized. This includes the electrostatic parameters, i.e. partial charges, electronic polarizabilities (α) and the Thole atomic dipole-dipole screening factor (a), as well as the Lennard-Jones (LJ) parameters (ε and R_min). Accurate representation of the above terms provides a solid foundation for describing both short and long-range interactions. Intramolecular parameters including bond, angle, dihedral and improper terms were then optimized iteratively, with the non-bonded parameters reevaluated upon completion of the bonded parameter optimization.

2.2 Intermolecular or Nonbonded Parameters

The partial charges, polarizabilities and Thole screening parameters of the sp² carbons and charge of the associated hydrogens were initially optimized by targeting the QM electrostatic potentials for the four alkene model compounds (Figure 1) calculated at the B3LYP/aug-cc-pVDZ level.^33–37 All the QM calculations in this study were performed using the Gaussian 09 program.³⁸ More details about the method and the choice of initial parameters are provided in previous studies.^39,40 The net charge of sp² carbon group including one carbon and one bonded hydrogen was constrained to be neutral, consistent with the general convention used in the Drude force field.³⁹ The electrostatic parameters for sp³ carbons and the associated hydrogens were taken from previous work on saturated alkanes.³² The value of the atomic intramolecular Thole screening factor a_i for the 1–2 and 1–3 induced electrostatic interactions of the sp² carbon was initially set to a value of 1.3 as in the saturated hydrocabons, and subsequently optimized to a value of 0.750 by targeting the molecular polarizabilities from QM; the Thole screening factor for the (i,j)-pair is given by a_ij = a_i+a_j according to Eq. (5) in Harder et al ⁴¹. We note that, as for our previous work on alkanes, the atomic polarizabilities determined from the QM calculations were not scaled. The LJ parameters are given in in Supplementary Table S1. Details about the molecular dipole moments and polarizabilities of the model compounds are given in in Supplementary Tables S2 and S3. The electrostatic properties of the model compounds (dipoles, polarizabilities, etc) are in relatively good aggreement with the QM results and the deviations are similar to what was observed in previous studies.³

The LJ parameters of the alkene carbon and hydrogen atoms were optimized targeting the density and enthalpy of vaporization (ΔH_vap) of neat liquids at room temperature, together with specific QM target data. The model compounds considered were 2-butene, 2-pentene and 2-hexene. The QM data is comprised of the minimum interaction energies and distances of the 3 model compounds with individual water molecules or with noble gas atoms (neon and helium).⁴² The density and enthalpy of vaporization of the neat liquids were calculated using MD simulations in the NPT ensemble with periodic boundary conditions from systems comprising 216 molecules. The enthalpy of vaporization was calculated as,

$$\mathrm{\Delta }{H}_{\text{vap}}=E_{\text{pot}}(g)-E_{\text{pot}}(l)+RT$$ (1)

where E_pot(g) and E_pot(l) represent the mean potential energy of the molecule in the gas and the condensed liquid phase, respectively. The mean potential energy of the molecule in the gas phase was calculated from a simulation of a single isolated molecule. The condensed liquid phase simulations were carried out in the NPT ensemble at a constant pressure of 1 atm, as described in the following paragraph. All the MD simulations were carried out with NAMD 2.10.⁴³ Molecular mechanical (MM) calculations were carried out with CHARMM (version c38b1).⁴⁴

To avoid the inefficient self-consistent field (SCF) condition at each step, MD simulations of the polarizable Drude models were generated by propagating the systems as an extended Lagrangian with a timestep of 1 fs using a dual Langevin thermostat implemented in NAMD.^8,12 The temperature of the reduced-mass Drude-nucleus pair was maintained at 1 K, yielding a dynamical behavior that is nearly indistinguishable from SCF.⁸ Periodic boundary conditions (PBC) were imposed for all simulation systems. Electrostatic interactions were treated using the particle mesh Ewald (PME) lattice sum method.⁴⁵ A smooth switching function active from 10 to 12 Å was used for the van der Waals forces. An analytical long-range correction for the van der Waals forces was included. Covalent bonds associated with hydrogen atoms and geometries of water molecules were constraint with the SETTLE procedure.⁴⁶

An initial set of parameters for each model compound was determined from a grid-scan of the LJ parameters to best match the target density and enthalpy of the neat liquid. These initial parameters were then refined based on interactions of the model compounds with individual noble gas atoms or water molecules. QM interaction energies were evaluated as a function of distance between the noble gas atoms and atoms of interest at the MP3 level of theory with the 6–311++g(3d,3p) basis set.^47,48 Interaction energies with noble gas atoms are documented in Supplementary Figure S1. Interactions with water involved optimization at the MP2/6–31G(d) and single point energies at the MP2/cc-pVQZ level. More information about the interaction energies with water is provided in Supplementary Tables S4 and S5. Basis-set Superposition Error (BSSE) corrections were included for all interaction energies by the counterpoise method.⁴⁹ All non-linear optimizations procedure were carried out with in-house programs or scripts utilizing the NLopt library.⁵⁰

2.3 Intramolecular parameters

The internal parameters of the alkene model compounds (bonds, angles, dihedrals and impropers torsions) were optimized by minimizing the differences between Drude and QM optimized geometries, potential energy scans, and vibrational spectra. The QM vibrational frequencies were calculated at the MP2 level with the 6–31g(d, p) basis set, using scaling factors from Scott and Radom.^51,52 The vibrational spectra of the molecular mechanical models were calculated with the VIBRAN module in CHARMM.⁴⁴ The vibrational analysis module MOLVIB⁵³ in CHARMM was employed to analyze contributions from the internal coordinates to the spectra.⁴⁴ Details are provided in in Supplementary Table S6. Internal coordinates matrices were constructed according to the method suggested by Pulay.⁵⁴ Potential energy surfaces along the dihedral angles were calculated at the MP2 level with the correlation-consistent double-Zeta basis set (cc-pVDZ).³⁷ In the Drude force field, the double bond dihedral parameter is assigned as X-CD2C1A=CD2C1A-X, where “X” may represent any of the connecting carbon atoms. In the optimization of the dihedral parameters, stable conformers were weighted according to their relative energy.⁴⁰ The intramolecular parameters were adjusted iteratively to remain consistent with the nonbond parameters.

2.4 Refinement of the head group using maximum entropy

We previously developed a polarizable DPPC model based on the classical Drude oscillator.³ While the overall properties from this model were comparable to those from the CHARMM26 (C36) force field, the deuterium order parameters S_CD of carbon atoms at sites G_3S and G₂ along the polar head group were substantially underestimated compared with experimental measurements. Improving the accuracy of the head group representation was thus one important objective of the present effort. Nevertheless, identifying the underlying cause of the problem and exploiting the information from deuterium order parameters is challenging for two main reasons. First, the experimental data reflect an ensemble average; no simple information about the behavior of a single molecule can be extracted directly from the data. Furthermore, the deuterium order parameters S_CD of the carbon atoms in the different parts of the lipid molecule are strongly coupled to one another. The polar head group alone includes about 30 atoms, yielding over 30 different dihedral angle potentials, each comprising a superposition of about 1–4 cosine functions of different amplitudes. Searching through such a high-dimensional space of parameters to improve the deuterium order parameters at a few specific sites is very difficult.

Designing a systematic strategy to rapidly optimize the parameters of a model to match experimental data is an objective of general interest from the point of view of force field development. One way to make progress is to try to first identify the (hopefully few) degrees of freedoms that are most strongly correlated with the most inaccurate S_CD’s. To this end, we employed a maximum entropy approach realized via the restrained-ensemble MD (re-MD) simulation method.⁵⁵ The maximum entropy/re-MD simulation method is a powerful approach to translate experimental data into structural information about macromolecular systems with the least amount of undesired arbitrary biases.^56,57 Briefly, the re-MD method considers N replicas of a system of interest with coordinate X_S. The ensemble average value of a property q_i is calculated from the N replicas,

$${\overline{q}}_i({\mathbf{X}}_1,{\mathbf{X}}_2,\dots ,{\mathbf{X}}_N)=\frac{1}{N}{\sum }_{s=1}^N{q}_i({\mathbf{X}}_S)$$ (2)

These ensemble-averaged properties q̄i may not agree with their proper experimental value $Q_i^{exp}$. To drive each of these ensemble-averaged properties toward their proper experimental value, a global biasing potential U_RE is introduced for each observable,

$$U_{RE}({\mathbf{X}}_1,{\mathbf{X}}_2,\dots ,{\mathbf{X}}_N)=\frac{1}{2}{\sum }_{i}K{({\overline{q}}_i({\mathbf{X}}_1,{\mathbf{X}}_2,\dots ,{\mathbf{X}}_N)-Q_i^{exp})}^2$$ (3)

It can be shown that such a bias is, in a maximum entropy sense, the least disruptive of the configurations of the system.⁵⁷ For the present application, the re-MD simulation approach was implemented through a tcl script for NAMD 2.10.⁴³ Analytical derivatives of the effective potential were included to evaluate the forces acting on the atoms of interest. While one could treat all the S_CD of the DPPC molecule via re-MD, in principle the computational overhead becomes prohibitive. For this reason, we tried to limit the number of S_CD that must be treated simultaneously via the re-MD to a maximum of 2 or 3 sites.

The maximum entropy-guided parameter optimization cycle may be summarized in the following way. A first re-MD simulation was generated to drive the S_CD of the deuterium quadrupolar splitting at sites G_3S and G₂ toward their correct experimental values. From the re-MD simulation re-directing those S_CD toward their proper experimental value, it was observed that a single torsion located in the polar head and glycerol backbone region, P-O11-C1-C2, was the most affected compared to an unbiased MD. The implication is that, in a maximum entropy sense, the potential function associated with this torsion is incompatible with the experimental S_CD values. From this information, the parameters of the P-O11-C1-C2 dihedral were optimized to reduce the deviation of the calculated S_CD relative to the experimental data using a genetic algorithm, through simultaneous mutation of the parameters in restricted space, each trial requiring a long unbiased MD simulation of the membrane bilayer (on the order of 50 ns) to evaluate the S_CD. Once no further improvement could be obtained, the cycle was repeated. A second re-MD simulation was generated to re-direct the most inaccurate deuterium order parameters toward their correct experimental value. This identified O11-C1-C2-O21 and C1-C2-O21-C21 as the most relevant torsions to optimize in the second cycle using the genetic algorithm with long unbiased MD simulation of the membrane bilayer. In total, four cycles of re-MD simulation and parameter optimization via the genetic algorithm were carried out, until a satisfactory agreement of all S_CD was reached. Ultimately, the parameters of 7 dihedral angles were refined to improve the previous Drude force field model of DPPC. Those are P-O11-C1-C2, O11-C1-C2-O21, C1-C2-O21-C21, C11-O12-P-O11, O11-C1-C2-C3, C3-C2-O21-C21, and O21-C2-C3-O31. The improved dihedrals of the PC head group were also used for DMPC, DLPC, POPC and DOPC.

2.5 MD simulations of hydrated lipid bilayers

The properties of solvated membrane bilayers formed by DPPC, DMPC, DOPC, POPC, DOPE, POPE and DPPE were extracted from extended MD simulations. A complete list of the membrane simulations is given in Table 1. Each system is comprised of 72 lipid molecules, with 36 in the upper and lower leaflets. The ratio of water to lipid molecules (~30) was chosen to match experimental conditions, yielding about 30,000 particles in each system (including nuclei, Drude particles and lone pairs). The SWM4-NDP water model was employed for all the simulations.²¹ The simulation temperatures for the all the systems were kept above the lipid-crystalline phase transition temperature (315 K for pure DPPC bilayer, 337 K for DPPE bilayer, 270 K for POPC bilayer).^58–60 Larger bilayer systems comprising 288 DPPC molecules (144 in the upper and lower leaflets) were constructed, and simulated in the NPT ensemble at 323 K for 200 ns to determine the lateral diffusion of the lipid molecules in the membrane plane. The remaining simulation protocols were as those described above for the neat liquids.

Table 1.

Bilayer systems modeled in this study. All bilayer system comprise 72 lipid molecules, with equal number in the upper and lower leaflet (DPPC† is a larger system comprising 288 lipid molecules).

System	Temperature (K)	Hydration Ratio (Nwater/Nlipid)
DPPC	323	30.4
DPPC†	323	30.4
DMPC	303	25.7
DLPC	303	31.3
POPC	293, 303, 323, 333	31.1
DOPC	293, 303, 323, 333	33.5
DPPE	342	32.0
POPE	303	32.0
DOPE	298	32.0

The starting configurations of the solvated bilayers were generated by the CHARMM-GUI web server.⁶¹ In the simulation systems, the membrane bilayer extends in the x-y plane and their normal is aligned to the z-axis. Each system was first optimized by energy minimization for 1000 steps with the steepest-descent algorithm followed by 10,000 steps of initial equilibration MD with a short timestep of 0.1 fs to allow the initial relaxation of the Drude particles. The systems were then fully equilibrated at the desired temperatures under an isotropic constant pressure of 1 atm in the NPT ensemble with a 1 fs timestep, during which the simulation box size was allowed to adjust in all three dimensions. The first 50–100 ns of each simulation were discarded for the analysis. All structural and dynamical properties were calculated over 200 ns of production simulation for each system. Average structural properties (area per lipid, lipid volume, and thermal expansivitiy) were analyzed by dividing the remaining simulation trajectories into equal blocks with errors estimated using a block-averaging approach (three blocks were used for the area per lipid and lipid volume properties, and two blocks were used for thermal expansivitiy).

3. Results and discussion

The present molecular mechanical (MM) Drude force field model for DPPC, DMPC, DLPC, POPC, DOPC, DPPE, POPE, and DOPE builds on the previous work on DPPC by Chowdhary et al.³ The lipid force field parameters are available online via the web site http://mackerell.umaryland.edu/charmm_ff.shtml as well as the Drude-Prepper module of the CHARMM-GUI web-server.⁶¹ The optimized Drude force field for the lipids is compatible with the remainder of the Drude force field including the SWM4-NDP water model,²¹ ions,^10,23 protein,^7,11 nucleic acids,^24–26 and carbohydrates.^27–29 In the following, we present the validation of the Drude force field for lipids. The validation effort includes on QM computations based on a series of small compounds as well as a broad range of experimental data on lipid membranes.

3.1 Properties of the model compounds

Structural and geometric properties of the small model compounds, calculated from the optimized Drude polarizable force field and the C36 additive force field, are compared with the results of QM calculations in Table 2. The structural properties are reported for the lowest energy conformer. In addition, geometric data for small molecules containing alkene moieties taken from a survey of the Cambridge Structural Database (CSD) are also included.⁶² The good agreement with the QM computations indicates that the MM force field models are representative of the compounds isolated in vacuum. The context is slightly different with the CSD survey data because it provides information about the compounds in a condensed crystalline phase. Nevertheless, the results collected in Table 2 show that the structural geometric properties from the MM force fields and QM calculations and the CSD survey are generally in excellent agreement for the model compounds considered here. For all bonds in the model compounds, deviations between the QM and the MM force fields (Drude and C36) representations are smaller than 0.01 Å. For valence angles, the Drude force field shows a slightly better performance than the additive C36 force field; the largest deviation of angle between the QM calculation and the Drude model being ~0.4 °. In comparison, the largest deviation for the C36 additive force field was 1.7 ° in the case of the Θ₄ angle in 2-hexene. For dihedral angles, both the Drude model and the C36 additive force field are in very good agreement with the QM results. The largest deviation is smaller than ~2 °. The results regarding the dihedral torsion angles are slightly more complex, as they may be affected by steric interactions. Furthermore, it is expected that the averaged dihedral angles from the CSD survey could deviate somewhat from the optimal values of the model compounds in the gas-phase. Nevertheless, the overall consistency of the MM models, QM calculations and CSD survey shows that the present strategy for the optimization of bonds, angles and dihedrals parameters can successfully predict correct molecular geometries.

Table 2.

Geometric properties of minimum energy rotamers of the alkene model compounds from QM calculations, the Drude polarizable force field and the C36 additive force field, along with data collected from the Cambridge Structural Database (CSD).⁶² For the CSD data, averaged structural properties are reported. Crystal structures with alkenes in ring systems or that contain ions were omitted. A threshold of the crystallographic R-factor was set to <= 0.05. For dihedral angles, median values were used instead of averaged properties. Bonds, angles, and dihedrals are defined as shown in Figure 1.

Method	Dihedrals			Angles				Bonds (Å)
	Ψ1	Ψ2	Ψ3	Θ1	Θ2	Θ3	Θ4	r1	r2	r3	r4	r5
2-butene
QM	180.0	-	-	124.7	124.7	-	-	1.50	1.34	1.50	-	-
Drude	180.0	-	-	125.4	125.1	-	-	1.50	1.34	1.50	-	-
C36	180.0	-	-	124.0	124.1	-	-	1.51	1.34	1.51	-	-
CSD	−178.2	-	-	124.7	124.7	-	-	1.50	1.32	1.49	-	-
2-pentene
QM	−178.9	116.9	-	124.7	124.8	111.9	-	1.50	1.34	1.50	1.53	-
Drude	−179.7	116.9	-	125.1	124.0	110.1	-	1.50	1.34	1.50	1.53	-
C36	−179.8	116.0	-	124.0	124.8	111.0	-	1.51	1.34	1.51	1.54	-
CSD	48.7	149.7	-	126.0	126.2	112.9	-	1.49	1.32	1.49	1.53	-
2-hexene
QM	179.4	116.8	−65.0	124.6	125.0	112.4	112.5	1.53	1.50	1.34	1.50	1.53
Drude	179.4	116.8	−65.0	124.6	125.0	112.4	112.5	1.52	1.50	1.34	1.50	1.52
C36	179.7	118.6	−65.8	124.0	124.8	112.7	114.2	1.53	1.51	1.34	1.51	1.53
CSD	165.1	−133.5	177.8	126.9	127.0	112.6	114.0	1.53	1.49	1.32	1.49	1.53
3-hexene
QM	116.6	180.0	−116.5	111.8	124.9	124.9	111.8	1.53	1.50	1.34	1.50	1.53
Drude	116.6	180.0	−116.6	111.9	124.9	124.9	111.8	1.53	1.50	1.34	1.50	1.53

Table 3 presents the molar volumes and enthalpies of vaporization (ΔH_vap) of the neat liquids of the model compounds, 2-butene, 2-pentene and 2-hexene. As the chain length of the alkene molecules increases, the Drude polarizable models accurately predict the molar volumes. The accuracy of the polarizable and additive force field is similar for 2-pentene and 2-hexene, with errors in the molar volumes being less than 1.6 cm³. However, the deviation in the molar volume is less than 1.0 cm³ for 2-butene, which is an improvement over the C36 additive force field. Importantly, while the enthalpy of vaporization from C36 additive force field are within a reasonable range for all the compounds, the results from the Drude polarizable force field are in even better agreement with experimental data. The largest error with the Drude force field is only 0.3 kcal/mol for 2-butene, whereas the largest error with the C36 additive force field was 1.1 kcal/mol in the case of 2-pentene. The calculated hydration free energy of 2-hexene is 7.24 kcal/mol, which matches the experimental value of 7.24 kcal/mol.⁶³ The dielectric constant (electrostatic permittivity) of the polarizable model is 1.98, which is in good accord with the experimental value of 2.14 (both the calculated value and experimental measurements considered the trans conformation of 2-hexene), supporting the use of the unscaled atomic polarizabilities as with the alkanes.

Table 3.

Molar volume and enthalpy of vaporization (ΔH_vap) of the model compounds from experimental measurements, Drude simulations and C36 additive force field simulations. Experimental data were taken from Smith et. Al.¹¹¹ Properties from of the Drude force field simulations are average values from multiple calculations.

Compound	Molar Volume (cm3)			ΔHvap (kcal/mol)
	Expt.	Drude	C36	Expt.	Drude	C36
2-butene	93.823 (298.15 K)	94.290	96.551	5.11	5.42	4.50
2-pentene	108.207(293.15 K)	109.203	109.920	6.40	6.36	7.50
2-hexene	122.468(293.15K)	124.042	124.093	7.55	7.70	6.75

Interestingly, the resulting binding energies of the model compounds with water or noble gas tend to be not as attractive as the values from QM (given in Supplementary Tables S4 and S5 and Supplementary Figure S1). The final models were optimized to yield accurate condensed behavior for the molar volume and enthalpy of vaporization (Table 3). A possible explanation for such systematic deviation is that the van der Waals parameters in the final Drude force field must have indirectly incorporated some van der Waals many-body effects, by virtue of the optimization to yield accurate condensed behavior for the molar volume and enthalpy of vaporization. Such many-body effects are absent in the context of a single model compound and a water molecule or a noble gas atom. The latter context only probes the 2-body van der Waals interactions, which is too negative. A 3-body correction would be unfavorable and would effectively contribute to reduce the van der Waals interactions probed only at the 2-body level.⁶⁴

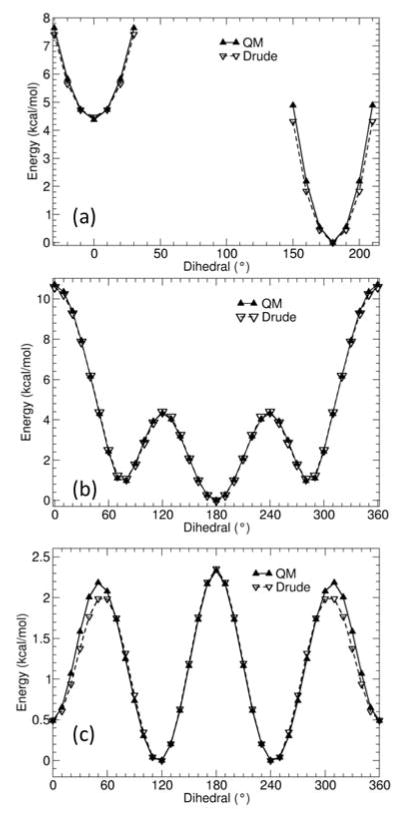
The QM dihedral energy surfaces for 2-butene, 2-pentene, and 2-hexene are shown in Figures 2, 3, 4 and 5. The agreement between QM and the final optimized Drude force field for the alkenes is satisfactory. By comparison with the QM surfaces, it is clear that the Drude force field correctly predicts the relative energy of the trans and gauche conformations, with a deviation smaller than about 0.2 kcal/mol. The largest discrepancy occurs for high relative energy rotamers. Because 2-butene and 2-pentene both contain less than 6 carbon atoms, contributions from steric interactions from terminal alkane moieties may not be fully captured (Figure 1). These interactions are accounted for in 2-hexene. The 3-hexene model compound, which was not included in the parameter optimization process, was used to assess the dihedral parameter for rotation about the double bond. The Drude polarizable force field predicts that the trans conformer is 1.2 kcal/mol more stable than the cis conformer, consistent with the QM surface at the MP2/cc-pVDZ level.

Figure 2.

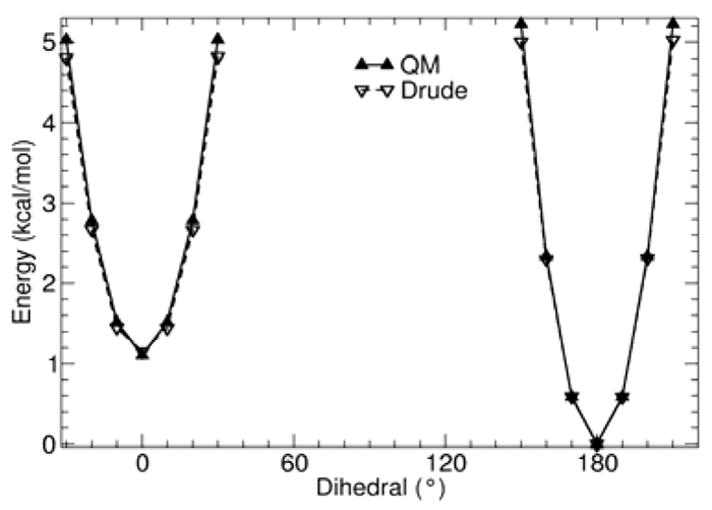
QM (solid lines) and Drude (dashed lines) calculated potential energy surface for rotating dihedral angle CD33A-CD2C1A-CD2C1A-CD33A in 2-butene. Other degrees of freedom were allowed to relax in both QM (MP2/cc-pVDZ) and the Drude calculations.

Figure 3.

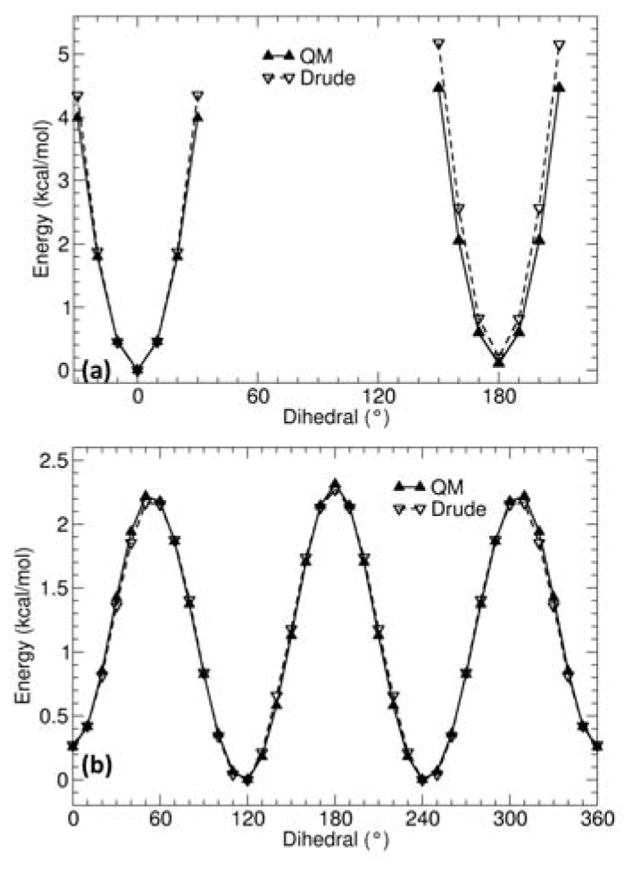
QM (solid lines) and Drude (dashed lines) calculated potential energy surfaces for rotating dihedral angle CD33A-CD2C1A-CD2C1A-CD32A (a), and CD2C1A-CD2C1A-CD32A-CD33C (b) in 2-pentene.

Figure 4.

QM (solid lines) and Drude (dashed lines) calculated potential energy surfaces for rotating dihedral angle CD33A-CD2C1A-CD2C1A-CD32A (a), CD2C1A-CD2C1A-CD32A-CD32A (b), and CD2C1A-CD32A-CD32A-CD33A (c) in 2-hexene.

Figure 5.

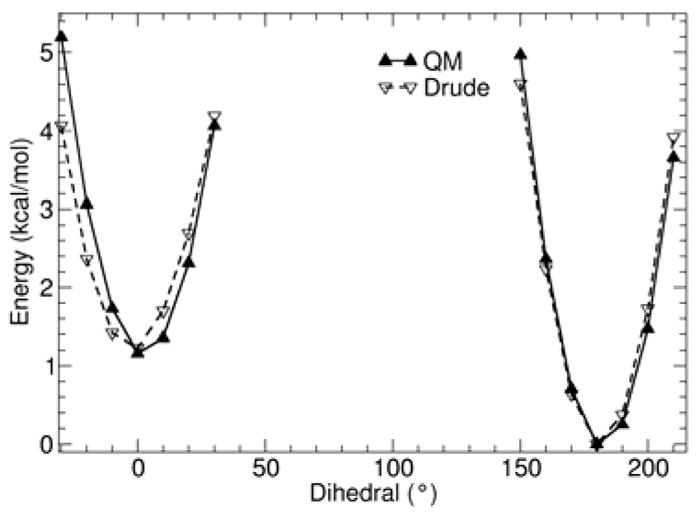
QM (solid lines) and Drude (dashed lines) calculated potential energy surfaces for rotating dihedral angle CD33A-CD2C1A-CD2C1A-CD33A in 3-hexene. Other degrees of freedom were allowed to relax in both QM and the Drude calculations.

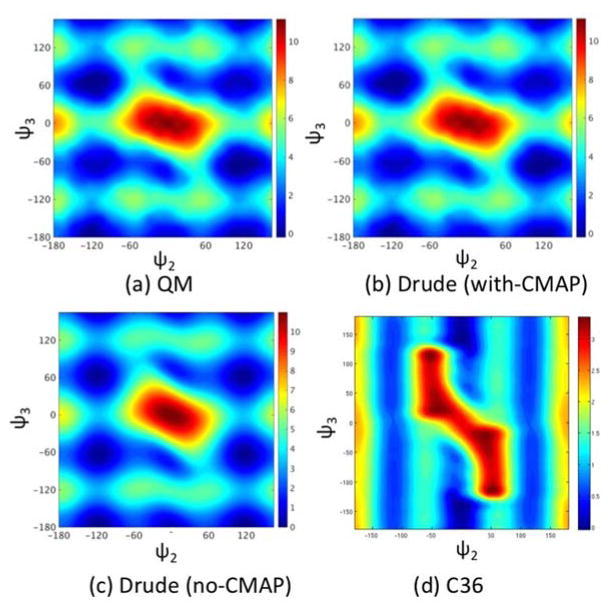
Anticipating that torsions around the carbon-carbon single bond adjacent to the double bond might display some complex coupling effects that could be difficult to represent accurately with independent torsion potentials, we examined the entire two-dimensional (2D) potential energy surface for dihedral ψ₂ and ψ₃ in 2-hexene and compared the accuracy of two models with the analogous QM data. The 2D map is shown in Figure 6a. The first model included only independent torsion potentials over ψ₂ and ψ₃, while the second model introduced a 2D (ψ₂, ψ₃) grid-based spline following the correction map (CMAP) procedure that was introduced previously for the (φ, ψ) dihedrals of the protein backbone.⁶⁵ As shown in Figure 6b and 6c, the Drude polarizable force field correctly predicts the relative depth of the minima at (±120°, ±60°) and (±120°, 180°), whether a (ψ₂, ψ₃)-CMAP correction is included or not. Further analysis indicates that for most regions, the difference between the two models is located in small regions, suggesting that the impact would be negligible. By comparison, the (ψ₂, ψ₃) torsion potentials calculated from the C36 additive force field is qualitatively incorrect. As observed in Figure 6d, periodicity along ψ₃ is completely missing, leading to only two stable conformations at (ψ₂, ψ₃) = (0°, ±110°). The model with CMAP corrections was used to generate the present membrane simulations. Alternatively, given the similarity of the two-dimensional (ψ₂, ψ₃) potential energy surface with and without CMAP correction, the simpler representation based on independent torsion potentials could also be used.

Figure 6.

Potential energy surfaces of model compound 2-hexene as a function of dihedral ψ₂ angle and ψ₃, as defined in Figure 1. (a) Benchmark data from QM calculation. (b) Drude force field with CMAP between dihedral ψ₂ and ψ₃ included, (c) Drude force field without CMAP correction (d) C36 nonpolarizable force field.

3.2 NMR deuterium order parameters

NMR deuterium order parameters, S_CD, extracted from NMR deuterium quadrupolar splittings measurements are an important benchmark for accessing the quality of a force field. The S_CD characterizes the average orientation of a carbon-deuterium (C-D) bond vector in the lipid molecule with respect to the membrane normal. It is defined as,

$$S_{\text{CD}}=\mid \langle \frac{3{cos}^2(\theta )-1}{2}\rangle \mid$$ (4)

where θ is the angle between the C-D bond vector and the normal to the lipid bilayer. A value of S_CD that is too small is either indicative of a lack of orientational order in this region of the molecule or of an incorrect local conformation.

While the overall properties of the 2013 Drude force field for DPPC were generally good, the S_CD at a few specific sites along the polar head group were substantially underestimated compared with experimental measurements.³ Thus, improving the accuracy of the head group representation with respect to the average orientational order as reported by the S_CD was one important objective of the present effort. To refine the force field, we employed a maximum entropy approach realized via the restrained-ensemble MD (re-MD) simulation method.⁵⁵ This enabled a rapid identification of the problematic torsions in the polar head group region, which could then be refined iteratively. As shown in Figure 7, the calculated order parameters for a hydrated DPPC bilayer simulated at 323 K with the improved Drude polarizable force field agrees very well with the available experimental S_CD.^66–71 The excellent agreement indicates the statistical order of the DPPC molecules in fluid phase bilayer membranes is correctly represented in these simulations.

Figure 7.

NMR deuterium order parameters (S_CD) for a hydrated DPPC bilayer. Shown are the S_CD calculated using the new Drude polarizable force field (red), C36 additive force field (blue), and measured from experiments (black). The results for the C36 force field were taken from Klauda et. al.¹⁶ Experimental data were taken from Seelig and co-workers.^66–69 and Strenk et al;⁷⁰ the data for the Sn-2 chain is taken from Douliez and et al.⁷¹ The temperature of the MD simulations and the experimental data is 323 K. The axis labels follow the original naming convention from Seelig, where the glycerol carbon attached to phosphorous is called G3 where the palmitic chains are bonded to carbons 1 and 2 of the glycerol. The CHARMM force field and topology follows the Sundaralingam¹²⁵ notation given by the following: β is C12-H12A and C12-H12B, α is C11-H11A and C11-H11B, G1R is C3-HX, G1S is C3-HY, G2 is C2-HS, G3R is C1-HA, G3S is C1-HB, C2 is C22-H2R and C22-H2S, and C2R is C32-H2X.

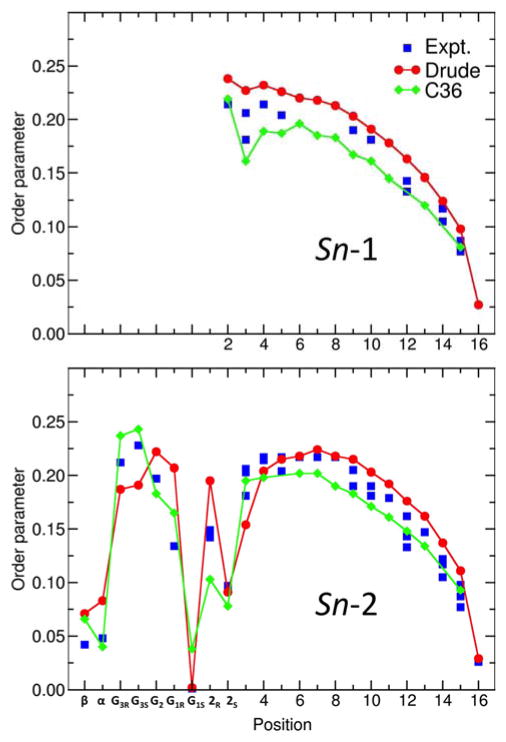
We also examined the NMR order parameters for the unsaturated lipids. As shown in Figure 8, the calculated S_CD for a hydrated POPC bilayer from the Drude polarizable force field are in good agreement with experimental data,⁷² with a few minor differences. In particular, the order parameters from the experiments at positions 9 and 10, corresponding to the double bond, are smaller compared with the results from both force fields. In addition, the order parameter at position 2 for the C22-H2R bond vector appears to be overestimated in the Drude force field compared to experiment and C36. On the other hand, the order parameter for the C22-H2S bond vector from the Drude force field (value of 0.060) is in better agreement with experiment (value of 0.064) relative to C36 (value of 0.093). Such small deviations in S_CD are indicative of differences in the average conformation of the Sn-2 chain near the glycerol backbone region of the POPC molecule. Furthermore, it is worth noting that there is some spread is the measured NMR order parameters.⁷³ To gain some perspective and appreciate the significance of small deviations in S_CD, the following analysis is helpful. The average 〈(3cos²(θ) − 1)/2〉 calculated from the POPC simulations based on the Drude force field for the C22-H2R bond vector is −0.221, while the experimental value of the S_CD is 0.096. The sign of a deuterium quadrupolar splitting cannot be measured experimentally. Assuming that the experimental value also carries a negative sign, the difference in value would translate into a shift of about 58° to 64° in the average orientation of the bond vector. This shows that fairly small deviations in the average conformation of the POPC molecule can lead to differences in the S_CD. The calculated S_CD for the two unsaturated chains of DOPC are very similar to those of the unsaturated Sn-2 chain of POPC (data not shown), but do not display the slight upward shift (~0.02) that is observed experimentally.⁷⁴ The order parameters along the unsaturated Sn-2 chain of POPC or DOPC decrease by about 0.02 when the temperature is raised from 303 K to 323K (data not shown), indicates a slight increase in fluctuations that is consistent with experiment.⁷⁴

Figure 8.

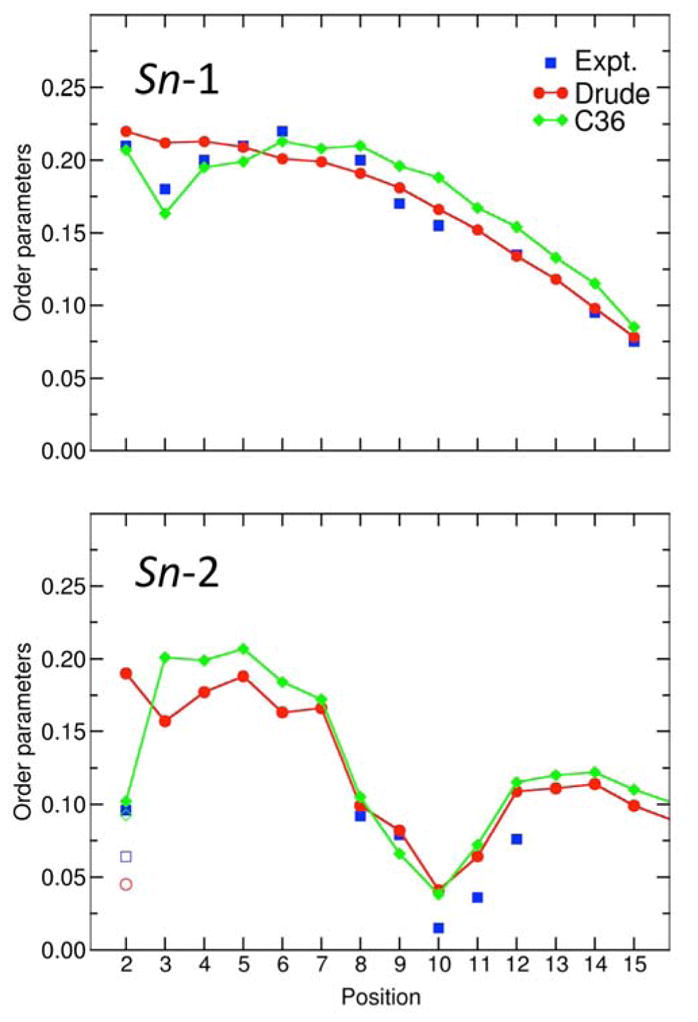
NMR deuterium order parameters (S_CD) for a hydrated POPC bilayer. Shown are the S_CD calculated using the new Drude polarizable force field (red), C36 additive force field (blue), and measured from experiments (black). The results for the C36 force field were taken from Klauda et. al.¹⁶ The MD values were calculated at 303 K. The experimental data collected at 300 K is from Seelig and Seelig.⁷² The open symbols at position 2 of the Sn-2 chain represent the split values of the order parameters for HR and HS.

A comparison of the calculated and experimental order parameters for a hydrated POPE bilayer is shown in Figure 9. The results from the Drude polarizable force field are fairly similar to the values from the C36 force field,¹⁶ and are in general agreement with experimental data.^75,76 Differences between the experiments and calculations similar to those noted above with respect to POPC are observed with respect to the 9th and 10th positions, and the magnitude of the C22-H2R and C22-H2S splittings.

Figure 9.

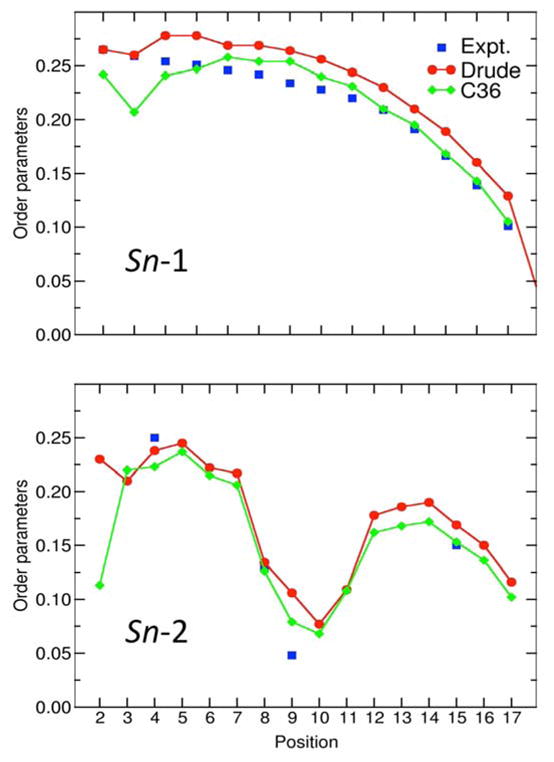
NMR deuterium order parameters (S_CD) for a hydrated POPE bilayer. Shown are the S_CD calculated using the new Drude polarizable force field at 303 K (red), C36 additive force field at 310 K (blue), and measured from experiments at 310 K (black). The results for the C36 force field were taken from Klauda et. al.¹⁶ The experimental data is taken from Seelig and co-workers.^75,76

3.3 Electron Density Profiles

The lipid bilayer form factor F(q) was determined by taking the Fourier transform of the electron density profile (EDP), ρ(z),³

$$F(q)=\mid {\int }_{-d/2}^{d/2}[\rho (z)-{\rho }_{\mathrm{W}}]cos(qz)dz\mid$$ (5)

where d represents the length of the simulation cell in the z direction, and ρw is the electron density profile of pure water. For DPPC, the electronic density profile was calculated by assuming that electron charge is equivalent to the difference between the atomic number and partial charge of the atom, which includes the charge on the atoms and their associated Drude particles (including the charge on the lone-pairs particles when present). In practice, the magnitude of the experimental form factor is arbitrary and can be scaled to best fit the data from simulations.⁷⁷

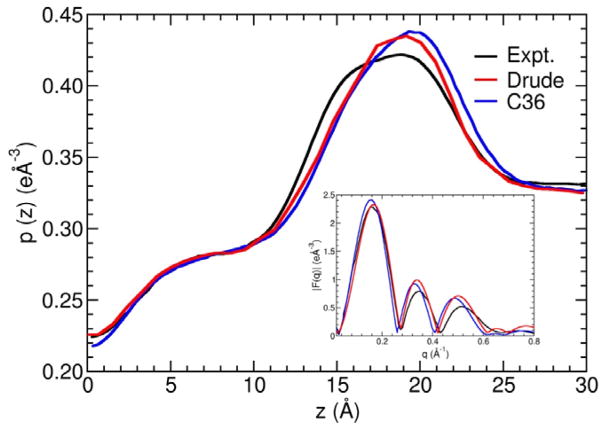
Figure 10 shows a comparison of the electron density profile from MD simulations and from X-ray experiment for a hydrated DPPC bilayer at 323 K.^78–80 There are two main peaks located at about z=±20 Å from the center of the membrane corresponding to the phosphate headgroup region. Beyond the main peaks the electron density quickly decays to 0.33 in the bulk water region. In the density profile calculated from the Drude model, the position of the main peaks matches the experimental data very well. The density peaks are strongly correlated with the thickness of the lipid bilayer, suggesting that the latter is correctly predicted by the simulation. However, the magnitude of the electron density at the main peak is slightly overestimated, which suggests that the polar headgroup region might be slightly too ordered. Toward the center of the bilayer, the electron densities quickly decreased to 0.28, in an almost linear manner, then reaches a plateau before it finally drops to 0.22 at the center of the bilayer (z=0 Å). All these trends are reproduced very well by the optimized Drude polarizable force field, which displays a net quantitative improvement over the C36 additive force field. The RMSD relative to the experimental electron density profile is 0.0076 for the Drude polarizable force field and 0.0115 for the C36 additive force field. In the inset of Figure 10, the form factors and electron densities obtained in Drude simulations are compared to experimental data and the fitted experimental data. The peak position and minima in the experimental form factors are reproduced quite well, with only some small offset in the magnitude of the second peak (at about q=0.3 Å⁻¹). The good agreement between the two indicates that the optimized Drude polarizable force field accurately predicts the average structural features of the DPPC lipid bilayer. The electron density profiles as well as the scattering form factors for the other lipids are shown in Supplementary Figures S2 and S3, respectively. A comparison of the calculated scattering form factor with available experimental data of Kučerka et al. for DPPC,^78–80 DMPC,^79,80 DLPC,^79,80 POPC,⁸⁰ DOPC,^79–81 and POPE⁸² is shown in Supplementary Figures S4–S9. The good agreement indicates that the average structure of the simulated membranes is reasonable.

Figure 10.

Electron density profiles and x-ray scattering form factor (inset) of the DPPC bilayer system of DPPC at 323 K, obtained from experiment (black line), compared with the results from MD simulations generated using the Drude polarizable force field (red), and the C36 additive force field (blue). The experimental data comes from Kučerka et al,^78–80 and the results for the C36 force field were taken from Chowdhary et al.³ The RMSD between the experimental data and the MD simulations is 0.0076 for the new Drude polarizable force field and 0.0115 for the C36 additive force field.

3.5 Membrane dipole potential

The transmembrane dipole potential is an important feature of bilayer membranes. ^83–85 Its magnitude governs the permeability of ions and charged molecules^86–88 as well as a host of biological processes.^89,90 A previous simulation study showed that an accurate representation of the transmembrane dipole is greatly affected by the induced polarization of the lipid hydrocarbon chains near the solvent-membrane interface.² The system electrostatic potential ψ(z) is related to the charge density profile ρ_q(z) along the normal through the Poisson equation, ²

$$\frac{d^2\psi (z)}{d{z}^2}=-\frac{\rho q(z)}{{\epsilon }_0}$$ (6)

where ε₀ is the permittivity constant of vacuum. Therefore ψ(z) can be computed from the MD simulations by evaluating the double integral

$$\psi (z)-\psi (0)=-\frac{1}{{\epsilon }_0}{\int }_0^{z}d{z}^{\prime }{\int }_z^{\infty }{\rho }_q(z^{″})d{z}^{″}$$ (7)

The particle type of summation (P-sum) in the above equation, also known as the Galvani potential, represents the potential difference that a probing charge experiences as it moves across interfaces.² As the probe charge is assumed to be a point with zero-radius, such Galvani potential is not truly a quantity that is measurable by experiment. As a reference, the potential at the center of bulk water region, under the PBC condition, has been set to zero.⁹¹ The electric field E(z) was evaluated by taking the integral of the charge density ρ_q(z),

$$E(z)=\frac{1}{2{\epsilon }_0}[{\int }_{-l}^z{\rho }_q(z^{\prime })dz-{\int }_z^l{\rho }_q(z^{\prime })dz].$$ (8)

The dipole potentials of the DPPC, DMPC, and DLPC membranes calculated from MD simulations based on the Drude polarizable force field are shown in Figure 11 and compared with results from the C36 nonpolarizable force field. For all the membrane simulations based on the polarizable force field, the dipole potential at the center of the bilayer is around 560 mV relative to the bulk water region. The corresponding value for the DPPC simulation based on the C36 nonpolarizable force field is around 650 mV, which is considerably larger. The main disparity between the two force fields occurs near the water-membrane interface region. In both cases, the dipole potential rapidly increases to reach a high positive value at the headgroup region relative to the bulk. However, while it remains high for the simulation based on the C36 nonpolarizable force field, the potential drops by about 500 mV from −18 to −10 Å along the z axis corresponding to the start of the hydrocarbon chains with the Drude models. The large drop indicates that there is a significant induced polarization response from the hydrocarbon chains to the local electrostatic field. Accordingly, the major difference between the electrostatic profiles for the two force fields must primarily be due to differences in electrostatic representation of the hydrocarbon, water, and water headgroup interactions. Induced polarization in the interfacial region, where the average electric field is the largest, is a particularly important feature that cannot be captured by a force field with fixed partial charges. The importance of the polarizability of the lipid molecules near the water-membrane interface noted here is consistent with recent electrostatic force microscope experiments which estimated that the dielectric constant was around 3 in this region.⁹² In contrast, the C36 additive force field displays essentially no response in this region, which reflects a nonpolarizable material with a vacuum-like dielectric constant close to 1.

Figure 11.

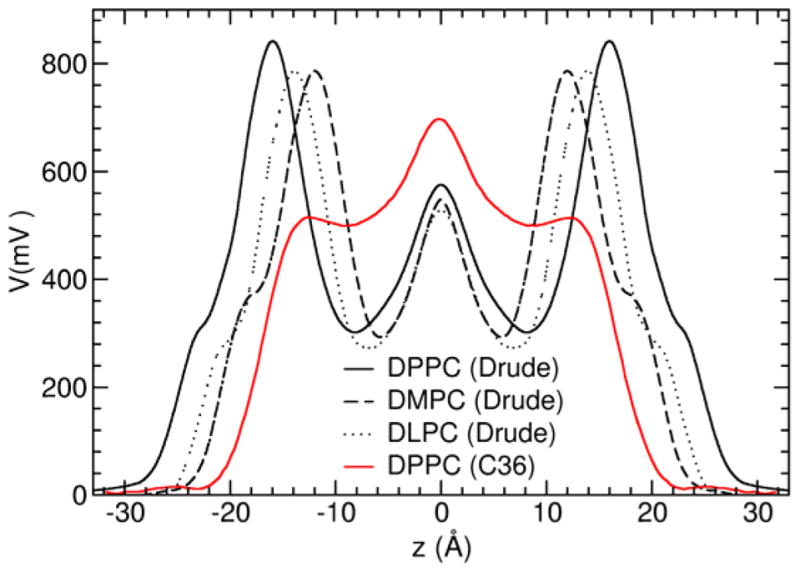
Transmembrane dipole potential of the DLPC (black dotted line), DMPC (black dashed line) and DPPC (black solid line) membranes from the Drude simulations and from the C36 additive force field for DPPC (red solid line).

3.6 Membrane Areas, Volumes, and Thickness

Hydrated bilayer membranes are essentially thin two-dimensional sheets. Important structural features include the average interfacial area per lipid molecule (A), the average hydrophobic thickness of the bilayer (D_B), the average volume per lipid molecule (V_L).⁹³ How such simple properties are simulated provides an important assessment of the accuracy of a force field. The volume per lipid molecule, V_L, was calculated as the time-average of the difference between the volume of the PBC simulation box (V_B) and the total volume taken by water molecules,

$$V_{\mathrm{L}}=\frac{V_{\mathrm{B}}-n_{\mathrm{W}}{V}_{\mathrm{W}}}{n_{\mathrm{L}}}$$ (9)

where n_W and n_L represents the number of water molecules and lipid molecules in the simulation system, respectively, and V_W is the specific volume of a water molecule (calculated from NPT simulation for the SWM4 water model at the given temperature). One may note that an assumption implicit with this expression is that the volume occupied by the small water molecules is independent of their location. The area per lipid head group of various fully hydrated lipid bilayers at fluid phase have been measured by Gravimetric X-ray approach, NMR and small-angle neutron scattering.⁹⁴ There are several approaches for determining the area per lipid A from MD simulations. The most straightforward method, of course, is to is divide the total area of the PBC simulation box in the x-y bilayer plane by the number of lipid per leaflet, yielding

$$A=\frac{L_x{L}_y}{(n_{\mathrm{L}}/2)}$$ (10)

where n_L is the number of lipid molecules in the simulation system. A second, more indirect, approach to is to divide the total effective volume of the lipid membrane V_L by the bilayer thickness D_B,

$$A=\frac{V_{\mathrm{L}}}{D_{\mathrm{B}}}$$ (11)

which may operationally be defined from the spatial distribution of water ρ_W(z) along the z direction normal to the membrane-bulk interface by assuming based on the Gibbs-Luzzatti prescription⁷⁹ that the integrated water probability on the left of the interface is equal to the integrated deficit of water probability on the right side of the surface,

$${\int }_0^{D_{\mathrm{B}}/2}{\rho }_{\mathrm{W}}(z)dz={\int }_{D_{\mathrm{B}}/2}^{z\ast }({\overline{\rho }}_{\mathrm{w}}-{\rho }_{\mathrm{W}}(z))dz$$ (12)

where z* represents an arbitrary position beyond which the water density is assumed to be equal to the bulk value ρ̄_w.

Table 4 reports the average interfacial area per lipid molecule (A), the hydrophobic thickness of the bilayer (D_B), and volume per lipid molecule (V_L) for DOPC, POPC, DOPE, POPE, DPPE, DMPC, DPPC, and DLPC. It is observed that the Drude polarizable model achieves a reasonable agreement with the experimental measures area per lipid. Experimental areas per lipid for POPE and DMPC are reproduced very well, while the area per lipid for POPC, DPPC and DLPC is slightly underestimated by about 1 Ų. For DPPE, the Drude force field slightly underestimates the area per lipid by about 3 Ų, a deviation that is similar to that from the C36 additive force field. It is worth noting that, due to the fluctuation of fluid phase lipid bilayer and experimental techniques, lipid structural properties such as the area per lipid reported in literatures often deviate by a few Ų between different studies, which may be indicative of some limitations in the precision of the experimental data.⁹⁵ Furthermore, the bilayer thickness D_B determined by fitting x-ray scattering data ⁷⁸ tends to provide a lower estimate than the value determined by fitting neutron scattering data.⁷⁹ For both DOPC and POPC, the area per lipid increases as a function of simulation temperature. With regards to the volume per lipid molecule, both the polarizable Drude force field and the C36 additive force field show high consistency with experimental data. However, C36 appears to slightly underestimate the volume by roughly 30–40 ų. The membrane thickness for DMPC, DLPC, and DPPC calculated with the Drude force field is also very consistent with the experimental estimates. For DOPC, the thickness is slightly overestimated by about 1.0 Å. The membrane thickness may also be determined from the position of the maximum in the electron density profile, corresponding to the phosphate group (see Supplementary Figure S2). The results are compiled in Supplementary Table S7. According to this criterion, the thinnest membrane is DLPC, closely followed by DMPC, while the thickest are DPPC, DPPE, and POPE. As observed from Supplementary Figure S3, the overall shape and the oscillations of the lipid bilayer form factor F(q_z) are highly sensitive to the position of the density maximum corresponding to the phosphate group of the polar head. The membrane thickness associated with the position of the maximum in the electron density profile gives rise to the dominant first peak in the scattering form factor at low values of q observed in Figure 10 and Supplementary Figure S3. The average scattering form factor for the different lipids, shown in Supplementary Figures S4–S9, clearly reflects the variations in membrane thickness. According to Eq. (5), a simple scaling of the Fourier-space q-axis of the scattering form factor corresponds to a scaling of the real-space Z-axis of the electron density profile by 1/s. This simple analysis can be used to match the position of the first minimum in the experimental scattering form factor (Supplementary Figure S10), suggesting that the thickness of these simulated model membranes is correct within 4% (Supplementary Table S7).

Table 4.

Properties of the fully hydrated pure lipid membranes comparing experimental measurements with simulations using the Drude polarizable force field and the C36 additive force field; A, surface area per lipid; D_B, Luzzatti bilayer membrane thickness; V_L, specific volume per lipid molecule. Error estimations are based on block-averaging approach by dividing the simulation trajectories into three blocks. Hydration numbers are listed in Table 1.

Lipid	T (K)	Surface area per lipid (Å2)			Bilayer thickness DB (Å)			Specific volume per lipid VL (Å3)
		Expt.	Drude	Additive‡	Expt.	Drude	Additive	Expt.	Drude	Additive
DPPC	323	63.079,95	61.8±0.5	62.8±3.03 61.8±0.3112	39.0±0.879	39.7	39.616	123295	1219.8	1201113
	323	63.0114	-	63.0114	-	-	-	-	-	-
DMPC	303	60.678 60.6114	61.1±1.9	60.8±0.216 61.7114	36.378	36.2	36.216	1096115 110195	1095.1	1060113
DLPC	303	63.278	61.6±0.4	64.4±0.3112	31.478 32.6±0.716	32.0	31.016	99178	985.2	951113
POPC	293	62.7±1.380	62.1±0.2	63.7±0.3112	39.8±0.8	39.6	38.316	-	1229.6	1200116
	303	64.3±1.380 68.3114	63.2±0.01	64.7±0.216 66.0114	39.1±0.8	39.4	37.416	1223117 125681	1246.4	1213116
	323	67.3±1.380	65.6±1.2	67.8±0.3112	37.9±0.8	38.3	37.316	-	1265.2	1235116
	333	68.1±1.494	66.1±0.7	68.7±0.3112	37.7±0.8	39.2	37.016	-	1297.6	1241116
DOPC	293	69.1118	63.2±1.1	67.3±0.4116	-	40.7	38.3116	1288118	1285.7	1260116
	298	67.479 72.478	-	68.9	-	-	-	-	-	-
	303	67.479 72.5118	65.3±0.2	69.0±0.316 68.0±0.5116	38.779	39.7	37.2116	130395	1296.5	1262116
	323	75.5118	68.4±0.4	70.3±0.6116	36.1	38.5	36.6116	1318118	1317.0	1285116
	333	-	70.3±0.4	71.4±0.5116	38.7	37.8	36.2116	-	1328.8	1292116
DPPE	342	60.594 55.4119	56.7±0.2 59.8±0.6§	56.4±0.5116	-	41.1	40.4116	-	1173.0	1141116
POPE	303	56.6120	56.6±0.2 62.4±0.8§	59.2±0.316	-	41.7	41.6116	-	1182.3	1153116
	310	59.8121 60.8114	-	58.8114	-	-	-	-	-	-
DOPE	298	-	60.6±0.2 62.9±0.9§	60.4±0.5116 62.3114	-	41.7	38.2116	-	1229.3	1196116

^‡Results for additive force fields were taken from simulations with the CHARMM C36¹⁶ force field and other related models^113,116

^§Values obtained from simulations generated with a pair-specific Lennard-Jones R_min (NBFIX) of 3.91 Å between the amino nitrogen and phosphate oxygen rather than the value of 3.71 Å generated from the standard combination rule.¹²².

3.7 Isothermal area compressibility modules

The isothermal area compressibility module (K_A) relates to the fluctuations of the area per lipid. It is calculated from a constant pressure simulation using the following expression,⁹⁶

$$K_A=\frac{k_{B}T\langle A\rangle }{\langle \delta A^2\rangle }$$ (13)

where T is the simulation temperature, and 〈A〉 and 〈δA²〉 are the averaged and quadratic fluctuations of the total area of the simulated membrane system, respectively. The results from the simulations together with experimental data are given in Table 5. It is observed that the Drude polarizable force field tends to overestimate K_A by a factor of 1.5 to 2 in some cases. In the particular case of lipids with a PE head group, the Drude model leads to very large overestimation of the compressibility modules. In comparison, the calculated K_A values from the C36 additive force field are in reasonable agreement with experiment.

Table 5.

Compressibility (K_A) of the fully hydrated pure lipid membrane comparing experimental measurements with simulations using the Drude polarizable force field and the C36 additive force field. Error estimations are based on block-averaging approach by dividing the simulation trajectories into two blocks. Hydration numbers are listed in Table 1.

Lipid	T (K)	K A(mN/m)
		Expt.	Drude	Additive
DPPC	323	23195 231114	393±11	238±35113 220114
DMPC	303	23418 234114	550±65	250±29113 210114
DLPC	303	-	288±17	268±24113
POPC	293	-	627±100	254±28116
	303	180–330114,123	709±26	298±30116 260114
	323	-	324±38	267±32116
	333	-	313±29	272±30116
DOPC	293	264118	452±139	282±34116
	298	300114	-	285114
	303	184–26518,118,124	623±40	256±29116
	323	254118	305±41	246±31116
	333	26518	378±15	242±36116
DPPE	342	-	503±15 431.8±24§	271±22116
POPE	303	233114	1594±11 363.6±0.3§	282±29116
	310	233114	-	270114
DOPE	298	-	1479±98 215±10§	282±23116
	298	-	-	255114

^‡Results for additive force field were taken from published studies with the CHARMM C36¹⁶ force field and other related models^113,116

^§Values obtained from simulations generated with a pair-specific Lennard-Jones R_min (NBFIX) of 3.91 Å between the amino nitrogen and phosphate oxygen rather than the value of 3.71 Å generated from the standard combination rule.

Such a large discrepancy with experiment is unexpected. Qualitatively, the implication is that the lateral packing of the lipid bilayer must be insufficiently flexible. In principle, the relative incompressibility of the membrane could arise from the interactions between the carbon chains or the polar head group region, or from some subtle factors affecting the hydration of the membrane surface. Identifying the physical origin of the discrepancy in a detailed all-atom force field remains, however, difficult. A recent study by Aksimentiev and co-workers aimed at improving the accuracy of lipid force fields suggests an interesting line of attack.⁹⁷ Specifically, they showed that the area per lipid of DPPE in simulations based on the nonpolarizable additive C36 lipid force field could be improved by introducing pair-specific LJ parameters (NBFIX) between the amino nitrogen and the phosphate oxygen in the PE head group.⁹⁷ Further simulation to calculate the osmotic pressure confirmed the inaccuracy of the standard combination rule.^98,99 In practice, interactions between oppositely charged atoms are often overestimated by the combination rule for a number of reasons, including charge transfer effects. The use of a pair-specific NBFIX in these cases is justified because the standard combination rule is only a convenient approximation to generate LJ parameters between different atom types. For example, a previous study showed that the osmotic pressure of concentrated electrolytes is highly sensitive to small adjustments to the pair-specific LJ between the cation and the anion.¹⁰⁰ While the PE headgroup is neutral, there is a strong cation-anion interaction between the positively charged amino group and the negatively charged phosphate group.

Inspired by these ideas, we explored the possibility of improving the force field for the PE lipids by changing the pair-specific LJ parameter R_min between the amino nitrogen and the oxygen atoms of the phosphate group (O13 and O14). The LJ parameter R_min was increased from its combination rule default value of 3.71 Å to 3.91 Å, a change of only 0.2 Å. The interaction between the phosphate group (C11 H11A H11B P O13 O14 O11 O12 C1 HA HB) and the amino group (N HN1 HN2 HN3 C12 H12A H12B) is −147.7 kcal/mol with the combination rule default parameter (3.71 Å), and it is reduced to −138.1 kcal/mol with the pair-specific R_min parameter. Thus, while the change is very small in terms of geometry, it yields a shift of 9.6 kcal/mol (7%) for this very strong interaction. In a 200 ns simulation of a DPPE membrane at 342 K, it was observed that the area per lipid increased to 59.8 Ų from its initial value of 56.7 Ų, while the isothermal area compressibility module decreased to ~432 nM/m from its initial value of 503 nM/m. The same amino nitrogen-phosphate oxygen NBFIX parameter decreased the isothermal compressibility of a DOPE bilayer at 298 K from to 215.1 nM/m from its initial value of about 1500 nM/m. Similarly, a POPE bilayer simulated at 303 K with the same NBFIX parameter, yielded an isothermal compressibility of 363.6 nM/m, which is close to the experimental value of 282 nM/m. While more work would be needed to systematically optimize the pair-specific LJ parameters for the polar headgroups, these preliminary tests show that this is a viable route for improving the physical accuracy of the current model.

3.8 Thermal expansion properties

The thermal area expansivity coefficient ${\alpha }_A^T$ of the bilayer can be evaluated by taking the temperature derivative of the lipid volume

$${\alpha }_V^T=\frac{1}{V}{(\frac{\partial V}{\partial T})}_{\mathrm{\Pi }}$$ (14)

where Π represents simulation under constant pressure. In the study, the area expansivitiy coefficients were determined from linear fitting of the lipid specific volume at various temperatures. It has two major components, the area thermal expansivity, ${\alpha }_A^T={(\partial A/\partial T)}_{\mathrm{\Pi }}/\langle A\rangle$, and bilayer thickness thermal contractivity, ${\alpha }_D^T={(\partial D/\partial T)}_{\mathrm{\Pi }}/D$. By taking the slope of volumetric data in Table 4, the evaluated area and thermal expansion properties show trends consistent with the experimental data. As the temperature increases, the areas and volumes of lipid bilayers tend to have a reduced rate of expansion. The results are given in Table 6, showing that the Drude force field yields a satisfactory agreement with experiment. The area expansivities are slightly too large for DOPC, and are slightly too small for POPC, suggesting that the model reached an acceptable compromise.

Table 6.

Area and volume thermal expansivitiy of POPC and DOPC at different temperatures, evaluated using area per lipid and volume per lipid data in Table 5.

Lipid	T (K)	${\mathit{\alpha }}_{\mathbf{A}}^{\mathbf{T}}$ (degree−1)		${\mathit{\alpha }}_{\mathbf{V}}^{\mathbf{T}}$ (degree−1)
		Expt.80	Drude	Expt.80	Drude
POPC	293	0.0022	0.0017	-	0.00126
	303	0.0021	0.0016	-	0.00124
	323	0.0021	0.0016	-	0.00122
	333	0.0020	0.0016	-	0.00119
DOPC	293	0.0019	0.0027	0.00075	0.00083
	303	0.0018	0.0026	0.00074	0.00083
	323	0.0018	0.0025	0.00073	0.00081
	333	0.0017	0.0024	-	0.00080

3.9 Translational diffusion

The rate of lateral diffusion of lipid molecules within the 2D-plane of the bilayer leaflets reflects an important aspect of membrane dynamics and fluidity. A number of experimental techniques have been employed for measuring the coefficient of lateral diffusion in lipids in bilayers, with values ranging from 0.1 to 22.4×10⁻⁷cm²/s depending on the experimental technique employed.^101–106 The short-time diffusion coefficient estimated from quasi-elastic neutron scattering experimental is on the order of 2 to 5×10⁻⁷ cm²/s,¹⁰² while the long-time diffusion coefficient display more variability. One value estimated from fluorescence recovery photobleaching (FRAP) experimental is on the order of 2 to 30×10⁻⁸ cm²/s.^103,104 Another value estimated from spin-labeling the head-groups of the phosphate lipid molecules in multilayers is on the order of 8.5 to 12×10⁻⁸ cm²/s.¹⁰⁵ Lastly, a more recent study using ¹H pulsed field gradients magic angle spinning NMR spectroscopy reported a lateral diffusion coefficient of about 15×10⁻⁸ cm²/s.¹⁰⁶

The lateral diffusion coefficient D_p of DPPC molecule within the plane of the bilayer was examined by evaluating the translational mean-square displacement (MSD) for the center of mass (COM) of lipid molecules,

$$D_{\mathrm{p}}=\underset{t\to \infty }{lim}\frac{1}{4}\frac{d}{dt}\langle {\mid {\mathbf{r}}_{xy}(t+t_0)-{\mathbf{r}}_{xy}(t_0)\mid }^2\rangle$$ (15)

where r_xy stands for the position of the lipid COM projected within the x-y membrane plane. The diffusion coefficient was then evaluated through linear fitting of the simulation data. In calculating the autocorrelation function, the time origin t₀ was shifted by steps of 100 ps. The diffusion coefficient was calculated as a time average for the individual lipid molecules, and then averaged over all the lipid molecules in the system.¹⁰⁷ To remove the artifact due to random relative motions of the upper and lower lipid monolayers, the coordinates of lipid molecules were corrected by subtracting the COM of the monolayer where it resides.¹⁰⁸ Simulation system consisting of 72 DPPC molecules and 288 DPPC molecules were both examined. For both the 72 DPPC and 288 DPPC systems, lipid molecules have local diffusional motion on the timescale of about 10 ps. The fast motion is mainly due to the “rattling” movements of the lipid chains in a cage-like environment while the positions of the hydrophilic head groups remains relatively stable.¹⁰⁹ Because of the considerable finite size effects on the lipid diffusion coefficient calculated from simulations,¹¹⁰ we mainly focus of the values extracted from the membrane system with 288 DPPC molecules. Standard errors were evaluated by dividing the simulation trajectory into three blocks.

The diffusion of DPPC lipid molecules, shown in Figure 12, exhibits behavior on two distinct orders of magnitudes. The short-time diffusion coefficient extracted from the present simulations is about 4.5 to 6.0×10⁻⁷cm²/s, a value that is roughly consistent with the estimate of 2–5×10⁻⁷ cm²/s from quasi-elastic neutron scattering.¹⁰² The long-time lateral diffusion coefficient extracted from the present simulations is about 1.0 to 2.5×10⁻⁸cm²/s. The calculated value overlaps with the broad range of 2 to 30×10⁻⁸ cm²/s estimated from fluorescence recovery.¹⁰⁴ It is, however, smaller than the experimental estimate of 8.5 to 12×10⁻⁸ cm²/s and of 15×10⁻⁸ cm²/s from spin-label,¹⁰⁵ and field gradients NMR,¹⁰⁶ respectively. The discrepancy can be partly explained by finite-size effects with the simulations. Theoretical analysis indicates that the lateral diffusion coefficient D_p of lipid molecules determined from MD simulations of membrane bilayers is expected to exhibit a very strong size dependence with respect to the dimension of the simulation cell.¹¹⁰ In simulations based on a finite MD system with PBC, the apparent lateral diffusion of the lipid molecules is effectively reduced because of the viscous drags arising from the nearby periodic images. The computational tool provided by Venable et al (https://diffusion.lobos.nih.gov) suggests that the D_p determined from the present simulation system of 288 lipids would increase by about a factor of 3 if we could simulate an infinite system, which would bring the calculated long-time lateral diffusion coefficient in closer agreement with the experimental estimates.^105,106

Figure 12.

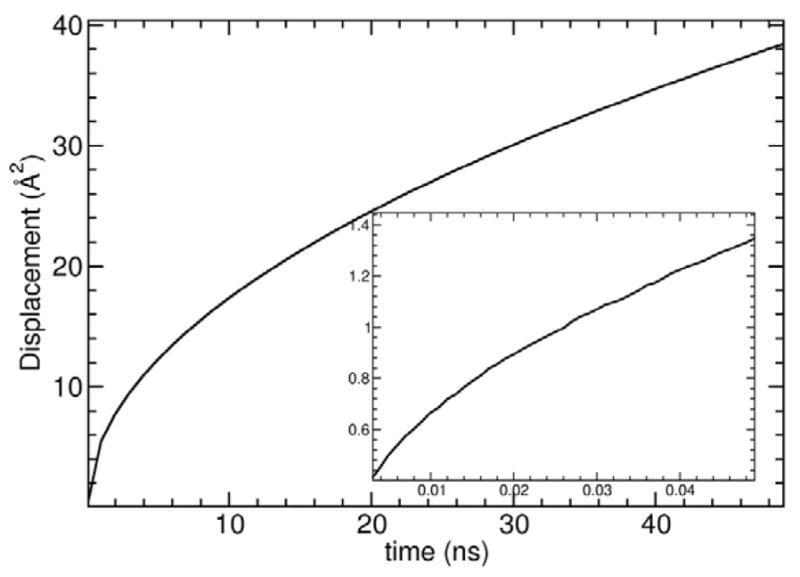
Mean-square displacement (MSD) of DPPC molecules within the membrane x-y plane. The movement of the center of mass of the lipids was removed. The displacement at short-time is given in the inset. The MD system comprised 288 DPPC molecules. The short-time diffusion coefficient fitted from the slope of the MSD is 6 Ų/ns in the interval 0.03–0.05 ns and 4.5 Ų/ns in the interval 0.0–0.05 ns. The long-time diffusion coefficient fitted from the slope of the MSD is 0.25Ų/ns in the interval 10–20 ns and 0.1Ų/ns in the interval 30–50 ns.

Conclusion

The polarizable force field based on the classical Drude oscillator offers a promising framework for modeling macromolecules using a more physically correct treatment of electrostatics as compared to traditional additive force field.¹⁴ The different components of the Drude force field for a biomolecular system, e.g., water,^21,22 ions,^10,23 carbohydrates,^27,28 proteins,^7,11 nucleic acids,²⁴ and lipids,³ have been developed with a consistent philosophy and thus are compatible with each other allowing for simulations of heterogenous systems. Simulations based on more accurate force fields will ultimately allow for a better understanding of the interplay between biological macromolecules and their environment. In the present study, we have sought to improve the representation of DPPC, especially with regards to the NMR order parameters of the polar headgroup region. This was achieved via a parametrization strategy based on a maximum entropy methodology. The force field was also expanded to incorporate several phospholipid molecules with mono-unsaturated hydrocarbon chains by using a series of alkene molecules as the model compounds. The iterative protocol employed in this study led to lipid models that have achieved good balance between reproducing QM calculations of model compounds and predicting condensed phase properties that are comparable to experimental measurements. Various properties, including densities and enthalpies of vaporization of model compounds, as well as volumes, thickness, areas, and electron densities of the lipid bilayers, agree well with experimental measurements. The results indicate that the polarizable lipid force field is capable of describing several features accurately. Most importantly, the transmembrane dipole potential predicted using the Drude polarizable agrees well from that the most-recent experimental data, highlighting the fact that a dielectric constant greater than 1 in the hydrocarbon chain region of the membrane is critical for a physically correct representation of electrostatics in these systems. As exemplified by the impact on pair-specific LJ parameters on the lateral compressibility of the membranes, the current Drude models could be further improved. Simulation studies of membrane-protein systems based on the Drude force field are currently under way.