Discrimination of curvature from motion during smooth pursuit eye movements and fixation

Even though motion trajectories in the real world are frequently curved, most studies of smooth pursuit and motion perception have investigated linear motion. We show that pursuit initially underestimates the curvature of target motion and is able to reproduce the target curvature ∼300 ms after pursuit onset. Temporal integration of target motion over longer periods is necessary for pursuit to reach the level of precision found in perceptual discrimination of curvature.

Abstract

Smooth pursuit and motion perception have mainly been investigated with stimuli moving along linear trajectories. Here we studied the quality of pursuit movements to curved motion trajectories in human observers and examined whether the pursuit responses would be sensitive enough to discriminate various degrees of curvature. In a two-interval forced-choice task subjects pursued a Gaussian blob moving along a curved trajectory and then indicated in which interval the curve was flatter. We also measured discrimination thresholds for the same curvatures during fixation. Motion curvature had some specific effects on smooth pursuit properties: trajectories with larger amounts of curvature elicited lower open-loop acceleration, lower pursuit gain, and larger catch-up saccades compared with less curved trajectories. Initially, target motion curvatures were underestimated; however, ∼300 ms after pursuit onset pursuit responses closely matched the actual curved trajectory. We calculated perceptual thresholds for curvature discrimination, which were on the order of 1.5 degrees of visual angle (°) for a 7.9° curvature standard. Oculometric sensitivity to curvature discrimination based on the whole pursuit trajectory was quite similar to perceptual performance. Oculometric thresholds based on smaller time windows were higher. Thus smooth pursuit can quite accurately follow moving targets with curved trajectories, but temporal integration over longer periods is necessary to reach perceptual thresholds for curvature discrimination.

NEW & NOTEWORTHY Even though motion trajectories in the real world are frequently curved, most studies of smooth pursuit and motion perception have investigated linear motion. We show that pursuit initially underestimates the curvature of target motion and is able to reproduce the target curvature ∼300 ms after pursuit onset. Temporal integration of target motion over longer periods is necessary for pursuit to reach the level of precision found in perceptual discrimination of curvature.

efficient processing of visual motion is essential for successful interactions with our environment (Burr and Thompson 2011; Nakayama 1985; Nishida 2011). Eye movements play an important role by guiding our actions, such as grasping or reaching (Bahill and LaRitz 1984; Bennett et al. 2010; Brenner and Smeets 2007, 2009, 2015; Johansson et al. 2001; Land and Hayhoe 2001). When a moving object appears in the visual field, subjects spontaneously pursue it with their eyes when they are required to intercept the object without being instructed to do so (Brenner and Smeets 2009, 2011; Mrotek and Soechting 2007a; Soechting et al. 2009). Continuous eye rotations, known as smooth pursuit eye movements, ensure that moving objects remain on the fovea and thus allow for dynamically sustained high-acuity percepts (Robinson 1965). These percepts may be used to build predictive models of future motion, which in turn enable accurate actions in the face of sensorimotor time lags (Schlag and Schlag-Rey 2002). The effects of smooth pursuit on motion perception and the relationship between pursuit and perception have long been a topic of research and debate (for recent reviews see Gegenfurtner 2016; Kowler 2011; Schütz et al. 2011; Spering and Montagnini 2011).

A number of researchers have evaluated the influence of smooth pursuit eye movements on motion perception. Much of the initial work on this topic showed that pursuit influence was detrimental. As early as the nineteenth century researchers found that pursued moving objects were perceived as slower compared with the same object movement during fixation (Aubert 1886; Fleischl 1882). Filehne (1922) found that a stationary flash during pursuit of another object appears to move in the opposite direction of pursuit. Since then many others have found that pursuit causes inaccuracies in the perception of speed and direction (Festinger et al. 1976; Freeman and Banks 1998; Haarmeier and Thier 1998; Morvan and Wexler 2009; Souman et al. 2005; Wertheim and Van Gelder 1990).

However, other researchers have demonstrated better psychophysical performance during pursuit for heading perception (Royden et al. 1992), relative motion (Braun et al. 2010), or isoluminant speed judgments (Braun et al. 2008). Spering et al. (2011) showed that subjects’ predictions about whether or not a briefly presented target (ball) would hit a small line segment (goal) were more accurate while subjects where actively pursuing the ball compared with a condition in which subjects fixated the ball as the goal moved toward it. In addition, perceptual performance was better in trials with better pursuit. Also, Fooken et al. (2016) found that accuracy in a two-dimensional interception task was higher during trials with better pursuit. Together these results suggest that smooth pursuit may be beneficial for motion perception and the prediction of motion trajectories.

In the real world objects rarely move along perfectly linear trajectories, but still little is known about the relationship between pursuit eye movements and perception for curvilinear motion stimuli. Eisenkolb et al. (2000) examined curvature discrimination of briefly (125 ms) presented motions and found that subjects were able to discriminate curvature from motion but that sensitivity decreased as a function of curvature. Mrotek et al. (2006) studied smooth pursuit with targets that first moved linearly and then followed the arc of circles with different radii. Target speed was kept constant and also the angular velocity. They found that when the target began to gradually change directions along the arc, the angular velocity of pursuit was fairly accurate after an initial overshoot 200–350 ms after onset of curved motion but that the pursuit direction consistently lagged behind the target. In a similar experiment Mrotek and Soechting (2007b) examined the ability of observers to predict curvilinear motion across a brief interval of target occlusion. They investigated to which extent extraretinal signals about future target direction could also incorporate predictions about gradual changes in movement direction as for curved trajectories during the occlusion. Again, the pursuit target moved straight initially and then along the arc of a circle. It disappeared behind an occluder in the first experiment but reappeared in the second. Then subjects were asked to point to the location where they believed the target would reappear. When the target did not reappear, subjects continued pursuit along the last target direction and their pointing behavior indicated that they expected a linear path of the target. When the target reappeared after following a curvilinear occluded path, pursuit also gradually changed direction and followed a curvilinear target motion during the occlusion. This demonstrated that subjects extracted the motion curvature of the target to build a predictive model, which enabled them to pursue with fairly accurate angular velocities for 200 ms after target disappearance.

None of the above-mentioned studies directly compared perception and pursuit of curved target movements; therefore the aim of the present study was twofold. First, we investigated whether or not pursuit affects the ability to discriminate different degrees of motion curvature and compared the sensitivity of curvature discrimination during pursuit and fixation. Second, we assessed the sensitivity of the smooth pursuit system to curved target movements over time.

METHODS

Observers.

Fifteen observers (6 men, 9 women) from Justus Liebig University of Giessen voluntarily participated in the study after providing written informed consent and had normal or corrected-to-normal vision. Experimental procedures were in accordance with the Declaration of Helsinki and were approved by the local ethics committee (LEK 2013-0018).

Display.

All stimuli were presented on a 22.5-in. VIEWPixx monitor (VPixx Technologies) at a refresh rate of 120 Hz, set to a spatial resolution of 1,920 (h) × 1,080 (v) pixels. Observers viewed stimuli binocularly from a distance of 48.5 cm with their head stabilized by a chin and forehead rest. At this distance the display subtended 61 × 34 degrees of visual angle (°); however, stimulus presentation was restricted to the central 32° × 19° portion. The pursuit target and fixation spot (white Gaussian dot, SD = 0.15°) were presented on a uniform black background. To prohibit the use of any external reference frames as indicators of target position or motion curvature, experiments took place in a dark, windowless, and completely light-shielded room with black walls. All light sources (e.g., from computers or power supplies) were covered with black tape. The black background had a luminance of <0.09 cd/m², and white pixels had a luminance of 31.44 cd/m².

Stimuli.

In every trial a stimulus consisting of a single white spot moving on a black background (see Display) along the arc of a circle was shown in each of the two intervals. The set of radii consisted of a standard radius of 7.9° and 10 comparison radii, which were the standard radius ± 0.16°, 0.63°, 1.43°, 2.54°, and 4.12°. Speed (11.4°/s) and arc length (11.4°) were held constant within and across all radii. Stimulus presentation was controlled with MATLAB (MathWorks, Natick, MA) and the Psychtoolbox (Brainard 1997; Pelli 1997).

Procedure.

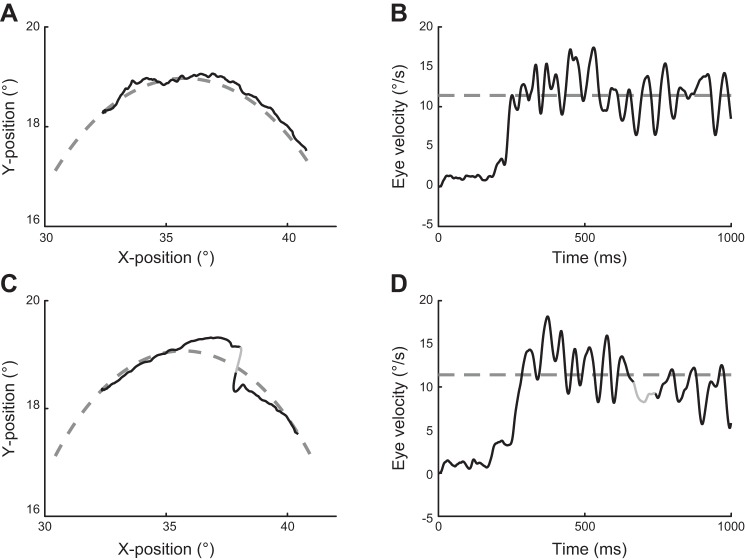
For pursuit trials we used the classical step-ramp paradigm introduced by Rashbass (1961) to reduce the number of initial saccades. A typical pursuit trial followed the sequence depicted in Fig. 1. Every trial started with the appearance of a fixation spot, and subjects were required to fixate it before pressing a button to start the experimental trial. All stimuli were presented in the central 18° (h) × 12° (v) region of the display. The position of the initial fixation spot was randomly chosen within a 4.3° × 3° rectangle centered at screen center. If subjects’ fixation was >2° away from the fixation spot, a beep was played to remind them to fixate. Since online drift correction is not a part of the EyeLink 1000 software, calibration was run again if the drift check failed more than twice. After the button press, there was a 300-ms delay. Then the “fixation” spot started to move. All motion was along an invisible circle with the given radius. The spot first stepped in one direction along the circular trajectory and then moved at a constant speed along the opposite direction for 1 s, crossing the initial fixation location after ~200 ms (Rashbass 1961). The end point of the dot’s motion was at the same vertical position as its starting point. After the first interval a black screen was displayed for 500 ms before a new fixation spot appeared at a different randomly selected position within the same central region. After this 1,500-ms period the second interval started and the second curvature stimulus was presented for 1 s followed by a black screen for 500 ms. Then subjects were asked to indicate which motion path was flatter by pressing one of two assigned buttons. The curvature stimuli could move either clockwise or counterclockwise along the top or bottom of the invisible circle (4 basic motion directions). The basic motion direction of the stimulus in the second interval was the same as in the first but started from a different position. The standard curvature stimulus was presented randomly in either the first or second interval. No feedback was given.

Fig. 1.

Sequence of events of a 2-interval pursuit trial. Each trial begins with the appearance of the first fixation spot for 1 s. After a button press the movement of the first curved step ramp starts and lasts 1 s. After a 500-ms delay the second interval starts with the 1-s appearance of the second fixation spot at a different location. Then the second curved step-ramp movement is shown for 1 s. After a black screen for 500 ms the subject is asked for a curvature judgment via button press.

Fixation trials were similar except that the subject was asked to always fixate a spot identical to the pursuit target at the center of the motion path such that the moving dot would pass through the position of the fixation spot after 500 ms. The viewing condition (fixation and pursuit) was blocked. Subjects ran four 50-trial sessions for each viewing condition. Fixation and pursuit conditions were run on separate visits to the laboratory, counterbalanced across subjects.

Eye movement recordings and analyses.

Eye movements were recorded with a tower-mounted EyeLink 1000 (SR Research, Mississauga, ON, Canada) utilizing the EyeLink toolbox (Cornelissen et al. 2002). The display was viewed binocularly, but only the position of the right eye was recorded (1,000 Hz). The spatial resolution was 0.01°. Since online drift correction is not a part of the EyeLink 1000 software, all eye traces were drift corrected off-line based on 100 ms of fixation data before the start of motion. All position traces were then filtered with a low-pass Butterworth filter with a frequency cutoff of 30 Hz. Velocity traces were computed by digitally differentiating the filtered position traces. For analysis based on the eye speed we used the velocity in x and y and projected it onto the vector of the target movement at each frame. Saccades were detected with the EyeLink’s default detection parameters, which consisted of a velocity threshold of 22°/s and an acceleration threshold of 3,800°/s². The average velocity in the last 40 ms was added to the velocity threshold, which allowed saccade detection even during ongoing smooth pursuit eye movements. We removed saccades from the velocity traces by interpolating the projected velocity between 30 ms before the detected onset and 30 ms after the offset each saccade. We used a linear interpolation between the velocities at the two end points. To avoid sharp transitions at the beginning and end of the interpolated segments, we gradually phased in and out the interpolation function with respect to the actual eye velocity. After interpolation the velocity trace was filtered with a low-pass Butterworth filter with a frequency cutoff of 20 Hz. Pursuit onset was detected by first determining a baseline velocity during 50 ms of fixation and then finding the first point in time when 50 consecutive velocity samples exceeded baseline velocity by 3 standard deviations or more. These 50 samples were also required to exceed 50% of stimulus velocity. The pursuit acceleration was defined as the slope of a line fitted to the pursuit onset and the following 30 samples of the velocity trace. Because of oscillations of the velocity trace we included also a criterion for the acceleration, which had to be faster than 50°/s² and slower than 300°/s². For calculations of pursuit gain, velocity vectors were projected onto the target trajectory as described for the projected velocity. All individual eye traces were inspected to ensure accurate saccade and pursuit detection.

Pursuit trials were only included if 1) the pursuit onset was detected and was found to be later than 50 ms and earlier than 400 ms after target motion onset and 2) the mean two-dimensional position error from pursuit onset until the end of the trial was <2° and during this time never >4°. Fixation trials were only included if 1) no pursuit onset was found and 2) the mean eye position remained within a 2° circle centered at the fixation target position. As a result of these criteria 284 pursuit trials and 239 fixation trials (a total of 523 trials or 9%) were removed. All analyses are based on the remaining 2,716 pursuit responses and 2,761 fixation trials (a total of 5,477 trials).

For the analysis of the curvature dynamics (see Fig. 8), we excluded the data for one participant because for one of the curvatures in one segment he only had trials with saccadic eye movements. To compare trials with saccades and pure pursuit across all subjects we selected random samples of 35 trials for each of the different radii with a certain oculomotor response (for both pursuit and saccadic trials we had on average ∼100 trials available for each radius). With those trials we again computed the psychometric function and extracted the parameters and repeated this process 1,000 times. To compare the sensitivity of the pursuit system to that of the perceptual system, oculometric functions were computed (Kowler and McKee 1987). To use the eye response to the different motion curvatures for the construction of oculometric functions, a circle was fit (Pratt 1987) either to the whole eye trajectory or to segments of 150, 200, 300, and 400 ms (samples) of eye position at different points in time (20-ms steps) relative to pursuit onset. To translate the eye movement response into curvature judgments, radii of the best-fitting circles were compared for the standard stimulus (radius of 7.9°) and comparison stimulus in each trial of the two intervals and the interval with the larger radius was considered to be the eye’s response to the question “which motion path was flatter?” These responses were then converted into proportion of “comparison flatter” responses for all levels of curvature. Then psignifit 4.0 (Schütt et al. 2015) was used to fit a cumulative Gaussian to the data where the mean was taken to be the point of subjective equality (PSE) and the standard deviation was taken to be the just-noticeable difference (JND). Perceptual responses were analyzed in the same way.

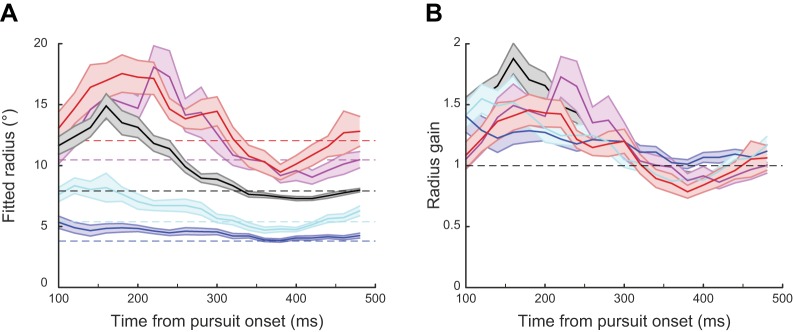
Fig. 8.

A: results of the circle fit analysis to 200-ms eye position segments averaged across subjects in response to 5 stimulus curvatures. Segments were aligned on pursuit onset and start 100 ms after onset. The different colors of the curves indicate the stimulus radius as indicated by the dashed horizontal lines. Here only the fittings to the 2 largest and the 2 smallest stimulus curvatures are shown; the black curve shows the fits for the standard stimulus with a radius of 7.9°, the shaded areas represent the SE. B: ratios between the radius of the fitted circle and the radius of the 5 stimulus curvatures over time starting 100 ms after pursuit onset. Black dashed line indicates a gain of 1. Values above the line indicate pursuit movement curvature with a higher radius, i.e., an underestimation of curvature.

RESULTS

First we compare the psychometric performance of curvature discrimination in the pursuit and fixation conditions. Then we present the results of the eye movement analysis regarding the specific characteristics of smooth pursuit and catch-up saccades in response to different motion curvatures. In the last part of results we compare the oculometric performance for curvature discrimination with the psychometric performance and test whether the pursuit quality is related to the perceptual thresholds.

Since two recent studies (Fooken et al. 2016; Spering et al. 2011) reported beneficial effects of pursuit on motion direction prediction and interception accuracy, we compared curvature discrimination during fixation and pursuit to test whether active pursuit improves the sensitivity for motion curvature. All our subjects were able to discriminate motion curvature with a high precision. Figure 2 shows psychometric functions for motion curvature discrimination during pursuit and fixation for two representative observers: observer ma (Fig. 2A) has a steeper psychometric function during fixation and observer mm (Fig. 2B) has a steeper function for the pursuit condition.

Fig. 2.

Psychometric functions for motion curvature discrimination during pursuit and fixation for 2 representative subjects. The proportions of trials in which the curvature was reported as being “flatter” than the comparison motion curvature are plotted as a function of the comparison standard curvature with a radius of 7.93°. Psychometric functions are plotted in gray for fixation and in black for pursuit. A: a subject whose discrimination performance was better during fixation. B: a subject whose performance was better during pursuit.

This was typical for our observers. Roughly half of our 15 observers were more precise during the fixation condition. On average, psychophysical discrimination thresholds were 1.43° during fixation and 1.41° during pursuit. This small difference in discrimination performance was not significant (t₁₄ = 0.07, P = 0.95). Thus no benefit was present for curvature discrimination when the moving target was pursued before the motion curvature judgment. As expected, there was no systematic difference in the PSE (t₁₄ = 0.97, P = 0.35; see Fig. 3B). Neither the JNDs (r₁₅ = 0.36, P = 0.20) nor the PSEs (r₁₅ = −0.03, P = 0.92) were correlated across participants.

Fig. 3.

Perceptual JNDs (A) and PSEs (B) for pursuit vs fixation conditions. Each filled circle denotes a single subject. Open circles display the JNDs and PSEs of the 2 example subjects depicted in Fig. 2, and gray squares show the average values. Dashed line indicates identity, and error bars depict SE. In B the light gray cross shows the size of the standard stimulus.

Analysis of pursuit properties for curved stimulus motion.

Next we present the properties of the pursuit responses to the differently curved target trajectories. Figure 4 displays XY eye positions of single pursuit responses of three observers to the standard stimulus curvature (Fig. 4, center) and to the stimuli with the smallest (Fig. 4, left) and the largest (Fig. 4, right) radius. Although the motion direction (clockwise and counterclockwise and up- or downward) was randomly chosen on each trial, data have been aligned here to a canonical direction and location for the purposes of plotting. To make it easier to compare individual traces, only five traces are shown for each subject.

Fig. 4.

Two-dimensional eye (black) and stimulus (gray) positions for the standard stimulus (center) and the stimuli with the smallest (left) and largest (right) radius. Each row depicts the last 5 eye traces of the last block collected from 3 subjects (zm, il, ma). Depending on the stimulus curvature, the vertical components of eye traces differ; they are largest for the smallest radius. Note that eye traces were aligned horizontally and/or flipped by 180°.

Figure 4 shows individual differences in pursuit quality and a clear modulation of pursuit depending on the degree of motion curvature. The flatter the curvature, i.e., the larger the radius, the smoother the pursuit response. Differences in pursuit quality were also present for single-eye responses to the same curvature as shown in Fig. 5. In ~40% of the trials subjects used a pure pursuit response as depicted in Fig. 5, A and B, while in the other 60% the eye position was realigned by one or more small catch-up saccades (Fig. 5C). It should be noted that the saccadic signal was interpolated for the velocity trace in Fig. 5D (see methods) and that the eye velocities of both trials roughly matched the target velocity of 11.4°/s.

Fig. 5.

A and C: XY eye position for a pure pursuit response (A) and a pursuit response including a catch-up saccade (C). The corresponding eye velocities, after projection onto the target trajectory, are plotted in B and D. XY eye positions and eye velocities are black, and target position is shown by the gray dashed line. The catch-up saccade is shown in C by the solid gray line. In the graph of eye velocity (D), the gray line segment indicates the time of the catch-up saccade and the interval used for the interpolation of the eye velocity during the saccade. In both trials the eye first moves more or less straight in a diagonal direction and develops curved pursuit later. It reaches the target velocity of 11.4°/s as indicated by the gray dashed line in B and D. In C the longer linear pursuit and the upcoming position error is corrected by a catch-up saccade.

Next we quantify pursuit performance as a function of stimulus motion curvature averaged across all subjects (Fig. 6). We computed for each single trial the open-loop acceleration as the slope of a line fitted to the velocity trace and the closed-loop gain in the interval 300–500 ms after pursuit onset. These analyses were based on the projected velocity, which takes the stimulus direction into account (see methods). The gain here is reflecting the angular gain because we used the projected velocity, which is proportional to the angular velocity. The plots of open-loop acceleration and closed-loop gain revealed that subjects were quite proficient in starting and speeding up their eyes to reach the target and then to smoothly follow various motion curvatures. We found that the open-loop acceleration was significantly influenced by curvature (F_9,126 = 2.933, P = 0.003); less curved stimuli, i.e., those with a high radius, resulted in a higher pursuit acceleration (see Fig. 6A). Also, pursuit gain was influenced by the curvature of motion (F_9,126 = 2.730, P = 0.006); it was higher for less curved stimuli (see Fig. 6B). However, in general we found that pursuit eye speed closely matched stimulus speed, and even pursuit gain for the most curved stimulus was close to perfect at 96% (SD = 7%).

Fig. 6.

Quality of smooth pursuit responses as a function of stimulus motion curvature. Open-loop acceleration (A), pursuit gain (B), and the average position error during the trial after pursuit onset (C) are shown. Means across subjects are plotted as gray circles for the 10 comparison curvatures; error bars indicate ± 1 SE. The linear regression line (black line) fitted to the data shows the direction of the significant main effect of curvature.

To further investigate pursuit quality for motion curvature, we calculated the average position error from pursuit onset until the end of the trial. Because we were mainly interested in the quality of pursuit of curvilinear movements, we removed in each trial all segments containing saccades from the calculation. We found a significant influence of the stimulus curvature on the position error (F_9,126 = 15.889, P < 0.001 position error). The position error increased with the amount of curvature (see Fig. 6C), suggesting that the pursuit system was less capable of producing smooth eye responses to more curved stimuli, which was also reflected in the lower pursuit gain.

Catch-up saccades during pursuit of stimuli with different degrees of motion curvature.

To examine the relationship between motion curvature and catch-up saccades during pursuit, we analyzed various saccadic parameters. We looked up the number of saccades and also computed the amplitude and latency of the first catch-up saccade occurring after pursuit initiation (Fig. 7). Of all trials, roughly 40% contained one corrective saccade during the tracking response, 40% contained no saccade, and the rest of the trials contained two or more saccades. The first catch-up saccades had amplitudes in the range of 0.55–0.7° and were short in duration. In line with the finding that the position errors during pursuit were larger for the highly curved stimuli, we found also more saccades (F_9,126 = 3.86, P < 0.001; see Fig. 7A) with a larger amplitude (F_9,117 = 2.771, P = 0.006; see Fig. 7B) for the stimuli with lower radii. The amplitude of the corrective saccade for the different curvatures was also highly correlated with the position error during the pursuit (r₁₀ = 0.89, P < .001). No systematic influence of stimulus curvature was present for the latency of the first catch-up saccade; they tended to occur roughly 240 ms after pursuit onset (see Fig. 7C) (F_9,117 = 1.116, P = 0.357). These results suggest that the curved target trajectories are tracked by a combination of saccadic and smooth pursuit eye movements and that the amplitudes of the first catch-up saccades correct inaccurate pursuit responses to the motion curvature.

Fig. 7.

Number of saccades (A), saccade amplitude (B), and saccadic onsets with respect to (w.r.t.) pursuit onset (C) during pursuit of curved motion. Means across subjects are plotted as points, and error bars indicate ± 1 SE. Black line indicates a linear regression fitted to the data.

Pursuit curvature over time.

To examine the spatiotemporal relationship between eye and stimulus, circles were fit (see methods) to the eye positions at varying points in time (see Fig. 8A). First, the eye movements of each trial were aligned on the pursuit onset for each of the 10 comparison curvatures and the standard curvature. For each trial we separated the eye movement response into segments of 200 ms starting at different time points and shifted the center of the window in 20-ms steps. To avoid a confounding influence by catch-up saccades, we took only segments without corrective saccades into account. In addition, we also performed the analysis with all segments, including those containing saccades, and got qualitatively identical results. We took the median of all the fitted radii for each subject to avoid a distortion of our measurement by almost straight segments where the circle fit provided extremely large radii of >100°.

Because of our chosen time window, the radii of the circles fitted to the eye position segments at pursuit onset are influenced by the eye positions during the initial fixation; therefore we focused our analysis of pursuit curvature on the time course starting 100 ms after pursuit onset. Already at 100 ms after pursuit onset the radii for fitted circles to the eye position in response to the different target curvatures start to diverge (see Fig. 8A). Around the end of the open-loop phase a pattern starts to emerge. For all target curvatures the radii of the fitted circles are larger than the actual target radius, which can also be seen in the radius gain shown in Fig. 8B. This suggests that initially the curvature of the moving target is underestimated and the pursuit movement is too straight with respect to target curvature. Around 300 ms after pursuit onset, this underestimation starts to vanish and in some cases turns into a transient overestimation of curvature. Later during steady-state pursuit responses become quite accurate and reach a radius gain of close to unity.

To test this observation statistically we studied the radius gain at 100, 200, 300, and 400 ms after pursuit onset for all curvatures and conducted a repeated-measures ANOVA with the factors Time and Curvature. We found a significant main effect of Time (F_3,39 = 16.292, P < 0.001) but not for Curvature (F_9,117 = 0.778, P = 0.637), which suggests that the ability of the pursuit system to track different curvatures develops over time and similarly for all curvatures. The interaction between Time and Curvature was also significant (F_27,351 = 1.576, P = 0.036). To test for the main effect of Time we ran post hoc t-tests comparing the two early points in time, where we still see the overshoot, with the two later points and found a significant decrease (t₁₃ = 4.501, P < 0.001) of the radius gain from 1.52 (SD = 0.43) to 1.03 (SD = 0.10). The gain during the later phase is not different from 1 (t₁₃ = 0.975, P = 0.348). To investigate the interaction more closely we ran again a repeated-measures ANOVA with only the factor Curvature for each of our four time points separately. We did not find any significant difference between the curvatures for each of the time points (all P > 0.124), suggesting that the interaction is mainly depending on the differences between the different time points. We tested for this by calculating the difference between the radius gain values for one time point and the following one. We found a significant difference between the curvatures between 100–200 ms and 200–300 ms after pursuit onset (F_9,126 = 1.985, P = 0.046 and F_9,126 = 1.995, P = 0.045, respectively) but not for 300–400 ms (F_9,126 = 0.824, P = 0.596). As shown in Fig. 8B, there is underestimation of curvature early on in the pursuit, followed by quite accurate tracking after ~300 ms.

Comparison of oculometric and psychometric performance.

Although pursuit curvature did improve over time, it is still not clear whether or not pursuit curvature will be sensitive enough to discriminate the curvature of stimuli to the same degree as is possible during perception. To answer this question, we compared the oculometric performance directly with the perceptual performance during pursuit, i.e., for the same trials (Fig. 9). We used the circle fit analysis for the eye trajectory of the whole trial for both the standard and the comparison stimulus for each trial. We compared the radii of the fitted circles and assigned an eye response similar to the perceptual one, i.e., “which curve is flatter.”

Fig. 9.

A: oculometric and perceptual psychometric function for 1 representative subject. The psychometric function during the pursuit condition is in black and the oculometric function for the same trials in gray. B: JNDs for perceptual vs oculometric functions. JNDs for all subjects are represented by filled circles; only the example subject is represented by an open circle. The dashed line indicates identity, and the gray square shows the average. Error bars depict SE.

We found that the oculometric sensitivity for curvature was quite reliable. The average oculometric threshold was 1.67° compared with 1.41° for the perceptual threshold, a difference that amounts to <4% of the standard radius. This difference was not significant (t₁₄ = 1.82, P = 0.091). Interestingly, we also found a correlation between the oculometric thresholds and the perceptual JNDs (r₁₅ = 0.51, P = 0.05), suggesting a relationship between the quality of the oculomotor behavior and the perceptual thresholds.

Because we used the whole eye movement trajectory for the circle fit analysis irrespective of the presence of a corrective saccade in the segment, this discrimination threshold could be influenced by catch-up saccades. In theory, it is possible to fit a circle to trajectories composed of straight pursuit segments and small catch-up saccades. In this case, the analysis method would imply that pursuit follows the curvature of the stimulus, although pursuit is actually straight and the curvature is mainly created by saccades. To account for this problem, we compared the oculometric performance for trials with or without catch-up saccades. Because for some subjects we only found a few trials per combination of radius and oculomotor behavior, we computed the overall effect across all subjects. We used all trials from our subjects and used bootstrapping to estimate the JND based on the oculomotor behavior (see methods). The estimated JND for oculometric functions without any catch-up saccades was 1.78° (95% CI = 1.42–2.15°) and not significantly different from the JND for trials with one catch-up saccade (1.88°, CI = 1.49–2.27°). This confirms that the pursuit system is able to produce eye movements that accurately follow different curvatures.

Oculometric performance over time.

Our results so far show that eye movement and perceptual curvature discrimination are roughly similar. This was based on an analysis of the complete 1-s trial. However, we have shown before that the curvature of pursuit varies substantially over time. Therefore we now compare oculometric functions over time for different integration intervals to perceptual data with equivalent presentation durations. Figure 10 shows that oculometric thresholds increased massively with shorter analysis intervals, reaching radius differences as large as 10° for 300-ms intervals and up to 20° for the 150-ms intervals. Psychophysical thresholds also increased for shorter presentation durations, but to a much lesser degree. Even for brief 150-ms presentations radius discrimination had thresholds of ~5°. The difference between the oculometric and perceptual thresholds for 150 ms (t₅ = 2.839, P = 0.036) as well as for 300 ms (t₅ = 2.723, P = 0.042) was significant. This indicates that pursuit eye movements need longer temporal integration until they are able to reflect target curvature with the same precision as the corresponding perceptual judgments.

Fig. 10.

JNDs of different oculometric and psychometric functions: direct comparison of the average oculometric threshold between 250 and 350 ms after pursuit for different given integration windows compared with perceptual results measured for different presentation durations. Squares indicate oculometric data; circles indicate perceptual data. Note that the perceptual data for short durations of 150 and 300 ms were measured with 6 observers during fixation. Error bars depict SE. SEs for the perceptual results are covered by the markers. Asterisks (*) indicate significance at 5% level.

Relation between pursuit quality and perception of target curvature.

We also tested whether the quality of pursuit was related to perceptual performance of our subjects (Fig. 11). We defined pursuit accuracy as the mean of the absolute angular deviations of the eye from pursuit onset until the end of the trial. Thus, if the eye position at one instant during pursuit was at an angle of 89° with respect to the center of the circle and the target stimulus was at 90°, the angular deviation would be 1°. We also calculated the precision of the eye movements as the standard deviation of the angular deviations for each trial. We averaged the values for each subject and correlated them with the perceptual JND during pursuit. We found significant positive relationships between the angular accuracy of the eye movements (r₁₅ = 0.61, P = 0.02) and perceptual JNDs as well as between the angular precision (r₁₅ = 0.56, P = 0.03) and perceptual JNDs. Comparable results were obtained when we computed the radial deviations for each participant. However, we did not observe any significant relationship between the pursuit quality and the perceptual threshold measured during the fixation condition (r₁₅ = −0.03, P = 0.92 for angular error; r₁₅ = 26, P = 0.35 for angular standard deviation). These results suggest that although we do not find a better performance for curvature discrimination during pursuit compared with the fixation condition, pursuit quality is still significantly related to perceptual performance during pursuit.

Fig. 11.

Relationship between perceptual JND during pursuit and mean angular pursuit error (accuracy) (A) or the average angular standard deviation (precision) (B) of each single trial for all 15 subjects denoted by black dots. Solid black line shows a linear regression fitted to the data.

DISCUSSION

Curved target trajectories are common in our natural environment, for example, as prominent features of many ball games (e.g., Bahill and Karnavas 1993; Shapiro et al. 2010). So far surprisingly little is known about how well we can pursue and distinguish targets moving along differently curved trajectories. Here we asked subjects to pursue and to discriminate different motion curvatures and found that larger motion curvatures led to a general decrease in pursuit quality. Overall, it took at least 300 ms to build up pursuit responses that reflected the curvature of the target trajectory, but oculometric thresholds for motion curvature discrimination based on the whole 1-s trajectory reached the level of perceptual discrimination performance. Oculometric thresholds based on smaller time windows were higher also compared with perceptual thresholds for similar target presentation durations during fixation. Therefore, smooth pursuit can accurately follow moving targets with curved trajectories, but temporal integration over larger segments is necessary to reach perceptual thresholds. While we could not find an additional perceptual benefit for pursuit compared with fixation, we did find better perceptual performance for observers who exhibited better pursuit.

Oculomotor behavior for different curvatures.

The curvature of the target trajectory has some known effects on the initiation of pursuit eye movement (Baloh et al. 1988; Collewijn and Tamminga 1984). More curved stimuli tended to elicit lower open-loop accelerations, which might be a direct consequence of the linearity of the initial pursuit. If the initial target trajectory was misinterpreted as being linear, the initial speed would be underestimated for targets with higher curvatures. In addition to acceleration, pursuit gain and position errors were also influenced by target curvature. We found that the overall quality of pursuit for curved target trajectories is lower; pursuit responses had lower velocity gains and higher position errors for the more curved stimuli, especially for the stimulus with the highest curvature. For pursuit, curved motion led in general to a higher position error as our values varied between 0.5° and 0.7°, whereas for linear motions for similar velocities the average position error is typically below 0.2° (Spering et al. 2005).

In ~60% of all trials small catch-up saccades were needed to correct for the accumulating mismatch between eye and target position, and their frequency and size were related to the pursuit quality and target curvature. This suggests a tight coupling of pursuit and saccadic eye movements (see, e.g., Orban de Xivry and Lefèvre 2007). Latencies of the first catch-up saccades were similar for the different degrees of curvature, indicating that the detection of the position error was independent of the amount of curvature. Overall the oculomotor system is capable of tracking curved targets with curved pursuit and invokes additional saccadic eye movements only when the position error gets too large. This is a reasonable strategy, as saccadic eye movements impair perception by suppressing visual sensitivity (for reviews see Krock and Moore 2014; Ross et al. 2001).

Curved pursuit takes time compared with direction and velocity.

In general, the tracking of curved target trajectories is more difficult than tracking linear movements since the movement directions change over time so that the visual system has to analyze the motion directions continuously to predict future target locations. To be able to predict the target curvature the oculomotor system would need access to the derivative of the position information. Our results show that pursuit seems to have problems with this kind of target movement, as it needs a long time until the curvature is accurately reflected. Interestingly, the pursuit system is also worse in estimating acceleration, which is the derivative of velocity over time in comparison to constant speed (Watamaniuk and Heinen 2003). Bennett et al. (2007) could show that the pursuit system is capable of estimating the acceleration of a moving target, but it also takes at least 500 ms and even then the estimate is not perfect. This seems quite similar to our findings for the evolution of curvature in pursuit, where we found accurate curvature also ∼300 ms after pursuit onset or ∼500 ms after target motion onset.

For linear target movements with constant speeds the pursuit system works remarkably well. Pursuit seems to be very good in quickly estimating the direction of motion (Braun and Gegenfurtner 2016; Mukherjee et al. 2015; Osborne et al. 2004). Directional thresholds for linear motion of pure pursuit responses for similar target speeds reached asymptotic values of 1.5–2.5° within ∼100–150 ms after pursuit motion onset and were similar to perceptual threshold during fixation (Braun and Gegenfurtner 2016; Mukherjee et al. 2015). Although another study found higher direction discrimination thresholds for pursuit than for perception, both measures were similarly affected by noise, suggesting a common motion processing stage (Watamaniuk and Heinen 1999). For speed, it is debated whether the pursuit estimate reaches its best level already during open loop (Boström and Warzecha 2010; Mukherjee et al. 2015; Osborne et al. 2005, 2007; Rasche and Gegenfurtner 2009). Our study shows that for motion curvature the most accurate pursuit is reached ∼300 ms after pursuit onset (see Figs. 8 and 10), which is much later than for linear target movements.

For linear target movements the oculometric thresholds were similar to the perceptual thresholds with time segments of 40 ms (Braun and Gegenfurtner 2016), whereas here we found similar thresholds only if we considered the whole eye trajectory of 1,000 ms; accordingly, oculometric thresholds for smaller integration windows of 150 ms were much higher than the perceptual threshold. Also, when we directly compared the oculometric thresholds with perceptual judgments with similar presentation durations, oculometric thresholds were higher. Perceptually participants were able to discriminate the different curvatures quite well even for the short presentation durations (Eisenkolb et al. 2000), but oculometric thresholds were significantly higher for similar durations (see Fig. 10). Thus oculometric performance for curved trajectories develops more slowly and needs more temporal integration until a precise estimation of target curvature can be extracted from the observed pursuit traces. Only when taking into account the whole pursuit trajectory did we find thresholds similar to the perceptual performance, perhaps reflecting an asymptotic maximum level of performance that could suggest a common motion processing stage for oculometric and perceptual performance (Watamaniuk and Heinen 1999).

The behavior of the pursuit system reflects this need for more temporal integration. Initially, there is an underestimation of the target curvature with too linear pursuit with respect to the different radii. Since this pattern is present for all stimuli, even for the motion curvature with the largest radius, it seems to represent a more general predictive strategy of the pursuit system. This pursuit strategy also seems to be present in the study of Fooken et al. (2016); the visually guided pursuit responses to the first 100–300 ms of nonlinear targets trajectories were more or less straight and showed curvature only later after target disappearance, which fits very well with our observations of accurate curvature after ∼300 ms. This result is in line with the study of Mrotek et al. (2006), who found that the gaze angular velocities initially overshot target angular velocity but after ~350 ms began to oscillate around target angular velocity.

Starting pursuit almost linearly in the open-loop phase seems to be a good strategy to gain some additional processing time so that continuous and moderate pursuit adjustments can be made in the closed-loop phase to improve its precision for a given task or intention (Pack and Born 2001; Rasche and Gegenfurtner 2009). It seems to be a general strategy of the pursuit system to initially pick an approximate answer when confronted with ambiguous or uncertain motion signals. This is also the case when multiple potential motion directions are present; here pursuit initially follows the vector average (Lisberger and Ferrera 1997). In situations where a reward varies for different directions, pursuit only gradually changes toward the motion signals with higher reward (Schütz et al. 2015).

Pursuit directional anisotropy.

One additional topic that must be discussed with respect to pursuit to curved targets is the anisotropy in direction gain (Baloh et al. 1988; Collewijn and Tamminga 1984; Krukowski and Stone 2005; Liston and Stone 2014; Rottach et al. 1996). The quality of pursuit differs; it is best along the horizontal axis, good for the vertical, and reduced for oblique movements. Curved motion trajectories always consist of oblique movements with different ratios of horizontal and vertical components depending on the radius. Because the start and end points of each trajectory were horizontally aligned in our study, the different target curvatures mainly differed in their vertical component, i.e., the smaller the radius the larger the vertical component. This can explain to some extent our findings of the pursuit behavior, since we found less acceleration, lower pursuit gain, and higher position errors for movements with larger vertical components, which is in line with previous findings for asymmetry in the control of vertical and horizontal pursuit (Baloh et al. 1988; Krukowski and Stone 2005; Liston and Stone 2014; Rottach et al. 1996).

Overall, the initial use of a linear approximation seems to be a general strategy as we found it for all curvatures. This initial underestimation of target curvature scaled with the actual target curvature and therefore seems to be independent of the horizontal and vertical components. Only when retinal errors signal a deviation from linearity, pursuit is adjusted and becomes more curved. The fact that additional processing time is needed for adjustments of the pursuit responses so that they accurately reflect the target curvature suggests that the pursuit system is not very sensitive to motion curvature, the derivative of position. This is similar to the results obtained for acceleration, the derivative of speed.

Curvature perception during fixation and pursuit.

Smooth pursuit not only provides best visual acuity for the recognition of moving targets, it can also improve the ability to predict target trajectories in space and time (Land and McLeod 2000; Spering et al. 2011) and the accuracy of eye-hand coordination (Brenner and Smeets 2009; Mrotek and Soechting 2007a; Wilmut et al. 2006). On the basis of these findings, we expected superior perceptual performance of motion curvature discrimination for the pursuit compared with the fixation condition. However, in our study we found that thresholds for curvature discrimination from motion were similar during the pursuit and fixation conditions (see Fig. 3). Why is curvature discrimination not improved by active pursuit?

Initially until pursuit onset the visual input, the retinal slip caused by the moving target, was similar in the pursuit and fixation conditions. At the beginning of each trial the target moved toward the fixated location in both conditions. In our fixation condition, the fixation point was in the center of the motion curvature path and the target movement stimulated symmetrical locations of the stationary retina with respect to the fovea, which may support curvature discrimination. In principle the fixation spot could serve as an external cue to estimate the curvature. During our pursuit condition, the retinal input was similar to the fixation condition, only the starting point of the target movement was closer to the fovea. With pursuit onset after ~150–200 ms, visual perception was modified dynamically during the whole trial. After initiation, the retinal slip velocity was consistently reduced until after ~300 ms pursuit was fast and curved enough to stabilize the moving target on the fovea beside typical small oscillations during pursuit. When catch-up saccades occurred, visual sensitivity was reduced (Burr et al. 1994). In addition to retinal signals, extraretinal signals also become available for the pursuit system. Thus in our study the retinal input was not comparable for the pursuit and fixation conditions; the judgments of our subjects therefore could be based on different cues and signals, but in the conditions we investigated here there was no simple solution of making the retinal inputs equivalent, as was done in previous studies (Spering et al. 2011). Also, neither the retinal signals nor the extraretinal signals are noise free (Freeman and Banks 1998; Lisberger 2010; Osborne et al. 2005; Rasche and Gegenfurtner 2009).

The differences between the conditions could also explain why there was no relationship between the pursuit quality and the perceptual thresholds during the fixation condition. Subjects with high pursuit quality could better extract the target curvature during pursuit for their perceptual responses but had to rely on different cues and signals in the fixation condition. A further reason for the lack of perceptual improvement during pursuit might be that accurate pursuit curvature took longer to develop than for linear motion and pursuit performance was poorer overall. For example, oculometric thresholds were only in the range of the perceptual thresholds when the whole trajectory was taken into account. The need for more temporal integration makes it more difficult during pursuit to obtain accurate extraretinal information about the target trajectory, which would be beneficial for the discrimination of motion curvature. Because we were interested in the temporal evolution and quality of pursuit of curved trajectories our targets were never occluded and presented for a full second. This is 3–10 times longer than the short target durations of 100–300 ms used by Spering et al. (2011) and Fooken et al. (2016), who measured pursuit responses mainly during the open-loop phase. Such short target durations for the comparison of curvature discrimination performance between pursuit and fixation were not possible in our study because the pursuit was still more or less straight during the open-loop period. In the study of Fooken et al. (2016) subjects knew the initial target directions before motion onset and therefore showed anticipatory smooth pursuit, and this predictive mechanism might support motion perception. In our study we did not find anticipatory smooth pursuit.

There is one more major difference between our study and the studies that found a benefit of pursuit performance over a fixation condition. In many of the previous studies subjects had the task of intercepting a moving object (Bahill and LaRitz 1984; Brenner and Smeets 2009, 2011) or predicting its future motion path (Spering et al. 2011). In these dynamic tasks it was necessary to quickly gather online information to enhance the performance by fast and accurate movement predictions. In our discrimination task there was enough time to integrate all the relevant information for curvature comparison and a final judgment. No predictions were necessary, which might conceal the benefits of additional extraretinal information in a more dynamic task.

Pursuit supports perception.

Despite the fact that we did not find the expected superior performance for the pursuit condition, there still was a strong relationship between the pursuit quality and the perceptual thresholds. Subjects with higher pursuit quality also showed better perceptual performance in the pursuit condition. Theoretically this correlation might point toward a common factor limiting both the quality of pursuit as well as the perceptual performance. This could be a task-specific factor, related to the processing of motion curvature, or an unspecific factor, such as attentional resources. Alternatively, perceptual performance and pursuit quality might be causally related, such that better pursuit facilitates perceptual performance directly. Since pursuit quality was only related to perceptual performance in pursuit but not in fixation trials, it is most likely that pursuit quality influenced perceptual performance. Research on training effects in different sport disciplines has revealed a close relationship between task performance and strategic eye movement behavior (Bahill and LaRitz 1984; Fooken et al. 2016; Land and McLeod 2000; Palidis et al. 2017). Elite athletes excelling at a task fixate or track the task-relevant item earlier, longer, and more closely than novices, a behavior that has been termed “quiet eye” (e.g., Vickers 2007, 2016). This is important because in many ball sports the ball speed is too fast for the pursuit system and the ball movement time itself is often very short. Athletes therefore learn to make appropriate saccadic and pursuit movements to the right locations at the right point in time in order to pick up the relevant cues about ball direction, speed, and spin within 200–300 ms (Bahill et al. 2005).

Conclusions.

Target motion curvature leads to lower pursuit gains and higher position errors and as a consequence larger corrective saccades. Curved pursuit takes time to develop; in the initial phase pursuit responses are too straight with respect to target curvature. The pursuit system needs ~300 ms after onset to match the pursuit response to curved target trajectories. The oculometric thresholds for motion curvature discrimination were similar to the perceptual performance when the whole 1-s pursuit movement was taken into account. With shorter time intervals the oculometric performance is worse compared with perceptual thresholds for similar intervals. This suggests that the pursuit system needs longer temporal integration periods of the extraretinal signal to compute an accurate estimate of target curvature. Despite this, participants with higher pursuit quality also showed better perceptual performance during pursuit.

GRANTS

This work was supported by Deutsche Forschungsgemeinschaft SFB TRR 135 “Cardinal mechanisms of perception.”

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the author(s), readers are herein alerted to the fact that additional materials related to this manuscript (kinematic data and participants' responses from the detection task) may be found at http://doi.org/10.5281/zenodo.820846. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

N.M.R. performed experiments; N.M.R. and A.G. analyzed data; N.M.R., A.G., A.C.S., D.I.B., and K.R.G. interpreted results of experiments; N.M.R. and A.G. prepared figures; N.M.R. and A.G. drafted manuscript; N.M.R., A.G., A.C.S., D.I.B., and K.R.G. approved final version of manuscript; A.C.S., D.I.B., and K.R.G. conceived and designed research; A.G., A.C.S., D.I.B., and K.R.G. edited and revised manuscript.