Aging does not affect the intralimb coordination elicited by slip-like perturbation of different intensities

This study was aimed at investigating how aging affects the intralimb coordination of lower limb segments, described by the planar covariation law, during unexpected slip-like perturbations of increasing intensity. Results revealed that neither the aging nor the perturbation intensity affects this coordination strategy. Accordingly, we proposed that the balance control emerges from an invariant set of control schemes shared across different sensory motor contexts and despite age-related neuromuscular adaptations.

Abstract

This study was aimed at verifying whether aging modifies intralimb coordination strategy during corrective responses elicited by unexpected slip-like perturbations delivered during steady walking on a treadmill. To this end, 10 young and 10 elderly subjects were asked to manage unexpected slippages of different intensities. We analyzed the planar covariation law of the lower limb segments, using the principal component analysis, to verify whether elevation angles of older subjects covaried along a plan before and after the perturbation. Results showed that segments related to the perturbed limbs of both younger and older people do not covary after all perturbations. Conversely, the planar covariation law of the unperturbed limb was systematically held for younger and older subjects. These results occurred despite differences in spatio-temporal and kinematic parameters being observed among groups and perturbation intensities. Overall, our analysis revealed that aging does not affect intralimb coordination during corrective responses induced by slip-like perturbation, suggesting that both younger and older subjects adopt this control strategy while managing sudden and unexpected postural transitions of increasing intensities. Accordingly, results corroborate the hypothesis that balance control emerges from a governing set of biomechanical invariants, that is, suitable control schemes (e.g., planar covariation law) shared across voluntary and corrective motor behaviors, and across different sensory contexts due to different perturbation intensities, in both younger and older subjects. In this respect, our findings provide further support to investigate the effects of specific task training programs to counteract the risk of fall.

NEW & NOTEWORTHY This study was aimed at investigating how aging affects the intralimb coordination of lower limb segments, described by the planar covariation law, during unexpected slip-like perturbations of increasing intensity. Results revealed that neither the aging nor the perturbation intensity affects this coordination strategy. Accordingly, we proposed that the balance control emerges from an invariant set of control schemes shared across different sensory motor contexts and despite age-related neuromuscular adaptations.

several studies have widely documented that the elevation angles of lower limb segments covary during numerous walking-related motor tasks (Borghese et al. 1996; Cappellini et al. 2010; Courtine and Schieppati 2004; Grasso et al. 1998; Ivanenko et al. 2007; Noble and Prentice 2008). This intralimb coordination strategy, also named planar covariation law (PCL; see Intralimb coordination for more details), has been shown to simplify the control of both posture (Lacquaniti et al. 1990) and locomotion (Ivanenko et al. 2008) and is thought to be result of coupling between neural oscillators within the spinal cord and mechanical oscillators involved in locomotion control (Lacquaniti et al. 1999).

Recent findings have further extended this notion, revealing that the PCL observed during steady locomotion is also adopted when young adults either are subjected to floor disturbances (Funato et al. 2015) or manage unexpected slip-like perturbations while walking (Aprigliano et al. 2016). Accordingly, the intralimb coordination described by the PCL appears as a control strategy shared across several volitional and likely involuntary motor behaviors and seems to reflect the relationship between intersegmental coordination and control of the dynamic balance in humans (Aprigliano et al. 2016; Funato et al. 2015).

Aging does not affect intralimb coordination during steady walking described by the PCL (Bleyenheuft and Detrembleur 2012; Noble and Prentice 2008), although aging involves neuromuscular adaptations that can modify kinematic, kinetic, and muscle activity. In particular, adults aged 62–82 yr have more conservative or less destabilizing walking patterns than adults aged 23–34 yr; that is, elderly subjects are characterized by reduced walking speed and step length, increased step width, stance and double support phases, and redistribution of the workload between proximal and distal leg joints (Grabiner et al. 2001; Maki 1997; Menz et al. 2003; Monaco and Micera 2012; Monaco et al. 2009; Winter et al. 1990). The absence of the influence of aging on the PCL observed during steady walking further corroborates the hypothesis that the main roles underlying the timed organization of the neuromuscular system are hardwired into the motoneuronal networks involved in locomotion (Monaco et al. 2010).

On the other hand, many studies have documented that aging per se involves substantial loss of muscle strength (Aoyagi and Shephard 1992; Brooks and Faulkner 1994; Doherty et al. 1993), slower rate of muscle force development (Porter et al. 1997; Thelen et al. 1996), and deterioration of neural and sensory systems (Maki and McIlroy 2006). Accordingly, the biomechanical response of elderly people while managing unexpected perturbations is characterized mostly by shorter steps (Carty et al. 2011) and slower compensatory movements (Lockhart et al. 2005; Martelli et al. 2017; Thelen et al. 1997), thus making balance control more challenging (Martelli et al. 2017; Tang and Woollacott 1998; 1999). Based on this evidence, it is possible to hypothesize that age-related modifications of the neuromuscular system can affect the control of dynamic balance while managing unexpected perturbations, thus compromising the coordination of lower limb segments.

The main goal of this study was to verify whether aging modifies the intralimb coordination underlying corrective responses induced by unexpected slip-like perturbations delivered during steady walking. In addition, we investigated the extent to which the intensity of the perturbation further affects the intralimb coordination strategy in elderly people that is still debated (Hsiao-Wecksler and Robinovitch 2007; Rogers et al. 2001; Tropea et al. 2015a). In this respect, we hypothesized that aging and intensity of the perturbation significantly affect lower limb intersegmental coordination of the corrective response elicited by unexpected slippages. The results are expected to provide novel understanding concerning the context-dependent strategies used by elderly people while managing unexpected perturbations.

MATERIALS AND METHODS

Subjects, experimental setup, and protocol.

Twenty healthy subjects, 10 younger (range: 22–30 yr) and 10 older (range: 63–80 yr) participants matched for height and body mass, were enrolled for the study. Age, anthropometric features, and walking speed for both groups are shown in Table 1. Volunteers were selected according to the following inclusion criteria: living autonomously, being able to walk over ground and on the treadmill without any walking aid, no falls experienced within 1 yr before testing, not reporting significant neuromuscular skeletal diseases, and not practicing competitive sports.

Table 1.

Age, anthropometric parameters, and walking speed for both groups

	Young	Elders
Age, yr	24.4 (2.5)	66.3 (5.1)
Mass, kg	63.1 (9.1)	66.9 (10.8)
Height, m	1.69 (0.07)	1.66 (0.08)
Leg length, m	0.80 (0.04)	0.79 (0.04)
Walking speed, m/s	1.08 (0.03)	1.08 (0.02)

Values are means (SD).

The experimental setup and the protocol have already been described in our previous studies (Aprigliano et al. 2015; Tropea et al. 2015a) and are recapped here. Participants were asked to manage unexpected slip-like perturbations delivered while steadily walking. Perturbations were supplied by SENLY, a split-belt treadmill whose belts can be independently controlled to emulate multidirectional slip-like perturbations (Bassi Luciani et al. 2012). SENLY is also provided with force sensors, which are used to identify the heel strike of the foot being perturbed and, accordingly, to deliver the perturbation (Fig. 1B).

Fig. 1.

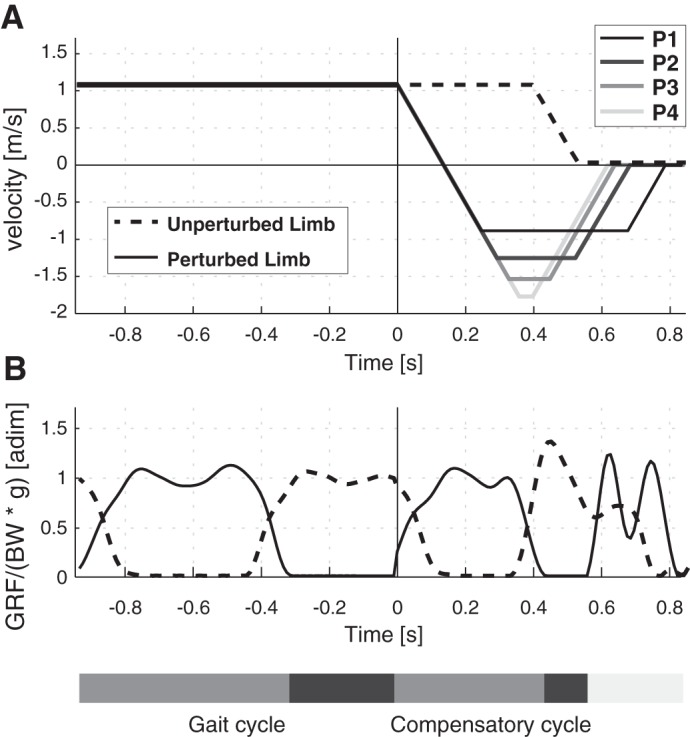
Belt velocity profiles (A) and vertical component (B) of the ground reaction force (GRF), normalized to subjects’ body weight (BW) and gravitational acceleration (g), referred to the perturbed and unperturbed limbs (solid and dashed lines, respectively). The time course (in s) of the gait and compensatory cycles is represented along the horizontal axes; 0 s corresponds to the onset of the perturbation. Stance and swing phases of the gait and compensatory cycles are reported in light and dark gray bars, respectively.

In this study, perturbations were delivered in the forward direction while subjects were walking at normalized speeds corresponding to a Froude number (Vaughan and O’Malley 2005) equal to 0.15. The Fr was also used to normalize the intensity of the four different perturbations (i.e., P1, P2, P3, and P4), which were delivered when the heel strike of the foot being perturbed was detected by SENLY. Specifically, the speed of the perturbing belt was brought to the maximum amplitude and then to zero with an acceleration of 8 m/s², and the whole belt displacement was set to 60% of leg length; the maximum speed of the belt was set at Fr equal to 0.1, 0.2, 0.3, and 0.4 for P1, P2, P3, and P4, respectively. After the onset of the perturbation, the speed of the contralateral belt was maintained for a further 0.4 s and then brought to zero in 0.15 s with constant acceleration (Fig. 1A).

Before the recording sessions were started, the enrolled subjects performed a 5-min period of acclimation while walking at normalized speeds; then, they were exposed to an initial set of random perturbations delivered on both sides to prevent the first perturbation-related bias (Bhatt et al. 2006; Oude Nijhuis et al. 2009). Participants wore a safety harness attached to an overhead track to prevent impact with the ground in case of irrecoverable lack of balance.

After the acclimation period, each trial began while the participant was walking steadily, starting ∼1 min before the perturbation was delivered to include at least 10 consecutive unperturbed strides and ending after the subject recovered the balance. Perturbations were delivered to both the right and left legs. Only data referring to the right perturbations were adopted for offline analysis. In addition, the protocol accounted for four further trials where no perturbation was delivered. Overall, enrolled participants underwent 12 experimental trials (i.e., 4 right perturbations, 4 left perturbations, 4 instances of unperturbed walking). To prevent bias in the results, 1) participants did not know whether they would be perturbed or not, 2) participants did not know which side (i.e., right or left) would be perturbed, and 3) the 12 trials were supplied in random order.

During the experimental sessions, the three-dimensional (3D) lower limb kinematics was recorded at 100 Hz by means of a Vicon Motion Analysis System (Oxford, UK) provided with six cameras. Specifically, a set of 25 reflective spherical markers (14 mm in diameter) was attached to the following body landmarks: sacrum, anterior iliac spines, external surface of the greater trochanters, lateral and medial epicondyle of the femurs, head of the fibulas, lateral and medial malleolus, first and fifth metatarsal heads of both feet, both calcaneus, and additional markers rigidly attached to a wand over the midfemurs and the midshaft of the tibias. The global reference frame was located at the center of SENLY, with the x-axis along the anterior/posterior direction, the y-axis vertical, and the z-axis defined by the right-hand rule along the medial/lateral direction.

Onset of the perturbation and records of marker trajectory were synchronized by means of a logic pulse generated by SENLY.

Research procedures conformed to the Declaration of Helsinki and were approved by the Institutional Ethics Committee of the Fondazione Don Gnocchi (Florence, Italy). Informed consent was obtained from all participants before the experimental sessions began.

Data processing.

The 3D marker trajectory was low-pass filtered (zero-lag, fourth order Butterworth with cutoff frequency at 10 Hz) to remove high frequency-related noise. Heel strike and toe off were identified based on the maximum and minimum elevation of the limb axis in compliance with the literature (Borghese et al. 1996; Ivanenko et al. 2006).

For each subject and each trial, data were subdivided into two subsets: data recorded before and after the onset of the perturbation (i.e., heel strike of the perturbed foot). The former referred to the last five unperturbed strides in which each cycle started with the heel strike of the foot being perturbed. Each stride was time-interpolated over 101 points, and all strides were averaged to have a representative unperturbed gait cycle. The latter referred to the compensatory stride; that is, it started simultaneously with the onset of the perturbation and ended with the following ipsilateral heel strike. Data referring to the perturbed stride were also time-interpolated over 101 points.

Spatio-temporal parameters (i.e., duration of the stride and stance phase, step length, and width) were evaluated both before and after the onset of the perturbation. The duration of the stride (stride) was evaluated as the interval between two consecutive heel contacts of the perturbed foot; the stance phase, expressed as a percentage of the gait cycle (stance%), was defined as the period during which the perturbed foot was on the ground; the step length and width were calculated as the anterior/posterior and medial/lateral displacements, respectively, between consecutive right and left heel strikes (i.e., from the perturbed to the unperturbed foot).

Lower limbs [i.e., perturbed (PL) and unperturbed limbs (UL)] were modeled as three-link (i.e., thigh, shank, and foot) chains connected by spherical joints (i.e., hip, knee, and ankle) whose centers were estimated in accordance with our previous study (Martelli et al. 2013).

The 3D elevation angles of all limb segments (i.e., thigh, shank, and foot) were computed using the method described in the literature (Allard 1997). The range of motion (RoM) of elevation angles was calculated as the difference between the maximum and the minimum values during both unperturbed gait and compensatory cycle (i.e., before and after the onset of the perturbation, respectively).

Intralimb coordination.

The intralimb coordination strategy related to the UL and PL, before and after the onset of the perturbation, was investigated by analyzing the planar covariation law, that is, an algebraic approach aimed at highlighting the covariance of elevation angles (Barliya et al. 2009; Borghese et al. 1996; Ivanenko et al. 2008; Lacquaniti et al. 1990). To go into further detail, when the elevation angles of thigh, shank, and foot are plotted one vs. the others in a 3D space, they describe regular trajectory loops. If these loops are constrained close to a plane, it is possible to state that thigh, shank, and foot elevation angles do not evolve independently of each other, but they covary along an attractor plane. This relationship among elevation angles is usually called planar covariation law, and it is investigated by using the principal component analysis (PCA).

Here, data sets before and after the onset of the perturbation were parsed out by means of the PCA of their correlation matrix. The outcome of the PCA consisted of three principal components, namely PC₁, PC₂, and PC₃, ordered according to their explained data variance. If elevation angles were weakly correlated, the explained variance related to each of the three components would be significantly different from zero. Otherwise, if the explained variance related to the PC₃ was close to zero, elevation angles would result in being correlated, and the three elevation angles would lie on a plane. From the theoretical viewpoint, it was also possible that the explained variance of the last two components was negligible, suggesting that the three elevation angles could be represented by scaling one independent component. However, this condition did not occur in our data analysis (see results).

We assumed that kinematic variables would lie on a plane if the cumulative explained variance (CEV%) accounted for by PC₁ and PC₂ was ≥99%, as previously reported (Borghese et al. 1996; Courtine and Schieppati 2004). If confirmed, this condition reveals that the three elevation angles are correlated to each other and can be represented by the linear combination of only two independent components. The misalignment between covariation planes pertaining to two different data sets was estimated by means of the dot product between their third weight coefficient vectors (i.e., W₃). Specifically, two covariation planes would be coinciding if the dot product of their W₃, named dot_W3, was 1. Because data sets were noisy, we adopted 0.99 as a threshold (Aprigliano et al. 2016).

Statistical analysis.

To investigate the effects of perturbation and aging (“time window” and “group” factors), the two-way mixed design, repeated-measures ANOVA (within-subjects factor – 2 levels: pre- and postperturbation; between-subjects factor – 2 levels: young and elderly group) was performed on all spatio-temporal parameters (i.e., step length and width, stride, and stance%), kinematics (i.e., RoM of elevation angles), and PCA outcomes (i.e., CEV%). Moreover, considering only data recorded after the onset of the perturbation (i.e., data POST), the effects of “perturbation intensity” (i.e., P1, P2, P3, and P4) and group (i.e., young and elderly people) were analyzed by using the two-way mixed design, repeated-measures ANOVA (within-subjects factor – 4 levels: P1–P4; between-subjects factor – 2 levels: young and elderly group).

The effects of perturbation intensity and group on the misalignment between the covariation planes before and after the perturbation (i.e., dot_W3) were analyzed by means of the two-way mixed design, repeated-measures ANOVA. When required, the one-sample t-test was used to verify whether the dot_W3 was significantly lower than the threshold. The t-test for independent samples was also used to analyze possible differences between the two groups.

For each dependent measure, the Lilliefors and the Mauchly’s tests were preliminarily performed to check the normality and sphericity assumptions. The Huynd-Feldt correction was applied if data violated the sphericity condition. Data analysis was carried out offline by means of customized MATLAB (The MathWorks, Cambridge, MA) scripts, and the statistical significance was set at P < 0.05.

RESULTS

Spatio-temporal parameters.

The groups did not show any significant differences in anthropometric features or walking speed (P > 0.05; Table 1). Specifically, younger and older subjects walked at average speeds of 1.08 ± 0.03 (range: 1.04–1.15 m/s) and 1.08 ± 0.02 m/s (range: 1.05–1.12 m/s), respectively. Inspection of all videos recorded during the experimental sessions confirmed that, after the perturbation, all participants were able to recover their balance without falling and without being assisted by the safety harness.

For each condition (i.e., PRE, P1, P2, P3, and P4) and each group (i.e., younger and older adults), the temporal (stride and the stance%) and spatial (step length and width) parameters are shown in Fig. 2.

Fig. 2.

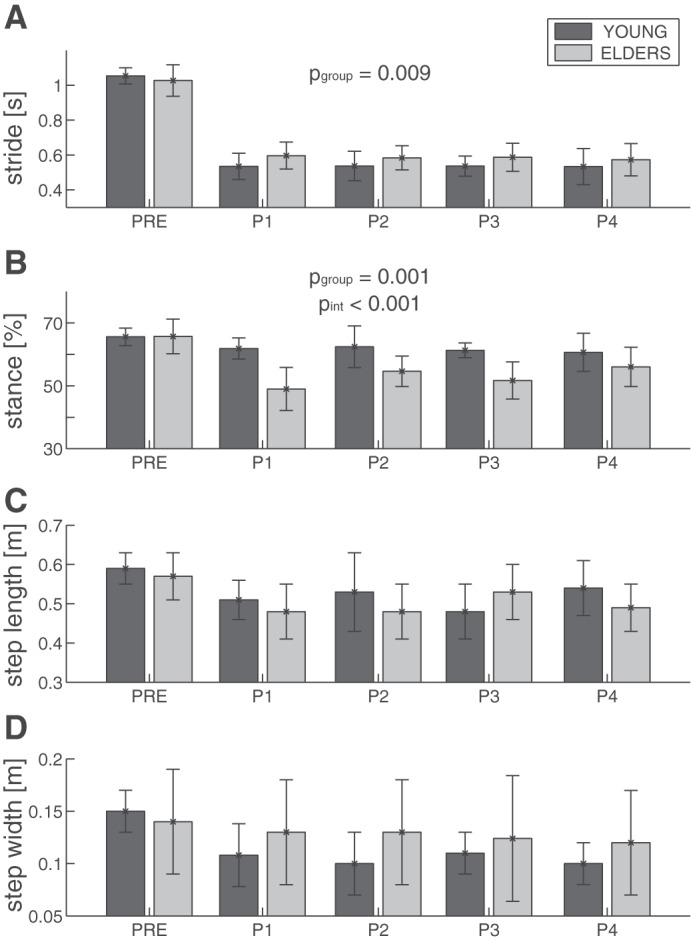
Temporal (stride duration and stance%; A and B) and spatial (step length and width; C and D) parameters are expressed as mean and 1 SD and refer to the perturbed limb (PL). Bars refer to young (dark gray; n = 10) and elderly (light gray; n = 10) people for all experimental conditions (i.e., PRE, P1, P2, P3, and P4). Significant P values related to the 2-way ANOVA on data POST are reported for group (p_goup) and perturbation intensity (p_int) factors.

Temporal parameters significantly decreased as a result of perturbation (P < 0.001; Table 2 and Fig. 2, A and B): 1) the stride decreased from 1.04 ± 0.07 to 0.56 ± 0.05 s (means  ± SD over all subjects), and 2) the stance% decreased from 65.6 ± 1% for both groups to 62.3 ± 6.9% for younger subjects and to 53.1 ± 5.7% for the older ones (p_group = 0.002). The effect of interaction of both factors (i.e., time window × group) was significant (P < 0.001) for both metrics. Specifically, after the perturbation the greatest reduction of the stride was observed in young subjects, whereas the greatest reduction of the stance% was observed in older participants.

Table 2.

Two-way ANOVA on spatio-temporal parameters measured before and after the perturbations: effects of “time window” and “group” factors

	Time Window		Group		Time Window × Group
Metric	P value	F value	P value	F value	P value	F value
Stride	<0.001	3,390.31	0.515	0.44	<0.001	23.25
Stance%	<0.001	156.28	0.002	12.92	<0.001	52.84
Step length	<0.001	115.85	0.319	1.04	0.915	0.01
Step width	<0.001	79.37	0.752	0.10	<0.001	13.11

Spatial parameters changed significantly as a result of perturbation (P < 0.001; Table 2 and Fig. 2, C and D): 1) the step length after the perturbation decreased from 0.58 ± 0.05 to 0.51 ± 0.08 m for younger and older adults, and 2) the step width decreased from 0.15 ± 0.04 to 0.12 ± 0.04 m for both groups.

The two-way ANOVA on data POST revealed significant effects of the factor group (Table 3) on stride (0.53 ± 0.04 and 0.58 ± 0.06 s for younger and older adults, respectively) and on stance%, as reported above. The factor perturbation intensity involved an increased trend for the stance% from P1 to P4 (P < 0.001; Fig. 2B and Table 3). No interaction between perturbation intensity and group factors was observed (P > 0.05; Table 3).

Table 3.

Two-way ANOVA on spatio-temporal parameters after the onset of the perturbations: effects of “perturbation intensity” and “group” factors

	Perturbation Intensity		Group		Perturbation Intensity × Group
Metric	P value	F value	P value	F value	P value	F value
Stride	0.483	0.83	0.009	8.25	0.794	0.34
Stance%	<0.001	7.59	0.001	13.81	0.073	2.47
Step length	0.828	0.30	0.388	0.78	0.094	2.25
Step width	0.903	0.19	0.284	1.21	0.917	0.17

Elevation angles.

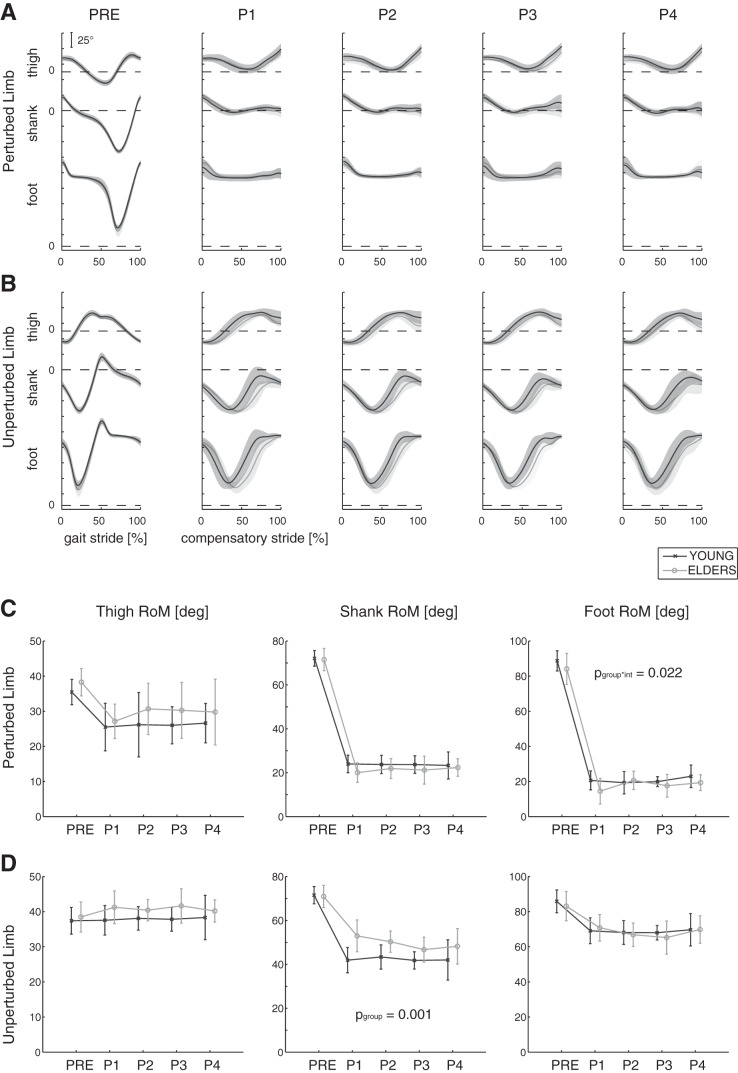
Elevation angles of thigh, shank, and foot and their RoM (RoM_T, RoM_S, and RoM_F) are reported in Fig. 3.

Fig. 3.

A and B: elevation angle profile of thigh, shank, and foot. The time course (in %) of the gait and compensatory cycles is represented along the horizontal axes for both the perturbed (PL; A) and the unperturbed limbs (UL; B); 0 and 100% correspond to 2 consecutive heel strikes of the PL. Mean (bold lines) and 1 SD (shaded areas) are shown for each group (young: n = 10, dark gray; elders: n = 10, light gray) and for all experimental conditions (i.e., PRE, P1, P2, P,3 and P4). C and D. Range of motion (RoM) of elevation angles (means ± 1 SD) is represented for young and elders (dark and light gray, respectively) and for all trials. Significant P values, related to the 2-way ANOVA on data POST, are reported for group (p_goup) and perturbation intensity (p_int) factors.

During steady walking (i.e., before the perturbation), elevation angles were similar to those described in the literature at the same speed (Aprigliano et al. 2016; Noble and Prentice 2008) and out of phase between limbs (Fig. 3, A and B). As expected, these kinematic variables were significantly altered as a result of the perturbation, involving a significant reduction of the RoM for all limb segments (P < 0.001; Table 4 and Fig. 3, C and D). In one case (i.e., RoMs of the UL), the statistical analysis revealed a different RoM between the groups. In addition, significant interactions of the two factors (i.e., time window and group) were observed for the RoM_S and RoM_T pertaining to the UL; the young group showed the greatest reduction in the range of motion at the shank and the thigh after the onset of the perturbation.

Table 4.

Two-way ANOVA on RoM of elevation angles (thigh, shank, and foot) in both limbs (UL and PL) measured before and after the perturbations: effects of “time window” and “group” factors

	Time Window		Group		Time Window × Group
Limb (Metric)	P value	F value	P value	F value	P value	F value
UL
RoMT	<0.001	20.35	0.276	1.25	0.006	7.78
RoMS	<0.001	911.95	0.008	8.65	<0.001	22.74
RoMF	<0.001	398.48	0.420	0.68	0.137	2.24
PL
RoMT	<0.001	170.35	0.063	3.87	0.664	0.19
RoMS	<0.001	9,610.77	0.365	0.86	0.107	2.64
RoMF	<0.001	7,933.99	0.099	3.00	0.142	2.18

RoM, range of motion (RoM_T, RoM_S, and RoM_F are range of motion for thigh, shank, and foot, respectively); UL, unperturbed limb; PL, perturbed limb.

The two-way ANOVA on data POST showed that the RoM of the shank, considering UL, in the older people was significantly greater than that of the younger participants (P = 0.001; Table 5). Conversely, the “perturbation intensity” did not affect the RoM of elevation angles (P > 0.05; Table 5). A significant interaction of the two factors (i.e., perturbation intensity and group) was observed for the RoM_F at PL (P = 0.022; Table 5); the older group showed the greatest reduction in the range of motion at the foot with perturbations of increasing intensity (Fig. 3C).

Table 5.

Two-way ANOVA on RoM of elevation angles (thigh, shank, and foot) in both limbs (UL and PL), measured after the perturbations: effects of “perturbation intensity” and “group” factors

	Perturbation Intensity		Group		Perturbation Intensity × Group
Limb (Metric)	P value	F value	P value	F value	P value	F value
UL
RoMT	0.331	1.17	0.118	2.66	0.854	0.26
RoMS	0.469	0.86	0.001	16.49	0.528	0.75
RoMF	0.354	1.11	0.837	0.03	0.544	0.72
PL
RoMT	0.420	0.96	0.194	2.09	0.779	0.36
RoMS	0.388	1.03	0.238	1.48	0.662	0.53
RoMF	0.095	2.24	0.145	2.29	0.022	3.50

RoM, range of motion (RoM_T, RoM_S, and RoM_F are range of motion for thigh, shank, and foot, respectively); UL, unperturbed limb; PL, perturbed limb.

Intersegmental coordination.

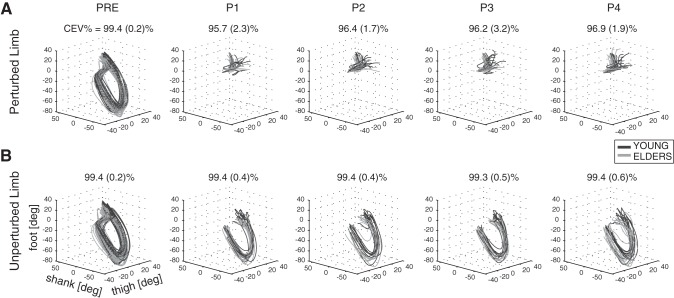
The lower limb intersegmental coordination was examined by plotting the elevation angles one vs. the others in a 3D-position space graph (Fig. 4).

Fig. 4.

Planar covariation of elevation angles at thigh, shank, and foot (3-dimensional position/space) are shown for PL (A) and UL (B). Dark and light gray lines describe trajectories obtained for young (n = 10) and elderly people (n = 10), respectively. Trials performed by each subject are superimposed. The CEV% [i.e., mean value (1 SD) across all subjects] is represented for each limb (PL and UL) and each experimental condition (PRE, P1, P2, P3, and P4).

According to the adopted criteria, the planar covariation of elevation angles was observed only for the UL across all experimental conditions (i.e., PRE, P1, P2, P3, and P4) and for both groups (i.e., younger and older subjects). As a matter of fact, in these cases the CEV% for the first two components was always greater than the threshold (Fig. 4). Conversely, the elevation angles of limb segments pertaining to the PL after the onset of the perturbation did not show any tight coupling (P = 0.007 related to time window factor; Table 6), which was in accord with the findings reported in previous studies (Aprigliano et al. 2016; Noble and Prentice 2008). Because elevation angles of PL did not lay close to a plane, the analysis of the similarity of the covariation planes between data recorded before and after the perturbation (i.e., dot_w3) could not be performed.

Table 6.

Two-way ANOVA on cumulative explained variance measured before and after the perturbations: effects of “time window” and “group” factors

	Time Window		Group		Time Window × Group
Limb	P value	F value	P value	F value	P value	F value
UL	0.316	1.01	0.333	0.98	0.387	0.75
PL	0.007	7.51	0.417	0.68	0.382	0.77

UL, unperturbed limb; PL, perturbed limb.

The orientation of the covariation planes related to the UL was quantified by analyzing the dot_W3 calculated between data recorded before and after the onset of the perturbation (i.e., PRE vs. P1, PRE vs. P2, PRE vs. P3, and PRE vs. P4). Results revealed that the dot_W3 ranged from 0.97 to 0.99 (means ± SD: 0.99 ± 0.01), which was higher or comparable with the threshold across all conditions and for both groups. Accordingly, covariation planes before and after the perturbations could be considered as congruent across subjects and trials.

DISCUSSION

In this study, we investigated the effects of aging and intensity of the perturbation on lower limb intersegmental coordination, assessed by the PCL, resulting after an unexpected slippage induced while steady walking. We hypothesized that both factors can significantly affect lower limb intersegmental coordination during the corrective motor response.

Results related to UL instead rejected our hypothesis, showing that elevation angles in older people were tidily coupled both before and after the perturbation (Fig. 4B). In addition, the analysis of the misalignment of covariation planes revealed that their orientation was comparable across conditions (i.e., before and after perturbations of increasing intensities) and groups (i.e., younger and older subjects), even though several differences were observed between younger and older participants in temporal and kinematic parameters (see Figs. 2 and 3 and Tables 2 and 3). Overall, our findings confirm that the intralimb coordination underlying steady walking and corrective response is led by the PCL.

Concerning PL, results extended the outcome of our previous study (Aprigliano et al. 2016) with regard to the elderly population, confirming that, after a perturbation, the movement of the PL is led by a kinematic pattern different from that observed during steady locomotion. Specifically, the movement of the belt constrains the foot to cover a certain displacement while the subject enables strategies to prevent the knee hyperextension. As a result, elevation angles of lower limb segments of the PL do not covary as much as during the unperturbed locomotion, thus involving an altered intralimb coordination strategy (Fig. 4A). For this reason the intralimb coordination strategy employed by the PL after the perturbation violated the PCL.

Effects of intensity of the perturbation on intralimb coordination.

The increasing intensity of the perturbation did not modify the intralimb coordination during the corrective behavior of younger and older subjects but involved an incremental trend of stance% from P1 to P4 (see Fig. 2B). These findings corroborate the hypothesis that intralimb coordination is a kinematic invariant across several locomotion-related motor tasks (Borghese et al. 1996; Cappellini et al. 2010; Courtine and Schieppati 2004; Ivanenko et al. 2008; Lacquaniti et al. 1999), and accordingly, it is supposed to be achieved mainly by a suitable tuning of the stride timing (i.e., duration of swing and stance phases).

Remarkably, during the corrective responses, the time courses of elevation angles of the UL are adapted to the increased biomechanical demand, even if their mutual relationship still relies on the covariation law described by the PCL (Fig. 4B and Table 7). This invariant feature of the intralimb coordination raises the hypothesis that the PCL represents a functional optimization rule governing the dynamic balance across several conditions. In this respect, our results extend previous findings concerning the phase coupling between elevation angles and net mechanical power while walking (Bianchi et al. 1998; Lacquaniti et al. 1999) toward a more general principle linking the PCL with the overall biomechanical demand underlying the control of the dynamic balance. Further experimental results are required to deeply investigate this hypothesis.

Table 7.

Two-way ANOVA on cumulative explained variance after the onset of the perturbations: effects of “perturbation intensity” and “group”

	Perturbation Intensity		Group		Perturbation Intensity × Group
Limb	P value	F value	P value	F value	P value	F value
UL	0.458	0.88	0.395	0.76	0.503	0.79
PL	0.362	1.09	0.452	0.52	0.686	0.50

UL, unperturbed limb; PL, perturbed limb.

To the best of our knowledge, the effect of the intensity of the perturbation on the balance recovery response has not yet been completely investigated, above all in elderly people. As a matter of fact, few studies have demonstrated that the intensity of the perturbation can differently alter the corrective behavior of older adults. Specifically, older individuals can generate rapid stepping movements in response to moderate levels of perturbations, although they seem to be unable to deal with more challenging perturbations (Hsiao-Wecksler and Robinovitch 2007; Rogers et al. 2001; Tropea et al. 2015a). Accordingly, it is not clear to what extent the intensity of the perturbation may modify the planning and the execution of effective motor responses based on any intralimb coordination law.

From the biomechanical viewpoint, we have already observed that the intensity of the perturbation alters the behavioral corrective response of young subjects, revealing a direct relationship between intensity of the perturbation and stability (Aprigliano et al. 2015). Others also corroborated the evidence that the difficulty of maintaining balance while the dynamic stability of a steady locomotion is challenged increases proportionally with both the intensity of the perturbation (Ilmane et al. 2015) and the baseline speed (Bhatt et al. 2005; Ilmane et al. 2015).

Recently, other authors have examined trial-to-trial changes in the balance recovery response to a wide range of magnitudes to investigate whether the acquired adaptive changes could be appropriately scaled to a higher-intensity perturbation (Patel and Bhatt 2015). Their results revealed that the central nervous system is able to calibrate the adaptive response to a higher intensity of perturbation based on previous experience of less intense perturbations. This conclusion is in agreement with earlier findings concerning the positive effects of a controlled perturbation-based paradigm on balance control and fall outcomes (Grabiner et al. 2012; Mansfield et al. 2010; Shimada et al. 2004; Yang et al. 2013). Noticeably, all of these studies have investigated the effects of a perturbation-based training as an adaptive strategy to manage unexpected perturbations.

Results presented in our work revealed that although the biomechanical demand required to maintain balance was modified by the amplitude of the perturbation (Fig. 2 and Table 2), mainly in terms of the timing of the compensatory stride, the corrective response of older people is characterized by a consistent intralimb coordination strategy, as described by the PCL. Current results raise the hypothesis that balance control emerges from a governing set of biomechanical invariants, that is, suitable kinematic patterns (e.g., PCL) shared across voluntary and corrective motor behaviors and across sensory contexts. If confirmed, this would shed light on the mechanisms underlying the efficiency of the central nervous system (CNS) to coordinate the whole body response to achieve balance control. Further experiments are required to test this hypothesis.

Effects of aging on the intralimb coordination.

One of the main findings of this study was that aging does not affect the PCL during corrective responses induced by unexpected perturbations of walking. In particular, the results revealed that the intralimb coordination strategy underlying the UL after the onset of the perturbation in both groups and across all experimental conditions was the same as that adopted during unperturbed walking (Fig. 4B and Table 6). Accordingly, the age-related modifications of the neuromuscular system do not seem to significantly alter the interaction among motoneuronal networks involved in the control of dynamic balance, thus preserving intralimb coordination during the compensatory movements of the UL. In this respect, our results suggest that in older people, as well as in younger ones (Aprigliano et al. 2016), the intralimb coordination strategy elicited by unexpected perturbations likely resembles that observed during unperturbed walking.

Actually, this result was unexpected since it seems to be against the evidence that aging per se significantly affects the corrective response of elderly people, making their balance control more challenging (Liu and Lockhart 2009; Pai et al. 2006; Pijnappels et al. 2005). In particular, combining the present findings with those reported in the literature, it is possible to argue that although younger and older people adopt the same rule to regulate intralimb coordination during a corrective behavior, the effectiveness of the balance recovery of the latter group is usually worse than that of the former one.

We believe that one of the key factors underlying this discrepancy may be the latency of the corrective behavior of older people. Actually, our results highlighted an age-related delay in completing the compensatory stride (i.e., increased stride duration after the perturbation, see Fig. 2A), thus suggesting that declined reflex reactions and muscle weakness may be the main actors influencing the corrective response of the older people. As a matter of fact, it has been widely demonstrated that the age-related deterioration of neural, sensory, and musculoskeletal systems affects in a negative fashion the ability of elderly people to detect the onset of instability and to rapidly plan and execute an effective stepping reaction (Liu and Lockhart 2009; Lockhart et al. 2005; Maki and McIlroy 2006; Pijnappels et al. 2005).

The consistency of intralimb coordination patterns observed in older participants across different experimental conditions (i.e., steady walking and managing unexpected slippages of different intensities) suggests that the adopted perturbation-based paradigm targets specific neuromuscular skills. They are supposed to be encrypted in the lower part of the CNS (Dietz 2002; Ivanenko et al. 2008; Lacquaniti et al. 2002) and do not seem to be altered by aging (Monaco et al. 2010). Accordingly, the continuous exposure to the proposed perturbations could hence allow older adults to reinforce their ability to elicit suitable coordination strategies.

Actually, our findings allow us to also speculate that a perturbation-based paradigm can even be used to elicit unaltered motor programs in subjects affected by diseases of the supraspinal networks of the CNS. As matter of fact, previous studies (Morton and Bastian 2006; Mummel et al. 1998; Reisman et al. 2007; Rinaldi and Monaco 2013) have already revealed that suitable experimental protocols lead people affected by damages of the upper part of the CNS (e.g., post-stroke or cerebellar patients) to adopt healthy-like behaviors. Accordingly, we can hypothesize that perturbation-based paradigms can elicit hardwired neuromuscular skills as well, thus leading patients to recover unaltered motor schemes. However, further investigations are required to confirm this hypothesis.

In conclusion, this study shows that lower limb intersegmental coordination described by the PCL was not affected by aging, even during challenging postural transitions (i.e., high-intensity perturbations). In this respect, the intralimb coordination strategy elicited by unexpected perturbations likely resembles that observed during unperturbed walking. Accordingly, our findings provide further support to investigate the effects of a perturbation-based paradigm to rehabilitate walking capabilities in subjects with balance disorders.

Limitations of the study.

This study was limited by three main factors. First, enrolled elderly participants were relatively high functioning with no falling history, and thus only successful responses to perturbations were observed during the experimental sessions. Further studies are required to extend these results to subjects characterized by higher risk of falling (i.e., fragile elderly individuals).

Second, it is well known that multiple exposures to perturbations can modify subjects’ corrective responses (Barrett et al. 2012). However, our experimental protocol (see Subjects, experimental setup, and protocol) was designed specifically to prevent any adaptation mechanisms in accordance with previous literature (Bolger et al. 2014; Carpenter et al. 2004).

Finally, the results cannot be fully generalized due to the adopted experimental setup (i.e., SENLY). On the other hand, our platform allows us to test repeatable experimental conditions across subjects and sessions (Aprigliano et al. 2015, 2016; Martelli et al. 2017; Martelli et al. 2013, 2014; Monaco et al. 2017; Tropea et al. 2015a, 2015b), thus guaranteeing reliable data sets.

GRANTS

This work was supported partly by the European Union Commission within the CYBERLEGs (The CYBERnetic LowEr-Limb CoGnitive Ortho-prosthesis, ICT 287894), the CYBERLEGs Plus Plus (The CYBERnetic LowEr-Limb CoGnitive Ortho-prosthesis Plus Plus, ICT 731931), and the I-DONT-FALL (Integrated prevention and Detection sOlutioNs Tailored to the population and Risk Factors associated with FALLs, CIP-ICT-PSP-2011-5-297225) projects, by Fondazione Pisa within the IUVO Project (project no. 154/11), and by institutional funds from The BioRobotics Institute, Scuola Superiore Sant’Anna.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

F.A., S.M., and V.M. conceived and designed research; F.A., D.M., P.T., and G.P. performed experiments; F.A., D.M., P.T., and V.M. analyzed data; F.A. and V.M. interpreted results of experiments; F.A. and P.T. prepared figures; F.A., S.M., and V.M. drafted manuscript; F.A., D.M., P.T., G.P., S.M., and V.M. edited and revised manuscript; F.A., D.M., P.T., G.P., S.M., and V.M. approved final version of manuscript.