Contrasting speed-accuracy tradeoffs for eye and hand movements reveal the optimal nature of saccade kinematics

The optimality of saccade kinematics has been suggested by modeling studies but experimental evidence is lacking. However, we observed that, when subjects voluntarily modulated their hand velocity, the velocity of saccades accompanying these hand movements was also modulated, suggesting a shared kinematic plan for eye and hand movements. We leveraged this modulation to show that saccades had less endpoint accuracy when their velocity decreased, illustrating that normometric saccades have optimal speed and accuracy.

Abstract

In contrast to hand movements, the existence of a neural representation of saccade kinematics is unclear. Saccade kinematics is typically thought to be specified by motor error/desired displacement and generated by brain stem circuits that are not penetrable to voluntary control. We studied the influence of instructed hand movement velocity on the kinematics of saccades executed without explicit instructions. When the hand movement was slow the saccade velocity decreased, independent of saccade amplitude. We leveraged this modulation of saccade velocity to study the optimality of saccades (in terms of velocity and endpoint accuracy) in relation to the well-known speed-accuracy tradeoff that governs voluntary movements (Fitts’ law). In contrast to hand movements that obeyed Fitts' law, normometric saccades exhibited the greatest endpoint accuracy and lower reaction times, relative to saccades accompanying slow and fast hand movements. In the slow condition, where saccade endpoint accuracy suffered, we observed that targets were more likely to be foveated by two saccades resulting in step-saccades. Interestingly, the endpoint accuracy was higher in two-saccade trials, compared with one-saccade trials in both the slow and fast conditions. This indicates that step-saccades are a part of the kinematic plan for optimal control of endpoint accuracy. Taken together, these findings suggest normometric saccades are already optimized to maximize endpoint accuracy and the modulation of saccade velocity by hand velocity is likely to reflect the sharing of kinematic plans between the two effectors.

NEW & NOTEWORTHY The optimality of saccade kinematics has been suggested by modeling studies but experimental evidence is lacking. However, we observed that, when subjects voluntarily modulated their hand velocity, the velocity of saccades accompanying these hand movements was also modulated, suggesting a shared kinematic plan for eye and hand movements. We leveraged this modulation to show that saccades had less endpoint accuracy when their velocity decreased, illustrating that normometric saccades have optimal speed and accuracy.

despite dissimilar movement durations, reach and saccadic eye movements are characterized by stereotypical bell-shaped velocity profiles, consisting of an initial acceleration phase and a subsequent deceleration phase. Yet, paradoxically, their kinematics is thought to be represented in distinct ways. It is now well accepted that some aspects of the hand kinematics are represented in dorsal premotor (Churchland et al. 2006; Cisek and Kalaska 2005), ventral premotor (Kakei et al. 2001), parietal (Averbeck et al. 2005; Kalaska et al. 1990), and motor (Georgopoulos et al. 1982; Kakei et al. 1999; Moran and Schwartz 1999) cortices, allowing hand velocity to be voluntarily modulated. In contrast, saccade kinematics is thought to be a derived attribute that is not explicitly represented in higher oculomotor areas (Fuchs et al. 1985; Henn and Cohen 1976; Luschei and Fuchs 1972; Sparks 2002; Van Gisbergen et al. 1981, but see Goossens and van Opstal, 2012), and consequently not under explicit voluntary control. Thus the computation of saccade trajectory is highly stereotypical and is governed by the main sequence relationship where the duration is linearly related to the amplitude, and the velocity is monotonically related to the amplitude (Bahill et al. 1975; Collewijn et al. 1988).

Nevertheless, some aspects of saccade kinematics such as saccade velocity can be modulated by certain task conditions. For example, saccades made in the dark compared with saccades to well-illuminated targets (Becker and Fuchs 1969; Sharpe et al. 1975), saccades made to auditory targets compared with visual targets (Zambarbieri et al. 1982), saccades made to predictive targets compared with random targets (Bronstein and Kennard 1987), memory-guided saccades and anti-saccades compared with pro-saccades (Smit et al. 1987), saccades to nonrewarded locations compared with rewarded locations (Takikawa et al. 2002), and saccades made in isolation compared with those accompanying hand movements (Snyder et al. 2002; van Donkelaar et al. 2004) have lower peak saccadic velocities, respectively. Recent studies have also shown that as subjective value of the stimulus increases, saccade peak velocity increases (Reppert et al. 2015). Also, subjects tend to make faster saccades in anticipation of seeing a face, rather than an object or visual noise (Xu-Wilson et al. 2009). However, most of these studies varied the task conditions (like changing the stimuli) rendering saccades noncomparable between the conditions. Inspired by studies that have shown saccade velocity modulation when accompanied by hand movement, we tested whether voluntary modulation in hand velocity led to a modulation in saccade velocity, which would suggest a shared kinematic representation for coordinated eye-hand movements.

In addition, we also hoped to leverage the possible modulation of saccade velocity to test the optimality of saccades. According to speed-accuracy tradeoff, movements should be more accurate when movement duration (or velocity) is more (or less) (Fitts 1954; Harris and Wolpert 1998). While this law has been tested for hand movements (Fitts 1954; Jax et al. 2007; Rosenbaum et al. 1993), it has not been examined for saccades. Saccades are considered to be optimal (Harris and Wolpert 1998; Todorov and Jordan 2002), and simulation studies have suggested that the stereotypical nature of saccades is ideal to minimize endpoint error (maximize endpoint accuracy) while maintaining the appropriate saccade duration and velocity in the presence of noise (Harris and Wolpert 2006; van Beers 2008). However, in the absence of voluntary control of saccade kinematics, experimental support of such optimized speed-accuracy tradeoff is lacking. In this study, we experimentally test the optimal nature (speed-accuracy relationship) of saccadic eye movements.

METHODS

Subjects

Eighteen right-handed subjects (checked by modified Edinburgh Handedness Index) participated in the study. They were aged between 21 and 29 yr (mean age = 24.2 ± 2.3 yr, equal number of men and women) and had normal or corrected-to-normal vision. Except for one subject who is an author in this paper, all the other subjects were naive to the purpose of the study. Written, informed consent was obtained in accordance with the Institutional Human Ethics Committee of the Indian Institute of Science, which approved the protocol. Subjects were paid for their participation in the study.

Setup

Data was collected using TEMPO/VIDEOSYNC software (Reflective Computing) that also displayed the stimuli and recorded behavior in real time. Eye movements were tracked at 240 Hz by a head-mounted infrared pupil tracker (ETL-200, RK-706-PCI, ISCAN). Hand movements were tracked at 240 Hz by an electromagnetic position and orientation measuring system (LIBERTY, Polhemus) consisting of a source (central transmitter) and a tracker (small receiver) which was placed on the forefinger of the subject. Data was acquired and stored by TEMPO, which interfaced with both eye and hand tracking systems in real time with a delay of 8 ± 1 ms.

A virtual reality setup consisting of a slightly tilted semitransparent mirror was used to minimize the distortions of the electromagnetic field used for hand tracker. The targets were presented on an inverted 20″ Dell LED monitor (refresh rate 60 Hz) housed on a wooden frame above the mirror. When subjects sat looking down through the mirror they saw a virtual image of overhead monitor below the mirror. An acrylic sheet was placed below the mirror, in the plane of the virtual image so that the subjects got an impression of touching the screen. Subjects performed the task by moving one hand on this sheet to point to the targets [see Gopal et al. (2015) for an image of the setup]. All the recordings were done in a dark room. Subjects sat with the chin resting on a chin rest and head immobilized with head bars positioned on both sides of the temple. To provide visual feedback of the pointing finger in the dark, a LED was fixed at the tip of the pointing finger (right index finger) and kept ON throughout the task.

Behavioral Paradigm

Velocity task.

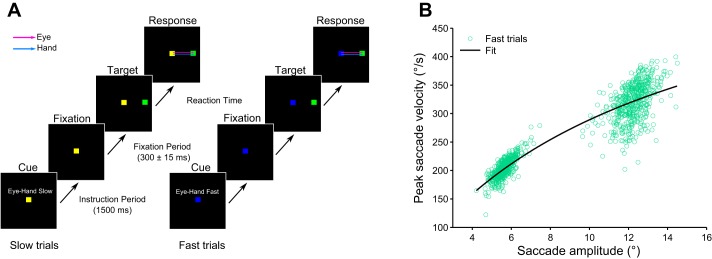
Subjects (n = 8) were instructed to make slow or fast hand movements to peripherally appearing targets. Each trial began with a cue period of 1,500 ms, which indicated whether the subject would have to make a slow (yellow fixation spot) or fast (blue fixation spot) hand movement during which no active fixation was required. Additionally, written instruction of “Eye-Hand Slow” and “Eye-Hand Fast” was displayed in the appropriate trials just above the fixation spot; however, no information was provided regarding target position. The presence of a cue period, therefore could allow enough time for subjects to plan for the appropriate velocity movement and hence not affect the reaction times. Following the cue, a white fixation spot of ~1° appeared at the center of the screen. Subjects had to fixate eyes and hand on it for 300 ± 15 ms, after which a peripheral green target (size ~1°) appeared either left or right of the fixation spot at an eccentricity of 6° (Amp6) or 13° (Amp13). Subjects were encouraged to make a slow movement that reached the target within 5 s in the slow trials and make a movement as fast as possible in the fast trials. Online monitoring of hand velocity was done on the basis of movement time, i.e., the time taken by the hand to exit the fixation electronic window (a region that is specified in the behavioral monitoring system and invisible to the subject, ~3°) and enter the target electronic window (~3°). Trials in which subjects could successfully reach the target with the correct velocity were indicated by a tone (1 KHz, ~70 dB). No explicit instructions were given for eye movements. Additionally, trials were grouped such that each group of trials had 8 conditions (2 target positions: left and right × 2 velocity conditions: slow and fast × 2 target eccentricities: 6° and 13°) that were presented pseudo-randomly within each group. Subjects performed ~1,000 trials in two sessions each containing greater than 63 groups of trials.

Before the task began, each subject performed ~60 practice trials where the movement times for the slow and fast conditions were determined. The subject-specific movement time measured during the practice session was used for the main experiment.

Normal velocity task.

On a separate day, six of the eight subjects also made normative hand movements. Each trial began with a white fixation spot of ~1° appearing at the center of the screen. The subjects had to fixate their eyes and hand on it for 300 ± 15 ms, after which a peripheral green target (size ~1°) appeared either left or right of the fixation spot at an eccentricity of 6° (Amp6) or 13° (Amp13). Subjects were instructed to point to these targets with no instruction given for eye movements. Unlike the velocity task, there was no explicit velocity instruction for hand movements while performing the task. The subjects performed the pointing task using their natural predisposed velocity in this task and this was operationally defined as a normative movement. The data was collected in a single session with subjects performing ~500 trials.

Modified velocity task.

We also recorded 10 naive subjects on a modified velocity task where the subjects executed all the three velocity conditions in the same session. First, subjects performed ~300 trials of the normal velocity condition. This was same as the normal velocity task, except that there a written instruction cue of “Normal Hand” was displayed for 1,500 ms before each trial. There was no explicit velocity instruction in this condition and subjects performed the pointing task using their natural predisposed velocity. The mean + 2 standard deviation (SD) of the hand movement duration in the normal condition was used to set the movement duration cutoffs in the slow condition. However, some subjects by default had a low movement duration (high velocity) in the normal velocity trials and were unable to make faster hand movements that had movement duration less than mean − 2 SD in the fast velocity condition. For these subjects the cutoff was set to fixed level (Amp6: 25 ms to reach the target, Amp13: 100 ms to reach the target). After the normal velocity condition, subjects were given ~70 trials of practice to get acclimatized to the slow and fast velocity cutoffs. Thereafter they performed ~800 trials of the velocity task (Fig. 1A). The only difference between these trials and those in the velocity task was that the instruction cue was modified to “Slow Hand” or “Fast Hand.”

Fig. 1.

Task and performance. A: subjects were instructed to make a slow or fast pointing movement to a green target (6° or 13°) that appeared peripherally on either side of fixation. Slow and fast trials were indicated by yellow and blue central cues, respectively. B: fitting Eq. 1 to the main sequence of saccades made in the fast trials for the exemplar subject. Each green dot represents a trial, while the black line represents the fit.

Tracker Accuracy

The eye and hand trackers were calibrated while subjects pointed and fixated at the fixation spot as well at the target positions. To quantify the accuracy of the eye and hand trackers, the SD of the horizontal and vertical components of eye and hand trajectory for 20 ms before saccade/hand onset and after saccade/hand offset was calculated for each trial. This value measures the noise in the tracker at the fixation spot and at the target locations and is related to the accuracy of the tracker. Across all the subjects in the slow and fast velocity experiments, noise in the tracker at the fixation in the eye signal was 0.40 ± 0.31° while the noise in the hand signal was 0.05 ± 0.08 cm. The tracker noise at the target positions for the eye (0.50 ± 0.33°) and hand signals (0.14 ± 0.17 cm) were also quantified. In the normal velocity experiment, across all the subjects, fixation noise (Eye: 0.42 ± 0.31°, Hand: 0.03 ± 0.09 cm) and the target noise (Eye: 0.40 ± 0.28°, Hand: 0.14 ± 0.09 cm) in trackers were also quantified. There was no significant difference in the accuracy of the trackers between the two experimental sessions (Velocity task vs. Normal velocity task) at both fixation and target, across subjects. In the experiment where the subjects performed slow, normal, and fast velocity trials in the same session, the noise in the eye and hand tracker at the fixation spot was 0.62 ± 0.14° and 0.04 ± 0.03 cm, respectively, while the noise in the eye and hand tracker at the target location was 0.64 ± 0.17° and 0.07 ± 0.02 cm, respectively.

Data Analysis

All analysis was done offline using MATLAB (MathWorks, Natick, MA).

Saccade detection.

The data was smoothed using a boxcar filter of 20 ms. The beginning and ending of saccades were demarcated depending on when the instantaneous velocity exceeded and dropped below 30°/s. The acceleration-deceleration profile, i.e., whether the peak in acceleration was followed by a peak in deceleration within 60 ms or less, was used as an additional criterion to distinguish saccades. The saccade beginning and ending was further adjusted to the point where the velocity dropped below 10% of the peak eye velocity during the saccade. Finally, to be considered a valid first saccade, the saccade had to satisfy a duration criterion (>24 ms and <140 ms) and an amplitude criterion (>2° and <20°). The amplitude criterion of the second and third saccade was >1° and <20°. If the saccade velocity crossed 700°/s anytime during the duration of a saccade it was considered a blink-perturbed saccade and was omitted from the analysis.

Hand onset detection.

The data was smoothed using a boxcar filter of 20 ms. A velocity criterion of 6 cm/s was used to mark hand movement onset as well as offset. Movement beginnings and ends were further modified using the criterion of 10% of the peak hand velocity of the movement, similar to the criterion used for saccades. All these movements had to satisfy an amplitude criterion (>1 cm) and a duration criterion (>40 ms). If the instantaneous hand velocity crossed 300 cm/s anytime during the duration of the movement, the trial was omitted from the analysis.

Cutoffs for reaction time.

Eye and Hand reaction times (RTs) were calculated as the time between target presentation and the detected saccade and hand movement beginning, respectively. RTs were corrected for the system delays of 8 ± 1 ms. Initially, Eye RT < 80 ms and Hand RT < 200 ms were removed from the analysis. Subsequently, a cutoff of a mean ± 2 SD of the eye RT and hand RTs were used to remove outliers from the analysis. These criteria removed <6% of the trials.

Classification of trials.

For offline assessment of correct velocity trials, we used a cutoff of 40 cm/s for Amp6 trials and a cutoff of 60 cm/s for Amp13 trials. Trials in the slow condition in which the peak hand velocity was below the respective cutoffs were judged as correct trials, while trials in the fast condition in which the peak hand velocity was above the respective cutoffs were judged as correct trials. Approximately five percent of the data was excluded based on the above criterion. In addition to using such a velocity cutoff, we also used K-means clustering to divide the hand trials into fast and slow conditions and then into Amp6 and Amp13 conditions. The results were consistent with the earlier method. Hence, we report only the results in which the velocity criterion was used to classify trials.

Saccade vigor.

To test whether saccade velocity is influenced by factors other than their corresponding amplitudes, saccade vigor was computed (Choi et al. 2014; Reppert et al. 2015). Briefly, a hyperbolic function was fitted to characterize the relationship between the saccade amplitude and peak saccade velocity (main sequence relationship) in the fast condition using both Amp6 and Amp13 trials (Fig. 1B). The function had the form

$$v=\alpha \left(1-\frac{1}{1+\mathrm{\beta x}}\right)$$ (1)

where x is the saccade amplitude, v is the peak saccade velocity, and α and β represent parameter values that are unique to each subject. These coefficients were used to predict the peak saccade velocity for each saccade in the slow condition. The ratio of observed to predicted velocity is defined as saccade vigor. A value <1 suggests that peak velocity of the saccade was lower than what is expected by the main sequence relationship.

Endpoint accuracy.

Endpoint accuracy was determined using two metrics: endpoint error and endpoint scatter. Amplitudes in each trial was calculated as the Euclidean distance between the eye positions before saccade onset and after saccade offset based on both the horizontal and vertical eye positions as

$$\mathrm{Amplitude}=\sqrt{{\left(x_{\mathrm{final}}-x_{\mathrm{initial}}\right)}^2+{\left(y_{\mathrm{final}}-y_{\mathrm{initial}}\right)}^2}$$ (2)

where x_final and x_initial are the final and initial horizontal positions, respectively, while y_final and y_initial are the final and initial vertical positions, respectively. The target amplitude combined the horizontal and vertical components of the movement into a one-dimensional quantity. We further confirmed that the vertical component of the movement was negligible compared with the horizontal component since the target was displayed only on the horizontal axis.

Endpoint error was then calculated as the mean of the difference between movement and target amplitudes. Thus negative endpoint errors indicate movements that undershot the target, while positive endpoint errors indicate that which overshot the target. Endpoint scatter was calculated as the SD of the difference between the movement endpoint and target amplitude. Hence, the larger the endpoint scatter, the more scattered is the endpoint of the movement. For most of the analyses, the first eye and hand movement have been considered, except where it is explicitly mentioned otherwise.

Statistical tests.

In this paper, values x ± y indicate the mean and standard deviation (SD). The data was first checked for normality using Lilliefors test. If the data satisfied normality then a paired t-test (two-tailed unless specified otherwise) or a Wilcoxon signed-rank test was conducted. For multiple comparisons across groups of data either repeated-measures ANOVA (for data satisfying normality) or Kruskal-Wallis/Friedman’s test was used. Unless otherwise mentioned the level of significance (α) was fixed to 0.05. Cohen’s d and partial eta squared η², which measures the effect size, have also been reported.

RESULTS

To test the existence of shared kinematic representation of coordinated eye-hand movements, subjects performed fast or slow pointing movements to a peripherally appearing target, with no explicit instruction for eye movements. We hypothesized that a shared kinematic representation would lead to a change in saccade velocity when hand velocity was changed. Thereafter, we also compared saccades accompanying nondefault hand velocity movements (slow and fast hand movements) and those accompanying default or normal velocity hand movements. The aim of these analyses was to describe speed accuracy tradeoff for saccades and determine whether normative saccades are optimal relative to slow and fast saccades. Although we have usually used two-way repeated-measures ANOVA with velocity condition (Slow, Fast, and Normal) and amplitude condition (Amp6 and Amp13) as factors, for the sake of brevity we present the results of the influence of the velocity condition alone. This is because an increase in velocity and amplitude of saccade and hand movements is expected when instructed task amplitude increases from Amp6 to Amp13.

Saccade Velocity Modulation

A two-way repeated-measures ANOVA showed a significant main effect of velocity condition [F(1,17) = 250.1, P < 0.001, η² = 0.94) on peak hand velocity, suggesting that subjects performed the (velocity and modified velocity) task as instructed. We then tested whether the instructed change in the hand velocity was accompanied by a corresponding change in saccade kinematics in the slow (mean hand velocity: Amp6 = 21 ± 2 cm/s, Amp13 = 33 ± 3 cm/s) and fast trials (mean hand velocity: Amp6 = 119 ± 26 cm/s, Amp13 = 167 ± 36 cm/s). Only those trials where subjects foveated the target with a single saccade were included in this analysis. A two-way repeated-measures ANOVA showed that there was a significant main effect of velocity condition [F(1,17) = 33.0, P < 0.001, η² = 0.97] on peak saccade velocity, suggesting that it was modulated by hand velocity (mean peak eye velocity; Slow-Amp6 = 188 ± 25°/s; Fast-Amp6 = 198 ± 21°/s; Slow-Amp13 = 300 ± 40°/s; Fast-Amp13 = 320 ± 37°/s). Interestingly, saccade amplitude also increased in the fast trials (mean saccade amplitude: Amp6 = 5.8 ± 0.4°; Amp13 = 12.5 ± 0.6°) compared with the slow trials (mean saccade amplitude: Amp6 = 5.5 ± 0.5°; Amp13 = 12.2 ± 0.8°). A two-way repeated-measures ANOVA revealed significant main effect of velocity condition [F(1,17) = 15.4, P = 0.001, η² = 0.47] on saccade amplitude. This raised the possibility that the change in saccade peak velocity observed between the two velocity conditions could be a result of the increased saccade amplitude.

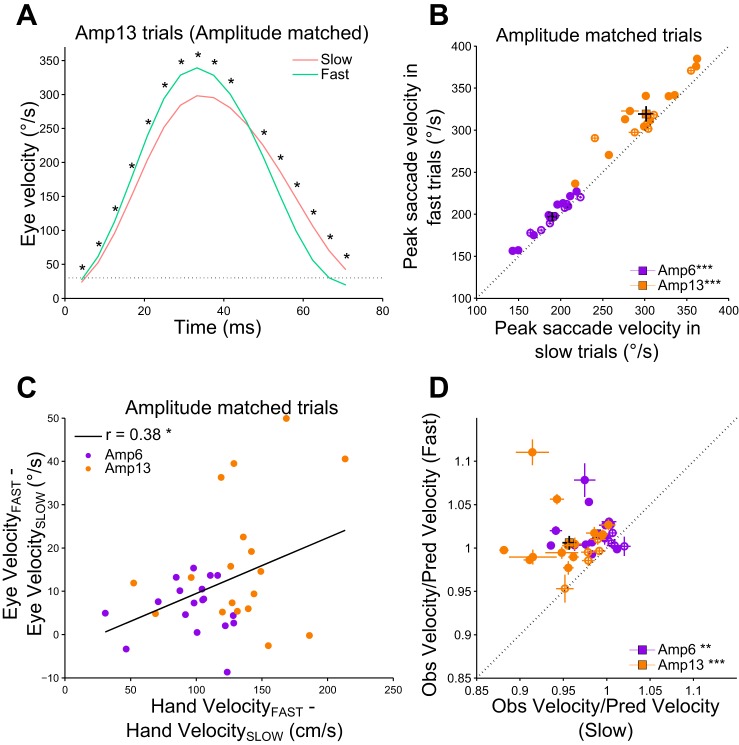
To verify the influence of hand velocity on saccades, independent of saccade amplitude, we matched the mean saccade amplitude in fast and slow trials for each subject. We sequentially removed trials from both the lower and upper tail of saccade amplitude distributions (depending on which value was furthest from the mean) from both the fast and slow trials, till the mean saccade amplitude was matched, and the P value was >0.05 (two-tailed t-test). The mean amplitude matched distributions in the fast and slow trials were from the same continuous distribution (P > 0.05, two-tailed Kolmogorov-Smirnov test) in 16/18 subjects in both Amp6 and Amp13 conditions. A three-way ANOVA with target direction (Left vs. Right), amplitude (Amp6 vs. Amp13), and velocity condition (Slow vs. Fast) as factors showed that the velocity condition was not a significant factor influencing the direction of amplitude matched saccades in any 18/18 subjects. Furthermore, the Bayes factor in favor of the null hypothesis (saccade direction in Slow and Fast trials are not significantly different) was less than 0.3 in 32/36 conditions (18 subjects × 2 target directions) suggesting that the direction of saccades was similar between Slow and Fast trials. Despite such amplitude and direction matching, the average saccade velocity profiles were distinct between the slow and fast trials (Fig. 2A, Amp13 condition in an exemplar subject). The peak saccade velocity was significantly greater in fast trials compared with slow trials in 11/18 subjects in Amp6 [mean peak saccade velocity; Slow = 191 ± 24°/s; Fast = 198 ± 21°/s; t(17) = 4.3, P < 0.001, d = 0.3] and 12/18 subjects in Amp13 [mean peak saccade velocity; Slow = 304 ± 40°/s; Fast = 321 ± 37°/s; t(17) = 4.6, P < 0.001, d = 0.4] condition (Fig. 2B). At a population level, a two-way repeated-measures ANOVA showed that even after matching the amplitudes of slow and fast trials, there was a significant main effect of hand velocity condition [F(1,17) = 23.8, P < 0.001, η² = 0.58] on peak saccade velocity. This represents an increase of 5 ± 5% of peak saccade velocity in the fast trials compared with the slow trials. To quantify the relation between eye and hand velocities we computed an index of velocity modulation as the difference between the mean peak velocities during fast and slow conditions. Interestingly, we found that the observed modulation in saccade velocity (Fast − Slow) was positively correlated with the modulation in hand velocity (r = 0.38, P = 0.024), suggesting that the instructed change in hand velocity between the two velocity conditions influenced the change in peak eye velocity (Fig. 2C).

Fig. 2.

Change in peak saccade velocity with hand velocity in amplitude matched trials. A: the average saccade velocity profile for a representative subject in the Amp13 condition. The mean of the instantaneous velocity of the amplitude matched saccades for the fast (green) and slow (red) hand velocity conditions. The time bins at which there is statistical significant difference between the average instantaneous velocities of the saccades are marked with a black asterisk (*P < 0.05). The dotted line represents the velocity cutoff used for detection of saccades. B: comparison of peak saccade velocity in the Amp6 and Amp13 conditions. Each dot and cross-hairs represents the mean ± SE of the peak saccade velocity for a single subject (purple, Amp6; orange, Amp13). Filled circles represent significant difference in peak saccade velocity between the 2 velocity conditions. The square and black cross-hair represents the mean ± SE across the population. The unity line is represented as a black dotted line. C: correlation between the modulation in peak hand velocity and the modulation in peak saccade velocity. Each dot indicates a subject (purple, Amp6; orange, Amp13). The least squares line is shown as a black line. D: comparison of saccade vigor (ratio of the observed peak saccade velocity to the predicted peak saccade velocity) between the fast and the slow trials. Other marking conventions are the same as in B (**P < 0.01 and P > 0.001; ***P < 0.001).

To test whether the modulation in saccade velocity was observed not only at its peak, we computed the average saccade velocity over the entire duration of the saccade (average saccade duration; Slow-Amp6: 54 ± 8 ms, Fast-Amp6: 55 ± 8 ms, Slow-Amp13: 75 ± 13 ms, Fast-Amp13: 76 ± 13 ms). Fourteen of 18 subjects and 13/18 subjects had greater average saccade velocity in the fast trials compared with the slow trials in the Amp6 (average saccade velocity; Slow = 122 ± 13°/s, Fast = 127 ± 11°/s; t(17) = 4.7, P < 0.001, d = 0.3) and Amp13 (average saccade velocity; Slow = 197 ± 22°/s, Fast = 207 ± 20°/s; t(17) = 5.3, P < 0.001, d = 0.5) conditions, respectively, indicating that the saccade velocity in the slow trials was indeed less than that in the fast trials.

To complement the previous analyses where we removed trials to match saccade amplitudes between the two velocity conditions, we also tested the saccade velocity modulation using a vigor analysis (see methods; Choi et al. 2014; Reppert et al. 2015) in which all trials were included. The ratio of the observed to predicted peak saccade velocity in the fast condition was ~1. In the event of modulation in the peak saccade velocity in the slow trials compared with the fast trials, the ratio of the observed to predicted peak saccade velocity in the slow conditions should be lesser than the ratio in the fast condition. Consistent with this idea, the ratio was significantly less in 11/18 and 13/18 subjects in the slow trials compared with the fast trials in the Amp6 and Amp13 conditions, respectively (Fig. 2D). This result was reflected at the population level as well, in both Amp6 (Saccade vigor ratio; Slow = 0.99 ± 0.02, Fast = 1.01 ± 0.02; W = 17, P = 0.003, d = 1.2) and Amp13 conditions (Saccade vigor ratio; Slow = 0.96 ± 0.03, Fast = 1.00 ± 0.03, W = 0, P < 0.001, d = 1.5). This indicates that saccade vigor changed depending on the velocity of the accompanying hand movements.

To additionally validate the influence of hand velocity condition on peak eye velocity, we constructed an analysis of covariance (ANCOVA) model where

$$\mathit{\text{Peak Eye Velocity}}={\beta }_0+\left(\mathit{\text{Eye Amplitude}}\right){\beta }_1+\left(\mathrm{Hand}\mathrm{velocity}\mathrm{condition}\right){\beta }_2+\mathrm{their}\mathrm{interactions}+\epsilon$$

In this analysis, the hand velocity condition was considered as a categorical variable (slow or fast). We found that the hand velocity condition was a significant factor influencing peak eye velocity in 14/18 subjects.

We also verified whether the trial by trial variation of peak hand velocity influenced the peak eye velocity by constructing a linear regression model which had the same form as the above equation (hand velocity was now considered as a continuous variable). We found that the coefficient for peak hand velocity was significant for 14/18 subjects, suggesting that trial-by-trial variations in peak hand velocity influenced the peak eye velocity.

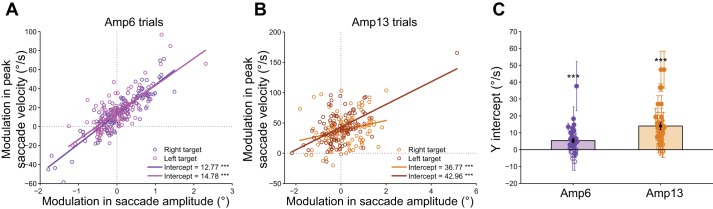
The task design provided us an additional way to check the effect of hand velocity on saccade velocity. As mentioned in the methods, the trials were grouped into sets of eight trials; each group containing two target positions: right and left, two amplitude conditions: 6° and 13°, and two velocity conditions: slow and fast, pseudo-randomly presented to the subjects. Within each group of trials we computed the difference in saccade velocity and the difference in saccade amplitude between a fast and slow trial, separately for each target position and amplitude condition. To quantify the relationship between the differences in saccade amplitudes (Fast − Slow) and the difference in peak saccade velocities (Fast − Slow) we fitted a regression line to the distribution of points and the y-intercept was computed. A positive y-intercept indicates an increase in peak saccade velocity when the difference between the eye amplitudes in the fast and slow trials is 0. As evident in the representative subject, the y-intercept was significantly greater than 0 in Amp6 (Fig. 3A, intercept for right target = 12.77°/s, P < 0.001, intercept for left target = 14.78°/s, P < 0.001) and in Amp13 condition (Fig. 3B, intercept for right target = 36.77°/s, P < 0.001; intercept for left target = 42.96°/s, P < 0.001). The y-intercept was significantly greater than 0 in 44/72 conditions (2 directions × 2 amplitudes × 18 subjects). Across the population, the intercept was significant in both Amp6 [mean intercept = 5.4 ± 8.0°/s; t(35) = 4.0, P < 0.001] and Amp13 [mean intercept = 14.0 ± 12.1°/s; t(35) = 6.9, P < 0.001] conditions (Fig. 3C).

Fig. 3.

Modulation of peak saccade velocity in blocks. A: scatter plot of the modulation in the amplitudes and the modulation in the peak velocities of saccades in the slow and fast condition within each block of trials in a single subject for Amp6 trials. The left (reddish purple) and right (bluish purple) target and their best fit regression lines are shown. The lines, x = 0 and y = 0 are shown as black dotted lines. The intercept for each target and its significance value is indicated in the bottom right of the figure. B: same as A but for the Amp13 condition. The left (darker orange) and right (lighter orange) target and their least-square fit lines are shown. Other conventions are same as in A. C: bar plot showing the mean ± SE of the intercepts across the population for the 2 amplitude conditions. The mean ± SE of the intercepts for each subject which is significantly different from 0 (filled circle and cross-hairs) and not significant (unfilled circle and cross-hairs) are also shown. ***P < 0.001.

Taken together, the previous analyses clearly demonstrate that saccade velocity was correlated to changes in hand velocity. We leveraged this modulation to test the applicability of Fitts’ law for saccades. To obtain a suitable measure to compare slow and fast trials, we also recorded the eye and hand movements of 16 of the original participants while they performed the same pointing task under normal hand velocities. In the succeeding sections, we contrast the speed-accuracy tradeoff results for saccades and hand movements in the three velocity conditions.

Confirming Fitts’s Law for Hand Movements

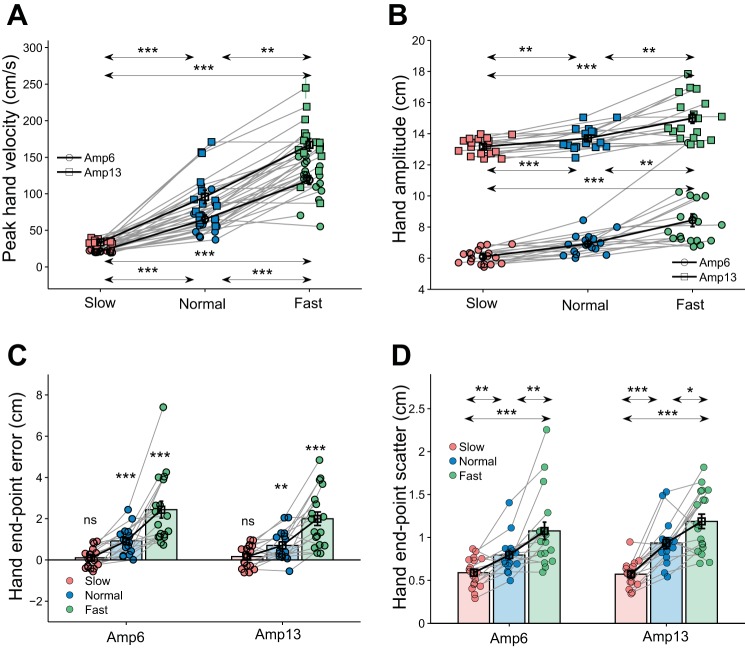
A two-way repeated-measures ANOVA showed a significant main effect of velocity condition [F(2,30) = 112.4, P < 0.001, η² = 0.99] on peak hand velocity, suggesting that subjects performed the (velocity, normal velocity, and modified velocity) task as instructed. The peak hand velocity in normal trials was intermediate between slow and fast movements (Fig. 4A; mean peak hand velocity; Amp6: Slow = 21 ± 2 cm/s, Normal = 65 ± 24 cm/s, Fast = 119 ± 26 cm/s; Amp13: Slow = 33 ± 3 cm/s, Normal = 96 ± 36 cm/s, Fast = 167 ± 36 cm/s). The mean peak hand velocity in the normal trials was significantly greater than that in the slow trials [Amp6: t(15) = 7.5, P < 0.001, d = 2.7; Amp13: t(15) = 6.8, P < 0.001, d = 2.5; both P values were less than the Bonferroni-corrected α of 0.017] and significantly less than that in the fast trials [Amp6: t(15) = 7.4, P < 0.001, d = 2.2; Amp13: t(15) = 8.2, P < 0.001, d = 2.0; both P values were less than the Bonferroni-corrected α of 0.017] in both the amplitude conditions. Not surprisingly, a two-way repeated-measures ANOVA showed a significant main effect of velocity condition [F(2,30) = 28.3, P < 0.001, η² = 0.65] on hand amplitude. The hand amplitude in the normal trials (mean hand amplitude: Amp6: Slow = 6 ± 0.5 cm, Normal = 6.9 ± 0.7 cm, Fast = 8.4 ± 1.7 cm; Amp13: Slow = 13.2 ± 0.5 cm, Normal = 13.7 ± 0.7 cm, Fast = 15.0 ± 1.4 cm) was intermediate between the slow and fast trials (Fig. 4B). In the Amp6 condition, the hand amplitude in the normal trials was significantly greater than that in the slow trials [t(15) = 5.2, P < 0.001, d = 1.4] and was lower than that in the fast trials [t(15) = 4.1, P < 0.001, d = 1.1]. In the Amp13 condition, the hand amplitude in the normal trials was significantly greater than that in the slow trials [t(15) = 3.1, P = 0.008, d = 0.8] but was significantly less than that in the fast trials [t(15) = 4.3, P < 0.001, d = 1.1]. These results suggest that subjects voluntarily modulated their hand velocity as instructed.

Fig. 4.

Hand endpoint accuracy in the 3 velocity conditions. A: comparison of the peak hand velocity across the 3 velocity conditions. Each dot and cross-hair represents the mean ± SE of peak hand velocity for each subject for slow (red), normal (blue), and fast (green) trials, for the Amp6 (circles) and Amp 13 (squares) conditions. The population mean ± SE is indicated with black unfilled circles and cross-hairs (for Amp6) and black unfilled squares and cross-hairs (for Amp13). The arrows between different groups at the bottom are for the Amp6 condition. B: comparison of hand amplitude across the 3 velocity conditions. The marking conventions are the same as in A. C: comparison of hand endpoint error between the 3 velocity conditions in the Amp6 and Amp13 conditions. Each dot represents a subject (red, slow; blue, normal; green, fast), while the bar and cross-hair represents the mean ± SE across the population. D: comparison of hand endpoint scatter between the 3 velocity conditions in the Amp6 and Amp13 conditions. Other marking conventions are the same as in C. Arrows show statistical comparisons between groups, indicated by the arrowheads. *P < 0.05 and P ≥ 0.01; **P < 0.01 and P ≥ 0.001; ***P < 0.001.

Based on Fitts’ law we speculated that hand endpoint accuracy should be maximum for slow movements and progressively decrease for normal and fast movements. As expected, a two-way repeated-measures ANOVA showed a significant main effect of velocity on both hand endpoint error [F(2,30) = 28.3, P < 0.001, η² = 0.65] and hand endpoint scatter [F(2,30) = 32.6, P < 0.001, η² = 0.68]. The hand endpoint error was greatest in the fast trials (mean hand endpoint error: Amp6 = 2.4 ± 1.7 cm; Amp13 = 2.0 ± 1.4 cm), followed by normal trials (mean hand endpoint error: Amp6 = 0.9 ± 0.7 cm; Amp13 = 0.7 ± 0.7 cm), with least error in the slow trials (mean hand endpoint error: Amp6 = 0.1 ± 0.5 cm; Amp13 = 0.2 ± 0.5 cm) (Fig. 4C). The hand endpoint error was not significantly different from 0 in the slow trials but was significant greater in both normal and fast trials in both amplitude conditions [Amp6: Slow: t(17) = 0.9, P = 0.380; Normal: t(15) = 5.4, P < 0.001; Fast: t(17) = 6.0, P < 0.001; Amp13: Slow: t(17) = 1.3, P = 0.213; Normal: t(15) = 3.8, P = 0.002; Fast: t(17) = 6.1, P < 0.001]. Similarly, hand endpoint scatter also followed the same trend, with highest endpoint scatter in the fast trials (mean hand endpoint scatter; Amp6: 1.1 ± 0.4 cm; Amp13: 1.2 ± 0.4 cm), followed by the normal trials (mean hand endpoint scatter; Amp6: 0.8 ± 0.2 cm; Amp13: 0.9 ± 0.3 cm), and lowest in the slow trials (mean hand endpoint scatter; Amp6: 0.6 ± 0.2 cm; Amp13: 0.6 ± 0.1 cm) as predicted by the Fitts’ law [Fig. 4D; Amp6: Slow vs. Normal: W = 9, P = 0.002, d = 1.0; Normal vs. Fast: W = 5, P = 0.001, d = 0.8; Slow vs. Fast: W = 1, P < 0.001, d = 1.5; Amp13: Slow vs. Normal: W = 1, P < 0.001, d = 1.7; Normal vs. Fast: W = 21, P = 0.015, d = 0.8; Slow vs. Fast: t(17) = 6.1, P < 0.001, d = 2.3; all P values were less than the Bonferroni-corrected α of 0.017]. Furthermore, a one-way repeated-measures ANOVA (as RT did not change with target amplitude, mean RT was calculated for each subject after combining both amplitudes together) showed that there was a significant main effect of velocity condition on hand RT [F(2,34) = 10.1, P < 0.001 η² = 0.43] and that hand RT was least in the normal trials compared with both slow and fast trials [mean hand RT; Slow = 353 ± 60 ms; Normal = 289 ± 27 ms; Fast = 343 ± 44 ms; Slow vs. Normal: t(15) = 3.8, P = 0.002, d = 1.4; Normal vs. Fast: t(15) = 4.0, P = 0.001, d = 1.5; Slow vs. Fast: t(15) = 0.9, P = 0.364, d = 0.2].

Testing Fitts’ Law for Saccades

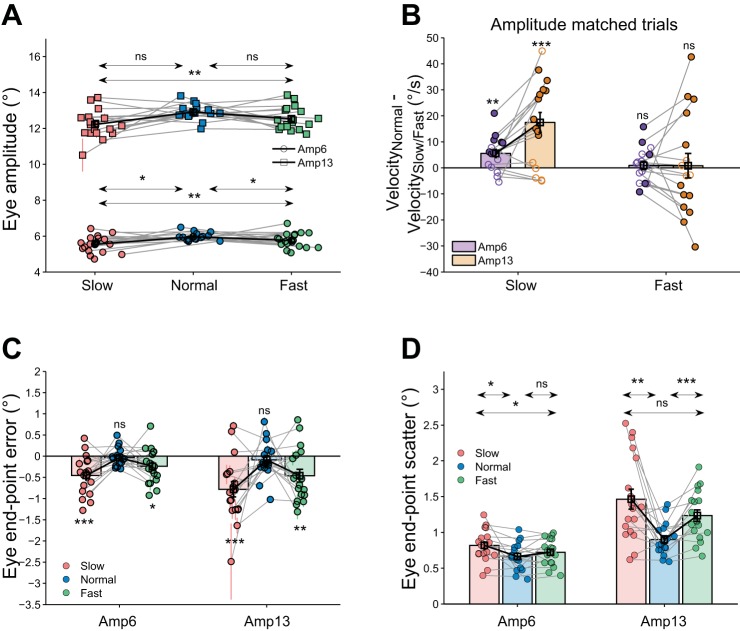
We then tested the applicability of Fitts’ law of speed/accuracy tradeoff for saccades (trials where the target was foveated with a single saccade) in the different velocity conditions. We first compared saccade amplitudes in the slow (mean eye amplitude; Amp6: 5.5 ± 0.5°; Amp13: 12.2 ± 0.8°), normal (mean eye amplitude; Amp6: 6.0 ± 0.2°; Amp13: 12.9 ± 0.4°), and fast trials (mean eye amplitude; Amp6: 5.8 ± 0.4°; Amp13: 12.5 ± 0.6°) (Fig. 5A). A two-way repeated-measures ANOVA showed that there was a significant effect of velocity condition on saccade amplitude [F(2,30) = 6.5, P = 0.005, η² = 0.30]. Thus, to compare the peak velocity of saccades accompanying slow, normal, and fast hand movements, we matched the amplitudes of saccades separately for slow and normal conditions, and for fast and normal conditions, for each subject. The difference between mean peak saccade velocity in slow trials and normal trials was significantly greater than 0 in 9/16 subjects in Amp6 [mean peak saccade velocity; Slow = 196 ± 20°/s; Normal = 202 ± 17°/s; difference = 6 ± 7°/s; t(15) = 3.4, P = 0.004, d = 0.3) and 10/16 subjects in Amp13 condition [mean peak saccade velocity; Slow = 310 ± 40°/s; Normal = 328 ± 35°/s; difference = 17 ± 16°/s; t(15) = 4.3, P < 0.001, d = 0.5; Fig. 5B]. A two-way repeated-measures ANOVA demonstrated a main effect of velocity condition [F(1,15) = 20.2, P < 0.001, η² = 0.57], showing that peak eye velocity in the slow condition was less than that observed in the saccades accompanying normal velocity hand movements. In contrast, when the saccade velocity in fast and normal conditions were compared, peak saccade velocity was either comparable (Amp6: 11/16 subjects, Amp13: 4/16 subjects) or less (Amp6: 2/16 subjects; Amp13: 7/16 subjects) or greater (Amp6: 3/16 subjects; Amp13: 5/16 subjects). The difference between the mean peak saccade velocity in the fast and normal conditions was not significantly different in both Amp6 [mean peak saccade velocity; Fast = 202 ± 18°/s, Normal = 203 ± 17°/s; difference = 1 ± 7°/s; t(15) = 0.5, P = 0.538, d = 0.1) and Amp13 [mean peak saccade velocity; Fast = 328 ± 35°/s; Normal = 329 ± 35°/s; difference = 1 ± 20°/s; t(15) = 0.2, P = 0.869, d = 0.02] conditions (Fig. 5B). A two-way repeated-measures ANOVA showed an insignificant main effect of velocity condition on peak saccade velocity [F(1,15) = 0.090, P = 0.768, η² = 0.006], suggesting that the peak saccade velocity is comparable between the normal and fast trials.

Fig. 5.

Eye endpoint accuracy in the 3 velocity conditions. A: comparison of eye endpoint amplitude across the slow (red), normal (blue), and fast (green) velocity conditions. Marking conventions are the same as 4B. B: difference between the peak saccade velocity in the normal trials and the slow/fast velocity condition. Each dot represents a subject (purple, Amp6; orange, Amp13), with the unfilled dots representing subjects with no significant difference between normal and the other velocity conditions. The bar and cross-hair represents the mean ± SE across the population. C: comparison of eye endpoint error between the 3 velocity conditions. Other marking conventions are same as in Fig. 4C. D: comparison of eye endpoint scatter across the 3 conditions. Other conventions are same as in Fig. 4D. *P < 0.05 and P ≥ 0.01; **P < 0.01 and P ≥ 0.001; ***P < 0.001; ns, not significant.

According to Fitts’ law, the saccade endpoint accuracy should be greatest for the slow trials (which had lowest saccade velocity) and decrease for the normal and fast hand trials. A two-way repeated-measures ANOVA showed significant effect of velocity condition on both eye endpoint error [F(2,30) = 6.5, P = 0.005, η² = 0.30] and scatter [F(2,30) = 11.0, P < 0.001, η² = 0.42]. However, contrary to the prediction of Fitts’ law, the eye endpoint error was highest in the slow condition, intermediate in the fast condition, and lowest in the normal trials (mean eye endpoint error; Amp6: Slow = −0.5 ± 0.5°; Normal = −0.04 ± 0.2°; Fast = −0.2 ± 0.4°; Amp13: Slow = −0.8 ± 0.8°; Normal = 0.1 ± 0.4°; Fast = −0.5 ± 0.6°) (Fig. 5C). The mean eye endpoint error was significantly less than 0 in both slow and fast trials but not in the normal trials [Amp6: Slow: t(17) = 4.2, P < 0.001; Normal: t(15) = 0.6, P = 0.539; Fast: t(17) = 2.4, P = 0.026; Amp13: Slow: t(17) = 4.3, P < 0.001; Normal: t(15) = 0.8, P = 0.437; Fast: t(17) = 3.1, P = 0.007]. Similarly, eye endpoint scatter was highest in the slow trials and lowest in the normal trials (Fig. 5D; mean eye endpoint scatter: Amp6: Slow = 0.8 ± 0.2°; Normal = 0.7 ± 0.2°; Fast = 0.7 ± 0.2°; Amp13: Slow = 1.4 ± 0.6°; Normal = 0.9 ± 0.2°; Fast = 1.2 ± 0.3°) [Amp6: Slow vs. Normal: t(15) = 2.8, P = 0.013, d = 0.7; Normal vs. Fast: t(11) = 1.3, P = 0.215, d = 0.3; Slow vs. Fast: t(15) = 2.7, P = 0.014, d = 0.5; Slow vs. Normal and Slow vs. Fast comparisons had P values less than the Bonferroni-corrected α of 0.017; Amp13: Slow vs. Normal: t(15) = 3.3, P = 0.005, d = 1.2; Normal vs. Fast: t(15) = 4.7, P < 0.001, d = 1.1; Slow vs. Fast: t(15) = 1.8, P = 0.094, d = 0.5; Slow vs. Normal eye endpoint scatter had a P value less than the Bonferroni-corrected α of 0.017].

Furthermore, a one-way repeated-measures ANOVA (as RT did not change with target amplitude, mean RT was calculated for each subject after combining both amplitudes together) showed that there was a significant main effect of velocity condition on eye RT [F(2,30) = 5.8, P = 0.009, η² = 0.27] and that eye RT tended to be lowest in the normal condition [mean eye RT; Slow = 214 ± 41 ms; Normal = 192 ± 37 ms; Fast = 208 ± 40 ms; Slow vs. Normal: t(15) = 2.6, P = 0.018; Normal vs. Fast: t(15) = 2.1, P = 0.054; Slow vs. Fast: t(15) = 1.4, P = 0.161; Slow vs. Normal eye RT tended to the Bonferroni-corrected α of 0.017]. Thus, not only was eye endpoint accuracy highest in the normal trials, the eye RT tended to be the least. This suggests that, in terms of speed-accuracy relations, normometric saccades were optimal (high velocity, lowest RT, and higher endpoint accuracy) compared with those in the slow and fast trials (Fig. 5).

Control of Endpoint Accuracy with Step-Saccade

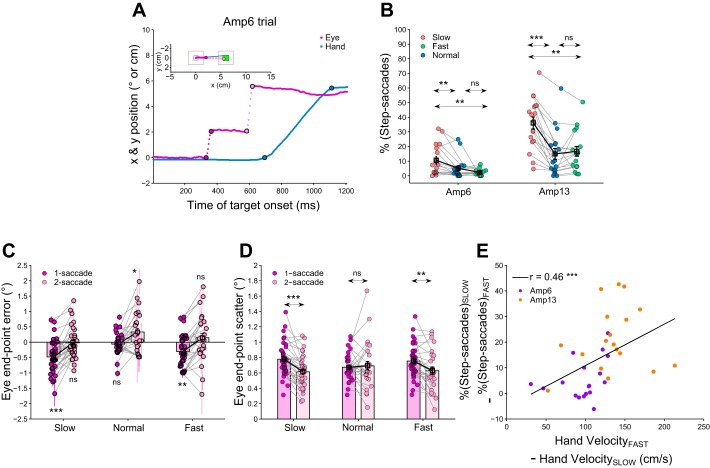
Saccades accompanying slow hand movements were least accurate and hence the most suboptimal. To understand whether and how the brain compensates for such suboptimal performance, we analyzed the saccades accompanying slow hand movement further. We observed that while subjects usually made one saccade to foveate the target before the hand movement ended, they sometimes reached the target with two saccades (Fig. 6A, example Amp6 trial from an exemplar subject), and rarely with three saccades (~1% trials). Since, three-saccade trials were rare and often not present in some subjects, we did not consider the three-saccade trials for the subsequent analyses.

Fig. 6.

Step-saccade trials. A: eye and hand displacement across time for an Amp6 trial in a representative subject. The maroon dots indicate eye displacements, while the blue dots indicate the hand displacements. Movement onsets and ends are demarcated using filled circles (maroon, first saccade, pink, second saccade; blue, first hand movement). Inset shows the eye and hand trajectories from the central fixation [white square at (0,0)] to the green peripheral target [green square at (6,0)]. The maroon dotted lines indicate the first saccade, the pink dotted line indicates the second saccade, and the blue dotted line indicates the first hand movement. The larger squares indicate the electronic windows (used for online monitoring and not visible to the subjects). B: comparison of percentage of occurrence of saccade breakage trials in the slow (red), normal (blue), and fast (green) conditions. Each dot represents a subject. The black unfilled squares and cross-hairs indicate the population mean ± SE. C: comparison of eye endpoint error between the 1-saccade (maroon) and 2-saccade (pink) trials. Each dot and cross-hair represent the mean ± SE of a subject. The bar and cross-hair represents the mean ± SE across the population. D: comparison of eye endpoint scatter between the 1-saccade and 2-saccade trials. Marking conventions are the same as in C. E: correlation between the modulation in hand velocity and the modulation in percentage of step-saccade trials between the slow and fast conditions. Each dot indicates a subject (purple, Amp6; orange, Amp13). The least squares fit is indicated as a black line. The correlation coefficient is indicated on the top left of the figure. *P < 0.05 and P ≥ 0.01; **P < 0.01 and P ≥ 0.001; ***P < 0.001.

To test whether step-saccade trials are related to the suboptimality of saccades we calculated the probability of occurrence of two-saccade trials for the three velocity conditions (Fig. 6B). A Kruskal-Wallis test showed that there was significant main effect of velocity condition on the probability of step-saccade trials in both Amp6 (χ² = 8.2, P = 0.017) and Amp13 (χ² = 14.0, P < 0.001) conditions. The probability of step-saccade trials was significantly greater in the slow condition [mean %(Step-saccades); Amp6 = 10.6 ± 10.3%; Amp13 = 36.1 ± 17.3%] compared with both normal [mean %(Step-saccades); Amp6 = 5.1 ± 7.1%; Amp13 = 14.9 ± 15.6%] and fast conditions [mean %(Step-saccades); Amp6 = 2.3 ± 2.2%; Amp13 = 16.7 ± 14.1%] (Amp6: Slow vs. Normal: W = 25, P = 0.008; Normal vs. Fast: W = 32, P = 0.376; Slow vs. Fast: W = 16, P = 0.007; Amp13: Slow vs. Normal: W = 0, P < 0.001; Normal vs. Fast: W = 38, P = 0.121; Slow vs. Fast: W = 7, P = 0.002). This implies that step-saccades may be a means of improving endpoint accuracy when the saccade was suboptimal, and hence most frequently observed in the slow condition.

We tested this hypothesis further and observed that in the slow and fast conditions, the final eye endpoint error in the two-saccade trials was not significantly different from 0 [mean final eye endpoint error; Slow: −0.02 ± 0.5°, t(32) = 0.42 P = 0.818; Fast: 0.1 ± 0.8°, t(24) = 0.9, P = 0.368], while the final eye endpoint error in one-saccade trials was significantly less than 0 [mean final eye endpoint error; Slow: −0.5 ± 0.5°, t(35) = 5.4, P < 0.001; Fast: −0.3 ± 0.5°, t(35) = 3.6, P = 0.001], suggesting that step-saccades might be a way of improving endpoint accuracy (Fig. 6C). In contrast, in the normal trials, the final eye endpoint error in the one-saccade trials was not significantly different from 0 [mean final eye endpoint error; −0.1 ± 0.4°, t(31) = 1.0, P = 0.319], while in the two-saccade trials the final eye endpoint error was significantly greater than 0 [mean final eye endpoint error; 0.3 ± 0.7°, t(24) = 2.5, P = 0.018], suggesting that normal saccades are accurate by default while step-saccades in the normal condition makes them overshoot the target (Fig. 6C).

Eye endpoint scatter also showed a similar trend with higher endpoint scatter in the one-saccade compared with the two-saccade trials in the slow [mean saccade endpoint scatter; one-saccade = 0.8 ± 0.2°, two-saccade = 0.6 ± 0.3°; t(32) = 6.5, P < 0.001, d = 0.8] and fast [mean saccade endpoint scatter; one-saccade = 0.8 ± 0.2°, two-saccade = 0.6 ± 0.3°; t(24) = 3.7, P = 0.001, d = 0.5] conditions, but not in the normal (mean saccade endpoint scatter; one-saccade = 0.7 ± 0.2°, two-saccade = 0.7 ± 0.3°; W = 141, P = 0.563, d = 0.1) condition (Fig. 6D). Furthermore, the probability of step-saccades in the slow trials was negatively correlated with the final saccade endpoint error (r = −0.35, P = 0.034) and scatter (r = −0.65, P < 0.001), suggesting that subjects who had a higher propensity of making step-saccades had greater endpoint accuracy. Taken together, these results validate the hypothesis that step-saccades improve endpoint accuracy in the slow and fast conditions when saccades are suboptimal.

To further quantify the relationship between step-saccades and hand velocity, we calculated an index of hand velocity modulation for a subject as the difference between the mean peak velocities of fast and slow hand movements. Similarly, we also calculated an index of step-saccade modulation for each subject as difference between the probabilities of step-saccade trials in the slow and fast hand trials (Fig. 6E). Interestingly, we observed a linear relationship (r = 0.46, P < 0.001) between hand velocity modulation and step-saccade modulation, indicating that step-saccade trials were influenced by hand velocity.

Interestingly, the pattern of step-saccades observed in our data was quite different from the typical pattern of saccadic responses. A typical saccadic response includes a primary saccade that covers 90% of target distance followed by a corrective saccade of 10%. However, in the slow trials, the first saccade of the step-saccade trials fell short by 46 ± 29% and 37 ± 24% of the target distance in the Amp6 and Amp13 conditions, respectively. In the fast trials, the first saccade fell short by 23 ± 32% and 33 ± 28% of the target distance in the Amp6 and Amp13 conditions, respectively, while in the normal trials, the first saccade fell short by 9 ± 24% (sometimes the first saccade overshot the target) and 13 ± 31% of the target distance in the Amp6 and Amp13 conditions, respectively. Thus, while step-saccade profiles in the normal velocity condition seem to be consistent with that typically reported in the literature, the saccades in the slow and fast conditions fell short by a much larger distance. This suggests that the step-saccades that we observed in the data were mechanistically different from the typical saccadic response and helped to increase the endpoint accuracy.

DISCUSSION

In contrast to hand movements, the relatively stereotypical trajectories of saccades have prevented a systematic exploration of speed-accuracy tradeoffs. In this study, we used the voluntary control of hand movement velocity and showed systematic modulations of kinematic profiles of saccades, which in turn allowed us to test the applicability of Fitts’ law to saccades. We observed that normative saccades are already optimized for endpoint accuracy and velocity of movement. The modulation of saccade kinematics by hand movements further suggests that some aspect of the kinematics maybe shared between the two effectors.

Modulation of Saccade Kinematics

Saccade kinematics are typically considered impervious to voluntary control (Bahill et al. 1975; Collewijn et al. 1988). However, studies have demonstrated that the main sequence gets modulated by conditions like light (Becker and Fuchs 1969; Sharpe et al. 1975), task conditions (Bronstein and Kennard 1987; Smit et al. 1987; Snyder et al. 2002; van Donkelaar et al. 2004; Zambarbieri et al. 1982), and reward (Takikawa et al. 2002). In these studies the physical attributes of the saccadic targets or the cognitive context of the task were varied. In contrast, in the present study, saccades were executed to the same visual targets, under the same cognitive context, suggesting that the modulation in peak velocity was driven by instructed hand velocity.

Two previous studies have also demonstrated the influence of hand movements on saccade velocity. Snyder et al. (2002) found that the peak velocity of the saccades accompanying hand movements was 4% higher compared with saccades executed in isolation, which is comparable to that observed here. Notably, unlike Snyder et al. (2002), subjects naturally coupled eye and hand movements without any explicit instructions to eye movements per se, making this study comparable to natural reaching behaviors that we execute in our daily lives. In another study, van Donkelaar et al. (2004) manipulated the kinetics of the hand movement while keeping the kinematics constant, and found that the peak saccade velocity increased when the force applied by the hand was greater. Although we have not disentangled the effect of hand kinetics and kinematics, in our study, faster hand movements would have required a greater force for execution, which according to van Donkelaar et al. (2004) should have increased peak saccade velocity. In contrast, we observed that peak saccade velocity during the fast and the normal hand movements were comparable, while peak saccade velocity decreased when accompanied by a slow hand movement. Interestingly, these differences suggest that kinematic modulation maybe distinct from dynamic modulation. A similar dichotomy between kinematic and dynamic representations have been reported in the context of motor learning as well (Krakauer et al. 1999).

The increased peak saccade velocity in the fast condition could potentially also be attributed to increased saccade amplitude due to the influence of greater hand amplitude. A number of studies have demonstrated that hand amplitude is modulated by the instructed change in eye amplitude (Bekkering et al. 1995; de Graaf et al. 1995; de Grave et al. 2006; Van Donkelaar et al. 2000). Here we observed the converse—that the change in hand amplitude is reflected in a change in saccade amplitude as well—which has not been reported before. However, the modulation in peak saccade velocity could not be ascribed to increased saccade amplitude in the fast hand velocity condition as we observed increased peak saccade velocity even after factoring out the effect of increased amplitude. Additionally, most saccades observed here were executed before the hand movement onset as described in earlier studies (Biguer et al. 1984; de Boer et al. 2013; Lünenburger et al. 2000; Prablanc et al. 1979; Sailer et al. 2000). Hence, the modulation in peak saccade velocity could not be attributed to the online feedback from the hand. Instead, our data suggests a sharing of the kinematic plan between the two effectors that enables the modulation of peak and average saccade velocity based on hand velocity before the initiation of the hand movement. This idea is also consistent with the finding that eye system possesses an efference copy of the hand motor plan (Ariff et al. 2002).

Optimality of Normometric Saccades

Saccade velocity varies widely across healthy people but is highly consistent within the same person. Between subject differences in saccade peak velocity do not appear to be associated with different endpoint accuracy (Choi et al. 2014), i.e., people who have fast saccades are not less accurate. Here, we have shown that within the same subject saccades slowed down when accompanied by a slow hand movement and the endpoint accuracy was also lower. We also observed that peak velocity of saccades executed in conjunction with normal and fast hand movements were surprisingly similar. Having high saccade velocity might be of evolutionary advantage as it brings the object of interest onto the fovea quickly (Clark and Stark 1975; Enderle and Wolfe 1987). However, greater velocity comes with the added disadvantage of decreased accuracy in the presence of signal-dependent noise (Harris and Wolpert 1998; van Beers et al. 2004). In contrast to the expectation of speed-accuracy tradeoff (Fitts 1954), saccades were both fast and accurate in the normal condition compared with slow and fast conditions. This suggests that normometric saccades are already optimal for speed as well as accuracy and may not be amenable to further increase. Such counterintuitive results have also been reported by Takikawa et al. (2002), who observed that saccades were both accurate and fast when made to rewarded locations.

These results also support the idea that the main sequence relationship may exist so as to optimize speed-accuracy tradeoff (Harris and Wolpert 2006; Shadmehr et al. 2010). In the studies of Harris and Wolpert, simulations of a control signal having signal-dependent noise assumed a fixed duration of saccades, and the kinematics of saccades that resulted were optimal in that they minimized endpoint accuracy. Since they did not vary durations of the saccade in their simulations it is not clear what the predictions would be for slow vs. fast saccades. However, according to their model slower saccades would be expected to have a smaller control signal and therefore a smaller endpoint variance (in accordance with Fitts' law). Thus our finding is at odds with their model. However, in the work of van Beers, the Harris and Wolpert model was extended to include a noise term that was a function of duration and is expected to decrease accuracy for longer duration saccades. However, since the signal-dependent noise term is also expected to reduce for long-duration saccades, the combined effect of both the noise terms on speed accuracy tradeoff is unspecified. Nevertheless, our empirical observation that slower saccades are less accurate than normal saccades (in violation of Fitts' law) indicates that normometric saccades are optimal to begin with. A corollary of optimality of normometric saccades may be that even small deviations of 5% from the optimal peak saccade velocity manifests as a significant decrease in saccade endpoint accuracy, as observed here.

Previous modeling studies have also proposed the existence of an optimal controller (Enderle and Wolfe 1987; Goossens and van Opstal 2012; Todorov 2004; Todorov and Jordan 2002) that plays a major role in the execution of saccades by maintaining the main sequence relationship. Here we have shown that the deviation from the normal main sequence relationship resulted in lower endpoint accuracy. Despite providing sufficient time (1.5 s) to plan the upcoming movement velocity, the optimal controller was ostensibly not able to adapt to the requirement of the task. This suggests that the controller is likely to be hardwired and less adaptable to task-specific requirements. To compensate for the inflexible nature of the controller other corrective mechanisms like step-saccades may help improve endpoint accuracy.

Step-Saccade Trials

Step-saccades were an additional manifestation of altered saccade kinematics due to the influence of hand kinematics. A saccade undershoot of ~10% has been reported previously (Collewijn et al. 1988; Harris 1995; Kapoula and Robinson 1986; Robinson 1973) and has been attributed to factors like maintaining the target representation in the same cerebral hemisphere (Robinson 1973), energy minimization (Becker 1989), a “lazy” strategy where peripheral vision is used to gather information about the target without actually reaching the target (Kapoula and Robinson 1986), and flight time minimization (Harris 1995). However, to the best of our knowledge, no study has analyzed the metrics of undershot saccades accompanying hand movements. Interestingly, the patterns of saccade breakage observed in the slow and fast conditions were quite distinct from the 10% saccade undershoot reported by previous studies and also observed in the normal velocity condition. More interestingly, the prevalence of saccade breakage was more during the slow hand movement condition, reiterating our suggestion that there is shared kinematic planning between the two effectors. This kinematic cross talk between the two systems may enable the breaking of saccades even though it was executed before the initiation of the hand movement and increase the saccadic endpoint accuracy during slow and fast conditions.

Step-saccades may be construed as a different strategy employed by the subjects to accomplish the slow velocity trials. For example, one could imagine that saccades in the slow condition tracked the hand movements instead of being executed to the target directly, resulting in step-saccades. Examples of such saccades can be seen in Ariff et al. (2002) (where subjects were instructed to look where they thought their hand was; see Fig. 1, C and D), and in the literature describing gaze anchoring (Neggers and Bekkering 2000, 2001) and in Reina and Schwartz (2003). In typical hand-tracking saccades, the second saccade does not start till the hand reaches the first saccade endpoint. In contrast, in our data set the second saccade often started long before the hand reached the first saccade amplitude. This time difference in the slow trials was less than 0 in both Amp6 [mean = −75 ± 147 ms; t(16) = 2.1, P = 0.051] and Amp13 [mean = −159 ± 126 ms; t(17) = 5.3, P < 0.001] conditions, suggesting that the step-saccade trials in the slow condition may not be due to hand tracking.

Although it is difficult to conclusively prove that subjects did not change their strategy between the different velocity conditions, the data suggests that they did not. First, less than 30% of the slow trials had step-saccades while the majority of trials were suboptimal one-saccade trials. Presumably, a different strategy if implemented should be applicable to the majority of the trials and not just to a minority of trials. Second, we have shown that subjects who had a greater propensity of making step-saccades were more accurate validating our hypothesis that step-saccades may be a corrective measure to improve endpoint accuracy. Last but not the least, Fitts’ law is a principle followed by different effectors performing a variety of tasks engaging different strategies. Hence, this law should have been applicable to the slow condition irrespective of the strategy used to accomplish the task. Even if slow trials engage a different strategy, our result regarding the violation of the Fitts’ law holds true.

Neural Substrates for Eye-Hand Kinematic Modulation

Edelman and Goldberg (2001) demonstrated that neurons in the superior colliculus (SC) fired at a higher level during the perisaccadic period when saccades were made to visible targets compared with lower velocity memory-guided or anti-saccades, implicating the role of SC in influencing saccade velocity. In agreement with Snyder et al. (2002), we believe the interaction between eye and hand peak velocity may involve the SC for several reasons. First, there are neurons in the deep layers of SC that are modulated by accompanying hand movements (Philipp and Hoffmann 2014; Stuphorn et al. 2000). Second, inactivation of the SC leads to deficit in hand target selection (Song et al. 2011). Third, SC has been implicated in eye-hand coordination (Lünenburger et al. 2001). Finally, there exists an anatomical connection between SC and dorsal premotor and motor cortex (Fries 1984, 1985) which is modulated by the velocity of the upcoming hand movement (Churchland et al. 2006; Moran and Schwartz 1999). Thus information regarding the velocity of the hand movement could be accessible to the saccadic system in the SC, which may modulate the gains of the saccadic burst generators (Katnani et al. 2012), resulting in a lower peak velocity of the ensuing saccade. Taken together, our data suggest that optimized speed-accuracy tradeoff may be implemented in the SC, as proposed in a model by Goossens and van Opstal (2012).

GRANTS

The study was supported by grants from the Department of Science and Technology (IRPHA), Government of India and a DBT-IISc partnership program grant and a Department of Biotechnology grant to A. Murthy. S. Jana was supported by a fellowship from the Council of Scientific and Industrial Research, India and the Indian Institute of Science. A. Gopal was supported by a fellowship from National Brain Research Centre, India.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.G, S.J., and A.M. conceived and designed the experiments; A.G. and S.J. performed the experiments and analyzed the data; A.G., S.J., and A.M. interpreted the results of the experiments; A.G. and S.J. prepared the figures and drafted the manuscript; A.G., S.J., and A.M. edited, revised, and approved the final version of the manuscript.