Semiparametric regression on cumulative incidence function with interval-censored competing risks data

Abstract

Many biomedical and clinical studies with time-to-event outcomes involve competing risks data. These data are frequently subject to interval censoring. This means that the failure time is not precisely observed, but is only known to lie between two observation times such as clinical visits in a cohort study. Not taking into account the interval censoring may result in biased estimation of the cause-specific cumulative incidence function, an important quantity in the competing risk framework, used for evaluating interventions in populations, for studying the prognosis of various diseases and for prediction and implementation science purposes. In this work we consider the class of semiparametric generalized odds-rate transformation models in the context of sieve maximum likelihood estimation based on B-splines. This large class of models includes both the proportional odds and the proportional subdistribution hazard models (i.e., the Fine-Gray model) as special cases. The estimator for the regression parameter is shown to be semiparametrically efficient and asymptotically normal. Simulation studies suggest that the method performs well even with small sample sizes. As an illustration we use the proposed method to analyze data from HIV-infected individuals obtained from a large cohort study in sub-Saharan Africa. We also provide the R function ciregic that implements the proposed method and present an illustrative example.

1. Introduction

Many biomedical studies with time-to-event outcomes involve competing risk data. The basic identifiable quantities from such data, are the cause-specific hazard and the cause-specific cumulative incidence function. The latter quantity plays a key role in the evaluation of interventions on populations, in studying the prognosis of various diseases, and in prediction. Prediction in turn, is especially useful in quality of life studies and for general implementation science purposes. Frequently, competing risks data are subject to interval censoring, that is, the times to the occurrence of an event are only known to lie between two observation times. An important example of interval-censored competing risk data, and the motivation for the present paper, comes from studies in HIV care and treatment programs. Individuals living with HIV who receive care in these programs may die while in care or become lost to care. Patients not retained in care are less likely to receive antiviral treatment (ART) and, frequently, any other clinical services. They are thus more likely to experience adverse clinical outcomes including death and viral rebound. The resulting increased infectivity of these patients may in addition significantly contribute to further expansion of the HIV epidemic in their communities. Identifying factors associated with mortality while in care and loss to care is useful for optimizing interventions, especially in sub-Saharan Africa, the region most affected by the HIV epidemic and the locus of the present study.

In many cases in this context, when a death has occurred, the corresponding death date is known to be between the date the death was reported and the last clinic visit of the deceased patient. Also, since loss to care is defined as no clinic visits for a certain period (e.g., three months from the last observed clinic visit or for the maximum period that a patient may have adequate medication supplies), the actual date of disengagement from care (being alive but not receiving anti-HIV care) is unknown. Consequently, studies in this context involve interval-censored competing risk data where death and loss to care are competing events. This research was motivated from studies in this setting and the fact that the issue of interval censoring in this context has, to our knowledge, been largely ignored in the literature.

Both nonparametric and fully parametric approaches have been proposed to estimate the cause-specific cumulative incidence function with interval-censored competing risk data. For example, Hudgens et al. [1] proposed a nonparametric maximum likelihood estimator for the cause-specific cumulative incidence under interval censoring. More recently, a parametric estimation method for the cause-specific cumulative incidence under a Gompertz distribution assumption was developed by Hudgens et al. [2]. These methods however do not consider covariates. To incorporate covariate information into a regression setting, fully parametric likelihood methods for the cause-specific cumulative incidence can be modified to deal with interval-censored competing risk data. For example, Jeong and Fine [3] proposed a parametric maximum likelihood approach along with a generalized odds-rate transformation [4] to model the cause-specific cumulative incidence under the Gompertz distribution. On the other hand, Cheng [5] proposed a three-parameter modified logistic model, while Shi et al. [6] considered a parametric method for explicitly modeling the cause-specific cumulative incidence of the cause of interest based on the generalized odds-rate transformation [4] and the modified three-parameter logistic function proposed by Cheng [5].

A key limitation of the fully parametric methods is that they make strong distributional assumptions about the true cause-specific cumulative incidence functions. Additionally, using more flexible three-parameter distributions may be challenging computationally and may lead to non-convergence problems as in univariate survival analysis, as cautioned by Lambert et al. [7] for example. A general approach to overcome the limitations of the fully parametric methods is to consider a semiparametric model. This approach was used successfully by Zhang et al. [8] for the Cox model with interval-censored (univariate) survival data. The authors used a sieve maximum likelihood estimation methodology [9] along with monotone B-splines to approximate the baseline hazard of the Cox proportional hazards model. Recently, Li [10] used the estimation approach by Zhang et al. [8] to the problem of semiparametric regression of the cumulative incidence function with interval-censored competing risk data under the proportional subdistribution hazards or the Fine-Gray model [11]. However, the assumption of proportional subdistribution hazards may not be correct and also the resulting parameter estimates are somewhat difficult to interpret as reported by Fine [12]. As we show in the illustration of our proposed methodology, using a proportional subdistribution hazard model for both competing risks did not provide a good fit to the data in our motivating HIV study compared to other models which better fit these data. Consequently, considering a more general class of semiparametric models for the cumulative incidence function, which also includes models which are easily interpretable by practitioners, such as, for example, the proportional odds model [12, 13], has important practical implications.

The main goal of this paper is to extend the B-spline sieve maximum likelihood estimator for interval-censored data used by [8] and [10], to the class of semiparametric generalized odds rate transformation models for the cause-specific cumulative incidence function and evaluate its asymptotic and finite sample properties. The large class of the generalized odds rate transformation models includes both the proportional odds model and the proportional subdistribution hazards model (i.e., the Fine-Gray model) [11] as special cases. Additionally, we explicitly incorporate the boundedness constraint of the cumulative incidence functions during the likelihood maximization. This is not the case with many existing methods for right-censored competing risk data that analyze each cause of failure separately and which can produce cumulative incidence estimates having a sum, over all possible causes of failure, which is greater than 1. For example, in the illustration presented by Choi and Huang [14], the analysis based on the Fine-Gray model [11] produced cumulative incidence estimates that added to 1.29. This may indicate a model misspecification and may adversely influence the validity of any predictions based on these estimates. The boundedness constraint was not considered by Li [10]. Finally, we develop and illustrate the R function ciregicthat easily implements the proposed estimation methodology for general interval-censored competing risks data.

We show that the B-spline sieve maximum likelihood estimator for the regression (Euclidean) parameter is shown to be semiparametrically efficient and asymptotically normal. We also demonstrate that the estimator for the functional parameter (baseline cause-specific cumulative incidence functions) converges at the optimal rate for nonparametric regression, which is nevertheless slower than the usual parametric $\sqrt{n}$ rate. Simulation studies suggest that the method performs well even with small sample sizes. We illustrate our methods by considering a number of candidate models like the proportional subdistribution and proportional odds model in the analysis of death and loss to care in the context of data from HIV care and treatment programs. Finally, we conclude this manuscript with a discussion, while examples on how to use the R function ciregiccreated to fit these models and asymptotic theory proofs are reserved for the Appendix.

2. Data and method

We assume the existence of a finite number k of competing risks. The cause of failure is denoted by C, the actual failure time is denoted by T, whereas (U₁, …, U_m) denote the m ∈ (0, ∞) distinct observation times. Observation times could be clinical visits, laboratory tests and all other occasions where the sampling unit (e.g., a patient) is actually observed. The number of observation times m may differ from subject to subject. To facilitate our further discussion let V ∈ {0, U₁, …, U_m} correspond to the last observation time prior to the failure and U ∈ {U₁, …, U_m, ∞} the first observation time after the failure. Using this notation a left-censored observation will correspond to (V, U) = (0, U₁), while a right-censored observation to (V, U) = (U_m, ∞). For j = 1, …, k, if a subject fails from the j-th cause of failure before the first observation time U₁ (i.e. it is left-censored), we observe ${\delta }_j^1=1$. If he/she fails between V > U₁ and U ≤ U_m, we observe δ_j = 1. But if he/she is right-censored (i.e. T > U_m), then we observe $\delta ={\sum }_{j=1}^k({\delta }_j+{\delta }_j^1)=0$. We assume the observation interval to be [a, b], that is a = U₁ < U_m = b. Along with the C, V, U, ${\{{\delta }_j\}}_{j=1}^k$ and ${\{{\delta }_j^1\}}_{j=1}^k$, we also observe a vector of covariates Z ∈ ℝ^d, whose effects are the primary parameters of interest. We further assume the following two fundamental conditions:

• A1The observation times (U₁, …, U_m) are independent of (T, C) conditional on Z.
• A2The distribution of (U₁, …, U_m) does not contain the parameters that govern the distribution of (T, C) (non-informative interval censoring).

The cause-specific cumulative incidence function is defined as

$$F_j(t;z)=Pr(T\le t,C=j\mid Z=z),j=1,\dots ,k$$

and corresponds to the cumulative probability of failure from the j-th cause of failure in the presence of the remaining causes of failure, conditional on the covariates. Given the two assumptions above, the likelihood function in terms of the cause-specific cumulative incidence functions is

$$L(\theta ;D)\propto \prod _{i=1}^n\left\{\prod _{j=1}^k{[F_j(u_i;z_i,{\theta }_j)-F_j(v_i;z_i,{\theta }_j)]}^{{\delta }_{ij}}\right\}\left\{\prod _{j=1}^k{[F_j(v_i;z_i,{\theta }_j)]}^{{\delta }_{ij}^1}\right\}\times {\left[1-\sum _{j=1}^k{F}_j(u_i;z_i,{\theta }_j)\right]}^{1-{\delta }_i},$$ (1)

where $\theta ={({\theta }_1^{\prime },\dots ,{\theta }_k^{\prime })}^{\prime }$ is a parameter that includes, in our case, regression coefficients for the effect of the covariate vector Z on each cause-specific cumulative incidence function and unspecified functions of time. A natural choice for the model for F_j is the class of semiparametric transformation models [11, 3, 15]:

$$g_j[F_j(t;z)]={\varphi }_j(t)+{\beta }_j^{\prime }z,j=1,\dots ,k$$ (2)

where g_j is a known increasing cause-specific link function and ϕ_j is an unspecified, strictly increasing and invertible function of time. A special subset of the class of semiparametric transformation models is the class of the generalized odds rate transformation models [4, 16, 12, 3]:

$$g_j(F_j;{\alpha }_j)=\{\begin{array}{ll}log\left[\frac{{(1-F_j)}^{-{\alpha }_j}-1}{{\alpha }_j}\right]\hfill & \text{if}0<{\alpha }_j<\infty \hfill \\ log[-log(1-F_j)]\hfill & \text{if}{\alpha }_j=0\hfill \end{array}$$

for j = 1, …, k. The proportional odds model and the proportional subdistribution hazards model [11] are special cases of the generalized odds rate transformation with α_j = 1 and α_j = 0, respectively [3]. Note that the link functions for different causes of failure are allowed to be different. All authors considering general classes of models assume that the true link functions are known [16, 17, 12, 18] and we adopt this assumption in our present work as well. This is because estimating α is not always possible because not all models with unknown α are identifiable from the data as in the non-competing-risk setting [19]. Even when there is no non-identifiability issues, reliable estimation of α requires very large sample sizes [19, 18].

As in [8] and [10], we avoid imposing parametric assumptions on ϕ_j in (2) and thus the likelihood involves k infinite-dimensional or functional parameters. In general, maximization of the likelihood function with an infinite-dimensional parameter θ ∈ Θ over Θ may lead to inconsistent maximum likelihood estimates [9]. One approach to overcome this problem is to use sieve maximum likelihood estimation. A sieve [9] is a sequence {Θ_n}_n≥1 of parameter spaces that approximate in a certain sense the original parameter space Θ, with the approximation error tending to zero as n → ∞. A sieve maximum likelihood estimate is the estimate obtained by maximizing the likelihood function over Θ_n. Another practical advantage of using the sieve maximum likelihood approach is that it reduces the dimensionality of the optimization problem, and, thus, the computational burden, compared to a fully semiparametric likelihood approach [8]. This is because the dimension of Θ_n is significantly smaller (i.e., it involves fewer number of parameters to be estimated) compared to that of the full parameter space Θ in finite samples. The computational advantage of the sieve maximum likelihood approach compared to a fully semiparametric maximum likelihood approach for interval-censored survival data has been shown in the simulation study by Zhang et al. [8]. In our case, the sequence of approximating functional parameter spaces is chosen to be spaces of monotone (due to the monotonicity of the cumulative incidence function) B-spline functions as defined in [8], i.e.,

$${\mathcal{M}}_n({\gamma }_j,N_j,m_j)=\left\{\varphi :\varphi (t;{\gamma }_j)=\sum _{s=1}^{N_j+m_j}{\gamma }_{j,s}{B}_{s,m_j}(t),{\gamma }_j\in {ℝ}^{N_j+m_j+1},{\gamma }_{j,1}<\dots <{\gamma }_{j,N_j+m_j}\right\},$$

for j = 1, …, k, where N_j and m_j are the number of internal knots and the order of the B-spline for the j-th cause of failure, γ_j are the unknown control points and t ∈[a, b], with a and b being the minimum and maximum observation times in the study. The number of internal knots N_j increases with sample size and is selected to satisfy N_j ≈ n^ν such that max_1≤t≤Nj+1 (c_{t, j} − c_{t−1, j}) = O(n^−ν), where c_{t, j} is the place of the t-th knot for the j-th cause-specific cumulative incidence function. During the likelihood maximization we impose the monotonicity constraints

$${\gamma }_{j,s}<{\gamma }_{j,s+1},$$

for every s = 1, …, N_j + p_j and j = 1, …, k. Additionally, the constraint max

$$\underset{z}{max}\left\{\sum _{j=1}^k{F}_j(b;z,{\theta }_j)\right\}<1$$ (3)

is needed to ensure that the sum of the estimated cumulative incidence functions at the maximum follow-up time b is bounded above by 1, where the maximum is over all the observed covariate patterns.

Let the true parameter values be denoted by ${\theta }_0={({\beta }_0^{\prime },{\varphi }_0^{\prime })}^{\prime }$, where ${\beta }_0={({\beta }_{1,0}^{\prime },\dots ,{\beta }_{k,0}^{\prime })}^{\prime }$ and ϕ₀ = (ϕ_1,0, …, ϕ_k,0)′ and the corresponding estimator by ${\widehat{\theta }}_n={({\widehat{\beta }}_n^{\prime },{\widehat{\varphi }}_n^{\prime })}^{\prime }$, where ${\widehat{\beta }}_n={({\widehat{\beta }}_{1,n}^{\prime },\dots ,{\widehat{\beta }}_{k,n}^{\prime })}^{\prime }$ and ϕ̂_n = (ϕ̂_1,n, …, ϕ̂_k,n)′. Also, define the L₂-metric for the distance between two parameters θ₁ = (β^(1)′, ϕ^(1)′)′ and θ₂ = (β^(2)′, ϕ^(2)′)′ as

$$d({\theta }_1,{\theta }_2)={\left(\sum _{j=1}^k{\Vert {\beta }_j^{(1)}-{\beta }_j^{(2)}\Vert }^2+\sum _{j=1}^k{\Vert {\varphi }_j^{(1)}-{\varphi }_j^{(2)}\Vert }_{\mathrm{\Phi }}^2\right)}^{\frac{1}{2}},$$

where

$${\Vert {\varphi }_j^{(1)}-{\varphi }_j^{(2)}\Vert }_{\mathrm{\Phi }}^2=E{\left[{\varphi }_j^{(1)}(V)-{\varphi }_j^{(2)}(V)\right]}^2+E{\left[{\varphi }_j^{(1)}(U)-{\varphi }_j^{(2)}(U)\right]}^2,j=1,\dots ,k$$

and ||·|| denotes the Euclidean norm. Here we assume that each unspecified function ϕ_{0, j}(t), j = 1, …, k, is smooth in the sense that it has a bounded p-th derivative in [a, b] for p ≥ 1 and that the first derivative of ϕ_{0, j}(t) is strictly positive and continuous on [a, b], along with some other technical regularity conditions that are listed in the Appendix. Our regularity conditions are similar to those used in [8]. Given assumptions A1, A2 and regularity conditions C1–C6, it can be shown that

$$d({\widehat{\theta }}_n,{\theta }_0)\stackrel{p}{\to }0$$

if the number of internal knots N_j = O(n^ν) for all j = 1, …, k, where ν satisfies 1/[2(1 + p)]< ν < 1/(2p) (more details on the selection of the number of internal knots are presented in subsection 2.1). Therefore, the B-spline-based sieve maximum likelihood estimator is consistent. Additionally,

$$d({\widehat{\theta }}_n,{\theta }_0)=O_p\left\{n^{-min[p\nu ,(1-\nu )/2]}\right\}.$$

This implies that the convergence rate of the estimator for the functional parameters is slower that the usual $\sqrt{n}$ rate. This estimator achieves the optimal convergence rate for nonparametric regression estimators which is n^−p/(1+2p) when one chooses ν = 1/(1 + 2p) [8]. Finally,

$$\sqrt{n}({\widehat{\beta }}_n-{\beta }_0)\stackrel{d}{\to }N[0,I^{-1}({\beta }_0)],$$

which implies that the convergence rate of the estimator for the Euclidean parameter is $\sqrt{n}$. This also points to the efficiency of this estimator as the corresponding variance matrix attains the semiparametric efficiency bound I(β₀). The definition of the information matrix I(β₀) is provided in the Appendix. Since finding I(β₀) involves solving an integral equation with no explicit solution, estimation of I(β₀) by I(β̂_n) is not straightforward [8, 10]. Consequently, one could either use the approach by Zhang et al. [8] and Li [10] for standard error estimation or rely on the computationally simpler nonparametric bootstrap method. The validity of the bootstrap for the Euclidean parameter estimates in general semiparametric M-estimation problems has been verified by Cheng and Huang [20]. The above mentioned asymptotic properties are proved in the Appendix.

2.1. Practical implementation of the method

The proposed methodology can be easily implemented using our R function ciregic. An example on how to use this function is provided in the Appendix. In this subsection we discuss the three steps that are crucial for applying our methodology in practice. The first and third steps are automatically implemented using our ciregicfunction.

The first step to apply the methodology is to consider the number and the placement of the knots for the B-splines. As it was mentioned previously, to achieve the optimal nonparametric convergence rate for the functional parameters, one has to select the knots based on the smoothness of the underlying unspecified parameters ϕ_{0, j}(t), j = 1, …, k, as measured by the order p of the derivatives of these parameters that are bounded. However, this degree of smoothness will be unknown in practice. In this case, one can impose the weakest possible assumption that only the first derivative is bounded, i.e. p = 1, and proceed with setting ν = 1/(1 + 2p) = 1/3. Under this choice, the number of internal knots N_j has the order of n^1/3 and, therefore, N_j can be set equal to [n^1/3] which corresponds to the largest integer that is smaller than or equal to n^1/3. The price, however, for imposing the weakest possible assumption regarding the smoothness of the functional parameters is that the convergence rate of the estimator for the baseline cause-specific cumulative incidence function is n^1/3. This is the slowest achievable rate for this estimator using the B-spline-based sieve maximum likelihood approach. Based on our simulation study presented in the next Section, the performance of this approach is quite satisfactory even with small sample sizes. It has to be noted that this minimal assumption (i.e., p = 1) has been imposed in our R function ciregic. The placement of knots for the B-splines is an easier task since, due to the monotonicity constraints, these splines have better behavior compared to unconstrained B-splines and are less sensitive to the placement of the knots. Consequently, placing the knots at the quantiles of the empirical distribution of the observation times provides a reasonable and simple approach to knot placement.

Next, selecting the link function parameters is needed in cases where the true link functions are unknown a priori (as it is usually the case in practice). In this case, we propose, following [18], performing a grid search over a plausible combination of α₁, …, α_k values and selecting the combination with the largest maximized likelihood value. We must acknowledge however, that the additional uncertainty due to this type of model selection procedure is very difficult to estimate and this is still an open problem in the literature [19, 18]. For this reason we assumed in all theoretical derivations that the true link functions are a priori known.

The final step is to obtain the parameter estimates of the model by maximizing the likelihood function (1) through a constrained optimization algorithm. The monotonicity constraints are linear inequality constraints and they can be easily incorporated in the optimization by using for example the logarithmic barrier method. However, incorporating the boundedness costraint (3) is more challenging as this is a nonlinear inequality constraint. For the special case with k = 2 and α₁ = α₂ = 1, i.e. with two competing risks and logit link functions for both risks, the boundedness constraint is equivalent to a linear inequality constraint. In this special case the optimization can be performed using a constrained optimization package such as the R package constrOptim, which can handle linear inequality constraints through the logarithmic barrier method. If there are more than 2 competing risks or one needs to fit a wide variety of models under different combinations of α values, then an optimization algorithm that incorporates nonlinear inequality constraints is needed. In this case, the R package alabamaprovides a useful set of functions for optimization under both linear and nonlinear inequality constraints. Our ciregicfunction automatically imposes the monotonicity and boundedness constraints using the alabamapackage.

3. Simulation study

In order to evaluate the finite sample performance of our method, we performed a series of simulation experiments. We considered two causes of failure and two covariates, one binary (Z₁) and one continuous (Z₂), in the simulations. The covariates Z = (Z₁, Z₂)′ were generated from the Bernoulli distribution with probability of success 0.4 and from the standard normal distribution, respectively. The cumulative incidence for causes 1 and 2 were considered to have a proportional odds form:

$$F_j(t)=\frac{exp\left[{\varphi }_j(t)+{\beta }_j^{\prime }Z\right]}{1+exp\left[{\varphi }_j(t)+{\beta }_j^{\prime }Z\right]},j=1,2$$

where exp [ϕ₁(t)] = 0.4 [1 − exp(−0.6t)]/0.6 and exp [ϕ₂(t)] = 0.75 [1 − exp(−0.5t)]/0.5 following a Gompertz distribution [3]. The true values for the regression parameters were β₁ = (β₁₁, β₁₂)′ = (0.5, −0.3) and β₂ = (β₂₁, β₂₂)′ = (−0.5, 0.3).

Based on these models, we simulated the failure times and causes of failure. The first observation time U_1i (e.g. clinic visit) was simulated based on the exponential distribution with a hazard parameter equal to 3. Each one of the next observations were placed after time V from the previous observation, with V being generated based on the exponential distribution with a hazard parameter equal to 3, for a maximum period of 3 years. This choice led to an average time of four months between two consecutive observations. The number of simulated data sets was 1,000, with the sample size per data set ranging between 200, 350 and 500. The proposed methodology was applied in each data set using cubic B-splines, and the number of knots was set equal to the larger integer up to and including N^1/3, with N being the total number of distinct time points V_i and U_i for the non-right-censored observations, plus the number of right-censored observations. The knots were placed at the corresponding percentiles of the distribution of the observed times (V_i,U_i). The nonparametric bootstrap method was used for standard error estimation of the parameter of interest β, based on 50 bootstrap samples. More specifically, for each simulated dataset, 50 random samples of size n were drawn with replacement from the dataset, and then the model was fitted to each of these samples. The standard deviation of the corresponding 50 regression parameter estimates was the estimated standard error of β̂_n.

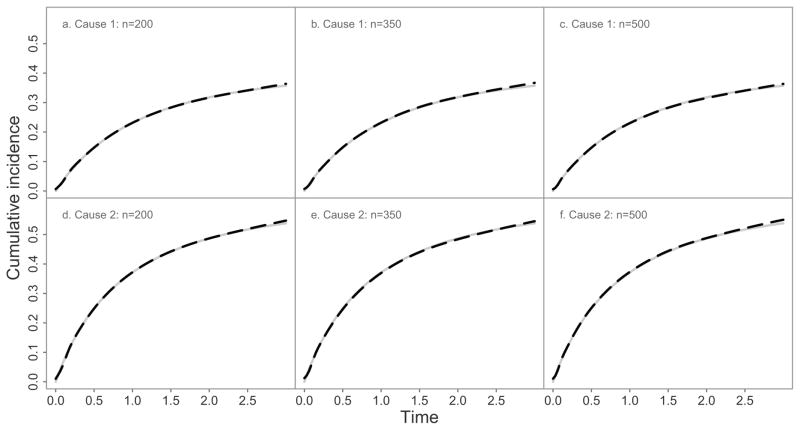
Simulation results regarding the baseline cumulative incidence functions are presented in Figure 1. Even with a sample size of 200, the average of the estimated baseline cumulative incidence functions were in close agreement with the corresponding true quantities. Regarding the regression parameter (Table 1), the method performs well, with the bias being very small and the empirical coverage probability staying close to the nominal 95% level in all cases.

Figure 1.

True (grey lines) and average estimated (black dashed lines) baseline cumulative incidence functions based on 1,000 simulation replications according to cause of failure and sample size n.

Table 1.

Simulation results regarding the Euclidean parameter β = (β₁₁, β₁₂, β₂₁, β₂₂)′ based on 1,000 replications. Bootstrap based on 50 bootstrap samples was used for standard error estimation.

n		β11	β12	β21	β22
200	% bias	−0.311	3.239	2.631	2.950
	MCSD	0.281	0.134	0.279	0.134
	ASE	0.275	0.133	0.273	0.133
	ECP	0.943	0.945	0.938	0.947
350	% bias	0.464	−0.037	2.626	0.085
	MCSD	0.196	0.095	0.191	0.095
	ASE	0.203	0.098	0.204	0.098
	ECP	0.952	0.941	0.955	0.941
500	% bias	−1.403	0.640	−0.137	0.622
	MCSD	0.169	0.082	0.171	0.082
	ASE	0.169	0.081	0.168	0.081
	ECP	0.945	0.940	0.946	0.938

MCSD: Monte Carlo standard deviation of the estimates;

ASE: Average standard error of the estimates;

ECP: Empirical coverage probability

4. Analysis of the HIV data

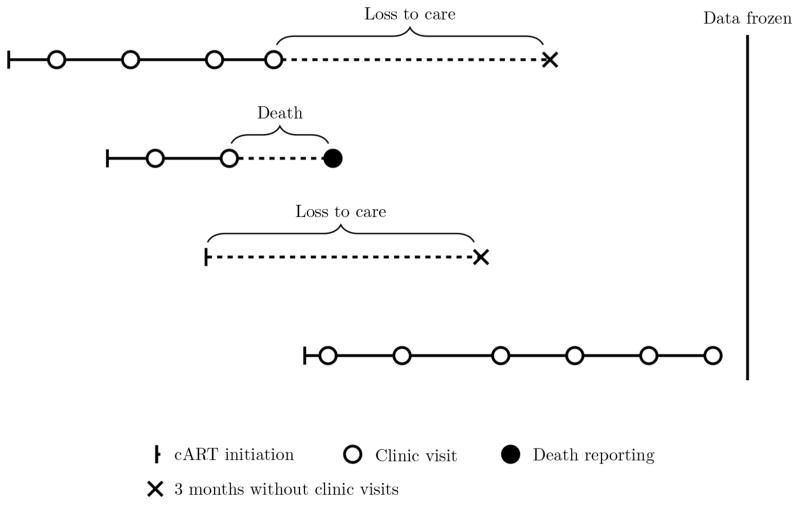
The methodology is applied to the evaluation of risk factors for the cause-specific cumulative incidence of being lost to care and of death while in care. Loss to care is a measure of patient non-retention in care, and thus is an extremely important measure for the success of any intervention program for the HIV/AIDS epidemic, since patients who have disengaged from HIV care do not receive antiretroviral treatment (ART) and thus have increased HIV-related mortality and morbidity, are more infectious and contribute to further expanding the HIV epidemic. The data came from the East Africa IeDEA (International Epidemiologic Databases to Evaluate AIDS) Regional Consortium, a network of HIV care and treatment programs in Kenya, Uganda and Tanzania. The working definition of loss to care was having no clinic visits for a 3-month period. This cutoff was chosen by the clinicians because typically patients on ART are expected to have run out of medication if they have not had a clinic visit within a 3-month period. A schema of typical patient temporal trajectories is presented in Figure 2. Based on this figure it is clear that neither loss to care nor death times are exactly known due to interval censoring. In the current analysis we included patients with a CD4 count of at least 100 cells/μl at ART initiation. Basic descriptive characteristics of the study sample are presented in Table 2.

Figure 2.

Example of four patients in a typical HIV care and treatment program.

Table 2.

Descriptive characteristics of the study sample.

	In HIV care (n=2,232) n (%)	LTC1 (n=690) n (%)	Death2 (n=131) n (%)
Gender
Male	681 (30.5)	207 (30.0)	62 (47.3)
Female	1,551 (69.5)	483 (70.0)	69 (52.7)
HIV status disclosed
No	763 (34.2)	279 (40.4)	57 (43.5)
Yes	1,469 (65.8)	411 (59.6)	74 (56.5)
	Median (IQR)	Median (IQR)	40.9 (35.0, 50.8)
Age3 (years)	37.1 (30.4, 44.9)	35.2 (28.6, 41.7)
CD43 (cells/μl)	199 (152, 276)	188 (140, 262)	163 (131, 213)

¹Loss to care

²While in HIV care

³At ART initiation

Similarly to the simulation study, we applied the proposed methodology using cubic B-splines and with the number of knots being equal to the larger integer up to and including N^1/3, with N being the total number of distinct time points V_i and U_i for the non-right-censored patients plus the number of right-censored patients. The knots were placed at the corresponding percentiles of the distribution of the observed times (V_i,U_i). The nonparametric bootstrap method was used for standard error estimation of the parameter of interest, based on 50 bootstrap samples, as described in the simulation study Section. The analysis was performed using our R function ciregicthat is illustrated in the Appendix.

In order to perform the analysis we needed to select the α = (α₁, α₂) parameter indexing the link functions for loss to care and death while in care. To do so we performed a grid search over all possible combinations of α₁ ∈ {0, 0.2, …, 10} and α₂ ∈ {0, 0.2, …, 10}. The maximum log-likelihood value (−3144.47) was achieved at the point α = (2, 1.2). The maximized log-likelihood value for the popular Fine-Gray proportional subdistribution hazards model for both competing risks (FGFG), i.e., α = (0, 0), was −3147.05. Consequently, the fit of the FGFG model is clearly not optimal. In order to illustrate our method for the Fine-Gray model and the proporitonal odds model, which are the most popular choices in practice, we also fitted a model which assumes a proportional subdistribution hazards model for loss to care and a proportional odds model for death (FGPO model). In this case α was set equal to (0, 1). The maximized log-likelihood for the FGPO model was −3146.91. The results of the analysis based on the FGPO and the optimal model are presented in Table 3.

Table 3.

Comparison between the results from the Fine-Gray – proportional odds model (FGPO) with α = (0, 1) and the optimal based on the grid search model with α = (2, 1.2)

Outcome	Covariate	α = (0, 1) mRR1/β̂(p-value)	α = (2, 1.2) β̂ (p-value)
A. Loss to care	Age at ART initiation
	per 10 years	0.7832/−0.244 (<0.001)	−0.348 (<0.001)
	Gender
	Male vs Female	1.1702/0.157 (0.031)	0.273 (0.005)
	CD4 at ART initiation
	per 100 cells/μl	1.0022/0.002 (0.947)	0.001 (0.976)
B. Death	Age at ART initiation
	per 10 years	1.3603/0.308 (<0.001)	0.329 (<0.001)
	Gender
	Male vs Female	1.7583/0.564 (0.008)	0.567 (0.008)
	CD4 at ART initiation
	per 100 cells/μl	0.6993/−0.358 (0.003)	−0.346 (0.006)

¹Measure of relative risk

²Subdistribution hazard ratio

³Odds ratio

Based on Table 3, lower age at ART initiation and male gender are associated with an increased cumulative incidence of loss to care. Specifically, the estimate associated with age implies that patients older by 10 years have 21.7% lower subdistribution hazard [11] of being lost to care (p-value<0.001). In addition, males have 17.0% higher subdistribution hazard of being lost to care compared to females (p-value=0.031). Also, there is no evidence for an association between CD4 count at ART initiation and the cumulative incidence of loss to care (p-value=0.947). Older age, male gender and lower CD4 count at ART initiation are strongly associated with an increased odds of death while in care. It is clear that the interpretability of the estimated regression parameter for death while in care as odds ratios is very desirable, especially for non-statistically inclined investigators. We also compared the results from the FGPO model with those from the optimal model based on the grid search with α = (2, 1.2). The estimated regression coefficients are presented in Table 3 as well. The results from the two analyses are qualitatively similar. However, the regression coefficient estimates for gender and age differ substantially between the two models for the loss to care outcome. As a comparison, we also performed a naïve analysis based on the midpoint imputation approach, under the optimal model with α = (2, 1.2). Using this approach, the unknown failure times are replaced by the midpoint between the two observation times that surround the true failure time, and then the data are analyzed as usual right-censored data. The estimate for the effect of CD4 on loss to care, based on the naïve analysis, was 10.9 times larger (0.011 versus 0.001) compared to the estimate from the proposed approach, although this effect was still not statistically significant. Additionally, the estimate of the effect of age on death was attenuated by 8.3% based on the naïve analysis compared to the estimate from the proposed method. However, this effect was still statistically significant. The difference between the rest estimates from the two approaches was less than 3.4%.

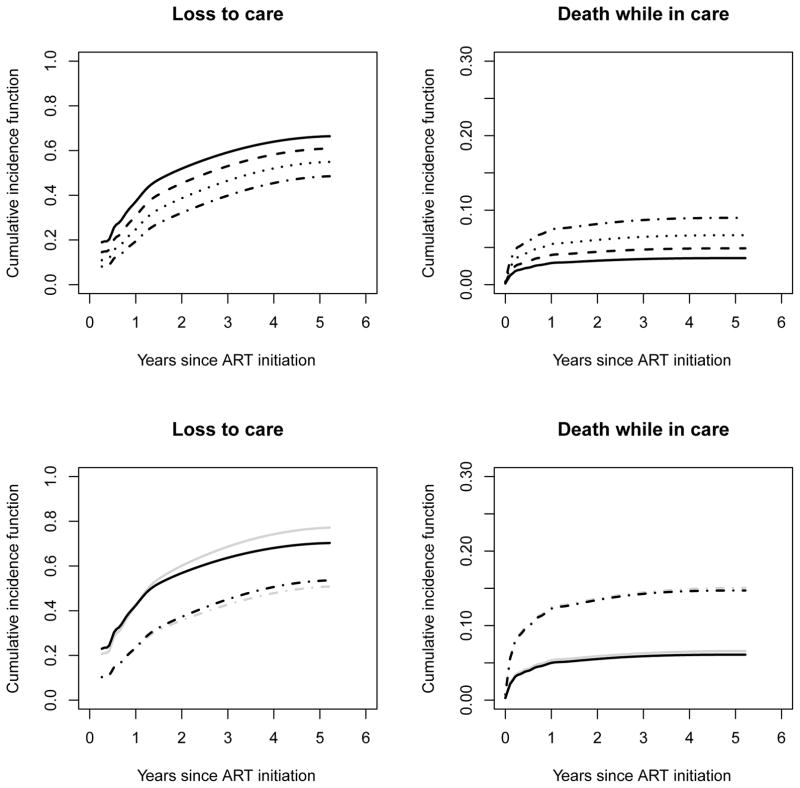
It is straightforward to derive predicted cause-specific cumulative incidence functions for specific patient subgroups. Figure 3 presents results of these quantities, based on the estimates from the optimal model, for a female patient with CD4 count at ART initiation of 120 cells/μl, by age at ART initiation. Such predictions are useful for evaluating program effectiveness and can also be used as inputs to mathematical models of cost-effectiveness analyses to identify the best strategy to optimize care in our setting. The comparison between the predictions from the optimal model and the FGPO model are presented in the bottom row of Figure 3. For the loss to care outcome, the predicted cumulative incidences for a 40-year old male patient with a CD4 count at ART initiation of 120 cells/μl from the two models differ substantially. More specifically, the difference between the two age groups is smaller after the first year based on the optimal model compared to the FGPO model. This provides some evidence for the violation of the proportional subdistribution hazards assumption of the Fine-Gray model. However, when considering the death outcome, the predicted cumulative incidences from the two models are quite close, and this is because the difference between the link function parameters in the two models is somewhat small (i.e., α₂ = 1.2 for the optimal model and α₂ = 1 for the FGPO model).

Figure 3.

Estimated cumulative incidence of loss to care (top left panel) and of death (top right panel) for a female patient with a CD4 count of 120 cells/μl at ART initiation, according to age at ART initiation (solid lines = 20 years; dashed lines = 30 years; dotted lines = 40 years; dashed-dotted lines = 50 years) based on the optimal model according to the grid search, with α = (2, 1.2), and estimated cumulative incidence of loss to care (bottom left panel) and of death (bottom right panel) for a male patient with a CD4 count of 120 cells/μl at ART initiation, according to age (solid lines = 20 years; dashed-dotted lines = 50 years), based on the optimal model (black lines) and the Fine-Gray – proportional odds model (gray lines) with α = (0, 1).

5. Discussion

In this paper we extended the work by Li [10] on semiparametric analysis of the proportional subdistribution hazards or the Fine-Gray model [11] for cumulative incidence incidence estimation with interval-censored competing risk data, to the class of the semiparametric generalized odds rate transformation models. This general class includes the proportional odds model [3, 6] and the proportional subdistribution hazards model as special cases. This extension is very important for medical and epidemiological applications when the proportional subdistribution hazards model does not provide good fit to the data, as was the case with our HIV data analysis. Unlike [10], we also explicitly incorporate the boundedness of the cause-specific cumulative incidence function constraint into the optimization, and we also provide and illustrate an R function called ciregic, that easily implements the proposed method.

We have showed that the B-spline sieve maximum likelihood estimator for the regression (Euclidean) parameter, under the class of the generalized odd rate transformation models is consistent, semiparametrically efficient and asymptotically normal. It was also shown that the estimator for the functional parameter (baseline cumulative incidence functions) is consistent in an L₂-metric and converges at the optimal rate for nonparametric regression which is nevertheless slower than the usual parametric $\sqrt{n}$ rate. This methodology is also applicable to the case of current status data [21, 22] since these data are special cases of interval-censored data [8]. It is straightforward to show that our results also hold for the more general class of semiparametric transformation models.

Throughout this paper we assumed that the true link functions are known as in [16, 17, 12, 18]. A practical issue regarding the application of the proposed method in practice is when this assumption is not true. To this end, and simiarly to Mao and Wang [18], we proposed performing a grid search over a plausible set of combinations of (α₁, …, α_k) and choosing the combination with the largest maximized likelihood value. This approach for selecting the proper link function parameter values was illustrated in an analysis of data from a large network of HIV care and treatment programs in sub-Saharan Africa. The issue of the additional variability due to this type of model selection is still an open problem and requires further investigation.

Our approach simultaneously estimates the models for all causes of failure in contrast to many semiparametric methods for right-censored competing risk data. Analysis of all the competing causes of failure is essential for a more complete understanding of the underlying competing risks process. However, this comes at the cost of specifying a model for every cause of failure and can increase the risk of model misspecification, even though our method is very flexible in terms of the baseline cumulative incidence functions and the link functions.

In general, fully parametric methods can be straightforwardly extended to the case of interval censoring, and have the advantage of being efficient. However, the validity of these methods relies on strong assumptions for each cause of failure and this limits their generality. One solution is to adopt more flexible 3-parameter distributions as in [5] and [6]. However, while these distributions are clearly less flexible than the B-spline approximations used in this paper, they may also be plagued by non-convergence issues such as in univariate survival analysis [7]. By contrast, when using our proposed methods, we did not face non-convergence problems in either in the simulations or the analysis of the HIV data. A disadvantage of our method, compared to parametric approaches, is that it does not provide estimates of the long term proportions for each cause of failure. Even though this is possible with parametric approaches as well [23, 3, 6, 2], care is needed when making extrapolations beyond the observable time interval as mentioned by Jeong and Fine [3].

In this paper, we did not consider the asymptotic distribution of the estimated baseline and covariate-specific cumulative incidence functions as the slower rate of convergence of this estimator make this task considerably difficult. However, evaluating the uncertainty of model-based predictions of the cumulative incidence is very useful from a clinical and implementation science perspective. Therefore, it would be useful to study the asymptotic properties of the estimated baseline and covariate-specific cumulative incidence functions and propose a method for the calculation of confidence intervals and simultaneous confidence bands. Additionally, the issue of quantifying the uncertainty due to the link function selection is another interesting and challenging issue for future research.

Appendix

The R function ciregic

The R function ciregic, which can be found in the online material of this manuscript, implements the methods proposed in this work. This function depends on the package alabama that performs optimization with both linear and nonlinear inequality constraints. Therefore, prior installation of this package is required in order to use the ciregic function. The first step is to install/define the ciregic function, which can be done by either running the script ciregic.R provided in the online material of this manuscript, or by storing it in the working folder and then using the command

source(“ciregic.R”)

In this illustration we use the HIV dataset that was analyzed in this manuscript. We load and list the first records of these data using the commands

The variables v and u are the lower and upper observation times V and U, respectively. These times correspond to years since ART initiation. The variable c is the cause of failure, where the loss to care event is coded as c=1, the death event as c=2, and the right-censoring as c=0. Note that the u values for the right-censored observations (i.e., c=0) are not included in any calculation. This is because in theory, U = ∞ for right-censored observations. Therefore, these times have been previously replaced with the lower observation times v plus 1 day as

data$u<-(data$v+1/365.25)*(data$c==0)+data$u*(data$c>0)

Performing the analysis that was presented in the HIV data example section based on the Fine-Gray model for loss to care and the proportional odds model for death, which correspond to α = (0, 1), requires the commands

In order to achieve reproducibility of the standard error estimates, as they are based on the bootstrap, we need to manually set a random seed as presented above. The first argument in the Surv2 function is the lower observation time V, the second is the upper observation time U, and the third is the cause of failure variable. The last variable should include 0 for right-censored observations, and 1 and 2 for causes of failure 1 and 2, respectively. Currently, we allow for only two competing risks, but we plan to extend this to three or more in the near future. The output presented above corresponds to the first column of Table 3. Note that in that table, the effects of age and CD4 count have been multiplied by 10 and 100, respectively, for interpretation purposes. The object fit.01 is a list that contains an output of the analysis in the first component, the regression parameter estimates and the corresponding variance-covariance matrix in the second and third components respectively, and the value of the maximized log-likelihood in the eighth component. Indication of successful convergence of the optimization algorithm is stored in the ninth component of fit.01. The components 4 to 7, include the estimated baseline cumulative incidence functions and some other elements that are useful for estimating the covariate- specific cumulative incidence function using our pred.cif function. The estimation with 50 bootstrap replications and a dataset of 3,053 observations required 11.65 minutes. We plan to optimize the computational efficiency of our function by utilizing multiple cores, and to upload it in CRAN as a package. Estimation of the optimal model for this analysis with α = (2, 1.2) can be performed using the command

set.seed(20835)
fit.opt<-ciregic(formula=Surv2(v, u, c)∼ male + age_art + cd4_art,
                         data=data, alpha=c(2,1.2), nboot=50)

Incorporation of an interaction effect between gender and age at ART initiation could be simply incoprorated as

fit.opt<-ciregic(formula=Surv2(v, u, c)∼ male*age_art + cd4_art,
                         data=data, alpha=c(2,1.2), nboot=50)

Estimation of the covariate-specific cumulative incidence function can be easily performed using the pred.cif function. The first argument in this function is the object containing the results from the model fit generated by the ciregic function, and the second the desired covariate pattern as a vector. For example, in order to estimate the cumulative incidence function of loss to care and death for a 20-year old female with a CD4 count of 120 cells/μl at ART initiation, we need the command

f20.01<-pred.cif(fit.01, covp=c(0,20,120))
head(f20.01)
##            t         cif1        cif2
## 1 0.00000000 4.996004e-15 0.001595043
## 2 0.05265523 7.882583e-15 0.007162271
## 3 0.10531046 5.606626e-14 0.012532213
## 4 0.15796569 1.477572e-07 0.015031502
## 5 0.21062092 4.201278e-02 0.017972113
## 6 0.26327615 1.896563e-01 0.019366670

The option covp should include the desired covariate values, in the same order as the listing order of the corresponding covariates in the right side of the formula argument in ciregic function. As in any other prediction problem, these covariate values should not be outside the observable range of covariate values in order to avoid extrapolation. The function pred.cif returns a data frame that includes times and the estimated cumulative incidence functions for both failure causes and for the desired covariate pattern. Plotting the object f20.01 in the example above (e.g., with the plot function) will provide the estimated cumulative incidences that are depicted in the second row of Figure 3 as solid grey lines.

Proof of consistency

Empirical process theory techniques will be applied to derive the consistency of the B-spline sieve maximum likelihood estimator. As usual P f = ∫_𝒳 f (x)d P(x) and ${\mathbb{P}}_{n}f=n^{-1}{\sum }_{i=1}^{n}f(X_i)$, which is the empirical process indexed by the function f evaluated at $X_i=(V_i,U_i,{\delta }_{i1},\dots ,{\delta }_{ik},{\delta }_{i1}^1,\dots ,{\delta }_{ik}^1,{\delta }_i,Z_i)$, the sample point of individual i, with 𝒳 denoting the sample space. Also, let C denote a general constant which may differ in different settings. The following regularity conditions are assumed

• C1E(Z Z′) is non-singular and Z is bounded, i.e. there exists a z₀ > 0 such that P(||Z|| ≤ z₀) = 1.
• C2β_j ∈ ℬ_j, where ℬ_j is a compact subset of ℝ^d for every j = 1, …, k.
• C3There exists an η > 0 such that P(U − V ≥ η) = 1 and the union of the supports of V and U are contained in [a, b], where 0 < a < b < ∞ and $0<{min}_{j\in \{1,\dots ,k\}}{F}_j(a)<{\sum }_{j=1}^k{F}_j(b)<1$.
• C4ϕ_{0, j} ∈ Φ, where Φ is a class of functions with bounded p-th derivative in [a, b] for p ≥ 1 and the first derivative of ϕ_{0, j} is strictly positive and continuous on [a, b]. This holds for all j = 1, …, k.
• C5The conditional density of (V,U) given Z has bounded partial derivatives with respect to (v, u) and the bounds of these derivatives do not depend on (v, u, z).
• C6For some κ ∈ (0, 1), a′Var(Z|V)a ≥ κa′E(ZZ′|V)a a.s. and a′Var(Z|U)a ≥ κ a′E(ZZ′|U)a a.s. for all α ∈ ℝ^d.

Let ℱ₁ = {l(θ; X): θ ∈ Θ_n} denote the class of log-likelihood functions indexed by the parameter space ${\mathrm{\Theta }}_n={\times }_{j=1}^k({\mathcal{B}}_j\times {\mathcal{M}}_{n,j})$. The Euclidean parameters are β_j ∈ ℬ_j and the functional parameters are ϕ_j ∈ℳ_{n, j}, for j = 1, …, k. The functional parameter space ℳ_{n, j} ≡ ℳ_n(γ_j, N_{n, j}, p_j) is the space of monotone B-spline functions defined on the observation time interval [a, b]. Convergence will be proved in the L₂-metric

$$d({\theta }_1,{\theta }_2)={\left(\sum _{j=1}^k{\Vert {\beta }_j^{(1)}-{\beta }_j^{(2)}\Vert }^2+\sum _{j=1}^k{\Vert {\varphi }_j^{(1)}-{\varphi }_j^{(2)}\Vert }_{\mathrm{\Phi }}^2\right)}^{\frac{1}{2}},$$

for θ₁ = (β⁽¹⁾′, ϕ⁽¹⁾′)′ and θ₂ = (β⁽²⁾′, ϕ⁽²⁾′)′, where

$${\Vert {{\varphi }_j^{(1)}}^{\prime }-{{\varphi }_j^{(2)}}^{\prime }\Vert }_{\mathrm{\Phi }}^2=E{\left[{{\varphi }_j^{(1)}}^{\prime }(V)-{{\varphi }_j^{(2)}}^{\prime }(V)\right]}^2+E{\left[{{\varphi }_j^{(1)}}^{\prime }(U)-{{\varphi }_j^{(2)}}^{\prime }(U)\right]}^2,j=1,\dots ,k.$$

Let 𝕄(θ) = Pl(θ; X) and 𝕄_n(θ) = ℙ_nl(θ; X), which leads to 𝕄_n(θ) − 𝕄(θ) = (ℙ_n − P)l(θ; X) for each θ ∈ Θ_n. In order to prove that $d({\widehat{\theta }}_n,{\theta }_0)\stackrel{p}{\to }0$ we need to verify the following conditions:

1. ${sup}_{\theta \in {\mathrm{\Theta }}_n}\mid {\mathbb{M}}_n(\theta )-\mathbb{M}(\theta )\mid \stackrel{p}{\to }0$

2. sup_{θ: d(θ, θ0)≥ε} 𝕄(θ) < 𝕄(θ₀)

3. The sequence of estimators θ̂_n satisfy 𝕄_n(θ̂_n) ≥ 𝕄_n(θ₀) − o_p(1)

It has been shown that there exists a set of brackets {[ ${\varphi }_{i,j}^L,{\varphi }_{i,j}^U$]: i = 1, …, (1/ε)^{Cq_{n, j}}}, where C is a constant and q_{n, j} = N_{n, j} + p _j + 1, with N_{n, j} and p _j being the number of internal knots and the degree of the B-spline for the j-th cause of failure, such that ${\mathbb{P}}_n\mid {\varphi }_{i,j}^U-{\varphi }_{i,j}^L\mid \le \epsilon$ and ${\varphi }_{i,j}^L(t)\le {\varphi }_j(t)\le {\varphi }_{i,j}^U(t)$ for any t ∈ [a, b] and i = 1, …, (1/ε)^{Cq_{n, j}} [9]. By condition C2, ℬ_j ⊂ ℝ^d is compact and thus it can be covered by C(1/ε)^d ε-balls, i.e. for any β ∈ ℬ_j there exists an s = 1, …,C(1/ε)^d such that β ∈ B(β_{s, j}) ≡ {b ∈ ℬ_j: |b − β_{s, j} | ≤ ε}. By condition C1 it follows that for any β ∈ ℬ_j and any z, ${\beta }^{\prime }z\in [{\beta }_{s,j}^{\prime }z-C\epsilon ,{\beta }_{s,j}^{\prime }z+C\epsilon ]$. Let ${\eta }_j(t,z)\equiv {\varphi }_j(t)+{\beta }_j^{\prime }z$. Then, for any j = 1, …, k we can construct a set of brackets{[ ${\eta }_{j,s,i}^L,{\eta }_{j,s,i}^U$]: i = 1, …, (1/ε) ^{Cq_{n, j}}; s = 1, …,C(1/ε)^d }, with ${\eta }_{j,s,i}^L(t,z)={\varphi }_{i,j}^L(t)+{\beta }_{s,j}^{\prime }z-C\epsilon$ and ${\eta }_{j,s,i}^U(t,z)={\varphi }_{i,j}^U(t)+{\beta }_{s,j}^{\prime }z+C\epsilon$, such that ${\mathbb{P}}_n\mid {\eta }_{j,s,i}^U-{\eta }_{j,s,i}^L\mid \le C\epsilon$ and ${\eta }_j(t,z)\in [{\eta }_{j,s,i}^L(t,z),{\eta }_{j,s,i}^U(t,z)]$ for any t ∈ [a, b] and z ∈ Z. So, for any cause of failure j = 1, …, k it is straightforward to construct a set of brackets {[ $F_{j,s,i}^L,F_{j,s,i}^U$]: i = 1, …, (1/ε)^{Cq_{n, j}}; s = 1, …,C(1/ε)^d } with:

$$F_{j,s,i}^L=g_j^{-1}\left({\eta }_{j,s,i}^L;{\alpha }_j\right)$$

and

$$F_{j,s,i}^U=g_j^{-1}\left({\eta }_{j,s,i}^U;{\alpha }_j\right)$$

such that there exists an s = 1, …,C(1/ε)^d and an i = 1, …, (1/ε)^{Cq_{n, j}} such that $F_j(t,z)\in [F_{j,s,i}^L(t,z),F_{j,s,i}^U(t,z)]$ for any t ∈ [a, b] and z ∈ Z. Using Taylor approximation along with conditions C1, C2 the constraint ${\sum }_{j=1}^k{F}_j(b;z,{\theta }_j)<1$ and the fact that α_j < ∞ for all j = 1, …, k, we can show that ${\mathbb{P}}_n\mid F_{j,s,i}^U-F_{j,s,i}^L\mid \le C\epsilon$ and the bracketing number with the L₁(ℙ_n)-norm is bounded by C(1/ε)^{d+Cq_{n, j}}, for any j = 1, …, k, s = 1, …,C(1/ε)^d and i = 1, …, (1/ε)^{Cq_{n, j}} . Consequently, we can construct a set of brackets {[ $l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^L,l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^U$]: i_j = 1, …, (1/ε)^{Cq_{n, j}}, s_j = 1, …, C_j (1/ε)^ν}, where k is the fixed and finite number of competing risks, with

$$\begin{array}{lll}{l}_{i_1,\dots ,i_k,s_1,\dots ,s_k}^L(X)\hfill & =\hfill & \sum _{j=1}^k{\delta }_j^{l}log\left[F_{j,s_j,i_j}^L(V,Z)\right]+\sum _{j=1}^k{\delta }_{j}log\left[F_{j,s_j,i_j}^L(U,Z)-F_{j,s_j,i_j}^U(V,Z)\right]\hfill \\ \hfill & +\hfill & (1-\delta )log\left[1-\sum _{j=1}^k{F}_{j,s_j,i_j}^U(U,Z)\right],\hfill \end{array}$$

where ${\delta }_j^l=I_{\{X\le V,\delta =j\}}$, δ_j = I_{V<X≤U,_δ=j}, $\delta ={\sum }_{j=1}^k({\delta }_j+{\delta }_j^1)$ and

$$\begin{array}{lll}{l}_{i_1,\dots ,i_k,s_1,\dots ,s_k}^U(X)\hfill & =\hfill & \sum _{j=1}^k{\delta }_j^{l}log\left[F_{j,s_j,i_j}^U(V,Z)\right]+\sum _{j=1}^k{\delta }_{j}log\left[F_{j,s_j,i_j}^U(U,Z)-F_{j,s_j,i_j}^L(V,Z)\right]\hfill \\ \hfill & +\hfill & (1-\delta )log\left[1-\sum _{j=1}^k{F}_{j,s_j,i_j}^L(U,Z)\right]\hfill \end{array}$$

such that for any j = 1, …, k there exists an i _j = 1, …, (1/ε)^{Cq_{n, j}}, s_j = 1, …,C_j (1/ε)^ν so that $l(\theta ;X)\in [l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^L(X),l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^U(X)]$ for any sample point X ∈ 𝒳. Using Taylor approximation and regularity conditions C1–C3 it can be shown that ${\mathbb{P}}_n[l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^U-l_{i_1,\dots ,i_k,s_1,\dots ,s_k}^L]\le C\epsilon$, for any j, i _j and s _j . Additionally, the bracketing number N_[](Cε,ℱ₁, L₁(ℙ_n)) is bounded by ${\prod }_{j=1}^k{C}_j{(1/\epsilon )}^{\nu +C{q}_{n,j}}$. Since q_{n, j} = n^r_j + m, with r _j ∈ (0, 1), it follows that log N_[](Cε,ℱ₁, L₁(ℙ_n)) = o(n), for any ε > 0. Also, due to condition C3 there exists an envelope F for the class of likelihood functions ℱ₁ such that P^*F < ∞ and log N(ε,ℱ₁, L₁(ℙ_n)) ≤ log N_[](2ε,ℱ₁, L₁(ℙ_n)) [8]. Consequently, ℱ₁ is Glivenko-Cantelli by Theorem 2.4.3 of [24]. Consequently

$$\underset{\theta \in {\mathrm{\Theta }}_n}{sup}\mid {\mathbb{M}}_n(\theta )-\mathbb{M}(\theta )\mid \stackrel{p}{\to }0$$

Next we are going to show that condition 2., i.e. sup_{θ: d(θ, θ0)≥}ε 𝕄(θ) < 𝕄(θ₀), holds. By definition we have:

$$\begin{array}{lll}\mathbb{M}({\theta }_0)-\mathbb{M}(\theta )\hfill & =\hfill & E\{\sum _{j=1}^k{F}_j^0(V,Z)log\frac{F_j^0(V,Z)}{F_j(V,Z)}\hfill \\ \hfill & \hfill & +\sum _{j=1}^k\left[F_j^0(U,Z)-F_j^0(V,Z)\right]log\frac{F_j^0(U,Z)-F_j^0(V,Z)}{F_j(U,Z)-F_j(V,Z)}\hfill \\ \hfill & \hfill & +\left[1-\sum _{j=1}^k{F}_j^0(U,Z)\right]log\frac{1-{\sum }_{j=1}^k{F}_j^0(U,Z)}{1-{\sum }_{j=1}^k{F}_j(U,Z)}\}\hfill \\ \hfill & =\hfill & E\{\sum _{j=1}^k{F}_j(V,Z)m\left[\frac{F_j^0(V,Z)}{F_j(V,Z)}\right]\hfill \\ \hfill & \hfill & +\sum _{j=1}^k[F_j(U,Z)-F_j(V,Z)]m\left[\frac{F_j^0(U,Z)-F_j^0(V,Z)}{F_j(U,Z)-F_j(V,Z)}\right]\hfill \\ \hfill & \hfill & +\left[1-\sum _{j=1}^k{F}_j(U,Z)\right]m\left[\frac{1-{\sum }_{j=1}^k{F}_j^0(U,Z)}{1-{\sum }_{j=1}^k{F}_j(U,Z)}\right]\},\hfill \end{array}$$

where, as in [8], m(x) = x log x − x + 1 ≥ (1/4)(x − 1)² for x ∈ [0, 5], and thus for any θ in a sufficiently small neighbourhood of θ₀ we have

$$\begin{array}{lll}\mathbb{M}({\theta }_0)-\mathbb{M}(\theta )\hfill & \ge \hfill & \frac{1}{4}E\{\sum _{j=1}^k{F}_j(V,Z){\left[\frac{F_j^0(V,Z)}{F_j(V,Z)}-1\right]}^2\hfill \\ \hfill & \hfill & +\sum _{j=1}^k[F_j(U,Z)-F_j(V,Z)]{\left[\frac{F_j^0(U,Z)-F_j^0(V,Z)}{F_j(U,Z)-F_j(V,Z)}-1\right]}^2\hfill \\ \hfill & \hfill & +\left[1-\sum _{j=1}^k{F}_j(U,Z)\right]{\left[\frac{1-{\sum }_{j=1}^k{F}_j^0(U,Z)}{1-{\sum }_{j=1}^k{F}_j(U,Z)}-1\right]}^2\}\hfill \\ \hfill & =\hfill & \frac{1}{4}E\{\sum _{j=1}^k\frac{1}{F_j(V,Z)}{\left[F_j^0(V,Z)-F_j(V,Z)\right]}^2\hfill \\ \hfill & \hfill & +\sum _{j=1}^k\frac{1}{F_j(U,Z)-F_j(V,Z)}{\left[F_j^0(U,Z)-F_j^0(V,Z)-F_j(U,Z)+F_j(V,Z)\right]}^2\hfill \\ \hfill & \hfill & +\frac{1}{F_j(U,Z)}{\left[\sum _{j=1}^k{F}_j^0(U,Z)-\sum _{j=1}^k{F}_j(U,Z)\right]}^2\}\hfill \\ \hfill & \ge \hfill & \frac{1}{4}E\{\sum _{j=1}^k{\left[F_j^0(V,Z)-F_j(V,Z)\right]}^2\hfill \\ \hfill & \hfill & +\sum _{j=1}^k{\left[F_j^0(U,Z)-F_j^0(V,Z)-F_j(U,Z)+F_j(V,Z)\right]}^2\hfill \\ \hfill & \hfill & +{\left[\sum _{j=1}^k{F}_j^0,(U,Z)-\sum _{j=1}^k{F}_j(U,Z)\right]}^2\}\hfill \\ \hfill & \ge \hfill & \frac{1}{4}E\left(\sum _{j=1}^k{\left[F_j^0(V,Z)-F_j(V,Z)\right]}^2+{\left\{\sum _{j=1}^k\left[F_j^0(U,Z)-F_j(U,Z)\right]\right\}}^2\right)\hfill \\ \hfill & \ge \hfill & \frac{1}{4}E\left({\left\{\sum _{j=1}^k\left[F_j^0(V,Z)-F_j(V,Z)\right]\right\}}^2+{\left\{\sum _{j=1}^k\left[F_j^0(U,Z)-F_j(U,Z)\right]\right\}}^2\right)\hfill \\ \hfill & =\hfill & CE({\left\{\sum _{j=1}^k[{({\beta }_{0,j}-{\beta }_j)}^{\prime }Z+({\varphi }_{0,j}-{\varphi }_j)(V)]\right\}}^2\hfill \\ \hfill & \hfill & +{\left\{\sum _{j=1}^k[{({\beta }_{0,j}-{\beta }_j)}^{\prime }Z+({\varphi }_{0,j}-{\varphi }_j)(U)]\right\}}^2)\hfill \end{array}$$

where the last equality follows from a Taylor expansion around the value of the linear predictor η_j (X). Using the same arguments as in [25], pp. 2126–2127, along with regularity conditions C1–C6 it follows that

$$\mathbb{M}({\theta }_0)-\mathbb{M}(\theta )\ge C\left(\sum _{j=1}^k{\Vert {\beta }_j-{\beta }_{j,0}\Vert }^2+\sum _{j=1}^k{\Vert {\varphi }_j-{\varphi }_{j,0}\Vert }_{\mathrm{\Phi }}^2\right)=C{d}^2({\theta }_0,\theta ).$$

Consequently

$$\begin{array}{lll}\underset{\theta :d(\theta ,{\theta }_0)\ge \epsilon }{sup}\mathbb{M}(\theta )\hfill & \le \hfill & \underset{\theta :d(\theta ,{\theta }_0)\ge \epsilon }{sup}\left[\mathbb{M}({\theta }_0)-C{d}^2({\theta }_0,\theta )\right]\hfill \\ \hfill & =\hfill & \mathbb{M}({\theta }_0)-\underset{\theta :d(\theta ,{\theta }_0)\ge \epsilon }{inf}C{d}^2({\theta }_0,\theta )\hfill \\ \hfill & =\hfill & \mathbb{M}({\theta }_0)-C{\epsilon }^2\hfill \\ \hfill & <\hfill & \mathbb{M}({\theta }_0)\hfill \end{array}$$

and we have proven condition 2.

Finally, we prove condition 3, i.e. that the sequence of estimators θ̂_n satisfy 𝕄_n(θ̂_n) ≥ 𝕄_n(θ₀) − o_p(1). It has been shown that for ϕ_{0, j} ∈ Φ there exists a θ_{0,n, j} ∈ℳ_{n, j} of order m ≥ p + 2 such that ${\Vert {\varphi }_{0,n,j}-{\varphi }_{0,j}\Vert }_{\infty }\le C{q}_n^{-p}=O(n^{-p\nu })$ [26]. This also implies that ${\Vert {\varphi }_{0,n,j}-{\varphi }_{0,j}\Vert }_{\mathrm{\Phi }}\le C{q}_n^{-p}=O(n^{-p\nu })$ [8]. Of course the previous result holds for any j = 1, …, k. Letting θ_0,n = (β₀, ϕ_0,n) it follows that

$$\begin{gathered} {\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_0)={\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_{0,n})+{\mathbb{M}}_n({\theta }_{0,n})-{\mathbb{M}}_n({\theta }_0) \\ \ge {\mathbb{M}}_n({\theta }_{0,n})-{\mathbb{M}}_n({\theta }_0) \\ ={\mathbb{M}}_n({\theta }_{0,n})-{\mathbb{M}}_n({\theta }_0)+\mathbb{M}({\theta }_{0,n})-\mathbb{M}({\theta }_{0,n})+\mathbb{M}({\theta }_0)-\mathbb{M}({\theta }_0) \\ =({\mathbb{P}}_n-P)[l({\theta }_{0,n};X)-l({\theta }_0;X)]+\mathbb{M}({\theta }_{0,n})-\mathbb{M}({\theta }_0) \end{gathered}$$ (4)

Similar to [8], we consider the class of functions ℱ₂ = {l(β₀, ϕ; X) − l(β₀, ϕ₀; X): ϕ_j ∈ℳ_j,n, ||ϕ_j − ϕ_{0, j}||_Φ ≤ Cn^−pν for any j = 1, …, k} and construct a set of ε-brackets with L₂(P))-norm bounded by ${(1/\epsilon )}^{{\sum }_{j=1}^k{C}_j{q}_{n,j}}$. Consequently, the corresponding bracketing integral

$$\begin{array}{lll}{J}_{[]}(1,{\mathcal{F}}_2,L_2(P))\hfill & \equiv \hfill & {\int }_0^1\sqrt{log{N}_{[]}(\epsilon ,{\mathcal{F}}_2,L_2(P))}d\epsilon \hfill \\ \hfill & \le \hfill & \sqrt{\sum _{j=1}^k{C}_j{q}_{n,j}}{\int }_0^1\sqrt{log(1/\epsilon )}d\epsilon \hfill \\ \hfill & =\hfill & \sqrt{\sum _{j=1}^k{C}_j{q}_{n,j}}{\int }_0^{\infty }{u}^{1/2}{e}^{-u}du\hfill \\ \hfill & <\hfill & \infty \hfill \end{array}$$

because the integral above is bounded by 1 [27] and thus by theorem 19.5 of [28] ℱ₂ is P-Donsker. Using the fact that ||ϕ_j − ϕ_{0, j}||_Φ ≤ Cn^−pν in ℱ₂ and the boundedness of l(·; X), along with the dominated convergence theorem we can show that lim_n→∞ P[l(β₀, ϕ; X) − l(β₀, ϕ₀; X)]² = 0. Using the fact that for a P-Donsker class of functions there exists a semimetric ρ_p that makes that class totally bounded and that ${\mathbb{G}}_{n}f=\sqrt{n}({\mathbb{P}}_n-P)f$ is asymptotically equicontinuous by corollary 2.3.12 of [24] it follows that:

$$({\mathbb{P}}_n-P)[l({\theta }_{0,n};X)-l({\theta }_0;X)]=o_p(n^{-1/2})$$

Next, for the remaining term in (4) we can again use the boundedness of the loglikelihood function for any sample point X ∈ 𝒳 and that ||ϕ_{0,n, j} − ϕ_{0, j}||_Φ = O(n^−pν), along with the dominated convergence theorem it follows that

$$\mathbb{M}({\theta }_{0,n})-\mathbb{M}({\theta }_0)>-o(1)$$

as n → ∞. Thus

$${\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_0)\ge o_p(n^{-1/2})-o(1)=-o_p(1)$$

and this proves the final consistency condition. Consequently

$${\left(\sum _{j=1}^k{\Vert {\widehat{\beta }}_{j,n}-{\beta }_{j,0}\Vert }^2+\sum _{j=1}^k{\Vert {\widehat{\varphi }}_{j,n}-{\varphi }_{j,0}\Vert }_{\mathrm{\Phi }}^2\right)}^{\frac{1}{2}}\stackrel{p}{\to }0$$

Proof of rate of convergence

Derivation of the rate of convergence will be based on theorem 3.2.5 of [24]. We showed in the proof of consistency that

$$\mathbb{M}({\theta }_0)-\mathbb{M}(\theta )\ge C{d}^2({\theta }_0,\theta ).$$

and that

$${\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_0)\ge I_{1,n}+I_{2,n},$$

where I_1,n = (ℙ_n − P)[l(β₀, ϕ_0,n; X) − l(β₀, ϕ₀; X)] and I_2,n = P[l(β₀, ϕ_0,n; X) − l(β₀, ϕ₀; X)]. Applying a Taylor expansion leads to

$$I_{1,n}=({\mathbb{P}}_n-P)\left[{\dot{l}}_2({\beta }_0,\stackrel{\sim }{\varphi };X)({\varphi }_{0,n}-{\varphi }_0)\right]=n^{-p\nu +\epsilon }({\mathbb{P}}_n-P)\left[{\dot{l}}_2({\beta }_0,\stackrel{\sim }{\varphi };X)\frac{{\varphi }_{0,n}-{\varphi }_0}{n^{-p\nu +\epsilon }}\right]$$

for any 0 < ε < 1/2 − pν. The uniform boundedness of l̇₂(β₀, ϕ̃; X) due to the conditions C1–C4 and the fact that ||ϕ_0,n − ϕ₀||_∞ = O(n^−pν) [26] lead to

$$P{\left[{\dot{l}}_2({\beta }_0,\stackrel{\sim }{\varphi };X)\frac{{\varphi }_{0,n}-{\varphi }_0}{n^{-p\nu +\epsilon }}\right]}^2\to 0.$$

Since ℱ₂ is P-Donsker and by corollary 2.3.12 of [24] we have that

$$({\mathbb{P}}_n-P)\left[{\dot{l}}_2({\beta }_0,\stackrel{\sim }{\varphi };X)\frac{{\varphi }_{0,n}-{\varphi }_0}{n^{-p\nu +\epsilon }}\right]=o_p(n^{-1/2}).$$

Consequently,

$$I_{1,n}=o_p(n^{-p\nu +\epsilon }{n}^{-1/2})=o_p(n^{-2p\nu }).$$

Since the function m(x) = x log x − x + 1 is bounded by ≤ (x − 1)² in a neighbourhood of x = 1, it follows that

$$\mathbb{M}({\theta }_0)-\mathbb{M}({\theta }_{0,n})\le C{\Vert {\varphi }_0-{\varphi }_{0,n}\Vert }_{\mathrm{\Phi }}^2=O(n^{-2p\nu })$$

and thus

$$I_{2,n}=\mathbb{M}({\theta }_{0,n})-\mathbb{M}({\theta }_0)\ge -O(n^{-2p\nu }).$$

Consequently,

$${\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_0)\ge -O_p(n^{-2p\nu })=-O_p(n-2min(p\nu ,(1-\nu )/2)).$$

Defining the class of functions ℱ₃(η) = {l(θ; X) − l(θ₀; X): ϕ_j ∈ℳ_{n, j} and d(θ, θ₀) ≤ η} and using similar arguments as in the proofs of consistency, we have that

$$log{N}_{[]}(\epsilon ,{\mathcal{F}}_3(\eta ),L_2(P))\le Ck(N_j+p_j)log(\eta /\epsilon )$$

and thus

$$J_{[]}(\eta ,{\mathcal{F}}_3(\eta ),L_2(P))={\int }_0^{\eta }\sqrt{1+log{N}_{[]}(\epsilon ,{\mathcal{F}}_3(\eta ),L_2(P))}d\epsilon \le Ck{(N_j+p_j)}^{1/2}\eta .$$

Now, using the uniform boundedness of l(θ; X) as a result of conditions C1 and C3, and theorem 3.4.1 of [24], the function ϕ_n(η) of theorem 3.2.5 [24] is

$${\varphi }_n(\eta )={(N_j+p_j)}^{1/2}\eta +\frac{(N_j+p_j)}{n^{1/2}}.$$

Also, we have that

$$n^{2p\nu }{\varphi }_n(1/n^{p\nu })=n^{p\nu }{n}^{\nu /2}+\frac{n^{2p\nu }{n}^{\nu }}{n^{1/2}}=n^{1/2}\left[n^{p\nu -(1-\nu )/2}+n^{2p\nu -(1-\nu )}\right].$$

Consequently, if pν ≤ (1 − ν)/2 then n^2pνϕ_n(1/n^pν) ≤ n^1/2. Based on this and in accordance with [8] we conclude that if we choose r_n = min(pν, (1 − ν)/2), then $r_n^2{\varphi }_n(1/r_n)\le n^{1/2}$ and ${\mathbb{M}}_n({\widehat{\theta }}_n)-{\mathbb{M}}_n({\theta }_0)\ge -O_p(r_n^{-2})$. Therefore

$$d({\widehat{\theta }}_n,{\theta }_0)=O_p(n^{-r_n})$$

Proof of asymptotic normality

In order to prove the asymptotic normality of the estimator for Eucidean parameter β̂_n we need to verify that the information matrix I (β₀) is nonsingular and also the conditions of theorem 3 of [8]. These conditions are

• B1ℙ_nl̇₁(β̂_n, β̂_n; X) = o_p(n^−1/2) and ℙ_nl̇₂(β̂_n, ϕ̂_n; X)(ξ ₀) = o_p(n^−1/2)
• B2(ℙ_n − P)[l^*(β̂_n, ϕ̂_n; X) − l^*(β₀, ϕ₀; X)] = o_p(n^−1/2)
• B3P[l^*(β̂_n, ϕ̂_n; X) − l^*(β₀, ϕ₀; X)] = −I (β₀)(β̂_n − β₀) + o_p(||β̂_n − β₀||) + o_p(n^−1/2)

Information for β

At first we will show that the information matrix I (β₀) is nonsingular. Generically, the likelihood for an individual observation is

$$\begin{array}{lll}l(\beta ,\varphi ;X)\hfill & =\hfill & \sum _{j=1}^k{\delta }_j^{1}log[F_j(V;Z,{\alpha }_j)]+\sum _{j=1}^k{\delta }_{j}log[F_j(U;Z,{\alpha }_j)-F_j(V;Z,{\alpha }_j)]\hfill \\ \hfill & +\hfill & (1-\delta )log\left[1-\sum _{j=1}^k{F}_j(U;Z,{\alpha }_j)\right],\hfill \end{array}$$

where

$$F_j(t;Z,{\alpha }_j)=\{\begin{array}{ll}\hfill 1-{\{1+{\alpha }_{j}exp[{\varphi }_j(t)+{\beta }_j^{\prime }Z]\}}^{-\frac{1}{{\alpha }_j}}& \text{if}0<{\alpha }_j<\infty \hfill \\ \hfill 1-exp\{-exp[{\varphi }_j(t)+{\beta }_j^{\prime }Z]\}& \text{if}{\alpha }_j=0.\hfill \end{array}$$

We will carry out the calculations for the proportional subdistribution hazards model (i.e. α_j = 0). The proof for any other combination of link functions with 0 ≤ α_j < ∞, follows from similar arguments and calculations. The likelihood for an individual observation, under α_j = 0 for all j = 1, …, k is:

$$\begin{array}{lll}l(\beta ,\varphi ;X)\hfill & =\hfill & \sum _{j=1}^k{\delta }_{j}log\left[e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]\hfill \\ \hfill & +\hfill & \sum _{j=1}^k{\delta }_j^{1}log\left[1-e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}\right]\hfill \\ \hfill & +\hfill & (1-\delta )log\left\{1-\sum _{j=1}^k\left[1-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]\right\},\hfill \end{array}$$

where Λ_j = exp(ϕ_j) is the cumulative subdistribution hazard for the j-th cause of failure [11]. The score function for β_j (j = 1, …, k) is

$$\begin{array}{lll}{\stackrel{.}{l}}_{{\beta }_j}\hfill & =\hfill & {\delta }_j\frac{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}[-{\mathrm{\Lambda }}_j(V)Z{e}^{{\beta }_j^{\prime }Z}]-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}[-{\mathrm{\Lambda }}_j(U)Z{e}^{{\beta }_j^{\prime }Z}]}{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}\hfill \\ \hfill & \hfill & +{\delta }_j^1\frac{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}{\mathrm{\Lambda }}_j(V)Z{e}^{{\beta }_j^{\prime }Z}}{1-e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}+(1-\delta )\frac{e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\left[-{\mathrm{\Lambda }}_j(U)Z{e}^{{\beta }_j^{\prime }Z}\right]}{1-{\sum }_{j=1}^k\left[1-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]}\hfill \\ \hfill & =\hfill & -{\delta }_{j}Z{e}^{{\beta }_j^{\prime }Z}\frac{{\mathrm{\Lambda }}_j(V)e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-{\mathrm{\Lambda }}_j(U)e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}\hfill \\ \hfill & \hfill & +{\delta }_j^{1}Z{e}^{{\beta }_j^{\prime }Z}\frac{{\mathrm{\Lambda }}_j(V)e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}{1-e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}+(1-\delta )Z{e}^{{\beta }_j^{\prime }Z}\frac{{\mathrm{\Lambda }}_j(U)e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{1-{\sum }_{j=1}^k\left[1-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]}.\hfill \end{array}$$

Let

$$h_j={\frac{\partial {\mathrm{\Lambda }}_{j,s}}{\partial s}|}_{s=0}.$$

The score operator for Λ_j (j = 1, …, k) is

$$\begin{array}{lll}{\stackrel{.}{l}}_s^j\hfill & =\hfill & -{\delta }_j{e}^{{\beta }_j^{\prime }Z}\frac{h_j(V)e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-h_j(U)e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}\hfill \\ \hfill & \hfill & +{\delta }_j^1{e}^{{\beta }_j^{\prime }Z}\frac{h_j(V)e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}{1-e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}\hfill \\ \hfill & \hfill & -(1-\delta )e^{{\beta }_j^{\prime }Z}\frac{h_j(U)e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{1-{\sum }_{j=1}^k\left[1-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]}.\hfill \end{array}$$

Let

$$\begin{array}{lll}\hfill {\alpha }_1^j& =\hfill & \frac{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}{1-e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}},{\alpha }_2^j=\frac{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}}{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}={\alpha }_3^j+1,\hfill \\ \hfill {\alpha }_3^j& =\hfill & \frac{e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}},{\alpha }_4^j=\frac{e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}}{1-{\sum }_{j=1}^k\left[1-e^{-{\mathrm{\Lambda }}_j(U)e^{{\beta }_j^{\prime }Z}}\right]},\hfill \\ \hfill \frac{{\alpha }_1^j}{1-{\alpha }_1^j}& =\hfill & e^{-{\mathrm{\Lambda }}_j(V)e^{{\beta }_j^{\prime }Z}}.\hfill \end{array}$$

Then,

$$\begin{array}{lll}{\stackrel{.}{l}}_{{\beta }_j}\hfill & =\hfill & Z{e}^{{\beta }_j^{\prime }Z}\left[-{\delta }_j{\alpha }_3^j{\mathrm{\Lambda }}_j(U)+{\delta }_j{\alpha }_2^j{\mathrm{\Lambda }}_j(V)+{\delta }_j^1{\alpha }_1^j{\mathrm{\Lambda }}_j(V)-(1-\delta ){\mathrm{\Lambda }}_j(U){\alpha }_4^j\right]\hfill \\ \hfill & =\hfill & Z{e}^{{\beta }_j^{\prime }Z}\left\{{\delta }_j^1{\mathrm{\Lambda }}_j(V){\alpha }_1^j-{\delta }_j\left[{\mathrm{\Lambda }}_j(V){\alpha }_3^j-{\mathrm{\Lambda }}_j(U){\alpha }_2^j\right]-(1-\delta ){\mathrm{\Lambda }}_j(U){\alpha }_4^j\right\}\hfill \end{array}$$

and

$${\stackrel{.}{l}}_s^j=e^{{\beta }_j^{\prime }Z}\left\{{\delta }_j^1{h}_j(V){\alpha }_1^j-{\delta }_j\left[h_j(V){\alpha }_3^j-h_j(U){\alpha }_2^j\right]-(1-\delta )h_j(U){\alpha }_4^j\right\}.$$

Next, for any j = 1, …, k, we need to find

$$E({\stackrel{.}{l}}_{{\beta }_j}\mid T_1=t_1,\dots ,T_k=t_k,Z)$$

and

$$E({\stackrel{.}{l}}_s^j\mid T_1=t_1,\dots ,T_k=t_k,Z).$$

The random variables here are ( ${\delta }_j^1$, δ_j, δ,U, V). Assume U, V the same for all j = 1, …, k and that condition C3 holds. Since the event ${\delta }_j^1=1$ is equivalent to T_j < V and T_j ≤ T_l for any l = 1, …, k we have that

$$E({\delta }_j^1=1\mid T_1=t_1,\dots ,T_k=t_k,Z)=I(t_j\le t_l,l=1,\dots ,k){\int }_{t_j}^{b}g(v,u\mid z){\int }_{v+\eta }^b\mathit{dvdu},$$

where g(v, u|z) if the density of (V,U) conditinal on Z = z. Similarly, since the event δ_j = 1 is equivalent to T_j ∈ (V,U) and T_j ≤ T_l for any l = 1, …, k we have that

$$E({\delta }_j=1\mid T_1=t_1,\dots ,T_k=t_k,Z)=I(t_j\le t_l,l=1,\dots ,k){\int }_a^{t_j}{\int }_{t_j}^{b}g(v,u\mid z)I(u-v\ge \eta )\mathit{dvdu}.$$

Finally, we have that

$$\begin{array}{lll}E(\delta =0\mid T_1=t_1,\dots ,T_k=t_k,Z)\hfill & =\hfill & P(U\le t_j,j=1,\dots ,k,U-V\ge \eta )\hfill \\ \hfill & =\hfill & {\int }_a^{t-\eta }{\int }_{v+\eta }^{t}g(v,u\mid z)\mathit{dvdu},\hfill \end{array}$$

where t = min(t_j: j = 1, …, k). We also have that,

$${({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_{{\theta }_j}=E_{Z}E({\stackrel{.}{l}}_{{\theta }_j}\mid T_1=t_1,\dots ,T_k=t_k,Z).$$

Now

$$\begin{array}{lll}E({\stackrel{.}{l}}_{{\beta }_j}\mid T_1=t_1,\dots ,T_k=t_k,Z)\hfill & =\hfill & Z{e}^{{\beta }_j^{\prime }Z}\{I(t_j\le t_l,l=1,\dots ,k){\int }_{t_j}^b{\int }_{v+\eta }^b{\mathrm{\Lambda }}_j(v){\alpha }_1^{j}g(v,u\mid z)\mathit{dvdu}\hfill \\ \hfill & -\hfill & I(t_j\le t_l,l=1,\dots ,k)\times \hfill \\ \hfill & \hfill & {\int }_a^{t_j}{\int }_{t_j}^b[{\mathrm{\Lambda }}_j(v){\alpha }_3^j-{\mathrm{\Lambda }}_j(u){\alpha }_2^j]I(u-v\ge \eta )g(v,u\mid z)\times \hfill \\ \hfill & \hfill & I(u-v\ge \eta )\mathit{dvdu}\hfill \\ \hfill & -\hfill & {\int }_a^{t-\eta }{\int }_{v+\eta }^t{\mathrm{\Lambda }}_j(u){\alpha }_4^{j}g(v,u\mid z)\mathit{dvdu}\}.\hfill \end{array}$$

Similarly,

$${({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_s^j=E_{Z}E({\stackrel{.}{l}}_s^j\mid T_1=t_1,\dots ,T_k=t_k,Z).$$

Now,

$$\begin{array}{lll}E({\stackrel{.}{l}}_s^j\mid T_1=t_1,\dots ,T_k=t_k,Z)\hfill & =\hfill & e^{{\beta }_j^{\prime }Z}\{I(t_j\le t_l,l=1,\dots ,k){\int }_{t_j}^b{\int }_{v+\eta }^b{h}_j(v){\alpha }_1^{j}g(v,u\mid z)\mathit{dvdu}\hfill \\ \hfill & -\hfill & I(t_j\le t_l,l=1,\dots ,k)\times \hfill \\ \hfill & \hfill & {\int }_a^{t_j}{\int }_{t_j}^b[h_j(v){\alpha }_3^j-h_j(u){\alpha }_2^j]I(u-v\ge \eta )g(v,u\mid z)\times \hfill \\ \hfill & \hfill & I(u-v\ge \eta )\mathit{dvdu}\hfill \\ \hfill & -\hfill & {\int }_a^{t-\eta }{\int }_{v+\eta }^t{h}_j(u){\alpha }_4^{j}g(v,u\mid z)\mathit{dvdu}\}.\hfill \end{array}$$

Let,

$$\begin{array}{lll}{b}_1^j(v,u)\hfill & =\hfill & E_Z[e^{{\beta }_j^{\prime }Z}{\alpha }_1^{j}g(u,v\mid z)]\hfill \\ b_2^j(v,u)\hfill & =\hfill & E_Z[e^{{\beta }_j^{\prime }Z}{\alpha }_2^{j}g(u,v\mid z)]\hfill \\ b_3^j(v,u)\hfill & =\hfill & E_Z[e^{{\beta }_j^{\prime }Z}{\alpha }_3^{j}g(u,v\mid z)]\hfill \\ b_4^j(v,u)\hfill & =\hfill & E_Z[e^{{\beta }_j^{\prime }Z}{\alpha }_4^{j}g(u,v\mid z)].\hfill \end{array}$$

Then,

$$\begin{array}{lll}{({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_s^j\hfill & =\hfill & I(t_j\le t_l,l=1,\dots ,k){\int }_{t_j}^b{\int }_{v+\eta }^b{h}_j(v)b_1^j(v,u)g(v,u\mid z)\mathit{dvdu}\hfill \\ \hfill & -\hfill & I(t_j\le t_l,l=1,\dots ,k)\times \hfill \\ \hfill & \hfill & {\int }_a^{t_j}{\int }_{t_j}^b[h_j(v)b_3^j(v,u)-h_j(u)b_2^j(v,u)]I(u-v\ge \eta )g(v,u\mid z)I(u-v\ge \eta )\mathit{dvdu}\hfill \\ \hfill & -\hfill & {\int }_a^{t-\eta }{\int }_{v+\eta }^t{h}_j(u)b_4^j(v,u)g(v,u\mid z)\mathit{dvdu}.\hfill \end{array}$$

Let,

$$\begin{array}{lll}{c}_1^j(v,u)\hfill & =\hfill & E_Z[Z{e}^{{\beta }_j^{\prime }Z}{\alpha }_1^{j}g(u,v\mid z)]\hfill \\ c_2^j(v,u)\hfill & =\hfill & E_Z[Z{e}^{{\beta }_j^{\prime }Z}{\alpha }_2^{j}g(u,v\mid z)]\hfill \\ c_3^j(v,u)\hfill & =\hfill & E_Z[Z{e}^{{\beta }_j^{\prime }Z}{\alpha }_3^{j}g(u,v\mid z)]\hfill \\ c_4^j(v,u)\hfill & =\hfill & E_Z[Z{e}^{{\beta }_j^{\prime }Z}{\alpha }_4^{j}g(u,v\mid z)].\hfill \end{array}$$

Then,

$$\begin{array}{lll}{({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_{{\beta }_j}\hfill & =\hfill & I(t_j\le t_l,l=1,\dots ,k){\int }_{t_j}^b{\int }_{v+\eta }^b{\mathrm{\Lambda }}_j(v)c_1^j(u,v)g(v,u\mid z)\mathit{dvdu}\hfill \\ \hfill & -\hfill & I(t_j\le t_l,l=1,\dots ,k)\times \hfill \\ \hfill & \hfill & {\int }_a^{t_j}{\int }_{t_j}^b[{\mathrm{\Lambda }}_j(v)c_3^j(v,u)-{\mathrm{\Lambda }}_j(u)c_2^j(v,u)]I(u-v\ge \eta )g(v,u\mid z)I(u-v\ge \eta )\mathit{dvdu}\hfill \\ \hfill & -\hfill & {\int }_a^{t-\eta }{\int }_{v+\eta }^t{\mathrm{\Lambda }}_j(u)c_4^j(v,u)g(v,u\mid z)\mathit{dvdu}.\hfill \end{array}$$

Denote,

$${({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_s^j=\left(\begin{array}{c}{L}_1(t_1)\\ .\\ .\\ .\\ L_k(t_k)\end{array}\right)$$

and

$${({\stackrel{.}{l}}_s^j)}^T{\stackrel{.}{l}}_{{\beta }_j}=\left(\begin{array}{c}{R}_1(t_1)\\ .\\ .\\ .\\ R_k(t_k)\end{array}\right)$$

We need to find h₁, …, h_k s.t.

$$L_j(t_j)=R_j(t_j),j=1,\dots ,k.$$

or equivalently

$$\frac{\partial L_j(t_j)}{\partial t_j}=\frac{\partial R_j(t_j)}{\partial t_j},j=1,\dots ,k.$$

We have that

$$\begin{array}{lll}\frac{\partial L_j(t_j)}{\partial t_j}\hfill & =\hfill & \{-{\int }_{t_j+\eta }^b{h}_j(t_j)b_1^j(u,t_j)du\hfill \\ \hfill & -\hfill & {\int }_{t_j}^b[h_j(t_j)b_3^j(u,t_j)-h_j(u)b_2^j(u,t_j)]I(u\ge t_j+\eta )du\hfill \\ \hfill & +\hfill & {\int }_a^{t_j}[h_j(v)b_3^j(t_j,v)-h_j(t_j)b_2^j(t_j,v)]I(u\ge t_j+\eta )du\hfill \\ \hfill & -\hfill & {\int }_a^{t_j-\eta }{h}_j(t_j)b_4^j(t_j,v)dv\}I(t_j\le t_l,l=1,\dots ,k)\hfill \end{array}$$

Let,

$$\begin{array}{lll}{b}_j(t_j)\hfill & =\hfill & {\int }_{t_j+\eta }^b{b}_1^j(u,t_j)du+{\int }_{t_j+\eta }^b{b}_2^j(u,t_j)du\hfill \\ \hfill & +\hfill & {\int }_a^{t_j-\eta }{b}_3^j(t_j,v)dv+{\int }_a^{t_j-\eta }{b}_4^j(t_j,v)dv.\hfill \end{array}$$

Then,

$$\begin{array}{lll}\frac{\partial L_j(t_j)}{\partial t_j}\hfill & =\hfill & -b_j(t_j)h_j(t_j)+{\int }_{t_j+\eta }^b{h}_j(x)b_3^j(x,t_j)dx\hfill \\ \hfill & +\hfill & {\int }_a^{t_j-\eta }{h}_j(x)b_2^j(t_j,x)dx\hfill \end{array}$$

for t_j ≤ t_l, for any l = 1, …, k. Similarly let

$$\begin{array}{lll}{c}_j(t_j)\hfill & =\hfill & {\int }_{t_j+\eta }^b{c}_1^j(u,t_j)du+{\int }_{t_j+\eta }^b{c}_2^j(u,t_j)du\hfill \\ \hfill & +\hfill & {\int }_a^{t_j-\eta }{c}_3^j(t_j,v)dv+{\int }_a^{t_j-\eta }{c}_4^j(t_j,v)dv.\hfill \end{array}$$

Then,

$$\begin{array}{lll}\frac{\partial R_j(t_j)}{\partial t_j}\hfill & =\hfill & -c_j(t_j){\mathrm{\Lambda }}_j(t_j)+{\int }_{t_j+\eta }^b{\mathrm{\Lambda }}_j(x)c_3^j(x,t_j)dx\hfill \\ \hfill & +\hfill & {\int }_a^{t_j-\eta }{\mathrm{\Lambda }}_j(x)c_2^j(t_j,x)dx\hfill \end{array}$$

for t_j ≤ t_l, for any l = 1, …, k. Therefore

$$h_j^{★}(t_j)-\int K(t_j,x)h_j^{★}(x)dx=m(t_j),$$

where

$$\begin{array}{c}{h}_j^{★}(t_j)=b_j(t_j)h_j(t_j),\\ K(t_j,x)=\frac{b_3^j(x,t_j)I(t_j+\eta <x<b)+b_2^{j}I(a<x<t_j-\eta )}{b_j(t_j)}\end{array}$$

and

$$m(t_j)=-\frac{\frac{\partial R_j(t_j)}{\partial t_j}}{b_j(t_j)}.$$

Now, as in [29] by lemma 6.1 [29], the fact that K(t_j, x) is a bounded kernel and Fredholm integral equations results, there exists a 0(t_j, x) such that

$$h_j^{★}(t_j)=m(t_j)-\int \mathrm{\Gamma }(t_j,x)m(x)dx.$$

Thus, similarly to [29] (pp. 159), $h_j^{★}$ is differentiable with a bounded derivative.

Verification of conditions B1–B3

For condition B1 we need to show that

$${\mathbb{P}}_n{\stackrel{.}{l}}_2({\widehat{\beta }}_n,{\widehat{\varphi }}_n;X)({\xi }_0)=o_p(n^{-1/2})$$

since ℙ_nl̇₁(β̂_n, ϕ̂_n; X) = 0. ξ₀ has a bounded derivative and it is also a function with bounded variation [8]. Define S_n(D_n, K_n,m) to be the space of polynomial spline functions s of order m ≥ 1, with the restriction of s to any of the K_n subinterval being a polynomial of order m ≤ K_n and for m ≥ 2 and 0 ≤ m′ ≤ m − 2, s is m′ times continuously differentiable on [a, b]. Then it can be shown using the argument in [30] pp. 435–436 that there exists a ξ_0,n ∈ S_n(D_n, K_n, m) such that

$${\Vert {\xi }_{0,n}-{\xi }_0\Vert }_{\mathrm{\Phi }}=O(q_n^{-1})=O(n^{-\nu })$$

and ℙ_nl̇₂(θ̂_n; X)(ξ_0,n) = 0. Consequently,

$${\mathbb{P}}_n{\stackrel{.}{l}}_2({\widehat{\theta }}_n;X)({\xi }_0)=I_{3,n}+I_{4,n},$$

where

$$I_{3,n}=({\mathbb{P}}_n-P){\stackrel{.}{l}}_2({\widehat{\theta }}_n;X)({\xi }_0-{\xi }_{n,0})$$

and

$$I_{4,n}=P\left[{\stackrel{.}{l}}_2({\widehat{\theta }}_n;X)({\xi }_0-{\xi }_{n,0})-{\stackrel{.}{l}}_2({\theta }_0;X)({\xi }_0-{\xi }_{n,0})\right].$$

Let ℱ₄ = {l̇₂(θ; x)(ξ₀ − ξ): θ ∈ℳ_n, ξ ∈ S_n(D_n, K_n,m) and ||ξ₀ − ξ||_Φ ≤ n^−ν }. Similarly, it can be shown that

$$N_{[]}(\epsilon ,{\mathcal{F}}_4,L_2(P))\le C{(1/\epsilon )}^d{(1/\epsilon )}^{Ck(N_j+p_j)}{(1/\epsilon )}^{Ck(N_j+p_j)},$$

and this leads to ℱ₄ being Donsker. Also, for any r ∈ ℱ₄, Pr² → 0 as n → ∞ and thus I_3,n = o_p(n^−1/2) by corollary 2.3.12 of [24]. Finally, based on the Cauchy-Schwartz inequality and regularity conditions C1–C4 we have that

$$\begin{array}{lll}{I}_{4,n}\hfill & \le \hfill & Cd({\widehat{\theta }}_n,{\theta }_0){\Vert {\xi }_0-{\xi }_{0,n}\Vert }_{\mathrm{\Phi }}\hfill \\ \hfill & =\hfill & O_p(n-min(p\nu ,(1-\nu )/2)n^{-\nu })\hfill \\ \hfill & =\hfill & O_p(n-min(\nu (p+1),(1+\nu )/2)))\hfill \\ \hfill & =\hfill & o_p(n^{-1/2}),\hfill \end{array}$$

and thus we proved condition B1.

For condition B2 define the class of functions

$${\mathcal{F}}_5(\eta )=\{l^{★}(\theta ;x)-l^{★}({\theta }_0;x):{\theta }_j\in {\mathcal{M}}_{j,n}\text{and}d(\theta ,{\theta }_0)\le \eta \}.$$

Using similar arguments as before, we can show that ℱ₅(η) is P-Donsker and that for any r ∈ ℱ₅, Pr² → 0 as η → ∞ and therefore condition B2 holds. Finally, it is a straightforward task to show condition B3 based on Taylor expansion and the convergence rate of the estimator. Thus

$$\sqrt{n}({\widehat{\beta }}_n-{\beta }_0)\stackrel{d}{\to }N[0,I^{-1}({\beta }_0)]$$