Design of pilot studies to inform the construction of composite outcome measures

Abstract

Introduction

Composite scales have recently been proposed as outcome measures for clinical trials. For example, the Preclinical Alzheimer's Cognitive Composite (PACC) is the sum of z-score normed component measures assessing episodic memory, timed executive function, and global cognition. Alternative methods of calculating composite total scores using the weighted sum of the component measures that maximize the signal-to-noise ratio of the resulting composite score have been proposed. Optimal weights can be estimated from pilot data, but it is an open question how large a pilot trial is required to calculate reliably optimal weights.

Methods

We describe the calculation of optimal weights and use large-scale computer simulations to investigate the question as how large a pilot study sample is required to inform the calculation of optimal weights. The simulations are informed by the pattern of decline observed in cognitively normal subjects enrolled in the Alzheimer's Disease Cooperative Study Prevention Instrument cohort study, restricting to n = 75 subjects aged 75 years and older with an APOE ε4 risk allele and therefore likely to have an underlying Alzheimer's disease neurodegenerative process.

Results

In the context of secondary prevention trials in Alzheimer's disease and using the components of the PACC, we found that pilot studies as small as 100 are sufficient to meaningfully inform weighting parameters. Regardless of the pilot study sample size used to inform weights, the optimally weighted PACC consistently outperformed the standard PACC in terms of statistical power to detect treatment effects in a clinical trial. Pilot studies of size 300 produced weights that achieved near-optimal statistical power and reduced required sample size relative to the standard PACC by more than half.

Discussion

These simulations suggest that modestly sized pilot studies, comparable to that of a phase 2 clinical trial, are sufficient to inform the construction of composite outcome measures. Although these findings apply only to the PACC in the context of prodromal Alzheimer's disease, the observation that weights only have to approximate the optimal weights to achieve near-optimal performance should generalize. Performing a pilot study or phase 2 trial to inform the weighting of proposed composite outcome measures is highly cost-effective. The net effect of more efficient outcome measures is that smaller trials will be required to test novel treatments. Alternatively, second generation trials can use prior clinical trial data to inform weighting, so that greater efficiency can be achieved as we move forward.

1. Introduction

Composite endpoints have received increasing attention as potential outcome measures for clinical trials in Alzheimer's disease (AD). Composites can be defined as the sum of items taken from component instruments of a cognitive battery [1]. Or, more simply, composites can be defined as the sum of established cognitive instruments. One such composite is the Preclinical Alzheimer's Cognitive Composite (PACC) [2]. The PACC is constructed from component measures assessing episodic memory, timed executive function, and global cognition and is the primary outcome measure for a major ongoing trial [3]. We have described how the performance of a composite endpoint depends on the weighting used and how optimal weights can be derived if the multivariate distribution of change scores on component measures is known [4]. The multivariate distribution of change scores of the component measures is typically not known but can be estimated if pilot data are available, for example, from a prior trial or from a prior representative registry study using the component instruments. An important consideration is whether prior data are sufficient to inform weighting parameters for a composite outcome measure and, in particular, how large a sample size would be required to meaningfully inform calculation of weights. In this article, we use data from a completed registry trial to describe calculation of optimal weights and to investigate the question of what size pilot study is sufficient to inform calculation of optimal weights.

2. Methods

In overview, we use simulations informed by data from a completed registry trial, the Alzheimer's Disease Cooperative Study Prevention Instrument (PI) trial, to demonstrate optimal weighting and investigate the question as how large a pilot study is required to determine weights that improve the performance of the PACC. In the text that follows we briefly describe the PACC and the PI trial and then formally characterize optimal weights and computer simulation procedures.

2.1. Preclinical Alzheimer's Cognitive Composite

We use the PACC [2] to demonstrate the influence of weighting on characteristics of the composite scale. The PACC is a weighted sum of well recognized and validated component instruments, the Mini-Mental Status Examination (MMSE) assessing global cognition function [5], the Free and Cued Selective Reminding task (FCSRT) assessing episodic memory [6], and the WAIS-R Digit Symbol task (Digit Symbol), a timed test of processing speed and memory function [7], and the WMS-R Logical Memory story delayed recall task (Logical Memory) [8].

2.2. Prodromal AD PI cohort

Pilot study longitudinal data for the PACC to inform instrument behavior and clinical trial design are not available [2]. However, roughly comparable component instruments are available from the PI protocol conducted by the Alzheimer's Disease Cooperative Study [9]. The PI protocol performed annual neuropsychometric and functional assessments of 644 cognitively normal older persons (age 75 years and older). Although there was no randomization to treatment, the PI enrollment and assessment procedures mimicked that of a clinical trial, with primary purpose to assess the utility of the components of the assessment battery as potential endpoints for an Alzheimer's disease prevention trial, and these data were used in the initial description of the PACC [2]. The PACC components that were not assessed in the PI study were the MMSE and the Logical Memory test. Comparable domain-specific instruments used in their stead were the modified MMSE [10] substituting for the MMSE, and the New York University Paragraph delayed recall test [11] substituting for the Logical Memory test. When the distinction is relevant, we call the resulting composite the PI-PACC to distinguish it from the PACC constructed from the MMSE, FCSRT, Digit Symbol, and Logical Memory test.

Donohue et al. [2] restricted their analysis to subjects with an APOE ε4 risk allele, and we follow suit. Subjects aged 75 years and older with this genetic risk profile have with high likelihood an underlying Alzheimer's disease neurodegenerative process, and hence these subjects are an approximate representation of clinically normal, AD biomarker positive subjects that are the target of contemporary secondary prevention trials [2]. We call this subset of the PI cohort the PI Prodromal AD cohort. Baseline through month 36 data are available for 75 of these subjects (mean age at baseline 78.5 years [standard deviation 2.9 years], 59% female), and these longitudinal data are used to inform the simulations reported here.

2.3. Optimal weights

We assume the primary analysis is mixed model repeated measure (MMRM) comparing change first to last in treatment versus change first to last in control [2]. To simplify presentation, we assume complete data for all simulations. Including missing values in simulations would reduce power given a total sample size, but would not appreciably impact the relative efficiency of trial designs and endpoints, which is the focus of this article. We further make the usual assumption that an effective treatment would shift the mean change but not affect the variability of change (constant variance of change in treatment and control arms). Under these assumptions, optimal weights for constructing a composite endpoint are a simple function of two sets of parameters, the expected change and the covariance of change of the component measures [4]. Given the vector μ of expected change scores of component measures and covariance matrix Σ of change scores, weights that maximize the signal-to-noise ratio of the composite (and therefore statistical power of clinical trials using the composite) are

$$\text{Optimal}\text{weights}=c\ast {\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}^{\prime }$$

The c is an arbitrary scalar constant—any nonzero value of c will produce equally optimal weights. A useful convention is to set c so that the weights sum in absolute value to 1. The distribution of component change scores is typically unknown, but can be estimated, for example, from prior clinical trials that included the component measures or from registry trials specifically designed to investigate properties of potential outcome measures.

2.4. Computer simulations

We used computer simulations to investigate the properties of weights estimated from pilot registry study data performed before a formal randomized clinical trial. We simulated 40,000 pilot study–clinical trial dyads, using pilot study sample sizes of 100 to 300 persons, and clinical trial sample sizes of 100 to 1600 subjects per arm. The pilot study component of the dyad could be a prior nonintervention study registry trial or the placebo arm of a previously completed trial with comparable inclusion criteria. Simulations assumed multivariate normality of component change scores with the mean and covariance structure observed in the PI prodromal AD cohort. A 25% shift in mean change was added to the treatment arm to simulate data from a trial with an effective treatment. For each dyad, we calculated the standard PACC [2] and optimal PACC from the simulated component scores, with weights for the optimal PACC estimated from the simulated pilot study and weights for the standard PACC calculated from baseline data of the clinical trial, reflecting how these endpoints would be calculated in practice. An MMRM model testing the hypothesis that the mean 3-year decline was different in the treatment and control arms was fit to the respective composite measures. Statistical power of the PACC and optimal PACC was calculated as the percentage of simulations for which a statistically significant difference was observed at α = 0.05 significance level. All data simulations and statistical analyses were performed using the R statistical programming language, with model fitting performed using the nlme package [12].

3. Results

Baseline characteristics and 3-year change observed in the PI prodromal AD cohort are summarized in Table 1. The ratio of mean change to the standard deviation of change (the mean to standard deviation ratio (MSDR), aka the signal-to-noise) for each component instrument of the PI-PACC is also summarized in Table 1. Instruments with high MSDR are more sensitive to change and are more powerful endpoints for clinical trials [13]. Among the components of the PI-PACC, the paragraph recall test has the greatest MSDR (Table 1). PACC and optimal PACC weights, standardized to sum in absolute value to 1, are summarized in the bottom two rows of the table. Both composites give relatively lower weight to the modified MMSE and the Digit Symbol test. A primary difference between the PACC and the optimal PACC is a greater weight to the FCSRT by the PACC and greater weight to the paragraph recall test by the optimal PACC (Table 1).

Table 1.

Mean (standard deviation) of component item scores at baseline and year 3 visit, mean to standard deviation ratio of the component scores, and component weights used to construct the weighted sum composite scores

Summary statistic	FCSRT	mMMSE	NYU Paragraph	Digit Symbol
Mean (SD)
Baseline	47.88 (0.47)	95.97 (2.84)	7.39 (2.49)	41.29 (12.04)
Year 3	46.63 (4.18)	91.88 (15.44)	5.69 (3.25)	38.64 (11.10)
Change	−1.27 (4.11)	−4.09 (15.02)	−1.69 (3.15)	−2.65 (9.33)
Mean to standard deviation ratio (MSDR)
	0.31	0.27	0.54	0.28
Item weights
PACC	0.72	0.12	0.14	0.03
Optimal PACC	0.25	0.06	0.65	0.04

Abbreviations: Digit Symbol, WAIS-R Digit Symbol task; FCSRT, Free and Cued Selective Reminding task; mMMSE, modified Mini-Mental Status Examination; NYU Paragraph, New York University Paragraph delayed recall test; PACC, Prodromal Alzheimer's Cognitive Composite.

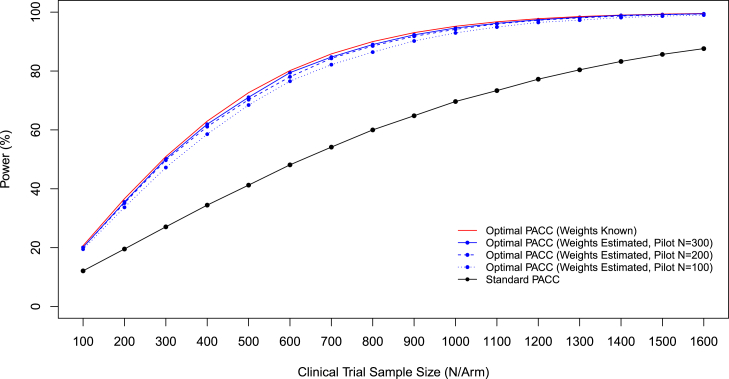
Power to detect treatment effects as a function of sample size is summarized in Fig. 1. As a reference point, the theoretical maximum power achievable if the true covariance of component change scores was known is also plotted in the figure. A three year clinical trial using weights informed by a three year pilot study of size 300 subjects achieves near-optimal power, with obtained power deviating from optimal power by less than 1% in the critical region of the power curve with power of 80% and higher (Fig. 1). Power of pilot study–clinical trial dyads decreases if smaller pilot studies are used to inform weights, but only modestly. Power obtained was within 1.2 percentage points of the theoretical maximum achievable power when pilot sample size is 200 subjects, and within 2.4 percentage points of the theoretical maximum when pilot sample size is 100 subjects. Nonetheless, it is important to note that there is some loss of power, and a modest inflation of estimated sample size would be prudent if the pilot study data used to estimate optimal weights were also used to estimate sample size for a future clinical trial, on the order of 3% (pilot N = 300) to 10% (pilot N = 100) for the scenarios reported here.

Fig. 1.

Power to detect a 25% slowing in cognitive decline as a function of sample size per arm and outcome measure used. For optimal composites, power is also a function of the size of pilot study used to inform optimal weights. (Clinical trial with equal allocation to, two-sided hypothesis testing, and type I error rate α = 0.05.)

4. Discussion

The optimal weighting formula as implemented here assumes a treatment effect that shifts the mean change from baseline to last visit but assumes a constant variance of change in treatment and control. This is the usual assumption used in power calculations (e.g., [14]^, [15]^, [16]). Alternative treatment effects may be plausible. For example, instead of assuming a percentage shift in mean location, we could assume a percentage decrease in rate of decline in all subjects, so that the variance of change scores would be decreased; for example, under this assumed treatment effect, a 25% shift in mean would be accompanied by a 0.75 squared = 0.5625 reduction in variance in the treatment arm and accompanying increase in power. We prefer the more conservation mean shift assumption for several reasons. First, given the general uncertainty in parameter estimates used to inform power calculations, conservative assumptions provide some margin of error in sample size calculations. Second, an alternative scenario that is plausible and even likely is that response to treatment will be variable within the treatment arm. In other words, the variance of change in the treatment arm will be the sum of variance in rate of decline plus the variance of response to treatment. Under this plausible and likely scenario, the total variance will be larger than the variance in the placebo arm, meaning the percent shift hypothesis would be highly anticonservative and result in underestimates of required sample size and underpowered trials.

The MMRM analysis plan typically includes baseline level of the outcome variable as a covariate [17]. When this term was added to the MMRM model fits to each simulated data set the power increased slightly, less than one percentage point for most of the range of sample sizes simulated for both the PACC and optimal PACC. Hence, the observations regarding relative efficiency of the PACC and optimally weighted PACC are unchanged by inclusion on the baseline covariate term.

5. Conclusions

We have investigated the magnitude of sample size required to estimate weights that optimize the performance of a cognitive composite endpoint and found that pilot studies of as small as 100 to 300 subjects are sufficient to inform composite weighting and achieve near-optimally powerful composite endpoints. In other words, trials of the size of a typical phase 2 trial are sufficient to estimate weighting parameters for defining an optimal weighted composite endpoint. This finding is similar to previously reported findings in Ard et al. [4] for a two-component composite instrument. Ard et al. used computer simulations to document near-optimal composite performance with weights estimated from pilot studies as small as 100 subjects for the two-component composite. The current article replicates and meaningfully extends those results by (1) assessing the prospective performance of a composite currently in use in a major Alzheimer's disease clinical trial, and (2) using data from a completed registry trial to determine realistic simulation parameters.

A related concern is the representativeness of the pilot study used to train weights—weights optimal in one clinical trial target population may not be optimal in a different population. Raghavan et al. [18] addressed this latter question and found substantial robustness of cognitive composites to the training data set. They found that weights estimated from longitudinal data obtained relatively earlier or later in the prodromal AD spectrum were comparable and consistently improved trial efficiency regardless of the prodromal AD stage recruited to the ultimate clinical trial. As we observed in our investigation of pilot study sample size, even approximate information about the distribution of change scores was sufficient to inform the calculation of optimal weights and improve the efficiency of composite scales. On the basis of these observations we speculate that, within the context of prodromal AD trials, weights optimal in one sample will be optimal or near-optimal for future trials with similar design and inclusion criteria, and that an optimal PACC defined using optimal weights estimated from a single registry trial (or completed clinical trial) would be an appropriate endpoint for future trials with similar design and inclusion criteria. In contrast, the PACC as originally described is redefined on a trial-by-trial basis—it is the sum of z-score normed component instruments, with z-score normative values estimated from baseline visit data of the respective clinical trial [2]. In other words, the PACC is measured on a different scale and has a different interpretation for each clinical trial. A single established optimally weighted PACC would have the dual advantages of improved statistical power and of being comparable study to study, so that future pooled meta-analyses would be possible. The clear tradeoff and downside of optimal endpoints is that a pilot study is required, a real cost in terms of both time and resources. For the “PI-PACC” assuming the distribution of change scores observed in the PI Prodromal AD cohort, the optimal PACC is relatively cost efficient even considering the time and cost of a pilot registry trial—assuming this distribution of change scores, a trial with 80% power to detect a 25% slowing of decline using the optimal PACC would require 600 subjects per arm (1200 subjects total), whereas a trial powered to detect the same percentage slowing in the PI-PACC would require more than 2500 subjects.

Given the critical importance of statistical power in clinical trials, any method of improving power and trial efficiency should be seriously considered. More power means there is less likelihood of false negative trials missing effective treatments or conversely more power means that we can perform smaller trials with equivalent power, so that we may perform more clinical trials and test more treatments with the limited study subject pool available for prodromal AD studies. In the long run, more efficient trials will shorten the time till effective treatments are identified and we begin to make meaningful progress against the epidemic of AD.

Research in Context.

• 1.Systematic review: Composite scales, typically defined as the weighted sum of established component assessment scales, have recently been proposed as outcome measures for clinical trials. Composite scales can be severely inefficient endpoints if suboptimal weights are used to construct the composite. Optimal weights can be estimated from pilot data, but it is an open question as how large a pilot trial is required to calculate reliably optimal weights.
• 2.Interpretation: We demonstrated with large-scale computer simulations that pilot trials of size 100 to 300 subjects, the size of typical phase 2 clinical trials, are sufficient to determine optimal weights that maximize the sensitivity and statistical power of composite outcomes to detect treatment effects.
• 3.Future directions: The potential utility of optimally weighted composites has been well demonstrated. A practical demonstration of utility using data from completed trials would further validate this approach to clinical trial endpoint development.