Accurate nanoscale flexibility measurement of DNA and DNA–protein complexes by atomic force microscopy in liquid

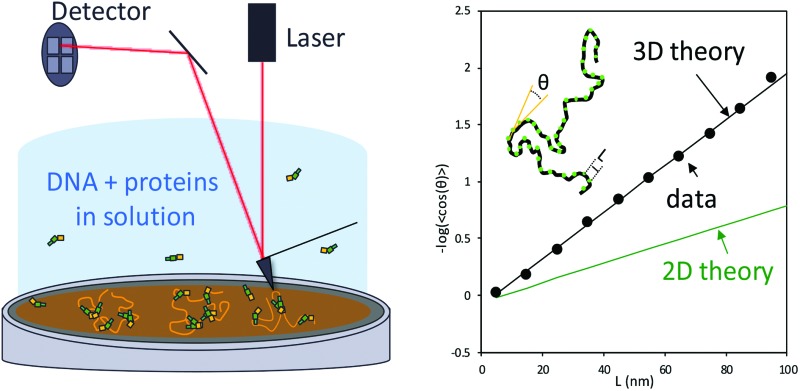
We obtain accurate three-dimensional persistence length measurements for DNA and DNA–protein complexes using liquid AFM imaging, validated by optical tweezers.

Abstract

The elasticity of double-stranded DNA (dsDNA), as described by its persistence length, is critical for many biological processes, including genomic regulation. A persistence length value can be obtained using atomic force microscopy (AFM) imaging. However, most AFM studies have been done by depositing the sample on a surface using adhesive ligands and fitting the contour to a two-dimensional (2D) wormlike chain (WLC) model. This often results in a persistence length measurement that is different from the value determined using bulk and single molecule methods. We describe a method for obtaining accurate three-dimensional (3D) persistence length measurements for DNA and DNA–protein complexes by using a previously developed liquid AFM imaging method and then applying the 3D WLC model. To demonstrate the method, we image in both air and liquid several different dsDNA constructs and DNA–protein complexes that both increase (HIV-1 Vpr) and decrease (yeast HMO1) dsDNA persistence length. Fitting the liquid AFM-imaging contour to the 3D WLC model results in a value in agreement with measurements obtained in optical tweezers experiments. Because AFM also allows characterization of local DNA properties, the ability to correctly measure global flexibility will strongly increase the impact of measurements that use AFM imaging.

Introduction

DNA is a polymer that stores the genetic information necessary for cellular function. For this genomic DNA to fit into the limited available cellular space, it must be strongly compacted, inhibiting access required for gene expression. To address this challenge, unfolding of specific genomic DNA regions must be dynamically regulated in the cell. Because the extent of DNA compaction can be controlled by the stiffness of polymeric DNA, this regulation requires modification of DNA mechanical properties. Many proteins participate actively in altering DNA flexibility through bending and looping. An example is the high mobility group type B (HMGB) class of proteins found in eukaryotic cells.1,2 From a biophysical perspective, an accurate measurement of DNA flexibility, reflected in part by the parameter known as the persistence length, is critical to advance our understanding of the functions of DNA-interacting proteins and small molecules. Accurate determination of the effects of proteins on DNA persistence length is necessary for understanding the functions of many important cellular proteins.3

Atomic force microscopy (AFM) is a powerful technique to study the biophysical properties of single DNA molecules, including DNA flexibility. AFM directly probes the conformations and interactions of DNA and proteins locally, with nanometer and picoNewton resolutions.1,4–11 Describing the flexibility of DNA deposited on a surface has been challenging because of the surface treatment required for DNA immobilization. Surface treatment affects DNA deposition and conformation. DNA molecules can be deposited on the surface in two main ways. In most cases, molecules can either be equilibrated or kinetically trapped on the surface. For studies reported to date, the approach used to estimate the persistence length involves either the two-dimensional Worm-Like-Chain (2D WLC) model, used for 2D equilibrium binding, or measurement of the projection on the surface of the three-dimensional Worm-Like-Chain (3D WLC) in the kinetic trapping case. According to surface treatments and solution condition both methods can result in values of the persistence length that deviate from the values measured using several other methods.7,12–15 Most AFM studies to characterize the double-stranded DNA (dsDNA) persistence length have been performed in air. Under these conditions the biophysical properties of the DNA are changed during drying, and this is reflected in the persistence length estimate.1,7,12,13,15 Obtaining high-resolution images of DNA and DNA–protein complexes in more physiologically-relevant liquid environments has been challenging.16,17 For example, scanning of DNA molecules in liquid yields blurry images if attachment is not sufficiently strong.18,19

It has been argued that AFM imaging of DNA in liquid preserves the DNA B-form structure,20 whereas air imaging may disturb the helical rise for various salt concentrations,7,20–23 thus perturbing the mechanical properties of the DNA. Solutions of divalent metal ions such as Mg²⁺ (ref. 7, 24 and 25) or Ni²⁺ (ref. 16, 26 and 27) are commonly used for DNA immobilization to mica surfaces prior to air drying,28,29 possibly altering the structure and functions of nucleic acids and proteins.30 Thus, although AFM is powerful in its direct imaging of DNA to determine local flexibility, the accuracy of persistence length determination by this method seems to vary, and surface deposition methods may alter the physical properties of the DNA.

Here we avoid the problems described above by imaging DNA in liquid without added metal ions. To do this, we first treat a mica surface with 3-aminopropyl-trietoxy silane (APTES). The modified surface becomes positively charged in the absence of divalent cations.31–33 We then image DNA in liquid, as previously described by others.32,33 Here, we extend this method to quantitatively characterize DNA flexibility. To demonstrate the broad applicability of the method, we characterize several DNA constructs of different lengths and composition. We first characterize three different DNA constructs (plasmids pUC18, pBR322 and a portion of mitochondrial genomic DNA (mtDNA)) and calculate the persistence length of each construct. We show that to accurately characterize the flexibility of the DNA when imaged in liquid, the three-dimensional Worm-Like-Chain (3D WLC) model must be applied. This suggest that DNA molecules adopt a three-dimensional conformation on the surface by preserving its bend angles under these conditions. We find that fitting image data to a 3D WLC model yields persistence length estimates that agree with those obtained in optical tweezers experiments where DNA is stretched in solution. To extend these results, we also tested the effects of two different classes of proteins on the measured DNA persistence length. We tested the high-mobility group B (HMGB) protein HMO1, and the HIV-1 Viral protein R (Vpr), which strongly alter DNA flexibility in opposite ways. In both cases, we find that fitting AFM data in liquid using the 3D WLC model yields quantitative persistence length measurements in agreement with DNA stretching measurements using optical tweezers. We conclude that AFM imaging in liquid can be an excellent method to quantitatively probe the flexibility of DNA and DNA–protein complexes.

Experimental

Atomic force microscopy

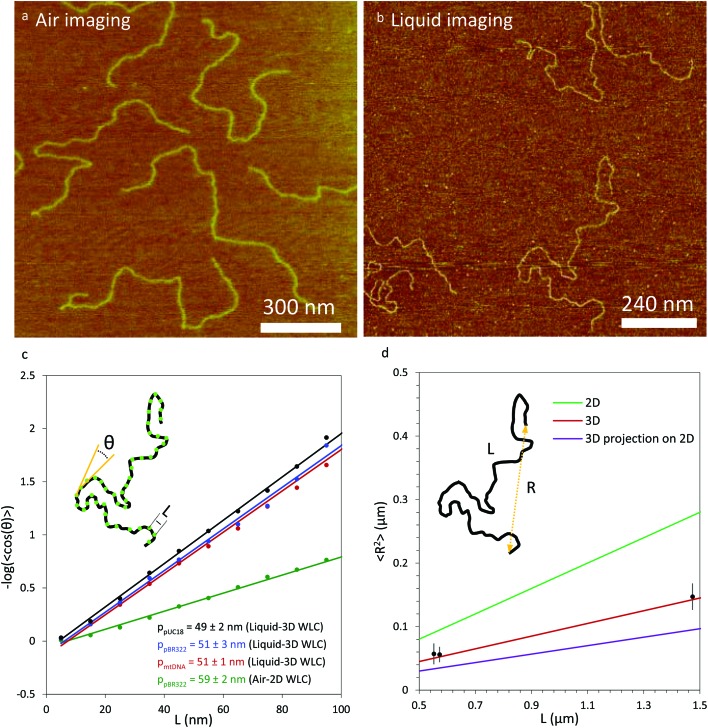
High-resolution atomic force microscopy images were obtained using a Bruker Nanoscope V MultiMode 8 instrument with PeakForce Tapping™ (PeakForce) mode. By controlling and lowering the force settings for this mode, the PeakForce method enabled us to scan delicate samples without causing damage.1,12,34 The peak force setting was varied from 70 pN to 120 pN and the vertical adjustment was varied from 500 nm to 1 μm to optimize image quality. Under these settings, the sample is gently touched by the tip, pushing it down as it scans the surface. Both experiments in air and in liquid were performed at room temperature and at atmospheric pressure. For air imaging, we used a silicon cantilever (resonance frequency = 70 kHz, spring constant = 0.4 N m^–1, and tip radius = 2 nm). The scan size varied from 1 μm × 1 μm to 5 μm × 5 μm and from 512 × 512 to 1024 × 1024 pixels, all scanned at a rate of 1.00 Hz. For liquid imaging, we used a silicon cantilever (resonance frequency = 150 kHz, spring constant = 0.7 N m^–1, and tip radius = 2 nm) submerged in a flow cell. The flow cell contained a solution of 30 μL. The scan size varied from 868 nm × 868 nm to 1.2 μm × 1.2 μm at 512 × 512 pixels, all scanned at a rate of 1.00 Hz. Image processing was done using Nanoscope analysis software, using the flattening function to remove planar artifacts. Tracing of DNA molecules was carried out using NCTracer software.12 The persistence length p was characterized in the absence and presence of proteins. To do this, orientation differences, θ, for different locations along the DNA were measured as a function of contour length, L. Thus, for each data point along the contour obtained from NCTracer, a second data point a distance L away along the DNA contour, was determined, and a line was drawn between these two points. This process was repeated for the next two data points and the angle θ between the two lines was determined, as shown in the inset of Fig. 1c. This was then repeated over the length of each molecule for values of L ranging from 5 nm to 100 nm and plotted in Fig. 1c. The results were then fit to the 2D WLC model1,7,12,13 and 3D WLC7,35,36 model for imaging in air and in liquid, respectively.

cos(θ) = e^–L/2p (2D) 1

cos(θ) = e^–L/p (3D) 2

Fig. 1. Comparison of the measured persistence length for multiple DNA constructs imaged in liquid and in air. (a) Air imaging of pBR322 DNA. (b) Liquid imaging of pBR322 DNA. (c) DNA constructs pUC18 (black), pBR322 (blue) and mtDNA (red) imaged in liquid show a value of the persistence length which agrees with the three dimensional value of the DNA persistence length. Air imaging of pBR322 DNA (green) shows a value of the persistence length that is higher than the value of the three dimensional persistence length obtained with optical tweezers experiments. The inset represents DNA local bends. Each point (in green) along the DNA is separated by a distance L. The local angle θ between two segments (in yellow), which represent the tangent between two adjacent points is separated by a distance L. Each data point represents an average of measured angles for between 17 and 47 molecules, depending on the construct. Statistical uncertainties in each data point (SEM) are smaller than the data point in each case. Uncertainties in the persistence length value shown are 95% confidence interval from fits to eqn (1) or (2). (d) End-to-end distance measurements as a function of contour length. The data for the three DNA constructs are represented in solid black symbols. The green line represents the values from eqn (3) for DNA equilibrated in 2D. The red line represents the values from eqn (4) for DNA in 3D. The purple line represents the values from eqn (5) for DNA in 3D projected on a 2D surface. For all three equations, a value of 50 nm was used for the persistence length. The inset shows a diagram of a DNA molecule with the end-to-end distance R and the full DNA contour length L. Error bars are standard error for end-to-end distance measurements from 13 to 47 molecules.

Although cos(θ) was determined as a function of L ranging from 5 nm to 100 nm, the data were fit over a range of 25 nm ≤ L ≤ 70 nm to give an optimal value of p, as previously described.12,13 Each measurement was obtained for a number of molecules ranging from 17 to 47, depending on the construct. As discussed in Abels et al.,36 although the image obtained is in 2D, the resulting contour reflects local bending angles in 3D. For this method, all DNA molecules without loops were fully analyzed and the non-looped parts of the molecules containing loops were also analyzed starting more than one persistence length away from the loop. Thus, about 90% of the DNA on a given surface was analyzed.

To further test the mechanical properties of DNA on the surface we also obtained the end-to-end distance measurements in 2D (eqn (3)), 3D (eqn (4)) and 3D projection on a 2D (eqn (5)) surface for each molecule (Table 2).7,36

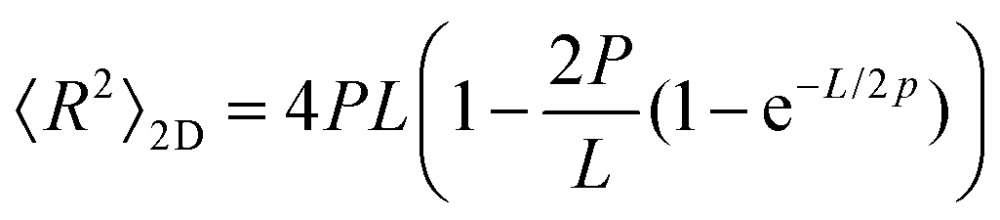3

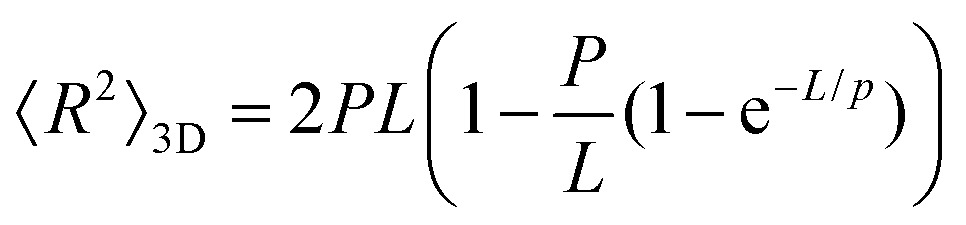4

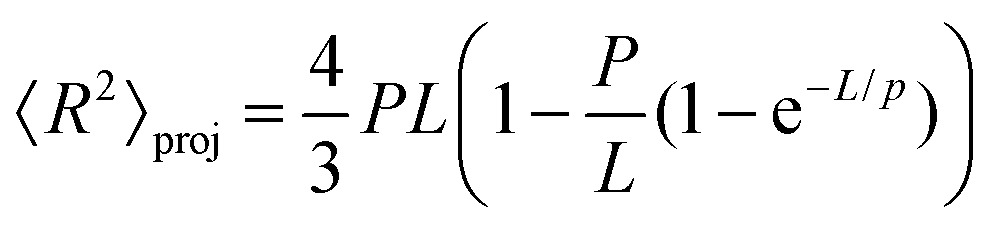5

Table 2. Measured value of the contour length and measured persistence length from end-to-end distance measurements, fit to models for two-dimensional WLC, three-dimensional WLC, and projection of 3D WLC onto a 2D surface, as described by eqn (3), (4), and (5). Uncertainty in measured length is standard error for at least 13 measurements. Uncertainty in persistence length is propagated from uncertainty in end-to-end distance (Fig. 1d) and contour length measurements.

Construct	DNA length (bp)	DNA measured length (bp)	2D persistence length using end-to-end distance (nm)	3D persistence length using end-to-end distance (nm)	Persistence length from projection of 3D on 2D (nm)
pUC18	1650	1624 ± 96	26 ± 2.5	51.7 ± 5.1	77.5 ± 7.6
mtDNA	1663	1684 ± 21	24.5 ± 2	48.9 ± 3.6	73.4 ± 5.4
pBR322 (air)13	4361	4353 ± 324	57 ± 6
pBR322 (liquid)	4361	4334 ± 116	25 ± 1	49.9 ± 2.4	74.9 ± 3.6

For this method, only molecules that did not contain loops were used, such that about 76% of the molecules on a given image were used in this analysis.

DNA and protein–DNA sample preparation for AFM

Air imaging was done using 4361 bp linearized plasmid pBR322 DNA deposited on a freshly cleaved mica surface, using 5 mM Mg²⁺ as a bridging agent.12,13 Vpr (11 kDa)37 and HMO1 (25 kDa)38–40 protein concentrations were 5 nM and 3 nM, respectively, corresponding to a ratio of protein to DNA bp ([DNA]/[Vpr]/[DNA]*(DNA chain length in bp)) of 0.01 and 0.06. The sample for liquid imaging was prepared using a freshly cleaved mica surface coated with 3-aminopropyl-trietoxy silane (APTES). To prepare the surface, ten freshly cleaved mica surfaces were placed in a vacuum desiccator along with a 30 microliter solution of APTES and 10 microliters of N,N-diisopropylethylamine (DIPEA) in a small container. The desiccator was evacuated with the APTES and DIPEA, then left to evaporate and coat the mica for 2 hours. The desiccator was then purged with argon gas for 2 minutes and then opened to the air to remove the APTES and DIPEA solutions. It was then purged again with argon for 2 minutes and evacuated and left under vacuum for two days to cure before imaging.33,41 The coated surfaces were stored under vacuum until used. The surfaces typically last for several weeks, depending on exposure to air during exchange. The concentration of DNA for pUC18, pBR322 and mtDNA used in these experiments was 0.11 nM. The pBR322 was linearized with Puv II as previously described.13

For the mtDNA construct, a fragment of mtDNA (CRS, NC_012920) that contains the LSP, HSP1 and IPR, region 1 to 741, was cloned into pUC18 between the BamH I and Hind III sites. Dual promoter DNA templates were prepared by PCR using the pUC-mtDNA (1–741) as template and the forward primer, LSP + 510-For, (5′-CTTCCGGCTCGTATGTTGTGTGGAATTG-3′) and reverse primer, HSP1 + 1000-Rev, (5′-ACTTTAAAAGTGCTCATCATTGG-3′). PCR products were purified with Wizard SV gel and PCR Clean-up System (Promega), DNA was eluted in 80 μL TE (10 mM Tris-HCl, pH 8.0 buffer and 0.1 mM EDTA) and finally diluted to 1 μM in TE buffer. Extinction coefficients for each DNA construct were calculated with IDT DNA technologies tool (http://biophysics.idtdna.com/UVSpectrum.html). The concentration of Vpr and HMO1 proteins used in these experiments was 2 nM and 1 nM, respectively, corresponding to a ratio of protein to DNA bp of 0.01 and 0.06. In liquid, the AFM experiment was carried out in 38 mM Na⁺, 25 mM Hepes at pH 7.5. For dry imaging of Vrp-DNA complexes, the same solution of 38 mM Na⁺, 25 mM Hepes at pH 7.5 was used on a 5 mM Mg²⁺ treated mica surface. For dry imaging of HMO1-DNA complexes, 10 mM Tris-HCl (pH 8.0) and 5 mM Mg²⁺ was used for deposition on mica.

Optical tweezers

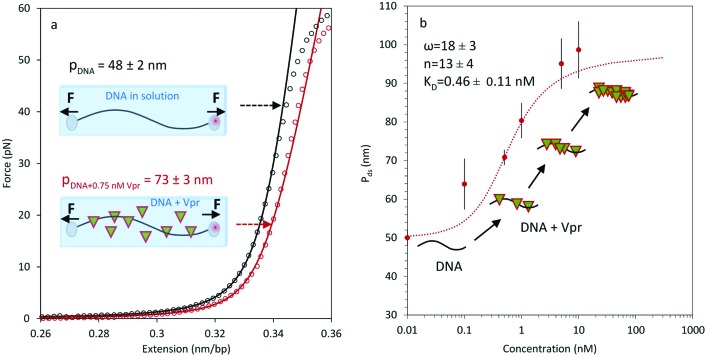
To characterize Vpr-DNA interactions, a single phage-λ DNA molecule (48 500 base pairs) was captured and extended in the absence and in the presence of proteins using optical tweezers. The experimental buffer used was 10 mM Hepes, pH 7.5, and 50 mM Na⁺. The change in the force–extension curve was quantified using the Extensible Worm-Like Chain (WLC).1,42

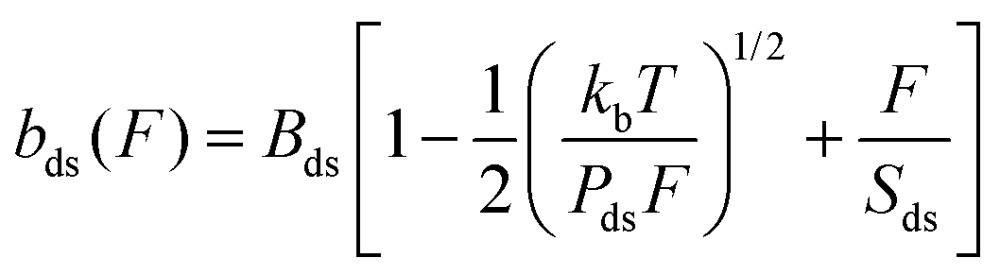6

where b_ds and F are the measured extension and force respectively, P_ds is the persistence length, B_ds is the contour length of the DNA measured in the unit of nm bp^–1, and S_ds represents the elastic modulus, which takes into account the backbone extensibility.

To quantify the binding of Vpr to DNA,12 we used the cooperative McGhee–von Hippel binding isotherm, which is given by1,43,44

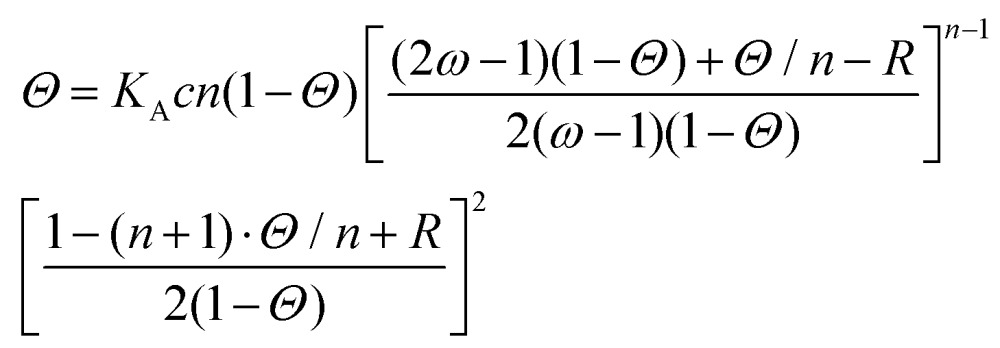7

where K_A is the equilibrium DNA binding affinity, Θ is the DNA fractional site occupancy, n is the binding site size, ω is the cooperativity parameter and c is the concentration of proteins in solution. The cooperative equilibrium dissociation constant for the protein binding to the lattice is K_D = 1/K_Aω.

The persistence length is given by

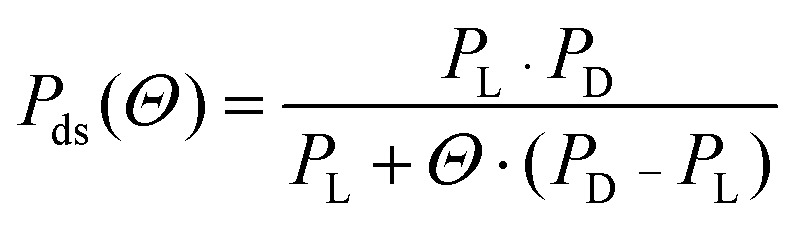8

where P_D is the protein-free value of P_ds and P_L is the protein-saturated value of P_ds.1 Optical tweezers data with HMO1 was taken from previously published work.12 Although the salt concentration is slightly different in the optical tweezers experiments relative to the AFM imaging experiments, the range of salt concentrations used varies between 38 mM Na⁺ to 100 mM Na⁺. Over this range, the DNA persistence length does not change significantly.45

Results

3D WLC fitting of AFM images of DNA in liquid yield correct persistence length value

Local bending angle fitting to determine persistence length

To investigate the mechanical properties of DNA molecules adsorbed to a mica surface we used AFM to map the conformations of the molecules. We imaged pBR322 in air (Fig. 1a) and found that using the standard method to fit the contour of the molecule to the 2D WLC model (eqn (1)), the persistence length of naked DNA was estimated to be 59 ± 2 nm,12 (Fig. 1c, green), a value which agrees with other values in the literature for AFM measurement on a dried surface.7,13 For comparison, we imaged in solution linearized plasmids pBR322 (4361 bp, Fig. 1b), pUC18 (1650 bp), and a mitochondrial DNA sequence (1663 bp, mtDNA). The resulting measurements are shown in black, blue, and red, respectively in Fig. 1c. The inset depicts the concept of local DNA bends used to estimate the persistence length. Each point (in green) along the DNA contour is separated by a distance L. The local angle θ between two linear segments (in yellow) represents the tangent between two adjacent points separated by a distance L. The measured values of the persistence length of DNA alone for these three constructs, when fit to the 3D WLC model (eqn (2)), are 49 ± 2 nm, 51 ± 3 nm, and 51 ± 1 nm, respectively (Fig. 1c). As shown in Table 1, the values we obtained agree, within uncertainty, with the results of single molecule DNA stretching experiments using optical tweezers in solution.1,15 Given the conventional method of fitting DNA dried on a mica surface to a 2D WLC model, we were initially surprised that only fitting to the 3D WLC model gave the correct DNA persistence length for experiments in liquid. Therefore, we used another method to also find the persistence length.

Table 1. Comparison between AFM and optical tweezers measured persistence length fit to two-dimensional and three-dimensional WLC model. For DNA only we present the weighted mean for the three constructs. The conditions for Vpr and HMO1 correspond to those presented in Table 3. Optical tweezers values are calculated at the effective concentration determined from the liquid AFM measurements (0.75 nM for Vpr and 0.86 nM for HMO1, Table 3) from fits to eqn (6)–(8). See for example the fit line shown in Fig. 3b for Vpr. Uncertainties are 95% confidence interval from fits to eqn (1) (2D, air AFM) or eqn (2) (3D, liquid AFM). For optical tweezers measurements, uncertainties were determined from fits to eqn (7) and (8) using the χ² + 1 method60.

	Persistence length	Persistence length	Persistence length
	DNA only (nm)	DNA + HMO1 (nm)	DNA + Vpr (nm)
2D fit AFM air	59 ± 2	39 ± 2	108 ± 2
3D fit AFM air	118 ± 4	78 ± 4	216 ± 4
2D fit AFM liquid	25.3 ± 0.7	10.5 ± 1.5	34 ± 3
3D fit AFM liquid	50.6 ± 1.4	21 ± 3	68 ± 5
Optical tweezers (liquid AFM conditions)	50 ± 2	16 ± 3	75 ± 3
Optical tweezers (air AFM conditions)	50 ± 2	17 ± 3	78 ± 3

End-to-end distance fitting to determine persistence length

To test whether the local flexibility is also manifested in overall molecule flexibility, we also measured the end-to-end distance distribution for the molecules tested in liquid. We observe that when fitted with 2D end-to-end distance (eqn (3)) the weighted average DNA persistence length for the three constructs is 25 ± 1 nm. Additionally, using a model for measurements of the end-to-end distance after projection of the 3D WLC model on the 2D surface gives 75 ± 3 nm for the weighted average (eqn (5)). In contrast, the end-to-end distance measurements assuming a pure 3D WLC model (eqn (4)) give a weighted average persistence length value of 50 ± 2 nm, which agrees with the value obtained using bending angles above, as illustrated in Fig. 1d and Table 2. The results suggest that these DNA molecules deposited on APTES in liquid adopt equilibrium 3D conformations as described by the 3D WLC model. To test whether this observation holds for molecules of different flexibilities, we also measure the persistence length of DNA–protein complexes.

Measuring persistence lengths for DNA–protein complexes of varying flexibility

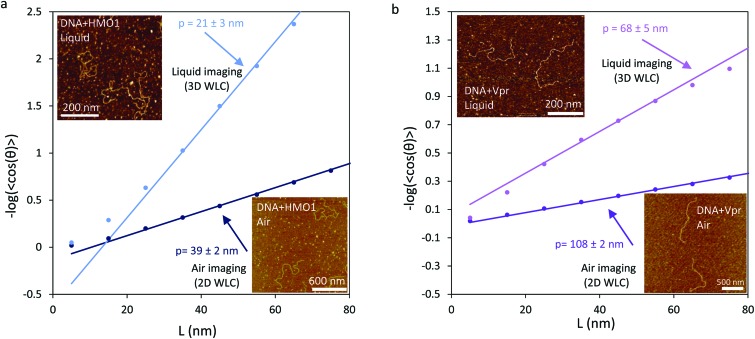
AFM can detect conformations of DNA–protein complexes with nanometer resolution, allowing characterization of protein–DNA interactions.12,32,46–48 We recently performed experiments with HMO1, a yeast nucleolar architectural DNA bending high-mobility group B (HMGB) protein. HMO1 is involved in chromatin structure maintenance and facilitation of ribosomal RNA transcription.1,12,39,40 By imaging HMO1-DNA complexes in air at 0.06 proteins/DNA bp, and fitting to the 2D WLC (eqn (1)), we measured a persistence length of 39 ± 2 nm. To compare AFM data with many DNA molecules and optical tweezers data with only a single molecule we use the effective concentration, reflecting the depletion of protein in solution when binding to the many DNA molecules in solution in the AFM experiments. In contrast, because there is only one DNA molecule in solution in the optical tweezers experiments, the protein concentration added is the same as the concentration in solution. Using the DNA binding affinity for HMO1 to calculate the effective concentration in solution in the AFM experiments (0.76 nM),49 the persistence length measured in optical tweezers (eqn (6)) under these conditions corresponds to 17 ± 3 nm.12 Although in both dried AFM imaging and in optical tweezers experiments we observe a decrease in persistence length relative to DNA only (39 ± 2 nm compared to 17 ± 3 nm), the values obtained in these two experiments disagree (Table 3). This discrepancy might be due to the fact that the AFM measurements were carried out on a dried, Mg²⁺-coated surface, which can result in the quasi-absence of monovalent salt or other artifacts of the washing process.50 When HMO1-DNA complexes are imaged in a liquid environment at 0.06 proteins/DNA bp, corresponding to an effective HMO1 protein concentration of 0.86 nM (Table 3), we also observe a decrease in the persistence length. By fitting these AFM liquid imaging data to the 3D WLC we found the persistence length to be 21 ± 3 nm, a value that agrees, within uncertainty, with optical tweezers measurements (Table 3).

Table 3. Exact binding conditions used for all AFM measurements along with effective concentration determined by calculating the amount bound to DNA of different lengths. This effective concentration was used to determine the optical tweezers persistence length conditions in Table 1. The DNA concentration used in all AFM experiments was 0.11 nM DNA molecules.

	[Protein]/[bp]	Effective concentration for optical tweezers comparison (nM)	Measured DNA length without proteins (bp ± SD)	Number of bp
DNA + 5 nM Vpr (air)	0.01	0.87	4353 ± 324 (pBR322)	4361
DNA + 2 nM Vpr (liquid)	0.01	0.75	1624 ± 96 (pUC18)	1650
DNA + 3 nM HMO1 (air)	0.06	0.76	4353 ± 324 (pBR322)	4361
DNA + 1 nM HMO1 (liquid)	0.06	0.86	1624 ± 96 (pUC18)	1650

Upon binding DNA, proteins may decrease the apparent DNA persistence length, as in the case of HMO1,12 increase the DNA persistence length,51 or leave DNA flexibility unaffected. To further test whether AFM measurements in liquid accurately reflect solution properties of the polymer, we performed additional AFM and optical tweezers experiments to study protein–DNA complexes with increased apparent persistence length. We studied DNA complexes with HIV-1 Viral protein R (Vpr) and characterized their mechanical properties (Fig. 2b and 3). Human immunodeficiency virus type 1 (HIV-1) encodes two regulatory proteins and four accessory proteins in addition to gag, pol and env proteins. Viral protein R (Vpr) is an accessory protein composed of 96 amino acids. Vpr is packaged into virions and is essential for maintaining the virulence of the virus,37 Vpr contains three alpha-helices, a flexible N-terminal region, and a flexible C-terminal region.52 The functions of Vpr remain mysterious, though in vivo functions attributed to Vpr include modulation of transcription of the virus, disruption of cell-cycle control by releasing cytochrome c from mitochondria, nuclear transport of the HIV-1 pre-integration complex (PIC), facilitating reverse transcription, suppression of the immune activation, and reduction of the HIV mutation rate.53 It has also been suggested that Vpr uses the cellular machinery to transfer proviral DNA to the nucleus.53 Optical tweezers data obtained here show that Vpr increases the apparent DNA persistence length in Vpr-DNA complexes.

Fig. 2. The yeast nucleolar HMGB protein HMO1 and the HIV-1 Viral protein R decrease and increase the persistence length of the DNA, respectively. (a) The apparent DNA persistence length in DNA-HMO1 complexes (lower-right inset) imaged in air (dark blue) is 39 ± 2 nm when fit to the 2D WLC (eqn (1)). The apparent DNA persistence length in DNA-HMO1 complexes (upper-left inset) imaged in liquid (light blue) is 21 ± 3 nm when fit to the 3D WLC (eqn (2)). (b) The apparent DNA persistence length in DNA-Vpr complexes (lower-right inset) imaged in air (dark purple) is 108 ± 2 nm when fit to the 2D WLC. The apparent DNA persistence length in DNA-Vpr complexes (upper-left inset) imaged in liquid (light purple) is 68 ± 5 nm when fit to the 3D WLC. Uncertainties are 95% confidence intervals from fits to the corresponding WLC model.

Fig. 3. Measurements of apparent DNA persistence length in the presence of HIV-1 Viral protein R (Vpr) proteins. (a) The binding of Vpr to DNA increases its apparent persistence length. DNA in the absence (black circle) and presence (red circle) of 0.75 nM Vpr is illustrated, along with a corresponding theoretical WLC curve, obtained from the average of three measurements, each fit to eqn (6). Uncertainty in the fit is SEM from the three measurements. The schematic diagrams represent DNA in solution and DNA in the presence of Vpr proteins (triangle symbols). A force F is exerted on both beads, allowing us to stretch the DNA and then to measure the mechanical properties of DNA. (b) The apparent DNA persistence length as a function of concentration is fit to the McGhee–von Hippel binding isotherm to obtain ω = 18 ± 3, n = 13 ± 4, and K_D = 0.46 ± 0.11 nM. Error bars are SEM for 3 or more measurements. Uncertainties in the fit parameters were determined from fits to eqn (7) and (8) using the χ² + 1 method.60.

The value of the DNA-Vpr complex persistence length was obtained by fitting optical tweezers data to the Extensible WLC model (eqn (6), Fig. 3a) at different protein concentrations (Fig. 3b). Measurement of the persistence length as a function of protein concentration enabled us to extract equilibrium binding parameters by fitting P_ds to the McGhee–von Hippel binding isotherm (eqn (7) and (8)). From the fit we estimate the binding cooperativity parameter, ω = 18 ± 3, and the cooperative equilibrium dissociation constant for the protein binding to the DNA lattice K_D = 0.46 ± 0.11 nM, with a binding site size n = 13 ± 4 bp. The AFM-measured value of the persistence length in air (2D WLC) is 108 ± 5 nm at a 0.01 protein to DNA bp ratio. Using the K_D value measured here, the effective concentration in solution for these conditions is 0.87 nM, yielding an optical tweezers persistence length of 78 ± 3 nm, which does not agree with the AFM measurements taken in air. In contrast, using liquid AFM imaging and fitting to the 3D WLC model at a 0.01 protein to DNA bp ratio, the measured persistence length is 68 ± 5 nm. Again using the K_D value measured here, the effective concentration of Vpr in solution for AFM imaging in liquid is 0.75 nM. A representative force–extension curve for DNA in the absence of Vpr (Fig. 3a, black curve) and in the presence of 0.75 nM Vpr is shown in Fig. 3a (red curve). The persistence length of 75 ± 3 nm, obtained in optical tweezers experiments under the equivalent liquid AFM imaging conditions, agrees within uncertainty with the persistence length of 68 ± 5 nm from AFM imaging in liquid under the same conditions when fit to the 3D WLC model (Table 3). These Vpr results demonstrate that accurate apparent persistence length measurements can be obtained by AFM in liquid for DNA stiffened by protein binding.

Discussion

By combining AFM imaging in liquid with optical tweezers experiments, we have demonstrated that the persistence length of DNA of multiple different lengths as well as DNA–protein complexes of varying flexibilities can be accurately described by the 3D WLC model. These results are obtained both from local bending angle measurements as well as measurements of DNA end-to-end distances. In contrast, previous measurements of DNA flexibility were obtained on samples prepared on a mica surface in the presence divalent cations, which were used as adhesive ligands either in air or in liquid. In those cases, the drying process or the presence of adhesive ligands apparently impedes equilibration of the DNA conformation on the surface, or otherwise alters the mechanical properties of the DNA. Consequently, the measurements thus obtained typically overestimate the persistence length of the DNA for long molecules.1,7,12,13 Some other studies showed that divalent cations such as magnesium interact with the bases and the backbone of the DNA,30,54 which may alter the mechanical properties of the DNA, changing the measured persistence length. All of these studies have shown that DNA adsorbed on the surface follow a 2D WLC model.7 In contrast, some other studies in a dry environment have shown that a 3D conformation can be captured through kinetic trapping either by polylysine and using local curvature analysis36,55 or APTES.56 However, although it was found that an accurate 3D persistence length could be determined by kinetic trapping, the use of polylysine may alter protein–DNA interactions by binding directly to the DNA molecules. These kinetic trapping methods also required drying of the DNA on the surface, which may alter its properties. It was also shown that for DNA deposited on APTES and then dried the physiological B form is preserved. In this case, persistence length varied from 51 ± 5 nm to 55 ± 5 nm for length constructs from 3 times the DNA persistence length to 5 times the DNA persistence length, with the high uncertainty likely reflecting significant variability in DNA flexibility after drying.56 Finally, some previous studies were also performed using AFM imaging in liquid, but Mg²⁺ ions were used to anchor the DNA molecules to the surface. The authors found that adding NaCl resulted in entropy gain by the polymer through competition with Mg²⁺ binding, resulting in a decrease in the observed persistence length at high salt. Thus, at 1 mM MgCl₂ and without NaCl, the authors obtained a persistence length of 37 ± 3 nm using the 2D WLC model. This value is consistent with the expected decrease in persistence length due to binding of multivalent ions.54,57 At 1 mM MgCl₂ and 100 mM NaCl the authors obtained a value of 25 ± 2 nm for the DNA persistence length when fit to the 2D WLC model.50 However, a 25 nm persistence length in the 2D WLC model would be 50 nm in the 3D WLC model, which is the known value for these conditions. This illustrates the difficulty with using MgCl₂, as the appropriate model for fitting the data appears to change from the 2D WLC to the 3D WLC as Mg²⁺ is titrated off the DNA by Na⁺. Table 4 illustrates the results from different surface preparation methods used to determine the persistence length of DNA.

Table 4. Persistence length of DNA for different surface preparations and AFM imaging conditions.

Surface coating	Imaging conditions	DNA surface trapping	WLC model	Persistence length (nm)	DNA length (nm)	Ref
Magnesium	Dry	2D equilibrium	2D	57 ± 6	1480 ± 110	13
				59 ± 2	1480 ± 110	12
				53	L < 1000	7
				71	922	7
				147	2038	7
Magnesium	Liquid	2D equilibrium	2D	84 ± 8 [1 mM NaCl]	From 60 to 10 200	50
				25 ± 2 [100 mM NaCl]		50
Polylysine	Dry	Kinetic trapping	3D	55 ± 2	318 ± 16	36
APTES	Dry	Kinetic trapping	3D	51 ± 5	163 ± 8	56
				55 ± 5	281 ± 10	56
APTES (this work)	Liquid	Kinetic trapping	3D	49 ± 2 nm	552 ± 32
				51 ± 1 nm	573 ± 7
				51 ± 3 nm	1474 ± 39

By performing AFM experiments both in air and in liquid, and comparing to the results of optical tweezers experiments, we demonstrate that the persistence length value obtained by fitting the local bending angles and end-to-end distances obtained from liquid AFM data to the 3D WLC model (P = 50.6 ± 1.4 nm) agrees, within uncertainty, with single molecule optical tweezers measurements (P = 50 ± 2 nm). The fits to the local bending angle assume that the angle θ measured on our 2D image reflects the 3D configuration adopted in 3D equilibrium by the molecule, as discussed in Abels et al.36 The end-to-end distance measurements, however, do not need to make this assumption. The measurements are also not consistent with a projection of the 3D conformation onto the surface, but rather with a configuration that preserves the 3D angular and end-to-end distance distributions when binding to the surface. The most likely explanation for our observation of 3D behavior is that the DNA is kinetically trapped on the 2D surface and that the surface attachment preserves the 3D angles, as discussed above. Although the persistence length of DNA was previously quantified for kinetically trapped DNA after drying, these measurements have not previously been reported for DNA imaged on APTES in liquid.

Thus, the DNA deposition and liquid imaging method used here allows us to capture the three-dimensional persistence length using two different types of measurements on images of DNA obtained in liquid. In contrast, AFM carried out on a dry surface in air with 5 mM MgCl₂ yielded an overestimated value of P = 59 ± 2 nm.12 It is possible to use lower amounts of MgCl₂, which may yield more accurate persistence length values, but we found it difficult to obtain good DNA–surface attachment at low MgCl₂ concentrations for long DNA molecules (greater than 1600 bp). Moreover, DNA–protein complexes formed with yeast HMO1 and HIV-1 Vpr both yielded apparent persistence length values from liquid AFM imaging that agreed, within uncertainty, with optical tweezers measurements. Measurements obtained in air did not (Table 3).

While our previous studies with HMO1 showed that it reduced the apparent DNA persistence length, the measurements reported here are the most accurate measurements of this effect. Although these measurements could also be obtained using optical tweezers, AFM images also yield distributions of local DNA bending angles as well as looping interactions induced by protein binding.12,58 When obtained on APTES-coated surfaces, these additional features can be more accurately determined and quantitated. There are no previous reports of the effect of Vpr on DNA elasticity. However, the results shown here demonstrate that Vpr significantly increases the DNA persistence length. This result explains the unusual mechanism of DNA compaction by Vpr, in which rodlike structures are alternated with strong DNA bends. This compaction mechanism may allow Vpr to facilitate transport of HIV-1 proviral DNA into the nucleus of infected cells.59

In summary, we have demonstrated that depositing DNA and DNA–protein complexes on APTES surfaces, followed by AFM imaging in liquid yields the correct persistence length when compared to that obtained in solution using optical tweezers. We showed that measurements of the local bending angle and the end-to-end distance of the deposited complexes reveal the correct persistence length value when fit to the 3D WLC model. This shows that the configuration revealed in the image reflects the 3D equilibrium conformation of the molecule. Thus, application of this AFM imaging method in liquid allows measurement of the 3D properties of DNA and DNA–protein complexes in solution without requiring the use of multivalent ions, which may interfere with the DNA–protein interactions being studied, and without requiring drying of the surface, which may alter the polymer properties. Such images can be used to measure local protein–DNA interaction characteristics that are not available from solution methods that determine average DNA bending properties.

Funding

This work was supported by the National Institutes of Health [R01GM072462 to M.C.W., R01GM075965 to L.J.M.]; and the National Science Foundation [MCB-1243883 to M.C.W.].

Author contributions

D.M. designed and performed experiments and analyzed data. S.B., L.J.M., C.E.C. contributed reagents. N.E.I. provided analysis advice. M.C.W. designed experiments. All authors wrote the paper.