Tutorial on Biostatistics: Linear Regression Analysis of Continuous Correlated Eye Data

Abstract

Purpose

To describe and demonstrate appropriate linear regression methods for analyzing correlated continuous eye data.

Methods

We describe several approaches to regression analysis involving both eyes, including mixed effects and marginal models under various covariance structures to account for inter-eye correlation. We demonstrate, with SAS statistical software, applications in a study comparing baseline refractive error between one eye with choroidal neovascularization (CNV) and the unaffected fellow eye, and in a study determining factors associated with visual field data in the elderly.

Results

When refractive error from both eyes were analyzed with standard linear regression without accounting for inter-eye correlation (adjusting for demographic and ocular covariates), the difference between eyes with CNV and fellow eyes was 0.15 diopters (D; 95% confidence interval, CI −0.03 to 0.32D, P=0.10). Using a mixed effects model or a marginal model, the estimated difference was the same but with narrower 95% CI (0.01 to 0.28D, P=0.03). Standard regression for visual field data from both eyes provided biased estimates of standard error (generally underestimated) and smaller P-values, while analysis of the worse eye provided larger P-values than mixed effects models and marginal models.

Conclusion

In research involving both eyes, ignoring inter-eye correlation can lead to invalid inferences. Analysis using only right or left eyes is valid, but decreases power. Worse-eye analysis can provide less power and biased estimates of effect. Mixed effects or marginal models using the eye as the unit of analysis should be used to appropriately account for inter-eye correlation and maximize power and precision.

INTRODUCTION

In ophthalmic research, an outcome measurement, eg, visual acuity, is often taken from both eyes of a person to evaluate its association with eye-specific or person-specific characteristics. This requires the eye to be the unit of statistical analysis. Because the outcomes measured from both eyes are usually positively correlated, appropriate data analysis requires using both-eye data and accounting for the inter-eye correlation to make a valid assessment of the association. In addition to the risk factor of interest, there are often other covariates (person-specific or eye-specific) that may affect the outcome, necessitating the use of multivariable regression approaches.

Correlated eye data are often analyzed using one of the following approaches^1,2:

1. Using data from each eye and ignoring the inter-eye correlation. Estimators of regression coefficients are unbiased, but the variance of the estimates is not correct.

2. Using data of one eye per subject, where the eye is chosen randomly or as the left, or as the right eye. Estimators of regression coefficients are unbiased, but because half of the data is not used, the variance of the estimators is greater than if all of the data is used with appropriate accommodation of the correlation. Furthermore, power is often reduced.

3. Using data of one eye per subject, where the eye is the worse eye or better eye, sometimes designated as “the study eye”. In addition to the loss of precision noted in 2), the association between the outcome of the worse (better) eye with covariates may be different than for all eyes, thus producing a biased estimate of the overall association.

4. Performing two separate analyses, one for left eye data, another for right eye data. Each of the analyses has the limitations noted in 2). In addition, estimates may differ between the two regression analyses when there is no biological basis for the associations to be affected by laterality.

5. Creating a person-specific outcome value by averaging across eyes. Estimators of regression coefficients are unbiased and the variance estimate is similar to using all of the data with appropriate accommodation of the correlation; however, eye-specific covariates cannot be accommodated.

The development of new statistical methodology and statistical software over the last 30 years allows for the use of multivariable regression models for analyzing ocular level data that can adjust for the inter-eye correlation. The computational procedures for mixed effects modelling³ and population-average (marginal) modelling using the generalized estimating equations (GEE) approach⁴ are now available in a number of statistical software packages (eg, SAS, R, Stata, etc). In this article, we examine the use of these linear regression techniques and illustrate their use by analyzing correlated continuous eye data from two real clinical studies of eye disease.

MATERIALS AND METHODS

Mixed effects model and marginal model

Two commonly used approaches that can accommodate correlated data are the mixed effects or random effects model using maximum likelihood estimation³ and the marginal model using GEE.⁴ The comparisons of these two approaches and the standard linear regression model are summarized in Table 1.

Table 1.

Comparisons of standard linear regression models, Mixed effects models and marginal models using generalized estimating equations (GEE)

	One-eye analysis	Two-eyes analysis
Characteristics of models	Standard linear regression models	Standard linear regression models	Mixed effects models	Marginal models using GEE
Assumption	Measure from an eye of a subject is independent of measure from other subjects	Measures from both eyes of a subject are independent, and also independent of measures from other subjects	Measures from both eyes of a subject are correlated, but independent of measures from other subjects	Measures from both eyes of a subject are correlated, but independent of measures from other subjects
Approach for accounting for inter-eye correlation	Not needed, as inter-eye correlation does not exist	None	By using random effects	By using “working correlation” for residuals of standard linear model
Estimation method	Least squares	Least squares	Maximum Likelihood	GEE
Estimate for mean response	Least squares means	Least squares means	Conditional on the random effects, the eye-specific outcomes are independent	Marginal, conditional only on covariates and not on other responses or random effects
Estimate of within-subject correlation	Not needed	None	Estimated together with the fixed effects	Separate from the estimate of marginal mean response
Regression coefficient estimate	Estimates change in mean value of an outcome corresponding to change in the covariate while holding constant other covariates	Estimates change in mean value of an outcome corresponding to change in the covariate while holding constant other covariates	Estimates change in expected mean value of outcome for an individual eye corresponding to change in the eye-specific covariates while holding constant other eye-specific covariates	Estimates change in mean value of all individuals corresponding to change in the covariate while holding constant other covariates
Interpretation of regression coefficient	Change in mean ocular outcome for a unit change of a covariate across all subjects	Change in mean ocular outcome for a unit change of a covariate across all subjects	Change in expected mean ocular outcome for a unit change in a covariate of a subject while keeping random effect fixed	Change in mean ocular outcome for a unit change in a covariate across all subjects
Missing data	Can handle data missing completely at random	Can handle unbalanced data and data missing completely at random	Can handle unbalanced data and missing at random	Can handle unbalanced data and missing completely at random
Advantage	Simplicity	Simplicity	Flexibility	Robustness to the mis-specification of covariance structure
Disadvantage	Loss of statistical power	Invalid inference	Easy to mis-specify the model (either random effect or fixed effect or covariance structure), lead to biased inference	May lose efficiency if covariance structure mis-specified or sample size too small
SAS procedure	PROC REG PROC GLM	PROC REG PROC GLM	RANDOM statement of PROC MIXED	PROC GENMOD
Stata procedure	REGRESS	REGRESS	XTMIXED	XTGEE

The mixed effects model is a statistical model containing both fixed effects and random effects (thus called mixed effects model). It is useful in settings where repeated measurements are made on the same subjects (such as in a longitudinal study), or where measurements are made on clusters of related statistical units (such as both eyes of a subject). In contrast to the standard regression model that assumes the intercept and the effect of each covariate on an outcome are the same across all subjects, mixed effects models assume that the effect of some factors are the same for all subjects (ie, the fixed effects) while the effect of other covariates may vary with different subjects (ie, the random effects). The mixed effects model explicitly accounts for the correlations between paired eyes of subjects by adding a random effect (such as a random intercept, assuming that the intercept is the same for both eyes of a subject, but different across different subjects) in addition to the fixed effects of interest that may be either person- or eye-specific. In the mixed effects model, the subject-specific random effect accounts for the inter-eye correlation, and the model provides the conditional mean of the outcome given covariates and random effects. An important assumption is that the distribution of the random effects is assumed to be normal. In addition, the interpretation of the covariate effects is conditional on the random effects. Thus, in an ophthalmic setting, one can estimate the expected change in outcome between both eyes of a subject given corresponding changes in covariate levels between eyes. The mixed effects model requires correct specifications for both fixed effects and random effects. In SAS, the mixed effects model is executed using PROC MIXED through a RANDOM statement.

The marginal model using the GEE approach provides the estimate of changes in the population mean corresponding to changes in covariates. Although GEE was initially developed to analyze correlated data from longitudinal repeated measures,⁴ it has been extended to other types of correlated data, including observations from paired eyes.⁵ Different from the mixed effects model, the GEE approach does not require distributional assumptions because estimation of the marginal model depends only on correctly specifying the linear function relating the mean outcome (or a transformation of the mean outcome referred to as the link function) to the covariates. In the GEE approach, a correlation function for the subunits within a cluster needs to be selected and a robust estimator of the variance of the regression coefficients, the “sandwich” estimator, is employed. In contrast to the mixed model which has a subject-specific interpretation, GEE is a marginal model approach, as it does not incorporate any random effects into the model. The marginal model takes account of the inter-eye correlation by estimating the covariance among all the residuals from a single subject, assuming the residuals from a subject are correlated, while the standard linear regression model assumes the residuals are independent with constant variance. The marginal model is usually executed in SAS using PROC GENMOD, or PROC MIXED using a REPEATED statement. In the latter case, PROC MIXED uses a likelihood-based approach assuming a normally distributed outcome variable, but allows for correlation among subunits within a cluster, without applying random effects. In the former case, normality is not assumed and a quasi-likelihood approach is employed that also takes account of correlation between subunits.

To model correlated data using the mixed effects models or marginal model, a covariance structure or working correlation must be specified. The observations may be correlated with each other in several different ways. The pattern of correlation is known as the correlation structure or covariance structure. For cross-sectional correlated eye data (ie, with the inter-eye correlation from both eyes of a subject but not repeated measures over time), the most commonly used covariance structures are unstructured covariance, compound symmetry, and working independence covariance matrix, as shown below.

1. Unstructured $\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_{12}\\ {\sigma }_{12}& {\sigma }_2^2\end{array}\right)$

   where the variance in one eye, ${\sigma }_1^2$, and the contralateral eye, ${\sigma }_2^2$, may differ, and ${\sigma }_{12}$ is their covariance. This covariance structure involves 3 parameters (ie, ${\sigma }_1^2$, ${\sigma }_{12}$ and ${\sigma }_2^2$).

2. Compound Symmetry $\left(\begin{array}{cc}{\sigma }^2& {\sigma }_{cs}^2\\ {\sigma }_{cs}^2& {\sigma }^2\end{array}\right)$

   where ${\sigma }_{cs}^2$ is the covariance between both eyes, and the variance of measurements in both eyes of a subject is the same and equal to ${\sigma }^2$. Of note, this covariance structure involves two parameters (ie, ${\sigma }_{cs}^2$ and ${\sigma }^2$).

   The above two covariance structures have a different number of parameters to estimate from the data. Compound symmetry is appropriate when the variances from both eyes are equal, and their inter-eye correlations are the same for an outcome measure from paired eyes. The variances are generally expected to be the same if both eyes are unaffected by disease or both are affected similarly and treated similarly. If no such assumption can be imposed, the unstructured covariance can be used, but fitting a model with an unstructured covariance structure may require a larger dataset than other approaches. The variances may be different when one eye is diseased and the other is not because the disease process may cause more variability in the outcome than in the normal state. Similarly, variances may be different if one eye (eg, the right eye) is always tested first and there are fatigue effects associated with the testing.

3. Working independence covariance matrix $\left(\begin{array}{cc}{\sigma }^2& 0\\ 0& {\sigma }^2\end{array}\right)$. This covariance structure only involves one parameter ${\sigma }^2$.

   Although the “working independence” covariance appears to ignore the correlation between eyes by specifying a correlation of 0, the GEE approach uses a robust variance estimator that provides asymptotically unbiased variance estimators for the regression coefficients. In GEE, with the working independence covariance structure, the regression coefficients are the same as for the standard linear regression model, but standard errors (SEs) are adjusted for the correlated data. With the compound symmetry correlation structure, both the regression coefficients and SEs differ from the standard linear regression model. When there is little knowledge available to choose between the unstructured and compound symmetry correlation structures, the working independence covariance matrix may be the best choice.

While the choice of covariance structure should be based on the biological or clinical context, in the cross-sectional paired eyes setting, we expect the choice of covariance structure will have minimal impact on the statistical inference as demonstrated in the following examples.

We demonstrate the application of the mixed effects model and marginal models to analyze cross-sectional correlated eye data from two clinical studies as described below. The institutional review board associated with each clinical center approved the study protocol and informed consent was obtained from each patient, and each study adhered to the tenets of the Declaration of Helsinki.

All statistical analysis were performed in SAS 9.4 (SAS Institute Inc, Cary, NC, USA), and the SAS codes are included in the Appendix.

Example 1: Analysis of refractive error data from a clinical trial

We first demonstrate the linear regression models by analyzing baseline refractive error data from the Comparison of Age-related Macular Degeneration Treatments Trials (CATT).⁶ CATT was a multi-center randomized clinical trial to assess the efficacy and safety of ranibizumab and bevacizumab when administered monthly or as needed. The study enrolled 1,185 participants aged ≥50 years, untreated active choroidal neovascularization (CNV) in the study eye due to AMD (the fellow eye could have or not have CNV), and visual acuity between 20/25 and 20/320. In CATT, refractive error was measured by subjective refraction, and spherical equivalent in diopters (D) was calculated as the sphere plus half of the cylinder.

We hypothesized that the morphological changes in the retina from active CNV would impact refractive error by changing the axial length of the eye. To test this hypothesis, we compared the baseline spherical equivalent between study eyes with active CNV and their fellow eyes among patients without CNV in the fellow eye at baseline. To eliminate the effect of lens status on refractive error, we restricted this comparison to 355 patients who had pseudophakic eyes.

Example 2: Analysis from visual field data from a cross-sectional study

Data were from 394 eyes of 197 patients aged 65 years or older who were seen for glaucoma treatment or were evaluated for a possible diagnosis of glaucoma in the Glaucoma Consultation Service of the Massachusetts Eye and Ear Infirmary. All patients had perimetry via an Octopus perimeter (Haag-Streit AG, Koeniz, Switzerland[AU: confirm?]) in each eye.^7–8 The percentage of normal visual field in an eye was calculated as the average threshold in the central 30° standardized by the normal value for a 65-year-old person. Distance visual acuity was assessed with the use of spectacles with and without pinhole, and the better of the two measures was taken as the Snellen visual acuity in an eye. Visual acuity was then transformed to a measure of percent impairment. Other measures assessed at the glaucoma examination included lens status in each eye and history of systemic hypertension. We are interested in determining the factors associated with visual field data, including person-specific factors (age, sex, and hypertension status) and eye-specific factors (lens status and visual acuity).

RESULTS

Comparison of refractive error in study eyes with CNV and fellow eyes without CNV in the CATT

Among 1,185 CATT participants randomized, 355 participants had active CNV only in the study eye and were pseudophakic in both eyes at baseline. The distributions of baseline refractive error in study eyes with CNV and their fellow eyes without CNV are shown in Figure 1.

Figure 1.

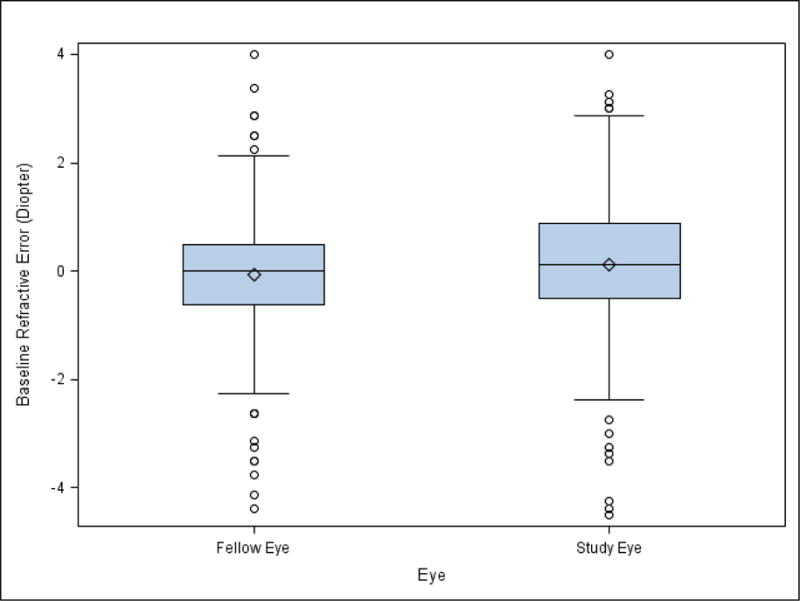
Boxplot for refractive error in study eyes with choroidal neovascularization (CNV) and fellow eyes without CNV in the Comparison of Age-related Macular Degeneration Treatments Trials

Because of the paired design (study eye with CNV, fellow eye without CNV) and the fact that the distribution of baseline refractive error is approximately normally distributed, the simplest analysis is to use a paired t-test to assess the mean difference in refractive error between study eyes and fellow eyes.

The mean baseline refractive error was 0.12D (standard deviation, SD 1.17D) in study eyes with CNV, and −0.03D (SD 1.21D) in the fellow eyes without CNV. The inter-class correlation coefficient between the study eyes and fellow eyes was 0.43 (95% confidence interval, CI, 0.35–0.52), so the statistical analysis needs to account for the inter-eye correlation in baseline refractive error.

The mean difference between study eyes and fellow eyes was 0.15 (95% CI 0.02–0.28), and the paired t-test provided a P-value of 0.02. An equivalent analysis is to calculate the refractive error difference between paired study eye and fellow eye for each participant, then perform a one sample t-test on the differences (which had a symmetric distribution as shown in Figure 2) to test whether the mean difference was statistically different from 0 or not.

Figure 2.

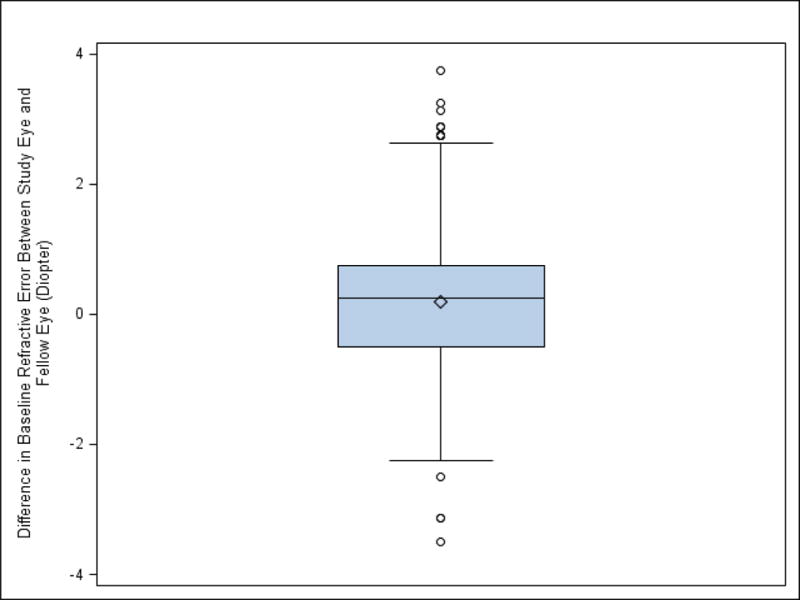
Boxplot for the difference in baseline refractive error between study eyes with choroidal neovascularization (CNV) and fellow eyes without CNV in the Comparison of Age-related Macular Degeneration Treatments Trials

To adjust for demographic covariates (age, sex, and smoking status) and ocular covariates (geographic atrophy, and glaucoma), we used multivariable linear regression models. The estimates of the difference in baseline refractive error from various analysis approaches between study eyes with CNV and fellow eyes without CNV are shown in Table 2. Without adjustment for any covariates, the paired t-test, mixed effects model and marginal models essentially provide the same statistically significant results (P=0.02), suggesting that refractive error is on average about 0.15D higher in study eyes with CNV compared to their fellow eyes without CNV. However, the standard regression analysis and the 2-group independent t-test that do not account for the inter-eye correlation provide results that are not statistically significant (P=0.09).

Table 2.

Comparison of baseline refractive error between study eyes with active choroidal neovascularization (CNV) and fellow eyes without CNV in the Comparison of Age-related Macular Degeneration Treatments Trials

Analysis approaches	The mean difference between study eyes with CNV and fellow eyes without CNV (95% CI), in diopters	P-value
Unadjusted analysis
Independent-sample t-test	0.15 (−0.03, 0.33)	0.09
Standard linear regression model	0.15 (−0.03, 0.33)	0.09
Paired t-test	0.15 (0.02, 0.28)	0.02
Mixed model, compound symmetry or unstructured	0.15 (0.02, 0.28)	0.02
Marginal model, PROC MIXED using REPEATED, unstructured	0.15 (0.02, 0.28)	0.02
Marginal model, GEE, working independent	0.15 (0.02, 0.28)	0.02
Covariates-adjusted analysis§
Standard linear regression	0.15 (−0.03, 0.32)	0.10
Mixed model, compound symmetry or unstructured	0.15 (0.01, 0.28)	0.03
Marginal model, PROC MIXED using REPEATED, unstructured	0.15 (0.01, 0.28)	0.03
Marginal model, GEE, working independence	0.15 (0.01, 0.28)	0.03
Marginal model, GEE, compound symmetry	0.15 (0.01, 0.28)	0.03

^§Adjusted for age, sex, current smoking status, geographic atrophy and glaucoma.

CI, confidence interval; GEE generalized estimating equation

The covariance matrix estimates from PROC MIXED using a REPEATED statement (see SAS code in Appendix) are as following:

• Unstructured covariance = $\left(\begin{array}{cc}1.456& 0.613\\ 0.613& 1.365\end{array}\right)$

• Compound symmetry covariance = $\left(\begin{array}{cc}1.410& 0.613\\ 0.613& 1.410\end{array}\right)$

The unstructured (using type=UN) and compound symmetry (using type=CS) provided identical off-diagonal covariance estimates (0.613), however, their diagonal variance estimates are similar but not identical.

In the regression model-based comparison of refractive error between study eyes with CNV vs fellow eyes without CNV with adjustment for covariates, the point estimates from the various models are the same, but the SE and their 95% CIs are not identical (Table 2). In this paired design, the standard linear regression analysis without accounting for inter-eye correlation provides a wider 95% CI than other analytic approaches that account for inter-eye correlation. The mixed model and marginal models provide identical results with respect to the estimated mean difference, 95% CI, and P-value.

The estimates for the baseline subject-specific (age, sex, smoking status) and eye-specific covariates including presence of geographic atrophy (yes/no) and glaucoma (yes/no), are shown in Table 3. The different regression models provide very similar point estimates for all of the regression coefficients, yet the SEs are different for some covariates, leading to different P-values. The covariate P-values are usually smaller in the standard linear regression models than other models that account for the inter-eye correlation. Particularly for the effect of glaucoma on refractive error, the standard regression model provides a P-value of 0.08, while the P-value from the other regression models that account for the inter-eye correlation are larger, 0.31 to 0.32 from the GEE models, 0.14 from marginal model using PROC MIXED with REPEATED and 0.16 from the mixed effects model using a RANDOM intercept.

Table 3.

Effect of covariates on baseline refractive error in study eyes with choroidal neovascularization (CNV) and fellow eyes without CNV using various regression approaches, Comparison of Age-related Macular Degeneration Treatments Trials

Covariates	Standard linear regression model		Mixed model, random intercept (unstructured or compound symmetry)		Marginal model: PROC MIXED with REPEATED unstructured		Marginal model: GEE, working independence		Marginal model: GEE, compound symmetry
	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value
Group (study eye vs fellow)	0.15 (0.09)	0.10	0.15 (0.07)	0.03	0.15 (0.07)	0.03	0.15 (0.07)	0.03	0.15 (0.07)	0.03
Age (per year)	0.01 (0.01)	0.20	0.01 (0.01)	0.29	0.01 (0.01)	0.29	0.01 (0.01)	0.21	0.01 (0.01)	0.22
Sex (female vs male)	0.05 (0.10)	0.58	0.05 (0.12)	0.66	0.06 (0.12)	0.62	0.05 (0.10)	0.60	0.05 (0.10)	0.61
Current smoking (yes vs no)	0.21 (0.18)	0.24	0.21 (0.21)	0.33	0.20 (0.21)	0.33	0.21 (0.23)	0.38	0.21 (0.23)	0.37
Geographic atrophy (no vs yes)	0.07 (0.16)	0.64	0.03 (0.15)	0.82	0.04 (0.15)	0.78	0.07 (0.20)	0.71	0.03 (0.19)	0.85
Glaucoma (no v. yes)	0.25 (0.14)	0.08	0.24 (0.17)	0.16	0.25 (0.17)	0.14	0.25 (0.24)	0.31	0.24 (0.24)	0.32

GEE, generalized estimating equation; SE, standard error

As demonstrated in Table 3, in evaluating the association of covariates with an eye-specific outcome, ignoring the inter-eye correlation has an impact on the statistical inference (SE and P-value). The direction (increase or decrease in SE or P-value) of this impact depends on the inter-eye correlation of the covariate. For both geographic atrophy and glaucoma, there is a positive correlation between both eyes (both had an inter-eye correlation coefficient of 0.37), and ignoring the inter-eye correlation makes the SE and P-value too small. Group status (study eye vs fellow eye) has a negative inter-eye correlation coefficient of −1.0 (due to the paired design) and ignoring the inter-eye correlation makes the SE and P-value too large.

The fit of the model can be assessed by a residual plot from the mixed model as shown in Figure 3. These plots indicate that the residuals show no specific pattern (ie, random) and are approximately normally distributed, indicating reasonable fit to the data by the model.

Figure 3.

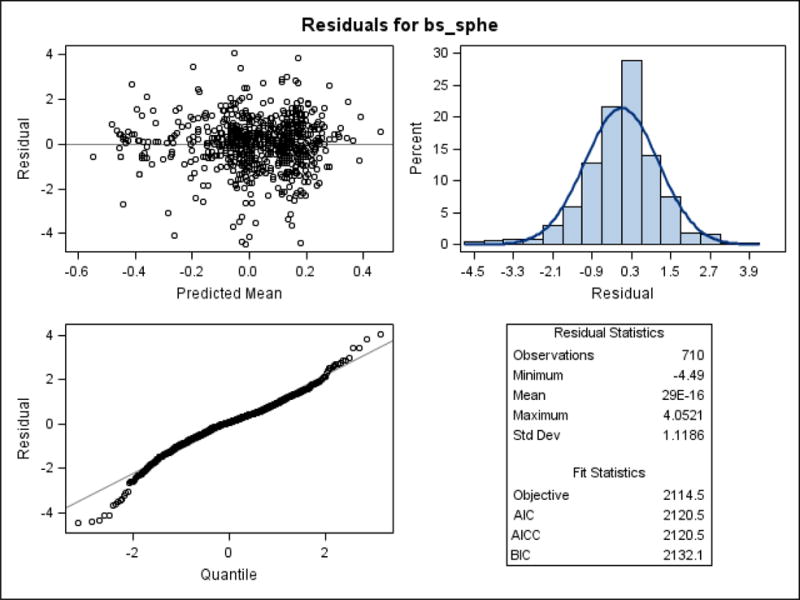
Residual plots for baseline refractive error between eyes with choroidal neovascularization (CNV) and fellow eyes without CNV from the multivariable mixed model in the Comparison of Age-related Macular Degeneration Treatments Trials

Risk factors for visual field loss in a cross-sectional study

Linear regression models were applied to evaluate how each factor (age, sex, hypertension, lens status and visual acuity) was independently associated with visual field data. However, the visual field data from both eyes of a patient are moderately correlated with an inter-class correlation coefficient of 0.56 (95% CI 0.46–0.65), justifying the need to account for the inter-eye correlation.

For comparison, we first fitted the standard linear regression model that ignores the inter-eye correlation for data from both eyes, and for data from the worse eye (ie, the eye with the worse visual field). We then fit the mixed effects model using a RANDOM intercept, marginal models using both GEE and PROC MIXED with REPEATED statement. We fitted the mixed effects model using both an unstructured covariance and a compound symmetry covariance. Their covariance estimates are extremely similar as shown below.

• Unstructured covariance = $\left(\begin{array}{cc}324.3& 179.4\\ 179.4& 324.8\end{array}\right)$

• Compound symmetry = $\left(\begin{array}{cc}324.6& 179.4\\ 179.4& 324.6\end{array}\right)$

The results for the independent effect of each covariate on visual field data are summarized in Table 4. Results show that while the standard linear regression model without accounting for the inter-eye correlation provided valid point estimates of the regression coefficients, their SE estimates were biased (generally underestimated), thus the P-value was smaller than those from the appropriate models that account for the inter-eye correlation. For example, the P-value for the age effect is 0.008 from the standard regression model, and 0.02 from mixed effects model or marginal models.

Table 4.

Comparison of results from various regression approaches for visual field data in patients tested for glaucoma (n=197 patients; 394 eyes)

Variable	Standard linear regression model for both eyes		Standard linear regression model for worse eye§		Mixed model, random intercept (unstructured or compound symmetry)		Marginal model: PROC MIXED with REPEATED, unstructured		Marginal model: GEE, working independence		Marginal model: GEE, compound symmetry
	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value
Age (per year)	−0.53 (0.20)	0.008	−0.55 (0.31)	0.07	−0.57 (0.25)	0.02	−0.57 (0.25)	0.02	−0.53 (0.24)	0.02	−0.57 (0.23)	0.01
Female sex	0.31 (1.86)	0.87	0.74 (2.89)	0.80	0.15 (2.32)	0.95	0.15 (2.32)	0.95	0.31 (2.22)	0.89	0.15 (2.24)	0.95
Hypertension (yes)	−3.05 (1.88)	0.11	−2.03 (2.92)	0.49	−3.02 (2.35)	0.20	−3.02 (2.35)	0.20	−3.05 (2.29)	0.18	−3.02 (2.30)	0.19
Aphakic	−18.4 (3.8)	<0.001	−22.1 (5.4)	<0.001	−18.5 (3.5)	<0.001	−18.5 (3.5)	<0.001	−18.4 (4.8)	<0.001	−18.5 (5.8)	0.001
% acuity loss (per %)	−0.48 (0.08)	<0.001	−0.38 (0.10)	0.0002	−0.41 (0.07)	<0.001	−0.41 (0.07)	<0.001	−0.48 (0.12)	<0.001	−0.41 (0.09)	<0.001

^§From the eye with worse visual field.

GEE, generalized estimating equation; SE, standard error

The worse eye analyses provide somewhat different results in terms of regression coefficient, SE and associated P-value (Table 4) as compared to other approaches of analyzing data of both eyes. The regression coefficient can be either larger or smaller than other approaches, while the SE and P-values tended to be larger than other approaches, in part due to the reduced number of observations. For example, the age effect from the worse eye analysis was not significant (P=0.07), while P-values from other approaches were all statistically significant (Table 4).

To compare these various analysis approaches when the sample size is small, we took a random sample of 40 patients (80 eyes) from the visual field study and performed the same analysis as described previously. The visual field data from both eyes of a patient are moderately correlated with an inter-class correlation coefficient of 0.50 (95% CI 0.22–0.70). The estimates of the covariance matrix using an unstructured and a compound symmetry covariance model differed, particularly for the variance terms. The variability in the right eye was greater than in the left eye in the unstructured model:

• Unstructured covariance = $\left(\begin{array}{cc}468.7& 145.7\\ 145.7& 197.3\end{array}\right)$

• Compound symmetry = $\left(\begin{array}{cc}334.1& 144.1\\ 144.1& 334.1\end{array}\right)$

With a smaller sample size, the differences in results from various modeling approaches and under different covariance structures became more substantial (Table 5). For example, the results for the aphakic effect across different model approaches are very different, with regression coefficients ranging from −7.72 (SE 5.12; P=0.14) in the marginal model using PROC MIXED with REPEATED statement to −14.5 (SE 6.3; P=0.03) in the standard linear regression model of both eyes data without accounting for inter-eye correlation. Interestingly, GEE under different covariance structures also provides different results with P-value 0.04 under working independence as compared to P-value 0.14 under compound symmetry, likely due to the very different estimates of right eye and left eye variances as shown above. In this case, the analyses using an unstructured or working independence covariance structure are more appropriate.

Table 5.

Comparison of results from various regression approaches for visual field data from 40 randomly selected patients tested for glaucoma (n=40 patients; 80 eyes)

Variable	Standard linear regression model for both eyes		Standard linear regression model for worse eye§		Mixed model, random intercept (unstructured or compound symmetry)		Marginal model: PROC MIXED with REPEATED: unstructured		Marginal model: GEE, working independence		Marginal model: GEE, compound symmetry
	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value	Regression coefficient (SE)	P-value
Age (per year)	0.17 (0.46)	0.71	0.16 (0.70)	0.82	0.11 (0.55)	0.85	0.03 (0.48)	0.95	0.17 (0.54)	0.76	0.11 (0.52)	0.83
Female sex	7.55 (4.17)	0.07	7.16 (6.63)	0.29	7.05 (5.02)	0.17	6.45 (4.46)	0.16	7.55 (5.03)	0.13	7.06 (4.93)	0.15
Hypertension – (yes)	−7.77 (4.10)	0.06	−0.66 (6.42)	0.92	−7.89 (4.97)	0.12	−10.7 (4.43)	0.02	−7.77 (4.70)	0.10	−7.89 (4.76)	0.10
Aphakic	−14.5 (6.3)	0.03	−16.9 (9.0)	0.07	−11.7 (6.1)	0.06	−7.72 (5.12)	0.14	−14.5 (7.1)	0.04	−11.7 (8.0)	0.14
% acuity loss (per %)	−0.70 (0.22)	0.002	−0.64 (0.32)	0.06	−0.61 (0.22)	0.009	−0.66 (0.19)	0.001	−0.70 (0.21)	0.0008	−0.61 (0.19)	0.001

^§From the eye with worse visual field.

GEE, generalized estimating equation; SE, standard error

DISCUSSION

In this paper, we introduced and demonstrated the mixed effects models and marginal models for analyzing continuous correlated two-eyes data from cross-sectional studies. We have seen that ignoring the correlation between eyes of the same subject can lead to inaccurate estimates of SEs of coefficients, confidence intervals, and P-values, and the analysis of one eye (eg, worse eye) only data may produce biased or inefficient estimates of the association. In clinical trials, when the eyes are in different treatment groups and the correlation is ignored, the SEs for the treatment effect and P-values are generally too large. In observational studies, when the eyes are in the same group or category, or in clinical trials where both eyes receive the same treatment, the SEs and P-values are generally too small. Changing from an analytic approach that ignores the correlation to one that appropriately accommodates the correlation can have a substantial impact on inference. The impact on inference between the choice of mixed effects models and GEE models to accommodate the correlation tends to be small, especially in the large samples used as examples here. When the sample size becomes small, the choice of analysis models and covariance structure can have substantial impact on the regression coefficients, SE and P-values as shown in the example of 40 randomly selected subjects.

When specifying a mixed model in SAS, the inter-eye correlation is accounted for by the RANDOM statement. In general, use of a REPEATED statement in PROC MIXED is a type of marginal model; however, the estimates of the variance-covariance matrix for the parameter estimates are calculated differently from that of a GEE model, because they are based on a multivariate normal likelihood. Conversely, the use of the RANDOM statement in PROC MIXED is a true mixed effects model. In linear mixed effects models for a normally distributed continuous outcome using a subject-specific random effect, the parameter estimates will be the same as for GEE models with a compound symmetry working correlation structure.⁹

The mixed effects model and GEE model have different interpretations and one model can be more appropriate than another depending on the study question. The interpretation of the linear mixed effects models may be more germane, especially in clinical trials for treatment group comparisons within same subject; what is the change expected within an individual when a different treatment is applied? In contrast, the marginal model used in the GEE approach provides an estimate of the difference in the population mean when a different treatment is applied. In observational studies, where the interest is on how a subject-specific covariate (such as age) is associated with an eye-specific outcome, the interpretation of the covariate effects from mixed effects model is conditional on the subject-specific random effect, eg, are changes in glaucoma status between fellow eyes correlated with corresponding changes in refractive error? With marginal models, a different question is addressed; on average, do eyes with glaucoma have a higher (or lower) refractive error than eyes without glaucoma? In observational studies, the marginal model is generally more relevant. However, the difference is subtle and in practice the estimated effect may be similar. Not having to worry too much about the exact specification of the correlation matrix and robust variance estimation with the GEE approach is very appealing; however, these advantages hold only for large samples and may produce estimates of variance that are either too large or too small with moderate or small (≈<40) sized samples.

In summary, data from both eyes of a subject are correlated. The standard regression models that ignore inter-eye correlation can lead to incorrect conclusions. The mixed model and marginal model are the two major appropriate approaches for analyzing correlated eye data. Both the mixed effects model and marginal model required the specification of covariance or correlation structure. In marginal model using GEE, even when the structure of the correlation matrix is mis-specified, it still provides asymptotically unbiased estimates of the regression coefficients and variance. While in mixed effects models, mis-specification of the covariance structure for the random effects may lead to biased estimates of regression coefficients. Different from the mixed effects model which has a subject-specific interpretation, GEE is a marginal model approach, as it does not incorporate any random effects into the model. The major limitation of the mixed model is the dependency of unbiased parameter estimates on the correct model specification of both fixed effects and random effects, while valid estimation from GEE is dependent on a large enough sample size. A detailed comparison of mixed models and the GEE approach can be found in papers by Hubbard et al⁹ and Gardiner et al.¹⁰ In our two examples of analyzing cross-sectional continuous correlated eye data with large sample size, the mixed effects models and marginal models provided similar results, and various specification of covariance/correlation structure provided almost the same results, this is likely due to the similarity of various covariance structures in the cross-sectional eye data (ie, only with two measures per subject). When the number of measurements from a subject becomes larger (such as in a longitudinal eye study), we expect their differences will be more substantial.